Introduction

The mathematical model of groundwater flow and solute transport is an effective tool for scientific and rational development, utilization, and protection of the groundwater resources. The hydrogeological parameters are quantitative indicators describing the characteristics of groundwater aquifers. Correct identification of hydrogeological parameters is a prerequisite for the use of this mathematical model. The main problems of hydrogeology are to obtain the numerical model parameters of the groundwater and establish the model. At present, the hydrogeological parameters are mainly obtained through two methods: model establishment in laboratory and field pumping test. The field pumping test is the main method to investigate the hydrological parameters of groundwater, because the test data are safe and reliable due to field survey (Şahin 2018). After acquiring the hydrogeological parameters through the pumping test, the depth of water level drop is observed through the observation hole, and the hydrogeological parameters are identified by solving the corresponding inverse problems. The direct and indirect solutions are commonly used to solve the inverse problems (Abdelaziz et al. 2019). Due to the poor stability of the direct solution, the indirect method is currently used more. Indirect solutions such as the simplex method, modified Gauss-Newton method, and optimization method are optimization methods related to the initial point, which are easy to fall into the local optimum (Neighbors et al. 2017). In order to compensate this shortcoming, many scholars have proposed to solve the hydrogeological parameters by the intelligent algorithms, such as neural network algorithm, simulated annealing algorithm, and ant colony algorithm. However, these algorithms generally have the defects of slow convergence speed and low calculation accuracy (Dragonetti et al. 2017), resulting in the distortion of the parameters for construction of the hydrogeological model, and large error between the constructed model and the actual model.

Particle swarm optimization, as a kind of global optimization algorithm (Zhang et al. 2020), is an intelligent optimization algorithm based on the observation of the behaviors of animal groups. Compared with other intelligent algorithms, PSO is featured with simple form and high performance. At the same time, it has a memory mechanism to store and maintain the best solutions found by each particle and the entire group, to ensure that no degradation occurs during the iteration process, so that it has been used widely in many fields. However, the PSO suffers from a premature convergence in the application. Current scholars in China and overseas have proposed a variety of improved algorithms to overcome the premature convergence of the PSO (Moayedi et al. 2020; Nhu et al. 2020). Most of them refer to combine the PSO with other algorithms to promote strengths and avoid weaknesses, so that the advantages of both algorithms can be exerted effectively. This algorithm can enhance the local convergency ability of the PSO, but the calculating process is complex and the time consumption is high.

Based on the shortcomings of other algorithms and the advantages of PSO as well as the characteristics of premature convergence of the PSO, the calculation method of PSO algorithm is optimized in this paper. The gradient descent method with faster convergence in the traditional method is used to form an intelligent optimization algorithm with derivatives to improve the accuracy, sensitivity, and convergence of PSO algorithm. Thus, it is used in the calculation of hydrogeological parameters to provide a reliable algorithm basis for constructing the hydrogeological models and establishing the parameters of aquifer.

Methodology

Calculation method of PSO

In the PSO algorithm, the individuals are regarded as particles without mass and volume in order to describe the complexity of the algorithm. The particle population is set as m, the spatial search dimension is set as n, the position of particle i is set as xi = [xi1, xi2, …, xin], the flying speed is set as vi = [vi1, vi2, …, vin] i = 1, 2, …m, the historical optimal search position of particle i is set as Pi = (Pi1, Pi2, …Pin), and the historical optimal search position of the entire population is set as Pg = (Pg1, Pg2, …Pgn). The calculation equations of the position and velocity of the particle are as below:

$$ {\mathrm{v}}_{ik}\left(\mathrm{t}+1\right)={wv}_{\mathrm{ik}}(t)+{c}_1r\left[{p}_{ik}(t)-{x}_{ik}(t)\right]+{c}_2r\left[{p}_{gk}(t)-{x}_{ik}(t)\right] $$
(1)
$$ {\mathrm{v}}_{ik}\left(t+1\right)={x}_{ik}(t)+{v}_{ik}\left(t+1\right) $$
(2)
$$ \mathrm{w}={w}_{\mathrm{max}}-k\frac{w_{\mathrm{max}}-{w}_{\mathrm{min}}}{T} $$
(3)
$$ {\mathrm{x}}_{ik}={x}_i+{v}_{ik} $$
(4)

In the equation, c1 and c2 are acceleration factors and non-negative constants; w is inertia weight coefficient; wmax and wmin are the maximum and minimum values of inertia weight coefficients, respectively, and r is a pseudo-random number distributed randomly in [0, 1], which can increase the search traversal; particle speed is usually limited within \( \left[\hbox{-} {\mathrm{v}}_k^{\mathrm{max}},{v}_k^{\mathrm{max}}\right] \). k is the actual number of iteration, and the T is the maximum number of iteration.

Calculation method of optimized PSO

The individuals are regarded as particles without mass and volume. The particle population is set as m, the spatial search dimension is set as n, the position of particle i is set as xi = [xi1, xi2, …, xin], the flying speed is set as vi = [vi1, vi2, …, vin] i = 1, 2, …m, the historical optimal search position of particle i is set as Pbest, and the historical optimal search position of the entire population is set as gbest. The appropriate value of the particle is solved by di =  −  ∇ f(xi). r is a randomly distributed pseudo-random number within [0, 1], w is an inertial weight coefficient, a is the set step size, thus, the calculation equations of the position and velocity of the particle are as below:

$$ {\mathrm{v}}_{ik}\left(\mathrm{t}+1\right)={wv}_{\mathrm{ik}}(t)+{c}_1r\left[{p}_{best}(t)-{x}_{ik}(t)\right]+{c}_2r\left[{g}_{best}(t)-{x}_{ik}(t)\right] $$
(5)
$$ {\mathrm{x}}_{ik}={x}_i+{v}_{ik}+{ad}_i $$
(6)

Calculating process of optimized PSO

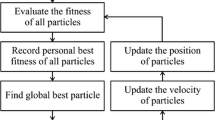
The specific calculating process of the optimized PSO is shown as below: the number of population in the PSO algorithm m is determined firstly, the particle length is set to l, the maximum number of iterations is set to T, and the particle velocity vi and position xi are initialized within the feasible solution range; then, the fitness value of each particle is calculated or the optimal fitness value of particle is acquired, and a judgment is made to check if the function is derivable. If it is possible, the ∇f(xi) is calculated, otherwise the approximate derivative is calculated. The step is set to a, and di =  −  ∇ f(xi); the speed and position of the particle is calculated with the optimized algorithm. If the termination condition is met, it can exit; otherwise, it has to return. The specific algorithm flowchart is shown in Fig. 1 as below.

Fig. 1
figure 1

Algorithm flowchart of optimized PSO

Full size image

Convergence analysis of optimized PSO

The convergence of the PSO algorithm with derivatives is tested through Sphere function, Rosenbrock function, and Griewank function, which are used widely. The Sphere function is a commonly used single-peak function with the intelligent optimization algorithm test (De et al. 2020), and its calculation method is as below:

$$ {f}_1=\sum \limits_{i=1}^N{x}_i^2 $$
(7)

Scope of xi is ‐100 ≤ xi ≤ 100. If xi = 0, the function has the optimal value fmin(xi) = 0.

The Rosenbrock function (Moslehi and Haeri 2020) is a non-convex single-peak function, commonly used for the test of intelligent optimization algorithm. The Rosenbrock function can be calculated with below equation:

$$ {f}_2=\sum \limits_{i=1}^N\left[100{\left({x}_{i+1}-{x}_i\right)}^2+{\left(1-{x}_i\right)}^2\right] $$
(8)

Scope of xi is ‐100 ≤ xi ≤ 100. If xi = 1, the function has the optimal value fmin(xi) = 0

The Griewank function is also a commonly used test function of standard intelligent optimization algorithm (Huang et al. 2019), and its calculation method is as below:

$$ {f}_3(x)=\frac{1}{4000}\sum \limits_{i=1}^N{x_i}^2-\prod \limits_{i-1}^N\cos \left(\frac{x_i}{\sqrt{i}}\right)+1 $$
(9)

If xi = 0, the function has the global minimum fmin(xi) = 0.

Model establishment of hydrogeological parameters

Regarding the establishment of hydrogeological models, the Theis equation is commonly used for pumping test currently to determine the hydrogeological parameters (Zech et al. 2016). It is assumed that each aquifer is homogeneous and isotropic, and can be extended indefinitely without boundaries. The thickness of the aquifer is equal to the thickness of the permeable layer, floor of the aquifer is in a horizontal state, and the pumping velocity in the aquifer is constant. Thus, the drop depth of the pumping water level can be calculated with below equation:

$$ h=\frac{Q}{4\pi A}W(u) $$
(10)

In the equation, h is the drop depth of pumping water level drop depth, expressed as m; Q is the pumping velocity of aquifer, expressed as m3/s; A is the parameter coefficient of aquifer, expressed as m2/s; and W(u) is the Theis function. Its calculation method is as given below:

$$ W(u)=\underset{u}{\overset{\infty }{\int }}\frac{\exp \left(-x\right)}{x} dx $$
(11)

In the equation, u represents the dimensionless time, and its calculation equation is given in equation (12). μ is the flow coefficient of elastic release, and t is the pumping time, expressed as s:

$$ u=\frac{{\mathrm{r}}^2\mu }{4 At} $$
(12)

Combining the PSO algorithm with derivatives to solve the parameters, the aquifer parameter A and u are estimated based on the approximate expressionist of Srivastava R. Thus, the model of the hydrogeological parameters can be established as below.

$$ \min \varphi \left(A,\mu \right)=\sum \limits_{i=1}^N{\left({\mathrm{h}}_i^0-{h}_i^c\right)}^2 $$
(13)

In which, A ∈ (0, 3.0), and μ ∈ (0, 0.1); \( {\mathrm{h}}_i^0 \) is the actual drop depth of aquifer water level detected at the ith moment of pumping; \( {h}_i^c \) is the drop depth of aquifer water level at the ith moment calculated with the Theis function; and A and u are to be estimated. The optimization of model is mainly to obtain the optimal value of A and u, so that the square sum of the difference between the actual drop depth of the aquifer water level and the calculated values of parameters to be estimated can be minimal.

The data obtained during the actual pumping test are recorded in this study. It can be known that the pumping flow is Q = 9.54 m3/s, the pumping duration is 580 min, and the distance between the observation hole and the pumping well is r = 21.63 m. The recorded data of the drop depth of the water layer within 580 min are given in Table 1 below.

Table 1 Data of the pumping test
Full size table

Optimized PSO to solve the hydrogeological parameters

The calculation method and conditions of equation (13) are used in combination with the PSO algorithm with derivatives to solve the hydrogeological parameters. Different number of particles, the step size, the number of iterations, and the multiple of the parameter to be estimated are respectively utilized in this study, and the convergence condition is set as that the objective function is less than 2 × 10−2; otherwise, it is regarded as non-convergence. The operation time after each calculation is analyzed. Solving process of the hydrogeological parameters is shown in Fig. 2 as below.

Fig. 2
figure 2

Solving process of the hydrogeological parameters

Full size image

Results

Convergence analysis of optimized PSO

The convergence of PSO algorithm with derivatives is verified by Sphere function, Rosenbrock function, and Griewank function. The verification results using the Sphere function are shown in Table 2. It can be seen from the table that the calculated average values are 0.097 × 10−5, 0.127 × 10−3, 0.193 × 10−3, −0.118 × 10−3, 0.549 × 10−3, and −0.296 × 10−3 respectively after the independent calculation using the PSO with derivatives is performed for 50 times when the number of particles is 10, the step size is 10−2, and the maximum number of iterations is 600. Differences between such values and the theoretical value 0 of the Sphere function are small. The Rosenbrock function is used to further verify the convergence of the PSO algorithm with derivatives. The results are shown in Table 3. As it reveals that the calculated average values are 0.015 × 10−2, 0.098, 1.001, 1.006, 0.095, and 1.004 respectively after the independent calculation using the PSO with derivatives is performed for 50 times when the number of particles is 20, the step size is 10−2, and the maximum number of iterations is 400. Differences between such values and the theoretical value 1 are small. The Griewank function is used to verify the convergence of the PSO algorithm with derivatives, and the results are shown in Table 4. As can be seen from the table that the calculated average values are 1.19 × 10−6, −0.296 × 10−3, 0.321 × 10−3, −0.157 × 10−3, 0.373 × 10−3, and −0.254 × 10−3 respectively after the independent calculation using the PSO with derivatives is performed for 50 times when the number of particles is 100, the step size is 10−2, and the maximum number of iterations is 1000. Differences between such values and the theoretical value 0 are small.

Table 2 Verification results of Sphere function on PSO algorithm with derivatives
Full size table
Table 3 Verification results of Rosenbrock function on PSO algorithm with derivatives
Full size table
Table 4 Verification results of Griewank function on PSO algorithm with derivatives
Full size table

Hydrogeological parameters to validate the accuracy of PSO algorithm

In order to validate the accuracy of the optimized PSO algorithm, the drop depth of water layer at each time is calculated with the PSO algorithm and the optimized PSO algorithm under the same conditions, and the calculated values are compared with the actual observed values, as shown in Fig. 3. It can be seen that drop depth of water layer at each time calculated with the optimized PSO algorithm is very close to the observed value, and the error between the two is small. Of which, the maximum absolute error between value calculated by the optimized PSO algorithm and the observed value is 0.011, the maximum relative error is 8.1%, the minimum absolute error is 0.002, and the minimum relative error is 0.25%. While, there are some differences between the drop depths of water layer calculated by the PSO and the observation values, the maximum absolute error is 0.021, the maximum relative error is 29.1%, the minimum absolute error is 0.004, and the minimum relative error is 0.76%.

Fig. 3
figure 3

Comparison between actual drop depth and calculated value of water layer in the observation hole

Full size image

Reliability analysis of PSO

The parameters of the aquifer are calculated and numbers of iterations are compared with the PSO algorithm and the optimized PSO algorithm respectively under the same conditions. The results are shown in Fig. 4. It can be seen that the convergence speed of optimized PSO is faster than the unoptimized PSO under the same conditions with the average number of iterations of 87 times; the convergence speed of unoptimized PSO is relatively slow with the number of iterations of 450 times to reach the optimal value. At the same time, the parameters of the aquifer are calculated with the PSO algorithm and the optimized PSO algorithm under the same conditions. The results are shown in Table 5. It can be seen that the objective function φ (T, μ) is 0.00659 calculated by the optimized PSO algorithm and 0.00684 calculated by the unoptimized PSO algorithm, respectively. Thereby, the objective function calculated with the optimized PSO algorithm is obviously smaller than that calculated with the unoptimized PSO algorithm.

Fig. 4
figure 4

Comparison between calculating process of the optimized PSO and unoptimized PSO

Full size image
Table 5 Calculation results of the optimized PSO and unoptimized PSO
Full size table

Sensitivity analysis of water conductivity coefficient

The hydrogeological parameter A = 2.745 calculated with the optimized PSO algorithm. The parameter is disturbed at −20%, −10%, −5%, 5%, 10%, and 20%, respectively, with no change of the other parameters. The drop depths of the aquifer water level at 90 min, 180 min, and 580 min of the pumping time are calculated under such conditions, and then the calculated values are compared with the actual detection values to analyze the relationship between the water conductivity coefficient and the drop depth of water level. The results are shown in Table 6. It can be seen that the A increases with the increase of the disturbance coefficient, and A changes accordingly as the disturbance coefficient is disturbed between −20 and 20%. Compared with the case without disturbance, the maximal absolute error of A change is 0.218, the minimum absolute error is 0.03, the maximum relative error is 7.9%, and the minimum relative error is 0.65%. In addition, it can be seen from the table that the larger the A, the smaller the drop depth of aquifer.

Table 6 Drop depths of aquifer and calculated values under different water conductivity coefficients
Full size table

Sensitivity analysis of water storage coefficient

The hydrogeological parameter is A = 2.745 calculated with the optimized PSO algorithm. The parameter is disturbed at −20%, −10%, −5%, 5%, 10%, and 20%, respectively, with no change of the other parameters. The drop depths of the aquifer water level at 90 min, 180 min, and 580 min of the pumping time are calculated under such conditions, and then the calculated values are compared with the actual detection values to analyze the relationship between the water storage coefficient and the drop depth of water level. The results are shown in Table 7. It can be seen that the μ increases with the increase of the disturbance coefficient, and μ changes accordingly as the disturbance coefficient is disturbed between −20 and 20%. Compared with the case without disturbance, the maximal absolute error of μ change is 0.012, the minimum absolute error is 0.002, the maximum relative error is 21%, and the minimum relative error is 3.5%. In addition, it can be seen from the table that the larger the μ, the smaller the drop depth of aquifer.

Table 7 Drop depths of aquifer and calculated values under different water storage coefficient
Full size table

Discussion

PSO is a random optimization algorithm emphasizing the groupness based on swarm intelligence. Compared with traditional optimization algorithms, it has the advantages of high computational efficiency, simple operation, and wide application range. The PSO has been widely used in construction, hydrology and geology, electricity, and transportation vehicles. However, the PSO suffers from a premature convergence in the application. Current scholars have proposed a variety of improved algorithms to optimize the PSO. Delice et al. (2017) (Delice et al. 2017) have optimized the calculation process of PSO algorithm, which not only enhances the ability to solve of PSO algorithm but also can search different points in the solution space with high effectiveness, and solves the problem of two-sided pipeline balance in the hybrid model. Taherkhan et al. (2016) (Taherkhani and Safabakhsh 2016) have proposed an adaptive inertial weighting method based on the stability. It can determine the inertial weight of each particle in different dimensions through the performance of the particles and the distance of the best position. In addition, it is applied to the radar system design for validation. The experimental results suggest that the adaptive inertial weighting method based on the stability can improve the convergence speed of PSO in both static and dynamic state. Based on previous researches, the PSO algorithm is optimized by derivation of its particle moderation value to avoid the premature convergence of the PSO algorithm, and enhance the accuracy and sensitivity of the PSO algorithm. The results reveal that calculated values with the optimized PSO algorithm are very close to the theoretical value in the three commonly used intelligent optimization algorithm tests, which indicates that the optimized PSO algorithm has certain correctness and effectiveness, providing reliable algorithm basis for construction of the hydrogeological model and the establishment of aquifer parameters.

At the same time, the accuracy and reliability of the PSO algorithm are analyzed in this study. By comparing the optimized and unoptimized PSO algorithm, it is found that the maximum absolute error is 0.011, and the maximum relative error is 8.1% between the calculated value with optimized PSO algorithm and the observed value; the maximum absolute error is 0.021, and the maximum relative error is 29.1% between the calculated value with PSO algorithm and the observation value. It fully demonstrates that the degree of fitting between the calculated value of the optimization algorithm and the actual observation value is high. The average number of iterations of the optimized PSO algorithm is 87, while it of the unoptimized PSO is 450 to reach the optimal value. In addition, the target function calculated with the optimized PSO algorithm is obviously much smaller than that of calculated with the PSO, which is consistent with the research results of Delice et al. It further validates that the reliability and feasibility of the optimized PSO algorithm. Finally, the sensitivity of the water conductivity coefficient and the sensitivity of water storage coefficient are analyzed in this study. The results reveal that the water conductivity coefficient and water storage coefficient are inversely related to the drop depth of the aquifer under various interference coefficients, and both the sensitivity of water conductivity and the sensitivity of water storage coefficient are high.

Conclusion

In this study, the calculation method of PSO algorithm is optimized and applied to hydrogeological parameters, and the convergence, accuracy, and sensitivity are analyzed, respectively. The results indicate that, compared with the unoptimized PSO, the accuracy of optimized PSO algorithm is significantly higher with good convergence and sensitivity, which can provide a reliable algorithm basis for the construction of hydrogeological model and the establishment of aquifer parameters better. However, there are still some shortcomings in this study. The optimized PSO algorithm is compared with the unoptimized PSO algorithm only, and is not compared with other algorithms such as simplex algorithm and genetic algorithm to analyze its advantages. In future, it will continue to compare and analyze the optimized PSO algorithm with other intelligent optimization algorithms to get the superiorities of the optimized PSO algorithm. In conclusion, the accuracy and sensitivity are enhanced through the optimization of PSO algorithm, providing a reliable algorithm basis for the construction of hydrogeological model and the establishment of aquifer parameters.