1 Introduction

Generally, there are numerous methods for predicting flood wave forms so that preventative measures may be taken to protect lives and property during a flood. Forecasting can also improve water transfer methods in natural or artificial waterways. In 1871, Saint–Venant formulated the first one-dimensional unsteady flow theory. Given the complexity in solving such equations, simplified and approximate methods were then developed (Maidment 1993). Complications of dynamic models and difficulty in estimation of discharge using river bathymetry and bed roughness has led to the use of simplified models derived from the Saint–Venant equations. On the other hand, detailed data on the river bathymetry required in the Saint–Venant method is not available (Oubanas et al. 2018). Due to nonlinearity of the equations and interactions between fluxes, acceleration terms, and pressure gradients, the Saint–Venant equations are prone to instability in severe transitions (Yu et al. 2021). The transition from hydrological river models to dynamic models remains challenging. The key in dynamic models is that "problems at a single river cross-section can form a pinch point with numerical errors rapidly cascading through large sections of the network" (Yu et al. 2021). In addition, to simplify the calculation process of the Saint–Venant equations, the characteristics of the simplified cross-section, which is significantly different from the exact and main cross-section of the river, are used (Yu et al. 2021). Numerical instabilities and fluctuations in the complete solution of Saint–Venant equations such as the presence of lateral flows, initial conditions and significant changes in river geometry were studied in (Nujić 1995; Garcia-Navarro and Vazquez-Cendon 2000; Sanders 2001; Tseng 2004; Xing 2014; Li et al. 2017; Kvočka et al. 2015; Yang et al. 2012). However, there is no simple, universal or fixed solution (Yu et al. 2021). Complete solution of the Saint–Venant equations or the dynamic wave causes stability and convergence problems and mass conservation issues (Rossman and Huber 2017) and often leads researchers to use kinematic wave equations (Yu et al. 2021). Kinematic wave theory was used for flow simulation in border irrigation (Chari et al. 2019) and deformable channels (Krutov et al. 2021). In addition, efficiency and accuracy of the kinematic wave was studied in (Shultz et al. 2008; Roohi et al. 2020; Eizeldin and Almasalmeh 2019; SABZEVARI et al. 2019; Prawira et al. 2019). Flood routing and sediment load estimation are of great importance in water resources management and flood management (Patel and Sarkar 2022). (Farsirotou and Kotsopoulos 2015) experimentally studied changes in the river bottom sills and evaluated their effect on the depth of flood to protect the river. To calculate flood damage, it is essential to have the accurate water depth value during the flood or the degree of flood damage proportional to the water depth, as proposed by previous studies (Smith 1994; Kok et al. 2005; Hall et al. 2005a; Meyer and Messner 2005; Merz and Thieken 2009; Thieken et al. 2008) employing the damage-depth water curve method. In most cases, researchers focus on solving the uncertainty of hydrologic elements, such as water depth (De Moel and Aerts 2011). In contrast, the analyzes by (Dutta et al. 2003; Apel et al. 2004, 2006, 2008; Hall et al. 2005b; Merz et al. 2007) explored the uncertainty of hydraulic elements. (Fiorillo et al. 2022) used Harmony Search (HS) algorithm to study the drainage network optimization to decrease flood risks. (Razmi et al. 2022) studied compound floods using bivariate frequency analysis methods.

Although hydraulic methods are more accurate, hydrologic methods are widely used in river engineering because of their simplicity and popularity (Tsai 2005). One of the hydrologic methods utilized extensively in flood routing is the Muskingum approach. Assessment of the water surface profile downstream is of great importance in determining which areas will be submerged during a flood in downstream.

In order to utilize hydraulic routing, solve Saint–Venant equations in river engineering designs, evaluate the transfer and expansion path of floods, and analyze water surface profiles, it is necessary to derive section specifications along the river at appropriate intervals accurately. Then, to calculate the water depth, Saint–Venant equations must be solved by employing complex numerical methods and determining upstream and downstream boundary conditions as well as roughness coefficients along the path. On the other hand, surveying and obtaining section specifications, especially in mountain rivers and impassable areas, is expensive and time-consuming. Moreover, section specifications change over time and should be extracted periodically for accurate calculation of flood routing and water depth. However, hydrologic approaches of flood routing, such as the linear Muskingum method, are not only less expensive but also provide acceptable accuracy and can be used to analyze the downstream flood of a study river reach. Although the Muskingum method is often utilized to calculate the outflow hydrograph (discharge changes over the time) (Chu and Chang 2009; Moghaddam et al. 2016; Bazargan and Norouzi 2018), the current study introduces a new approach to determine downstream water depth changes over time. Rather than calculating the outflow hydrograph, the proposed method employs the linear Muskingum approach and kinematic wave relations. In doing so, the present study recognizes the importance of water depth calculation in engineering and flood management. On the other hand, as its available data are from kinematic waves, the current work first employs the particle swarm optimization (PSO) algorithm to optimize the inflow and outflow discharge values as a function of the inflow and outflow depths. Then, with the resulting functions and linear Muskingum equations, the proposed method uses the time-depth curves (flow depth in terms of time) in the upstream and downstream of the study river reach, instead of the inflow and outflow hydrographs, to optimize the values of X, K, and Δt. Then, the outflow depth (temporal changes in downstream depth) is calculated with the optimized parameters instead of the outflow discharge. In other words, collection of the required data to analyze unsteady flow in hydraulic and hydrodynamic routing methods, or using Hec-Ras or Mike 11 numerical models is difficult, time consuming, complicated, and costly. While hydrological methods such as linear Muskingum method are easy, inexpensive, and fast with enough accuracy. In addition, mentioned data in hydraulic and hydrodynamic routing methods have uncertainties due to the model structure, model parameters and field measurements, which in most cases is unexpectedly costly and significantly affect the process of hydraulic projects. In other words, the solution presented in the present study is suitably accurate to estimate the temporal changes in flow depth and reduces the cost and accelerates the process of hydraulic projects.

2 Materials and Methods

2.1 Study Area

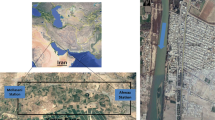
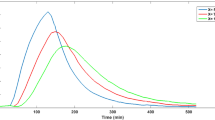
In the present study, data recorded by the research center of a water resources management company for two hydrometric stations is used: Mollasani (Station No.: 21-308, 48˚53′ E, 31˚35′N) and Ahwaz (Station No.: 21-309, 48˚41′E, 31˚20′N) located in the upstream and downstream of the study reach on the Karun River, respectively (Fig. 1). The first flood data (Fig. 2, occurred on 2012/02/26 to 2012/03/01) with inflow discharge changes of 221 to 565 m3/s and inflow depth changes of 1.30 to 2.83 (m) were used as the flood baseline (observational) to optimize the parameters of the linear Muskingum method (X, K, Δt) and the coefficients related to the depth-discharge equations. The main advantage of the Muskingum method is that the estimated parameters of the flood baseline (the flood whose input and output values are recorded) can be used for routing other floods occurring in the study reach (i.e. determining downstream flood specifications), provided that the river morphology remains the same. Therefore, the current study employs the following parameters: the estimated parameters of the first flood (observational) to calculate water depth values (Y at the time of flooding), the second flood (Fig. 2, occurred in 2012/02/02 to 2012/02/05) with inflow discharge changes between 222 and 494 m3/s and inflow depth changes of 1.32 to 2.45 (m). It should be noted that the first and second floods belong to the reach of the hydrometric stations of Mollasani (upstream) and Ahwaz (downstream) in the Karun River.

Fig. 1
figure 1

Study Area

Full size image
Fig. 2
figure 2

Discharge and depth data of the first and second floods

Full size image
figure a

2.2 Saint–Venant Equations

Saint–Venant equations are hyperbolic partial differential systems which the current study presents in their general form, save for that of the lateral flow (Vente 1959).

Continuity equation:

$$\frac{\partial Q}{\partial x}+\frac{\partial A}{\partial t}=0$$
(1)

Momentum equation:

(2)

where:

A = cross-sectional area of flow; Q = discharge; S0 = channel bottom slope; Sf = slope of the energy-grade line or friction slope; v = average flow velocity; h = flow depth; g = acceleration due to gravity; x = distance along the channel length; and t = time; \(\frac{\partial h}{\partial x}\) = water surface slope; and \(\frac{v}{g}\frac{\partial v}{\partial x}\) and \(\frac{1}{g}\frac{\partial v}{\partial t}\) are inertia terms.

According to the terms of the momentum equation, hydraulic routing methods are categorized into 1) kinematic waves, 2) diffusion waves, and 3) dynamic waves. The most simplified form of hydraulic routing is the kinematic wave in which pressure, translational, and local acceleration terms are excluded from the momentum equation (Chow et al. 1988).

2.3 Kinematic Wave

It is the most simplified form for solving Saint–Venant equations. Many authors have studied the field of kinematic waves, among which are (Katopodes 1982).

Kinematic wave equations are given as:

$$\frac{\partial Q}{\partial x}+\frac{\partial A}{\partial t}=0$$
(3)
$${S}_{f}={S}_{0}$$
(4)

In the present study, the available data was of the kinematic wave type.

  1. 1.

    Eq. (4) shows that, in the momentum equation, temporal and spatial changes of velocity (v) and spatial changes of flow depth (h) are negligible compared to those of the bed slope. The study of available data and cross sectional characteristics of the Mollasani and Ahwaz stations (upstream and downstream, respectively) showed that the terms \(\frac{\partial h}{\partial x}\), \(\frac{v}{g}\frac{\partial v}{\partial x}\), \(\frac{1}{g}\frac{\partial v}{\partial t}\) are negligible compared to those of the bed slope (S0). As the results in Table 1 show, these terms have a lower percentage than the bed slope and so that can be excluded.

    As shown in Table 1, the mean values of \(\frac{\partial h}{\partial x}\) in the upstream and downstream sections of the study reach (the Mollasani and Ahwaz hydrometric stations) were 0.398 and 0.180 times the S0, respectively. The mean values of \(\frac{v}{g}\frac{\partial v}{\partial x}\) in the upstream and downstream sections of the study reach were 0.002 and 0.006 times the S0, respectively. Moreover, the mean values of \(\frac{1}{g}\frac{\partial v}{\partial t}\) in the upstream and downstream sections were calculated as 0.046 and 0.074 times the S0. Hence, compared to the value of S0, the \(\frac{\partial h}{\partial x}\), \(\frac{v}{g}\frac{\partial v}{\partial x}\) and \(\frac{1}{g}\frac{\partial v}{\partial t}\) values can be excluded with an appropriate accuracy.

  2. 2.

    In the case of the kinematic wave, changes in the flow depth is expressed as a single-valued relationship. However, in the dynamic wave, these changes are transformed to a loop curve (Chow 1959; Jain 2000), as shown in Fig. 3.

    Figures 4 shows changes in water depth of the first flood upstream (YI) and downstream (YO) of the study reach, respectively, as well as water depth changes of the input discharge of the first flood (upstream) in both the ascending and descending areas of the inflow hydrograph and water depth changes of the output discharge of the first flood (downstream) in both the ascending and descending areas of the outflow hydrograph.

    As shown in Fig. 4, temporal changes in water depth overlap in both the ascending and descending branches of the first flood, i.e. they are not loop-shaped. Again, the figure proves that the available data for the current study is related to the kinematic waves.

Table 1 Kinematic wave results
Full size table
Fig. 3
figure 3

Schematics of the flow depth changes in the dynamic wave type

Full size image
Fig. 4
figure 4

Water depth changes of the input discharge

Full size image

2.4 Linear Muskingum Method

This approach is best suited for rivers where the effects of inertia and backwater have insignificant values (Chang et al. 1983).

In the linear Muskingum method, continuity and storage relations are developed as follows:

Continuity:

$$\frac{dS}{dt}\approx \frac{\Delta S}{\Delta t}=I-O$$
(5)

Storage:

$$S=K\left[XI+\left(1-X\right)O\right]$$
(6)

where S = storage; I = inflow; O = outflow; t = time; ΔS = Δt = changes in storage during the time interval Δt; K = storage time constant; and X = dimensionless weighting factor.

Given the continuity of flow and simplification of Eqs. (5) and (6):

$${O}_{j+1}={C}_{1}{I}_{j+1}+{C}_{2}{I}_{j}+{C}_{3}{O}_{j}$$
(7)

where C1, C2 and C3 are given as:

$${C}_{1}=\frac{0.5\Delta t-KX}{K-KX+0.5\Delta t}$$
(8)
$${C}_{2}=\frac{0.5\Delta t+KX}{K-KX+0.5\Delta t}$$
(9)
$${C}_{3}=\frac{K-KX-0.5\Delta t}{K-KX+0.5\Delta t}$$
(10)
$${C}_{1}+{C}_{2}+{C}_{3}=1$$
(11)

According to Fig. 4, the inflow and outflow discharges can be expressed as a function of water depth. In other words:

$$I={M}_{1}{Y}_{I}^{\alpha }$$
(12)
$$O={M}_{2}{Y}_{O}^{\beta }$$
(13)

In previous study, the outflow hydrograph was calculated using Eq. (7) and the linear Muskingum method. As discussed in Introduction, calculation of water depth during a flood is essential in order to analyze and assess the flood in downstream, especially for damage appraisal and flood management and engineering. However, calculation of water depth using hydraulic routing method is a time-consuming and costly process due to the characteristics of river sections and their requirements. The present study introduces a new approach for calculation of the flood specifications downstream of a study reach by the use of the linear Muskingum method and kinematic wave equations. In this approach, the inflow and outflow functions in terms of water depth are applied instead of the inflow and outflow discharge of these equations. In other words, for calculation of the downstream (YO) water depth, substituting Eqs. (12) and (13) in Eq. (7) resulted in Eq. (14):

$${\left({Y}_{O}\right)}_{j+1}={\left[\frac{{M}_{1}}{{M}_{2}}\left[{C}_{1}{\left({Y}_{I}\right)}_{j+1}^{\alpha }+{C}_{2}{\left({Y}_{I}\right)}_{j}^{\alpha }\right]+{C}_{3}{\left({Y}_{O}\right)}_{j}^{\beta }\right]}^{\frac{1}{\beta }}$$
(14)

The PSO algorithm was used in the present study for optimization for its accuracy, efficiency and high speed.

Particle swarm optimization (PSO) algorithm is a population-based evolutionary algorithm and is used in civil engineering and water resources optimization problems such as reservoir performance (Kumar and Reddy 2007), water quality management (Afshar et al. 2011; Lu et al. 2002; Chau 2005), and optimization of the Forchheimer equation coefficients (Norouzi et al. 2021, 2022).

Various algorithms have been used to optimize the parameters of the Muskingum method and other methods and issues that need to be optimized, one of the fastest, most acceptable and most widely used of which is the PSO algorithm, which has been confirmed by (the meaning of the sentence is not clear) (Jahandideh-Tehrani et al. 2020). Therefore, particle swarm optimization (PSO) was used in the present study for the optimization of linear Muskingum parameters (X, K, Δt) and values (M1, M2, α, β). Minimization of the Mean Relative Error (MRE), as defined by Eq. (15), was used as the target function in the PSO:

$$MRE=\frac{1}{n}\sum_{i=1}^{n}\left|\frac{{Y}_{i}-{y}_{i}}{{Y}_{i}}\right|*100$$
(15)

where Yi is the observational flow depth (recorded in the hydrometric station), yi is the computational flow depth (calculated using the equations presented in the present study), and n is the number of data.

Figure 5 presents the flowchart depicting optimization of the linear Muskingum parameters by the PSO and the MRE function.

Fig. 5
figure 5

Particle Swarm Optimization (PSO) algorithm flowchart

Full size image

3 Results and Discussion

In flood management and engineering, calculation of water depth in downstream of a river during a flood is essential for economic analysis and damage assessment. In this study, inflow and outflow discharges were actually estimated as functions of water depth. Then, by substituting the functions in Eq. (7), the values of downstream water depth, rather than the discharge of the output flow were obtained. In the resulting equation (Eq. 14), it should be noted that, in order to calculate the linear Muskingum parameters (X, K, Δt), the input water depth variation (YI - t) was used instead of the inflow discharge (I - t) and the output water variation was used instead of the outflow discharge variation (O-t). In other words, M1, α, M2, β, X, K, and ∆t parameters were optimized using linear Muskingum method, PSO algorithm and first flood data. Then, by application of the linear Muskingum method (using the parameters obtained from a flood to calculate the flow characteristics downstream of any other flood in the same river reach, provided that the river morphology is unchanged), using the parameters obtained from the first flood and temporal changes in flow depth in upstream (Mollasani hydrometric station), temporal changes in depth in downstream of the study river reach (Ahwaz hydrometric station) were calculated.

Overall, the present study composed of the following steps:

  1. 1.

    Estimation of the inflow-outflow functions of the first flood (observational flood) in terms of the water depth in Eqs. (12) and (13). Optimization of the values of M1, M2, α, and β using the PSO algorithm, the results of which are presented in Table 2.

  2. 2.

    Using the PSO algorithm to optimize the linear Muskingum parameters (X, K, Δt) by the temporal changes in YI (input water depth) in the first flood (YI - t) and the temporal changes in YO (output water depth) in the first flood (YO - t), as presented in Table 2. It is worth mentioning that the previous study used inflow-outflow hydrographs (Q - t) to optimize such parameters and Eq. (7) to calculate the outflow hydrograph, while the present study used Eq. (14) to calculate output water depth changes with respect to time.

  3. 3.

    Calculation of the temporal changes in output water depth of the second flood (YO - t) by using the input water depth changes with respect to the time of the second flood (YI - t) and the optimized values of the linear Muskingum parameters (X, K, Δt) together with the optimized values of M1, M2, α, and β estimated from the first flood. In other words, according to the linear Muskingum method, the estimated parameters of a flood, which have already been recorded in the study reach (base flood), can be used to estimate the outflow characteristics, such as the downstream discharge and water depth of the same study reach, provided that the river morphology has not changed.

Table 2 Optimized values of the linear Muskingum parameters (X, K, Δt) and M1, M2, α, and β by using the first flood
Full size table

The calculation process of the temporal changes in output depth for the second flood when using the parameters obtained from the first flood (Table 2), the MRE of the whole flood, the MRE of the peak section and the DPO are given in the Table 3.

Table 3 The calculation process of the second flood using the parameters obtained from the first flood
Full size table

In Table 3:

$${C}_{1}=\frac{0.5\Delta t-KX}{K-KX+0.5\Delta t}=\frac{0.5*0.907-12.461*0.359}{12.461-12.461*0.359+0.5*0.907}=-0.476$$
$${C}_{2}=\frac{0.5\Delta t+KX}{K-KX+0.5\Delta t}=\frac{0.5*0.907+12.461*0.359}{12.461-12.461*0.359+0.5*0.907}=0.584$$
$${C}_{3}=\frac{-0.5\Delta t-KX+K}{K-KX+0.5\Delta t}=\frac{-0.5*0.907-12.461*0.359+12.461}{12.461-12.461*0.359+0.5*0.907}=0.892$$

In Table 3, In order to apply Eq. (14), the value of the output water depth at the start of a flood (YO)1 should be known. As in the linear Muskingum method, the value of the outflow discharge at the start of a flood (O1) is assumed to be equal to the inflow discharge at the start of the flood (I1). Then, in order to calculate (YO)1, the function O = 341.266 YO1.196 is used because the values of M2 and β are optimized as 341.266 and 1.196, respectively. If the value of O1 = I1 = 287 (m3/s) is considered, according to the above function, then the value of (YO)1 is calculated to be equal to 0.865 (m). In addition, for the second flood, temporal changes in input flow depth, temporal changes in the observational and computational output flow depth are shown in Fig. 6.

Fig. 6
figure 6

Computational and observational values of water depth of the second flood

Full size image

4 Conclusion

For proper design of hydraulic structures and flood control, as well as issues related to economic analysis and flood-related damages, the calculation of flood depth is more important than flood discharge. Hydraulic (Saint–Venant equations) and hydrological methods are used for the flood routing in rivers. To use hydraulic methods, upstream and downstream boundary conditions, roughness coefficients as well as cross-section properties must be available along the path and at appropriate intervals, which is time consuming and costly in many rivers. While hydrological methods such as the linear Muskingum method, in addition to the need for much less data and low cost for flood routing, are more accurate in engineering works. In previous studies, the outflow hydrograph (changes in discharge over time in downstream) has been routed using the linear Muskingum method. While in the present study, according to the flow wave type formed in the study river reach and using the linear Muskingum method and the PSO algorithm, a solution to calculate the flood depth in downstream was presented. Since a kinematic wave type was formed in the studied river reach of the Karun River, an equation was presented to calculate discharge changes in terms of flow depth. In other words, in the kinematic wave, the slope of the energy-grade line or friction slope (Sf) is equal to the channel bottom slope (S0) and the flow discharge changes in terms of flow depth can be obtained using Eqs. (12) and (13). Then, by substituting the mentioned equations in the equations of the linear Muskingum method, instead of calculating the temporal changes in outflow discharge, the temporal changes in outflow depth in downstream were calculated. The results indicated that the solution presented in the present study is highly accurate so that the mean relative error to the total flood, the mean relative error related to the peak section of the inflow hydrograph and the value of DPO were calculated as 1.29, 0.24 and 1.16%, respectively.