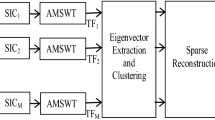
Abstract
According to the theory of single channel blind source separation (SCBSS), the algorithm based on virtual channel expansion must be established in a known source number, and most algorithms can only separate two source signals. When separating multiple source signals, the performance will deteriorate sharply. Since the existing methods of this kind use only a single algorithm for virtual channel expansion, they cannot retain all the source signals’ valuable information and effectively separate the multiple source signals. From the perspective of making the constructed virtual multi-channel signal contain enough information of the source signals as much as possible, this paper proposes a SCBSS algorithm based on improved wavelet packet and variational mode decomposition (IWP-VMD-SCBSS). Firstly, the source number is estimated according to the interval sampling method and the minimum description length (MDL) criterion. Secondly, the signal reconstruction method based on improved wavelet packet decomposition (IWPD) is used to reconstruct multiple purer virtual signals. Then the virtual signals are combined with the first intrinsic mode function (IMF) of two-level variational mode decomposition (VMD) and the original single-channel observed signal to constitute a virtual multi-channel signal. Finally, the joint approximate diagonalization of eigen-matrices (JADE) algorithm is used to process the virtual multi-channel observed signal to achieve BSS and obtain estimated source signals. The simulation results indicate that the IWP-VMD-SCBSS algorithm can achieve a lower symbol error rate (SER) than existing algorithms and lower computational complexity. It can solve the SCBSS problem of multiple communication signals effectively under an unknown source number.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Blind source separation (BSS) refers to recover each source signal when only the observed signals are known. The prior information of source signals and the characteristics of the transmission channel are unknown in this case [1]. According to the relationship between the source signals’ number and the observed signals’ number, BSS can be divided into underdetermined BSS, positive definite BSS and overdetermined BSS. Moreover, single channel blind source separation (SCBSS) is extremely ill-conditioned in underdetermined BSS, requiring only single channel to receive the observed signal. Only this single-channel observed signal is used to recover the collected source signals [2]. Estimating many quantities with very few quantities is required, so it is tough to solve this problem. Currently, most BSS algorithms are aimed at the overdetermined mixed situation or positive-definite mixed situation in multi-channel BSS. That is, the known source number, and the number of observed signals is not less than that of source signals. Unfortunately, the source signals’ number is generally unknown, and the observed signals’ number is also less than source number in practical applications. Even in some scenarios, only a single sensor can be placed to collect source signals, which is an extremely ill-conditioned underdetermined mixed situation. However, the advantage of the SCBSS technology is that the required hardware equipment is significantly reduced, and the installation and application are convenient. It is widely applied to communication countermeasures [3, 4], speech signal separation [5,6,7], mechanical fault diagnosis [8,9,10], biomedical signal processing [11, 12] and many other fields. Therefore, the research of SCBSS algorithms has important practical significance and broad application value.
Traditional BSS algorithms are not suitable for SCBSS. At present, there are several ways to solve SCBSS problems: methods based on virtual multi-channel [13,14,15,16], methods based on transform domain filtering [17] and methods based on a finite set of symbols [18, 19], etc. The methods based on virtual multi-channel do not require the characteristic information of source signals, which can use delay, interval sampling, wavelet decomposition, variational mode decomposition (VMD), empirical mode decomposition (EMD), ensemble empirical mode decomposition (EEMD) and other methods to construct a virtual multi-channel signal. Then, the mature independent component analysis (ICA) algorithm [20] or the JADE algorithm [1, 21] is used to separate source signals. The methods based on transform domain filtering refer to the use of Fourier transform, discrete cosine transformation (DCT) domain Wiener filtering or cyclic spectrum transform methods to transform the time-domain overlapping signals to other domains to realize BSS in the transform domain. However, this method requires source signals’ prior information, which is not entirely blind in the real sense. In addition, when the actual application environment becomes more and more complex and source signals’ number is large, how to use this algorithm to achieve the SCBSS needs further research. The methods based on a finite set of symbols can accurately describe communication signals by symbol sequences and parameters according to the characteristics of the limited symbol set. Therefore, the idea of sequence detection and joint parameter estimation can realize the BSS, among which the per survivor processing (PSP) algorithm and particle filter algorithm are the most used. Nevertheless, the complexity of both algorithms is too high, so further research is needed to improve the operation speed. The methods based on a finite set of symbols are difficult to apply in practice at present. In addition to those as mentioned above mainstream SCBSS algorithms, recently proposed some other practical separation algorithms, such as the non-negative matrix factorization (NMF) algorithms [22,23,24] and the current hot SCBSS algorithms based on deep neural networks [25, 26] etc. Nevertheless, the development of these algorithms is not yet complete. There is no mature related BSS theory as a support, so we do not carry out detailed research on such methods in this paper.
Given the advantages that the methods based on virtual multi-channel do not require prior information of the source signals and have low complexity, they have been widely used. Many scholars applied the EMD algorithm to deal with the SCBSS problem, which does not need source signals’ prior information, but with mode mixing and poor anti-noise performance problems [13, 15, 27]. On this basis, some scholars proposed EEMD algorithm, which can solve the problem of mode mixing to a certain extent, but with large computation cost. Moreover, the added Gaussian white noise cannot be neutralized entirely, so the EEMD algorithm is still affected by noise and cannot completely solve the problems of endpoint effect and mode mixing [28,29,30,31]. Konstantin Dragomireskiy [32] proposed VMD algorithm, which has a solid mathematical theoretical foundation and can essentially solve the mode mixing problem. What is more, it has a fast convergence speed and has been widely used in biomedical signal processing and fault diagnosis, but the accuracy of signal decomposition is corrupted by the penalty factor and decomposition level [16, 33,34,35]. Pang et al. reconstructed the virtual multi-channel signal using the optimal approximate component obtained by wavelet decomposition and achieved BSS through the FastICA algorithm. However, this method is difficult to represent the signal containing a large amount of detailed information [14]. In this regard, Zhao et al. used wavelet packet decomposition (WPD) to improve the performance of SCBSS when separating high-frequency signals dominated by detailed information. However, how to select proper wavelet basis and decomposition layers will directly affect the separation performance of source signals [36].
In addition, the above-mentioned SCBSS algorithms based on virtual multi-channel must be established with a known source number. Most algorithms can only separate two source signals. To solve the above problems, this paper proposes a SCBSS algorithm based on improved wavelet packet and variational mode decomposition (IWP-VMD-SCBSS). On the one hand, the virtual signals reconstructed by an improved method of wavelet packet signal reconstruction (IMWPSR) can better retain the information of source signals. On the other hand, the virtual multi-channel observed signal which combined by the reconstructed signals, the first intrinsic mode function (IMF) of two-level VMD and the single channel observed signal can retain the information of source signals both in the variable frequency domain and wavelet domain, which makes the source signals’ information more complete. The proposed algorithm can effectively improve the performance when separating multiple source signals, achieving higher estimation accuracy and lower computational complexity. In a word, the proposed algorithm can effectively estimate source number and separate other doped interference signals in the SCBSS problem. Moreover, the proposed algorithm has more evident advantages in separating multiple signals than existing SCBSS algorithms, and it has certain practicability.
The contents of this paper are organized as follows. Section 2 provides a mathematical model of signal mixing and problem-solving for SCBSS. In order to transform the SCBSS mixed model into a virtual multi-channel BSS mixed model, Sect. 3 introduces the related theoretical framework of WPD and VMD, and suggests the basic principles of the JADE algorithm for subsequent BSS simultaneously. Section 4 introduces the proposed IWP-VMD-SCBSS algorithm in detail, including the source number estimation and the realization of SCBSS. To verify its feasibility and effectiveness, Sect. 5 evaluates the the proposed algorithm and compares it with existing SCBSS algorithms. In the end, conclusions are summarized in Sect. 6.
2 Mathematical model of SCBSS
Assuming observed signals \({\mathbf{X}}(t){ = [}x_{1} (t),x_{{2}} {\text{(t),}} \ldots, \, x_{N} {\text{(t)]}}^{T}\) received by \(N\) sensors are obtained by the linear mixture of \(M\) source signals \(s_{1} (t),s_{{2}} {\text{(t),}} \ldots, \, s_{M} (t)\) at a certain instant. Suppose the source signal vector is \({\mathbf{s}}(t) = [s_{1} (t),s_{{2}} {\text{(t),}} \ldots, \, \)\(s_{M} (t)]^{T}\), then the mathematical model of BSS can be expressed as:
It can also be equivalent to
where \(t = 1,2, \ldots,T\) indicates the sampling time, \({\mathbf{a}}_{m} \in {\mathbf{R}}^{N \times 1}\) is mixed coefficient vector, \({\mathbf{A}} = [{\mathbf{a}}_{1} \;{\mathbf{a}}_{2} \; \cdots \;{\mathbf{a}}_{M} ]\) is the column full-rank mixed matrix with \(N\) in \(M\) order, and \({\mathbf{v}}(t)\) is additive white Gaussian noise.
The problem of BSS can be described as making full use of the different characteristics of the observed signals received by each sensor when the source signal vector \({\mathbf{s}}(t)\) characteristics and the mixed matrix \({\mathbf{A}}\) are unknown, using corresponding algorithm to process the multi-channel observed signal \({\mathbf{X}}(t)\) and obtain separation matrix \({\mathbf{W}}\). Then according to Eq. (3) to estimate source signals are, so as to realize the effective separation of each source signal.
When the mixed coefficient matrix \({\mathbf{A}}\) rows are 1, it becomes an extremely ill-conditioned underdetermined mixed situation. That is, the SCBSS signal mixed model, which can be expressed by Formula (4).
where \(x(t)\) is the single-channel signal, and \({\mathbf{a}} = [a_{1} ,a_{2} , \ldots ,a_{M} ]\) is mixed coefficient vector.
For the solution of the single channel mixed model, the virtual channel expansion method is used to construct multiple virtual signals, so as to meet the basic requirements of non-underdetermined BSS. Then the SCBSS problem can be solved by using the relevant algorithm of multi-channel BSS to separate each source signal.
3 Preliminaries and existing methods
3.1 Signal reconstruction method based on WPD
Compared with wavelet decomposition, WPD can provide a signal decomposition method with higher time–frequency resolution, which can decompose signal with low-frequency and high-frequency components simultaneously. There is neither redundancy nor omission in this decomposition process.
The essence of WPD is to divide the signal into arbitrary frequency bands by a set of low orthogonal pass and high orthogonal pass filters with the same bandwidth, and the frequency information is stored in wavelet packet node coefficients. For the convenience of expression, assuming that the scale function and the corresponding wavelet function are \(\mu_{0} (t) = \varphi (t)\) and \(\mu_{1} (t) = \psi (t)\) respectively, the scale equation of WPD can be expressed as:
where \(h(k)\) and \(g(k)\) are the low and high pass filter coefficients respectively, and \(g(k) = ( - 1)^{k} h(1 - k)\).
The function \(\left\{ {\mu_{n} (t)} \right\}\) defined recursively by formula (6) is the wavelet packet determined by the scale function \(\mu_{0} (t) = \varphi (t)\). The structure of the WPD tree can be represented by Fig. 1.
Firstly, the optimal wavelet base is selected, and then we determine the number of WPD layers on the basis of the source number, taking into account the requirements of speed and accuracy. The single channel signal \(x(t)\) is carried out by \(M\)-layer WPD, and the \(M\)-th layer can get \(2^{M}\) WPD nodes, from which \(2^{M}\) virtual signals can be reconstructed. When choosing different wavelet packet nodes to reconstruct the virtual signals, the performance of SCBSS will also be different. In general, nodes with larger energy contain more information of the source signals, and the virtual signal reconstructed by the node with the largest energy has the highest similarity with the source signals, and the performance of SCBSS using this virtual signal is the best (for the specific formula of energy calculation, see Sect. 4.2).
3.2 Variational mode decomposition
Unlike the EMD algorithm that only carries out cyclic filtering [13, 15, 27], the essence of the VMD algorithm is adaptive Wiener filtering [32]. By constructing a completely non-recursive constrained variational model and solve its optimal solution, the complex signal is adaptively decomposed to a series of narrow-band intrinsic mode functions (IMFs), which surround each constantly varying center frequency. The objective function of the VMD algorithm is to minimize the sum of each estimated IMFs’ bandwidths, and its constraint condition is to make the equation of each IMFs’ sum and the single-channel observed signal \(x(t)\) to be decomposed.
Firstly, each analytic signal is calculated by Hilbert transform, and its spectrum is modulated to the fundamental band of the estimated center frequency \(\omega_{k}\).
Using Gaussian smoothing to estimate each IMF’s bandwidth, the variational problem can be written as Eq. (8).
where \(\left\{ {u_{k} } \right\} = \left\{ {u_{1} , \ldots , \, u_{{\text{K}}} } \right\}\) is the set of mode functions and \(\left\{ {\omega_{k} } \right\} = \left\{ {\omega_{1} , \ldots , \, \omega_{{\text{K}}} } \right\}\) is the set of center frequencies of each variational mode function.
In order to obtain the optimal solution of the above constrained variational problem, the quadratic penalty factor \(\alpha\) and Lagrange multiplication operator \(\lambda (t)\) are led to construct an augmented Lagrange function, so that the constrained variational problem can be transformed into an unconstrained variational problem, namely Eq. (9).
where the value of the quadratic penalty factor \(\alpha\) can ensure the reconstruction accuracy of the signal with Gaussian noise to be decomposed, and the Lagrange multiplication operator \(\lambda (t)\) can keep the constraint conditions strict.
We use alternate direction method of multipliers (ADMM) to update \(u_{k}\), \(\omega_{k}\) and \(\lambda\) alternately in the frequency domain to solve the augmented Lagrange function’s minimum point. The introduction of Wiener filtering can make the VMD algorithm more robust to noise. The Fourier transforms of \(u(t)\), \(x(t)\) and \(\lambda (t)\) are denoted by \(\hat{u}(\omega )\), \(\hat{x}(\omega )\) and \(\hat{\lambda }(\omega )\) respectively, and the iterative update formulas for obtaining the mode functions \(u_{k}\) and the center frequencies \(\omega_{k}\) are shown in Formulas (10) and (11).
where \(\hat{u}_{k}^{n + 1} (\omega )\) is the mode function at \(n + 1\)-th loop iteration, and \(\omega_{{_{k} }}^{n + 1}\) is the power spectrum’s center frequency of the mode function \(\hat{u}_{k}^{n + 1} (\omega )\) at the \(n + 1\)-th loop iteration. Perform inverse Fourier transform on \(\left\{ {\hat{u}_{k} (\omega )} \right\}\) and then take the real part of them, the time-domain mode functions \(\left\{ {u_{k} (t)} \right\}\) can be obtained.
The decision criterion for stopping the loop iteration is
where \(\varepsilon\) is convergence tolerance.
When the iteration stop criterion is satisfied, the single channel signal \(x(t)\) is decomposed into \(\left\{ {u_{k} (t)} \right\} = \left\{ {u_{1} (t), \ldots , \, u_{{\text{K}}} {(}t{)}} \right\}\) by the VMD algorithm, which are used to form the virtual multi-channel signal \({\mathbf{X}}(t)\).
3.3 Basic principles of JADE algorithm
JADE algorithm is an improved independent decomposition algorithm on the basis of the diagonalization of the fourth-order cumulant matrix proposed by Cardoso, which can separate source signals well when the frequency difference between the signals is slight [1, 21]. This algorithm constructs fourth order cumulant matrices of multiple variables based on the characteristic that the mutual cumulant between independent signals is zero. Then the separation matrix \({\mathbf{W}}\) is solved by joint approximate diagonalization of cumulant matrices, which improves the robustness of separation results. In brief, the JADE algorithm include whitening process and orthogonal transform process, as shown in Fig. 2.
The concrete steps of JADE algorithm are as follows:
-
(1)
Whitening of observed signals.
We assume the virtual multi-channel signal \({\mathbf{X}}(t)\) is obtained by multiplying a \(N \times M\) dimensional mixed matrix \({\mathbf{A}}\) and \(M\) independent source signals \({\mathbf{s}}(t)\), the whitening matrix \({\mathbf{Q}}\) can be obtained.
where \(\mu_{1} ,\mu_{2} , \ldots,\mu_{N}\) are the \(N\) largest different eigenvalues of the covariance matrix of \({\mathbf{X}}(t)\), \({{\varvec{\upalpha}}}_{1} ,{{\varvec{\upalpha}}}_{2} , \ldots,{{\varvec{\upalpha}}}_{N}\) are the eigenvectors corresponding to the different eigenvalues, and \(\sigma\) is noise variance.
The signals after whitening can be formulated as
From Eq. (14), we can estimate unitary matrix \({\mathbf{U}}\) to realize the estimation of mixed matrix \({\mathbf{A}}\). Moreover, it can be known that the unitary matrix \({\mathbf{U}}\) is orthogonal in paper [21].
-
(2)
Calculation of the fourth-order cumulant of whitening signal \({\mathbf{z}}(t)\).
The fourth-order cumulant of \({\mathbf{z}}(t)\) is expressed as:
For any \(N \times N\)-order weight matrix \({\mathbf{P}}\), define its fourth-order cumulant matrix \({\mathbf{Q}}_{{\mathbf{Z}}} ({\mathbf{P}})\) related to \({\mathbf{z}}(t)\), then the element in \(i\)-th row and \(j\)-th column of \({\mathbf{Q}}_{{\mathbf{Z}}} ({\mathbf{P}})\) can be expressed as:
where \(p_{ef}\) is the element corresponding to the \(e\)-th row and \(f\)-th column of \({\mathbf{P}}\), so the cumulant matrix \({\mathbf{V}} = {\mathbf{Q}}_{{\mathbf{z}}} {\mathbf{(P)}}\) can be obtained.
Depending on the nature of the cumulant, Eq. (17) can be obtained.
where \(cum(s_{d} ,s_{d}^{ * } ,s_{d} ,s_{d}^{ * } )\) represents the fourth order cumulant of the \(d\)-th column of source signals \({\mathbf{s}}(t)\), and \({{\varvec{\upchi}}}_{d}\) is the \(d\)-th column of the orthogonal unitary matrix \({\mathbf{U}}\), and \({{\varvec{\Lambda}}}_{{\mathbf{P}}} = diag(k_{1} {{\varvec{\upchi}}}_{1}^{H} {\mathbf{P\chi }}_{1} ,k_{2} {{\varvec{\upchi}}}_{2}^{H} {\mathbf{P\chi }}_{2} , \ldots,k_{N} {{\varvec{\upchi}}}_{N}^{H} {\mathbf{P\chi }}_{N} )\).
From Eq. (17), it can be known that the orthogonal matrix that makes the matrix \({\mathbf{U}}^{H} {\mathbf{Q}}_{{\mathbf{z}}} ({\mathbf{P}}){\mathbf{U}}\) diagonal to any matrix \({\mathbf{P}}\) is the unitary matrix \({\mathbf{U}}\) to be sought.
-
(3)
Selection of weight matrix \({\mathbf{P}}_{n}\).
Assume \(({\tilde{\mathbf{Q}}})_{hg} = cum(z_{i} ,z_{j}^{ * } ,z_{e} ,z_{f}^{ * } )\), where \(g = k + (l - 1)N\) and \(h = i + (j - 1)N\). It can be easily seen from Eq. (15) that \({\tilde{\mathbf{Q}}}\) is \(N^{2} \times N^{2}\) dimension Hermit matrix. The eigenvalue decomposition of \({\tilde{\mathbf{Q}}}\) is carried out, and the \(N^{2} \times 1\)-dimensional eigenvectors corresponding to the \(N\) maximum eigenvalues of matrix \({\tilde{\mathbf{Q}}}\) are selected, and they are rearranged into \(N\) \(N \times N\)-dimensional matrices, which can be used as the weight matrices \({\mathbf{P}}_{n} , \, n = 1,2, \ldots,N\).
-
(4)
Determination of the unitary matrix \({\mathbf{U}}\).
For each selected weight matrix \({\mathbf{P}}_{n} , \, n = 1,2, \ldots,N\), its cumulant matrix set \({\mathbf{V}}_{n} = {\mathbf{Q}}_{{\mathbf{z}}} {\mathbf{(P}}_{n} {\mathbf{)}}(n = 1,\) \(2, \ldots,N)\) can be obtained. By maximizing the cost function shown in formula (18), the unitary matrix \({\mathbf{U}}\) can maximize the diagonalization of each cumulant matrix \({\mathbf{V}}_{n} = {\mathbf{Q}}_{{\mathbf{z}}} {\mathbf{(P}}_{n} {\mathbf{)}}\). The unitary matrix \({\mathbf{U}}\) can be obtained.
(5) Estimation of the mixed matrix \({\hat{\mathbf{A}}}\) and the source signals \({\hat{\mathbf{s}}}(t)\)
4 Proposed SCBSS algorithm
At present, SCBSS algorithms based on virtual channel expansion must be established in a known source number, and most algorithms can only separate two source signals, and the performance will deteriorate sharply when multiple source signals are separated. In order to solve the problem, this paper proposes a SCBSS algorithm based on improved wavelet packet and variational mode decomposition (IWP-VMD-SCBSS). The flow-process diagram is shown in Fig. 3. Firstly, the source number is estimated by interval sampling method combined with MDL criterion (IS-MDL). Secondly, we improve the traditional wavelet packet signal reconstruction method, transforming to use multiple groups of nodes with larger energy to reconstruct the virtual signals \({\mathbf{Y}}(t) = [y_{1} (t),y_{2} (t), \ldots,y_{M - 1} (t)]\) which can better retain source signals’ information. Then, the reconstructed virtual signals \({\mathbf{Y}}(t)\), the first IMF \(u_{1} (t)\) of the two-level VMD and the original single channel observed signal \(x(t)\) are recombined into a virtual multi-channel observed signal \({\mathbf{X}}(t) = [x(t),y_{1} (t), \ldots,y_{M - 1} (t),u_{1} (t)]\). Finally, we apply the JADE algorithm to process the \({\mathbf{X}}(t)\) to realize the BSS.
4.1 Source number estimation
The estimation of source number mainly relies on the theory of spatial spectrum estimation, that is, the covariance matrix is obtained by decomposing multivariate data under certain conditions, whose large eigenvalues correspond to source signals and small eigenvalues correspond to noise. The number of large eigenvalues can preliminarily estimate the source number. However, most estimation methods are for multi-channel array signals, and the array signals’ number should be more than that of source signals, so these methods cannot be used to estimate the source number directly for the single channel observed signal. Therefore, it is necessary to expand the single channel signal into multiple virtual signals.
In order to realize multi-channel expansion, we propose an interval sampling method in this paper, which refers to re-sampling the input signal to obtain some new data vectors to form a multi-dimensional matrix. Assuming that the received single channel observed signal is \(x(t)\), the discrete form \(\tilde{x}(l) = x(lT_{1} )\) of the \(x(t)\) is obtained by sampling it at an interval of \(T_{1}\); then the discrete observed signal \(\tilde{x}(l)\) is sampled once every \(B\) point, and the discrete single-channel observed signal \(\tilde{x}(l)\) can be rearranged into \(B\)-channel virtual signals \(\tilde{x}_{1} (l),\tilde{x}_{2} (l), \ldots,\tilde{x}_{B} (l)\) through interval sampling, as shown in Eq. (20).
Then the expanded virtual multi-channel observed signal matrix \({\tilde{\mathbf{X}}}_{B} (l)\) can be obtained, as shown in Eq. (21).
Finally, the expanded virtual multi-channel signal matrix \({\tilde{\mathbf{X}}}_{B} (l)\) can directly estimate the source signals’ number. The advantage of this method is that the performance of each channel signal obtained by multi-channel expansion is very close, and it can accurately estimate the source number with low complexity only by ensuring that the number of the \({\tilde{\mathbf{X}}}_{B} (l)\) is not less than that of source signals.
Given the limitation of carrier frequency interval (CFI) and signal-to-noise ratio (SNR) in the specific working environment, when the covariance matrix is decomposed into eigenvalues under actual conditions, the noise eigenvalues will be close to the signal eigenvalues, and the difference between them is no longer noticeable. As a result, the source number cannot be correctly distinguished, and the spatial covariance matrix eigenvalue estimation method will be invalid. To solve this problem, this paper discusses several existing effective methods in source number estimation, including the Akaike Information Criterion (AIC) [37] and the Minimum Description Length (MDL) [38] in Information Theoretical Criteria (ITC), and the Gerschgorin Disk Estimator (GDE) method based on Gerschgorin Disk theorem [38]. After theoretical research and experimental simulation, the MDL criterion is selected to process the \({\tilde{\mathbf{X}}}_{B} (l)\) estimate source number.
Rissane proposed the principle of minimum description length (MDL) in his work on general coding, which is based on ITC. The mathematical model of ITC can be described as: If the observed data is recorded as \({\mathbf{X}}_{B} = [X_{B} (1){,}X_{B} (2), \cdots ,X_{B} (L)]^{T}\), and the parameterized probability model is \(f({\mathbf{X}}_{B} /\theta )\), then only the model with the best fitting degree with the observed data \({\mathbf{X}}_{B}\) needs to be found. Assuming \(m\) source signals in the virtual multi-channel observed signal matrix \({\tilde{\mathbf{X}}}_{B} (l)\), the covariance matrix of \({\tilde{\mathbf{X}}}_{B} (l)\) is obtained and denoted as \({\mathbf{R}}_{{\mathbf{X}}}\). Then, the spectral decomposition of the covariance matrix \({\mathbf{R}}_{{\mathbf{X}}}\) can be expressed as follows:
where \(\lambda_{b}\) is the eigenvalue of the covariance matrix \({\mathbf{R}}_{{\mathbf{X}}}\) after singular value decomposition, and \({\mathbf{c}}_{b}\) is the corresponding eigenvector of \(\lambda_{b}\), \(\delta\) represents unknown scalar.
The method of ITC can be summarized as follows in a unified functional formula.
where \(L(m)\) is the likelihood function, \(P(m)\) is the penalty function, and \(J(m)\) is the random distribution function that decreases at first and then increases. Taking different values of \(L(m)\) and \(P(m)\), different estimation algorithms on the basis of ITC can be obtained. The formula of the MDL criterion can be described as:
where \(L\) is the number of sample points and \(B\) is the array signals’ number (that is, the number of signal paths of the virtual multi-channel observed signal matrix \({\tilde{\mathbf{X}}}_{B} (l)\)).
In a word, we propose a source number estimation method using the proposed interval sampling method combined with the MDL criterion (IS-MDL method) to estimate the source number in the SCBSS problem. Next, we verify the effectiveness of the proposed source number estimation method through experimental simulation. Perform 1000 Monte Carlo simulation experiments, and calculate the estimation accuracy under different carrier frequency intervals (CFIs, denoted as \(\Delta f\)) and the different source number (denoted as \(M\)), as shown in Fig. 4.
Figure 4 shows the estimation accuracy when the proposed IM-MDL method estimates the different source number when the signal CFI is from 0.3 to 0.7 MHz. As the results, it can be seen that when the SNR is low, the estimation accuracy of the proposed IM-MDL method increases with the increase of the signal CFI and decreases when the actual number of source signals increases. When the SNR increases, the estimation accuracy will also increase. Even when the CFI is 0.3 MHz, the proposed method can also achieve 100% estimation accuracy. When M = 2, 3 and 4 respectively, the estimation accuracy of the proposed IS-MDL method can reach 100% when the SNR is above − 9, − 5, and 0 dB respectively. In short, this paper proposes the IM-MDL source number estimation method that combines the interval sampling method with the MDL criterion, which lay a solid foundation for the subsequent SCBSS process.
4.2 Single channel blind source separation process
4.2.1 Reconstruction of the virtual multi-channel observed signal model
In order to better extract source signals’ information, this paper starts from the variational frequency domain and the wavelet domain to reconstruct the virtual signals which is used to constitute the multi-channel observation signal model.
Firstly, we make some appropriate improvements to the signal reconstruction method based on WPD to reconstruct \(M - 1\) virtual signals with the complete information of source signals. Before performing WPD, it is essential to select the optimal wavelet basis, that is, a group of orthogonal filters most suitable for the corresponding signal to be decomposed. Since this paper is aimed at the blind separation of communication signals, we define the wavelet function and scale function of the Meyer wavelet in the frequency domain. In addition, the Meyer wavelet is not tightly supported with fast convergence rate. The discrete Meyer wavelet, namely Dmeyer wavelet, can be selected as the wavelet packet generating function based on these characteristics. It is an approximation of Meyer wavelet based on finite impulse response (FIR), which is widely used to calculate of fast discrete wavelets and is more suitable for the decomposition of communication signals.
Considering the needs of decomposition speed and the accuracy of reconstructed signals, the decomposition layers is set as the source number \(M\). Then WPD is performed for the single channel observed signal \(x(t)\), and the \(M\)-th layer can obtain \(2^{M}\) wavelet packet nodes.
In the WPD, the \(q\)-th node of the \(m\)-th layer decomposition is denoted as \((m,q)\), and the \(i\)-th coefficient of node \((m,q)\) is denoted as \(d_{m}^{q} (i)\), and the energy value of the \(q\)-th node of the \(m\)-th layer decomposition can be calculated by norm-2.
where \(I\) is the total number of coefficients of node \((m,q)\).
The energy of the \(m\)-th layer of WPD is the sum of the energy values of each node.
Next, the proportion of the energy can be obtained for each node.
Since the node with a smaller energy proportion contains less information about source signals, these nodes can be considered to be caused by noise, while the node with a larger energy proportion contains more information about source signals, which can be conducive to correct separation. According to this theory, the threshold of energy proportion is set in the nodes of the \(M\)-th layer of WPD, which is generally about 3%. Firstly, the nodes whose energy proportion \(\eta_{q}\) is less than the energy threshold are eliminated. Then, the nodes with high energy are selected as many as possible from the remaining nodes to reconstruct the \(M - 1\) virtual signals \({\mathbf{Y}}(t) = [y_{1} (t),y_{2} (t), \ldots,y_{M - 1} (t)]\) with the same length as the original single channel signal \(x(t)\) by different combinations. The reconstructed virtual signals can better retain the information of the source signals, and they have a narrower bandwidth and higher SNR than the \(x(t)\). The above process is an improvement of the signal reconstruction method based on WPD in this paper, which is called the improved method of wavelet packet signal reconstruction (IMWPSR).
In order to express the proposed IMWPSR more intuitively, take three communication signals (namely \(M = 3\)) as an example to show the reconstruction process of the virtual signals in detail. The WPD is performed on the \(x(t)\)(The SNR is 10 dB), and the energy proportion of each frequency band in the \(M\)-th layer decomposition is drawn, as shown in Fig. 5.
After removing the nodes whose energy proportion is less than the threshold (the energy proportion threshold is set to 3% based on experience), that is to remove nodes 5 and 6 in the above figure. Then the third layer nodes 1–4, 7 and 8 are selected to reconstruct the virtual signal \(y_{1} (t)\), and the third layer nodes 2–4, 7 and 8 are selected to reconstruct the virtual signal \(y_{2} (t)\). Thus, we can obtain two purer virtual signals with the same length as the \(x(t)\).
Secondly, we use the VMD algorithm to decompose the \(x(t)\) in variable frequency domain to generate other virtual signals. VMD algorithm has a solid mathematical theoretical basis, which can essentially overcome mode mixing with fast convergence speed and good noise resistance [32]. Firstly, the relevant parameters of VMD are initialized, the penalty factor \(\alpha = 2000\), bandwidth \(\tau = 0\), convergence tolerance \(\varepsilon = 1 \times 10^{ - 7}\), and the decomposition levels \(K\) is set to 2. Then the \(x(t)\) is decomposed by VMD to obtain two intrinsic mode functions (IMFs) \(u_{1} (t)\) and \(u_{2} (t)\). The first mode function \(u_{1} (t)\) is purer than the second mode function \(u_{2} (t)\), that is, it contains more information of source signals and less noise, so that it can be selected as one virtual signal of \({\mathbf{X}}(t)\).
In the end, since the single channel observed signal \(x(t)\) contains all the information of source signals, it can be used as one of the virtual signals, combined with the virtual signal matrix \({\mathbf{Y}}(t)\) obtained by the IMWPSR and the first IMF \(u_{1} (t)\) decomposed by VMD to compose \({\mathbf{X}}(t) = [x(t),y_{1} (t), \ldots,y_{M - 1} (t),u_{1} (t)]\).
4.2.2 The separability of the reconstruction model
Since there is almost no source signals’ prior knowledge and the mixed channel, it is difficult to recover each source signal based on the reconstructed virtual multi-channel observed signal. In order to successfully separate each source signal, not only must the source signals meet specific statistical characteristics, but the mixed channel model must also meet certain prior conditions. Next, this paper demonstrates the following points.
-
(1)
Meet the essential requirement of positive definite BSS. The \({\mathbf{X}}(t)\) always satisfies that the number of signal components is more than the source number. The dimension of \({\mathbf{X}}(t)\) can be reduced to a positive definite BSS model through the whitening method. At the same time, and the correlation between each component can be removed to simplify the BSS algorithm and improve the separation performance.
-
(2)
For the channel noise problem of BSS, this paper adopts the additive noise model. The application of the IMWPSR, which uses higher energy nodes to reconstruct the virtual signals, can effectively weaken the effect of noise. The VMD algorithm has good anti-noise performance, and the first IMF in the two-level VMD corresponds to the source signals and almost contains no noise. Therefore, combining these two algorithms can reduce the influence of channel noise to a certain extent.
The JADE algorithm can also separate source signals when the frequency difference is slight, its operation speed is fast, and the separation result is robust [1, 21]. Therefore, this paper selects this algorithm to perform BSS of the constructed virtual multi-channel observed signal \({\mathbf{X}}(t)\), and all the estimated source signals \({\hat{\mathbf{s}}}(t)\) with high estimation accuracy can be obtained in the end.
In summary, this paper has proposed a SCBSS algorithm based on improved wavelet packet and variational mode decomposition (IWP-VMD-SCBSS), suitable for the condition where the source number is unknown. The algorithm steps are summarized as follows:
-
Step 1: The interval sampling method is proposed to expand the single channel observed signal \(x(t)\) into \(B\)-channel signal, which is recorded as the virtual multi-channel observed signal matrix \({\tilde{\mathbf{X}}}_{B} (l)\), and the source number \(M\) is estimated based on the MDL criterion.
-
Step 2: The single channel signal \(x(t)\) is decomposed by \(M\)-layer WPD and the IMWPSR is applied to reconstruct the virtual signal matrix \({\mathbf{Y}}(t) = [y_{1} (t),y_{2} (t), \ldots,y_{M - 1} (t)]\) with the same length as the \(x(t)\).
-
Step 3: Two intrinsic mode functions (IMFs) \(u_{1} (t)\) and \(u_{2} (t)\) are obtained by two-level VMD of the \(x(t)\).
-
Step 4: The single channel signal \(x(t)\), the virtual signal matrix \({\mathbf{Y}}(t)\) reconstructed by the IMWPSR and the first IMF \(u_{1} (t)\) decomposed by VMD are reorganized into the virtual multi-channel observed signal \({\mathbf{X}}(t) = [x(t),y_{1} (t), \ldots,y_{M - 1} (t),u_{1} (t)]\).
-
Step 5: The JADE algorithm is used to process the \({\mathbf{X}}(t)\), and each source signal can be estimated.
5 Algorithm simulation and performance analysis
In this section, the performance of the proposed IWP-VMD-SCBSS algorithm is simulated and analyzed, and compared with different SCBSS algorithms such as the VMD-SCBSS algorithm [16], the WPD-SCBSS algorithm [36] and the EEMD-PCA-SCBSS algorithm [28].
5.1 Experiment setup
The proposed method is demonstrated by separating communication source signals. The communication signals used as the source signals are cyclostationary signals include BPSK and QPSK signals with good anti-noise characteristics and frequency band utilization. In the simulation, two QPSK signals and two BPSK signals are used as the source signals. The carrier frequencies of the four source signals are 60, 60.5, 61 and 61.5 MHz respectively (can be adjusted with different experiments), the signal amplitudes are all 1, the symbol rates are all 0.25Mbit/s. The down-conversion method is adopted, and the sampling frequency is set to 5 MHz or 7 MHz based on the sampling theorem, which can ensure separation accuracy and increase calculation speed at the same time. (Due to the increase of source signals to be separated, sampling points need to increase, so the sampling frequency is changed to 7 MHz when separating four source signals.) Then the white Gaussian noise \(v(t)\) is added, the single channel signal \(x(t) = \sum_{m = 1}^{4} {a_{m} s_{m} (t)} + v(t)\) can be obtained.
Because the valuable information of communication signals is mainly contained in transmitted symbol sequences, it is not necessary to thoroughly estimate each signal's waveform. As long as the symbols of the recovered signals can be guaranteed to be equal to that of the source signals, the SCBSS algorithm can achieve the desired effect. Therefore, after each recovered signal is obtained, the symbol sequence obtained by its demodulation can be compared with the symbol sequence of the source signal transmitted in each channel, and we calculate the symbol error rate (SER) to measure the performance of the corresponding SCBSS algorithm. For the separation effect, the lower the SER, the better the performance of the SCBSS algorithm.
5.2 Verification of the effectiveness of the proposed algorithm
We apply the IWP-VMD-SCBSS algorithm to the separation of three source signals (\(a_{4} = 0\)), and its performance is shown by the scatter diagrams, and the SER will be further calculated. From Sect. 4.2, when three source signals are separated at the SNR of 10 dB, we propose the IMWPSR can obtain two virtual signals \(y_{1} (t)\), \(y_{2} (t)\) that can better retain the information of source signals. Then, the virtual signals \(y_{1} (t)\), \(y_{2} (t)\), the first IMF \(u_{1} (t)\) decomposed by VMD, the single channel observed signal \(x(t)\) are recombined into the virtual multi-channel observed signal \({\mathbf{X}}(t) = [x(t),y_{1} (t),y_{2} (t),u_{1} (t)]\). Finally, BSS is realized by the JADE algorithm, which can obtain estimated three source signals \(\hat{s}_{1} (t)\), \(\hat{s}_{2} (t)\) and \(\hat{s}_{3} (t)\). The scatter diagrams of the three estimated source signals and that of the \(x(t)\) are compared as follows:
Comparing the scatter diagram of the \(x(t)\) and the estimated source signals, the mixed three source signals have been successfully separated, and the SCBSS has achieved the desired effect. It intuitively shows the effectiveness of the IWP-VMD-SCBSS algorithm (Figs. 6, 7).
Next, we will further test and verify the effectiveness of the IMPWSR and the IWP-VMD-SCBSS algorithm by calculating SER, comparing the performance of the proposed IWP-VMD-SCBSS algorithm, the traditional WPD-SCBSS algorithm, and the WPD-SCBSS algorithm optimized by the IMWPSR, which is called the IWPD-SCBSS algorithm. We carry out 100 Monte Carlo simulation experiments to calculate the average SER of the three estimated source signals as shown in Fig. 8.
From Fig. 8, we can see that the separation performance of the IWPD-SCBSS algorithm is better than that of the WPD-SCBSS algorithm. The SER of the improved algorithm is reduced by two orders of magnitude compared with that before the optimization when the SNR is 10 dB. As the SNR increases, the improvement effect becomes more apparent. It indicates that the information of source signals is more complete for separating three source signals when multiple nodes with larger energy are used to reconstruct virtual signals than when only the node with the largest energy is used to reconstruct virtual signals. In other words, the IMWPSR is helpful to improve the performance of SCBSS. In addition, when the VMD algorithm is introduced for further improvement, the average SER of the IWP-VMD-SCBSS algorithm proposed in this paper is significantly reduced. When the SNR is 10 dB, it can achieve accurate separation without symbol error, far better than the 0.1% SER of the IWPD-SCBSS algorithm. It shows that the IMWPSR combined with the VMD algorithm can further improve the separation effect. The reason is that the IWP-VMD-SCBSS algorithm simultaneously introduces WPD and VMD algorithms to reconstruct the virtual multi-channel observed signal, which can retain the source signals' information both in the variable frequency domain and wavelet domain simultaneously. Moreover, the application of the IMWPSR, which uses higher energy nodes to reconstruct the virtual signals, can weaken the influence of noise to a certain extent. The VMD algorithm also has good noise immunity. Therefore, the IWP-VMD-SCBSS algorithm can effectively suppress noise and significantly improve separation performance.
5.3 Comparison proposed algorithm with other existing SCBSS algorithms
5.3.1 Performance comparison under different source number
In order to further demonstrate the superiority of the IWP-VMD-SCBSS algorithm, we apply traditional WPD-SCBSS algorithm [16], VMD-SCBSS algorithm [36] and EEMD-PCA-SCBSS algorithm [28] to separate two source signals (\(a_{3} = 0, \, a_{4} = 0\)), three source signals (\(a_{4} = 0\)) and four source signals respectively, and the performance of these three SCBSS algorithms in the separation of a different number of source signals (denoted as \(M\)) are compared with the IWP-VMD-SCBSS algorithm. The average SER curves of different algorithms, as shown in Fig. 9.
From Fig. 9, the VMD-SCBSS algorithm has a large SER regardless of the source number, which cannot achieve the desired separation effect. The reason is that the VMD algorithm needs to set a penalty factor \(\alpha\) and decomposition levels \(K\) in advance. When the source signals’ CFI is 0.5 MHz, the decomposition levels \(K\) is directly set to the source number \(M\), leading to the information hybridity of decomposition signals and the loss of some information of source signals, and it will still be affected by noise. When the WPD-SCBSS algorithm separates two source signals, the SER will gradually decrease as the SNR increases. It can achieve a fairly good separation effect when the SNR increases to 6 dB. However, when the source signals is more than two, only reconstructing the virtual signals by the node with the largest energy will lose some information of the source signals, resulting in poor separation effect. The performance of the EEMD-PCA-SCBSS algorithm is weaker than that of the WPD-SCBSS algorithm when separating two source signals, and the separation performance will further deteriorate when separating multiple signals, which cannot achieve a good separation effect. The reason is that the EEMD algorithm fails to solve the edge effect and mode mixing problems completely. Too few IMFs selected to reconstruct the virtual multi-channel signal will miss some information of the source signals, while too many IMFs selected to reconstruct the virtual multi-channel signal will not achieve a good de-noising effect.
Given the many shortcomings of existing algorithms, there is an urgent need for a new SCBSS algorithm to solve these above problems, especially an algorithm suitable for multiple source signals separation. Therefore, this paper proposes the IWP-VMD-SCBSS algorithm, which combines the improved wavelet packet method and the 2-level VMD algorithm. The average SER of the IWP-VMD-SCBSS algorithm is significantly lower than other SCBSS algorithms regardless of M = 2, 3 and 4. When the SNR is 8 dB, the average SER of the proposed IWP-VMD-SCBSS algorithm is at least three orders of magnitude lower than other algorithms. The proposed algorithm can achieve accurate separation without symbol error when the SNR is 10 dB.
In addition, when separated source signals increases, the separation performance of existing algorithms will deteriorate. Especially, they cannot achieve effective separation of the four source signals. As the SNR increases, the SER remains high, indicating that these algorithms have failed. However, the IWP-VMD-SCBSS algorithm can still maintain good separation effect when separate four source signals. When the SNR is more than 8 dB, it can still realize the separation of four source signals without SER. On the whole, the proposed algorithm has the best separation performance. The reason is that the IWP-VMD-SCBSS algorithm simultaneously introduces WPD and VMD algorithms to reconstruct the virtual multi-channel observed signal \({\mathbf{X}}(t)\), which can retain the source signals' information both in the variable frequency domain and wavelet domain simultaneously. It can effectively prohibit noise without mode mixing and the lack of some information of source signals in the EEMD-PCA-SCBSS algorithm.
5.3.2 Performance comparison under different CFIs
Keep other conditions unchanged, and change the source signals' CFIs (denoted as \(\Delta f\)) to 0.3 MHz, 0.4 MHz and 0.5 MHz respectively. Since the VMD-SCBSS algorithm is poor when comparing the performance of separating the different number of source signals, it will not be considered when comparing the closer CFI. In addition, other existing SCBSS algorithms have poor performance when separating four source signals, so we only compare the performance of different algorithms when separating two and three source signals. Under different CFIs, the separation performance of the IWP-VMD-SCBSS algorithm is observed with the WPD-SCBSS algorithm and the EEMD-PCA-SCBSS algorithm that have a good separation effect. The average SER curves as shown in Fig. 10.
From Fig. 10 it appears that the separation effect of all algorithms will deteriorate with the reduction of CFI. The separation effect of the IWP-VMD-SCBSS algorithm is significantly better than that of the EEMD-PCA-SCBSS algorithm. The reason is that the separation effect of the EEMD-PCA-SCBSS algorithm will be affected by the white Gauss noise added in the EEMD process, which cannot be completely neutralized. Furthermore, the problem of edge effect and mode mixing cannot be solved entirely. All the IMFs cannot be selected to reconstruct the virtual multi-channel observed signal, resulting in lacking some source signals’ information.
Next, we compare the proposed algorithm with the WPD-SCBSS algorithm. For the separation of two source signals, the SER of the IWP-VMD-SCBSS algorithm is higher than that of the WPD-SCBSS algorithm when the SNR is lower than 3 dB, and the separation effect is no better than that of the WPD-SCBSS algorithm. The IWP-VMD-SCBSS algorithm has lower SER and better separation performance than the WPD-SCBSS algorithm when the SNR is higher than 4 dB. The reason is that when the SNR is low, there will be some noise mixed in the first IMF of VMD added to the IWP-VMD-SCBSS algorithm. The reconstructed virtual multi-channel signal \({\mathbf{X}}(t)\) is contaminated by noise, resulting in a poor separation effect. Although the performance of the IWP-VMD-SCBSS algorithm is not as good as that of the WPD-SCBSS algorithm when the SNR is below 3 dB, the SER of both algorithms is high. The separation performance of both algorithms is poor in this case, so it is not easy to carry out practical applications. In comparison, when the SNR is above 4 dB, the separation effect of the IWP-VMD-SCBSS algorithm is significantly better than that of the WPD-SCBSS algorithm with low SER, which has good practical value. For the separation of three source signals, the WPD algorithm will not achieve a good separation as the SNR increases, and its performance will worsen with the reduction of CFI. For the proposed IWP-VMD-SCBSS algorithm, when the CFI of source signals is 0.3 MHz, the average SER is very high, and the reduction of the SER with the increase of the SNR is not apparent, so the separation effect is unsatisfactory. When the CFI of source signals is higher than 0.4 MHz, the average SER gradually decreases as the SNR increases, and the separation effect is fairly good. The reason is that when the SNR and CFI increase, the virtual multi-channel observed signal reconstructed by WPD and VMD can contain more information of the source signals without frequency mixing between the source signals and almost no noise.
Based on the comprehensive analysis, the proposed IWP-VMD-SCBSS algorithm perform more superior than other SCBSS algorithms when separating source signals with different CFIs and holds application values and excellent foreground.
To further explore the performance of the IWP-VMD-SCBSS algorithm in separating source signals with more CFIs, taking the separation of three source signals as an example, we study the performance changes when the CFI continues to increase. The average SER with the change the SNR is as drawn as Fig. 11.
Figure 11 shows that when the CFI increases to more than 0.5 MHz, the separation performance of the IWP-VMD-SCBSS algorithm basically reaches the maximum excellent. It is less affected by the CFI but is greatly affected by the SNR at this time. The reason is that when the CFI is 0.5 MHz, it has reached twice the symbol rate, there is no frequency mixing between the source signals, and the reconstructed virtual multi-channel signal \({\mathbf{X}}(t)\) can retain all the information of each source signal well. The proposed algorithm has been able to separate three source signals effectively, so the improvement of separation performance is not obvious when the CFI increases continously.
5.4 Computational time complexity analysis
We compare and analyze the computational complexity of the IWP-VMD-SCBSS algorithm and various traditional SCBSS algorithms in this section. The simulation is performed on the platform of MATLAB R2018b with the same computer, which has AMD Ryzen 5 3550H processor and 16 GB memory. The average calculation time required for one execution of various SCBSS algorithms is compared and recorded in Table 1.
Table 1 shows that compared with the WPD-SCBSS algorithm, the IWP-VMD-SCBSS algorithm has a longer computation time and higher complexity. However, the separation performance of the IWP-VMD-SCBSS algorithm is significantly improved regardless of separating two, three or four source signals, which is significantly better than the WPD-SCBSS algorithm. Compared with the VMD-SCBSS algorithm, the computational time of the IWP-VMD-SCBSS algorithm is comparable to that of the VMD-SCBSS algorithm when separating two source signals. The computational time of the IWP-VMD-SCBSS algorithm is shorter than that of the VMD-SCBSS algorithm when separating multiple source signals. The reason is that when separating multiple source signals, the preset number of decomposition modes of the VMD process in the VMD-SCBSS algorithm should be set to the source number \(M\), so its complexity will increase sharply. However, the VMD process's preset number of decomposition modes in the IWP-VMD-SCBSS algorithm is always 2, reducing the computational time complexity to a certain extent. When the source number increases, the complexity of the IWP-VMD-SCBSS algorithm decreases more noticeable compared with the VMD-SCBSS algorithm, and the separation effect of the IWP-VMD-SCBSS algorithm is significantly better than that of the VMD-SCBSS algorithm. Compared with the EEMD-PCA-SCBSS algorithm, no matter how many source signals are separated, the running time of the IWP-VMD-SCBSS algorithm will be significantly less, and the IWP-VMD-SCBSS algorithm has better separation performance. Therefore, from the perspectives of algorithm complexity and separation effect, compared with other existing SCBSS algorithms, the comprehensive performance of the IWP-VMD-SCBSS algorithm is the best. It can effectively separate multiple source signals and has low computational time complexity and the most superior separation performance.
6 Conclusion
In this paper, we proposed the IWP-VMD-SCBSS algorithm with high separation performance. Firstly, the source number is estimated by the interval sampling method combined with the MDL criterion. Secondly, the signal reconstruction method based on WPD is improved and combined with the VMD algorithm to reconstruct multiple virtual signals that can better retain the source signals’ information. Then the single channel observed signal is used as one of the virtual signals, combined with other virtual signals to compose a virtual multi-channel signal. Finally, we use the JADE algorithm to process the virtual multi-channel signal to obtain the estimated source signals. The simulation results show that the IWP-VMD-SCBSS algorithm can effectively solve the SCBSS problem of multiple communication signals, with superior performance and good anti-noise performance. Moreover, the proposed algorithm yields outstanding performance over the existing SCBSS algorithms. It has low computational complexity and is feasible.
-
(1)
An interval sampling method combined with MDL criterion is proposed to realize source number estimation, which can estimate the source number with 100% accuracy in a noisy environment, providing a foundation for the subsequent SCBSS process.
-
(2)
We improve the signal reconstruction method based on wavelet packet decomposition, transforming to use multiple nodes with larger energy to reconstruct the virtual signals, which can better retain the information of the source signals and effectively improve the separation effect.
-
(3)
From the point of view of joint excellence, a new virtual channel expansion method is proposed, which combines the IMWPSR and the VMD algorithm. It can effectively retain the information in the variable frequency domain and the wavelet domain and suppress the noise component simultaneously, effectively improving the performance of SCBSS.
Availability of data and materials
The datasets generated or analyzed and material during this current study are available from the corresponding author on reasonable request.
Code availability
The codes during this current study are available from the corresponding author on reasonable request.
References
Wei, L. L., Liu, Y. S., & Cheng, D. F. (2018). A novel partial discharge ultra-high frequency signal de-noising method based on a single channel blind source separation algorithm. Electronics Newsweekly, 11(3), 509–516.
Pang, L. H., & Deng, X. R. (2016). A SCBSS methodology for time-frequency overlapped signals using non-negative matrix factorization. International Journal of Electronics, 104(4), 624–634.
Wu, C. L., Liu, Z., Wang, X., Jiang, W. L., & Ru, X. H. (2016). Single-channel blind source separation of co-frequency overlapped GMSK signals under constant-modulus constraints. IEEE Communications Letters, 20(3), 486–489.
Zhao, M. C., Yao, X. J., Wang, J., & Dong, S. H. (2021). Single-channel blind source separation of spatial aliasing signal based on Stacked-TCN. Systems Engineering and Electronics, 43(9), 2628–2636.
Al-Tmeme, A., Woo, W. L., Dlay, S. S., & Gao, B. (2018). Single channel informed signal separation using artificial-stereophonic mixtures and exemplar-guided matrix factor deconvolution. International Journal Adaptive Control and Signal Processing, 32(9), 1259–1281.
Sun, L. H., Xie, K. L., Gu, T., Chen, J., & Yang, Z. (2019). Joint dictionary learning using a new optimization method for single-channel blind source separation. Speech Communication, 106, 85–94.
Tengtrairat, N., & Woo, W. L. (2015). Single-channel separation using underdetermined blind autoregressive model and least absolute deviation. Neurocomputing, 147(1), 412–425.
He, P. J., She, T. T., Li, W. H., & Yuan, W. B. (2018). Single channel blind source separation on the instantaneous mixed signal of multiple dynamic sources. Mechanical Systems and Signal Processing, 113, 22–35.
Lian, J. J., Wang, X. Q., Ma, B., & Liu, D. M. (2018). Improvement to the sources selection to identify the low frequency noise induced by flood discharge. Mechanical Systems and Signal Processing, 110, 139–151.
Oliveira, D. R. D., Lima, M. A. A., Silva, L. R. M., Ferreira, D. D., & Duque, C. A. (2021). Second order blind identification algorithm with exact model order estimation for harmonic and interharmonic decomposition with reduced complexity. International Journal of Electrical Power & Energy Systems, 125, 106415.
Jiang, X., Geng, D. Y., & Zhang, Y. Y. (2019). BCG signal de-noising method research based on EMD-ICA. Chinese Journal of Biomedical Engineering, 38(2), 139–148.
Xie, Y., Xie, K., & Xie, S. (2019). Underdetermined blind source separation for heart sound using higher-order statistics and sparse representation. IEEE Access, 7, 87606–87616.
Gao, B., Woo, W. L., & Dlay, S. S. (2011). Single-channel source separation using EMD-subband variable regularized sparse features. IEEE Transactions on Audio, Speech, and Language Processing, 19(4), 961–976.
Pang, L. H., & Tang, B. (2017). Wavelet-FastICA-based separation method for single-channel and time-frequency overlapped signal in electromagnetic surveillance. International Journal of Information and Communication Technology., 11(2), 187–201.
Prasanna Kumar, M. K., & Kumaraswamy, R. (2017). Single-channel speech separation using combined EMD and speech-specific information. International Journal of Speech Technology., 20(4), 1037–1047.
Zhang, Y. N., Qi, S. B., & Zhou, L. (2018). Single channel blind source separation for wind turbine aeroacoustics signals based on variational mode decomposition. IEEE Access, 6(1), 73952–73964.
Dong, S. J., Tang, B. P., & Zhang, Y. (2012). A repeated single channel mechanical signal blind separation method based on morphological filtering and singular value decomposition. Measurement, 45(8), 2052–2063.
Liu, X., Guan, Y. L., Koh, S. N., Liu, Z., & Wang, P. (2018). Low-complexity single-channel blind separation of co-frequency coded signals. IEEE Communications Letters, 22(5), 990–993.
Yang, Y., Zhang, D. L., & Peng, H. (2018). Single-channel blind source separation for paired carrier multiple access signals. IET Signal Processing, 12(1), 37–41.
Zhu, H., Zhang, S., & Zhao, H. (2016). Single-channel source separation of multi-component radar signal with the same generalized period using ICA. Circuits, Systems, and Signal Processing, 35(1), 353–363.
Fu, W. H., Yang, X. N., & Liu, N. A. (2008). Robust algorithm for communication signal blind separation fourth-order-cumulant-based. Journal of Electronics & Information Technology, 30(8), 1853–1856.
Al-Tmeme, A., Woo, W. L., Dlay, S. S., & Gao, B. (2017). Underdetermined convolutive source separation using GEM-MU with variational approximated optimum model order NMF2D. IEEE Transactions on Audio, Speech and Language Processing., 25(1), 31–45.
He, P. J., Qi, M., Liu, G. Y., Yu, Z. J., & Fu, Q. (2019). An adaptive single channel EMD-TNMF blind source separation algorithm for both instantaneous and convolutive mixed signal. Conference Series: Materials Science and Engineering., 658(1), 012003.
Parathai, P., Tengtrairat, N., & Woo, W. L. (2019). Single-channel signal separation using spectral basis correlation with sparse nonnegative tensor factorization. Circuits, Systems, and Signal Processing, 38, 5786–5816.
He, J., Chen, W., & Song, Y. X. (2020). Single channel blind source separation under deep recurrent neural network. Wireless Personal Communications, 115(2), 1277–1289.
Zhou, H. J., Jiao, L. C., Zheng, S. J., Yang, L. F., Shen, W. G., & Yang, X. N. (2020). Generative adversarial network-based electromagnetic signal classification: A semi-supervised learning framework. China Communications, 17(10), 157–169.
Yue, G., Li, X., Chen, S. Y., & Li, X. L. (2021). An automatic ocular artifacts removal approach for multi-channel EEG data based on NMF and EMD. Journal of Neural Engineering, 18(5), 6012–6017.
Liu, X. L., Wang, H., & Huang, Y. M. (2021). A SCBSS signal de-noising method of integrating EEMD and ESMD for dynamic deflection of bridges using GBSAR. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 14, 2845–2856.
Shang, H. K., Lo, K. L., & Li, F. (2017). Partial discharge feature extraction based on ensemble empirical mode decomposition and sample entropy. Entropy, 19(9), 439–456.
Song, H. L., Dong, H. B., Yuan, Z. W., Zhu, J., Zhang, H. Y., & Huang, Y. J. (2019). An EEMD-based electromagnetic induction method for nondestructive testing of buried metal conductors. IEEE Access, 7(1), 142261–142271.
Zhao, L. H., Hong, G., Wang, Z. L., Chen, W. W., & Long, W. (2021). Research on fault vibration signal features of GIS disconnector based on EEMD and kurtosis criterion. IEEJ Transactions on Electrical and Electronic Engineering, 16(5), 677–686.
Dragomiretskiy, K., & Zosso, D. (2014). Variational mode decomposition. IEEE Transactions on Signal Processing, 62(3), 531–544.
Bhattacharjee, A., Fattah, S. A., Zhu, W. P., & Ahmad, M. O. (2018). VMD-RiM: Rician modeling of temporal feature variation extracted from variational mode decomposed EEGs signal for automatic sleep apnea detection. IEEE Access, 6(1), 77440–77453.
Ma, Z. Q., Li, Y. C., Liu, Z., & Guang, C. J. (2016). Rolling bearings’ fault feature extraction based on variational mode decomposition and Teager energy operator. Journal of Vibration and Shock, 35(13), 134–139.
Wang, R., Xu, L., & Liu, F. K. (2020). Bearing fault diagnosis based on improved VMD and DCNN. Journal of Vibro-Engineering, 22(5), 1055–1068.
Zhao, Z. J., & Huang, Y. B. (2017). Single-channel blind-source separation algorithm based on wavelet packet decomposition. Communications Technology, 50(3), 425–429.
Wu, Y., Li, X. K., & Cao, Z. M. (2020). Source number estimation based on a novel multi-view meta-hierarchical classification framework. Measurement Science and Technology., 31(6), 14–29.
Dong, Z., Hu, J. P., Du, B. L., & He, Y. Z. (2017). Improvement of source number estimation method for single channel signal. PLoS ONE, 11(10), e0164654.
Acknowledgements
We gratefully acknowledge the anonymous reviewers who read the drafts and provided many helpful suggestions.
Funding
This work is sponsored by the Natural Science Foundation of Shanghai (19ZR1454000).
Author information
Authors and Affiliations
Contributions
Wensheng Zhao and Weihong Fu wrote the main manuscript text. All authors reviewed the manuscript. The authors have no relevant financial or non-financial interests to disclose.
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Zhao, W., Fu, W. A single-channel blind source separation algorithm based on improved wavelet packet and variational mode decomposition. Telecommun Syst 86, 127–142 (2024). https://doi.org/10.1007/s11235-024-01115-8
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11235-024-01115-8