A New Method for Separating EMI Signal Based on CEEMDAN and ICA

Abstract

Aiming at the problem of electromagnetic interference signal separation, we propose a single-channel blind source separation method based on complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) and independent component analysis (ICA). Firstly, decompose the mixed interference signal by CEEMDAN to obtain a series of intrinsic mode functions (IMF). Secondly, combine them into a new multi-dimensional signal and solve its correlation matrix, and use singular value decomposition to obtain the eigenvalues of the matrix, and then use it to estimate the source number. Thirdly, select those IMFs whose correlation coefficients with the observed signal are bigger and regard them together with the original signal after denoising as new observed signals. Finally, recover the source signals by fast independent component analysis (Fast-ICA). We also extend our method to multi-channel BBS, and experiment results show that our method can eliminate unnecessary noise in the signal and perform well.

1 Introduction

The rapid development of technology has made electronic equipment more and more modern, but the electromagnetic environment caused by it has become more and more complicated. While external electromagnetic interference harms the electronic equipment, the electromagnetic interference (EMI) signal emitted by itself is also harmful to other external devices. Therefore, considerable attention has been paid to overcoming EMI [1, 2]. EMI often results from multiple sources, but only one observed signal is known. In order to obtain useful information from it, it is necessary to find a way to separate the EMI noise from the observed signal. As Li said [3], the EMI noise and the useful signals are usually very different in the frequency range. Therefore, after decomposing the mixed signal into basis functions of different frequencies, the EMI noise can be determined and reduced.

Fourier transform (FT) is a classic signal separation method. It can know the frequency component of the signal and the amplitude and phase of the signal at the corresponding frequency. However, it is impossible to know the moment when a specific frequency component appears and its corresponding change. Therefore, it cannot handle the nonlinear non-stationary signal, which is very common in EMI signals. In order to overcome the limitations of FT and obtain the time–frequency local characteristics of the signal, methods such as short-time Fourier transform (STFT) and wavelet analysis have been proposed. However, these methods also have some weakness. For example, the fundamental uncertainty principle limits the wavelet theory [4].

In order to better analyse the characteristics of nonlinear non-stationary signals, Huang et al. have proposed the empirical mode decomposition (EMD) method [5]. EMD can adaptively decompose the signal into some intrinsic mode functions (IMF) according to the characteristics of the input signal without any prior knowledge. Therefore, it is considered to be a breakthrough in linear and steady-state spectrum analysis based on FT for nearly two hundred years which is widely used in many aspects such as machine fault diagnosis [6], disease detection [7], economic analysis [8] and so on. However, when there is intermittence in the time domain of the high-frequency components, the consequence of the method will occur “mode mixing” [9]. It means that a single IMF contains signals with very different frequency differences, or signals of the same frequency are decomposed into completely different IMFs. In [10], Wu et al. have put forward the ensemble empirical mode decomposition (EEMD) to solve the above problem. They add Gaussian white noise to the signal, taking advantage of the uniform distribution of the white noise spectrum. When the signal is applied to the white noise background distributed over the entire time–frequency space, the signals of different time scales are automatically distributed to the appropriate reference scale. And then it weakens the effect of white noise by averaging, thereby reducing the mode mixing.

However, the IMFs obtained by EEMD contain residual noise, and different realisations of signal plus noise may get a different number of IMFs. Yeh et al. [11] have added positive and negative paired noise to the original signal and proposed a complementary EEMD (CEEMD) method, which significantly alleviated the reconstruction problem. However, the completeness property cannot be proven, and the final averaging is difficult for the number of IMFs obtained each time may change. Torres et al. [12] add adaptive noise at each stage of EMD decomposition, proposing CEEMDAN method, and obtains each IMF by calculating its specific margin. CEEMDAN effectively solves the above two problems, the reconstruction error is almost zero, the decomposition is complete, and the calculation cost is reduced.

In this paper, we discuss a new method for separating EMI signals based on CEEMDAN and ICA. We first decompose the mixed signal by CEEMDAN and then select some of them to recover source signals by ICA, which does well in simulation experiments. The rest of the paper is organised as follows. In Sect. 2, we provide a brief introduction of the EMD, CEEMDAN and ICA method. Section 3 describes the details of our algorithm. Section 4 is devoted to the single-channel blind source separation experiment, and Sect. 5 is about the multi-channel blind source separation and comparative analysis. Section 6 concludes the paper.

The innovations of this paper have the following two aspects. First, we explore a method for estimating the source number using SVD and correlation coefficient. Second, we put forward a single-channel blind source separation (BSS) method combining CEEMDAN and ICA. When there are multiple observations, it can be combined with ICA to achieve BSS of any channel, including underdetermined, positive definite and overdetermined BSS.

2 EMD, CEEMDAN and ICA

2.1 The EMD Method

The EMD method assumes that any signal is composed of several IMFs. Each IMF should satisfy two conditions: the number of extreme points and that of zero-crossing points must be equal or differ at most by one; the local mean of the upper and lower envelopes must be zero.

For a given signal $x$, the main steps of EMD are as follows [4]:

• 1. Find all the maxima of the original signal $x$, and get the upper envelope $e_{ + }$ by cubic spline interpolation. And then find all the minima of the original signal $x$, and get the lower envelope $e_{ - }$ by cubic spline interpolation.

• 2. Calculate the mean of the upper and lower envelopes as the mean envelope of the original signal $m_{1}^{1}$:

$$ \begin{array}{*{20}c} {m_{1}^{1} = \frac{{e_{ + } + e_{ - } }}{2} } \\ \end{array} $$

(1)

Extract the difference between $x$ and $m_{1}^{1}$ as $h_{1}^{1}$:

$$ \begin{array}{*{20}c} {h_{1}^{1} = x - m_{1 }^{1} } \\ \end{array} $$

(2)

If $h_{1}^{1}$ does not satisfy the two conditions, take it as a new signal and repeat the above steps:

$$ \begin{array}{*{20}c} {h_{2}^{1} = h_{1}^{1} - m_{2 }^{1} } \\ \end{array} $$

(3)

$$ \begin{array}{*{20}c} \begin{aligned} h_{3}^{1} = h_{2}^{1} - m_{3 }^{1} \hfill \\ \vdots \hfill \\ \end{aligned} \\ \end{array} $$

(4)

After repeating $k$ times, $h_{k}^{1} \left( t \right)$ satisfies the two conditions, and then the first IMF is obtained as:

$$ \begin{array}{*{20}c} {c_{1} = imf_{1} = h_{k}^{1} } \\ \end{array} $$

(5)

In practice, the mean of the upper and lower envelopes cannot be zero, and the conditions are usually considered to be satisfied when the following formula is satisfied:

$$ \begin{array}{*{20}c} {\frac{{\sum \left[ {h_{k - 1}^{1} \left( t \right) - h_{k}^{1} \left( t \right)} \right]^{2} }}{{\sum \left[ {h_{k - 1}^{1} \left( t \right)} \right]^{2} }} \le \varepsilon ,\quad \varepsilon \in \left[ {0.2, 0.3} \right]} \\ \end{array} $$

(6)

• 3. Extract the difference between $x$ and $c_{1}$ as residual $r_{1}$:

  $$ \begin{array}{*{20}c} {r_{1} = x - c_{1} } \\ \end{array} $$

  (7)

Let $r_{1}$ be a new signal and repeat the above step 1) and step 2) to obtain the other IMFs and the residuals:

$$ \begin{array}{*{20}c} {r_{2} = r_{1} - c_{2} } \\ \end{array} $$

(8)

$$ \begin{aligned} \begin{array}{*{20}l} {r_{3} = r_{2} - c_{3} } \\ \end{array} \hfill \\ \vdots \hfill \\ \end{aligned} $$

(9)

Until $c_{n}$ or $r_{n}$ is less than the default value, or $r_{n}$ is a monotonic function or constant, the EMD method stops, and the original signal can be expressed as:

$$ \begin{array}{*{20}l} {x = \mathop \sum \limits_{i = 1}^{n} c_{i} + r_{n} } \\ \end{array} $$

(10)

The frequencies of the IMFs are arranged from high to low.

2.2 The CEEMDAN Method

The CEEMDAN method is based on EMD. Without loss of generality, let $E_{k} \left( \cdot \right)$ be the operator producing the $kth$ IMF obtained by EMD and let $\omega^{\left( i \right)}$ be a realisation of zero mean unit variance white noise.

For a given signal $x$, the main steps of CEEMDAN are as follows [12]:

• 1. For signal $x^{\left( i \right)} = x + \beta_{0} \omega^{\left( i \right)} ,i = 1,2, \ldots ,I$, decompose it by EMD until getting its first IMF $d_{1}^{\left( i \right)}$. Define the first IMF of CEEMDAN as:

  $$ \begin{array}{*{20}c} {\tilde{d}_{1} = \frac{1}{I}\mathop \sum \limits_{i = 1}^{I} d_{1}^{\left( i \right)} = \bar{d}_{1} } \\ \end{array} $$

  (11)

• 2. Calculate the first residual as:

  $$ \begin{array}{*{20}c} {r_{1} = x - \tilde{d}_{1} } \\ \end{array} $$

  (12)

• 3. For signal $r_{1} + \beta_{1} E_{1} \left( {\omega^{\left( i \right)} } \right),i = 1,2, \ldots ,I$, obtain its first IMF by EMD. Define the second IMF of CEEMDAN as:

  $$ \begin{array}{*{20}c} {\tilde{d}_{2} = \frac{1}{I}\mathop \sum \limits_{i = 1}^{I} E_{1} \left( {r_{1} + \beta_{1} E_{1} \left( {\omega^{\left( i \right)} } \right)} \right) } \\ \end{array} $$

  (13)

• 4. For $k = 2, \ldots ,K$, calculate the kth residual as:

  $$ \begin{array}{*{20}c} {r_{k} = r_{{\left( {k - 1} \right)}} - \tilde{d}_{k} } \\ \end{array} $$

  (14)

• 5. For signal $r_{k} + \beta_{k} E_{k} \left( {\omega^{\left( i \right)} } \right),i = 1,2, \ldots ,I$, obtain its first IMF by EMD. Define the $\left( {k + 1} \right)th$ IMF of CEEMDAN as:

  $$ \begin{array}{*{20}c} {\tilde{d}_{{\left( {k + 1} \right)}} = \frac{1}{I}\mathop \sum \limits_{i = 1}^{I} E_{1} \left( {r_{1} + \beta_{1} E_{1} \left( {\omega^{\left( i \right)} } \right)} \right) } \\ \end{array} $$

  (15)

• 6. For the next $k$ go to step (4).

Repeat step (4) to step (6) until the residual obtained cannot be decomposed by EMD, either because it satisfies the conditions of IMF or the number of its local extrema is less than three. The final residual is:

$$ \begin{array}{*{20}c} {r_{k} = x - \mathop \sum \limits_{k = 1}^{K} \tilde{d}_{k} } \\ \end{array} $$

(16)

with $K$ being the total number of IMF so that signal $x$ can be expressed as:

$$ \begin{array}{*{20}c} {x = \mathop \sum \limits_{k = 1}^{K} \tilde{d}_{k} + r_{k} } \\ \end{array} $$

(17)

The coefficients $\beta_{k} = \varepsilon_{k} std\left( {r_{k} } \right)$ allow the selection of SNR in each iteration with $std\left( \cdot \right)$ being standard deviation operator.

2.3 ICA

Based on a higher-order moment of input signals, ICA is considered as an effective BSS technique [13].

For $n$ statistically independent unknown source signal $s_{1} ,s_{2} , \ldots ,s_{n}$, their linear combination generates $n$ random variables $x_{1} ,x_{2} , \ldots ,x_{n}$:

$$ \begin{array}{*{20}c} {x_{i} = a_{i1} s_{1} + a_{i2} s_{2} + \ldots + a_{in} s_{n} , i = 1,2, \ldots ,n} \\ \end{array} $$

(18)

In the formula (18), $a_{ij} \left( {i,j = 1,2, \ldots ,n} \right)$ is real coefficient. Let $X = \left[ {x_{1} ,x_{2} , \ldots ,x_{n} } \right]^{T}$, $S = \left[ {s_{1} ,s_{2} , \ldots ,s_{n} } \right]^{T}$, $A$ is the matrix of element $a_{ij}$, thus:

$$ \begin{array}{*{20}c} {X = AS} \\ \end{array} $$

(19)

where $A$ is a regular mixing matrix, and $X$ and $S$ are matrices whose rows contain samples of mixed and original signals, respectively. The goal of ICA is to separate the source signal $S$ as much as possible using the observed signal $X$ in the case where both $A$ and $A$ are unknown. It can construct a separation matrix $W$ to solve it, thus $Y = WX$, where $Y$ is an estimate of $S$. The algorithm of ICA can be expressed as:

$$ \begin{array}{*{20}c} {Y = WX = WAS = S} \\ \end{array} $$

(20)

The idea of ICA is to constantly update $W$ so that the estimator is closer to the source signal, and Fast-ICA [14] is widely adopted.

3 A Novel Method for Separating EMI Signal Using CEEMDAN and ICA

Based on CEEMDAN and ICA, we propose a new method for separating the EMI signal, which can reduce the calculation cost and restore source signals with less noise.

3.1 Single-Channel BSS

If there is only one observed signal, we can directly perform single-channel BSS. The main steps are as follows:

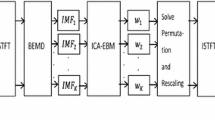
• (1) Discompose the original signal $s\left( t \right)$ using CEEMDAN and obtain several IMFs.

  Like EEMD, the CEEMD method also needs to select appropriate white noise standard deviation $\varepsilon$ and the number of times $N$ that white noise added. When using the EEMD method, if the noise amplitude is constant, the more noise is added, the result of the final decomposition is closer to the true value, but the larger the calculation time overhead [15]. As for the amplitude of the added noise, if the amplitude is too small and the signal-to-noise ratio is too high, the noise will not affect the selection of the pole, and thus loses the role of the supplementary scale. Wu and Huang suggest that $\varepsilon$ does better if it is equal to the standard deviation of the input signal multiplied by a fraction. Moreover, they believe that when $\varepsilon$ is appropriate, the increase of $N$ is not evident for the improvement of the results. During experiments, we find it does well when $\varepsilon$ is 0.01 to 0.5 times the standard deviation of the original signal and $N$ is equal to 100.

• (2) Estimate the source number of the original signal.

  Combine the IMFs into a new multi-dimensional signal $s_{imf} \left( t \right)$.

  $$ \begin{array}{*{20}c} {s_{imf} \left( t \right) = \left( {c_{1} \left( t \right),c_{2} \left( t \right), \ldots ,c_{K} \left( t \right)} \right)^{T} } \\ \end{array} $$

  (21)

  Solve the correlation matrix of $s_{imf} \left( t \right)$:

  $$ \begin{array}{*{20}c} {R_{s} = E\left[ {s_{imf} \left( t \right)s_{imf}^{H} \left( t \right)} \right]} \\ \end{array} $$

  (22)

  Use SVD to obtain the eigenvalues $\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{m}$ of the matrix $R_{s}$, and exclude the elements whose values are 0 and calculate the ratios of adjacent eigenvalues:

  $$ \begin{array}{*{20}c} {\Delta = Max\left( {\frac{{\lambda_{1} }}{{\lambda_{2} }},\frac{{\lambda_{2} }}{{\lambda_{3} }}, \ldots ,\frac{{\lambda_{m - 1} }}{{\lambda_{m} }}} \right) } \\ \end{array} $$

  (23)

  Calculate the correlation coefficients between the IMFs and $s\left( t \right)$, and set the number of IMFs corresponding to a strong correlation (beyond 0.5) as $X$, then let $M = X + 1$. Take Fig. 1 as an example, firstly find local maxima points whose abscissa are $i = 3$ and $i = 5$. If $M$ is the abscissa of a local maximum point, which means $M = 3,5$, we can estimate the source number $x$ is equal to $M$. Otherwise we can find which local maxima point abscissa is closest to $M$. Then we can assume that $x$ is equal to the abscissa of that point. For example, when $M = 2$, it can be assumed that $x = 3$.

  Fig. 1

  

  Ratio curve of adjacent eigenvalues

• (3) Denoise the original signal.

  As the IMFs of high-frequency are mostly high-frequency noise, we can observe the time-domain diagram of IMFs. And then select the first few IMFs whose correlation coefficient with the original signal is less than 0.2, subtracting these components from the original signal and getting the denoised signal $s^{\prime}\left( t \right)$.

• (4) Reconstruct new observed signals.

  Select $\left( {x - 1} \right)$ IMFs with more significant correlation coefficients and $s^{\prime}\left( t \right)$ to form a new multi-dimensional matrix, whose dimension is equal to the estimated source number $x$.

  The denoised signal and some IMFs are selected to reconstruct the multi-dimensional matrix, instead of only selecting the IMFs. It can not only eliminate the interference of the pseudo component and residual component due to the decomposition but also remain the information carried by the original signal as much as possible [16].

• (5) Use the reconstructed matrix as the input signal to apply the Fast-ICA algorithm, and each independent component is obtained.

  Solve the correlation coefficient between each independent component $ICA_{i} \left( t \right)$ and $s\left( t \right)$, and an independent component corresponding to a correlation coefficient greater than 0.4 can be selected as a source signal. The more effective way is as follows. Firstly, sort the independent components according to the absolute value of the correlation coefficient from large to small. Secondly, superimpose the components one by one and figure out the correlation coefficient between the mixed signal and $s\left( t \right)$ every time, observing the change of coefficient and filtering out the appropriate number of independent components as source signals. The algorithm flow chart is shown in Fig. 2.

  Fig. 2

  

  Our single-channel blind source separation

It should be noted that when using CEEMDAN method, it needs to determine $\varepsilon$ and $N$ through experiments. Moreover, even the same $\varepsilon$ and $N$ are used, the obtained eigenvalues have absolute randomness. What’s more, it is necessary to add or subtract the component according to its positive or negative correlation coefficient when superimposing it.

3.2 Multi-Channel BSS

If there are multiple observed signals $s^{1} \left( t \right),s^{2} \left( t \right), \ldots , s^{N} \left( t \right)$, it can achieve multi-channel BSS using the method above. The main steps are as follows:

• (1) Decompose each of the original signals by the method above, and obtain a series of source signals $s_{1} \left( t \right),s_{2} \left( t \right), \ldots ,s_{M} \left( t \right)$, with $M$ being the total number of source signals.

• (2) Cluster the source signals based on their correlation coefficients.

  • i. Assume that all source signals are self-contained and get sets $C_{1}^{1} ,C_{2}^{1} ,..,C_{{M_{1} }}^{1}$.

  • ii. Solve the correlation coefficient of any one signal of $C_{1}^{1}$ (only $s_{1} \left( t \right)$ now) and any one signal of $C_{2}^{1} ,C_{3}^{1} ,..,C_{{M_{1} }}^{1}$, and classify $C_{i}^{1}$ and $C_{1}^{1}$ into one set if the correlation coefficient between them is greater than 0.9, thus getting new sets $C_{1}^{2} ,C_{2}^{2} ,..,C_{{M_{2} }}^{2}$.

  • iii. Solve the correlation coefficient of any one signal of $C_{2}^{2}$ and any one signal of $C_{3}^{2} ,C_{4}^{2} ,..,C_{{M_{2} }}^{2}$, and classify $C_{i}^{2}$ and $C_{i}^{2}$ into one set if the correlation coefficient between them is greater than 0.9.

  • iv. Repeat steps similar to the above and finally get sets $C_{1}^{T} ,C_{2}^{T} ,..,C_{{M_{T} }}^{T}$.

• (3) For each set $C_{i}^{T}$, reconstruct the signals in it into a multi-dimensional matrix and use it as an input signal to apply the Fast-ICA algorithm. Then choose any one signal of $C_{i}^{T}$ and solve the correlation coefficient between the signal and each independent component. Finally, sort all the correlation coefficients and select the component corresponding to the biggest correlation coefficient as a source signal. The algorithm flow chart is shown in Fig. 3.

  Fig. 3

  

  Our multi-channel blind source separation

4 Single-Channel BSS Experiment

4.1 Simulation Experiment Data

Simulation signal is as follows:

$$ \begin{array}{*{20}c} {s\left( t \right) = s_{1} \left( t \right) + s_{2} \left( t \right) + s_{3} \left( t \right) } \\ \end{array} $$

(24)

where $s_{1} \left( t \right)$ is a sine signal, $s_{2} \left( t \right)$ is a sawtooth signal and $s_{3} \left( t \right)$ is intermittent noise. The time-domain waveform diagrams of each signal and mixed simulation signal are shown in Fig. 4.

Fig. 4

Source signals and mixed simulation signal

4.2 Method Performance Criteria

Since the waveform of the separated signal has changed, we use correlation coefficient $\rho$ and vestigial quadratic mismatch (VQM) to measure the performance of the method.

Correlation coefficient is calculated as follows [17]:

$$ \begin{array}{*{20}c} {\rho = \frac{{cov\left( {s,s^{\prime}} \right)}}{{cov\left( {s,s} \right)*cov\left( {s^{\prime},s^{\prime}} \right)}} } \\ \end{array} $$

(25)

$s$ and $s^{\prime}$ are source signal and separated signal. The closer the absolute value of the correlation coefficient is to 1, the closer the separation signal is to the source signal, and the better the separation is.VQM is calculated as follows [18]:

$$ \begin{array}{*{20}c} \begin{aligned} VQM & = 10\lg \frac{{E\left[ {\left| {s^{\prime}\left( t \right) - rs\left( t \right)} \right|^{2} } \right]}}{{E\left[ {\left| {rs\left( t \right)} \right|^{2} } \right]}} \\ r & = \frac{{E\left[ {\left| {s^{\prime}\left( t \right)s\left( t \right)} \right|} \right]}}{{E\left[ {\left| {s\left( t \right)} \right|^{2} } \right]}} \\ \end{aligned} \\ \end{array} $$

(26)

The smaller the value of VQM, the better the separation is. Usually, when the value is less than -23 dB, the separation is considered to be excellent [19].

4.3 Results and Analyses

Decompose signal $s\left( t \right)$ by EMD, EEMD and CEEMDAN. The results are exhibited in Fig. 5.

Fig. 5

Decomposition results of mixed simulation signal by different methods. a EMD, b EEMD, c CEEMDAN

It shows that the results of EMD occur mode mixing, producing some pseudo components, while the EEMD and CEEMDAN overcome mode mixing effectively.

Use the method mentioned in Sect. 3 to estimate the source number. Figure 6 shows the ratios of adjacent eigenvalues.

Fig. 6

Ratios curve of adjacent eigenvalues

From Fig. 6, we can find local maxima points whose abscissa are $i = 3$, $i = 5$ and $i = 7$. Then calculate the correlation coefficients between the IMFs and $s\left( t \right)$, which are 0.04389,0.16006,0.18198,0.21212,0.22849,0.40522,0.49507,0.74823,0.69006,0.04532,0.05580 and 0.03713. The number of IMFs corresponding to a correlation greater than 0.5 is 2. Thus we can estimate the source number is 3.

Select the eighth IMF, the ninth IMF and $s\left( t \right)$ to form a new multi-dimensional signal. Use the signal as input to apply Fast-ICA algorithm and remove the less relevant component. Figure 7 shows two separated signals.

Fig. 7

Separated signals obtained by our method

4.4 Real Signal Experiment

We choose the EEG dataset from Bonn University, Germany [20]. The dataset has five subsets, each of whom contains 100 segments of EEG signals, and the number of sampling points is 4097. We select the first 1000 sampling points of a random EEG signal. The time-domain waveform diagram of it is shown in Fig. 8.

Fig. 8

EEG signal

Decompose the signal by the method we proposed, and the result is showed in Fig. 9. It can be seen that the two separated signals are more regular than the origin EEG signal, and the correlation coefficients between the two separated signals and the original signal are -0.83266 and -0.53014, both of whom are greater than 0.5, which means strong correlation. Combine the signals into a new signal, and the correlation coefficient between it and the original signal is 0.96365, which is very close to 1, indicating that the separation is excellent. Figure 10 shows the reconstructed signal (red) and the original signal (blue), whose waveforms are very similar.

Fig. 9

Separated signals obtained by our method

Fig. 10

Comparison of the reconstructed signal and the original signal

5 Multi-Channel BSS Experiment

5.1 Simulation Experiment Data

We use two sine signals of different frequencies and one sawtooth signal and mix any two of them with different intermittent noise, thus getting three observed signals. The source signals and observed signals are shown in Fig. 11a, b.

Fig. 11

Different signals. a Source signals, b Observed signals

5.2 Method Performance Criteria

We use the same performance criteria as we mention in the single-channel BSS experiment.

5.3 Results and Analyses

Decompose the mixed signals by Fast-ICA directly and our method. Figure 12a, b show the results. Comparing the results, we can see that our method removes the extra intermittent noise and obtains better separation signals. In order to quantitatively measure the effect of the method, we use different methods to decompose the same signals, such as EFICA [21], WASOBI [22] and FCOMBI [23]. Comparison tables are shown in Table 1, Tables 2 and 3.

Fig. 12

Separated signals obtained by different methods. a Fast-ICA, b our method

Table 1 Comparison of separation results about $s_{1} \left( t \right)$

Table 2 Comparison of separation results about $s_{2} \left( t \right)$

Table 3 Comparison of separation results about $s_{3} \left( t \right)$

For sine signal $s_{1} \left( t \right)$, the correlation coefficient of our method is larger than that of other methods, and the VQM of our method is smaller than that of other methods, which means the separation is excellent.

We can also see that for sine signal $s_{2} \left( t \right)$, the correlation coefficient of our method is larger than that of other methods, and the VQM of our method is smaller than that of other methods, which means the signal is accurately separated.

Table 3 shows that for sawtooth signal $s_{3} \left( t \right)$. The correlation coefficient of our method is larger than 0.9, close to 1, and the VQM of our method is less than − 20 dB. Compared to other methods, our method seems to not handle the sawtooth signal well.

To sum up, we can know that for sine signals $s_{1} \left( t \right)$ and $s_{2} \left( t \right)$, our method does better than other methods but do worse for sawtooth signal $s_{3} \left( t \right)$. Observing the result images, we can find that our method entirely eliminates intermittent noise and the separated sawtooth signal deviates from the local maximum and minimum points. Although our method is generally effective from the evaluation criteria for the sawtooth signal, the results of other methods remain most of the noise, destroying the characteristics of the source signals. It can be inferred that the algorithm causes the error of the signal at the extreme points when eliminating the noise leads to the unsatisfactory calculation of the correlation coefficient and the VQM.

6 Conclusions

The consequences of traditional EMD method may occur mode mixing, and the decomposition of EEMD method includes residual noise. In this paper, we propose a new method for separating the EMI signal based on CEEMDAN and ICA. The single-channel and multi-channel simulation experiments show that our method overcomes the “mode mixing” phenomenon and reduces residual auxiliary noise. And not only do the separated signals eliminate the noise, but also they perform well in evaluation criteria. Besides, the components separated from the EEG signal by our method are more regular. It is believed that the method can achieve excellent results in the separation of the EMI signal.