Single-Channel Blind Source Separation using Adaptive Mode Separation-Based Wavelet Transform and Density-Based Clustering with Sparse Reconstruction

Abstract

In this paper, the problem of single-channel blind source separation (SCBSS) is addressed using a novel approach that combines the adaptive mode separation-based wavelet transform (AMSWT) and the density-based clustering with sparse reconstruction. The proposed method is performed in the time–frequency domain and in a reverberant environment. First, using the Fourier transform, the amplitude spectrum of the observed mixture signal is obtained. Then, using variational scaling and wavelet functions, the AMSWT is used to adaptively extract spectral intrinsic components (SICs). To obtain a better time–frequency resolution, the AMSWT is applied to each mode. Thus, the SCBSS problem is transformed into a non-underdetermined. Then, for each frequency bin, the density-based clustering, reformulated to the eigenvector clustering problem, is performed to estimate the mixing matrix. Finally, sparse reconstruction is used to reconstruct the sources. The proposed method is evaluated using objective measures of separation quality. A computational complexity evaluation based on time consumption is also performed. Simulation results show that the proposed method is very effective for solving the SCBSS problem and provides better separation performances than the reference methods. However, the proposed method is computationally expensive.

1 Introduction

Blind source separation (BSS) aims to separate the source signals from the mixed signals without any information. The BSS has been applied in many areas such as medical imaging and engineering [2, 44], astrophysics [40], image processing [11], geophysical data processing [35], speech processing [21,22,23, 32], detection and radar localization [28], communication systems [43], automatic transcription of speech [13], musical instrument identification [34], mechanical flaw detection [18], multichannel telecommunications [38], multispectral astronomical imaging [33] and speech recognition [4].

In the literature, the BSS methods are classified as being linear and nonlinear, instantaneous and convolutive, and overcomplete and underdetermined. The convolutive mixture model of BSS is an effective way to represent the speech signal mixing mechanism in a reverberant environment [7, 30]. The BSS problem can be formulated either in the time domain or in the frequency domain. The BSS can be also treated in the joint time–frequency (TF) domain where computationally efficient BSS algorithms are available.

In most situations and for many practical uses, only one-channel recording of mixture signals is available. This particular instance of the underdetermined source separation problem called single-channel source separation (SCSS) has been the subject of many studies. To address the single-channel audio source separation problem, numerous strategies have been proposed in the literature [12]. In [14], the authors attempted to combine the maximum-likelihood estimation and nonnegative matrix factorization (NMF) based on the Itakura–Saito divergence measurement. The short-time Fourier transform (STFT) representation of the observed single-channel signal has been subjected to the NMF-based approach in [39]. The method requires the use of extra training data. A combination of the empirical mode decomposition (EMD) and independent component analysis (ICA), as well as wavelet transformations, has been suggested in [31]. However, the wavelet transform needs some specified basis functions to represent a signal, and there is no rigorous mathematical theory underpinning the EMD or its improved algorithms [20]. The bark scale aligned wavelet packet decomposition has been introduced in [26] where the separation step has been performed using the Gaussian mixture model (GMM), which was employed before the Fourier transform. In [45], the authors proposed the variational mode decomposition (VMD) method to solve the SCBSS problem. The separation process is performed using joint approximate diagonalization based on the fourth-order cumulant matrices. In [36], the authors presented a novel method for SCBSS in a noisy environment. The method is based on selecting the TF units of signal presence and computing the mixture spectral amplitude. The separation process is performed using TF masking. In [25], an adaptive signal separation has been proposed. The method uses a time-varying parameter that adapts locally to instantaneous frequencies and a linear chirp (linear frequency modulation) to model the signal components. The single-channel technique has been explored for muscle artifact removal from multichannel EEG [6].

The classic TF representation is computed using the STFT. The STFT does not reflect the time-varying information. Moreover, it yields a time–frequency representation with only uniform time and frequency resolution. A new adaptive mode separation-based wavelet transform (AMSWT) has been proposed in [24] based on [10, 16]. The AMSWT method involves solving a recursive optimization problem to adaptively extract spectral intrinsic components (SICs). The limited support of each spectral mode is implemented to establish the spectral boundaries for wavelet bank configuration. Then, the spectral boundaries of the created wavelet bank configuration are used to highlight the spectral information. The AMSWT strategy is fully adaptive in the sense that one does not require prior knowledge.

In [41], a new method to solve the underdetermined BSS problem for convolutive mixture has been proposed. The method operates in the time–frequency domain, and it combines the density-based grouping and sparse source reconstruction. The density-based clustering is introduced to estimate the mixing matrix, which is converted to an eigenvector clustering issue. The rank-one structure of the local covariance matrices of the mixture TF vectors is first used to extract the eigenvectors. By combining weight clustering and density-based clustering, the eigenvectors are subsequently grouped and tweaked to provide an approximated mixing matrix. The source reconstruction is transformed into a $l_{p}$-norm minimization using an iterative Lagrange multiplier method. The Lagrange multiplier used to solve optimization problems under constraints aims to enforce the constraint, while the quadratic penalty improves the convergence. In the iterative formula, both the primal and dual variables are updated iteratively.

In this paper, a new method to solve the SCBSS problem is proposed. The method combines the AMSWT [24] and density-based clustering with the sparse reconstruction method introduced in [41]. The method is performed in three stages: (i) The amplitude spectrum of the observed mixture signal is obtained using STFT. The convolution in the time domain can be approximated by a multiplication in the STFT domain. (ii) A better TF resolution is obtained using the variational scaling and wavelet functions, which are applied to the spectral intrinsic components (SICs) extracted adaptively using the AMSWT. By creating virtual multichannel signals of the TF representation, the underdetermined single-channel problem is transformed to a non-underdetermined problem. (iii) For each TF representation and each frequency bin, the density-based clustering, which is converted to an eigenvector clustering problem, and the sparse reconstruction, which is converted to a minimization problem, are, respectively, performed to estimate the mixing matrix and sources.

The BSSeval toolbox [15] is used to evaluate the proposed method’s performance. The evaluation is performed in terms of many criteria such as source-to-distortion ratio (SDR), source-to-artifact ratio (SAR) and source-to-interference ratio (SIR). The proposed method is compared to the variational mode decomposition (VMD) method [45], adaptive spectrum amplitude estimator and masking method [36] and the nonnegative tensor factorization of modulation spectrograms method [3].

The following sections make up the remaining content. The SCBSS problem formulation is presented in Sect. 2. The AMSWT method, the density-based clustering method and the source reconstruction are the main focus of Sect. 3. Simulation results are presented in Sect. 4. Finally, conclusions and discussions are given in Sect. 5.

2 Convolutive Mixture Model

Let $\mathbf{x}\left(t\right)={[{x}_{1}\left(t\right),.., {x}_{M}(t)]}^{T}$ be a vector of M observed sources obtained via the mixing of N independent sources $\mathbf{s}\left(t\right)={[{s}_{1}\left(t\right),.., {s}_{N}(t)]}^{T}$. The BSS problem aims to estimate the $N$ sources from the $M$ mixtures. The convolutive mixture occurs through the propagation of the sound through space and multiple paths caused by reflections from different objects, especially in rooms and closed environments. The convolutive mixture is modeled as follows:

$${x}_{j}\left(t\right)=\sum_{i=1}^{N}\sum_{k=0}^{K-1}{h}_{ji}(k){s}_{i}(t-k), j=1, \dots , M$$

(1)

The matrix form is given as:

$${\varvec{x}}\left(t\right)={\varvec{H}}*{\varvec{s}}\left(t\right)=\sum_{k=0}^{K-1}{{\varvec{H}}}_{k}{\varvec{s}}(t-k)$$

(2)

where ${h}_{ji}$ denotes the impulse response from source $i$ to sensor $j$, and ${\varvec{H}}$ is an $M\mathrm{x}N$ matrix that contains the kth filter coefficients.

In most cases and for many practical purposes, only one-channel recording is accessible. Numerous studies have examined this instance known as single-channel source separation. In this case, M $=1$. The convolutive SCBSS in the time–frequency domain is described as follows:

$${\varvec{X}}\left(t,f\right)=\sum_{i=1}^{N}{X}_{i}(t,f)$$

(3)

where X_i(t, f) is the STFT of x_i(t).

The conventional source separation techniques are ineffective in this scenario. The issue in SCBSS might be viewed as a single observation combined with numerous unidentified sources.

3 Single-Channel Blind Source Separation Method

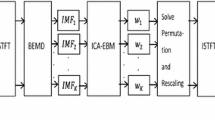
The different steps of the proposed method for single-channel blind source separation are summarized by the flowchart shown in Fig. 1.

Fig. 1

Proposed method for single-channel blind source separation.

The spectrum of the observed signal is obtained by the STFT. The convolution in the time domain is transformed into a multiplication in the STFT domain. The AMSWT approach is used to obtain an optimal spectral mode separation. Thus, the SCBSS problem is transformed into a non-underdetermined problem by establishing virtual multichannel signals of the TF representation of the observed signals. Then, the $M$ time–frequency representations of the mixture are divided into $Q$ nonoverlapping blocks.

As a preprocessing step at the mixing matrix estimation stage, the TF representation of the observed signal is whitened for each frequency bin ${\mathbf{x}}_{d}$. The whitening process is performed using the eigenvector matrix ${\mathbf{U}}_{\mathbf{x}}$ and the eigenvalue matrix ${{\varvec{\Sigma}}}_{\mathbf{x}}$ of $E({\mathbf{x}}_{d}{{\mathbf{x}}_{d}}^{H})$, and it is expressed by ${{\mathbf{x}}_{d}}^{w}={{\varvec{\Sigma}}}_{\mathbf{x}}^{-1/2}{\mathbf{U}}_{\mathbf{x}}^{H}{\mathbf{x}}_{d}$.

The estimation of the mixing matrix is reformulated into an eigenvector clustering issue. The ambiguity of scaling is solved by rescaling the estimated mixing matrix by restricting the first row. The order of the reconstructed sources is aligned, by grouping the nearby source TF vectors based on their correlation, in terms of power ratio, to resolve the permutation ambiguity [10].

The post-processing stage involves de-whitening the predicted mixing matrix by $\widehat{\mathbf{H}}={{\mathbf{U}}_{\mathrm{x}}{\varvec{\Sigma}}}_{\mathbf{x}}^{1/2}\widetilde{\mathbf{H}}$. Then, the source reconstruction is reformulated into a sparse minimization problem, whose solution was achieved using an initialization-corrected iterative Lagrange multiplier approach.

Finally, the estimated sources are obtained in the TF domain, which are transformed into the time domain using the modified method proposed in [27].

3.1 Adaptive Mode Separation-Based Wavelet Transform

The STFT is a TF representation, which has an even bandwidth distribution across all frequency channels and suffers from the TF resolution limitation due to the fixed window size. The speech signal is substantially nonperiodic and nonstationary. Therefore, the use of the STFT will result in mistakes, particularly when complex transitory phenomena like voice mixing occur in the signal.

The AMSWT performs a time–frequency analysis using variational scaling and wavelet functions. The method is built on the alternating direction method of multiplier (ADMM) solver [19], which then defines a bank of variational scaling functions and wavelets depending on the spectral boundaries that have been defined. As a result, the approximation coefficients are obtained as the inner product of the analyzed signal $x$ with variational scaling function. The inner product of the analyzed signal $x$ with variational wavelets yields the detail coefficients, which are expressed as:

$${W}_{x}\left(t,0\right)=\langle x,{\varnothing }_{1}\rangle =\int x\left(\tau \right){\overline{\varnothing } }_{1}\left(\tau -t\right)d\tau $$

(4)

and

$${W}_{x}\left(t,k\right)=\langle x,{\psi }_{k}\rangle =\int x\left(\tau \right){\overline{\psi }}_{k}\left(\tau -t\right)d\tau $$

(5)

where $x$ is the input signal.

In [24], under the amplitude-modulated and frequency-modulated (AM-FM) assumption, the intrinsic modes $u(t)$ have distinguishable features in the frequency domain. Using the ADMM solver, the spectral modes can be adaptively obtained similarly to the intrinsic mode functions (IMFs) extraction, to estimate compact modes:

$$\underset{{u}_{k},{\omega }_{k}}{\mathrm{min}}\begin{array}{c}\left\{\sum_{k}{\Vert {\partial }_{t}\left[\left(\delta \left(t\right)+\frac{j}{\pi t}\right)*{u}_{k}\left(t\right)\right]{e}^{j{\omega }_{k}t}\Vert }_{2}^{2}\right\}\\ s.t. \sum_{K}{u}_{k}=x(t)\end{array}$$

(6)

where $x\left(t\right)$ is the signal to be decomposed under the constraint that over all modes’ summation should be equal to the input signal, $\delta \left(.\right)$ is the Dirac impulse and $\left(\delta \left(t\right)+\frac{j}{\pi t}\right)*{u}_{k}(t)$ denotes the original data and its Hilbert transform. The variables ${u}_{k}$, ${\omega }_{k}$ and $k$ denote the modes, their central frequencies and the mode number, respectively.

The spectral segmentation boundary number can be determined empirically as follows:

$$\widetilde{K}=min\left\{n\in {\mathbb{Z}}^{+}|n\ge 2\rho \mathrm{ln}N\right\}$$

(7)

where $N$ is the signal length and $\rho$ is the scaling exponent determined by the detrended fluctuation analysis (DFA).

According to [24], (6) is solved using a quadratic penalty term; the parameter $\lambda$ denotes the Lagrangian multiplier used to render the problem unconstrained

$$ L\left( {u_{k} ,\omega _{k} ,\lambda } \right) = \eta \sum\limits_{k} {\left\| {\delta _{t} \left[ {\left( {\delta \left( t \right) + \frac{j}{{\pi t}}} \right)*u_{k} (t)} \right]e^{{j\omega _{k} t}} } \right\|_{2}^{2} } + \langle \lambda ,x - \sum\limits_{K} {u_{k} } \rangle + \left\| {x - \sum\limits_{K} {u_{k} } } \right\|_{2}^{2} $$

(8)

Therefore, ${u}_{k}$ is determined recursively as

$${\widehat{u}}_{k}^{n+1}\left(\omega \right)=\frac{X\left(\omega \right)-\sum_{i\ne j}{\widehat{u}}_{i}^{n+1}\left(\omega \right)+\frac{{\widehat{ \lambda }}^{n}}{2}}{1+2\eta {(\omega -{\omega }_{k}^{n})}^{2}}$$

(9)

where $X\left(\omega \right)$, $\widehat{{u}_{i}}\left(\omega \right)$ and $\widehat{\lambda } (\omega )$ denote, respectively, the Fourier transforms of the input signal $x(t)$, the mode function ${u}_{i}(t)$ and $\lambda (t)$. $\eta$ denotes the balancing parameter of the data-fidelity constraint. The center frequencies ${\omega }_{k}^{n+1}$ are updated as the center of gravity of the corresponding mode’s power spectrum using the following equation

$${\omega }_{k}^{n+1}=\frac{{\int }_{0}^{\infty }\omega {\left|{\widehat{u}}_{k}^{n+1}\left(\omega \right)\right|}^{2}d\omega }{{\int }_{0}^{\infty }{\left|{\widehat{u}}_{k}^{n+1}\left(\omega \right)\right|}^{2}d\omega }$$

(10)

As a result, rather than using a predefined wavelet bank, we create adaptive wavelet banks based on spectral modes and their corresponding center frequencies, which represent the intrinsic components.

Authors in [24] used the mode bandwidth and central frequencies to define the boundaries between each mode; however, in the literature, some authors just used the average of the two central frequencies as spectral boundary, which ignores the spectrum distribution.

Consider the $kth$ mode with an average frequency ${\omega }_{k}$ and a spectral bandwidth ${\beta }_{k}$. Then, the boundary ${{\varvec{\Omega}}}_{k}$ between the $kth$ mode and the $\left(k+1\right)th$ mode is given by

$${{\varvec{\Omega}}}_{k}=\frac{{\omega }_{k}+\frac{{\beta }_{k}}{2}+{\omega }_{k+1}-\frac{{\beta }_{k+1}}{2}}{2}$$

(11)

where ${{\varvec{\Omega}}}_{0}=0$ and ${{\varvec{\Omega}}}_{k}=\pi$.

The authors apply the same principle used in the production of both Littlewood–Paley and Meyer’s wavelets [9] for variational scaling functions and wavelets based on spectral boundaries. ${\widehat{\varnothing }}_{k}$ and ${\widehat{\psi }}_{k}$ are, respectively, defined by the following equation, with $\gamma$ is the parameter that ensures no overlap between the two consecutive transitions.

$${\widehat{\varnothing }}_{k}=\left\{\begin{array}{l}1, \omega \le (1-\gamma ){{\varvec{\Omega}}}_{k}\\ \mathrm{cos}\left(\frac{\pi }{2}\alpha \left(\gamma ,{{\varvec{\Omega}}}_{k}\right)\right), \left(1-\gamma \right){{\varvec{\Omega}}}_{k}\le \omega \le (1+\gamma ){{\varvec{\Omega}}}_{k}\\ 0\,\, otherwise\end{array}\right.$$

(12)

and

$${\widehat{\psi }}_{k}=\left\{\begin{array}{l}1, \left(1+\gamma \right){{\varvec{\Omega}}}_{k}\le \omega \le (1-\gamma ){{\varvec{\Omega}}}_{k+1}\\ \mathrm{cos}\left(\frac{\pi }{2}\alpha \left(\gamma ,{{\varvec{\Omega}}}_{k+1}\right)\right), \left(1-\lambda \right){{\varvec{\Omega}}}_{k+1}\le \omega \le (1+\lambda ){{\varvec{\Omega}}}_{k+1}\\ \mathrm{sin}\left(\frac{\pi }{2}\alpha \left(\gamma ,{{\varvec{\Omega}}}_{k}\right)\right), \left(1-\lambda \right){{\varvec{\Omega}}}_{k}\le \omega \le (1+\lambda ){{\varvec{\Omega}}}_{k} \\ 0\,\, otherwise\end{array}\right.$$

(13)

where $\alpha \left(\gamma ,{{\varvec{\Omega}}}_{k}\right)=\beta \{\left(\frac{1}{2\gamma {{\varvec{\Omega}}}_{k}}\right)\left[\left|\omega \right|-\left(1-\gamma \right){{\varvec{\Omega}}}_{k}\right]\}]$ and $\beta (\nu )$ is an arbitrary function defined as follows:

$$\beta \left(\nu \right)=\left\{\begin{array}{l}0, \nu \le 0\\ 1, \nu >1\\ \beta \left(\nu \right)+\beta \left(1-\nu \right)=1, 0<\nu <1\end{array}\right.$$

(14)

The adaptive mode separation-based wavelet transform algorithm is summarized as follows:

• Step 1: Time–frequency representation

• Input: Observed mixture.

  • Using the Fourier transform, obtain the amplitude spectrum signal.

  • Obtain the appropriate spectrum spectral modes (segments). Execute the first inner loop and the second inner loop to update ${u}_{k}$ according to (9), and update ${\omega }_{k}$ according to (10), respectively

  • Compute the proper spectral boundaries using (11). Then, using (12) and (13), the bank of variational scaling functions and wavelets based on the spectral boundaries is defined.

  • Finally, using (4) and (5), respectively, apply variational scaling and wavelet functions to each mode to obtain the time–frequency distribution.

• Output: time–frequency distribution of the observed mixture.

3.2 Density-Based Clustering

In [41], the authors introduced the eigenvector clustering as an alternative to estimate the mixing matrix. The eigenvector clustering is based on two factors, which are the local density ${\rho }_{q}$ and the minimum distance ${\delta }_{q}$ that may be taken between the point q and any additional points with a higher density. They are given, respectively, by

$${\rho }_{q}\triangleq \sum_{k\ne q}{e}^{-\frac{{\upsilon }_{qk}^{2}}{{\tau }_{c}^{2}}}$$

(15)

and

$${\delta }_{q}=\underset{k:{\rho }_{k}>{\rho }_{q}}{\mathrm{min}}({\upsilon }_{qk})$$

(16)

where the region for each data point is defined by a cut-off distance ${\tau }_{c}$, and ${\upsilon }_{qk}$ are the elements of the similarity matrix:

$${\varvec{V}}\triangleq \left[\begin{array}{ccc}{\upsilon }_{11}& \cdots & {\upsilon }_{1Q}\\ \vdots & \ddots & \vdots \\ {\upsilon }_{Q1}& \cdots & {\upsilon }_{QQ}\end{array}\right]$$

(17)

From the eigenvectors ${\varvec{A}}$ whose elements are ${{\varvec{a}}}_{q}$, the similarity matrix ${\varvec{V}}$ is generated as follows:${\upsilon }_{qk}={\Vert {{\varvec{a}}}_{q}-({{\varvec{a}}}_{q}^{H}{{\varvec{a}}}_{k})\Vert }_{F}^{2}$ , where ${\Vert .\Vert }_{F}$ denotes Frobenius norm [29] expressed as follows:

$$ \left\| {a_{q} - (a_{q}^{H} a_{k} )} \right\|_{F}^{2} = \sum\limits_{{q = 1}}^{Q} {\sum\limits_{{k = 1}}^{Q} {\left| {a_{q} - (a_{q}^{H} a_{k} )} \right|^{2} } } = {\text{trace}}\left( {\left( {a_{q} - \left( {a_{q}^{H} a_{k} } \right)} \right)\left( {a_{q} - (a_{q}^{H} a_{k} )} \right)^{H} } \right) $$

(18)

where ${(.)}^{H}$ denotes the conjugate transpose.

The eigenvector extraction is based on the local covariance matrix ${{\varvec{R}}}_{q}^{\mathrm{\rm X}}=\sum_{i=1}^{N}{\sigma }_{i,q}^{2}{h}_{i}{h}_{i}^{H}$ where ${h}_{i}$ is called the steering vector representing each direction of the mixing matrix. According to [41], there is at least one subblock indexed as ${q}_{i}$ for which the associated local covariance ${{\varvec{R}}}_{{q}_{i}}^{\mathrm{\rm X}}$ has roughly a rank-one structure. This condition is exploited in [16] where the authors applied the eigenvalue decomposition (EVD) to the local covariance matrix ${{\varvec{R}}}_{q}^{\mathrm{\rm X}}$, which results in the following equation:

$${{\varvec{R}}}_{q}^{\mathrm{\rm X}}={{\varvec{U}}}_{q}{{\varvec{\Sigma}}}_{q}{{\varvec{U}}}_{q}^{H}$$

(19)

where ${{\varvec{U}}}_{q}$ and ${{\varvec{\Sigma}}}_{q}$ denote the eigenvector matrix and eigenvalue matrix, respectively.

The extracted vector denoted ${\mathbf{a}}_{q}$ corresponds to the largest eigenvalue of ${{\varvec{\Sigma}}}_{q}$ and also represents the first eigenvector in ${{\varvec{U}}}_{q}$. To obtain the eigenvector matrix $\mathbf{A}\triangleq [{\mathbf{a}}_{1},\dots ,{\mathbf{a}}_{Q}]$, the eigenvector extraction is done subblock wisely.

According to [41], the global maximum in the density indexed as ${q}^{*}$ has a minimum distance ${\delta }_{{q}^{*}}$ defined as follows:${\delta }_{{q}^{*}}=\underset{q,k=1,\dots ,Q}{\mathrm{max}}({\upsilon }_{qk})$ if ${\rho }_{{q}^{*}}=\underset{q=1,\dots ,Q}{\mathrm{max}}({\rho }_{q})$(20)

The two components are multiplied together to provide the following score:

$${\gamma }_{q}={\rho }_{q} \times { \delta }_{q}$$

(21)

To get ${\left\{{\gamma }_{q}\right\}}_{q=1}^{Q}$ , the scores from (20) are applied to all of the subblocks. The obtained scores are then arranged in a decreasing order. As a result, the eigenvectors with the greatest $N$ scores define the clusters, which are denoted by $\mathbf{C}\triangleq [{{\varvec{c}}}_{1},..., {{\varvec{c}}}_{N}]$.

As mentioned in [41], it would be difficult to cluster the eigenvectors using solely the density-based strategy described above. To address this issue, a weight clustering approach to further tune the projected clusters is used [42]. The procedure of the weighted eigenvector clustering can be summarized in three steps.

First, the eigenvector is weighted by a kernel function defined as follows:

$${{\varvec{b}}}_{qk}\triangleq {e}^{{\omega }_{qk}^{2}/{\tau }_{0}^{2}} {{\varvec{a}}}_{q}$$

(22)

where $k=1,..,N$ and ${\omega }_{qk}={\Vert {{\varvec{a}}}_{q}-\left({{{\varvec{a}}}_{q}}^{H} {{\varvec{c}}}_{k}\right){\boldsymbol{ }{\varvec{c}}}_{k}\Vert }_{F}^{2}$.

Then, the weighted covariance matrix is created as:

$${{\varvec{R}}}_{k}^{\mathrm{b}}=\sum_{q=1}^{Q}{{\varvec{b}}}_{qk} {{{\varvec{b}}}_{qk}}^{H}$$

(23)

Finally, the EVD is applied to the weighted covariance matrix ${{\varvec{R}}}_{k}^{b}$:

$${{\varvec{R}}}_{k}^{\mathrm{b}}={{\varvec{U}}}_{qk}{{\varvec{\Sigma}}}_{qk}{{{\varvec{U}}}_{qk}}^{H}$$

(24)

As an updated of cluster ${{\varvec{c}}}_{k}$ where $k = 1,..., N$, the eigenvector that corresponds to the largest eigenvalue from the equation (24) is extracted.

The mixing matrix estimation algorithm is summarized as follows:

Step 2 : Mixing matrix estimation

Input : X which represents the TF representation of the observed signal whose elements ${\mathbf{x}}_{d}.$

• For each block $\mathrm{q}\in \mathrm{Q}$ do

  • Calculate the local covariance matrix of ${\mathbf{R}}_{\mathrm{q}}^{\mathrm{\rm X}}$ using ${\widehat{\mathbf{R}}}_{f,q}^{\mathbf{\rm X}}=\frac{1}{p} \sum_{d=q\left(P-1\right)+1}^{qP}{\mathbf{x}}_{f,d} {\mathbf{x}}_{f,d}^{H}$

  • Construct the eigenvector matrix $\mathbf{A}$ using (19).

• End

  • Using the eigenvector matrix $\mathbf{A}$, compute the similarity matrix defined by (17)

• For each block $\mathrm{q}\in \mathrm{Q}$ do

  • Calculate the local density ${\uprho }_{\mathrm{q}}$ and the minimum distance ${\updelta }_{\mathrm{q}}$ and the score ${\upgamma }_{\mathrm{q}}$ using (15), (16) and (21), respectively

• End

  • Calculate ${\updelta }_{{\mathrm{q}}^{*}}$ using (20), then, obtain the score sequence $\Upsilon =[{\upgamma }_{1},\dots , {\upgamma }_{Q}]$.

  • To obtain the score sequence $\Upsilon$, record the eigenvector matrix with the same permutation of decreasing alignment. So, to get the estimated clusters $\mathbf{C}=[{\mathbf{c}}_{1},\dots , {\mathbf{c}}_{N}]$, truncate the first $N$ reordered eigenvectors.

• For $k=1\, {\it{to}}\, N \,{\it{do}}$

• For each subblock $\mathrm{q}\in \mathrm{Q}$ do

  • Calculate the weighted eigenvector ${\mathbf{b}}_{\mathrm{qk}}$ using ${\mathbf{a}}_{\mathrm{q}}$ and ${\mathbf{c}}_{\mathrm{k}}$, then calculate ${\mathbf{R}}_{\mathrm{qk}}^{\mathrm{b}}$ using (22) and (23), respectively.

  • Calculate ${\widetilde{\mathbf{h}}}_{\mathrm{k}}$ using (24)

• End

• End

Output: Estimated mixing matrix $\widehat{\mathbf{H}}$ .

3.3 Source Reconstruction

In [41], the sparsity-based method has been introduced as an alternative to reconstruct the estimated source signal using a $l_{p}$-norm-based minimization measurement. (The convergence is guaranteed for $0< p<1.$) The method consists of converting the source reconstruction problem to a sparse reconstruction minimization problem. A designed iterative Lagrange multiplier approach with an appropriate initialization procedure is used to solve this minimization problem.

The source reconstruction is performed to find the sparsest term of ${s}_{d}$. For this, the maximum posterior likelihood of ${s}_{d}$ is expressed as:

$$\underset{{s}_{d}}{\mathrm{max}}\prod_{i=1}^{N}P\left(\left|{s}_{i,d}\right|\right)$$

$$s.t. {\mathbf{x}}_{d}=\widehat{\mathbf{H}}{s}_{d}$$

(25)

where the complex-valued super-Gaussian distribution $P\left(\left|{s}_{i,d}\right|\right)$ is given by:

$$P\left(\left|{s}_{i,d}\right|\right)=p\frac{{\gamma }^{1/p}}{\Gamma (\frac{1}{p})}{e}^{-{\left|{s}_{i,d}\right|}^{p}}$$

(26)

where $p$ and $\gamma$ control the shape and variance of the probability function, $\Gamma$ denotes the gamma function and $\widehat{\mathbf{H}}$ represents the estimated mixing matrix.

The problem returns to solve the equivalent optimization problem given as follows:

$$\underset{{s}_{d}}{\mathrm{min}}\sum_{i=1}^{N}{|{s}_{i,d}|}^{p}$$

$$s.t. {\mathbf{x}}_{d}=\widehat{\mathbf{H}}{s}_{d}$$

(27)

The Lagrange multiplier method is used to solve the optimization problem. Hence, the problem is reformulated to an unconstrained optimization problem as follows:

$$\underset{{s}_{d},\alpha }{\mathrm{min}}\mathcal{F}({s}_{d},\alpha )\triangleq \sum_{i=1}^{N}{|{s}_{i,d}|}^{p}+{\alpha }^{H}({\mathbf{x}}_{d}-\widehat{\mathbf{H}}{s}_{d})$$

(28)

where $\alpha$ is the Lagrange multiplier.

The implicit solution of the problem is given as follows:

$${s}_{d}={\Psi }^{-1}( {s}_{d}) {\widehat{\mathbf{H}}}^{H} {(\widehat{\mathbf{H}} {\Psi }^{-1}{(s}_{d} {)\widehat{\mathbf{H}}}^{H} )}^{-1} {\mathbf{x}}_{d}$$

(29)

where ${\Psi }^{-1}( {s}_{d})\triangleq \left[\begin{array}{ccc}{|{s}_{1,d}|}^{2-p}& \cdots & 0\\ \vdots & \ddots & \vdots \\ 0& \cdots & {|{s}_{N,d}|}^{2-p}\end{array}\right]$

The iterative scheme to obtain the solution ${s}_{d}$ is given as follows:

$${\widehat{s}}_{d}^{\left(iter+1\right)}=\left\{\begin{array}{c}{\Psi }^{-1}\left( {{\widehat{s}}_{d}}^{\left(\mathrm{iter}\right)}\right){\widehat{\mathbf{H}}}^{H} {\left(\widehat{\mathbf{H}} {\Psi }^{-1}\left({{\widehat{s}}_{d}}^{\left(\mathrm{iter}\right)}\right){\widehat{\mathbf{H}}}^{H} \right)}^{-1} {\mathbf{x}}_{d} if {\Vert {{\widehat{s}}_{d}}^{\left(\mathrm{iter}\right)}\Vert }_{0}\ge M \\ {\Psi }^{-1}\left( {{\widehat{s}}_{d}}^{\left(\mathrm{iter}\right)}\right){\widehat{\mathbf{H}}}^{H} {\left(\widehat{\mathbf{H}} {(\Psi }^{-1}\left( {{\widehat{s}}_{d}}^{\left(\mathrm{iter}\right)}\right)+\epsilon \mathbf{I}{)}^{-1} {\widehat{\mathbf{H}}}^{H} \right)}^{-1} {\mathbf{x}}_{d } elseif \Vert {{\widehat{s}}_{d}}^{\left(\mathrm{iter}\right)}\Vert <M\end{array}\right.$$

(30)

The source reconstruction algorithm is summarized as follows:

• Step 3: Estimation of the TF representation of the sources

• Input: Time–frequency representation of the observed signal denoted X whose elements ${\mathbf{x}}_{d}$ and estimated mixing matrix $\widehat{\mathbf{H}}$

  For each frequency bin $\mathrm{do}$

  • Initialize the sources as ${\widehat{s}}_{d}^{(0)}=\sum_{j=1}^{{C}_{N}^{M}}{\omega }_{j}{\mathrm{y}}_{j,d}$

    Repeat

    • Update ${\widehat{s}}_{d}^{\left(\mathrm{iter}\right)}$ using (30)

    • $iter= iter+1$

    Until ${{\Vert {{\widehat{s}}_{d}}^{\left(\mathrm{iter}\right)}\Vert }_{p}}^{p}-{{\Vert {{\widehat{s}}_{d}}^{\left(\mathrm{iter}+1\right)}\Vert }_{p}}^{p}$ is less than a given threshold.

    End

    Aware that ${{\Vert {{\widehat{s}}_{d}}^{\left(\mathrm{iter}\right)}\Vert }_{p}}^{p}\triangleq \sum_{i=1}^{N}{|{{s}^{\left(\mathrm{iter}\right)}}_{i,d}|}^{p}$ .

• Output: time–frequency representation of the estimated sources.

For each frequency bin $d$, since the iterative method computes successive approximations to the solution of the problem, the stopping criterion minimizes the iterative absolute error. The tolerance or threshold of the stopping criteria is determined to guarantee the best algorithm performance without resulting in a high computing time.

4 Simulation Results

To investigate the effectiveness of the proposed method, numerical simulations have been performed in a reverberant environment. The TIMIT database [37] and NOIZEUS database [1] were used to build the speech dataset, which was chosen at random (available online). The sampling rate of the speech signals is ${f}_{s} = 16 \mathrm{kHz}$, and the speakers might be either female or male. Using the technique outlined in [17], the propagation environment is simulated as a reverberant room shown in Fig. 2.

Fig. 2

Sources—microphone configuration.

The room impulse response from the source $i$ to the sensor is illustrated in Fig. 3. By adjusting the reverberant time, a variety of convolutive mixed signals can be produced. It is crucial to evaluate the transmission duration of the signal decay to 60 dB to reflect the room reverberation.

Fig. 3

Room impulse responses from the source $i$ to the microphone.

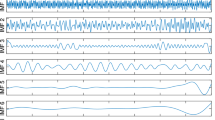
As an illustration, let the three sources shown in Fig. 4a. The three sources are convolutedly mixed in the virtual room shown in Fig. 1 using the room impulse responses shown in Fig. 2. The observed single-channel signal is shown in Fig. 4b. Figure 4c shows a frame of 1024 sample length of the observed signal. The obtained modes are shown in Fig. 4d. For this example, the decomposition of the observed signal results in 24 modes. The TF representations of the obtained modes are shown in Fig. 4e. A comparison between the STFT of the estimated frame and the original frame of the observed signal is shown in Fig. 4f. The estimated sources are shown in Fig. 4g. A comparison between the TF representations of original sources and estimated sources is shown in Fig. 4h.

Fig. 4

Illustration example of the single-channel separation of a convolutive mixture of three speech signals based on the proposed method.

As can be seen, the estimated sources are highly similar to the original sources. The proposed method based on the AMSWT method and density-based clustering with sparse reconstruction provides an accurate estimate of the source signals and results in a spectral content located with high accuracy.

The BSSeval toolbox [15] is used to analyze the performance of the proposed approach. The estimated sources are expressed as $\widehat{s}={s}_{\mathrm{target}}+{e}_{\mathrm{interf}}+{e}_{\mathrm{noise}}+{e}_{\mathrm{artif}}$ for the objective performance criteria measurement, where ${s}_{target}$ refers to the source signals, ${e}_{\mathrm{interf}}$ stands for interference from other sources, ${e}_{\mathrm{noise}}$ stands for distortion brought on by noise and ${e}_{\mathrm{artif}}$ includes all other artifacts introduced by the separation algorithm.

The parameter $p$ of the $l_{p}$-norm-based minimization method can have a significant impact on source reconstruction performance [41]. Many tests have been performed using different values of $p$ to assess its effect on the source-to-distortion ratio (SDR) using the given dataset. Table 1 displays the obtained SDRs for the parameter p varying from 0.1 to 0.9 by a step of 0.2.

Table 1 SDRs evaluation for different values of the parameter p

As can be seen, the SDR marginally increases as p increases and reaches its maximum when $p = 0.7$. The parameter p is set to 0.7 in the subsequent experiments. Changing the value of the parameter p to take advantage of the source sparsity proves that the sparse reconstruction based on $l_{p}$-norm-based minimization method is very effective.

The estimated sources’ performances are evaluated using the SDR, the source-to-artifact ratio (SAR) and the source-to-interference ratio (SIR) criteria, and compared with the performances of the estimated sources obtained via the VMD method [45], adaptive spectrum amplitude estimator and masking method [36] and the nonnegative tensor factorization of modulation spectrograms method [3]. The SDR, SAR and SIR are defined as follows:

$$\mathrm{SDR}=10{\mathrm{log}}_{10}\frac{{\Vert {s}_{\mathrm{target}}\Vert }^{2}}{{\Vert {e}_{\mathrm{interf}}+{e}_{\mathrm{noise}}+{e}_{\mathrm{artif}}\Vert }^{2}}$$

(31)

$$\mathrm{SAR}=10{\mathrm{log}}_{10}\frac{{\Vert {s}_{\mathrm{target}}+{e}_{\mathrm{interf}}+{e}_{\mathrm{noise}}\Vert }^{2}}{{\Vert {\mathrm{e}}_{\mathrm{artif}}\Vert }^{2}}$$

(32)

$$\mathrm{SIR}=10 {\mathrm{log}}_{10}\frac{{\Vert {s}_{\mathrm{target}}\Vert }^{2}}{{\Vert {e}_{\mathrm{interf}}\Vert }^{2}}$$

(33)

Figure 5 shows the mean square error (MSE) between the original signal and the estimated sources obtained via the proposed method and reference methods. The comparison is performed for different reverberation conditions where the reverberation time is varied from 100 ms to 500 ms by a step of 50 ms. As observed, the proposed method provides the smallest MSE even in a highly reverberant environment.

Fig. 5

Comparison in terms of mean square errors (MSEs) between the original signal and the estimated sources obtained via the proposed method and reference methods.

Figures 6, 7 and 8 show, respectively, the SDR, SAR and SIR obtained by the proposed method and reference methods for different reverberant times. As can be seen, the proposed method results in a better performance in terms of the three criteria compared to the VMD, adaptive spectrum amplitude estimator and masking and nonnegative tensor factorization of modulation spectrogram methods in a reverberant environment. The proposed method results in higher performance criteria even in a highly reverberant environment.

Fig. 6

Comparison in terms of SDR between the original signal and the estimated sources obtained via the proposed method and reference methods.

Fig. 7

Comparison in terms of SAR between the original signal and the estimated sources obtained via the proposed method and reference methods.

Fig. 8

Comparison in terms of SIR between the original signal and the estimated sources obtained via the proposed method and reference methods.

The proposed method has been compared to the reference methods in terms of time computing. In general, the computational complexity [5, 8] is a measure of the execution time. The Fourier transform of a signal of length N has a computational complexity of ${\rm O}(N log N)$ [5, 8]. Then, using variational scaling and wavelet functions, the AMSWT is introduced to adaptively extract spectral intrinsic components (SICs). The AMSWT method is built on the ADMM solver, with a computational complexity of $O\left({n}^{2}\right).$ The density-based clustering has a computational complexity of $O\left({n}^{3}\right).$ The computational complexity required to compute the similarity matrix is $O\left({n}^{2}\right)$, and the sparse reconstruction used to reconstruct the estimated source has a computational complexity of $O\left({n}^{3}\right)$. The sparse methods are computationally expansive.

The experiments have been carried out using a PC with a 2.4 GHz processor and 4 GB of RAM. The comparison has been performed for reverberation time conditions of 100 ms and 400 ms. The obtained results are shown in Fig. 9. As can be seen, the proposed method has a computational cost than the reference methods both in a weakly reverberant environment and in a highly reverberant environment. The SCBSS methods in the time–frequency domain are computationally expensive.

Fig. 9

Comparison between the computational complexity of the proposed method and reference methods in terms of time running (sec).

5 Conclusion

A new method to solve the SCBSS problem has been presented. The method combines the adaptive mode separation-based wavelet transform (AMSWT) with adaptive mode separation and the density-based clustering with sparse reconstruction. The SCBSS problem is transformed into a non-underdetermined. The method operates in the time–frequency domain and a reverberant environment. The proposed method has been tested on speech datasets constructed from TIMIT and NOIZEUS databases for various reverberation time conditions. Simulation experiments indicate that the proposed method results in the smallest MSE and the highest values of SIR, SAR and SDR compared to the reference methods. The simulation results demonstrate the effectiveness of the proposed method to solve the SCBSS problem even in a highly reverberant environment. In terms of computational complexity, the proposed method is expensive.