Introduction. Cylindrical shells of finite length, including the thick-walled ones, are used in vessels, enclosures, and protective structures intended for withstanding significant hydro- and gas-dynamic loads and suitable as a containment for environmentally hazardous products of explosions, in particular in emergency cases. These are the air- and spacecraft equipment, containers for storage and transportation of explosive and toxic substances, chambers for explosive thermonuclear fusion power generation processes, and others. Such structural elements (SE) are made of metal, multilayer woven and filament-wound composite materials (CM), metal-composite (MC) material consisting of an internal metal layer (steel, titanium alloys, etc.) and an external multilayer composite, and others. There have been numerous reviews [1,2,3,4,5] and other publications [6,7,8,9,10,11] dedicated to theoretical and experimental studies of the stress-strain state (SSS) and strength of cylindrical metal, multilayer filament-wound composite, and MC shells of finite length under internal explosive loading in air as well as to strength criteria for anisotropic materials. Except for [6] (addressing the isotropic metal shells), the known experimental investigations were performed only for an explosive charge positioned along the axis at mid-height (central axisymmetric explosive loading). For this loading case, the experiments demonstrated the advantages of woven and filament-wound composites over metal, of filament-wound composites over woven ones, and of MC over woven composites. Voitenko et al. [6] studied also the influence of the radial shift of an explosive charge in the central section (the central non-axisymmetric loading) on the strength. In [2] we noted the limitation of experimental methods versus the theoretical ones.

The theoretical studies of SSS and strength of isotropic metal, anisotropic filament-wound multilayer composites, and MC cylindrical shells of finite length under internal explosive loading within the framework of the shell approximations were undertaken in [8, 9, 12,13,14,15,16]; the theoretical analyses using equations of 3D elastoplasticity were performed in [7, 10, 11, 17,18,19,20,21,22,23,24,25,26,27]. It was only the publications [7, 15, 25] which addressed the case of an explosive charge positioned at mid-height and radially shifted (the central non-axisymmetric loading), and the publication [24] which considered the radially and axially shifted position of an explosive charge (the nonaxisymmertic loading). The strength was discussed only in [8,9,10,11, 15, 16, 25, 26]. In [10, 11] we used the criteria of maximum stresses, maximum strains, the Hoffman criterion, and the generalized Mises criterion; in [25] the Ashkenazi strength criterion was applied for the materials whose ultimate tensile and compression strengths are equal and the Mises criterion was used for the materials whose ultimate tensile and compression strengths are different; in [26] we used the generalized Mises criterion, in [8, 9, 15, 16]. Abrosimov et al. applied the Hoffman criterion to the matrix and the maximum stress criterion to the reinforcing elements. The metal-composite materials were studied in the publications [9, 10, 26]. Noteworthy is that in all the theoretical investigations, except for [7, 10, 11, 27], the external load during the explosion of a spherical explosive charge in air was modeled by the procedure [28], while in the publications [7, 10, 11, 27] it was done by following the procedure [29].

Taking into account the insufficient knowledge of SSS and especially strength of the multilayer filamentwound composite and metal-composite cylinders of finite length under the non-axisymmetric internal loading and the drawbacks of the shell approximations versus the theory of elasticity for solving such problems [2], we will undertake here a study of SSS and strength of the SE at hand using the equations of the 3D theory of elasticity and the phenomenological strength criteria for anisotropic materials, which are most widely spread in the relevant applications.

Object of Investigation. The investigation was carried out for a general case of multilayer filament-wound metal-composite cylinders of finite length, generally loaded with a non-central non-axisymmetric pressure impulse generated through explosion of a spherical explosive charge in air. The problems are considered in the elastic linear statement without regard for plasticity. Here, the notion “layer” is taken to mean a part of the structural element (even if such part has been technologically fabricated through multi-ply winding), within which the elastic characteristics and directions of main anisotropy axes can be assumed to be constant. We will use cylindrical coordinates x,  φ, r. The origin of coordinates is positioned at the shell center of symmetry (x = φ = r = 0), with the explosive charge located in the plane φ = 0. In the case of the filament-wound (spirally transtropic) layer one of the principal axes of anisotropy will always coincide with the reinforcement direction (x′), while the other two (r′ and φ′) lying in the isotropy plane will be taken to coincide respectively with the radial coordinate r and the direction normal to the plane (x′r′). Consequently, the axes (x′ and φ′), with the reinforcement (winding) angle α being nonzero, are turned with respect to the global coordinate axes x and φ through a winding angle which is constant within the layer under consideration. The extreme cases α = 0 and ± 90° correspond to the axial and circumferential reinforcement, respectively, with the spiral orthotropy degenerating into the cylindrical one. The isotropic layers are considered to be a particular case of spirally orthotropic ones, provided that the appropriate identical equality expressions for a series of elastic, plastic, and strength characteristics of the material are met, with the reinforcement angle α being arbitrary. The mathematical statement and the method of solving the 3D non-stationary problem have been detailed in [2, 24, 25] and are omitted here.

The strength was assessed by three criteria: the maximum-stress criterion (σmax), the maximum-strain criterion (εmax), and the generalized Mises criterion on the following condition [2, 5, 25, 26, 30,31,32,33]:

$$ \Phi <1, $$
(1)

where Φ is the strength function that correspond to one of the above-mentioned criteria. In case condition (1) is not met, the material undergoes fracture at the computational point at hand.

The geometrical dimensions of the thick-walled cylindrical shells were as follows (unless otherwise specified): inner radius R1 = 0.15 m, outer radius R2 = 0.19 m (thus, the total wall thickness H = 0.04 m), and the cylinder length L = 0.6 m. The loading was performed by detonating a spherical TNT/RDX charge arbitrarily positioned inside the shell at a point (x0 , r0 ) so that, according to [2, 8, 9, 13,14,15,16,17,18,19,20,21,22,23,24,25,26], the pressure at the inner surface of the cylinder was given by

$$ P\left(x,\kern0.5em \upvarphi, t\right)={P}_0\frac{H\left({R}_1{a}^{-1}\sqrt{1+{\uplambda}^2+{\upeta}^2-2\uplambda \cos \upvarphi}-t\right)}{\sqrt{{\left(1+{\uplambda}^2+{\upeta}^2-2\uplambda \cos \upvarphi \right)}^3}}, $$
(2)

where \( \uplambda ={r}_0/{R}_1,\upeta =\left(x-{x}_0\right)/{R}_1,\kern1em a=2.857\sqrt{q}=6310\mathrm{m}/\mathrm{s},{P}_0 \) is the nominal pressure at a distance of R1 from the charge center, \( {P}_0=0.35{qM}_{ch}/{R}_1^3,{x}_0 \) and r0 are the axial and radial coordinates of the charge center, respectively, q is the explosive heat value, q = 4.877 MJ/kg, M ch is the explosive charge mass, and H(t ) is the Heaviside function.

Generally, the shell can be made of an internal metal isotropic layer and external unidirectionally reinforced spirally (or cylindrically) transtropic composite single layer or two layers with equal thickness of the same composite with an orthogonal reinforcement arrangement [α; α ± 90∘], where α denotes the reinforcement angle for the internal layer (with respect to the two-layered composite), while (α ± 90°) is the reinforcement angle for external layer. The explosive charge mass M ch was selected such that the mass ratio of the charge was constant [2, 26, 34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50],

$$ \upchi ={M}_{ch}/{M}_0=\mathrm{const}, $$
(3)

where M0 is the total mass of the shell. Hence,

$$ {M}_{ch}\left(\upbeta \right)=\uppi \upchi LH\left\{{\uprho}_c\left(1-\upbeta \right)\left[2{R}_1+H\left(1+\upbeta \right)\right]+{\uprho}_m\upbeta \left(2{R}_1+\upbeta H\right)\right\},\kern1em 0\le \upbeta ={h}_m/H\le 1, $$
(4)

where ρ c is the composite density, ρ m is the metal density, h m is the metal layer thickness, and β is the relative thickness of the metal layer. The quantity χ, which, according to [34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50], serves as a measure of the specific load on the shell under explosive loading is hereinafter taken to be χ = 0.0006, thus making the maximum values of the strength functions on each of the three criteria vary in the vicinity of 1.

The metal layer of the shell is made of steel 50 with the following characteristics [51]: ρ m  = 7800kg/m3, the Young modulus E = 2.02 ⋅ 105 MPa, Poisson’s ratio v = 0.3, σ Y  = 380 MPa, τ Y = 220 MPa, ε Y  = 0.19%, and γ Y  = 0.14%, where σ Y and τ Y , ε Y and γ Y are the yield points at normal and tangential stresses, and the normal and shear yield strains, respectively. Metal was assumed to work in the elastic region; therefore, during the strength verification the ultimate strength values were assumed to be equal to the respective yield points. The reasons for using this approach were threefold. First, it raises the conservatism of the calculated results; second, the application software package (ASP) [52] being used permits handling the non-axisymmetric problems only in the linear (elastic) statement; and third, in the discussion to follow we will demonstrate that in the cases at hand the fracture (if any) always occurred in the composite part of the metal-composite cylinder and metal worked in the elastic region under these loads.

′

The composite part of the shell was taken to be made of a spirally transtropic unidirectionally reinforced (along x′) epoxy-glass composite VMPS-ÉDT-10 with the following physical-mechanical characteristics along the principal axes of anisotropy [10]: ρ c = 1880 kg/m3, E′ = 37,900 MPa, E = 8900 MPa, G′ = 2840 MPa, \( {v}^{\prime }=0.28,v=0.36,\kern1em {\upsigma}_t^{\prime }=1831\kern1em \mathrm{MPa},{\upsigma}_c^{\prime }=634\kern0.5em \mathrm{MPa},{\upsigma}_t=36.75\kern1em \mathrm{MPa},\kern0.5em {\upsigma}_c=193\kern1em \mathrm{MPa} \), τ = 63.1 MPa, τ = 48.6 MPa, \( {\varepsilon}_t^{\prime }=4.83\%,{\upvarepsilon}_c^{\prime }=1.67\%,\kern0.5em {\upvarepsilon}_t=0.41\%,\kern0.5em {\upvarepsilon}_c=2.14\%,\kern1em {\upgamma}^{\prime }=1.11\% \) and γ = 0.74%. Herein we use the following notation: E and E′ are the Young moduli in the isotropy plane and along filaments, respectively, G′ is the shear modulus in the plane parallel to filaments v and v′ are the Poisson’s ratios in the isotropy plane and in the plane parallel to filaments, \( {\upsigma}_t^{\prime } \) is the ultimate tensile strength along filaments, \( {\upsigma}_c^{\prime } \) is the ultimate compressive strength along filaments, σ t is the ultimate tensile strength in the isotropy plane, σ c is the ultimate compressive strength in the isotropy plane, τ′ is the ultimate shear strength in the plane parallel to filaments, τ is the ultimate shear strength in the isotropy plane, \( {\upvarepsilon}_t^{\prime } \) is the ultimate tensile strain along filaments, \( {\upvarepsilon}_c^{\prime } \) is the ultimate compression strain along filaments, ε t is the ultimate tensile strain in the isotropy plane, ε c is the ultimate compression strain in the isotropy plane, γ′ is the ultimate shear strain in the plane parallel to filaments, and γ is the ultimate shear strain in the isotropy plane.

The ultimate values of the strains \( {\upvarepsilon}_t^{\prime },{\upvarepsilon}_c^{\prime },{\upvarepsilon}_c^{\prime },{\upvarepsilon}_t,{\upvarepsilon}_c,{\upgamma}^{\prime } \), and γ were found from Hooke’s law for a transtropic body [53] in terms of the respective ultimate strength values in stresses. We took into account that CM worked in the elastic region until failure.

Thus, with β = 0 we have a composite shell, while with β = 1 it is a metal one; with intermediate values β it is a metal-composite shell. The metal cylinder was always made up of a single layer [steel 50]; the composite one could be a unidirectionally reinforced single-layer [α] or an equal-thickness orthogonally reinforced bilayer [α; α ± 90°]; the metal-composite cylinder could be a bi-layer [steel 50; α] or three-layer design [steel 50; α; α ± 90°] with equal-thickness intermediate and external composite layers.

The calculations were performed for different values of β and, hence, charge masses M ch . These values are used in further calculations. For β = 0, 0.25, 0.5, 0.75, and 1, the respective values of M ch are 29, 50, 72, 95.5, and 121 g.

Choice of Steps of a Finite-Difference Grid and Boundary Conditions at Cylinder Edges and Comparison of 2D and 1D Calculations. Use the non-axisymmetric (3D) option of ASP [52]. Analyze the time variation of radial stresses in the cylinder central section in its mid-thickness for the cases of β = 0, 0.5, and 1 under the central axisymmetric loading (with the explosive charge positioned at the point x0 = r0 = 0). In all the variants, the composite part of the shell was taken to be of a single-layer design with circumferential reinforcement. The shell edges were assumed to be slip-supported. We considered discretization into 10, 20, 40, and 80 elements over the total cylinder thickness H, the axial spacing being always twice the radial one. The numerical experiment demonstrated that the discrepancy between the results for the 40- and 80-element discretizations over H was within 5%; therefore, for further calculations we chose the finite-difference grid of the following dimensions: ∆r = H/ 40 and ∆x = 2∆r = H/20. For the non-axisymmetric problems we calculated the first 20 harmonics, while for the axisymmetric problems only the zero-th harmonic was computed.

From the strength standpoint, it is the first semi-period of radial vibration which is the most critical for the cylinders that experience only a single explosion loading during its operation. For the SEs under consideration, it takes a rather short time – about 100 μs. This is not long enough for the disturbance to run from the shell edges to the central section; and if the explosive charge is located at the center or nearby the SE strength will not depend on the boundary conditions at the edges. In case the charge is positioned in the central section of the cylinder (x0 = 0), it is this section which will be the most critical one [4, 11,12,13,14, 21]. Therefore, in further calculations for the central or near-central axisymmetric and non-axisymmetric explosion loading we used the slip-supported edge conditions as the most simple ones. We will illustrate this through numerical calculations for the central axisymmetric loading. We studied the time variation of the maximum value of the strength function Φ with β = 0.25 for three different boundary conditions at the edges: free, fixed, or slip-supported ones for a central inner point, and the maximum value of the function over the entire cylinder. The composite part of the shell was made of a single layer with circumferential reinforcement. The explosive charge was positioned at the center of symmetry of the shell (x0 = r0 = 0). The maximum-stress criterion was applied as the strength criterion. For each of the three variants of calculation no discrepancy was observed between the respective curves – the fit was perfect.

Let us now compare the axisymmetric 2D (the central axisymmetric loading) and one-dimensional (the plane strain state – PSS) problems for the cylinder as considered above (β = 0.25). For the 2D problem we specified the slip-support conditions at the edges. In the one-dimensional problem the pressure along the axial coordinate remains constant but in time it varies in the same manner as in the 2D problem in the central section of the cylinder on the inner surface under detonation of a spherical explosive charge in air. The calculated results are summarized in Fig. 1. The plots demonstrate the time variation of hoop and axial stresses and are seen to have a poor fit. The plane (one-dimensional) calculation overestimates the values of σφ and gives essentially higher values of σ x in comparison with the 2D calculation. This is due to the fact that the explosion load (2) essentially depends on the distance to the charge and, therefore, noticeably varies both in duration and in amplitude along the axial coordinate x. It has a pronounced maximum in amplitude and minimum in duration at the point closest to the charge (x = 0; r = R1 ). The plane approximation of PSS gives a distorted pattern of SSS and thus of the object strength. On the other hand, it is more conservative and can be used for approximate strength analysis of the cylinder.

Fig. 1.
figure 1

A comparative analysis of 2D and 1D calculations: (1) 2D analysis of a cylinder of length L = 0.6 m at the inner point of the central section below the charge (x = 0; r = R1); (2) one-dimensional (PSS) calculation for the same point.

Full size image

Numerical Results. Let us consider the axisymmetric 2D problem for the same cylinder and the same explosive charge as above, except that the charge is now positioned at one of the edges:x0 =  ± L/2. Figure 2 illustrates the time variation of the maximum values of the strength function for the maximum-stress criterion, maximum-strain criterion, and the generalized Mises criterion. It is seen from the plots that the cases of free and slip-supported edges give close, though not identical, results in Φmax. In the case of the fixed-edge boundary conditions, we have the results that essentially differ quantitatively and qualitatively from those in the other two cases. For all the fracture criteria considered, the largest values of Φmax are observed in the case of fixed edges.

Fig. 2.
figure 2

Behavior of strength functions by the maximum stress criterion (a), maximum strain criterion (b), and the generalized Mises criterion (c) for three different boundary conditions at edges: (1) free, (2) slipsupported, and (3) fixed edges.

Full size image

Hereinafter, unless specified otherwise, the explosive charge is positioned in the shell central section x0 = 0 and the slip support conditions are applied at the shell edges.

Let us define the optimal reinforcement for the composite part of the shell. We analyzed metal-composite shells for β = 0.25 , with two equal-thickness composite layers [steel 50; α; α ± 90°] or a single composite layer [steel 50; α]. The results of the strength analysis by three different criteria (as mentioned above) in the first semi-period of radial vibration (0 ≤ t ≤ 100 μs) are summarized in Table 1 which shows the maximum values of the strength function by each of the criteria within this time period. The explosive charge was positioned at the center of symmetry of the shell x0 = r0 = 0. It is seen from Table 1 that the best case, from the strength standpoint, is to have a two-layered shell [steel 50; 90°] with circumferential reinforcement of its composite part.

Table 1. Choosing the Optimal Reinforcement for the Composite Part of the Cylinder
Full size table

Further calculations were performed for this shell design [steel 50; 90°], with β and r0 being varied.

Let us assess the influence of radial shift of the explosive charge location on the strength. The charge was positioned in the cylinder central section x0 = 0; the calculations were carried out for the time interval 0 ≤ t ≤ 100 μs.

The radial shift of the explosive charge position was varied from 0 to 50 mm. With r0 = 0 we had the axisymmetric statement, where it sufficed to compute the zeroth harmonic only. With r0 ≠ 0 the problem became the nonaxisymmetric one and we had to compute the first 20 harmonics. Table 2 demonstrates the variation of the maximum values of the strength function for different r0 and β, as assessed by the maximum-stress and maximum-strain criteria and by the generalized Mises criterion.

Table 2. The Influence of Radial Shift of Explosive Charge Location on the Strength
Full size table

It is seen from Table 2 that for all the criteria considered the strength functions grow with increasing radial shift of the explosive charge. This also follows indirectly from formula (2): the maximum amplitude of the explosive loading is inversely proportional to the cubed minimum distance between the cylinder inner wall and the explosive charge location. With 0 ≤ r0 ≤ 20 mm, the strength condition was fulfilled for all the shells at hand, while with r0 ≥ 30 mm it could be violated. The strength functions varied in the vicinity of 1. With β ≥ 0.75 the strength condition in all the criteria studied was met even at the maximum charge shift r0 = 50 mm; with smaller β it could be violated in one, two, or three criteria altogether, depending on r0. The generalized Mises criterion turned out to be the most conservative, while the maximum strain criterion was the least conservative one. Note that with max being essentially higher than 1 the error of determination of SSS and strength grows due to the fact that the stress–strain curve for steel deviates from Hooke’s law when the yield point is exceeded. Therefore, for such cases the present calculation provide but approximate data.

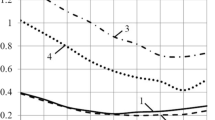
The most critical point had the following axial and angular coordinates: x = x0 = 0,  φ = φ0 = 0, while its radial coordinate depended on β and r0. In the case of the purely composite cylinder (β = 0), the point was generally located near the mid-thickness: r ≈ R1 + H/2. For the steel shell (β=) the most critical point lied on the inner surface r = R1. With intermediate steel layer thicknesses (0.25 ≤ β ≤ 0.75) the location of the critical point depended both on the strength criterion applied and on r0. In the cases of the maximum-stress and maximum-strain criteria with small radial shifts of the explosive charge, the critical point was located on the inner surface of the steel internal layer, while with increasing r0 it fell into the external composite part of the cylinder. When the generalized Mises criterion was applied, the critical point was usually located inside the external composite layer. Let us discuss this effect in more detail though the example of β = 0.25. Figure 3 shows the time variation of the maximum values of the strength functions for r0 = 0 and 50 mm. In both cases, according to the generalized Mises criterion it is the composite layer which turned out to be the critical part – see peaks of curves 3 in Fig. 3 at t ≈ 40 and 80 μs. From the standpoint of the maximum stress and maximum strain criteria, the most critical point under the axisymmetric explosive loading is located on the inner surface of the steel layer (the peaks of curves 1 and 2 at t ≈ 60 μs in Fig. 3a), while in the case of non-axisymmetric loading the critical part is the composite layer (peaks of curves 1 and 2 at t ≈ 40 and 80 μs in Fig. 3b). According to all the criteria, the strength was ensured under the axisymmetric explosion and failed under the non-axisymmetric explosive loading.

Fig. 3.
figure 3

Behavior of strength functions with β = 0.25 for r0 = 0 (a) and 50 mm (b). Here and in Figs. 4–6: (1) σmax criterium; (2) εmax criterium; (3) generalized Mises criterion.

Full size image

A study of radial stresses has demonstrated that during the axisymmetric explosion a wave σ r of amplitude about 15 MPa propagates in the composite layer, while in the case of the non-axisymmetric explosion at r0 = 50 mm the amplitude is approx 40 MPa. It is because of the low radial tensile strength of this composite (σ t = 36.75 MPa < 40 MPa) that the strength conditions for this loading fail in all the criteria considered.

The use of such transtropic and unidirectionally reinforced CMs that have a low ultimate strength in the isotropy plane (and thus along the radial coordinate too) will be ineffective for cylindrical SE to be subjected to internal explosive loading. In terms of the strength of the shell as a whole, the calculations can give even somewhat contradictory results. We will demonstrate this by way of the following example.

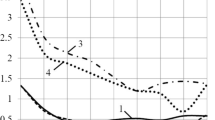
Let us consider a steel cylinder: β = 1, M ch = 121g, and h m = H = 40mm.With 0 ≤ r0 ≤ 50mm the strength conditions in all three criteria will be fulfilled with at least 17% margin, and in some cases the margin will be even more than 50% (see Table 2). Without changing the charge mass M ch or the thickness of the steel internal layer h m = H, we will increase the cylinder thickness by adding an extra external circumferentially reinforced composite layer of thickness h add that will vary within the range 0 ≤ h add  ≤ 50 mm. The calculations of maximum values of the strength functions for this shell as a whole demonstrate that the cylinder can deteriorate. Figure 4 shows the curves of Φmax vs. h add for the cases of r0 = 0 and 50 mm. It is evident that with h add = 0 the strength condition for the steel shell holds for each of the three criteria. With h add > 0, the strength under the axisymmetric explosion (Fig. 4a) is also ensured for all thicknesses of the metal-composite shell. Furthermore, assessed by the maximumstress criterion and generalized Mises criterion the values of the strength functions of the metal-composite shell can in some cases exceed those for the steel shell, i.e., with no composite layer (h add = 0). With the charge positioned non-axisymmetrically, the strength conditions for the cylinder as a whole start failing usually for the majority of h add values (except for the purely steel shell and for the steel shell with additional composite layers of small thicknesses). For the most of h add values, the generalized Mises criterion has been found to be the most conservative, while the maximum-strain criterion is seen to be the least conservative one (see Fig. 4b). This is due to the fact that with no composite layer (h add = 0) the wave σ r is isolated within the steel layer that has a high ultimate strength; with the explosive charge taken, this wave will not be critical for the cylinder and thus the strength conditions will be fulfilled. If an external composite layer (h add > 0) with a low radial strength is added, some portion, though a small one, of the wave σ r will enter the composite and can cause its fracture; this is what Fig. 4 illustrates. The strength of the internal steel layer will become higher, for a portion of the energy will go outwards into the composite layer. For the shell as a whole, it can lead to fracture of the external composite layer.

Fig. 4.
figure 4

On the paradoxes of hardening a steel shell by an outer composite layer: dependence of Φmax vs. h add for the cases of r0 = 0 (a) and 50 mm (b).

Full size image

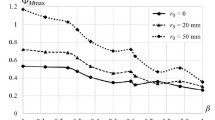
Figure 5 shows the variation of maximum values of the strength function vs. β for r0 = 0 and 50 mm. It is seen that because of the low radial strength of the composite the optimal shell, from the strength standpoint, will be the all-metal one (β = 1) (except for some small thicknesses of the composite layer, with the explosive charge mass ratio χ being equal). This again confirms inexpediency of using CM with low radial ultimate strength values for cylindrical shells to withstand internal explosive loading.

Fig. 5.
figure 5

Strength of a metal-composite cylinder as a function of β for the cases of r0 = 0 (a) and 50 mm (b).

Full size image

As mentioned earlier in [2, 25, 26], the axial shift of the explosive charge location has a weak effect on the strength of a composite cylinder under internal explosion in case the shell edges are free or slip-supported. Let us illustrate this through the following calculation. Table 3 shows the maximum values of the strength functions on three criteria for the most critical case from among the metal-composite shells at hand (β = 0.25,  r0 = 50 mm) for various values of the axial shift of the charge location from the central section (x0 = 0) to the edge (x0 = 300 mm). It is evident that Φmax for the maximum stress criterion is independent of the axial shift x0 , while for other two criteria it only weakly depends on x0 . These conclusions remain valid for the remaining values of β and r0 considered.

Table 3. The Influence of Axial Shift of Explosive Charge Location on the Strength
Full size table

A different situation arises when the cylinder has its edges rigidly fixed. Figure 6 illustrates a variation in Φmax as a function of x0 for the same problem (β = 0.25, r0 = 50 mm) with the shell edges rigidly fixed (non-monotonic plots) and slip-supported (the horizontal straight lines corresponding to Table 3). It is seen that with |x0| ≥ 200 mm = L/6 the shell strength depends on neither the explosive charge shift nor the boundary conditions at the shell edges. On the other hand, with |x0| ≥ 200 mm = L/3 it is essentially dependent on x0 if the edges are rigidly fixed and is independent of x0 if they are slip-supported. In the case of the rigidly fixed edges, the most critical explosive charge location, in terms of all the strength criteria considered, will be near the edge x =  ± L/2.

Fig. 6.
figure 6

The influence of boundary conditions at edges on the strength of cylindrical shell.

Full size image

Conclusions

1. The axial shift of the explosive charge has a weak effect on the strength of a composite cylinder with free or slip-supported edges and has quite a significant influence in the case of the explosive charge positioned close to a shell edge with fixed shell edges. According to all the strength criteria considered, the most critical explosive charge location will be that near the edge x =  ± L/2 for a shell with fixed edges.

2. The radial shift of the explosive charge has a great effect on the shell strength. The larger the radial shift of the charge, the lower the SE strength.

3. The shell strength is determined by the section x = x0 passing through the charge and is independent of the boundary conditions at edges if the charge is located quite far from the edges. In this case, the PSS model gives a distorted picture of SSS in the critical section x = x0 of the shell; however, these plane problems are more conservative and can be used for approximate strength analysis of structures.

4. The critical point in the shell under the central non-axisymmetric loading lies within the interval x = x0, φ = φ0 = 0, or on the shell inner surface (r = R1), or, a for a MMC cylinder, in the external composite layer (R1 + h m  < r < R2). Its position depends on the strength criterion applied as well on the radial shift of the explosive charge, r0. With small r0 values, the most critical point is usually located on the inner surface, while with significant r0 values it is inside the external composite layer.

5. The use of CM with low ultimate tensile strength values in the radial direction is ineffective for the shells considered. An all-metal shell (β = 1) with no composite layer will nearly always be an optimal one from the strength standpoint, with a constant charge mass ratio, in comparison with similar CM shells. The reinforcement of the steel shell with external composite layers will be ineffective. With decreasing strength function in the internal steel layer, the strength of the cylinder as a whole will not be ensured because of the fracture of the external composite layer in the radial tensile stress relief waves.