Introduction. The dynamic stress-strain state and strength of hollow multilayer wound rotational metal- composite (MC) shells on the internal explosion of a spherical charge in air are little investigated, with a small number of theoretical and experimental studies devoted this problem. The literature review is given in the previous paper of the authors [1], there it is noted that to date, the thickness of elastoplastic metal layers and the mechanical characteristics of composite layers that provide the best carrying capacity of MC cylinders under internal explosive loading have not been determined.

The one-dimensional dynamic stress-strain state and strength of wound MC cylinders were numerically studied and the thickness of elastoplastic metallic layers that provide the highest carrying capacity of cylinders under internal explosive loading in air was evaluated in [1]. At the same time, only one specific composite was studied as the outer layer of the MC cylinder. This investigation is going on with a study [1] to determine the optimum thickness in terms of strength for elastoplastic metallic layers and mechanical characteristics of composite layers from four different composites. As in [1], the explosive loading is simulated using the CONWEP program [2, 3] and the generalized Mises strength criterion [4], the simplest of the Tsai–Wu ones, is correct (i.e., satisfies the necessary and sufficient conditions for the strength surface existence), it can also adequately assess the composite strength at the lowest costs spent for criterial experiments.

The object of the study is: to numerically investigate the strengthening behavior of an MC cylindrical double- layer (metal–composite) shell of the total constant thickness H under internal dynamic pressure from the explosion of a spherical charge located in the center of cylinder symmetry at the constant total-to-running charge mass ratio, to identify the best thicknesses of metallic layers and physicomechanical characteristics of composites that provide the highest carrying capacity of the double-layer MC cylinder. The inner layer is isotropic elastoplastic steel, and the outer layer is a circularly reinforced cylindrically transtropic elastic composite. The dynamic problem is solved in the 1D statement of the plane strain state at the cylinder ends to obtain the most qualitative and illustrative results.

Mathematical Formulation and Solution Method. Consider the plane strain state of a double-layer cylinder under axisymmetric internal dynamic pressure from the explosion of a charge evenly distributed lengthwise and located in line with the axis of symmetry. In this case, the pressure pulse corresponds to the explosion of a spherical charge of a certain mass M in air at a distance equal to the inner radius of the cylinder. The inner layer is isotropic elastoplastic steel of full strength in tension–compression (the equations of the Prandtl–Reuss nonhardening material flow theory were used [5]). The outer layer is a circularly reinforced cylindrically transtropic fully elastic composite of unequal tensile–compression strength with the ideal layer-to-layer contact. The problem is numerically solved by the finite difference method (FDM) in the cylindrical Eulerian coordinates x, φ, r, in view of the axial symmetry and plane strain state on any end planes x = const. The finite-difference Lagrangian mesh is frozen in the medium and moves in space and time with it. Thus, we have the computational domains for the 1D problem: R ≤ r -≤ + h for the inner and R + h ≤ r ≤ R + H for the outer layers of the cylinder, where R is the inner radius of the inner cylinder, h is the thickness of the inner steel layer, H is the total thickness of the cylinder, and H - h is the thickness of the outer composite layer. The complete system of differential equations together with initial, boundary, and contact conditions is given in [1].

The strength of a double-layer cylinder is estimated by the generalized Mises criterion [4], which for a circularly remforced cylindrically transtropic composite at the plane strain state is as follows:

$$\Phi =\left({\sigma }_{x}+{\sigma }_{r}\right)\left(\frac{1}{{\sigma }_{+}}-\frac{1}{{\sigma }_{-}}-\frac{{\upsigma }_{\varphi }}{\sqrt{{\sigma }_{\varphi }+{\sigma }_{\varphi }-{\sigma }_{+}{\sigma }_{-}}}\right)+{\sigma }_{\varphi }\left(\frac{1}{{\sigma }_{\varphi +}}-\frac{1}{{\sigma }_{\varphi -}}\right)+\frac{{\sigma }_{x}^{2}+{\sigma }_{r}^{2}-{\sigma }_{x}{\sigma }_{r}}{{\sigma }_{+}{\sigma }_{-}}+\frac{{\sigma }_{x}^{2}}{{\sigma }_{\varphi +{\sigma }_{\varphi -}}}<1,$$
(1)

where \({\sigma }_{\varphi +}\) and \({\sigma }_{\varphi -}\) are the ultimate strengths of the circular reinforcement direction in tension–compression, respectively, σ+ and σ- are the same in the isotropy plane xr (<p = const), Φ is the strength function, and σx, σrr and σφ are the stress tensor components. If (1) is fulfilled, the strength is maintained. Otherwise, (Φ ≥ 1), the strength criterion is not satisfied, and the material is fractured in this point. The cases of isotropic and/or materials of full strength in tension–compression are easily obtained from (1) as partial (degenerate). Note that in all further calculations, the inner (first) layer is made of isotropic steel of full sirength in tension-compression and for it, the Mises criterion (1) degenerates into the classical fourth theory of strength [6].

The dynamic 1D boundary problem is numerically solved with the application package earlier developed by the authors [7]. The solution method is the Wilkins time-explicit finite-difference integro-interpolation algorithm [8], modified by the authors for anisotropic materials and included in this package. The strength, i.e., Φ function, is calculated at each time step in each finite-difference element of the computational domain. If its maximum value over the entire volume of the computational domain Φmax was less than unity, the object was recognized as strong; otherwise, the strength of the cylinder as a whole was believed to be deteriorated, and the failure was recorded.

Materials. The inner layer is isotropic elastoplastic St20 steel of full strength in tension–compression with the physicomechanical characteristics [6]: density p = 7860 kg/m3, Young’s modulus E = 212000 MPa, Poisson’s ratio v = 0.3, yield strength aY = 250 MPa, and σ+ = σ- = σμ = 420 MPa.

The outer layer is a cylindrically transtropic circularly reinforced elastic composite of unequal tensile– compression strength. The four composites were examined:

C No. 1: T300/5208 graphite epoxy with the volume fiber content V = 70% and physicomechanical characteristics [9]: p = 1583 kg/m3, E = 14,900 MPa, v = 0.386, Eφ = 162,000 MPa, vφ = 0.283, σ+ = 52.6 MPa, σ- = 260 MPa, σφ+ = 1744 MPa, and σφ- = 1650 MPa. Here, Eφ is Young’s modulus in the circumferential direction, v<p is Poisson’s ratio corresponding to the circumferential direction [1, 4, 10].

C No. 2: T300/5208 graphite epoxy with the volume fiber content V = 40% and physicomechanical characteristics [9]: ρ = 1406 kg/m3, E = 7900 MPa, v = 0.436, Eφ = 94,100 MPa, vφ = 0.309, σ+ = 49.5 MPa, σ- = 220 MPa, σφ+ = 1013 MPa, and σφ- = 940 MPa.

C No. 3: E-glass epoxy with the volume fiber content V = 65% and physicomechanical characteristics [9]: ρ = 2112 kg/m3, E = 15,300 MPa, v = 0.332, Eφ = 48,000 MPa, vφ = 0.315, σ+ = 27.8 MPa, σ- = 150 MPa, σφ+ = 1297 MPa, and σφ- = 820 MPa.

C No. 4: E-glass epoxy with the volume fiber content V = 40% with physicomechanical characteristics [9]: ρ = 1750 kg/m3, E = 8300 MPa, v = 0.395, Eφ = 30,900 MPa, vφ = 0.327, σ+ = 27.1 MPa, σ- = 140 MPa, σφ+ = 798 MPa, and σφ- = 480 MPa.

For convenience and shortening the text, the composites to be calculated will be specified by the above numbers.

Object Geometry. The inner radius R of the cylindrical MC shell remained constant in all calculations, viz R = 150 mm. The three versions of MC double-layer shells classified under their total thickness H are examined:

(i) thin: H = 10 mm, H⁄R = 0.067;

(ii) medium thickness: H = 20 mm, H⁄R = 0.133;

(iii) thick: H = 40 mm, H⁄R = 0.267.

The thickness of the inner steel layer h varied within (0–0.8)H. Thus, the thickness ratio of the metal (β = h/H varied within 0–0.8. At (β = 0, we have a single-layer composite shell; at (β > 0, we have a double-layer MC shell. There was no point to discuss the (β > 0.8 cases as unattractive in terms of their practical application.

Loading. As in [1], the explosive charge mass in the TNT equivalent M was dependent on H and (β so that the mass ratio (ξ= M/m remained constant for each of the three shell versions. Here, m is the running mass (per unit length) of the shell:

$$m=\pi \pi H\left[{\rho }_{m}\beta \left(2R+\beta H\right)+{\rho }_{c}\left(1-\beta \right)\left(2R+H+\beta H\right)\right],$$
(2)

where ρm is the metal density and ρc is the composite density.

Thus, M(β) in each case was calculated by the formula

$$M\left(\beta \right)=\xi m,$$
(3)

where m((β, H) is determined from (2).

Hereinafter ξ is constant and equal to ξ = 1.421 mm = const. The M calculations were carried out by scheme (2)–(3). Since the 3 H values (10, 20, and 40 mm), the 4 composites (ρc discretely varied from 1406 to 2112 kg/m3) and a wide β interval (0–0.8) were discussed, the charge mass M was also examined over a fairly wide range, from 19.46 g for the thin-walled (H = 10 mm) single-layer (β = 0) composite cylinder [C No. 2] to 400.86 g for the thick- walled (H = 40 mm) double-layer (β = 0.8) MC cylinder [St20; C No. 3].

Finite-Difference Mesh Parameters. With the application package [7], the mesh step along the radial coordinate was constant and equal to dr = 0.1 mm. This ensured sufficient and equal calculation accuracy for all three shell versions. Thus, at H = 10, 20, and 40 mm, the cylinder was partitioned across its width into 100, 200, and 400 finite-difference elements, respectively. The contact surface should always coincide with the node of the computational domain, so the thickness h of the inner steel layer could discretely change with the step dr = 0.1 mm. The time step was chosen automatically subject to the Kurant stability condition. The calculations were carried out to the point in time of 100–200 µs to fit H and β values and cover the first half-period of radial shell vibrations, the most dangerous in terms of strength [4]. If the dynamics (vibrations) of cylinders in a wider time range were of interest, some calculations were sometimes performed on a half as fine (and more accurate) finite-difference mesh with dr = 0.05 mm. Hereinafter the notation is adopted: ΦmaxC is the maximum value of the Mises strength function Φ, which is achieved across the whole width of the outer composite layer at the first half-period of radial vibrations for the total calculated time interval tcalc, i.e., the global Φ maximum in the open rectangle (R + h < r < R + H; 0 < t < tcalc).

Numerical Results.

Thin-Walled Cylinders

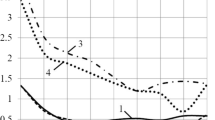
Determination of Optimum β (hereafter βopt) and an Outer Composite Layer of Optimum Strength. Thin- walled (H = 10 mm; H/R= 10/150 = 0.0667) double-layer MC cylinders [St20; C] were examined for four outer composite layers and nine β values, from 0 to 0.8 with a step of 0.1 (at β = 0, we have single-layer composite cylinders). The data obtained were used to plot Fig. 1, where the solid, dashed, dot-and-dash, and dotted curves correspond to the MC cylinders of [St20; C No. 1], [St20; C No. 2], [St20; C No. 3], and [St20; C No. 4], respectively. As is seen, the MC cylinders [St20; C No. 1] and [St20; C No. 2] are of higher strength than [St20; C No. 3] and [St20; C No. 4]. Even single-layer (β = 0) shells [C No. 1] and [C No. 2] possessed quite a high safety margin in contrast to similar [C No. 3] and [C No. 4]. At the same time, if the MC cylinder [St20; C No. 3] started to satisfy the strength condition already at β ≥ 0.02, [St20; C No. 4] only at β > 0.3. The MC cylinders [St20; C No. 2] were found to be of the highest strength, while [St20; C No. 3] were the most dangerous. Although the corresponding strength limits in C No. 1 are higher than those in C No. 2, and those in C No. 3 are higher than those in C No. 4, the MC cylinders [St20; C No. 2] are stronger than [St20; C No. 1], and [St20; C No. 4] are stronger than [St20; C No. 3]. The reason is that the strength of such composttes under explosive loading is primarily determined by the tensile strength σ+ in the isotropy plane, i.e., in the radial (r) and axial (x) directions. With an increase in the volume content V of reinforcing fibers from 40 to 70% in C No. 1 compared to C No. 2 and from 40 to 65% in C No. 3 compared to C No. 4, these strength limits increased insignificantly compared to the density of the composites. Therefore, at fixed ξ, the growth of the mass M of the explosive charge will occur faster than the growth of the corresponding strength limits σ+, and thus, the strength of the MC cylinder will decrease.

Fig. 1.
figure 1

The ΦmaxC vs β for four composites in the outer layers of thin-walled MC cylinders: (1) [St20; C No. 1], (2) [St20; C No. 2], (3) [St20; C No. 3], and (4) [St20; C No. 4].

Full size image

From Fig. 1, determine the optimum thickness ratio βopt of the steel layer in which the corresponding ΦmaxC are minimum:

for MC shell [St20; C No. 1] βopt = 0.4; ΦmaxC(βopt) = min = 0.2138<<1;

for [St20; C No. 2] βopt = 0.5; ΦmaxC(βopt) = min = 0.1988<<1;

for [St20; C No. 3] βopt = 0.7; ΦmaxC(βopt) = min = 0.7072<1;

for [St20; C No. 4] βopt = 0.7; ΦmaxC(βopt) = min = 0.4176<<1.

The composite of optimum strength for the outer layer was C No. 2, and the most dangerous was C No. 3.

Effect of Plastic Deformation of the Inner Metallic Layer on the Stress-Strain State and Strength of the Outer Composite Layer. In all the above cases of examining the MC cylinders (0.1-5 (] -50.8), the inner steel layer underwent significant plastic strains. Let us prove it by specific numerical calculations.

Denote the maximum radial displacement and circumferential strain by umax and εφ- max = (umax/R) × 100%, respectively, of the inner steel layer surface r = R reached at the first half-period of radial vibrations of the MC cylinder. With β from 0.1 to 0.8, the following results for the MC cylinders were obtained:

[St20; C No. 1]: umax monotonically increases from 0.3272 to 0.567 mm, εφ- max monotonically increases from 0.218 to 0.378%;

[St20; C No. 2]: umax monotonically increases from 0.4293 to 0.6182 mm, εφ - max monotonically increases from 0.286 to 0.412%;

[St20; C No. 3]: umax monotonically increases at 0.1≤ β ≤ 0.3 from 0.6814 to 0.6868 mm and then at 0.3 ≤ β ≤ 0.8 monotonically decreases from 0.6868 to 0.6759 mm; εφ - max monotonically increases at 0.1 ≤ β ≤ 0.3 from to 0.4579% and then at 0.3 ≤ β ≤ 0.8 monotonically decreases from 0.4579 to 0.4506%;

[St20; C No. 4]: umax monotonically decreases from 0.7985 to 0.6922 mm, εφ- max monotonically decreases from 0.5323 to 0.4615%.

The global minimum and maximum of umax (and hence Eφ- max as well) for the MC cylinders are as follows:

(umax)min = 0.3292 mm and (εφ - max)min = 0.218% for [St20; C No. 1] at β = 0.1;

(umax)min = 0.7985 mm and (εφ - max)min = 0.5323% for [St20; C No. 4] also at β = 0.1.

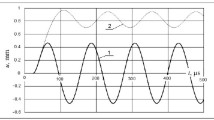
For these two extreme cases at β = 0.1, Fig. 2 for [St20; C No. 1]) and Fig. 3 for [St20; C No. 4]) are plotted. They depict the time variations of the radial displacement u and circumferential stress σφ of the inner steel layer surface r = R. As is seen, the plastic steel deformation is responsible for a significant difference in the curves, even for the “weakest” case [St20; C No. 1] in terms of the plastic flow (Fig. 2). For [St20; C No. 4], the displacements and strains were almost 2.5 times larger than those in [St20; C No. 1], and the corresponding plots differ much more (Fig. 3). The plastic deformation brings about an increase in umax at the first half-period of radial vibrations, but then their amplitude and frequency become smaller compared to ideally elastic solutions. The reason is that elastoplastic steel is more pliable than ideally elastic, and at the first half-period, when the pressure pulse from the explosion acts on the inner surface, it receives a larger deflection (more precisely, buckling). Starting from the second half-period and further, the explosive loading has practically no effect, but in the elastoplastic layer, the irreversible energy losses for its plastic deformation have managed to occur and, therefore, the vibration amplitude will be smaller than for the ideally elastic case in which there are no energy losses by definition and vibrations occur without damping. As regards σφ, starting from the first half-period and further in the elastoplastic problem, their amplitude is much smaller than in the ideally elastic one since for the case of the nonhardening material flow theory [1, 5], the stress intensity can never exceed σY = 250 MPa.

Fig. 2.
figure 2

Variations of u(t) (a) and σφ(t) (b) of the inner surface of the thin-walled MC cylinder [St20; C No. 1] at β = 0.1. [Here and in Figs. 3, 4, 7, 8, and 9: the solid line corresponds to the elastoplastic inner steel layer (σY = 250 MPa), and the dashed one corresponds to the case when St20 was considered ideally elastic (σY = ∞).]

Full size image
Fig. 3.
figure 3

Variations of u(t) (a) and σφ(t) (b) of the inner surface of the thin-walled MC cylinder [St20; C No. 4] at β = 0.1.

Full size image

The global minimum and maximum of the largest deflection (buckling) of the inner surface are reached for the MC cylinders with the thinnest (β = 0.1) inner steel layer. Therefore, for completeness of examination, Fig. 4 is constructed, similar to Figs. 2 and 3 with the only difference that it corresponds to the MC cylinder [St20; C No. 4] with the thickest (β = 0.8) of the inner steel layers. At β = 0.8, this MC shell was most buckled among the four ones: umax = 0.6922 mm>0.6759 mm for [St20; C No. 3] >0.6122 mm for [St20; C No. 2] >0.567 mm for [St20; C No. 1].

Fig. 4.
figure 4

Variations of u(t) (a) and σφ(t) (b) of the inner surface of the thin-walled MC cylinder [St20; C No. 4] at β = 0.8.

Full size image

Figure 4 turned out to be most representative: it clearly shows the residual plastic deflection (buckling) of about 0.44 mm in the elastoplastic formulation around which harmonic vibrations of the shell occur after the drop of looding. Strictly speaking, the residual deflection was also in other elastoplastic formulations, perhaps, somewhat smaller and not so clearly defined.

In conclusion of this discussion, take a look at the effect of plastic deformation of the inner steel layer on the strength of the outer composite one. Let us consider the most durable and the most dangerous MC cylinders in their optima, i.e., at their β = β opt. These are, respectively, MC cylinders [St20; C No. 2] at β = 0.5, where in the elastoplastic formulation ΦmaxC(βopt = 0.5) = min = 0.1988 and [St20; C No. 3] at β = 0.7, where in the elastoplastic formulation ΦmaxC(βopt = 0.7) = min = 0.7072. Time variations of ΦmaxC for [St20; C No. 2] at β = and [St20; C No. 3] at β = 0.7 are shown in Fig. 5.

Fig. 5.
figure 5

Variations of ΦmaxC(t) for the optimum thin-walled MC cylinders [St20; C No. 2] (a) and [St20; C No. 3] (b). (Here and in Fig. 10: solid lines are elastoplastic calculation and dashed lines are ideally elastic one.)

Full size image

The curves of the elastic and elastoplastic calculations qualitatively differ significantly from each other. With this, either the most dangerous points r = rcr or the corresponding critical moments of time t = tcr did not also coincide. The quantitative difference is insignificant:

for [St20; C No. 2] at β = 0.5, ΦmaxC was equal to 0.1988 in the elastoplastic and 0.1996 in the elastic formulations. The relative excess of the elastic calculation over the elastoplastic one equals: δ = (0.1996 – 0.1988)×100%/0.1988 = 0.4024% < 0.5%;

for [St20; C No. 3] at β = 0.7, ΦmaxC was 0.7072 in the elastoplastic and 0.7414 in the elastic formulations. The relative excess of the elastic calculation over the elastoplastic one equals: δ = (0.7414 – 0.7072)×100%/0.7072 = 4.836% < 5%.

Medium-Thickness Cylinders.

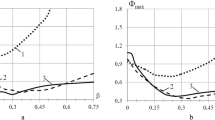
Determination of βopt and an Outer Composite Layer of Optimum Strength. Double-layer medium-thickness MC cylinders [St20; C] (H = 20 mm; H/R= 20/150 = 0.1333) were examined for four outer composite layers and nine β values, from 0 to 0.8 with a step of 0.1 (at β = 0, we have single-layer composite cylinders). The data obtained were used to plot Fig. 6. The MC cylinders [St20; C No. 1] and [St20; C No. 2] as well as thin-walled cylinders are of higher strength than [St20; C No. 3] and [St20; C No. 4]. Even single-layer (β = 0) shells [C No. 1] and [C No. 2] possessed quite a high safety margin in contrast to similar [C No. 3] and [C No. 4]. At the same time, if the MC cylinder [St20; C No. 4] started to satisfy the strength condition already at β > 0.27, [St20; C No. 4] only at β > 0.515. As before, the MC cylinders [St20; C No. 2] were the most durable, while [St20; C No. 3] were the most dangerous. The MC cylinders [St20; C No. 2] are stronger than [St20; C No. 1] and [St20; C No. 4] are stronger than [St20; C No. 3] for the same reasons as for thin-walled cylinders.

Fig. 6.
figure 6

The ΦmaxC vs β for four composites in the outer layers of medium-thickness MC cylinders: (1) [St20; C No. 1], (2) [St20; C No. 2], (3) [St20; C No. 3], and (4) [St20; C No. 4].

Full size image

From Fig. 6, determine the optimum thickness ratio βopt of the steel layer in which the corresponding ΦmaxC are minimum:

for MC cylinder [St20; C No. 1] βopt = 0,6; ΦmaxC(βopt) = min = 0.287<<1; for [St20; C No. 2] βopt = 0.7; ΦmaxC(βopt) = min = 0.2079<<1;

for [St20; C No. 3] βopt = 0.6; ΦmaxC(βopt) = min = 0.8792<1; for [St20; C No. 4] βopt = 0.7; ΦmaxC(βopt) = min = 0.5773<<1.

The composite of optimum strength for the outer layer was C No. 2, and the most dangerous was C No. 3.

Effect of Plastic Deformation of the Inner Metallic Layer on the Stress-Strain State and Strength of the Outer Composite One. In all the above cases of examining MC cylinders (0.1-5 (] -5 0.8), the inner steel layer underwent significant plastic strains. Let us prove this by specific numerical calculations: with β from 0.1 to 0.8, the following results were obtained:

[St20; C No. 1]: umax monotonically grows from 0.3026 to 0.5012 mm; εφ-max monotonically grows from 0.202 to 0.334%;

[St20; C No. 2]: umax monotonically grows from 0.4067 to 0.5402 mm; εφ-max monotonically grows from 0.271 to 0.360%;

[St20; C No. 3]: umax monotonically decreases from 0.6289 to 0.5853 mm, εφ-max monotonically decreases from 0.419to 0.390%;

[St20; C No. 4]: umax monotonically decreases from 0.7235 to 0.5958 mm, εφ-max monotonically decreases from 0.482 to 0.397%.

The global minimum and maximum of umax (and hence εφ-max as well) for all MC cylinders are as follows:

(umax)min = 0.3026 mm and (εφ- max)min = 0.202% for [St20; C No. 1] at β = 0.1;

(umax)min = 0.7235 mm and (εφ- max)min = 0.482% for [St20; C No. 4] also at β = 0.1.

For these two extreme cases at (] = 0.1, Fig. 7 for [St20; C No. 1] and Fig. 8 for [St20; C No. 4] are plotted. They depict the time variations of the radial displacement u and circumferential stress σφ of the inner steel layer surface r = R. As is seen, the plastic steel deformation is responsible for a significant difference in the curves even for the “weakest” case [St20; C No. 1] in terms of the plastic flow (Fig. 7). For [St20; C No. 4], the displacements and strains were almost 2.4 times larger than those in [St20; C No. 1], and the corresponding plots differ much more (Fig. 8). The qualitative effects of plastic deformation of the inner steel layer are the same as those for the thin-walled cylinders.

The global minimum and maximum of the largest inner surface deflection (buckling) are also reached for the MC cylinders with the thinnest (β = 0.1) inner steel layer. Therefore, for completeness of examination, Fig. 9 is constructed, similar to Figs. 7 and 8 with the only difference that it corresponds to the MC cylinder [St20; C No. 4] with the thickest (β = 0.8) of the inner steel layers. At β = 0.8, this MC shell was most buckled among the four ones: umax = 0.5958 mm>0.5853 mm for [St20; C No. 3] >0.5402 mm for [St20; C No. 2]>0.5012 mm for [St20; C No. 1].

Fig. 7.
figure 7

Variations of u(t) (a) and σφ(t)(b) of the inner surface of the medium-thickness MC cylinder [St20; C No. 1] at β = 0.1.

Full size image
Fig. 8.
figure 8

Variations of u(t) (a) and σφ(t)(b) of the inner surface of the medium-thickness MC cylinder [St20; C No. 4] at β = 0.1.

Full size image
Fig. 9.
figure 9

Variations of u(t) (a) and σφ(t)(b) of the inner surface of the medium-thickness MC cylinder [St20; C No. 4] at β = 0.8.

Full size image

As before, Fig. 9 turned out to be most representative: it clearly shows the residual plastic deflection (buckling) of about 0.36 mm in the elastoplastic formulation around which the harmonic vibrations of the shell occur after the drop of loading. Strictly speaking, the residual deflection was also in other elastoplastic formulations, perhaps, somewhat smaller and not so clearly defined.

In conclusion of this discussion, take a look at the effect of plastic deformation of the inner steel layer on the strength of the outer composite one. Let us consider the most durable and the most dangerous MC cylinders in their optima, i.e., at their β = βopt. These are, respectively, MC cylinders [St20; C No. 2] at β = 0.7, where in the elastoplastic formulation, ΦmaxC(βopt = 0.7) = min = 0.2079 and [St20; C No. 3] at β = 0.6, where in the elastoplastic formulation, ΦmaxC(βopt = 0.6) = min = 0.8792. Time variations of ΦmaxC for [St20; C No. 2] at (] = 0.7 and [St20; C No. 3] at β = 0.6 are shown in Fig. 10.

Fig. 10.
figure 10

Variations of ΦmaxC(t) for the optimum medium-thickness MC cylinders [St20; C No. 2] (a) and [St20; C No. 3] (b).

Full size image

The curves of the elastic and elastoplastic calculations differ significantly from each other both qualitatively and quantitatively. With this, either the most dangerous points r = rcr or the corresponding critical moments of time t = tcr did not also coincide. The quantitative difference in contrast to the thin-walled shells can also be significant: for [St20; C No. 2] at β = 0.7, ΦmaxC was equal to 0.2079 in the elastoplastic and 0.2702 in the elastic formulations. The relative excess of the elastic calculation over the elastoplastic one equals: δ = (0.2702 – 0.2079)×100%/0.2079 = 30%;

for [St20; C No. 3] at β = 0.6, ΦmaxC was 0.8792 in the elastoplastic and 1.314 in the elastic formulations. The relative excess of the elastic calculation over the elastoplastic one equals: δ = (1.314 – 0.8792)×100%/0.8792 = 49.454% ≈ 50%.