Composite materials (CM) are widely applied in the modern engineering, in particular, in structures subjected to nonstationary loads. Such structures include vessels, shells/cases and protective housings intended for confinement in their body of considerable hydro- or gas-dynamical loads [1,2], etc. The CM manufacturing technology and structure, in contrast to conventional isotropic structural materials, stipulate their essential quantitative and qualitative distinctions in response to both static and dynamic loads. Scientific and technical applications frequently involve multilayered shells of rotation fabricated of composite layers/plies, which are spirally reinforced at a certain angle α to the generatrix. Such shells are orthotropic, while their principal axes of anisotropy x′, φ′, r do not coincide with the global cylindrical coordinate system axes frame x, φ, r, but are turned at the reinforcement angle around axis r. It is known from [1–4] that, in studies of stress-strain state (SSS) and strength assessments, it is necessary to consider the effects caused by incongruity of principal directions of elasticity with the direction of coordinate axes.

The SSS studies of such structures have been mainly performed in the axisymmetric statement [3,4] with no consideration of strength issues. In cases of non-axisymmetric nonstationary load, finite length of a cylindrical structural component, and stress localization, the problem under study involves three spatial coordinates x, φ, r and time t. The numerical integration of such four-dimensional boundary problems is performed, as a rule, using the state-of-the-art commercial software packages based on three-dimensional (3D) dynamic finite-element method (FEM).

However, when the problem is linear and dependence of the SSS on angle φ is caused only by non-axisymmetric loading, more rational solving procedure, which does not require application of 3D-elements, is available for bodies of revolution and elastic strains. Study [5] has shown an adequate applicability of the numerical-and-analytical method based on expansion of variables into Fourier series by angle φ, which results in the initial nonstationary three-dimensional boundary problem reduction to a set of two-dimensional ones. This method has been successfully applied to study of the dynamic three-dimensional SSS of multilayer isotropic and cylindrically orthotropic cylinders [5], and then it has been modified for a case of non-axisymmetric dynamic loading of thick-walled multilayered spirally orthotropic cylinders of final length [6].

The aim of this study is to modify the developed and tested in [6] applied software package (ASP) for strength estimation of a considered cylindrical structural component within the total time range and to execute several calculations illustrating the effect pulse load non-axisymmetic pattern on calculated strength of the cylinder. As strength criteria, we have used the well-known modern criteria of the orthotropic material fracture by Ashkenazi [2] or Tsai–Wu [7–10].

Work [6] describes the mathematical statement of a boundary problem and the numerical-and-analytical method of its solving based on expansion of variables into trigonometric Fourier series by angular coordinate φ with the subsequent application of the Wilkins two-dimensional linearized integro-interpolation algorithm [11] to the obtained set of independent two-dimensional problems. Noteworthy is that cylinder edges in [6] were considered to be rigidly fixed. As it is known from [12], such boundary conditions imply strain and stress singularities in the vicinity of edge angular points, i.e., the strength condition in these points will be certainly violated using dense enough FEM meshes. Therefore, in the present study, the following kinematic boundary conditions are set at the plane of symmetry:

$$ {u_x} = \frac{{\partial {u_r}}}{{\partial x}} = \frac{{\partial {u_\varphi }}}{{\partial x}} = 0,\quad x = \frac{{\pm L}}{2}, $$
(1)

which correspond to plane strain conditions at the edges and to frictionless sliding fixation conditions for isotropic or cylindrically orthotropic cylinders. Here u x , u φ, and u r are components of displacement vector in the cylindrical coordinate system (x, φ, r) with origin (similarly to [6]) located in the centre of symmetry of a cylindrical shell and L is the cylinder length.

Similarly to [6], impact loading is provided by a spherical charge of trotyl-cyclonyte explosive (TCE), and according to [4,6,13] pressure at the internal surface of the cylinder is

$$ P\left( {x,\varphi, t} \right) = {P_0}\frac{{H\left( {{R_1}a_0^{ - 1}\sqrt {{1 + {\lambda^2} + {\eta^2} - 2\lambda \cos \varphi - t}} } \right)}}{{\sqrt {{{{\left( {1 + {\lambda^2} + {\eta^2} - 2\lambda \cos \varphi - t} \right)}^3}}} }}, $$
(2)

where λ is relative radial offset of the explosive charge, λ = r 0/R 1, η = (x − x 0 )/R 1, a 0 = 6310 km/s, P 0 is nominal pressure at the distance R 1 from the explosive charge centre, R 1 is internal radius of the cylinder, and x 0 and r 0 are axial and radial coordinates of the explosive charge centre, respectively. In calculations, the internal pressure P 0 = 34 MPa was taken, which corresponded to the mass of explosive charge equal to 0.02 kg, and the internal radius R 1 = 0.1 m.

Strength of a thick-walled cylinder during variation of its dynamic three-dimensional SSS is evaluated by means of the modern fracture criteria of Ashkenazi [2] or Tsai–Wu [7–10]. The Ashkenazi criterion in the anisotropy principal axes x′, φ′, r for the general case of three-axial SSS has the following form [2]

$$ \begin{array}{*{20}{c}} {\Phi \leqslant 1,} \\ {\Phi = \frac{{a\sigma_{x'}^2 + b\sigma_{\varphi '}^2 + c\sigma_r^2 + d\tau_{x'\varphi '}^2 + e\tau_{\varphi 'r}^2 + f\tau_{rx'}^2 + g{\sigma_{x'}}{\sigma_{\varphi '}} + h{\sigma_{\varphi '}}{\sigma_r} + m{\sigma_r}{\sigma_{x'}}}}{{\sqrt {{\sigma_{x'}^2 + \sigma_{\varphi '}^2 + \sigma_r^2 + \tau_{x'\varphi '}^2 + \tau_{\varphi 'r}^2 + \tau_{rx'}^2 + {\sigma_{x'}}{\sigma_{\varphi '}} + {\sigma_{\varphi '}}{\sigma_r} + {\sigma_r}{\sigma_{x'}}}} }}} \\ \end{array}, $$
(3)

where

$$ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {a = \frac{1}{{{\sigma_{ux'}}}},} & {a = \frac{1}{{{\sigma_{u\varphi '}}}},} & {c = \frac{1}{{{\sigma_{ur}},}},} & {d = \frac{1}{{{\tau_{ux'\varphi '}}}},} & {e = \frac{1}{{{\tau_{u\varphi 'r}}}},} & {f = \frac{1}{{{\tau_{urx'}}}},} \\ \end{array} } \\ {g = \frac{4}{{\sigma_{ux'\varphi '}^{45}}} - a - b - d,\quad h = \frac{4}{{\sigma_{u\varphi 'r}^{45}}} - b - c - e,\quad m = \frac{4}{{\sigma_{urx'}^{45}}} - c - a - f,} \\ \end{array} $$

σ ux′ , σ uφ′, and σ ur are ultimate strengths under tensile or compressive loading conditions in corresponding directions, τ ux′φ, τ uφ′r , and τ urx′ are ultimate strengths in case of pure shear in corresponding planes, and \( \sigma_{ux'\varphi '}^{45} \), \( \sigma_{u\varphi 'r}^{45} \), and \( \sigma_{urx'}^{45} \) are ultimate strengths in the diagonal direction at angle 45° to the axes of symmetry shafts in a plain which corresponds to the lower indices.

As seen from formulas (3), the Ashkenazi criterion implies the equal strength of a composite material in tension and compression, which is quite rare for real materials. Therefore, in the state-of-the-art strength calculations, the Tsai–Wu criterion [8–10] is used, which is deprived of the above deficiency and takes the following form in the principal axes of the material anisotropy

$$ F \leqslant 1, $$
(4)
$$ F = {\sigma_{x'}}\left( {\frac{1}{{\sigma_{ux'}^{+} }} - \frac{1}{{\sigma_{ux'}^{-} }}} \right) + {\sigma_{\varphi '}}\left( {\frac{1}{{\sigma_{u\varphi '}^{+} }} - \frac{1}{{\sigma_{u\varphi '}^{-} }}} \right) + {\sigma_r}\left( {\frac{1}{{\sigma_{ur}^{+} }} - \frac{1}{{\sigma_{ur}^{-} }}} \right) $$
$$ + \frac{{\sigma_{x'}^2}}{{\sigma_{ux'}^{+} \sigma_{ux'}^{-} }} + \frac{{\sigma_{\varphi '}^2}}{{\sigma_{u\varphi '}^{+} \sigma_{u\varphi '}^{-} }} + \frac{{\sigma_r^2}}{{\sigma_{ur}^{+} \sigma_{ur}^{-} }} + \frac{{\tau_{x'\varphi '}^2}}{{\tau_{ux'\varphi '}^2}} + \frac{{\tau_{\varphi 'r}^2}}{{\tau_{u\varphi 'r}^2}} + \frac{{\tau_{rx'}^2}}{{\tau_{urx'}^2}} $$
$$ - \frac{{{\sigma_{x'}}{\sigma_{\varphi '}}}}{{\sqrt {{\sigma_{ux'}^{+} \sigma_{ux'}^{-} \sigma_{u\varphi '}^{+} \sigma_{u\varphi '}^{-} }} }} - \frac{{{\sigma_{\varphi '}}{\sigma_r}}}{{\sqrt {{\sigma_{u\varphi '}^{+} \sigma_{u\varphi '}^{-} \sigma_{ur}^{+} \sigma_{ur}^{-} }} }} - \frac{{{\sigma_r}{\sigma_{x'}}}}{{\sqrt {{\sigma_{ur}^{+} \sigma_{ur}^{-} \sigma_{ux'}^{+} \sigma_{ux'}^{-} }} }}, $$

where indices “+” and “−” correspond to ultimate strengths in tension and compression, respectively.

Functions Φ from (3) or F from (4), depending on the applied strength criterion, define the area, at the boundary of which the critical SSS is reached: if the condition Φ < 1 (or F < 1) is valid, no fracture occurs, while violation of this condition means fracture and strength collapse. Since criteria (3) and (4) are formulated in the coordinate system coinciding with the principal axes of anisotropy, while the SSS is calculated in the global cylindrical coordinate system, the stress tensor should be turned at the respective reinforcement angle α using the available formulas [14], in order to calculate stresses figuring in these criteria. The strength evaluation procedure should be executed in each finite-difference cell of the calculation area at each time step. Moreover, it is necessary to vary the angular coordinate φ with small enough step (no more than 20°). Thus, if the condition Φ < 1 (or F < 1) is satisfied within the total calculation area and in the total calculated time range, the structure’s strength can be considered sufficient. If this condition is violated at least in one point and at any instant, the strength criterion is not satisfied.

The limiting surface of Tsai–Wu (4) is a classical surface of the second order, which is always convex in six-dimensional stress space. Differing strength values of a composite material in tension and in compression is caused by the offset of the centre (4) relative to the coordinate system origin. The Ashkenazi limiting surface (3) always has a central symmetry, is a particular case of the fourth order surface, it can have alternating curvature and consist of convex and concave sections, which are absolutely smoothly integrated with each other [2].

Noteworthy is that a load in the form of function (2) is discontinuous in time and space. Therefore, its Fourier-series expansion by angle φ is inevitably accompanied by the Gibbs parasitic effect [6,15], consisting in occurrence of the function false spike in the vicinity of points of breaks. In order to eliminate this deficiency, several options have been applied:

  1. (i)

    as any approximate numerical method, the Wilkins algorithm [4–6,11] is characterized by individual numerical viscosity due to approximation of derivatives by finite differences;

  2. (ii)

    in order to ensure stability of computing process and smoothing of steep, first of all explosive, wave fronts, an artificial viscosity in the linear and square forms [6,11] is used;

  3. (iii)

    strength verification is provided not for a continuous interval, but for a discrete set of angular coordinates φ i with step φ i+1 − φ i  ≈ 20°, which has practically no effect on the computation process of SSS estimation;

  4. (iv)

    the Gibbs effect is, first of all, induced by higher harmonics and exhibits itself during summation of quite a large number of Fourier series terms [15]; whereas the number of harmonics in problems under study did not exceed 11, including the zero harmonic;

  5. (v)

    if the Gibbs effect is observed, despite the aforesaid in clauses (i)–(iv), the error obtained will increase the safety margin.

Numerical studies have been performed for single- and two-layered cylinders (with internal radius R 1 = 0.1 m, thickness H = 0.02 m, and length L = 0.4 m) from graphite-epoxide T300/976, with such physicomechanical and strength characteristics [10]: E x  = 156,000 MPa, E φ = E r  = 9090 MPa, G φx  = G rx  = 6960 MPa, G φr  = 3240 MPa, ν xφ = 0.228, νφr  = 0.4, ν rx  = 0.013, the material density ρ = 1540 kg/m3, \( \sigma_{ux}^{+} \) = 1520 MPa, \( \sigma_{ux}^{-} \)= 1590 MPa, \( \sigma_{u\varphi }^{+} \) =\( \sigma_{ur}^{+} \) = 45 MPa, \( \sigma_{u\varphi }^{-} \)= \( \sigma_{ur}^{-} \) = 252 MPa, and τ uxφ = τ uφr  = τ urx  = 105 MPa. Here E i , G ij , ν ij (i, j = x, φ, r, i ≠ j) are technical characteristics of elasticity of orthotropic material in the anisotropy principal axes with reinforcement angle α = 0, i.e., in case of cylindrically orthotropic body with anisotropy principal axes coinciding with the global cylindrical coordinate axes [15]: E i are elastic moduli, G ij are shear moduli, and ν ij are Poisson’s ratios in the respective directions and planes. The strength characteristics are also given for a zero reinforcement angle. In this case, equations [14] should hold:

$$ {E_i}{\nu_{ji}} = {E_j}{\nu_{ij}},\quad i \ne j, $$
(5)

while for real materials the compliance matrix determinant is more than zero and it can be converted into a stiffness matrix.

In a single-layered cylinder, a reinforcement angle α = 45° is used. In case of a two-layered shell, layers have the same thickness H/2, whereas the reinforcement angle of the internal layer is 45° and of the external one is −45°. Insofar as the ultimate strength of the given material in tension and compression is different, the cylinder strength is evaluated via the Tsai–Wu criterion (4).

The number of calculated harmonics depends on the location of the explosive charge. If it is located at the longitudinal axis of symmetry of the cylinder [at x-axis, which corresponds to λ = 0 in Eq. (2)], the problem becomes axisymmetric and thus only zero harmonic should be considered, since harmonics of higher order become identically equal to zero. If the explosive charge has a radial offset relative to shell centre (0 < λ < 1), then, similarly to [6], the adequate representation of non-axisymmetric SSS (and, consequently, strength) requires calculation of 11 harmonics, including the zero one. In addition, two-dimensional dynamic calculations in polar coordinates r, φ were executed for infinitely long cylinders under non-axisymmetric plane strain conditions, whereas η = 0 was taken in Eq. (2). Provided condition λ = 0 was also satisfied, i.e., for zero radial offset of the explosive charge, the two-dimensional nonstationary boundary problem degenerates into the unidimensional one.

Table 1 indicates the maximal values of strength function F by the Tsai–Wu criterion (4), which occur in a single- and two-layered cylindrical elements with boundary conditions (1) at the edges for the calculated time interval T calc = 2∙10−4 s, depending on the axial offset x 0 of the explosive charge. During the time interval T calc the action of pulse load (2) has excited cylinder oscillations, and several complete periods of radial and other oscillations have already took place. Zero radial offset of the explosive charge is considered (λ = 0).

Table 1 Effect of the Axial Offset of Explosive Charge on Calculated Strength of Cylinders
Full size table

As follows from data in Table 1, strength of structural components is ensured for any axial offset of the explosive charge. In this case, value of x 0 has a feeble effect on the cylindrical shell strength: variation of x 0 from zero to L/2 results in variation of F max within the range 0.708 ± 0.025 for single-layered and of 0.6165 ± 0.0335 for two-layer cylinder. Therefore, in all calculations the explosive charge was placed in plane of the central cross section of the cylinder x = 0, i.e., with no axial offset (x 0 = 0). Additionally it has been revealed that substitution of a single-layered cylindrical package by orthogonally-symmetrically reinforced (α1,2 = ±45°) two- layered one of the same thickness and from the same composite material results in the safety margin increase from 11.1 to 18.3 % depending on the explosive charge location.

The effect of explosive charge radial offset characterized by dimensionless parameter λ = r 0/R 1 on dynamic strength of similar cylinders has been also studied for the same calculated time interval (2∙10−4 s) and the results are tabulated in Table 2.

Table 2 Effect of the Radial Offset of Explosive Charge on Calculated Strength of Cylinders
Full size table

Comparison of data in Tables 1 and 2 shows that radial offset of the explosive charge has a stronger effect on the shell strength, than axial one. Increase in λ results in the safety margin reduction. The latter makes about 30 % for single-layered and about 40 % for two-layered cylinders at λ = 0, but at λ = 0.08 the strength criterion does not hold for shells.

The two-dimensional approach can be applied as the first approximation to strength calculations of cylinders from the considered composite (graphite-epoxide T300/976) with use of the Tsai–Wu criterion for loads of type (2). According to Table 2, the results of 2D- and 3D-calculations of the minimum strength by the Tsai-Wu criterion show quite good fit. Thus, in the most, but not all, cases, 3D-calculation is more conservative (e.g., at λ = 0.1 for one-layered cylinder and at λ = 0 for two-layered one). The maximal discrepancy in F max values of 2D- and 3Dcalculations does not exceed 8.3 %. Unfortunately, generalization of the above findings for other pulse loads different from (2), materials and strength criteria requires additional verification. It will shown further that, despite close results on F max, the distinction in the SSS of cylinders calculated by 2D- and 3D-methods is essential.

Considerable effect on dynamic strength of shells is rendered by 3D-effects, as well as by non-axisymmetry of load and the SSS. The increase of λ from zero to 0.08 results, according to formula (2), in the increase in maximum pressure value at the internal surface only by 28.4 %, while the time of its action is diminished by 8 %. Nevertheless, as seen from Table 2, even safety margin exceeding 40 % turned out to insufficient for the two-layered cylinder for λ = 0 to satisfy the strength criterion at radial offset of the explosive charge λ = 0.08.

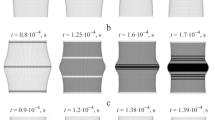
From all the above cases, the strength function attains its maximum F max in the time interval from 15 to 30 μs, i.e., in the first quarter of the period of radial oscillations of the cylinder. The most critical is the zone (x = x 0, Φ = 0), which is located at the minimal distance from the centre of explosive charge [see formula (2)]. For two-layered cylinders, in certain cases, the most dangerous becomes the edge zone (x = ± L/2), which has the minimal distance from explosive charge. No strongly manifested effects of “swing” type [4,16], induced by excitation of shell bending oscillation forms of “barrel-saddle” type and leading to axial runout/flapping, which occur after about 5–10 periods of radial oscillations and later, have been observed. This is attributed to the fact that such “swing” is usually an intrinsic feature of dynamics of shells with free edges [4,16]. In case under study, kinematic boundary conditions (1) at the shell edges make it possible to increase shell stiffness, as compared to that with free edges, and essentially hinder excitation of free bending oscillations, which initiating a “swing.” Noteworthy is that at λ = 0, i.e., under non-axisymmetric loading conditions, oscillating effects of flapping type occurêed, which were visually similar to a “swing,” but had a physical nature not related to bending oscillation forms. These effects are caused by excitation of wave processes along the circumferential coordinate, while being absent at λ = 0, they increase with growth of λ and become most strongly manifested in case of 2D-calculations, where no bending oscillation forms can take place by definition.

Figure 1 illustrates the results of 2D-calculations of the SSS at the internal surface of a single-layered cylinder. It is visible that flapping oscillations occur in antiphase in shell points located in the opposite angular coordinates and grow with increase in λ. A similar pattern was observed for the two-layered cylinder. Therefore, in order to ensure reliability of results obtained in strength calculations of shells subjected to strongly non-axisymmetric pulse pressure, it is necessary to increase the calculation time range to no less than 10 complete periods of radial oscillations of the cylinder.

Fig. 1
figure 1

Kinetics of σφ for various values of φ at the internal surface of a single-layered cylinder: (a)λ = 0; (b) λ = 0.2; (c) λ = 0.4. (Solid lines correspond to φ = 0; dashed lines to φ = π.)

Full size image

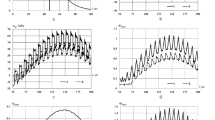
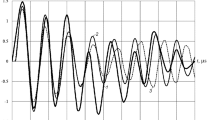
It has been already mentioned that, despite close fit of results on the minimum safety margin (F max), the SSS estimations of shells via 2D- and 3D-methods are essentially different. This is illustrated by Figs. 2 and 3, where stress variation kinetics in various points of single- and two-layered cylinders are shown for the case of explosive charge location (x 0 = 0, λ = 0.1). Frequencies of radial oscillations practically coincide, while the peak values of stresses calculated by a 2D-method essentially (twice and more) exceed those calculated by a 3D-method. Quite unexpectedly, in strength estimations by the Tsai–Wu criterion, the 3D-calculations in the most cases yielded more conservative results than the two-dimensional ones (see Table 2). Hence, in estimations of both the dynamic three-dimensional SSS, and strength, there are no strict substantiations for application of the simplified 2D-methods of calculation of similar thick-walled cylindrical structural components, insofar as under conditions of nonaxisymmetric pulse loading depending on circumferential and longitudinal coordinates simultaneously, a comprehensive account of wave processes along all three coordinates (x, φ, and r) based on the general three-dimensional theory should be applied, in order to obtain adequate results.

Fig. 2
figure 2

Stresses in various points of a single-layered cylinder. [Here and in Fig. 3: (a) x = 0, r = R 1, φ = 0; (b) x = 0, r = R 1, φ = 0; solid lines = 3D-calculations, dashed lines = 2D-calculations.]

Full size image
Fig. 3
figure 3

Stresses in various points of a two-layered cylinder.

Full size image

Conclusions

  1. 1.

    A numerical-analytical method and software package for calculation of nonstationary three-dimensional non-axisymmetric SSS and strength (with use the Ashkenazi or Tsai–Wu strength criteria) of multilayer thick-walled elastic cylindrical shells with spiral orthotropy of layers have been developed.

  2. 2.

    Using particular boundary problems as an example, possibilities of the proposed method have been shown and some recommendations have been made on calculation of multilayer nonstationary SSS and strength of similar structures subjected to internal shock loading by an explosive charge with an offset relative to the shell centre of symmetry.