Introduction. This work is focused on specific numerical dynamic strength analysis of metal-composite thick-walled cylindrical shells and, as limiting cases, purely metal or purely composite ones. The overall dimensions of the cylinders, internal explosion loading conditions, and the relevant notations were as used earlier in [1].

Object of Research. In a general case, a shell can be fabricated of two materials: an internal isotropic metallic layer and an external unidirectionally reinforced composite layer which in turn can be either a spirally (or cylindrically transtropic) single ply or equi-thickness double ply with an orthogonal reinforcement configuration [α; α ± 90°] where α is the reinforcement angle for the inner ply (with respect to the double ply) and (α ± 90°) for the outer ply.

The charge mass M ch was chosen such that the relative explosive charge mass was constant [2]:

$$ \chi =\frac{{{M_{ch }}}}{{{M_0}}}=\mathrm{const}, $$
(1)

where M 0 is the shell’s total mass.

Hence, we have

$$ {M_{ch }}\left( \beta \right)=\pi \chi L\left( {{R_2}-{R_1}} \right)\left\{ {{\rho_c}\left( {1-\beta } \right)\left[ {2{R_1}+\left( {{R_2}-{R_1}} \right)\left( {1+\beta } \right)} \right]+{\rho_m}\beta \left[ {2{R_1}+\beta \left( {{R_2}-{R_1}} \right)} \right]} \right\};\quad 0\leqslant \beta =\frac{{{h_m}}}{{{R_2}-{R_1}}}\leqslant 1, $$
(2)

where ρ c is the density of the composite, ρ m is the metal density, h m is the metal layer thickness, and β is the metal layer thickness ratio. In the calculations hereinafter the quantity χ was taken to be 0.003.

For the metal layer we used steel 20 with the following physical-mechanical characteristics [3]: ρ m = 8000 kg/m3, the Young modulus E = 2.02∙105 MPa, Poisson’s ratio ν = 0.3, and yield stress σ Y = 250 MPa. This steel was able to deform elastically and elastoplastically and obeyed the equations of the no-hardening flow theory; the Mises criterion was used as a condition for the onset of plastic deformation.

The composite part of the shell was assumed to be made of an elastic spirally transtropic unidirectionally reinforced (along x′) graphite epoxide with the following physical-mechanical characteristics along the principal anisotropy axes [4]: ρ c = 1600 kg/m3, E x′ = 150,000 MPa, E φ′ = E r = 9000 MPa, ν x′φ′ = 1/3, νφ′r = 1/2, G x′φ′ = G x′r = 6000 MPa, σ+ ux′ = 2000 MPa, σ- ux′ = 1500 MPa, σ+ uφ′ = σ+ ur = 40 MPa, σ- uφ′ = σ- ur = 150 MPa, τ ux′φ′ = τ urx′ = 80 MPa, and τ uφ′r = 45 MPa. This composite deforms elastically up till failure.

Thus, we have a composite shell when β = 0, a metal shell when β = 1, and a metal-composite one in the case of intermediate β values. The metal cylinder was always a single layer [steel 20]; the composite one could be a unidirectionally reinforced single-ply [α] or an equi-thickness orthogonally reinforced double-ply [α; α ± 90°]; the metal-composite cylinder could be a two-layer [steel 20; α] or three-layer design [steel 20; α; α ± 90°] with equi-thickness intermediate and external composite plies.

It can be easily verified that the Hoffman strength criterion for this graphite epoxide material does not meet the condition of invariance in the anisotropy plane, while the Tsai–Wu criterion does obey this condition. The Ashkenazi criterion and the updated linearly quadratic criterion [1] are suitable only for the materials that have equal strength in tension and compression. Based on the rules stated in [1], considering that the overwhelming majority of cases, except for a confluent extreme case of β = 1, deal with a composite whose tensile and compressive strength essentially differ, it is only the Tsai–Wu criterion which can be used as a strength criterion in the calculations. Therefore, during further analysis the strength of dynamically loaded shells was assessed by the Tsai–Wu failure criterion.

Numerical Investigations. The calculations were performed in five stages:

  • (i) choosing an optimal reinforcement configuration for the composite part of the shell;

  • (ii) clarifying the influence of the axial location of an explosive charge on the strength of the optimally reinforced composite shell;

  • (iii) choosing an optimal steel layer thickness ratio β of the metal-composite cylinder with the optimal reinforcement configuration of its composite part in the cases of the most and least dangerous axial locations of the explosive charge;

  • (iv) checking the optimal metal-composite cylinder design [as defined at stage (iii)] for optimal reinforcement angle of the composite part;

  • (v) discussing the findings and performing additional analyses, making up conclusions.

The design time interval was limited to the first half-period of radial vibrations of the shell because it is this half-period which is the most critical one from the strength standpoint, as was mentioned earlier in [1]. Therefore, the numerical computation was stopped as soon as the value of the radial displacement of the cylinder’s internal point closest to the charge (x = x 0; r = R 1) upon the start of loading action became zero and changed its sign.

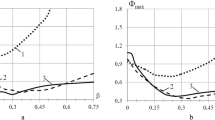
Choosing an Optimal Reinforcement Configuration. We set β = 0; in this case, the explosive charge mass M ch was 0.0265 kg according to (2). The charge was placed at the cylinder’s center of symmetry (x 0 = 0). Figure 1 shows the variation of values of the strength function Ψmax by the Tsai–Wu criterion versus the reinforcement angle and configuration for the cylinder. It is evident that the optimal case (from among those considered) for strength is to fabricate the composite part of the shell in the form of an equi-thickness orthogonally reinforced double ply [0; ± 90°]. With this reinforcement configuration the strength condition is met, while with other reinforcement configurations, as well as in the case of a single-layer cylinder, the strength criterion for the structural element is not obeyed.

Fig. 1
figure 1

For choosing an optimal reinforcement configuration for the composite part of the shell. (Solid line – single-layer cylinder, dashed line – equi-thickness two-layer cylinder.)

Full size image

Clarifying the Influence of the Explosive Charge Axial Location on Strength of the Composite Shell. For the optimal equi-thickness double-ply composite shell with reinforcement [0; ± 90°] the explosive charge location – the value of x 0 was varied from 0 to L/2. The resulting values of Ψmax were in the range 0.98 ± 0.03. This suggests that the axial location of the explosive charge has only a slight effect on the strength of dynamically loaded composite cylinder. The analysis has revealed that the explosive charge location near the end of the cylinder (x 0 = L/2) presents the greatest danger – the strength function in this case was able to reach and exceed unity, i.e., a local failure of the shell material was noted; the explosive charge location near the cylinder center of symmetry (x 0 = 0) was the least dangerous – the Ψmax values did not exceed 0.95.

Choosing an Optimal Steel Layer Thickness Ratio β of the Metal-Composite Cylinder. We considered a three-layer metal-composite shell [steel 20; 0; ± 90°] whose external composite part is an equi-thickness double ply with an optimal reinforcement configuration as outlined above. The metal layer thickness ratio β was varied from zero to unity. In this case, the corresponding explosive charge mass M ch was computed by (2) and varied from M ch (0) = 0.0265…M ch (1) = kg. The calculated results are shown in Fig. 2. Figure 2a and 2b illustrates the respective variations of the strength function Ψmax and hoop strain εφ max at the shell’s internal point closest to the explosive charge location (with coordinates x = x 0; r = R 1) versus β. It is evident that εφ max increases monotonically with β from zero to unity; for the centrally located charge this dependence is close to linear one. Despite this fact, the optimum for strength is achieved at an intermediate value of the metal layer thickness, namely: at β ≈ 1/3 for both the central and end locations of the explosive charge. Thus, the optimal (from the strength standpoint) layer thickness ration for the three-layer metal-composite shell [steel 20; 0; ± 90°] to (1) is 1/1/1, i.e., the optimally subject designed three-layer metal-composite cylinder should have equi-thickness layers.

Fig. 2
figure 2

For choosing an optimal metal layer thickness ratio for the metal-composite cylinder. [Solid line corresponds to the central location of the explosive charge (x 0 = 0) and dashed one to the end location (x 0 = L/2.]

Full size image

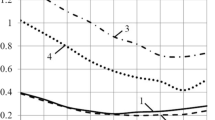
It should be mentioned that this (optimal) metal-composite cylinder the influence of the axial location of the explosive charge on the strength is quite significant (Fig. 3). It is obvious that the presence of an internal elastic-plastic metal layer (the calculations have demonstrated that in all of the above-mentioned cases the cylinder’s metal part undergoes plastic deformation) leads to a situation where the end location of the explosive charge is more dangerous in comparison to its central location.

Fig. 3
figure 3

The influence of axial location of explosive charge on strength of the metal-composite cylinder.

Full size image

Checking the Metal-Composite Cylinder Design for Optimal Reinforcement Angle. Since the solution of the optimization problem for the previous three stages is not quite strict (it is based on some engineering assumptions and common sense considerations), it is necessary to verify whether the equi-thickness three-layer metal-composite shell [steel 20; α; α ± 90°] will be optimal for strength at α = 0. Figure 4 shows the variation of Ψmax versus α for the central and end locations of the explosive charge. It is seen that the strength optimum for the equi-thickness three-layer cylinder is indeed achieved in the case of an orthogonal lateral-axial reinforcement [0; ± 90°] of its double-ply composite part. The optimal cylinder should have a three-layer design: its internal layer being an isotropic metallic material, the intermediate layer being a cylindrically transtropic composite with axial reinforcement, and the external layer being a cylindrically transtropic composite with circumferential reinforcement; the layer thickness ratio should be 1/1/1. At this point the solution of the optimization problem can be considered completed.

Fig. 4
figure 4

The effect of the reinforcement configuration of the composite part of the shell on strength of the metal-composite cylinder. (Solid line – central location of the explosive charge; dashed line – end location of the explosive charge.)

Full size image

As evident from the data in Figs. 3 and 4, the explosive charge location near the shell end is the most dangerous: the stress-strain state (SSS) and strength are unpredictable in this case. It is seen from Fig. 4 that even minor deviations of the reinforcement angle from the optimal one can lead to an almost three-fold increase of values of the Ψmax function. Furthermore, in the case of central location of the explosive charge with any orthogonal reinforcement configurations [α; α ± 90°] of the external equi-thickness composite double-ply the cylinder strength was ensured with a given margin, while in the case of the end location of the charge the condition for strength was obeyed only by the optimal reinforcement [0; ± 90°] of the composite part of the shell.

Discussion. The calculations demonstrate that in the majority of cases considered the following zones turned out to present the greatest danger from the strength standpoint: for a single-layer cylinder: the vicinity of section (x = x 0) which lies closest to the charge location; for the two-and three-layer cylinders: the vicinity of the same section and a zone near the shell end (x = ± L/2) located closest to the explosive charge. Also, in the multi-layer cylinders there are special points near the shell end – the places where the contact cylindrical surface reaches the free flat end – where singularities may even arise at certain combinations of elastic characteristics of the layers in contact [5]. In the case of the end location of the explosive charge (x = ± L/2), these zone merge and SSS becomes most critical.

The presence of possible singularities in multilayer shells imposes additional requirements on the numerical calculation procedure during the solution of optimization problems, namely: all the calculations for cylinders with constant preset dimensions (R 1, R 2, and L) should be performed on the same finite-difference mesh with invariable discretization steps in axial and radial coordinates (in this particular case, the radial step Δr = 1.25 mm, the axial step Δx = 2Δr = 2.5 mm). Then, even if some unnaturally large stresses are noted near the singular points, their minimum (and thus the minimum of the strength function Ψ) will be attained only with the optimal reinforcement configuration and layer thickness ratio of the multilayer cylinder. For the quantitative assessment of the strength margin or the extent to which the strength is exceeded one should apply other criteria (energy-based, integral, etc.) that characterize SSS in a volume rather than at a point. The criteria as considered above (Ashkenazi’s, Tsai–Wu’s, Hoffman’s, etc.) deal with SSS just at a point; therefore, the validity of their application to bodies with irregular boundaries and singular points is arguable.

The analysis performed for the equi-thickness three-layer shell [steel 20; α; α ± 90°] with an end location of the explosive charge (x 0 = L/2) has shown the reinforcement configuration with α ≈ 22° (Fig. 4) to be the most dangerous. In this case, danger arises from the vicinity of the end contact zone between the intermediate and external layers, which is located in the intermediate layer: x → x 0, -0, r → [(R 1 + 2R 2)/3]-0. The stress-strain state near this zone is as follows: σ x = τ xφ = τ xr = 0 in view of boundary conditions at the free end.

The calculations have demonstrated that the function Ψ reaches its maximum at an instant far exceeding the duration of the internal pressure action on the cylinder inner surface, namely: at a quarter-period of radial vibrations of the cylinder. At this instant, in the above-mentioned zone the stresses σφ and τ rφ are maximum, while σ r is insignificant. Therefore, it can be inferred that the shell strength is governed mostly by the values of σφ max and τ rφ max in the vicinity of this zone. The data on variations of these quantities versus the reinforcement angle are summarized in Table 1.

Table 1 Variation of Stress State at a Dangerous Point Versus Reinforcement Angle of the External Composite Double-Ply
Full size table

A comparison between the data given in Fig. 4 and Table 1 shows that the most dangerous (from the strength standpoint) situation arises when τ rφ max and the ratio τ rφ max/σφ max simultaneously reach their maxima as functions of α (τ rφ max/σφ max > 1 at α = 22°). An almost ten-fold increase in σφ max at α = 90° (in comparison to the case with α = 22°) with almost no τ rφ was less dangerous because with such reinforcement the intermediate composite layer had the maximum circumferential strength.

The composites under consideration feature an essential anisotropy of both elastic and strength properties: depending on the direction the ultimate strength can vary from 40 to 2000 MPa in tension, from 150 to 1500 MPa in compression, and from 45 to 80 MPa in shear. The Tsai–Wu’s linearly quadratic strength criterion involves shear terms in the form of purely quadratic additives [1], and the emergence of new off-diagonal stress tensor components will most likely be undesirable from the strength standpoint.

The most optimal orthogonal reinforcement configuration for the composite double-ply seems to be the configuration [0; 90°] whereby the spiral orthotropy degenerates into the cylindrical one, all the torsional modes are identically absent, and two out of three shear components of the stress tensor are identically nullified: τ xφ ≡ τ rφ ≡ 0. The configuration [90°; 0] has all these properties too; however, the calculations have demonstrated that the configuration [0; 90°] is more optimal and leads to lower values of the strength function Ψ. Any deviations from this reinforcement configuration results merely in higher Ψ.

The dependence of the function Ψ on normal stresses has a more complex trend. Furthermore, the scatter of strength characteristics with regard to normal stresses versus the direction is much larger (up to 50-fold). Considering that for similar problems (cylindrical shells under the action of internal transient pressure) it is the normal (hoop) stress which is the governing stress in most cases, the optimal reinforcement configuration, optimal layer thickness ratio for a three-layer metal-composite shell, and the most dangerous location of the explosive charge can be found only on the basis of preliminary numerical optimization strength analysis.

As mentioned above and in [1], the irreversible energy lossess in an internal steel layer under plastic deformation lead to an increase in strength margin of a multilayer metal-composite shell. Let us consider an optimally designed equi-thickness (β = 1/3) three-layer metal-composite cylinder [steel 20; 0; ± 90°] under the action of a central symmetric (x 0 = 0) explosion. The data in Figs. 2–4 show that this is the safest case from the stength standpoint. The calculations reveal that the most dangerous point lies in the intermediate composite layer near the interface with the internal steel layer {r → [(2R 1 + R 2)/3] + 0} in the central section closest to the explosive charge. We will demonstrate that even in this case the influence of plastic strains in the metal on the global SSS and strength of the multilayer cylinder will be quite significant.

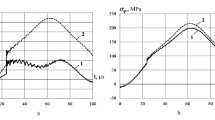
The effect of plastic deformation of the steel layer on SSS and strength of the cylinder is illustrated by Fig. 5.

Fig. 5
figure 5figure 5figure 5figure 5figure 5figure 5

The influence of plastic deformation of the internal metal layer on SSS and strength of the metal-composite cylinder: (a) maximum values of the strength function; (b) hoop strain at the inner central point (x = 0; r = R 1); (c) hoop stress at the same point; (d) axial stress at the same point; (e) hoop stress at the dangerous point {x = 0; r → [(2R 1 + R 2)/3] + 0}; (f) axial stress at the same point. [Solid lines – data obtained for elastic-plastic steel 20 (σ Y = 250 MPa); dashed lines – assumption that steel is perfectly elastic (σ Y = ∞).]

Full size image

Radial stresses at the internal central point correspond to the boundary condition [1] σ r = -P 0 H(t 0 - t), where P 0 = 104 MPa and t 0 = 15.85 μs. At the dangerous point the dependence of σ r on t is more complex, and the maximum magnitude of the stresses is always lower than P 0. Nevertheless, the radial stresses have an essential effect on strength of the shell for the ultimate strength values of this composite in the radial direction are fairly low: 40 MPa in tension and 150 MPa in compression (irrespective of reinforcement configuration and direction of spiral reinforcement because the radial direction in these problems always coincides with one of the principal directions of anisotropy, which features the minimum stiffness and strength). There are no shear stresses in the entire central section (x = 0).

Analysis of data given in Fig. 5 shows that the plastic deformation of the internal steel layer permits lowering the level of maximum values of the strength function Ψ by a factor of 1.5 in comparison to the elastic problem statement (with σ Y = ∞) – Fig. 5a. The plastic transition in the steel has an essential influence not only on SSS of the steel layer (Fig. 5b–d) but also on SSS of the elastic composite layers (Fig. 5e). In this case, the level of maximum stresses is lower than that for the elastic problem statement with σ Y = ∞ [except for σ x at the dangerous point (Fig. 5f), but in this case the discrepancy between the curves is very small]. This is due to irreversible losses of energy, which was taken by the system from the explosion loading, for plastic deformation of the metal.

Thus, during the design of structural elements of an explosion-proof chamber (EPC) a thing of great importance is to choose the right steel grade for the internal layer. For example, it is not recommended to use alloyed steels (such as 20KhNZA, 30KhGSA, 40KhNMA, etc.) for they have a fairly high yield stress (850–1600) MPa [3] and tend to deform almost elastically under such loading. Taking into account that density and elastic characteristics of all steel grades differ only slightly [3], during the SSS and strength analysis one encounters an unfavorable situation close to that corresponding to dashed lines in Fig. 5. For such EPCs it is recommended to use plastic steels (such as grade 20) with a comparatively low yield stress and high ultimate strain ε u at failure.

Note that although an all-metal shell (β = 1) made of steel 20 will be strong enough to withstand the explosion loading conditions with a charge mass ratio χ = 0.003 in all of the above-mentioned cases {the maximum hoop strain does not exceed 1% (Fig. 2b), while ε u for steel 20 is at least one order of magnitude, if not 20 times, higher [3]}, this cylinder will unpractical regarding the materials consumption: it is almost 2.16 times heavier than the optimal (β = ± 1/3) three-layer [steel 20; 0; ± 90°] shell.

Conclusions

1. With the materials considered (steel 20 and transtropic unidirectionally reinforced graphite epoxide) for a cylinder of fixed dimensions and a charge mass ratio, the equi-thickness three-layer metal-composite shell [steel 20; 0; ± 90°] has turned out to be the most optimal for strength (by the Tsai–Wu criterion).

2. It has been found out that the most dangerous location of the explosive charge is near one of free ends of the cylinder and the least dangerous location at the shell’s center of symmetry.

3. The most dangerous points are localized either in the cross-section x =const closest to the charge or at the end closest to the charge.

4. The irreversibel energy losses for plastic deformation of the internal metal layer result in a larger strength margin of the multilayer cylinder as a whole. Therefore, it is not advisable to use high-quality steel grades (such as 20KhNZA, 30KhGSA, 40KhNMA, etc.) with a high yield stress for internal structural elements of EPCs. Most recommended steels are the plastic ones with a relatively low yield stress and high ultimate strain at failure.