Intertemporal choice as a tradeoff between cumulative payoff and average delay

Abstract

Intertemporal choice involves outcomes that are received in different moments of time. This paper presents a new framework for analyzing intertemporal choice as a tradeoff between the cumulative payoff of a stream of intertemporal outcomes and its average delay (similar to the mean–variance approach in modelling risk preferences). Ceteris paribus, a decision maker prefers a stream of intertemporal payoffs with a higher cumulative payoff and a lower average delay. A decision maker with such time preferences always dislikes a partial delay in consumption (splitting one payoff into two, one of which is slightly delayed in time). In contrast, many existing models (e.g. discounted utility, quasi-hyperbolic discounting, generalized hyperbolic discounting or liminal discounting) imply a preference for partial delay. Our proposed model is compatible with the common difference effect (corresponding to a horizontal fanning-out of indifference curves) and the absolute magnitude effect (corresponding to a vertical fanning-in of indifference curves). The proposed model is applied to the standard consumption-savings problem with a constant interest rate. A simple experimental test of the proposed model vs. discounted utility and quasi-hyperbolic discounting is presented.

1 Introduction

Intertemporal choice involves outcomes that are received in different moments of time. It arises in many economic situations such as consumption/savings decisions, financial investment, education planning and career choice, dynamic games and bargaining etc. Samuelson (1937) proposed a classic model of time preferences known as discounted utility or constant (exponential) discounting. This model gained momentum in economics after Koopmans (1960) provided its axiomatization. Discounted utility of a stream of intertemporal payoffs is given by the exponentially-discounted sum of utilities of its payoffs.

Thaler (1981) argued that a decision maker may prefer to consume one apple today over two apples tomorrow and have a reversed preference when both consumptions are delayed for one year. Such time preferences cannot be rationalized by discounted utility. This descriptive limitation of discounted utility became known as the common difference effect (Loewenstein and Prelec 1992). It motivated the development of numerous generalizations of discounted utility. These include, inter alia, quasi-hyperbolic discounting (Phelps and Pollak 1968), generalized hyperbolic discounting (Loewenstein and Prelec 1992) and liminal discounting (Pan et al. 2015). Yet, these generalizations, like discounted utility itself, share a common counter-intuitive property: splitting one intertemporal payoff into two payoffs, one of which is slightly delayed in time, may increase overall utility.

Blavatskyy (2015) gives an example of a decision maker who chooses between receiving two million dollars now and receiving one million dollars now as well as one million dollars at a later moment of time. If this later moment of time is sufficiently close to the present moment, a decision maker with a concave¹ utility function prefers the delayed split payment due to Jensen’s inequality. As Baucells and Sarin (2007a, 2007b) put it: “… we would like the intertemporal models to satisfy … local substitutability: as the time distance between periods becomes small, the marginal rate of substitution should approach one. Otherwise, a receipt of two dollars, as compared to one dollar now and one dollar a bit later, could produce a utility jump.” Blavatskyy (2016) proposed a generalization of the present discounted value—rank-dependent discounted utility—which cannot increase when one payoff is split into two payoffs, one of which is slightly delayed in time.

This paper presents a new framework for analyzing intertemporal decision making. Any stream of intertemporal payoffs can be characterized by two objective statistics: its cumulative payoff and its average delay. A cumulative payoff is a desirable attribute and an average delay is an undesirable attribute. A decision maker, who decides over time, trades off the cumulative payoff of a stream of intertemporal outcomes against its average delay according to her subjective time preferences. A very patient decision maker opts for a stream of intertemporal payoffs that yields the highest cumulative payoff. A very impatient decision maker opts for a stream of intertemporal payoffs that yields the shortest average delay. Our presented model of intertemporal choice is similar to the mean–variance approach of Markowitz (1952) for modeling risk preferences in financial decision making.

Scholten and Read (2010) were the first to consider a tradeoff between differences in valued outcomes and differences in weighted delays. Read and Scholten (2012) extended the model of Scholten and Read (2010) and characterized a sequence of intertemporal outcomes by its cumulative payoff (exactly as in this paper) and its adjusted delay. The average delay considered in this paper is a special case of the adjusted delay (the weighted average) in Read and Scholten (2012). The model of Read and Scholten (2012) overlaps with the model presented in this paper when the adjusted delay in Scholten and Read (2010) is the weighted average and utility function that integrates cumulative payoff and average delay in this paper takes a specific form proposed by Scholten and Read (2010). Scholten et al. (2016) consider a different adjusted delay where time periods are weighted by cumulative utilities of outcomes.

Manzini et al. (2010) proposed another model of multi-criteria decision making over time. In their model, a decision maker first compares streams of intertemporal outcomes according to their discounted utility. If one stream is far superior than other streams in terms of discounted utility, then it is chosen straight away. If all streams are similar in terms of discounted utility, a decision maker decides according to the second criterion. This criterion is assumed to be one prominent, possibly context-dependent, attribute (e.g. either outcome or time dimension).

Rubinstein (2003) proposed a three-stage procedure for intertemporal choice that closely resembles the similarity approach of Rubinstein (1988) developed for choice under risk. In this procedure, a decision maker first checks for temporal dominance: if one alternative yields a larger monetary outcome at an earlier moment of time, then this dominant alternative is chosen straight away. If neither alternative dominates the other, the decision maker checks if the two alternatives are similar either in temporal or in outcome dimension. If the two alternatives are similar in the temporal dimension but not in the outcome dimension, the alternative with a larger outcome is chosen. If the two alternatives are similar in the outcome dimension but not in the temporal dimension, the alternative with a shorter delay is chosen. If the two alternatives are similar both in the temporal and in the outcome dimension, then a decision maker decides according to another (not specified) criterion.

The remainder of the paper is organized as follows. A model of intertemporal choice as a tradeoff between cumulative payoff and average delay is presented in Sect. 2. Section 3 illustrates that time preferences in this model are monotone with respect to advanced payments (unlike in discounted utility theory and many of its generalizations). Section 4 shows that the common difference effect implies a horizontal fanning-out of indifference curves in our proposed model. Section 5 shows that the absolute magnitude effect implies a vertical fanning-in of indifference curves in our proposed model. Section 6 presents an application to the standard consumption-savings problem with a constant interest rate. Section 7 presents an experimental test of the proposed model vs. discounted utility and its popular generalization—quasi-hyperbolic discounting. Section 8 concludes.

2 The framework

A vector ${\varvec{x}}\stackrel{\scriptscriptstyle\mathrm{def}}{=}({x}_{0}, {x}_{1}, \dots , {x}_{T})\in {\mathbb{R}}_{+}^{T+1}$ denotes a stream of intertemporal payoffs x_t ∊ ℝ₊ that a decision maker receives in moments of time t ∊ {0, 1, …, T}, for some T ≥ 1. Payoffs are numbered in a chronological order so that t = 0 denotes the present moment of time and t < s denotes the moment of time t ∊ {0,1,…,T} that precedes the moment of time s ∊ {1, …, T}. We consider objective time though the framework could be adopted to a non-linear subjective time perception (cf. Bradford et al. 2019). The cumulative payoff of stream ${\varvec{x}}\in {\mathbb{R}}_{+}^{T+1}$ is given by

$$CP\left({\varvec{x}}\right)=\sum_{t=0}^{T}{x}_{t}$$

(1)

The average delay of stream ${\varvec{x}}\in {\mathbb{R}}_{+}^{T+1}$ is given by

$$AD\left({\varvec{x}}\right)=\sum_{t=0}^{T}\frac{{x}_{t}}{CP\left({\varvec{x}}\right)}t$$

(2)

The average delay of a stream is the sum of all moments of time, at which the stream yields positive payoffs, weighted by the corresponding payoff’s share in the total cumulative payoff of the stream (over all moments of time). A stream that yields only one positive payoff x_t > 0 at moment of time t has the average delay of t. For simplicity, we assume that the stream (0, 0, …, 0) that yields no positive payoffs has the average delay of zero.

Ceteris paribus, a decision maker prefers a stream of intertemporal payoffs with a higher cumulative payoff and a lower average delay. In other words, temporal preferences are represented by a real-valued utility function $U\left(CP\left({\varvec{x}}\right),AD\left({\varvec{x}}\right)\right)$ that is increasing in the first argument and decreasing—in the second argument. We assume that such function U(.,.) is continuous and differentiable. Utility function U(.,.) can be represented with upward sloping indifference curves on a Cartesian plane where cumulative payoff of streams is plotted on the vertical axis and the average delay—on the horizontal axis (cf. Fig. 1).

Fig. 1

Indifference curves in the CP-AD plane

Figure 2 shows indifference curves of a very patient decision maker who opts for streams with the highest cumulative payoff (no intertemporal discounting). Figure 3 shows indifference curves of a very impatient decision maker who opts for streams with the shortest delay. Our model of time preferences as a tradeoff between cumulative payoff and average delay is similar to the mean–variance model of risk preferences as a tradeoff between expected value and risk, as measured by variance or standard deviation (Markowitz 1952).

Fig. 2

Indifference curves of a very patient decision maker (no intertemporal discounting)

Fig. 3

Indifference curves of a very impatient decision maker

3 Advanced payments

Let us consider three streams of intertemporal outcomes. Stream A yields outcome x > 0 now (and nothing in all other moments of time). Stream B yields outcome x/2 now, outcome x/2 at a later moment of time t > 0 and nothing in all other moments of time. Stream C yields outcome x > 0 at time t (and nothing in all other moments of time).²

All three streams yield the same cumulative payoff x. The average delay of stream A is zero, the average delay of stream B is t/2 and the average delay of stream C is t. Thus, in this example, there is no real tradeoff between a cumulative payoff and an average delay: all three streams yield the same cumulative payoff, but stream A yields it sooner, stream B—later and stream C—the latest. According to the model presented in the previous section, any decision maker should prefer A over B over C.

In contrast, a decision maker with an additively-separable non-linear utility function u(.) and discount function D(.), with the conventional normalization D(0) = 1, prefers A over B when

$$u\left(x\right)>u\left(\frac{x}{2}\right)+D\left(t\right)u\left(\frac{x}{2}\right)$$

(3)

and prefers B over C when

$$u\left(\frac{x}{2}\right)+D\left(t\right)u\left(\frac{x}{2}\right)>D\left(t\right)u\left(x\right)$$

(4)

If moment of time t is very close to the present moment, then the right-hand-side of inequality (3) and the left-hand-side of inequality (4) both converge to 2u(x/2); and the right-hand-side of inequality (4) converges to u(x). Thus, if t is sufficiently close to zero then both inequalities (3) and (4) cannot hold at the same time. Either inequality (3) is satisfied but inequality (4) is violated (for a decision maker with a strictly convex utility function) or inequality (4) is satisfied but inequality (3) is violated (for a decision maker with a strictly concave utility function). In other words, a decision maker whose time preferences are represented by discounted utility theory or one of its popular generalizations (quasihyperbolic discounting, generalized hyperbolic discounting or liminal discounting) with a non-linear utility function can reveal either a preference for A over B or a preference for B over C but not both preferences at the same time (when moment of time t is sufficiently close to zero).

Next, we characterize the condition when the model presented in Sect. 2 satisfies the first-order temporal dominance. One stream of intertemporal outcomes first-order temporally dominates another stream if and only if the dominant stream is obtained from the dominated stream through a series of increased and/or advanced payments (Blavatskyy 2018, proposition 1). An advanced payment results from shifting a positive consumption from a later moment of time to an earlier moment of time. Thus, any advanced payment inevitably reduces the average delay while holding the cumulative payoff constant. According to the model presented in Sect. 2, any advanced payment can only increase the desirability of a stream.

An increased payment results from improving the payoff received at some moment of time. An increased payment reduces the average delay (2) if it occurs not later than the average delay. Thus, the model from Sect. 2 always satisfies the first-order temporal dominance if the dominant stream is obtained from the dominated stream through a series of advanced payments and/or increased payments at moments of time proceeding the average delay of the dominated stream.

If the dominant stream is obtained from the dominated stream x through an increased payment at moments of time occurring after the average delat $AD\left({\varvec{x}}\right)$, the model from Sect. 2 satisfies the first-order temporal dominance if inequality (5) holds for all $t>AD\left({\varvec{x}}\right)$.

$$\frac{\partial U\left(CP\left({\varvec{x}}\right),AD\left({\varvec{x}}\right)\right)}{\partial CP\left({\varvec{x}}\right)} +\frac{\partial U\left(CP\left({\varvec{x}}\right),AD\left({\varvec{x}}\right)\right)}{\partial AD\left({\varvec{x}}\right)}\frac{t-AD\left({\varvec{x}}\right)}{CP\left({\varvec{x}}\right)}>0$$

(5)

4 The common difference effect and horizontal fanning-out

The common difference effect is observed when a decision maker prefers to receive a smaller outcome x now rather than to receive a larger outcome y > x at a later time t > 0, but, at the same time, she prefers to receive y in time t + s rather than to receive x in time s, for some s > 0 (Loewenstein and Prelec 1992).³ The common difference effect cannot be rationalized with Samuelson (1937) discounted utility. It implies a violation of one of its axioms, known as stationarity (Koopmans 1960).

Point A on Fig. 4 represents a stream that yields a smaller outcome x now. Point B on Fig. 4 represents a stream that yields a larger outcome y > x at a later time t > 0. If a decision maker prefers A to B then A should be located on a higher indifference curve so that indifference curves are relatively vertical in the vicinity of A and B.

Fig. 4

The common difference effect and horizontal fanning-out of indifference curves

Point C on Fig. 4 represents a stream that yields a larger outcome y at time s + t. Point D on Fig. 4 represents a stream that yields a smaller outcome x at time s. If a decision maker prefers C to D then C should be located on a higher indifference curve so that indifference curves are relatively horizontal in the vicinity of C and D. Thus, the model presented in Sect. 2 with indifference curves that fan out in the horizontal dimension (cf. Fig. 4) is compatible with the common difference effect.

When temporal delays are relatively short, several studies report a reverse common difference effect when subjects choose a larger outcome at a later moment of time over a smaller outcome available immediately but reverse their preference when both outcomes are delayed by the same time (e.g. Holcomb and Nelson 1992; Scholten and Read 2006; Sayman and Öncüler 2009). For example, Sayman and Öncüler (2009) report that 19 out of 38 subjects (50%) choose €10 in the day after tomorrow over €7 today but, at the same time, choose €7 tomorrow over €10 delayed in 3 days. Such reverse common difference effect is compatible with the model presented in Sect. 2 with a horizontal fanning in of indifference curves in the vicinity of zero (i.e. for very short temporal delays).

Figure 5 illustrates the reverse common difference effect for relatively short temporal delays. Point A represents the outcome €7 today, point B represents the outcome €10 in the day after tomorrow, point C represents the outcome €10 delayed in 3 days and point D represents the outcome €7 tomorrow. The reverse common difference effect is observed when the indifference curves between points A and B are relatively flat compared to the indifference curves between points C and D, i.e. when the indifference curves fan in along the horizontal axis in the vicinity of zero. Interestingly, mixed horizontal fanning of temporal indifference curves (fanning in for very short delays and fanning out for longer delays) is similar to the mixed fanning of risk indifference curves along the horizontal axis of Marschak-Machina probability triangle.

Fig. 5

The reverse common difference effect and horizontal fanning-in of indifference curves in the vicinity of zero (short temporal delays)

5 The absolute magnitude effect and vertical fanning-in

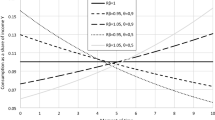
The absolute magnitude effect is observed when a decision maker is relatively impatient with small outcomes and relatively patient—with large outcomes (Loewenstein and Prelec 1992). For example, Thaler (1981) reports that a median subject is indifferent between receiving 15 dollars now and 60 dollars in one year, as well as between receiving 3000 dollars now and 4000 dollars in one year. Figure 6 shows the implied indifference curves in our model for this example. Our model is compatible with the absolute magnitude effect when indifference curves fan in in the vertical direction (cf. Fig. 6).

Fig. 6

The absolute magnitude effect and vertical fanning-in of indifference curves

6 Application: Consumption-savings problem

Let us now apply our proposed model to the standard consumption-savings problem with a constant interest rate. A decision maker has income Y₀ > 0 at the present moment of time t = 0. This can be interpreted as a discounted present value of her total lifelong income. The decision maker decides how to divide this income between consumption and savings in T + 1 periods, $T\in {\mathbb{N}}$. Whichever income is saved at period $t\in \left\{\mathrm{0,1},\dots ,T-1\right\}$ earns a constant interest rate R ≥ 1. Any income that is saved in the last period T perishes. Let ${Y}_{t}\in \left[0,Y{R}^{t}\right]$ denote disposable income in period $t\in \left\{\mathrm{0,1},\dots ,T\right\}$ and ${S}_{t}\in \left[0,{Y}_{t}\right]$ denote savings in period $t\in \left\{\mathrm{0,1},\dots ,T\right\}$ so that ${Y}_{t+1}=R{S}_{t}$ for all $t\in \left\{\mathrm{0,1},\dots ,T-1\right\}$.

A decision maker with income Y_T in the last period T who decides to save S_T ≥ 0 faces a stream of intertemporal payoffs with cumulative payoff Y_T — S_T and average delay 0. Thus, it is optimal to set S_T = 0. Savings are never optimal in the last period if they perish afterwards.

In the before-last period $T-1$ the decision maker knows that any disposable income in the last period will be entirely consumed in the last period. Thus, the decision maker with income ${Y}_{T-1}$ in the before-last period $T-1$ who decides to save ${S}_{T-1}\ge 0$ faces a stream of intertemporal payoffs that yields ${Y}_{T-1}-{S}_{T-1}$ immediately and $R{S}_{T-1}$ delayed for one period. This stream has cumulative payoff $CP={Y}_{T-1}+\left(R-1\right){S}_{T-1}$ and average delay $R{S}_{T-1}/CP$. Therefore, the problem of the decision maker is to choose the optimal level of savings ${S}_{T-1}\in \left[0,{Y}_{T-1}\right]$ to maximize utility $U\left(CP,R{S}_{T-1}/CP\right)$. Instead of considering utility function $U\left(CP,R{S}_{T-1}/CP\right)$ it is more convenient to introduce an auxiliary utility function $V\left(CP,R{S}_{T-1}\right)\equiv U\left(CP,R{S}_{T-1}/CP\right)$ that is increasing in the first argument and decreasing in the second argument. Consumption-savings problem in the before-last period $T-1$ then becomes

$${S}_{T-1}^{*}=\underset{{S}_{T-1}\in \left[0,{Y}_{T-1}\right]}{\mathrm{argmax}} V\left({Y}_{T-1}+\left(R-1\right){S}_{T-1},R{S}_{T-1}\right)$$

(6)

Differentiating auxiliary utility function with respect to savings ${S}_{T-1}$ yields $\frac{dV}{d{S}_{T-1}}=\left(R-1\right)\frac{\partial V}{\partial {x}_{1}}+R\frac{\partial V}{\partial {x}_{2}}$. If the value of a partial derivative $\frac{\partial V}{\partial {x}_{2}}$ is relatively small (as, for example, in the case of indifference curves illustrated on Fig. 2) then the derivative $\frac{dV}{d{S}_{T-1}}$ is positive for all ${S}_{T-1}$ and it is optimal to save all disposable income. In other words, a very patient decision maker opts for 100% saving. If either the value of a partial derivative $\frac{\partial V}{\partial {x}_{1}}$ is relatively small (as, for example, in the case of indifference curves illustrated on Fig. 3) or the interest rate is very close to one then the derivative $\frac{dV}{d{S}_{T-1}}$ is negative for all ${S}_{T-1}$ and it is optimal to consume all disposable income. In other words, a very impatient decision maker (or any decision maker in case of a low interest rate) opts for 100% consumption. If neither is the case, the first-order condition for optimal savings is given by

$$-\frac{\partial V/\partial {x}_{2}}{\partial V/\partial {x}_{1}}=\frac{R-1}{R}$$

(7)

Example 1

Consider auxiliary utility function $V\left({x}_{1},{x}_{2}\right)={x}_{1}^{\alpha }-\theta {x}_{2}$ where $\alpha \in \left(\mathrm{0,1}\right)$ is a subjective parameter that can be interpreted as diminishing sensitivity to cumulative payoff (similar to the curvature of nonlinear utility function) and $\theta >0$ is a subjective parameter that can be interpreted as aversion to temporal delay. In this case the solution to problem (6) is given by (8).

$${S}_{T-1}^{*}=\left\{\begin{array}{cc}0,& \theta \ge \alpha \frac{R-1}{R}{Y}_{T-1}^{\alpha -1}\\ \frac{1}{R-1}\left[{\left(\frac{\theta R}{\alpha \left(R-1\right)}\right)}^{\frac{1}{\alpha -1}}-{Y}_{T-1}\right],& \alpha \frac{R-1}{R}{\left(R{Y}_{T-1}\right)}^{\alpha -1}\le \theta \le \alpha \frac{R-1}{R}{Y}_{T-1}^{\alpha -1}\\ {Y}_{T-1},& \theta \le \alpha \frac{R-1}{R}{\left(R{Y}_{T-1}\right)}^{\alpha -1}\end{array}\right.$$

(8)

Solution (8) is quite intuitive. On the one hand, relatively impatient decision makers (with high values of temporal aversion $\theta$) optimally decide to consume all disposable income and save nothing. On the other hand, relatively patient decision makers (with low values of temporal aversion $\theta$) optimally decide to save all disposable income as consume nothing. Last but not least, decision makers with intermediate values of temporal aversion $\theta$ optimally decide to save a fraction of their disposable income and consume the rest. If interest rate R is close to one then the only solution (8) is to save nothing and consume all disposable income. When savings yield no interest, all decision makers opt for immediate consumption. Blavatskyy (2016) finds a similar result for rank-dependent discounted utility.

Consider now a decision maker who optimally decides to save nothing in the before-last period. In period $T-2$ this decision maker knows that any disposable income in the before-last period will be entirely consumed in that period. Thus, the decision maker with income ${Y}_{T-2}$ in period $T-2$ who decides to save ${S}_{T-2}\ge 0$ faces a stream of intertemporal payoffs that yields ${Y}_{T-2}-{S}_{T-2}$ immediately and $R{S}_{T-2}$ delayed for one period. The optimal savings are then given by (9).

$${S}_{T-2}^{*}=\underset{{S}_{T-2}\in \left[0,{Y}_{T-2}\right]}{\mathrm{argmax}} V\left({Y}_{T-2}+\left(R-1\right){S}_{T-2},R{S}_{T-2}\right)$$

(9)

Optimization problem (9) is mathematically equivalent to problem (8). Thus, if it is optimal to save nothing in period $T-1$ then it is also optimal to save nothing in period $T-2$ and, by induction, in all preceding periods as well. In other words, a very impatient decision maker (or any decision maker if interest rate is very close to one) opts for 100% consumption already in the current period t = 0.

Example 1 (continued)

If $\theta \ge \alpha \frac{R-1}{R}{Y}_{0}^{\alpha -1}$ then ${S}_{t}^{*}=0$ for all $t\in \left\{\mathrm{0,1},\dots ,T\right\}$.

Consider now a decision maker who optimally decides to save all disposable income in the before-last period. In the period $T-2$ this decision maker knows that any disposable income in the before-last period will be entirely saved in that period. Thus, the decision maker with income ${Y}_{T-2}$ in period $T-2$ who decides to save ${S}_{T-2}\ge 0$ faces a stream of intertemporal payoffs that yields ${Y}_{T-2}-{S}_{T-2}$ immediately and ${R}^{2}{S}_{T-2}$ delayed for two periods. The optimal savings are then given by (10).

$${S}_{T-2}^{*}=\underset{{S}_{T-2}\in \left[0,{Y}_{T-2}\right]}{\mathrm{argmax}} V\left({Y}_{T-2}+\left({R}^{2}-1\right){S}_{T-2},{2R}^{2}{S}_{T-2}\right)$$

(10)

Differentiating auxiliary utility function with respect to savings ${S}_{T-2}$ yields $\frac{dV}{d{S}_{T-2}}=\left({R}^{2}-1\right)\frac{\partial V}{\partial {x}_{1}}+2{R}^{2}\frac{\partial V}{\partial {x}_{2}}$. If the value of a partial derivative $\frac{\partial V}{\partial {x}_{2}}$ is smaller than $\frac{{R}^{2}-1}{2{R}^{2}}\frac{\partial V}{\partial {x}_{1}}$ then the derivative $\frac{dV}{d{S}_{T-1}}$ is positive for all ${S}_{T-1}$ and it is optimal to save all disposable income in period $T-2$. By induction, it is optimal to save all disposable income in every but last period when partial derivative $\frac{\partial V}{\partial {x}_{2}}$ is smaller than $\frac{{R}^{T}-1}{T{R}^{T}}\frac{\partial V}{\partial {x}_{1}}$.

Example 1 (continued)

If $\theta \le \alpha \frac{{R}^{T}-1}{T{R}^{T}}{\left({R}^{T}{Y}_{0}\right)}^{\alpha -1}$ then ${S}_{t}^{*}={R}^{t}{Y}_{0}$ for all $t\in \left\{\mathrm{0,1},\dots ,T-1\right\}$ and ${S}_{T}^{*}=0$.

7 Experimental test

7.1 Design

Our experimental test is designed to contrast the prediction of the model presented in Sect. 2 with that of discounted utility and its popular generalization—quasi-hyperbolic discounting (Phelps and Pollak 1968). Arguably the simplest such test is a binary choice between two streams of intertemporal outcomes. The first stream yields x > 0 euros now as well as x euros at a later moment of time t > 0. The second stream yields 2 x euros at a moment of time t/2 (and nothing at any other moment of time).

Both streams yield the same cumulative payoff 2 x euros. Moreover, both streams have the same average delay t/2. Thus, according to our model a decision maker is indifferent between these two streams of intertemporal outcomes (regardless of her time preferences).

In contrast, discounted utility and its popular generalization—quasi-hyperbolic discounting—predict that a decision maker should strictly prefer the first stream over the second stream. Notice that (1-β)² > 0 for any discount factor β < 1. This inequality can be rearranged as 1 + β² > 2β. Multiplying both sides of this inequality by u(x) yields u(x) + β²u(x) > 2βu(x), where u(.) denotes a utility function. For a concave utility function, Jensen’s inequality implies 2u(x) ≥ u(2x) so that we can write u(x) + β²u(x) > βu(2x). Multiplying both sides of this inequality by the present-bias parameter δ ≤ 1 yields

$$u\left(x\right)+\delta {\beta }^{2}u\left(x\right)\ge \delta u\left(x\right)+\delta {\beta }^{2}u\left(x\right)>\delta \beta u\left(2x\right)$$

(11)

The left-most part of inequality (11) is the quasi-hyperbolic discounted utility of the first stream that yields x euros now as well as x euros at time t. The right-most part of inequality (11) is the quasi-hyperbolic discounted utility of the second stream that yields 2 x euros at time t/2. Discount utility is the special case when the present-bias parameter δ is one. Therefore, discounted utility and its popular generalization—quasi-hyperbolic discounting—predict that the first stream is always chosen over the second stream in a direct binary choice (for any subjective time preference parameters β and δ and any concave utility function).

If time t is close to the present moment of time, then two streams of intertemporal payoffs are similar to each other. In this case, it is plausible that a decision maker can choose either stream in a direct binary choice between the two. This supports the prediction of our model but challenges the prediction of discounted utility and quasi-hyperbolic discounting. For example, Blavatskyy and Maafi (2018) presented 75 experimental subjects with a binary choice between two streams when x = 10 and t is two months. Choice decision was repeated four times. Blavatskyy and Maafi (2018) found that 27 subjects (36%) have chosen the first stream on at least one occasion and the second stream—on at least one occasion as well. At the same time, 24 subjects (32%) have always consistently chosen the first stream. The remaining 24 subjects (32%) have always consistently chosen the second stream.

Scholten et al. (2016) report that 154 out of 356 subjects (43.26%) choose £300 at time t plus another £300 at time 3t rather than £600 at time 2t in unrepeated hypothetical choice. They also report that 213 out of 347 subjects (61.38%) reveal the same preference when sequences are presented including zero outcomes, i.e. the first sequence is presented as £300 at time t, £0 at time 2t, and £300 at time 3t. In other words, Scholten et al. (2016) find that an inconsequential additional presentation of zero payoffs reverses the modal choice between two streams of intertemporal payoffs. Arguably, this finding can be interpreted as evidence that most subjects are largely indifferent between these streams.

7.2 Implementation

We set outcome x at ten euros and time t at two weeks. Collecting data on time preferences in a laboratory experiment with time-contingent monetary payoffs requires an assumption that subjects do not integrate their payments received in the experiment with their money or consumption plans outside the experimental laboratory (there is no arbitrage). Andreoni et al. (2018) found no strong evidence of arbitrage (see, however, Andreoni and Sprenger 2015; Sprenger 2015). To minimize the possibility of arbitrage in our experiment, subjects were not rewarded with cash/cheque envelopes mailed at specific dates. Instead, at the end of the experiment, subjects received €10 or €20 discount coupons from a major supermarket chain. These discount coupons function like a gift card but they are valid only on one specific day. Most of our subjects were familiar with the discount coupons (that are routinely used by supermarket chains to encourage shopping on public holidays in France). During subject recruitment, prospective subjects were informed in advance that they will be rewarded with discount coupons valid for one day only (no delayed cash/cheque payments).

To elicit indifference between two streams, subjects were presented with a direct binary choice between these streams twice. On the second repetition, the left-hand side and the right-hand side choice options were interchanged. Subjects faced between two and four distractor choice tasks between two repetitions.

One hundred MBS students (56% female) were recruited for ten experimental sessions. Each session lasted around 15 min (no subject participated in more than one session). At the end of the experiment, every subject received €20 worth of discount coupons, but their validity date varied across subjects (depending on their choices made in the experiment).

The experiment was administered as a paper-and-pencil experiment. At the beginning of the experiment, each subject received experimental instructions (a translation is presented in the Appendix) and a 6-page booklet with six binary choice problems, each printed on a separate page. The order of questions was randomized subject to a restriction that at least two distractor tasks appeared between the repetitions of the same question. The presentation of the left-hand side and the right-hand side choice options was randomized as well.

Subjects answered six questions at their own pace. A subject who answered all six questions was invited to the experimenter’s table. The subject then rolled a standard 6-sided die. She received discount coupons according to her choice in the question that appeared on the page number corresponding to the number that came up on the die.

7.3 Results

We did not find any order effects between subjects who initially faced the first stream on the left (on the second repetition it was presented on the right) and subjects who initially faced the first stream on the right (on the second repetition it was presented on the left). Twenty-eight subjects consistently choose the first stream (€10 now plus €10 in two weeks) on both repetitions. Twenty-three subjects consistently choose the second stream (€20 in one week) on both repetitions. The remaining 49 subjects once choose the first stream and once choose the second stream.

Thus, only 28% of revealed choice patterns are consistent with discounted utility (or quasi-hyperbolic discounting) and 72% of revealed choice patterns contradict discounted utility (or quasi-hyperbolic discounting). Freeman and Halton (1951) extension of the Fisher exact probability test for the hypothesis that all subjects choose the first stream is 2.993e-31 (a chi-squared test is χ² = 112.5, p = 0). In other words, the hypothesis that all subjects strictly prefer €10 now plus €10 in two weeks over €20 in one week is soundly rejected.

On the other hand, at least 49% and at most 92%⁴ of revealed choice patterns are consistent with the model presented in Sect. 2. Freeman-Halton extension of the Fisher exact probability test for the hypothesis that all subjects are equally likely to choose either stream is 0.868 (a chi-squared test is χ² = 0.26, p = 0.878). Our experimental results confirm the intuition presented at the end of Sect. 6.1—when temporal delays are relatively short, a temporal spread of payoffs is similar to the pooled payoff (at the median delay) so that many decision makers are likely to be indifferent between the two.

8 Conclusion

Empirical violations of Koopmans (1960) stationarity condition highlighted descriptive limitations of Samuelson (1937) discounted utility and motivated the development of various generalizations of the latter. Many generalizations, however, keep the additively separable form of temporal utility and differ from each other only in their proposed discount function—quasi-hyperbolic (Phelps and Pollak 1968), generalized hyperbolic (Loewenstein and Prelec 1992), liminal (Pan et al. 2015) or varying in the short- and long-term (Blavatskyy 2015). Additively separable temporal utility with a non-linear (i.e., either strictly concave or strictly convex) utility function implies a rather counter-intuitive preference for a partial delay in consumption (cf. Blavatskyy 2016). Empirical estimates of additively separable temporal utility often find near-linear utility function (e.g., Andreoni and Sprenger 2012; Andreoni et al. 2015; Abdellaoui et al. 2018; Cheung 2019) with a relatively poor goodness of fit (e.g., Blavatskyy and Maafi 2018; Cheung 2019). As Cheung (2019) puts it: “This points to the exciting opportunities for future … research to focus not only on the forms of the utility and discount functions, but also on alternatives to the discounted utility model itself”.

Our paper proposes an alternative framework how to conceptualize intertemporal choice as a multi-criteria decision problem: a tradeoff between the cumulative payoff of a stream of intertemporal outcomes and its average delay. A cumulative payoff is a desirable attribute whereas an average delay is an undesirable attribute (analogously how the expected return is a desirable attribute and risk is an undesirable attribute in Markowitz (1952) mean–variance approach). Our proposed model always implies aversion to a partial delay in consumption (unlike the additively separable temporal utility). The proposed model is compatible with several empirical regularities such as the common difference effect (which is equivalent to the horizontal fanning-out of indifference curves in the CP-AD plane) and the absolute magnitude effect (which is equivalent to the vertical fanning-in of indifference curves in the CP-AD plane). A new simple experimental test of our proposed model versus discounted utility and quasi-hyperbolic discounting (with a concave utility function) soundly rejects the latter two models in favor of the former one.

On the other hand, some empirical findings cannot be rationalized by our proposed model. For example, Varey and Kahneman (1990) found that subjects preferred streams of discomforting outcomes declining rather than increasing over time. In a similar vein, Loewenstein and Sicherman (1991) found that many museum visitors prefer increasing streams of wages over constant or decreasing streams of wages with the same cumulative payoff, i.e. they reveal a preference for streams with a longer average delay. Loewenstein and Prelec (1991) found that many students prefer a sequence of dining experiences that yields a dinner at a fancy French restaurant later rather than sooner (again implying a preference for a longer average delay).

A preference for streams of intertemporal outcomes increasing over time elicited in hypothetical questionnaires, however, is not replicated in experiments with streams of real monetary outcomes. For example, Gigliotti and Sopher (1997) find that a modal choice pattern is to choose a decreasing stream over a constant stream and the latter—over an increasing stream of real monetary payoffs (with the same cumulative payoff).⁵ Similarly, Manzini et al. (2010) find that “a majority of subjects prefers decreasing to increasing sequences” when choosing between streams of real monetary payoffs. Our proposed model (like most models of temporal discounting) can rationalize a reference for decreasing streams over increasing streams of real monetary payoffs but it cannot account for a reversed preference discovered in hypothetical questionnaires.

Loewenstein (1988) found that subjects expecting to receive a VCR in one year were willing to pay, on average, $54 to receive it now; but subjects expecting to receive a VCR now were willing to accept, on average, $126 for its delivery being delayed for one year. Such “delay-speed up” asymmetry is a violation of a basic consequentialist premise that only the sequence of outcomes (and not its presentational framing) is relevant for decision making. Our proposed model (like any model based on the consequentialist premise) cannot account for a “delay-speed up” asymmetry.

A significant progress has been recently done in the empirical research on time preferences, specifically in disentangling intertemporal discounting from the curvature of instantaneous utility (e.g. Cheung 2019). This richness of new data and new elicitation methods of time preferences challenge the workhorse theoretical model of intertemporal choice—an additively separable utility function—and create a demand for more descriptive representations of time preferences. While behavioral regularities in choice under risk, such as the Allais paradox or the common ratio effect, motivated the development of numerous non-expected utility theories, “well into double figures” (Starmer 2000), the number of theoretical models of intertemporal choice remained on a relatively modest level. Models of multicriteria decision making over time are particularly rare (cf. Rubinstein 2003; Manzini et al. 2010). This paper attempts to fill this gap with a model that tradeoffs the outcome dimension (as captured by the cumulative outcome) versus the temporal dimension (as captured by the average delay). An interesting possible extension of this model is to incorporate another criterion—“temporal skewness”—analogously to how a preference for positive skewness is sometimes added in the mean–variance approach in finance. Another interesting extension is to consider non-monetary outcomes that cannot be easily cumulated across time periods such as health outcomes (cf. Attema et al. 2018).

Appendix

1.1 Experimental Instructions

Welcome to our experiment! This is an experiment in choice over time. It is financed from research funds. We would like to ask you to take six decisions in this experiment.

At the end of the experiment you will receive one or two discount coupons for a supermarket chain valid only on a specific day. Your payoff depends only on your decisions and the realization of random events. Your payoff does not depend on the decisions of other participants. Your anonymity will be preserved during and after the experiment.

During the experiment you need to answer six questions printed in your booklet. Please note that that there are no right or wrong answers in this experiment. Here is an example of a typical question that you may face during the experiment:

1.2 Question 1

Please choose your preferred alternative:

Please raise your hand when you answered all six questions. We will ask you to come forward with your booklet to our table. We then ask you to toss a die to randomly select one question number. This question will be used to determine your payoff.

For instance, suppose that the die comes up one. Then question 1 is selected. Suppose that question 1 in your booklet is the question shown above. If you have ticked the right alternative in this question, you receive one discount coupon worth €20 valid only on May 8th.

Please note that any question can be randomly selected at the end to determine your payoff. So it is in your best interest to answer all six questions carefully. Good luck!