A monotone model of intertemporal choice

Abstract

Existing models of intertemporal choice such as discounted utility (also known as constant or exponential discounting), quasi-hyperbolic discounting and generalized hyperbolic discounting are not monotone: A decision maker with a concave utility function generally prefers receiving $1 m today plus $1 m tomorrow over receiving $2 m today. This paper proposes a new model of intertemporal choice. In this model, a decision maker cannot increase his/her satisfaction when a larger payoff is split into two smaller payoffs, one of which is slightly delayed in time. The model can rationalize several behavioral regularities such as a greater impatience for immediate outcomes. An application of the model to intertemporal consumption/saving reveals that consumers may exhibit dynamic inconsistency. Initially, they commit to saving for future consumption, but, as time passes, they prefer to renegotiate such a contract for an advance payment. Behavioral characterization (axiomatization) of the model is presented. The model allows for intertemporal wealth, complementarity and substitution effects (utility is not separable across time periods).

1 Introduction

Intertemporal choice involves payoffs to be received at different points in time. Samuelson (1937) proposed a classical model of intertemporal choice that is known as discounted utility or constant (exponential) discounting. The model is parsimonious and analytically convenient, but its descriptive validity has been questioned. For instance, Thaler (1981, p. 202) argued that some people may prefer one apple today over two apples tomorrow, but, at the same time, they may prefer two apples in 1 year plus 1 day over one apple in 1 year. Discounted utility cannot account for such a switching choice pattern. The descriptive limitations of discounted utility motivated the development of alternative models such as quasi-hyperbolic discounting (Phelps and Pollak 1968) and generalized hyperbolic discounting (Loewenstein and Prelec 1992). These models replaced a constant (exponential) discount factor in discounted utility with a more general discount function.

Discounted utility and its subsequent generalizations such as quasi-hyperbolic and generalized hyperbolic discounting may produce rather counterintuitive results which are seldom discussed in the literature. These models may violate intertemporal monotonicity when utility function is concave (as usually assumed in economics). For example, consider a decision maker who receives 1 million dollars now as well as 1 million dollars at a later moment of time t (with a convention that $t=0$ denotes the present moment).¹ According to the above-mentioned models, this decision maker behaves as if maximizing utility

$$\begin{aligned} u\left( {\$1\,\hbox {m}} \right) +D\left( t \right) u\left( {\$1\,\hbox {m}} \right) \end{aligned}$$

(1)

where $u(\cdot )$ is utility function and $D(\cdot )$ is a discount function. According to the same models, receiving 2 million now yields utility u($2 m). For a decision maker with a concave utility function $u(\cdot )$ and enough patience (i.e., with a discount function D(t) sufficiently close to one), utility (1) is greater than u($2 m) due to Jensen’s inequality. Moreover, in a continuous time framework, for any decision maker with a concave utility function $u(\cdot )$ it is always possible to find a moment of time t sufficiently close to the present moment such that utility (1) is greater than u($2 m) due to the property $\mathop {\lim }\nolimits _{t\rightarrow 0} D\left( t \right) =1$ (cf. Figure 1 in Loewenstein and Prelec 1992, p. 581). In other words, the above-mentioned models predict that a decision maker with a concave utility function prefers receiving 1 million now plus 1 million at a later moment of time t over receiving 2 million immediately.

More generally, according to the existing models of intertemporal choice, the desirability of any payoff may increase if this payoff is split into two smaller payoffs one of which is slightly delayed in time. Such an implication is clearly testable in a controlled laboratory experiment. Yet, readers would probably agree with my tentative conjecture that very few people are likely to reveal such a preference. Most people would find no real tradeoff in receiving the same sum of money sooner rather than later, no matter whether they have patient or impatient time preferences. The failure of a model of intertemporal choice to accommodate such a preference is akin to the violation of first-order stochastic dominance in a theory of decision making under risk.

This paper considers an intuitive analogy between intertemporal choice and choice under risk/uncertainty. When intertemporal payoffs are framed as payoffs in an uncertain future and risk preferences are represented by rank-dependent utility, we obtain a new model of intertemporal choice that does not violate intertemporal monotonicity. The main contribution of this paper is to show that rank-dependent utility with plausible parameters (inverse S-shaped probability weighting function and concave utility function) can be successfully used for rationalizing behavioral regularities in intertemporal choice. Thus, economists could benefit from one unified theory for choice under risk and over time. This contrasts with the current trend of developing alternative models that deal either with intertemporal choice (e.g., Frederick et al. 2002, Section 5, p. 365) or with choice under risk (e.g., Starmer 2000). A unified theory of choice under risk and over time brings the benefits of consistency in economic modeling (e.g., we avoid the violations of monotonicity described above) and allows viewing separate behavioral regularities from a larger perspective (e.g., violations of independence in choice under risk and a greater impatience for immediate outcomes in intertemporal choice may be two sides of the same coin).

The remainder of the paper is organized as follows. Section 2 presents our model of intertemporal choice and discusses its properties. Section 3 applies this model to the problem of intertemporal consumption/savings. Behavioral characterization (axiomatization) of the model is presented in Sect. 4. Section 5 concludes with a general discussion.

2 A model of uncertain future

We first consider intertemporal choice in a discrete time framework, which is later extended into a continuous time framework. Consider a decision maker who receives payoffs $x_{t}\ge 0$ in moments of time $t\in \{0, 1, 2, {\ldots }\}$ with a convention that $t=0$ denotes the present moment. For an intuitive understanding of our proposed model, it may be helpful to think about intertemporal choice in the following manner. The main difference between the payoff received in the current moment of time and payoffs to be received in the subsequent moments of time is that the future payoffs cannot be counted upon with certainty. One way of modeling this uncertain future is to assume that there is a survival probability $\beta \in (0,1)$. With probability $\beta$ the decision maker “survives” to the next moment of time and enjoys the receipt of any payoffs due in that moment. With probability $1-\beta$, the decision maker “dies” and receives no future payoffs. The probability $1-\beta$ does not necessarily reflect the likelihood of physical death. For example, it may reflect the likelihood that the standard contracts are no longer implementable due to force majeure (e.g., a Russian invasion). For parsimony, we assume that $\beta$ is constant at all moments of time. Probability $\beta$ is a subjective parameter of the model.

Given probability $\beta$, we can reframe the problem of intertemporal choice as choice under risk. Let $t\in \{0, 1, 2, {\ldots }\}$ denote a state of the world when the decision maker “dies” at a moment of time t. Table 1 shows the probabilities of the states of the world as well as the associated payoffs.

Table 1 States of the world, probabilities and the associated payoffs

If the decision maker maximizes expected utility, then there is a (Bernoulli) utility function $u(\cdot )$ such that a stream of payoffs $\{x_{0}, x_{1}, x_{2}, {\ldots }\}$ received in moments of time $t\in \{0, 1, 2, {\ldots }\}$ yields utility (2).

$$\begin{aligned} U\left( {\left\{ {x_0,x_1,x_2,\ldots } \right\} } \right) =\left( {1-\beta } \right) \mathop \sum \limits _{t=0}^\infty \beta ^{t}u\left( {\mathop \sum \limits _{s=0}^t x_s } \right) \end{aligned}$$

(2)

It is relatively straightforward to rearrange utility formula (2) into formula (3).

$$\begin{aligned} U\left( {\left\{ {x_0,x_1,x_2 ,\ldots } \right\} } \right) =u\left( {x_0 } \right) +\mathop \sum \limits _{t=1}^\infty \beta ^{t}\left[ {u\left( {\mathop \sum \limits _{s=0}^t x_s } \right) -u\left( {\mathop \sum \limits _{s=0}^{t-1} x_s } \right) } \right] \end{aligned}$$

(3)

If utility function $u(\cdot )$ is linear, then formula (3) simplifies into classical discounted linear utility (4).

$$\begin{aligned} U\left( {\left\{ {x_0 ,x_1 ,x_2 ,\ldots } \right\} } \right) =\mathop \sum \limits _{t=0}^\infty \beta ^{t}x_t \end{aligned}$$

(4)

Thus, if Bernoulli utility function $u(\cdot )$ is approximately linear (e.g., when payoffs are small), then model (3) practically coincides with the classical model of Samuelson (1937) with a discount factor $\beta$.

If Bernoulli utility function $u(\cdot )$ is nonlinear (e.g., when payoffs are large), then model (3) diverges from the classical model of Samuelson (1937). Samuelson (1937) assumed that a decision maker behaves as if maximizing the sum of discounted utilities of future payoffs. Thus, his model is also known as discounted utility. In contrast, model (3) assumes that a decision maker behaves as if maximizing the sum of discounted incremental utilities of future payoffs. A decision maker aggregates the stock of payoffs and subsequent future payoffs are evaluated by their contribution to the overall utility of this stock. Thus, if we consider parameter $\beta$ to be a discount factor rather than a survival probability, then model (3) can be called “discounted incremental utility.”

To illustrate model (3), let us return to the first example from the introduction. Consider a decision maker who receives 2 million at a moment of time $T\ge 0$ and nothing in all other periods. For simplicity, let us normalize the utility of zero to zero. Utility (3) of the 2 million to be received at a moment of time T is then given by (5), which resembles the formula of discounted utility.

$$\begin{aligned} U\left( {x_T =\$2\,\hbox {m}} \right) =\beta ^{T}u\left( {\$2\,\hbox {m}} \right) \end{aligned}$$

(5)

Consider now the same decision maker who receives 1 million at a moment of time T as well as 1 million at a moment of time $T+\tau , \tau \ge 0$ (and nothing in all other periods). Utility (3) of this stream of payments is then given by (6), which differs from the formula of discounted utility.

$$\begin{aligned} U\left( {x_T =\$1\,\hbox {m};x_{T+\tau } =\$1\,\hbox {m}} \right) =\beta ^{T}u\left( {\$1\,\hbox {m}} \right) +\beta ^{T+\tau }\left[ {u\left( {\$2\,\hbox {m}} \right) -u\left( {\$1\,\hbox {m}} \right) } \right] \end{aligned}$$

(6)

In the limit, as $\tau$ goes to zero, utility value (6) converges to utility value (5), as one should expect from a continuous utility function. Thus, utility (3) avoids violations of temporal continuity. Moreover, for all $\tau >0$ utility value (6) is strictly smaller than utility value (5) provided that the Bernoulli utility function $u(\cdot )$ is monotone. In other words, irrespective of the subjective parameters of a decision maker (survival probability/discount factor $\beta$ and the curvature of utility function u), he or she always prefers to receive the same amount of money sooner rather than later.

Model (3) assumes that discount factor/survival probability $\beta$ is constant at all moments of time. Such a model is ideally suited for dealing with payoffs that are received at regular time intervals (moments of time are equally spaced in time). When a decision maker receives outcomes at irregular points in time, it may be more convenient to consider a continuous time line instead of discrete time periods. In this case, it is conventional to switch from a discount factor/survival probability $\beta$ to a continuously compounded discount rate $\delta \in (0,1)$. Specifically, if $m\in {\mathbb {N}}$ denotes the number of compounding periods, then we replace $\beta$ with formula (7).

$$\begin{aligned} \beta =\mathop {\lim }\limits _{{{m}}\rightarrow \infty } \left( {1-\frac{{\delta }}{m}} \right) ^{{{m}}}=e^{-\delta } \end{aligned}$$

(7)

Given a continuous time line $t\in {\mathbb {R}}_{+}$, payoffs are described by payoff function x: ${\mathbb {R}}_{+}\rightarrow {\mathbb {R}}_{+}$ so that x(t) denotes a payoff received at a moment of time t. With this notation, model (3) becomes Eq. (8).

$$\begin{aligned} U\left( x \right) =u\circ x\left( 0 \right) +\mathop \sum \limits _{t>0} e^{-\delta t}\left[ {u\left( {\mathop \sum \limits _{s\le t} x\left( s \right) } \right) -u\left( {\mathop \sum \limits _{s<t} x\left( s \right) } \right) } \right] \end{aligned}$$

(8)

If payoff function $x(\cdot )$ is continuous, then payoffs received between the present moment of time ($t=0$) and a future moment of time $t>0$ are given by cumulative payoff function (9).

$$\begin{aligned} y\left( t \right) =\mathop \int \limits _0^t x\left( s \right) \hbox {d}s \end{aligned}$$

(9)

Payoffs received between the present moment ($t=0$) and a future moment $T>0$ then yield utility (10).

$$\begin{aligned} U\left( x \right) =\mathop \int \limits _0^T e^{-\delta t}\hbox {d}u\circ y\left( t \right) \end{aligned}$$

(10)

If utility (10) function $u(\cdot )$ is differentiable, then utility (10) can be written as (11).

$$\begin{aligned} U\left( x \right) =\mathop \int \limits _0^T e^{-\delta t}u^{\prime }\left( {\mathop \int \limits _0^t x\left( s \right) \hbox {d}s} \right) x\left( t \right) \hbox {d}t \end{aligned}$$

(11)

If utility function $u(\cdot )$ is linear (i.e., $u'(y)=1$ for all $y\in {\mathbb {R}}_{+})$, then model (11) simplifies into a standard formula (12) of a discounted present value—a special case of the Samuelson (1937) model with linear utility. However, for a nonlinear utility function $u(\cdot )$, model (11) diverges from the discounted utility model of Samuelson (1937).

$$\begin{aligned} U\left( x \right) =\mathop \int \limits _0^T e^{-\delta t}x\left( t \right) \hbox {d}t \end{aligned}$$

(12)

Our model of intertemporal choice is analogous to expected utility theory of choice under risk/uncertainty. One of the cornerstones of expected utility theory is the independence axiom. Yet, empirical studies found systematic violations of the independence axiom such as the common consequence effect (e.g., Allais 1953, p. 527; Blavatskyy 2013a) and the common ratio effect (e.g., Kahneman and Tversky 1979, Problem 3, p. 266; Blavatskyy 2010). In response to these empirical findings, several generalizations of expected utility theory were proposed in the literature (see Starmer 2000, for a review). One such popular generalized nonexpected utility theory that fits well to experimental data is Quiggin (1981) rank-dependent utility. As the next step, we generalize “discounted incremental utility” to rank-dependent discounted utility, which is analogous to rank-dependent utility in choice under risk/uncertainty.

We begin by reconsidering the problem of intertemporal choice in a discrete time setting. A decision maker receives payoffs $x_{t}\ge 0$ in moments of time $t\in \{0, 1, 2, {\ldots }\}$. As before, for an intuitive understanding of the model it may be helpful to think about discount factor $\beta \in (0,1)$ as a survival probability. The problem of intertemporal choice can be then reframed as choice under risk/uncertainty: a decision maker receives payoff $\mathop \sum \nolimits _{s=0}^t x_s$ with probability $\beta ^{t}\left( {1-\beta } \right)$, for all $t\in \{0,1,2,{\ldots }\}$. If risk preferences are represented by rank-dependent utility, then a decision maker behaves as if maximizing utility

$$\begin{aligned} U\left( {\left\{ {x_0 ,x_1 ,x_2 ,\ldots } \right\} } \right) =u\left( {x_0 } \right) +\mathop \sum \limits _{t=1}^\infty w\left( {\beta ^{t}} \right) \left[ {u\left( {\mathop \sum \limits _{s=0}^t x_s } \right) -u\left( {\mathop \sum \limits _{s=0}^{t-1} x_s } \right) } \right] \end{aligned}$$

(13)

where $w{:}\,[0,1]\rightarrow [0,1]$ is a strictly increasing weighting function satisfying $w(0)=0$ and $w(1)=1$. In a special case, when this function is linear, i.e., $w(p)=p$ for all $p\in [0,1]$, model (13) becomes model (3).

To illustrate the behavioral implications of model (13), let us consider several well-known behavioral regularities in intertemporal choice. We begin with the common difference effect (Loewenstein and Prelec 1992, section II.1, p. 574). Some people may prefer $110 in 31 days over $100 in 30 day,s and, at the same time, they may prefer $100 today over $110 tomorrow (e.g., Frederick et al. 2002, p. 361). According to model (13), a decision maker prefers $100 today over $110 tomorrow if inequality (14) holds (utility of $0 is normalized to zero and $\beta$ is a daily discount factor).

$$\begin{aligned} u\left( {\$100} \right) >w\left( \beta \right) u\left( {\$110} \right) \end{aligned}$$

(14)

The same decision maker prefers to receive $110 in 31 days rather than $100 in 30 days if (15) holds.

$$\begin{aligned} w\left( {\beta ^{31}} \right) u\left( {\$110} \right) >w\left( {\beta ^{30}} \right) u\left( {\$100} \right) \end{aligned}$$

(15)

Thus, a decision maker reveals dynamically inconsistent preferences when inequality (16) is satisfied.

$$\begin{aligned} w\left( \beta \right) <\frac{u\left( {\$100} \right) }{u\left( {\$110} \right) }<\frac{w\left( {\beta ^{31}} \right) }{w\left( {\beta ^{30}} \right) } \end{aligned}$$

(16)

If weighting function $w(\cdot )$ is linear, the leftmost-hand side of inequality (16) is equal to the rightmost-hand side of inequality (16). In other words, model (3), like the model of Samuelson (1937), cannot account for the common difference effect. Yet, if function $w(\cdot )$ is nonlinear, the leftmost-hand side of inequality (16) can be smaller than the rightmost-hand side of inequality (16) and a decision maker can exhibit a greater impatience for immediate rewards. Moreover, for an inverse S-shaped function $w(\cdot )$ that is concave near zero and convex near one, which is often elicited in experimental studies (e.g., Abdellaoui 2000, pp. 1507–1508), the leftmost-hand side of inequality (16) is smaller than the rightmost-hand side. For example, Table 2 shows the values of the leftmost-hand and the rightmost-hand side of inequality (16) for several values of parameter $\beta \in (0,1)$ and the weighting function (17) proposed by Tversky and Kahneman (1992, p. 309) with $\gamma =0.61$ (a median parameter elicited in the experiment of Tversky and Kahneman 1992, p. 312).

$$\begin{aligned} w\left( q \right) =\frac{q^{\gamma }}{\left( q^{\gamma }+\left( {1-q} \right) ^{\gamma } \right) ^{\frac{1}{\gamma }}} \end{aligned}$$

(17)

Table 2 The leftmost-hand and the rightmost-hand side of inequality (16) for function (17), $\gamma =0.61$

Thaler (1981) provides another (related) example of dynamically inconsistent preferences. Consider a decision maker who is indifferent between receiving $15 now and $z in t quarters. Using equation $\beta ^{t}z=15$, we can infer an implicit discount factor $\beta \in (0,1)$ that would apply if this decision maker were to maximize the discounted present value. For instance, Thaler (1981) found a median value of $z to be $30 when a delay t is one quarter, $60 when a delay t is 1 year and $100 when a delay t is 3 years. In this case, using formula $\beta =\root t \of {15/z}$, an implicit quarterly discount factor would be 0.5 for payoffs in one quarter, $0.25^{0.25}\approx 0.707$ for payoffs in 1 year, and $0.15^{1/12}\approx 0.854$ for payoffs in 3 years. Thus, it appears as if a decision maker used a higher discount factor for payoffs in the more distant future—a phenomenon that some authors call hyperbolic discounting (e.g., Frederick et al. 2002, section 4.1, p. 360).

According to our proposed model (13), however, a decision maker behaves as if using a discount factor $\beta$ that is implicitly defined by Eq. (18).

$$\begin{aligned} w\left( {\beta ^{t}} \right) u\left( {\$z} \right) =u\left( {\$15} \right) \end{aligned}$$

(18)

As an illustration, let us consider a probability weighting function (17) proposed by Tversky and Kahneman (1979, p.309) and a power utility function $u\left( {\$x} \right) =x^{\alpha }$, with parameter values $\gamma =0.56$ and $\alpha =0.225$ that Camerer and Ho (1994, p. 188) estimated from experimental data reported in eight studies of decision making under risk. Under this parameterization, a quarterly discount factor implicitly defined by Eq. (18) would be 0.9852 for payoffs in one quarter, 0.9854 for payoffs in 1 year, and 0.9905 for payoffs in 3 years. Thus, a discount factor inferred from Eq. (18) may be almost constant over time if we use an inverse S-shaped weighting function $w(\cdot )$ and a concave utility function $u(\cdot )$. At the same time, an inferred discount factor would be increasing over time if we used a misspecified model with a linear weighting function and a linear utility function.²

Another example from Thaler (1981) illustrates the so-called absolute magnitude effect (cf. Loewenstein and Prelec 1992, section II.2, p. 575; Frederick et al. 2002, section 4.2.2, p. 363). Consider a decision maker who is indifferent between receiving $250 now and $y in t quarters. Thaler (1981) found that a median value of $y is $300 when a delay t is one quarter, $350 when a delay t is 1 year and $500 when a delay t is 3 years. If a representative decision maker maximized the discounted present value, then his or her implicit quarterly discount factor would be $\beta =\root t \of {250/y}$. Thus, an inferred discount factor would be $6/7\approx 0.8571$ for payoffs in one quarter, $0.75^{0.25}\approx 0.9306$ for payoffs in 1 year, and $0.5^{1/12}\approx 0.9439$ for payoffs in 3 years. As in the previous example, these discount factors increase over time—it appears as if a decision maker is more impatient for payoffs that are closer to the present moment. Moreover, discount factors inferred from the indifference between $250 now and $y in t quarters exceed the corresponding discount factors inferred from the indifference between $15 now and $z in t quarters. In other words, a decision maker appears to be more impatient when dealing with small payoffs (i.e., small payoffs are apparently discounted at a relatively higher rate compared to large payoffs).

Yet, if a decision maker maximizes utility (13), then his or her discount factor is implicitly defined by $w\left( {\beta ^{t}} \right) u\left( {\$y} \right) =u\left( {\$250} \right)$. For illustration, let us consider the same parametric form of model (13) as in the previous example: the weighting function (17) and a power utility function with parameters estimated by Camerer and Ho (1994, p. 188). In this case, an inferred discount factor would be 0.9988 for payoffs in one quarter as well as in 3 years and 0.9990 for payoffs in 1 year. Two observations are apparent. First, as in the previous example, these discount factors are almost identical (do not increase over time horizon). Second, they are similar to the corresponding discount factors inferred from Eq. (18) under the same parameterization of model (13). Thus, model (13) with a constant discount factor $\beta$ can generate behavior that looks like hyperbolic discounting (a greater impatience for immediate payoffs) and an absolute magnitude effect (a greater impatience for small payoffs) when we ignore nonlinear weighting and utility functions.

3 An application: the problem of intertemporal consumption/savings

Model (13) can be applied to finding an optimal consumption/savings plan. This problem can be summarized as follows. At the current moment of time $t=0$, a decision maker receives income $Y>0$, which can be interpreted as a discounted present value of a total lifetime income. A decision maker decides how to split this income Y for consumption at $T+1$ moments of time, $T\ge 2$. Any saved income that is not consumed at moment of time $t\in \{0, 1, 2, {\ldots }T-1\}$ is transferred to the subsequent moment of time multiplied by an interest rate $R>1$. Any income that is not consumed at the last moment of time $t=T$ perishes (alternatively, a decision maker “dies” after the last moment of time T).

Let $Y_{t}\in [0, YR ^{t}]$ denote total income disposable at moment of time $t\in \{0, 1, {\ldots }T\}$. Let $C_{t}\in [0,Y_{t}]$ denote consumption at moment of time $t\in \{0, 1, {\ldots }T\}$. Then we must have $Y_{0}=Y$ and for all $t\in \{1, 2, {\ldots }T\}$:

$$\begin{aligned} Y_t =\left( Y_{t-1} -C_{t-1} \right) R= YR ^{t}-\sum _{s=0}^{t-1} {C_s R^{t-s}} \end{aligned}$$

(19)

Since all unconsumed income perishes after the last moment of time T, a decision maker with any monotone utility function consumes all disposable income at the last moment: $C_{T}=Y_{T}$. Knowing this, at the penultimate moment of time a decision maker who maximizes utility (13) solves problem (20).

$$\begin{aligned} \mathop {\max }\limits _{C_{T-1} \in \left[ {0,Y_{T-1} } \right] } \left[ {1-w\left( \beta \right) } \right] u\left( {C_{T-1} } \right) +w\left( \beta \right) u\left( Y_{T-1} R-C_{T-1} \left( {R-1} \right) \right) \end{aligned}$$

(20)

3.1 Case 1: consumption of all disposable income at the current moment of time and no savings

Let us consider first a situation when a decision maker chooses to consume all disposable income immediately and saves nothing for the later moment of time. Consuming all disposable income at the penultimate moment of time (and consuming nothing at the last moment of time) yields utility $u(Y_{T-1})$. Thus, utility $u(Y_{T-1})$ must be greater than the objective function in (20) for all $C_{T-1}<Y_{T-1}$ in order for zero savings to be an optimal solution.³ This condition can be written as inequality (21).

$$\begin{aligned}&\left[ {1-w\left( \beta \right) } \right] \frac{u\left( {Y_{T-1} } \right) -u\left( {C_{T-1} } \right) }{Y_{T-1} -C_{T-1} }>w\left( \beta \right) \left( {R-1} \right) \nonumber \\&\quad \frac{u\left( {Y_{T-1} R-C_{T-1} \left( {R-1} \right) } \right) -u\left( {Y_{T-1} } \right) }{\left( {Y_{T-1} -C_{T-1} } \right) \left( {R-1} \right) } \end{aligned}$$

(21)

The ratio on the left-hand side of inequality (21) denotes the slope of utility function between $C_{T-1}$ and $Y_{T-1}>C_{T-1}$. The ratio on the right-hand side of inequality (21) denotes the slope of utility function between $Y_{T-1}$ and $Y_{T-1}R-C_{T-1}(R-1)>Y_{T-1}$. One of the properties of a concave utility function is a declining slope, i.e., the ratio on the left-hand side of (21) is strictly greater than the ratio on the right-hand side of (21) for all $C_{T-1}\in [0, Y_{T-1})$. Thus, inequality (21) always holds if $1-w(\beta )$ is greater than or equal to $w(\beta )(R-1)$, which can be rewritten as condition (22). Note that condition (22) is always satisfied as interest rate R is lowered to one—savings are never optimal when they bring no interest.

$$\begin{aligned} w(\beta )\le \frac{1}{R} \end{aligned}$$

(22)

If utility function is differentiable, then inequality (22) is not only a sufficient condition for zero savings but a necessary condition as well. The necessity follows from the following observation. For a differentiable utility function, in the limit as $C_{T-1}$ goes to $Y_{T-1}$, the ratio on the left-hand side of (21) converges to the ratio on the right-hand side of (21). Thus, if inequality (22) does not hold, so that $1-w(\beta )$ is less than $w(\beta )(R-1)$, then it is possible to find $C_{T-1}$ sufficiently close to $Y_{T-1}$ such that inequality (21) does not hold as well.

Condition (22) is rather intuitive. If a decision maker is sufficiently impatient (so that $w(\beta )\le 1{/}R$), then it is optimal to consume all disposable income at the penultimate moment of time without saving anything for the last moment of time. In fact, such a decision maker would even prefer to run into a debt (to have a negative consumption at the last moment) if debts were allowed.

For a linear weighting function, condition (22) simply requires a discount factor not to exceed 1 / R, i.e., a decision maker must not be very patient. For an inverse S-shaped weighting function (that is convex in the neighborhood of one), the upper bound imposed by condition (22) on a subjective discount factor is even higher than 1 / R. Table 3 shows the upper bound on $\beta$ imposed by condition (22) for weighting function (17) with parameter $\gamma =0.61$ (elicited in the experiment of Tversky and Kahneman 1992, p. 312) and $\gamma =0.56$ (estimated by Camerer and Ho 1994, p. 188). For example, if income increases by 10 % from one moment of time to another, a decision maker with weighting function (17) and $\gamma =0.61$ chooses not to save at the penultimate moment of time if $\beta \le 0.9895$.

Table 3 The upper bound imposed by condition (22) on a subjective discount factor $\beta$ for various values of an interest rate R and several weighting functions w($\cdot$)

An impatient decision maker with $w(\beta )\le 1{/}R$ chooses to consume all income Y already at the current moment $t=0$ leaving nothing for consumption at all future moment of time $t\in \{1, 2, {\ldots }T\}$. This conclusion follows from the following observation. We already established that $C_{T}=0$ and $C_{T-1}=Y_{T-1}$ if $w(\beta )\le 1{/}R$. Knowing this, a decision maker faces problem (23) at the before-penultimate moment $T-2$.

$$\begin{aligned} \mathop {\max }\limits _{C_{T-2} \in \left[ {0,Y_{T-2} } \right] } \left[ {1-w\left( \beta \right) } \right] u\left( {C_{T-2} } \right) +w\left( \beta \right) u\left( {C_{T-2} +Y_{T-1} } \right) \end{aligned}$$

(23)

Using budget constraint (19), we can transform problem (23) into a problem that is equivalent to problem (20). Since we deal with the case $w(\beta )\le 1{/}R$, the optimal solution to (23) is then $C_{T-2}=Y_{T-2}$ so that $Y_{T-1}=(Y_{T-2}-C_{T-2})R=0$ and, consequently, $C_{T-1}=0$. Iterating this argument for all preceding moments of time, we come to the conclusion that a decision maker with $w(\beta )\le 1{/}R$ always chooses to consume all disposable income as soon as possible (leaving nothing for consumption at the subsequent moments). Thus, such a decision maker consumes all income Y already at the current moment $t=0$.

Impatient consumers with $w(\beta )\le 1{/}R$ would never voluntarily hold any savings (and even try to accumulate a credit card debt if it were possible). Such decision makers prefer to consume all income immediately and “starve” in the subsequent periods. To prevent such behavior, a social planner can either increase an interest rate (so that condition $w(\beta )\le 1{/}R$ is rarely satisfied) or introduce restrictions on the intertemporal movement of income (e.g., a system of social security). The latter option appears to be more effective. Table 3 shows that a large increase in the interest rate is required for any substantial decrease in the upper bound on $\beta$ when weighting function $w(\cdot )$ is inverse S-shaped.

3.1.1 Dynamic inconsistency with a nonlinear weighting function

Consumers with a nonlinear weighting function $w(\cdot )$ may be dynamically inconsistent. At the current moment $t=0$, they can commit to a consumption path that saves a part of a disposable income for consumption in the future periods. Yet, at a later time moment $t>0$ they prefer to renegotiate such a contract in order to get an advance payment. For example, consider the problem of intertemporal consumption/savings when a decision maker has to choose a consumption path at moment $t=0$ (and it cannot be changed at the subsequent moments). A maximizer of utility (13) then solves problem (24).

$$\begin{aligned}&{\mathop {\mathop {\max }\limits _{ C_1 ,\ldots ,C_{T-1} \ge 0}} \limits _{\sum \limits _{t=0}^{T-1} {C_t R^{T-t}} \le YR^{T}}} \sum _{t=0}^{T-1} {\left[ {w\left( {\beta ^{t}} \right) -w\left( {\beta ^{t+1}} \right) } \right] u\left( {\sum _{s=0}^t {C_s } } \right) }\nonumber \\&\qquad +\,w\left( {\beta ^{T}} \right) u\left( { YR ^{T}-\sum _{t=0}^{T-1} {C_t \left( {R^{T-t}-1} \right) } } \right) \end{aligned}$$

(24)

Using an argument analogous to the one presented above for problem (20) without the possibility of pre-commitment, we can show that a decision maker with a concave utility function decides to pre-commit at the current moment $t=0$ to zero consumption at the last moment $t=T$ if condition (25) holds. Condition (25) is not only sufficient but also necessary if the utility function is differentiable. Note that condition (22), which we derived before for a situation without commitment, can be viewed as a special case of condition (25) when $T=1$ (a commitment only for one period).

$$\begin{aligned} \frac{w\left( {\beta ^{T}} \right) }{w\left( {\beta ^{T-1}} \right) }\le \frac{1}{R} \end{aligned}$$

(25)

If weighting function $w(\cdot )$ is linear, then condition (25) is identical to condition (22) for all $T\ge 2$ (in this case both conditions simplify to $\beta \le 1{/}R)$. In other words, consumers with a linear weighting function do not have the problem of dynamic inconsistency that we described above. If such decision makers optimally decide not to save at the penultimate moment of time, then they also pre-commit to such a decision at any earlier moment of time.

For an inverse S-shaped weighting function $w(\cdot )$ condition, (25) is stronger than condition (22). In this case, inequality (25) may be violated even though condition (22) is satisfied. For example, Table 4 shows the upper bound imposed by condition (25) on a subjective discount factor $\beta$ when $T=50$ for weighting function (17) with parameter $\gamma =0.61$ (elicited in the experiment of Tversky and Kahneman 1992, p. 312) and $\gamma =0.56$ (estimated by Camerer and Ho 1994, p. 188).

Table 4 The upper bound imposed by condition (25) on a subjective discount factor $\beta$ when $T=50$ for various values of the interest rate R and two weighting functions w ($\cdot$)

A comparison of the corresponding cells in Tables 3 and 4 shows the scope of dynamic inconsistency. Consider the case when income increases by 10 % from one moment of time to another and a decision maker has a weighting function (17) with $\gamma =0.61$. Without the possibility of commitment, the decision maker chooses not to save at the penultimate moment of time iff $\beta \le 0.9895$. This decision maker pre-commits to the same zero-savings decision 50 periods in advance iff $\beta \le 0.8536$. Thus, consumers with a discount factor $\beta \in (0.8536, 0.9895]$ are dynamically inconsistent—at the current moment they would pre-commit to a positive consumption at the last moment of time; but after 50 periods, they would try to empty their savings account at the penultimate moment of time.

Whereas $w(\beta )\le 1{/}R$ is a condition for zero savings not only at the penultimate moment of time but also at all earlier moments of time as well, the corresponding condition with the possibility of commitment may differ from inequality (25). At $t=0$, a decision maker with a concave utility function decides not to save at moment of time $k\in \{0, 1, {\ldots }T-1\}$, i.e., he or she pre-commits to zero consumption from moment $k+1\in \{1, 2, {\ldots }T\}$ onwards, if condition (26) holds. Condition (26) is not only sufficient but also necessary when the utility function is differentiable. Condition (25) is a special case of condition (26) when $k=T-1$. Condition (26) is the same as condition (25) and condition (22) when weighting function $w(\cdot )$ is linear. For an inverse S-shaped weighting function, condition (26) gets progressively stronger as k decreases to zero.

$$\begin{aligned} \frac{w\left( {\beta ^{T}} \right) }{w\left( {\beta ^{k}} \right) }\le \frac{1}{R^{T-k}} \end{aligned}$$

(26)

Without the possibility of commitment, a decision maker chooses to consume all income at the current moment $t=0$ when $w(\beta )\le 1{/}R$. At the same time, this decision maker pre-commits at $t=0$ to consuming all income at the same moment of time only when $w(\beta ^{T})\le 1{/}R^{T}$. These two conditions are identical when weighting function $w(\cdot )$ is linear. Yet, for an inverse S-shaped weighting function $w(\cdot )$ these two conditions can vastly differ, particularly for a large T. For example, consider the case when income increases by 10 % from one moment of time to another, $T=50$ and a decision maker has a weighting function (17) with $\gamma =0.61$. Without the possibility of commitment, the decision maker chooses to consume all income at the current moment of time $t=0$ iff $\beta \le 0.9895$. This decision maker pre-commits at $t=0$ to such a decision iff $\beta \le 0.0004$. Thus, a decision maker with a wide range of discount factors $\beta \in (0.0004, 0.9895]$ exhibits some form of dynamic inconsistency (he or she may pre-commit to zero savings close to the last moment $t=T$ but not close to the current moment $t=0$).

3.2 Case 2: saving of all disposable income for the next moment of time and no consumption

When is it optimal to save all disposable income for the next moment of time so that there is no consumption except at the last moment of time T? If a decision maker consumes nothing at $t=T-1$, then all disposable income $Y_{T-1}$ is transferred to the last moment of time. Thus, consumption at the last moment of time is $Y_{T-1}R$ and utility (13) of consumption at moments of time $T-1$ and T is given by

$$\begin{aligned} \left[ {1-w\left( \beta \right) } \right] u\left( 0 \right) +w\left( \beta \right) u\left( {Y_{T-1} R} \right) \end{aligned}$$

(27)

Utility (27) must be greater than the objective function in (20) for all $C_{T-1}>0$ in order for 100 %-savings to be an optimal solution. This condition can be written as inequality (28).

$$\begin{aligned}&w\left( \beta \right) \left( {R-1} \right) \frac{u\left( {Y_{T-1} R} \right) -u\left( {Y_{T-1} R-C_{T-1} \left( {R-1} \right) } \right) }{C_{T-1} \left( {R-1} \right) }\nonumber \\&\quad >\left[ {1-w\left( \beta \right) } \right] \frac{u\left( {C_{T-1} } \right) -u\left( 0 \right) }{C_{T-1} } \end{aligned}$$

(28)

The ratio on the right-hand side of inequality (28) denotes the slope of utility function between 0 and $C_{T-1}>0$. For a concave utility function $u(\cdot )$, this slope decreases in $C_{T-1}$. Thus, the right-hand side of inequality (28) attains its highest possible value in the limit as $C_{T-1}$ converges to zero.

The ratio on the left-hand side of (28) denotes the slope of utility function between points $Y_{T-1}R-C_{T-1}(R-1)$ and $Y_{T-1}R$. For a concave utility function $u(\cdot )$, this slope decreases as $Y_{T-1}R-C_{T-1}(R-1)$ approaches $Y_{T-1}R$ (from below). Thus, the left-hand side of inequality (28) attains its lowest possible value in the limit as $Y_{T-1}R-C_{T-1}(R-1)$ approaches $Y_{T-1}R$, i.e., as $C_{T-1}$ converges to zero. Hence, inequality (28) holds for all $C_{T-1}>0$ if and only if it holds in the limit as $C_{T-1}$ converges to zero.

Let $u'(Y_{T-1}R)$ denote the limit of the ratio on the left-hand side of (28) as $C_{T-1}$ converges to zero (i.e., the marginal utility of consumption at $Y_{T-1}R)$. Let $u'$(0) denote the limit of the ratio on the right-hand side of (28) as $C_{T-1}$ converges to zero (i.e., the marginal utility of consumption at zero). A necessary and sufficient condition for 100 %-savings at the penultimate moment is then (29).

$$\begin{aligned} w\left( \beta \right) >\frac{1}{1+\left( {R-1} \right) \frac{{u}'\left( {Y_{T-1} R} \right) }{{u}'\left( 0 \right) }} \end{aligned}$$

(29)

The intuition behind condition (29) is rather simple—a decision maker saves all disposable income at the penultimate period of time if he or she is sufficiently patient so that $w(\beta )$ is greater than a certain threshold. Note that this threshold [the right-hand side of (29)] converges to one as an interest rate R is lowered to one. Since $w(\beta )$ cannot exceed one, saving all disposable income is never an optimal strategy if those savings bring a very low interest rate R.

If utility function is linear, then the marginal utility of consumption is constant at all levels, i.e., $u'(Y_{T-1}R)=u'(0)$. In this case, condition (29) simplifies to $w(\beta )>1{/}R$, which is a complementary condition to inequality (22). Thus, for a linear utility only two optimal solutions are possible—either a decision maker is impatient and consumes all disposable income [inequality (22) holds] or he/she is patient and saves all disposable income [inequality (29) holds]. This aligns with a standard solution for Samuelson (1937) discounted linear utility (a maximization of the discounted present value).

If condition (29) is satisfied, then a decision maker is very patient and consumes nothing at the penultimate moment of time $T-1$ postponing all consumption to the last moment of time T. With this knowledge, such a decision maker faces problem (30) at the before-penultimate moment of time $T-2$.

$$\begin{aligned} \mathop {\max }\limits _{C_{T-2} \in \left[ {0,Y_{T-2} } \right] } \left[ {1-w\left( {\beta ^{2}} \right) } \right] u\left( {C_{T-2} } \right) +w\left( {\beta ^{2}} \right) u\left( {Y_{T-1} R^{2}-C_{T-1} \left( {R^{2}-1} \right) } \right) \nonumber \\ \end{aligned}$$

(30)

Problem (30) is the same as problem (20) with a squared discount factor and a squared interest rate. Thus, a decision maker optimally chooses to consume nothing in period $T-2$ if condition (31) holds.

$$\begin{aligned} w\left( {\beta ^{2}} \right) >\frac{1}{1+\left( {R^{2}-1} \right) \frac{{u}'\left( {Y_{T-2} R^{2}} \right) }{{u}'\left( 0 \right) }} \end{aligned}$$

(31)

Iterating this argument for all preceding periods, we come to the conclusion that a decision maker postpones all consumption to the last moment of time T (and consumes nothing at all previous moments of time) if and only if condition (32) is satisfied for all $s\in \{1, 2, {\ldots }T\}$.

$$\begin{aligned} w\left( {\beta ^{s}} \right) >\frac{1}{1+\left( {R^{s}-1} \right) \frac{{u}'\left( {YR^{T}} \right) }{{u}'\left( 0 \right) }} \end{aligned}$$

(32)

For a linear utility function (with a constant marginal utility of consumption at all levels), condition (32) simplifies to $w(\beta ^{s})>1{/}R^{s}$ for all $s\in \{1, 2, {\ldots }T\}$. If weighting function is linear as well, then this condition simplifies further to $\beta >1{/}R$, which is a complementary inequality to inequality (22). This is a standard result—a decision maker, who maximizes discounted present value, consumes all income either at the present moment $t=0$ (when $\beta \le 1{/}R)$ or at the last moment $t=T$ (when $\beta >1{/}R$).

This result also holds for a linear utility function and a nonlinear weighting function that is convex in the neighborhood of one that contains values $\{\beta , \beta ^{2}, {\ldots }, \beta ^{T}\}$. In this case, condition (32) imposes the highest lower bound on a subjective discount factor $\beta$ when $s=1$. In other words, if condition (32) is satisfied for $s=1$, then it is also satisfied for all $s\in \{2, 3, {\ldots }T\}$. Thus, condition (32) again simplifies to $w(\beta )>1{/}R$. A decision maker with a linear utility function and a weighting function that is convex in the neighborhood of one (such as an inverse S-shaped function often found in empirical studies) consumes all income either at the present moment $t=0$ (when $w(\beta )\le 1{/}R)$ or at the last moment $t=T$ (when $w(\beta )>1{/}R)$. Thus, when it comes to a small income (where utility function is approximately linear), consumers either spend it straight away or deposit it in their savings account.

Condition (32) is stronger for a concave utility function (with a declining marginal utility) than for a linear utility. In the limiting case, when a marginal utility of income $YR^{T}$ is infinitesimally small compared to the marginal utility of zero consumption, the right-hand side of (32) becomes one, i.e., condition (32) is always violated. In such a case, a decision maker never saves all disposable income for the next moment of time and consumes at least some portion of it. For example, this happens if a decision maker has a constant relative risk aversion utility function $u(x)=x^{1-r}/(1-r)$ for $x\ge 0$ and $r\ne 1$.

In an economy with a low or moderate interest rate, only a small range of discount factors (very close to one) satisfies condition (32) for 100 %-savings, but a wide range of discount factors satisfies condition (22) for 0 %-savings (cf. Table 3). This fits well with a stylized fact that few people over-save but many people over-consume. A social planner who wants to eliminate both excessive savings and excessive consumption can achieve the two goals by lowering an interest rate and introducing restrictions on the movement of income to early periods (such as social security).

3.3 Optimal consumption path with a possibility of a debt (negative consumption)

In Sect. 3.1, we established that consumers with $w(\beta )\le 1{/}R$ choose to consume all disposable income as soon as possible if there is no possibility of pre-commitment to a consumption plan that saves a part of their income for consumption at future moments of time. Yet, this result depends on the restriction that consumers cannot borrow (have a negative consumption at later moments). This section considers a modification of the problem of optimal consumption/saving when consumers can have a negative consumption at some moments of time. An intertemporal budget constraint remains intact—the discounted present value of all consumption must not exceed income Y available at $t=0$.

At the penultimate moment of time, a decision maker then faces problem (20) without the restriction that consumption $C_{T-1}$ must be between zero and $Y_{T-1}$. In case when $w(\beta )<1{/}R$, it becomes optimal to consume more than the income that is disposable at the moment $t=T-1$. A decision maker effectively “borrows” from the consumption at the last moment of time, which becomes negative. For an illustration, let us consider a decision maker with a constant absolute risk aversion (CARA) utility function $u(x)=a- be^{-\mathrm{d}x}$, where $a\in {\mathbb {R}}$ and $b,d>0$; d is the Arrow–Pratt coefficient of absolute risk aversion. In this case, a solution to problem (20) with an unrestricted $C_{T-1}$ is given by (33).⁴

$$\begin{aligned} C_{T-1} =Y_{T-1} -\frac{1}{Rd}\ln \frac{R-1}{1/{w\left( \beta \right) }-1} \end{aligned}$$

(33)

From budget constraint (19), it follows that the optimal consumption at the last moment $t=T$ is (34).

$$\begin{aligned} C_T =\frac{1}{d}\ln \frac{R-1}{1/{w\left( \beta \right) }-1} \end{aligned}$$

(34)

Optimal consumption at the preceding moments $t\in \{1, 2, {\ldots }T-1\}$ is then recursively defined by (35).⁵

$$\begin{aligned} C_t =\frac{1}{d}\ln \left( {e^{C_{t+1} d}+\frac{R-1}{1-w\left( \beta \right) }w\left( {\beta ^{T-t+1}} \right) \left[ {e^{-d\sum \limits _{s=t+1}^T {C_s } }-e^{-d\sum \limits _{s=t+1}^{T-1} {C_s } }} \right] } \right) \end{aligned}$$

(35)

Finally, consumption at the present moment $t=0$ is given by $C_0 =Y-\sum \nolimits _{t=1}^T {C_t R^{-t}}$.

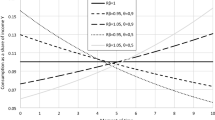
With a possibility of a debt (a negative consumption at later periods), the optimal consumption path defined by (34)–(35) has an interesting pattern. Figure 1 plots consumption path (34)–(35) for Tversky and Kahneman (1992) weighting function (17) with parameters $\gamma =1$ (a linear function), $\gamma =0.61$ (elicited in the experiment of Tversky and Kahneman 1992, p. 312) and $\gamma =0.56$ (estimated by Camerer and Ho 1994, p. 188). We fix $T=50,\,R=1.02$ and the Arrow–Pratt coefficient $d=10^{-5}$.

Fig. 1

Optimal consumption path with a possibility of a debt (negative consumption) for a consumer with CARA utility function (the Arrow–Pratt coefficient $d=10^{-5}$) and Tversky and Kahneman (1992) weighting function ($T =50, R=1.02$)

Figure 1 shows that optimal consumption is nearly constant at the initial moments of time (if T is sufficiently large). This is a standard result. The problem faced by a consumer at one of the early moments is not much different from the problem faced at the subsequent moment (provided that the number of future periods is very large). Thus, the optimal solution does not change much either.

Optimal consumption, however, starts to decline at the later moments of time. There is practically no consumption at the penultimate moment of time and a debt (negative consumption) at the last moment of time. Impatient decision makers (with a low $\beta$) have a higher level of constant consumption at the initial moments and a higher level of debt at the last moment. Compared to this effect, a change in the curvature of the weighting function has a relatively modest effect. As the weighting function (17) converges to a linear function (i.e., parameter $\gamma$ increases to one), a decision maker consumes less at the initial moments of time and has a lower debt at the last moment of time.

4 Behavioral characterization (axiomatization) of rank-dependent discounted utility

There is a totally ordered nonempty set S that can be finite or infinite. An element $t\in S$ is called a moment of time. A total order on the set S is called a chronological order. There is a sigma-algebra $\Sigma$ of the subsets of S that are called time periods. There is a connected set Y. An element $y\in Y$ is called a cumulative outcome. A program $f{:}\,S\rightarrow Y$ is a $\Sigma$-measurable function from S to Y. The set of all programs is denoted by ${\mathcal {F}}$. Aconstant program that yields one cumulative outcome $y\in Y$ in all moments of time is denoted by ${{\mathbf {y}}}\in {\mathcal {F}}$.

A decision maker has a preference relation $\succcurlyeq$ on ${\mathcal {F}}$. The symmetric part of $\succcurlyeq$ is denoted by $\sim$, and the asymmetric part of $\succcurlyeq$ is denoted by $\succ$. The preference relation $\succcurlyeq$ is represented by a function $U{:}\,{\mathcal {F}}\rightarrow {\mathbb {R}}$ if $f\succcurlyeq g$ implies $U(f)\ge U(g)$ and vice versa for all $f,\,g\in {\mathcal {F}}$. We assume that the preference relation $\succcurlyeq$ is a weak order (Axioms 1 and 2).

Axiom 1

(Completeness) For all $f,\,g\in {\mathcal {F}}$ either $f\succcurlyeq g$ or $g \succcurlyeq f$ (or both).

Axiom 2

(Transitivity) For all $f,\,g,\,h\in {\mathcal {F}}$ if $f\succcurlyeq g$ and $g \succcurlyeq h$, then $f\succcurlyeq h$.

First, we derive utility representation when f(t) is a step function. Subsequently, this representation is extended to all other programs. Consider a partition $\{T_{0}, T_{1}, {\ldots },T_{n}\}$ of the time space S into $n+1$ time periods for some $n\in {\mathbb {N}}$ (i.e., $T_{i }\in \Sigma$ for all $i\in \{0, 1,{\ldots },n\},\,T_{0}\bigcup T_{1}\bigcup {\ldots } \bigcup T_{n}=S$ and $T_{i }\bigcap T_{j }=\emptyset$ for all $i,\,j\in \{0, 1,{\ldots },n\},\,i\ne j)$. We assume that time periods in partition $\{T_{0}, T_{1}, {\ldots },T_{n}\}$ are numbered in the chronological order, i.e., time period $T_{0}$ is the earliest and time period $T_{n}$ is the latest. Let $\{y_{0}, T_{0}; y_{1}, T_{1}; {\ldots }; y_{n} ,T_{n}\}$ denote a step program that yields a cumulative outcome $y_{i}\in Y$ at a moment of time $t\in T_{i},\,i\in \{0, 1,{\ldots }, n\}$. We assume that cumulative outcomes do not become less desirable over time (in other words, a decision maker receives only desirable payoffs over time). This assumption guarantees that all step programs are rank-ordered (comonotonic), i.e., ${{{\mathbf {y}}}}_{{{\mathbf {n}}}} \succcurlyeq {{{\mathbf {y}}}}_{{{\mathbf {n}}}-1} \succcurlyeq {\cdots } \succcurlyeq {{{\mathbf {y}}}}_{{{\mathbf {0}}}}$ for any partition $\{T_{0}, T_{1}, {\ldots },T_{n}\}$ that is ordered in the chronological order.⁶ Let $\mathbb {F}\subset {\mathcal {F}}$ denote the set of all step programs.

For compact notation, let $y Tf \in \mathbb {F}$ denote a step program that yields a cumulative outcome $y\in Y$ at all moments of time $t\in T$ within a time period $T\in \Sigma$; and outcome f(t)—at all other moments of time $t\in S\backslash T$. A time period $T\in \Sigma$ is null (or inessential) if $y Tf \succcurlyeq z Tf$ for all $y,\,z\in Y$ and all $f{:}\,S \backslash T\rightarrow Y$. Otherwise, a time period is nonnull (or essential). If there is only one nonnull time period, we additionally assume that Y is a separable set (i.e., Y contains a countable subset whose closure is Y). This assumption is needed for the existence of a continuous utility function within one time period (cf. Debreu 1954, Theorem I, p.162).

Traditionally, a real-valued utility representation is derived through a connected topology approach that assumes continuous preferences (Axiom 3 below). Yet, we actually need only two implications of continuity that are known as solvability and Archimedean property (Axioms 3a and 3b below). Thus, we can assume these two properties directly, instead of assuming continuity. This alternative is known as an algebraic approach (Wakker 1988; Köbberling and Wakker 2003, p. 398).

Axiom 3

(Step-continuity) For any partition $\{T_{0}, T_{1}, {\ldots }, T_{n}\}$ of the set S into $n+1$ time periods and any step program $\{y_{0}, T_{0};y_{1},T_{1};{\ldots };y_{n},T_{n}\}\in \mathbb {F}$ the sets { $(z_{0}, z_{1}, {\ldots }, z_{n})\in Y^{n+1 }{:}\, \{z_{0},T_{0}; {\ldots }; z_{n},T_{n}\} \succcurlyeq \{y_{0},T_{0};{\ldots }; y_{n},T_{n}\} \}$ and $\{(z_{0}, z_{1}, {\ldots }, z_{n})\in Y^{n+1 }{:}\, \{y_{0},T_{0}; {\ldots }; y_{n},T_{n}\} \succcurlyeq \{z_{0},T_{0};{\ldots }; z_{n},T_{n}\} \}$ are closed with respect to the product topology on $Y^{n+1}$.

Axiom 3a

(Solvability) For all cumulative outcomes $x,\,y\in Y$, time period $T\in \Sigma , f{:}\,S\backslash T\rightarrow Y$ and a step program $g\in \mathbb {F}$ such that $x Tf \succcurlyeq g\succcurlyeq y Tf$, there exists a cumulative outcome $z\in Y$ such that $g\sim z Tf$.

Axiom 3b

(Archimedean Axiom) A sequence of cumulative outcomes $\{y_{i}\}_{i\in {\mathbb {N}}}$ such that $y_{i} Tg \sim y_{i-1} Tf$ and $x Tf \succcurlyeq y_{i} Tf \succcurlyeq z Tf$ for some $x, z\in Y$ is finite for all $y_{0}\in Y$, a nonnull time period $T\in \Sigma$, and $f,\,g{:}\,S \backslash T\rightarrow Y$ such that either $y_{0} Tf \succ y_{0} Tg$ or $y_{0} Tg \succ y_{0} Tf$.

In choice under uncertainty, a separable utility representation is traditionally derived from an axiom known as tradeoff consistency (Wakker 1984, 1989) or Reidemeister closure condition in geometry (Blaschke and Bol 1938). Blavatskyy (2013b) recently showed that this condition can be weakened to an axiom known as cardinal independence or standard sequence invariance (e.g., Krantz et al. 1971, Section 6.11.2).

Axiom 4

(Cardinal independence) If $x Tf \succcurlyeq y Tg , x Tg \succcurlyeq z Tf$, and $yAh \succcurlyeq xAk$, then $xAh \succcurlyeq zAk$ for all $x,\,y,\,z \in Y$; $f,\,g{:}\,S\backslash T \rightarrow Y$; $h,\,k{:}\,S\backslash A \rightarrow Y$, any nonnull time period $T\in \Sigma$ and any time period $A\in \Sigma$.

Proposition 1

(Blavatskyy 2013b) A preference relation $\succcurlyeq$ satisfies Axioms 1, 2, 4 and either 3 or 3a and 3b if and only if it admits representation (36), where $p_{i}\in [0,1]$ for all $i\in \{0, 1, {\ldots }, n\},\,p_{0}+p_{1}+{\cdots }+p_{n}=1$, and function $u{:}\,Y\rightarrow {\mathbb {R}}$ is continuous. Constants $p_{i}\in [0,1]$ are unique except for the trivial case when all time periods in $\{T_{0}, T_{1}, {\ldots },T_{n}\}$ are null. Function $u{:}\,Y \rightarrow {\mathbb {R}}$ is unique up to a positive affine transformation if at least two time periods in $\{T_{0}, T_{1}, {\ldots }, T_{n}\}$ are nonnull.

$$\begin{aligned} U\left( \left\{ y_0 ,T_0 ;y_{1} ,T_{1} ;\ldots ;y_n ,T_n \right\} \right) =\sum _{i=0}^n {p_i \cdot u\left( {y_i } \right) } \end{aligned}$$

(36)

The proof follows immediately from Proposition 1 in Blavatskyy (2013b) when Axiom 3 is used, and Proposition 3 in Blavatskyy (2013b) when Axioms 3a and 3b are used.

Formula (36) can be rewritten as (37) by introducing notation $w_i =\sum \nolimits _{k=i}^n {p_k }$ for all $i\in \{0, 1, {\ldots }, n\}$. Since $p_{i} \ge 0$ for all $i\in \{0, 1, {\ldots }, n\}$ and $p_{0}+p_{1} +{\cdots }+ p_{n}=1$, we must have $1=w_{0}\ge w_{2}\ge {\cdots }\ge w_{n}=p_{n}\ge 0$.

$$\begin{aligned} U\left( \left\{ {y_0 ,T_0 ;y_{1} ,T_{1} ;\ldots ;y_n ,T_n } \right\} \right) =u\left( {y_0 } \right) +\sum _{i=1}^n {w_i \left[ {u\left( {y_i } \right) -u\left( {y_{i-1} } \right) } \right] } \end{aligned}$$

(37)

Consider a decision maker who receives a payoff $x_{0}$ at the present moment t=0, a payoff $x_{1}$ at a later moment of time $t=1$ and so forth till the last payoff $x_{n}$ at the latest moment of time $t=n$, for some $n\in {\mathbb {N}}$. If the time space S is ${\mathbb {R}}_{+}$, then this decision maker receives a cumulative outcome $y_{0}=x_{0}$ at any moment of time that belongs to the time period $T_{0}=[0,1)$; a cumulative outcome $y_{1}=x_{0}+x_{1}$ at any moment of time that belongs to the time period $T_{1}=[1,2)$; and so forth till cumulative outcome $y_{n}=x_{0}+x_{1} +{\cdots }+ x_{n}$ at any moment of time in the time period $T_{n}=[n,\infty )$. According to formula (37), the stream of payoffs $\{x_{0}, x_{1}, {\ldots }, x_{n}\}$ received in moments of time $t\in \{0, 1, {\ldots }, n\}$ then yields utility

$$\begin{aligned}&U\left( {\left\{ {x_0 ,\left[ {0,1} \right) ;\ldots ;\sum _{s=0}^n {x_s } ,\left[ {n,\infty } \right) } \right\} } \right) \nonumber \\&\quad =u\left( {x_0 } \right) +\sum _{i=1}^n {w_i \left[ {u\left( {\sum _{s=0}^i {x_s } } \right) -u\left( {\sum _{s=0}^{i-1} {x_s } } \right) } \right] } \end{aligned}$$

(38)

Finally, if we introduce a function $w{:}\,[0,1]\rightarrow \{w_{0}, w_{1}, {\ldots }, w_{n}\}$ such that $w(\beta ^{i})=w_{i}$ for all $i\in \{0,1,{\ldots }, n\}$ and some constant $\beta \in (0,1)$, then formula (38) coincides with model (13).

Representation (37) for step programs can be extended to all other programs. A standard method is to enclose any bounded program $f\in {\mathcal {F}}$ by step programs that period-wise dominate (approximation from above) or are period-wise dominated (approximation from below) by program $f\in {\mathcal {F}}$. For this method to work, we need the following Axioms 5–7 (cf. Lemma 2.3 in Wakker 1993).

Axiom 5

(Nontriviality) $f \succcurlyeq g$ holds not for all $f,\,g\in {\mathcal {F}}$.

Axiom 6

(Monotonicity) For all $f,\,g\in {\mathcal {F}}$ if ${{\mathbf {f}}}({{\mathbf {t}}}) \succcurlyeq {{\mathbf {g}}}({{\mathbf {t}}})$ for all $t\in S$ then $f\succcurlyeq g$.

Axiom 7

(Step-equivalence) For any program $f\in {\mathcal {F}}$, there exists a step program $g\in \mathbb {F}$ such that $f\sim g$.

For unbounded programs, either enclosure by step programs from above or from below (or both) is not possible. We approximate unbounded programs by truncated bounded programs defined as follows. For any $f\in {\mathcal {F}}$ and any $y\in Y$, let $f_{<y}\in {\mathcal {F}}$ denote a program that yields a cumulative outcome y at any moment of time $t\in S$ such that ${{\mathbf {f}}}({{\mathbf {t}}} )\succ {{\mathbf {y}}}$ and cumulative outcome f(t) at all other moments of time. Furthermore, let $f_{>y}\in {\mathcal {F}}$ denote a program that yields a cumulative outcome y at any moment of time $t\in S$ such that ${{\mathbf {y}}}\succ {{\mathbf {f}}}({{\mathbf {t}}})$ and cumulative outcome f(t) at all other moments of time. Axiom 8 below ensures the existence of truncated bounded programs.

Axiom 8

(Truncation richness) For all $x\in Y$ and any $f\in {\mathcal {F}}$, there exists $y\in Y$ such that ${{\mathbf {y}}}\succ {{\mathbf {x}}}$ and $f_{<y}\in {\mathcal {F}}$, and there exists $z\in Y$ such that ${{\mathbf {x}}}\succ {{\mathbf {z}}}$ and $f_{>z}\in {\mathcal {F}}$.

Axiom 9

(Truncation continuity) For all $f\in {\mathcal {F}}$ and all $g\in \mathbb {F}$ if $f \succ g$, then there exists $x\in Y$ such that $f_{<x}\in {\mathcal {F}},\,f_{<x} \succcurlyeq g$ and if $g \succ f$, then there exists $y\in Y$ such that $f_{>y}\in {\mathcal {F}},\, g \succcurlyeq f_{>y}$.

Proposition 2

(Wakker 1993) Preference relation $\succcurlyeq$ satisfies Axioms 1, 2, 4–9 and either 3 or 3a and 3b if and only if it admits representation $U\left( f \right) =\int _S {u\circ f\left( t \right) dw\left( t \right) }$ where a (Bernoulli) utility function $u{:}\,Y\rightarrow {\mathbb {R}}$ is continuous and determined up to an increasing linear transformation; a capacity $w{:}\,\Sigma \rightarrow [0,1]$ is unique; and the integral is a Choquet integral with respect to capacity w.

The proof follows immediately from Proposition 1 and Theorem 2.5 in Wakker (1993, p.463).

If payoffs received between $t=0$ and a future moment of time $t>0$ are described by cumulative payoff function (9), then utility representation in Proposition 2 can be written as $\int \nolimits _{t=0}^\infty {w\left( {e^{-\delta t}} \right) \hbox {d}u\circ y\left( t \right) }$, where $w{:}\,[0,1]\rightarrow [0,1]$ is a strictly increasing function, $w(0)=0$ and $w(1)=1$, and $\delta \in (0,1)$ is a constant.

5 General discussion

The main contribution of this paper is a new model of intertemporal choice that is analogous to rank-dependent utility in choice under risk/uncertainty. Recently, Blavatskyy (2014) showed that a special case of rank-dependent utility with a linear utility⁷ and a cubic weighting function is practically equivalent to the model of optimal portfolio investment in finance that is based on a tradeoff between expected return, risk and skewness of assets. This unexpected relationship together with the results of the current paper demonstrate that it is possible to construct a unified microeconomic theory for risk/uncertainty, finance and time under the umbrella of rank-dependent utility.

A rank-dependent utility representation appears rather naturally in intertemporal choice when a decision maker receives only desirable payoffs over time. In this case, cumulative outcomes are always rank-ordered (comonotonic) when time periods are arranged in a chronological order. In contrast, in choice under risk/uncertainty there is no such equivalent total order on the state space.

The situation is more complex when a decision maker may receive an undesirable payoff at some moment in time. In this case, cumulative outcomes are not necessarily rank-ordered (comonotonic) when time periods are arranged in a chronological order. As a result, the behavior of a decision maker may differ when he or she faces desirable and undesirable payoffs.

Consider the following example from Thaler (1981). A representative individual is indifferent between receiving $15 now and $30 in 3 months as well as between losing $15 now and losing $16 in 3 months. If a representative individual maximized discounted present value, then we would infer a quarterly discount factor $\beta _{+}=0.5$ from a choice between desirable payoffs and a quarterly discount factor $\beta _{-}=0.9375$ from a choice between undesirable payoffs. Thus, it appears as if people discount undesirable payoffs to a smaller extent than desirable payoffs (e.g., Frederick et al. 2002, section 4.2.1, p. 362; Loewenstein and Prelec 1992, section II.3, p. 575).

In order to apply our proposed model to undesirable payoffs, it may be helpful once again to interpret a quarterly discount factor $\beta$ as a survival probability. Thus, a decision maker, who loses $15 now, loses $15 for sure, but a decision maker, who loses $16 in 3 months, loses $16 only with a probability $\beta$. A rank-dependent utility maximizer is indifferent between these two options when Eq. (39) holds (for simplicity, we normalized the utility of zero to zero).

$$\begin{aligned} u\left( {-\$15} \right) =\left[ {1-w\left( {1-\beta } \right) } \right] u\left( {-\$16} \right) \end{aligned}$$

(39)

A rank-dependent utility maximizer is indifferent between receiving $15 now and receiving $30 in 3 months when Eq. (18) holds for $t=1,\,z=30$. As an illustration, let us consider a weighting function (17) proposed by Tversky and Kahneman (1992, p. 309) and a power utility function $u\left( {\$x} \right) =\mathrm{sign}\left( x \right) *\left| x \right| ^{\alpha }$, with parameter values $\gamma =0.56$ and $\alpha =0.225$ estimated by Camerer and Ho (1994, p. 188). In this case, a quarterly discount factor inferred from Eq. (39) is $\beta _{-}=0.9995$ and a quarterly discount factor inferred from Eq. (18) is $\beta _{+}=0.9852$. Thus, a discount factor can be very similar for gains and losses when we allow for a nonlinear weighting function and a nonlinear utility even though gains appear to be discounted at a significantly higher rate under the assumption of linear weighting and utility functions. Note that this example does not even require different weighting functions for gains and losses and/or the possibility of loss aversion as in cumulative prospect theory (Tversky and Kahneman 1992).

Any model involves a tradeoff between descriptive realism and parsimony/analytical convenience. In choice under risk/uncertainty, rank-dependent utility can rationalize a wide range of behavioral regularities such as Allais (1953) common consequence effect, the common ratio effect (e.g., Bernasconi 1994) and systematic violations of the betweenness axiom (e.g., Camerer and Ho 1994). Yet, rank-dependent utility also fails to accommodate some behavioral patterns such as the reflection example (Machina 2009; Blavatskyy 2013c) and the troika paradox (Blavatskyy 2012).⁸ Similarly, our proposed model can rationalize numerous behavioral regularities in intertemporal choice (and new examples from the introduction), but it cannot possibly accommodate all of them.

Consider the following example of “subadditive” time preferences (Scholten and Read 2010, anomaly 1, p. 928).⁹ A decision maker prefers to receive $100 in 19 months rather than $118 in 22 months. He/she also prefers to receive $136 in 22 months rather than $100 in 16 months. Let $\beta$ denote a monthly discount factor and let us normalize the utility function so that u($0) $=$ 0. According to model (13) a decision maker reveals the above-mentioned choice pattern if inequality (40) holds.

$$\begin{aligned} \frac{w\left( {\beta ^{16}} \right) }{u\left( {\$136} \right) }<\frac{w\left( {\beta ^{22}} \right) }{u\left( {\$100} \right) }<\frac{w\left( {\beta ^{19}} \right) }{u\left( {\$118} \right) } \end{aligned}$$

(40)

If utility function $u(\cdot )$ is linear/concave, then inequality (40) holds only when weighting function $w(\cdot )$ is sufficiently concave in the domain containing $\beta ^{16},\,\beta ^{19}$ and $\beta ^{22}$. An inverse S-shaped weighting function, which is often found in empirical studies, is concave only in the neighborhood of zero. Thus, for a typical parameterization of rank-dependent utility with a concave utility and an inverse S-shaped weighting function, inequality (40) can hold only when a discount factor $\beta$ is sufficiently small so that values $\beta ^{16},\,\beta ^{19}$ and $\beta ^{22}$ are in the neighborhood of zero.¹⁰ Yet, such a low monthly discount factor (that is close to zero when compounded over 16–22 months) does not appear to be realistic.

If utility function $u(\cdot )$ is convex, then inequality (40) can hold for a high discount factor $\beta$ (so that values $\beta ^{16},\,\beta ^{19}$ and $\beta ^{22}$ are in the neighborhood of one where a conventional inverse S-shaped weighting function is convex). For example, consider weighting function (17) proposed by Tversky and Kahneman (1992) with a parameter $\gamma =0.56$ estimated by Camerer and Ho (1994, p.188). Let a monthly discount factor be $\beta =0.999$. In this case, inequality (40) holds when utility function $u(\cdot )$ is sufficiently convex so that u($118) $<$ 1.0139u($100) but u($136) $>$ 1.0293u($100). Figure 2 illustrates these bounds on a convex utility function $u(\cdot )$. Thus, our proposed model (13) can accommodate “subadditive” time preferences found in Scholten and Read (2010) if we allow for nonstandard parameters: either a low monthly discount factor or a (slightly) convex utility function.

Fig. 2

The “least convex” utility function required for inequality (40) to hold for $\beta =0.999$ and Tversky and Kahneman (1992) weighting function (17) with a parameter $\gamma =0.56$: utility of $118 must not exceed 1.0139 u($100) and utility of $136 must not fall below 1.0293 u($100)

Finally, let us consider an example of “superadditive” time preferences from Scholten and Read (2010, anomaly 2, p. 929). A decision maker prefers to receive $10,250 in 24 months rather than $8250 in 12 months. The same decision maker also prefers to receive $6250 in 12 months rather than $10,250 in 36 months. Let $\beta$ denote an annual discount factor and let u($0) $=$ 0. Model (13) then represents the above-mentioned “superadditive” time preferences if inequality (41) holds.

$$\begin{aligned} \frac{w\left( {\beta ^{3}} \right) }{u\left( {\$6250} \right) }<\frac{w\left( \beta \right) }{u\left( {\$10{,}250} \right) }<\frac{w\left( {\beta ^{2}} \right) }{u\left( {\$8250} \right) } \end{aligned}$$

(41)

For a linear or concave utility function $u(\cdot )$, inequality (41) holds only if weighting function $w(\cdot )$ is concave on the domain that contains $\beta ,\,\beta ^{2}$ and $\beta ^{3}$. Yet, for a convex utility function, inequality (41) may hold when weighting function $w(\cdot )$ is convex or linear on the domain that contains $\beta ,\,\beta ^{2}$ and $\beta ^{3}$. For example, consider weighting function (17) with $\gamma =0.56$ and an annual discount factor $\beta =0.99$. In this case, inequality (41) holds when utility function $u(\cdot )$ is sufficiently convex so that u($6250) $>$ 0.9077u($10,250), but u($8250) $<$ 0.9463u($10,250). Figure 3 illustrates these bounds. Thus, model (13) can rationalize “superadditive” time preferences if we allow for convex utility function.

Fig. 3

The “least convex” utility function required for inequality (41) to hold for $\beta =0.99$ and Tversky and Kahneman (1992) weighting function (17) with a parameter $\gamma =0.56$: utility of $6250 must exceed 0.9077 u($10,250) and utility of $8250 must fall below 0.9463 u($10,250)

A drawback of discounted utility as well as its subsequent generalizations such as quasi-hyperbolic and generalized hyperbolic discounting is that these models assume independence (cf. Postulate 3, Koopmans 1960, p. 292). This assumption can be summarized as follows. If, at some point in time, all available choice alternatives yield the same payoff, then a choice decision does not depend on such a payoff (e.g., Bleichrodt et al. 2008, p. 342). Even though this assumption is quite problematic in intertemporal choice, it is seldom discussed in the literature (cf. Frederick et al. 2002, Section 3.2, p. 357). To illustrate the limitations of independence, let us consider a choice between

• (A) One million in 2 years

• (B) Two million in 6 years

as well as a choice between

• (C) Ten million now plus 1 million in 2 years

• (D) Ten million now plus 2 million in 6 years

Some people may choose A over B, for example, because the marginal utility of their first million is much higher than the marginal utility of their second million. At the same time, they may choose D over C. Upon receiving 10 million, the comparative advantage of getting another million in 2 years (in C) may fade away in front of the investment possibility to double that amount in 4 years (in D). In other words, there may be an intertemporal wealth effect—a large payoff received in an earlier time period may affect the decision maker’s preference between payoffs in the subsequent periods.

Our proposed model can rationalize such intertemporal wealth effects. For simplicity, let us consider model (13) with a linear weighting function $w(\cdot )$, i.e., we consider “discounted incremental utility” model (3). According to model (3), a decision maker prefers to receive 1 million in 2 years (option A) rather than 2 million in 6 years (option B) if and only if inequality (42) holds (with $\beta$ denoting an annual discount factor).

$$\begin{aligned} \beta ^{2}u\left( {\$1\,\hbox {m}} \right) >\beta ^{6}u\left( {\$2\,\hbox {m}} \right) \end{aligned}$$

(42)

At the same time, this decision maker prefers to receive (D) 10 million now plus 2 million in 6 years rather than (C) 10 million now plus 1 million in 2 years if and only if inequality (43) holds.

$$\begin{aligned} u\left( {\$10\,\hbox {m}} \right) {+}\beta ^{6}\left[ {u\left( {\$12\,\hbox {m}} \right) {-\,}u\left( {\$10\,\hbox {m}} \right) } \right] >u\left( {\$10\,\hbox {m}} \right) {+}\beta ^{2}\left[ {u\left( {\$11\,\hbox {m}} \right) {-\,}u\left( {\$10\,\hbox {m}} \right) } \right] \nonumber \\ \end{aligned}$$

(43)

Inequalities (42) and (43) cannot hold simultaneously if utility function $u(\cdot )$ is linear. Yet, if the utility function is nonlinear, both inequalities are satisfied whenever condition (44) is met.

$$\begin{aligned} \frac{u\left( {\$11\,\hbox {m}} \right) -u\left( {\$10\,\hbox {m}} \right) }{u\left( {\$12\,\hbox {m}} \right) -u\left( {\$10\,\hbox {m}} \right) }<\beta ^{4}<\frac{u\left( {\$1\,\hbox {m}} \right) }{u\left( {\$2\,\hbox {m}} \right) } \end{aligned}$$

(44)

For a concave utility function $u(\cdot )$, the ratio on the left-hand side of (44) is always smaller than the ratio on the right-hand side of (44). In other words, a concave (convex) utility function is necessary for systematic violations of independence when people reveal greater patience (impatience) when receiving large outcomes in the present period. Thus, model (3) predicts that a decision maker with a concave utility function may have a systematic tendency to choose (A) over (B) but (D) over (C).

So far, we considered only monetary payoffs, but our proposed model can be also applied to more general outcomes such as vectors of consumption goods/services (i.e., when $x_{t}\in {\mathbb {R}}^{n}$ for $n\in {\mathbb {N}})$. For illustration, let us consider a choice between the following plans for a summer vacation:

• (E) France this year and Hawaii next year

• (F) Hawaii this year and Hawaii next year

as well as a choice between

• (G) France this year and France next year

• (H) Hawaii this year and France next year

Some people may find it boring to visit the same destination 2 years in a row, even if it is their favorite destination. Such decision makers would prefer plan (I) over plan (J), but, at the same time, they would prefer plan (L) over plan (K), in violation of the assumption of payoff independence. In other words, there may be an intertemporal substitution effect. A stream of diversified intertemporal payoffs may satisfy a decision maker to a greater extent than a stream that yields the same payoff in every time period (even if this payoff is the most desirable one in one-shot choice).

On the other hand, there may be people who prefer visiting the same destination year after year. Such decision makers would prefer plan (J) over plan (I) and plan (K) over plan (L) due to their habit formation. Again, such behavior violates the independence assumption. Loewenstein and Prelec (1993, Example 4, p. 95) provide another similar example of independence violation.

We shall denote outcomes as vectors with two elements. The first (second) element denotes the number of summer vacations spent in France (Hawaii). Consequently, the domain of utility function $u(\cdot )$ is ${\mathbb {R}}^{2}$. Finally, let $\beta$ be an annual discount factor. According to model (3), a decision maker prefers vacation plan (I) over vacation plan (J) if inequality (45) is satisfied.

$$\begin{aligned} u\left( {1,0} \right) +\beta \left[ u\left( {1,1} \right) -u\left( {1,0} \right) \right] >u\left( {0,1} \right) +\beta \left[ u\left( {0,2} \right) -u\left( {0,1} \right) \right] \end{aligned}$$

(45)

At the same time, this decision maker prefers plan (L) over plan (K) if inequality (46) holds.

$$\begin{aligned} u\left( {0,1} \right) +\beta \left[ {u\left( {1,1} \right) -u\left( {0,1} \right) } \right] >u\left( {1,0} \right) +\beta \left[ {u\left( {2,0} \right) -u\left( {1,0} \right) } \right] \end{aligned}$$

(46)

Inequalities (45) and (46) can hold simultaneously if and only if inequality (47) is satisfied.

$$\begin{aligned} \beta \left[ {u\left( {1,1} \right) -u\left( {0,2} \right) } \right] >\left( {1-\beta } \right) \left[ {u\left( {0,1} \right) -u\left( {1,0} \right) } \right] >\beta \left[ {u\left( {2,0} \right) -u\left( {1,1} \right) } \right] \end{aligned}$$

(47)

A necessary condition for (47) to hold is inequality (48), which defines a concave utility function $u(\cdot )$.

$$\begin{aligned} u\left( {1,1} \right) >\frac{u\left( {2,0} \right) +u\left( {0,2} \right) }{2} \end{aligned}$$

(48)

Thus, a decision maker with a concave utility function $u(\cdot )$ can systematically violate independence by choosing vacation plan (I) over vacation plan (J) as well as vacation plan (L) over vacation plan (K). This is a standard result from consumer choice—people with concave utility prefer a diversified consumption basket because substituting goods/commodities that are consumed in large quantities with goods/commodities that are consumed in small quantities increases overall satisfaction.

Similarly, for a convex utility function $u(\cdot )$ the rightmost-hand side of inequality (47) is greater than the leftmost-hand side of inequality (47). Thus, a decision maker with a convex utility function can also systematically violate intertemporal independence. In this case, however, the pattern of violations is different—a decision maker prefers to visit the same destination year after year.

The above examples illustrate that “discounted incremental utility” can be used for modeling a variety of time preferences. The model has the same number of parameters as the discounted utility of Samuelson (1937). Yet, despite this parsimony, the model can accommodate a large set of behavioral regularities including intertemporal wealth, complementarity and substitution effects. Apparently, an improvement in the descriptive realism does not sacrifice analytical convenience.

The separability of utility in intertemporal choice may not be normatively appealing because payoffs are not mutually exclusive. They are merely received at different points in time, and there still may be strong wealth, complementarity or substitution effects (as our examples above illustrate). Arguably, the separability of utility is more appealing in choice under risk/uncertainty where payoffs occur in mutually exclusive states of the world. Yet, even in this case, there are well-known violations of independence (e.g., Allais 1953, p. 527; Kahneman and Tversky 1979, p. 266).

The classical work of Samuelson (1937) catalyzed economic modeling of intertemporal choice. Most of the subsequent developments in the literature adopted some elements of Samuelson’s discounted utility. This paper tries to avoid such a legacy. As a result, our proposed model of intertemporal choice avoids such problems as the discontinuity of time preferences, increasing satisfaction from splitting payoffs across two periods close in time and payoff independence.