Introduction

Hedging is the act of taking a futures market position in order to reduce the degree of risk associated with holding a specific asset. Although there exists a futures market for an underlying asset, that futures market is so illiquid that it is functionally useless (Hull 2014). One problem with using futures contracts to hedge a portfolio of spot assets is that a perfect futures contract may not exist, and as a consequence, a perfect hedge cannot be achieved. In order to allow an efficient alignment of risk and reward, the well-known hedging ratio is implemented.

The selection of an optimal hedging ratio is a central issue in the risk management practices. Traditionally, the optimal hedge ratio is defined as the ratio of futures holdings to a spot position that minimizes the risk of the hedged portfolio (Conlon et al. 2016). A hedge ratio is the comparative value of an open position’s hedge to the aggregate size of the position itself. It is expressed as a decimal or fraction and is used to quantify the amount of risk exposure one has assumed through remaining active in an investment or trade. It can be calculated based on correlation of both spot and future price and standard deviation of the future (Hull 2014).

The strategy of the hedging ratio is very simple and involves the adoption of a fixed hedge which consists of taking a futures position that is equal in magnitude, but opposite in sign to the spot position. If price changes in the futures market exactly match those in the spot market, the adoption of a one-to-one strategy will be enough to eliminate the price risk. However, in practice the prices in the spot and futures markets do not move exactly together and a hedge ratio derived from the traditional beta hedge strategy would not minimize the risk. In particular, Casillo (2004) shows that mispricing adds 20% to the volatility of the futures contract. Since the futures contract is more volatile than the underlying index, the use of the beta as a sensitivity adjustment would over-hedged the portfolio. The fundamental of optimal hedge ratio is derived by maximizing the mean–variance expected utility of the hedged portfolio (Benet 1992; Tong 1996; Brooks and Chong 2001). The previous literature presents the estimation of static hedge ratio by the ordinary least squares technique (Ehsani and Lien 2015). However, several papers are supportive of dynamic hedging strategies (Bollerslev 1986; Engle and Kroner 1995; Engle and Sheppard 2001; Engle 2002). Consequently, we employ the GARCH specification to estimate a time-varying hedge ratio, and we demonstrate that the dynamic hedging strategy provides greater risk reduction than the static one.

Because of the mixed results found in the literature, the research question on the optimal hedge ratio is still of paramount importance. Numerous papers attempt to derive the optimal of hedging ratio by considering different extensions. Chen et al. (2014) compute the optimal hedge ratio by minimizing the riskiness of hedged portfolio returns. The authors show that the riskiness-minimizing hedge ratio is effective in reducing the riskiness of the spot as compared to the variance-minimizing hedge ratio. Choudhry (2003) shows that the time-varying hedge ratio based on bivariate GARCH and bivariate GARCH-X models outperforms the constant minimum variance hedge ratio.

Most of the above hedging models assume that both returns of spot and futures follow a multivariate normal distribution with linear dependence. However, this hypothesis is not confirmed by empirical studies, which show that financial asset returns are skewed, leptokurtic and asymmetrically dependent (Longin and Solnik 2001; Ang and Chen 2002; Patton 2006). The purpose of this paper is to improve the effectiveness of dynamic hedging by specifying the joint distribution of spot and futures returns more realistically. Accordingly, we use a GARCH model based on copula. The copula function describes the dependence structure between the spot and futures returns, and the joint distribution can be decomposed into its marginal distributions and its dependence structure. The contribution of this article is to develop GARCH model and test it for several types of assets (exchange rate, stocks, energy and commodity indices) using different copulas to specify the joint distribution. With this more realistic hedging ratio, this paper tries to provide a better tool for risk management. Our results show that the GARCH family models based on copula improve the hedging effectiveness.

The remaining part of the paper is organized as follows: Sect. 2 presents the hedging ratio measures, Sect. 3 discusses the empirical results and provides the economic implications for designing optimal portfolios and formulating optimal hedging strategies, and Sect. 4 gives some concluding comments.

Methodology

The hedging model

Following Hull (2014), let St and ft be the respective changes in the spot and futures prices at time t. If the joint distribution of spot and futures returns remains the same over time, then the conventional risk-minimizing hedge ratio \(\delta\) will be defined as the ratio of covariance between the spot and the future divided by the variance of the future:

$$\delta = \frac{{\text{cov} \left( {S_{t } , f_{t} } \right)}}{{\text{var} \left( {f_{t} } \right)}}$$
(1)

Estimation of this stat hedge ratio is easily computed from the least squares regression of \(S_{t } on f_{t}\). However, the joint distribution of these assets may be time varying, in which case the static hedging strategy is not suitable for an extension to multi-period futures hedging.

The dynamic hedge ratio depends on the way in which the conditional variances and covariances are specified. Thus, scholars (Jondeau and Rockinger 2006; Karakas 2016; Han et al. 2017) propose to use GARCH models to compute the conditional variances.

The GARCH(p, q), generalized autoregressive conditional heteroscedasticity, model was introduced by Bollerslev (1986). According to this model, the conditional variance is a linear function of lagged squared error terms and lagged conditional variance terms. The GARCH (p, q) model successfully captures several characteristics of financial time series, such as thick tailed returns and volatility clustering (Baba et al. 1990).

The conditional mean and variance equations of the GARCH (1,1) model can be expressed as:

$$\begin{aligned} r_{t} & = \mu + \phi r_{t - 1 } + \varepsilon_{t} , \\ \varepsilon_{t} & = \sqrt {h_{t} z_{t} } \\ h_{t} & = w + \alpha \varepsilon_{t - 1}^{2} + \beta h_{t - 1} \\ \end{aligned}$$
(2)

where rt denotes return at time t, μt is the conditional mean at t, ht is the conditional variance at t and w, α and β are nonnegative parameters with the restriction that the sum α + β is less than one to ensure stationarity and the positive of conditional variance as well.

The dynamic conditional correlation (DCC)-GARCH model proposed by Engle and Sheppard (2001) and Engle (2002) releases the constant correlation and improves the flexibility of the hedging models. Also, this specification allows the correlation to be time varying. All the above models are estimated under the assumption of multivariate normality, whereas most of these dynamic hedging models assume that the spot and futures returns follow a multivariate normal distribution with linear dependence.

This assumption is at odds with numerous empirical studies, which show that financial asset returns are skewed, leptokurtic and asymmetrically dependent. Various explanations for these empirical facts have been provided, such as leverage effects and asymmetric responses to uncertainty. Hence, these characteristics should be considered in the specifications of any effective hedging model. The use of a copula function allows us to consider the marginal distributions and the dependence structure both separately and simultaneously. Therefore, the joint distribution of the asset returns can be specified with full flexibility, which will thus be more realistic. Copula functions enable flexible modeling of the dependence structure between random variables by allowing the construction of multivariate densities that are consistent with the univariate marginal densities. Hence, copulas can be considered as a powerful tool for identifying and modeling dependence structure (Koirala et al. 2014).

The advantage of using copulas relies in the fact that marginal distributions and dependence structure that is entirely represented by the copula functions can be separated (Nelson 1999; Cherubini et al. 2004). An important property of copulas is that they are invariant under strictly increasing transformations of the variables. This invariance property guarantees that variables and their logarithms have the same copula.

Following Hsu et al. (2008), we specify the the Glosten–Jagannathan–Runkle (GJR)-ARCH models for shocks in the spot and futures returns. Under the same error correction model, the conditional variance for asset i, i = s, f, is given by:

$$\begin{aligned} h_{i,t}^{2} = c_{i} + b_{i} h_{i,t - 1}^{2} + a_{i,1} \varepsilon_{i,t - 1}^{2} + a_{i,2} k_{i, t - 1} \varepsilon_{i, t - 1}^{2} \hfill \\ \varepsilon_{it} = h_{i,t} z_{i,t } ; z_{i,t} \sim {\text{skewed}} - t\left( {z_{i} /\eta_{i} , \phi_{i} } \right) \hfill \\ \end{aligned}$$
(3)

with ki,t−1 = 1 when εi,t−1 is negative; otherwise, ki,t−1 = 0. The density function of the skewed t distribution is:

$${\text{Skewed}} - t\left( {z/\eta , \phi } \right) = \left\{ {\begin{array}{*{20}c} {bc \left( {1 + \frac{1}{\eta - 2}\left( {\frac{bz + a}{1 - \phi }} \right)^{2} } \right)^{{\frac{\eta + 1}{2}}} ;\quad z < - \frac{a}{b}} \\ {bc \left( {1 + \frac{1}{\eta - 2}\left( {\frac{bz + a}{1 + \phi }} \right)^{2} } \right)^{{\frac{\eta + 1}{2}}} ;\quad z \ge - \frac{a}{b}} \\ \end{array} } \right.$$
(4)

The values of a, b and c are defined as:

$$a \equiv 4\phi \frac{\eta - 2}{\eta - 1} ;\quad b \equiv 1 + 3\phi^{2} - a^{2} ;\quad c \equiv \frac{{\varGamma \left( {\frac{\eta + 1}{2}} \right)}}{{\sqrt {\pi \left( {\eta - 2} \right)} \varGamma \left( {\frac{\eta }{2}} \right)}}$$
(5)

where η is the kurtosis parameter and \(\emptyset\) is the asymmetry parameter. These are restricted to 4 < η < 30 and − 1 <  \(\emptyset\)  < 1. Thus, the specified marginal distributions of spot and futures returns are asymmetric, fat-tailed and non-Gaussian. Assume that the conditional cumulative distribution functions of zs and zf are Gs,t (zs,t|Ψt−1) and Gf,t (zf,t|Ψt−1), respectively. Ψt−1is the information set at time t − 1.

The conditional copula function, denoted as Ct(ut,vt|Ψt−1), is defined by the two time-varying cumulative distribution functions of random variables

$$u_{t} = G_{s,t} (z_{s,t} |\varPsi_{t - 1} ){\text{ and }}v_{t} = Gf,t(z_{f,t} |\varPsi_{t - 1} ).$$
(6)

Let Φt be the bivariate conditional cumulative distribution functions of zs,t and zf,t. Using the Sklar theorem, we obtain:

$$\varPhi_{t} \left( {z_{s,t} , z_{f,t} /\varPsi_{t - 1} } \right) = C_{t} \left( {u_{t} ,v_{t} /\varPsi_{t - 1} } \right) = C_{t} \left( {G_{s,t} \left( {z_{s,t} /\varPsi_{t - 1} } \right),G_{f,t} \left( {z_{f,t} /\varPsi_{t - 1} } \right)/\varPsi_{t - 1} } \right)$$
(7)

The bivariate conditional density function of zs,t and zf,t can be constructed as:

$$\begin{aligned} \varphi_{t} \left( {z_{s,t} , z_{f,t} /\varPsi_{t - 1} } \right) & = c_{t} \left( {G_{s,t} \left( {z_{s,t} /\varPsi_{t - 1} } \right), G_{f,t} \left( {z_{f,t} /\varPsi_{t - 1} } \right)/\varPsi_{t - 1} } \right) \\ & \quad \times g_{s,t} \left( {z_{s,t} /\varPsi_{t - 1} } \right) \times g_{f,t } \left( {z_{f,t} /\varPsi_{t - 1} } \right) \\ \end{aligned}$$
(8)

where

$$c_{t} \left( {u_{t} ,v_{t} /\varPsi_{t - 1} } \right) = \frac{{\partial^{2} C_{t} \left( {u_{t} ,v_{t} /\varPsi_{t - 1} } \right)}}{{\partial u_{t} \partial v_{t} }} ; \quad g_{s,t } \left( {z_{s,t} /\varPsi_{t - 1} } \right)$$
(9)

is the conditional density of zs,t and gf,t (zf,t |Ψt−1) is the conditional density of zf,t.

The literature proposes several copulas such as elliptical, Archimedean, archimax and extreme value copulas (Ewing and Malik 2013). In our paper, we focus on Archimedean copulas. Archimedean copulas are a prominent class of copulas with a common method of construction involving one-dimensional generator functions (Joe 1997 and Nelson 1999). This version of copulas functions is suitable for our study as it presents desirable properties such as associatively and symmetry and they are capable of capturing wide ranges of dependence (Malevergne and Sornette 2003). Archimedean copulas have no linear dependence parameter in their density function. Prior to their use in financial application, Archimedean copulas have been successfully used in actuarial applications (Frees and Valdez 1998). Many extreme value copulas are introduced in the literature, and the most known are Gumbel, Frank, BB7, Joe and Kimeldorf–Sampson copulas (Joe 1997; Nelson 1999).

  • Gumbel copula

The Gumbel copula is an Archimedean copula, which can capture a different sense of risk occurring during periods of stress. It has the following form:

$$C\left( {u_{1},u_{2}} \right) \, = \, \exp \left\{ { - \left[ {\left( { - \, \log u_{1}} \right)^{\theta} + \, \left( { - \, \log u_{2}} \right)^{\theta} } \right]^{1/\theta} } \right\}$$
(10)

with θ ≥ 1 expressing the degree of dependence.

  • Frank copula

The Frank copula (1979) takes the following form:

$$C\left( {\mu_{1} , \mu_{2} ; \,\theta } \right) = - \theta^{ - 1} \log \left\{ {1 + \frac{{\left( {e^{{ - \theta \omega_{1} }} - 1} \right)\left( {e^{{ - \theta \mu_{2} }} - 1} \right)}}{{e^{ - \theta } - 1}}} \right\}$$
(11)

The dependence parameter may assume any real value (− ∞; ∞). Values of − ∞, 0 and ∞ correspond to the Frechet lower bound, independence and Frechet upper bound, respectively. Consequently, the Frank copula can be used to model outcomes with strong positive or negative dependence.

  • BB7 copula

This family was introduced by Joe and Xu. It has the following form:

$$C\left( {\mu ,\upsilon ,\theta ,\delta } \right) = 1 - \left( {1 - \left[ {\left( {1 - \mu^{ - \theta} } \right)^{ - \delta} + \left( {1 - \theta ^{ -\theta} } \right) ^{ -\delta} - 1} \right]^{ -1/\delta} } \right)^{ 1/\theta}$$
(12)

with θ ≥ 1, δ ≻ 0.

Where μ = 1 − μ, θ = 1 − θ and generator function φ(t) = [1 − (1 − t)θ]−δ − 1. The lower and upper tail dependences for the BB7 copula are λL = 2−1/δ and λμ = 2 − 21/θ, respectively.

It is worth emphasizing that parameter θ allows us to capture the upper tail dependence only, whereas δ is related to the lower tail dependence. For this characteristic, the BB7 copula plays an important role among all the two-parameter Archimedean copulas.

  • Joe copula

Joe copula can be presented as follows:

$$C\left( {\mu 1,\mu 2:\delta } \right) = 1 - \left( {\left( {1 - \mu 1} \right)\delta + \left( {1 - \mu 2} \right)\delta - \left( {1 - \mu 1} \right)\delta \left( {1 - \mu 2} \right)\delta \left( {1 - \mu 2} \right)\delta } \right)1/\delta ,$$
(13)

where δ ≥ 1 and the generator function is φt = − ln(1 − (1 − t)δ).

  • Kimeldorf–Sampson

The Kimeldorf and Sampson copula has the following form:

$$C\left( {\mu , \, \theta } \right) \, = \, \left( {\mu - \delta + \, \theta - \delta - \, 1} \right) - 1/\delta ,$$
(14)

where 0 ≺ δ ≺ ∞0 and the generator function is φ(t) = t−δ − 1. This copula is also known as the Clayton copula.

Following Patton (2006) and Bartram et al. (2007), we assume that the dependence parameters \(\rho_{t}\) or \(\tau_{t}\) rely on the previous dependences and historical information. These time-varying parameters are specified, respectively, as:

$$\left( {1 - \theta_{1} L} \right)\left( {1 - \theta_{2} L} \right)\rho_{t} = \omega + \gamma \left( {u_{t - 1} - 0.5} \right)\left( {v_{t - 1} - 0.5} \right)$$
(15)
$$\left( {1 - \theta_{1} L} \right)\left( {1 - \theta_{2} L} \right)\tau_{t} = \omega + \gamma \left( {u_{t - 1} - 0.5} \right)\left( {v_{t - 1} - 0.5} \right)$$
(16)

where both \(\beta_{1}\) and \(\beta_{2}\) are positive, and then, the copula parameters are:

$$\theta_{c } = \left( {\theta_{1} , \theta_{2} , \omega , \gamma } \right)$$
(17)

In our study, extreme dependence between spot and futures returns is modeled by one of these five copulas. We consider that the best and the more appropriate copula is the one that minimizes Akaike criteria (AIC). The IMF (inference function for margins) method allows estimation of the parameters of the distributions and those of the function copulates separately, using the maximum likelihood method for each one.

After estimating the parameters in different copula-based GARCH models, the conditional variances \(h_{st}^{2}\) and \(h_{ft}^{2}\) are obtained (using Eq. 3):

$$h_{i,t}^{2} = c_{i} + b_{i} h_{i,t - 1}^{2} + a_{i,1} \varepsilon_{i,t - 1}^{2} + a_{i,2} k_{i, t - 1} \varepsilon_{i, t - 1}^{2}$$
(18)

The dynamic hedge ratios for the copula-based GARCH models are then calculated as the conditional covariance of the spot S and futures f prices (Eq. 18) on the conditional variance of the future f including the dependence defined by the copulas (Eqs. 10, 11, 12, 13 and 14):

$$\widehat{\delta }_{t}^{*} = {\raise0.7ex\hbox{${h_{sf,t} }$} \!\mathord{\left/ {\vphantom {{h_{sf,t} } {h_{f,t}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${h_{f,t}^{2} }$}}$$
(19)

Hence, the steps of our approach can be summarized hereafter:

  1. 1.

    Check the nature and the behavior of the data.

  2. 2.

    Use the sample of innovations to estimate the parameters of the selected copula functions.

  3. 3.

    Estimate the parameters and covariances of the GJR-ARCH model including the copula in the skewed distribution, as developed in the Sklar’s theorem.

  4. 4.

    Use the covariances and variances obtained to estimate the hedging ratio.

Effectiveness of hedging

For checking the effectiveness of copula-GARCH models for hedging ratio, we use DCC-GARCH model as benchmark.

To developp this benchmark, we use a multivariate GARCH with bivariate error correction, following Kroner and Sultan (1993) and Kroner and Ng (1998). For St−1 and Ft−1, the spot and futures prices:

$$s_{t} = \varphi_{0s} + \varphi_{1s} \left( {S_{t - 1} - \lambda F_{t - 1} } \right) + \varepsilon_{st}$$
$$f_{t} = \varphi_{0f} + \varphi_{1f} \left( {S_{t - 1} - \lambda F_{t - 1} } \right) + \varepsilon_{ft}$$

with \(\left( {\varepsilon_{st } \varepsilon_{ft} } \right) \sim {\mathcal{N}}\left( {o,H_{t} } \right)\)

$$H_{t} = \left[ {\begin{array}{*{20}c} {k_{st} } & 0 \\ 0 & {k_{ft} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 & \rho \\ \rho & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {k_{st} } & 0 \\ 0 & {k_{ft} } \\ \end{array} } \right] = D_{t} RD_{t} = D_{t} J_{t} Q_{t} J_{t} D_{t}$$

And \(h_{it}^{2} = \alpha_{i} + \beta_{i} \varepsilon_{i t - 1}^{2} + \gamma_{i} h_{i t - 1}^{2}\)And \(Q_{t} = \left( {1 - \alpha_{1} - \alpha_{2} } \right)\overline{Q} + \alpha_{1} \xi_{t - 1} \xi_{t - 1}^{,} + \alpha_{2} Q_{t - 1}\) with \(\xi_{t} \sim {\mathcal{N}}\left( {O,I} \right)\)

The benchmark hedging ratio is the respective changes in the spot S and futures f prices using the DCC model. Including correlation between them:

$$\widehat{\delta }_{t}^{*} = {\raise0.7ex\hbox{${k_{sf,t} }$} \!\mathord{\left/ {\vphantom {{k_{sf,t} } {k_{f,t}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${k_{f,t}^{2} }$}}$$

For computing the effectiveness, we evaluate the hedging performance of the different copula-GARCH models, by computing the variance of the return of the hedged portfolio. Knowing a portfolio is composed of a spot asset \(s_{t}\) and \(\delta_{t}\) units of futures \(f_{t}\). We have:

$$\text{var} \left( {s_{t} - \delta_{t}^{*} f_{t} } \right)$$

where \(\delta_{t}^{*}\) represents the estimated hedge ratio. The effectiveness of hedging across different models can be evaluated by comparison with the benchmark.

Empirical analysis

The aim of this study is to improve the effectiveness of dynamic hedging using GARCH model based on several types of copula. To test the effectiveness of our hedging ratio, we collect from Bloomberg, data dealing with daily spot and futures prices for different asset indices: S&P 500 for stocks, Brent for energy, Wheat for commodities, Gold for precious metals and Euro/Dollar for exchange rate market. All the asset prices cover the period from January 2, 2010, to October 31, 2015. The continuously compounded daily returns are defined and calculated as the difference in the logarithms of daily future prices multiplied by 100.

Table 1 presents descriptive statistics of all the assets composing our sample. The measures for skewness and excess kurtosis show that most return series are obviously skewed and highly leptokurtic with respect to the normal distribution. J–B is the Jarque–Bera test for normality. The Jarque–Bera statistics indicate that daily returns for each asset of our sample are not normally distributed. In fact, the Ljung–Box statistic is used to test for the hypothesis of no autocorrelation up to order of 12. On the basis of Ljung–Box Q-statistic and for raw returns series, the hypothesis that all correlation coefficients up to 12 are jointly zero is rejected. The Ljung–Box statistics of order 12 applied to squared returns is highly significant, indicating that there is no serial correlation over the time. These findings justify the use of the GARCH model based on copula specification, as financial asset returns are skewed, leptokurtic and asymmetrically dependent.

Table 1 Descriptive statistics
Full size table

Table 2 reports the estimates of parameters for conditional means, variances and marginal distributions for the copula-based GARCH models. The coefficient β1 is significant for all the indices, which confirms the asymmetric effect on volatility, i.e., negative shocks have greater impacts than positive shocks on the conditional variances. Concerning the estimation of parameters for different copula functions, it seems that the autoregressive parameter \(\theta_{1}\) is greater than 0.9 for all copulas and portfolios, which implies that shocks to the dependence structure between the spot and futures returns can persist for some considerable time and in turn affect the estimated hedge ratio. The parameter γ is significantly positive at the 1% level, suggesting that the latest information on returns is an appropriate measure for modeling the dynamic dependence structure. In terms of model fitting, it seems that the Franck and Joe copulas have the highest log-likelihood. This finding is consistent with the results of Bartram et al. (2007).

Table 2 Parameters estimation for the copula-based GARCH models
Full size table

Table 3 presents the estimation of the parameters of GARCH (1,1) model. The parameters are estimated by using the maximum likelihood technique. We notice the AR (1) term, φ1, in the mean equation is significant in all cases. The coefficients of the lagged squared residuals, α0 and α1, are highly statistically significant in all cases, which suggests that volatility of series returns is more readily affected by relevant information at time t − 1. The coefficients of lagged variance of the volatility, β1, are highly significant in all cases, implying that the volatility at time t depends on the volatility at time t − 1.

Table 3 Parameters estimates of GARCH (1,1) model for each asset
Full size table

Given the availability of the estimates of GARCH (1, 1) models, we turn to estimate five copula functions for each pair of spot and futures.

Table 4 reports the estimates of parameters for the DCC-GARCH. In terms of model fitting, both the log-likelihood functions and the Kolmogorov–Smirnov goodness of fit validate the DCC-GARCH models. We also notice that the coefficients \(\alpha_{1}\) and \(\alpha_{2}\) are close and less than 1, which implies that the correlations between the futures and their underlying assets are highly persistent. This means that shocks can push the correlation away from its long-run average for some considerable time.

Table 4 Estimation of the DCC-GARCH model
Full size table

Tables 5 and 6 present the hedging performance of the different models. A hedged portfolio is composed of a spot asset and δ units of futures. The effectiveness of a hedge becomes relevant only if there is a significant change in the value of the hedged item. A hedge is effective if the price movements of the hedged item and the hedging derivative roughly offset each other.

Table 5 Effectiveness of hedging. Comparison with DCC-GARCH model: portfolio variance
Full size table
Table 6 Effectiveness of hedging
Full size table

The results show that the copula-based GARCH models outperform the dynamic hedging models for all types of assets. The improvement over the DCC benchmark model varies from 12 to 17%, from 15 to 25%, from 11 to 29%, from 3 to 16% and from 3 to 25%, for the Gumbel copula, for the Franck copula, for the BB7, for the Joe copula and for the Kimeldorf Sampson copula, respectively. As expected, the dynamic hedging models outperform the conventional hedging model for all types of assets. The copula-based GARCH models are the most effective in reducing the variances of hedged portfolios.

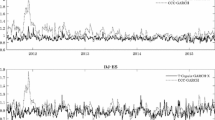
Figure 1 compares the optimally performing hedge ratios obtained from the copula-GARCH models with respect to those obtained from the DCC-GARCH benchmark model. Overall, this figure suggests that the proposed models provide greater hedging effectiveness than the conventional model. These observations support that when estimating the optimal hedge ratio, it is extremely important to have time-varying variances and to employ suitable distribution specifications for the time series, as demonstrated by the superior performance of the copula-based GARCH models. Our findings are in line with those of Conlon et al. (2016), Ehsani and Lien (2015), Ewing and Malik (2013) and Han et al. (2017).

Fig. 1
figure 1

Variance reduction in each copula-GARCH model with respect to the DCC-GARCH benchmark model. Notes Figure compares the variance reduction in each copula-GARCH model with respect to the DCC-GARCH benchmark model

Full size image

Conclusion

In this paper, we have proposed a class of new copula-based GARCH models to estimate risk-minimizing hedge ratios. We have compared the hedging effectiveness of our model with other conventional models, especially the dynamic conditional correlation GARCH hedging models. Through different copula functions, the proposed models allow to specify the joint distribution of the spot and futures returns with full flexibility. Since the marginal and joint distributions can be specified separately and simultaneously, we estimate the conditional variance and covariance to obtain the optimal hedge ratio without the restrictive assumption of multivariate normality. Our results highlight that the hedging effectiveness based on the proposed models is improved compared to the conventional model. Therefore, we show that a better specification of the joint distribution of the asset can effectively help to manage the risk exposure of portfolios. Our findings are useful for investors, hedgers and risk managers as they allow to improve the hedging performance using the same quantity of futures contract or to obtain the same effectiveness of hedging using less futures contracts. Finally, in our study the hedging effectiveness is investigated based on futures. An extension of our work is to take into account options as a hedging instrument.