Two-photon phase gate with linear optical elements and atom–cavity system

Abstract

We propose a protocol for implementing $\pi$ phase gate of two photons with linear optical elements and an atom–cavity system. The evolution of the atom–cavity system is based on the quantum Zeno dynamics. The devices in the present protocol are simple and feasible with current experimental technology. Moreover, the method we proposed here is deterministic with a high fidelity. Numerical simulation shows that the evolution in cavity is efficient and robust. Therefore, the protocol may be helpful for quantum computation field.

1 Introduction

In the recent years, many interests have been attracted by the developments in quantum information processing (QIP) [1–5]. As one of the most important research fields in QIP, quantum computation has shown great advantages [6–9]. Comparing with a classical electronic computer, a quantum computer has much higher running speed [6, 7]. Moreover, a quantum computer can solve many special problems [7–9] which cannot be solved by a classical electronic computer. To achieve quantum computation, quantum logic gates are the essential elements because it has been shown that a quantum computation network can be decomposed into a series of logic gates [10–12]. That is, any multiqubit gates can be decomposed into single-qubit operations and two-qubit logic gates. Therefore, numerous researches have been focus on the realization of the one-qubit unitary gates and the two-qubit logic gates in different physical systems, such as ion traps [13], cavities [14], quantum dots [15], NMR systems [16], superconductor systems [17] and so on. It is worth noting that the cavity quantum electrodynamics (CQED) system has been proved to be very promising for QIP. And it is a preferably alternative for implementations of logic gates [18–28]. For example, Deng et al. [18] have used the controlled phase flip (CPF) gates, which are constructed with CQED system, to construct atomic phase gates by single-photon interference. The CPF gates have been also used by Duan and Kimble [20] to implement a controlled Not (CNOT) gate for photons. Ren et al. have proposed two interesting protocols [21, 22] for photonic hyper-CNOT gates with quantum dot–microcavity coupled systems. Chudzicki et al. [27] have proposed a protocol for deterministic and cascadable conditional phase gate for photonic qubits. Moreover, many protocols [29–31] for realizing CQED systems in experiments have been proposed in past several years. Therefore, the CQED system is a perfect alternate candidate for preparing phase gates.

Quantum Zeno dynamics is previously considered to restrain the evolution of the initial state by performing frequent measurements, which are experimentally tested [32]. And it is improving by numerous following researches [33–35], which have indicated that the dynamics does not necessarily freeze in evolution with quantum Zeno dynamics and the system will evolve away from its initial state in a subspace called “Zeno subspace” [33, 36], by frequently projecting onto a multidimensional subspace. Furthermore, as shown in Refs. [35, 37], with quantum Zeno effect expressed in terms of a continuous measurement one can obtain the same physical effects as the case when quantum Zeno effect expressed by projection operators and nonunitary dynamics. The quantum Zeno dynamics in terms of continuous coupling can be described as following. Supposing a dynamical evolution process is governed by the Hamiltonian $H_K=H_{\mathrm{obs}}+KH_{\mathrm{mean}}$, where $H_{\mathrm{obs}}$ is the Hamiltonian of the quantum system investigated, K is a coupling constant, and $H_{\mathrm{meas}}$ is viewed as an additional interaction Hamiltonian performing the measurement. The system will remain in the same Zeno subspace including its initial state, in the limit $K\rightarrow \infty$, and the evolution operator can be written by $U(t)=\exp [-it\sum _{\iota }(K\eta _\iota P_\iota + P_\iota H_{\mathrm{obs}}P_\iota )]$, in which $P_\iota$ denotes the eigenvalue projection of $H_{\mathrm{meas}}$ with eigenvalues $\eta _\iota$ ($H_{\mathrm{meas}}=\sum _{\iota }\eta _\iota P_\iota )$. As it provides a large amount of interesting application in CQED system, quantum Zeno dynamics attracts many interests [38–41]. For example, Li and Huang [38] have proposed a protocol for the generation of a three-dimensional entangled state for two atoms trapped in a cavity via quantum Zeno dynamics. The method proposed in protocol [38] is robust against the cavity decay since the evolution of the system is restricted to a subspace with null-excitation cavity fields. Chen et al. [39] have proposed an efficient scheme to drive two atoms in two coupled cavities into a two-atom singlet state via quantum Zeno dynamics and virtual excitations by one step, which is robust against both the cavity decay and atomic spontaneous emission.

On the other hand, photons are known as the ideal carriers for information between quantum nodes in a quantum network, as they can be transmitted over long distance through optical fibers or even in a free space with high speed [42, 43]. Moreover, photons have good operability, as their polarization, spatial, momentum, frequency and some other degrees of freedom can be operated easily by linear or nonlinear optical elements. For example, Sheng and Deng [44] have presented an efficient scheme to realize quantum entanglement distribution over an arbitrary collective-noise channel between two users, where the quantum information is encode in polarization degree of freedom of photons. Li et al. [45] have proposed a faithful qubit transmission scheme with linear optics against collective noise. Moreover, Kang et al. [46] have exploited the photon frequency degree of freedom to generate entanglement in quantum nodes. Therefore, it is worthwhile to realize quantum information tasks with photon systems.

Combining the advantages of photons and quantum Zeno dynamics in CQED system, in this paper, we propose a protocol for implementing $\pi$ phase gate of two photons with linear optical elements and atom–cavity system. The evolution of the atom–cavity system is based on the quantum Zeno dynamics. The present protocol has the following advantages. Firstly, the devices in the present protocol are simple, and feasible with current experimental technology. Secondly, the implementation of the two-photon phase gate can be achieved in one step. The method we propose here is deterministic with a high fidelity. Numerical simulation shows that the evolution in cavity is efficient and robust. Thirdly, auxiliary photons are not required in our protocol, which can save physical resources. Therefore, our protocol may be helpful for quantum computation field.

Fig. 1

Schematic diagram of the atom energy levels

The article is organized as follows. In Sect. 2, we will introduce the evolution of the atom–photon system. In Sect. 3, we will describe the process for implementation of a two-photon $\pi$ phase gate with linear optical elements and atom–cavity system. Discussion and conclusions are shown in Sect. 4.

2 The evolution of the atom–cavity system

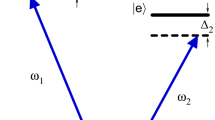
We consider an atom with a ground state $|g\rangle$ and three excited states $|e_L\rangle$, $|e_0\rangle$ and $|e_R\rangle$, which is shown in Fig. 1. Suppose that the atomic transition $|g\rangle \leftrightarrow |e_L\rangle$ ($|g\rangle \leftrightarrow |e_R\rangle$) is resonantly coupled to the input left (right) circularly polarized photon $|L\rangle$ ($|R\rangle$) with coupling constant $\lambda _L$ ($\lambda _R$), $|g\rangle \leftrightarrow |e_0\rangle$ is resonantly driven through a laser pulse with Rabi frequency $\Omega$. The total Hamiltonian in the interaction picture can be written by $(\hbar =1)$

$$\begin{aligned} H_I= & {} H_{c}+H_{l},\nonumber \\ H_{c}= & {} \sum _{k=L,R}\lambda _k|e_k\rangle \langle g|a_k+H.c.,\nonumber \\ H_{l}= & {} \Omega |e_0\rangle \langle g|+H.c., \end{aligned}$$

(1)

where $a_k$ is the annihilation operator for the k-polarization photon $(k=L,R)$.

In the present paper, assuming that the initial state of the atom is $|e_0\rangle$, according to the setups of the linear optical elements, no more than two photons will be injected into the cavity. There are three cases: (1) No photons are injected into the cavity. (2) A R-polarized photon or an L-polarized photon is injected into the cavity. (3) A R-polarized photon and an L-polarized photon are both injected into the cavity. Therefore, the system will evolve in the Hilbert subspace spanned by

$$\begin{aligned} |\psi _0\rangle= & {} |g\rangle |0\rangle _{L}|0\rangle _{R},\quad |\psi _1\rangle =|e_0\rangle |0\rangle _{L}|0\rangle _{R},\quad |\psi _2\rangle =|g\rangle |1\rangle _{L}|0\rangle _{R},\nonumber \\ |\psi _3\rangle= & {} |e_L\rangle |0\rangle _{L}|0\rangle _{R},\quad |\psi _4\rangle =|e_0\rangle |1\rangle _{L}|0\rangle _{R},\quad |\psi _5\rangle =|g\rangle |0\rangle _{L}|1\rangle _{R},\nonumber \\ |\psi _6\rangle= & {} |e_R\rangle |0\rangle _{L}|0\rangle _{R},\quad |\psi _7\rangle =|e_0\rangle |0\rangle _{L}|1\rangle _{R},\quad |\psi _8\rangle =|g\rangle |1\rangle _{L}|1\rangle _{R},\nonumber \\ |\psi _9\rangle= & {} |e_L\rangle |0\rangle _{L}|1\rangle _{R},\quad |\psi _{10}\rangle =|e_R\rangle |1\rangle _{L}|0\rangle _{R},\quad |\psi _{11}\rangle =|e_0\rangle |1\rangle _{L}|1\rangle _{R}, \end{aligned}$$

(2)

in which $|m\rangle _{R}$ ($|m'\rangle _{L}$) $(m,m'=0,1,2,\ldots )$ are the photon number states of R (L)-polarization. The Hamiltonian can be rewritten with the eigenstates $|\phi _{n}\rangle$ $(n=1,2,\ldots ,7)$ of $H_{c}$ as

$$\begin{aligned} H_I= & {} H_{c}+H_{l},\nonumber \\ H_{c}= & {} \sum \limits _{n=1}^{7}\varepsilon _n|\phi \rangle _n\langle \phi |,\nonumber \\ H_{l}= & {} \Omega (|\psi _0\rangle \langle \psi _1|+|\phi _6\rangle \langle \psi _{11}|+|\phi _7\rangle \langle \psi _{11}|)\nonumber \\&+\,\frac{\Omega }{\sqrt{2}}(|\phi _1\rangle \langle \psi _4|+|\phi _2\rangle \langle \psi _4|+|\phi _3\rangle \langle \psi _7|+|\phi _4\rangle \langle \psi _7|)+H.c., \end{aligned}$$

(3)

where $\varepsilon _1=\lambda _L$, $\varepsilon _2=-\lambda _L$, $\varepsilon _3=\lambda _R$, $\varepsilon _4=-\lambda _R$, $\varepsilon _5=0$, $\varepsilon _6=\chi$ and $\varepsilon _7=-\chi$, $(\chi =\sqrt{\lambda _L^2+\lambda _R^2})$, and

$$\begin{aligned} |\phi _1\rangle= & {} \frac{1}{\sqrt{2}}(|\psi _2\rangle +|\psi _3\rangle ),\quad |\phi _2\rangle =\frac{1}{\sqrt{2}}(|\psi _2\rangle -|\psi _3\rangle ),\nonumber \\ |\phi _3\rangle= & {} \frac{1}{\sqrt{2}}(|\psi _5\rangle +|\psi _6\rangle ),\quad |\phi _4\rangle =\frac{1}{\sqrt{2}}(|\psi _5\rangle -|\psi _6\rangle ),\nonumber \\ |\phi _5\rangle= & {} \frac{1}{\chi }(\lambda _R|\psi _9\rangle -\lambda _L|\psi _{10}\rangle ),\quad |\phi _6\rangle =\frac{1}{\sqrt{2}\chi }(\chi |\psi _{8}\rangle +\lambda _L|\psi _9\rangle +\lambda _R|\psi _{10}\rangle ),\nonumber \\ |\phi _7\rangle= & {} \frac{1}{\sqrt{2}\chi }(\chi |\psi _{8}\rangle -\lambda _L|\psi _9\rangle -\lambda _R|\psi _{10}\rangle ). \end{aligned}$$

(4)

That means under the Zeno condition $\Omega \ll \lambda _k$ ($k=L,R$), the Hilbert subspace will split into eight subspaces

$$\begin{aligned} S_1= & {} \{|\psi _0\rangle ,|\psi _1\rangle \},\quad S_2=\{|\phi _1\rangle \}, \quad S_3=\{|\phi _2\rangle \},\nonumber \\ S_4= & {} \{|\phi _3\rangle \},\quad S_5=\{|\phi _4\rangle \},\quad S_6=\{|\phi _6\rangle \},\nonumber \\ S_7= & {} \{|\phi _7\rangle \},\quad S_8=\{|\phi _5\rangle \}. \end{aligned}$$

(5)

If we define projectors as following

$$\begin{aligned} P_q=|\phi _q\rangle \langle \phi _q|\ (q=1,2,\ldots ,7), \end{aligned}$$

(6)

according to Ref. [35], the effective Hamiltonian of the system can be written by

$$\begin{aligned} H_{\mathrm{eff}}= & {} \sum \limits _{q}\varepsilon _qP_q+P_qH_{l}P_q\nonumber \\= & {} \Omega (|\psi _0\rangle \langle \psi _1|+|\psi _1\rangle \langle \psi _0|)+\sum \limits _{q=1}^7\varepsilon _q|\phi _q\rangle \langle \phi _q|. \end{aligned}$$

(7)

Then, we can further write Hamiltonians of these eight subspaces as

$$\begin{aligned} H_{S_1}= & {} \Omega (|\psi _0\rangle \langle \psi _1|+|\psi _1\rangle \langle \psi _0|),\quad H_{S_2}=\lambda _L|\phi _1\rangle \langle \phi _1|,\quad H_{S_3}=-\lambda _L|\phi _2\rangle \langle \phi _2|,\nonumber \\ H_{S_4}= & {} \lambda _R|\phi _3\rangle \langle \phi _3|,\quad H_{S_5}=-\lambda _R|\phi _4\rangle \langle \phi _4|,\quad H_{S_6}=\chi |\phi _6\rangle \langle \phi _6|,\nonumber \\ H_{S_7}= & {} -\chi |\phi _7\rangle \langle \phi _7|,\quad H_{S_8}=0. \end{aligned}$$

(8)

Under Zeno condition $\Omega \ll \lambda _k$ ($k=L,R$), the evolution operators of eight subspaces can be written by

$$\begin{aligned} U_{S_1}(t)= & {} e^{-iH_{S_1}t}=e^{-i\Omega (|\psi _0\rangle \langle \psi _1|+|\psi _1\rangle \langle \psi _0|)t},\quad U_{S_2}(t)=e^{-iH_{S_2}t}= e^{-i\lambda _L|\phi _1\rangle \langle \phi _1|t},\nonumber \\ U_{S_3}(t)= & {} e^{-iH_{S_3}t}= e^{i\lambda _L|\phi _2\rangle \langle \phi _2|t},\quad U_{S_4}(t)=e^{-iH_{S_4}t} =e^{-i\lambda _R|\phi _3\rangle \langle \phi _3|t},\nonumber \\ U_{S_5}(t)= & {} e^{-iH_{S_5}t}= e^{i\lambda _R|\phi _4\rangle \langle \phi _4|t},\nonumber \\ U_{S_6}(t)= & {} e^{-iH_{S_6}t}= e^{-i\chi |\phi _6\rangle \langle \phi _6|t},\quad U_{S_7}(t)=e^{-iH_{S_7}t}= e^{i\chi |\phi _7\rangle \langle \phi _7|t},\quad U_{S_8}=I. \end{aligned}$$

(9)

3 The $\pi$ phase gate of two photons with linear optical elements and atom–cavity system

Now, we describe the implementation of two-photon phase gate with linear optical elements and atom–cavity system. The schematic diagram of the devices is shown in Fig. 2. As shown in Fig. 2, HWP is a half-wave plate for transformation $|R\rangle \leftrightarrow |L\rangle$. $\hbox {PBS}_1$ and $\hbox {PBS}_2$ are two polarizing beam splitters in the circular basis, which transmit the input right circularly polarized photons $|R\rangle$ and reflect the left circularly polarized photons $|L\rangle$. K is an optical switch with two different states: one is transmitting state and the other is reflecting state. a and b denote two different paths. We assume that the side-leakage $\kappa _s$ of the cavity is large enough, so that the input photons can be injected into and emitted out the cavity easily. Moreover, if we design the length of each path carefully, the input photons will arrive at $\hbox {PBS}_1$, $\hbox {PBS}_2$ and the cavity at the same time. The arrival time $t_0$ of the input photons can be calculated when the length of each path and the speed of photons are known. We assume that the optical switch K is initially in transmitting state, and we change switch K to the reflecting state at time $t_0$, so that the injected photons will be not emitted from the cavity during the interaction. Then, after the evolution in the cavity, we change switch K back to the transmitting state at time $t_0+t_f$ ($t_f$ is the evolution time in the cavity), so that the photons may be emitted from the cavity. In addition, toggling the switch K should be precise to avoid the gate error.

Fig. 2

Schematic diagram of the two-photon phase gate with linear optical elements and atom–cavity system. HWP is a half-wave plate for transformation $|R\rangle \leftrightarrow |L\rangle$. $\hbox {PBS}_1$ and $\hbox {PBS}_2$ are two polarizing beam splitters in the circular basis, which transmit the input right circularly polarized photons $|R\rangle$ and reflect the left circularly polarized photons $|L\rangle$. a and b denote two different paths

Suppose that the two input photons are injected to the devices from paths a and b, respectively. The initial state of the two photons is

$$\begin{aligned} x_1|R\rangle _{a}|R\rangle _{b}+x_2|R\rangle _{a}| L\rangle _{b}+x_3|L\rangle _{a}|R\rangle _{b}+x_4|L\rangle _{a}|L\rangle _{b}, \end{aligned}$$

(10)

where $|x_1|^2+|x_2|^2+|x_3|^2+|x_4|^2=1$. Therefore, the state of the whole atom–photon system is

$$\begin{aligned} |e_0\rangle (x_1|R\rangle _{a}|R\rangle _{b}+x_2|R\rangle _{a}|L\rangle _{b}+x_3|L\rangle _{a}|R\rangle _{b}+x_4|L\rangle _{a}|L\rangle _{b}). \end{aligned}$$

(11)

After the photons in paths a and b passing $\hbox {PBS}_1$ (See Fig. 2), the state in Eq. (11) changes into

$$\begin{aligned} |e_0\rangle (x_1|R\rangle _{d}|R\rangle _{c}+x_2|R\rangle _{d}|L\rangle _{d}+x_3|L\rangle _{c}|R\rangle _{c}+x_4|L\rangle _{c}|L\rangle _{d}). \end{aligned}$$

(12)

Then, the photon in path c passing though HWP, the total state of the atom–photon system will be

$$\begin{aligned} |e_0\rangle (x_1|R\rangle _{d}|L\rangle _{c}+x_2|R\rangle _{d}|L\rangle _{d}+x_3|R\rangle _{c}|L\rangle _{c}+x_4|R\rangle _{c}|L\rangle _{d}). \end{aligned}$$

(13)

Next, the photons in paths c and d passing $\hbox {PBS}_2$, the state of the whole system changes into

$$\begin{aligned} |e_0\rangle (x_1|R\rangle _{a'}|L\rangle _{a'}+x_2|R\rangle _{a'}|L\rangle _{b'}+x_3|R\rangle _{b'}|L\rangle _{a'}+x_4|R\rangle _{b'}|L\rangle _{b'}). \end{aligned}$$

(14)

From Fig. 2, we can see that the photon(s) in path $a'$ will be injected into the cavity and coupled with the trapped atom. Therefore, the state of the whole atom–photon system in Eq. (14) can be written as

$$\begin{aligned}&(x_1|e_0\rangle |1\rangle _{R}|1\rangle _{L}|0\rangle _{a'}|0\rangle _{a'}+x_2|e_0\rangle |0\rangle _L|1\rangle _{R}|0\rangle _{a'}|L\rangle _{b'}\nonumber \\&\qquad +x_3|e_0\rangle |1\rangle _L|0\rangle _R|R\rangle _{b'}|0\rangle _{a'}+x_4|e_0\rangle |0\rangle _L|0\rangle _R|R\rangle _{b'}|L\rangle _{b'})\nonumber \\&\quad =(x_1|\psi _{11}\rangle |0\rangle _{a'}|0\rangle _{a'}+x_2|\psi _7\rangle |0\rangle _{a'}|L\rangle _{b'} +x_3|\psi _4\rangle |R\rangle _{b'}|0\rangle _{a'}+x_4|\psi _1\rangle |R\rangle _{b'}|L\rangle _{b'}).\nonumber \\ \end{aligned}$$

(15)

According to the evolution operators in Sect. 2, by setting the Rabi frequency $\Omega$ of laser beam and the interaction time $t_f$ suitably, that is, satisfying $\Omega t_f=\pi$, the evolution in cavity will be $|\psi _{11}\rangle \rightarrow |\psi _{11}\rangle$, $|\psi _7\rangle \rightarrow |\psi _7\rangle$, $|\psi _4\rangle \rightarrow |\psi _4\rangle$ and $|\psi _1\rangle \rightarrow -|\psi _1\rangle$. So, when the evolution is over, the atom–photon system will be in state

$$\begin{aligned}&U(t_f)(x_1|\psi _{11}\rangle |0\rangle _{a'}|0\rangle _{a'}+x_2|\psi _7\rangle |0\rangle _{a'}|L\rangle _{b'} +x_3|\psi _4\rangle |R\rangle _{b'}|0\rangle _{a'}+x_4|\psi _1\rangle |R\rangle _{b'}|L\rangle _{b'})\nonumber \\&\quad =(x_1|\psi _{11}\rangle |0\rangle _{a'}|0\rangle _{a'}+x_2|\psi _7\rangle |0\rangle _{a'}|L\rangle _{b'} +x_3|\psi _4\rangle |R\rangle _{b'}|0\rangle _{a'}-x_4|\psi _1\rangle |R\rangle _{b'}|L\rangle _{b'})\nonumber \\&\quad =(x_1|e_0\rangle |1\rangle _{R}|1\rangle _{L}|0\rangle _{a'}|0\rangle _{a'}+x_2|e_0\rangle |0\rangle _L|1\rangle _{R}|0\rangle _{a'}|L\rangle _{b'}\nonumber \\&\qquad +x_3|e_0\rangle |1\rangle _L|0\rangle _R|R\rangle _{b'}|0\rangle _{a'}-x_4|e_0\rangle |0\rangle _L|0\rangle _R|R\rangle _{b'}|L\rangle _{b'})\nonumber \\&\quad =|e_0\rangle (x_1|1\rangle _{R}|1\rangle _{L}|0\rangle _{a'}|0\rangle _{a'}+x_2|0\rangle _L|1\rangle _{R}|0\rangle _{a'}|L\rangle _{b'}\nonumber \\&\qquad +x_3|1\rangle _L|0\rangle _R|R\rangle _{b'}|0\rangle _{a'}-x_4|0\rangle _L|0\rangle _R|R\rangle _{b'}|L\rangle _{b'}). \end{aligned}$$

(16)

Next, we trace out the atom state. Subsequently, photons in cavity will be emitted from the cavity to the path $a'$, and photons in path $b'$ will be straightly reflected by the mirror. Therefore, the state of the two photons will be

$$\begin{aligned} x_1|R\rangle _{a'}|L\rangle _{a'}+x_2|R\rangle _{a'}|L\rangle _{b'}+x_3|R\rangle _{b'}|L\rangle _{a'}-x_4|R\rangle _{b'}|L\rangle _{b'}. \end{aligned}$$

(17)

Then, the two photons will pass back through $\hbox {PBS}_2$, HWP and $\hbox {PBS}_1$ in sequence again, and the process can be described as

$$\begin{aligned}&x_1|R\rangle _{a'}|L\rangle _{a'}+x_2|R\rangle _{a'}|L\rangle _{b'}+x_3|R\rangle _{b'}|L\rangle _{a'}-x_4|R\rangle _{b'}|L\rangle _{b'}\nonumber \\&\quad {\underrightarrow{\hbox {PBS}_2}}\ \ x_1|R\rangle _{d}|L\rangle _{c}+x_2|R\rangle _{d}|L\rangle _{d}+x_3|R\rangle _{c}|L\rangle _{c}-x_4|R\rangle _{c}|L\rangle _{d}\nonumber \\&\quad {\underrightarrow{\hbox {HWP}}}\ \ x_1|R\rangle _{d}|R\rangle _{c}+x_2|R\rangle _{d}|L\rangle _{d}+x_3|L\rangle _{c}|R\rangle _{c}-x_4|L\rangle _{c}|L\rangle _{d}\nonumber \\&\quad {\underrightarrow{\hbox {PBS}_1}}\ \ x_1|R\rangle _{a}|R\rangle _{b}+x_2|R\rangle _{a}|L\rangle _{b}+x_3|L\rangle _{a}|R\rangle _{b}-x_4|L\rangle _{a}|L\rangle _{b}. \end{aligned}$$

(18)

From Eq. (18), we can see that the implementation of the two photons phase gate with linear optical elements and atom–cavity system is completed.

Fig. 3

The fidelity F(t) of the state in the cavity versus $\lambda t$

Fig. 4

The final fidelity $F(t_f)$ of the state in the cavity versus $\Omega /\lambda$

4 Discussion and conclusions

In this section, let us make some discussion. Firstly, we calculate the fidelity of the system’s state in the cavity. Because when the evolution process in the cavity is completed as expectation, the state of the trapped atom should be $|g\rangle$. In other cases, the gate operation is failure. When the gate operation is succeed, we trace the state of the trapped atom, which has nothing to do with the photons’ state. Therefore, we use the fidelity of the atom–cavity state to describe the gate fidelity when the linear optical elements outside the cavity are considered to be perfect. The fidelity is defined as $F(t)=|\langle \Phi _{\mathrm{ideal}}|\rho (t)|\Phi _{\mathrm{ideal}}\rangle |$ with $|\Phi _{\mathrm{ideal}}\rangle =x_1|\psi _{11}\rangle +x_2|\psi _7\rangle +x_3|\psi _4\rangle -x_4|\psi _1\rangle$ and $\rho (0)=|\Psi (0)\rangle \langle \Psi (0)|$. ($|\Psi (0)\rangle =x_1|\psi _{11}\rangle +x_2|\psi _7\rangle +x_3|\psi _4\rangle +x_4|\psi _1\rangle$.) For simplification, we set $\lambda _L=\lambda _R=\lambda$. According to the differential equation $\dot{\rho }(t)=i[\rho (t),H_I(t)]$, in which $\rho (t)$ is the density operator of the system, we plot the fidelity F(t) versus $\lambda t$ in Fig. 3. As shown in Fig. 3, the fidelity continuously increases with the increasing of the interaction time, and the final fidelity $F(t_f)$ is 0.9989 with the parameters $t_f=50/\lambda$ ($\Omega =\pi /t_f=\pi \lambda /50$) and $x_1=x_2=x_3=x_4=1/2$. Moreover, we plot $F(t_f)$ versus $\Omega /\lambda$, when $\Omega$ is variational, which is shown in Fig. 4, with $x_1=x_2=x_3=x_4=1/2$. As indicated in Fig. 4, the final fidelity $F(t_f)$ vibrates with the change of $\Omega {/}\lambda$. The vibration is intensified with the increasing of $\Omega {/}\lambda$ because large $\Omega$ means the Zeno condition is not satisfied well. Therefore, we should choose a suitable value of $\Omega {/}\lambda$ to obtain a maximum $F(t_f)$.

Fig. 5

The final fidelity $F(t_{f'})$ of the two-photon phase gate versus $\delta t_f/t_f$ and $\delta \Omega /\Omega$

Secondly, since most of the parameters are hard to faultlessly achieve in experiment, we need to investigate the variations in the parameters induced by the experimental imperfection. We consider that there are little deviations of interaction time $t_f$ and the Rabi frequency of laser pulses $\Omega$, which are denoted by $\delta t_f$ and $\delta \Omega$, respectively. In Fig. 5, we plot the final fidelity $F(t_{f'})$ of the system’s state in cavity versus the variations ($\delta t_f$ and $\delta \Omega$) in total operation time $t_f'$ $(t_f'=t_f+\delta t_f)$ and laser amplitude $\Omega '$ $(\Omega '=\Omega +\delta \Omega )$ with $t_f=50/\lambda$ and $x_1=x_2=x_3=x_4=1/2$. Moreover, we calculate the exact values of $F(t_{f'})$ at some boundary points of Fig. 5 and show the results in Table 1. We find that the final fidelity $F(t_{f'})$ is still 0.996 % even when the deviation $\delta \Omega _{0}/\Omega _{0}=\delta t_{f}/t_{f}=5\,\%$. So, we can say the protocol is robust against the variations of the parameters $t_f$ and $\Omega$. Furthermore, from Fig. 5 and Table 1, we find that $F(t_{f'})$ decreases little when $\delta t_f$ and $\delta \Omega$ have the opposite sign (one positive and the other negative). On the contrary, $F(t_{f'})$ decreases larger when $\delta t_f$ and $\delta \Omega$ have the same sign (both positive or both negative). That is easy to understand, as $t_f$ and $\Omega$ should satisfy the condition $\Omega t_f=\pi$. Therefore, when $\Omega$ ( $t_f$) decreases, $t_f$ ($\Omega$) should increase.

Table 1 Samples of the final fidelity $F(t_{f'})$ with corresponding $\delta \Omega {/}\Omega$ and $\delta t_f{/}t_f$

On the other hand, once we set $t_f=C/\lambda$ ($C=$ constant), we have $\delta t_f=\delta (C/\lambda )\simeq -C\delta \lambda /\lambda ^2$. The deviation of $\lambda$ will directly lead the deviation of $t_f$. So, the influence due to the deviation of $\lambda$ has similar effects as the influence due to the deviation of $t_f$ on the final fidelity $F(t_f)$. Therefore, for the sake of integrality for discussion, taking $\delta \lambda$ instead of $\delta t_f$, we plot $F(t_{f})$ versus $\delta \Omega$ and $\delta \lambda$ in Fig. 6. Also, samples of $F(t_{f})$ with $\delta \Omega /\Omega$ and $\delta \lambda /\lambda$ are shown in Table 2. Seeing from Fig. 6 and Table 2, the protocol is also robust against the variations of $\Omega$ and $\lambda$. Therefore, we can conclude that the protocol is robust against the variations of the parameters $t_f$, $\Omega$ and $\lambda$.

Fig. 6

The final fidelity $F(t_f)$ of the two-photon phase gate versus $\delta \lambda /\lambda$ and $\delta \Omega /\Omega$

Table 2 Samples of the final fidelity $F(t_f)$ with corresponding $\delta \Omega /\Omega$ and $\delta \lambda /\lambda$

Thirdly, let us discuss the fidelity F(t) of the system’s state in cavity with decoherence mechanisms, such as the atomic spontaneous emission and the cavity decay being considering. The evolution of the system can be described by a master equation in Lindblad form as following with the decoherence being considered,

$$\begin{aligned} \dot{\rho }=i[\rho ,H_I]+\sum \limits _{l}\left[ L_l\rho L_l^{\dagger }-\frac{1}{2}\left( L_l^{\dagger }L_l\rho +\rho L_l^{\dagger }L_l\right) \right] , \end{aligned}$$

(19)

where $L_l$ ($l=1,2,\ldots ,5$) is the Lindblad operator. There are six Lindblad operators

$$\begin{aligned} L_{1}= & {} \sqrt{\Gamma _L}|g\rangle \langle e_L|,\quad L_{2}=\sqrt{\Gamma _R}|g\rangle \langle e_R|,\nonumber \\ L_{3}= & {} \sqrt{\Gamma _0}|g\rangle \langle e_0|,\quad L_{4}=\sqrt{\kappa _L}a_L,\nonumber \\ L_{5}= & {} \sqrt{\kappa _R}a_R, \end{aligned}$$

(20)

in which $\Gamma _s$ $(s=R,L,0)$ are the atomic spontaneous emissions, $\kappa _r$ $(r=R,L)$ are the cavity decays. We suppose $\Gamma _s=\Gamma /2$ $(s=R,L,0)$ and $\kappa _r=\kappa$ $(r=R,L)$ for simplicity.

Fig. 7

The fidelity F(t) of the evolution in the cavity versus $\lambda t$ when decoherence is considered

Fig. 8

The final fidelity $F(t_f)$ of the evolution in the cavity versus $\kappa /\lambda$ and $\Gamma /\lambda$

We plot the fidelity F(t) versus $\lambda t$ with $t_f=50/\lambda$, $\kappa =0.001\lambda$, $\Gamma =0.001\lambda$ and $x_1=x_2=x_3=x_4=1/2$ in Fig. 7. From Fig. 7, we can see that the fidelity increases from 0.25 to 1 during the evolution. Comparing with the result shown in Fig. 3, where the decoherence mechanism has been considered, the final fidelity $F(t_f)$ with these parameters is 0.9392 here, and it is 1 in Fig. 3. We also consider the final fidelity $F(t_f)$ versus $\kappa /\lambda$ and $\Gamma /\lambda$ in Fig. 8, with $t_f=50/\lambda$ and $x_1=x_2=x_3=x_4=1/2$. The trend of evolution is similar to that in Fig. 4, but $F(t_f)$ cannot reaches 1. Because the gate is based on photon polarization, photon losses leading by cavity decays will destroy the gate. On the other hand, the atomic spontaneous emissions may not destroy photons, but it will lead the uncertain phase shifts because the evolution will not go along the path been designed. This also deceases the fidelity of the gate. Therefore, a strong coupling regime may require here to restrain the atomic spontaneous emission and the cavity decay. In current experimental conditions, it is reported by protocols [47–49] that $\lambda =2\pi \times 750$, $\kappa =2\pi \times 3.5$ and $\Gamma =2\pi \times 2.62$ MHz are realizable with the optical cavity mode wavelength in a range between 630 and 850 nm. These data give the ratios $\kappa /\lambda =0.0047$ and $\Gamma /\lambda =0.0035$. By submitting the ratios into Eq. (20), we have the gate fidelity $F(t_{f})=0.7745$. By adding nondemolition measurement detectors [20, 50] on paths a and b, we can know whether or not the photon losses are occurred in the process. If there is no photon loss, the gate fidelity will be 0.9263. Therefore, nondemolition measurement detectors are quite helpful here. When photon losses are occurred, we can know that from the nondemolition measurement detectors’ results, and then, restart the process. Moreover, with the rapid development in strong coupling regime, the atomic spontaneous emission and the cavity decay will be restrained better in the near feature, so that our protocol can work better as well.

Fourthly, in experiment, the atomic energy level structure can be realized with ${}^{87}$Rb, whose structure is shown in Fig. 9. The state $|g\rangle$ corresponds to $F=1$, $m=0$ of hyperfine state of $5^2$S$_{1/2}$ electronic ground state. The state $|e_0\rangle$ ($|e_L\rangle$, $|e_R\rangle$) corresponds to $F=1$, $m=0$ ($m=-1$, $m=1$) of hyperfine state of $5^2$P$_{1/2}$ electronic state.

Fig. 9

The energy level structure of ${}^{87}$Rb

Fifthly, the linear optical elements such as HWPs and PBSs are used in our protocol. They are simple, powerful, effective and widely used in optical protocols [51–61]. For example, Sheng and Deng [54] have proposed a protocol for deterministic entanglement purification and complete nonlocal Bell-state analysis with hyperentanglement, where PBSs are exploited to preform unitary transformations for polarization and spatial degrees of freedom of photons. Deng [58] has proposed an optimal nonlocal entanglement concentration protocol for multiphoton systems in a partially entangled pure state with the projection measurement on an additional photon, in which PBSs are used to offer helps to the parity checks.

In conclusion, we have proposed a protocol for implementing $\pi$ phase gate of two photons with linear optical elements and atom–cavity system. The evolution of the atom–cavity system is based on the quantum Zeno dynamics. The devices in the present protocol are simple, and feasible with current experimental technology. The implementation of the two-photon phase gate can be achieved in only one step. The method is deterministic with a high fidelity. Numerical simulation shows that the evolution in cavity is efficient and robust. Moreover, auxiliary photons are not required in our protocol, which can save physical resources. Therefore, our protocol may be helpful for quantum computation field.