1 Introduction

Wave-particle duality is one of most counterintuitive behaviors for quantum particles, which lies at the heart of quantum mechanics [1]. Bohr explains this phenomenon with the complementarity principle, which states that quantum particles can behave like particle or wave depending on using which kind of experimental apparatus to measure them [2]. To see such complementarity, one can assume the quantum particle as a photon and send it into a Mach-Zehnder (MZ) interferometer. The photon is first split through a beam splitter (BS) and then travels along two pathes in the interferometer. The two paths is up to a tunable phase φ. In the presence of the second BS, the two paths are recombined and the probability for detecting the photon in the detector is a sinusoidal function of φ, which yields wavelike interference fringes. On the other hand, without the second BS, the experiment reveals which path the photon followed, the photon is detected in one or the other detector with equal probability 1/2, thus behaving like a particle.

However, the complementarity principle has been intensively debated in the past. In particular, the supporters of hidden-variable theories suggested that quantum particles may in fact know in advance which kind of measurement they will be confronted through a hidden variable, thus could decide which behavior to appear [3]. To challenge this theory, Wheeler has formulated an experiment in which one randomly chooses whether to insert the second BS after the photon passes through the first BS and enters the interferometer [4, 5]. Such experiment now is called as delay-choice experiment. In this way, the photon can not know in advance which kind of measurement it will meet and thus can not select which behavior the photon will exhibit. This delay-choice experiment concurs with Bohr’s complementarity principle and denies the hidden-variable theories.

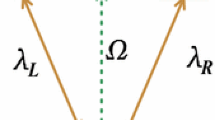
Recently, Ionicioiu and Terno have further proposed a quantum version of Wheeler’s delay-choice experiment, where the presence of second BS is determined by the state of a quantum ancilla [6]. The details of this scheme is shown in Fig. 1. In which, each beam splitter is replaced by a Hadamard (H) operation, and the second H operation is controlled by the ancillary qubit. The quantum system shows wavelike behavior when the ancillary qubit is in the state |1〉 and the second H operation is applied. While if the ancillary qubit is instead in the state |0〉, the second H gate is not performed and the system displays particlelike behavior. In contrast, when the ancillary qubit is prepared in a superposition state, the result is a wave-particle superposition state. It means that the wave and particle feature can be measured simultaneously in a single experimental setup, which points toward a redefinition of complementarity in quantum mechanics. Then, this quantum delay-choice experiment recently has attracted much attentions [7] and also has been experimentally realized with linear optics [8–11] and superconducting circuit systems [12].

Fig. 1
figure 1

Schematic circuit for the quantum delay-choice experiment

Full size image

In this paper, we present a simple experimental scheme to realize the quantum delay-choice experiment with cavity quantum electrodynamics (QED) and observe the photonic wave-particle superposition state. In our scheme, the basic building blockade is the cavity input-output process. We show that such process can provide a simple method to realize a controlled operation between the atom and the photon. With such gate, we can test the wave-particle complementarity principle based on single-photon or single-atom. Compared to the quantum delay choice experiment with superconducting circuit [12], our scheme is more nature and also very simple, which does not require dynamical evolution and coherent state detection. Besides, through measuring the atom as a superposition state, we can prepare the photon in a superposition of wavelike and particle like states, which could simulate further redefinition of wave-particle complementarity principle.

2 Cavity Input-Output Process

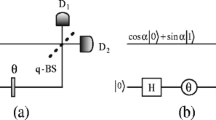
Let us consider a three-level atom trapped in a single-sided cavity as shown in Fig. 2a. In which, the qubit is represented by different hyperfine levels |0〉 and |1〉 in the atomic ground-state manifold (see Fig. 1b). The atomic transition |1〉 ↔ |e〉 is coupled to the cavity mode a h and driven by the h (horizontal) polarization component of the input single-photon pulse, while the state |0〉 is decoupled from the cavity mode due to the large hyperfine splitting. Now we introduce a detailed theoretical model to illustrate the cavity input-output process [13]. In the rotating frame with respect to the frequency of input pulse, the interaction between the atom and the cavity mode is described by the Hamiltonian given by

$$ H=\hbar g(a_{h}\sigma_{+}+a_{h}^{\dagger }\sigma_{-}), $$
(1)

where σ + = |e〉〈1|, g is the atom-cavity coupling rate. The cavity mode a h is driven by the input field \( a_{h}^{in}\). Then we can easily obtain the Heisenberg-Langevin equations for the internal cavity field and the atomic operator [14–16]

$$\begin{array}{@{}rcl@{}} \dot{a}_{h} &=&-i[a_{h},H]-\frac{\kappa }{2}a_{h}-\sqrt{\kappa }a_{h}^{in}, \end{array} $$
(2)
$$\begin{array}{@{}rcl@{}} \dot{\sigma}_{-} &=&-i[\sigma_{-},H]-\frac{\gamma }{2}\sigma_{-}, \end{array} $$
(3)

where κ and γ are respectively the cavity decay rate and the spontaneous emission rate for the excited level, σ z = |e〉〈e|−|1〉〈1|. The output field \(a_{h}^{out}\) is connected with the input by the standard cavity input-output relation \(a_{h}^{out}=a_{h}^{in}+\sqrt { \kappa }a_{h}.\) The input field meets the standard commutation relations \( [a_{h}^{in}(t),a_{h}^{in\dagger }(t^{\prime })]=\delta (t-t^{\prime })\). If the cavity decay rate κ is sufficiently large, the atom will have a weak excitation. So the component |e〉〈e| is negligible. Under this approximation, −σ z can be replaced with the population 1 for the atom in the state |1〉. In the steady state, the Eqs. 2 and 3 can be solved analytically, and the output field is

$$ a_{h}^{out}=\frac{4g^{2}+\kappa\gamma}{4g^{2}-\kappa\gamma}a_{h}^{in}, $$
(4)

From the above expression, we find that, if the input single-photon pulse is decoupled with the single atom in the cavity, it will get an extra phase shift π after reflection. However, if the pulse is couled with the single atom and g 2/κ γ >> 1, it will not acquire a phase shift. With this state-dependent mechanism, one can realize a controlled phase shift (CPS) gate between atom and photon. We can encode the photon qubit with horizontal (h) and vertical (v) polarization, and encode atomic quabit with the internat state |0〉 and |1〉. Then one can find that, when the atom-photon system is in the state |1h〉, it will have a coupling between the atom and the photon, otherwise the atom and photon is decoupled. In this way, one can realize a CPS gate U C P F between the atom and the photon as follows

$$\begin{array}{@{}rcl@{}} \begin{array}{ll} |0v\rangle&\rightarrow-|0v\rangle\\ |0h\rangle&\rightarrow-|0h\rangle\\ |1v\rangle&\rightarrow-|1v\rangle\\ |1h\rangle&\rightarrow|1h\rangle \end{array} \end{array} $$
(5)

In the following, we will show how to employ the above cavity input-output process to implement quantum delay-choice experiment for observing the wave-particle superposition of single photon.

Fig. 2
figure 2

(Color online) (a) Schematic setup for the basic building blocks. b Level structure of the atom confined in the cavity and the coupling induced by cavity fields. c Schematic circuit for implementing quantum delay-choice experiments with cavity input-output process, where the red dash-line box denotes the realization of controlled H gate based on one CPS gate and two single qubit rotation gates

Full size image

3 Seeing Wave-Particle Superposition

As shown in the introduction section, the MZ interferometer for realizing the quantum delay-choice experiment can be transformed into a quantum circuit consisting of one testing particle and one ancillary qubit. The key point in such circuit is a controlled H gate between the ancillary qubit and the testing particle. In the following, we will go to test the wave-particle feature of single photon by employing the single atom as an ancillary qubit and the cavity input-output process as a mean to realize the controlled H gate. In this manner, one can finally find that whether the photon appears as particle and wave dependents on the state of the atomic state.

The detailed circuit based on the cavity input-output process implementing quantum delay-choice experiment is shown in Fig. 2c. We find that the controlled H gate U C H between the atom and the photon can be generated through two single-photon rotation operations (R) and one CPS gate U C P F . It is easy to check that

$$\begin{array}{@{}rcl@{}} U_{CH}=R\cdot U_{CPF}\cdot R, \end{array} $$
(6)
$$\begin{array}{@{}rcl@{}} R=\left[\begin{array}{ll} \cos{\pi/8} & \sin{\pi/8} \\ \sin{\pi/8} & -\cos{\pi/8} \end{array}\right] \end{array} $$
(7)

In the circuit, the single-photon rotation gate H is denoted as

$$\begin{array}{@{}rcl@{}} H=\left[\begin{array}{ll} \cos{\pi/4} & \sin{\pi/4} \\ \sin{\pi/4} & -\cos{\pi/4} \end{array}\right] \end{array} $$
(8)

Experimentally, R and H gates can be readily realized using linear optical elements [17], which is well-developed in the current linear optical systems laboratory. The phase shifter will introduce a phase shift φ on the h polarization.

Now we detailedly show the principle of the above circuit to realize a quantum delay-choice experiment. Firstly, we assume the atom and the photon is in the following state

$$\begin{array}{@{}rcl@{}} |\psi_{i}\rangle=\psi_{a}\bigotimes\psi_{p} =(\cos(\theta)|0\rangle+\sin(\theta)|1\rangle)\bigotimes|h\rangle \end{array} $$
(9)

For the initial atomic state preparation, one can apply one classical laser pulse on the atom and generate an atomic superposition state cos(𝜃)|0〉+ sin(𝜃)|1〉, where 𝜃 is determined by the time of the laser pulse applying on the atom. After the operations in the circuit network, the final state of the system becomes

$$\begin{array}{@{}rcl@{}} |\psi_{f}\rangle=\cos(\theta)|0\rangle|\text{particle}\rangle -\sin(\theta)|1\rangle|\text{wave}\rangle \end{array} $$
(10)

where the wave function of the particlelike state is \(|\text {particle}\rangle =(|v\rangle -e^{i\varphi }|h\rangle )/\sqrt {2}\), and the wavelike state is |wave〉 = e iφ/2(cos(φ/2)|h〉−isin(φ/2)|v〉). As one can see, if the atomic state is |0〉 and |1〉, it means that the interferometer is open and close, which yields the particle and wave interference pattern. Nontrivially, if we detect the atom in the basis \({|\pm \rangle =(|0\rangle \pm |1\rangle )/\sqrt {2}}\), one can prepare a photonic wave-particle superposition state. In particular, the outcomes |±〉 will project the photon into the following wave-particle superposition state

$$ \psi_{wp}=\cos(\theta)|\text{particle}\rangle\mp\sin(\theta)|\text{wave}\rangle $$
(11)

So, with our cavity input-output system, we can easily prepare the photon simultaneously in a wave and particle state. This method can also be generalized to test wave-particle feature of single atom state. The above counterintuitive phenomenon is important for people to further understand some fundamental phenomenons in quantum mechanics, especially to redefine wave-particle complementarity principle.

4 Experimental Discussion

Before conclusion, we will give a brief discussion on the experimental detection and practical parameters. Note that, with current cavity QED technology, the atonic state can be probed though resonant fluorescence, and the photonic polarization state can be selected to click the photon detector by the polarization-dependent beam splitter. If the atom is finally measured in the state |0〉, the final detection probability for the photon state in |h〉 is I h = cos2(𝜃)/2. While if the atom is in the state |1〉, the final detection probability is I h = sin2(𝜃)cos2(φ/2). In contrast, if we don’t measure the atomic state and just detect the photon state, then the probability for horizontal polarization is

$$ I_{h}(\varphi,\theta)=\frac{1}{2}\cos^{2}(\theta) +\sin^{2}(\theta)\cos^{2}(\varphi/2) $$
(12)

The detailed result is numerically plotted in Fig. 3. When 𝜃 = 0,π/2, the photon will collapse into particlelike and wavelike state. Thus, one can find that, the morphing behavior between the wave and particle can be continuously modified through changing 𝜃. Note that recent experiment has demonstrated the controlled phase shift operation between atom and photon [18], which makes our proposal very promising. In their experiment, they consider a trapped Rb atom in a cavity, with the involved parameters as (g,κ,γ)=(6.7,2.5,3)×2π MHz, the fidelity of the CPS gate approaches 0.83. Considering the reduction on fidelity due to imperfection in the single-photon rotation gate is very small, so the fidelity of our scheme is expected to still over 0.8, it is sufficient to see the wave-particle superposition feature.

Fig. 3
figure 3

(Color online) The probability of detecting a photon at horizontal polarization as a function of the angles φ and 𝜃

Full size image

5 Summary

In summary, we have proposed an experimental scheme to implement the quantum delay-choice experiment with cavity input-output process. Through a controlled phase shift gate between single-atom and single-photon, we show that the circuit network for quantum delay-choice experiment could be naturally achieved. The photon can be easily prepared into a superposition of wavelike and particlelike states, which could simulate further deeply understanding of wave-particle complementarity principle.