Abstract
We propose a scheme for implementing a two-qubit quantum phase gate in which the photonic qubits encoded on the cavity modes and a three-level V-type atom passes through the cavity. The location of the resonance is predicted from the use of the theory of multiphoton resonance. Further, we investigate the influence of variations in parameters such as the coupling strengths and detunings on the gate fidelity. We also use the wave-function and the density matrix approaches to analyze theoretically and numerically the effects of decoherence in the implementation of the gate.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
In the field of quantum computation, the principle of coherent superposition and quantum entanglement can be utilized for building quantum computers [1]. In comparison to conventional computers, it has been shown that quantum computers provide more efficient and faster solutions for certain computational problems. An evidence for the power of quantum computers had been shown by finding the prime factors of an integer and by conducting a search of an object in an unsorted database with N elements [2, 3]. Quantum logic gates are fundamental building blocks of quantum computers. In [4, 5], a set of gates containing of a one-bit unitary gate and a two-bit gate can build a universal quantum computer. Many physical systems were suggested to implement the concept of quantum computing: trapped ions [6], liquid-state nuclear magnetic resonance (NMR) [7], cavity quantum electrodynamics (QED) [8, 9], etc.
Cavity QED systems have been shown to provide an enhancement in the interactions between atoms and photons compared to such interactions in free space, and then these systems can be used to implement quantum logic [8,9,10,11]. Quantum information in cavity QED systems can be represented by qubits in atoms, by qubits in cavity modes, or by qubits in atoms and cavity modes together. A number of proposals for realizing quantum logic gates were proposed such as schemes in [12,13,14]. In quantum communication, the use of cavity QED systems is favored since they provide an interface between computation and communication (i.e., between atoms and photons) and then they hold great promise as basic tools for quantum networks [15, 16].
In [17], a scheme for realizing quantum gates with photonic qubits to be encoded on cavity modes is proposed. In this theoretical scheme, the authors utilize both the technique of adiabatic elimination from atomic physics developed by [18] and dual-rail qubits approach for the interaction of multilevel atoms with multimode cavities so that a set of universal gates is realized. In more details, by assuming a four-level atom in double-\(\Lambda \) configuration to be coupled to two dual-rail qubits the two-qubit iSWAP gate has been formed. Then, by adding two more transitions to the iSWAP gate configuration (i.e., a six-level atom interacts with six cavity modes) the Fredkin gate can be built. In [19], it is shown that applying the multiphoton resonance theory has significantly improved the speed of quantum iSWAP gate in the previous scheme. Furthermore, a study of the influence of the decoherence processes on the performance of both the iSWAP and the Fredkin operations shows that these operations are insensitive to the atomic and photonic decays, and therefore, these gates are good candidates for applications in quantum information processing.
In this paper, we follow the same procedure of using the multiphoton resonance theory in Refs. [17, 19] to implement a two-qubit gate in which a three-level atom in Vee configuration passes through a cavity with two photons. As a comparison with the previous scheme, in our scheme we reduce the number of the states of an atom and the number of photons inside a cavity to only three atomic levels and two cavity modes, and therefore, the requirements in the physical system in our scheme can be met in a physically reasonable scenario.
This paper is organized as follows. In Sect. 2 we describe the model and discuss how multiphoton resonance theory is used so that the two-qubit quantum phase gate is performed. We then examine the robustness of our scheme to variations in significant parameters of the model in Sect. 3, and we also study the variation in the gate fidelity due to decoherence processes in Sect. 4. Finally, we conclude the paper in Sect. 5 with a summary.
2 Quantum phase gate
2.1 The model
We consider a V-configuration of the energy levels of a three-level atom in which  represents the ground state and \(|e\rangle \) and \(|\textit{i}\rangle \) are two excited states, each coupled to the ground state via a dipole allowed transition but not to each other. The atom interacts with two EM modes inside a high Q cavity, and these modes have the resonant frequencies \(\omega _1\) and \(\omega _2\) (see Fig. 1). We choose the Fock states \(|0\rangle \) and \(|1\rangle \) to be the logical states 0 and 1. All the possible states in the cavity field are therefore given by \(|00\rangle \), \(|01\rangle \), \(|10\rangle \), and \(|11\rangle \). In this paper, we use the notation \(|\alpha , \beta , \delta \rangle \equiv |\alpha \rangle |\beta _1\rangle |\delta _2\rangle \) where
represents the ground state and \(|e\rangle \) and \(|\textit{i}\rangle \) are two excited states, each coupled to the ground state via a dipole allowed transition but not to each other. The atom interacts with two EM modes inside a high Q cavity, and these modes have the resonant frequencies \(\omega _1\) and \(\omega _2\) (see Fig. 1). We choose the Fock states \(|0\rangle \) and \(|1\rangle \) to be the logical states 0 and 1. All the possible states in the cavity field are therefore given by \(|00\rangle \), \(|01\rangle \), \(|10\rangle \), and \(|11\rangle \). In this paper, we use the notation \(|\alpha , \beta , \delta \rangle \equiv |\alpha \rangle |\beta _1\rangle |\delta _2\rangle \) where  represents atomic state, while \(|\beta _1\rangle \) and \(|\delta _2\rangle \) denote that cavity fields have \(\beta \) photon in mode 1 and \(|\delta \rangle \) photon in mode 2 with \((\beta , \delta \in 0, 1)\).
represents atomic state, while \(|\beta _1\rangle \) and \(|\delta _2\rangle \) denote that cavity fields have \(\beta \) photon in mode 1 and \(|\delta \rangle \) photon in mode 2 with \((\beta , \delta \in 0, 1)\).
In the standard qubit basis \({|00\rangle , |01\rangle , |10\rangle , |11\rangle }\), the quantum phase gate (QPG) we want to realize is given, in matrix form, by
We consider an atom with such a configuration (see Fig. 1) in its ground state  passing through the cavity with two photons in its modes. Obviously, the initial state then is
passing through the cavity with two photons in its modes. Obviously, the initial state then is  . It is apparent that the initial state \(|0_1, 0_2\rangle \) does not evolve with the time, and for the initial states
. It is apparent that the initial state \(|0_1, 0_2\rangle \) does not evolve with the time, and for the initial states  and
and  we will see in the following sections that proper values for detunings, the interaction time between the three-level atom and the cavity modes, and the global phases will keep these states in their initial states. This means the cavity state \(|0_1, 0_2\rangle \) is unaffected, the cavity states \(|0_1, 1_2\rangle \), \(|1_1, 0_2\rangle \) remain in their initial states, and therefore, a \(\pi \) phase shift for the state \(|1_1, 1_2\rangle \) is only needed so that we meet the conditional evolution for implementing the quantum phase gate.
we will see in the following sections that proper values for detunings, the interaction time between the three-level atom and the cavity modes, and the global phases will keep these states in their initial states. This means the cavity state \(|0_1, 0_2\rangle \) is unaffected, the cavity states \(|0_1, 1_2\rangle \), \(|1_1, 0_2\rangle \) remain in their initial states, and therefore, a \(\pi \) phase shift for the state \(|1_1, 1_2\rangle \) is only needed so that we meet the conditional evolution for implementing the quantum phase gate.
The Hamiltonian describes the level scheme in Fig. 1 in the Schrödinger picture which can be given, in the dipole and rotating-wave approximations, as

where the coupling strengths are \(\textit{g}_j (j=1, 2)\), the atomic operators  and
and  , and \(\hat{a}_j\) is the photon annihilation operator for the cavity mode. Now, we can set \(\hbar =1\). For the system initially in the state
, and \(\hat{a}_j\) is the photon annihilation operator for the cavity mode. Now, we can set \(\hbar =1\). For the system initially in the state  and after interaction time t, the state of the system is given by
and after interaction time t, the state of the system is given by

and therefore the Hamiltonian describing this system in an interaction picture can take the form

with  and
and  .
.
2.2 Effective Hamiltonian
We now discuss how to use the adiabatic elimination technique to implement the quantum phase gate in Eq. (1). This technique provides a theoretical method for isolating two-level behavior from the more general N-level rotating-wave approximation Schrödinger equation [18]. In [17, 19], this technique has been used to construct effective three-level, four-level, and even five-level systems with a multiphoton resonance in order to implement universal quantum gates. Here, we use this technique to reduce the system in Eq. (3) to an effective two-level system. We now define two orthogonal projection operators P and Q where \(P+Q=1\), \(PP=P\), \(QQ=Q\), and \(PQ=QP=0\).
Assuming we set \(|\textit{i}\rangle \) to be far from resonance and the states of interest correspond to the subspace \(|\psi \rangle _P\) spanned by P, then  . In this assumption \(\Delta _1 \gg \textit{g}_j\) with \(\textit{g}_j (j=1,2)\) are all of coupling constants, whereas \(\Delta _2\) to be small and its proper value will be determined later to ensure resonance. We use the two-level effective Hamiltonian defined by \(H_{\mathrm{eff}} = H_0 - BA^{-1} B^{\dag }\) where \(H_0 = PH_IP\), \(A=QH_IQ\), \(B=PH_IQ\), and \(H_I\) is given by Eq. (4). For convenience, we use matrix form to represent the Hamiltonian in Eq. (4). That is, in the basis
. In this assumption \(\Delta _1 \gg \textit{g}_j\) with \(\textit{g}_j (j=1,2)\) are all of coupling constants, whereas \(\Delta _2\) to be small and its proper value will be determined later to ensure resonance. We use the two-level effective Hamiltonian defined by \(H_{\mathrm{eff}} = H_0 - BA^{-1} B^{\dag }\) where \(H_0 = PH_IP\), \(A=QH_IQ\), \(B=PH_IQ\), and \(H_I\) is given by Eq. (4). For convenience, we use matrix form to represent the Hamiltonian in Eq. (4). That is, in the basis  one can rewrite \(H_I\) as
one can rewrite \(H_I\) as
Selecting levels  and \(|e\rangle \) as our P space, one can then partition \(H_I\) into the matrices:
and \(|e\rangle \) as our P space, one can then partition \(H_I\) into the matrices:
After a trivial energy shift, the effective two-level Hamiltonian is
where the operators  and
and  . The effective coupling \(\textit{g}_{\mathrm{eff}}\) and the resonance condition \(\Delta _2\) (by setting \(\Delta _{\mathrm{eff}}=0\)) are given by
. The effective coupling \(\textit{g}_{\mathrm{eff}}\) and the resonance condition \(\Delta _2\) (by setting \(\Delta _{\mathrm{eff}}=0\)) are given by
The system for the states of interest evolves in time, therefore, according to

Quantum phase gate using the two-level behavior of Eqs. (8) and (9) for parameters in the Hamiltonian (4). In this figure, the state  is represented by the black-solid line, the state \(|\textit{i}, 0_1, 1_2\rangle \) is in red-dotted line, and the state \(|e, 1_1, 0_2\rangle \) is the blue-dashed line. Parameters: \(\textit{g}_1=\textit{g}_2=\textit{g}\), \(\Delta _1=25 \textit{g}\), and the value of \(\Delta _2\) is determined by the resonance condition in Eq. (9). The inset shows a zoom for the population of the state \(|\textit{i}, 0_1, 1_2\rangle \) for the same parameters (Color figure online)
is represented by the black-solid line, the state \(|\textit{i}, 0_1, 1_2\rangle \) is in red-dotted line, and the state \(|e, 1_1, 0_2\rangle \) is the blue-dashed line. Parameters: \(\textit{g}_1=\textit{g}_2=\textit{g}\), \(\Delta _1=25 \textit{g}\), and the value of \(\Delta _2\) is determined by the resonance condition in Eq. (9). The inset shows a zoom for the population of the state \(|\textit{i}, 0_1, 1_2\rangle \) for the same parameters (Color figure online)
With the time evolution to be \((|\textit{g}_{\mathrm{eff}}t|=\pi )\) a \(\pi \) shift for the state \(|1_1, 1_2\rangle \) is introduced. The three other logical states \(|0_1, 0_2\rangle \), \(|0_1, 1_2\rangle \), and \(|1_1, 0_2\rangle \) remain in their initial states as a result for the parameters in Eqs. (8) and (9), for the large value of \(\Delta _1\), and for the gate operating time \(|\textit{g}_{\mathrm{eff}}t|=\pi \). A two-qubit phase gate is, therefore, realized. It is worth noting that our proposal requires the atom state to be  in and out the cavity, such a condition provides a simple error correction. If the atom is not detected to be in the ground state, the logic operation must be aborted.
in and out the cavity, such a condition provides a simple error correction. If the atom is not detected to be in the ground state, the logic operation must be aborted.
In Fig. 2, we use the parameters in Eqs. (8) and (9) to numerically integrate the full Hamiltonian (4). In this plot it is apparent that a two-level behavior occurs between the states  and \(|e, 1_1, 0_2\rangle \), and the system in Eq. (3) returns to its initial state
and \(|e, 1_1, 0_2\rangle \), and the system in Eq. (3) returns to its initial state  after an interaction time \(|\textit{g}_{\mathrm{eff}}t|=\pi \), which is completely in agreement with the analytical dynamics in Eq. (10). In Fig. 3 we also numerically integrate the Hamiltonian (4) to check the validity of our proposal by measuring the fidelity of the system in Eq. (3) for being in the qubit state
after an interaction time \(|\textit{g}_{\mathrm{eff}}t|=\pi \), which is completely in agreement with the analytical dynamics in Eq. (10). In Fig. 3 we also numerically integrate the Hamiltonian (4) to check the validity of our proposal by measuring the fidelity of the system in Eq. (3) for being in the qubit state  for different values of \(\Delta _1/\textit{g}\).
for different values of \(\Delta _1/\textit{g}\).
Variation of the fidelity of the quantum phase gate as a function of \(\Delta _1/\textit{g}\), where \(\textit{g}_1=\textit{g}_2=\textit{g}\) and the value of \(\Delta _2\) is set by the resonance condition in Eq. (9). The inset shows a zoom for the fidelity in the region \(0< \Delta _1/\textit{g} \le 5 \) for the same parameters
3 Impacts of variations in couplings and detunings
Here, we discuss the impact of variations in significant parameters such as the coupling constant \(\textit{g}\) and the detuning \(\Delta \) on the fidelity of our gate. Theoretically, the proper values for the coupling strengths and the detunings are determined by Eqs. (8) and (9). In reality, however, there is always uncertainty in these parameters that must be taken into account. For example, it is reported in [8] that the uncertainty in atom velocity ranges between \(\pm \,2\) m/s, and then the atomic position of each atom can be determined with a \(\pm \,1\) mm precision. It is found in [20] that the variation of the atom-field strength over the cross section of the atomic beam (0.5 mm) is in order 2%. Considering such variations in the parameters of \(\textit{g}\) and \(\Delta \) and by the use of the full Hamiltonian (4), we plot the fidelity of QPG in Fig. 4, where we allow the values of \(\textit{g}\) and \(\Delta _2\) to vary slightly around the theoretical values. The system appears to be reasonably insensitive to variations in parameters.
Variation of the fidelity of the quantum phase gate as a function of \(\Delta _2/\textit{g}\). Parameters: \(\textit{g}_1=\textit{g}_2=\textit{g}\), \(\Delta _1=25 \textit{g}\), and the value of \(\Delta _2\) is determined by the resonance condition in Eq. (9). The solid line shows the effect of both the variation of the atom-field strength in order 2% and the variation of \(\Delta _2\)
4 Effects of decoherence
Since the birth of quantum computing, it was realized that decoherence will be one of the difficulties to build quantum computers. Here, we study the influence of decoherence to examine with how much efficiency the desired outcome can be produced. In our treatment, two dominant channels of the decoherence decay, namely via cavity and atomic relaxations, are only considered in the study of the effects of decoherence.
4.1 Input state: \(|\psi \rangle =|g, 1_1, 1_2\rangle \)
Firstly, we study the effect of dissipative processes when the initial state to be  . For this purpose, we recall Liouville’s equation (or general master equation) that can be written, in the density matrix framework, as
. For this purpose, we recall Liouville’s equation (or general master equation) that can be written, in the density matrix framework, as
The first term in Eq. (11) describes the atom-field coupling for the system \(H_I\) in Eq. (4), and the second term \(\mathcal {L}\rho \) is known as Liouville’s operator and contains the effects of dissipations. At zero temperature, the Liouvillian \(\mathcal {L} \rho \) has the so-called Lindblad form [21]
where \(\eta \) represents the loss of population. In our case \(\eta \) may refer to the spontaneous emission \(\gamma \) or to the cavity field rate \(\kappa \). The operators L and \(L^{\dag }\) are the corresponding system operators. By using Eqs. (11) and (12), numerical calculations in Fig. 5 show the variation in fidelity when atomic and photonic decays to be considered.
In the following we seek to derive an analytical solution that enables us to explain the numerical results provided by Eq. (11). For convenience, we rewrite the previous Lindblad form in an another equivalent form as
The Liouvillian operator in this formula gives further details for the population decays from the excited states and the quantum jumps events in the damped systems [22].
Applying the general master equation in Eq. (11) on the system described by the state vector (3) shows that the decay of the cavity field from the state, for example, \(|e, 1_1, 0_2\rangle \) takes the system to state \(|e, 0_1, 0_2\rangle \) and the decay of state \(|\textit{i}, 0_1, 1_2\rangle \) due to the atomic relaxation takes the system to state  . Both states
. Both states  and \(|e, 0_1, 0_2\rangle \notin \mathcal {H}\), as \(\mathcal {H}\) represents the Hilbert space where the Hamiltonian \(H_I\) acts on \(|\psi (t)\rangle \). Indeed, both decays via atomic and photonic relaxations take the system outside the Hilbert space
and \(|e, 0_1, 0_2\rangle \notin \mathcal {H}\), as \(\mathcal {H}\) represents the Hilbert space where the Hamiltonian \(H_I\) acts on \(|\psi (t)\rangle \). Indeed, both decays via atomic and photonic relaxations take the system outside the Hilbert space  . This means our system is not closed and decays in our system result in an irreversible loss of population. This actually indicates that we can use the wave-function approach [23] instead of density matrix approach in Eq. (11) and therefore an analytical solution can be deduced. To this end, we rewrite the previous Liouville’s equation as
. This means our system is not closed and decays in our system result in an irreversible loss of population. This actually indicates that we can use the wave-function approach [23] instead of density matrix approach in Eq. (11) and therefore an analytical solution can be deduced. To this end, we rewrite the previous Liouville’s equation as
where \(H^{\prime } = H_I -\frac{i}{2} \sum \nolimits _{i} \eta _{i} L^{\dag }_i L_i\) and \(J \rho = \sum \nolimits _{i} \eta _{i} \ L_i \rho \ L_i^{\dag }\). Since decays in our system result in an irreversible loss of population, we can propagate the wave function \(|\psi (t)\rangle \) (instead of the density matrix \(\rho \)) with the Schrödinger equation using the non-Hermitian Hamiltonian \(H^{\prime }\), i.e., \(\frac{\partial }{\partial t}|\psi (t)\rangle = -i\ H^{\prime } |\psi (t)\rangle \). The Hamiltonian describing the system when decays to be considered is

where \(\kappa _1\) and \(\kappa _2\) are the cavity field rates of the two modes and  is the atomic relaxation from state \(|e\rangle \) to state
is the atomic relaxation from state \(|e\rangle \) to state  . Shore’s method [18] can be modified so that \(H^{\prime }_{\mathrm{eff}}= H_{\mathrm{eff}} -\frac{i}{2} \sum \nolimits _i \eta _i L^{\dag }_i L_i\) and, therefore, the effective two-level Hamiltonian with decays can be given as
. Shore’s method [18] can be modified so that \(H^{\prime }_{\mathrm{eff}}= H_{\mathrm{eff}} -\frac{i}{2} \sum \nolimits _i \eta _i L^{\dag }_i L_i\) and, therefore, the effective two-level Hamiltonian with decays can be given as

The Hamiltonian \(H^{\prime }_{\mathrm{eff}}\) acts on the subsystem  which is nothing but the system \(|\psi (t)\rangle \) spanned by the projector P, i.e., \(|\chi (t)\rangle = P|\psi (t)\rangle \). The time evolution of the probability amplitudes in the subsystem \(|\chi (t)\rangle \), therefore, can be described by (with \(\textit{g}_{\mathrm{eff}}=\textit{g}_2\) and assuming exact resonance, \(\Delta _{\mathrm{eff}}=0\))
which is nothing but the system \(|\psi (t)\rangle \) spanned by the projector P, i.e., \(|\chi (t)\rangle = P|\psi (t)\rangle \). The time evolution of the probability amplitudes in the subsystem \(|\chi (t)\rangle \), therefore, can be described by (with \(\textit{g}_{\mathrm{eff}}=\textit{g}_2\) and assuming exact resonance, \(\Delta _{\mathrm{eff}}=0\))

We may write the equations of motion (17) in matrix form as

The solutions for \(\lambda \) are obtained from the \(2 \times 2\) determinant of the coefficients, which yields the quadratic equation (where we set \(\kappa _1=\kappa _2= \kappa \) and  )
)
The distinct roots (in the strong coupling regime \(\textit{g}_2 > \kappa , \gamma \)) are reduced into
It follows that the general solutions for \(c_i(i=1,2)\) may have the forms
where the values of the coefficients are determined by the initial values \((c_1(t=0)=1\) and \(c_2(t=0)=0)\) and by the initial values of their first and second derivatives obtained from the equations of motion in Eq. (17). The solutions for \((c_1(t)\) and \(c_2(t))\) can be then given as

Variation of the fidelity in the presence of dissipation processes. Parameters of couplings and detunings can be found in Fig. 4, and \(F_0\) represents the fidelity of the system at the resonance condition and in the absence of any decay (see Fig. 4). a For \(\kappa =0\) and at the resonance condition, the fidelity is \(F=(0.9, 0.75, 0.5)F_0\) at \(\gamma /g_2 \sim -\frac{2}{\pi } \text{ ln }(F)\). b Similarly \(F=(0.9, 0.75, 0.5)F_0\) at \(\kappa /g_2 \sim -\frac{2}{3\pi } \text{ ln }(F)\), where \(\gamma =0\)
The norm of the system \(|\chi (t)\rangle \) therefore decreases according to \(\langle \chi (t)|\chi (t)\rangle = |c_1(t)|^2+|c_2(t)|^2 \simeq e^{-(\frac{3\kappa +\gamma }{2})t}\), i.e., it decays with the rate \(\frac{1}{2}(3\kappa +\gamma )\). We plot the dynamics of the states  and \(|e, 1_1, 0_2\rangle \) and compare the results by Eq. (21) with the numerical integration of Eq. (11) as shown in Fig. 6.
and \(|e, 1_1, 0_2\rangle \) and compare the results by Eq. (21) with the numerical integration of Eq. (11) as shown in Fig. 6.
Dynamics of the two-level system in Fig. 2 in the presence of dissipation processes and in strong coupling regime, \(\textit{g}=4\gamma \) and \(\kappa =\gamma \). The inset shows the relative population \(R=|P_\mathrm{th}-P_\mathrm{num}|/P_\mathrm{num}\) where \(P_\mathrm{th}\) represents population of  given by theoretical calculation, i.e.,
given by theoretical calculation, i.e.,  (see Eq. (21)), and \(P_\mathrm{num}\) is population of
(see Eq. (21)), and \(P_\mathrm{num}\) is population of  by numerical integration of Eq. (11). This inset indicates the deviations between theoretical and numerical calculations and reflects the agreement between the results provided by the density operator approach and the wave-function method
by numerical integration of Eq. (11). This inset indicates the deviations between theoretical and numerical calculations and reflects the agreement between the results provided by the density operator approach and the wave-function method
4.2 Input states: \(|g, 1_1, 0_2\rangle \), \(|g, 0_1, 1_2\rangle \)
Following the same procedure in previous sections, we now briefly discuss the effects of decoherence processes on the initial states  and
and  . For the initial state
. For the initial state  , the time evolution of this state is
, the time evolution of this state is  , and for the initial state
, and for the initial state  its wave function at some time later is
its wave function at some time later is  . From Liouville’s equation, both systems are not closed and in each system there are two relaxation channels. In more detail, upper states in these systems, namely \(|\textit{i}, 0_1, 0_2\rangle \) and \(|e, 0_1, 0_2\rangle \), decay to the state
. From Liouville’s equation, both systems are not closed and in each system there are two relaxation channels. In more detail, upper states in these systems, namely \(|\textit{i}, 0_1, 0_2\rangle \) and \(|e, 0_1, 0_2\rangle \), decay to the state  due to atomic relaxations, and both initial states
due to atomic relaxations, and both initial states  and
and  decay to
decay to  due to photonic relaxations. By integrating Eq. (11), one can find the effects of atomic and photonic decays on the populations of the previous initial states at any time.
due to photonic relaxations. By integrating Eq. (11), one can find the effects of atomic and photonic decays on the populations of the previous initial states at any time.
Finally, we briefly give a discussion of the experimental feasibility for implementing our scheme within cavity QED. Here we use the parameters in Rydberg atom microwave cavity QED experiment performed at ENS in Paris by Haroche et al. [8]. In this experiment the three important parameters for the cavity–atom interaction system are \((\textit{g}, \kappa , \gamma )/2\pi \sim (47, ,0.16, 0.005)\ \text{ kHz }\). Considering these parameters, the gate fidelities in our scheme \(F> 0.98\). The gate fidelities become \(F>0.99\) for the parameters in [24], where further improvements in the field energy damping time (with \(T_c=130\ \text{ ms }\) at \(\omega /2\pi =51\ \text{ GHz }\)) have been introduced.
5 Conclusion
In summary, we have proposed a simple scheme that realizes a cavity QED based two-qubit phase gate. In this scheme, a three-level atom in Vee configuration interacts with a two-mode high Q cavity, where we use quantum logic with stored cavity photons. We utilize the theory of multiphoton resonance to determine the appropriate values for detunings, coupling constants, and the interaction time indicated in Eqs. (8) and (9). We also discuss the influence of the atomic and photonic decays, and deviation of \(\textit{g}\) and \(\Delta \) on the fidelity. In general, it is apparent that the system is reasonably insensitive to variations in such parameters and therefore the scheme can be experimentally realized.
The three-level V-type atom is realistic and has interesting applications. This system, for example, has been widely used in experimental observations of quantum jumps of single trapped ions [25,26,27]. Moreover, polarization spectroscopy in V-type configuration in Rb atoms has been reported in [28].
In this scheme, we consider the interaction of the atom–cavity to be in the strong coupling domain. Basically, our scheme requires the cavity to have an extremely high Q factor and the cavity modes to be confined in a small mode volume for extended periods of times. Recently, most of cavity QED techniques work in the regime of strong coupling [24, 29,30,31,32]. Further, experimental realizations of multimode strong coupling in cavity QED have been recently reported in [33, 34], which promises that the strong interaction between a multimode field and a multilevel atom simultaneously inside one cavity can be achievable and, therefore, our scheme can be realized by the present cavity QED techniques.
References
Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2000)
Shor, P.W.: Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Comput. 26(5), 1484–1509 (1997)
Grover, L.K.: Quantum mechanics helps in searching for a needle in a haystack. Phys. Rev. Lett. 79(2), 325–328 (1997)
Barenco, A., Bennett, C.H., Cleve, R., DiVincenzo, D.P., Margolus, N., Shor, P., Sleator, T., Smolin, J.A., Weinfurter, H.: Elementary gates for quantum computation. Phys. Rev. A 52(5), 3457–3467 (1995)
DiVincenzo, D.P.: Two-bit gates are universal for quantum computation. Phys. Rev. A 51(2), 1015–1022 (1995)
Cirac, J.I., Zoller, P.: Quantum computations with cold trapped ions. Phys. Rev. Lett. 74(20), 4091–4094 (1995)
Jonathan, A.J., Michele, M., Rasmus, H.H.: Implementation of a quantum search algorithm on a quantum computer. Nature 393, 344–346 (1998)
Raimond, J.M., Brune, M., Haroche, S.: Manipulating quantum entanglement with atoms and photons in a cavity. Rev. Mod. Phys. 73(3), 565–582 (2001)
Mabuchi, H., Doherty, A.C.: Cavity quantum electrodynamics: coherence in context. Science 298(5597), 1372–1377 (2002)
van Enk, S.J., Kimble, H.J., Mabuchi, H.: Quantum information processing in cavity-QED. Quantum Inf. Process. 3(1–5), 75–90 (2004)
Haroche, S., Raimond, J.-M.: Exploring the Quantum: Atoms, Cavities, and Photons. OUP, Oxford (2013)
Pellizzari, T., Gardiner, S.A., Cirac, J.I., Zoller, P.: Decoherence, continuous observation, and quantum computing: a cavity qed model. Phys. Rev. Lett. 75(21), 3788–3791 (1995)
Zubairy, M.S., Kim, M., Scully, M.O.: Cavity-QED-based quantum phase gate. Phys. Rev. A 68(3), 033820 (2003)
Rauschenbeutel, A., Nogues, G., Osnaghi, S., Bertet, P., Brune, M., Raimond, J.M., Haroche, S.: Coherent operation of a tunable quantum phase gate in cavity QED. Phys. Rev. Lett. 83(24), 5166–5169 (1999)
Hacker, B., Welte, S., Rempe, G., Ritter, S.: A photon–photon quantum gate based on a single atom in an optical resonator. Nature 536, 193–196 (2016)
Reiserer, A., Rempe, G.: Cavity-based quantum networks with single atoms and optical photons. Rev. Mod. Phys. 87(4), 1379–1418 (2015)
Everitt, M.S., Garraway, B.M.: Multiphoton resonances for all-optical quantum logic with multiple cavities. Phys. Rev. A 90(1), 012335 (2014)
Shore, B.W.: Two-level behavior of coherent excitation of multilevel systems. Phys. Rev. A 24(3), 1413–1418 (1981)
Alqahtani, M.M., Everitt, M.S., Garraway, B.M.: Cavity QED photons for quantum information processing. arXiv:1407.0654v1 [quant-ph]
Meschede, D., Walther, H., Müller, G.: One-atom maser. Phys. Rev. Lett. 54(6), 551–554 (1985)
Lindblad, G.: On the generators of quantum dynamical semigroups. Commun. Math. Phys. 48(2), 119–130 (1976)
Barnett, S.M., Radmore, P.M.: Methods in Theoretical Quantum Optics. Clarendon, Oxford (2002)
Dalibard, J., Castin, Y., Mølmer, K.: Wave-function approach to dissipative processes in quantum optics. Phys. Rev. Lett. 68(5), 580–583 (1992)
Kuhr, S., Gleyzes, S., Guerlin, C., Bernu, J., Hoff, U.B., Deléglise, S., Osnaghi, S., Brune, M., Raimond, J.M., Haroche, S., Jacques, E., Bosland, P., Visentin, B.: Ultrahigh finesse Fabry–Pérot superconducting resonator. Appl. Phys. Lett. 90, 164101 (2007)
Leibfried, D., Blatt, R., Monroe, C., Wineland, D.: Quantum dynamics of single trapped ions. Rev. Mod. Phys. 75(1), 281–324 (2003)
Bergquist, J.C., Hulet, R.G., Itano, W.M., Wineland, D.J.: Observation of quantum jumps in a single atom. Phys. Rev. Lett. 57(14), 1699–1702 (1986)
Nagourney, W., Sandberg, J., Dehmelt, H.: Shelved optical electron amplifier: observation of quantum jumps. Phys. Rev. Lett. 56(26), 2797–2799 (1986)
Cha, E.H., Jeong, T., Noh, H.: Two-color polarization spectroscopy in \(V\)-type configuration in rubidium. Opt. Commun. 326, 175–179 (2014)
Vahala, K.J.: Optical microcavities. Nature 424, 839–846 (2003)
Ritter, S., Nölleke, C., Hahn, C., Reiserer, A., Neuzner, A., Uphoff, M., Mücke, M., Figueroa, E., Bochmann, J., Rempe, G.: An elementary quantum network of single atoms in optical cavities. Nature 484, 195–200 (2012)
McKeever, J., Buck, J.R., Boozer, A.D., Kuzmich, A., Nägerl, H.-C., Stamper-Kurn, D.M., Kimble, H.J.: State-insensitive cooling and trapping of single atoms in an optical cavity. Phys. Rev. Lett. 90(13), 133602 (2003)
Walther, H., Varcoe, B.T.H., Englert, B.G., Becker, T.: Cavity quantum electrodynamics. Rep. Prog. Phys. 69(5), 1325 (2006)
Kollár, A.J., Papageorge, A.T., Vaidya, V.D., Guo, Y., Keeling, J., Lev, B.L.: Supermode-density-wave-polariton condensation with a Bose–Einstein condensate in a multimode cavity. Nat. Commun. 8(14386), 17 (2017)
Sundaresan, N.M., Liu, Y., Sadri, D., Szőcs, L.J., Underwood, D.L., Malekakhlagh, M., Türeci, H.E., Houck, A.A.: Beyond strong coupling in a multimode cavity. Phys. Rev. X 5(2), 021035 (2015)
Acknowledgements
The author wishes to thank F. Maiz for helpful discussions and comments on the manuscript.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Alqahtani, M.M. Quantum phase gate based on multiphoton process in multimode cavity QED. Quantum Inf Process 17, 211 (2018). https://doi.org/10.1007/s11128-018-1979-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11128-018-1979-6


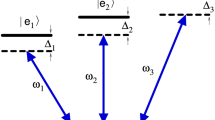

 and
and  . This level scheme is used to realize a two-qubit quantum phase gate
. This level scheme is used to realize a two-qubit quantum phase gate



