New optical soliton solutions to the Biswas–Milovic equations with power law and parabolic law nonlinearity using the Sardar-subequation method

Abstract

This investigation delves into the analytic optical exploration of the Biswas–Milovic equation featuring both parabolic and power law nonlinearity. It provides valuable insights into the distinctive characteristics of optical soliton solutions, enhancing our comprehension of soliton dynamics in diverse optical systems. Employing the potent Sardar-subequation analytical method, we construct a variety of wave structures, revealing a spectrum of optical soliton solutions that span trigonometric and hyperbolic functions. Thorough validation with Mathematica software ensures precision and dynamic visual representations depict soliton solutions that exhibit diverse patterns. These patterns include bright solitons, dark solitons, singular solitons, king solutions, bell-shaped patterns, as well as parabolic-shaped and hyperbolic-shaped patterns. These solutions hold significance in the realms of optical fiber and wave dynamics within various optical systems. Our approach above demonstrates versatility and applicability in solving a wide range of mathematical and physical problems, indicating its usefulness in generating such optical solutions.

1 Introduction

Nonlinear equations (NLEs) are nature’s language, describing the intricate dances of phenomena from heat flow to light waves. Unlike the simple lines of linear equations, NLEs twist and turn, capturing the true complexity of our world. These equations weave stories of solitons, solitary waves that dance through optical fibers, and their solutions hold the key to understanding a vast array of scientific mysteries. From the scorching heat flow in a furnace to the shimmering ripples of light pulses, NLEs provide a powerful narrative tool. By unlocking their secrets, mathematicians, and engineers can harness the behavior of these phenomena, building better fiber optic networks, designing efficient heat transfer systems, and even delving into the mysteries beyond the realm of light (Tozar et al. 2021; Rasid et al. 2023; Eslami and Mirzazadeh 2016; Liu et al. 2019). In addition, comprehending and managing soliton dynamics are imperative for diverse optical applications, spanning optical communication, nonlinear optics, and ultrafast photonics. Optical solitons present distinct advantages, including stable propagation across extensive distances and the preservation of pulse shape and integrity. Consequently, precise modeling of soliton dynamics holds paramount importance in the development and enhancement of optical devices and systems tailored for these specific applications (Shaikh et al. 2023; Mirzazadeh 2015; Hossain et al. 2024a; Zou and Guo 2023). Among various NLEs, the BME also known as the generalized nonlinear Schrödinger equation, represents a significant advancement in modeling optical solitons in nonlinear media. Unlike the standard nonlinear Schrödinger equation (NLSE), it includes additional terms for higher-order effects like self-steepening, self-frequency shift, and third-order dispersion. These terms are crucial in shaping optical pulse behavior. By incorporating them, the BME provides a comprehensive framework for studying soliton propagation, especially in regimes with significant nonlinear effects. This enhanced model facilitates accurate prediction and analysis of soliton behavior in various optical systems, driving advancements in optical communication, nonlinear optics, and ultrafast photonics. It’s a valuable tool for designing and optimizing optical devices for applications ranging from long-distance communication to nonlinear signal processing (Altun et al. 2022; Ozdemir 2023; Gupta and Yadav 2023). Additionally, the equation is integrable, implying that it possesses an infinite number of conservation laws. The interplay of Parabolic and Power law nonlinearities within the BME is the focus of this investigation. The form of BME is as follows (Altun et al. 2022):

$$ i\left\{ {\Upsilon^{n} } \right\}_{t} - \left\{ {\left( {\beta F\left| \Upsilon \right|^{2} } \right) - W} \right\}\Upsilon^{n} - {\mathbb{C}}\left\{ {\left\{ {\Upsilon^{n} } \right\}_{xx} + \left\{ {\Upsilon^{n} } \right\}_{yy} } \right\} = 0. $$

(1)

In this equation, $\Upsilon =\Upsilon (x,y,t)$ represents the complex function,${\left\{{\Upsilon }^{n}\right\}}_{t}=\frac{\partial {\Upsilon }^{n}}{\partial t}$, ${\left\{{\Upsilon }^{n}\right\}}_{xx}=\frac{{\partial }^{2}{\Upsilon }^{n}}{\partial {x}^{2}}$ and ${\left\{{\Upsilon }^{n}\right\}}_{yy}=\frac{{\partial }^{2}{\Upsilon }^{n}}{\partial {y}^{2}}$. Equation (1) comprises three terms: the first denotes the overall evolution, the second term involving the function$\text{F}$, embodies the nonlinearity term, and the third term, the general form of group velocity dispersion. Here, $\text{F}$ is a real-valued algebraic function, and $n$ serves as a parameter that extends from the NLSE to the BME. The variables$x$,$y$, and $t$ are independent spatial and temporal variables, while$\mathcal{B}$,${\mathbb{C}}$, and $W$ are real quantities.

In a general context, $n$ is greater than or equal to 1, and when $n$ equals 1, Eq. (1) simplifies to the (2 + 1)-dimensional NLSE form of the BME. This study focuses on Eq. (1), which exhibits distinct nonlinearity, with the assumption that $n$ equals 1 is an essential NLSE form for optical fibers.

Numerous scholars have developed diverse approaches to derive precise solutions for nonlinear equations, utilizing approaches like the (${G}{\prime}/G$,$1/G$)-expansion method (Li et al. 2010; Hossain et al. 2024b), the $\left(\frac{{{\varvec{G}}}^{\boldsymbol{^{\prime}}}}{{{\varvec{G}}}^{\boldsymbol{^{\prime}}}+G+A}\right)$ technique (Iqbal et al. 2023a; Mia et al. 2023), the finite-gap integration method (Niu and Guo 2023), the Riccati equation method (Yomba 2005; Elsayed and Khaled 2015), the Hirota bilinear method (Chen et al. 2023; Kumar et al. 2022a), Lie group method (Jafari et al. 2015; Buckwar and Luchko 1998), the $\left({G}{\prime}/G\right)$-expansion technique (Mohanty et al. 2023; Naher and Abdullah 2012), the extended Jacobi elliptic function method (Zafar et al. 2020; Wen and Lü 2009), the exp-function method (Islam et al. 2022), the exp $\left\{-\varphi \left(\xi \right)\right\}$ method (Khan et al. 2024; Roshid and Rahman 2014), the functional variable technique (Babajanov and Abdikarimov 2022; Bekir and San 2012), the homogeneous balance method (Wang et al. 1996; Fan et al. 1998), the fractional approach (Tandel et al. 2022), the new auxiliary equation method (Islam et al. 2023; Zhang 2013), the sine–Gordon expansion scheme (Kumar et al. 2022b), the first integral method (Taghizadeh and Mirzazadeh 2011), the tanh–function method (Parkes and Duffy 1996; Fan 2000), the simple equation technique (Islam et al. 2024; Nofal 2016), the unified auxiliary equation method (Ali et al. 2023), the generalized $\left({G}{\prime}/G\right)$-expansion technique (Kaur 2014), the tanh–coth method (Kumar and Pankaj 2015; Mamun et al. 2022), the generalized Kudryshov method (Habib et al. 2019; Islam et al. 2015), the Hirota bilinear formulation (Fokas and Lenells 2012; Abdel-Gawad and Osman 2015) and so on.

Among various methods, the Sardar subequation method is a highly valuable analytical technique employed for solving NLEs (Rehman et al. 2023). This method is a particular case of the transformed rational function method given in Yasin et al. (2024) and is easier than this method. It hinges on representing solutions as power series, with coefficients determined by a single variable. The method derives these coefficients by substituting the series into the equation and equating coefficients of like terms. This approach has extensive applications in revealing analytical solutions and has been utilized by several investigators to uncover solutions for various NLEs (Ibrahim et al. 2023; Rezazadeh et al. 2020; Rehman et al. 2022; Cinar et al. 2022; Iqbal et al. 2023b). In the past, numerous researchers have employed various mathematical laws such as the parabolic law, Kerr law, power law, and Kudryashov’s quintuple power law, among others, to explore optical soliton solutions of BME using diverse solving techniques (Eslami and Mirzazadeh 2016; Altun et al. 2022; Gupta and Yadav 2023). The majority of these studies focused on revealing bright and dark soliton solutions. This study, however, aims to explore a wide range of soliton patterns, including bright solitons, dark solitons, singular solitons, king solutions, bell-shaped patterns, as well as parabolic-shaped and hyperbolic-shaped patterns. As of now, there has been no exploration of the above-mentioned equation, which incorporates parabolic and power law nonlinearity, using the Sardar subequation method. The main objective of this work is to use the previously established techniques to obtain soliton solutions for the mentioned nonlinear equations. The paper is organized into the following sections: (i) Sect. 2 provides an overview of the methodology. (ii) Sect. 3 discusses the parabolic and power law nonlinearity. (iii) In Sect. 4, the methodology is applied to the equations, resulting in the derivation of the necessary solutions. (iv) In Sect. 5, we explore dynamic representations using contour, 3D, and 2D graphs to illustrate the intriguing characteristics of various soliton solutions. (v) Sect. 6 contains concluding observations. (vi) Lastly, the paper ending with the list of references.

2 Sardar-subequation approach

This section provides a concise overview of the Sardar-subequation method, a highly effective technique for obtaining exact solutions to various nonlinear partial differential equations (Ibrahim et al. 2023; Rezazadeh et al. 2020; Rehman et al. 2022; Cinar et al. 2022; Iqbal et al. 2023b). Facilitating this analytical journey, assume the NLEs involves three independent variables $x,y$ and $t$ which is expressed as:

$$T\left(\Upsilon,{\Upsilon}_{x},{\Upsilon}_{xx},{\Upsilon}_{y},{\Upsilon}_{yy},{\Upsilon}_{xy},{\Upsilon}_{t},{\Upsilon}_{tt},{\Upsilon}_{xt},\dots \dots \dots \right)=0.$$

(2)

In this framework, $T$ corresponds to a polynomial function that depends upon the variables compressed in $\Upsilon$ and ${\Upsilon}_{x}=\frac{\partial \Upsilon}{\partial x}$, ${\Upsilon}_{y}=\frac{\partial \Upsilon}{\partial y}$, ${\Upsilon}_{t}=\frac{\partial \Upsilon}{\partial t}$, ${\Upsilon}_{xx}=\frac{{\partial }^{2}\Upsilon}{\partial {x}^{2}}$, ${\Upsilon}_{yy}=\frac{{\partial }^{2}\Upsilon}{\partial {y}^{2}}$, ${\Upsilon}_{tt}=\frac{{\partial }^{2}\Upsilon}{\partial {t}^{2}}$, ${\Upsilon}_{xt}=\frac{\partial \Upsilon}{\partial x\partial t}$, ${\Upsilon}_{xy}=\frac{\partial \Upsilon}{\partial x\partial y}$ and so on.

We establish a new variable $\Psi$, which is governed by the following relation, in order to transform Eq. (2):

$$ \Upsilon \left( {x,y,t} \right) = e^{i\Theta } \Re \left( \Psi \right),\;\Theta = x + y + \sigma t + \zeta_{0} \;and\;\Psi = \delta_{1} x + \delta_{2} y + \vartheta t $$

(3)

where $\vartheta$ represents the wave velocity, $\Theta$ denotes the phase component, ${\zeta }_{0}$ stands for the phase constant, and ${\delta }_{1}$, ${\delta }_{2}$, and $\sigma$ be nonzero real values need to be determined.

Therefore, Eq. (2) is converted into an ordinary differential equation that can be put together as follows using Eq. (3),

$$S\left(\mathfrak{R},{\mathfrak{R}}{\prime},{\mathfrak{R}}^{{\prime}{\prime}},{\mathfrak{R}}^{{\prime}{\prime}{\prime}},\dots \dots \dots \right)=0.$$

(4)

The new polynomial in this case that holds $\mathfrak{R}$ and its ordinary derivatives is called $S$, ($\mathfrak{R}=\mathfrak{R}\left(\Psi \right), {\mathfrak{R}}{\prime}=\frac{d\mathfrak{R}}{d\Psi },{\mathfrak{R}}^{{\prime}{\prime}}=\frac{{d}^{2}\mathfrak{R}}{d{\Psi }^{2}},{\mathfrak{R}}^{{\prime}{\prime}{\prime}}=\frac{{d}^{3}\mathfrak{R}}{d{\Psi }^{3}},\dots \dots \dots$).

The general solution of Eq. (4) is given by the following equation as mentioned in the Sardar-subequation method:

$$\mathfrak{R}\left(\Psi \right)=\sum_{j=0}^{P}{a}_{j}{\mathcal{H}}^{j}\left(\Psi \right),$$

(5)

subsequent in:

$$ {\mathcal{H}^{\prime}}\left( \Psi \right) = \sqrt {{\mathcal{H}}^{4} \left( \Psi \right) + \omega {\mathcal{H}}^{2} \left( \Psi \right) + \epsilon } , $$

(6)

where ‘′’ is called the derivative with respect to $\Psi$, ${a}_{j}$,$(j=1, 2, 3, \dots \dots \dots , P)$, $\upomega$ and $\epsilon$ are the arbitrary constants and here, P is defined as a balance number that needs to be figured out.

The solutions offered by Eq. (6) depend on the characteristics of the parameters ($\upomega$ and $\epsilon$) and manifest in the following manner:

Scenario I. When ${\upomega } > 0$ but $\epsilon = 0$ then

$$ {\mathcal{H}}_{1}^{ \pm } \left( \Psi \right) = \pm \sqrt {h\ell \omega } cosech_{h\ell } \left( {\sqrt \omega \Psi } \right), $$

(7)

$$ {\mathcal{H}}_{2}^{ \pm } \left( \Psi \right) = \pm \sqrt { - h\ell \omega } sech_{h\ell } \left( {\sqrt \omega \Psi } \right), $$

(8)

where ${cosech}_{h{\ell}}\left( \Psi \right)=\frac{2}{h{e}^{\Psi }-{{\ell}e}^{-\Psi }}$ and ${sech}_{h{\ell}}\left( \Psi \right)=\frac{2}{h{e}^{\Psi }+{{\ell}e}^{-\Psi }}$.

Scenario II. When $\upomega <0$ but $\epsilon =0$ then

$$ {\mathcal{H}}_{3}^{ \pm } \left( \Psi \right) = \pm \sqrt { - h\ell \omega } cosec_{h\ell } \left( {\sqrt { - \omega } \Psi } \right), $$

(9)

$$ {\mathcal{H}}_{4}^{ \pm } \left( \Psi \right) = \pm \sqrt { - h\ell \omega } sec_{h\ell } \left( {\sqrt { - \omega } \Psi } \right), $$

(10)

where ${cosec}_{h{\ell}}\left( \Psi \right)=\frac{2i}{h{e}^{i\Psi }-{{\ell}e}^{-i\Psi }}$ and ${sec}_{h{\ell}}\left( \Psi \right)=\frac{2}{h{e}^{i\Psi }+{{\ell}e}^{-i\Psi }}$.

Scenario III. When $\upomega <0$ but $\epsilon = \frac{{\omega^{2} }}{4}$ then

$$ {\mathcal{H}}_{5}^{ \pm } \left( \Psi \right) = \pm \sqrt { - \frac{\omega }{2}} tanh_{h\ell } \left( {\sqrt { - \frac{\omega }{2}} \Psi } \right), $$

(11)

$$ {\mathcal{H}}_{6}^{ \pm } \left( \Psi \right) = \pm \sqrt { - \frac{\omega }{2}} coth_{h\ell } \left( {\sqrt { - \frac{\omega }{2}} \Psi } \right), $$

(12)

$$ {\mathcal{H}}_{7}^{ \pm } \left( \Psi \right) = \pm \sqrt { - \frac{\omega }{2}} \left\{ {tanh_{h\ell } \left( {\sqrt { - 2\omega } \Psi } \right) \pm i\sqrt {h\ell } sech_{h\ell } \left( {\sqrt { - 2\omega } \Psi } \right)} \right\}, $$

(13)

$$ {\mathcal{H}}_{8}^{ \pm } \left( \Psi \right) = \pm \sqrt { - \frac{\omega }{2}} \left\{ {coth_{h\ell } \left( {\sqrt { - 2\omega } \Psi } \right) \pm \sqrt {h\ell } cosech_{h\ell } \left( {\sqrt { - 2\omega } \Psi } \right)} \right\}, $$

(14)

$$ {\mathcal{H}}_{9}^{ \pm } \left( \Psi \right) = \pm \sqrt { - \frac{\omega }{8}} \left\{ {tanh_{h\ell } \left( {\sqrt { - \frac{\omega }{8}} \Psi } \right) + coth_{h\ell } \left( {\sqrt { - \frac{\omega }{8}} \Psi } \right)} \right\}, $$

(15)

where ${tanh}_{h{\ell}}\left( \Psi \right)=\frac{h{e}^{\Psi }-{{\ell}e}^{-\Psi }}{h{e}^{\Psi }+{{\ell}e}^{-\Psi }}$ and ${coth}_{h{\ell}}\left( \Psi \right)=\frac{h{e}^{\Psi }+{{\ell}e}^{-\Psi }}{h{e}^{\Psi }-{{\ell}e}^{-\Psi }}$.

Scenario IV. When $\upomega >0$ but $\epsilon = \frac{{\omega^{2} }}{4}$ then

$$ {\mathcal{H}}_{10}^{ \pm } \left( \Psi \right) = \pm \sqrt {\frac{\omega }{2}} tan_{h\ell } \left( {\sqrt {\frac{\omega }{2}} \Psi } \right), $$

(16)

$$ {\mathcal{H}}_{11}^{ \pm } \left( \Psi \right) = \pm \sqrt {\frac{\omega }{2}} cot_{h\ell } \left( {\sqrt {\frac{\omega }{2}} \Psi } \right), $$

(17)

$$ {\mathcal{H}}_{12}^{ \pm } \left( {\Psi } \right) = \pm \sqrt {\frac{\omega }{2}} \left\{ {tan_{h\ell } \left( {\sqrt {2\omega } {\Psi }} \right) \pm \sqrt {h\ell } sec_{h\ell } \left( {\sqrt {2\omega } {\Psi }} \right)} \right\}, $$

(18)

$$ {\mathcal{H}}_{13}^{ \pm } \left( {\Psi } \right) = \pm \sqrt {\frac{\omega }{2}} \left\{ {cot_{h\ell } \left( {\sqrt {2\omega } {\Psi }} \right) \pm \sqrt {h\ell } cosech_{h\ell } \left( {\sqrt {2\omega } {\Psi }} \right)} \right\}, $$

(19)

$$ {\mathcal{H}}_{14}^{ \pm } \left( {\Psi } \right) = \pm \sqrt {\frac{\omega }{8}} \left\{ {tan_{h\ell } \left( {\sqrt {\frac{\omega }{8}} {\Psi }} \right) + cot_{h\ell } \left( {\sqrt {\frac{\omega }{8}} {\Psi }} \right)} \right\}, $$

(20)

where ${tan}_{h{\ell}}\left( \Psi \right)=-i\frac{h{e}^{i\Psi }-{{\ell}e}^{-i\Psi }}{h{e}^{i\Psi }+{{\ell}e}^{-i\Psi }}$ and ${cot}_{h{\ell}}\left( \Psi \right)=i\frac{h{e}^{i\Psi }+{{\ell}e}^{-i\Psi }}{h{e}^{i\Psi }-{{\ell}e}^{-i\Psi }}$.

Next, we advance to the subsequent stages to derive exact solutions for the NLEs:

Stage 1: The homogeneous balance method is applied in order to determine the balance number P. Using this strategy, the equation’s highest-order derivative term and highest-degree nonlinear term are balanced.

Stage 2: The left side of Eq. (4) is converted into a polynomial that contains the terms $\mathcal{H}$ by changing the value of P in Eq. (5) and then adding that modified equation into Eq. (4) and using Eq. (6). When terms with matching powers inside the polynomial have their coefficients set to 0, an algebraic system of equations involving ${a}_{j}$, $\omega$, and other terms is established. The more details of this technique are given in the references (Ibrahim et al. 2023; Rezazadeh et al. 2020; Rehman et al. 2022; Cinar et al. 2022; Iqbal et al. 2023b).

3 Application of nonlinearities law

In this portion, we examined Eq. (1) by employing both Parabolic law nonlinearity and Power law nonlinearity.

3.1 Parabolic law

To explore Eq. (1) with Parabolic law nonlinearity, specifically when $\text{F}\left(\Pi \right)={\mathcal{B}}_{1}\Pi +{\mathcal{B}}_{2}{\Pi }^{2}$, the NLSE corresponding to Eq. (1) assumes the following form (Zhou et al. 2016; Biswas 2004):

$$i{\left\{\Upsilon\right\}}_{t}-\left\{\left({\beta }_{1}{\left|\Upsilon\right|}^{2}\right)+\left({\beta }_{2}{\left|\Upsilon\right|}^{4}\right)-W\right\}\Upsilon-{\mathbb{C}}\left\{{\left\{\Upsilon\right\}}_{xx}+{\left\{\Upsilon\right\}}_{yy}\right\}=0.$$

(21)

Upon substituting Eq. (3) into Eq. (21) and organizing the resulting expression, we derive the following equations from the imaginary and real components:

$$ \left( {\delta_{1} + \delta_{2} } \right)\left( {\vartheta - 2{\mathbb{C}}} \right)\Re^{\prime}\left( \Psi \right) = 0, $$

(22)

$$ and \left( {W - \delta_{1} + 2{\mathbb{C}}} \right)\Re \left( \Psi \right) - \beta_{1} \left( {\Re \left( \Psi \right)} \right)^{3} - \beta_{2} \left( {\Re \left( \Psi \right)} \right)^{5} - {\mathbb{C}}\left( {\delta_{1}^{2} + \delta_{2}^{2} } \right)\Re^{\prime\prime}\left( \Psi \right) = 0. $$

(23)

As $\mathfrak{R}\left(\Psi \right)$ is non-zero and possesses second-order derivatives, Eq. (22) yields the following constraint on the velocity:

$$\vartheta =2\left({\delta }_{1}+{\delta }_{2}\right){\mathbb{C}}.$$

(24)

Thus, Eq. (23) represents the NODE (Nonlinear Ordinary Differential Equation) form of Eq. (21) with Parabolic law nonlinearity, subject to the constraint specified in Eq. (24).

3.2 Power law

To investigate Eq. (1) with power law nonlinearity, particularly when $\text{F}\left(\Pi \right)={\Pi }^{n}$, the NLSE associated with Eq. (1) takes the following form (Zhou et al. 2016; Biswas 2004):

$$ i\left\{ \Upsilon \right\}_{t} - \left\{ {\left( {\beta \left| \Upsilon \right|^{2n} } \right) - W} \right\}\Upsilon - {\mathbb{C}}\left\{ {\left\{ \Upsilon \right\}_{xx} + \left\{ \Upsilon \right\}_{yy} } \right\} = 0. $$

(25)

Under this circumstance, for stability, it is necessary that $0<n<2$ (Zhou et al. 2016). Upon substituting Eq. (3) into Eq. (25) and arranging the resulting expression, the following equations are obtained:

$$ \left( {\delta_{1} + \delta_{2} } \right)\left( {\vartheta - 2{\mathbb{C}}} \right)\Re^{\prime}\left( \Psi \right) = 0, $$

(26)

$$ and \left( { - \beta \left( {\Re \left( \Psi \right)} \right)^{2n} + W - \delta_{1} + 2{\mathbb{C}}} \right)\Re \left( \Psi \right) - {\mathbb{C}}\left( {\delta_{1}^{2} + \delta_{2}^{2} } \right)\Re^{\prime\prime}\left( \Psi \right) = 0. $$

(27)

As $\mathfrak{R}\left(\Psi \right)$ is non-zero and possesses second-order derivatives, Eq. (26) yields the following constraint on the velocity:

$$\vartheta =2\left({\delta }_{1}+{\delta }_{2}\right){\mathbb{C}}.$$

(28)

Thus, Eq. (27) represents the NODE form of Eq. (25) with power law nonlinearity, subject to the constraint specified in Eq. (28).

4 Method’s application

Here, we use the procedure described in Sect. 2 to obtain the optical soliton solution for Eq. (1):

4.1 Parabolic law

Considering Eq. (5), (6), and (23) collectively, and employing the balancing principle, we get the balance number $P=1/2$, so it is essential to establish the following relationship:

$$\mathfrak{R}\left(\Psi \right)={{\rm X}\left(\Psi \right)}^\frac{1}{2}$$

(29)

Reorganizing Eq. (23) in accordance with Eq. (29) yields the following equation:

$$ \begin{aligned} & 4\left\{ {W - \delta_{1} + 2{\mathbb{C}} - \beta_{1} {\rm X}\left( \Psi \right) - \beta_{2} \left( {{\rm X}\left( \Psi \right)} \right)^{2} } \right\}\left( {{\rm X}\left( \Psi \right)} \right)^{2} \\ & \quad + {\mathbb{C}}\left( {\delta_{1}^{2} + \delta_{2}^{2} } \right)\left( {{\rm X}^{\prime}\left( \Psi \right)} \right)^{2} - 2{\mathbb{C}}\left( {\delta_{1}^{2} + \delta_{2}^{2} } \right){\rm X}\left( \Psi \right){\rm X}^{\prime\prime}\left( \Psi \right) = 0. \\ \end{aligned} $$

(30)

Reapplying the balance principle and acquiring $P=1$, so that, the solution takes on the following structure:

$${\rm X}\left(\Psi \right)={a}_{0}+{a}_{1}\mathcal{H}\left(\Psi \right).$$

(31)

In this equation, the constants ${a}_{0}$ and ${a}_{1}$ are coefficients that need to be figured out. When applying the discussed methodology, the resulting coefficients are as follows:

$$ a_{0} = - \frac{{3\beta_{1} }}{{8\beta_{2} }}\;and\;a_{1} = \pm \frac{{\sqrt 3 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{2\sqrt { - \beta_{2} } }},\;{\upomega } = \frac{{9\beta_{1}^{2} - 32 \delta_{1} \beta_{2} + 32W\beta_{2} + 64{\mathbb{C}}\beta_{2} }}{{8\left( {\delta_{1}^{2} + \delta_{2}^{2} } \right){\mathbb{C}}\beta_{2} }} $$

(32)

Utilizing Eqs. (3), (5), (29), (31), and (32), the solutions for Eq. (1) are derived as follows:

Scenario I. When $\upomega >0$ but $\epsilon = 0$ then

$$ {\Upsilon }_{1}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left[ { - \frac{{3\beta_{1} }}{{8\beta_{2} }} \pm \frac{{\sqrt 3 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{2\sqrt { - \beta_{2} } }}\sqrt {h\ell \omega } cosech_{h\ell } \left( {\sqrt \omega \Psi } \right)} \right]^{\frac{1}{2}} , $$

(33)

$$ {\Upsilon }_{2}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left[ { - \frac{{3\beta_{1} }}{{8\beta_{2} }} \pm \frac{{\sqrt 3 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{2\sqrt { - \beta_{2} } }}\sqrt { - h\ell \omega } sech_{h\ell } \left( {\sqrt \omega \Psi } \right)} \right]^{\frac{1}{2}} , $$

(34)

Scenario II. When ${\upomega } < 0$ but $\epsilon = 0$ then

$$ {\Upsilon }_{3}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left[ { - \frac{{3\beta_{1} }}{{8\beta_{2} }} \pm \frac{{\sqrt 3 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{2\sqrt { - \beta_{2} } }}\sqrt { - h\ell \omega } cosec_{h\ell } \left( {\sqrt { - \omega } \Psi } \right)} \right]^{\frac{1}{2}} , $$

(35)

$$ {\Upsilon }_{4}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left[ { - \frac{{3\beta_{1} }}{{8\beta_{2} }} \pm \frac{{\sqrt 3 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{2\sqrt { - \beta_{2} } }}\sqrt { - h\ell \omega } sec_{h\ell } \left( {\sqrt { - \omega } \Psi } \right)} \right]^{\frac{1}{2}} , $$

(36)

For scenarios (scenario I and scenario II) we have $\Psi ={\delta }_{1}x+{\delta }_{2}y+2\left({\delta }_{1}+{\delta }_{2}\right){\mathbb{C}}t$, ${\beta }_{2}<0$ and constrain condition, $15 {\beta }_{1}^{2}+64 {\beta }_{2}\left(2 c+w-{\delta }_{1}\right)=0.$

Scenario III. When $\upomega <0$ but $\epsilon = \frac{{\omega^{2} }}{4}$ then

$$ {\Upsilon }_{5}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left[ { - \frac{{3\beta_{1} }}{{8\beta_{2} }} \pm \frac{{\sqrt 3 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{2\sqrt { - \beta_{2} } }}\sqrt { - \frac{\omega }{2}} tanh_{h\ell } \left( {\sqrt { - \frac{\omega }{2}} \Psi } \right)} \right]^{\frac{1}{2}} , $$

(37)

$$ {\Upsilon }_{6}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left[ { - \frac{{3\beta_{1} }}{{8\beta_{2} }} \pm \frac{{\sqrt 3 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{2\sqrt { - \beta_{2} } }}\sqrt { - \frac{\omega }{2}} coth_{h\ell } \left( {\sqrt { - \frac{\omega }{2}} \Psi } \right)} \right]^{\frac{1}{2}} , $$

(38)

$$ \Upsilon_{7}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left( { - \frac{{3\beta_{1} }}{{8\beta_{2} }} \pm \frac{{\sqrt 3 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{2\sqrt { - \beta_{2} } }}} \right.\left. {\left[ {\sqrt { - \frac{\omega }{2}} \left\{ {\tanh_{h\ell } \left( {\sqrt { - 2\omega } \Psi } \right) \pm i\sqrt {h\ell } {\text{sech}}_{h\ell } \left( {\sqrt { - 2\omega } \Psi } \right)} \right\}} \right]} \right)^{\frac{1}{2}} , $$

(39)

$$ \Upsilon_{8}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left( { - \frac{{3\beta_{1} }}{{8\beta_{2} }} \pm \frac{{\sqrt 3 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{2\sqrt { - \beta_{2} } }}\left[ {\sqrt { - \frac{\omega }{2}} \left\{ {coth_{h\ell } \left( {\sqrt { - 2\omega } \Psi } \right) \pm \sqrt {h\ell } cosech_{h\ell } \left( {\sqrt { - 2\omega } \Psi } \right)} \right\}} \right]} \right)^{\frac{1}{2}} , $$

(40)

$$ \Upsilon_{9}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left( { - \frac{{3\beta_{1} }}{{8\beta_{2} }} \pm \frac{{\sqrt 3 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{2\sqrt { - \beta_{2} } }}\left[ {\sqrt { - \frac{\omega }{8}} \left\{ {tanh_{h\ell } \left( {\sqrt { - \frac{\omega }{8}} \Psi } \right) + coth_{h\ell } \left( {\sqrt { - \frac{\omega }{8}} \Psi } \right)} \right\}} \right]} \right)^{\frac{1}{2}} , $$

(41)

Scenario IV. When $\upomega >0$ but $\epsilon = \frac{{\omega^{2} }}{4}$ then

$$ {\Upsilon }_{10}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left\{ { - \frac{{3\beta_{1} }}{{8\beta_{2} }} \pm \frac{{\sqrt 3 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{2\sqrt { - \beta_{2} } }}\sqrt {\frac{\omega }{2}} tan_{h\ell } \left( {\sqrt {\frac{\omega }{2}} \Psi } \right)} \right\}^{\frac{1}{2}} , $$

(42)

$$ {\Upsilon }_{11}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left\{ { - \frac{{3\beta_{1} }}{{8\beta_{2} }} \pm \frac{{\sqrt 3 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{2\sqrt { - \beta_{2} } }}\sqrt {\frac{\omega }{2}} cot_{h\ell } \left( {\sqrt {\frac{\omega }{2}} \Psi } \right)} \right\}^{\frac{1}{2}} , $$

(43)

$$ {\Upsilon }_{12}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left\{ { - \frac{{3\beta_{1} }}{{8\beta_{2} }} \pm \frac{{\sqrt 3 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{2\sqrt { - \beta_{2} } }}\left[ {\sqrt {\frac{\omega }{2}} \left\{ {tan_{h\ell } \left( {\sqrt {2\omega } \Psi } \right) \pm \sqrt {h\ell } sec_{h\ell } \left( {\sqrt {2\omega } \Psi } \right)} \right\}} \right]} \right\}^{\frac{1}{2}} , $$

(44)

$$ \Upsilon_{13}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left\{ { - \frac{{3\beta_{1} }}{{8\beta_{2} }} \pm \frac{{\sqrt 3 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{2\sqrt { - \beta_{2} } }}\left[ {\sqrt {\frac{\omega }{2}} \left\{ {\cot_{h\ell } \left( {\sqrt {2\omega } \Psi } \right) \pm \sqrt {h\ell } \cos ech_{h\ell } \left( {\sqrt {2\omega } \Psi } \right)} \right\}} \right]} \right\}^{\frac{1}{2}} , $$

(45)

$$ \Upsilon_{14}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left\{ { - \frac{{3\beta_{1} }}{{8\beta_{2} }} \pm \frac{{\sqrt 3 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{2\sqrt { - \beta_{2} } }}\left[ {\sqrt {\frac{\omega }{8}} \left\{ {tan_{h\ell } \left( {\sqrt {\frac{\omega }{8}} \Psi } \right) + cot_{h\ell } \left( {\sqrt {\frac{\omega }{8}} \Psi } \right)} \right\}} \right]} \right\}^{\frac{1}{2}} . $$

(46)

For scenarios (scenario III and scenario IV) we have $\Psi ={\delta }_{1}x+{\delta }_{2}y+2\left({\delta }_{1}+{\delta }_{2}\right){\mathbb{C}}t$, ${\beta }_{2}<0$ and constrain condition, $3{\beta }_{1}^{2}+16 {\beta }_{2}\left(2 c+w-{\delta }_{1}\right)=0.$

4.2 Power law

Considering Eqs. (5), (6), and (27) collectively, and employing the balancing principle we obtain $P=1/n$, therefore, the following relation can be defined:

$$\mathfrak{R}\left(\Psi \right)={{\rm X}\left(\Psi \right)}^\frac{1}{n}$$

(47)

So, Eq. (27) transforms into the following form:

$$ \begin{aligned} & \left( {W - \delta_{1} + 2{\mathbb{C}}} \right)n^{2} \left( {{\rm X}\left( \Psi \right)} \right)^{2} - \beta n^{2} \left( {{\rm X}\left( \Psi \right)} \right)^{4} \\ & \quad + {\mathbb{C}}\left( {\delta_{1}^{2} + \delta_{2}^{2} } \right)\left( {n - 1} \right)\left( {{\rm X}^{\prime}\left( \Psi \right)} \right)^{2} - n{\mathbb{C}}\left( {\delta_{1}^{2} + \delta_{2}^{2} } \right){\rm X}\left( \Psi \right){\rm X}^{\prime\prime}\left( \Psi \right) = 0. \\ \end{aligned} $$

(48)

Once again applying the balance principle and obtaining $P=1$, the solution assumes the following structure:

$${\rm X}\left(\Psi \right)={a}_{0}+{a}_{1}\mathcal{H}\left(\Psi \right).$$

(49)

Now, the constants ${a}_{0}$ and ${a}_{1}$ are coefficients that need to be figured out. When applying the discussed method, the resulting coefficients are as follows:

$$ a_{0} = 0,\;and\;a_{1} = \pm \frac{{\sqrt 2 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{\sqrt { - \beta } }}\;{\text{where}}\;{\upomega } = \frac{{ - \delta_{1} + W + 2{\mathbb{C}}}}{{\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}}} $$

(50)

Operating Eqs. (3), (5), (47), (49) and (50), the solutions for Eq. (1) are obtained as follows:

Scenario I. When $\upomega >0$ but $\epsilon = 0$ then

$$ {\Upsilon }_{15}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left[ { \pm \frac{{\sqrt 2 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{\sqrt { - \beta } }}\sqrt {h\ell \omega } cosech_{h\ell } \left( {\sqrt \omega \Psi } \right)} \right]^{1/n} , $$

(51)

$$ {\Upsilon }_{16}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left[ { \pm \frac{{\sqrt 2 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{\sqrt { - \beta } }}\sqrt { - h\ell \omega } sech_{h\ell } \left( {\sqrt \omega \Psi } \right)} \right]^{\frac{1}{n}} , $$

(52)

Scenario II. When ${\upomega } < 0$ but $\epsilon = 0$ then

$$ {\Upsilon }_{17}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left[ { \pm \frac{{\sqrt 2 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{\sqrt { - \beta } }}\sqrt { - h\ell \omega } cosec_{h\ell } \left( {\sqrt { - \omega } \Psi } \right)} \right]^{\frac{1}{n}} , $$

(53)

$$ {\Upsilon }_{18}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left[ { \pm \frac{{\sqrt 2 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{\sqrt { - \beta } }}\sqrt { - h\ell \omega } sec_{h\ell } \left( {\sqrt { - \omega } \Psi } \right)} \right]^{\frac{1}{n}} , $$

(54)

Scenario III. When ${\upomega } < 0$ but $\epsilon = 0$ then

$$ {\Upsilon }_{19}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left[ { \pm \frac{{\sqrt 2 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{\sqrt { - \beta } }}\sqrt { - \frac{\omega }{2}} tanh_{h\ell } \left( {\sqrt { - \frac{\omega }{2}} \Psi } \right)} \right]^{\frac{1}{n}} , $$

(55)

$$ {\Upsilon }_{20}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left[ { \pm \frac{{\sqrt 2 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{\sqrt { - \beta } }}\sqrt { - \frac{\omega }{2}} coth_{h\ell } \left( {\sqrt { - \frac{\omega }{2}} \Psi } \right)} \right]^{\frac{1}{n}} , $$

(56)

$$ \Upsilon_{21}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left( { \pm \frac{{\sqrt 2 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{\sqrt { - \beta } }}\left[ {\sqrt { - \frac{\omega }{2}} \left\{ {tanh_{h\ell } \left( {\sqrt { - 2\omega } \Psi } \right) \pm i\sqrt {h\ell } sech_{h\ell } \left( {\sqrt { - 2\omega } \Psi } \right)} \right\}} \right]} \right)^{\frac{1}{n}} , $$

(57)

$$ \Upsilon_{22}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left( { \pm \frac{{\sqrt 2 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{\sqrt { - \beta } }}\left[ {\sqrt { - \frac{\omega }{2}} \left\{ {coth_{h\ell } \left( {\sqrt { - 2\omega } \Psi } \right) \pm \sqrt {h\ell } cosech_{h\ell } \left( {\sqrt { - 2\omega } \Psi } \right)} \right\}} \right]} \right)^{\frac{1}{n}} , $$

(58)

$$ \Upsilon_{23}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left( { \pm \frac{{\sqrt 2 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{\sqrt { - \beta } }}\left[ {\sqrt { - \frac{\omega }{8}} \left\{ {tanh_{h\ell } \left( {\sqrt { - \frac{\omega }{8}} \Psi } \right) + coth_{h\ell } \left( {\sqrt { - \frac{\omega }{8}} \Psi } \right)} \right\}} \right]} \right)^{\frac{1}{n}} , $$

(59)

Scenario IV. When $\upomega >0$ but $\epsilon = \frac{{\omega^{2} }}{4}$ then

$$ \Upsilon_{24}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left\{ { \pm \frac{{\sqrt 2 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{\sqrt { - \beta } }}\sqrt {\frac{\omega }{2}} tan_{h\ell } \left( {\sqrt {\frac{\omega }{2}} \Psi } \right)} \right\}^{\frac{1}{n}} , $$

(60)

$$ {\Upsilon }_{25}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left\{ { \pm \frac{{\sqrt 2 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{\sqrt { - \beta } }}\sqrt {\frac{\omega }{2}} cot_{h\ell } \left( {\sqrt {\frac{\omega }{2}} \Psi } \right)} \right\}^{\frac{1}{n}} , $$

(61)

$$ \Upsilon_{26}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left\{ { \pm \frac{{\sqrt 2 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{\sqrt { - \beta } }}\left[ {\sqrt {\frac{\omega }{2}} \left\{ {tan_{h\ell } \left( {\sqrt {2\omega } \Psi } \right) \pm \sqrt {h\ell } sec_{h\ell } \left( {\sqrt {2\omega } \Psi } \right)} \right\}} \right]} \right\}^{\frac{1}{n}} , $$

(62)

$$ \Upsilon_{27}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left\{ { \pm \frac{{\sqrt 2 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{\sqrt { - \beta } }}\left[ {\sqrt {\frac{\omega }{2}} \left\{ {cot_{h\ell } \left( {\sqrt {2\omega } \Psi } \right) \pm \sqrt {h\ell } cosech_{h\ell } \left( {\sqrt {2\omega } \Psi } \right)} \right\}} \right]} \right\}^{\frac{1}{n}} , $$

(63)

$$ \Upsilon_{28}^{ \pm } = e^{{i\left( {x + y + \sigma t + \zeta_{0} } \right)}} \left\{ { \pm \frac{{\sqrt 2 \sqrt {\delta_{1}^{2} {\mathbb{C}} + \delta_{2}^{2} {\mathbb{C}}} }}{{\sqrt { - \beta } }}\left[ {\sqrt {\frac{\omega }{8}} \left\{ {tan_{h\ell } \left( {\sqrt {\frac{\omega }{8}} \Psi } \right) + cot_{h\ell } \left( {\sqrt {\frac{\omega }{8}} \Psi } \right)} \right\}} \right]} \right\}^{\frac{1}{n}} , $$

(64)

For scenarios (scenario I, scenario II, scenario III, and scenario IV) we have, $\Psi ={\delta }_{1}x+{\delta }_{2}y+2\left({\delta }_{1}+{\delta }_{2}\right){\mathbb{C}}t$, n = 1, ${\beta }_{2}<0$.

Remark: We checked all extracted new solutions in our article by back substitution to the original PDEs via the Mathematica package program. We confirmed that all results are valid solutions of the Biswas–Milovic equation for both power and parabolic law.

5 Graphs and physical interpretations

Using the advanced mathematical computing program Mathematica, we were able to unravel the complex graphical patterns that the BME with power law nonlinearity and the BME with parabolic law nonlinearity displayed. We used a wide range of graphic aids in our presentation, including contour plots, 2D graphical displays, and 3D renderings. We were able to acquire a thorough grasp of the graphical behavior of these NLEs and shed light on their subtleties over a large range of parameter values for each relevant variable.

For each scenario, we chose four representative solution sets in order to keep things concise and clear (BME with parabolic law nonlinearity and BME with power law nonlinearity) from our extensive results for visual representation. For simplicity, we standardized only four graphs, including 3D, 2D, and contour plots out of 14 equations for each case. The relevant figure captions contain the specific constants related to each graph. By changing the parameter t in 2D graphs, we were able to integrate several solutions into a single figure.

5.1 Visualization of the BME with parabolic law nonlinearity

Figure 1 derived from Eq. (34); this figure effectively illustrates a bell-shaped wave patterns soliton solution. Here in (a) 3D visualization of the bell-shaped wave patterns soliton, (b) 2D plot illustrating variations over time, and (c) a contour representation of the bell-shaped wave patterns soliton. The advantages of bell-shaped soliton solutions in optical physics encompass their smooth energy distribution, mitigated dispersion effects, suitability for pulse compression, association with nonlinear effects, waveform stability, precision in imaging, relevance in optical signal processing, predictable interactions, and diminished intensity fluctuations. These attributes render bell-shaped solitons invaluable in a myriad of optical applications and technologies.

Fig. 1

Graphical representations of Eq. (34) for ${\mathbb{C}}=0.05, \omega =2.6, {\beta }_{1}=1.1,{\beta }_{2}=0.1 h=-0.3, l=0.1, { \delta }_{1}=0.1$ and ${\delta }_{2}=0.2$: a A 3D representation of bell-shape soliton b A 2D representation of bell-shape soliton and c Contour representation of bell-shape soliton

Figure 2, resulting from the application of Eq. (36), aptly demonstrates the solution’s parabolic shape. In a, a 3D visualization, b a 2D display showcasing variations of time, and c contour plot. In the realm of optical physics, these solutions characterized by parabolic profiles offer a versatile and valuable range of possibilities.

Fig. 2

Graphical representations of Eq. (36) for ${\mathbb{C}}=0.06, \omega =-0.1, {\beta }_{1}=.01, {\beta }_{2}=-1.09 h=0.3, l=0.1, { \delta }_{1}=0.1$ and ${\delta }_{2}=0.01$: a 3D parabolic representation b 2D parabolic representation and c Contour parabolic representation

They can be utilized for various technological advancements and applications in optics, encompassing optical fiber design, pulse compression, and the customization of spatial and temporal characteristics within optical fields, among other uses.

Figure 3, obtained through the utilization of Eq. (37), prominently showcases the distinctive soliton characterized by a kink shaped. In panel (a), a 3D representation, (b) offers a 2D representation and (c) exhibits a contour plot. The advantages of these kink solitons in optical physics would be rooted in their stability during propagation, predictable interaction properties, energy localization capabilities, and versatile applicability to various optical communication and signal processing applications.

Fig. 3

Graphical representations of Eq. (37) for ${\mathbb{C}}=0.41, \omega =-5.25, {\beta }_{1}=1.1, {\beta }_{2}=-0.9 h=0.3, l=0.1, { \delta }_{1}=0.1$ and ${\delta }_{2}=0.2$: a 3D kink shaped representation b 2D kink shaped representation and c Contour representation

Figure 4, obtained through the utilization of Eq. (45), illustrates singular soliton solutions characterized by a distinctive single-soliton structure: (a), a 3D singular representation, (b) provides a 2D plot, and (c) showcases a singular contour representation. Singular solitons in optics, as exemplified in Fig. 4, offer advantages in pulse shaping, optical switching, waveguide design, exploration of nonlinear optical effects, precision optics, wavefront control, optical amplification, and optical imaging. The unique characteristics of singular solitons make them valuable tools in a variety of optical applications and technologies.

Fig. 4

Graphical representations of Eq. (45) for ${\mathbb{C}}=0.05, \omega =5.5, {\beta }_{1}=0.1, {\beta }_{2}=-0.1 h=0.3, l=0.1, { \delta }_{1}=0.1$ and ${\delta }_{2}=0.2$: a 3D singular representation of soliton b 2D singular representation of soliton and c Contour singular representation of soliton

5.2 The Graphical representation of the BME with power law nonlinearity

Figure 5, obtained through the utilization of Eq. (52), vividly showcases dynamic solutions characterized by bright soliton. In (a), 3D representation, (b) offer 2D view of soliton, and (c) displays a contour representation. This graphical representation enables us to clearly identify the inherent periodic behavior within the bell-shaped wave patterns soliton solutions of the BME with parabolic law nonlinearity. The observation of bright soliton behavior is particularly significant as it reflects a delicate balance between nonlinear and dispersive effects, which inherently influence the focusing and spreading characteristics of the pulse.

Fig. 5

Graphical representations of Eq. (52) for ${\mathbb{C}}=0.5, \omega =0.44, \beta =-0.1, h=-3.3, l=0.1, n=1, { \delta }_{1}=0.81$ and ${\delta }_{2}=0.4$: a 3D representation of bright soliton b 2D representation of bright soliton and c Contour bright representation of soliton

Figure 6, obtained through the utilization of Eq. (53), prominently features soliton solutions characterized by a hyperbolic pattern with a regular singularity. In (a), 3D representation, (b) offers a 2D presentation and (c) displays a contour representation. The advantages of hyperbolic-shaped soliton solutions in optical physics, as illustrated in Fig. 6, encompass their ability to localize energy, provide propagation stability, associate with nonlinear effects, find applications in optical fiber design, exhibit predictable interactions with other solitons, offer precision in imaging, demonstrate suitability for optical signal processing, show reduced sensitivity to perturbations, and prove effective in pulse compression. These features establish hyperbolic-shaped solitons as valuable components in a range of optical applications and technologies.

Fig. 6

Graphical representations of Eq. (53) for ${\mathbb{C}}=0.5, \omega =-0.5, \beta =-3.1, h=0.3, l=0.1, n=1, { \delta }_{1}=-0.1$ and ${\delta }_{2}=0.1$: a 3D representation of hyperbolic solution b 2D representation of hyperbolic solution and c Contour representation of the hyperbolic solution

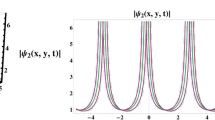
Figure 7 displays distinctive dark soliton solutions with a specific periodicity derived from Eq. (57). The 3D representation in (a) showcases their unique characteristics, while (b) offers a 2D view and (c), a contour representation further illustrates these soliton solutions. Dark solitons provide advantages like energy localization, association with specific nonlinear effects, propagation stability, applications in optical fiber design, controlled interaction with other solitons, suitability for optical switching, waveform stability, precision in imaging, and effectiveness in pulse compression. These features underscore the significance of dark solitons in diverse optical applications and technologies.

Fig. 7

Graphical representations of Eq. (57) for ${\mathbb{C}}=0.1, \omega =-0.7, \beta =0.1, h=-0.3, l=1, n=1, { \delta }_{1}=0.6$ and ${\delta }_{2}=0.1$: a 3D dark representation of soliton b 2D dark representation of soliton and c Contour dark representation of soliton

Figure 8, based on Eq. (63), reveals unique uniform singular soliton patterns. In (a), 3D representation showcases their characteristics, (b) provides a 2D view of temporal patterns, and (c) displays a contour representation. These solitons offer advantages like energy localization, propagation stability, predictable interactions, precision in optical switching, applications in waveguide design, exploration of nonlinear optical effects, imaging precision, reduced intensity fluctuations, and suitability for optical signal processing in optical physics.

Fig. 8

Graphical representations of Eq. (63) for ${\mathbb{C}}=0.01, \omega =0.5, \beta =-0.09, h=0.3, l=0.1, n=1, { \delta }_{1}=0.1$ and ${\delta }_{2}=-5.2$: a A 3D representation of uniform singular soliton b A 2D representation of uniform singular soliton and c Contour representation of uniform singular soliton

6 Conclusion

We applied the Sardar-subequation method, yielding numerous accurate optical soliton solutions for both parabolic and power law nonlinearities of BME. We used an analytical approach to generate several types of nonlinear wave patterns inside these nonlinearities, and different exact solutions in rational, hyperbolic, and trigonometric forms were revealed. Preciseness was guaranteed by rigorous validation using Mathematica software, and dynamic visual representations showed various patterns of soliton solutions, such as bell-shaped, parabolic-shaped, hyperbolic-shaped, and dark, bright, and singular soliton solutions. These optical soliton solutions offered advantages such as energy localization, propagation stability, predictable interactions, precision in optical switching, applications in waveguide design, exploration of nonlinear optical effects, imaging precision, reduced intensity fluctuations, and suitability for optical signal processing in optical physics. Our study’s demonstration of the flexibility of the Sardar subequation approach allowed us to investigate a wide range of optical soliton solutions. Crucially, in comparison to other methods, the optical soliton solutions obtained using this technology demonstrated its effectiveness, dependability, and ease of use. We hope that our current study will have a significant influence on contemporary optical phenomena.