1 Introduction

Advancements in nonlinear optics have given rise to a range of NLS equations with broader applicability. NLS equations naturally describe the propagation of pulses in optical fibers, making them a fundamental tool in optics research. The universal applicability of NLS equations extends their usefulness to a broad range of nonlinear physical systems in various domains, encompassing electrical engineering, mathematics, and optical physics (such as light transmission through optical fibers, chaos, and photonics) (Baskonus et al. 2021; Kumar et al. 2020). Among the myriad NLS equations, the resonant NLS equation has gained renown for its apt description of nonlinear optical phenomena, particularly in the realms of optical fibers and telecommunications. In the realm of optical fibers, the resonant NLS equation serves as a mathematical description for the journey of optical pulses through these systems, accommodating the influences of nonlinearity, dispersion, and various other factors. This equation takes the following form (Tozar et al. 2021; Zayed and Alurrfi 2016):

$${\mathrm{i\Upsilon}}_{t}+{p\Upsilon }_{xx}+\Upsilon \left({q\left|\Upsilon \right|}^{2}+s{\left|\Upsilon \right|}^{4}\right)+w\left(\frac{{\left|\Upsilon \right|}_{xx}}{\left|\Upsilon \right|}\right)\Upsilon =0, \quad {\text{i}}=\surd -1$$
(1)

In this equation \(p\), (\(q, s,\) \(w\)), and \(\Upsilon =\Upsilon (x,t)\), respectively symbolize the coefficient of dispersion, coefficients of nonlinearity, and the normalized complex amplitude of the pulse confined within the optical fiber.

Tozar et al. (2021) used the functional variable method to find a variety of soliton solutions with different structures for this model. In Zayed and Alurrfi (2016), the auxiliary equation method proposed by Sirendaoreji and Kudryashov is extended to construct new types of Jacobi elliptic function solutions for Eq. (1).

The resonant NLS equation, serving as a versatile model in the realm of optical physics, holds immense significance for understanding a wide spectrum of optical phenomena. It unravels the mysteries of wave transmission, the formation of optical solitons, and the intricate nonlinear behaviors observed within optical fibers and related media. Esteemed by scholars, this equation delves into the dynamic behavior of optical waves in diverse scenarios. It paves the way for innovative optical solitons, exploration of intricate optical wave interactions, and scrutiny of light pulse propagation in nonlinear optical materials. Researchers employ a blend of mathematical methodologies and numerical simulations to decode the secrets concealed within this equation, thus gaining profound insights into the intricate behavior of optical waves within complex optical systems.

Numerous scholars have developed a wide array of methodologies to extract precise solutions for NLS equations and other nonlinear evolution equations, employing techniques such as the Riccati equation method (Yomba 2005; Elsayed and Alurrfi 2015), Lie symmetries (Jafari et al. 2015; Hosseini et al. 2023a), the (\(\dot{G}/G\))-expansion technic (Mohanty et al. 2023; Naher and Abdullah 2012), the extended Jacobi elliptic function method (Hosseini et al. 2023b; Wen and Lü 2009), the (G′/G2)-expansion method (Rehman et al. 2022a), He's semi-inverse scheme (Mirzazadeh 2015), the new modified simple equation method (Irshad et al. 2017), the functional variable technic (Babajanov and Abdikarimov 2022; Bekir and San 2012), Homogeneous balance method (Wang et al. 1996; Fan and Zhang 1998), the fractional approach (Tandel et al. 2022), the new auxiliary equation method (Islam et al. 2023; Zhang 2013), the sine–Gordon expansion scheme (Kumar et al. 2022), the first integral method (Taghizadeh and Mirzazadeh 2011), the tanh–function method (Parkes and Duffy 1996; Fan 2000), the generalized (G'/G)-expansion technique (Kaur 2014), the tanh–coth method (Kumar and Pankaj 2015; Mamun et al. 2022), the generalized Kudryshov method (Habib et al. 2019; Islam et al. 2015), the exp(− φ(ξ))-expansion method (Roshid et al. 2014), the unified method (Fokas and Lenells 2012; Abdel-Gawad and Osman 2015), the first extended rational sinh-Gordon method (Rehman and Ahmad 2023), the Galilean transformation and its bifurcation analysis (Hosseini et al. 2023c), the modified rational sine–cosine and sinh-cosh methods (Rehman et al. 2023), and other different techniques (Akram et al. 2023; Islam et al. 2024; Ahmad et al. 2023; Rehman et al. 2022b; Boakye et al. 2024; Ma 2023; El-Sherif et al. 2005; Ma et al. 2010; Fetoh et al. 2019; Abdel-Gawad and Osman 2013; Ganie et al. 2024).

The double (\(\dot{{\varvec{G}}}/{\varvec{G}}\),\(1/{\varvec{G}}\))-expansion method is a highly valuable analytical technique used to solve nonlinear partial differential equations featuring variable coefficients. It relies on representing solutions as power series with coefficients figured out by two variables (G and 1/G), and it derives these coefficients by substituting the series into the equation and matching coefficients of like terms. This method finds extensive application in uncovering solitary and optical wave solutions within a range of NLS equations. A number of investigators (Iqbal et al. 2023; Chowdhury et al. 2023) have utilized this technique to reveal solutions for NLS equations. As of now, there has been no exploration of optical solutions for the resonant NLS equation using the double (\(\dot{{\varvec{G}}}/{\varvec{G}}\),\(1/{\varvec{G}}\))-expansion method. The aim of this research is to acquire optical soliton solutions for this nonlinear equation through the application of this method. The paper follows the following structure: (i) Sect. 2 elucidates the methodology employed. (ii) In Sect. 3, we apply the aforementioned method to the Resonant NLS equation and obtain the requisite solutions. (iii) Sect. 4 is dedicated to the exploration of dynamic representations, visually illustrating the captivating behaviors of various solitons using 2D, 3D, and contour graphs. (iv) Sect. 5 offers concluding remarks.

2 Methodology

Within this discussion, we provide a comprehensive overview of the essential steps required for the application of the (\(\dot{G}/G\),\(1/G\))-expansion method, a technique introduced by some researchers (Iqbal et al. 2023; Chowdhury et al. 2023), in the analysis of NLS equations. Indeed, facilitating this analytical process necessitates the introduction of an auxiliary linear ordinary differential equation. This auxiliary equation is meticulously formulated to complement the methodology, enabling a systematic exploration of nonlinear phenomena and their solutions, which is constructed as follows:

$$\ddot{G}\left(\varsigma \right)+\lambda G\left(\varsigma \right)=\beta$$
(2)

In the above equation, the sign ‘.’ stands for the differentiation as regards \(\varsigma\) in addition the variables agree like this:

$${\Phi } = \dot{G}\left( \varsigma \right)/G\left( \varsigma \right) \,{\text{and}}\,{\Psi } = 1/G\left( \varsigma \right)$$
(3)

Equation (3) satisfied the following relationships:

$$\dot{\Phi }={-\Phi }^{2}+\beta\Psi -\lambda \quad {\text{and}} \quad \dot{\Psi }=-\mathrm{\Phi \Psi }$$
(4)

It is worth noting that \(\Phi\) and \(\Psi\) are the functions of \(\varsigma .\)

The Eq. (2) mentioned above yields different results subject to the value of λ, which can be classified into three distinct scenarios:

Case I. If \(\lambda >0\) (positive values).

In this case, Eq. (2) yields the general solution (GS) as follows:

$$G\left( \varsigma \right) = C_{1} {\text{sin}}\left( {\varsigma \sqrt \lambda } \right) + C_{2} {\text{cos}}\left( {\varsigma \sqrt \lambda } \right) + \beta /\lambda$$
(5)
$$\mathrm{which\, produces}:{\Psi }^{2}=\left(\frac{{\Phi }^{2}-2\beta\Psi +\lambda }{{{\alpha }_{1}\lambda }^{2}-{\beta }^{2}}\right)\lambda$$
(6)

where \({\alpha }_{1}={C}_{1}^{2}+{C}_{2}^{2}\) stands for the arbitrary constants.

Case II. If \(\lambda <0\) (negative values)

In this consequence, Eq. (2) produces the GS in the following manner:

$$G\left(\varsigma \right)={C}_{1}s{\text{inh}}\left(\varsigma \sqrt{-\lambda }\right)+{C}_{2}{\text{cosh}}\left(\varsigma \sqrt{-\lambda }\right)+ \beta /\lambda$$
(7)

resulting in:

$${\Psi }^{2}=-\lambda \left(\frac{{\Phi }^{2}-2\beta\Psi +\lambda }{{{\alpha }_{2}\lambda }^{2}+{\beta }^{2}}\right), where {\alpha }_{2}={C}_{1}^{2}-{C}_{2}^{2}$$
(8)

Case III. If \(\lambda =0\)

Within this context, Eq. (2) produces the GS in the following manner:

$$G\left(\varsigma \right)=\frac{\beta {\varsigma }^{2}}{2}+{C}_{1}\varsigma +{C}_{2}$$
(9)
$$\mathrm{which delivers}: {\Psi }^{2}=\left(\frac{{\Phi }^{2}-2\beta\Psi }{{{C}_{1}}^{2}-2\beta {C}_{2}}\right)$$
(10)

Now, let's assume the general form of an NLS equation that encompasses three independent variables (x, y, and t) can be represented as:

$$\mathcal{H}\left(\Upsilon ,{\Upsilon }_{x},{\Upsilon }_{xx},{\Upsilon }_{y},{\Upsilon }_{yy},{\Upsilon }_{xy},{\Upsilon }_{t},{\Upsilon }_{tt},{\Upsilon }_{xt},\dots \dots \dots \right)=0$$
(11)

Within this context, \(\mathcal{H}\) represents a polynomial function that is contingent upon the variables encapsulated in \(\Upsilon\) and \({\Upsilon }_{x}=\frac{\partial\Upsilon }{\partial x}\), \({\Upsilon }_{y}=\frac{\partial\Upsilon }{\partial y}\), \({\Upsilon }_{t}=\frac{\partial\Upsilon }{\partial t}\), \({\Upsilon }_{xx}=\frac{{\partial }^{2}\Upsilon }{\partial {x}^{2}}\), \({\Upsilon }_{yy}=\frac{{\partial }^{2}\Upsilon }{\partial {y}^{2}}\), \({\Upsilon }_{tt}=\frac{{\partial }^{2}\Upsilon }{\partial {t}^{2}}\), \({\Upsilon }_{xt}=\frac{\partial\Upsilon }{\partial x\partial t}\), \({\Upsilon }_{xy}=\frac{\partial\Upsilon }{\partial x\partial y}\) and so on.

In order to transform Eq. (11), we introduce a new variable \(\varsigma\), which is governed by the following relations:

$${\Upsilon }\left( {x,t} \right) = e^{{i\chi \left( {x,t} \right)}} v\left( \varsigma \right),\chi \left( {x,t} \right) = \tau - kx + lt,\varsigma = \left( {x - at} \right)$$
(12)

where \(k\) is the wave number, \(\tau\) represents the constant and \(l\) is the wave frequency.

Equation (11), now converted into an ordinary differential equation which can be written as follows:

$$J\left(v,\dot{v},\ddot{v},\dddot{v},\dots \dots \dots \right)=0$$
(13)

Here, \(J\) represents the new polynomial that contains \(v\) with its ordinary derivatives.

Consider the following equation, which represents the GS of Eq. (13) utilizing the previously discussed method:

$$v\left(\varsigma \right)={a}_{0}+\sum_{i=1}^{M}{a}_{i}{\Phi }^{i}\left(\varsigma \right)+\sum_{i=1}^{M}{b}_{i}{\Phi }^{i-1}\left(\varsigma \right)\Psi \left(\varsigma \right)$$
(14)

In the above equation \({a}_{0}\), \({a}_{i}\) and \({b}_{i} (i=1, 2, 3, \dots \dots \dots , M)\) are the arbitrary constant fulfilling the requirement \({a}_{M}^{2}+{b}_{M}^{2}\ne 0\) and the parameter M is defined as a positive homogeneous balance number in this context. To figure out these arbitrary constants, we employ the previously mentioned method, following these phases:

Phase 1: To find the balance number M, the homogeneous balance method is employed. This method entails balancing the highest-order derivative and the nonlinear terms with the highest degree.

Phase 2: By inserting the value of M into Eq. (14) and subsequently substituting this modified equation into Eq. (13), while utilizing Eqs. (4) and (6) (illustrated through Case I as an example), the left-hand side of Eq. (13) is transformed into a polynomial that incorporates \(\Phi\) and \(\Psi\). In this polynomial, the degree associated with \(\Psi\) does not exceed 1, whereas the degree of \(\Phi\) ranges from 0 to any integer. Setting the coefficients of terms with matching powers within the polynomial to 0 leads to the establishment of a system of algebraic equations involving \({a}_{i}\), \({b}_{i}\), λ (when λ > 0), \(\beta\) and others.

Phase 3: Utilizing Mathematica software to solve the algebraic equations obtained in Step II, we determine the values of \({a}_{i},\) \({b}_{i}\), λ (where λ > 0), and \(\beta\). Subsequently, these values are substituted into the transformed Eq. (14), allowing us to derive the optical solutions represented by the trigonometric functions as described in Eq. (5). This comprehensive procedure ultimately yields the optical solution for Eq. (1), following the coordinate change outlined in Eq. (12).

Phase 4: Following a process similar to Steps II and III, we obtain the optical solutions for Eq. (13), particularly Eq. (11), which are represented as a combination of hyperbolic functions and rational functions.

3 Method’s application

In this part, we implement the aforementioned method outlined in Sect. 2 to acquire the optical solution of the resonant NLS equation.

Upon applying the transformation described in Eq. (12), Eq. (1) can be expressed as an ordinary differential equation after separating the real and imaginary components in the following manner:

Real part:

$$\left(p+w\right)\ddot{v}-\left(l+p{k}^{2}\right)v+{qv}^{3}+{sv}^{5}=0$$
(15)

Imaginary part:

$$a=-2kp$$
(16)

Operating the homogeneous balance technique, we find out the balance number M to be \(\frac{1}{2}\). However, since it is not an integer number, we introduce an additional transformation as follows:

$${\mathcal{F}}^\frac{1}{2}=v$$
(17)

Now, utilizing this transformation in Eq. (15), we obtain:

$$\left(p+w\right)\left(2\mathcal{F}\ddot{\mathcal{F}}-{\dot{\mathcal{F}}}^{2}\right)-4\left\{\left(l+p{k}^{2}\right){\mathcal{F}}^{2}-{q\mathcal{F}}^{3}-{s\mathcal{F}}^{4}\right\}=0$$
(18)

Once more, we apply the homogeneous balance law to Eq. (18), resulting in: \(M=1\) and the solution of Eq. (18) can be written as follows:

$$\mathcal{F}\left(\varsigma \right)={a}_{0}+{a}_{1}\Phi \left(\varsigma \right)+{b}_{1}\Psi \left(\varsigma \right)$$
(19)

In this equation, the constants \({a}_{0}\), \({a}_{1}\), and \({b}_{1}\) are coefficients that need to be figured out. We will now apply the three cases, as discussed in the methodology section.

Case I. \(\lambda >0\) (For trigonometric solutions).

To obtain the required solution, Eq. (19) is substituted into Eq. (18) and Eqs. (2) and (3) are applied, the left side of Eq. (18) is switched to a polynomial that encompasses \(\Phi\) and \(\Psi\). Setting each coefficient of this polynomial to zero leads to a system of algebraic equations involving the coefficients \({a}_{0}\), \({a}_{1}\), and \({b}_{1}\). The solution to these algebraic systems supplies the values for the arbitrary constants as results:

$${a}_{0}=0, { a}_{1}=0, q=\frac{4s\lambda \beta {b}_{1}}{3\sqrt{-{\beta }^{2}+{{\alpha }_{1}\lambda }^{2}}}, w=\frac{3p{\beta }^{2}-3p{{\alpha }_{1}\lambda }^{2}-4s\lambda {b}_{1}^{2}}{3\left({-\beta }^{2}+{{\alpha }_{1}\lambda }^{2}\right)} and l=\frac{3p{k}^{2}{\beta }^{2}-3p{k}^{2}{{\alpha }_{1}\lambda }^{2}+s{\lambda }^{2}{b}_{1}^{2}}{3\left({-\beta }^{2}+{{\alpha }_{1}\lambda }^{2}\right)}$$
(20)

Now, employing these computed values in Eq. (19), we obtain the following:

$$\mathcal{F}\left(\varsigma \right)={b}_{1}\frac{1}{{C}_{1}{\text{sin}}\left(\varsigma \sqrt{\lambda }\right)+{C}_{2}{\text{cos}}\left(\varsigma \sqrt{\lambda }\right)+ \beta /\lambda }$$
(21)

where \({b}_{1}\ne 0\).

By reverting Eq. (21) to its initial form with the assistance of Eq. (12) and Eq. (17), we obtain the following:

$$\Upsilon \left(x,t\right)={e}^{i\left\{\tau -kx+\left(\frac{3p{k}^{2}{\beta }^{2}-3p{k}^{2}{{\alpha }_{1}\lambda }^{2}+s{\lambda }^{2}{b}_{1}^{2}}{3\left({-\beta }^{2}+{{\alpha }_{1}\lambda }^{2}\right)}\right)t\right\}}{\left({b}_{1}\frac{1}{{C}_{1}{\text{sin}}\left((x-at)\sqrt{\lambda }\right)+{C}_{2}{\text{cos}}\left((x-at)\sqrt{\lambda }\right)+\beta/\lambda}\right)}^\frac{1}{2}$$
(22)

where \({b}_{1}\ne 0\).

If we set both \(\beta\) and \({C}_{2}\) to zero while ensuring \({C}_{1}\) is non-zero simplifies Eq. (22) to the solitary wave solution as:

$$\Upsilon \left(x,t\right)={e}^{i\left\{\tau -kx+\left(\frac{-3p{k}^{2}{C}_{1}^{2}+s{b}_{1}^{2}}{3{C}_{1}^{2}}\right)t\right\}}{\left(\frac{{b}_{1}}{{C}_{1}}{\text{cosec}}\left((x-at)\sqrt{\lambda }\right)\right)}^\frac{1}{2}$$
(23)

where \({b}_{1}\ne 0\).

Furthermore, if we set both \(\beta\) and \({C}_{1}\) to zero while ensuring that \({C}_{2}\) is non-zero, Eq. (22) simplifies to return the solitary wave solution as follows:

$$\Upsilon \left(x,t\right)={e}^{i\left\{\tau -kx+\left(\frac{-3p{k}^{2}{C}_{2}^{2}+s{b}_{1}^{2}}{3{C}_{2}^{2}}\right)t\right\}}{\left(\frac{{b}_{1}}{{C}_{2}}{\text{sec}}\left((x-at)\sqrt{\lambda }\right)\right)}^\frac{1}{2}$$
(24)

where \({b}_{1}\ne 0\).

Case II. \(\lambda <0\) (For hyperbolic solutions)

In this scenario, we follow a similar procedure that is described in case I to derive the necessary solution. We start the process by inserting Eq. (19) into Eq. (18) and implementing Eqs. (2) and (3). This series of operations results in the left side of Eq. (18) being converted into a polynomial that incorporates \(\Phi\) and \(\Psi\). Upon equating each coefficient of this polynomial to zero, we derive a system of algebraic equations involving the coefficients \({a}_{0}\), \({a}_{1}\),and \({b}_{1}\). The solution to these algebraic systems provides the values for the arbitrary constants as follows:

Set 1:

$$\begin{aligned} a_{0} & = - \frac{{\lambda b_{1} }}{{\sqrt {\beta^{2} + \alpha_{2} \lambda^{2} } }}, a_{1} = \pm \frac{{\sqrt { - \lambda } b_{1} }}{{\sqrt {\beta^{2} + \alpha_{2} \lambda^{2} } }}, q = \frac{{8s\lambda b_{1} }}{{3\sqrt {\beta^{2} + \alpha_{2} \lambda^{2} } }}, w = \frac{{ - 3p\beta^{2} - 3p\alpha_{2} \lambda^{2} + 16s\lambda b_{1}^{2} }}{{3\left( {\beta^{2} + \alpha_{2} \lambda^{2} } \right)}}\,{\text{and}} \\ l & = \frac{{ - 3pk^{2} \beta^{2} - 3pk^{2} \alpha_{2} \lambda^{2} - 4s\lambda^{2} b_{1}^{2} }}{{3\left( {\beta^{2} + \alpha_{2} \lambda^{2} } \right)}} \\ \end{aligned}$$
(25)

By incorporating these values into Eq. (19), we arrive at the solution in the following manner:

$$\mathcal{F}\left(\varsigma \right)=-\frac{\lambda {b}_{1}}{\sqrt{{\beta }^{2}+{{\alpha }_{2}\lambda }^{2}}}\pm \frac{\sqrt{-\lambda }{b}_{1}}{\sqrt{{\beta }^{2}+{{\alpha }_{2}\lambda }^{2}}}\sqrt{-\lambda }\frac{\left({C}_{1}{\text{cosh}}\left(\varsigma \sqrt{-\lambda }\right)+{C}_{2}{\text{sinh}}\left(\varsigma \sqrt{-\lambda }\right)\right)}{{C}_{1}{\text{sinh}}\left(\varsigma \sqrt{-\lambda }\right)+{C}_{2}{\text{cosh}}\left(\varsigma \sqrt{-\lambda }\right)+\beta/\lambda}+{b}_{1}\frac{1}{{C}_{1}{\text{sinh}}\left(\varsigma \sqrt{-\lambda }\right)+{C}_{2}{\text{cosh}}\left(\varsigma \sqrt{-\lambda }\right)+\beta/\lambda}$$
(26)

where \({b}_{1}\ne 0\).

By substituting the transformation variables outlined in Eq. (12) into this equation, it is transformed into the following GS form:

$$\Upsilon \left(x,t\right)={e}^{i\left\{\tau -kx+\left(\frac{-3p{k}^{2}{\beta }^{2}-3p{k}^{2}{{\alpha }_{2}\lambda }^{2}-4s{\lambda }^{2}{b}_{1}^{2}}{3\left({\beta }^{2}+{{\alpha }_{2}\lambda }^{2}\right)}\right)t\right\}}{\left(-\frac{\lambda {b}_{1}}{\sqrt{{\beta }^{2}+{{\alpha }_{2}\lambda }^{2}}}\pm \frac{\sqrt{-\lambda }{b}_{1}}{\sqrt{{\beta }^{2}+{{\alpha }_{2}\lambda }^{2}}}\sqrt{-\lambda }\frac{{C}_{1}{\text{cosh}}\left((x-at)\sqrt{-\lambda }\right)+{C}_{2}{\text{sinh}}\left((x-at)\sqrt{-\lambda }\right)}{{C}_{1}{\text{sinh}}\left((x-at)\sqrt{-\lambda }\right)+{C}_{2}{\text{cosh}}\left((x-at)\sqrt{-\lambda }\right)+\beta/\lambda}{+b}_{1}\frac{1}{{C}_{1}{\text{sinh}}\left((x-at)\sqrt{-\lambda }\right)+{C}_{2}{\text{cosh}}\left((x-at)\sqrt{-\lambda }\right)+\beta/\lambda}\right)}^\frac{1}{2}$$
(27)

Where \({b}_{1}\ne 0\).

When both \(\beta\) and \({C}_{2}\) are set to zero, with the condition that \({C}_{1}\) is non-zero, Eq. (27) simplifies to supply the solitary wave solution as follows:

$$\Upsilon \left(x,t\right)={e}^{i\left\{\tau -kx+\left(\frac{-3p{k}^{2}{C}_{1}^{2}-4s{b}_{1}^{2}}{3{C}_{1}^{2}}\right)t\right\}}{\left(-\frac{{b}_{1}}{{C}_{1}}\pm \frac{{b}_{1}}{{C}_{1}}{\text{coth}}\left((x-at)\sqrt{-\lambda }\right)+\frac{{b}_{1}}{{C}_{1}}{\text{cosech}}\left((x-at)\sqrt{-\lambda }\right)\right)}^\frac{1}{2}$$
(28)

Where \({b}_{1}\ne 0\).

Set 2:

$$\begin{aligned} a_{0} & = \frac{{\lambda b_{1} }}{{\sqrt {\beta^{2} + \alpha_{2} \lambda^{2} } }}, a_{1} = \pm \frac{{\sqrt { - \lambda } b_{1} }}{{\sqrt {\beta^{2} + \alpha_{2} \lambda^{2} } }}, q = - \frac{{8s\lambda b_{1} }}{{3\sqrt {\beta^{2} + \alpha_{2} \lambda^{2} } }}, w = \frac{{ - 3p\beta^{2} - 3p\alpha_{2} \lambda^{2} + 16s\lambda b_{1}^{2} }}{{3\left( {\beta^{2} + \alpha_{2} \lambda^{2} } \right)}}\,{\text{and}} \\ l & = \frac{{ - 3pk^{2} \beta^{2} - 3pk^{2} \alpha_{2} \lambda^{2} - 4s\lambda^{2} b_{1}^{2} }}{{3\left( {\beta^{2} + \alpha_{2} \lambda^{2} } \right)}} \\ \end{aligned}$$
(29)

Incorporating these determined values into Eq. (19), we arrive at the solution in the following manner:

$$\mathcal{F}\left(\varsigma \right)=\frac{\lambda {b}_{1}}{\sqrt{{\beta }^{2}+{{\alpha }_{2}\lambda }^{2}}}\pm \frac{\sqrt{-\lambda }{b}_{1}}{\sqrt{{\beta }^{2}+{{\alpha }_{2}\lambda }^{2}}}\sqrt{-\lambda }\frac{\left({C}_{1}{\text{cosh}}\left(\varsigma \sqrt{-\lambda }\right)+{C}_{2}{\text{sinh}}\left(\varsigma \sqrt{-\lambda }\right)\right)}{{C}_{1}{\text{sinh}}\left(\varsigma \sqrt{-\lambda }\right)+{C}_{2}{\text{cosh}}\left(\varsigma \sqrt{-\lambda }\right)+\beta/\lambda}+{b}_{1}\frac{1}{{C}_{1}{\text{sinh}}\left(\varsigma \sqrt{-\lambda }\right)+{C}_{2}{\text{cosh}}\left(\varsigma \sqrt{-\lambda }\right)+\beta/\lambda}$$
(30)

where \({b}_{1}\ne 0\).

Upon substituting the transformation variables as defined in Eq. (12) into this equation, it transforms into the following generalized solution form:

$$\Upsilon \left(x,t\right)={e}^{i\left\{\tau -kx+\left(\frac{-3p{k}^{2}{\beta }^{2}-3p{k}^{2}{{\alpha }_{2}\lambda }^{2}-4s{\lambda }^{2}{b}_{1}^{2}}{3\left({\beta }^{2}+{{\alpha }_{2}\lambda }^{2}\right)}\right)t\right\}}{\left(\frac{\lambda {b}_{1}}{\sqrt{{\beta }^{2}+{{\alpha }_{2}\lambda }^{2}}}\pm \frac{\sqrt{-\lambda }{b}_{1}}{\sqrt{{\beta }^{2}+{{\alpha }_{2}\lambda }^{2}}}\sqrt{-\lambda }\frac{{C}_{1}{\text{cosh}}\left((x-at)\sqrt{-\lambda }\right)+{C}_{2}{\text{sinh}}\left((x-at)\sqrt{-\lambda }\right)}{{C}_{1}{\text{sinh}}\left((x-at)\sqrt{-\lambda }\right)+{C}_{2}{\text{cosh}}\left((x-at)\sqrt{-\lambda }\right)+\beta/\lambda}{+b}_{1}\frac{1}{{C}_{1}{\text{sinh}}\left((x-at)\sqrt{-\lambda }\right)+{C}_{2}{\text{cosh}}\left((x-at)\sqrt{-\lambda }\right)+\beta/\lambda}\right)}^\frac{1}{2}$$
(31)

Where \(b_{1} \ne 0\).

If both \(\beta\) and \(C_{2}\) are set to zero, with the condition that \(C_{1}\) is non-zero, Eq. (31) simplifies to supply the solitary wave solution as follows:

$${\Upsilon }\left( {x,t} \right) = e^{{i\left\{ {\tau - kx + \left( {\frac{{ - 3pk^{2} C_{1}^{2} - 4sb_{1}^{2} }}{{3C_{1}^{2} }}} \right)t} \right\}}} \left( {\frac{{b_{1} }}{{C_{1} }} \pm \frac{{b_{1} }}{{C_{1} }}{\text{coth}}\left( {\left( {x - at} \right)\sqrt { - \lambda } } \right) + \frac{{b_{1} }}{{C_{1} }}{\text{cosech}}\left( {\left( {x - at} \right)\sqrt { - \lambda } } \right)} \right)^{\frac{1}{2}}$$
(32)

where \(b_{1} \ne 0\).

Set 3:

$$\begin{aligned} a_{0} & = 0, a_{1} = 0, q = \frac{{4s\lambda \beta b_{1} }}{{3\sqrt {\beta^{2} + \alpha_{2} \lambda^{2} } }}, w = \frac{{ - 3p\beta^{2} - 3p\alpha_{2} \lambda^{2} + 4s\lambda b_{1}^{2} }}{{3\left( {\beta^{2} + \alpha_{2} \lambda^{2} } \right)}}\,{\text{and}} \\ l & = \frac{{ - 3pk^{2} \beta^{2} - 3pk^{2} \alpha_{2} \lambda^{2} - s\lambda^{2} b_{1}^{2} }}{{3\left( {\beta^{2} + \alpha_{2} \lambda^{2} } \right)}} \\ \end{aligned}$$
(33)

Utilizing these computed values in Eq. (19), the solution can be expressed as follows:

$${\mathcal{F}}\left( \varsigma \right) = b_{1} \frac{1}{{C_{1} {\text{sinh}}\left( {\varsigma \sqrt { - \lambda } } \right) + C_{2} {\text{cosh}}\left( {\varsigma \sqrt { - \lambda } } \right) + {\raise0.7ex\hbox{$\beta $} \!\mathord{\left/ {\vphantom {\beta \lambda }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\lambda $}}}}$$
(34)

where \(b_{1} \ne 0\).

Reverting Eq. (34) to its original form with the assistance of Eq. (12) and Eq. (17), we arrive at the following:

$${\Upsilon }\left( {x,t} \right) = e^{{i\left\{ {\tau - kx + \left( {\frac{{ - 3pk^{2} \beta^{2} - 3pk^{2} \alpha_{2} \lambda^{2} - s\lambda^{2} b_{1}^{2} }}{{3\left( {\beta^{2} + \alpha_{2} \lambda^{2} } \right)}}} \right)t} \right\}}} \left( {b_{1} \frac{1}{{C_{1} {\text{sinh}}\left( {\left( {x - at} \right)\sqrt { - \lambda } } \right) + C_{2} {\text{cosh}}\left( {\left( {x - at} \right)\sqrt { - \lambda } } \right) + {\raise0.7ex\hbox{$\beta $} \!\mathord{\left/ {\vphantom {\beta \lambda }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\lambda $}}}}} \right)^{\frac{1}{2}}$$
(35)

where \(b_{1} \ne 0\).

When \(\beta\) and \(C_{2}\) to zero while ensuring \(C_{1}\) is non-zero shortens Eq. (35) to the solitary wave solution as follows:

$${\Upsilon }\left( {x,t} \right) = e^{{i\left\{ {\tau - kx + \left( {\frac{{ - 3pk^{2} C_{1}^{2} - sb_{1}^{2} }}{{3C_{1}^{2} }}} \right)t} \right\}}} \left( {\frac{{b_{1} }}{{C_{1} }}{\text{cosech}}\left( {\left( {x - at} \right)\sqrt { - \lambda } } \right)} \right)^{\frac{1}{2}}$$
(36)

where \(b_{1} \ne 0\).

Furthermore, when we set both \(\beta\) and \(C_{1}\) to zero while ensuring that \(C_{2}\) is non-zero, Eq. (35) simplifies to return the solitary wave solution as follows:

$${\Upsilon }\left( {x,t} \right) = e^{{i\left\{ {\tau - kx + \left( {\frac{{ - 3pk^{2} C_{2}^{2} + sb_{1}^{2} }}{{3C_{2}^{2} }}} \right)t} \right\}}} \left( {\frac{{b_{1} }}{{C_{2} }}{\text{sech}}\left( {\left( {x - at} \right)\sqrt \lambda } \right)} \right)^{\frac{1}{2}}$$
(37)

where \(b_{1} \ne 0\).

Case III. \(\lambda = 0\) (For rational solutions)

In this instance, we follow a procedure like the one expressed in cases I and II to obtain the required solution. The process begins with the substitution of Eq. (19) into Eq. (18) and the application of Eqs. (2) and (3). This manipulation converts the left side of Eq. (18) into a polynomial containing \({\Phi }\) and \({\Psi }\). By equating each coefficient of this polynomial to zero, we set up a system of algebraic equations that involve the constants \(a_{0}\), \(a_{1}\) and \(b_{1}\). The solution to these algebraic systems furnishes the values for the arbitrary constants as follows:

Set 1:

$$\begin{aligned} a_{0} & = \frac{{2\beta b_{1} }}{{C_{1}^{2} - 2\beta C_{2} }}, a_{1} = 0, q = \frac{{4s\beta b_{1} }}{{ - C_{1}^{2} + 2\beta C_{2} }}, w = \frac{{ - 3pC_{1}^{2} + 6p\beta C_{2} - 4sb_{1}^{2} }}{{3\left( {C_{1}^{2} - 2\beta C_{2} } \right)}}\,and \\ l & = \frac{{ - pk^{2} C_{1}^{4} + 4pk^{2} \beta C_{1}^{2} C_{2} - 4pk^{2} \beta^{2} C_{2}^{2} - 4s\beta^{2} b_{1}^{2} }}{{\left( {C_{1}^{2} - 2\beta C_{2} } \right)^{2} }} \\ \end{aligned}$$
(38)

Incorporating these values into Eq. (19), we obtain the solution as follows:

$${\mathcal{F}}\left( \varsigma \right) = \frac{{2\beta b_{1} }}{{C_{1}^{2} - 2\beta C_{2} }} + b_{1} \frac{1}{{\frac{\beta }{2}\varsigma^{2} + C_{1} \varsigma + C_{2} }}$$
(39)

where \(b_{1} \ne 0\).

Substituting the transformation variables defined in Eq. (12) into the above equation yields the following generalized solution form:

$${\Upsilon }\left( {x,t} \right) = e^{{i\left\{ {\tau - kx + \left( {\frac{{ - pk^{2} C_{1}^{4} + 4pk^{2} \beta C_{1}^{2} C_{2} - 4pk^{2} \beta^{2} C_{2}^{2} - 4s\beta^{2} b_{1}^{2} }}{{\left( {C_{1}^{2} - 2\beta C_{2} } \right)^{2} }}} \right)t} \right\}}} \left( {\frac{{2\beta b_{1} }}{{C_{1}^{2} - 2\beta C_{2} }} + b_{1} \frac{1}{{\frac{\beta }{2}\left( {x - at} \right)^{2} + C_{1} \left( {x - at} \right) + C_{2} }}} \right)^{\frac{1}{2}}$$
(40)

where \(b_{1} \ne 0\).

If both \(\beta\) and \(C_{2}\) are set to zero, with the condition that \(C_{1}\) is non-zero, Eq. (40) simplifies to supply the solitary wave solution as follows:

$${\Upsilon }\left( {x,t} \right) = e^{{i\left\{ {\tau - kx - pk^{2} t} \right\}}} \left( {\frac{{b_{1} }}{{C_{1} }}\frac{1}{{\left( {x - at} \right)}}} \right)^{\frac{1}{2}}$$
(41)

where \(b_{1} \ne 0\).

Set 2:

$$a_{0} = 0, a_{1} = 0, q = \frac{{4s\beta b_{1} }}{{4(C_{1}^{2} - 2\beta C_{2} )}}, w = \frac{{ - 3pC_{1}^{2} + 6p\beta C_{2} - 4sb_{1}^{2} }}{{3\left( {C_{1}^{2} - 2\beta C_{2} } \right)}}\,{\text{and}}\,l = - pk^{2}$$
(42)

Incorporating these values into Eq. (19), we obtain the solution as follows:

$${\mathcal{F}}\left( \varsigma \right) = \frac{{b_{1} }}{{\frac{\beta }{2}\varsigma^{2} + C_{1} \varsigma + C_{2} }}$$
(43)

where \(b_{1} \ne 0\).

When the transformation variables defined in Eq. (12) are substituted into the equation mentioned above, it results in the following generalized solution form:

$${\Upsilon }\left( {x,t} \right) = e^{{i\left\{ {\tau - kx - pk^{2} t} \right\}}} \left( {\frac{{b_{1} }}{{\frac{\beta }{2}\left( {x - at} \right)^{2} + C_{1} \left( {x - at} \right) + C_{2} }}} \right)^{\frac{1}{2}}$$
(44)

where \(b_{1} \ne 0\).

4 Graphs and their associated physical interpretations

In this section, we employed Mathematica, a modern mathematical computational tool, to reveal unique graphical patterns displayed by the resonant NLS equation. Our presentation featured a diverse set of visual representations, including 3D renderings, 2D graphical displays, and contour plots. These graphics spanned a broad spectrum of parameter values for each relevant variable. The goal was to provide a comprehensive insight into the graphical behavior of the resonant NLS equation, elucidating its intricacies across a diverse parameter space.

In the interest of clarity and brevity, we have chosen to visually depict a limited selection of five solution sets from our comprehensive results. To keep simplicity, we have standardized the x-axis (− 10 to 10) for all the graphs. The constants specific to each graph are provided in the corresponding figure captions. In 2-D graphs, we have consolidated multiple solutions within a single figure by varying the parameter t.

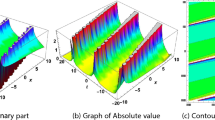
Figure 1 is obtained from Eq. (22), effectively illustrates the multi-periodic soliton solution. In (a), we provide a 3D visualization of these solutions, (b) offers a 2D display with time variations, and (c) features a contour representation of the solution. This graphical depiction allows us to discern the recurring and bell-shaped patterns that define these solutions, offering a visual understanding of the unique characteristics of the Resonant NLS equation.

Fig. 1
figure 1

Graphical representations of the solutions \(\left| {{\Upsilon }\left( {x,t} \right)} \right|\) of Eq. (22) for \(b_{1} = - .2, \lambda = .1, a = - 3.3, C_{1} = - .2, C_{2} = 0.1,\) and \(\beta = 1\): (a) A 3D representation (b) A 2D representation and (c) Contour representation

Full size image

It is evident that the behavior of the derived solutions, including the amplitude and width of the solitary wave, was unaffected by the nonlinear parameters.

Figure 2, is found from Eq. (23), effectively illustrates a specific solution derived from Eq. (22), prominently displaying its singular multi-periodic characteristics. In (a), we offer a 3D visualization of these solutions; (b) provides a 2D display showcasing time variations, and (c) includes a contour representation of the solution. This graphical representation enables us to clearly identify the periodic behavior inherent in the solutions within the context of the Resonant NLS equation.

Fig. 2
figure 2

Graphical representations of the solutions \(\left| {{\Upsilon }\left( {x,t} \right)} \right|\) of Eq. (23) for \(b_{1} = .2, \lambda = .2, a = 2.3,\) and \(C_{1} = .9\): (a) A 3D representation (b) A 2D representation and (c) Contour representation

Full size image

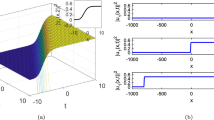
Figure 3, derived from Eq. (31), prominently highlights singular soliton features characterized by a semi-bell-shaped behavior. In (a), a 3D representation of these solutions is provided, while (b) offers a 2D view with time variations, and (c) showcases a contour representation of the solution. This graphical representation affords a clear visualization of the distinctive behavior inherent in the solutions of the Resonant NLS equation.

Fig. 3
figure 3

Graphical representations of the solutions of Eq. (31) for and: (a) A 3D representation (b) A 2D representation and (c) Contour representation

Full size image

It is evident that the graph's structure in Figs. 2 and 3 is made up of singular-periodic solutions. We claim that a singular wave solution is essential for studying many physical phenomena. For instance, a singular wave is formed when a sudden force is applied, such an earthquake that might generate a disastrous tsunami wave. Moreover, a sudden temperature shock might also result in a thermal tsunami for a porous medium.

Figure 4, obtained from Eq. (36), illustrates a specific solution derived from Eq. (35), emphasizing a bright soliton solution with a half-bell-shaped structure within the singular soliton. In (a), a 3D representation of these solutions is displayed, while (b) presents a 2D view with time variations, and (c) showcases a contour representation of the solution. This graphical depiction offers a clear visualization of the unique bright soliton solution with a half-bell-shaped structure inherent in the solutions of the Resonant NLS equation.

Fig. 4
figure 4

Graphical representations of the solutions of Eq. (36) for and: (a) A 3D representation (b) A 2D representation and (c) Contour representation

Full size image

Figure 5, derived from Eq. (37), which is a particular solution of Eq. (35), prominently showcases bright soliton solutions characterized by a specific periodicity and bell-shaped profiles. In (a), a 3D representation of these solutions is presented, while (b) offers a 2D view displaying varying time patterns, and (c) showcases a contour representation of the solution. This graphical depiction provides a clear visualization of the distinct bright soliton solutions with bell-shaped profiles inherent in the solutions of the Resonant NLS equation.

Fig. 5
figure 5

Graphical representations of the solutions of Eq. (37) for and: (a) A 3D representation (b) A 2D representation and (c) Contour representation

Full size image

It is evident that the behavior of the derived solutions, including the amplitude and width of the solitary wave, was unaffected by the nonlinear parameters.

By contrasting the results we obtained in this paper with the well-known results from Tozar et al. (2021) and Zayed and Alurrfi (2016), we can conclude that while the other solutions in the paper are new and unpublished, our results (36) and (37) are equivalent to the solutions \(W_{13,14} {\text{and}} W_{15,16}\) in Tozar et al. (2021), respectively. While our results (23), (24), and (37) are equivalent to the solutions (3.44), (3.47), and (3.54) obtained in Zayed and Alurrfi (2016), respectively.

5 Conclusion

The double (\(\dot{G}/G\),\(1/G\))-expansion method is investigated to get numerous precise optical solutions for the resonant NLS equation. This equation is essential to understanding the dynamics of optical soliton in optical fiber theory. By constructing several nonlinear wave structures inside this equation, new traveling pulse responses are obtained. Flexible forms are created that include rational, hyperbolic, and trigonometric functions. A range of behaviors are examined, including brilliant solitons, single solitons, singular and multiperiodic patterns, and semi-bell-shaped structures. These optical solutions, characterized by varying parameter values, hold substantial promise for advancing the field of optical physics, impacting both light and electron optics. The versatility of the double (\(\dot{G}/G\),\(1/G\))-expansion method that employed in our study empowered us to explore a diverse spectrum of optical solutions. Significantly, the optical soliton solutions derived through this method underscore its efficacy, reliability, and simplicity when contrasted with alternative techniques. In the near future, this model will be discussed by other different techniques when its coefficients are not constants.