1 Introduction

In recent years, the nonlinear evolution equations (NLEEs) have attracted an increasingly attention from mathematics and physicists. It is well known that the research of nonlinear physics phenomena is a very interesting topic. NLEEs can display many interesting nonlinear dynamic behaviors, such as plasma physics, optical fibers, chaos theory, hydrodynamics and other nonlinear fields. The properties corresponding to NLEEs are flourishing, including integrability, dispersion effects, solitary wave solutions, bilinear expressions, periodic wave solutions. There are many works for the NLEEs in this field [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15].

A variety of straightforward methods can be used to solve the NLEEs. For instance, inverse scattering transformation (IST) [16], Darboux transformation (DT) [17], Hirota’s bilinear method (HBM) [18], Lie group symmetry (LGS) [19, 20], multiple exp-function method [21], etc.

As we know that the most classic Kadomtsev–Petviashvili (KP)-type equation [22] reads

$$\begin{aligned} (u_{t}+6uu_{x}+u_{3x})_{x}+3u_{yy}=0, \end{aligned}$$
(1)

which can characterize the growth of shallow water waves in quasi one-dimension, with the weak influence of surface tension and viscosity. There are many KP-type equations. For example, a \((3+1)\)-dimensional B-type KP equation (BKP) [23] is presented by

$$\begin{aligned} u_{ty}-u_{xxxy}-3(u_{x}u_{y})_{x}+3u_{xz}=0. \end{aligned}$$
(2)

When \(y=z\), it can be read the \((2+1)\)-dimensional BKP equation, which has a great influence in both the phase shift and the dispersion connection of each extended nonlinear evolution equation. There are many works to study the multiple wave solutions and lump solutions, Bäcklund transformation and shock wave type solutions for such kind of equations [24,25,26,27,28,29,30].

In this work, we mainly study a \((3+1)\)-dimensional BKP–Boussinesq equation [31] given by

$$\begin{aligned} u_{ty}-u_{xxxy}-3(u_{x}u_{y})_{x}+u_{tt}+3u_{xz}=0, \end{aligned}$$
(3)

where u is a differential function about x, y, z and t. It is easy to find that the \((3+1)\)-dimensional BKP–Boussinesq equation denotes the \((3+1)\)-dimensional BKP equation plus a partial derivative of u with respect to t, i.e. \(u_{tt}\). The equation is proposed by Wazwaz and El-Tantawy [31]. This equation possesses the properties of both Boussinesq and BKP equations, which can be used to depict the propagation of long waves in shallow water. It also describes other waves, such as nonlinear lattice waves, iron sound waves in a plasma. Furthermore, it has many applications in physical field, such as the percolation of water in porous subsurface of a horizontal layer of material. Actually, BKP–Boussinesq equation plays an important role in describing the processes of interaction of exponentially localized structures. A bilinear representation belong to the equation is presented. We know that the equation can depict more interesting phenomena than other KP-type equations.

To the best of our knowledge, the lump solutions in NLEEs have attracted more and more attention, which are reflected in the interaction phenomena between lump solutions and other rational solutions, such as [32,33,34,35,36,37,38,39,40,41]. The main goal in this paper is to derive its traveling wave solutions by a Bäcklund transformation method, and obtain rogue wave solutions and interaction phenomena between the double kink solitary waves and lump solution by using a bilinear expression of (3).

The structure of this paper is as follows. In Sect. 2, based on the Hirota’s bilinear method and Bell’s polynomial theory, we compute the bilinear representation for the \((3+1)\)-dimensional BKP–Boussinesq equation. Then, in Sect. 3, its Bäcklund transformation is presented by using a bilinear equation. Moreover, according to a group of Bäcklund transformation formulas, we also get the corresponding traveling wave solutions of the equation. Section 4 uses an ansätz function to obtain rogue wave solutions and rational breather waves for the Eq. (3). In Sect. 5, we present its one-, two- and N-kink solitary wave solutions in a very natural way. In Sect. 6, by virtue of a special function, we find the interaction solutions between lump and other waves.

2 Bilinear representation

Let us introduce the following potential transformation

$$\begin{aligned} u=cq_{x}, \end{aligned}$$
(4)

where c is a constant. Taking \(c=1\), substituting (4) into (3), and integrating the result with respect to x once, then one obtains

$$\begin{aligned} E(q)=q_{ty}-(q_{3xy}+3q_{xx}q_{xy})+q_{tt}+3q_{xz}=\sigma ,\nonumber \\ \end{aligned}$$
(5)

where \(\sigma \) is an integrable constant. Based on the results provided in Refs. [42,43,44,45,46,47,48,49,50,51,52,53], and we obtain \(E(q)=P_{ty}-P_{xxxy}+P_{tt}+3P_{xz}=\sigma \). Supposing \(\sigma =0\), we have

$$\begin{aligned} E(q)=P_{ty}-P_{xxxy}+P_{tt}+3P_{xz}=0, \end{aligned}$$
(6)

with the following variable transformation

$$\begin{aligned} q=2 \ln F \Longleftrightarrow u=2[\ln F]_{x}. \end{aligned}$$
(7)

Then one obtains

$$\begin{aligned} \left( D_{t}D_{y}-D_{x}^{3}D_{y}+D_{t}^{2}+3D_{x}D_{z}\right) F\cdot F=0, \end{aligned}$$
(8)

where F is a real function about x, y, z and t. \(D_{s}\) \((s=x, y, z, t)\) denote some Hirota’s bilinear operators [18].

3 Bäcklund transformation and traveling wave solutions

3.1 Bilinear Bäcklund transformation

In order to derive the Bäcklund transformation of Eq. (3), we assume that there exists another real function solution in bilinear Eq. (8); then, we can obtain a similar bilinear form as

$$\begin{aligned} \left( D_{t}D_{y}-D_{x}^{3}D_{y}+D_{t}^{2}+3D_{x}D_{z}\right) f'\cdot f'=0. \end{aligned}$$
(9)

By constructing a key function given by

$$\begin{aligned} M= & {} \left[ \left( D_{t}D_{y}-D_{x}^{3}D_{y}+D_{t}^{2}\right. \right. \nonumber \\&\left. \left. +\,3D_{x}D_{z}\right) f'\cdot f'\right] f\cdot f \nonumber \\&-\,\left[ \left( D_{t}D_{y}-D_{x}^{3}D_{y}+D_{t}^{2}\right. \right. \nonumber \\&\left. \left. +\,3D_{x}D_{z}\right) f\cdot f\right] f'\cdot f', \end{aligned}$$
(10)

and supposing \(M=0\), we have

$$\begin{aligned}&\left[ \left( D_{t}D_{y}-D_{x}^{3}D_{y}+D_{t}^{2}+3D_{x}D_{z}\right) f'\cdot f'\right] f\cdot f \nonumber \\&\quad =\left[ \left( D_{t}D_{y}-D_{x}^{3}D_{y}+D_{t}^{2}+3D_{x}D_{z}\right) f\cdot f\right] f'\cdot f'.\nonumber \\ \end{aligned}$$
(11)

According to above equation, we can show that \(f'\) can be used to solve the Eq. (8) if and only if \(f'\) also denotes a solution of Eq. (9). By exchanging the dependent variables f and \(f'\), Eq. (10) satisfies \(M=0\). Next, we introduce several types of exchange formulas for bilinear operator as follows [18]

$$\begin{aligned}&\left( D_{i}D_{j}f'f'\right) ff-\left( D_{i}D_{j}ff\right) f'f'=2D_{j}\left( D_{i}f'f\right) ff', \end{aligned}$$
(12)
$$\begin{aligned}&2\left( D_{i}^{3}D_{j}f'f'\right) ff-2\left( D_{i}^{3}D_{j}ff\right) f'f'\nonumber \\&\quad =D_{i}\left[ \left( 3D_{i}^{2}D_{j}f'f\right) ff'+\left( 3D_{i}^{2}f'f\right) \left( D_{j}ff'\right) \right. \nonumber \\&\quad \quad \left. +\left( 6D_{i}D_{j}f'f\right) \left( D_{i}ff'\right) \right] +D_{j}\left[ \left( D_{i}^{3}f'f\right) ff'\right. \nonumber \\&\quad \quad \left. +\left( 3D_{i}^{2}f'f\right) \left( D_{i}ff'\right) \right] , \end{aligned}$$
(13)

where \(i,j=x,y,z,t\). It is easy to find that

$$\begin{aligned} \left( D_{i}D_{j}f'f\right) ff'=\left( D_{j}D_{i}f'f\right) ff'. \end{aligned}$$
(14)

Based on the exchange formulas (12)–(14) of bilinear operators, the Bäcklund transformation related to the Eq. (3) are given by

$$\begin{aligned} \begin{aligned} B_{1}f'f&=-\left( 3D_{x}^{2}D_{y}+\epsilon _{1}D_{y}+\epsilon _{2}\right. \\&\quad \left. +\,4\epsilon _{8}D_{t}+12D_{z}\right) f'f=0,\\ B_{2}f'f&=-\left( 3D_{x}^{2}+\epsilon _{3}D_{y}+\epsilon _{4}\right) f'f=0,\\ B_{3}f'f&=-\,6\left( D_{x}D_{y}+\epsilon _{5}D_{x}\right) f'f=0,\\ B_{4}f'f&=\left( 4D_{t}-D_{x}^{3}+\epsilon _{1}D_{x}-\epsilon _{6}-4\epsilon _{9}D_{t}\right) f'f=0,\\ B_{5}f'f&=-\left( 3D_{x}^{2}+\epsilon _{7}D_{x}-\epsilon _{4}\right) f'f=0,\\ B_{6}f'f&=4\left( D_{t}+\epsilon _{8}D_{x}+\epsilon _{9}D_{y}\right) f'f=0. \end{aligned} \end{aligned}$$
(15)

We provide the detailed calculation as follows

$$\begin{aligned} 2M&=2\left[ \left( D_{t}D_{y}f'f'\right) ff-\left( D_{t}D_{y}ff\right) f'f'\right] \nonumber \\&\quad -2\left[ \left( D_{x}^{3}D_{y}f'f'\right) ff -\left( D_{x}^{3}D_{y}ff\right) f'f'\right] \nonumber \\&\quad +2\left[ \left( D_{t}^{2}f'f'\right) ff-\left( D_{t}^{2}ff\right) f'f'\right] \nonumber \\&\quad +6\left[ \left( D_{x}D_{z}f'f'\right) ff-\left( D_{x}D_{z}ff\right) f'f'\right] \nonumber \\&=4D_{y}\left( D_{t}f'f\right) ff'-D_{x}\left[ \left( 3D_{x}^{2}D_{y}f'f\right) ff' \right. \nonumber \\&\quad \left. +\left( 3D_{x}^{2}f'f\right) \left( D_{y}ff'\right) \right. \nonumber \\&\quad \left. +\left( 6D_{x}D_{y}f'f\right) \left( D_{x}ff'\right) \right] \nonumber \\&\quad -D_{y}\left[ \left( D_{x}^{3}f'f\right) ff' \right. \nonumber \\&\quad \left. +\left( 3D_{x}^{2}f'f\right) \left( D_{x}ff'\right) \right] \nonumber \\&\quad +4D_{t}\left( D_{t}f'f\right) ff' +12D_{z}\left( D_{x}f'f\right) ff'\nonumber \\&=4D_{y}\left( D_{t}f'f\right) ff'-D_{x}\left[ \left( 3D_{x}^{2}D_{y}f'f\right. \right. \nonumber \\&\quad \left. +\epsilon _{1}D_{y}f'f +\epsilon _{2}f'f\right) ff'\nonumber \\&\quad +\left( 3D_{x}^{2}f'f+\epsilon _{3}D_{y}f'f\right. \nonumber \\&\quad \left. +\epsilon _{4}f'f\right) \left( D_{y}ff'\right) +\left( 6D_{x}D_{y}f'f\right. \nonumber \\&\quad \left. \left. +6\epsilon _{5}D_{x}f'f\right) \left( D_{x}ff'\right) \right] \nonumber \\&\quad -D_{y}\left[ \left( D_{x}^{3}f'f -\epsilon _{1}D_{x}f'f \right. \right. \nonumber \\&\quad \left. +\epsilon _{6}f'f\right) ff'+\left( 3D_{x}^{2}f'f+\epsilon _{7}D_{x}f'f\right. \nonumber \\&\quad \left. \left. -\epsilon _{4}f'f\right) \left( D_{x}ff'\right) \right] +4D_{t}\left( D_{t}f'f+\epsilon _{8}D_{x}f'f\right. \nonumber \\&\quad \left. +\epsilon _{9}D_{y}f'f\right) ff'-4D_{x}\left( \epsilon _{8}D_{t}f'f\right) ff'\nonumber \\&\quad -4D_{y}\left( \epsilon _{9}D_{t}f'f\right) ff'+12D_{x}\left( D_{z}f'f\right) ff'\nonumber \\&=D_{x}\left( B_{1}f'f\right) ff'+D_{x}\left( B_{2}f'f\right) \left( D_{y}ff'\right) \nonumber \\&\quad +D_{x}\left( B_{3}f'f\right) \left( D_{x}ff'\right) \nonumber \\&\quad +D_{y}\left( B_{4}f'f\right) ff'+D_{y}\left( B_{5}f'f\right) \left( D_{x}ff'\right) \nonumber \\&\quad +D_{t}\left( B_{6}f'f\right) ff'. \end{aligned}$$
(16)

For the above reduction and \(D_{i}ff=0\), the parameters \(\epsilon _{i}, (i=2,3,5,6,7)\) will be equal to zero. Based on the expression (14), we can obtain \(\epsilon _{j}=0, (j=1,4,8,9)\).

Fig. 1
figure 1

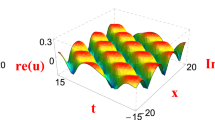
(Color online) Rational solution (23) for Eq. (3) by choosing suitable parameters: \({\hat{a}}_{1}=1,{\hat{a}}_{2}=1.2,{\hat{a}}_{3}=0.9,{\hat{a}}_{4}=2.1,z=0,t=3\). a Perspective view of the real part of the wave. b The overhead view of the wave. c The wave propagation pattern of the wave along the x axis

Full size image

3.2 Traveling wave solutions

Let us substitute a solution \(f=1\) into the \((3+1)\)-dimensional BKP–Boussinesq Eq. (3), which is reduced to the initial variable u with \(u=2(\ln f)_{x}=0\). One has

$$\begin{aligned} D_{s}^{n}gf=D_{s}^{n}g=\frac{\partial ^{n}}{\partial s^{n}}g,\quad n\ge 1. \end{aligned}$$
(17)

The Bäcklund transformation (15) related to \(f=1\) will be a group of linear equations given by

$$\begin{aligned} \left\{ \begin{aligned}&3f'_{xxy}+\epsilon _{1}f'_{y}+\epsilon _{2}f'+4\epsilon _{8}f'_{t}+12f'_{z}=0,\\&3f'_{xx}+\epsilon _{3}f'_{y}+\epsilon _{4}f'=0,\\&f'_{xy}+\epsilon _{5}f'_{x}=0,\\&4f'_{t}-f'_{xxx}+\epsilon _{1}f'_{x}-\epsilon _{6}f'-4\epsilon _{9}f'_{t}=0,\\&3f'_{xx}+\epsilon _{7}f'_{x}-\epsilon _{4}f'=0,\\&f'_{t}+\epsilon _{8}f'_{x}+\epsilon _{9}f'_{y}=0. \end{aligned} \right. \end{aligned}$$
(18)

We introduce a function given by

$$\begin{aligned} f'=1+\mu \exp \left( {\hat{a}}_{1}x+{\hat{a}}_{2}y+{\hat{a}}_{3}z-{\hat{a}}_{4}t\right) ,~~{\hat{a}}_{1}\ne 0,\nonumber \\ \end{aligned}$$
(19)

where \({\hat{a}}_{1}, {\hat{a}}_{2}, {\hat{a}}_{3}, {\hat{a}}_{4}\) are some constants. Taking \(\epsilon _{2}, \epsilon _{4}, \epsilon _{6}=0\) to the above equations (18), then one has

$$\begin{aligned} \begin{aligned} \epsilon _{1}&=\frac{{\hat{a}}_{1}^{3}+4{\hat{a}}_{4}-4\epsilon _{9}{\hat{a}}_{4}}{{\hat{a}}_{1}},\\ \epsilon _{3}&=-\frac{3{\hat{a}}_{1}^{2}}{{\hat{a}}_{2}},\quad \epsilon _{5}=-{\hat{a}}_{2},\quad \epsilon _{7}=-\,3{\hat{a}}_{1},\\ {\hat{a}}_{3}&=\frac{\epsilon _{8}{\hat{a}}_{1}{\hat{a}}_{4}-{\hat{a}}_{1}^{3}{\hat{a}}_{2}+{\hat{a}}_{2}{\hat{a}}_{4}+\epsilon _{9}{\hat{a}}_{2}{\hat{a}}_{4}}{3{\hat{a}}_{1}},\\ {\hat{a}}_{4}&=\epsilon _{8}{\hat{a}}_{1}+\epsilon _{9}{\hat{a}}_{2}. \end{aligned} \end{aligned}$$
(20)

So, we obtain the following exponential wave solution

$$\begin{aligned} u=2\left[ \ln f'\right] _{x}, \end{aligned}$$
(21)

where \(f'=1+\mu \exp \left[ {\hat{a}}_{1}x+{\hat{a}}_{2}y+ \frac{\epsilon _{8}{\hat{a}}_{1}{\hat{a}}_{4} -{\hat{a}}_{1}^{3}{\hat{a}}_{2}+{\hat{a}}_{2}{\hat{a}}_{4}+\epsilon _{9}{\hat{a}}_{2}{\hat{a}}_{4}}{3{\hat{a}}_{1}}z-(\epsilon _{8}{\hat{a}}_{1}+\epsilon _{9}{\hat{a}}_{2})t\right] \). Then above u solves the BKP–Boussinesq Eq. (3).

Next, we use a first-order function as follows

$$\begin{aligned} f'={\hat{a}}_{1}x+{\hat{a}}_{2}y+{\hat{a}}_{3}z-{\hat{a}}_{4}t, \end{aligned}$$
(22)

by substituting (22) into a class of equations (18), and taking \(\epsilon _{i}=0,(2\le i\le 7)\). The Eq. (18) are limited by \(({\hat{a}}_{4}-{\hat{a}}_{2}){\hat{a}}_{4}-3{\hat{a}}_{1}{\hat{a}}_{3}=0\), which satisfies the existence of \(\epsilon _{1}, \epsilon _{8}\) and \(\epsilon _{9}\). We can obtain the following rational solution of the BKP–Boussinesq equation

$$\begin{aligned} u=\frac{2{\hat{a}}_{1}}{{\hat{a}}_{1}x+{\hat{a}}_{2}y+{\hat{a}}_{3}z-{\hat{a}}_{4}t}. \end{aligned}$$
(23)

The graphic of the rational solution (23) for Eq. (3) is plotted in Fig. 1 by choosing suitable parameters.

Fig. 2
figure 2

(Color online) Rational breather wave solution (26) for Eq. (3) by choosing suitable parameters: \({m_{1}=1.35},m_{7}=1,y=0,z=0\). a Perspective view of the real part of the wave. b The overhead view of the wave. c The wave propagation pattern of the wave along the x axis

Full size image

4 Rogue wave solutions

In order to seek the rogue wave solutions for the BKP–Boussinesq equation, we assume that

$$\begin{aligned} F= & {} 1+\left( m_{1}x+m_{2}y+m_{3}z+m_{4}t\right) ^{2}+m_{5}x^{2}\nonumber \\&+m_{6}\left( y+z\right) ^{2}+m_{7}t^{2},~~\left( m_{1}\ne 0\right) , \end{aligned}$$
(24)

where \(m_{i} (i=1,2,3,4,5,6,7)\) are free constants. Substituting the ansätz (24) into the bilinear Eq. (8), with the aid of mathematica, one can obtain the following results

$$\begin{aligned} m_{2}= & {} -\frac{m_{7}}{3m_{1}^{3}},~m_{3}=\frac{m_{7}\left( 36m_{1}^{6}+m_{7}\right) }{108m_{1}^{7}},\nonumber \\ m_{4}= & {} \frac{m_{7}}{6m_{1}^{3}},~m_{5}=0,~m_{6}=0. \end{aligned}$$
(25)

Then, substituting (24) and (25) into \(u=[\ln F]_{x}\) yields the following solutions

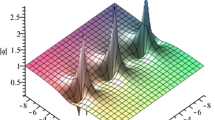
$$\begin{aligned} u=\frac{4\left[ m_{1}^{2}x-\frac{m_{7}}{3m_{1}^{2}}y+\frac{m_{7}\left( 36m_{1}^{6}+m_{7}\right) }{108m_{1}^{6}}z+\frac{m_{7}}{6m_{1}^{2}}t\right] }{1+\left( m_{1}x-\frac{m_{7}}{3m_{1}^{3}}y+\frac{m_{7}\left( 36m_{1}^{6}+m_{7}\right) }{108m_{1}^{7}}z+\frac{m_{7}}{6m_{1}^{3}}t\right) ^{2}+m_{7}t^{2}}.\nonumber \\ \end{aligned}$$
(26)

For the solution (26), we call it as the new-type rational breather wave solution [27]. By choosing appropriate parameters, its graph is plotted in Fig. 2. We can show that Fig. 2a exists a pair of peaks in the opposite direction. Furthermore, it is also called as the bright and dark soliton waves. We can see that its one down wave locates below the plane wave. Then, it can be said that the rational breather wave is not a kinky wave. Actually, the wave is a local form in the (x, t) plane. There exist two similar wave shapes of the rogue wave. So it can also be called as the two-dimensional rogue wave for Eq. (3).

We consider

$$\begin{aligned}&{\tilde{u}}=u_{x} =\frac{4\left[ -\left( m_{1}^2x-\frac{m_{7}}{3m_{1}^{2}}y +\frac{m_{7}\left( 36m_{1}^{6}+m_{7}\right) }{108m_{1}^{6}}z+\frac{m_{7}}{6m_{1}^{2}}t\right) ^{2} +m_{1}^{2}m_{7}t^{2}+m_{1}^{2}\right] }{\left[ 1+\left( m_{1}x-\frac{m_{7}}{3m_{1}^{3}}y+\frac{m_{7} \left( 36m_{1}^{6}+m_{7}\right) }{108m_{1}^{7}}z+\frac{m_{7}}{6m_{1}^{3}}t\right) ^{2}+m_{7}t^{2}\right] ^{2}}. \end{aligned}$$
(27)

It is not hard to find that \({\tilde{u}}\) is also a solution of Eq. (3). By choosing proper parameters, we provide one group of graphs related to the solution (27) shown in Fig. 3. It is a rogue wave form. We can find that upper dominant peak and two holes exist in Fig. 3a. Its velocity, amplitude and width keep unchanged, in the process of propagation. We also find that the symmetry of rogue wave will be influenced by some parameters. Moreover, it is the highest wave in these waves, and forming in a very short time. Figure 3b shows its density. Then, Fig. 3c depicts the corresponding amplitude of \({\tilde{u}}\) in different time.

Fig. 3
figure 3

(Color online) Rogue wave solution (27) for Eq. (3) by choosing suitable parameters: \({m_{1}=1.35},m_{7}=1,y=0,z=0\). a Perspective view of the real part of the wave. b The overhead view of the wave. c The wave propagation pattern of the wave along the x axis

Full size image

5 Multi kink solitary wave solutions

In this part, we consider the kink solitary wave solutions for Eq. (3) by expanding F about the small parameter \(\epsilon \) given by

$$\begin{aligned} F=1+\epsilon F^{(1)}+\epsilon ^{(2)}F^{2}+\epsilon ^{3}F^{(3)}+\cdots . \end{aligned}$$
(28)

Substituting (28) into (8) and equating the coefficients of all powers of \(\epsilon ^{n}\) to zero, one has

$$\begin{aligned}&F_{ty}^{\left( 1\right) }-F_{3xy}^{\left( 1\right) }+F_{2t}^{\left( 1\right) }+3F_{xz}^{\left( 1\right) }=0,\end{aligned}$$
(29)
$$\begin{aligned}&2\left( F_{ty}^{\left( 2\right) }-F_{3xy}^{\left( 2\right) }+F_{2t}^{\left( 2\right) }+3F_{xz}^{\left( 2\right) }\right) \nonumber \\&\quad =-\left( D_{t}D_{y}-D_{x}^{3}D_{y}+D_{t}^{2}+3D_{x}D_{z}\right) F^{\left( 1\right) }\cdot F^{\left( 1\right) },\end{aligned}$$
(30)
$$\begin{aligned}&\left( F_{ty}^{\left( 2\right) }-F_{3xy}^{\left( 2\right) }+F_{2t}^{\left( 2\right) }+3F_{xz}^{\left( 2\right) }\right) \nonumber \\&\quad =-\left( D_{t}D_{y}-D_{x}^{3}D_{y}+D_{t}^{2}+3D_{x}D_{z}\right) F^{\left( 1\right) }\cdot F^{\left( 2\right) }. \end{aligned}$$
(31)

From the formula (29), we can obtain a solution of F given by

$$\begin{aligned} F=1+\exp (\xi _{1}), \end{aligned}$$
(32)

in which \(\xi _{1}=k_{1}x+l_{1}y+\alpha _{1}z+\omega _{1}t+\delta _{1}\). Substituting F into bilinear form (8), we get \(\omega _{1}=\frac{-l_{1}\pm \sqrt{l_{1}^{2}+4k_{1}^{2}l_{1}-12k_{1}\alpha _{1}}}{2}\), (\(\triangle =l_{1}^{2}+4k_{1}^{2}l_{1}-12k_{1}\alpha _{1}\ge 0\)). Taking \(F^{(2)}=F^{(3)}=\cdots =0\), then one kink soliton solution is given by

$$\begin{aligned} u_{1}=2\left[ \ln \left( 1+\exp (\xi _{1})\right) \right] _{x}. \end{aligned}$$
(33)
Fig. 4
figure 4

(Color online) One kink soliton solution (33) for Eq. (3) by choosing suitable parameters: \(k_{1}=1.2,l_{1}=1.2,\delta _{1}=0,\alpha _{1}=0.02\). a Perspective view of the real part of the wave. b The overhead view of the wave. c The wave propagation pattern of the wave along the x axis

Full size image
Fig. 5
figure 5

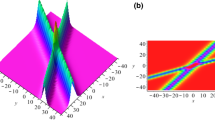
(Color online) Double kink soliton solution (34) for Eq. (3) by choosing suitable parameters: \(k_{1}=-\,1.1,k_{2}=1,l_{1}=1,l_{2}=2,\alpha _{1}=2,\xi _{2}=-\,1.1,\alpha _{2}=2,\omega _{1}=1,\omega _{2}=-\,2,\delta _{1}=-\,1.2,\delta _{2}=-\,1\). a Perspective view of the real part of the wave. b The overhead view of the wave. c The wave propagation pattern of the wave along the x axis

Full size image

According to the above way, one can find the double kink soliton solutions of (3) as follows

$$\begin{aligned} u_{2}&=2\left[ \ln \left( 1+\exp \left( \xi _{1}\right) \right. \right. \nonumber \\&\quad \left. \left. +\,\exp \left( \xi _{2}\right) +\exp \left( \xi _{1}+\xi _{2}+C_{12}\right) \right) \right] _{x},\end{aligned}$$
(34)
$$\begin{aligned} \xi _{i}&=k_{i}x+l_{i}y+\alpha _{i}z+\omega _{i}t+\delta _{i}, \nonumber \\ \omega _{i}&=\frac{-l_{i}\pm \sqrt{l_{i}^{2}+4k_{i}^{2}l_{i}-12k_{i}\alpha _{i}}}{2}, \end{aligned}$$
(35)
$$\begin{aligned} C_{12}&=\frac{\left( \omega _{1}-\omega _{2}\right) \left( l_{1}-l_{2}\right) -\left( k_{1}-k_{2}\right) ^{3}\left( l_{1}-l_{2}\right) +\left( \omega _{1}-\omega _{2}\right) ^{2}+3\left( k_{1}-k_{2}\right) \left( \alpha _{1}-\alpha _{2}\right) }{\left( \omega _{1}+\omega _{2}\right) \left( l_{1}+l_{2}\right) -\left( k_{1}+k_{2}\right) ^{3}\left( l_{1}+l_{2}\right) +\left( \omega _{1}+\omega _{2}\right) ^{2}+3\left( k_{1}+k_{2}\right) \left( \alpha _{1}+\alpha _{2}\right) }, \end{aligned}$$
(36)

where \(k_{i},l_{i},\alpha _{i},\delta _{i}\) are some constants \((i=1,2)\).

Similarly, the N-kink solitary wave solutions are derived by

$$\begin{aligned} u_{N}&=2[\ln F]_{x},\end{aligned}$$
(37)
$$\begin{aligned} F&=\sum _{\rho =0,1}\exp \left( \sum _{j=1}^{N}\rho _{i}\xi _{i}+\sum _{1\le i<j\le N}\rho _{i}\rho _{j}C_{ij}\right) , \end{aligned}$$
(38)
$$\begin{aligned} C_{ij}= & {} \frac{\left( \omega _{i}-\omega _{j}\right) \left( l_{i}-l_{j}\right) -\left( k_{i}-k_{j}\right) ^{3}\left( l_{i}-l_{j}\right) +\left( \omega _{i}-\omega _{j}\right) ^{2}+3\left( k_{i}-k_{j}\right) \left( \alpha _{i}-\alpha _{j}\right) }{\left( \omega _{i}+\omega _{j}\right) \left( l_{i}+l_{j}\right) -\left( k_{i}+k_{j}\right) ^{3}\left( l_{i}+l_{j}\right) +\left( \omega _{i}+\omega _{j}\right) ^{2}+3\left( k_{i}+k_{j}\right) \left( \alpha _{i}+\alpha _{j}\right) }, \end{aligned}$$
(39)

The graphics of one kink soliton solution (33) and double kink soliton solutions (34) for Eq. (3) are plotted in Figs. 4 and 5 by choosing suitable parameters.

6 Interaction phenomena

In this section, by considering the characteristics of interaction between lump and kink wave solutions, we discuss their corresponding phenomena. By introducing a dependent transformation \(u=2(\ln f)_{x}\), and based on the Bell’s polynomial theory [42, 46, 47], we can also obtain the same bilinear form of \((3+1)\)-dimensional BKP–Boussinesq equation

$$\begin{aligned}&\left( D_{t}D_{y}-D_{x}^{3}D_{y}+D_{t}^{2}+3D_{x}D_{z}\right) f\cdot f\nonumber \\&\quad =2f_{ty}f-2f_{t}f_{y}-2f_{3xy}f+6f_{xxy}f_{x}\nonumber \\&\qquad -6f_{xy}f_{xx}+2f_{3x}f_{y}+2f_{tt}f\nonumber \\&\qquad -2f_{t}^{2}+6f_{xz}f-6f_{x}f_{z}=0. \end{aligned}$$
(40)

In order to construct the interaction solutions, based on the results in [33, 39], we take following form

$$\begin{aligned} f=g^{2}+h^{2}+k\cosh (m)+a_{11}, \end{aligned}$$
(41)

where g, h and m are, respectively, expressed by

$$\begin{aligned}&g=a_{1}x+a_{2}y+a_{3}z+a_{4}t+a_{5},\end{aligned}$$
(42)
$$\begin{aligned}&h=a_{6}x+a_{7}y+a_{8}z+a_{9}t+a_{10},\end{aligned}$$
(43)
$$\begin{aligned}&m=k_{1}x+k_{2}y+k_{3}z+k_{4}t, \end{aligned}$$
(44)

and \(a_{i}, (i=1,2,\ldots ,11)\), \(k, k_{1}, k_{2}, k_{3}, k_{4}\) are all the real parameters. Substituting Eqs. (42)–(44) into the bilinear Eq. (40), then we obtain a polynomial equation about x, y, z and t. Collecting the coefficients of the terms, such as \(x, y, z, t, \cosh (m)\) and \(\sinh (m)\), and taking them to be zero, we get a class of algebraic equations. Solving them, two cases about these parameters are derived. Substituting the limitations in Cases 1 and 2 into the Eq. (41) and \(u=2(\ln f)_{x}\), we can obtain these interaction solutions between lump and kink wave solutions for the BKP–Boussinesq equation.

Case 1. The limitations are provided by

$$\begin{aligned} \begin{aligned} a_{1}&=a_{5}=a_{10}=a_{11}=0,a_{j}=a_{j},\\&\quad \left( j=2,3,4,6,7,8,9\right) \\ k&=k,k_{i}=k_{i},(i=1,3,4),k_{2}\\&=\frac{-3a_{6}a_{7}k_{1}^{2}+a_{2}a_{4} +a_{4}^{2}+3a_{6}a_{8}+a_{7}a_{9}+a_{9}^{2}}{3a_{6}^{2}k_{1}}. \end{aligned}\nonumber \\ \end{aligned}$$
(45)

Then, we get the interaction solution as follows

$$\begin{aligned} u=\frac{2a_{6}\left( a_{6}x+a_{7}y+a_{8}z+a_{9}t\right) +kk_{1}\sinh \left( k_{1}x+\frac{-3a_{6}a_{7}k_{1}^2+a_{2}a_{4} +a_{4}^2+3a_{6}a_{8}+a_{7}a_{9}+a_{9}^2}{3a_{6}^2k_{1}}y +k_{3}z+k_{4}t\right) }{\left( a_{2}y+a_{3}z+a_{4}t\right) ^{2}+\left( a_{6}x+a_{7}y +a_{8}z+a_{9}t\right) ^{2}+k\cosh \left( k_{1}x+\frac{-3a_{6}a_{7}k_{1}^2 +a_{2}a_{4}+a_{4}^2+3a_{6}a_{8}+a_{7}a_{9}+a_{9}^2}{3a_{6}^2k_{1}}y+k_{3}z+k_{4}t\right) }.\nonumber \\ \end{aligned}$$
(46)

The graphic of the interaction solution (46) for Eq. (3) is plotted in Fig. 6 by choosing suitable parameters.

Fig. 6
figure 6

(Color online) Interaction solution (46) for Eq. (3) by choosing suitable parameters: \(a_{2}=\frac{7200}{1357},a_{3}= 1,a_{4}=3,a_{6}=12,a_{7}=-\frac{1}{68},a_{8}=1,a_{9}=1,k=2,k_{1}= \frac{5}{6},k_{3}=2,k_{4}= 2,(c1)~ t=-\,3,(c2)~ t=0,(c3)~ t=3\). a Perspective view of the real part of the wave. b Contour plot. c The wave propagation pattern of the wave along the x axis

Full size image

Case 2. The limitations are provided by

$$\begin{aligned} \begin{aligned} a_{1}&=a_{4}=a_{10}=0, \quad a_{j}=a_{j}, \quad \left( j=2,5,6,7\right) ,\\ a_{3}&=\frac{a_{2}\left( k_{1}^{3}-k_{4}\right) }{3k_{1}},\\ a_{8}&=-\frac{\left( a_{6}k_{1}^{3}-a_{6}k_{4}-a_{7}k_{1}\right) \left( k_{1}^{3}-k_{4}\right) }{3k_{1}^{2}},\\ a_{9}&= -\frac{a_{6}\left( k_{1}^{3}-k_{4}\right) }{k_{1}},\quad a_{11}=-a_{5}^{2},\quad k=k,\quad k_{i}=k_{i}, \\&\quad \left( i=1,3,4\right) , \quad k_{2}= -\frac{a_{7}k_{1}}{a_{6}}. \end{aligned} \end{aligned}$$
(47)

Then, we get the corresponding interaction solution as follows

$$\begin{aligned} u=\frac{2a_{6}\left( a_{6}x+a_{7}y+a_{8}z+a_{9}t\right) +k k_{1}\sinh \left( k_{1}x-\frac{a_{7}k_{1}}{a6}y+k_{3}z+k_{4}t\right) ]^{2}}{\left( a_{2}y+\frac{a_{2}\left( k_{1}^{3}-k_{4}\right) }{3k_{1}}z+a_{5}\right) ^2+\left( a_{6}x+a_{7}y-\frac{\left( a_{6}k_{1}^{3}-a_{6}k_{4}-a_{7}k_{1}\right) \left( k_{1}^{3}-k_{4}\right) }{3k_{1}^{2}}z-\frac{a_{6}\left( k_{1}^{3}-k_{4}\right) }{k_{1}}t\right) ^{2}+k\cosh \left( k_{1}x-\frac{a_{7}k_{1}}{a6}y+k_{3}z+k_{4}t\right) -a_{5}^2}.\nonumber \\ \end{aligned}$$
(48)

The graphic of the interaction solution (48) for Eq. (3) is plotted in Fig. 7 by choosing suitable parameters.

Fig. 7
figure 7

(Color online) Interaction solution (48) for Eq. (3) by choosing suitable parameters: \(a_{2}=7,a_{5}=1,a_{6}=12,a_{7}=1,k=2,k_{1}=\frac{5}{6},k_{3}=\frac{2}{3},k_{4}=1,(c4)~t=-\,8,(c5)~t=0,(c6)~t=8\). a Perspective view of the real part of the wave. b Contour plot. c The wave propagation pattern of the wave along the x axis

Full size image

As shown in Figs. 6 and 7, in a certain period of time, we can see that the kink waves exist in (x, y) plane. Then, the lump appears from them, and continuously removes in the double kink waves. In reality, the oscillation amplitude of lump starts to increase at a moment, and detaches from one of the kink waves. It is a gradual process, which can be reflected in Fig. 7. From Figs. 6a2–b2, 7a2–b2, when \(t=0\), the level of separation reaches to a peak. Besides, lump locates in the center of double kink waves. Then, we find that the lump slowly closes to the another kink wave. Its oscillation amplitude gradually reduces with the distance of the lump and the kink wave getting smaller and smaller. Finally, the kink wave swallows the lump. The double kink waves will revert to the initial state. We can see that the velocity of final lump will become smaller than its initial state. Maybe it is affected by the kink solitary waves.

7 Conclusions and discussion

In this work, we have systematically investigated the \((3+1)\)-dimensional BKP–Boussinesq equation. By using the Hirota’s bilinear method, we have derived the bilinear expression and Bäcklund transformation of the equation. Based on that, we have obtained its traveling wave solutions, including rational solutions and exponential wave solutions. Furthermore, an effective way is proposed to get its kink solitary wave solutions, rational breather solution and rogue wave solution. Finally, we have shown that a special function can be provided to get the interaction solutions between the lump and double kink waves.

From our results obtained in this paper, the method presented here has been proved to be a very effective method for finding analytical solutions of NLEEs. It is hoped that our results can enrich the theories for the associated NLEEs in mathematical physics.