1 Introduction

There has long been a great deal of theoretical and practical interest in the propagation of laser beams over atmospheric turbulence (Hajjarian et al. 2010; Gbur et al. 2014; Benzehoua et al. 2023b; Chib et al. 2020; Nossir et al. 2021, 2023a). Due to the intricacy of oceanic turbulence, laser beam propagation through it is comparatively less studied than that via atmospheric turbulence. However, because of their potential uses in underwater optical communication, imaging and sensing, there has been a lot of interest in investigating the propagation of laser beams in oceanic turbulence during last decades (Korotkova 2015; Luo et al. 2018; Hou 2009; Ata and Baykal 2018; Cheng et al. 2016). The direction of polarization is influenced by oceanic turbulence and the polarization in turn affects the beam wander caused by the turbulence. Here, we just take into account the process of oceanic turbulence in clean water, ignoring the involvement of air bubbles, suspended particles and other phenomena. It is commonly recognized that variations in salinity and temperature affect the refractive index of oceanic turbulence. Research on the effects of oceanic water temperature and salinity fluctuations, as well as the degree of polarization, mutual coherence function, spreading spherical waves, scintillation index, beam wander and average aperture on laser beam propagation have all been extensively studied (Chen et al. 2013; Lu et al. 2014a, 2014b; Baykal 2016; Yang et al. 2017; Chib et al. 2023; Alharbi et al. 2022).

On the other hand, research on the behavior of laser beams propagating through oceanic turbulence has been a focus of attention up until now because underwater laser communications and imaging systems must perform various laser beams like pulsed vortex (Benzehoua and Belafhal 2023a), Gaussian Schell-model Vortex Beam (Huang et al. 2014), hollow higher-order cosh-Gaussian beam (Elmabruk and Bayraktar 2023), cosine-Gaussian-correlated Schell-model beam (Ding et al. 2015), partially coherent radially polarized doughnut beam (Fu and Zhang 2013), vortex cosine hyperbolic-Gaussian beam (Lazrek et al. 2022), hollow Gaussian beam (Li et al. 2019), partially coherent anomalous hollow vortex beam (Liu et al. 2019), partially coherent Lorentz-Gauss vortex beam (Liu et al. 2017), radial Gaussian beam (Lu et al. 2015), Gaussian array beam (Lu et al. 2014a, 2014b), partially coherent beam (Lu et al. 2006), rotating elliptical chirped Gaussian vortex beam (Ye et al. 2018), quasi-homogeneous beam (Chen et al. 2013) and hyperbolic sinusoidal Gaussian beam (Bayraktar 2020).

Our research group has recently investigated the propagation of the BHoChG beam through the optical system and atmospheric turbulence (Nossir et al. 2023b; Dalil-Essakali et al. 2023). One of the specific properties of this beam is that the Bessel-Gaussian beam is distinguished by a zero-core intensity surrounded by brilliant and dark rings for non-zero beam orders. Its prospective uses as optical manipulation, atomic confinement devices and guides have garnered a lot of interest. The BHoChG beam incorporates an additional intriguing function known as higher-order cosh because of its numerous applications, high-power extraction capacity and adaptable profile. Besides, the properties of higher-order of hyperbolic sinusoidal function take place the literature in several analyses and becomes a trending topic among scientists. By managing and modifying the beam's properties, new opportunities are created and the outcomes include and go beyond the findings on the other beams. The hollow profile of the BHoChG beam in particular, the cosh function which is essentially a superposition of Gaussian functions both demonstrate the beam's uniqueness. The BHoChG and beam BHoShG beam have one extra control parameter Ω which is a feature parameter that set these beams apart from other beams. One other advantage of these beams is that they have some parameters, which give them greater significance. This adaptability enables customized beam characteristics to satisfy certain application requirements.

To the best of our knowledge, no one has investigated the behavior of the BHoChG beam and compared it with the BHoShG beam traveling through oceanic turbulence. The rest of the paper is organized as follows: Sect. 2 is kept for the incident fields of the BHoChG beam and BHoShG beam and the general theory is based on the extended Huygens-Fresnel diffraction integral to evaluate the analytical expressions of the average intensity of the propagating through oceanic turbulence. In Sect. 3 the formulae of the axial intensity of the BHoChG beam and the BHoShG are derived. In Sect. 4, interesting specific cases of our studied beams are deduced. The impacts of source beam parameters and the oceanic turbulence parameters on the evolution properties of the received beams intensities have been examined using numerical examples in Sect. 5. Finally, the main results obtained are summarized in Sect. 6.

2 Principle of the propagation of the BHoChG beam and the BHoShG beam through oceanic turbulence

To study the theoretical investigation of the BHoChG beam passing through oceanic turbulence, we first introduced the source field expression of the beam at \(z = 0\) in the cylindrical coordinates system as (Nossir et al. 2023b; Dalil et al. 2023)

$$E\left( {r,\theta ,0} \right) = E_{0} \exp \left( {il\theta } \right)J_{l} \left( {\frac{\mu r}{{\omega_{0} }}} \right)ch^{n} \left( {\Omega r^{2} } \right)\exp \left( { - \frac{{r^{2} }}{{\omega_{0}^{2} }}} \right),$$
(1)

where \(r,\theta\) refers the coordinates at the source plane, \(E_{0}\) is the amplification factor, \(J_{l}\) denotes the l-th order Bessel function of the first kind, \(\omega_{0}\) is the waist width, \(\exp \left( {il\theta } \right)\) is the phase term for the beam, \(\Omega \,\) indicates the parameters associated to the cosh part, \(n\) is the beam order and \(\mu\) is the transverse component of the wave factor.

In the other hand, we can write the electric field of the BHoShG beam at source field \(z = 0\) as

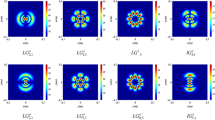
$$E\left( {r,\theta ,0} \right) = E_{0} \exp \left( {il\theta } \right)J_{l} \left( {\frac{\mu r}{{\omega_{0} }}} \right)sh^{n} \left( {\Omega r^{2} } \right)\exp \left( { - \frac{{r^{2} }}{{\omega_{0}^{2} }}} \right).$$
(2)

In Fig. 1, we illustrate the intensity distribution of the considered beams for different values of the Bessel order function l. From the plots of Fig. 1 (top row), it can be seen that, when \(l = \, 0\) the intensity distribution of the BHoChG beam is a single bright ring but the BHoShG beam has a dark-hollow intensity distribution at the original plane (bottom row).

Fig. 1
figure 1

Intensity distribution of the BHoChG beam (top row) and the BHoShG beam (bottom row) at z = 0 for \(n = 3,\) \(\Omega = 100m^{ - 1} ,\) \(n = 3,\) \(\mu = 0.6\) and \(\omega_{0} = 0.05m\): a \(l = 0,\) b \(l = 1\) and c \(l = 3\)

Full size image

However, in the case of the Bessel order is different to zero these beams profiles are characterized by a dark center region with zero intensity whose radius increases significantly with l. It is also shown that the intensity distribution of the BHoChG beam decreases when l becomes large. Figure 2 presents the contour graphs of the intensity distribution of the BHoChG beam and the BHoShG beam at the source plane \(\left( {z = 0} \right)\) for different values of the parameters \(\Omega \,\). One can clearly see that the considered beams have a central dark region. From these curves, we can observe that the intensity distribution of the two beams increases with increasing \(\Omega \,\) while, the depth of the center dark region becomes greater. We can also conclude from Figs. (1) and (2), that these beams are characterized by a ringed intensity pattern and the radius of the ring increases with the Bessel order function and \(\Omega\).

Fig. 2
figure 2

Intensity distribution of the BHoChG beam (top row) and the BHoShG beam (bottom row) at z = 0 for \(n = 3,\) \(l = 3\) and \(\mu = 0.6\): a \(\Omega = 60m^{ - 1}\)b \(\Omega = 200m^{ - 1}\) and c \(\Omega = 250m^{ - 1}\)

Full size image

We shall use the identity explicit equations of cosh (.) in the following (Abramowitz and Stegun 1970)

$$\cosh^{n} \left( {\rho^{2} } \right) = \frac{1}{{2^{n} }}\sum\limits_{s = 0}^{n} {\left( {\begin{array}{*{20}c} n \\ s \\ \end{array} } \right)e^{{a_{sn} \rho^{2} }} } ,$$
(3a)

with \(a_{sn} = 2s - n\), (3b).

where \(\left( {\begin{array}{*{20}c} n \\ s \\ \end{array} } \right)\) refers the binomial coefficient.

By the help of Eq. (3a), the input field of the BHoChG beam becomes

$$E\left( {r,\theta ,0} \right) = \frac{{E_{0} }}{{2^{n} }}\exp \left( {il\theta } \right)J_{l} \left( {\frac{\mu }{{\omega_{0} }}r} \right)\sum\limits_{s = 0}^{n} {\left( {\begin{array}{*{20}c} n \\ s \\ \end{array} } \right)\exp \left[ { - \left( {\frac{1}{{\omega_{0}^{2} }} - a_{sn} \Omega } \right)r^{2} } \right]} .$$
(4)

Based on the extended Huygens-Fresnel integral formula. The average intensity of laser beam spreading in the receiver plane can be written as (Andrews and Phillips 2005)

$$\begin{aligned} \left\langle {I\left( {\vec{\rho },z} \right)} \right\rangle = & \left\langle {E(\vec{\rho },z,t)E^{ * } (\vec{\rho },z,t)} \right\rangle = \frac{{k^{2} }}{{4\pi^{2} z^{2} }}\int\limits_{0}^{a} {\int\limits_{0}^{a} {\int\limits_{0}^{2\pi } {\int\limits_{0}^{2\pi } {\left\langle {E(\vec{r}_{1} ,0)E^{ * } (\vec{r}_{2} ,0)} \right\rangle } } } } \\ & \quad \times \exp \left[ {\frac{ik}{{2z}}\left( {\left( {\vec{r}_{1} - \vec{\rho }} \right)^{2} - \left( {\vec{r}_{2} - \vec{\rho }} \right)^{2} } \right)} \right]\left\langle {\exp \left[ {\psi \left( {\overrightarrow {{r_{1} }} ,\overrightarrow {\rho } } \right) + \psi^{*} \left( {\overrightarrow {{r_{2} }} ,\overrightarrow {\rho } } \right)} \right]\,} \right\rangle d\vec{r}_{1} d\vec{r}_{2} , \\ \end{aligned}$$
(5)

where * denote the complex conjugation and \(\left\langle . \right\rangle\) represents the ensemble average over the medium statistics, \(E(\vec{\rho },z)\) and \(E(\vec{r},0)\) at the output plane \(z\) and in the source plane \(z = 0\), respectively, \(\overrightarrow {r} = \left( {r,\theta } \right)\) and \(\overrightarrow {\rho } = \left( {\rho ,\phi } \right)\) indicate the position vectors of the fields in the source plane and the receiver one, respectively. \(k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0pt} \lambda }\) is the wave number with \(\lambda\) as the wavelength of laser light in vacuum and \(\psi \left( {\overrightarrow {r} ,\overrightarrow {\rho } } \right)\) denotes the random part due to the turbulent oceanic of the complex phase of a spherical wave propagating from the source plane to the output one.

The last term in angle brackets of Eq. (5) can be expressed as (Andrews and Phillips 2005)

$$\left\langle {\exp \left[ {\psi \left( {\overrightarrow {{r_{1} }} ,\overrightarrow {\rho } } \right) + \psi^{*} \left( {\overrightarrow {{r_{2} }} ,\overrightarrow {\rho } } \right)} \right]\,} \right\rangle = \exp \left[ {\frac{1}{{\rho_{0}^{2} }}\left( {2r_{1} r_{2} \cos \left( {\theta_{1} - \theta_{2} } \right)} \right)} \right]\exp \left[ { - \frac{1}{{\rho_{0}^{2} }}\left( {r_{1}^{2} + r_{2}^{2} } \right)} \right],$$
(6)

where \(\rho_{0}\) the coherence length of a spherical wave propagating in oceanic turbulence can be is given by

$$\rho_{0} = \left[ {\frac{{\pi^{2} k^{2} z}}{3}\int\limits_{0}^{\infty } {d\kappa \kappa^{3} } \Phi \left( \kappa \right)} \right]^{ - 1/2} ,$$
(7)

where \(\Phi \left( \kappa \right)\) is the spatial power spectrum of the refractive index fluctuations and \(\kappa\) is the spatial frequency for a homogeneous and isotropic turbulent ocean can be obtained as (Nikshov and Nikishov, 2000)

$$\begin{aligned} \Phi \left( \kappa \right) = & 0.388 \times 10^{ - 8} \varepsilon^{ - 11/3} \frac{{\chi_{T} }}{{\zeta^{2} }}\left[ {1 + 2.35\left( {\kappa \eta } \right)^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}} } \right] \\ & \quad \times \left( {\zeta^{2} \exp \left( { - A_{T} \delta } \right) + \exp \left( { - A_{s} \delta } \right) - 2\zeta \exp \left( { - A_{TS} \delta } \right)} \right), \\ \end{aligned}$$
(8)

where the oceanic turbulence parameters are:

\(\varepsilon\) is the rate of dissipation of turbulent kinetic energy per unit mass of fluid, which may vary in the range from \(10^{ - 1} m^{2} s^{ - 3} \,\) to \(10^{ - 10} m^{2} s^{ - 3}\), \(\chi_{T}\) is the dissipation rate of mean squared temperature having value in the range from \(10^{ - 4} K^{2} s^{ - 1}\) to \(\,10^{ - 10} K^{2} s^{ - 1} ,\) \(\zeta\) represents the relative strength of temperature and salinity fluctuations, which in the ocean water changes in the range from -5 to 0, \(\eta = 10^{ - 3}\) is the Kolmogorov inner scale, \(\delta = 8.284(\kappa \eta )^{4/3} + 12.978(\kappa \eta )^{2} ,\) \(A_{T} = 1.863 \times 10^{ - 2} ,\) \(A_{S} = 1.9 \times 10^{ - 4}\) and \(A_{TS} = 9.41 \times 10^{ - 3}\).

Substituting Eqs. (4) and (6) into Eq. (5) and after re-arranging the integrand function the received intensity can be expressed as

$$\begin{aligned} \left\langle {I_{c} \left( {\overrightarrow {\rho } ,z} \right)} \right\rangle = & \frac{{k^{2} E_{0}^{2} }}{{2^{2 + n + m} \pi^{2} z^{2} }}\sum\limits_{{s_{1} = 0}}^{n} {\left( {\begin{array}{*{20}c} n \\ {s_{1} } \\ \end{array} } \right)\sum\limits_{{s_{2} = 0}}^{m} {\left( {\begin{array}{*{20}c} m \\ {s_{2} } \\ \end{array} } \right)} } \int\limits_{0}^{ + \infty } {\int\limits_{0}^{ + \infty } {\int\limits_{0}^{2\pi } {\int\limits_{0}^{2\pi } {\exp \left\{ {\frac{ik}{z}\left[ {r_{2} \rho \cos \,\left( {\theta_{2} - \phi } \right) - r_{1} \rho \cos \left( {\theta_{1} - \phi } \right)} \right]} \right\}} } } } \\ & \quad \times \exp \left[ {\frac{{2r_{1} r_{2} }}{{\rho_{0}^{2} }}\cos \left( {\theta_{1} - \theta_{2} } \right)} \right]\exp \left( { - \beta_{1} r_{1}^{2} } \right)\exp \left( { - \beta_{2} r_{2}^{2} } \right)\exp \left[ {il\left( {\theta_{1} - \theta_{2} } \right)} \right] \\ & \quad \times J_{l} \left( {\frac{\mu }{{\omega_{0} }}r_{1} } \right)\,J_{l} \left( {\frac{\mu }{{\omega_{0} }}r_{2} } \right)\,d\overrightarrow {{r_{1} }} d\overrightarrow {{r_{2} }} , \\ \end{aligned}$$
(9)

where.

$$\beta_{1} = \frac{1}{{\omega_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} - a_{{s_{1} n}} \Omega - \frac{ik}{{2z}},$$
(10a)

and

$$\beta_{2} = \frac{1}{{\omega_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} - a_{{s_{2} m}} \Omega + \frac{ik}{{2z}}.$$
(10b)

In the following Section, we calculate the axial intensities of the BHoChG beam and the BHoShG beam propagating through oceanic turbulence.

3 Axial intensity of the propagation of the BHoChG beam and the BHoShG beam through oceanic turbulence

For the propagation on the axis, we put \(\rho = 0\) into Eq. (9). So, the expression of the axial intensity of BHoChG beam propagating in oceanic turbulence is given by

$$\begin{aligned} \left\langle {I_{c} \left( {0,z} \right)} \right\rangle = & \frac{{k^{2} E_{0}^{2} }}{{2^{2 + n + m} \pi^{2} z^{2} }}\sum\limits_{{s_{1} = 0}}^{n} {\left( {\begin{array}{*{20}c} n \\ {s_{1} } \\ \end{array} } \right)\sum\limits_{{s_{2} = 0}}^{m} {\left( {\begin{array}{*{20}c} m \\ {s_{2} } \\ \end{array} } \right)} } \int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\int\limits_{0}^{2\pi } {\int\limits_{0}^{2\pi } {\exp \left( { - \beta_{1} r_{1}^{2} } \right)} } } } \exp \left( { - \beta_{2} r_{2}^{2} } \right) \\ & \quad \times \exp \left[ {\frac{1}{{\rho_{0}^{2} }}\left( {2r_{1} r_{2} \cos \left( {\theta_{1} - \theta_{2} } \right)} \right)} \right]\exp \left[ {il\left( {\theta_{1} - \theta_{2} } \right)} \right]J_{l} \left( {\frac{\mu }{{\omega_{0} }}r_{1} } \right)J_{l} \left( {\frac{\mu }{{\omega_{0} }}r_{2} } \right)r_{1} dr_{1} d\theta_{1} r_{2} dr_{2} d\theta_{2} . \\ \end{aligned}$$
(11)

By using the following integrals (Abramowitz, and Stegun 1970)

$$\int\limits_{0}^{2\pi } {\exp \left[ { - im\theta_{1} + x\cos \left( {\theta_{1} - \theta_{2} } \right)} \right]} d\theta_{1} = 2\pi \exp \,\left( { - im\theta_{2} } \right)I_{m} \left( x \right),$$
(12)

and (Gradshteyn and Ryzhik 1994)

$$\begin{gathered} \int\limits_{0}^{\infty } {x\exp \left( { - \gamma x^{2} } \right)} J_{n} \left( {\alpha x} \right)J_{n} \left( {\beta x} \right)dx = \frac{1}{2\gamma }\exp \left( { - \frac{{\alpha^{2} + \beta^{2} }}{4\gamma }} \right)I_{n} \left( { - \frac{\alpha \beta }{{2\gamma }}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{with}}\,\,\left[ {{\text{Re}} n > - 1,\,\left| {\,\arg \left( \gamma \right)} \right|\langle \frac{\pi }{4},\alpha > 0,\beta > 0} \right], \hfill \\ \end{gathered}$$
(13)

with the modified Bessel function is \(I_{m} \left( z \right) = \left( { - i} \right)^{m} J_{m} \left( {iz} \right),\) and after some tedious calculations, we derive the most important results of the current study which describe the output field of the axial intensity of the BHoChG beam propagating through the oceanic turbulence as

$$\begin{aligned} \left\langle {I_{c} \left( {0,z} \right)} \right\rangle = & i^{l} \frac{{k^{2} E_{0}^{2} }}{{2^{2 + n + m} z^{2} }}\sum\limits_{{s_{1} = 0}}^{n} {\left( {\begin{array}{*{20}c} n \\ {s_{1} } \\ \end{array} } \right)\sum\limits_{{s_{2} = 0}}^{m} {\left( {\begin{array}{*{20}c} m \\ {s_{2} } \\ \end{array} } \right)} } \frac{1}{{\beta \beta_{1} }}\exp \left[ { - \frac{{\mu^{2} }}{{4\omega_{0}^{2} }}\left( {\frac{1}{\beta } + \frac{1}{{\beta_{1} }}} \right)} \right] \\ & \quad \times \exp \left( { - \frac{{\mu^{2} }}{{4\beta \beta_{1}^{2} \omega_{0}^{2} \rho_{0}^{4} }}} \right)J_{l} \left( { - \frac{{i\mu^{2} }}{{2\beta \beta_{1} \omega_{0}^{2} \rho_{0}^{2} }}} \right), \\ \end{aligned}$$
(14)

where

$$\beta = \beta_{2} - \frac{1}{{\beta_{1} \rho_{0}^{4} }}.$$
(15)

After some calculations, the analytical expression of the on-axis average intensity distribution of the BHoShG beam propagating through oceanic turbulence is expressed as

$$\begin{aligned} \left\langle {I_{s} \left( {0,z} \right)} \right\rangle = & i^{l} \frac{{k^{2} E_{0}^{2} }}{{2^{2 + q + f} z^{2} }}\sum\limits_{{t_{1} = 0}}^{q} {\left( {\begin{array}{*{20}c} q \\ {t_{1} } \\ \end{array} } \right)\left( { - 1} \right)^{{^{{_{{t_{1} }} }} }} \sum\limits_{{t_{2} = 0}}^{f} {\left( {\begin{array}{*{20}c} f \\ {t_{2} } \\ \end{array} } \right)} } \left( { - 1} \right)^{{^{{_{{t_{2} }} }} }} \frac{1}{{\alpha \alpha_{1} }}\exp \left[ { - \frac{{\mu^{2} }}{{4\omega_{0}^{2} }}\left( {\frac{1}{\alpha } + \frac{1}{{\alpha_{1} }}} \right)} \right] \\ & \quad \times \exp \left( { - \frac{{\mu^{2} }}{{4\alpha \alpha_{1}^{2} \omega_{0}^{2} \rho_{0}^{4} }}} \right)J_{l} \left( { - \frac{{i\mu^{2} }}{{2\alpha \alpha_{1} \omega_{0}^{2} \rho_{0}^{2} }}} \right), \\ \end{aligned}$$
(16)

where.

$$\alpha_{1} = \frac{1}{{\omega_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} + a_{{t_{1} q}} \Omega - \frac{ik}{{2z}},$$
(17a)
$$\alpha_{2} = \frac{1}{{\omega_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} + a_{{t_{2} f}} \Omega + \frac{ik}{{2z}},$$
(17b)

and

$$\alpha = \alpha_{2} - \frac{1}{{\alpha_{1} \rho_{0}^{4} }}.$$
(17c)

In the following Section, we will derive the results of some interesting laser beams treated as particular cases which can be obtained from our main research endings to investigate the propagation properties in oceanic turbulence.

4 Particular cases

Our study is a general one, which allows us to derive several new studies as special cases. These results and others that have not yet been treated previously in the literature will be discussed below.

4.1 Bessel cosh-Gaussian beam

With \(n = 1\) and \(m = 1\), Eq. (14) is simplified to the analytical expression of the axial intensity distribution of the Bessel cosh-Gaussian beam traveling in oceanic turbulence and it is expressed as

$$\begin{aligned} \left\langle {I_{c} \left( {0,z} \right)} \right\rangle = & i^{l} \frac{{k^{2} E_{0}^{2} }}{{4z^{2} }}\sum\limits_{{s_{1} = 0}}^{1} {\left( {\begin{array}{*{20}c} 1 \\ {s_{1} } \\ \end{array} } \right)\sum\limits_{{s_{2} = 0}}^{1} {\left( {\begin{array}{*{20}c} 1 \\ {s_{2} } \\ \end{array} } \right)} } \,\frac{1}{{\beta \beta_{1} }}\exp \left[ { - \frac{{\mu^{2} }}{{4\omega_{0}^{2} }}\left( {\frac{1}{\beta } + \frac{1}{{\beta_{1} }}} \right)} \right] \\ & \quad \times \exp \left( { - \frac{{\mu^{2} }}{{4\beta \beta_{1}^{2} \omega_{0}^{2} \rho_{0}^{4} }}} \right)J_{l} \left( { - \frac{{i\mu^{2} }}{{2\beta \beta_{1} \omega_{0}^{2} \rho_{0}^{2} }}} \right), \\ \end{aligned}$$
(18)

where \(\beta_{1}\) and \(\beta\) are achieved by the replacement \(a_{{s_{1} 1}}\) and \(a_{{s_{2} 1}}\) in Eqs. (10a) and (15), respectively. With \(I_{c} \left( {0,z} \right)\) is the analytical expression of the received intensity of the Bessel cosh-Gaussian beam propagating in oceanic turbulence.

4.2 Bessel sinh-Gaussian beam

For \(f = 1\) and \(q = 1\), we can easily get the expression of the axial intensity of the Bessel sinh-Gaussian beam spreading through oceanic turbulence by the help of Eq. (16). This intensity is characterized by the following formula as

$$\begin{aligned} \left\langle {I_{s} \left( {0,z} \right)} \right\rangle & = i^{l} \frac{{k^{2} E_{0}^{2} }}{{4z^{2} }}\sum\limits_{{t_{1} = 0}}^{1} {\left( { - 1} \right)^{{t_{1} }} \left( {\begin{array}{*{20}c} 1 \\ {t_{1} } \\ \end{array} } \right)\sum\limits_{{t_{2} = 0}}^{1} {\left( { - 1} \right)^{{t_{2} }} \left( {\begin{array}{*{20}c} 1 \\ {t_{2} } \\ \end{array} } \right)} } \frac{1}{{\alpha \alpha_{1} }}\exp \left[ { - \frac{{\mu^{2} }}{{4\omega_{0}^{2} }}\left( {\frac{1}{\alpha } + \frac{1}{{\alpha_{1} }}} \right)} \right] \\ & \quad \times \exp \left( { - \frac{{\mu^{2} }}{{4\alpha \alpha_{1}^{2} \omega_{0}^{2} \rho_{0}^{4} }}} \right)J_{l} \left( { - \frac{{i\mu^{2} }}{{2\alpha \alpha_{1} \omega_{0}^{2} \rho_{0}^{2} }}} \right), \\ \end{aligned}$$
(19)

where \(\alpha_{1}\) and \(\alpha\) are established by putting \(a_{{t_{1} 1}}\) and \(a_{{t_{2} 1}}\) in Eqs. (17a) and (17c), respectively. With \(I_{s} \left( {0,z} \right)\) is the analytical expression of the received intensity of the Bessel sinh-Gaussian beam spreading in oceanic turbulence.

4.3 Bessel-Gaussian beam

By the use of Eq. (14), the propagation formula of the expression of the axial intensity for the Bessel-Gaussian beam propagating through oceanic turbulence becomes for \(n = 0\) and \(m = 0\).

$$\begin{aligned} \left\langle {I_{c} \left( {0,z} \right)} \right\rangle = & \left( { - 1} \right)^{l} \frac{{k^{2} E_{0}^{2} }}{{4z^{2} }}\frac{1}{{\beta \beta_{1} }}\exp \left[ { - \frac{{\mu^{2} }}{{4\omega_{0}^{2} }}\left( {\frac{1}{\beta } + \frac{1}{{\beta_{1} }}} \right)} \right] \\ & \quad \times \exp \left( { - \frac{{\mu^{2} }}{{4\beta \beta_{1}^{2} \omega_{0}^{2} \rho_{0}^{4} }}} \right)I_{l} \left( { - \frac{{\mu^{2} }}{{2\beta \beta_{1} \omega_{0}^{2} \rho_{0}^{2} }}} \right), \\ \end{aligned}$$
(20)

where the parameters \(\beta_{1}\) and \(\beta\) appearing in this equation are derived from \(a_{{s_{1} n}} = a_{{s_{2} m}} = 0\) in Eqs. (10a) and (15), respectively. \(I_{c} \left( {0,z} \right)\) describes the axial intensity of the propagation of Bessel-Gaussian beam through oceanic turbulence.

4.4 Higher-order cosh-Gaussian beam

By letting \(\mu = 0\) and \(l = 0\), Eq. (14) simplifies to the analytical expression of the average intensity for the Higher-order cosh-Gaussian beam in oceanic turbulence which is written as

$$\left\langle {I_{c} \left( {0,z} \right)} \right\rangle = \frac{{k^{2} E_{0}^{2} }}{{2^{2 + n + m} z^{2} }}\sum\limits_{{s_{1} = 0}}^{n} {\left( {\begin{array}{*{20}c} n \\ {s_{1} } \\ \end{array} } \right)\sum\limits_{{s_{2} = 0}}^{m} {\left( {\begin{array}{*{20}c} m \\ {s_{2} } \\ \end{array} } \right)} } \frac{1}{{\beta \beta_{1} }},$$
(21)

where \(\beta_{1}\) and \(\beta\) are obtained in Eqs. (10a) and (15), respectively.

In the case of \(n = m = 1\), \(\mu = 0\) and \(l = 0,\) Eq. (14) is simplified to the analytical expression to the propagation of the cosh-Gaussian beam through the oceanic turbulence. \(I_{c} \left( {0,z} \right)\) represents the expression of the axial intensity of the Higher-order cosh-Gaussian beam spreading through oceanic turbulence.

4.5 Higher-order sinh-Gaussian beam

By setting \(\mu = 0\) and \(l = 0\) in Eq. (16) so, the analytical expression of the axial intensity distribution of the Higher-order sinh-Gaussian beam traveling in oceanic turbulence given by the following expression

$$\left\langle {I_{s} \left( {0,z} \right)} \right\rangle = \frac{{k^{2} E_{0}^{2} }}{{2^{2 + f + q} z^{2} }}\sum\limits_{{t_{1} = 0}}^{q} {\left( {\begin{array}{*{20}c} q \\ {t_{1} } \\ \end{array} } \right)\left( { - 1} \right)^{{t_{1} }} \sum\limits_{{t_{2} = 0}}^{f} {\left( {\begin{array}{*{20}c} f \\ {t_{2} } \\ \end{array} } \right)} } \left( { - 1} \right)^{{t_{2} }} \frac{1}{{\alpha \alpha_{1} }},$$
(22)

where \(\alpha_{1}\) and \(\alpha\) are derived by the use Eqs. (17a) and (17c), respectively.

Another case added to our results, it is the sinh-Gaussian beam through oceanic turbulence when \(q = f = 1\), \(\mu = 0\) and \(l = 0\) introduced in Eq. (16). \(I_{s} \left( {0,z} \right)\) indicates the axial intensity of the Higher-order sinh-Gaussian beam as it spreads across oceanic turbulence.

4.6 Gaussian beam

We explore our main result, the fundamental Gaussian beam which is considered a specific case of our findings when \(\mu = 0\), \(m = n = 0\) and \(l = 0\). Then, Eq. (14) yields

$$\left\langle {I_{c} \left( {0,z} \right)} \right\rangle = \frac{{k^{2} E_{0}^{2} }}{{4z^{2} }}\frac{1}{{\beta_{1} \beta }},$$
(23)

where the parameters \(\beta_{1}\) and \(\beta\) are obtained by putting \(a_{{s_{1} n}} = a_{{s_{2} m}} = 0\) in Eqs. (10a) and (15), respectively. The expression of the axial intensity of the Gaussian beam propagating in oceanic turbulence is \(I_{c}\).

We study numerically in the following, the evolution behavior of the BHoChG beam and the BHoShG beam after they spread over oceanic turbulence by using the results acquired in the preceding section.

5 Numerical results and analysis

In this Section, we numerically investigate the propagation characteristics of the BHoChG beam and the BHoShG beam propagating through oceanic turbulence based on Eqs. (14) and (16) by adjusting the parameters of the input beam and the propagation medium. The calculation parameters are set to be, unless other values are specified in the caption: \(\lambda = 1310nm,\,\) \(\Omega = 100m^{ - 1} ,\) \(\omega_{0,\,} = 0.05m,\) \(\chi_{T} = 10^{ - 8} K^{2} s^{ - 1} ,\,\,\) \(\zeta = - 2.5\) and \(\varepsilon = 10^{ - 7} m^{2} s^{ - 3}\).

Firstly, we analyzed the evolution of the normalized intensity distribution of the BHoChG beam in oceanic turbulence and compared it with the BHoShG beam. Figure 3 presents the normalized intensity distribution of these beams passing through oceanic turbulence for different values of the dissipation rate of the mean-square temperature parameter \(\chi_{T}\) at two values of the Bessel order \(l\). We can see from this figure that, the axial intensity of the BHoChG beam increases with the increase of the parameter of oceanic turbulence \(\chi_{T}\) until it reaches a maximum value at the position \(z_{\max } ,\) then it decreases gradually and vanishes for large values of \(z\). Meanwhile, it is observed that the BHoChG loses its first profile during the propagation under the short propagation distance and it becomes very focused when \(\chi_{T}\) are larger with the complete vanishing of its first dark spot at the position \(z_{\max }\) which means that the medium is turbulent.

Fig. 3
figure 3

Normalized intensity of the propagation of the BHoChG beam (top row) and the BHoShG beam (bottom row) for different values of \(\chi_{T}\): a \(l = 1\) and b \(l = 2\) with \(n = 3\)

Full size image

Therefore, the on-axis intensity decreases while increasing the Bessel order so, the propagation of the BHoChG beam is more resistant to oceanic turbulence, in this case the dark spot size becomes larger. However, plots in Fig. 3 show that the axial intensity of the BHoShG beam increases with the propagation distance \(z\). It is also seen that the propagating beam present two different behaviors, one for the near field which the beam spreads quickly in the medium and the second one for the far field. However, in the far field the beam loses its concentration and evolves to recover its original dark hollow properties due to the effect of the oceanic turbulence. Additionally, the axial intensity of the BHoShG beam increases with the Bessel order function. This study also concludes that the beam is resist more to the effects of oceanic turbulence for small values of \(\chi_{T}\).

The distribution of the on-axis intensity of the BHoChG beam and the BHoShG beam in oceanic turbulence versus the propagation distance is illustrated in Fig. 4 for two values of the Bessel order function by varying the ratio of temperature to salinity parameter \(\zeta\). From this illustration, we can see that the axial intensity of the BHoShG beam during the propagation occurs more rapidly by increasing the parameter \(\zeta\).

Fig. 4
figure 4

Normalized intensity as a function of the propagation distance z of the BHoChG beam (top row) and the BHoShG beam (bottom row) for different values of \(\zeta\) with \(n = 2\) and \(\mu = 2.5\): a \(l = 1\) and b \(l = 2\)

Full size image

It is also evident that more \(\zeta\) is smaller; the BHoChG beam propagates a larger distance before it loses its first central dark spot. However, we find out that by increasing the parameter \(\zeta\) the axial intensity of the BHoShG becomes smaller and can keep its original intensity profile. In this case, it is changing slowly by increasing the propagation distance and the beam becomes less focused. Based upon this, the axial intensity profile takes a wide shape with the decrease in the ratio of temperature to salinity parameter. We conclude that the BHoChG beam and the BHoShG beam have better capacity to resist the fluctuations created by oceanic turbulence for weak values of \(\zeta\).

The effect of the parameter \(\varepsilon\), which means the rate of dissipation of turbulent kinetic energy per unit mass of fluid on the intensity properties of the BHoChG beam and compared with the BHoShG beam propagating in the oceanic turbulence is treated in Fig. 5 for two values of the Bessel order function. Therefore, the numerical results show that the parameter \(\varepsilon\) has a significant impact on the output beam of the normalized intensity, which becomes weak as \(\varepsilon\) and \(l\) are higher.

Fig. 5
figure 5

Normalisszed intensity of the propagation the BHoChG beam (top row) and the BHoShG beam (bottom row) for different values of \(\varepsilon\) with \(n = 2\): a \(l = 1\) and b \(l = 2\)

Full size image

This means that more the parameter \(\varepsilon\) is larger, the beam travels a greater distance before the loses its first central dark spot at \(z = z_{\max }\) and the axial intensity profile takes wide shape. It can be inferred that the central dark core of the BHoChG beam will gradually increases with the parameter \(\varepsilon\) and the Bessel orders or the propagation distance increasing. Furthermore, the results reveal that the BHoShG beam spreads faster with small \(\varepsilon\) and weak axial intensity.

However, we can conclude from this figure that the spreading properties of the beams through oceanic turbulence can resist to stronger fluctuations of turbulence for larger values of \(\varepsilon\). Here, we present the impact of the beam order \(n\) on the evolution properties of the BHoChG beam and the BHoChG beam in oceanic turbulence. Figure 6 gives the on-axis average intensity of these beams propagating through the oceanic turbulence versus the propagation distance for different values of beam order \(n\) and for two values of the parameters \(\mu\).

Fig. 6
figure 6

Normalized intensity as a function of the propagation distance z of the BHoChG beam (top row) and the BHoShG beam (bottom row) for different values of \(n\) with \(l = 3\): a \(\mu = 1.5\) and b \(\mu = 2.5\)

Full size image

It should be noted that as the beam order increases, the axial intensity of the BHoChG beam increases. It means that the BHoChG beam spreads much faster for a low value of the beam order, showing that a laser beam has a weak resistance to the disturbances of the oceanic. It is found that on-axis intensity of the BHoShG beam vanishes at short propagation distances which means that the beam spreads more rapidly for higher order of the beam due to the diffraction process.

To learn about the spreading characteristics of a BHoChG beam and the BHoShG beam on the propagation in oceanic turbulence, we analyze the influence of the parameter \(\Omega\) based on the derived Eqs. (14) and (16). The evolution behavior of the variation of the on-axis average intensity of the two-beam propagating through this medium versus the propagation distance is plotted in Fig. 7. It is evident that the beams spread more rapidly as the parameter \(\Omega\) decreases. Moreover, this figure shows that the axial intensity distribution is larger as the value of \(\Omega\) increases but at small values of the Bessel order. We deduce that the BHoShG beam is more influenced by the decentered parameter compared to the BHoChG beam. That is to say, for a laser beam to resist more, its decentered parameter width should be large. To check the impact of the beam waist width \(\omega_{0}\) on the propagation through oceanic turbulence, we plot in Fig. 8 the on-axis average intensity of the BHoChG beam and the BHoShG beam versus the propagation distance for different values of the beam waist width. It can be observed that when the beam waist width increases, the axial intensity also increases which means that the beam can resist to stronger fluctuation of turbulence. Then, it decreases gradually with rising the propagation distance that is to say the propagating beam may lose its dark dip center faster in far field. This study also shows that is \(\omega_{0}\) has a significant impact on the propagation of the BHoShG beam compared to the BHoChG beam. We can deduce that the BHoChG beam and the BHoShG beam are more resistant to oceanic turbulence when \(\omega_{0}\) is large. In order to investigate the influence of the wavelength \(\lambda\) on the beam propagation, Fig. 9 gives the evolution of the on-axis average intensity of the BHoChG beam and the BHoShG beam traveling in oceanic turbulence as a function of the propagation distance for three values of the wavelength. From this figure, the intensity distribution increases when the wavelength weakens. It was also found that as shown in Fig. 9, the normalized intensity distribution of the BHoShG beam increases with the wavelength. In addition, one can clearly deduce that the propagation of these beams is more resistant to the oceanic turbulence when the wavelength is small. That means that the considered beams spread more rapidly when \(\lambda\) is longer.

Fig. 7
figure 7

Normalized intensity of the propagation of the BHoChG beam (top row) and the BHoShG beam (bottom row) versus the propagation distance \(z\) for different values of \(\Omega\) with \(\mu = 0.5\) and \(n = 3\): a \(l = 1\) and b \(l = 2\)

Full size image
Fig. 8
figure 8

Normalized intensity of the BHoChG beam (top row) and the BHoShG beam (bottom row) for different values of \(\omega_{0}\) with \(\mu = 2.5\) and \(n = 3\): a \(l = 1\) and b \(l = 2\)

Full size image
Fig. 9
figure 9

Normalized intensity of the BHoChG beam (top row) and the BHoShG beam (bottom row) for different values of \(\lambda\) with \(\mu = 40,\) \(n = 3\) and \(l = 1\): a \(\varepsilon = 10^{ - 1} \,m^{2} s^{ - 3}\) and b \(\varepsilon = 10^{ - 3} \,m^{2} s^{ - 3}\)

Full size image

6 Conclusion

In this paper, the evolution of the average intensity of the BHoChG beam and BHoShG beam spreading through oceanic turbulence is investigated analytically, benefiting the extended Huygens-Fresnel integral and analyzed numerically. The axial intensity of various laser beams has been derived from our results as particular cases of the BHoChG beam and the BHoShG beam. Additionally, this study analyzes the impact of oceanic turbulence parameters and the source beam parameters such as the beam waist width and the parameter \(\Omega \,.\) It is shown that the BHoChG beam and BHoShG beam travel a long distance in the oceanic turbulence after losing their original profiles, which means that our beams can resist strong oceanic turbulence with small dissipation rates of temperature variance, large rates of dissipation of kinetic energy per unit mass of fluid, lower relative strength of temperature and salinity fluctuations, wider beam waist and a higher decentered parameter. The findings in this work will help researchers better understand the propagation parameters of the BHoChG beam compared with the BHoShG beam in oceanic turbulence, which will be beneficial for optical underwater communication, remote sensing, imaging and other applications.