Introduction of Bessel higher-order cosh-Gaussian beam and its propagation through a paraxial ABCD optical system

Abstract

In this paper, we introduce a new laser beam called Bessel higher-order cosh-Gaussian (BHChG) beam and analyzed its propagation properties through a paraxial ABCD optical system. The analytical expression of the diffracted beam is derived based on the extended Huygens–Fresnel integral and some numerical examples of BHChG beam propagating in a free space, through a thin lens and a Fractional Fourier transform system are exposed. The results reveal that the behavior of the output BHChG beam is affected by the optical system and the source beam parameters. The propagation of some laser beams through a paraxial ABCD optical system is deduced as particular case from the present study such as the fundamental Gaussian beam, the Bessel-Gaussian beam, the cosh-Gaussian beam, the Bessel-cosh-Gaussian beam and the Higher-order-cosh-Gaussian beam. The outcomes can be helpful for free-space optical communication, remote sensing and optical micromanipulation.

1 Introduction

The Bessel higher-order cosh-Gaussian (BHChG) beam is a model light beam proposed to describe a laser beam including Bessel cosh-Gaussian, Bessel-Gaussian and Gaussian beams regarded as special cases of this beam. Introducing the higher-order cosh function in BHChG beam presents advantage practical use of Gaussian function in laser physics due to its high-power extraction capabilities and its profile flexibility. Additionally, the Bessel-Gaussian beam is obtained from the Bessel beam modulated by a Gaussian envelope known as a solution of the paraxial Helmholtz equation in cylindrical coordinates. Higher-order Bessel beams show a dark central core surrounded by consecutive brilliant and dark rings, unlike the zeroth-order Bessel beam which presents bright center core with intense intensity. Bessel beams can have helical wavefronts and an optical axis phase singularity, defining them as vortex beams.

Apart from that, the usual optical devices often used to guide the light beams from a source plane to a reception plane, have known a considerable interest for laser applications over the years. As an example, free-space optical communication systems which have increased their level of competition in broadband access networks. So fundamental research area is interested in studying the propagation of laser beams through paraxial optical systems as thin lens and FRFT system (Nossir et al. 2020; Belafhal and Dalil-Essakali 2000; Monin and Ustinov 2018; Augustyniak et al. 2020; Benzehoua and Belafhal 2023a, b; Chib et al. 2022; Boufalah et al. 2019). This later system was initially developed by Namias (1980) as a mathematical tool to address issues in quantum mechanics and later applied to the optics field by several researchers (Zhou 2009; Chen et al. 2009; Mendlovic and Ozaktas 1993; Ozaktas and Mendlovic 1993).

The propagation properties of laser beams through paraxial optical systems have been extensively developed since several years due to their potential applications in various fields such as metrology, micromanipulation of particles, atom guidance, optical trapping and tweezers (Soskind and Soskind 2015; Arlt et al. 2001; Xu et al. 2000; Ashkin et al. 1987; Ho and Hoang 2012). During the last years, the transformation properties through optical systems is investigated for large kinds of light beams modulated with cosine-hyperbolic function such as pulsed Laguerre higher-order cosh-Gaussian (Benzehoua and Belafhal 2023a, b), higher-order cosh-Gaussian beam (Zhou and Zheng 2009), elegant Hermite cosh-Gaussian laser beams (Yu et al. 2002), Circular cosine-hyperbolic-Gaussian beam (Hricha et al. 2022; El Halba et al. 2022), vortex Hermite-cosh-Gaussian beams (El Halba et al. 2021) and Hollow higher-order cosh-Gaussian beams (Saad and Belafhal 2021) and so on.

Furthermore, we introduce a new laser beam family named Bessel higher-cosh-Gaussian (BHChG) beam that is derived from the Laguerre higher-order cosh-Gaussian (LHChG) beam (Benzehoua and Belafhal 2023a, b). Based on the work of Kotlyar et al. (2022) and Saad et al. (2017) and by expressing Laguerre-Gaussian beams versus Bessel beams (Mendoza-Hernández et al. 2015) in some conditions, the field distribution of BHChG beam is evaluated. The experimental realization of this beam can be made as it was described by Durnin (1987) and Durnin et al. (1987), where Bessel-Gaussian beams can be obtained by the modulation of Bessel beam with a Gaussian aperture. The higher order-cosh function appearing in the formula of BHChG beam, which is as a superposition of Gaussian functions, is considered as a Gaussian truncation. Subsequently, the BHChG beam is created experimentally.

In the present study, we investigate the evolution of BhChG beam upon the propagation through a paraxial ABCD optical system. The studied beam has the advantage that it covers a broad range of beams such as the Gaussian beam, the Bessel-Gaussian beam, the cosh-Gaussian beam, the Bessel-cosh-Gaussian beam and higher-order cosh-Gaussian beam. The initial parameters of BHChG beam can be adjusted to increase the freedom of controlling the beam profile's features. This particularity of beam is important for some applications including free space optics, higher power efficiency techniques and micro-optics. The manuscript is structured: In the following section, the field distribution of the BHChG beam is exposed and its evolution profile is discussed with numerical illustrations. In the third section, the analytical expression of the diffracted beam is derived based on the Huygens–Fresnel integral ABCD Collins formula. In the fourth Section, some numerical examples are performed in free space, thin lens and FRFT system and discussed. Finally, the main results are summarized in the conclusion part.

2 Field distribution of Bessel higher-order cosh-Gaussian beam

We introduce a new laser beam family named Bessel higher-order cosh-Gaussian (BHChG). It is a versatile laser beam that can be used to describe a wide range of laser beams, including the Bessel higher-order cosh-Gaussian, Bessel-Gaussian, cosh-Gaussian and Gaussian beams as special cases. Hence, the field distribution of the considered beam can be written, in the polar coordinates, at the source plane as

$$E\left( {r,\theta ,0} \right) = E_0 \exp \left( {il\theta } \right)J_l \left( {\frac{\mu r}{{\omega_0 }}} \right)ch^n \left( {\Omega r^2 } \right)\exp \left( { - \frac{r^2 }{{\omega_0^2 }}} \right),$$

(1)

where $E_0$ is the amplitude of the field, $J_l$ denotes the l-th order Bessel function of the first kind, $\omega_0$ is the waist width of the fundamental Gaussian mode, $\theta$ is the phase term of the beam, $\Omega$ designates the parameter associated with the cosh part, $n$ is the beam order and $\mu$ is the transverse component of the wave factor. Applying the following explicit formulae of cosh (.) (Abramowitz and Stegun 1970)

$$ch^n \left( {\Omega r^2 } \right) = \frac{1}{2^n }\sum_{s = 0}^n {\frac{n!}{{\left( {n - s} \right)!s!}}\exp \left( {a_{sn} \Omega r^2 } \right)} ,$$

(2)

where the exclamation mark $!$ indicates the factorial $n! = \Gamma \left( {n + 1} \right)$ and $a_{sn} = 2s - n$.

Equation (1) can be written as

$$E\left( {r,\theta ,0} \right) = E_0 \frac{1}{2^n }\exp \left( {il\theta } \right)J_l \left( {\frac{\mu }{\omega_0 }r} \right)\sum_{s = 0}^n {\left( {\begin{array}{*{20}c} n \\ s \\ \end{array} } \right)\exp \left[ { - \left( {\frac{1}{\omega_0^2 } + a_{sn} \Omega } \right)r^2 } \right]} ,$$

(3)

where $\left( {\begin{array}{*{20}c} n \\ s \\ \end{array} } \right)$ is the binomial coefficient.

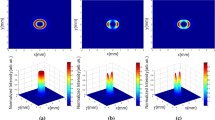
In Fig. 1, we illustrate the intensity distribution of BHChG beam given by Eq. (3) for different beams orders $(n,l)$ and with fixed values of $\Omega$ and $\mu$. From the plots of the figure, we can note that the intensity distribution of the laser beam corresponds to that of Bessel-Gaussian beam of zero-order when the beam order $l$ takes on a zero value.

Fig. 1

Three-dimensional intensity distribution of BHChG beam at the source plane. for different values of $n$ and $l$: a $l = 0$, b $l = 1$ and c $l = 3$ with $\Omega = 0.2\,{\text{mm}}^{ - 1}$ and $\mu = 3$. Top row $n = 0$, middle row $n = 1$ and bottom row $n = 3$

When $l > 0$, the beam profile is characterized by a dark center region with zero intensity whose radius expands noticeably with increasing $(n,l)$. In this latter case, the beam keeps its invariant profile and shows two pics with a light intensity distribution that increases with beams orders. Because of its unique features, the BHChG beam can be expected to be useful in trapping and manipulating microscopic particles.

To show the impact of the source parameters on the behavior of BHChG beam, typical illustrations of the intensity distribution for three values of $l$ are given in Fig. 2. It is seen from the plots that the intensity distribution of BHChG beam decreases when $l$ becomes large. From the graphics, one can also see for all values of $l$ that the intensity increases and the positions of the two lobes move towards the higher values of the transverse coordinate $r/\omega_0$ with further increasing the two parameters $\mu$ and $\Omega$.

Fig. 2

Intensity distribution of BHChG beam at the initial plane for different values of $l$: a $l = 1$, b $l = 2$ and c $l = 3$ with $\Omega = 0.2\,{\text{mm}}^{ - 1}$, $n = 3$ and $\mu = 3$

3 Propagation of BHChG beam through a paraxial ABCD optical system

The field distribution of the BHChG beam propagating through a paraxial ABCD optical system along the z-direction is expressed, in the cylindrical coordinates system, by using the Huygens–Fresnel diffraction integral in the paraxial approximation as (Collins 1970)

$$E\left( {\rho ,\varphi ,z} \right) = - \frac{ik}{{2\pi B}}\exp \left( {ikz} \right)\int_0^{ + \infty } {\int_0^{2\pi } {E_0 \left( {r,\theta ,0} \right)} } \exp \left[ {\frac{ik}{{2B}}\left( {Ar^2 - 2\rho r\cos \left( {\theta - \varphi } \right) + D\rho^2 } \right)} \right]rdrd\theta ,$$

(4)

where $\left( {r,\theta ,0} \right)$ and $\left( {\rho ,\varphi ,z} \right)$ are the coordinates of the field at the input and the output planes respectively, $z$ is the optical path length along the propagation axis from the initial plane to the output plane. A, B and D represent the transfer matrix elements of the paraxial optical system and $k = \frac{2\pi }{\lambda }$ designates the wavenumber with $\lambda$ is the wavelength of laser light.

Substituting Eq. (3) into Eq. (4) and using the following identity (Gradshteyn and Ryzhik 1994)

$$\int_0^{2\pi } {\exp \left( {il\varphi_0 } \right)\exp } \left[ { - i\frac{k\rho }{B}r\cos \left( {\varphi - \varphi_0 } \right)} \right]d\varphi = i^l 2\pi J_l \left( {\frac{k\rho }{B}r} \right)\exp \left( {il\varphi } \right).$$

(5)

By recalling the following formula (Ditkine and Proudnikov 1978)

$$\int_0^\infty {x\exp \left( { - \gamma x^2 } \right)} J_n \left( {\alpha x} \right)J_n \left( {\beta x} \right)dx = \frac{1}{2\gamma }\exp \left( { - \frac{\alpha^2 + \beta^2 }{{4\gamma }}} \right)I_n \left( {\frac{\alpha \beta }{{2\gamma }}} \right),$$

(6)

here $I_n$ is the modified Bessel function of the order $n$.

One obtains the analytical expression of the field distribution at the output plane of the BHChG beam propagating through a paraxial ABCD optical system

$$\begin{aligned} E\left( {\rho ,\varphi ,z} \right) & = - \frac{{ki^{l + 1} }}{{2^{n + 1} B}}E_0 \exp \left( {il\varphi } \right)\exp \left[ {ik\left( {z + \frac{D\rho^2 }{{2B}}} \right)} \right] \\ & \quad \times \sum_{s = 0}^n {\left( {\begin{array}{*{20}c} n \\ s \\ \end{array} } \right)} \frac{1}{\alpha }\exp \left[ { - \frac{1}{4\alpha }\left( {\frac{\mu^2 }{{\omega_0^2 }} + \frac{k^2 \rho^2 }{{B^2 }}} \right)} \right]J_l \left( {i\frac{k\mu \rho }{{2B\alpha \omega_0 }}} \right), \\ \end{aligned}$$

(7)

where

$$\alpha = \frac{1}{\omega_0^2 } - a_{sn} \Omega - i\frac{kA}{{2B}}.$$

(8)

The expression of Eq. (7) can be expressed as

$$\begin{aligned} E\left( {\rho ,\varphi ,z} \right) & = - \frac{iN_B }{{2^n A\omega_0^2 }}E_0 \exp \left( {il\varphi } \right)\exp \left( {\frac{2izBN_B }{{A\omega_0^2 }}} \right)\exp \left( {\frac{iDN_B }{{A\omega_0^2 }}\rho^2 } \right) \\ & \quad \times \sum_{s = 0}^n {\left( {\begin{array}{*{20}c} n \\ s \\ \end{array} } \right)} \frac{1}{\alpha }\exp \left( { - \frac{\mu^2 }{{4\alpha \omega_0^2 }}} \right)\exp \left( { - \frac{N_B^2 }{{\alpha A^2 \omega_0^4 }}\rho^2 } \right)J_l \left( {\frac{iN_B \mu }{{\alpha A\omega_0^3 }}\rho } \right), \\ \end{aligned}$$

(9)

where

$$N_B = \frac{k\omega_0^2 A}{{2B}}.$$

(10)

Equation (7) is the main result of this paper. In the following, we present particular cases of beams propagating through a paraxial ABCD optical system deduced from our study.

3.1 Particular cases

3.1.1 Bessel cosh-Gaussian beam

By letting $n = 1$, Eq. (1) reduces to that of a Bessel cosh-Gaussian beam written as

$$E\left( {r,\theta ,0} \right) = E_0 \exp \left( {il\theta } \right)J_l \left( {\frac{\mu r}{{\omega_0 }}} \right)ch\left( {\Omega r^2 } \right)\exp \left( { - \frac{r^2 }{{\omega_0^2 }}} \right).$$

(11)

The analytical formula of the Bessel cosh-Gaussian beam diffracted by a paraxial ABCD optical system is derived from Eq. (7) as

$$\begin{aligned} E\left( {\rho ,\varphi ,z} \right) & = - \frac{{ki^{l + 1} }}{2B}E_0 \exp \left( {il\varphi } \right)\exp \left[ {ik\left( {z + \frac{D\rho^2 }{{2B}}} \right)} \right] \\ & \quad \times \sum_{s = 0}^1 {\left( {\begin{array}{*{20}c} 1 \\ s \\ \end{array} } \right)} \frac{1}{\alpha }\exp \left[ { - \frac{1}{4\alpha }\left( {\frac{\mu^2 }{{\omega_0^2 }} + \frac{k^2 \rho^2 }{{B^2 }}} \right)} \right]J_l \left( {i\frac{k\mu \rho }{{2B\alpha \omega_0 }}} \right), \\ \end{aligned}$$

(12)

with

$$\alpha = \frac{1}{\omega_0^2 } - \Omega \left( {a_{01} + a_{11} } \right) - i\frac{k}{2B}.$$

(13)

3.1.2 Bessel-Gaussian beam

By setting $n = 0$, Eq. (1) is simplified to the field distribution of Bessel-Gaussian beam given by

$$E\left( {r,\theta ,0} \right) = E_0 \exp \left( {il\theta } \right)J_l \left( {\frac{\mu r}{{\omega_0 }}} \right)\exp \left( { - \frac{r^2 }{{\omega_0^2 }}} \right).$$

(14)

Equation (7) reduces to the field distribution of Bessel-Gaussian beam diffracted by a paraxial ABCD optical system expressed as

$$E\left( {\rho ,\varphi ,z} \right) = - \frac{{i^{l + 1} k}}{2B\alpha }E_0 \exp \left( {il\varphi } \right)\exp \left[ {ik\left( {z + \frac{D\rho^2 }{{2B}}} \right)} \right]\exp \left[ { - \frac{1}{4\alpha }\left( {\frac{\mu^2 }{{\omega_0^2 }} + \frac{k^2 \rho^2 }{{B^2 }}} \right)} \right]J_l \left( {i\frac{k\mu \rho }{{2B\alpha \omega_0 }}} \right),$$

(15)

where

$$\alpha = \frac{1}{\omega_0^2 } - i\frac{k}{2B}.$$

(16)

This finding agrees with the result given by Belafhal and Dalil-Essakali study (2000) for the propagation of Bessel-Gaussian beam through a paraxial ABCD optical system.

3.1.3 Higher-order cosh-Gaussian beam

When $\mu = 0$ and $l = 0$, Eq. (1) is simplified to the initial field distribution of the Higher-order cosh-Gaussian beam and expressed as

$$E\left( {r,0} \right) = E_0 ch^n \left( {\Omega r^2 } \right)\exp \left( { - \frac{r^2 }{{\omega_0^2 }}} \right).$$

(17)

The analytical expression of the field distribution at the output plane is deduced from Eq. (7) and written as

$$E\left( {\rho ,z} \right) = - \frac{{i^{l + 1} k}}{{2^{n + 1} B}}E_0 \exp \left[ {ik\left( {z + \frac{D\rho^2 }{{2B}}} \right)} \right]\sum_{s = 0}^n {\left( {\begin{array}{*{20}c} n \\ s \\ \end{array} } \right)} \frac{1}{\alpha }\exp \left( { - \frac{1}{4\alpha }\frac{k^2 \rho^2 }{{B^2 }}} \right),$$

(18)

where

$$\alpha = \frac{1}{\omega_0^2 } - a_{sn} \Omega - i\frac{k}{2B}.$$

(19)

3.1.4 cosh-Gaussian beam

To find the cosh-Gaussian beam in the input plane, we put $n = 1$, $\mu = 0$ and $l = 0$ in Eq. (1). Then the field distribution is expressed as

$$E\left( {r,0} \right) = E_0 ch\left( {\Omega r^2 } \right)\exp \left( { - \frac{r^2 }{{\omega_0^2 }}} \right).$$

(20)

The analytical expression of the field distribution for cosh-Gaussian beam diffracted by a paraxial ABCD optical system is derived from Eq. (7) as

$$E\left( {\rho ,z} \right) = - \frac{ik}{{4B}}E_0 \exp \left[ {ik\left( {z + \frac{D\rho^2 }{{2B}}} \right)} \right]\sum_{s = 0}^1 {\left( {\begin{array}{*{20}c} 1 \\ s \\ \end{array} } \right)} \frac{1}{\alpha }\exp \left( { - \frac{k^2 \rho^2 }{{4\alpha B^2 }}} \right),$$

(21)

where

$$\alpha = \frac{1}{\omega_0^2 } - \Omega \left( {a_{01} + a_{11} } \right) - i\frac{k}{2B}.$$

(22)

3.1.5 Gaussian beam

When $\mu = 0$, $n = 0$ and $l = 0$ in the initial field of BHChG beam, Eq. (1) reduces to the field distribution of a Gaussian beam given by

$$E\left( {r,0} \right) = E_0 \exp \left( { - \frac{r^2 }{{\omega_0^2 }}} \right).$$

(23)

The spreading formula of a Gaussian laser beam propagating through a paraxial ABCD optical system deduced from Eq. (7) is written as

$$E\left( {\rho ,z} \right) = - \frac{ik}{{2B\alpha }}E_0 \exp \left[ {ik\left( {z + \frac{D\rho^2 }{{2B}}} \right)} \right]\exp \left\{ { - \frac{k^2 \rho^2 }{{4\alpha B^2 }}} \right\},$$

(24)

with

$$\alpha = \frac{1}{\omega_0^2 } - i\frac{k}{2B},$$

(25)

which corresponds to the result of Dickson (1970).

4 Numerical results and discussions

In this Section, we will illustrate numerical examples using the analytical expression given by the Eq. (7) to investigate the propagation features of BHChG beam in free space, thin lens and Fractional Fourier transform system. The simulations parameters are chosen as $\omega_0 = 1\,{\text{mm}}$, $\lambda = 632.8\,{\text{nm}}$, $\Omega = 0.2\,{\text{mm}}^{ - 1}$.

4.1 Free space propagation

In this part, we will treat the transformation of the BHChG beam in free space system represented by the following matrix

$$\left( {\begin{array}{*{20}c} A & B \\ C & D \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 1 & z \\ 0 & 1 \\ \end{array} } \right),$$

(26)

where z is the propagation distance between the reference planes.

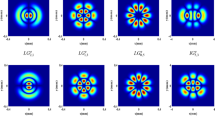
Figure 3 describes the intensity evolution of the BHChG beam propagating in free space with different values of propagation distance and for three values of the beam order l. From the illustrated plots, it is indicated that the BHChG beam presents a central dark region except for $l = 0$ where the beam takes the zero-order Bessel cosh-Gaussian beam profile. We can see from the plots that the intensity distribution BHChG beam decreases and the central dark region (for l > 0) gets wide as the beam order l increases. It is also seen that the intensity decreases and the width peak broadens upon propagation of BHChG beam in free space.

Fig. 3

Intensity profile of BHChG beam propagating in free space. for different values of $n$ and $l$: a $l = 0$, b $l = 1$ and c $l = 3$ for $\mu = 3$. Top row $\left( {z = 1000\,{\text{mm}}} \right)$, middle row $\left( {z = 2000\,{\text{mm}}} \right)$ and bottom row $\left( {z = 3000\,{\text{mm}}} \right)$

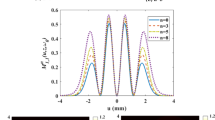
Figures 4, 5 and 6 describe the intensity evolution of the BHChG beam propagating in free space as a function of the transverse coordinate ${\rho / {\omega_0 }}$ with different parameters characterizing the diffracted BHChG beam and with three values of the beam order $l$. Figure 4 shows the comportment of BHChG beam by varying the beam waist and the wavelength of the light source.

Fig. 4

Intensity distribution of BHChG beam propagating in free space for different values of $l$: a $l = 0$, b $l = 1$ and c $l = 3$ with $n = 3$, $\mu = 3$ and $z = 1000\,{\text{mm}}$

Fig. 5

Intensity distribution of the BHChG beam propagating in free space for different values of $\mu$, $\Omega$ and $l$: a $l = 1$, b $l = 2$ and c $l = 3$ with $n = 3$, $z = 1000\,{\text{mm}}$, $\mu = 3$ and $N_B = \pi$

Fig. 6

Intensity distribution of BHChG beam propagating in free space for different values of $\mu$, $\Omega$ and $l$: a $l = 1$, b $l = 2$ and c $l = 3$ with $n = 3$, $z = 1000\,{\text{mm}}$, $\mu = 3$ and $N_B = \pi \cdot 10^{ - 3}$

One can point out that the output BHChG beam have a hollow profile and the width of the central dark region becomes greater by further increasing $l$. We can see from the plots that, the intensity distribution of the BHChG beam decreases by increasing $l$ and the wavelength and by decreasing the beam waist. It is also seen that the positions of the peaks move toward the high values of the transverse coordinate as the beam order $l$ and the wavelength $\lambda$ increase and the beam waist $\omega_0$ decreases.

In Fig. 5, we illustrate the intensity distribution of the BHChG beam traveling in free space versus the transverse coordinate ${\rho / {\omega_0 }}$ in the Fresnel diffraction region $\left( {N_B = \pi } \right)$. We can note that the diffracted beam keeps the same comportment as compared to the input beam.

Figure 6 indicates the intensity distribution of the BHchG beam in the Fraunhofer diffraction zone $\left( {N_B = \pi \cdot 10^{ - 3} } \right)$ for studying the propagation properties of the considered beam in this part.

The curves show that as $l$ grows, the central dark spot at the center of the diffracted beam becomes noticeably larger and the position of the two lobes tend toward the higher values of the transverse coordinate ${\rho / {\omega_0 }}$.

Figure 7 presents the phase distribution of the propagation of the BHChG across a free space optical system for four values of the $l$. It is shown that with increasing l from 1 to 4, the phase structure becomes more and more observable. Additionally, the vertical antisymmetry of the beam phase appeared for odd modes which could have promising utility in various fields of physics.

Fig. 7

The phase distribution of the BHChG propagating in a free space optical system with different values of l with $z = 2000\,{\text{mm}}$ and n = 3: a l = 1, b l = 2, c l = 3 and d l = 4

4.2 Thin lens in free space

Now, let us consider a thin lens in a free space represented by the transfer matrix as

$$\left( {\begin{array}{*{20}c} A & B \\ C & D \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\frac{1 - z}{f}} & z \\ { - \frac{1}{f}} & 1 \\ \end{array} } \right).$$

(27)

To investigate the propagation properties of BHChG beam through a thin lens in a free space, we display in Fig. 8 the intensity distribution of the diffracted beam given by Eq. (7) for various values of the beam order l and for three values of the focal length.

Fig. 8

Intensity distribution of BHChG beam propagating through a thin lens for different values of $l$ and $f$: a $f = 50\,{\text{mm}}$, b $f = 150\,{\text{mm}}$ and c $f = 250\,{\text{mm}}$ with $z = 500\,{\text{mm}}$, $\mu = 1.5$ and $n = 3$. Top row $l = 1$, middle row $l = 2$ and bottom row $l = 3$

As seen from the plots, the peak intensity progressively increases with the focused length while the breadth of the rings starts to contract and their position advances towards the tiny values of ${x / {\omega_0 }}$. This figure shows that even when the beam order is changed, the beam keeps a similar shape profile and comportment during free-space propagation through a thin lens. Figure 9 shows the phase distribution of the various forms of the BHChG beam for several beam orders l. From the plots, we can observe that the spiral phase structure can be rotated counterclockwise with the increase of the topological charge l. Moreover, in the case of the odd modes the phase distribution shows a vertical antisymmetry.

Fig. 9

The phase distribution of the BHChG propagating through a thin lens for different values of l with $z = 500\,{\text{mm}}$,$f = 150\,{\text{mm}},$$\mu = 1.5$ and n = 3: a l = 1, b l = 2, c l = 3 and d l = 4

4.3 Fractional Fourier transform system

The propagation properties of BHChG beam through a FRFT system will be examined in this section. The transfer matrix associated to this optical system is expressed as

$$\left( {\begin{array}{*{20}c} A & B \\ C & D \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\cos \phi } & {f\sin \phi } \\ { - {{\sin \phi } / f}} & {\cos \phi } \\ \end{array} } \right),$$

(28)

where $\phi = {{p\pi } / 2}$, $f$ is the standard focal length and $p = 2m + 1$ is the order of FRFT system with $m$ is a positive number.

The evolution of the intensity distribution of BHChG beam through a FRTF system is illustrated in Fig. 10 for different fractional order p and with the values of the other parameters are taken the same as that used in the previous paragraph. It is shown from the plots that the BHChG beam propagating across a FRET system maintains the same profile. As observed, the diffracted beam is gradually focused when $0 < p < 1$ until the beam spot size reaches the minimum size at $p = 1$. Then, the beam is gradually defocused when $1 < p < 2$ and returns to its original form at $p = 2$. Which explains that the intensity distribution of the BHChG beam is periodic through a FRTF system with a period $p = 2$.

Fig. 10

Intensity distribution of BHChG beam propagating through a FRTF system for different fractional order p with $n = 2$, $\mu = 1.5$ and $f = 1000\,{\text{mm}}$. Top row $l = 1$, middle row $l = 2$ and bottom row $l = 3$

The phase distribution is presented in Fig. 11 for four values of l. It is seen that when the increase of $l,$ the spiral phase structure changes and becomes more convergent and a vertical antisymmetry of the beam phase appears for the odd modes. Moreover, it can be turn in the counterclockwise direction with increasing l.

Fig. 11

The phase distribution of the propagation of the BHChG through a FRTF system for different values of l with $f = 1000\,{\text{mm}}$, $\mu = 1.5$ and n = 3: a l = 1, b l = 2, c l = 3 and d l = 4

5 Conclusion

The propagation properties of Bessel higher-order cosh-Gaussian beam, as a new laser beam introduced in this study, through a paraxial ABCD optical system are investigated. From the analytical formula of the intensity distribution for BHChG beam, developed by using the extended Huygens–Fresnel integral, we have discussed the comportment of the diffracted beam in free space, thin lens and FRFT system through numerical examples. We can conclude that BHChG beam behaves differently upon propagation through the studied optical systems. Also, the BHChG beam has many parameters that can be adjusted, which is advantageous for its use in some applications. The results of this study can be used in free-space optical communications and micromanipulation.