1 Introduction

Non-linear partial differential equations (PDEs) are significant and helpful within different fields like, sciences, engineering, computational mathematics, including computational physics. The exact solutions of non-linear equations perform a important part to study the dynamics of complex physical problems (Yalcınkaya et al. 2022). Evaluation and interpretation of the systems and processes behind different non-linear phenomena are found among numerous professional areas of study, combining hydrodynamics, fiber optics, viscoelastic materials, signal processing, biology, physical science, and others. Different analytical methods were recently created (Uddin et al. 2023). In modern science, a wide range of attractive non-linear models have developed, and other scientists and mathematicians have created important mathematical methods for obtaining exact solutions such as simplest equation methodology, (\(\frac{G^\prime}{G}\))-expansion technique (Jianguo et al. 2019), rational (\(\frac{G^\prime}{G}\)) technique (Islam et al. 2018), extended tanh-function methodology (Ali et al. 2023), Sine-cosine scheme (Ali et al. 2023), tanh function methodology (Ashraf et al. 2023), Riccati expansion (Huiling et al. 2023), unified expansion (Alshammari et al. 2023), Kudryashov expansion (Alquran 2021), the modified exponential-function scheme (Degon and Chowdhury 2022), Hirota bilinear methodology (Alshammari et al. 2023), differential transformation scheme (Verma and Rawani 2023), the homotopy analysis technique(Brociek et al. 2023) and so on. Different methods have been applied in the literature to solve nonlinear partial differential equations (NLPDE). Finding exact NLPDE solutions is necessary for understanding nonlinear physical phenomena properly (Seadawy et al. 2023). In this article, we examine the KDV equation. The classical KDV equation (Khan et al. 2023):

$$\begin{aligned} \frac{\partial }{\partial t} \mathbb {F} + \mathbb {F} \frac{\partial }{\partial x} \mathbb {F}+ \frac{\partial ^{3}}{\partial x^{3}} \mathbb {F}=0{,} \end{aligned}$$
(1)

was established in 1895 by de Vries along with Korteweg to identify particular theoretical physics occurrences related to quantum mechanics. To find analytical exact solitary wave solutions of the partial differential equations. Since the KDV equation has been initially derived in a study on canal waves in shallow water, It is involved in several different physics cases, particularly those providing traveling waves, solitons, and shock waves. It’s been investigated and used for a long time. Considering aerodynamics, continuum mechanics, and fluid dynamics, it provides a representation for shock wave creation, turbulence, and mass transfer. A lot of students were interested in this discovery because it was so important to research equatorial one-layer oceanic flows, by including the effects due to the Earth’s rotation over the fluid in Eq. (1), Geyer et al. modified it.

$$\begin{aligned} \frac{\partial }{\partial t}\mathbb {F}-\pi _{0} \frac{\partial }{\partial x}\mathbb {F}+\frac{3}{2}\mathbb {F} \frac{\partial }{\partial x} \mathbb {F}+\frac{1}{6} \frac{\partial ^{3}}{\partial x^{3}}=0{.} \end{aligned}$$
(2)

Many different techniques have been developed to solve KDV equations. For example, utilizing binary Bell polynomials to study the generalized variable coefficient Korteweg-de Vries equation in the fluid. Wazzan discovered the exact solutions of the KDV, modified KDV, potential KDV, and generalized KDV equations using the extended hyperbolic function approach. Geophysical KDV equation Eq. (2)’s solitary waves solution was calculated using a better expansion approach. Applying the Kudryashov approach, the solitons, conservation rules, and Geophysical KDV equation conservation equation Eq. (2). The geophysical KDV equation’s lump and interaction solutions were examined using Hiorta BLM. Studied the soliton solutions of the generalized perturbed KDV equation applying Hirota BLM. Generalized perturbed KDV equation as:

$$\begin{aligned} \mathbb {F}_{t}+\varrho \mathbb {F}_{x}+\Omega \mathbb {F} \mathbb {F}_{x}+\eta \mathbb {F}_{xxx}=0{,} \end{aligned}$$
(3)

where, \(\varrho\) is a perturbation factor that expresses the Coriolis effect. \(\Omega\) denoted the non-linearity as well as \(\eta\) is the dispersion factor, and \(\mathbb {F}\) is an analytic function of (x, t), free surface advancement is represented by \(\mathbb {F}(x,t)\). By choosing the \(\varrho =0\), \(\Omega =1\), and \(\eta =1\), the classical KDV Eq. (1) may become of Eq. (3). The generalization of standard KDV Eq. (1) and the geophysical KDV Eq. (2) is a generalized perturbed-KdV partial differential Eq. (3). By selecting \(\varrho =-\pi _{0}\), \(\Omega =32\), and \(\eta =16\), it is possible to obtain the geophysical KDV Eq. (2). The vibration transmission in fluids is explained by the perturbed-KDV equation, which is found in various fields such as healthcare engineering and mechanics. Non-linear systems are frequently determined using linear equations because dealing with nonlinear dynamical equations is challenging. As long as the input data has a particular precision and range, this works correctly, but chaos, singularities solitons, and other exciting components by linearization (Ali et al. 2023). Schrödinger’s equation combines the features of parabolic and hyperbolic equations from a mathematical perspective (Rizvi et al. 2023).

Lie symmetry analysis is a powerful method for finding precise solutions to complicated equations known as non-linear partial differential equations (PDEs). It involves a comprehensive and effective approach to unraveling these complex mathematical problems. In recent times, Lie’s approach has been addressed in several excellent textbooks and has been applied to the analysis of many engineering and physical modeling techniques. Lie symmetry analysis was used to explore the unstable isentropic Navier Stoke’s equations in 1-D about an ideal pressure formula (Jiwari et al. 2022). Lie symmetry technique was used to study the Fisher’s type diffusion equations (Verma et al. 2014). The Lie group was used to analyze the nonlinear regularised long wave system (Jiwari et al. 2017). To create the bright and dark soliton solution and study the nonlinear regularised long wave approach (Kumar et al. 2021). Determining non-linear evolution equations’ solutions, and implementation from symmetry analysis procedure is important (Akram et al. 2023). It is acknowledged that the pursuit of accurate solutions to non-linear evolution equations is a constant focal point in theoretical physics (Younas et al. 2023).

In 1918, Noether found another important feature of Lie symmetry. The concept of DEs has effects on conservation laws. Noether discovered a connection between conserved quantities and symmetry. The literature is full of references to the contributions made by numerous researchers in creating various approaches to create conservation rules (Rabia et al. 2023; Rizvi et al. 2023; Aziz et al. 2023). Scholar expands on what she finds in kumar and Dhiman (2022). The idea of self-adjointness has recently received a lot of attention (Freire 2011). According to Lie symmetry, the damped nonlinear elastic wave problem-solving will also be examined. To study partial differential equations, conservation principles are very important, for the reason why they deliver conserved quantities in each solution (Usman and Zaman 2023). The innovation of Lie symmetry analysis is the convenience and systematicity with which invariant functions can be created. For differential equations, there will be an association between Lie symmetries and conservation principles (Paliathanasis and Leach 2022). The equation’s symmetry group can be determined by using the Lie symmetry technique. Moreover, the equation can be simplified in the same way, and the symmetry transformation can produce new results for the equation (Yang et al. 2023).

In Sect. 1, we discuss the classical symmetries of the KDV equation. The optimal system of KDV equation is explained in Sect. 2. In Sect. 3, consists of symmetry reduction. This study explains the overview and analytical techniques in Sect. 4, and the graphical illustration developed. Section 5 covered the Conserved quantities. Section 6 consists of a graphical explanation. Then finally, the conclusion.

2 Classical symmetries of the generalized perturbed-KdV equation

One-parameter Lie group of infinitesimal transformation within generalized perturbed-KdV equation x, t, w is given,

$$\begin{aligned} x^{*}=x+\varepsilon \xi ^{1}(x,t,w)+\Theta (\xi ^{2}),\end{aligned}$$
(4)
$$\begin{aligned} t^{*}=t+\varepsilon \xi ^{2}(x,t,w)+\Theta (\xi ^{2}),\end{aligned}$$
(5)
$$\begin{aligned} w^{*}=w+\varepsilon \tau (x,t,w)+\Theta (\xi ^{2}), \end{aligned}$$
(6)

where, \(\varepsilon\)= small parameter, group parameter. \(\xi ^{1}\)= function of dependent or independent.

Suppose a vector field,

$$\begin{aligned} A=xi^{1}(x,t,w)\frac{\partial }{\partial x}+\xi ^{2}(x,t,w)\frac{\partial }{\partial t}+\tau (x,t,w)\frac{\partial }{\partial w}. \end{aligned}$$
(7)

The third prolongation of X provided by,

$$\begin{aligned} A^{|3|}= & {} \xi ^{1}(x,t,w)\frac{\partial }{\partial x}+\xi ^{2}(x,t,w)\frac{\partial }{\partial t}+\tau (x,t,w) \frac{\partial }{\partial w}\nonumber \\{} & {} +\tau ^{t} \frac{\partial }{\partial w_{t}}+\tau ^{x}\frac{\partial }{\partial w_{x}}+\tau ^{xxx} \frac{\partial }{\partial w_{xxx}}, \end{aligned}$$
(8)

with coefficients,

$$\begin{aligned} \tau ^{J}=D_{J}\left( \tau -\sum ^{2}_{i=1}\xi ^{i}w^{\alpha }_{j}\right) +\sum ^{2}_{i=1}\xi ^{i}w^{\alpha }_{J,i}. \end{aligned}$$
(9)

Utilizing the third prolongation \((A^{(3)})\) to the Eq. (1) .

$$\begin{aligned} A^{(3)}(W_{t}+\varrho W_{x}+\Omega W W_{x}+\eta W_{xxx})|_{(1)=0}=0. \end{aligned}$$
(10)

The Lie algebra of the Eq. (1) (generalized perturbed-KdV equation) is generated through vector field,

$$\begin{aligned} A=\xi ^{1}(x,t,w)\frac{\partial }{\partial x}+\xi ^{2}(x,t,w)\frac{\partial }{\partial t}+\tau (x,t,w)\frac{\partial }{\partial w}. \end{aligned}$$
(11)

The generalized perturbed-KdV equation has Lie point symmetries that are,

$$\begin{aligned} A_{1}=\frac{\partial }{\partial t},\ A_{2}=\frac{\partial }{\partial x},\ A_{3}=\Omega t \frac{\partial }{\partial x}+\frac{\partial }{\partial w},\ A_{4}=w \frac{\partial }{\partial w}-\frac{3}{2} t \frac{\partial }{\partial t}+ \left( \frac{-1}{2}x-\varepsilon t\right) \frac{\partial }{\partial x}. \end{aligned}$$
(12)

These vector fields’ commutation relations are displayed in the table 1, and each ith row and jth column entry is identified as \([X_{i},X_{j}] = A_{i}A_{j} - A_{j}A_{i},\ i, j = 1, 2, 3, 4.\)

Table 1 Commutator table
Full size table

3 Optimal system of generalized perturbed-KdV equation

To create the most effective structure for subgroups, we could create an ideal structure of subgroups to achieve our goal. Since they are equivalent. The ideal structure for one-dimensional subalgebras is equivalent to the orbit categorization using the adjoint representations. An adjoint representation \(Ad(exp(\varepsilon A_{i}))\) is defined by the Lie series,

$$\begin{aligned} Ad(exp(\varepsilon .A_{i}).A_{j}) = A_{j} - \varepsilon [A_{i},A_{j}] +\frac{\varepsilon ^{2}}{2} [A_{i}, [A_{i},A_{j}]]-..., \end{aligned}$$
(13)

where, \([A_{i},A_{j}]\) is the Lie algebra’s commutator, \(\varepsilon\) is a parameter, and i, j = 1, 2, 3, 4. We provide an overview of all adjoint characterizations of the algebraic generalized perturbed-KdV equation generator in Table 2, where the (i, j)th entry indicates \(Ad(exp(\varepsilon A_{i}))A_{j}\).

Table 2 The adjoint form that represents the generalized perturbed-KdV equation
Full size table

4 Symmetry reduction

In the following section, we determine the generalized perturbed-KdV equation’s symmetries together with associated reductions. The generalized perturbed-KdV equation can be written as (x, t, w). Therefore, to make the equation easier, to use a certain set of coordinates. Therefore, it is necessary to reduce the number of variables that are dependent within the generalized perturbed-KdV equation. A PDE can be converted to either an ODE or a more simple PDE by reducing its number of independent parameters. The above generalized perturbed-KdV in the context of (x, t, w) can be transformed as an ODE in parameters of (r, w). We are now able to get the simplified equation, through a chain rule. As for concerning the operator,

Family 1:

$$\begin{aligned} A_{1}=\frac{\partial }{\partial t}, \end{aligned}$$
(14)

we have,

$$\begin{aligned} \frac{dx}{0}=\frac{dt}{1}=\frac{dw}{0}, \end{aligned}$$
(15)

the similarity variables are as follows:

$$\begin{aligned} x=r,\ w=\ell (r). \end{aligned}$$
(16)
$$\begin{aligned} w=\ell (r) \Rightarrow w=x. \end{aligned}$$
(17)

In order to identify the syntax of the function \(\ell (r)\), substitute Eq. (17) into Eq. (3), which satisfied following conditions:

$$\begin{aligned} \varrho \ell '(r)+\Omega \ell (r) \ell '(r)+\eta \ell '(r) \ell '''(r)=0. \end{aligned}$$
(18)

Similarly,

Family 2:

$$\begin{aligned} A_{2}=\frac{\partial }{\partial x}, \end{aligned}$$
(19)

we obtain,

$$\begin{aligned} \frac{dx}{1}=\frac{dt}{0}=\frac{dw}{0}, \end{aligned}$$
(20)

the similarity variables are as follows:

$$\begin{aligned} t= & {} r,\ w=\ell (r). \end{aligned}$$
(21)
$$\begin{aligned} w= & {} \ell (r) \Rightarrow w=t, \end{aligned}$$
(22)

We anticipate that when \(\ell (r)\) is substituted into Eq. (1), it will satisfy the following condition:

$$\begin{aligned} \ell '(r)=0. \end{aligned}$$
(23)

Similarly

Family 3:

$$\begin{aligned} A_{3}=\Omega t \frac{\partial }{\partial x}+\frac{\partial }{\partial w}. \end{aligned}$$
(24)

In this particular instance, the defining equation is:

$$\begin{aligned} \frac{dx}{\Omega t}= & {} \frac{dt}{0}=\frac{dw}{1}, \end{aligned}$$
(25)
$$\begin{aligned} \Omega \frac{t^{2}}{2}= & {} r,\ \frac{x}{\Omega t}=w+\ell (r), \end{aligned}$$
(26)
$$\begin{aligned} w-\frac{x}{\Omega t}= & {} \ell (r) \Rightarrow \ w=\frac{x}{\Omega t}-\ell (r), \end{aligned}$$
(27)

After substituting it into Eq. (1), the apparent form of \(\ell (r)\) is revealed. Through this substitution, we ascertain the existence of a solution for the following equation, \(\ell (r)\):

$$\begin{aligned} \frac{x}{\Omega t^{2}}+\Omega t \ell '(r)+\frac{\varrho }{\Omega }+\frac{x}{\Omega ^{2} t^{2}}-\frac{z}{t}=0. \end{aligned}$$
(28)

Family 4:

$$\begin{aligned} A_{4}=w \frac{\partial }{\partial w}-\frac{3}{2} t \frac{\partial }{\partial t}+\left( \frac{-1}{2}x-\varepsilon t\right) \frac{\partial }{\partial x}. \end{aligned}$$
(29)

In the present situation, the main equation is:

$$\begin{aligned} \frac{dx}{(\frac{-1}{2}x-\varepsilon t)}=\frac{dt}{(\frac{-3}{2}t)}=\frac{dw}{w}, \end{aligned}$$
(30)
$$\begin{aligned} -tx+\varepsilon \frac{t^{2}}{2}=r,\ w=-\ell (r)-\frac{2}{3}t, \end{aligned}$$
(31)

whenever it is substituted within (1), it appears as though \(\ell (r)\) would fulfill the equation:

$$\begin{aligned} \frac{\eta \ell '''(r) t^{\frac{4}{3}}+3\Omega \ell '(r) t \ell (r)+2 \Omega \ell '(r) t^{2}-2 t^{\frac{4}{3}}-\ell '(r)t\varepsilon +\ell '(r)x}{4 t^{\frac{4}{3}}}=0. \end{aligned}$$
(32)

Family 5:

$$\begin{aligned} A_{1}+A_{2}=\frac{\partial }{\partial t}+\frac{\partial }{\partial x}. \end{aligned}$$
(33)

In the present situation, the characteristic equation is:

$$\begin{aligned} \frac{dx}{1}=\frac{dt}{1}=\frac{dw}{0}, \end{aligned}$$
(34)
$$\begin{aligned} r=x-t,\ w=\ell (r), \end{aligned}$$
(35)

since it is substituted through Eq. (1), it appears as though \(\ell (r)\) would fulfill the equation:

$$\begin{aligned} -\ell '(r)+\varrho \ell '(r)+\Omega \ell (r) \ell '(r)+\eta \ell '''(r)=0. \end{aligned}$$
(36)

5 Application of new extended direct algebraic method

To use a new extended direct algebraic method to find an exact solution for the generalized perturbed-KdV equation, specifically focusing on solitary waves in an analytical manner (Asghar et al. 2022; Bakar et al. 2022; Hussain et al. 2023; Faridi et al. 2023; Iqbal et al. 2023; Shahzad et al. 2023). Let us pick Eq. (3) due to its generality. we have,

$$\begin{aligned} -\ell '(r)+\varrho \ell '(r)+\Omega \ell (r) \ell '(r)+\eta \ell '''(r)=0. \end{aligned}$$
(37)

Integrating Eq. (37) with regard to the r and constant is zero if integration,

$$\begin{aligned} \eta \ell ''(r)+\ell (r)(\varrho -1)+\frac{1}{2} \Omega \ell ^{2}(r)=0. \end{aligned}$$
(38)

By adjusting the homogeneous balancing parameter of Eq. (38), a solution can be seen,

$$\begin{aligned} \ell (r)=c_{0}+c_{1}\,S(r)+c_{2}\,S(r)^{2}. \end{aligned}$$
(39)

As we put the solution Eq. (39) within the Eq. (38) and count the difference in power coefficients:

$$\begin{aligned} \begin{aligned}&S(r)^{0}:\ \eta \,c_{{1}}\beta \, \left( \ln \left( \varpi \right) \right) ^{2} \alpha +2\,\eta \,c_{{2}}{\alpha }^{2} \left( \ln \left( \varpi \right) \right) ^{2}+c_{{0}}\varrho -c_{{0}}+1/2\,\Omega \,{c_{{0}}}^{2}=0{,}\\&S(r)^{1}:\ \eta \,c_{{1}}{\beta }^{2} \left( \ln \left( \varpi \right) \right) ^{2} +2\,\eta \,c_{{1}}\gamma \, \left( \ln \left( \varpi \right) \right) ^{2 }\alpha \\&\quad +6\,\eta \,c_{{2}}\alpha \, \left( \ln \left( \varpi \right) \right) ^{2}\beta +c_{{1}}\varrho -c_{{1}}+\Omega \,c_{{0}}c_{{1}} =0{,}\\&S(r)^{2}:\ 3\,\eta \,c_{{1}}\beta \, \left( \ln \left( \varpi \right) \right) ^{2} \gamma +8\,\eta \,c_{{2}}\alpha \, \left( \ln \left( \varpi \right) \right) ^{2}\gamma +4\,\eta \,c_{{2}}{\beta }^{2} \left( \ln \left( \varpi \right) \right) ^{2}\\&\quad +c_{{2}}\varrho -c_{{2}}+\Omega \,c_{{0}}c_{{2 }}+1/2\,\Omega \,{c_{{1}}}^{2} =0{,}\\&S(r)^{3}:\ 2\,\eta \,c_{{1}}{\gamma }^{2} \left( \ln \left( \varpi \right) \right) ^{2}+10\,\eta \,c_{{2}}\beta \, \left( \ln \left( \varpi \right) \right) ^{2}\gamma +\Omega \,c_{{1}}c_{{2}} =0{,}\\&S(r)^{4}:\ 6\,\eta \,c_{{2}}{\gamma }^{2} \left( \ln \left( \varpi \right) \right) ^{2}+1/2\,\Omega \,{c_{{2}}}^{2} =0. \end{aligned} \end{aligned}$$
(40)

The solution of above system of algebraic Eq. (40) with the help of Mathematica,

Set 1:

$$\begin{aligned}{} & {} \bigg [\varrho = 4ln \left( \varpi \right) ^{2}\gamma \alpha \eta -ln\left( \varpi \right) ^{2} \beta ^{2} \eta +1, \nonumber \\{} & {} \quad c_{0}=\frac{-12ln \left( \varpi \right) ^{2}\gamma \alpha \eta }{\Omega },\ c_{1}=-\frac{12 \eta \gamma ln\left( \varpi \right) ^{2} \beta }{\Omega },\ c_{2}=\frac{-12 \eta \gamma ^{2} ln\left( \varpi \right) ^{2}}{\Omega } \bigg ]. \end{aligned}$$
(41)

Set 2:

$$\begin{aligned}{} & {} \bigg [\varrho =-4ln\left( \varpi \right) ^{2}\gamma \alpha \eta -ln\left( \varpi \right) ^{2} \beta ^{2} \eta +1,\nonumber \\{} & {} \quad c_{0}=\frac{-2\eta ln\left( \varpi \right) ^{2}\left( 2\alpha \gamma + \beta ^{2}\right) }{\Omega },\ c_{1}=-\frac{12 \eta \gamma ln\left( \varpi \right) ^{2} \beta }{\Omega },\ c_{2}=\frac{-12 \eta \gamma ^{2} ln\left( \varpi \right) ^{2}}{\Omega } \bigg ]. \end{aligned}$$
(42)

The general solution of the Eq. (3) is obtaining by putting the Eq. (41) in the Eq. (39) is:

$$\begin{aligned} \mathbb {F}(x,t)=\frac{-12ln(\varpi )^{2}\gamma \alpha \eta }{\Omega }-\frac{12 \eta \gamma ln(\varpi )^{2} \beta }{\Omega }[S_{i}(r)]-\frac{-12 \eta \gamma ^{2} ln(\varpi )^{2}}{\Omega }\,[S_{i}(r) ]^{2}, \end{aligned}$$
(43)

where,

$$\begin{aligned} \Theta =\frac{3ln\left( \varpi \right) ^{2} \eta }{\Omega },\ \Lambda =\beta ^{2}-4\alpha \gamma . \end{aligned}$$
(44)

We just deal with the first set, in order to find the results and describe each result in the form of various cases as follows,

(Group 1): When \(\beta ^2 - 4\alpha \gamma < 0\), and \(\gamma \ne 0,\) the following is the derivation of mixed trigonometric solutions,

$$\begin{aligned} \mathbb {F}_{1}(x,t)= & {} -\Theta \bigg [4\alpha \gamma -2\beta ^{2}+2\beta \sqrt{-\Lambda }tan_{\kappa }\left( \frac{\sqrt{-\Lambda }}{2}(r)\right) \nonumber \\{} & {} +\left( -\beta +\sqrt{-\Lambda }tan_{\kappa }\left( \frac{\sqrt{-\Lambda }}{2}(r)\right) \right) ^{2}\bigg ], \end{aligned}$$
(45)
$$\begin{aligned} \mathbb {F}_{2}(x,t)= & {} -\Theta \bigg [4\alpha \gamma -2\beta ^{2}-2\beta \sqrt{-\Lambda }cot_{\kappa }\left( \frac{\sqrt{-\Lambda }}{2}(r)\right) \nonumber \\{} & {} +\left( -\beta +\sqrt{-\Lambda }cot_{\kappa }\left( \frac{\sqrt{-\Lambda }}{2}(r)\right) \right) ^{2}\bigg ], \end{aligned}$$
(46)
$$\begin{aligned} \mathbb {F}_{3}(x,t)= & {} -\Theta \bigg [ 4\alpha \gamma -2\beta ^{2}+2\beta \sqrt{-\Lambda } \left( tan_{\kappa }\left( \sqrt{-\Lambda }(r)\right) \pm \sqrt{mn}\left( sec_{\kappa }\sqrt{-\Lambda }(r)\right) \right) \nonumber \\{} & {} +\left( -\beta +\sqrt{-\Lambda }\left( tan_{\kappa }\left( \sqrt{-\Lambda }(r)\right) \pm \sqrt{mn}sec_{\kappa }\left( \sqrt{-\Lambda }(r)\right) \right) \right) ^{2}\bigg ], \end{aligned}$$
(47)
$$\begin{aligned} \mathbb {F}_{4}(x,t)= & {} -\Theta \bigg [ 4\alpha \gamma -2\beta ^{2}+2\beta \sqrt{-\Lambda }\left( cot_{\kappa }\left( \sqrt{-\Lambda }(r)\right) \pm \sqrt{mn}\left( csc_{\kappa }\sqrt{-\Lambda }(r)\right) \right) \nonumber \\{} & {} +\left( -\beta +\sqrt{-\Lambda }\left( cot_{\kappa }\left( \sqrt{-\Lambda }(r)\right) \pm \sqrt{mn}\left( csc_{\kappa }\sqrt{-\Lambda }(r)\right) \right) \right) ^{2}\bigg ], \end{aligned}$$
(48)
$$\begin{aligned} \mathbb {F}_{5}(x,t)= & {} -\Theta \bigg [ 4\alpha \gamma -2\beta ^{2}+2\beta \sqrt{-\Lambda }\left( tan_{\kappa }\left( \frac{\sqrt{-\Lambda }}{4}(r)\right) -cot_{\kappa }\left( \frac{\sqrt{-\Lambda }}{4}(r)\right) \right) \nonumber \\{} & {} +\left( -\beta +\frac{\sqrt{-\Lambda }}{2}\left( tan_{\kappa }\left( \frac{\sqrt{-\Lambda }}{4}(r)\right) -cot_{\kappa }\left( \frac{\sqrt{-\Lambda }}{4}(r)\right) \right) \right) ^{2}\bigg ]. \end{aligned}$$
(49)

(Group 2): When \(\beta ^2 - 4\alpha \gamma > 0\), and \(\gamma \ne 0\), we obtained the solutions of various format as following. Shock solution is achieved as,

$$\begin{aligned} \mathbb {F}_{6}(x,t)= & {} -\Theta \bigg [4\alpha \gamma -2\beta ^{2}-2\beta \sqrt{\Lambda }tanh_{\kappa }\left( \frac{\sqrt{\Lambda }}{2}(r)\right) \nonumber \\{} & {} +\left( -\beta -\sqrt{\Lambda }tanh_{\kappa }\left( \frac{\sqrt{\Lambda }}{2}(r)\right) \right) ^{2}\bigg ]. \end{aligned}$$
(50)

As a result, the singular solution is,

$$\begin{aligned} \mathbb {F}_{7}(x,t)= & {} -\Theta \bigg [4\alpha \gamma -2\beta ^{2}-2\beta \sqrt{\Lambda }coth_{\kappa }\left( \frac{\sqrt{\Lambda }}{2}(r)\right) \nonumber \\{} & {} \quad+\left( -\beta -\sqrt{\Lambda }coth_{\kappa }\left( \frac{\sqrt{\Lambda }}{2}(r)\right) \right) ^{2}\bigg ]. \end{aligned}$$
(51)

As a result, the mixed complex solitary wave solution is achieved,

$$\begin{aligned} \begin{aligned}&\mathbb {F}_{8}(x,t)=-\Theta \bigg [ 4\alpha \gamma -2\beta ^{2}+2\beta \sqrt{\Lambda }\left( -tanh_{\kappa }\left( \sqrt{\Lambda }r\right) \pm \iota \sqrt{mn}sech_{\kappa }\sqrt{\Lambda }\right) \\&\quad+\left( -\beta +\sqrt{\Lambda }\left( -tanh_{\kappa }\left( \sqrt{\Lambda }(r)\right) \pm \sqrt{mn}sech_{\kappa }\sqrt{\Lambda }(r)\right) \right) ^{2}\bigg ]. \end{aligned} \end{aligned}$$
(52)

The format for obtaining the mixed singular solution is as,

$$\begin{aligned} \begin{aligned} \mathbb {F}_{9}(x,t)=&-\Theta \bigg [ 4\alpha \gamma -2\beta ^{2}+2\beta \sqrt{\Lambda }\left( -coth_{\kappa }\left( \sqrt{\Lambda }(r)\right) \pm \iota \sqrt{mn}csch_{\kappa }\sqrt{\Lambda }(r)\right) \\&\quad+\left( -\beta +\sqrt{\Lambda }\left( -coth_{\kappa }\left( \sqrt{\Lambda }(r)\right) \pm \sqrt{mn}csch_{\kappa }\sqrt{\Lambda }(r)\right) \right) ^{2}\bigg ]. \end{aligned} \end{aligned}$$
(53)

Mixed shock singular solutions are achieved in the following format,

$$\begin{aligned} \begin{aligned} \mathbb {F}_{10}(x,t)=&-\Theta \bigg [ 4\alpha \gamma -2\beta ^{2}-2\beta \sqrt{\Lambda }\left( tanh_{\kappa }\left( \frac{\sqrt{\Lambda }}{4}(r)\right) +coth_{\kappa }\left( \frac{\sqrt{\Lambda }}{4}(r)\right) \right) \\&\quad+\left( -\beta +\frac{\sqrt{\Lambda }}{2}\left( tanh_{\kappa }\left( \frac{\sqrt{\Lambda }}{4}(r)\right) +coth_{\kappa }\left( \frac{\sqrt{\Lambda }}{4}(r)\right) \right) \right) ^{2}\bigg ]. \end{aligned} \end{aligned}$$
(54)

(Group 3): Since \(\alpha \gamma > 0\) as well as \(\beta =0,\) we obtained trigonometric solution as,

$$\begin{aligned} \mathbb {F}_{11}(x,t)=-4\Theta \alpha \gamma \bigg [1+\left( tan_{\kappa }\left( \sqrt{\alpha \gamma }(r)\right) \right) ^{2} \bigg ], \end{aligned}$$
(55)
$$\begin{aligned} \mathbb {F}_{12}(x,t)=-4\Theta \alpha \gamma \bigg [1+\left( -cot_{p}\left( \sqrt{\alpha \gamma }(r)\right) \right) ^{2} \bigg ]. \end{aligned}$$
(56)

These are the mixed trigonometric solutions,

$$\begin{aligned} \mathbb {F}_{13}(x,t)= & {} -4\Theta \alpha \gamma \bigg [1+\left( tan_{\kappa }\left( 2\sqrt{\alpha \gamma }(r)\right) \pm \sqrt{mn}sec_{\kappa }\left( 2\sqrt{\alpha \gamma }(r)\right) \right) ^{2} \bigg ], \end{aligned}$$
(57)
$$\begin{aligned} \mathbb {F}_{14}(x,t)= & {} -4\Theta \alpha \gamma \bigg [1+\left( -cot_{\kappa }\left( 2\sqrt{\alpha \gamma }(r)\right) \pm \sqrt{mn}csc_{\kappa }\left( 2\sqrt{\alpha \gamma }(r)\right) \right) ^{2} \bigg ], \end{aligned}$$
(58)
$$\begin{aligned} \mathbb {F}_{15}(x,t)= & {} -\Theta \alpha \gamma \bigg [4+\left( tan_{\kappa }\left( \frac{\sqrt{\alpha \gamma }}{2}(r)\right) -cot_{\kappa }\left( \frac{\sqrt{\alpha \gamma }}{2}(r)\right) \right) ^{2} \bigg ]. \end{aligned}$$
(59)

(Group 4): Since \(\alpha \gamma < 0\) as well as \(\beta =0,\) we acquired solutions in the format of the shock solutions,

$$\begin{aligned} \mathbb {F}_{16}(x,t)=-4\Theta \alpha \gamma \bigg [1+\iota \left( -tanh\left( \sqrt{-\alpha \gamma }(r)\right) \right) ^{2} \bigg ]. \end{aligned}$$
(60)

We obtained the singular as,

$$\begin{aligned} \mathbb {F}_{17}(x,t)=-4\Theta \alpha \gamma \bigg [1+\iota \left( -coth\left( \sqrt{-\alpha \gamma }(r)\right) \right) ^{2} \bigg ]. \end{aligned}$$
(61)

The distinct complex combo solutions are calculated as,

$$\begin{aligned} \mathbb {F}_{18}(x,t)= & {} -4\Theta \alpha \gamma \bigg [1+\iota \left( -tanh_{\kappa }\left( 2\sqrt{-\alpha \gamma }(r)\right) \pm i \sqrt{mn}sech_{\kappa }\left( 2\sqrt{-\alpha \gamma }(r)\right) \right) ^{2} \bigg ], \end{aligned}$$
(62)
$$\begin{aligned} \mathbb {F}_{19}(x,t)= & {} -4\Theta \alpha \gamma \bigg [1+\iota \left( -coth_{\kappa }\left( 2\sqrt{-\alpha \gamma }(r) \right) \pm i \sqrt{mn}csch_{\kappa }\left( 2\sqrt{-\alpha \gamma }(r)\right) \right) ^{2} \bigg ], \end{aligned}$$
(63)
$$\begin{aligned} \mathbb {F}_{20}(x,t)= & {} -\Theta \alpha \gamma \bigg [4+\iota \left( -\left( tanh_{p}\left( \frac{\sqrt{-\alpha \gamma }}{2}(r)\right) +coth_{p}\left( \frac{\sqrt{-\alpha \gamma }}{2}(r)\right) \right) \right) ^{2} \bigg ]. \end{aligned}$$
(64)

(Group 5): Since \(\beta = 0\) as well as \(\alpha =\gamma ,\) in the form of a periodic along with mixed periodic class, the periodic along with mixed periodic solutions are investigated.,

$$\begin{aligned} \mathbb {F}_{21}(x,t)= & {} -4\Theta \gamma ^{2}\bigg [1+\left( tan_{\kappa }((r)\gamma \right) ^{2} \bigg ], \end{aligned}$$
(65)
$$\begin{aligned} \mathbb {F}_{22}(x,t)= & {} -4\Theta \gamma ^{2}\bigg [1+\left( -cot_{\kappa }((r)\gamma \right) ^{2} \bigg ]{,} \end{aligned}$$
(66)
$$\begin{aligned} \mathbb {F}_{23}(x,t)= & {} -4\Theta \gamma ^{2}\bigg [1+\left( tan_{\kappa }\left( 2(r)\gamma \right) \pm \sqrt{mn}sec_{\kappa }\left( 2\gamma (r)\right) \right) ^{2} \bigg ], \end{aligned}$$
(67)
$$\begin{aligned} \mathbb {F}_{24}(x,t)= & {} -4\Theta \gamma ^{2}\bigg [1+\left( -cot_{\kappa }(2(r)\gamma \right) \pm \sqrt{mn}csc_{\kappa }\left( 2\gamma (r))\right) ^{2} \bigg ]{,} \end{aligned}$$
(68)
$$\begin{aligned} \mathbb {F}_{25}(x,t)= & {} -\Theta \gamma (r) \bigg [4+\left( tan_{\kappa }\left( \frac{\alpha }{2} (r)\right) -cot_{\kappa }\left( \frac{\alpha }{2}(r)\right) \right) ^{2} \bigg ]{.} \end{aligned}$$
(69)

(Group 6): When \(\beta = 0\) and \(\gamma =-\alpha ,\) the following class of single and mixed-wave compositions is acquired,

$$\begin{aligned} \mathbb {F}_{26}(x,t)= & {} 4\Theta \alpha ^{2}\bigg [1-\left( -tanh_{\kappa }\left( \alpha (r)\right) \right) ^{2} \bigg ], \end{aligned}$$
(70)
$$\begin{aligned} \mathbb {F}_{27}(x,t)= & {} 4\Theta \alpha ^{2}\bigg [1-\left( -coth_{\kappa }\left( \alpha (r)\right) \right) ^{2} \bigg ], \end{aligned}$$
(71)
$$\begin{aligned} \mathbb {F}_{28}(x,t)= & {} 4\Theta \alpha ^{2}\bigg [1-\left( -tanh_{\kappa }\left( 2(r)\alpha )\right) \pm \iota \sqrt{mn}sech_{\kappa }\left( 2\alpha (r)\right) \right) ^{2} \bigg ], \end{aligned}$$
(72)
$$\begin{aligned} \mathbb {F}_{29}(x,t)= & {} 4\Theta \alpha ^{2}\bigg [1-\left( -coth_{\kappa }\left( 2(r)\alpha \right) \pm \iota \sqrt{mn}sech_{\kappa }\left( 2\alpha (r)\right) \right) ^{2} \bigg ], \end{aligned}$$
(73)
$$\begin{aligned} \mathbb {F}_{30}(x,t)= & {} -\Theta \alpha ^{2}\bigg [4-\left( -tanh_{\kappa }\left( \frac{\alpha }{2}(r)\right) +coth_{\kappa }\left( \frac{\alpha }{2}(r)\right) \right) ^{2} \bigg ]. \end{aligned}$$
(74)

(Group 7): When \(\beta ^{2} =4\alpha \gamma ,\) then we have,

$$\begin{aligned} \mathbb {F}_{31}(x,t)= & {} 4 \Theta \bigg [-\alpha \gamma + \sqrt{\alpha \gamma }\left( \frac{2\sqrt{\alpha \gamma } (r) log[\varpi ]+1}{(r) log[\varpi ]} \right) \nonumber \\{} & {} -\left( \frac{-\left( \sqrt{\alpha \gamma } (r) log[\varpi ]+1\right) }{(r) log[\varpi ]} \right) ^{2} \bigg ]. \end{aligned}$$
(75)

(Group 8), as well as (Group 9) have the constant solutions,

(Group 10): Since \(\beta =0,\ \alpha =0\), then we have,

$$\begin{aligned} \mathbb {F}_{34}(x,t)=-4 \Theta \gamma ^{2} \bigg [\frac{-1}{\gamma log[\varpi ]^{2}} \bigg ]{.} \end{aligned}$$
(76)

(Group 11): When \(\alpha =0\), then we have,

$$\begin{aligned} \mathbb {F}_{35}(x,t)= & {} 4 \Theta \bigg [\left( \frac{\beta ^{2} m}{\left( \cosh _{\kappa }\left( \beta (r)\right) -\sinh _{\kappa }\left( \beta (r) \right) + m \right) }\right) \nonumber \\{} & {} -\left( \frac{-m \beta }{ \left( \cosh _{\kappa } \left( \beta (r) \right) -\sinh _{\kappa }\left( \beta (r) \right) + m \right) }\right) ^{2} \bigg ], \end{aligned}$$
(77)
$$\begin{aligned} \mathbb {F}_{36}(x,t)= & {} -4 \Theta \bigg [\beta \left( \frac{ -\beta \left( sin_{\kappa }\left( \beta (r)\right) +cosh_{\kappa }\left( \beta (r)\right) \right) }{\left( \sinh _{\kappa }\left( \beta (r)\right) +\cosh _{\kappa }\left( \beta (r) \right) + n\right) }\right) \nonumber \\{} & {} +\left( \frac{-\beta \left( sinh_{\kappa }\left( \beta (r)\right) +cosh_{\kappa }\left( \beta (r)\right) \right) }{ \gamma \left( \sinh _{\kappa } \left( \beta (r) \right) +\cosh _{\kappa }\left( \beta (r) \right) + n \right) }\right) ^{2} \bigg ]. \end{aligned}$$
(78)

(Group 12)::When \(\gamma =pq,\,(q\ne 0), \,\beta = p,\) and \({\alpha } =0\), we gain the plane solution as,

$$\begin{aligned} \mathbb {F}_{37}(x, t)=-4\Theta \kappa ^{2} q \times \bigg [\left( -\frac{m\kappa ^{P (r)}}{m-qn\kappa ^{P (r)}} \right) +q\left( -\frac{m\kappa ^{P (r)}}{m-qn\kappa ^{P (r)}} \right) ^2\bigg ]{.} \end{aligned}$$
(79)
Fig. 1
figure 1

Representation of solution \(\mathbb {F}_{1}(x, t)\) in 3-Dimension, 2-Dimension, and contour

Full size image
Fig. 2
figure 2

Representation of solution \(\mathbb {F}_{35}(x, t)\) in 3-Dimension, 2-Dimension, and contour

Full size image
Fig. 3
figure 3

Representation of solution \(\mathbb {F}_{27}(x, t)\) in 3-Dimension, 2-Dimension, and contour

Full size image

6 Graphical explanation

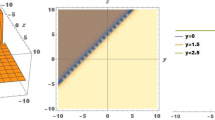
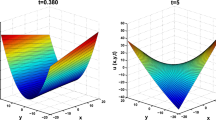
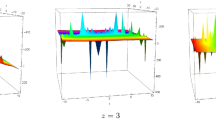
This section shows our results in the appearance of graphs through different parametric values. By choosing different parameter values, the diagrams display solutions that are different from those described in 3-D, 2-D, and their associated contours. Figure 1, shows the 2-D, 3-D and contour behaviour. The non-linearity \(\Omega =0.5\), dispersion factor \(\eta =2\), \(\alpha =1.5\), \(\beta =0.001\), \(\gamma =0.1\) and \(\kappa =4\). By choosing the specific values of variable deformation \(m=0.1\), \(n=0.7\) and fixing other parameter constants, the value of m and n is always greater than 0. For this purpose, we selected the solution \(\mathbb {F}_{1}(x, t)\) and discovered the presence of a combined bright-dark soliton in both two-dimensional (2-D) and three-dimensional (3-D) settings, represented visually through contour plots. Dark optical solitons manifest in the normal dispersion regime, where certain optical phenomena exhibit stability and propagate without distortion. This behavior stands in contrast to other dispersion regimes, highlighting the unique conditions under which dark solitons emerge. Figure 2, the non-linearity \(\Omega =2\), dispersion factor \(\eta =0.2\), \(\beta =0.5\). To select the \(m=0.001\), \(n=0.00002\) and \(\kappa =3\) then, We achieve a smooth, bright (non-topological solitary), or bell-shaped soliton, showcasing diverse soliton profiles. This versatility in soliton shapes is essential for understanding and manipulating wave behavior in various physical systems, providing valuable insights into nonlinear phenomena. The anomalous dispersion regime where the bright optical solitons occur. In Fig. 3, A singular kink soliton is identified, representing a distinct type of solitary wave with localized, abrupt changes. This observation holds significance in nonlinear dynamics, offering insights into the behavior of physical systems where kink solitons may arise, contributing to a deeper understanding of wave phenomena. In fields like optics and condensed matter physics, it is employed to describe and manipulate localized disturbances or abrupt changes, offering insights into wave behavior and facilitating the development of innovative technologies, such as signal processing and information transmission devices. The value of m and n is always greater-than 0 and m, and n are variables of constant deformation \(m=0.09\), and \(n=0.1\). Our conditions of \(\mathbb {F}_{27}(x, t)\) is that \(\beta =0\) and \(\gamma =-\alpha\) chose the \(\alpha =-1.7\), and \(\kappa =0.5\). These diverse results, encompassing various soliton types, are valuable for addressing nonlinear wave challenges in applied science and across multiple research domains. Their significance extends to enhancing our understanding of complex phenomena, impacting fields beyond applied science and contributing to broader advancements in scientific inquiry. The graphical illustrations of our newly discovered outcome.

7 Conserved quantities

Conservation means something that doesn’t change. A dynamical structure’s conserved quantity includes a function of the dependent variables, whose values stay constant throughout every phase of the entire system. Conserved quantities are important because expressing them requires the formulation of specific equations. This necessity to articulate these quantities in mathematical terms is crucial for understanding and applying fundamental principles to various scientific scenarios, and we may utilize that equation to comprehend how the variables will alter under various circumstances. When something is conserved, it indicates that regardless of what occurs, we are able to count on it to remain the same.

Full Fluxes (maybe involving arbitrary constants or functions).

$$\begin{aligned} \begin{aligned} { Flux_{t}}=&\frac{1}{2}\ {,} \mathbb {F} \left( { \mathfrak {C1}}\, \Omega t \mathbb {F}+{ \mathfrak {C2}}\, \mathbb {F} \right) +\mathbb {F} \left( \left( \varrho t-x \right) { \mathfrak {C1}}+{ \mathfrak {C3}} \right) , \\ { Flux_{x}}=&\frac{1}{3}\,{\mathbb {F}}^{2} \left( { \mathfrak {C1}}\,\Omega t \mathbb {F}+{ \mathfrak {C2}}\, \mathbb {F} \right) \Omega +\frac{1}{2}\,{\mathbb {F}}^{2} \left( \left( \varrho t-x \right) {\mathfrak {C1}}+{\mathfrak {C3}} \right) \Omega \\&+\frac{1}{2}\,\mathbb {F} \left( {\mathfrak {C1}}\, \Omega t \mathbb {F}+{\mathfrak {C2}}\,\mathbb {F} \right) \varrho + \frac{1}{2}\, \mathbb {F} \left( {\mathfrak {C1}}\, \Omega t+{\mathfrak {C2}} \right) \eta { \mathbb {F}xx}-\\&\frac{1}{2}\, \left( { \mathfrak {C1}}\, \Omega t+{\mathfrak {C2}} \right) \eta {{ \mathbb {F}x}}^{2}+\frac{1}{2}\,{\mathbb {F}xx}\, \left( {\mathfrak {C1}}\,\Omega t\mathbb {F}+{\mathfrak {C2}}\,\mathbb {F} \right) \eta +\mathbb {F} \left( \left( \varrho t-x \right) {\mathfrak {C1}}\right. \\&\left. +{\mathfrak {C3}} \right) \varrho +{\mathbb {F}x}\,{\mathfrak {C1}}\, \eta +{\mathbb {F}xx}\, \left( \left( \varrho t-x \right) {\mathfrak {C1}}+{\mathfrak {C3}} \right) \eta {.} \end{aligned} \end{aligned}$$
(80)

Cases separated with respect to free constants / functions:

(Case): \(\mathfrak {C1}\)

$$\begin{aligned} \aleph 1 \left( x,t,\mathbb {F} \right)= & {} \Omega t \mathbb {F} +\varrho t-x{,} \end{aligned}$$
(81)
$$\begin{aligned} Flux_t= & {} \frac{1}{2} \mathbb {F}^{2} t \Omega + \varrho t \mathbb {F} -\mathbb {F} x,\nonumber \\ Flux_x= & {} \frac{1}{3} \mathbb {F}^{3} t \Omega ^{2}+ \mathbb {F}^{2} t \Omega \varrho - \frac{1}{2} \Omega \mathbb {F}^{2} x +\mathbb {F} \Omega t \eta xx-\frac{1}{2} \Omega t \eta \mathbb {F} x^{2}\nonumber \\{} & {} \quad + \varrho ^{2} t \mathbb {F}-\varrho \mathbb {F} x+\eta \mathbb {F} x +\varrho \eta t \mathbb {F} xx- \eta \mathbb {F} xxx{.} \end{aligned}$$
(82)

(Case): \(\mathfrak {C2}\)

$$\begin{aligned}{} & {} \aleph 1 \left( x,t, \mathbb {F} \right) =\mathbb {F}{,} \end{aligned}$$
(83)
$$\begin{aligned}{} & {} Flux_t=\frac{1}{2} \mathbb {F}^{2},\nonumber \\{} & {} Flux_x=\frac{1}{3} \mathbb {F}^{3} \Omega + \frac{1}{2} \mathbb {F}^{2} \varrho +\mathbb {F} \eta \mathbb {F} xx-\frac{1}{2} \eta \mathbb {F} x^{2}{.} \end{aligned}$$
(84)

(Case:) \(\mathfrak {C3}\)

$$\begin{aligned}{} & {} \aleph 1 \left( x,t,\mathbb {F} \right) =1{,} \end{aligned}$$
(85)
$$\begin{aligned}{} & {} Flux_t= \mathbb {F},\nonumber \\{} & {} Flux_x=\frac{1}{2} \mathbb {F}^{2} \Omega + \mathbb {F} \varrho + \mathbb {F} xx \eta {.} \end{aligned}$$
(86)

8 Conclusion

This study deals with the generalized non-linear perturbed-KdV equation, exploring its properties and behaviors. By analyzing this equation, researchers sought to gain a deeper understanding of the underlying dynamics and potential applications in various scientific and mathematical contexts. The Lie symmetry analysis with optimal system and reduction method is performed. New extended direct algebraic approach is employed to get analytical solutions. The final results are,

  • The suggested model’s Lie algebra is established and also an optimal system of subalgebras is generated.

  • The transnational symmetry in space is connected with the conservation of mass and temporal symmetry is associated with conservation of energy, along with scaling symmetries for the generalized perturbed-KdV equation is produced.

  • The study successfully obtained generalized closed-form analytical solutions for a specific mathematical equation. Additionally, twelve distinct soliton groups were identified through the analysis, contributing to a comprehensive understanding of the equation’s behavior and providing valuable insights for applications in various scientific and mathematical domains.

  • The transmission of propagating solitary waves can be controlled by solitonic wave number.

  • The developed conserved vectors ensured that the total mass, energy, and momentum remain the same over time, even if it moves and changes shape.

In order to illuminate the graphical behavior of optical pulses, we strategically chose specific values for the involved free parameters. By assigning appropriate values, we create a visual representation that vividly showcases how optical pulses evolve. This graphical analysis serves as a valuable tool for interpreting the dynamics and characteristics embedded within the solution.