Electron-acoustic anti-kink, kink and periodic waves in a collisional superthermal plasma

Abstract

A qualitative analysis of the electron-acoustic wave is taken in a collisional plasma having two-temperature electrons with a fixed ion background, where hot electrons follow kappa distribution. The collision between stationary ions and cold electrons is considered. Using reduced perturbation technique, the Burgers equation for the plasma system is derived. Using traveling wave transformation, we obtain the dynamical system corresponding to the plasma system. Phase plane analysis is used in the dynamical system to study different kinds of wave features for the considered plasma system. Moreover periodic wave features and shock wave features are investigated in accordance to periodic orbits and heteroclinic orbits obtained in the phase portrait. Role of the superthermal parameter ($\kappa$), speed of the travelling wave (U) and $\alpha =n_{c_{0}}/n_{h_{0}}$ (where $n_{c_{0}}$ denotes the number density of cold electrons in equilibrium and $n_{h_{0}}$ denotes the number density of hot electrons in equilibrium) are shown on the electron-acoustic periodic waves and shock waves structures. The results hold relevance and significance in the context of space plasma.

1 Introduction

The study of electron-acoustic waves (EAW) continues to be of great interest, as they are observed in various plasma environments, including laboratory experiments, numerical simulations, and space plasma environments (Montgomery et al. 2001; Nikolic et al. 2002; Surendra and Graves 1991; Shukla et al. 2002; Akter and Hafez 2023). These waves occur in plasma containing stationary ions and two distinct populations of electrons (hot and cold) (Gary and Tokar 1985; Gary 1987). The cold electron fluid supplies inertia and hot electron fluid provides the force of restoration. The ions in the plasma act as a stable, unperturbed neutral background essential for the existence of EAWs (Gary 1987). The phase velocity ($v_{ph}$) of EAWs falls within the range of the thermal speeds of the hot and cold electrons, where the thermal speed of the cold electrons ($v_{tc}$) is given by $v_{tc}=\sqrt{T_{c}/m}$, and the thermal speed of the hot electrons ($v_{th}$) is given by $v_{th}=\sqrt{T_{h}/m}$, where $T_h$ denotes the temperature of the hot electrons, $T_c$ denotes the temperature of the cold electrons and m denotes the mass of an electron. For EAWs to exist, it is crucial that the number density of the cold electron species is much less compared to the number density of the hot electron species (i.e., $n_{h_{0}}>>n_{c_{0}}$), where $n_{h_{0}}$ denotes the number density of hot electrons in equilibrium and $n_{c_{0}}$ denotes the number density of cold electrons in equilibrium. So, the speed of EAWs is $C_{se}=\sqrt{(T_{h}/m)(n_{c_{0}}n_{h_{0}})}$. The linear mode analysis shows that EAWs follow a dispersion relation expressed as Gary and Tokar (1985), Mace et al. (1999), Singh and Lakhina (2001) $\omega ^2 = k^2c_{se}^2(1 + 3k^2\lambda _{Dc}^2)/(1 + k^2\lambda _{Dh}^2)$, where k denotes the wave number, $\omega$ denotes the wave frequency and $\lambda _{Dh}=\sqrt{T_{h}/4\pi n_{h_{0}}e^{2}}$ and $\lambda _{Dc}=\sqrt{T_{c}/4\pi n_{c_{0}}e^{2}}$ are Debye length of hot and cold electron respectively. In the long wavelength limit ($k^2\lambda _{Dh}^2<< 1$) and when the pressure from cold electrons is negligible compared to hot electrons, the dispersion relation simplifies to $\omega \approx kC_{se}$. Compared to ion acoustic waves, EAWs typically experience stronger damping due to the higher mobility of cold electrons. However, if cold electron density ($n_{c_{0}}$) is sufficiently low compared to the hot electron ($n_{h_{0}}$) density, and the cold electron temperature ($T_{c}$) is much lower than the hot electron temperature ($T_h$) (Gary 1987), the damping effect of EAWs is significantly reduced. This is because the wave propagation is enabled due to presence of the cold electron component while reducing the impact of Landau damping.

The presence and characteristics of EAWs have been confirmed through observations conducted by the Fast Auroral SnapshoT (FAST) mission in various regions of Earth’s magnetosphere (Gary and Tokar 1985; Gary 1987; Mace et al. 1999; Singh and Lakhina 2001; Cattell et al. 1999), including the intermediate auroral region (altitude less than 4000 km), geotail, and at higher altitude polar auroral region (approximately $2-8$ $R_E$, where $R_E$ denotes the Earth’s radius). These observations have revealed that the generation of most of the electrostatic high-frequency noise in the auroral plasma is due to EAWs (Pottelette and Treumann 2005). Under strong excitation, EAWs can undergo nonlinear evolution and give rise to various nonlinear structures, such as kink and anti-kink wave features, solitons, wave modulations (envelope solitons), turbulence, electron holes and shocks. These nonlinear structures have been observed in different regions of Earth’s magnetosphere, primarily in the polar magnetosphere and various auroral regions (Mozer et al. 1977; Temerin et al. 1982; Dubouloz et al. 1993; Berthomier et al. 2000; Ergun et al. 2004; Bostron 1992; Lakhina et al. 2008; Mace and Hellberg 1990; Kourakis and Shukla 2004; Chakrabarti and Sengupta 2011; Dutta et al. 2011), through satellite measurements. Similar observations of EAWs have also been made in laboratory settings (Anderegg et al. 2009). While analyzing the data collected by various satellites, it has been observed that the majority of the nonlinear structures in EAWs can be attributed to fluctuations in the parallel electric field (Evans 1974; Mozer and Kletzig 1998; Pottelette and Berthomier 2009).

In Yu and Shukla (1983) investigated linear and nonlinear modified EAWs in a plasma with two electron components (cold and hot). They found that the cold electron population density strongly influences the frequency of these EAWs. The study also discussed solitons associated with the modified EAWs. In Hellberg et al. (2000) conducted an experiment to observe electrostatic waves with high-frequency in a plasma with two temperature electrons. They observed that neither the bi-Maxwellian nor the Maxwellian-waterbag models could fully explain the damping and dispersion rates. However, by modelling the hot electron component using kappa-distribution function, they confirmed the presence of EAWs in the laboratory. In Singh and Lakhina (2001) examined the generation of EAWs in the magnetosphere using a plasma model with four components. They demonstrated that adding hot electrons to a three-component model reduced the excited wave growth rates and frequencies. The study applied the linear theory of EAWs to different regions of the magnetosphere and explained the presence of broadband electrostatic noise. In Lakhina et al. (2008) studied the nonlinear behavior of electron-acoustic and ion-acoustic waves in space plasma with multi-components. They applied the method of Sagdeev pseudopotential and identified three different types of solitary waves: ion-acoustic, slow ion-acoustic and electron-acoustic solitons. This study also discussed the effects of various plasma parameters on the amplitude of these solitons and their relevance to observations in the plasma sheet boundary layer.

In Han et al. (2013) investigated the existence and interactions of electron-acoustic shock waves with q-nonextensive distributed electrons in a non-Maxwellian plasma. They studied the role of collision on the propagation of shock waves, considering various parameters like the q non-extensive parameter and the ratio of number density of hot electrons to the number density of cold electrons. This study highlighted trajectory changes of shock waves with the combined role of dispersion and dissipation. In Han et al. (2014) conducted a theoretical inquiry into the nonlinear electron-acoustic shock and solitary waves propagation in a dissipative, nonplanar space plasma with $\kappa$ distributed hot electrons. They used the method of reductive perturbation to derive a modified KdV-Burgers equation for nonlinear waves in this plasma. The study examined the role of different parameters on the time evolution of shock wave profiles, nonlinear structures and nonplanar solitary waves resulting from the planar solitary wave collision. In Chowdhury et al. (2017) addressed the experimental observation of EAW propagation in a laboratory plasma. They overcame the challenge of heavy damping by introducing a small amount of drifting cold electrons in the Magnetized Plasma Linear Experimental device. This study revealed that the drift of electrons relaxes the conditions for wave destabilization and explained the observed phase velocity of the EAW. In Ali et al. (2017) studied the behavior of analytical electron acoustic solitary waves (EASWs) in the presence of a periodic force. They obtained a solution analytically for EASWs in the occurrence of a periodic force. The solution helped in exploring the role of various parameters on the characteristics of the EASWs. In Bansal et al. (2018) investigated obliquely propagating EASWs in a magnetized plasma with cold electrons, stationary ions and superthermal hot electrons. Using method of reductive perturbation, they derived the KdV-Burgers equation and investigated the variation of shock wave structure with various plasma parameters such as density of particle, superthermal parameter, temperature ratio of electrons, obliqueness, kinetic viscosity and magnetic field strength. The study aimed to understand the wave features observed in laboratory or space plasmas. In Sarkar et al. (2020) explored the formation of envelope solitons and solitary structures in EAWs in the inner magnetosphere plasma with suprathermal ions. Applying the method of reductive perturbation, they obtained the KdV equation and investigated the role of density, supra-thermality and Mach number on solitary wave structures. The study found that the parameters influenced the existence and profile of solitary waves, with higher densities and temperatures resulting in sharper profiles. The findings have implications for understanding astrophysical phenomena and data obtained from space missions. In Chatterjee and Mandi (2023) conducted a study on dust-ion-acoustic waves (DIAWs) in an unmagnetized dusty plasma and obtained one-soliton and two-soliton-shocks and other wave features.

In Abdelwahed et al. (2021) found new mathematical solutions for studying ionosphere plasma, with practical implications for fluid dynamics and ionosphere observations. Various types of wave propagations, including soliton waves, periodic waves, shock waves, explosive waves, and explosive-shock waves were successfully derived from the mathematical framework of the (MKP) equation. In Alharbi et al. (2022) developed a unified solver technique for creating new optical structures in stochastic nonlinear Schrödinger equations (NLSEs) with practical applications in fiber optics. These structures include various types and exhibit stochastic variations in amplitude and frequency due to nonlinear effects, making them important for advanced fiber communications. In Abdelwahed et al. (2023) utilized the Wiener process to investigate the (2+1)-dimensional chiral nonlinear Schrödinger equation (CNLSE), which relates to fractional Hall effect edge states in quantum physics. They applied the sine-Gordon expansion technique (SGET) to derive stochastic solutions, revealing various solitary behaviors like bright and dark solitons, periodic envelopes, and dissipative waves. These solutions changed significantly with variations in system parameters. The stochastic parameter played a key role in affecting damping, growth, and conversion effects, while noise intensity led to notable periodic envelope structures and shock-forced oscillations. This method holds promise for diverse nonlinear energy equations in applied sciences. In Azzam et al. (2023) studied electrostatic nonlinear Langmuir structures in dynamic environments like magnetospheres, clouds, and solar wind. They used theoretical models with stochastic elements to describe Langmuir waves, showing how stochastic factors influenced key behaviors. Their simplified method for obtaining stochastic solutions was crucial for understanding energy generation during the collapse of solar Langmuir wave bursts and clouds. This research had implications for studying energy phenomena and seeding in clouds, including electrostatic waves. It also explored the impact of noise parameters on solar wind Langmuir waves, relevant for real observations of energy processes in clouds. In Abdelwahed et al. (2023) examined how higher-order nonlinear Schrödinger equations (HONLSEs) impact energy and solitary transmission in optical fiber communications. They used a unified solver approach, accounting for factors like steepness, higher-order dispersions, and nonlinearity’s self-frequency effects. These HONLSE solutions revealed insights into complex wave energy phenomena and applications.

Singh et al. (2020) in 2020 studied the nonlinear electrostatic waves in a magnetized plasma, composed of cold ions and suprathermal $\kappa$-distributed electrons, were investigated. These waves propagated obliquely to the magnetic field. The researchers examined how parameters like initial electric field amplitude, wave Mach number, spectral index, propagation angle, and ion drift velocity influenced electric field structures. In Bibi et al. (2023) applied the $(m + (G'/G))$-expansion technique to find soliton solutions for the (3+1)-dimensional fractional modified Zakharov Kuznetsov (mZK) equation, which describes magnetic field effects on ion-acoustic waves in plasma. In Alkinidri et al. (2023) studied the impact of fluid flow and vibration on subsonic flow acoustics. They focused on noise generated by a convective gust interacting with a vibrating plate. Using the Wiener-Hopf technique, they analyzed how sound waves scatter when encountering a soft finite barrier. This research is valuable for understanding how structures interact with fluid flow in subsonic environments, with applications in aerospace engineering and noise reduction. Dutta et al. (2012), in 2012 investigated finite amplitude electron acoustic waves (EAW) in a collisional plasma using a fluid model to describe two-temperature electron species within a fixed ion background. They found that wave nonlinearity, dispersion, and dissipation due to electron-ion collisions, coupled with collective phenomena like plasma current, led to the formation of electron acoustic shock waves, as evidenced by both analytical and numerical analyses but they did not study the qualitative behavior of the electron-acoustic plasma waves. So, we are interested in this model to study the qualitative behavior of these electron-acoustic plasma waves in auroral plasma.

Most of the previous investigations were focused on EAWs focused on the collisionless regime. But, it is important to take into consideration the role of collisions in different plasma environments, both in the space plasma environment and in laboratory experiments. For instance, at the altitudes of the auroral ionosphere, collisions cannot be neglected (Volosevich and Galperin 1997). Therefore, it is crucial to study the attributes of nonlinear propagation of EAWs in the existence of dissipation caused by electron-ion collisions. There is no work on qualitative analysis of EAWs considering the collision between electrons and ions in the considered plasma system to the best of our knowledge. This paper explores the behavior of finite amplitude nonlinear EAWs in a plasma where collisions occur between electrons and ions. Specifically, we study the characteristics of propagation of these EAWs in a plasma environment that involves electron-ion collisions. Using Burgers equation, one can analyze the propagation, dispersion, and damping properties of EAWs in plasma. By solving this equation numerically and analytically, one can examine the nonlinear dynamics of the waves, including the formation of shock waves and analyze the impact of different plasma parameters on these wave features.

This paper is structured as follows: The plasma model and the basic equations are discussed in Sect. 2. Section 3 focuses on deriving the Burgers equation, which describes the propagation of the nonlinear EAWs. The transformation of the Burgers equation into planar dynamical systems is followed by both analytical and numerical solutions in Sect. 4. Section 5 is kept for the conclusion of the paper.

2 Basic equations

The plasma considered here is unbounded, meaning it does not have any specific boundaries or confinements. The plasma is also homogeneous, indicating that its properties and characteristics are uniform throughout its volume. Furthermore, the plasma is considered to be unmagnetized, implying that magnetic fields do not have a significant influence on its behavior. Space plasma often exhibit distribution functions that deviate from the Maxwellian distribution due to the presence of suprathermal particles with high-energy tails, which can be effectively described by the $\kappa$-distribution (Summers and Thorne 1991; Mace and Hellberg 1995). The plasma is composed of two main components: electrons, which can be categorized as both hot and cold, and ions, which are stationary. The primary collisions that occur within this plasma system involve interactions between the stationary ions and cold electrons. Relative to these EAWs, the hot electrons move so fast that they have enough time to conserve the thermodynamics equilibrium and hence with regard to this wave with low frequency, we can presume that hot electrons follow Kappa distribution. Ghosh (2017), Danehkar et al. (2011) given by

$$\begin{aligned} n_{h} = n_{h_{0}}\bigg [1-\frac{1}{(\kappa -\frac{3}{2})} \frac{e\phi }{T_{h}}\bigg ]^{-\kappa +\frac{1}{2}}, \end{aligned}$$

(1)

where $\kappa >\frac{3}{2}$ and $n_{h}$, $n_{h_{0}}$, e, $\phi$ and $T_{h}$ are number density of hot electrons, number density of hot electrons in equilibrium, magnitude of electric charge, electrostatic potential and temperature of hot electrons respectively.

In the momentum equation for the cold electrons, the pressure term has been neglected due to the significant difference between the hot electron temperature ($T_h$) and the cold electron temperature ($T_c$) in this plasma system. Usually, in the auroral region, $T_h$ ranges from 200 to 500 electron volts (eV), while $T_c$ ranges from 1 to 10 eV (Singh and Lakhina 2001). The equation of momentum (Dutta et al. 2012) for the cold electrons is given by

$$\begin{aligned} mn_{c}\bigg (\frac{\partial }{\partial t}+v_{c}\frac{\partial }{\partial x}\bigg )v_{c} = -n_{c}eE-mn_{c}\nu _{c}v_{c}, \end{aligned}$$

(2)

where $n_{c}$, $\nu _{c}$, $v_{c}$ and E are the number density of cold electrons, collision frequency between stationary background ions and cold electrons, cold electron fluid velocity and the electric field respectively.

The equation of continuity (Dutta et al. 2012) for cold electrons is

$$\begin{aligned} \frac{\partial n_{c}}{\partial t}+\frac{\partial }{\partial x}(n_{c}v_{c})=0, \end{aligned}$$

(3)

also from Maxwell’s equation (Dutta et al. 2012), we have

$$\begin{aligned} \frac{\partial E}{\partial x}= & {} 4\pi e(n_{0}-n_{c}-n_{h}),\end{aligned}$$

(4)

$$\begin{aligned} \frac{\partial E}{\partial t}= & {} 4\pi e n_{c}v_{c}. \end{aligned}$$

(5)

The majority of the observations revolve around instability in the parallel electric field (Evans 1974; Mozer and Kletzig 1998; Pottelette and Berthomier 2009), in the given Eq. (5), the balance is achieved between the particle current and the displacement current, assuming that the plasma is unmagnetized ($\nabla \times B =0$). Now using Eqs. (4) and (5) with $E=-\frac{\partial \phi }{\partial x}$ in Eq. (2), we get

$$\begin{aligned} \bigg (\frac{\partial }{\partial t}+v_{c}\frac{\partial }{\partial x}\bigg )v_{c}=\frac{e}{m}\frac{\partial \phi }{\partial x}+\frac{\nu _{c}}{4\pi e n_{c}}\frac{\partial }{\partial t}\bigg (\frac{\partial \phi }{\partial x}\bigg ). \end{aligned}$$

(6)

For convenience, we use normalized variables for the above equations to study the dynamics of the EAWs, hence we define ${\hat{t}}=\omega _{p_{c}}t$, ${\hat{x}}=\frac{x}{\lambda _{D_{h}}}$, $\hat{n_{c}}=\frac{n_{c}}{n_{c_{0}}}$, $\hat{n_{h}}=\frac{n_{h}}{n_{h_{0}}}$, ${\hat{\phi }}=\frac{e\phi }{T_{h}}$ and ${\hat{v}}=\frac{v_{c}}{v_{th}}$, where $\lambda _{D_{h}}=\sqrt{\frac{T_{h}}{4\pi n_{h_{0}}e^{2}}}$   denotes the Debye length of hot electron, $\omega _{p_{c}}=\sqrt{\frac{4\pi n_{c_{0}}e^{2}}{m}}$   denotes the plasma frequency of cold electrons, $v_{th}=\sqrt{\dfrac{T_{h}}{m}}$   denotes the thermal speed of hot electron.

Now using these normalized quantities in Eqs. (3),(4) and (6), we get

$$\begin{aligned}{} & {} \frac{\partial \hat{n_{c}}}{\partial {\hat{t}}}+\frac{\partial }{\partial \hat{}x}(\hat{n_{c}}{\hat{v_{c}}})=0,\end{aligned}$$

(7)

$$\begin{aligned}{} & {} \frac{\partial ^{2}{\hat{\phi }}}{\partial {{\hat{x}}^{2}}} =\bigg [1-\frac{{\hat{\phi }}}{(\kappa -\frac{3}{2})}\bigg ]^{-\kappa +\frac{1}{2}}+\alpha {\hat{n}}_{c}-\beta , \end{aligned}$$

(8)

$$\begin{aligned}{} & {} \bigg (\frac{\partial }{\partial {\hat{t}}}+\hat{v_{c}}\frac{\partial }{\partial {\hat{x}}}\bigg )\hat{v_{c}}=\frac{\partial {\hat{\phi }}}{\partial {\hat{x}}}+\frac{\nu _{c}}{\omega _{p_{c}} \hat{n_{c}}} \frac{\partial }{\partial {\hat{t}}}\bigg (\frac{\partial {\hat{\phi }}}{\partial {\hat{x}}}\bigg ), \end{aligned}$$

(9)

where $\alpha =n_{c_{0}}/n_{h_{0}}$ and $\beta =n_{0}/n_{h_{0}}$.

Equations (7)-(9) represent the normalized basic equations which describe the considered plasma model.

For simplicity, hereafter we remove cap from the variables in above equations and work with normalized variables.

3 The Burgers equation

In this segment, we will obtain the Burgers equation for the above considered plasma model using the method of reductive perturbation.

Let us consider the following stretching coordinates (Tamang and Saha 2019; Washimi and Taniuti 1966; Dwivedi and Pandey 1995; Shukla and Mamun 2001; Mamun 2008; Sarma and Dev 2014):

$$\begin{aligned} {\left\{ \begin{array}{ll} \xi =\epsilon (x-Mt),\\ \tau =\epsilon ^{2}t, \end{array}\right. } \end{aligned}$$

(10)

where M denotes the phase velocity of the EAW and $\epsilon$ denotes a dimensionless parameter that measures the order of the smallness of the perturbations.

Further we write the dependent variables $n_{c}$, $v_{c}$ and $\phi$ in the power series expansion of $\epsilon$ (Saha and Chatterjee 2014a, b; Ali et al. 2017) as:

$$\begin{aligned} \left. \begin{array}{ll} n_{c}=1+\epsilon n_{c_{1}}+\epsilon ^{2}n_{c_{2}}+\cdots , \\ v_{c}=0+\epsilon v_{c_{1}}+\epsilon ^{2}v_{c_{2}}+\cdots , \\ \phi =0+\epsilon \phi _{1}+\epsilon ^{2}\phi _{2}+\cdots . \\ \end{array} \right. \end{aligned}$$

(11)

To incorporate the effects of finite electron-ion collision, assuming that the ratio of the electron collision frequency $\nu _{c}$ to the plasma frequency $\omega _{p_{c}}$ is small but finite. So, we take

$$\begin{aligned} \frac{\nu _{c}}{\omega _{p_{c}}}=\nu . \end{aligned}$$

(12)

Now using Eqs. (10) and (11) in Eqs. (7)-(9), by considering the lowest powers of $\epsilon$, we obtain the following relations.

$$\begin{aligned} n_{c_{1}}= & {} -\frac{a}{\alpha }\phi _{1}, \end{aligned}$$

(13)

$$\begin{aligned} v_{c_{1}}= & {} -\frac{1}{M}\phi _{1},\end{aligned}$$

(14)

$$\begin{aligned} n_{c_{1}}= & {} -\frac{1}{M^{2}}\phi _{1}, \end{aligned}$$

(15)

where $a=\bigg [\frac{(\kappa -\frac{1}{2})}{(\kappa -\frac{3}{2})}\bigg ]$.

Using Eqs. (13)-(15), we get the dispersion relation as

$$\begin{aligned} M^{2}=\frac{\alpha }{a}. \end{aligned}$$

(16)

From next higher powers of $\epsilon$, we obtain the following relations

$$\begin{aligned}{} & {} -M\frac{\partial n_{c_{2}}}{\partial \xi }+\frac{\partial n_{c_{1}}}{\partial \tau }+\frac{\partial v_{c_{2}}}{\partial \xi }+\frac{\partial (n_{c_{1}}v_{c_{1}})}{\partial \xi }=0, \end{aligned}$$

(17)

$$\begin{aligned}{} & {} \alpha n_{c_{2}}+b\frac{\phi _{1}^{2}}{2}=-a\phi _{2}, \end{aligned}$$

(18)

$$\begin{aligned}{} & {} \frac{\partial v_{c_{1}}}{\partial \tau }+v_{c_{1}}\frac{\partial v_{c_{1}}}{\partial \xi }+\nu M\frac{\partial ^{2}\phi _{1}}{\partial \xi ^{2}}=\frac{\partial }{\partial \xi }(\phi _{2}+Mv_{c_{2}}), \end{aligned}$$

(19)

where $b=\bigg [\frac{(\kappa +\frac{1}{2})(\kappa -\frac{1}{2})}{(\kappa -\frac{3}{2})}\bigg ]$.

Finally, the Burgers equation for EAWs is obtained from Eqs. (17)-(19) after some substitutions in terms of $\phi _{1}$ as

$$\begin{aligned} \frac{\partial \phi _{1}}{\partial \tau }+A\phi _{1}\frac{\partial \phi _{1}}{\partial \xi } -B\frac{\partial ^{2}\phi _{1}}{\partial \xi ^{2}}=0, \end{aligned}$$

(20)

where $A=\bigg [-\frac{3}{2M}-\frac{bM}{2a}\bigg ]$ and $B=\bigg [\frac{\nu }{2}M^2\bigg ]$.

Equation (20) represents the Burgers equation for the electron-acoustic waves.

4 Phase plane analysis and nonlinear wave features

We consider the transformation

$$\begin{aligned} \eta =\xi -U\tau , \end{aligned}$$

(21)

where U denotes the speed of the wave and $\phi _{1}(\xi ,\tau )=\psi (\eta )$.

Using transformation (21), we convert the Burgers Eq. (20) into the following dynamical system (Strogatz 2015; Saha and Banerjee 2021; Abdikian et al. 2020):

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{d\psi }{d \eta }=z,\\ \frac{dz}{d \eta }=\frac{A^{2}}{2B^{2}}\psi ^{3}-\frac{3UA}{2B^{2}} \psi ^{2}+\frac{U^{2}}{B^{2}}\psi . \end{array}\right. } \end{aligned}$$

(22)

The dynamical system (22) is conservative because if we consider $\textbf{f}=(z,\frac{dz}{d\eta })$, then we get $\mathbf {\nabla }. \textbf{f}=0$.

For the equilibrium points of the dynamical system (22), we take

$$\begin{aligned} \frac{d\psi }{d\eta }=0 \text { ~~ and ~~} \frac{dz}{d\eta }=0. \end{aligned}$$

So, the equilibrium points of the dynamical system (22)  are  $E_{0}(0,0)$, $E_{1}(\frac{2U}{A},0)$ and $E_{2}(\frac{U}{A},0)$.

Now Jacobian matrix of the system (22) is given by

$$\begin{aligned} J=\left[ \begin{array}{cc} \frac{\partial {\dot{\phi }}}{\partial \phi }&{} \frac{\partial {\dot{\phi }}}{\partial z}\\ \frac{\partial {\dot{z}}}{\partial \phi }&{} \frac{\partial {\dot{z}}}{\partial z}\\ \end{array} \right] , \end{aligned}$$

where ${\dot{\phi }}=\frac{d\phi }{d\eta }$  and  ${\dot{z}}=\frac{dz}{d\eta }$.

$$\begin{aligned} \text {or,}\quad J=\left[ \begin{matrix} 0&{} 1\\ \frac{3A^2}{2B^2}\phi ^2-\frac{3UA}{B^2}+\frac{U^2}{B^2}&{} 0\\ \end{matrix} \right] . \end{aligned}$$

For equilibrium point $E_{0}(0,0)$, the eigenvalues are $\lambda _1=\frac{U}{B}$ and $\lambda _2=-\frac{U}{B}$ which are two real eigenvalues with opposite signs. So, $E_{0}(0,0)$ is a saddle point.

Now for equilibrium point $E_{1}(\frac{2U}{A},0)$, the eigenvalues are $\lambda _1=\frac{U}{B}$ and $\lambda _2=-\frac{U}{B}$, which are two real eigenvalues with opposite signs, Therefore $E_{1}(\frac{2U}{A},0)$ is a saddle point.

Now for equilibrium point $E_{2}(\frac{U}{A},0)$, the eigenvalues are $\lambda _1=\frac{U}{B}i$ and $\lambda _2=-\frac{U}{B}i$, which are two complex eigenvalues with real part equal to zero. Therefore, $E_{2}(\frac{U}{A},0)$ is a center.

Fig. 1

Phase portrait of the dynamical system (22) for the parameters $\kappa =2$, $\alpha =0.2$, $\nu =0.1$ and $U=0.2$

In the phase portrait given in Fig. 1, $E_{0}$ and $E_{1}$ are saddle points and $E_{2}$ is a center. Phase portrait shows a collection of periodic orbits encircling the the center $E_2$ and two heteroclinic orbits (one passing through $E_{0}$ towards $E_{1}$ and other passing through $E_{1}$ towards $E_{0}$). Similar phase portraits can be obtained for other values of $\kappa$, $\alpha$, $\nu$ and U. As those phase portraits carry the same feature, we ignore them. In the next section, we show nonlinear wave features of the plasma system that we have considered.

4.1 Analytical anti-kink and kink wave solutions

Now, Hamiltonian function for the dynamical system (22) is given by Saha and Banerjee (2021)

$$\begin{aligned} H(\psi ,z)=\frac{z^{2}}{2}-\frac{A^{2}}{2B^{2}}\frac{\psi ^{4}}{4} +\frac{3UA}{2B^{2}}\frac{\psi ^{3}}{3}-\frac{U^{2}}{B^{2}} \frac{\psi ^{2}}{2}. \end{aligned}$$

(23)

Hamiltonian function (23) gives the sum of kinetic energy and potential energy, i.e., the total energy of the system (22).

Now at (0, 0),   $H(0,0)=0=h$ (say).

So, $H(\psi ,z)=h$ for (0, 0), we have

$$\begin{aligned} z=\pm \sqrt{\frac{A^{2}}{B^{2}}\frac{\psi ^{4}}{4}-\frac{UA}{B^{2}}\psi ^{3} +\frac{U^{2}}{B^{2}}\psi ^{2}}. \end{aligned}$$

(24)

Using Eq. (24) in the first equation of system (22), we get

$$\begin{aligned} \psi =\frac{U}{A}\bigg [1\pm tanh\bigg (\frac{U}{2B}\eta \bigg )\bigg ]. \end{aligned}$$

(25)

The graph for anti-kink and kink waves features and effects of various parameters are shown in Figs. 2-6.

Fig. 2

Effect of $\kappa$ (for $\kappa \le 4$) on the anti-kink and kink wave features of Eq. (20) for $\alpha =0.2$, $\nu =0.1$ and $U=0.2$

Fig. 3

Effect of $\kappa$ (for $\kappa >4$) on the anti-kink and kink wave features of Eq. (20) for $\alpha =0.2$, $\nu =0.1$ and $U=0.2$

Fig. 4

Effect of $\alpha$ on the anti-kink and kink wave features of Eq. (20) for $\kappa =2$, $\nu =0.1$ and $U=0.2$

Fig. 5

Effect of U on the anti-kink and kink wave features of Eq. (20) for $\alpha =0.2$, $\nu =0.1$ and $\kappa =2$

Fig. 6

Effect of U on the anti-kink and kink wave features of Eq. (20) for $\alpha =0.2$, $U=0.2$ and $\kappa =2$

We have chosen the values of the parameter based on the environment of the auroral region (Dutta et al. 2012). The Figs. 2-6 show the behavior of anti-kink and kink wave features with varying parameter values. From Figs. 2 and 3 we observe that the amplitude of both anti-kink and kink waves tends to increase as the parameter $\kappa$ increases from 2 to 4. However, beyond $\kappa$ value 4, the amplitude starts to decrease. Additionally, from Fig. 4, we can observe that increasing the parameter $\alpha$ results in a higher amplitude for both anti-kink and kink waves. Furthermore, Fig. 5 illustrates that amplitude of anti-kink and kink waves increases as the parameter U increases. Finally, Fig. 6 shows that smoothness of anti-kink and kink waves improves with increasing values of the parameter $\nu$. The electron-acoustic periodic waves correspond to periodic orbits of the dynamical system (22). These waves refer to the waves with a repeating pattern that controls their frequency and wavelength.

4.2 Periodic wave solutions

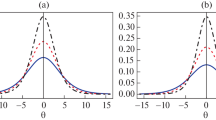
Using the Numerical method, the periodic wave solution is obtained. The graph for periodic wave features and effect of various parameters are shown in Figs. 7-11

Fig. 7

Effect of $\kappa$ (for $\kappa \le 4$) on the Periodic wave feature of the dynamical system (22) for the parameters $\alpha =0.2$, $\nu =0.1$ and $U=0.2$ with initial condition $(-0.02,0)$

Fig. 8

Effect of $\kappa$ (for $\kappa \ge 4$) on the periodic wave feature of the dynamical system (22) for the parameters $\alpha =0.2$, $\nu =0.1$ and $U=0.2$ with initial condition $(-0.02,0)$

Fig. 9

Effect of $\alpha$ on the periodic wave feature of the dynamical system (22) for the parameters $\kappa =2$, $\nu =0.1$ and $U=0.2$ with initial condition $(-0.02,0)$

Fig. 10

Effect of U on the periodic wave feature of the dynamical system (22) for the parameters $\alpha =0.2$, $\nu =0.1$ and $\kappa =2$ with initial condition $(-0.02,0)$

Fig. 11

Effect of $\nu$ on the periodic wave feature of the dynamical system (22) for the parameters $\alpha =0.2$, $U=0.2$ and $\kappa =2$ with initial condition $(-0.02,0)$

The Figs. 7-11 provide insights into the behavior of periodic wave features with varying parameter values. From Figs. 7 and 8 we observe that amplitude as well as width of the waves tend to increase as the parameter $\kappa$ increases from 2 to 4. However, beyond $\kappa$ value 4, amplitude starts to decrease while width of the wave increases. Additionally, from Fig. 9, we can observe that increasing the parameter $\alpha$ results in a higher amplitude and width of the waves. Furthermore, Fig. 10 illustrates that the amplitude of periodic waves increases while the width decreases as the value of the parameter U increases. Finally, Fig. 11 shows that the amplitude of the periodic waves remains the same but the width increases with increasing values of the parameter $\nu$. The electron-acoustic anti-kink and kink waves are produced by violent changes in the electrostatic potential due to the presence of small but finite effect of the ratio of electron collision frequency to the plasma frequency. The Higher is the amplitude of the wave, the higher is the energy of the wave.

5 Conclusion

Electron-acoustic waves with two-temperature electrons with a fixed ion background, where hot electrons follow kappa distribution have been considered. Applying the method of reductive perturbation, the Burgers equation has been obtained. Using traveling wave transformation, the dynamical system has been obtained from the plasma system. Phase plane analysis was used to study different kinds of electron-acoustic wave features for the considered plasma system. Moreover, periodic wave features and shock wave features (anti-kink and kink) have been investigated corresponding to the periodic orbits and heteroclinic orbits obtained in the phase portrait. Impact of the superthermal parameter ($\kappa$), speed of the travelling wave (U), $\alpha =n_{c_{0}}/n_{h_{0}}$ (where $n_{c_{0}}$ denote the number density of cold electrons in equilibrium and $n_{h_{0}}$ denote the number density of hot electrons in equilibrium) and $\nu$ are shown on the electron-acoustic periodic and shock waves structures. We have chosen the values of the parameter based on the environment of the auroral region (Dutta et al. 2012). So the results of the works are helpful to understand nonlinear Electron-acoustic wave features in the auroral region. The polar magnetosphere is known to have EAWs (Cattell et al. 1999), including electrostatic shock waves (Mozer et al. 1977). Observations of these shock waves in the polar magnetosphere provide valuable insights into their physics. Therefore, the outcomes of this study could be helpful in understanding the dynamics of shock waves specifically in the polar magnetosphere. Studying the variations in electric potential that results from the transmission of compressional shock waves hold great significance within the auroral plasma region. Previous investigations showed that in auroral plasma, the physical mechanism responsible for particle acceleration is attributed to the presence of anti-kink and kink wave characteristics (Temerin et al. 1982; Ergun et al. 2004; Bostron 1992).

Appendix

Here we have shown some steps for the derivation of the dynamical system (22) from the Burgers Eq. (20).

From equation (21) we get

$$\begin{aligned}{} & {} \frac{\partial \psi }{\partial \tau }= \frac{\partial \psi }{\partial \eta }. \frac{\partial \eta }{\partial \tau }=-U\frac{d\psi }{d \eta },\end{aligned}$$

(26)

$$\begin{aligned}{} & {} \frac{\partial \psi }{\partial \xi } = \frac{\partial \psi }{\partial \eta }. \frac{\partial \eta }{\partial \xi }=\frac{d\psi }{d \eta },\end{aligned}$$

(27)

$$\begin{aligned}{} & {} \quad \text {and}\quad \frac{\partial ^2\psi }{\partial \xi ^2} = \frac{d^2\psi }{d \eta ^2}. \end{aligned}$$

(28)

Now using Eqs. (26)-(28) in the Burgers Eq. (20), we get

$$\begin{aligned} -U\frac{d\psi }{d \eta }+A\psi \frac{d\psi }{d \eta }-B\frac{d^2\psi }{d \eta ^2}=0. \end{aligned}$$

(29)

Integrating the above Eq. (29) with respect to $\eta$, we get

$$\begin{aligned} -U\psi _{1}+A\frac{\psi ^{2}}{2}-B\frac{d\psi }{d \eta }=c_{1}, \end{aligned}$$

where $c_{1}$ is an integrating constant.

Using boundary conditions   $\psi \rightarrow 0$, $\frac{d\psi }{d \eta }\rightarrow 0$ as $\eta \rightarrow \infty$ or $\eta \rightarrow -\infty$, we get   $c_{1}=0$.

Then we have

$$\begin{aligned} \frac{d\psi }{d \eta }=A\frac{\psi ^{2}}{2B}-\frac{U\psi }{B}. \end{aligned}$$

(30)

Now using Eq. (30) in Eq. (29), we get

$$\begin{aligned} \frac{d^2\psi }{d \eta ^2}=\frac{A^{2}}{2B^{2}}\psi ^{3} -\frac{3UA}{2B^{2}}\psi ^{2}+\frac{U^{2}}{B^{2}}\psi . \end{aligned}$$

(31)

Now taking $\frac{d\psi }{d \eta }=z$, we get the dynamical system (22).