Nonlinear Wave Structures of Electron Acoustic Waves in Nonextensive Magnetized Electron–Positron–Ion Plasmas

Abstract

A multicomponent collisionless magnetized plasma system consisting of cold mobile electron fluid, hot electrons and positrons following the q-nonextensive distribution, and immobile positive ions is considered to study nonlinear propagation of electron acoustic waves. The reductive perturbation technique is used to reduce the basic set of fluid equations to the Laedke–Spatschek equation. By means of Painlevé integrability and Bäcklund transformation, some analytic solutions of the nonlinear evolution equation are presented. Furthermore, the effect of different plasma parameters on the characteristics of the nonlinear waves including single soliton, M-shaped soliton, breather, and periodic and rogue wave-type structures are graphically discussed.

1. INTRODUCTION

Nonlinear wave structures are of great importance among the most fascinating phenomena in the physical world. Numerous observations in space plasma region predict the existence of electron acoustic wave (EAW) in auroral acceleration region, plasma sheet boundary layer, terrestrial magnetosphere cusp region, Earth’s bow shock, geomagnetic tail, etc. [1–5]. EAWs are also observed in the laboratory experiments when the plasma consists of two distinct temperature ensembles of electrons, referred to as cold and hot electrons [6] and in numerical simulations [7]. It is basically an acoustic-type wave, in which the inertia comes from the cold electron fluid and the restoring force comes from the hot electron thermal pressure whereas the ions play the role of neutralizing background. The EAWs have been used to explain several wave emissions in different regions of the Earth’s magnetosphere [8]. It was first applied to interpret the hiss emissions observed in the polar cusp region in association with low energy (~100 eV) upward moving electron beams [9]. Also, the EA mode was employed to illustrate the generation of the broadband electrostatic noise (BEN) emissions detected in the plasma sheath [10] as well as in the auroral zone [8]. It is worth mentioning that EAWs usually suffer stronger damping because of the higher mobility of cold electrons than ions. To avoid Landau damping, it is necessary that the cold electron temperature (${{T}_{{\text{c}}}}$) should be much lower than the hot electron temperature (${{T}_{{\text{h}}}}$) and the equilibrium density of cold electrons is considered to be much lower than the equilibrium density of hot electrons [11]. Physically, for sufficiently low cold electron density compared to hot electron density, the damping of EAWs is heavily diminished while the cold electrons allow the wave to propagate. During the last few decades, the study of EAWs has been performed to investigate different types of collective nonlinear structures such as, solitons, shocks, double layers, t-urbulence, wave modulations, etc. [12–17]. The nonlinear propagation of EAWs in a plasma consisting of a   cold electron fluid, hot electrons obeying a trapped/vortex-like distribution, and stationary ions was studied in [18]. In [19], a theoretical investigation for understanding the properties of three dimensional (3D) EAW solitary waves in a magnetized plasmas containing stationary ions, magnetized cold electrons with electron beams, and magnetized hot electrons obeying a vortex-like distribution was carried out. Most of these nonlinear structures of EAWs were observed by several spacecraft missions [20, 21].

In contrast to ordinary two-component electron-ion plasma, it has been observed that the nonlinear waves in plasmas having an additional positron component behave differently [22]. Electron–positron–ion (EPI) plasmas occur in different regions of astrophysical contexts, such as the solar atmosphere [23], active galactic nuclei, pulsar magnetospheres, and near the polar cusp regions of the pulsars [24–26] and they have also been created in the laboratory [27]. Thus, it is pertinent to investigate the characteristics of plasma waves in EPI plasma. It is often noticed that the electrons and positrons are highly energetic particles that are present in astrophysical and space plasmas and are often represented by non-Maxwellian particle distribution. Accordingly, there has been a sustained research activity on the nonextensive statistical mechanics based on deviation from Boltzmann–Gibbs–Shannon (B–G–S) entropy measures to study electrostatic waves in plasma. Generalization of the B–G–S entropy was first recognized by Renyi [28] and subsequently Tsallis [29] extended the standard additivity of entropies to the nonlinear, nonextensive cases, where the entropic index q measures the amount of system nonextensivity. The q-nonextensive distribution has been effectively applied to various problems, including head-on collision of black holes, gravitational wave emission, and solar neutrino problem [30, 31]. During the last two decades, a large number of researches have been reported to investigate the different linear and nonlinear structures in various plasma physics models using q-nonextensive distribution of charged particles [32–35]. The properties of fully nonlinear EA solitary waves in an unmagnetized and collisionless EPI plasma with superthermal electrons and positrons were investigated in [36]. Cylindrical and spherical EA Gardner solitons and double layers in a two-electron-temperature plasma with nonthermal ions were studied [37]. The roles of nonextensive hot electrons and positrons on nonplanar EA shock waves in EPI plasmas were researched [38]. Bansal and Aggarwal [39] studied EA shock waves in unmagnetized nonplanar geometry with nonextensive electrons [39].

However, most of the above studies on the nonlinear waves are restricted to unmagnetized plasmas. Observations of space and astrophysical plasmas reveal that external magnetic field plays a significant role in linear and nonlinear plasma dynamics, as well as it influences the stability criteria of plasma waves. The model to study the 3D nonlinear waves in various magnetized plasma systems was presented in [40]. Inclusion of magnetic field in the plasma system completely changes the propagation dynamics of nonlinear waves. The 3D EAWs in a magnetized plasma featuring nonthermal hot electrons were investigated [41] and the propagation of linear and nonlinear electrostatic waves by deriving the Zakharov–Kuznetsov (ZK) equation in magnetized EPI plasma was studied [42]. Solitary wave solutions for the nonlinear 3D modified Korteweg–de Vries–ZK (KdV–ZK) equation were presented [43] by implementing the extended direct algebraic and fractional direct algebraic methods for nonlinear ion–acoustic waves in magnetized electron–positron plasma. The basic features of nonlinear propagation of electrostatic waves subjected to an external magnetic field in EPI plasma in presence of heavy particles were theoretically studied [44]. EA shock wave structures in EPI plasma under the influence of external magnetic field and superthermality were investigated in [45]. Recently, various nonlinear structures (such as soliton, periodic, quasi-periodic, and chaos) of collective ion dynamics in the presence of external magnetic field were theoretically investigated [46] by analyzing the novel nonlinear equation [47]. More recently, the propagation dynamics of EAWs in the presence of an external uniform weak magnetic field was studied [48], a generalized 3D KdV equation was derived and an exact solution with the help of Bäcklund transformation was presented. It may be mentioned here that the presence of nonextensive electrons and positrons in the presence of external magnetic field (modifying wave phase velocity) qualitatively modifies the nonlinear coherent structures of EAWs. Nonextensive particle distributions have become increasingly widespread throughout the physics of space plasma environments as they provide an efficient modeling of the observed particle distributions. Study of $q$-nonextensive statistics can provide a powerful and convenient frame for the analysis of many astrophysical and cosmological scenarios like planetary rings, solar winds, cometary tails [49], dark-matter halos [50], hadronic matter and quark-gluon plasmas [51], etc. Thus, it is expected that the presence of nonextensive electrons and positrons modifies the parametric region where EA nonlinear structures can exist. The main focus of our paper is to investigate the influence of $q$-nonextensive hot electrons and positrons, magnetic field strength and positron concentration on the characteristics of EAWs by deriving the Laedke–Spatschek equation [47]. The layout of this article is as follows. The basic equations and derivation of the nonlinear evolution equation are provided in Section 2. Verification of Painlevé integrability and analytical solutions of the nonlinear evolution equation using Bäcklund transformation are demonstrated in Section 3. Finally, brief conclusions of our results are presented in Section 4.

2. THEORETICAL MODEL AND NONLINEAR EVOLUTION EQUATION

We consider a homogeneous, collisionless and unbounded plasma medium consisting of inertial cold electrons, nonextensive hot electrons and positrons, and immobile positive ions in presence of externally applied uniform magnetic field ${\mathbf{B}} = {{B}_{0}}\hat {z}$, where $\hat {z}$ is the unit vector along the z axis. Ions having low energy and higher mass compared to electrons fail to respond in the fast timescale of electrons. Thus, the equilibrium condition reads ${{n}_{{{\text{c}}0}}} + {{n}_{{{\text{h}}0}}} = {{n}_{{{\text{p}}0}}} + {{n}_{{{\text{i}}0}}}$, where ${{n}_{{j0}}}$ is the unperturbed number densities of the species j (here, $j = {\text{c,h,p}}$, and i for cold electron, hot electron, hot positron, and positively charged ion, respectively). In such a magnetized plasma medium, the governing equations are given by

$$\frac{{\partial {{n}_{{\text{c}}}}}}{{\partial t}} + \nabla \cdot ({{n}_{{\text{c}}}}{{{\mathbf{u}}}_{{\mathbf{c}}}}) = 0,$$

(1)

$$\frac{{\partial {{{\mathbf{u}}}_{{\mathbf{c}}}}}}{{\partial t}} + ({{{\mathbf{u}}}_{{\mathbf{c}}}} \cdot \nabla ){{{\mathbf{u}}}_{{\mathbf{c}}}} = \frac{e}{{{{m}_{e}}}}\nabla \varphi - \frac{{e{{B}_{0}}}}{{{{m}_{e}}c}}({{{\mathbf{u}}}_{{\mathbf{c}}}} \times \hat {z}),$$

(2)

$${{\nabla }^{2}}\varphi = 4\pi e({{n}_{{\text{c}}}} + {{n}_{{\text{h}}}} - {{n}_{{\text{p}}}} - {{n}_{{{\text{i}}0}}}),$$

(3)

where ${{n}_{j}}$ is the number density of the plasma species j, ${{{\mathbf{u}}}_{{\text{c}}}}$ and below also ${{u}_{{\text{c}}}}$, ${{v}_{{\text{c}}}}$, ${{w}_{{\text{c}}}}$ are the cold electron fluid velocity in x, y, z directions, φ is electrostatic wave potential, and ${{m}_{e}}(e)$ is the mass (charge) of an electron.

In order to model the nonextensivity of plasma species (hot electrons and positrons), we employ the following q-nonextensive distribution as [32, 52]

$${{n}_{{\text{h}}}} = {{n}_{{{\text{h}}0}}}\mathop {\left[ {1 + (q - 1)\frac{{e\varphi }}{{{{k}_{{\text{B}}}}{{T}_{{\text{h}}}}}}} \right]}\nolimits^{\tfrac{{q + 1}}{{2(q - 1)}}} ,$$

(4)

$${{n}_{{\text{p}}}} = {{n}_{{{\text{p}}0}}}\mathop {\left[ {1 - (q - 1)\frac{{e\varphi }}{{{{k}_{{\text{B}}}}{{T}_{{\text{p}}}}}}} \right]}\nolimits^{\tfrac{{q + 1}}{{2(q - 1)}}} ,$$

(5)

where the parameter q indicates the strength of nonextensivity, ${{k}_{{\text{B}}}}$ is the Boltzman’s constant, and ${{T}_{{\text{p}}}}$ is the temperature of hot positrons. It can be mentioned here that in case of $q < - 1$, the q-distribution is not normalizable. In the extensive limiting case $(q \to 1)$, the well known Maxwell–Boltzmann distribution is recovered. For electrostatic plane wave propagation in a collisionless plasma, the dispersion relation in Tsallis formalism fits the experimental data very well when $q < 1$ [53]. For physically realistic Tsallis distribution function, the present study is restricted to values of q within the very limited range $0.6 < q \leqslant 1$ [54].

The nonlinear dynamics of EAWs is governed by the following normalized equations

$$\frac{{\partial {{n}_{{\text{c}}}}}}{{\partial t}} + \nabla \cdot ({{n}_{{\text{c}}}}{{{\mathbf{u}}}_{{\mathbf{c}}}}) = 0,$$

(6)

$$\frac{{\partial {{{\mathbf{u}}}_{{\mathbf{c}}}}}}{{\partial t}} + ({{{\mathbf{u}}}_{{\mathbf{c}}}} \cdot \nabla ){{{\mathbf{u}}}_{{\mathbf{c}}}} = \alpha \nabla \varphi - \Omega ({{{\mathbf{u}}}_{{\mathbf{c}}}} \times \hat {z}),$$

(7)

$$\begin{gathered} {{\nabla }^{2}}\varphi = \frac{{{{n}_{{\text{c}}}}}}{\alpha } + \mathop {\left[ {1 + (q - 1)\varphi } \right]}\nolimits^{\tfrac{{q + 1}}{{2(q - 1)}}} \\ \, - {{\mu }_{1}}\mathop {\left[ {1 - (q - 1)\sigma \varphi } \right]}\nolimits^{\tfrac{{q + 1}}{{2(q - 1)}}} + {{\mu }_{2}}, \\ \end{gathered} $$

(8)

where the particle densities ${{n}_{j}}$ and cold electron fluid velocity ${{{\mathbf{u}}}_{{\text{c}}}}$ are normalized by ${{n}_{{j0}}}$ and ${{C}_{e}} =$ ${{({{k}_{{\text{B}}}}{{T}_{{\text{h}}}}{\text{/}}\alpha {{m}_{e}})}^{{1/2}}}$, respectively, φ is normalized by ${{k}_{{\text{B}}}}{{T}_{{\text{h}}}}{\text{/}}e$, space and time scales are normalized in units of hot electron Debye length ${{\lambda }_{{{\text{Dh}}}}} = {{({{k}_{{\text{B}}}}{{T}_{{\text{h}}}}{\text{/}}4\pi {{n}_{{{\text{h}}0}}}{{e}^{2}})}^{{1/2}}}$ and cold electron plasma period $\omega _{{{\text{pc}}}}^{{ - 1}} = {{({{m}_{e}}{\text{/}}4\pi {{n}_{{{\text{c}}0}}}{{e}^{2}})}^{{1/2}}}$, respectively. Here, $\Omega = {{\Omega }_{{\text{c}}}}{\text{/}}{{\omega }_{{{\text{pc}}}}}$, where ${{\Omega }_{{\text{c}}}}{{n}_{{{\text{c}}0}}}{\text{/}}{{m}_{e}}c$ is the cold electron cyclotron frequency, ${{\mu }_{1}} = {{n}_{{{\text{p}}0}}}{\text{/}}{{n}_{{{\text{h}}0}}}$, ${{\mu }_{2}} =$ ${{n}_{{{\text{i}}0}}}{\text{/}}{{n}_{{{\text{h}}0}}} = 1 + {{\alpha }^{{ - 1}}} - {{\mu }_{1}}$, $\alpha = {{n}_{{{\text{h}}0}}}{\text{/}}{{n}_{{{\text{c}}0}}}$, and $\sigma = {{T}_{{\text{h}}}}{\text{/}}{{T}_{{\text{p}}}}$.

To study the nonlinear dynamics of EAWs in the presence of external magnetic field, we introduce the following stretched space-time coordinates

$$\xi = {{\varepsilon }^{{1/2}}}(z - Vt),\quad \zeta = \varepsilon x,\quad \eta = \varepsilon y,\quad \tau = {{\varepsilon }^{{3/2}}}t,$$

(9)

where V is the normalized phase speed of the EAWs and ε ($0 < \varepsilon < 1$) represents the amplitude of the weakly nonlinear wave. All the dependent variables are expanded in powers of parameter ε, as

$$\left( {\begin{array}{*{20}{c}} {{{n}_{{\text{c}}}}} \\ {{{u}_{{\text{c}}}}} \\ {{{{v}}_{{\text{c}}}}} \\ {{{w}_{{\text{c}}}}} \\ \varphi \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1 \\ 0 \\ 0 \\ 0 \\ 0 \end{array}} \right) + \varepsilon \left( {\begin{array}{*{20}{c}} {n_{{\text{c}}}^{{(1)}}} \\ {\sqrt \varepsilon u_{{\text{c}}}^{{(1)}}} \\ {\sqrt \varepsilon {v}_{{\text{c}}}^{{(1)}}} \\ {w_{{\text{c}}}^{{(1)}}} \\ {{{\varphi }^{{(1)}}}} \end{array}} \right) + {{\varepsilon }^{2}}\left( {\begin{array}{*{20}{c}} {n_{{\text{c}}}^{{(2)}}} \\ {\sqrt \varepsilon u_{{\text{c}}}^{{(2)}}} \\ {\sqrt \varepsilon {v}_{{\text{c}}}^{{(2)}}} \\ {w_{{\text{c}}}^{{(2)}}} \\ {{{\varphi }^{{(2)}}}} \end{array}} \right) + ....$$

(10)

To incorporate the effect of weak magnetic field on the nonlinear behavior of EAWs, we employ the scaling $\Omega \sim O(\sqrt \varepsilon )$. Substituting (9) and (10) into the equations (6)–(8), one can obtain different sets of equations in various powers of ε. In the lowest order of ε, we obtain the following relations:

$$\begin{gathered} w_{{\text{c}}}^{{(1)}} = Vn_{{\text{c}}}^{{(1)}},\quad {{\varphi }^{{(1)}}} = - \frac{{Vw_{{\text{c}}}^{{(1)}}}}{\alpha }, \\ n_{{\text{c}}}^{{(1)}} = - \alpha \left( {{{C}_{1}} - {{\mu }_{1}}{{D}_{1}}} \right){{\varphi }^{{(1)}}}, \\ \end{gathered} $$

(11)

where ${{C}_{1}}\;\, = \;\,(q\;\, + \;\,1){\text{/}}2$, ${{D}_{1}}\;\, = \;\, - {\kern 1pt} {{C}_{1}}\sigma$, and ${{V}^{2}}\;\; =$ ${{({{C}_{1}} - {{\mu }_{1}}{{D}_{1}})}^{{ - 1}}}$.

Combining all the higher-order terms in $\varepsilon$ and using the relations in (11), we obtain the following nonlinear Laedke–Spatschek equation [46, 47] for EAWs in nonextensive magnetized plasma

$$\begin{gathered} \left( {{{V}^{2}}\frac{{{{\partial }^{2}}}}{{\partial {{\xi }^{2}}}} + {{\Omega }^{2}}} \right)\left[ {\frac{{\partial n_{{\text{c}}}^{{(1)}}}}{{\partial \tau }} + An_{{\text{c}}}^{{(1)}}\frac{{\partial n_{{\text{c}}}^{{(1)}}}}{{\partial \xi }} + B\frac{{{{\partial }^{3}}n_{{\text{c}}}^{{(1)}}}}{{\partial {{\xi }^{3}}}}} \right] \\ \, + \frac{{{{V}^{3}}}}{2}\frac{\partial }{{\partial \xi }}\left[ {\frac{{{{\partial }^{2}}}}{{\partial {{\zeta }^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{\eta }^{2}}}}} \right]n_{{\text{c}}}^{{(1)}} = 0, \\ \end{gathered} $$

(12)

where $A = \left[ {3V + 2{{V}^{5}}({{C}_{2}} - {{\mu }_{2}}{{D}_{2}}){\text{/}}\alpha } \right]{\text{/}}2$, $B = {{V}^{3}}{\text{/}}2$ with ${{C}_{2}} = (q + 1)(3 - q){\text{/}}8$ and ${{D}_{2}} = {{C}_{2}}{{\sigma }^{2}}$.

Depending on the strength of the magnetic field, various comments of physical interest are as follows with respect to parameter space. In the absence of magnetic field, i.e., $(\Omega = 0)$ one can recover the Kadomtsev–Petviashvili (KP) equation [55] and in the one-dimensional motion (${{\partial }_{\zeta }} = {{\partial }_{\eta }} = 0$), the well known KdV equation [56] is recovered. Again, for strong magnetic field ${{\Omega }^{2}} \gg \partial _{\xi }^{2}$, an equation similar to ZK equation [40] is obtained.

3. PAINLEVÉ INTEGRABILITY AND ANALYTICAL SOLUTIONS

In this section, we perform Painlevé analysis to study the integrability of Eq. (12) and derive some interesting analytical solutions. For nonlinear partial differential equations (NPDEs), complete integrability is generally taken to mean the existence of an infinite set of conservation laws. Integrability plays a significant role in searching for the exact solutions of NPDEs. By investigating the integrability of a NPDE, one attains important observation into the nonlinear structure of the equation and the nature of its solutions [57, 58]. Since most of the dynamical systems from real physical problems have to involve nonlinearity, much attention has been focused on the integrability of nonlinear models. There are close relations between the integrability and the Painlevé property of NPDEs. Weiss, Tabor, and Carnevale (WTC) [59] proposed the Painlevé analysis approach of NPDEs, called the “WTC method of Painlevé analysis,” which is an effective method for not only testing Painlevé integrabilities but also constructing exact solutions of NPDEs. Later, in [60] the WTC method was simplified. A NPDE which possesses the Painlevé property must be single valued about the movable singularity manifold and the singularity manifold is noncharacteristic [60]. Applying the Painlevé criteria, according to WTC method, one can assume that $\psi (\xi ,\zeta ,\eta ,\tau )$ and ${{n}_{j}} = {{n}_{j}}(\xi ,\zeta ,\eta ,\tau )$ are analytic near the singularity manifold M given by

$$M = \{ (\xi ,\zeta ,\eta ,\tau )\,{\text{|}}\,\psi (\xi ,\zeta ,\eta ,\tau ) = 0\} ,$$

(13)

where $\psi (\xi ,\zeta ,\eta ,\tau ) = 0$ is an analytic function of $(\xi ,\zeta ,\eta ,\tau )$ near M and assume that

$$n_{{\text{c}}}^{{(1)}} = n_{{\text{c}}}^{{(1)}}(\xi ,\zeta ,\eta ,\tau ) = \sum\limits_{j = 0}^\infty {{n}_{j}}{{\psi }^{{j + p}}},$$

(14)

where p is an integer. We say that the Eq. (12) has Painlevé property when the solutions are single-valued about the movable M. After substitution of (14) into (12) and using leading order analysis, it turns out that $p = - 2$ and

$${{n}_{0}} = - \left( {\frac{{12B}}{A}} \right)\psi _{\xi }^{2}.$$

(15)

From the recursion relations for ${{n}_{j}}$, collecting terms involving ${{n}_{j}}$, it is found that

$$\begin{gathered} \psi _{\xi }^{5}{{n}_{j}}({{j}^{5}} - 20{{j}^{4}}{{H}^{3}} - 400{{j}^{2}} + 156j + 720) \\ \, = F({{n}_{{j - 1}}},\;...,{{n}_{0}},{{\psi }_{\zeta }},{{\psi }_{\eta }},{{\psi }_{\tau }}). \\ \end{gathered} $$

(16)

From (16), we can see that $j = - 1,\;4,\;5,\;6$ are the resonance points. The resonance at $j = - 1$ corresponds to the arbitrariness of ψ, which characterizes the singular hypersurface. In order to test whether the resonance points $j = 4,5,6$ satisfy the compatibility condition (16), following Kruskal ansatz [60] of the WTC method, we consider the following transformation:

$$\psi (\xi ,\zeta ,\eta ,\tau ) = \xi - \phi (\zeta ,\eta ,\tau ),\quad {{n}_{j}} = {{n}_{j}}(\tau ),$$

(17)

where $\phi {\kern 1pt} (\zeta ,\eta ,\tau )$ is an arbitrary function, and obtain the following recurrent relation for ${{n}_{j}}$:

$$\begin{gathered} {{\Omega }^{2}}\left[ {{{n}_{{j - 5,\tau }}} - (j - 6){{n}_{{j - 4}}}{{\phi }_{\tau }}} \right] \\ \, + A{{\Omega }^{2}}\sum\limits_{k = 0}^j \,(k - 4){{n}_{{k - 2}}}{{n}_{{j - k}}} \\ \, + B{{\Omega }^{2}}(j - 4)(j - 5)(j - 6){{n}_{{j - 2}}} \\ \end{gathered} $$

$$\begin{gathered} \, + {{V}^{2}}(j - 5)(j - 6)\left[ {{{n}_{{j - 3,\tau }}} - (j - 4){{n}_{{j - 2}}}{{\phi }_{\tau }}} \right] \\ \, + A{{V}^{2}}\sum\limits_{k = 0}^j \,(k - 2)(k - 3) \\ \, \times \left[ {(k - 4) + 3(j - k - 2)} \right]{{n}_{j}}{{n}_{{j - k}}} + (j - 5)(j - 6) \\ \end{gathered} $$

(18)

$$\begin{gathered} \times \,\left[ {B{{V}^{2}}(j - 2)(j - 3)(j - 4){{n}_{j}}} \right. \\ \, - \frac{{{{V}^{3}}}}{2}({{\phi }_{{\zeta \zeta }}} + {{\phi }_{{\eta \eta }}}){{n}_{{j - 3}}} \\ \, + \left. {\frac{{{{V}^{3}}}}{2}(j - 4)(\phi _{\zeta }^{2} + \phi _{\eta }^{2}){{n}_{{j - 2}}}} \right] = 0. \\ \end{gathered} $$

Putting $j = 0, \ldots ,6$ in the above recurrence relation (18), the following relations are obtained

$$\begin{gathered} {{n}_{0}} = \left( {\frac{{ - 12B}}{A}} \right),\quad {{n}_{1}} = 0,\quad {{n}_{2}} = \frac{{2{{\phi }_{\tau }} - V(\phi _{\zeta }^{2} + \phi _{\eta }^{2})}}{{2A}}, \\ {{n}_{3}} = \frac{{ - V({{\phi }_{{\zeta \zeta }}} + {{\phi }_{{\eta \eta }}})}}{{2A}}, \\ \end{gathered} $$

(19)

whereas, ${{n}_{4}}$, ${{n}_{5}}$, and ${{n}_{6}}$ are arbitrary. This shows that the nonlinear evolution Eq. (12) possesses Painlevé integrability in the sense of WTC method and hence it can be solved analytically.

3.1. Bäcklund Transformation for Finding Exact Solutions

We have studied the Painlevé property of Eq. (12), which demonstrates that the truncated Painlevé expansion to determine exact solutions of the Eq. (12) has the form [48, 61]

$$n_{{\text{c}}}^{{(1)}} = {{n}_{0}}{{\psi }^{{ - 2}}} + {{n}_{1}}{{\psi }^{{ - 1}}} + {{n}_{2}}.$$

(20)

After substitution of (20) into (12) and equating the coefficients of ${{\psi }^{{ - 6}}}$ and ${{\psi }^{{ - 7}}}$, we obtain

$${{n}_{0}} = \left( {\frac{{ - 12B}}{A}} \right)\psi _{\xi }^{2},\quad {{n}_{1}} = \left( {\frac{{12B}}{A}} \right){{\psi }_{{\xi \xi }}},$$

(21)

and for ${{\psi }^{0}}$ it is found that ${{n}_{2}}$ satisfies the nonlinear Eq. (12) which has the trivial solution ${{n}_{2}} = 0$. Starting with this trivial ${{n}_{2}} = 0$, the Bäcklund transform (BT) of Eq. (12) can be recast as

$$n_{{\text{c}}}^{{(1)}} = \left( {\frac{{12B}}{A}} \right)\frac{{{{\partial }^{2}}\ln(\psi )}}{{\partial {{\xi }^{2}}}}.$$

(22)

To determine the localized analytical solutions of Eq. (12) with the help of above BT (22), we assume a plane wave $\theta = \zeta + \eta + \xi - M\tau$ on the curved space $\psi$ such that $\psi = \psi (\theta )$, where M is the Mach number. On this $\theta$ plane, the BT can be assigned as

$$n_{{\text{c}}}^{{(1)}} = \left( {\frac{{12B}}{A}} \right)\frac{{{{d}^{2}}\ln(\psi (\theta ))}}{{d{{\theta }^{2}}}} = \left( {\frac{{12B}}{A}} \right)\left[ {\frac{{\psi {\kern 1pt} '{\kern 1pt} '}}{\psi } - \mathop {\left( {\frac{{\psi {\kern 1pt} '}}{\psi }} \right)}\nolimits^2 } \right].$$

(23)

Here, dash (') represents the derivative with respect to θ. Again, on the θ plane, the Eq. (12) is reduced (after single integration) to

$$\begin{gathered} \frac{{{{d}^{4}}n_{{\text{c}}}^{{(1)}}}}{{d{{\theta }^{4}}}} + \left[ {\frac{A}{B}n_{{\text{c}}}^{{(1)}} + \frac{{{{\Omega }^{2}}}}{{{{V}^{2}}}} + \frac{{V - M}}{B}} \right]\frac{{{{d}^{2}}n_{{\text{c}}}^{{(1)}}}}{{d{{\theta }^{2}}}} \\ \, + \frac{{3A}}{{2B}}\mathop {\left( {\frac{{dn_{{\text{c}}}^{{(1)}}}}{{d\theta }}} \right)}\nolimits^2 + \frac{{{{\Omega }^{2}}n_{{\text{c}}}^{{(1)}}}}{{B{{V}^{2}}}}\left( {An_{{\text{c}}}^{{(1)}} - M} \right) = 0. \\ \end{gathered} $$

(24)

For localized solution, we can take the integration constant as zero. Substituting (23) into (24) and equating the coefficients of different powers of ψ, we obtain a system of ordinary differential equations (ODEs) in ψ. For physically valid solutions, we consider ODE corresponding to the coefficients of ${{\psi }^{{ - 1}}}$, which yields

$$\frac{{{{d}^{2}}}}{{d{{\theta }^{2}}}}\left[ {\frac{{{{d}^{4}}}}{{d{{\theta }^{4}}}} + \left( {\frac{{{{\Omega }^{2}} + 2}}{{{{V}^{2}}}} - \frac{{2M}}{{{{V}^{3}}}}} \right)\frac{{{{d}^{2}}}}{{d{{\theta }^{2}}}} - \frac{{2M{{\Omega }^{2}}}}{{{{V}^{5}}}}} \right]\psi = 0.$$

(25)

Solution of Eq. (25) is given by

$$\begin{gathered} \psi (\theta ) = {{k}_{1}} + {{k}_{2}}\theta + {{k}_{3}}{{e}^{{ - {{\lambda }_{1}}\theta }}} + {{k}_{4}}{{e}^{{{{\lambda }_{1}}\theta }}} \\ \; + {{k}_{5}}{{e}^{{ - {{\lambda }_{2}}\theta }}} + {{k}_{6}}{{e}^{{{{\lambda }_{2}}\theta }}}, \\ \end{gathered} $$

(26)

where ${{k}_{i}}s\;(i = 1, \ldots ,6)$ are arbitrary integration constants and ${{\lambda }_{{1(2)}}} = \sqrt {{{\phi }_{{1(2)}}}}$ is the eigenvalue and

$$\begin{gathered} {{\phi }_{{1(2)}}} = \frac{1}{2}\left[ {\mathop {\left( {\frac{{2M}}{{{{V}^{3}}}} - \frac{{{{\Omega }^{2}} + 2}}{{{{V}^{2}}}}} \right)}\limits_{} } \right. \\ \, \mp \left. {\sqrt {\mathop {\left( {\frac{{{{\Omega }^{2}} + 2}}{{{{V}^{2}}}} - \frac{{2M}}{{{{V}^{3}}}}} \right)}\nolimits^2 + \frac{{8M{{\Omega }^{2}}}}{{{{V}^{5}}}}} } \right]. \\ \end{gathered} $$

(27)

By the above expressions it is found that the eigenvalue ${{\lambda }_{1}}$ is always purely imaginary as ${{\phi }_{1}} < 0$ and we put ${{\phi }_{1}} = i\lambda$, where λ is real. Moreover, the eigen value ${{\lambda }_{2}}$ is always real in the presence of external magnetic field. Finally, substituting (26) in the Eq. (23) we obtain the general solution of Eq. (12) as

$$\begin{gathered} n_{{\text{c}}}^{{(1)}}(\xi ,\zeta ,\eta ,\tau ) = \left( {\frac{{12B}}{A}} \right) \\ \, \times \left[ {\mathop {\frac{{\lambda _{1}^{2}({{k}_{3}}{{e}^{{ - {{\lambda }_{1}}\theta }}} + {{k}_{4}}{{e}^{{{{\lambda }_{1}}\theta }}}) + \lambda _{2}^{2}({{k}_{5}}{{e}^{{ - {{\lambda }_{2}}\theta }}} + {{k}_{6}}{{e}^{{{{\lambda }_{2}}\theta }}})}}{{{{k}_{1}} + {{k}_{2}}\theta + {{k}_{3}}{{e}^{{ - {{\lambda }_{1}}\theta }}} + {{k}_{4}}{{e}^{{{{\lambda }_{1}}\theta }}} + {{k}_{5}}{{e}^{{ - {{\lambda }_{2}}\theta }}} + {{k}_{6}}{{e}^{{{{\lambda }_{2}}\theta }}}}}}\limits_{} } \right. \\ \,\left. { - \mathop {\left( {\frac{{{{k}_{2}} - {{\lambda }_{1}}({{k}_{3}}{{e}^{{ - {{\lambda }_{1}}\theta }}} - {{k}_{4}}{{e}^{{{{\lambda }_{1}}\theta }}}) - {{\lambda }_{2}}({{k}_{5}}{{e}^{{ - {{\lambda }_{2}}\theta }}} - {{k}_{6}}{{e}^{{{{\lambda }_{2}}\theta }}})}}{{{{k}_{1}} + {{k}_{2}}\theta + {{k}_{3}}{{e}^{{ - {{\lambda }_{1}}\theta }}} + {{k}_{4}}{{e}^{{{{\lambda }_{1}}\theta }}} + {{k}_{5}}{{e}^{{ - {{\lambda }_{2}}\theta }}} + {{k}_{6}}{{e}^{{{{\lambda }_{2}}\theta }}}}}} \right)}\nolimits^2 } \right]. \\ \end{gathered} $$

(28)

3.2. Soliton Solutions

Now, for soliton solutions, putting k₁ = k₂ = k₃ = k₄ = 0 and ${{k}_{5}} = {{k}_{6}}$ in the general solution (28) and carrying out some simple algebra, we obtain

$$n_{{\text{c}}}^{{(1)}} = {{\left( {\frac{{12B\lambda _{2}^{2}}}{A}} \right)}^{2}}({{\lambda }_{2}}\theta ).$$

(29)

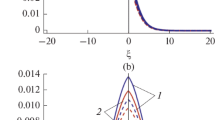
Thus, the nonlinear evolution Eq. (12) exhibits single peaked soliton solution (29). To have some numerical appreciations of our results, we choose the typical values of the parameters corresponding to the auroral zone [8, 19]: ${{T}_{{\text{c}}}} \simeq 5$ eV, ${{T}_{{\text{h}}}} \simeq 250$ eV, ${{n}_{{{\text{c}}0}}} \simeq 0.5$ cm^–3, and ${{n}_{{{\text{h}}0}}} \simeq 2.0$ cm^–3. These parameters correspond to $\alpha \simeq 4.0$. Furthermore, the present analysis is restricted to the range of values of the nonextensive parameter q satisfying $0.6 < q \leqslant 1$ [54]. In Fig. 1, we present the effect of nonextensive parameter q and positron concentration ${{\mu }_{1}}$ on the soliton solution, respectively. It is seen, that the soliton shrinks while its pulse amplitude increases with the increase of q and ${{\mu }_{1}}$, i.e., the nonextensivity and positron concentration can render the soliton more spiky. Physically, increasing the positron concentration leads to the decrease of ion number density (${{n}_{{i0}}}$) due to the quasineutrality condition and consequently, the soliton amplitude increases while its pulse width decreases. This feature can be attributed for diagnostic purpose when positron population can be introduced in electron–ion plasma.

Fig. 1.

Soliton solution of equation (12) as given in (29) for different values of (a) nonextensive parameter q ($q = 0.7$ (solid line), $q = 0.8$ (dotted line), and $q = 0.9$ (dashed line)) with ${{\mu }_{1}} = 0.3$ and (b) positron concentration ${{\mu }_{1}}$ (${{\mu }_{1}} = 0.3$ (solid line), ${{\mu }_{1}} = 0.4$ (dotted line), and ${{\mu }_{1}} = 0.5$ (dashed line)) with $q = 0.7$, where other parameters are $\Omega = 0.05$, $\sigma = 1$, $\alpha = 4$, and $M = 0.9$.

Moreover, putting ${{k}_{1}} = {{k}_{2}} = {{k}_{3}} = 0$, ${{k}_{5}} = {{k}_{6}} = P$, and ${{k}_{4}} = P{\text{/}}2$ in the general solution (28), we obtain M-shaped soliton solution. Figure 2 shows the M‑shaped solitons for different values of magnetic field strength Ω. It is observed that the amplitude of the soliton increases as the value of Ω increases. Moreover, the special extension (width) of M-shaped soliton decreases with the increase in external magnetic field. Therefore, increasing the magnetic field leads to an increase in the nonlinearity and a decrease in the dispersion and thus, the localized structures that are much taller and narrower. Physically, an increase in the magnetic field raises the frequency of the electron oscillation, leading to an increase in phase speed of the waves for constant wavelength. Then, the soliton propagates with greater speed. Since the soliton velocity is directly proportional to the soliton amplitude, the soliton evolves with higher amplitude.

Fig. 2.

M-Shaped soliton solution of equation (12) for different values of magnetic field ($\Omega = 0.06$ (solid line), $\Omega = 0.08$ (dotted line), and $\Omega = 0.1$ (dashed line)). Here, $q = 0.7$, ${{\mu }_{1}} = 0.3$, ${{k}_{1}} = {{k}_{2}} = {{k}_{3}} = 0$, ${{k}_{5}} = {{k}_{6}} = 1$, ${{k}_{4}} = 1{\text{/}}2$ and other parameters are same as in Fig. 1.

3.3. Periodic Solution

It is known from dynamical system theory that purely imaginary eigenvalues always correspond to the periodic solution of a nonlinear system. Therefore, to determine periodic solution from (28), we put ${{k}_{1}} = {{k}_{3}} = P$, ${{k}_{2}} = {{k}_{5}} = {{k}_{6}} = 0$ and ${{k}_{4}} = - P$, where P is a positive constant. Thus, the periodic solution of (12) is given by

$$n_{{\text{c}}}^{{(1)}} = \left( {\frac{{24B{{\lambda }^{2}}}}{A}} \right)\left[ {\frac{{(2 + i\sin (\lambda \theta ))}}{{{{{\{ 1 - 2i\sin (\lambda \theta )\} }}^{2}}}}} \right].$$

(30)

Figure 3 exhibits the variations of periodic solutions of the Eq. (12) for several values of nonextensive parameter q and external magnetic field strength Ω, respectively. It is observed from Fig. 3a that the oscillation amplitude as well as the number of oscillations decreases as q increases, while from Fig. 3b, it is clear that the influence of the magnetic field strength increases the number of oscillations and oscillation amplitude.

Fig. 3.

Periodic solution of equation (12) as given in (30) for different values of (a) nonextensive parameter ($q = 0.8$ (solid line), $q = 0.85$ (dotted line), and $q = 0.9$ (dashed line)) with ${{\mu }_{1}} = 0.3$, $\Omega = 0.01$ and (b) magnetic field strength ($\Omega = 0.01$ (solid line), $\Omega = 0.04$ (dotted line), and $\Omega = 0.08$ (dashed line)) with ${{\mu }_{1}} = 0.3$ and $q = 0.8$, ${{k}_{1}} = {{k}_{3}} = 1$, ${{k}_{2}} = {{k}_{5}} = {{k}_{6}} = 0$, ${{k}_{4}} = - 1$, where the other parameters are same as in Fig. 1.

3.4. Breather and Rogue Wave-Type Solutions

The name “breather” reflects the behavior of the wave profile in which energy concentrates in a localized and oscillatory fashion. By choosing ${{k}_{1}} = {{k}_{5}} = {{k}_{6}} = P$, ${{k}_{2}} = 0$, and ${{k}_{3}} = {{k}_{4}} = P{\text{/}}2$, where P is a positive constant, breather-like solution can be generated as

$$n_{{\text{c}}}^{{(1)}} = \left( {\frac{{12B}}{A}} \right)({{\lambda }_{2}}\theta )[2\lambda _{2}^{2} + (2\lambda _{2}^{2} - 2{{\lambda }^{2}})\cos(\lambda \theta )$$

$$\, + (4\lambda _{2}^{2} - {{\lambda }^{2}})\cosh({{\lambda }_{2}}\theta ) - {{\lambda }^{2}}\cos(\lambda \theta )({{\lambda }_{2}}\theta )$$

(31)

$$ + \;4\lambda {{\lambda }_{2}}\sin(\lambda \theta )\tanh({{\lambda }_{2}}\theta )]{{\{ 2 + \cos (\lambda \theta )({{\lambda }_{2}}\theta ) + ({{\lambda }_{2}}\theta )\} }^{2}}.$$

In order to illustrate the behavior of breather oscillations, the solution (31) is depicted in Fig. 4 by varying the values of nonextensive parameter q. It is found that the oscillations and envelope propagate at different speed. It is also observed that the number of oscillations and amplitude in the wave packet decrease with increasing q. The breather structures observed here are the outcome of interactions of multi phase waves. Thus, the formation of breather is the signature of the phase mixing of waves. On the other hand, rogue waves are strong wavelets that can “suddenly appear from nowhere and disappear with no trace” [62]. Rogue waves are now recognized as proper intrinsically nonlinear structures. Rogue waves are short-lived phenomena appearing suddenly out of normal waves and with a small probability. Substituting ${{k}_{1}} = {{k}_{5}} = {{k}_{6}} = P$, ${{k}_{2}} = {{k}_{3}} = 0$, and ${{k}_{4}} = - P$ into (28), the rogue wave-type solution can be obtained as

$$\begin{gathered} n_{{\text{c}}}^{{(1)}} = \left( {\frac{{12B}}{A}} \right)[4\lambda _{2}^{2} + 2(\lambda _{2}^{2} - \lambda _{2}^{2}{{e}^{{i\lambda \theta }}} + {{\lambda }^{2}}{{e}^{{i\lambda \theta }}})({{\lambda }_{2}}\theta ) \\ \, + {{(4\lambda _{2}^{2} - {{\lambda }^{2}}{{e}^{{i\lambda \theta }}})}^{2}}({{\lambda }_{2}}\theta ) + 4i\lambda {{\lambda }_{2}}{{e}^{{i\lambda \theta }}}\tanh({{\lambda }_{2}}\theta )({{\lambda }_{2}}\theta )] \\ \, \times {{\{ 2 + (1 - {{e}^{{i\lambda \theta }}})({{\lambda }_{2}}\theta )\} }^{{ - 2}}}. \\ \end{gathered} $$

(32)

Fig. 4.

Breather-like solution of equation (12) as given in (31) for different values of nonextensive parameter q for $\sigma = 1$, ${{\mu }_{1}} = 0.3$, $\Omega = 0.01$, $\alpha = 4$, and $M = 0.9$ with ${{k}_{1}} = {{k}_{5}} = {{k}_{6}} = 1$, ${{k}_{2}} = 0$, and ${{k}_{3}} = {{k}_{4}} = 1{\text{/}}2$.

This solution refers to an amount of the wave energy condensed in a relatively small area in space that is produced by the presence of nonlinear properties of the plasma medium and can be represented as rogue wave structure as shown in Fig. 5a. It is apparent from the figure that nonextensivity reduces the rogue wave amplitude. To extract another type of rogue-wave-like solution from relation (28), we take ${{k}_{1}} = {{k}_{3}} = {{k}_{4}} =$ ${{k}_{5}} = {{k}_{6}} = P$ and ${{k}_{2}} = 0$ and obtain

$$n_{{\text{c}}}^{{(1)}} = \left( {\frac{{12B}}{A}} \right)({{\lambda }_{2}}\theta )\left[ {\frac{{4(\lambda _{2}^{2} - {{\lambda }^{2}})\{ \cos (\lambda \theta ) + ({{\lambda }_{2}}\theta )\} + 8\lambda {{\lambda }_{2}}\sin (\lambda \theta )\tanh ({{\lambda }_{2}}\theta )}}{{{{{\{ 2 + (1 + 2\cos (\lambda \theta ))({{\lambda }_{2}}\theta )\} }}^{2}}}}} \right].$$

(33)

Fig. 5.

(a) Profile of rogue-wave-type solution (32) of equation (12) for different values of nonextensive parameter ($q = 0.75$ (solid line), $q = 0.8$ (dotted line), and $q = 0.86$ (dashed line)) with $\Omega = 0.01$ and ${{k}_{1}} = {{k}_{5}} = {{k}_{6}} = 1$, ${{k}_{2}} = {{k}_{3}} = 0$, and ${{k}_{4}} = - 1{\text{/}}2$ and (b) profile of another type of rogue wave structure (33) for different magnetic field strength ($\Omega = 0.05$ (solid line), $\Omega = 0.1$ (dotted line), and $\Omega = 0.15$ (dashed line)) with $q = 0.7$, ${{k}_{1}} = {{k}_{3}} = {{k}_{4}} = {{k}_{5}} = {{k}_{6}} = 1$, and ${{k}_{2}} = 0$, where other parameters are same as in Fig. 4.

The profile of solution (33) is displayed in Fig. 5b for different values of Ω. It is seen that the amplitude of the rogue wave structure is enlarged with the increase in Ω. Physically, the magnetic field in the plasma system enhances the coupling and generates new perturbations in the electron orbits. This nonlinearity introduced by the magnetic field creates new harmonics, and the rogue wave structures reveal these nonlinear phenomena. Usually, breathers and rogue wave structures are described through the well-known nonlinear Schrödinger equation [62, 63].

4. CONCLUSIONS

In this work, we have investigated the nonlinear propagation of EAWs in a magnetized plasma consisting of nonextensive hot electrons and positrons, mobile cold electrons, and immobile positive ions. Employing the standard reductive perturbation technique, Laedke–Spatschek equation is derived which governs the nonlinear dynamics of small-amplitude EAWs in nonextensive magnetized plasmas. We have used the Painlevé analysis to show the integrability of the nonlinear evolution equation. By implementing the Bäcklund transformation, a series of analytical solutions of Laedke–Spatschek equation are obtained. The solutions reveal that EAWs described by the nonlinear equation support various types of nonlinear structures, such as the single peaked soliton, M‑shaped soliton, and breather and rogue wave-like structures. It was found that these nonlinear structures are significantly modified by the relevant plasma parameters (entropic index q, magnetic field strength, positron concentration). The derived analytical results represent a wide class of fascinating coherent nonlinear phenomena and can be applicable in different fields of physical world [63, 64].