A study of optical solitons of Manakov model describing optical pulse propagation

Abstract

In nonlinear optical telecommunication networks and optical switching devices, the study of optical solitons is critical. In recent years, coupled nonlinear Schrödinger equations have been studied regarding the optical solitons and their collisions. When the coupled nonlinear Schrödinger equations are of Manakov type, the optical solitons collide with each other elastically and after collision their polarization may change depending on the polarization of incoming optical solitons. In order to develop and improve innovative optical devices, enhance the stability of optical communication networks, and minimize fiber losses, it is imperative to establish an analytical approach capable of generating a diverse range of optical solitons. The goal of this manuscript is the utilization of a specific integration scheme to produce a diverse range of optical solitons for the Manakov model, with the aim of reducing both experimental costs and time. In this study, the extended sinh-Gordon equation expansion method and the two variable $\left( G'/G, 1/G \right)$-expansion method are employed to enable a comparison of the solutions and demonstrate the originality of this research. For the considered expansion methods, optical soliton solutions such as dark-dark soliton, bright-bright soliton, combined dark-bright soliton, multi soliton and periodic solitary waves are achieved. Moreover, the graphical demonstration of these solitons is made in order to better understand the obtained results.

1 Introduction

The coupled nonlinear Schrödinger (CNLS) equations of Manakov type

$$\begin{aligned} {\iota } {U}_{1t} + {\alpha }_1 {U}_{1xx} + {\beta }_1 \left( |U_1|^2 + |U_2|^2 \right) U_1 = 0, \end{aligned}$$

(1.1)

$$\begin{aligned} {\iota } {U}_{2t} + {\alpha }_2 {U}_{2xx} + {\beta }_2 \left( |U_1|^2 + |U_2|^2 \right) U_2 = 0, \end{aligned}$$

(1.2)

is an integrable system where $U_1(x,t)$ and $U_2(x,t)$ are complex valued functions, representing the profile of the soliton pulse. The real constants ${\alpha }_i$ and ${\beta }_i$ correspond to group velocity dispersion and self-steeping nonlinearity, respectively. Manakov proposed the system (1) in 1973 to generalize the work of Zakharov and Shabat for constant polarization waves to arbitrary polarization of waves. He described that a nonlinear medium can act as a polarization filter upon entering the wave of varying polarization by splitting it into beams of constant polarization. Moreove, Manakov also provided the complete integrability of his modal by employing inverse scattering transformation (Shabat and Zakharov 1972; Manakov 1974).

The Manakov system has accommodated the development of new models to represent complex wave propagations, such as CNLS equations of three or multiple components (Kanna and Lakshmanan 2001), Manakov model with variable coefficients, varying potential and nonlinearities (Zhong et al. 2015; Su et al. 2013; Cheng et al. 2014), modified Manakov equations (Tsoy and Akhmediev 2006), coupled optical fiber system (Li and Guan 2021), two-component Gross–Pitaevskii equations (Li and Guan 2019) and others. The Manakov system has significant applications in biology (Scott 1984), finance (Yan 2011), fluid dynamics (Dhar and Das 1991), Bose–Einstein condensates (Busch and Anglin 2001), nonlinear fiber optics (Frisquet et al. 2015) etc. Yıldırım (2019), Gerdjikov and Todorov (2019), Mumtaz et al. (2012), Radhakrishnan et al. (1999), Özışık et al. (2022).

In nonlinear fiber optics, optical solitons are used as signal carriers because optical solitons do not change their shape while propagating and after colliding with other pulses, and they emerge as a consequence of the balance among linear and nonlinear effects in the optical medium. The first prediction of optical solitons in optical fibers was made by Hasegawa and Tappert (1973a, 1973b). Optical solitons can be categorized as (i) temporal soliton, which arises because of pulse dispersion and refractive nonlinearity’s combined effects, and (ii) spatial soliton, arises from the joined effects of beam diffraction and nonlinearity.

In communication networks, optical fiber is prioritized owing to its advantages like expanded bandwidth, lower weight, security from short circuits, and severe weather endurance. To make the optical soliton propagation effective, it is necessary to avoid the signal losses and this problem was tackled by imposing transparent boundary conditions on the Manakov system (Sabirov et al. 2021) and other nonlinear Schrödinger equations which made the solitons’ propagation reflectionless. Moreover, during the propagation in fibers, optical solitons face fiber nonlinearities and group velocity dispersion that broadened the shape of the solitons. Many mathematical systems have been introduced to overcome these complexities, including Hirota–Satsuma (Alquran et al. 2019), Fokas–Lenells (Yıldırım et al. 2022), Kaup–Newell (Esen et al. 2022), Biswas–Milovic (Zayed et al. 2021), Sasa–Satsuma (Yıldırım 2019), Gergjikov–Ivanov (Li et al. 2021), Triki–Biswas (Li and Lian 2022), Biswas–Arshad (Yıldırım 2019), Radhakrishanan–Kundu–Lakshmanan (Arnous et al. 2022), Lakshmanan–Porsezian–Daniel (Yıldırım et al. 2021), Schrödin-ger Hirota (Ozdemir et al. 2022), Chen–Lee–Liu (Yıldırım et al. 2020), Kudryashov equation (Zayed et al. 2021), the AB-system (Meng and Guo 2022), Kundu–Eckhaus (Mirzazadeh et al. 2018), Ginzbirg–Landau (Mohammed et al. 2021) and other equations.

In optical communication systems, various types of solitons, including dark, bright, combined, and multi-solitons, play a crucial role. To ensure seamless signal transmission through optical fibers, a diverse array of solitons has been generated through the application of various techniques, such as Darboux transformation (Guan and Li 2019), Hirota method (Radhakrishnan and Aravinthan 2007), trial equation method (Yıldırım 2019), modified simple equation method (Yıldırım 2019), extended simplest equation method (Ahmed et al. 2021) and auxiliary equation method (Ozisik et al. 2022), specifically on the Manakov system. Furthermore, the stability aspects of the Manakov system were explored through both linear stability analysis and modulation stability analysis (Younas and Ren 2022; Akram et al. 2023). The primary objective of this research is to achieve a diverse range of optical solitons that are beneficial for communication networks, using a single integrable method. This approach aims to maintain the simplicity, efficiency, and advancement to describe the propagation channels. In this article, the Manakov system has been explored to retrieve the optical soliton solutions using extended sinh-Gordon equation expansion method and $\left( G'/G, 1/G \right)$-expansion method. The first method is based on the sinh-Gordon equation and was constructed to find the Jacobi-elliptic function solutions of the nonlinear evolution equations (Mathanaranjan 2023, 2022; Mathanaranjan et al. 2022). The latter method was proposed by Li et al. (2010) based on $\left( G'/G \right)$-expansion method (Mathanaranjan et al. 2021; Mathanaranjan 2020), to establish the analytical wave solutions of nonlinear evolution equations that can be described in two variables, $\left( G'/G \right)$ and $\left( 1/G \right)$, where G satisfies the second order linear ordinary differential equation $G''({\theta }) + {\gamma } G({\theta }) = {\rho }$, ${\gamma }$ and ${\rho }$ are unknown constants. Implementation of two well known methods will provide an insightful comparison of the obtained results which will be helpful to discuss the novelty of this work.

The remaining article is organized as follows: Sect. 2 is the complete description of the extended sinh-Gordon equation expansion method and $\left( G'/G, 1/G \right)$-expansion method. Section 3 exhibits the mathematical analysis of Manakov system. The implementation of both methods on the nonlinear ordinary differential equation is in Sect. 4. Section 5 comprises the graphical depiction of the solutions and Sect. 6 is the conclusion.

2 Description of methods

The coupled nonlinear partial differential equations with independent variables x and t is considered, as

$$\begin{aligned} P_1 \left( p_1, p_{1x},p_{2x}, p_{1t},p_{2t},p_{1xx},p_{2xx},p_{1xt},p_{2xt},... \right) =0, \end{aligned}$$

(2.1)

$$\begin{aligned} P_2 \left( p_2, p_{1x},p_{2x}, p_{1t},p_{2t},p_{1xx},p_{2xx},p_{1xt},p_{2xt},... \right) =0. \end{aligned}$$

(2.2)

Implementation of traveling wave transformation

$$\begin{aligned} p_1 (x,t)= q_1 ({\theta }), \end{aligned}$$

(2.3)

$$\begin{aligned} p_2 (x,t)= q_2 ({\theta }), \end{aligned}$$

(2.4)

where ${\theta }= x- {\upsilon }t$, reduces Eqs. (2.1), (2.2) into ordinary differential equations (ODEs)

$$\begin{aligned} H_i \left( q_i, q_{i}', q_{i}'', q_{i}''',... \right) =0, ~ ~ ~ i=1,2. \end{aligned}$$

(2.5)

The constant ${\upsilon }$ is the velocity of the traveling wave.

2.1 Extended sinh-Gordon equation expansion method

The sinh-Gordon equation is written, as Chu et al. (2023)

$$\begin{aligned} u_{xt}= \sigma ~ \sinh (u), \end{aligned}$$

(2.6)

where $u = u(x,t)$ and $\sigma$ is a nonzero constants. Implementing traveling wave transformation $u(x,t)= r (\theta )$ where $\theta = x - {\upsilon }t$, the Eq. (2.6) reduces into a nonlinear patial differential equation (PDE)

$$\begin{aligned} r''(\theta )= - \frac{\sigma }{\upsilon } \sinh \left( r(\theta ) \right) . \end{aligned}$$

(2.7)

Integration of Eq. (2.7), gives

$$\begin{aligned} \left[ \left( \frac{r}{2} \right) ' \right] ^2 = - \frac{\sigma }{\upsilon }~\sinh ^2 \left( \frac{r}{2} \right) + m, \end{aligned}$$

(2.8)

where m is an integration constant. Setting $\frac{r}{2}= s(\theta )$ and $- \frac{\sigma }{\upsilon }=n$ in Eq. (2.8), yields

$$\begin{aligned} s' = \sqrt{m + n ~\sinh ^2(s)}. \end{aligned}$$

(2.9)

For distinct values of the parameters m and n, the following solutions are attained:

Case 1: When $m=0$ and $n=1$, Eq. (2.9) reduces to an ODE

$$\begin{aligned} s'= \sinh (s). \end{aligned}$$

(2.10)

Simplification of Eq. (2.10) yields the following solutions:

$$\begin{aligned} \sinh (s)= \pm {\iota } \text {sech} (\theta ), ~~ \cosh (s) = - \tanh (\theta ) \end{aligned}$$

(2.11)

and

$$\begin{aligned} \sinh (s) = \pm \text {csch} (\theta ), ~~ \cosh (s) = - \coth (\theta ) \end{aligned}$$

(2.12)

where $\iota = \sqrt{-1}$ is an imaginary number.

Case 2: When $m=n=1$, Eq. (2.9) reduces to an ODE

$$\begin{aligned} s'= \cosh (s). \end{aligned}$$

(2.13)

Simplification of Eq. (2.13) yields the following solutions:

$$\begin{aligned} \sinh (s) = \tan (\theta ), ~~ \cosh (s)= \pm \sec (\theta ) \end{aligned}$$

(2.14)

and

$$\begin{aligned} \sinh (s)= - \cot (\theta ), ~~ \cosh (s) = \pm \csc (\theta ). \end{aligned}$$

(2.15)

The solution of Eq. (2.5) can be considered, as

$$\begin{aligned} q_i (s)= \sum _{j=1}^K \cosh ^{j-1} (s) \left[ W_j~ \sinh (s) + V_j~ \cosh (s) \right] + V_0. \end{aligned}$$

(2.16)

The solution (2.16) together with Eqs. (2.10)–(2.12) can be presented, as

$$\begin{aligned} q_i (\theta )= \sum _{j=1}^K (-\tanh (\theta ))^{j-1} \left[ \pm \iota W_j~ \text {sech}(\theta ) - V_j \tanh (\theta ) \right] + V_0, \end{aligned}$$

(2.17)

and

$$\begin{aligned} q_i (\theta )= \sum _{j=1}^K (-\coth (\theta ))^{j-1} \left[ \pm W_j~ \text {csch}(\theta ) - V_j \coth (\theta ) \right] + V_0. \end{aligned}$$

(2.18)

Similarly, the solution (2.16) along Eqs. (2.13)–(2.15) can be presented, as

$$\begin{aligned} q_i (\theta )= \sum _{j=1}^K (\pm \sec (\theta ))^{j-1} \left[ W_j~ \tan (\theta ) \pm V_j \sec (\theta ) \right] + V_0, \end{aligned}$$

(2.19)

and

$$\begin{aligned} q_i (\theta )= \sum _{j=1}^K (\pm \csc (\theta ))^{j-1} \left[ - W_j~ \cot (\theta ) \pm V_j \csc (\theta ) \right] + V_0. \end{aligned}$$

(2.20)

The value of positive integer K can be determined by implementing homogeneous balancing principle on Eq. (2.5). Inserting the value of K in Eq. (2.16) and using Eq. (2.10), a polynomial equation in $s(\theta )$ is achieved. Comparing the coefficient of $\sinh ^j (s) \cosh ^j (s)$ to zero and solving the resulting algebraic system, the values of $W_j$ and $V_j$ are attained. Inserting these values in Eqs. (2.17), (2.18) gives the solitary wave solutions to Eq. (2.5) for Case 1. The procedure analogous to the first case is followed for the Case 2 using Eq. (2.13) along Eqs. (2.19), (2.20).

2.2 The $\left( \frac{G'}{G}, \frac{1}{G} \right)$-expansion method

The second order ordinary differential equation is considered, as

$$\begin{aligned} G'' (\theta ) + \gamma G (\theta ) = \rho , \end{aligned}$$

(2.21)

and setting

$$\begin{aligned} \psi = \frac{G~ '}{G}, ~ ~ \phi = \frac{1}{G} \end{aligned}$$

(2.22)

gives

$$\begin{aligned} {\psi }' = - {\psi }^2 + \rho \phi - \gamma , ~ ~ {\phi }'= - \psi \phi \end{aligned}$$

(2.23)

where $\gamma$ and $\rho$ are contants and $' = \frac{d}{d \theta }$. The general solutions of Eq. (2.21) can be written as follow:

For $\gamma <0$, the general solution is given, as

$$\begin{aligned} G(\theta )= B_1 \sinh \left( \sqrt{- \gamma }~ \theta \right) + B_2 \cosh \left( \sqrt{- \gamma }~ \theta \right) + \frac{\rho }{\gamma }, \end{aligned}$$

(2.24)

and it gives

$$\begin{aligned} {\phi }^2 = \frac{- \gamma }{{\gamma }^2 {\lambda }_1 + {\rho }^2}~ \left( {\psi }^2 - 2 {\rho } {\phi } + {\gamma }\right) \end{aligned}$$

(2.25)

where $B_1$ and $B_2$ are arbitrary constants and ${\lambda }_1= B_{1}^2 - B_{2}^2$.

For $\gamma >0$, the general solution is given, as

$$\begin{aligned} G(\theta )= B_1 \sin \left( \sqrt{\gamma }~ \theta \right) + B_2 \cos \left( \sqrt{\gamma }~ \theta \right) + \frac{\rho }{\gamma } \end{aligned}$$

(2.26)

and it gives

$$\begin{aligned} {\phi }^2 = \frac{\gamma }{{\gamma }^2 {\lambda }_2 - {\rho }^2} \left( {\psi }^2 -2 {\rho } {\phi } + {\gamma } \right) \end{aligned}$$

(2.27)

where $B_1$ and $B_2$ are arbitrary constants and ${\lambda }_2= B_{1}^2 + B_{2}^2$.

For $\gamma =0$, the general solution is given, as

$$\begin{aligned} G(\theta )= \frac{\rho }{2} ~{\theta }^2 + B_1 \theta + B_2, \end{aligned}$$

(2.28)

and it gives

$$\begin{aligned} {\phi }^2 = \frac{1}{B_{1}^2 -2 {\rho } B_2} \left( {\psi }^2 -2 {\rho } {\phi }\right) , \end{aligned}$$

(2.29)

where $B_1$ and $B_2$ are arbitrary constants.

The solution of Eq. (2.5) can be written in a polynomial of $\psi$ and $\phi$ variables, as

$$\begin{aligned} q_i(\theta )=c_0 + \sum _{j =1}^K c_{j}~ {\psi }^{j} + \sum _{j =1}^K d_{j}~ {\psi }^{j -1} {\phi } \end{aligned}$$

(2.30)

where $c_j$  $(j=0,1,2,...,K)$ and $d_j$  $(j=1,2,...,K)$ are unknown constants that satisfy the $c_{K}^2 + d_{K}^2 \ne 0$ condition. Implementation of homogeneous balancing principle on Eq. (2.5) gives the value of positive integer K. For the case ${\gamma }<0$, a polynomial in $\psi$ and $\phi$ is yielded by substituting Eq. (2.30) in Eq. (2.5) along Eqs. (2.23) and (2.25). Equating each coefficient of the polynomial to zero gives an algebraic set of equations that provides the values of $c_0$, $c_j$ and $d_j$. The traveling wave solution of Eqs. (1.1), (1.2) is deduced by inserting the values of $c_0$, $c_j$ and $d_j$ into Eq. (2.30). Similar steps are followed for the cases ${\gamma }>0$ and ${\gamma }=0$ using Eqs. (2.23), (2.27) and (2.29) into Eq. (2.30).

3 Mathematical analysis

A complex wave transformation for Eqs. (1.1), (1.2) is defined as follows:

$$\begin{aligned} U_1 (x,t)= q_1 ({\theta }) e^{\iota {\varphi }_1(x,t)}, \end{aligned}$$

(3.1)

$$\begin{aligned} U_2 (x,t)= q_2 ({\theta }) e^{\iota {\varphi }_2(x,t)}, \end{aligned}$$

(3.2)

with

$$\begin{aligned} \theta = x - {\upsilon }t, \end{aligned}$$

(3.3)

$$\begin{aligned} {\varphi }_i = - k_i x + {\omega }_i t + {\varsigma }_i, \end{aligned}$$

(3.4)

where ${\varphi }_i$, $q_i$, $k_i$, ${\omega }_i$, ${\upsilon }$ and ${\varsigma }_i$ $(i=1,2)$ are real valued and representing phase component, amplitude, frequency, wave number, velocity and phase constant, respectively.

Placing Eqs. (3.1), (3.2) in Eqs. (1.1), (1.2) with $i=1,2$ and $\hat{i}=3-i$, the imaginary part

$$\begin{aligned} {\upsilon }=- 2 {\alpha }_i k_i, \end{aligned}$$

(3.5)

and the real part

$$\begin{aligned} {\alpha }_i q''_{i} - \left( {\alpha }_i k_{i}^2 + {\omega }_i \right) q_i + {\beta }_i q_{i}^3 + {\beta }_i q_i q_{\hat{i}}=0, \end{aligned}$$

(3.6)

are deduced. Setting $q_i= q_{\hat{i}}$, Eq. (3.6) becomes

$$\begin{aligned} {\alpha }_i q''_{i} - \left( {\alpha }_i k_{i}^2 + {\omega }_i \right) q_i + 2 {\beta }_i q_{i}^3=0. \end{aligned}$$

(3.7)

4 Wave solutions of Manakov model

4.1 Implementation of extended ShGEEM

The extended sinh-Gordon equation expansion method is executed in this segment to analyze the solitary wave solutions of Eqs. (1.1), (1.2).

Case 1: $s'= \sinh (s)$

Exertion of balancing principle on the linear term $q''_{i}$ and nonlinear term $q_{i}^3$ of Eq. (3.7) gives $K=1$. For $K=1$, Eqs. (2.16)–(2.18) become

$$\begin{aligned} q_i(s)= W_1 \sinh (s) + V_1 \cosh (s) + V_0, \end{aligned}$$

(4.1)

$$\begin{aligned} q_i(\theta )= \pm \iota W_1 \text {sech}(\theta ) - V_1 \tanh (\theta ) + V_0, \end{aligned}$$

(4.2)

and

$$\begin{aligned} q_i(\theta )= \pm W_1 \text {csch}(\theta ) - V_1 \coth (\theta ) + V_0, \end{aligned}$$

(4.3)

where $W_1$ and $V_1$ can not be simultaneously zero.

Inserting Eq. (4.1) into Eq. (3.7) and associating all the coefficients of $\sinh ^j (s) \cosh ^j (s)$ to zero, a set of algebraic equations is obtained.

$$\begin{aligned} 12 {\beta }_i V_0 V_1 W_1&= 0, \\ 6 {\beta }_i V_0 V_{1}^2 + 6 {\beta }_i V_0 W_{1}^2&= 0, \\ 2 {\alpha }_i V_1 + 2 {\beta }_i V_{1}^3 + 6 {\beta }_i V_1 W_{1}^2&= {} 0, \\ 2 {\alpha }_i W_1 + 6 {\beta }_i V_{1}^2 W_1 + 2 {\beta }_i W_{1}^3&= 0, \\ - {\omega }_i V_0 - k_{i}^2 {\alpha }_i V_0 + 2 {\beta }_i V_{0}^3 - 6 {\beta }_i V_0 W_{1}^2 &= 0, \\ - {\omega }_i V_1 -2 {\alpha }_i V_1 - k_{i}^2 {\alpha }_i V_1 + 6 {\beta }_i V_{0}^2 V_1 - 6 {\beta }_i V_1 W_{1}^2 &= 0, \\ - {\omega }_i W_1 - {\alpha }_i W_1 - k_{i}^2 {\alpha }_i W_1 + 6 {\beta }_i V_{0}^2 W_1 -2 {\beta }_i W_{1}^3&= {} 0. \end{aligned}$$

The following results are obtained by resolving the above system.

Set 1: $V_0 = 0$, $V_1 = - \frac{\iota \sqrt{{\alpha }_i}}{\sqrt{{\beta }_i}}$, $W_1= 0$, $k_i= - \frac{\sqrt{- {\omega }_i -2 {\alpha }_i}}{\sqrt{{\alpha }_i}}$.

Putting the values given in Set 1 into Eqs. (4.2) and (4.3) and using Eq. (3.5), the solutions to Manakov system are attained as follows:

$$\begin{aligned} U_{1_{1}} (x,t)= \frac{ \sqrt{-{\alpha }_1}}{\sqrt{{\beta }_1}} \tanh \left( x - \frac{2 {\alpha }_1 \sqrt{- {\omega }_1 -2 {\alpha }_1}}{\sqrt{{\alpha }_1}} t\right) \times e^{\iota \left( \frac{\sqrt{- {\omega }_1 -2 {\alpha }_1}}{\sqrt{{\alpha }_1}} x + {\omega }_1 t + {\varsigma }_1\right) }, \end{aligned}$$

(4.4)

$$\begin{aligned} U_{2_{1}} (x,t)= \frac{ \sqrt{-{\alpha }_2}}{\sqrt{{\beta }_2}} \tanh \left( x - \frac{2 {\alpha }_2 \sqrt{- {\omega }_2 -2 {\alpha }_2}}{\sqrt{{\alpha }_2}} t\right) \times e^{\iota \left( \frac{\sqrt{- {\omega }_2 -2 {\alpha }_2}}{\sqrt{{\alpha }_2}} x + {\omega }_2 t + {\varsigma }_2\right) }, \end{aligned}$$

(4.5)

and

$$\begin{aligned} U_{1_{2}} (x,t)= & {} \frac{ \sqrt{-{\alpha }_1}}{\sqrt{{\beta }_1}} \coth \left( x - \frac{2 {\alpha }_1 \sqrt{- {\omega }_1 -2 {\alpha }_1}}{\sqrt{{\alpha }_1}} t\right) \nonumber \\{} & {} \times e^{\iota \left( \frac{\sqrt{- {\omega }_1 -2 {\alpha }_1}}{\sqrt{{\alpha }_1}} x + {\omega }_1 t + {\varsigma }_1\right) }, \end{aligned}$$

(4.6)

$$\begin{aligned} U_{2_{2}} (x,t)= & {} \frac{ \sqrt{-{\alpha }_2}}{\sqrt{{\beta }_2}} \coth \left( x - \frac{2 {\alpha }_2 \sqrt{- {\omega }_2 -2 {\alpha }_2}}{\sqrt{{\alpha }_2}} t\right) \nonumber \\{} & {} \times e^{\iota \left( \frac{\sqrt{- {\omega }_2 -2 {\alpha }_2}}{\sqrt{{\alpha }_2}} x + {\omega }_2 t + {\varsigma }_2\right) }. \end{aligned}$$

(4.7)

Set 2: $V_0 = 0$, $V_1 = - \frac{\iota \sqrt{{\alpha }_i}}{2 \sqrt{{\beta }_i}}$, $W_1= - \frac{\iota \sqrt{{\alpha }_i}}{2\sqrt{{\beta }_i}}$, $k_i= - \frac{\sqrt{- 2 {\omega }_i - {\alpha }_i}}{\sqrt{2{\alpha }_i}}$.

Inserting the values given in Set 2 into Eqs. (4.2) and (4.3) and using Eq. (3.5), the solutions to Manakov system are attained as follows:

$$\begin{aligned} U_{1_{3}}(x,t)= & {} \left[ \pm \frac{\sqrt{{\alpha }_1}}{2 \sqrt{{\beta }_1}}~ \text {sech} \left( x - \frac{2 {\alpha }_1 \sqrt{- 2 {\omega }_1 - {\alpha }_1}}{\sqrt{2{\alpha }_1}}t \right) \right. \nonumber \\{} & {} \left. + \frac{\sqrt{-{\alpha }_1}}{2\sqrt{{\beta }_1}} \tanh \left( x - \frac{2 {\alpha }_1 \sqrt{- 2 {\omega }_1 - {\alpha }_1}}{\sqrt{2{\alpha }_1}}t \right) \right] \nonumber \\{} & {} \times e^{\iota \left( \frac{\sqrt{- 2 {\omega }_1 - {\alpha }_1}}{\sqrt{2{\alpha }_1}} x + {\omega }_1 t + {\varsigma }_1\right) }, \end{aligned}$$

(4.8)

$$\begin{aligned} U_{2_{3}}(x,t)= & {} \left[ \pm \frac{\sqrt{{\alpha }_2}}{2 \sqrt{{\beta }_2}}~ \text {sech} \left( x - \frac{2 {\alpha }_2 \sqrt{- 2 {\omega }_2 - {\alpha }_2}}{\sqrt{2{\alpha }_2}}t \right) \right. \nonumber \\{} & {} \left. + \frac{ \sqrt{-{\alpha }_2}}{2\sqrt{{\beta }_2}} \tanh \left( x - \frac{2 {\alpha }_2 \sqrt{- 2 {\omega }_2 - {\alpha }_2}}{\sqrt{2{\alpha }_2}}t \right) \right] \nonumber \\{} & {} \times e^{\iota \left( \frac{\sqrt{- 2 {\omega }_2 - {\alpha }_2}}{\sqrt{2{\alpha }_2}} x + {\omega }_2 t + {\varsigma }_2\right) }, \end{aligned}$$

(4.9)

and

$$\begin{aligned} U_{1_{4}}(x,t)= & {} \left[ \mp \frac{\sqrt{-{\alpha }_1}}{2 \sqrt{{\beta }_1}}~ \text {csch} \left( x - \frac{2 {\alpha }_1 \sqrt{- 2 {\omega }_1 - {\alpha }_1}}{\sqrt{2{\alpha }_1}}t \right) \right. \nonumber \\{} & {} \left. + \frac{ \sqrt{-{\alpha }_1}}{2\sqrt{{\beta }_1}} \coth \left( x - \frac{2 {\alpha }_1 \sqrt{- 2 {\omega }_1 - {\alpha }_1}}{\sqrt{2{\alpha }_1}}t \right) \right] \nonumber \\{} & {} \times e^{\iota \left( \frac{\sqrt{- 2 {\omega }_1 - {\alpha }_1}}{\sqrt{2{\alpha }_1}} x + {\omega }_1 t + {\varsigma }_1\right) }, \end{aligned}$$

(4.10)

$$\begin{aligned} U_{2_{4}}(x,t)= & {} \left[ \mp \frac{\sqrt{-{\alpha }_2}}{2 \sqrt{{\beta }_2}}~ \text {csch} \left( x - \frac{2 {\alpha }_2 \sqrt{- 2 {\omega }_2 - {\alpha }_2}}{\sqrt{2{\alpha }_2}}t \right) \right. \nonumber \\{} & {} \left. + \frac{ \sqrt{-{\alpha }_2}}{2\sqrt{{\beta }_2}} \coth \left( x - \frac{2 {\alpha }_2 \sqrt{- 2 {\omega }_2 - {\alpha }_2}}{\sqrt{2{\alpha }_2}}t \right) \right] \nonumber \\{} & {} \times e^{\iota \left( \frac{\sqrt{- 2 {\omega }_2 - {\alpha }_2}}{\sqrt{2{\alpha }_2}} x + {\omega }_2 t + {\varsigma }_2\right) }. \end{aligned}$$

(4.11)

Set 3: $V_0 = 0$, $V_1 = 0$, $W_1= - \frac{\iota \sqrt{{\alpha }_i}}{\sqrt{{\beta }_i}}$, $k_i= - \frac{\sqrt{- {\omega }_i + {\alpha }_i}}{\sqrt{{\alpha }_i}}$.

Putting the values given in Set 3 into Eqs. (4.2) and (4.3) and using Eq. (3.5), the solutions to Manakov system are attained as follows:

$$\begin{aligned} U_{1_{5}}(x,t)= & {} \pm \frac{\sqrt{{\alpha }_1}}{\sqrt{{\beta }_1}}~ \text {sech} \left( x - \frac{2 {\alpha }_1 \sqrt{- {\omega }_1 + {\alpha }_1}}{\sqrt{{\alpha }_1}} \right) \nonumber \\{} & {} \times e^{\iota \left( \frac{\sqrt{- {\omega }_1 + {\alpha }_1}}{\sqrt{{\alpha }_1}}x + {\omega }_1 t + {\varsigma }_1 \right) }, \end{aligned}$$

(4.12)

$$\begin{aligned} U_{2_{5}}(x,t)= & {} \pm \frac{\sqrt{{\alpha }_2}}{\sqrt{{\beta }_2}}~ \text {sech} \left( x - \frac{2 {\alpha }_2 \sqrt{- {\omega }_2 + {\alpha }_2}}{\sqrt{{\alpha }_2}} \right) \nonumber \\{} & {} \times e^{\iota \left( \frac{\sqrt{- {\omega }_2 + {\alpha }_2}}{\sqrt{{\alpha }_2}}x + {\omega }_2 t + {\varsigma }_2 \right) }, \end{aligned}$$

(4.13)

and

$$\begin{aligned} U_{1_{6}}(x,t)= \mp \frac{\sqrt{-{\alpha }_1}}{\sqrt{{\beta }_1}}~ \text {csch} \left( x - \frac{2 {\alpha }_1 \sqrt{- {\omega }_1 + {\alpha }_1}}{\sqrt{{\alpha }_1}} \right) \times e^{\iota \left( \frac{\sqrt{- {\omega }_1 + {\alpha }_1}}{\sqrt{{\alpha }_1}}x + {\omega }_1 t + {\varsigma }_1 \right) }, \end{aligned}$$

(4.14)

$$\begin{aligned} U_{2_{6}}(x,t)= \mp \frac{\sqrt{-{\alpha }_2}}{\sqrt{{\beta }_2}}~ \text {csch} \left( x - \frac{2 {\alpha }_2 \sqrt{- {\omega }_2 + {\alpha }_2}}{\sqrt{{\alpha }_2}} \right) \times e^{\iota \left( \frac{\sqrt{- {\omega }_2 + {\alpha }_2}}{\sqrt{{\alpha }_2}}x + {\omega }_2 t + {\varsigma }_2 \right) }. \end{aligned}$$

(4.15)

Case 2: $s'= \cosh (s)$

Implementation of balancing principle on the linear term $q''_{i}$ and nonlinear term $q_{i}^3$ of Eq. (3.7) gives $K=1$. For $K=1$, Eqs. (2.16), (2.19) and (2.20) become

$$\begin{aligned} q_i(s)= W_1 \sinh (s) + V_1 \cosh (s) + V_0, \end{aligned}$$

(4.16)

$$\begin{aligned} q_i(\theta )= W_1 \tan (\theta ) \pm V_1 \sec (\theta ) + V_0, \end{aligned}$$

(4.17)

and

$$\begin{aligned} q_i(\theta )= - W_1 \cot (\theta ) \pm V_1 \csc (\theta ) + V_0, \end{aligned}$$

(4.18)

where $W_1$ and $V_1$ can not be simultaneously zero.

Inserting Eq. (4.16) into Eq. (3.7) and comparing all the coefficients of $\sinh ^j (s) \cosh ^j (s)$ to zero, a set of algebraic equation is obtained.

$$\begin{aligned} 12 {\beta }_i V_0 V_1 W_1&= 0, \\ 6 {\beta }_i V_0 V_{1}^2 + 6 {\beta }_i V_0 W_{1}^2&= 0, \\ 2 {\alpha }_i V_1 + 2 {\beta }_i V_{1}^3 + 6 {\beta }_i V_1 W_{1}^2&= 0, \\ 2 {\alpha }_i W_1 + 6 {\beta }_i V_{1}^2 W_1 + 2 {\beta }_i W_{1}^3&= {} 0, \\ - {\omega }_i V_0 - k_{i}^2 {\alpha }_i V_0 + 2 {\beta }_i V_{0}^3 - 6 {\beta }_i V_0 W_{1}^2&= 0, \\ - {\omega }_i W_1 - k_{i}^2 {\alpha }_i W_1 + 6 {\beta }_i V_{0}^2 W_1 -2 {\beta }_i W_{1}^3 &= 0, \\ - {\omega }_i V_1 - {\alpha }_i V_1 - k_{i}^2 {\alpha }_i V_1 + 6 {\beta }_i V_{0}^2 V_1 - 6 {\beta }_i V_1 W_{1}^2&= {} 0. \end{aligned}$$

Solving this system the following results are obtained. Set 4:  $V_0 = 0$,   $V_1 = \frac{\iota \sqrt{{\alpha }_i}}{\sqrt{{\beta }_i}}$,  $W_1= 0$,  $k_i= - \frac{\sqrt{- {\omega }_i - {\alpha }_i}}{\sqrt{{\alpha }_i}}$.

Putting the values specified in Set 4 into Eqs. (4.17) and (4.18) and using Eq. (3.5), the solutions to Manakov system are attained as follows:

$$\begin{aligned} U_{1_{7}}(x,t)= & {} \pm \frac{ \sqrt{-{\alpha }_1}}{\sqrt{{\beta }_1}} \sec \left( x - \frac{2 {\alpha }_1 \sqrt{- {\omega }_1 - {\alpha }_1}}{\sqrt{{\alpha }_1}}t \right) \times e^{\iota \left( \frac{\sqrt{- {\omega }_1 - {\alpha }_1}}{\sqrt{{\alpha }_1}}x + {\omega }_1 t + {\varsigma }_1 \right) }, \end{aligned}$$

(4.19)

$$\begin{aligned} U_{2_{7}}(x,t)= & {} \pm \frac{ \sqrt{-{\alpha }_2}}{\sqrt{{\beta }_2}} \sec \left( x - \frac{2 {\alpha }_2 \sqrt{- {\omega }_2 - {\alpha }_2}}{\sqrt{{\alpha }_2}}t \right) \times e^{\iota \left( \frac{\sqrt{- {\omega }_2 - {\alpha }_2}}{\sqrt{{\alpha }_2}}x + {\omega }_2 t + {\varsigma }_2 \right) }, \end{aligned}$$

(4.20)

and

$$\begin{aligned} U_{1_{8}}(x,t)= & {} \pm \frac{ \sqrt{-{\alpha }_1}}{\sqrt{{\beta }_1}} \csc \left( x - \frac{2 {\alpha }_1 \sqrt{- {\omega }_1 - {\alpha }_1}}{\sqrt{{\alpha }_1}}t \right) \times e^{\iota \left( \frac{\sqrt{- {\omega }_1 - {\alpha }_1}}{\sqrt{{\alpha }_1}}x + {\omega }_1 t + {\varsigma }_1 \right) }, \end{aligned}$$

(4.21)

$$\begin{aligned} U_{2_{8}}(x,t)= & {} \pm \frac{ \sqrt{-{\alpha }_2}}{\sqrt{{\beta }_2}} \csc \left( x - \frac{2 {\alpha }_2 \sqrt{- {\omega }_2 - {\alpha }_2}}{\sqrt{{\alpha }_2}}t \right) \times e^{\iota \left( \frac{\sqrt{- {\omega }_2 - {\alpha }_2}}{\sqrt{{\alpha }_2}}x + {\omega }_2 t + {\varsigma }_2 \right) }. \end{aligned}$$

(4.22)

Set 5:  $V_0 = 0$,  $V_1 = - \frac{\iota \sqrt{{\alpha }_i}}{2\sqrt{{\beta }_i}}$,  $W_1= - \frac{\iota \sqrt{{\alpha }_i}}{2\sqrt{{\beta }_i}}$,  $k_i= \frac{\sqrt{-2 {\omega }_i +{\alpha }_i}}{\sqrt{2{\alpha }_i}}$.

Inserting the values specified in Set 5 into Eqs. (4.17) and (4.18) and using Eq. (3.5), the solutions to Manakov system are attained as follows:

$$\begin{aligned} U_{1_{9}}(x,t)= & {} \left[ - \frac{ \sqrt{-{\alpha }_1}}{2 \sqrt{{\beta }_1}} \tan \left( x + \frac{2 {\alpha }_1 \sqrt{-2 {\omega }_1 +{\alpha }_1}}{\sqrt{2{\alpha }_1}}t \right) \right. \nonumber \\{} & {} \left. \mp \frac{\sqrt{-{\alpha }_1}}{2 \sqrt{{\beta }_1}} \sec \left( x + \frac{2 {\alpha }_1 \sqrt{-2 {\omega }_1 +{\alpha }_1}}{\sqrt{2{\alpha }_1}}t \right) \right] \nonumber \\{} & {} \times e^{\iota \left( - \frac{\sqrt{-2 {\omega }_1 +{\alpha }_1}}{\sqrt{2{\alpha }_1}} x + {\omega }_1 t + {\varsigma }_1\right) }, \end{aligned}$$

(4.23)

$$\begin{aligned} U_{2_{9}}(x,t)= & {} \left[ - \frac{ \sqrt{-{\alpha }_2}}{2 \sqrt{{\beta }_2}} \tan \left( x + \frac{2 {\alpha }_2 \sqrt{-2 {\omega }_2 +{\alpha }_2}}{\sqrt{2{\alpha }_2}}t \right) \right. \nonumber \\{} & {} \left. \mp \frac{ \sqrt{-{\alpha }_2}}{2 \sqrt{{\beta }_2}} \sec \left( x + \frac{2 {\alpha }_2 \sqrt{-2 {\omega }_2 +{\alpha }_2}}{\sqrt{2{\alpha }_2}}t \right) \right] \nonumber \\{} & {} \times e^{\iota \left( - \frac{\sqrt{-2 {\omega }_2 +{\alpha }_2}}{\sqrt{2{\alpha }_2}} x + {\omega }_2 t + {\varsigma }_2\right) }, \end{aligned}$$

(4.24)

and

$$\begin{aligned} U_{1_{10}}(x,t)= & {} \left[ \frac{ \sqrt{-{\alpha }_1}}{2 \sqrt{{\beta }_1}} \cot \left( x + \frac{2 {\alpha }_1 \sqrt{-2 {\omega }_1 +{\alpha }_1}}{\sqrt{2{\alpha }_1}}t \right) \right. \nonumber \\{} & {} \left. \mp \frac{ \sqrt{-{\alpha }_1}}{2 \sqrt{{\beta }_1}} \csc \left( x + \frac{2 {\alpha }_1 \sqrt{-2 {\omega }_1 +{\alpha }_1}}{\sqrt{2{\alpha }_1}}t \right) \right] \nonumber \\{} & {} \times e^{\iota \left( - \frac{\sqrt{-2 {\omega }_1 +{\alpha }_1}}{\sqrt{2{\alpha }_1}} x + {\omega }_1 t + {\varsigma }_1\right) }, \end{aligned}$$

(4.25)

$$\begin{aligned} U_{2_{10}}(x,t)= & {} \left[ \frac{ \sqrt{-{\alpha }_2}}{2 \sqrt{{\beta }_2}} \cot \left( x + \frac{2 {\alpha }_2 \sqrt{-2 {\omega }_2 +{\alpha }_2}}{\sqrt{2{\alpha }_2}}t \right) \right. \nonumber \\{} & {} \left. \mp \frac{ \sqrt{-{\alpha }_2}}{2 \sqrt{{\beta }_2}} \csc \left( x + \frac{2 {\alpha }_2 \sqrt{-2 {\omega }_2 +{\alpha }_2}}{\sqrt{2{\alpha }_2}}t \right) \right] \nonumber \\{} & {} \times e^{\iota \left( - \frac{\sqrt{-2 {\omega }_2 +{\alpha }_2}}{\sqrt{2{\alpha }_2}} x + {\omega }_2 t + {\varsigma }_2\right) }. \end{aligned}$$

(4.26)

Set 6:  $V_0 = 0$,  $V_1 = 0$,  $W_1= - \frac{\iota \sqrt{{\alpha }_i}}{\sqrt{{\beta }_i}}$,  $k_i= \frac{\sqrt{- {\omega }_i +2 {\alpha }_i}}{\sqrt{{\alpha }_i}}$.

Putting the values prescribed in Set 6 into Eqs. (4.17) and (4.18) and using Eq. (3.5), the solutions to Manakov system are attained as follows:

$$\begin{aligned} U_{1_{11}} (x,t)= & {} - \frac{ \sqrt{-{\alpha }_1}}{\sqrt{{\beta }_1}} \tan \left( x +\frac{2 {\alpha }_1 \sqrt{- {\omega }_1 +2 {\alpha }_1}}{\sqrt{{\alpha }_1}} t \right) \nonumber \\{} & {} \times e^{\iota \left( - \frac{\sqrt{- {\omega }_1 +2 {\alpha }_1}}{\sqrt{{\alpha }_1}}x + {\omega }_1 t + {\varsigma }_1\right) }, \end{aligned}$$

(4.27)

$$\begin{aligned} U_{2_{11}} (x,t)= & {} - \frac{ \sqrt{-{\alpha }_2}}{\sqrt{{\beta }_2}} \tan \left( x +\frac{2 {\alpha }_2 \sqrt{- {\omega }_2 +2 {\alpha }_2}}{\sqrt{{\alpha }_2}} t \right) \nonumber \\{} & {} \times e^{\iota \left( - \frac{\sqrt{- {\omega }_2 +2 {\alpha }_2}}{\sqrt{{\alpha }_2}}x + {\omega }_2 t + {\varsigma }_2\right) }, \end{aligned}$$

(4.28)

and

$$\begin{aligned} U_{1_{12}} (x,t)= \frac{ \sqrt{-{\alpha }_1}}{\sqrt{{\beta }_1}} \cot \left( x +\frac{2 {\alpha }_1 \sqrt{- {\omega }_1 +2 {\alpha }_1}}{\sqrt{{\alpha }_1}} t \right) \times e^{\iota \left( - \frac{\sqrt{- {\omega }_1 +2 {\alpha }_1}}{\sqrt{{\alpha }_1}}x + {\omega }_1 t + {\varsigma }_1\right) }, \end{aligned}$$

(4.29)

$$\begin{aligned} U_{2_{12}} (x,t)= \frac{ \sqrt{-{\alpha }_2}}{\sqrt{{\beta }_2}} \cot \left( x +\frac{2 {\alpha }_2 \sqrt{- {\omega }_2 +2 {\alpha }_2}}{\sqrt{{\alpha }_2}} t \right) \times e^{\iota \left( - \frac{\sqrt{- {\omega }_2 +2 {\alpha }_2}}{\sqrt{{\alpha }_2}}x + {\omega }_2 t + {\varsigma }_2\right) }. \end{aligned}$$

(4.30)

4.2 Implementation of $\left( \frac{G'}{G},\frac{1}{G}\right)$-expansion method

Exertion of the homogeneous balancing principle on the linear term $q_{i}''$ and nonlinear term $q_{i}^3$ of Eq. (3.7) yields $K=1$ and Eq. (2.30) becomes

$$\begin{aligned} q_i (\theta )= c_0 + c_1 {\psi } + d_1 {\phi }. \end{aligned}$$

(4.31)

The three cases will be discussed to attain the solitary wave solutions of Eqs. (1.1), (1.2).

Hyperbolic function solution: For ${\gamma }<0$, insertion of Eq. (4.31) together with Eqs. (2.23) and (2.25) into Eq. (3.7) gives a polynomial in ${\psi }$ and ${\phi }$. The values of unknowns are attained by simultaneously solving the system of equations which is yielded by equating all the coefficients of ${\psi }$ and ${\phi }$ equal to zero.

Set 7: $c_0 =0$,   $c_1 = -\frac{\iota \sqrt{{\alpha }_i}}{2 \sqrt{{\beta }_i}}$,  $d_1= - \frac{\sqrt{{\alpha }_i} \sqrt{{\rho }^2 + {\gamma }^2 {\lambda }_1}}{2 \sqrt{{\beta }_i {\gamma }}}$,   ${\omega }_i= \frac{1}{2} (-2 k_{i}^2 {\alpha }_i + {\alpha }_i {\gamma })$.

Putting the values stated in Set 7 into Eq. (4.31) and using Eq. (2.24), the solution to Manakov system is attained, as

$$\begin{aligned} U_{1_{13}} (x,t)= & {} \left[ - \frac{\sqrt{-{\alpha }_1}}{2 \sqrt{{\beta }_1}}\left( \frac{B_1 \sqrt{-{\gamma }}\cosh \left[ \sqrt{-{\gamma }}(x+ 2 {\alpha }_1 k_1 t) \right] +B_2 \sqrt{-{\gamma }}\sinh \left[ \sqrt{-{\gamma }}(x+ 2 {\alpha }_1 k_1 t) \right] }{\frac{\rho }{\gamma } + B_1 \sinh \left[ \sqrt{-{\gamma }}(x+ 2 {\alpha }_1 k_1 t) \right] + B_2 \cosh \left[ \sqrt{-{\gamma }}(x+ 2 {\alpha }_1 k_1 t) \right] } \right) \right. \nonumber \\{} & {} \left. - \frac{\sqrt{{\alpha }_1}}{2 \sqrt{{\beta }_1 {\gamma }}}\left( \frac{\sqrt{{\rho }^2 + {\gamma }^2 {\lambda }_1}}{\frac{\rho }{\gamma } + B_1 \sinh \left[ \sqrt{-{\gamma }}(x+ 2 {\alpha }_1 k_1 t) \right] + B_2 \cosh \left[ \sqrt{-{\gamma }}(x+ 2 {\alpha }_1 k_1 t) \right] } \right) \right] \nonumber \\{} & {} \times e^{\iota \left( -k_1 x + \frac{-2 k_{1}^2 {\alpha }_1 + {\alpha }_1 {\gamma }}{2} t + {\varsigma }_1 \right) }, \end{aligned}$$

(4.32)

$$\begin{aligned} U_{2_{13}} (x,t)= & {} \left[ -\frac{\sqrt{-{\alpha }_2}}{2 \sqrt{{\beta }_2}}\left( \frac{B_1 \sqrt{-{\gamma }}\cosh \left[ \sqrt{-{\gamma }}(x+ 2 {\alpha }_2 k_2 t) \right] +B_2 \sqrt{-{\gamma }}\sinh \left[ \sqrt{-{\gamma }}(x+ 2 {\alpha }_2 k_2 t) \right] }{\frac{\rho }{\gamma } + B_1 \sinh \left[ \sqrt{-{\gamma }}(x+ 2 {\alpha }_2 k_2 t) \right] + B_2 \cosh \left[ \sqrt{-{\gamma }}(x+ 2 {\alpha }_2 k_2 t) \right] } \right) \right. \nonumber \\ {}{} & {} \left. - \frac{\sqrt{{\alpha }_2}}{2 \sqrt{{\beta }_2 {\gamma }}}\left( \frac{\sqrt{{\rho }^2 + {\gamma }^2 {\lambda }_1}}{\frac{\rho }{\gamma } + B_1 \sinh \left[ \sqrt{-{\gamma }}(x+ 2 {\alpha }_2 k_2 t) \right] + B_2 \cosh \left[ \sqrt{-{\gamma }}(x+ 2 {\alpha }_2 k_2 t) \right] } \right) \right] \nonumber \\{} & {} \times e^{\iota \left( -k_2 x + \frac{-2 k_{2}^2 {\alpha }_2 + {\alpha }_2 {\gamma }}{2} t + {\varsigma }_2 \right) }, \end{aligned}$$

(4.33)

where ${\lambda }_1= B_{1}^2 -B_{2}^2$.

Precisely if $B_1=0$, $B_2>0$ and ${\rho }=0$ then from Eqs. (4.32), (4.33), the following solution is attained:

$$\begin{aligned} U_{1_{14}} (x,t)= & {} \left[ \frac{\sqrt{{\alpha }_1 {\gamma }}}{2 \sqrt{{\beta }_1}} \tanh \left[ \sqrt{-{\gamma }}(x+ 2 {\alpha }_1 k_1 t) \right] -\frac{\sqrt{-{\alpha }_1 {\gamma }}}{2 \sqrt{{\beta }_1}} \text {sech}\left[ \sqrt{-{\gamma }}(x+ 2 {\alpha }_1 k_1 t) \right] \right] \nonumber \\{} & {} \times e^{\iota \left( -k_1 x + \frac{-2 k_{1}^2 {\alpha }_1 + {\alpha }_1 {\gamma }}{2} t + {\varsigma }_1 \right) }, \end{aligned}$$

(4.34)

$$\begin{aligned} U_{2_{14}} (x,t)= & {} \left[ \frac{\sqrt{{\alpha }_2 {\gamma }}}{2 \sqrt{{\beta }_2}} \tanh \left[ \sqrt{-{\gamma }}(x+ 2 {\alpha }_2 k_2 t) \right] -\frac{\sqrt{-{\alpha }_2 {\gamma }}}{2 \sqrt{{\beta }_2}} \text {sech}\left[ \sqrt{-{\gamma }}(x+ 2 {\alpha }_2 k_2 t) \right] \right] \nonumber \\{} & {} \times e^{\iota \left( -k_2 x + \frac{-2 k_{2}^2 {\alpha }_2 + {\alpha }_2 {\gamma }}{2} t + {\varsigma }_2 \right) }. \end{aligned}$$

(4.35)

If $B_1>0$, $B_2=0$ and ${\rho }=0$ then from Eqs. (4.32), (4.33), the following solution is attained:

$$\begin{aligned} U_{1_{15}} (x,t)= & {} \left[ \frac{\sqrt{{\alpha }_1 {\gamma }}}{2 \sqrt{{\beta }_1}} \coth \left[ \sqrt{-{\gamma }}(x+ 2 {\alpha }_1 k_1 t) \right] -\frac{\sqrt{{\alpha }_1 {\gamma }}}{2 \sqrt{{\beta }_1}} \text {csch}\left[ \sqrt{-{\gamma }} (x+ 2 {\alpha }_1 k_1 t) \right] \right] \nonumber \\{} & {} \times e^{\iota \left( -k_1 x + \frac{-2 k_{1}^2 {\alpha }_1 + {\alpha }_1 {\gamma }}{2} t + {\varsigma }_1 \right) }, \end{aligned}$$

(4.36)

$$\begin{aligned} U_{2_{15}} (x,t)= & {} \left[ \frac{\sqrt{{\alpha }_2 {\gamma }}}{2 \sqrt{{\beta }_2}} \coth \left[ \sqrt{-{\gamma }}(x+ 2 {\alpha }_2 k_2 t) \right] -\frac{\sqrt{{\alpha }_2 {\gamma }}}{2 \sqrt{{\beta }_2}} \text {csch}\left[ \sqrt{-{\gamma }}(x+ 2 {\alpha }_2 k_2 t) \right] \right] \nonumber \\{} & {} \times e^{\iota \left( -k_2 x + \frac{-2 k_{2}^2 {\alpha }_2 + {\alpha }_2 {\gamma }}{2} t + {\varsigma }_2 \right) }. \end{aligned}$$

(4.37)

Trigonometric function solution: For ${\gamma }>0$, the insertion of Eq. (4.31) together with Eqs. (2.23) and (2.27) into Eq. (3.7) yields a polynomial in ${\psi }$ and ${\phi }$. The values of unknowns are deduced by resolving the system of equations which is obtained by equating all the coefficients of ${\psi }$ and ${\phi }$ to zero.

Set 8: $c_0 =0$,   $c_1 = -\frac{\iota \sqrt{{\alpha }_i}}{2 \sqrt{{\beta }_i}}$,  $d_1= - \frac{\sqrt{{\alpha }_i} \sqrt{{\rho }^2 - {\gamma }^2 {\lambda }_2}}{2 \sqrt{{\beta }_i {\gamma }}}$,   ${\omega }_i= \frac{1}{2} (-2 k_{i}^2 {\alpha }_i + {\alpha }_i {\gamma })$.

Putting the values specified in Set 8 into Eq. (4.31) and using Eq. (2.26), the solution to Manakov system is attained, as

$$\begin{aligned} U_{1_{16}} (x,t)= & {} \left[ - \frac{\sqrt{-{\alpha }_1}}{2 \sqrt{{\beta }_1}}\left( \frac{B_1 \sqrt{{\gamma }}\cos \left[ \sqrt{{\gamma }}(x+ 2 {\alpha }_1 k_1 t) \right] -B_2 \sqrt{{\gamma }}\sin \left[ \sqrt{{\gamma }}(x+ 2 {\alpha }_1 k_1 t) \right] }{\frac{\rho }{\gamma } + B_1 \sin \left[ \sqrt{{\gamma }}(x+ 2 {\alpha }_1 k_1 t) \right] + B_2 \cos \left[ \sqrt{{\gamma }}(x+ 2 {\alpha }_1 k_1 t) \right] } \right) \right. \nonumber \\{} & {} \left. - \frac{\sqrt{{\alpha }_1}}{2 \sqrt{{\beta }_1 {\gamma }}}\left( \frac{\sqrt{{\rho }^2 - {\gamma }^2 {\lambda }_2}}{\frac{\rho }{\gamma } + B_1 \sin \left[ \sqrt{{\gamma }}(x+ 2 {\alpha }_1 k_1 t) \right] + B_2 \cos \left[ \sqrt{{\gamma }}(x+ 2 {\alpha }_1 k_1 t) \right] } \right) \right] \nonumber \\{} & {} \times e^{\iota \left( -k_1 x + \frac{-2 k_{1}^2 {\alpha }_1 + {\alpha }_1 {\gamma }}{2} t + {\varsigma }_1 \right) }, \end{aligned}$$

(4.38)

$$\begin{aligned} U_{2_{16}} (x,t)= & {} \left[ - \frac{\sqrt{-{\alpha }_2}}{2 \sqrt{{\beta }_2}}\left( \frac{B_1 \sqrt{{\gamma }}\cos \left[ \sqrt{{\gamma }}(x+ 2 {\alpha }_2 k_2 t) \right] -B_2 \sqrt{{\gamma }}\sin \left[ \sqrt{{\gamma }}(x+ 2 {\alpha }_2 k_2 t) \right] }{\frac{\rho }{\gamma } + B_1 \sin \left[ \sqrt{{\gamma }}(x+ 2 {\alpha }_2 k_2 t) \right] + B_2 \cos \left[ \sqrt{{\gamma }}(x+ 2 {\alpha }_1 k_1 t) \right] } \right) \right. \nonumber \\{} & {} \left. - \frac{\sqrt{{\alpha }_2}}{2 \sqrt{{\beta }_2 {\gamma }}}\left( \frac{\sqrt{{\rho }^2 - {\gamma }^2 {\lambda }_2}}{\frac{\rho }{\gamma } + B_1 \sin \left[ \sqrt{{\gamma }}(x+ 2 {\alpha }_2 k_2 t) \right] + B_2 \cos \left[ \sqrt{{\gamma }}(x+ 2 {\alpha }_2 k_2 t) \right] } \right) \right] \nonumber \\{} & {} \times e^{\iota \left( -k_2 x + \frac{-2 k_{2}^2 {\alpha }_2 + {\alpha }_2 {\gamma }}{2} t + {\varsigma }_2 \right) }, \end{aligned}$$

(4.39)

where ${\lambda }_2= B_{1}^2 +B_{2}^2$.

If $B_1=0$, $B_2>0$ and ${\rho }=0$ then from Eqs. (4.38), (4.39), the following solution is attained:

$$\begin{aligned} U_{1_{17}} (x,t)= & {} \left[ \frac{\sqrt{-{\alpha }_1 {\gamma }}}{2 \sqrt{{\beta }_1}} \tan \left[ \sqrt{{\gamma }}(x+ 2 {\alpha }_1 k_1 t) \right] -\frac{\sqrt{-{\alpha }_1 {\gamma }}}{2 \sqrt{{\beta }_1}} \sec \left[ \sqrt{{\gamma }}(x+ 2 {\alpha }_1 k_1 t) \right] \right] \nonumber \\{} & {} \times e^{\iota \left( -k_1 x + \frac{-2 k_{1}^2 {\alpha }_1 + {\alpha }_1 {\gamma }}{2}t + {\varsigma }_1 \right) }, \end{aligned}$$

(4.40)

$$\begin{aligned} U_{2_{17}} (x,t)= & {} \left[ \frac{\sqrt{-{\alpha }_2 {\gamma }}}{2 \sqrt{{\beta }_2}} \tan \left[ \sqrt{{\gamma }}(x+ 2 {\alpha }_2 k_2 t) \right] -\frac{\sqrt{-{\alpha }_2{\gamma }}}{2 \sqrt{{\beta }_2}} \sec \left[ \sqrt{{\gamma }}(x+ 2 {\alpha }_2 k_2 t) \right] \right] \nonumber \\{} & {} \times e^{\iota \left( -k_2 x + \frac{-2 k_{2}^2 {\alpha }_2 + {\alpha }_2 {\gamma }}{2}t + {\varsigma }_2 \right) }. \end{aligned}$$

(4.41)

If $B_1>0$, $B_2=0$ and ${\rho }=0$ then from Eqs. (4.38), (4.39), the following solution is attained:

$$\begin{aligned} U_{1_{18}} (x,t)= & {} \left[ -\frac{\sqrt{-{\alpha }_1 {\gamma }}}{2 \sqrt{{\beta }_1}} \cot \left[ \sqrt{{\gamma }}(x+ 2 {\alpha }_1 k_1 t) \right] -\frac{\sqrt{-{\alpha }_1 {\gamma }}}{2 \sqrt{{\beta }_1}} \csc \left[ \sqrt{{\gamma }}(x+ 2 {\alpha }_1 k_1 t) \right] \right] \nonumber \\{} & {} \times e^{\iota \left( -k_1 x + \frac{-2 k_{1}^2 {\alpha }_1 + {\alpha }_1 {\gamma }}{2}t + {\varsigma }_1 \right) }, \end{aligned}$$

(4.42)

$$\begin{aligned} U_{2_{18}} (x,t)= & {} \left[ -\frac{\sqrt{-{\alpha }_2 {\gamma }}}{2 \sqrt{{\beta }_2}} \cot \left[ \sqrt{{\gamma }}(x+ 2 {\alpha }_2 k_2 t) \right] -\frac{\sqrt{-{\alpha }_2{\gamma }}}{2 \sqrt{{\beta }_2}} \csc \left[ \sqrt{{\gamma }}(x+ 2 {\alpha }_2 k_2 t) \right] \right] \nonumber \\{} & {} \times e^{\iota \left( -k_2 x + \frac{-2 k_{2}^2 {\alpha }_2 + {\alpha }_2 {\gamma }}{2}t + {\varsigma }_2 \right) }. \end{aligned}$$

(4.43)

Rational function solution: For ${\gamma }=0$, the insertion of Eq. (4.31) together with Eqs. (2.23) and (2.29) into Eq. (3.7) yields a polynomial in ${\psi }$ and ${\phi }$. The values of unknowns are deduced by resolving the system of equations which is obtained by equating all the coefficients of ${\psi }$ and ${\phi }$ to zero.

Set 9: $c_0 =0$,   $c_1 = -\frac{\iota \sqrt{{\alpha }_i}}{2 \sqrt{{\beta }_i}}$,  $d_1= \frac{{\iota } \sqrt{{\alpha }_i} \sqrt{B_{1}^2 - 2{\rho } {B}_2}}{2 \sqrt{{\beta }_i}}$,   ${\omega }_i= - k_{i}^2 {\alpha }_i$.

Putting the values specified in Set 9 into Eq. (4.31) and using Eq. (2.28), the solution to Manakov system is attained, as

$$\begin{aligned} U_{1_{19}} (x,t)= -\frac{\sqrt{-{\alpha }_1}}{\sqrt{{\beta }_1}}\frac{{\rho }(x + 2 {\alpha }_1 k_1 t)+ B_1 - \sqrt{B_{1}^2 -2 {\rho } B_2}}{{\rho } (x + 2 {\alpha }_1 k_1 t)^2 + 2 B_1 (x + 2 {\alpha }_1 k_1 t)+ 2 B_2} \times e^{\iota \left( -k_1 x - k_{1}^2 {\alpha }_1 t + {\varsigma }_1 \right) }, \end{aligned}$$

(4.44)

$$\begin{aligned} U_{2_{19}} (x,t)= -\frac{\sqrt{-{\alpha }_2}}{\sqrt{{\beta }_2}}\frac{{\rho }(x + 2 {\alpha }_2 k_2 t)+ B_1 - \sqrt{B_{1}^2 -2 {\rho } B_2}}{{\rho } (x + 2 {\alpha }_2 k_2 t)^2 + 2 B_1 (x + 2 {\alpha }_2 k_2 t)+ 2 B_2} \times e^{\iota \left( -k_2 x - k_{2}^2 {\alpha }_2 t + {\varsigma }_2 \right) }. \end{aligned}$$

(4.45)

5 Graphical observations

The obtained solutions of Manakov model using extended ShGEEM and $\left( G'/G, 1/G\right)$-expansion method are graphically exhibited in this segment. The deduced hyperbolic, trigonometric and rational functions represent dark-dark soliton, bright-bright soliton, combined dark-bright soliton, multi solitons and periodic solitary waves under suitable parametric values.

Fig. 1

Graphical simulations for $U_{1_{1}}(x,t)$ and $U_{2_{1}}(x,t)$ at ${\alpha }_1= {\beta }_1={\alpha }_2=1,~ {\beta }_2= 2,~{k}_1= -1,~ {k}_2=-\sqrt{2},~ {\omega }_1=-3,~{\omega }_2=-4,~ {\varsigma }_1={\varsigma }_2=1$

Fig. 2

Graphical simulations for $U_{1_{3}}(x,t)$ and $U_{2_{3}}(x,t)$ at ${\alpha }_1=1, ~{\beta }_1=-2, ~{\alpha }_2=2,~ {\beta }_2= -3,~{k}_1= - \frac{1}{\sqrt{6}},~ {k}_2=- \frac{1}{\sqrt{2}},~ {\omega }_1=-2,~{\omega }_2=-3,~ {\varsigma }_1={\varsigma }_2=1$

Fig. 3

Graphical simulations for $U_{1_{5}}(x,t)$ and $U_{2_{5}}(x,t)$ at ${\alpha }_1=1,~ {\beta }_1= -1,~ {\alpha }_2=\frac{1}{2},~ {\beta }_2= -\frac{1}{2},~{k}_1=-\sqrt{2},~ {k}_2= -\sqrt{3},~{\omega }_1={\omega }_2= -1,~ {\varsigma }_1={\varsigma }_2=1$

Fig. 4

Graphical simulations for $U_{1_{14}}(x,t)$ and $U_{2_{14}}(x,t)$ at ${\alpha }_1=1,~ {\beta }_1= 2,~ {\alpha }_2=1,~ {\beta }_2= 4,~ {\gamma }=-1,~{k}_1=1,~ {k}_2= 2,~{\omega }_1= -\frac{3}{2},~{\omega }_2= - \frac{9}{2},~ {\varsigma }_1={\varsigma }_2=1$

Fig. 5

Graphical simulations for $U_{1_{17}}(x,t)$ and $U_{2_{17}}(x,t)$ at ${\alpha }_1=1,~ {\beta }_1= 2,~ {\alpha }_2=1,~ {\beta }_2= 4,~ {\gamma }=1,~{k}_1=1,~ {k}_2= 2,~{\omega }_1= -\frac{1}{2},~{\omega }_2= - \frac{7}{2},~ {\varsigma }_1={\varsigma }_2=1$

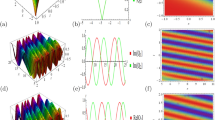
In Fig. 1, the solution $U_{1_{1}}(x,t)$, $U_{2_{1}}(x,t)$ is exhibited graphically for the parametric values taken as ${\alpha }_1= {\beta }_1={\alpha }_2=1,~ {\beta }_2= 2,~{k}_1= -1,~ {k}_2=-\sqrt{2},~ {\omega }_1=-3,~{\omega }_2=-4,~ {\varsigma }_1={\varsigma }_2=1$. Figure 1a represents modulus $|U_{1_{1}}|$ and $|U_{2_{1}}|$ in 3D, Fig. 1b refers to the 2D plot of $|U_{1_{1}}|$ and $|U_{2_{1}}|$, and Fig. 1c is the density plot of $|U_{1_{1}}|$ and $|U_{2_{1}}|$. Furthermore, Fig. 2d–f belong to imaginary value of $U_{1_{1}}$ and $U_{2_{1}}$ while Fig. 2g–i refer to real value of $U_{1_{1}}$ and $U_{2_{1}}$ in 3D, 2D and density plot, respectively.

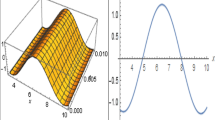
Figure 2 is graphical representation of the solution $U_{1_{3}}(x,t)$, $U_{2_{3}}(x,t)$ for the parametric values taken as ${\alpha }_1=1, ~{\beta }_1=-2, ~{\alpha }_2=2,~ {\beta }_2= -3,~{k}_1= - \frac{1}{\sqrt{6}},~ {k}_2=- \frac{1}{\sqrt{2}},~ {\omega }_1=-2,~{\omega }_2=-3,~ {\varsigma }_1={\varsigma }_2=1$. Figure 2a is the illustration of modulus $|U_{1_{3}}|$ and $|U_{2_{3}}|$ in 3D, Fig. 2b refers to the 2D plot of $|U_{1_{3}}|$ and $|U_{2_{3}}|$, and Fig. 2c is the density plot of $|U_{1_{3}}|$ and $|U_{2_{3}}|$. Furthermore, Fig. 2d–f belong to imaginary value of $U_{1_{3}}$ and $U_{2_{3}}$ while Fig. 2g–i refer to real value of $U_{1_{3}}$ and $U_{2_{3}}$ in 3D, 2D and density plot, respectively.

Figure 3 is the graphical illustration of the solution $U_{1_{5}}(x,t)$, $U_{2_{5}}(x,t)$ for the parametric values taken as ${\alpha }_1=1,~ {\beta }_1= -1,~ {\alpha }_2=\frac{1}{2},~ {\beta }_2= -\frac{1}{2},~{k}_1=-\sqrt{2},~ {k}_2= -\sqrt{3},~{\omega }_1={\omega }_2= -1,~ {\varsigma }_1={\varsigma }_2=1$. Figure 3a is the representation of modulus $|U_{1_{5}}|$ and $|U_{2_{5}}|$ in 3D, Fig. 3b is the depiction of $|U_{1_{5}}|$ and $|U_{2_{5}}|$ in 2D, and Fig. 3c is the density plot of $|U_{1_{5}}|$ and $|U_{2_{5}}|$. Figure 3d–f correspond to imaginary value of $U_{1_{5}}$ and $U_{2_{5}}$ and Fig. 3g–i belong to real value of $U_{1_{5}}$ and $U_{2_{5}}$ in 3D, 2D and density plot, respectively.

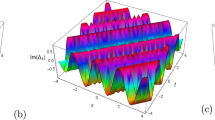
Figure 4 is the graphical representation of the solution $U_{1_{14}}(x,t)$, $U_{2_{14}}(x,t)$ for the parametric values taken as ${\alpha }_1=1,~ {\beta }_1= 2,~ {\alpha }_2=1,~ {\beta }_2= 4,~ {\gamma }=-1,~{k}_1=1,~ {k}_2= 2,~{\omega }_1= -\frac{3}{2},~{\omega }_2= - \frac{9}{2},~ {\varsigma }_1={\varsigma }_2=1$. Figure 4a illustration of modulus $|U_{1_{14}}|$ and $|U_{2_{14}}|$ in 3D, Fig. 4b exhibits $|U_{1_{14}}|$ and $|U_{2_{14}}|$ in 2D, and Fig. 4c depicts the density plot of $|U_{1_{14}}|$ and $|U_{2_{14}}|$. Furthermore, Fig. 4d–f refer to imaginary value of $U_{1_{14}}$ and $U_{2_{14}}$ while Fig. 4g–i belong to real value of $U_{1_{14}}$ and $U_{2_{14}}$ in 3D, 2D and density plot, respectively.

Figure 5 is the graphical illustration of the solution $U_{1_{17}}(x,t)$, $U_{2_{17}}(x,t)$ for the parametric values taken as ${\alpha }_1=1,~ {\beta }_1= 2,~ {\alpha }_2=1,~ {\beta }_2= 4,~ {\gamma }=1,~{k}_1=1,~ {k}_2= 2,~{\omega }_1= -\frac{1}{2},~{\omega }_2= - \frac{7}{2},~ {\varsigma }_1={\varsigma }_2=1$. Figure 5a representation of modulus $|U_{1_{17}}|$ and $|U_{2_{17}}|$ in 3D, Fig. 5b is the depiction of $|U_{1_{17}}|$ and $|U_{2_{17}}|$ in 2D, and Fig. 5c is the density plot of $|U_{1_{17}}|$ and $|U_{2_{17}}|$. Figure 5d–f correspond to imaginary value of $U_{1_{17}}$ and $U_{2_{17}}$ and Fig. 5g–i refer to real value of $U_{1_{17}}$ and $U_{2_{17}}$ in 3D, 2D and density plot, respectively.

6 Discussion and conclusion

In this article, optical solitons and other solitary wave solutions of the Manakov model are evaluated by employing the extended sinh-Gordon equation expansion method and $\left( G'/G, 1/G \right)$-expansion method. By executing these expansion methods, rational, trigonometric and hyperbolic functions are obtained. At some specific values of the parameters of the assumed system, dark-dark soliton, bright-bright soliton, combined dark-bright soliton, multi solitons and periodic solitary waves are obtained. These soliton solutions have fundamental applications in applied sciences, especially in nonlinear fiber optics since they can carry large amount of data at high speed owing to their stability during wave propagation. Bright solitons are extensively studied in optical communications and recently the transmission of dark solitons in optical fibers was discovered. Despite the fact that dark solitons have fewer fiber losses and less sensitivity to noise, bright solitons are preferred in communication network systems owing to their high intensity peaks. Combined dark-bright solitons represent a category of higher-order solitons that find application in optical fiber systems, ensuring the stable transmission of optical signals across extended distances (Bezgabadi and Bolorizadeh 2021). Furthermore, these soliton configurations possess the capacity to manipulate light properties through self-phase modulation effects, rendering them valuable for the advancement of optical devices. Multi-solitons, on the other hand, serve as tools for exploring noise characteristics and can be employed to reduce the duration of solitons in fiber-optic transmission systems (Zhang et al. 2019). Additionally, some of the wave results of the Manakov system are presented graphically to get a better understanding of the nature and propagation of solitary waves. The visual representation clearly demonstrates that the extended ShGEEM yields more accurate and valuable outcomes for the Manakov model when compared to the $\left( G'/G, 1/G \right)$-expansion method and prior literature. Given the significance of Manakov solitons in the field of optics, it is advantageous to possess a single method capable of obtaining all soliton types. Such a method would enhance efficiency, simplicity, facilitate interdisciplinary applications, reduce experimental costs, and contribute to technological advancements. In future, the proposed extended sinh-Gordon equation expansion method can be utilized to explore the dynamical behavior of other nonlinear mathematical models arising in optics. Moreover, the findings of this work can be utilized to suggest new numerical and laboratory experiments for optical devices and fiber optics.