Optical soliton solutions of Manakov model arising in the description of wave propagation through optical fibers

Abstract

In the field of nonlinear optics, soliton structures have been extensively investigated in recent years. Optical solitons can be used in communication systems as optical information carriers. The advantage of a optical soliton is that it does not alter its structure when it interacts with other pulses. Optical solitons are useful for signal processing applications like pulse compression, regeneration, and amplification, leading to cleaner, more reliable signals. They can also be explored in optical computing, sensing, and laser technology. Studying optical solitons provides insights into nonlinearity and dispersion in wave propagation, contributing to physics and paving the way for future discoveries. The purpose of this article is to strive for the optical soliton solutions of the Manakov model with the help of the modified auxiliary equation method and the extended trial equation method. The Manakov model is a simple, analytical, and numerical model that provides basic insights into soliton formation and propagation. This model is suitable for studying soliton properties like stability, interactions, and collisions. The study provides hyperbolic, trigonometric, rational, and notably, Jacobi-elliptic function solutions, which have not been explored for the considered system. Additionally, dark soliton, bright soliton, bright singular soliton, bright singular two-solitons, multi solitons and periodic solitary wave solutions are exhibited by their graphical representations.

1 Introduction

In nonlinear optics, optical solitons have been a substantial topic for exploration because of their potential applications in information technologies and ultrafast signal processing procedures. The balance arising between group velocity dispersion effect and nonlinear effect as a result of nonlinear variation in refractive index helps optical soliton to emerge (Haus and Wong 1996; Hasegawa 2000; Hasegawa and Tappert 1973). In optical soliton communications, the signal does not require to be transferred to an electric field for processing rather it is transmitted on the basis of the total internal reflection principle. Solitons are capable of ultrafast data transmission due to their unique shape and speed. They maintain their individuality, allowing multiple solitons to coexist within the same fiber without interference, thereby increasing channel capacity and overall communication capacity.

To study the optical solitons, ultrafast fiber lasers are regarded as an absolute commodity owing to their simplicity and rigorous control of the experimental parameters. Optical fiber communication has precedence over the regular cable communication system because of its extensive bandwidth, less weight, no risk of short circuits, and resistance to harsh temperatures. The propagation of optical pulses in fiber communication networks mostly has been studied using nonlinear Schödinger equations (Abbagari et al. 2023; Rehman et al. 2022; Baskonus et al. 2021; Badshah et al. 2023; Tariq et al. 2023; Kivshar and Peyrard 1992; Triki et al. 2022), while the complexities like dispersion (Houwe et al. 2023) and nonlinearity (Nguetcho and Wamba 2017; Tabi et al. 2022) have been tackled with the help of mathematical systems, including Biswas–Arshad (Yildirim 2019; Yildirim 2021), Triki-Biswas (Li and Lian 2022), Biswas–Milovic (Zayed et al. 2022), Radhakrishnan-Kundu-Lakshmanan (Ozdemir et al. 2021), Lakshmanan-Porsezian-Daniel (LPD) (Akram et al. 2021), Sasa–Satsuma (González-Gaxiola et al. 2021), Hirota-Satsuma (Alquran et al. 2019), Zakharov (Rehman et al. 2023), Schrödinger-Hirota (Ozdemir et al. 2022), Gergjikov-Ivanov (Li et al. 2021), Fokas–Lenells (Triki et al. 2022), Kundu-Eckhaus (Yildirim et al. 2019), complex Ginzburg-Landau (Abbagari et al. 2023), Chen-Lee-Liu (Ozdemir et al. 2021), Kaup–Newell (Esen et al. 2022), the AB-system (Meng and Guo 2022), Kudryashov (Iqbal et al. 2023), Manakov and other equations by utilizing novel techniques (Zhu et al. 2021; Yildirim and Yaşar 2017; Chou et al. 2023).

The Manakov model is an integrable system of two coupled nonlinear Schrödinger equations (NLSEs) whose complete integrability was established by Manakov Chen and Zhang (2015). He generalized the theory of arbitrary polarization of waves that was proposed by Zakharov and Shabat Shabat and Zakharov (1972). In his theory, he discussed the case of a polarization filter by demonstrating a wave with unstable polarization that will split into multiple streams whenever it enters in a nonlinear channel while the radiations in each beam have constant polarization. Manakov obtained the substantial result that a two-dimensional self-focused wave is associated with the problem of one-dimensional self-modulation of the electromagnetic wave of random polarization. In the collision process of these one-dimensional waves, which are considered solitons, their amplitudes and velocities remain unchanged, but their polarization does change. Manakov represented the above phenomena in mathematical form in terms of integrable coupled nonlinear Schrödinger equation of Manakov type (Manakov 1974), as

$$\begin{aligned} \iota {Q_1}_{t} + {\alpha }_{1} {Q_1}_{xx}+{\beta }_{1}( |{Q_1}|^2 + |{Q_2}|^2 ){Q_1} =0, \end{aligned}$$

(1)

$$\begin{aligned} \iota {Q_1}_{t} + {\alpha }_{2} {Q_2}_{xx}+{\beta }_{2}( |{Q_1}|^2 + |{Q_2}|^2 ){Q_2} =0, \end{aligned}$$

(2)

where ${Q_1}$ =${Q_1}(x,t)$, ${Q_2}$ = ${Q_2}(x,t)$ are the complex-valued functions that represent the profile of optical soliton pulses, ${\alpha }_{j}$, ${\beta }_{j}$ are real constants, coefficients of the group velocity dispersion and self-steeping nonlinearity, respectively.

The Manakov system arises in nonlinear optics (Abbagari et al. 2023), Bose–Einstein condensates (Busch and Anglin 2001), biology (Scott 1984), finance (Yan 2011), and hydrography (Dhar and Das 1991) etc. It captures essential features of light propagation in single-mode fibers, such as dispersion, self-phase modulation, and cross-phase modulation, and has been investigated by implementing mathematical techniques, including Hirota (Radhakrishnan and Aravinthan 2007), Darboux (Guan and Li 2019; Mukam et al. 2021), modified simple equation (Yildirim 2019), trial equation (Yildirim 2019), and extended simplest equation (Ahmed et al. 2021). Although, these studies provided the bright soliton, dark soliton, combined dark-bright soliton, kink soliton and rouge wave solutions but Jacobi elliptic function solutions have not been investigated for Manakov model. In this article, the modified auxiliary equation method (MAEM) and the extended trial equation method (ETEM) are utilized for the investigation of soliton structure of Manakov model.

The MAEM is an extension of the standard auxiliary equation method (Houwe et al. 2021) and it has been used to construct exact solutions of NLSE with Kerr law nonlinearity (Mahak and Akram 2020), Lakshamanan-Porsezian–Daniel model (Akram et al. 2022), Biswas–Arshed equation (Akram et al. 2022), Triki–Biswas equation (Akram and Gillani 2021) and many more. The ETEM is an extended form of trial equation method (Biswas et al. 2018 and has been applied to various nonlinear partial differential equations of higher order and fractional order Pandir et al. (2013) in mathematical physics to extract the optical solitons with anti-cubic nonlinearity Ekici et al. (2017). Although, MAEM and ETEM are powerful tools for solving nonlinear partial differential equations (NLPDEs), but they have limitations. The MAEM is primarily suited for specific NLPDEs, and its effectiveness may vary depending on the specific equation being studied. This method involves complex calculations and can lead to errors. Accuracy and control may not always be guaranteed, and the method may lead to multiple possible solutions, while the ETEM has limitations such as reliance on an initial hypothesis, analytical complexity, limited applicability, lack of uniqueness, and less rigorous theoretical framework.

The remaining paper is organized as follows: In Sect. 2, the complete description of the modified auxiliary method and the extended trial equation method is given. Section 3 presents the mathematical analysis of Manakov model. In Sect. 4, both methods are implemented for the nonlinear ordinary differential equation that is obtained using traveling wave transformation. Section 5 contains the graphical depiction, while Section 6 is the conclusion.

2 Description of methods

A coupled nonlinear partial differential equations can be considered, as

$$\begin{aligned} F_1\left( r_1,{r_1}_{x},{r_2}_{x},{r_1}_{t},{r_2}_{t},{r_1}_{xx},{r_2}_{xx},{r_1}_{xt},{r_2}_{xt},... \right) =0, \end{aligned}$$

(3)

$$\begin{aligned} F_2\left( r_2,{r_1}_{x},{r_2}_{x},{r_1}_{t},{r_2}_{t},{r_1}_{xx},{r_2}_{xx},{r_1}_{xt},{r_2}_{xt},... \right) =0. \end{aligned}$$

(4)

Using the traveling wave transformations,

$$\begin{aligned} r_1(x,t)= u_1(\theta ), \end{aligned}$$

(5)

$$\begin{aligned} r_2(x,t)= u_2(\theta ), \end{aligned}$$

(6)

where

$$\begin{aligned} {\theta }= x- p t. \end{aligned}$$

(7)

Substituting Eqs. (5), (6) into Eqs. (3), (4), the following ordinary differential equation (ODE) is deduced

$$\begin{aligned} V_j\left( u_j, u'_j, u''_j, u'''_j,... \right) =0. \end{aligned}$$

(8)

Here, $V_j$ $(j=1,2)$ is a polynomial of $u_j(\theta )$ and its derivatives. The parameter p represents velocity.

2.1 Modified auxiliary equation method

The general solution of Eq. (8) has the form

$$\begin{aligned} u_j(\theta )= g_{0} + \sum _{\ell =1}^N g_{{\ell }} K^{{\ell } f(\theta )} + \sum _{\ell =1}^N h_{{\ell }} K^{-{\ell } f(\theta )}, \end{aligned}$$

(9)

where $g_{0}$, $g_{{\ell }}$, $h_{{\ell }}$ and K are constants to be determined. The unknown constants $g_{{\ell }}$’s, $h_{{\ell }}$’s cannot simultaneously be zero and function $f(\theta )$ satisfies the auxiliary equation

$$\begin{aligned} f'(\theta )= \frac{\zeta + {\lambda } K^{- f(\theta )} + {\delta } K^{f(\theta )}}{\ln (K)}, \end{aligned}$$

(10)

where ${\zeta }$, ${\lambda }$ and ${\delta }$ are unknown parameters and $K >0$, $K \ne 1$. The value of N can be attained by implementing homogeneous balancing principle on Eq. (8). For the cases in which the value of N cannot be a positive integer, the following substitution can be used.

Case 1: When $N= \frac{m}{n}$, where m and n are co-prime, set

$$\begin{aligned} u_j(\theta )= \left( U(\theta )\right) ^{\frac{m}{n}}. \end{aligned}$$

(11)

Case 2: When $N= -d$ is a negative integer, set

$$\begin{aligned} u_j(\theta )= \left( U(\theta ) \right) ^{-d}. \end{aligned}$$

(12)

Substituting either Eq. (11) or Eq. (12) into Eq. (8), the value of N can be obtained by homogeneous balancing principle. Collecting all the coefficients of $K^{{\ell } f(\theta )}$ where $({\ell }= 0, \pm 1, \pm 2,...,\pm N)$ by inserting Eq. (9) along Eq. (10) into Eq. (8) and equating them to zero, an algebraic system of equations is attained. The values of unknown $g_{0}$, $g_{{\ell }}$, $h_{{\ell }}$, ${\zeta }$, ${\lambda }$ and ${\delta }$ are retrieved by solving the algebraic system.

The function $K^{f(\theta )}$ presumes the following values.

If ${\zeta }^2 - 4 {\lambda } {\delta } > 0$ and ${\delta } \ne 0$, then

$$\begin{aligned} K^{f(\theta )}= -\frac{ {\zeta } + \sqrt{{\zeta }^2 - 4 {\lambda }{\delta }}\tanh \left( \frac{1}{2}\sqrt{{\zeta }^2 - 4 {\lambda }{\delta }} ~\theta \right) }{2 {\delta }}, \end{aligned}$$

(13)

or

$$\begin{aligned} K^{f(\theta )}= - \frac{ {\zeta } + \sqrt{{\zeta }^2 - 4 {\lambda }{\delta }}\coth \left( \frac{1}{2}\sqrt{{\zeta }^2 - 4 {\lambda }{\delta }} ~\theta \right) }{2 {\delta }}. \end{aligned}$$

(14)

If ${\zeta }^2 - 4 {\lambda } {\delta } < 0$ and ${\delta } \ne 0$, then

$$\begin{aligned} K^{f(\theta )}= \frac{- {\zeta } + \sqrt{-{\zeta }^2 + 4 {\lambda }{\delta }}\tan \left( \frac{1}{2}\sqrt{-{\zeta }^2 + 4 {\lambda }{\delta }} ~\theta \right) }{2 {\delta }}, \end{aligned}$$

(15)

or

$$\begin{aligned} K^{f(\theta )}= - \frac{ {\zeta } + \sqrt{-{\zeta }^2 + 4 {\lambda }{\delta }}\cot \left( \frac{1}{2}\sqrt{-{\zeta }^2 + 4 {\lambda }{\delta }} ~\theta \right) }{2 {\delta }}. \end{aligned}$$

(16)

If ${\zeta }^2 - 4 {\lambda } {\delta } = 0$ and ${\delta } \ne 0$, then

$$\begin{aligned} K^{f(\theta )}= -\frac{2 + {\zeta } {\theta }}{2 {\delta }{\theta }}. \end{aligned}$$

(17)

The exact solutions of Eqs. (3), (4) can be obtained by putting the values of $g_{0}$, $g_{{\ell }}$, $h_{{\ell }}$, ${\zeta }$, ${\lambda }$, ${\delta }$ and substituting the values of $K^{f(\theta )}$ from Eqs. (13), (17) into Eq. (9) along the transformation Eq. (7).

2.2 Extended trial equation method

The solution of Eq. (8) can be written, as

$$\begin{aligned} u_j ({\theta }) = \sum _{m=0}^R {\tau }_{m} ~{\eta }^{m} ({\theta }), \end{aligned}$$

(18)

where

$$\begin{aligned} ({\eta }')^2 = {\Lambda } ({\eta }) = \frac{{\Omega }({\eta })}{{\gamma } ({\eta })}= \frac{{\mu }_{\sigma } {\eta }^{\sigma } +...+ {\mu }_{1} {\eta } + {\mu }_0}{{\chi }_{\rho } {\eta }^{\rho } +... + {\chi }_{1} {\eta } + {\chi }_{0}}. \end{aligned}$$

(19)

Using Eqs. (18), (19), the terms $(u'_j)^2$ and $u''_j$ are retrieved, as

$$\begin{aligned} (u'_j)^2 = \frac{{\Omega }({\eta })}{{\gamma } ({\eta })} ~\left( \sum _{m=0}^R m ~{\tau }_{m}~ {\eta }^{m-1}\right) ^2, \end{aligned}$$

(20)

and

$$\begin{aligned} u''_j = \frac{{\gamma } ({\eta }) {\Omega }' ({\eta }) - {\Omega } ({\eta }) {\gamma }' ({\eta })}{2 {\gamma }^2 ({\eta })} \left( \sum _{m=0}^R m~ {\tau }_{m} {\eta }^{m-1} \right) + \frac{{\Omega }({\eta })}{{\gamma } ({\eta })} \left( \sum _{m=0}^R m (m-1) {\tau }_{m}~ {\eta }^{m-2} \right) , \end{aligned}$$

(21)

where ${\Omega }({\eta })$ and ${\gamma } ({\eta })$ are polynomials of ${\eta }$. Inserting Eqs. (20), (21) into Eq. (8), a polynomial equation $\Theta (\eta )$ in ${\eta }$ is extracted, as

$$\begin{aligned} \Theta (\eta )= {\varrho }_{\epsilon } {\eta }^{\epsilon } +...+ {\varrho }_1 {\eta }+ {\varrho }_0=0. \end{aligned}$$

(22)

The suitable values are selected for the relation of $\sigma$, $\rho$ and R by implementing homogeneous balancing principle. Equating all the coefficients of $\Theta (\eta )$ to zero, gives an algebraic set of equations containing free parameters, as

$$\begin{aligned} {\varrho }_i =0, ~ i= 0,1,...,s. \end{aligned}$$

(23)

Solving this algebraic system of equation, the values of ${\mu }_0,...,{\mu }_{\sigma }$, ${\chi }_0,..., {\chi }_{\rho }$ and ${\tau }_{0j},...,{\tau }_{Rj}$ are attained.

Equation (19) can be exhibited in integral form, as

$$\begin{aligned} \pm ({\theta } -{\theta }_0) = \int \frac{1}{\sqrt{{\Lambda }({\eta })}}~ d{\eta }= \int \frac{\sqrt{{\gamma } ({\eta })}}{\sqrt{{\Omega }({\eta })}}~ d{\eta }. \end{aligned}$$

(24)

To classify the roots of ${\Omega }({\eta })$ in Eq. (24), a complete discrimination system for polynomials is used and exact traveling wave solutions of Eqs. (3), (4) are obtained.

3 Mathematical analysis

To obtain the nonlinear ODE form of Eqs. (1) and (2), a complex wave transformation is defined as follows:

$$\begin{aligned} {Q_1}(x,t)= {u}_{1}({\theta }) e^{{\iota }{\phi }_1 (x,t)}, \end{aligned}$$

(25)

$$\begin{aligned} {Q_2}(x,t)= {u}_{2}({\theta })e^{{\iota }{\phi }_2 (x,t)}, \end{aligned}$$

(26)

with

$$\begin{aligned} {\theta }= x- p t, \end{aligned}$$

(27)

$$\begin{aligned} {\phi }_j (x,t)= - {k}_{j} x + {\upsilon }_{j} t + {\xi }_{j}, \end{aligned}$$

(28)

where ${\phi }_j$, ${u}_{j}$, ${k}_{j}$, ${\upsilon }_{j}$, p, ${\xi }_{j}$, $(j=1,2)$ are real valued and represent phase component, amplitude element, frequency factor, wave number, velocity factor and phase constant, respectively.

Putting Eqs. (25), (26) in Eqs.(1), (2) with $j=1,2$ and $\hat{j}$ = $3 - j$, the imaginary component is retrieved as follow:

$$\begin{aligned} p = -2{\alpha }_{j} {k}_{j}, \end{aligned}$$

(29)

while the real part can be derived, as

$$\begin{aligned} {\alpha }_{j} {u}_{j}^{\prime \prime } - ({\alpha }_{j} {k}_{j}^{2} + {\upsilon }_{j} ){u}_{j} + {\beta }_{j} {u}_{j}^{3} + {\beta }_{j} {u}_{j} {u}_{\hat{j}}^{2} =0. \end{aligned}$$

(30)

For ${u}_{j} = {u}_{\hat{j}}$, Eq. (30) is yielded, as

$$\begin{aligned} {\alpha }_{j} {u}_{j}^{\prime \prime } - ({\alpha }_{j} {k}_{j}^{2} + {\upsilon }_{j} ){u}_{j} + 2 {\beta }_{j} {u}_{j}^{3} =0. \end{aligned}$$

(31)

4 Solitary wave solutions of Manakov model

4.1 Application of MAEM

In this segment, the modified auxiliary equation method is executing on Manakov model. Implementing the homogeneous balancing principle on the highest order linear term ${u}_{j}^{\prime \prime }$ and the nonlinear term of highest order ${u}_{j}^{3}$ in Eq. (31), $N=1$ is obtained and Eq. (9) gives

$$\begin{aligned} u_j(\theta )= g_{0} + g_{1} K^{f(\theta )} + h_{1} K^{-f(\theta )}. \end{aligned}$$

(32)

The following algebraic set of equations is obtained by inserting Eq. (32) along the auxiliary Eq. (10) into Eq. (31) and equating all the coefficients of $K^{{\ell } f(\theta )}$ to zero.

$$\begin{gathered} 2\alpha _{j} \delta ^{2} g_{1} + 2\beta _{j} g_{1}^{3} = 0, \hfill \\ 3\alpha _{j} \zeta \delta g_{1} + 6\beta _{j} g_{0} g_{1}^{2} = 0, \hfill \\ - \upsilon _{j} g_{1} - k_{j}^{2} \alpha _{j} g_{1} + \alpha _{j} \zeta ^{2} g_{1} + 2\alpha _{j} \lambda \delta g_{1} + 6\beta _{j} g_{0}^{2} g_{1} + 6\beta _{j} g_{1}^{2} h_{1} = 0, \hfill \\ - \upsilon _{j} h_{1} - k_{j}^{2} \alpha _{j} h_{1} + \alpha _{j} \zeta ^{2} h_{1} + 2\alpha _{j} \lambda \delta h_{1} + 6\beta _{j} g_{0}^{2} h_{1} + 6\beta _{j} g_{1} h_{1}^{2} = 0, \hfill \\ - \upsilon _{j} g_{0} - k_{j}^{2} \alpha _{j} g_{0} + 2\beta _{j} g_{0}^{3} + \alpha _{j} \zeta \lambda g_{1} + \alpha _{j} \zeta \delta h_{1} + 12\beta _{j} g_{0} g_{1} h_{1} = 0, \hfill \\ 3\alpha _{j} \zeta \lambda h_{1} + 6\beta _{j} g_{0} h_{1}^{2} = 0, \hfill \\ 2\alpha _{j} \lambda ^{2} h_{1} + 2\beta _{j} h_{1}^{3} = 0. \hfill \\ \end{gathered}$$

Solving this system of equations, the following solutions are attained:

Case 1.  $g_{0}= - \frac{{\iota } \sqrt{{\alpha }_j}~{\zeta }}{2 \sqrt{{\beta }_j}}$,   $g_{1} = - \frac{{\iota } \sqrt{{\alpha }_j}~{\delta }}{\sqrt{{\beta }_j}}$,  $h_{1} =0$,  $k_j = \pm \frac{\sqrt{-2 {\upsilon }_j - {\alpha }_j {\zeta }^2 + 4 {\alpha }_j {\lambda } {\delta }}}{\sqrt{2 {\alpha }_j}}$.

Case 2.  $g_{0}= - \frac{{\iota } \sqrt{{\alpha }_j}~{\zeta }}{2 \sqrt{{\beta }_j}}$,   $g_{1} = 0$,  $h_{1} = - \frac{{\iota } \sqrt{{\alpha }_j}~{\lambda }}{ \sqrt{{\beta }_j}}$,  $k_j = \pm \frac{\sqrt{-2 {\upsilon }_j - {\alpha }_j {\zeta }^2 + 4 {\alpha }_j {\lambda } {\delta }}}{\sqrt{2 {\alpha }_j}}$.

Substituting the values of parameters given in Case 1 into Eq. (32), the solitary wave solutions of Eqs. (1), (2) are obtained as follows:

For ${\zeta }^2 - 4 {\lambda } {\delta } > 0$ and ${\delta } \ne 0$,

$$\begin{aligned} Q_{1_1} (x,t)= \frac{ \sqrt{-{ \alpha }_1} \sqrt{{\zeta }^2 - 4 {\lambda } {\delta }}\tanh \left[ \frac{1}{2} \sqrt{{\zeta }^2 - 4 {\lambda } {\delta }}(x + 2 {\alpha }_1 k_1 t) \right] }{2 \sqrt{{\beta }_1}} \times e^{{\iota }\left( -k_1 x + {\upsilon }_1 t + {\xi }_1\right) }, \end{aligned}$$

(33)

$$\begin{aligned} Q_{2_1} (x,t)= \frac{ \sqrt{-{\alpha }_2} \sqrt{{\zeta }^2 - 4 {\lambda } {\delta }}\tanh \left[ \frac{1}{2} \sqrt{{\zeta }^2 - 4 {\lambda } {\delta }}(x + 2 {\alpha }_2 k_2 t) \right] }{2 \sqrt{{\beta }_2}} \times e^{{\iota }\left( -k_2 x + {\upsilon }_2 t + {\xi }_2\right) }, \end{aligned}$$

(34)

or

$$\begin{aligned} Q_{1_2} (x,t)=\frac{ \sqrt{-{\alpha }_1} \sqrt{{\zeta }^2 - 4 {\lambda } {\delta }}\coth \left[ \frac{1}{2} \sqrt{{\zeta }^2 - 4 {\lambda } {\delta }} (x + 2 {\alpha }_1 k_1 t) \right] }{2 \sqrt{{\beta }_1}} \times e^{{\iota }\left( -k_1 x + {\upsilon }_1 t + {\xi }_1\right) }, \end{aligned}$$

(35)

$$\begin{aligned} Q_{2_2} (x,t)=\frac{ \sqrt{-{\alpha }_2} \sqrt{{\zeta }^2 - 4 {\lambda } {\delta }}\coth \left[ \frac{1}{2} \sqrt{{\zeta }^2 - 4 {\lambda } {\delta }} (x + 2 {\alpha }_2 k_2 t) \right] }{2 \sqrt{{\beta }_2}} \times e^{{\iota }\left( -k_2 x + {\upsilon }_2 t + {\xi }_2\right) }. \end{aligned}$$

(36)

For ${\zeta }^2 - 4 {\lambda } {\delta } < 0$ and ${\delta } \ne 0$,

$$\begin{aligned} Q_{1_3} (x,t)= - \frac{ \sqrt{-{\alpha }_1} \sqrt{-{\zeta }^2 + 4 {\lambda } {\delta }}\tan \left[ \frac{1}{2} \sqrt{-{\zeta }^2 + 4 {\lambda } {\delta }} (x + 2 {\alpha }_1 k_1 t) \right] }{2 \sqrt{{\beta }_1}} \times e^{{\iota }\left( - k_1 x + {\upsilon }_1 t + {\xi }_1\right) }, \end{aligned}$$

(37)

$$\begin{aligned} Q_{2_3} (x,t)= - \frac{ \sqrt{-{\alpha }_2} \sqrt{-{\zeta }^2 + 4 {\lambda } {\delta }}\tan \left[ \frac{1}{2} \sqrt{-{\zeta }^2 + 4 {\lambda } {\delta }} (x + 2 {\alpha }_2 k_2 t) \right] }{2 \sqrt{{\beta }_2}} \times e^{{\iota }\left( - k_2 x + {\upsilon }_2 t + {\xi }_2\right) }, \end{aligned}$$

(38)

or

$$\begin{aligned} Q_{1_4} (x,t)=\frac{ \sqrt{-{\alpha }_1} \sqrt{-{\zeta }^2 + 4 {\lambda } {\delta }}\cot \left[ \frac{1}{2} \sqrt{-{\zeta }^2 + 4 {\lambda } {\delta }} (x + 2 {\alpha }_1 k_1 t) \right] }{2 \sqrt{{\beta }_1}} \times e^{{\iota }\left( -k_1 x + {\upsilon }_1 t + {\xi }_1\right) }, \end{aligned}$$

(39)

$$\begin{aligned} Q_{2_4} (x,t)=\frac{ \sqrt{-{\alpha }_2} \sqrt{-{\zeta }^2 + 4 {\lambda } {\delta }}\cot \left[ \frac{1}{2} \sqrt{-{\zeta }^2 + 4 {\lambda } {\delta }} (x + 2 {\alpha }_2 k_2 t) \right] }{2 \sqrt{{\beta }_2}} \times e^{{\iota }\left( -k_2 x + {\upsilon }_2 t + {\xi }_2\right) }, \end{aligned}$$

(40)

where $k_j = \pm \frac{\sqrt{-2 {\upsilon }_j - {\alpha }_j {\zeta }^2 + 4 {\alpha }_j {\lambda } {\delta }}}{\sqrt{2 {\alpha }_j}}$ for $j=1,2$.

Substituting the values of parameters given in Case 2 into Eq. (32), the solitary wave solutions of Eqs. (1), (2) are obtained as follows:

For ${\zeta }^2 - 4 {\lambda } {\delta } > 0$ and ${\delta } \ne 0$,

$$\begin{aligned} Q_{1_5} (x,t)= - \frac{\sqrt{-{\alpha }_1}}{2 \sqrt{{\beta }_1}} \frac{{\zeta }^2 - 4 {\lambda }{\delta }+ {\zeta }\sqrt{{\zeta }^2 - 4 {\lambda }{\delta }}\tanh \left[ \frac{1}{2} \sqrt{{\zeta }^2 - 4 {\lambda }{\delta }}(x + 2 {\alpha }_1 k_1 t) \right] }{{\zeta } +\sqrt{{\zeta }^2 - 4 {\lambda }{\delta }}\tanh \left[ \frac{1}{2} \sqrt{{\zeta }^2 - 4 {\lambda }{\delta }} (x + 2 {\alpha }_1 k_1 t)\right] } \times e^{{\iota }\left( -k_1 x + {\upsilon }_1 t + {\xi }_1\right) }, \end{aligned}$$

(41)

$$\begin{aligned} Q_{2_5} (x,t)=- \frac{\sqrt{-{\alpha }_2}}{2 \sqrt{{\beta }_2}} \frac{{\zeta }^2 - 4 {\lambda }{\delta }+ {\zeta }\sqrt{{\zeta }^2 - 4 {\lambda }{\delta }}\tanh \left[ \frac{1}{2} \sqrt{{\zeta }^2 - 4 {\lambda }{\delta }}(x + 2 {\alpha }_2 k_2 t) \right] }{{\zeta } + \sqrt{{\zeta }^2 - 4 {\lambda }{\delta }}\tanh \left[ \frac{1}{2} \sqrt{{\zeta }^2 - 4 {\lambda }{\delta }} (x + 2 {\alpha }_2 k_2 t)\right] } \times e^{{\iota }\left( -k_2 x + {\upsilon }_2 t + {\xi }_2\right) }, \end{aligned}$$

(42)

or

$$\begin{aligned} Q_{1_6} (x,t)= - \frac{\sqrt{-{\alpha }_1}}{2 \sqrt{{\beta }_1}} \frac{{\zeta }^2 - 4 {\lambda }{\delta }+ {\zeta }\sqrt{{\zeta }^2 - 4 {\lambda }{\delta }}\coth \left[ \frac{1}{2} \sqrt{{\zeta }^2 - 4 {\lambda }{\delta }}(x + 2 {\alpha }_1 k_1 t) \right] }{{\zeta } + \sqrt{{\zeta }^2 - 4 {\lambda }{\delta }}\coth \left[ \frac{1}{2} \sqrt{{\zeta }^2 - 4 {\lambda }{\delta }} (x + 2 {\alpha }_1 k_1 t)\right] } \times e^{{\iota }\left( -k_1 x + {\upsilon }_1 t + {\xi }_1\right) }, \end{aligned}$$

(43)

$$\begin{aligned} Q_{2_6} (x,t)= - \frac{\sqrt{-{\alpha }_2}}{2 \sqrt{{\beta }_2}} \frac{{\zeta }^2 - 4 {\lambda }{\delta }+ {\zeta }\sqrt{{\zeta }^2 - 4 {\lambda }{\delta }}\coth \left[ \frac{1}{2} \sqrt{{\zeta }^2 - 4 {\lambda }{\delta }}(x + 2 {\alpha }_2 k_2 t) \right] }{{\zeta } + \sqrt{{\zeta }^2 - 4 {\lambda }{\delta }}\coth \left[ \frac{1}{2} \sqrt{{\zeta }^2 - 4 {\lambda }{\delta }} (x + 2 {\alpha }_2 k_2 t)\right] } \times e^{{\iota }\left( -k_2 x + {\upsilon }_2 t + {\xi }_2\right) }. \end{aligned}$$

(44)

For ${\zeta }^2 - 4 {\lambda } {\delta } < 0$ and ${\delta } \ne 0$,

$$\begin{aligned} Q_{1_7} (x,t)= \frac{\sqrt{-{\alpha }_1}}{2 \sqrt{{\beta }_1}} \frac{-{\zeta }^2 + 4 {\lambda }{\delta }+ {\zeta }\sqrt{-{\zeta }^2 + 4 {\lambda }{\delta }}\tan \left[ \frac{1}{2} \sqrt{-{\zeta }^2 + 4 {\lambda }{\delta }}(x + 2 {\alpha }_1 k_1 t) \right] }{{\zeta } - \sqrt{-{\zeta }^2 + 4 {\lambda }{\delta }}\tan \left[ \frac{1}{2} \sqrt{-{\zeta }^2 + 4 {\lambda }{\delta }} (x + 2 {\alpha }_1 k_1 t) \right] } \times e^{{\iota }\left( -k_1 x + {\upsilon }_1 t + {\xi }_1\right) }, \end{aligned}$$

(45)

$$\begin{aligned} Q_{2_7} (x,t)= \frac{\sqrt{-{\alpha }_2}}{2 \sqrt{{\beta }_2}} \frac{-{\zeta }^2 + 4 {\lambda }{\delta }+ {\zeta }\sqrt{-{\zeta }^2 + 4 {\lambda }{\delta }}\tan \left[ \frac{1}{2} \sqrt{-{\zeta }^2 + 4 {\lambda }{\delta }}(x + 2 {\alpha }_2 k_2 t) \right] }{{\zeta } - \sqrt{-{\zeta }^2 + 4 {\lambda }{\delta }}\tan \left[ \frac{1}{2} \sqrt{-{\zeta }^2 + 4 {\lambda }{\delta }} (x + 2 {\alpha }_2 k_2 t) \right] } \times e^{{\iota }\left( -k_2 x + {\upsilon }_2 t + {\xi }_2\right) }, \end{aligned}$$

(46)

or

$$\begin{aligned} Q_{1_8} (x,t)= - \frac{\sqrt{-{\alpha }_1}}{2 \sqrt{{\beta }_1}} \frac{{\zeta }^2 - 4 {\lambda }{\delta }+ {\zeta }\sqrt{{\zeta }^2 - 4 {\lambda }{\delta }}\cot \left[ \frac{1}{2} \sqrt{-{\zeta }^2 + 4 {\lambda }{\delta }}(x + 2 {\alpha }_1 k_1 t) \right] }{{\zeta } + \sqrt{-{\zeta }^2 + 4 {\lambda }{\delta }}\cot \left[ \frac{1}{2} \sqrt{-{\zeta }^2 + 4 {\lambda }{\delta }} (x + 2 {\alpha }_1 k_1 t) \right] } \times e^{{\iota }\left( -k_1 x + {\upsilon }_1 t + {\xi }_1\right) }, \end{aligned}$$

(47)

$$\begin{aligned} Q_{2_8} (x,t)= - \frac{\sqrt{-{\alpha }_2}}{2 \sqrt{{\beta }_2}} \frac{{\zeta }^2 - 4 {\lambda }{\delta }+ {\zeta }\sqrt{{\zeta }^2 - 4 {\lambda }{\delta }}\cot \left[ \frac{1}{2} \sqrt{-{\zeta }^2 + 4 {\lambda }{\delta }}(x + 2 {\alpha }_2 k_2 t) \right] }{{\zeta } + \sqrt{-{\zeta }^2 + 4 {\lambda }{\delta }}\cot \left[ \frac{1}{2} \sqrt{-{\zeta }^2 + 4 {\lambda }{\delta }} (x + 2 {\alpha }_2 k_2 t) \right] } \times e^{{\iota }\left( -k_2 x + {\upsilon }_2 t + {\xi }_2\right) }, \end{aligned}$$

(48)

where $k_j = \pm \frac{\sqrt{-2 {\upsilon }_j - {\alpha }_j {\zeta }^2 + 4 {\alpha }_j {\lambda } {\delta }}}{\sqrt{2 {\alpha }_j}}$ for $j=1,2$.

4.2 Application of ETEM

In this segment, Eq. (31) is analyzed by extended trial equation method. Implementation of the balancing principle on the highest order linear term ${u}_{j}^{\prime \prime }$ and the nonlinear term of highest order ${u}_{j}^{3}$ in Eq. (31), gives

$$\begin{aligned} {\sigma } = {\rho } +2 R +2. \end{aligned}$$

(49)

If ${\rho } = 0$, $R=1$ then ${\sigma }= 4$ and Eq. (18) becomes

$$\begin{aligned} u_j ({\theta }) = {\tau }_{0} + {\tau }_{1} {\eta }, \end{aligned}$$

(50)

where ${\tau }_{0}$ and ${\tau }_{1}$ are unknown constants such that ${\tau }_{1} {\ne }~ 0$ and ${\eta }$ satisfy Eq. (19). Inserting Eq. (50) into Eq. (31), a polynomial in ${\eta } ({\theta })$ is extracted. Equating the coefficients of same powers of ${\eta } ({\theta })$ to zero, an algebraic set of equations is obtained.

$$\begin{aligned} {\alpha }_j {\mu }_1 {\tau }_{1} -2 {\upsilon }_j {\tau }_{0} {\chi }_0 - 2 {k}_{j}^2 {\alpha }_j {\tau }_{0} {\chi }_0 + 4 {\beta }_j {\tau }_{0}^3 {\chi }_0 = 0, \\ 2 {\alpha }_j {\mu }_2 {\tau }_{1} -2 {\upsilon }_j {\tau }_{1} {\chi }_0 - 2{k}_{j}^2 {\alpha }_j {\tau }_{1} {\chi }_0 + 12 {\beta }_j {\tau }_{0}^2 {\tau }_{1} {\chi }_0 = 0,\\ 3 {\alpha }_j {\mu }_3 {\tau }_{1} + 12 {\beta }_j {\tau }_{0} {\tau }_{1}^2 {\chi }_0 = 0, \\ 4 {\alpha }_j {\mu }_4 {\tau }_{1} + 4 {\beta }_j {\tau }_{1}^3 {\chi }_0 =0. \end{aligned}$$

Solving this system, the following values are deduced:

${\mu }_1 = \frac{2 ~{\tau }_{0} ( {\upsilon }_j + {k}_{j}^2 ~{\alpha }_j - ~2 {\beta }_j ~{\tau }_{0}^2 )~ {\chi }_0}{{\alpha }_j ~{\tau }_{1}}$,   ${\mu }_2 = \frac{({\upsilon }_j + {k}_{j}^2 ~ {\alpha }_j - 6 {\beta }_j ~{\tau }_{0}^2) ~{\chi }_0}{{\alpha }_j}$,   ${\mu }_3 =- \frac{ 4 ~{\beta }_j~ {\tau }_{0} ~{\tau }_{1}~ {\chi }_0}{{\alpha }_j}$,

${\mu }_4 = -\frac{{\beta }_j ~ {\tau }_{1}^2 ~ {\chi }_0}{{\alpha }_j}$,   ${\mu }_0 = {\mu }_0$,   ${\chi }_0 = {\chi }_0$,   ${\tau }_{0} = {\tau }_{0}$,   ${\tau }_{1} = {\tau }_{1}$.

Inserting these values in Eqs. (19) and (24), leads to

$$\begin{aligned} \pm ({\theta } -{\theta }_0) = H \int \frac{1}{\sqrt{{\Pi }({\eta })}}~ d{\eta }, \end{aligned}$$

(51)

where

$$\begin{aligned} {\Pi }({\eta }) = {\eta }^4 + \frac{{\mu }_3}{{\mu }_4} ~{\eta }^3 + \frac{{\mu }_2}{{\mu }_4}~ {\eta }^2 + \frac{{\mu }_1}{{\mu }_4} ~{\eta } + \frac{{\mu }_0}{{\mu }_4}, ~ H = \sqrt{\frac{{\chi }_0}{{\mu }_4}}. \end{aligned}$$

(52)

Using the above results, traveling wave solutions to Manakov model are produced as follows:

If ${\Pi } ({\eta }) = ({\eta }- {\omega }_1)^4$,

$$\begin{aligned} {Q_{1_9}} (x,t) = \left\{ {\tau }_{0} + {\tau }_{1} {\omega }_1 \pm \frac{{\tau }_{1} H}{x + 2 {\alpha }_1 k_1 t - {\theta }_0} \right\} \times e^{{\iota }(- k_1 x + {\upsilon }_1 t + {\xi }_1)}, \end{aligned}$$

(53)

$$\begin{aligned} {Q_{2_9}} (x,t) = \left\{ {\tau }_{0} + {\tau }_{1} {\omega }_1 \pm \frac{{\tau }_{1} H}{x + 2 {\alpha }_2 k_2 t - {\theta }_0} \right\} \times e^{{\iota }(- k_2 x + {\upsilon }_2 t + {\xi }_2)}. \end{aligned}$$

(54)

If ${\Pi } ({\eta }) = ({\eta }- {\omega }_1)^3 ({\eta }- {\omega }_2)$ and ${\omega }_2 > {\omega }_1$,

$$\begin{aligned} {Q_{1_{10}}} (x,t)= \left\{ {\tau }_{0} + {\tau }_{1} {\omega }_1 + \frac{4 H^2 ({\omega }_2 - {\omega }_1) {\tau }_{1}}{4 H^2 - \left[ ({\omega }_1 - {\omega }_2)( x+ 2 {\alpha }_1 k_1 t - {\theta }_0) \right] ^2 } \right\} \times e^{{\iota }(- k_1 x + {\upsilon }_1 t + {\xi }_1)}, \end{aligned}$$

(55)

$$\begin{aligned} {Q_{2_{10}}} (x,t) = \left\{ {\tau }_{0} + {\tau }_{1} {\omega }_1 + \frac{4 H^2 ({\omega }_2 - {\omega }_1) {\tau }_{1}}{4 H^2 - \left[ ({\omega }_1 - {\omega }_2)( x+ 2 {\alpha }_2 k_2 t - {\theta }_0) \right] ^2 } \right\} \times e^{{\iota }(- k_2 x + {\upsilon }_2 t + {\xi }_2)}. \end{aligned}$$

(56)

When ${\Pi } ({\eta }) = ({\eta }- {\omega }_1)^2 ~({\eta }- {\omega }_2)^2$,

$$\begin{aligned} {Q_{1_{11}}} (x,t) = \left\{ {\tau }_{0} + {\tau }_{1} {\omega }_2 + \frac{({\omega }_2 - {\omega }_1) {\tau }_{1}}{\exp \left[ \frac{{\omega }_1 - {\omega }_2}{H} (x + 2 {\alpha }_1 k_1 t - {\theta }_0) \right] -1} \right\} \times e^{{\iota }(-k_1 x + {\upsilon }_1 t + {\xi }_1)}, \end{aligned}$$

(57)

$$\begin{aligned} {Q_{2_{11}}} (x,t) = \left\{ {\tau }_{0} + {\tau }_{1} {\omega }_2 + \frac{({\omega }_2 - {\omega }_1) {\tau }_{1}}{\exp \left[ \frac{{\omega }_1 - {\omega }_2}{H} (x + 2 {\alpha }_2 k_2 t - {\theta }_0) \right] -1} \right\} \times e^{{\iota }(-k_2 x + {\upsilon }_2 t + {\xi }_2)}, \end{aligned}$$

(58)

and

$$\begin{aligned} {Q_{1_{12}}} (x,t) = \left\{ {\tau }_{0} + {\tau }_{1} {\omega }_1 + \frac{({\omega }_1 - {\omega }_2) {\tau }_{1}}{\exp \left[ \frac{{\omega }_1 - {\omega }_2}{H} (x + 2 {\alpha }_1 k_1 t - {\theta }_0) \right] -1} \right\} \times e^{{\iota }(-k_1 x + {\upsilon }_1 t + {\xi }_1)}, \end{aligned}$$

(59)

$$\begin{aligned} {Q_{2_{12}}} (x,t) = \left\{ {\tau }_{0} + {\tau }_{1} {\omega }_1 + \frac{({\omega }_1 - {\omega }_2) {\tau }_{1}}{\exp \left[ \frac{{\omega }_1 - {\omega }_2}{H} (x + 2 {\alpha }_2 k_2 t - {\theta }_0) \right] -1} \right\} \times e^{{\iota }(-k_2 x + {\upsilon }_2 t + {\xi }_2)}. \end{aligned}$$

(60)

When ${\Pi } ({\eta }) = ({\eta }- {\omega }_1)^2 ~({\eta }- {\omega }_2) ~ ({\eta }- {\omega }_3)$ and ${\omega }_1> {\omega }_2 > {\omega }_3$,

$$\begin{aligned} {Q_{1_{13}}} (x,t) = \left\{ {\tau }_{0} + {\tau }_{1} {\omega }_3 + \frac{({\omega }_2 - {\omega }_3) {\tau }_{1}}{1+ \frac{{\omega }_1 - {\omega }_2}{{\omega }_1 - {\omega }_3} \tanh ^2 \left[ \frac{\sqrt{({\omega }_1 - {\omega }_2) ({\omega }_1 - {\omega }_3)}(x + 2 {\alpha }_1 k_1 t - {\theta }_0)}{2 H} \right] }\right\} \times e^{{\iota }(-k_1 x + {\upsilon }_1 t + {\xi }_1)}, \end{aligned}$$

(61)

$$\begin{aligned} {Q_{2_{13}}} (x,t) = \left\{ {\tau }_{0} + {\tau }_{1} {\omega }_3 + \frac{({\omega }_2 - {\omega }_3) {\tau }_{1}}{1+ \frac{{\omega }_1 - {\omega }_2}{{\omega }_1 - {\omega }_3} \tanh ^2 \left[ \frac{\sqrt{({\omega }_1 - {\omega }_2) ({\omega }_1 - {\omega }_3)}(x + 2 {\alpha }_2 k_2 t - {\theta }_0)}{2 H} \right] }\right\} \times e^{{\iota }(-k_2 x + {\upsilon }_2 t + {\xi }_2)}. \end{aligned}$$

(62)

When ${\Pi } ({\eta }) = ({\eta }- {\omega }_1) ~({\eta }- {\omega }_2) ~ ({\eta }- {\omega }_3)~ ({\eta }- {\omega }_4)$ and ${\omega }_1> {\omega }_2> {\omega }_3 > {\omega }_4$,

$$\begin{aligned} {Q_{1_{14}}} (x,t) = \left\{ {\tau }_{0} + {\tau }_{1} {\omega }_3 + \frac{({\omega }_3 - {\omega }_1)({\omega }_4 - {\omega }_3) {\tau }_{1}}{({\omega }_1 - {\omega }_4) \text {sn}^2 \left[ \pm \frac{1}{2 H} \sqrt{({\omega }_1 - {\omega }_3)({\omega }_2 - {\omega }_4)}(x + 2 {\alpha }_1 k_1 t - {\theta }_0), \ell \right] - {\omega }_1 + {\omega }_3}\right\} \end{aligned}$$

$$\begin{aligned} \times e^{{\iota }(- k_1 x + {\upsilon }_1 t + {\xi }_1)}, \end{aligned}$$

(63)

$$\begin{aligned} {Q_{2_{14}}} (x,t) = \left\{ {\tau }_{0} + {\tau }_{1} {\omega }_3 + \frac{({\omega }_3 - {\omega }_1)({\omega }_4 - {\omega }_3) {\tau }_{1}}{({\omega }_1 - {\omega }_4) \text {sn}^2 \left[ \pm \frac{1}{2 H} \sqrt{({\omega }_1 - {\omega }_3)({\omega }_2 - {\omega }_4)}(x + 2 {\alpha }_2 k_2 t - {\theta }_0), \ell \right] - {\omega }_1 + {\omega }_3}\right\} \end{aligned}$$

$$\begin{aligned} \times e^{{\iota }(- k_2 x + {\upsilon }_2 t + {\xi }_2)}, \end{aligned}$$

(64)

where

$$\begin{aligned} {\ell }^2 = \frac{({\omega }_1 - {\omega }_4)({\omega }_2 - {\omega }_3 )}{({\omega }_2 - {\omega }_4)({\omega }_1 - {\omega }_3)}. \end{aligned}$$

(65)

Note that ${\omega }_i$ for $i = 1,...,4$ are the zeros of

$$\begin{aligned} {\Pi } ({\eta }) = 0. \end{aligned}$$

(66)

For ${\tau }_{0} = -{\tau }_{1} {\omega }_1$ and ${\theta }_0 = 0$, the rational function solutions are obtained from the solutions (53)–(56).

$$\begin{aligned} {Q_{1_{15}}} (x,t) = \left\{ \pm \frac{{\tau }_{1} H}{x + 2 {\alpha }_1 k_1 t } \right\} \times e^{{\iota }(- k_1 x + {\upsilon }_1 t + {\xi }_1)}, \end{aligned}$$

(67)

$$\begin{aligned} {Q_{2_{15}}} (x,t) = \left\{ \pm \frac{{\tau }_{1} H}{x + 2 {\alpha }_2 k_2 t} \right\} \times e^{{\iota }(- k_2 x + {\upsilon }_2 t + {\xi }_2)}, \end{aligned}$$

(68)

$$\begin{aligned} {Q_{1_{16}}} (x,t)= \left\{ \frac{4 H^2 ({\omega }_2 - {\omega }_1) {\tau }_{1}}{4 H^2 - \left[ ({\omega }_1 - {\omega }_2)( x+ 2 {\alpha }_1 k_1 t) \right] ^2 } \right\} \times e^{{\iota }(- k_1 x + {\upsilon }_1 t + {\xi }_1)}, \end{aligned}$$

(69)

$$\begin{aligned} {Q_{2_{16}}} (x,t) = \left\{ \frac{4 H^2 ({\omega }_2 - {\omega }_1) {\tau }_{1}}{4 H^2 - \left[ ({\omega }_1 - {\omega }_2)( x+ 2 {\alpha }_2 k_2 t ) \right] ^2 } \right\} \times e^{{\iota }(- k_2 x + {\upsilon }_2 t + {\xi }_2)}. \end{aligned}$$

(70)

Moreover, Eqs. (57)–(58) give hyperbolic function solution

$$\begin{aligned} {Q_{1_{17}}} (x,t) = \frac{({\omega }_2 - {\omega }_1) {\tau }_{1}}{2} \left\{ 1 + \coth \left[ \frac{({\omega }_1 - {\omega }_2)}{2 H} (x + 2 {\alpha }_1 k_1 t)\right] \right\} \times e^{{\iota }(- k_1 x + {\upsilon }_1 t + {\xi }_1)}, \end{aligned}$$

(71)

$$\begin{aligned} {Q_{2_{17}}} (x,t) = \frac{({\omega }_2 - {\omega }_1) {\tau }_{1}}{2} \left\{ 1 + \coth \left[ \frac{({\omega }_1 - {\omega }_2)}{2 H} (x + 2 {\alpha }_2 k_2 t)\right] \right\} \times e^{{\iota }(- k_2 x + {\upsilon }_2 t + {\xi }_2)}. \end{aligned}$$

(72)

For ${\tau }_{0} = - {\tau }_{1} {\omega }_2$ and ${\theta }_0 =0$, the hyperbolic function solution is obtained from Eqs. (59), (60).

$$\begin{aligned} {Q_{1_{18}}} (x,t) = \frac{({\omega }_1 - {\omega }_2) {\tau }_{1}}{2} \left\{ 1 + \coth \left[ \frac{({\omega }_1 - {\omega }_2)}{2 H} (x + 2 {\alpha }_1 k_1 t)\right] \right\} \times e^{{\iota }(- k_1 x + {\upsilon }_1 t + {\xi }_1)}, \end{aligned}$$

(73)

$$\begin{aligned} {Q_{2_{18}}} (x,t) = \frac{({\omega }_1 - {\omega }_2) {\tau }_{1}}{2} \left\{ 1 + \coth \left[ \frac{({\omega }_1 - {\omega }_2)}{2 H} (x + 2 {\alpha }_2 k_2 t)\right] \right\} \times e^{{\iota }(- k_2 x + {\upsilon }_2 t + {\xi }_2)}. \end{aligned}$$

(74)

For ${\tau }_{0} = - {\tau }_{1} {\omega }_3$ and ${\theta }_0 =0$, the hyperbolic function solution from (61), (62) is obtained, as

$$\begin{aligned} {Q_{1_{19}}} (x,t) =\left\{ \frac{B}{C + \tanh ^2 \left[ D(x + 2 {\alpha }_1 k_1 t) \right] } \right\} \times e^{{\iota }(- k_1 x + {\upsilon }_1 t + {\xi }_1)}, \end{aligned}$$

(75)

$$\begin{aligned} {Q_{2_{19}}} (x,t) =\left\{ \frac{B}{C + \tanh ^2 \left[ D(x + 2 {\alpha }_2 k_2 t) \right] } \right\} \times e^{{\iota }(- k_2 x + {\upsilon }_2 t + {\xi }_2)}, \end{aligned}$$

(76)

where

$$\begin{aligned} B = \frac{({\omega }_2 - {\omega }_3) ({\omega }_1 - {\omega }_3) {\tau }_{1}}{{\omega }_1 - {\omega }_2}, \\ C = \frac{{\omega }_1 - {\omega }_3}{{\omega }_1 - {\omega }_2}, \\ D = \frac{\sqrt{({\omega }_1 - {\omega }_2)({\omega }_1 - {\omega }_3)}}{2 H}. \end{aligned}$$

Here, B is the amplitude term and D is the inverse width component of soliton.

The existence criteria for all these solitons is ${\tau }_{1} < 0$.

For ${\tau }_{0} = - {\tau }_{1} {\omega }_3$ and ${\theta }_0 =0$, the Jacobi elliptic function solution (63), (64) is reduced to

$$\begin{aligned} {Q_{1_{20}}} (x,t) = \left\{ \frac{E}{F + \text {sn}^2 \left[ G_j (x + 2 {\alpha }_1 k_1 t ), {\ell } ~\right] }\right\} \times e^{{\iota }(- k_1 x + {\upsilon }_1 t + {\xi }_1)}, \end{aligned}$$

(77)

$$\begin{aligned} {Q_{2_{20}}} (x,t) = \left\{ \frac{E}{F + \text {sn}^2 \left[ G_j (x + 2 {\alpha }_2 k_2 t ), {\ell } ~\right] }\right\} \times e^{{\iota }(- k_2 x + {\upsilon }_2 t + {\xi }_2)}, \end{aligned}$$

(78)

where

$$\begin{aligned} E = \frac{({\omega }_3 - {\omega }_1)({\omega }_4 - {\omega }_3) {\tau }_{1}}{{\omega }_1 - {\omega }_4}, \\ F = \frac{{\omega }_3 - {\omega }_1}{{\omega }_1 - {\omega }_4}, \\ G_j = \frac{(-1)^j \sqrt{({\omega }_1 - {\omega }_3)({\omega }_2 - {\omega }_4)}}{2 H}, ~ j = 1,2. \end{aligned}$$

Remark 1

If the modulus term ${\ell } \rightarrow 1$, the hyperbolic function solution is emerged, as

$$\begin{aligned} {Q_{1_{21}}} (x,t) = \left\{ \frac{E}{F + \tanh ^2 \left[ G_j (x + 2 {\alpha }_1 k_1 t) \right] }\right\} \times e^{{\iota }(- k_1 x + {\upsilon }_1 t + {\xi }_1)}, \end{aligned}$$

(79)

$$\begin{aligned} {Q_{2_{21}}} (x,t) = \left\{ \frac{E}{F + \tanh ^2 \left[ G_j (x + 2 {\alpha }_2 k_2 t) \right] }\right\} \times e^{{\iota }(- k_2 x + {\upsilon }_2 t + {\xi }_2)}, \end{aligned}$$

(80)

for ${\omega }_1 = {\omega }_2$.

Remark 2

If the modulus term ${\ell } \rightarrow 0$, the periodic function solution is emerged, as

$$\begin{aligned} {Q_{1_{22}}} (x,t) = \left\{ \frac{E}{F + \sin ^2 \left[ G_j (x + 2 {\alpha }_1 k_1 t) \right] }\right\} \times e^{{\iota }(- k_1 x + {\upsilon }_1 t + {\xi }_1)}, \end{aligned}$$

(81)

$$\begin{aligned} {Q_{2_{22}}} (x,t) = \left\{ \frac{E}{F + \sin ^2 \left[ G_j (x + 2 {\alpha }_2 k_2 t) \right] }\right\} \times e^{{\iota }(- k_2 x + {\upsilon }_2 t + {\xi }_2)}, \end{aligned}$$

(82)

for ${\omega }_2 = {\omega }_3$.

5 Graphical observations

This segment includes graphical representations of some of the solution functions of Manakov model that are obtained using the modified auxiliary equation method and extended trial equation method. The obtained solutions are in terms of hyperbolic, trigonometric, rational and Jacobi elliptic functions. The graphical representations provide dark soliton, bright soliton, bright singular soliton, bright singular two-solitons, multi solitons and periodic solitary waves.

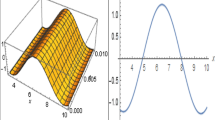
Figure 1 is the graphical representation of the solution $Q_{1_{1}}(x,t)$, $Q_{2_{1}}(x,t)$ for the parametric values taken as ${\alpha }_1 =2,~ {\beta }_1 = 3,~ {\alpha }_2= 3,~ {\beta }_2=2, ~ {\lambda }={\delta }=1,~ {\zeta }=3,~ k_1 =\frac{1}{\sqrt{2}},~ k_2= \sqrt{\frac{7}{10}},~{\upsilon }_1 =-6,~{\upsilon }_2= -8,~ {\xi }_1={\xi }_2=1$. Figure 1a is the illustration of modulus $|Q_{1_{1}}|$ and $|Q_{2_{1}}|$ in 3D, Fig. 1b exhibits $|Q_{1_{1}}|$ and $|Q_{2_{1}}|$ in 2D, and Fig. 1c depicts the density plot of $|Q_{1_{1}}|$ and $|Q_{2_{1}}|$. Furthermore, Fig. 1d–f refer to imaginary value of $Q_{1_{1}}$ and $Q_{2_{1}}$ while Fig. 1g–i belong to real value of $Q_{1_{1}}$ and $Q_{2_{1}}$in 3D, 2D and density plot, respectively.

Fig. 1

Graphs for ${Q_{1_{1}}}(x,t)$ and ${Q_{2_{1}}}(x,t)$ at ${\alpha }_1 =2,~ {\beta }_1 = 3,~ {\alpha }_2= 3,~ {\beta }_2=2, ~ {\lambda }={\delta }=1,~ {\zeta }=3,~ k_1 =\frac{1}{\sqrt{2}},~ k_2= \sqrt{\frac{7}{10}},~{\upsilon }_1 =-6,~{\upsilon }_2= -8,~ {\xi }_1={\xi }_2=1$

Figure  2 is the graphical illustration of the solution $Q_{1_{2}}(x,t)$, $Q_{2_{2}}(x,t)$ for the parametric values taken as ${\alpha }_1 =2,~ {\beta }_1 = 3,~ {\alpha }_2= 3,~ {\beta }_2=2, ~ {\lambda }={\delta }=1,~ {\zeta }=3,~ k_1 =\frac{1}{\sqrt{2}},~ k_2= \sqrt{\frac{7}{10}},~{\upsilon }_1 =-6,~{\upsilon }_2= -8,~ {\xi }_1={\xi }_2=1$. Figure 2a is the representation of modulus $|Q_{1_{2}}|$ and $|Q_{2_{2}}|$ in 3D, Fig. 2b is the depiction of $|Q_{1_{2}}|$ and $|Q_{2_{2}}|$ in 2D, and Fig. 2c is the density plot of $|Q_{1_{2}}|$ and $|Q_{2_{2}}|$. Figure 2d–f correspond to imaginary value of $Q_{1_{2}}$ and $Q({2_{2}})$ and Fig. 2g–i refer to real value of $Q_{1_{2}}$ and $Q_{2_{2}}$ in 3D, 2D and density plot, respectively.

Fig. 2

Graphs for ${Q_{1_{2}}}(x,t)$ and ${Q_{2_{2}}}(x,t)$ at ${\alpha }_1 =2,~ {\beta }_1 = 3,~ {\alpha }_2= 3,~ {\beta }_2=2, ~ {\lambda }={\delta }=1,~ {\zeta }=3,~ k_1 =\frac{1}{\sqrt{2}},~ k_2= \sqrt{\frac{7}{10}},~{\upsilon }_1 =-6,~{\upsilon }_2= -8,~ {\xi }_1={\xi }_2=1$

Figure 3 is the graphical representation of the solution $Q_{1_{3}}(x,t)$, $Q_{2_{3}}(x,t)$ for the parametric values taken as ${\alpha }_1 =2,~ {\beta }_1 = 1,~ {\alpha }_2= 5,~ {\beta }_2=3, ~ {\lambda }=3,~{\delta }=1,~ {\zeta }=2,~ k_1 =-\frac{3}{\sqrt{2}},~ k_2= -\frac{4}{\sqrt{3}},~{\upsilon }_1 =-1,~{\upsilon }_2= -4,~ {\xi }_1={\xi }_2=1$. Figure 3a is the illustration of modulus $|Q_{1_{3}}|$ and $|Q_{2_{3}}|$ in 3D, Fig. 3b exhibits $|Q_{1_{3}}|$ and $|Q_{2_{3}}|$ in 2D, and Fig. 3c depicts the density plot of $|Q_{1_{3}}|$ and $|Q_{2_{3}}|$. Furthermore, Fig. 3d–f refer to imaginary value of $Q_{1_{3}}$ and $Q_{2_{3}}$ and Fig. 3g–i belong to real value of $Q_{1_{3}}$ and $Q_{2_{3}}$ in 3D, 2D and density plot, respectively.

Fig. 3

Graphs for ${Q_{1_{3}}}(x,t)$ and ${Q_{2_{3}}}(x,t)$ at ${\alpha }_1 =2,~ {\beta }_1 = 1,~ {\alpha }_2= 5,~ {\beta }_2=3, ~ {\lambda }=3,~{\delta }=1,~ {\zeta }=2,~ k_1 =-\frac{3}{\sqrt{2}},~ k_2= -\frac{4}{\sqrt{3}},~{\upsilon }_1 =-1,~{\upsilon }_2= -4,~ {\xi }_1={\xi }_2=1$

Figure 4 is the graphical illustration of the solution $Q_{1_{5}}(x,t)$, $Q_{2_{5}}(x,t)$ for the parametric values taken as ${\alpha }_1 =2,~ {\beta }_1 = 3,~ {\alpha }_2= 3,~ {\beta }_2=2, ~ {\lambda }={\delta }=1,~ {\zeta }=3,~ k_1 =\frac{1}{\sqrt{2}},~ k_2= \sqrt{\frac{7}{10}},~{\upsilon }_1 =-6,~{\upsilon }_2= -8,~ {\xi }_1={\xi }_2=1$. Figure 4a representation of modulus $|Q_{1_{5}}|$ and $|Q_{2_{5}}|$ in 3D, Fig. 4b is the depiction of $|Q_{1_{5}}|$ and $|Q_{2_{5}}|$ in 2D, and Fig. 4c is the density plot of $|Q_{1_{5}}|$ and $|Q_{2_{5}}|$. Figure 4d–f correspond to imaginary value of $Q_{1_{5}}$ and $Q_{2_{5}}$ and Fig. 4g–i refer to real value of $Q_{1_{5}}$ and $Q_{2_{5}}$ in 3D, 2D and density plot, respectively.

Fig. 4

Graphs for ${Q_{1_{5}}}(x,t)$ and ${Q_{2_{5}}}(x,t)$ at ${\alpha }_1 =2,~ {\beta }_1 = 3,~ {\alpha }_2= 3,~ {\beta }_2=2, ~ {\lambda }={\delta }=1,~ {\zeta }=3,~ k_1 =\frac{1}{\sqrt{2}},~ k_2= \sqrt{\frac{7}{10}},~{\upsilon }_1 =-6,~{\upsilon }_2= -8,~ {\xi }_1={\xi }_2=1$

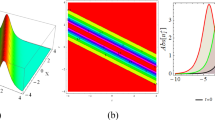
Figure 5 is the graphical illustration of the solution $Q_{1_{17}}(x,t)$, $Q_{2_{17}}(x,t)$ for the parametric values taken as $\omega _1=2, ~\omega _2=1,~,H=1, ~ \tau _1=1,~ {\alpha }_1 =1,~ {\alpha }_2= 2, ~ k_1 =2,~ k_2= 1,~{\upsilon }_1 =1, ~{\upsilon }_2= 3,~ {\xi }_1={\xi }_2=1$. Figure 5a is the representation of modulus $|Q_{1_{17}}|$ and $|Q_{2_{17}}|$ in 3D, Fig. 5b is the depiction of $|Q_{1_{17}}|$ and $|Q_{2_{17}}|$ in 2D, and Fig. 5c is the density plot of $|Q_{1_{17}}|$ and $|Q_{2_{17}}|$. Figure 5d–f correspond to imaginary value of $Q_{1_{17}}$ and $Q({2_{17}})$ and Fig. 5g–i refer to real value of $Q_{1_{17}}$ and $Q_{2_{17}}$ in 3D, 2D and density plot, respectively.

Fig. 5

Graphs for ${Q_{1_{17}}}(x,t)$ and ${Q_{2_{17}}}(x,t)$ at $\omega _1=2, ~\omega _2=1,~,H=1, ~ \tau _1=1,~ {\alpha }_1 =1,~ {\alpha }_2= 2, ~ k_1 =2,~ k_2= 1,~{\upsilon }_1 =1, ~{\upsilon }_2= 3,~ {\xi }_1={\xi }_2=1$

Figure 6 is the graphical representation of the solution $Q_{1_{19}}(x,t)$, $Q_{2_{19}}(x,t)$ for the parametric values taken as $\omega _1=3, ~\omega _2=2,~,H=1.5, ~ \tau _1=1.6,~ {\alpha }_1 =1,~ {\alpha }_2= 2, ~ k_1 =1.3,~ k_2= 1.5,~{\upsilon }_1 =1.2, ~{\upsilon }_2= 1.3,~ {\xi }_1={\xi }_2=1$. Figure 6a is the illustration of modulus $|Q_{1_{19}}|$ and $|Q_{2_{19}}|$ in 3D, Fig. 6b exhibits $|Q_{1_{19}}|$ and $|Q_{2_{19}}|$ in 2D, and Fig. 6c depicts the density plot of $|Q_{1_{19}}|$ and $|Q_{2_{19}}|$. Furthermore, Fig. 6d–f refer to imaginary value of $Q_{1_{19}}$ and $Q_{2_{19}}$ and Fig. 6g–i belong to real value of $Q_{1_{19}}$ and $Q_{2_{10}}$ in 3D, 2D and density plot, respectively.

Fig. 6

Graphs for ${Q_{1_{19}}}(x,t)$ and ${Q_{2_{10}}}(x,t)$ at $\omega _1=3, ~\omega _2=2,~,H=1.5, ~ \tau _1=1.6,~ {\alpha }_1 =1,~ {\alpha }_2= 2, ~ k_1 =1.3,~ k_2= 1.5,~{\upsilon }_1 =1.2, ~{\upsilon }_2= 1.3,~ {\xi }_1={\xi }_2=1$

Figure 7 is the graphical illustration of the solution $Q_{1_{21}}(x,t)$, $Q_{2_{21}}(x,t)$ for the parametric values taken as $\omega _1=4, ~\omega _2=3,~,H=2, ~ \tau _1=2.7,~ {\alpha }_1 =2.6,~ {\alpha }_2= 2.3, ~ k_1 =1.7,~ k_2= 1.6,~{\upsilon }_1 =1.4, ~{\upsilon }_2= 1.3,~ {\xi }_1={\xi }_2=1.2$. Figure 7a representation of modulus $|Q_{1_{21}}|$ and $|Q_{2_{21}}|$ in 3D, Fig. 7b is the depiction of $|Q_{1_{21}}|$ and $|Q_{2_{21}}|$ in 2D, and Fig. 7c is the density plot of $|Q_{1_{21}}|$ and $|Q_{2_{21}}|$. Figure 7d–f correspond to imaginary value of $Q_{1_{21}}$ and $Q_{2_{21}}$ and Fig. 7g–i refer to real value of $Q_{1_{21}}$ and $Q_{2_{21}}$ in 3D, 2D and density plot, respectively.

Fig. 7

Graphs for ${Q_{1_{21}}}(x,t)$ and ${Q_{2_{21}}}(x,t)$ at $\omega _1=4, ~\omega _2=3,~,H=2, ~ \tau _1=2.7,~ {\alpha }_1 =2.6,~ {\alpha }_2= 2.3, ~ k_1 =1.7,~ k_2= 1.6,~{\upsilon }_1 =1.4, ~{\upsilon }_2= 1.3,~ {\xi }_1={\xi }_2=1.2$

6 Discussion and conclusion

In this article, the optical solitons and other solitary wave solutions of the nonlinear Schrödinger equation of Manakov type is investigated. For this objective, modified auxiliary equation method and extended trial equation method are utilized. Trigonometric, hyperbolic, rational functions, and Jacobi elliptic function solutions were successfully obtained by applying these methods. Dark soliton, bright soliton, bright singular soliton, bright singular two-solitons, multi solitons and periodic solitary wave solutions are deduced with certain parameter restrictions in order to tackle the complexities of the system. The prior literature on Manakov model had soliton structures for hyperbolic and trigonometric functions Radhakrishnan and Aravinthan (2007); Guan and Li (2019); Yildirim (2019a, b); Ahmed et al. (2021) but not for Jacobi elliptic functions. Jacobi elliptic function is an effective tool for deciphering, comprehending, and forecasting the behavior of light pulses in optical communication networks. They are vital for study, development, and optimization of fiber optic communication systems because of their capacity to precisely depict complicated soliton structures, simplify computations, and reveal intricate propagation dynamics. They can represent a wide range of soliton solutions including bright solitons, dark solitons, breathing solitons as well as periodic and shock waves.

The bright singular two-solitons of Manakov model provided by the extended trial method, have potential applications in optical communication, quantum information processing, non-linear optics, and biosensor development. Two-solitons can generate entangled photon pairs for quantum computation and communication, accelerate quantum technology development, and switch and route optical signals in integrated photonic circuits. While a range of soliton structures is obtained using the modified auxiliary equation approach, the dark solitons are the only ones without the singularity. This may be used as leverage in fiber laser communication networks as it is possible to generate only non-singular solitons by adjusting settings, using filtering strategies, and taking advantage of soliton interactions. In fiber communication, dark soliton technology has several benefits such as improved signal-to-noise ratio (SNR), less dispersion effects, higher channel density, all-optical signal processing, and improved security. Cleaner signals and more channel capacity are achieved since they may propagate in an uninterrupted light backdrop without much contact. They are perfect for long-distance communication as they are less prone to dispersion. Dark solitons are also inherently stealthy and challenging to detect, making them useful for secure communication applications. Solitons are being explored for ultra-high-speed data transmission, long-distance communication, secure communication, all-optical signal processing, and biological systems (Shi et al. 2023). Their potential for logic operations and signal manipulation holds promise for future photonic integrated circuits.