1 Introduction

The main idea of this paper splits into two parts:

  1. (i)

    The first part concentrates on how we can enforce the PPAM (Kudryashov 2019; Bekir and Zahran 2021a, 2020, 2021b; Bekir et al. 2020) to construct the lump solutions of the PGIE (Gerdjikov and Ivanov 1983) which act for the dynamics of the propagation of solitons that carry quantic nonlinearity of Schrödinger's equation while Schrödinger's equation is classically explored with cubic nonlinearity. For this purpose, we will propose the dimensionless GI-equation

    $$i\,q_{t} + a\,q_{xx} + \,b\left| {q^{4} } \right|q\, + \,i\,c\,q^{2} \,q_{x}^{*} \, = 0\,.$$
    (1)

With \(q^{*} (x,t)\) denotes the complex conjugation of the complex valued wave structure \(q(x,t)\) with x and t as spatial and temporal variables sequentially. The first and last dimensionless terms of the PGIE represent the linear and the nonlinear dispersion stands for soliton temporal evolution respectively. All the involved parameters \(\mathrm{S}\) \(a,b\) and \(\mathrm{h}(\upxi )\)\(c\) are real-valued constants. For example, \(a\) gives dispersion of group velocity and \(b\) depends on coefficient of quantic form of nonlinearity.

The famous full nonlinearity structure of the perturbed GI- equation is

$$iq_{t} + a\,q_{xx} + \,b\left| {q^{4} } \right|\,q + \,i\,c\,q^{2} \,q_{x}^{*} \, = \,i\,[\alpha q_{x} + \lambda \left( {q\left| q \right|^{2m} } \right)_{x} + \,\mu (\left( {\left| q \right|^{2m} } \right)_{x} q].$$
(2)

where α, μ and λ represent the depiction of the inter-modal dispersion, the higher-order dispersion effect and the self-steepening for short pulses respectively, m signifies full nonlinearity effects. The current analysis concentrates on one such nonlinear evolution equation as GI equation (Bekir et al. 2020). The spectral problem and the associated perturbed GI hierarchy (Fan 2000a) of nonlinear evolution equations are presented and show that the GI hierarchy is integrable in a Liouville sense and possesses bi-Hamiltonian structure. Numerous efficient and influential methods have been projected for obtaining solutions of GI equation, such as algebra-geometric solutions (Dai and Fan 2004), soliton hierarchy (Guo 2009), bifurcations and travelling wave (He and Meng 2010), bright and dark soliton solutions (Lü et al. 2015), Darboux transformations (Yilmaz 2015) and many more being studied for more than a decade (Fan 2000b; Rogers and Chow 2012; Manafian and Lakestani 2016; Biswas et al. 2017, 2018; Triki et al. 2017; Zhang et al. 2017), Kaura and Wazwaz (2018) obtain the optical solitons for PGIE.

Let us now introduce this wave transformation:

$$q(x,t) = u(\zeta )\,e^{i\,\psi (x,t)} .$$
(3)
$$q_{t} = \left[ { - vu^{\prime} + i\,wu} \right]\,e^{i\,\psi (x,t)} .$$
(4)
$$q_{x} = \left[ {u^{\prime} - i\,ku} \right]\,e^{i\,\psi (x,t)} .$$
(5)
$$q_{xx} = \,\left[ {u^{\prime\prime} - 2iku^{\prime} - k^{2} u} \right]{\text{e}}^{i\,\psi (x,t)} .$$
(6)

With \(\zeta = x - \nu t,\,\,\psi (x,t) = \, - kx + wt + \theta \,,\,u(\zeta )\) represents the shape features of the wave pulse, \(\,\psi (x,t)\,\) is the phase component of the soliton, \(k\) is the soliton frequency, \(w\) is the wave number, \(\theta\) is the phase constant and \(\nu\) is the velocity of the soliton. Considering (3–6) into (1), followed by uncoupling of real and imaginary parts of the equation gives a pair of equations namely the real part is

$$au^{\prime\prime} - (w + ak^{2} + \alpha k)u - k\lambda u^{2m + 1} - cku^{3} + bu^{5} = 0.$$
(7)

And the imaginary part is

$$v = - 2\alpha k - \alpha + cu^{2} - [(2m + 1)\lambda + 2m\mu ]u^{2m} .$$
(8)

The velocity of the soliton can be extracted from Eq. (8), hence we can control the soliton arising while Eq. (7) can be solved to determine the soliton behaviour.

Now let us put \(m = 1\) and study Eq. (7) by putting implement the homogeneous balance between \(u^{\prime\prime},u^{5}\) that implies \(N = \frac{1}{2}\) which pushes us to take the transformation \(u = U^{\frac{1}{2}}\) hence Eq. (7) will be converted to

$$2aUU^{\prime \prime } - aU^{\prime 2} - 4(w + ak^{2} + \alpha k)U^{2} - 4k(\lambda + c)U^{3} + 4bU^{4} = 0.$$
(9)

Now, let us implement the homogeneous balance between \(UU^{\prime\prime}\) and either \(U^{{\prime}{2}}\) or \(U^{4}\) we get \(N = 1\).

  1. (ii)

    The second split concentrated on haw we can used the PPAM to obtain new soliton solutions of the PNSEWKL (Zhang et al. 2010; Moosaei et al. 2011; Biswas and Konar 2007; Zahran 2015; Eslami 2015; Salam 2018; Akramaand and Mahak 2018; Ahmed et al. 2018) that describes the propagation of waves in optical fibres

    $$iq_{t} + \,q_{xx} + \,\gamma \left| q \right|^{2} \,q\, + \,i\,\left\{ {\mu_{1} \,q_{xxx} + \mu_{2} \,\left| q \right|^{2} q_{x} + \mu_{3} \left( {\left| q \right|^{2} } \right)_{x} \,q} \right\} = 0.$$
    (10)

    where \(\gamma ,\mu_{1} ,\mu_{2} ,\mu_{3}\) are constants where \(\mu_{1} ,\mu_{2} ,\mu_{3}\) are the third order dispersion, the nonlinear dispersion and version of nonlinear dispersion respectively (Kaura and Wazwaz 2018). With the aid of the transformation

    $$q(x,t) = U(\zeta ){\text{e}}^{[i( - kx + wt)]} ,\,\zeta = x - vt.$$
    (11)

    where \(i = \sqrt { - 1}\) while \(k,w\) and \(v\) are constants.

Now, by using the transformation Eq. (11) into Eq. (10) the following two real and imaginary parts can be respectively emerged

$$\mu_{1} U^{\prime \prime \prime } + (2k - v - 3\mu_{1} k^{2} )\,U^{\prime } + (\mu_{2} + 2\mu_{3} )U^{2} U^{\prime } = 0.$$
(12)
$$(1 - 3\mu_{1} k)\,U^{\prime \prime } + (w - k^{2} + \mu_{1} k^{3} )U + (\alpha - \mu_{2} k)U^{3} = 0.$$
(13)

If we integrate Eq. (12) we obtain

$$\mu_{1} \,U^{\prime \prime } + (2k - v - 3\mu_{1} k^{2} )U + \frac{1}{3}(\mu_{2} + 2\mu_{3} )U^{3} = 0.$$
(14)

Equations (13), (14) are the same when

$$\frac{{\mu_{1} }}{{1 - 3k\mu_{1} }} = \frac{{2k - v - 3\mu_{1} k^{2} }}{{w - k^{2} + \mu_{1} k^{3} }} = \frac{{\frac{1}{3}(\mu_{2} + 2\mu_{3} )}}{{\alpha - \mu_{2} k}}.$$
(15)

From which we get the following relations

$$k = \frac{{w_{1} - \alpha \mu_{1} }}{{3w_{1} - \mu_{1} \mu_{2} }},\,w = \frac{{(1 - 3\mu_{1} k)(2k - v - 3\mu_{1} k^{2} )}}{{w_{1} }} + k^{2} - \mu_{1} k^{3} ,\;w_{1} = \frac{1}{3}\mu_{1} + \frac{2}{3}\mu_{3} .$$

Hence, we will solve any one of Eqs. (13) or (14) say Eq. (14) which is

$$\mu_{1} \,U^{\prime \prime } + (2k - v - 3\mu_{1} k^{2} )U + \frac{1}{3}(\mu_{2} + 2\mu_{3} )U^{3} = 0.$$
(16)

The NLPDE have been linked with nonlinear physical structures that concerning with several disciplines, like fluid dynamics, wave propagation, plasma physics, nonlinear telecommunication networks, optical fibres and so on to develop these phenomena and its applications. Discussion the studies for some NLPDE concerning their solutions through reasonable analytical, asymptotic and mixture methods to obtain the exact solution for the NLPDE have significant role in many nonlinear problems arising in various branches of science. Many forms of NLPDE have been studied to construct the exact solutions in terms of some parameters, when these parameters take definite values the soliton solutions could be detected. Some trials have been documented through some published articles via some authors to study various forms of shallow-water equations, see for example Kumar et al. (2021) who used the tanh–coth method to obtain the soliton solutions of RLW equations as well as used the mesh-free method to converts the RLW model into a system of nonlinear ordinary differential equations, solved the resultant system via Runge–Kutta method and discuss the stability for the extracted solutions, Jiwari and Gerisch (2021) who developed a mesh free algorithm based on local radial basis functions (RBFs) combined with the differential quadrature (DQ) method to provide numerical approximations of the solutions of time-dependent, nonlinear and spatially one-dimensional reaction–diffusion systems and to capture their evolving patterns, Jiwari et al. (2020) who employed the Lie Group method to reduce the compressible Navier–Stokes equations to a system of highly nonlinear ordinary differential equations with suitable similarity transformations and obtained exact solutions of the main equation and used the conservation laws multiplier to find the complete set of local conservation laws of this equation and Yadav and Jiwari (2019) who studied some soliton-type analytical solutions of Schrödinger equation, with their numerical treatment by Galerkin finite element method. There recent studies are implemented to discuss wave propagations in optical fibers see for example Younas and Ren (2021) who studied the propagation of waves through magneto-optic waveguides by using the extended Fan-sub equation method and extracted the exact solutions in the forms of Jacobi’s elliptic functions, trigonometric, hyperbolic, including solitary wave solutions like bright, dark, complex, singular, and mixed complex solitons, Younas et al. (2021) who extracted pure-cubic optical solitons in nonlinear optical fiber modeled by nonlinear Schrödinger equation with the effect of third-order dispersion, Kerr law of nonlinearity and with-out chromatic dispersion. The extracted soliton solutions in different forms like, Jacobi’s elliptic, hyperbolic, periodic, exponential function solutions including a class of solitary wave solutions such that bright, dark, singular, kink-shape, multiple-optical soliton, and mixed complex soliton solutions, Younas et al. (2022a) who investigated a series of abundant new soliton solutions to The Kraenkel-Manna-Merle model which expresses the nonlinear ultra-short wave pulse motions in ferrite’s materials having an external field with zero-conductivity, extracted the different forms of solutions like, Jacobi’s elliptic, hyperbolic, periodic, rational function solutions including a class of solitary wave solutions such that dark, singular, complex combo solitons, and mixed complex soliton solutions by using model expansion method, Younas et al. (2022b) who investigated the dynamical behavior of doubly dispersive equation which governs the propagation of nonlinear waves in the elastic Murnaghan’s rod, extracted a variety of solitary wave solutions with unknown parameters in different shapes such as bright, dark, kink-type, bell-shape, combine and complex soliton, hyperbolic, exponential, and trigonometric function solutions by using the new extended direct algebraic method and the generalized Kudryashov method, Younas et al. (2022c) who discussed the dynamical behavior of ill-posed Boussinesq dynamical wave equation that depicts how long wave made in shallow water propagates due to the influence of gravity, obtained different wave structures as novel breather waves, lump solutions, two-wave solutions, and rogue wave solutions by utilizing of Hirota's bilinear method and different test function approaches, Younas et al. (2022d) who secured the different soliton and other solutions in the magneto electro-elastic circular rod, obtained abundant solutions of the nonlinear longitudinal wave equation with dispersion caused by the transverse Poisson’s effect in a long circular rod by using the modified Sardar sub-equation method and extracted the soliton wave structures such as bright, dark, singular, bright-dark, bright-singular, complex, and combined and generate hyperbolic, trigonometric, exponential type and periodic solutions and Younas et al. (2022e) who secured the different forms of optical soliton solutions by using the new extended direct algebraic method to three-component Gross–Pitaevskii (tc-GP) system which describes the F = 1 spinor Bose–Einstein condensate, with F denoting the atom’s spin the spinor Bose–Einstein condensate, achieved different kinds of solitons, such as dark, singular, kink, bright–dark, complex and combined, are extracted.

The main target of our work focused on derived new types of soliton solutions for these two various models in the framework of the PPAM, the novelty our achieved solutions appears through the performance of the new behaviour of the extract solitons.

This article is prepared as follow, in the second and third sections the PPAM algorithm and its application to construct new types of soliton solutions for the two suggested models respectively, in the fourth section the conclusion is established.

2 The PPAM algorithm

Any nonlinear evolution equation can be written in the form

$$R(U,U_{x} ,U_{t} ,U_{xx} ,U_{tt} ,\cdot\cdot\cdot) = 0.$$
(17)

where R is defined in terms of \(U(x,t)\) and its partial derivatives, with using the transformation \(U(x,t) = U(\zeta ),\,\zeta = x - vt,\) Eq. (17) can be reduced to the following ODE:

$$S(U^{\prime } ,U^{\prime \prime } ,U^{\prime \prime \prime } ,\cdot\cdot\cdot) = 0.$$
(18)

where \(S\) in term of \(U(\zeta )\) and its total derivatives.

According to PPAM (Kudryashov 2019; Bekir and Zahran 2020, 2021a, b; Bekir et al. 2020) the exact solution for any nonlinear ordinary differential equation can be written in the following form

$$U(\zeta ) = A_{0} + \,A_{1} S(X)\,e^{ - N\zeta } ,\,X = R(\zeta ).$$
(19)

Or

$$U(\zeta ) = A_{0} + \,A_{1} S(X)\,e^{ - N\zeta } + A_{2} S^{2} (X)\,e^{ - 2N\zeta } ,\,X = R(\zeta ).$$
(20)

where \(X = R(\zeta ) = C_{1} - \frac{{e^{ - N\zeta } }}{N}\) and \(S(X)\) appearing in Eq. (18) and Eq. (19) surrenders to the Riccati-equation in the form \(S_{x} - AS^{2} = 0\) which has solution in the form

$$S(X) = \frac{1}{{SX + X_{0} }}.$$
(21)

Consequently

$$U^{\prime } = \, - NA_{1} \,Se^{ - N\zeta } - A_{1} \,A\,e^{ - 2N\zeta } S^{2} .$$
(22)
$$U^{\prime \prime } = \,A_{1} N^{2} \,S\,e^{ - N\zeta } + 3A_{1} ANS^{2} e^{ - 2N\zeta } + 2A_{1} A^{2} S^{3} e^{ - 3N\zeta } .$$
(23)

3 Applications

3.1 Firstly for the PGIE

In this section we are going to apply the PPAM to get new lump solutions for the PGIE, via inserting Eqs. (19), (22), (23) into Eq. (9) mentioned above and equating the coefficients of various powers \(S(\zeta )e^{ - N\zeta }\) to zero we obtained a system of equations whose solution is

$$\begin{array}{*{20}l} {(1)} \hfill & {\quad A_{0} = 0,a = - \frac{{3k^{2} c^{2} + 16b(w + \alpha k) + 6\lambda ck^{2} + 3\lambda^{2} k^{2} }}{{16bk^{2} }},} \hfill \\ {} \hfill & {\quad A = \frac{{8bkA_{1} }}{{\sqrt {9k^{2} c^{2} + 48b(w + \alpha k) + 18\lambda ck^{2} + 9\lambda^{2} k^{2} } }},} \hfill \\ {} \hfill & {\quad N = \frac{{ - 2\sqrt 3 k^{2} (c + \lambda )}}{{\sqrt {3k^{2} c^{2} + 16b(w + \alpha k) + 6\lambda ck^{2} + 3\lambda^{2} k^{2} } }}.} \hfill \\ \end{array}$$
(24)
$$\begin{array}{*{20}l} {(2)} \hfill & {\quad A_{0} = 0,\,\,\,a = - \frac{{3k^{2} c^{2} + 16b(w + \alpha k) + 6\lambda ck^{2} + 3\lambda^{2} k^{2} }}{{16bk^{2} }},} \hfill \\ {} \hfill & {\quad A = \frac{{ - 8bkA_{1} }}{{\sqrt {9k^{2} c^{2} + 48b(w + \alpha k) + 18\lambda ck^{2} + 9\lambda^{2} k^{2} } }},} \hfill \\ {} \hfill & {\quad N = \frac{{2\sqrt 3 k^{2} (c + \lambda )}}{{\sqrt {3k^{2} c^{2} + 16b(w + \alpha k) + 6\lambda ck^{2} + 3\lambda^{2} k^{2} } }}.} \hfill \\ \end{array}$$
(25)
$$\begin{array}{*{20}l} {(3)} \hfill & {\quad A_{0} = \frac{3k(c + \lambda )}{{4b}},\,\,a = - \frac{{3k^{2} c^{2} + 16b(w + \alpha k) + 6\lambda ck^{2} + 3\lambda^{2} k^{2} }}{{16bk^{2} }},} \hfill \\ {} \hfill & {\quad A = \frac{{ - 8bkA_{1} }}{{\sqrt {9k^{2} c^{2} + 48b(w + \alpha k) + 18\lambda ck^{2} + 9\lambda^{2} k^{2} } }},} \hfill \\ {} \hfill & {\quad N = \frac{{ - 2\sqrt 3 k^{2} (c + \lambda )}}{{\sqrt {3k^{2} c^{2} + 16b(w + \alpha k) + 6\lambda ck^{2} + 3\lambda^{2} k^{2} } }}.} \hfill \\ \end{array}$$
(26)
$$\begin{array}{*{20}l} {(4)} \hfill & {\quad A_{0} = \frac{3k(c + \lambda )}{{4b}},a = - \frac{{3k^{2} c^{2} + 16b(w + \alpha k) + 6\lambda ck^{2} + 3\lambda^{2} k^{2} }}{{16bk^{2} }},} \hfill \\ {} \hfill & {\quad A = \frac{{8bkA_{1} }}{{\sqrt {9k^{2} c^{2} + 48b(w + \alpha k) + 18\lambda ck^{2} + 9\lambda^{2} k^{2} } }},} \hfill \\ {} \hfill & {\quad N = \frac{{2\sqrt 3 k^{2} (c + \lambda )}}{{\sqrt {3k^{2} c^{2} + 16b(w + \alpha k) + 6\lambda ck^{2} + 3\lambda^{2} k^{2} } }}.} \hfill \\ \end{array}$$
(27)

Now, we will implement the solutions corresponding to the first and last result.

  1. (1)

    For the first result which is

$$\begin{gathered} A_{0} = 0,a = - \frac{{3k^{2} c^{2} + 16b(w + \alpha k) + 6\lambda ck^{2} + 3\lambda^{2} k^{2} }}{{16bk^{2} }}, \hfill \\ \,\,\,\,\,A = \frac{{8bkA_{1} }}{{\sqrt {9k^{2} c^{2} + 48b(w + \alpha k) + 18\lambda ck^{2} + 9\lambda^{2} k^{2} } }}, \hfill \\ \,\,\,\,\,\,N = \frac{{ - 2\sqrt 3 k^{2} (c + \lambda )}}{{\sqrt {3k^{2} c^{2} + 16b(w + \alpha k) + 6\lambda ck^{2} + 3\lambda^{2} k^{2} } }}. \hfill \\ \end{gathered}$$

That can be simplified to be

$$b = c = w = v = k = \lambda = \alpha = A_{1} = 1,A_{0} = 0,a = - 2.8,A = 0.7,N = - 1.1.$$
(28)

The solution in the framework of this result, according to the suggested method will be

$$U(\zeta ) = \frac{{e^{1.1\zeta } }}{{0.7(1 + \,\frac{{e^{1.1\zeta } }}{1.1}) + 1\,}}\,.$$
(29)
$$u(\zeta ) = \left( {\frac{{1.1e^{1.1\zeta } }}{{1.9 + 0.7\,e^{1.1\zeta } \,}}} \right)^{0.5} .\,$$
(30)
$$q(x,t) = \left( {\frac{{1.1e^{1.1\zeta } }}{{1.9 + 0.7\,e^{1.1\zeta } \,}}} \right)^{0.5} \times \,{\text{e}}^{i\psi (x,t)} .$$
(31)
$$q(x,t) = u(x,t)[\cos \psi (x,t) + i\sin \psi (x,t)].$$
(32)
$${\text{Re}} q(x,t) = \left( {\frac{{1.1e^{1.1\zeta } }}{{1.9 + 0.7\,e^{1.1\zeta } \,}}} \right)^{0.5} \times \cos \psi (x,t).$$
(33)
$${\text{Im}} q(x,t) = \left( {\frac{{1.1e^{1.1\zeta } }}{{1.9 + 0.7\,e^{1.1\zeta } \,}}} \right)^{0.5} \times \sin \psi (x,t).$$
(34)
  1. (2)

    For the last result which is

$$\begin{gathered} A_{0} = \frac{3k(c + \lambda )}{{4b}},a = - \frac{{3k^{2} c^{2} + 16b(w + \alpha k) + 6\lambda ck^{2} + 3\lambda^{2} k^{2} }}{{16bk^{2} }}, \hfill \\ \,\,\,\,\,A = \frac{{8bkA_{1} }}{{\sqrt {9k^{2} c^{2} + 48b(w + \alpha k) + 18\lambda ck^{2} + 9\lambda^{2} k^{2} } }}, \hfill \\ \,\,\,\,\,\,N = \frac{{2\sqrt 3 k^{2} (c + \lambda )}}{{\sqrt {3k^{2} c^{2} + 16b(w + \alpha k) + 6\lambda ck^{2} + 3\lambda^{2} k^{2} } }}. \hfill \\ \end{gathered}$$

That can be simplified to be

$$X_{0} = b = c = c_{1} = w = v = k = \lambda = \alpha = 1,A_{0} = 1.5,a = - 2.8,A = 0.7,N = 1.1.$$
(35)

The solution according to the suggested method and this result will be

$$U(\zeta ) = 1.5 + \frac{{1.1e^{ - 1.1\zeta } }}{{1.9 - 0.7e^{ - 1.1\zeta } \,}}\,.$$
(36)
$$u(\zeta ) = \left( {1.5 + \frac{{1.1e^{ - 1.1\zeta } }}{{1.9 - 0.7e^{ - 1.1\zeta } \,}}\,} \right)^{0.5} .\,$$
(37)
$$q(x,t) = \left( {1.5 + \frac{{1.1e^{ - 1.1\zeta } }}{{1.9 - 0.7e^{ - 1.1\zeta } \,}}\,} \right)^{0.5} \times {\text{e}}^{i\psi (x,t)} .$$
(38)
$${\text{Re}} q(x,t) = \left( {1.5 + \frac{{1.1e^{ - 1.1\zeta } }}{{1.9 - 0.7e^{ - 1.1\zeta } \,}}\,} \right)^{0.5} \times \cos \psi (x,t).$$
(39)
$${\text{Im}} q(x,t) = \left( {1.5 + \frac{{1.1e^{ - 1.1\zeta } }}{{1.9 - 0.7e^{ - 1.1\zeta } \,}}\,} \right)^{0.5} \times \sin \psi (x,t).$$
(40)

3.2 Secondly for the PNSEWKL

Via inserting Eqs. (19), (22–23) into Eq. (16) and by equating the coefficients of various powers of \(S(\zeta )e^{ - N\zeta }\) to zero we get a system of equations from which the following results will be detected

$$\begin{array}{*{20}c} {(1)} & {\quad A_{0} = - 1.8i\sqrt {\frac{{3k^{2} \mu_{1} + v - 2k}}{{\mu_{2} + 2\mu_{3} }}} ,\;A = - 0.4i\,A_{1} \,\sqrt {\frac{{\mu_{2} + 2\mu_{3} }}{{\mu_{1} }}} ,\,\;N = 1.4i\sqrt {\frac{{3k^{2} \mu_{1} + v - 2k}}{{\mu_{1} }}} .} \\ \end{array}$$
(41)
$$\begin{array}{*{20}c} {(2)} & {\quad A_{0} = - 1.8i\sqrt {\frac{{3k^{2} \mu_{1} + v - 2k}}{{\mu_{2} + 2\mu_{3} }}} ,\;A = 0.4i\,A_{1} \,\sqrt {\frac{{\mu_{2} + 2\mu_{3} }}{{\mu_{1} }}} ,\,\;N = - 1.4i\sqrt {\frac{{3k^{2} \mu_{1} + v - 2k}}{{\mu_{1} }}} .} \\ \end{array}$$
(42)
$$\begin{array}{*{20}c} {(3)} & {\quad A_{0} = 1.8i\sqrt {\frac{{3k^{2} \mu_{1} + v - 2k}}{{\mu_{2} + 2\mu_{3} }}} ,\,\,A = - 0.4i\,A_{1} \,\sqrt {\frac{{\mu_{2} + 2\mu_{3} }}{{\mu_{1} }}},\,N = - 1.4i\sqrt {\frac{{3k^{2} \mu_{1} + v - 2k}}{{\mu_{1} }}} .} \\ \end{array}$$
(43)
$$\begin{array}{*{20}c} {(4)} & {\quad A_{0} = 1.8i\sqrt {\frac{{3k^{2} \mu_{1} + v - 2k}}{{\mu_{2} + 2\mu_{3} }}} ,\,\,A = 0.4i\,A_{1} \,\sqrt {\frac{{\mu_{2} + 2\mu_{3} }}{{\mu_{1} }}}, \,N = 1.4i\sqrt {\frac{{3k^{2} \mu_{1} + v - 2k}}{{\mu_{1} }}} .} \\ \end{array}$$
(44)

From which we will discuss the first and the third results to get the corresponding solutions.

  1. (1)

    For the first result which is

$$A_{0} = - 1.8i\sqrt {\frac{{3k^{2} \mu_{1} + v - 2k}}{{\mu_{2} + 2\mu_{3} }}} ,A = - 0.4i\,A_{1} \,\sqrt {\frac{{\mu_{2} + 2\mu_{3} }}{{\mu_{1} }}} \,,N = 1.4i\sqrt {\frac{{3k^{2} \mu_{1} + v - 2k}}{{\mu_{1} }}} .$$

That can be simplified to be

$$X_{0} = k = v = c_{1} = B = w = \mu_{1} = \mu_{2} = \mu_{3} = A_{1} = 1,A_{0} = - 1.5i,A = - 0.7i\,,N = i.$$
(45)

The solution in the framework of this result, according to the suggested method will be

$$H(\zeta ) = \frac{{\,e^{\,\, - i\zeta } }}{{\,\, - 0.7i(1 - \frac{{\,e^{\,\, - i\zeta } }}{{^{i} }}\,) + 1\,}}.$$
(46)
$${\text{Re}} \,H(\zeta ) = \frac{\,0.7\sin \zeta + \cos \zeta + 0.7}{{\,\,0.98\sin \zeta + 1.4\cos \zeta + 1.98\,}}.$$
(47)
$${\text{Im}} \,H(\zeta ) = - 1.5 + \frac{\,0.7\cos \zeta - \sin \zeta }{{\,\,0.98\sin \zeta + 1.4\cos \zeta + 1.98\,}}.$$
(48)
$$q(x,t) = H(\zeta )\exp [i( - kx + wt + \theta )].$$
$$q(x,t) = \left\{ \begin{gathered} \left( {\frac{\,0.7\sin \zeta + \cos \zeta + 0.7}{{\,\,0.98\sin \zeta + 1.4\cos \zeta + 1.98\,}} + i\left( { - 1.5 + \frac{\,0.7\cos \zeta - \sin \zeta }{{\,\,0.98\sin \zeta + 1.4\cos \zeta + 1.98\,}}} \right)} \right) \times \hfill \\ \left( {\cos ( - kx + wt + \theta ) + i\sin ( - kx + wt + \theta )} \right) \hfill \\ \end{gathered} \right\}.$$
(49)
$${\text{Re}} \,\,q(\zeta ) = \left\{ \begin{gathered} \left( {\frac{\,0.7\sin \zeta + \cos \zeta + 0.7}{{\,\,0.98\sin \zeta + 1.4\cos \zeta + 1.98\,}}} \right) \times \cos ( - kx + wt + \theta ) \hfill \\ - \left( { - 1.5 + \frac{\,0.7\cos \zeta - \sin \zeta }{{\,\,0.98\sin \zeta + 1.4\cos \zeta + 1.98\,}}} \right) \times \sin ( - kx + wt + \theta ) \hfill \\ \end{gathered} \right\}\,.\,$$
(50)
$${\text{Im}} \,\,q(\zeta ) = \left\{ \begin{gathered} \left( {\frac{\,0.7\sin \zeta + \cos \zeta + 0.7}{{\,\,0.98\sin \zeta + 1.4\cos \zeta + 1.98\,}}} \right) \times \sin ( - kx + wt + \theta ) \hfill \\ + \left( { - 1.5 + \frac{\,0.7\cos \zeta - \sin \zeta }{{\,\,0.98\sin \zeta + 1.4\cos \zeta + 1.98\,}}} \right) \times \cos ( - kx + wt + \theta ) \hfill \\ \end{gathered} \right\}\,.\,$$
(51)
  1. (2)

    For the third result which is

$$A_{0} = 1.8i\sqrt {\frac{{3k^{2} \mu_{1} + v - 2k}}{{\mu_{2} + 2\mu_{3} }}} ,A = - 0.4i\,A_{1} \,\sqrt {\frac{{\mu_{2} + 2\mu_{3} }}{{\mu_{1} }}} \,,N = - 1.4i\sqrt {\frac{{3k^{2} \mu_{1} + v - 2k}}{{\mu_{1} }}} .$$

That can be simplified to be

$$X_{0} = k = v = c_{1} = B = w = \mu_{1} = \mu_{2} = \mu_{3} = A_{1} = 1,A_{0} = 1.5i,A = - 0.7i\,,N = - i.$$
(52)

The solution in the framework of this result, according to the suggested method will be

$$H(\zeta ) = \frac{{\,e^{\,\,i\zeta } }}{{\,\, - 0.7i(1 + \frac{{\,e^{\,\,i\zeta } }}{{^{i} }}\,) + 1\,}}.$$
(53)
$${\text{Re}} \,H(\zeta ) = \frac{\,\cos \zeta - 0.7\sin \zeta - 0.7}{{\,\,0.98\sin \zeta - 1.4\cos \zeta + 1.98\,}}.$$
(54)
$${\text{Im}} \,H(\zeta ) = 1.5 + \frac{\,0.7\cos \zeta + \sin \zeta }{{\,\,0.98\sin \zeta - 1.4\cos \zeta + 1.98\,}}.$$
(55)
$$q(x,t) = H(\zeta )\exp [i( - kx + wt + \theta )].$$
$$q(x,t) = \left\{ \begin{gathered} \left( {\frac{\,\cos \zeta - 0.7\sin \zeta - 0.7}{{\,\,0.98\sin \zeta - 1.4\cos \zeta + 1.98\,}} + i\left( {1.5 + \frac{\,0.7\cos \zeta + \sin \zeta }{{\,\,0.98\sin \zeta - 1.4\cos \zeta + 1.98\,}}} \right)} \right) \times \hfill \\ \left( {\cos ( - kx + wt + \theta ) + i\sin ( - kx + wt + \theta )} \right) \hfill \\ \end{gathered} \right\}.$$
(56)
$${\text{Re}} \,\,q(\zeta ) = \left\{ \begin{gathered} \left( {\frac{\,\cos \zeta - 0.7\sin \zeta - 0.7}{{\,\,0.98\sin \zeta - 1.4\cos \zeta + 1.98\,}}} \right) \times \cos ( - kx + wt + \theta ) \hfill \\ - \left( {1.5 + \frac{\,0.7\cos \zeta + \sin \zeta }{{\,\,0.98\sin \zeta - 1.4\cos \zeta + 1.98\,}}} \right) \times \sin ( - kx + wt + \theta ) \hfill \\ \end{gathered} \right\}\,.\,$$
(57)
$${\text{Im}} \,\,q(\zeta ) = \left\{ \begin{gathered} \left( {\frac{\,\cos \zeta - 0.7\sin \zeta - 0.7}{{\,\,0.98\sin \zeta - 1.4\cos \zeta + 1.98\,}}} \right) \times \sin ( - kx + wt + \theta ) \hfill \\ + \left( {1.5 + \frac{\,0.7\cos \zeta + \sin \zeta }{{\,\,0.98\sin \zeta - 1.4\cos \zeta + 1.98\,}}} \right) \times \cos ( - kx + wt + \theta ) \hfill \\ \end{gathered} \right\}\,.\,$$
(58)

4 Conclusion

Throughout of this study, the PPAM was implemented for the first time to achieve new lump solutions of the PGIE in various behaviour forms as bright soliton solution, dark soliton solution and rational soliton solution that are appear through Figs. 1, 2, 3 and 4. When the comparison imbed between our obtained lump solutions to PGIE with that previously achieved by Triki et al. (2017) that used other techniques, the agreements shown in some cases while the others are new. In a related subject, the suggested method has been used for construct new types of lump solutions for the PNSEWKL as bright soliton solution, dark soliton solution and trigonometric soliton solution that are appear through Figs. 5, 6, 7 and 8. When we compare the achieved lump solutions of the PNSEWKL with the previously achieved solutions by Zhang et al. (2017); Biswas et al. 2018; Kaura and Wazwaz 2018; Zhang et al. 2010; Moosaei et al. 2011; Biswas and Konar 2007; Zahran 2015; Eslami 2015) who used other techniques it is clear that the obtained solutions are new. Consequently, we can document new lump solutions for the two models via the PPAM which weren’t achieved before by any other methods. The new types of soliton solutions detected by adjusting the parameter have great contribution, significance in improve the quality of optical communications for the related applications such as recent telecommunication processes, few-cycle pulse propagation in metamaterials, the nonlinear refractive index cubic-quartic through birefringent fibers, helpful in the design optical amplifiers and so on. The prediction of the solitons appearing in this work is sufficient for the experimental observations. The achieved soliton solutions denote that the used method is effective and can be applied for any nonlinear evolution equations.

Fig. 1
figure 1

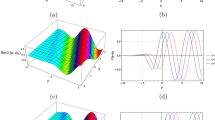
The plot \({\text{Re}} q(x,t)\) Eq. (33) in 2D and 3D with values: \(X_{0} = b = c = c_{1} = w = v = k = \lambda = \alpha = A_{1} = 1,A_{0} = 0,a = - 2.8,A = 0.7,N = - 1.1\)

Full size image
Fig. 2
figure 2

The plot \({\text{Im}} q(x,t)\) Eq. (34) in 2D and 3D with values: \(X_{0} = b = c = c_{1} = w = v = k = \lambda = \alpha = A_{1} = 1,A_{0} = 0,a = - 2.8,A = 0.7,N = - 1.1\)

Full size image
Fig. 3
figure 3

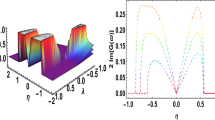
The plot \({\text{Re}} q(x,t)\) Eq. (39) in 2D and 3D with values: \(X_{0} = b = c = c_{1} = w = v = k = \lambda = \alpha = 1,\,A_{0} = 1.5,\,a = - 2.8,\,A = 0.7,N = 1.1\)

Full size image
Fig. 4
figure 4

The plot \({\text{Im}} q(x,t)\) Eq. (40) in 2D and 3D with values: \(X_{0} = b = c = c_{1} = w = v = k = \lambda = \alpha = 1,\,A_{0} = 1.5,\,a = - 2.8,\,A = 0.7,\,N = 1.1\)

Full size image
Fig. 5
figure 5

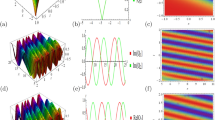
The plot \({\text{Re}} q(x,t)\) Eq. (50) in 2D and 3D with values: \(X_{0} = k = v = c_{1} = B = w = \mu_{1} = \mu_{2} = \mu_{3} = A_{1} = 1,A_{0} = - 1.5i,A = - 0.7i\,,N = i\)

Full size image
Fig. 6
figure 6

The plot \({\text{Im}} q(x,t)\) Eq. (51) in 2D and 3D with values: \(X_{0} = k = v = c_{1} = B = w = \mu_{1} = \mu_{2} = \mu_{3} = A_{1} = 1,\,A_{0} = - 1.5i,\,A = - 0.7i,\,N = i\)

Full size image
Fig. 7
figure 7

The plot \({\text{Re}} q(x,t)\) Eq. (57) in 2D and 3D with values: \(X_{0} = k = v = c_{1} = B = w = \mu_{1} = \mu_{2} = \mu_{3} = A_{1} = 1,\,A_{0} = 1.5i,\,A = - 0.7i,\,N = - i\)

Full size image
Fig. 8
figure 8

The plot \({\text{Im}} q(x,t)\) Eq. (58) in 2D and 3D with values: \(X_{0} = k = v = c_{1} = B = w = \mu_{1} = \mu_{2} = \mu_{3} = A_{1} = 1,\,A_{0} = 1.5i,A = - 0.7i,\,N = - i\)

Full size image