1 Introduction

Nonlinear partial differential equations (NLPDEs) are operated in order to model problems in various scientific and engineering areas. In addition to modeling NLPDEs, producing their analytical solutions is an area of great interest for researchers. Therefore, many techniques have been used in the literature to find the analytical solutions of NLPDEs like the F-expansion scheme (Ebaid and Aly 2012; Zhao 2013; Yıldırım 2021), Hirota bilinear approach (Hereman and Zhuang 1994; Satsuma 2003; Guo et al. 2020), the unified Riccati equation expansion method (Ozisik 2022; Cakicioglu et al. 2023; Ozisik et al. 2023; Esen et al. 2022), the generalized projective Riccati equations technique (Shahoot et al. 2018; Akram et al. 2021; Ozdemir 2022), enhanced Kudryashov method (Akbulut et al. 2022; Arnous et al. 2022; Arnous 2021; Arnous et al. 2022), generalized Kudryashov method (Arnous and Mirzazadeh 2016), the enhanced modified extended tanh expansion scheme (Onder et al. 2022; Ozisik et al. 2023), \(\left( \frac{G^\prime }{G^2}\right) \)-expansion method (Arshed and Raza 2020), \(exp(-\phi (\xi ))\)-expansion method (Raza et al. 2023; Javid and Raza 2019; Raza et al. 2019), extended trial equation method (Raza and Javid 2019), trial equation method (Arnous et al. 2016).

Nonlinear evolution equations (NLEEs) model some of the nonlinear dynamical systems in the field of applied sciences such as optics (Mirzazadeh et al. 2015; Arnous and Moraru 2022; Arnous 2022), plasma (Debnath 1994; Whitham 2011). From these systems, the nonlinear Schrödinger equation (NLSE) is the most basic example of nonlinear integrable systems. NLSEs have been utilized to explain the ultrashort pulse propagation in the optical fiber and the slow evolution of a nonlinear weak wave packet in deep water (Peregrine 1983). Davey-Stewartson system (DSS) that was derived by Davey (1974) is an extension of the NLSE. The following \((2+1)-\)dimensional DSS is studied by many researchers for the surface water wave packets with finite depth (Davey 1974; Zedan and Monaquel 2010):

$$\begin{aligned} \left\{ \begin{array}{cc} i \phi _t + \frac{1}{2}\mu ^2 (\phi _{xx}+\mu ^2 \phi _{yy}) + \gamma |\phi |^2 \phi - \psi _x \phi =0,\\ \psi _{xx}- \mu ^2 \psi _{yy} -2\gamma (|\phi |^2)_{x}=0, \end{array} \right. \end{aligned}$$
(1)

in which \(\phi (x,y,t)\) denotes the amplitude of the wave packet of the surface, \(\psi (x,y,t)\) is the velocity potential of the mean flow interacting with the surface wave; moreover, x, y represent the coordinates of the scaled spatial and t defines the coordinate of the scaled temporal. \(\mu \) represents the surface tension, so \(\mu = 1\) gives the DSI equation and \(\mu =i\) gives the DSII equation (Sun et al. 2018). Furthermore, focusing or defocusing cases are described with \(\gamma =\pm 1\). A general multiple-soliton solution form and the analytical traveling wave solutions for the DSS have been acquired via the simplest equation approach; besides, conservation law and the dispersion study have been analyzed in Selima et al. (2016). In Sun et al. (2018), through the Kadomtsev-Petviashvili hierarchy reduction, Sun et al. have produced the semi-rational solutions for eq. (1). Jafari et al. have obtained some novel analytical solutions including trigonometric and exponential functions for eq. (1) with the help of the first integral scheme in Jafari et al. (2012). Periodic and solitary wave solutions for the DSS have been derived through the sine-cosine approach in Zedan and Monaquel (2010). Gaballah et al. have produced the novel Jacobi elliptic wave function solutions of DSS utilizing the modified Jacobi elliptic function approach in Gaballah et al. (2022). Li et al. have acquired the lie symmetry algebra and some analytical solutions with the generalized sub-equation expansion approach for a generalized DSS in Li et al. (2008). Dark, singular, bright, periodic, and rational solitary wave solutions of the generalized DSS have been acquired through the first integral scheme, exp(\(-\Phi (\xi ))-\)expansion approach and first integral technique in Arshed et al. (2021). Moreover, the asymptotic attributes for the acquired family of the higher-order lump solutions of the DSII equation have been presented in Guo et al. (2022). Tang et al. introduced the resonant DSS in 2009 and its analytical solutions that define propagation, doubly periodic wave patterns have been produced with the multi-linear variable separation technique in Tang et al. (2009). Besides, for the \((2+1)-\)dimensional resonant DSS, it has been shown that the system is integrable by applying the Painleve test in Liang and Tang (2009). In order to derive bright, dark, and mixed dark-bright soliton solutions for the \((2+1)-\)dimensional resonant DSS, the sine-Gordon expansion technique has been utilized in Ismael et al. (2023). The new optical soliton solutions for the conformable coupled resonant DSS have been examined in Alabedalhadi et al. (2022) through the ansatz approach. Ismael et al. have produced dark, singular, bright, and singular solutions of the \((2+1)-\)dimensional resonant DSS with M-derivative in Ismael et al. (2021).

The new modified sine-Gordon technique has been used to get soliton solutions of variable-coefficient DSS in El-Shiekh and Gaballah (2020a). New Jacobi, periodic, and hyperbolic wave solutions have been retrieved for DSS with complex variable coefficients in El-Shiekh and Gaballah (2020b) via the direct similarity reduction technique.

The DSS was introduced as an extension of the NLSE. Although \((2+1)-\)dimensional DSS, generalized DSS, and resonant DSS have been studied before the parabolic law nonlinearity form has been adapted for the first time in this study. The \((2+1)-\)dimensional DSS (Ebadi et al. 2011) with the parabolic law nonlinearity is reads:

$$\begin{aligned} \left\{ \begin{array}{ll} i \phi _t + a (\phi _{xx}+\phi _{yy}) + b (c_1 |\phi |^2 + c_2 |\phi |^4)\phi -\alpha \phi \psi =0,\\ \psi _{xx}+\psi _{yy} + \beta (d_1 |\phi |^2 + d_2 |\phi |^4)_{xx}=0. \end{array} \right. \end{aligned}$$
(2)

The \((2+1)-\)dimensional DSS is one of the complex member of NLPDEs that arises in the study of several physical phenomena including nonlinear optics, plasma physics, and fluid dynamics. The motivation for examining this model is that the presented system can allow estimable mathematical and physical insights into the behavior of solitons, waves, and other nonlinear structures. As is known, especially when it comes to events related to nonlinear optics and the models designed for them, one of the areas of focus is the controllability and management of soliton transmission. At the forefront of the factors affecting soliton transmission is nonlinearity, and in the last 20 years, various forms of nonlinearity, with the general heading of self-phase modulation, have found their place in the literature. Examples such as the parabolic law, power law, dual power law, polynomial law, cubic-quintic-septic law, anti-cubic law, triple power law, cubic-quintic-septic-nonic law, Kudryashov’s law of refractive index, generalized anti-cubic law, and log law have been the subject of examination for many models in the literature. The primary focus is on controlling the form and amplitude of the soliton. In this context, the DSS model under investigation is also a widely studied area in the literature and has been the subject of many studies. Investigating the solutions and dynamics of the DSS with parabolic law may produce advancements in studying optical solitons and controlling wave patterns. Therefore, research in this area can have implications for solving real-world problems. The presented model comprises physics, mathematics, and engineering concepts. Hence, another motivating point is that this study is interdisciplinary and creates connections between different branches of science. We emphasize that there is no study on eq. (2) in the literature; therefore, we aim to implement the new Kudryashov method (nKM) and sinh-Gordon equation expansion method (ShGEEM) to the \((2+1)-\)dimensional DSS with parabolic law to obtain the analytical solutions.

There are various analytical methods in order to acquire the analytical solutions of NLPDEs in the literature. We can classify these approaches in many different ways like allowing effective results, and ease of implementation, including different kinds of soliton solutions, not requiring too much mathematical processing. In fact, each method has its own advantages and disadvantages. Thus, the selection of the correct and appropriate method for the problem under consideration depends on the specific requirements and choice of the researcher for their analysis. However, in this article, the reasons for choosing the nKM for the presented model are its widespread use and ease of implementation. Moreover, ShGEEM retrieves more comprehensive and different types of solution functions and soliton types.

The remainder of this manuscript is organized as follows: In Sect. 2, utilizing the wave transformation we present the mathematical analysis for Eq. (2). The nKM and its implementation to Eq. (2) is offered in Sect. 3. We give the definition and application of ShGEEM in section 4. In Sect. 5, we achieve the stability analysis. The graphical illustrations and interpretations are represented in Sect. 6. Finally, we give the Conclusion in Sect. 7.

2 Mathematical analysis of the adapted system given in Eq. (2)

In this section, in order to produce the ordinary differential equation (ODE), we implement the following wave transformation:

$$\begin{aligned} \begin{array}{cc} \phi (x,y,t)=U(\eta ) e^{i \theta (x,y,t)}, \,\,\, \psi (x,y,t)=V(\eta ),\\ \theta (x,y,t)=-\kappa _1 x-\kappa _2 y +\omega t +\Omega , \,\,\, \eta =p_1 x +p_2 y -vt, \end{array} \end{aligned}$$
(3)

in which \(U(\eta )\) and \(V(\eta )\) denote the scalar soliton profile for the complex \(\phi \) and scalar \(\psi \) functions, respectively. \(\theta (x,y,t)\) represents the phase component and \(p_1\), \(p_2\) are associated with the inverse widths of the soliton while v describes the velocity. \(\kappa _1\) and \(\kappa _2\) are the frequency of the soliton in the direction of x and y, respectively. While \(\omega \) represents the wave number, \(\Omega \) denotes the phase constant.

When we apply the wave transformation in eq. (3) to the first equation of Eq. (2), the following ODE is acquired:

$$\begin{aligned} a \left( p_1^2 + p_2^2\right) U^{\prime \prime } - \left( a \left( \kappa _1^2+\kappa _2^2 \right) +\omega \right) U - \alpha UV +b c_1 U^3 + b c_2 U^5 =0, \end{aligned}$$
(4)

which comes from the real part while the imaginary part serves the condition as follows:

$$\begin{aligned} v = - 2a({\kappa _1}{p_1} + {\kappa _2}{p_2}). \end{aligned}$$
(5)

When we use the wave transformation in Eq. (3) for the second equation of Eq. (2), we get the following relation:

$$\begin{aligned} V(\eta )=-\frac{\beta p_1^2 U(\eta )^2 \left( d_2 U(\eta )^2 +d_1 \right) }{p_1^2 + p_2^2}. \end{aligned}$$
(6)

Substituting Eq. (6) into Eq. (4), we derive the following ODE:

$$\begin{aligned}{} & {} a \left( p_1^2 + p_2^2\right) U^{\prime \prime } -\left( a\left( \kappa _1^2+\kappa _2^2 \right) +\omega \right) U + \left( bc_1 + \frac{\alpha \beta p_1^2 d_1}{p_1^2+p_2^2}\right) U^3 \nonumber \\{} & {} + \left( bc_2 + \frac{\alpha \beta p_1^2 d_2}{p_1^2+p_2^2}\right) U^5 =0. \end{aligned}$$
(7)

When applying the homogeneous balance rule between the highest order terms \(U^{\prime \prime }\) and \(U^5\), we get \(m+2=5m\), that is \(m=\frac{1}{2}\). Since the m is the balance number and it is considered as positive integer, we need to define the following simple transformation:

$$\begin{aligned} U=\sqrt{P}, \end{aligned}$$
(8)

where \(P=P(\eta )\) is a new function. When we substitute Eqs. (8) into (7), we have the following equation:

$$ \begin{aligned} & a\left( {p_{1}^{2} + p_{2}^{2} } \right)^{2} \left( {P^{\prime } } \right)^{2} - 2a\left( {p_{1}^{2} + p_{2}^{2} } \right)^{2} PP^{{\prime \prime }} + 4\left( {p_{1}^{2} + p_{2}^{2} } \right)\left[ {\left( {\kappa _{1}^{2} + \kappa _{2}^{2} } \right)a + \omega } \right]P^{2} \\ & \quad + \left[ {4\left( { - \alpha \beta d_{1} - bc_{1} } \right)p_{1}^{2} - 4p_{2}^{2} bc_{1} } \right]P^{3} + \left[ {4\left( { - \alpha \beta d_{2} - bc_{2} } \right)p_{1}^{2} - 4p_{2}^{2} bc_{2} } \right]P^{4} = 0. \\ \end{aligned} $$
(9)

Finally, balancing the terms \(PP^{\prime \prime }\) and \(P^4\), the balancing constant is found as \(m=1\).

3 Explanation and implementation of nKM

In this section, the presentation and application of the nKM method (Kudryashov 2020; Ozisik et al. 2022; Albayrak 2023), which is the first of the methods to be used in the article, are provided. One of the reasons for choosing the nKM method is that it is a contemporary method, easily applicable, secure, and has the capability to produce bright, dark, and singular soliton solutions, which are among the fundamental soliton types. The nKM method, like many methods commonly used in the literature, is based on an auxiliary differential equation, and many methods that use the same auxiliary equation have been used in the literature in recent years. Moreover, many of these methods contain a large number of solution functions. At this point, one of the advantages of the nKM method is that it does not contain repeating soliton solutions. Additionally, the ability of the nKM to be applied to a wide range of NLPDE equations constitutes another advantageous point. These fundamental features have been the main factors in selecting the nKM method. The nKM (Kudryashov 2020; Ozisik et al. 2022; Albayrak 2023) offers that the solution of eq. (2) in the following structure:

$$\begin{aligned} P(\eta ) = \sum _{s=0}^{m}\Lambda _{s}\vartheta ^{s}(\eta ), \end{aligned}$$
(10)

in which \(\Lambda _s\) are real constants to be determined, provided that \(\Lambda _m \ne 0\). m denotes the balancing constant found as \(m=1\) in eq. (2). Therefore, eq. (10) becomes,

$$\begin{aligned} P(\eta ) = \Lambda _{0}+ \Lambda _1 \vartheta (\eta ), \end{aligned}$$
(11)

where \(\vartheta (\eta )\) is the solution of the following formula:

$$\begin{aligned} \vartheta ^{\prime ^2}(\eta )=\delta ^2\vartheta ^2(\eta )[1-\lambda \vartheta ^2(\eta )], \end{aligned}$$
(12)

in which \(\delta \) and \(\lambda \) are real values. Additionally, the solution of eq. (12) is given as follows (Kudryashov 2020; Ozisik et al. 2022):

$$\begin{aligned} \vartheta (\eta )=\frac{4\tau }{4\tau ^2 e^{\delta \eta } + \lambda e^{-\delta \eta }}\,, \end{aligned}$$
(13)

in which \(\tau \) is a nonzero constant. Equation (13) gives the bright soliton when \(\lambda =4 \tau ^{2}\) and the singular soliton for \(\lambda = -4 \tau ^2\).

When substituting Eqs. (11) with  (12) into Eq. (9), collecting all \(\vartheta ^s(\eta )\) coefficients and equating them to zero, we reach the following algebraic system:

$$\begin{aligned} \begin{array}{ll} \vartheta ^0(\eta ): \left( \left( -M p_{1}^{2}-p_{2}^{2} b c_{2}\right) \Lambda _{0}^{2}+\left( -N p_{1}^{2}-p_{2}^{2} b c_{1}\right) \Lambda _{0} +S \left( a R+\omega \right) \right) \Lambda _{0}^{2}=0, \\ \vartheta ^1(\eta ): \left( 8\left( M p_{1}^{2}+ p_{2}^{2} b c_{2}\right) \sigma _{0}^{2}+6\left( N p_{1}^{2}+ p_{2}^{2} b c_{1}\right) \sigma _{0} +\left( a \delta ^{2} S-4 a R-4 \omega \right) S\right) \Lambda _{1} \Lambda _{0} =0,\\ \vartheta ^2(\eta ): \left( 24\left( M p_{1}^{2}+ p_{2}^{2} b c_{2}\right) \Lambda _{0}^{2} +12\left( N p_{1}^{2}+ p_{2}^{2} b c_{1}\right) \Lambda _{0} +\left( a \delta ^{2} S-4 a R-4 \omega \right) S \right) \Lambda _{1}^{2}=0, \\ \vartheta ^3(\eta ): \left( \left( -4\left( M p_{1}^{2} + p_{2}^{2} b c_{2}\right) \Lambda _{0}-N p_{1}^{2}-p_{2}^{2} b c_{1}\right) \Lambda _{1}^{2} +a \delta ^{2} \lambda S^{2}\Lambda _{0} \right) \Lambda _1=0, \\ \vartheta ^4(\eta ): \left( -4\left( M p_{1}^{2}+ p_{2}^{2} b c_{2}\right) \Lambda _{1}^{2}+3a \delta ^{2} \lambda S^{2} \right) \Lambda _1^2=0, \end{array} \end{aligned}$$
(14)

where \(M=\left( \alpha \beta d_{2}+b c_{2} \right) \), \(N=\left( \alpha \beta d_{1}+b c_{1}\right) \), \(S=\left( p_{1}^{2}+p_{2}^{2}\right) \) and \(R=\left( \kappa _{1}^{2}+\kappa _{2}^{2}\right) \). The solution sets of eq. (14) are derived as follows: Set 1:

$$\begin{aligned} \begin{array}{ll} p_{1}=\sqrt{\frac{- b c_{1}}{N}}\,p_{2}, \,\, \Lambda _{0}= 0, \,\, \Lambda _{1}=\sqrt{ \frac{-3 \lambda d_{1} \left( a R+\omega \right) }{b K}},\,\, \delta = 2 \sqrt{ \frac{ \left( a R+\omega \right) N}{a \alpha \beta d_{1} p_{2}^2}}, \end{array} \end{aligned}$$
(15)

Set 2:

$$\begin{aligned} \begin{array}{ll} \omega = \frac{-3 a R \lambda d_{1} -b K \Lambda _{1}^{2}}{3 d_{1} \lambda }, \, \, \Lambda _{1} = \Lambda _{1}, p_{1} = \frac{2 b \Lambda _{1} \, \sqrt{3 a \alpha \beta \lambda c_{1} K}}{3 a \alpha \beta \lambda \delta d_{1}}, \,\, p_{2} = \frac{2 \Lambda _{1} \sqrt{-3a \alpha \beta \lambda b K N}}{3 a \alpha \beta \lambda \delta d_{1}}, \\ \kappa _{1} = \kappa _{1}, \,\, \kappa _{2} = \kappa _{2}, \,\, \Lambda _{0} = 0, \end{array} \end{aligned}$$
(16)

Set 3:

$$\begin{aligned} \begin{array}{ll} \lambda = -\frac{4 b \Lambda _{1}^{2} K N}{3a \alpha \beta p_{2}^{2} d_{1}^{2} \delta ^{2}}, \,\, \omega = -\frac{ a \left[ \beta d_{1} \left( -p_{2}^{2} \delta ^{2}+4R\right) \alpha +4b c_{1} R\right] }{4 N}, p_{1}= \sqrt{\frac{- b c_{1}}{N} }\,p_{2}, \\ p_{2} = p_{2}, \,\, \Lambda _{0}= 0, \,\, \Lambda _{1} = \Lambda _{1} \end{array} \end{aligned}$$
(17)

Set 4:

$$\begin{aligned} \begin{array}{ll} \lambda = \frac{4 c_{1} \Lambda _{1}^{2} b^{2} K }{3 a \alpha \beta d_{1}^{2} \delta ^{2} p_{1}^{2}}, \,\, \omega = -\frac{a \left[ 4 b c_{1}\ R+\alpha \beta d_{1} \delta ^{2} p_{1}^{2}\right] }{4 b c_{1}}, \,\, \delta = \delta , p_{2} = \sqrt{-\frac{N}{b c_{1}}} \,p_{1}, \,\, \Lambda _{0} = 0, \,\, \Lambda _{1} = \Lambda _{1}. \end{array} \end{aligned}$$
(18)

where \(K=\left( c_{1} d_{2}-c_{2} d_{1}\right) \). After we substitute the sets in Eqs. (15)–(18) into Eq. (11) with Eq. (13) and utilize Eqs. (3),  (8), we acquire the following analytical solutions for Eq. (2):

$$\begin{aligned} \begin{array}{ll} \phi _{1,1}(x,y,t)= \left( \frac{4 \sqrt{ \frac{-3 \lambda d_{1} \left( a R+\omega \right) }{b K}} \tau }{4 \tau ^{2} {\mathrm e}^{\delta \eta }+\lambda {\mathrm e}^{-\delta \eta }} \right) ^\frac{1}{2} \times {\mathrm e}^{\textrm{i} \left( \omega t-x\kappa _{1}-y \kappa _{2}+\Omega \right) }, \end{array} \end{aligned}$$
(19)
$$\begin{aligned} \begin{array}{ll} \psi _{1,1}(x,y,t)=-\frac{4\beta \tau p_{1}^{2}}{S}\left( \frac{ \sqrt{ \frac{-3 \lambda d_{1} \left( a R+\omega \right) }{b K}} }{4 \tau ^{2} {\mathrm e}^{\delta \eta }+\lambda {\mathrm e}^{-\delta \eta }} \right) \left( d_{1} +d_{2} \left( \frac{4 \sqrt{ \frac{-3 \lambda d_{1} \left( a R+\omega \right) }{b K}} \tau }{4 \tau ^{2} {\mathrm e}^{\delta \eta }+\lambda {\mathrm e}^{-\delta \eta }}\right) \right) , \end{array} \end{aligned}$$
(20)

where \(p_1\), \(\delta \) are given in eq. (15).

$$\begin{aligned} \begin{array}{ll} \phi _{1,2}(x,y,t)= \sqrt{\frac{4 \Lambda _{1} \tau }{4 \tau ^{2} {\mathrm e}^{\delta \eta }+\lambda {\mathrm e}^{-\delta \eta }}} \times {\mathrm e}^{\textrm{i} \left( \frac{-3 a R \lambda d_{1} -b K \Lambda _{1}^{2}}{3 d_{1} \lambda } t-x\kappa _{1}-y \kappa _{2}+\Omega \right) }, \end{array} \end{aligned}$$
(21)
$$\begin{aligned} \begin{array}{ll} \psi _{1,2}(x,y,t)=-\frac{\beta p_{1}^{2}}{S} \left( \frac{4 \Lambda _{1} \tau }{4 \tau ^{2} {\mathrm e}^{\delta \eta }+\lambda {\mathrm e}^{-\delta \eta }}\right) \, \left( d_{1}+d_{2} \left( \frac{4 \Lambda _{1} \tau }{4 \tau ^{2} {\mathrm e}^{\delta \eta }+\lambda {\mathrm e}^{-\delta \eta }}\right) \right) , \end{array} \end{aligned}$$
(22)

where \(p_1\), \(p_2\) are described in Eq. (16).

$$\begin{aligned} \begin{array}{ll} \phi _{1,3}(x,y,t)=&\left( \frac{4 \Lambda _{1} \tau }{4 \tau ^{2} {\mathrm e}^{\delta \eta }-\frac{4 b \Lambda _{1}^{2} K N}{3a \alpha \beta p_{2}^{2} d_{1}^{2} \delta ^{2}} {\mathrm e}^{-\delta \eta }} \right) ^{\frac{1}{2}} \times {\mathrm e}^{\textrm{i} \left( -\frac{ a \left[ \beta d_{1} \left( -p_{2}^{2} \delta ^{2}+4R\right) \alpha +b c_{1}R \right] }{4N} t-x\kappa _{1}-y \kappa _{2}+\Omega \right) }, \end{array} \end{aligned}$$
(23)
$$\begin{aligned} \begin{array}{ll} \psi _{1,3}(x,y,t)=&-\frac{\beta p_{1}^{2}}{S}\left( \frac{4 \Lambda _{1} \tau }{4 \tau ^{2} {\mathrm e}^{\delta \eta }-\frac{4 b \Lambda _{1}^{2} K N}{3a \alpha \beta p_{2}^{2} d_{1}^{2} \delta ^{2}} {\mathrm e}^{-\delta \eta }}\right) \left( d_{1}+d_{2} \left( \frac{4 \Lambda _{1} \tau }{4 \tau ^{2} {\mathrm e}^{\delta \eta }-\frac{4 b \Lambda _{1}^{2} K N}{3a \alpha \beta p_{2}^{2} d_{1}^{2} \delta ^{2}} {\mathrm e}^{-\delta \eta }}\right) \right) , \end{array} \end{aligned}$$
(24)

where \(p_1\) is given in Eq. (17).

$$\begin{aligned} \begin{array}{ll} \phi _{1,4}(x,y,t)= \left( \frac{4 \Lambda _{1} \tau }{4 \tau ^{2} {\mathrm e}^{\delta \eta }+ \frac{4 c_{1} \Lambda _{1}^{2} b^{2} K }{3 a \alpha \beta d_{1}^{2} \delta ^{2} p_{1}^{2}} {\mathrm e}^{-\delta \eta }} \right) ^{\frac{1}{2}} \times {\mathrm e}^{\textrm{i} \left( -\frac{a \left[ 4 b c_{1} R+\alpha \beta d_{1} \delta ^{2} p_{1}^{2}\right] }{4b c_{1}} t-x\kappa _{1}-y \kappa _{2}+\Omega \right) }, \end{array} \end{aligned}$$
(25)
$$\begin{aligned} \begin{array}{ll} \psi _{1,4}(x,y,t)=-\frac{\beta p_{1}^{2}}{S}\left( \frac{4 \Lambda _{1} \tau }{4 \tau ^{2} {\mathrm e}^{\delta \eta }+ \frac{4 c_{1} \Lambda _{1}^{2} b^{2} K }{3 a \alpha \beta d_{1}^{2} \delta ^{2} p_{1}^{2}} {\mathrm e}^{-\delta \eta }}\right) \, \left( d_{1}+d_{2} \left( \frac{4 \Lambda _{1} \tau }{4 \tau ^{2} {\mathrm e}^{\delta \eta }+ \frac{4 c_{1} \Lambda _{1}^{2} b^{2} K }{3 a \alpha \beta d_{1}^{2} \delta ^{2} p_{1}^{2}} {\mathrm e}^{-\delta \eta }}\right) \right) , \end{array} \end{aligned}$$
(26)

where \(p_2\) is represented in Eq. (18). In Eqs. (19)–(26), \(v = -2a(\kappa _{1}p_{1}+\kappa _{2}p_{2})\), \(\eta =p_{1}x + p_{2}y-vt\) which are given in Eqs. (5) and  (3), respectively.

4 Description and enforcement of ShGEEM

In this section, efforts are being made to introduce and implement the ShGEEM, which is chosen as the second method (Yan 2003a, b; Mathanaranjan et al. 2022; Seadawy et al. 2018; Kumar et al. 2018; Foroutan et al. 2018; Kumar et al. 2018, 2019). In addition to being an effective method, the SHGEEM also has the capability to be applied to many problems. The ease of application and reliability of the method are among its other advantages. We take into account the following solution form in order to apply the proposed scheme:

$$\begin{aligned} P(\Theta )=\sigma _0 + \sum _{s=1}^m cosh^{s-1}(\Theta ) \left[ \sigma _s cosh(\Theta ) + \Upsilon _s sinh(\Theta ) \right] , \end{aligned}$$
(27)

where \(\sigma _s\) and \(\Upsilon _s\) are real values. Moreover, \(\Theta =\Theta (\eta )\) satisfies the following equation:

$$\begin{aligned} \frac{d\Theta }{d\eta }= \sqrt{sinh^2 (\Theta )+C}, \end{aligned}$$
(28)

where C represents the integration constant. Considering the \(C=0\), eq. (28) gives the following solutions:

$$\begin{aligned}{} & {} sinh(\Theta )=csch(\eta ), \, cosh(\Theta )=coth(\eta ), \end{aligned}$$
(29)
$$\begin{aligned}{} & {} sinh(\Theta )=i sech(\eta ), \, cosh(\Theta )=tanh(\eta ). \end{aligned}$$
(30)

Since we determined the balancing constant as \(m=1\) in eq. (2), therefore, eq. (27) converts into:

$$\begin{aligned} P(\Theta )=\sigma _0 + \sigma _1 cosh(\Theta ) + \Upsilon _1 sinh(\Theta ). \end{aligned}$$
(31)

After substituting Eqs. (31) and  (28) into Eq. (9), we produce a polynomial. If the coefficients of \(cosh^i(\Theta ) sinh^j(\Theta ), \, i=0,\ldots ,4,\, j=0,1\) are equated to zero, the following algebraic system is derived:

$$\begin{aligned} \begin{array}{ll} cosh^0(\Theta ) sinh^0(\Theta ): \left[ \left( -24 M \sigma _{0}^{2}-12 N \sigma _{0}+4 a p_{2}^{2} \right. +4 a R+4 \omega \right) p_{1}^{2} +2 a p_{1}^{4} \\ \left. +2 p_{2}^{2} \left( -12 \sigma _{0}^{2} b c_{2}-6 \sigma _{0} b c_{1}+a p_{2}^{2}+2 a R+2 \omega \right) \right] \Upsilon _{1}^2 +4\left( M p_{1}^{2}+ p_{2}^{2} b c_{2}\right) \Upsilon _{1}^{4} \\ - p_{2}^{2} \left( a p_{2}^{2} \sigma _{1}^{2}+4 \sigma _{0}^{2} \left( -\sigma _{0}^{2} b c_{2}-\sigma _{0} b c_{1}+ a R+\omega \right) \right) -a p_{1}^{4} \sigma _{1}^{2} \\ + \left[ -2 a p_{2}^{2} \sigma _{1}^{2}-4 \left( -M \sigma _{0}^{2}-N \sigma _{0}+ a R+\omega \right) \sigma _{0}^{2} \right] p_1^2=0, \\ \\ cosh^0(\Theta ) sinh^1(\Theta ):\\ \left( \begin{array}{ll} 2\left[ \left( 4 M \sigma _{0}+ N \right) p_{1}^{2}+4 p_{2}^{2} \left( \sigma _{0} c_{2}+\frac{c_{1}}{4}\right) b \right] \Upsilon _1^{2}\\ + \left[ \left( -8 M \sigma _{0}^{2}-6 N \sigma _{0}+2 a p_{2}^{2}+4 \left( a R+\omega \right) \right) p_{1}^{2} \right. \\ \left. + a p_{1}^{4} +\left( -8 \sigma _{0}^{2} b c_{2}-6 \sigma _{0} b c_{1}+a p_{2}^{2}+4 \left( a R+ \omega \right) \right) p_{2}^{2}\right] \sigma _0 \end{array}\right) \Upsilon _{1} =0,\\ \\ cosh^1(\Theta ) sinh^0(\Theta ): \\ \left( \begin{array}{ll} 3\left( \left( 4M \sigma _{0}+ N\right) p_{1}^{2}+4 p_{2}^{2} \left( \sigma _{0} c_{2}+\frac{c_{1}}{4}\right) b\right) \Upsilon _{1}^{2} \\ +\left[ \left( -4M \sigma _{0}^{2}-3N \sigma _{0}+2 a p_{2}^{2}+2 a R+2 \omega \right) p_{1}^{2}+a p_{1}^{4} \right. \\ \left. +p_{2}^{2} \left( -4 \sigma _{0}^{2} b c_{2}-3 \sigma _{0} b c_{1}+a p_{2}^{2}+2 a R+2 \omega \right) \right] \sigma _0 \end{array}\right) \sigma _1 =0, \\ \\ cosh^1(\Theta ) sinh^1(\Theta ):\\ \left( \begin{array}{ll} 4\left( M p_{1}^{2}+ p_{2}^{2} b c_{2} \right) \Upsilon _1^2 + \left[ -12M \sigma _{0}^{2} -6N \sigma _{0}+2 a p_{2}^{2}+2 a R+2 \omega \right] p_1^2 \\ + a p_{1}^{4} +\left[ -12 \sigma _{0}^{2} b c_{2}-6 \sigma _{0} b c_{1}+a p_{2}^{2}+2a R+2 \omega \right] p_2^2 \end{array}\right) \sigma _1 \Upsilon _1 =0, \\ \\ cosh^2(\Theta ) sinh^0(\Theta ): -8\left( \left( \alpha \beta d_{2}+c_{2} b\right) p_{1}^{2}+ p_{2}^{2} b c_{2}\right) \Upsilon _1^4 \\ -2\left( \begin{array}{ll} \left( -12M \sigma _{0}^{2}-6N \sigma _{0}+2 a p_{2}^{2}+2 a R+2 \omega \right) p_{1}^{2} \\ + a p_{1}^{4}+p_{2}^{2} \left( -12 \sigma _{0}^{2} b c_{2}-6 \sigma _{0} b c_{1}+a p_{2}^{2}+2 a R+2 \omega \right) \end{array}\right) \sigma _1^2 \\ +\left( \begin{array}{ll} \left( -24M \sigma _{1}^{2}+24M \sigma _{0}^{2}+12N \sigma _{0} -10 a p_{2}^{2} -4 a R-4 \omega \right) p_{1}^{2} -5 a p_{1}^{4} \\ - p_{2}^{2} \left( 24 \left( c_{2} b \sigma _{1}^{2}- \sigma _{0}^{2} b c_{2} \right) -12 \sigma _{0} b c_{1}+5a p_{2}^{2}+4a R+4 \omega \right) \end{array} \right) \Upsilon _1^2 =0, \\ \\ cosh^2(\Theta ) sinh^1(\Theta ): \\ \left( \begin{array}{ll} \left( \left( 4M \sigma _{0}+N\right) p_{1}^{2}+ p_{2}^{2} \left( 4\sigma _{0} c_{2}+c_{1}\right) b\right) \Upsilon _{1}^{2} +\left( 3\left( 4M \sigma _{0}+ N\right) \sigma _{1}^{2}+2 a p_{2}^{2} \sigma _{0}\right) p_{1}^{2} \\ +a \sigma _{0} p_{1}^{4} +p_{2}^{2} \left( 12 \left( \sigma _{0} c_{2}+\frac{c_{1}}{4}\right) b \sigma _{1}^{2}+a p_{2}^{2} \sigma _{0}\right) \end{array} \right) \Upsilon _1 =0, \\ \\ cosh^3(\Theta ) sinh^0(\Theta ): \\ \left( \begin{array}{ll} 3\left[ \left( 4M \sigma _{0}+N\right) p_{1}^{2}+4 p_{2}^{2} \left( \sigma _{0} c_{2}+\frac{c_{1}}{4}\right) b\right] \Upsilon _1^2 +\left( \left( 4M \sigma _{0}+N\right) \sigma _{1}^{2}+2 a p_{2}^{2} \sigma _{0}\right) p_{1}^{2} \\ +p_{2}^{2} \left( \left( 4\sigma _{0} c_{2}+c_{1}\right) b \sigma _{1}^{2}+a p_{2}^{2} \sigma _{0}\right) +a \sigma _{0} p_{1}^{4} \end{array} \right) \sigma _1 =0, \\ \\ cosh^3(\Theta ) sinh^1(\Theta ): \\ \left( \left( 8M p_{1}^{2}+8 p_{2}^{2} b c_{2}\right) \Upsilon _{1}^{2} +\left( 8M \sigma _{1}^{2}+6 a p_{2}^{2}\right) p_{1}^{2} +\left( 8 c_{2} b \sigma _{1}^{2}+3a p_{2}^{2}\right) p_{2}^{2} +3a p_{1}^{4} \right) \sigma _1 \Upsilon _1=0, \\ \\ cosh^4(\Theta ) sinh^0(\Theta ): \\ 3\left( a p_{1}^{4}+\left( 8M \sigma _{1}^{2}+2 a p_{2}^{2}\right) p_{1}^{2}+8 p_{2}^{2} \sigma _{1}^{2} b c_{2}+ a p_{2}^{4} \right) \Upsilon _1^2 +4\left( M p_{1}^{2}+ p_{2}^{2} b c_{2}\right) \Upsilon _{1}^{4} \\ + \left( 3a p_{1}^{4}+\left( 4M \sigma _{1}^{2}+6 a p_{2}^{2}\right) p_{1}^{2}+p_{2}^{2} \left( 4 c_{2} b \sigma _{1}^{2}+3a p_{2}^{2}\right) \right) \sigma _1^2=0, \end{array} \end{aligned}$$
(32)

where \(M=\left( \alpha \beta d_{2}+b c_{2} \right) \), \(N=\left( \alpha \beta d_{1}+b c_{1}\right) \), \(S=\left( p_{1}^{2}+p_{2}^{2}\right) \) and \(R=\left( \kappa _{1}^{2}+\kappa _{2}^{2}\right) \). Solving the system given in Eq. (32), the solution sets are retrieved as follows:

Family 1:

$$\begin{aligned} \begin{array}{cc} d_{1} = \frac{\left( 2a S- b c_{1} \sigma _{1}\right) S}{\sigma _{1} \alpha \beta p_{1}^{2}}, \,\, d_{2}=-\frac{ \left( 4 c_{2} b \sigma _{1}^{2}+ 3aS \right) S}{4 \alpha \beta p_{1}^{2} \sigma _{1}^{2}},\,\, \omega = a \left( S-R\right) ,\\ p_{1} =p_{1},\,\,p_{2} = p_{2},\sigma _{0}=\sigma _{1},\sigma _{1} = \sigma _{1}, \,\, \Upsilon _{1} =0. \end{array} \end{aligned}$$
(33)

Family 2:

$$\begin{aligned} \begin{array}{cc} \omega =\frac{\left( -\Upsilon _{1}^{2} b c_{2}-3 a R\right) d_{1}+b c_{1} d_{2} \Upsilon _{1}^{2}}{3 d_{1}},\,\, p_{1}=\frac{2 \, \sqrt{-3a \alpha \beta c_{1} K}\, \Upsilon _{1} b}{3 a \alpha \beta d_{1}}, \,\, p_{2} = \frac{2 \, \sqrt{3a \alpha \beta b K N}\, \Upsilon _{1}}{3 a \alpha \beta d_{1}}, \\ \kappa _{1}=\kappa _{1},\,\, \kappa _{2} = \kappa _{2}, \,\, \sigma _{0} = 0, \,\, \sigma _{1}= 0, \,\, \Upsilon _{1} = \Upsilon _{1}. \end{array} \end{aligned}$$
(34)

Family 3:

$$\begin{aligned} \begin{array}{cc} c_{1} = \frac{-2 \alpha \beta d_{1} p_{1}^{2} \sigma _{1}+a p_{1}^{4}+2 p_{1}^{2} a p_{2}^{2}+a p_{2}^{4}}{2 \sigma _{1} b S}, \,\, c_{2} = \frac{-16 p_{1}^{2} \sigma _{1}^{2} \alpha \beta d_{2}-3 a p_{1}^{4}-6 p_{1}^{2} a p_{2}^{2}-3 a p_{2}^{4}}{16 b \sigma _{1}^{2} S},\,\, \omega = \frac{a \left( p_{1}^{2}+p_{2}^{2}-4 \kappa _{1}^{2}-4 \kappa _{2}^{2}\right) }{4}, \\ \sigma _{0}= \sigma _{1}, \,\, \sigma _{1} = \sigma _{1}, \,\, \Upsilon _{1} = \sigma _{1}, \end{array} \end{aligned}$$
(35)

where \(K=\left( c_{1} d_{2}-c_{2} d_{1}\right) \). If Eqs. (33), (34), (35) are substituted into Eq. (31) by considering Eqs. (3), (8), (29), (30) the following solutions are acquired:

-With the set in Eq. (33):

$$\begin{aligned} \begin{array}{ll} \phi _{2,1}(x,y,t)=\sqrt{-\sigma _{1} \left( \coth \! \left( \eta \right) -1\right) }\, {\mathrm e}^{\textrm{i} \left( \left( S-R\right) a t -\kappa _{1} x-\kappa _{2} y+\Omega \right) }, \end{array} \end{aligned}$$
(36)
$$\begin{aligned} \begin{array}{ll} \psi _{2,1}(x,y,t)=\frac{\left( 4 b c_{2} \sigma _{1}^{2} \coth \! \left( \eta \right) +3 a \coth \! \left( \eta \right) S -4 c_{2} b \sigma _{1}^{2}+5 a p_{1}^{2}+5 a p_{2}^{2}-4 b c_{1} \sigma _{1}\right) \left( \coth \! \left( \eta \right) -1\right) }{4 \alpha }, \end{array} \end{aligned}$$
(37)
$$\begin{aligned} \phi _{2,2}(x,y,t)=\sqrt{\sigma _{1} \left( \tanh \! \left( \eta \right) +1\right) }\, {\mathrm e}^{\textrm{i} \left( \left( S-R\right) a t -\kappa _{1} x-\kappa _{2} y+\Omega \right) }, \end{aligned}$$
(38)
$$\begin{aligned} \begin{array}{ll} \psi _{2,2}(x,y,t)=\frac{\left( 4 b c_{2} \sigma _{1}^{2} \tanh \! \left( \eta \right) +3 a S \tanh \! \left( \eta \right) +4 c_{2} b \sigma _{1}^{2}-5 a S+4 b c_{1} \sigma _{1}\right) \left( \tanh \! \left( \eta \right) +1\right) }{4 \alpha }. \end{array} \end{aligned}$$
(39)

-With the set in Eq. (34):

$$\begin{aligned} \begin{array}{ll} \phi _{2,3}(x,y,t)= \sqrt{\frac{\Upsilon _{1}}{\sinh \! \left( \eta \right) }} \times {\mathrm e}^{\textrm{i} \frac{\left( \left( - \left( b c_{2}\Upsilon _{1}^{2} +3 a R\right) t- 3 \left( \kappa _{1} x+ \kappa _{2} y- \Omega \right) \right) d_{1}+ b t c_{1} d_{2} \Upsilon _{1}^{2}\right) }{3 d_{1}}}, \end{array} \end{aligned}$$
(40)
$$\begin{aligned} \begin{array}{ll} \psi _{2,3}(x,y,t)=\frac{\left( d_{1} \sinh \! \left( \eta \right) +d_{2} \Upsilon _{1}\right) c_{1} \Upsilon _{1} b}{\sinh \! \left( \eta \right) ^{2} \alpha d_{1}}, \end{array} \end{aligned}$$
(41)
$$\begin{aligned} \begin{array}{ll} \phi _{2,4}(x,y,t)=\sqrt{\frac{\Upsilon _{1} \textrm{i}}{\cosh \! \left( \eta \right) }}\, \times {\mathrm e}^{\textrm{i} \frac{\left( \left( - \left( b c_{2}\Upsilon _{1}^{2} +3 a R\right) t- 3 \left( \kappa _{1} x+ \kappa _{2} y- \Omega \right) \right) d_{1}+ b c_{1} d_{2} \Upsilon _{1}^{2} t\right) }{3 d_{1}}}, \end{array} \end{aligned}$$
(42)
$$\begin{aligned} \begin{array}{ll} \psi _{2,4}(x,y,t)=\frac{\textrm{i} \left( \textrm{i} d_{2} \Upsilon _{1}+d_{1} \cosh \! \left( \eta \right) \right) c_{1} \Upsilon _{1} b}{\cosh \! \left( \eta \right) ^{2} \alpha d_{1}}. \end{array} \end{aligned}$$
(43)

-With the set in Eq. (35):

$$\begin{aligned} \begin{array}{ll} \phi _{2,5}(x,y,t)=\sqrt{\frac{\sigma _{1} \left( 1-\cosh \! \left( \eta \right) +\sinh \! \left( \eta \right) \right) }{\sinh \! \left( \eta \right) }} \times {\mathrm e}^{ \textrm{i} \left( \frac{a \left( S-4R\right) t}{4}-\kappa _{1} x-\kappa _{2} y+\Omega \right) }, \end{array} \end{aligned}$$
(44)
$$\begin{aligned} \begin{array}{ll} \psi _{2,5}(x,y,t)=-\frac{p_{1}^{2} \beta \sigma _{1} \left( \left( 2 d_{2} \sigma _{1}+d_{1}\right) \cosh \! \left( \eta \right) -\left( 2 d_{2} \sigma _{1}+d_{1}\right) \sinh \! \left( \eta \right) +d_{1}\right) }{\left( \cosh \! \left( \eta \right) +1\right) \left( p_{1}^{2}+p_{2}^{2}\right) } \end{array} \end{aligned}$$
(45)
$$\begin{aligned} \begin{array}{ll} \phi _{2,6}(x,y,t)=\sqrt{\frac{\sigma _{1} \left( \textrm{i}+\sinh \! \left( \eta \right) +\cosh \! \left( \eta \right) \right) }{\cosh \! \left( \eta \right) }} \times {\mathrm e}^{ \textrm{i} \left( \frac{a \left( S-4R\right) t}{4}-\kappa _{1} x-\kappa _{2} y+\Omega \right) }, \end{array} \end{aligned}$$
(46)
$$\begin{aligned} \begin{array}{ll} \psi _{2,6}(x,y,t)=-\frac{p_{1}^{2} \beta \sigma _{1} \left( -\left( 2 d_{2} \sigma _{1}+d_{1}\right) \sinh \! \left( \eta \right) -\left( 2 d_{2} \sigma _{1}+d_{1}\right) \cosh \! \left( \eta \right) +\textrm{i} d_{1}\right) }{\left( -\sinh \! \left( \eta \right) +\textrm{i}\right) S}. \end{array} \end{aligned}$$
(47)

In Eqs.(36)–(47) \(v=-2 a \left( p_{1} \kappa _{1}+p_{2} \kappa _{2}\right) \) and \(\eta =-v t+p_{1} x+p_{2} y\).

It can be declared that all the acquired solutions satisfy the presented system. Although Eqs. (42),(43), (46) and (47) are solutions offered by the ShGEEM and given mathematically, they have not been evaluated in the article due to the definition given in Eq. (3).

5 Modulation instability

Substitute the followings into the Eq. (2);

$$\begin{aligned} \begin{aligned} \phi (x,y,t)=&\left( \Phi _0 + \epsilon \Phi _1(x,y,t)\right) e^{-i \Psi _0 t},\\ \psi (x,y,t) =&\Psi _0 + \epsilon \Psi _1(x,y,t), \end{aligned} \end{aligned}$$
(48)

where \(\Phi _0\) and \(\Psi _0\) are normalized optical power. Then linearized equations in terms of \(\Phi _1(x,y,t)\) and \(\Psi _1(x,y,t)\) are obtained as follows;

$$\begin{aligned} \begin{aligned}&\epsilon \left( a \left( \frac{\partial ^{2}}{\partial x^{2}}\Phi _1 \! \right) +a \left( \frac{\partial ^{2}}{\partial y^{2}}\Phi _1 \! \right) \right. \\&\left. +i \left( \frac{\partial }{\partial t}\Phi _1 \! \right) +\left( (5 b c_{2} \Phi _0^{3}+3 b c_{1} \Phi _0 +1 )\Phi _0 - \alpha \Psi _0 \right) \Phi _1 \! -\alpha \Psi _1 \! \Phi _0 \right) = 0,\\&{\epsilon \left( \frac{\partial ^{2}}{\partial x^{2}}\Psi _1 \! +\frac{\partial ^{2}}{\partial y^{2}}\Psi _1 \! +2 \beta d_{1} \left( \frac{\partial ^{2}}{\partial x^{2}}\Phi _1 \! \right) \Phi _0 +4 \beta d_{2} \left( \frac{\partial ^{2}}{\partial x^{2}}\Phi _1 \! \right) \Phi _0^{3}\right) }=0. \end{aligned} \end{aligned}$$
(49)

Substitute the followings into the linearized PDEs in Eq. (49):

$$\begin{aligned} \begin{aligned} \Phi _1(x,y,t) =&A_{1} {\mathrm e}^{i \left( \omega t-x \kappa _{1}-y \kappa _{2}\right) }+A_{2} {\mathrm e}^{\mathrm {-i} \left( \omega t-x \kappa _{1}-y \kappa _{2}\right) },\\ \Psi _1(x,y,t) =&B_{1} {\mathrm e}^{i \left( \omega t-x \kappa _{1}-y \kappa _{2}\right) }+B_{2} {\mathrm e}^{\mathrm {-i} \left( \omega t-x \kappa _{1}-y \kappa _{2}\right) }, \end{aligned} \end{aligned}$$
(50)

where \(\omega \), \(\kappa _1\) and \(\kappa _2\) are real values. Collecting the coefficients of \({\mathrm e}^{i \left( \omega t-x \kappa _{1}-y \kappa _{2}\right) }\) and \({\mathrm e}^{-i \left( \omega t-x \kappa _{1}-y \kappa _{2}\right) }\) and create a coefficient matrix as follows:

$$\begin{aligned} M=\begin{bmatrix} M_{11} &{} M_{12} \\ M_{21} &{} M_{22} \end{bmatrix}, \end{aligned}$$
(51)

where

$$\begin{aligned} \begin{aligned} M_{11} =&5 b c_{2} \Phi _0^{4} \epsilon A_{2}+3 b c_{1} \Phi _0^{2} \epsilon A_{2}-a \epsilon A_{2} \kappa _{1}^{2}-a \epsilon A_{2} \kappa _{2}^{2}-\alpha \Psi _0 \epsilon A_{2}-\alpha \epsilon B_{2} \Phi _0+\Phi _0 \epsilon A_{2}+\epsilon A_{2} \omega ,\\ M_{12} =&5 A_{1} \Phi _0^{4} b c_{2} \epsilon +3 A_{1} \Phi _0^{2} b c_{1} \epsilon -A_{1} a \epsilon \kappa _{1}^{2}-A_{1} a \epsilon \kappa _{2}^{2}-A_{1} \Psi _0 \alpha \epsilon -B_{1} \Phi _0 \alpha \epsilon +A_{1} \Phi _0 \epsilon -A_{1} \epsilon \omega ,\\ M_{21} =&-4 \beta d_{2} \epsilon A_{2} \kappa _{1}^{2} \Phi _0^{3}-2 \beta d_{1} \epsilon A_{2} \kappa _{1}^{2} \Phi _0-\epsilon B_{2} \kappa _{1}^{2}-\epsilon B_{2} \kappa _{2}^{2},\\ M_{22} =&-4 A_{1} \Phi _0^{3} \beta d_{2} \epsilon \kappa _{1}^{2}-2 A_{1} \Phi _0 \beta d_{1} \epsilon \kappa _{1}^{2}-B_{1} \epsilon \kappa _{1}^{2}-B_{1} \epsilon \kappa _{2}^{2}. \end{aligned} \end{aligned}$$
(52)

Solve the \(\omega \) in Eq. (51) in according to \(det(M)=0\):

$$\begin{aligned} \omega = \frac{-(A_{1} B_{2}-A_{2} B_{1})\left( a \kappa _{1}^{4} + \Omega _1 \kappa _1^2 + \Omega _2 \kappa _2^2\right) }{\Omega _3 \kappa _1^2 + \kappa _2^2(A_{1} B_{2}+A_{2} B_{1})}, \end{aligned}$$
(53)

where

$$\begin{aligned} \begin{aligned} \Omega _1 =&\left( -4 \alpha \beta d_{2}-5 b c_{2}\right) \Phi _0^{4}+\left( -2 \alpha \beta d_{1}-3 b c_{1}\right) \Phi _0^{2}-\Phi _0+2 a \kappa _{2}^{2}+\alpha \Psi _0, \\ \Omega _2 =&-5 b c_{2} \Phi _0^{4}-3 b c_{1} \Phi _0^{2}+a \kappa _{2}^{2}+\alpha \Psi _0-\Phi _0,\\ \Omega _3 =&8 A_{1} A_{2} \Phi _0^{3} \beta d_{2}+4 A_{1} A_{2} \Phi _0 \beta d_{1}+A_{1} B_{2}+A_{2} B_{1}. \end{aligned} \end{aligned}$$
(54)

Since Eq. (53) does not have a structure containing any complex form, it does not have an instability state. Therefore, modulation instability does not occur and the solutions of Eq. (2) are stable.

6 Results and discussion

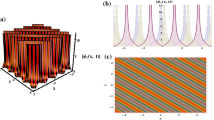
In this section, we showcase our results through graphical illustrations and provide interpretations of the gathered insights. Figs. 1a and  1b illustrate the 3D portraits for \(|\phi _{1,1}(x,1,t)|\) and \(\psi _{1,1}(x,1,t)\) at \(\tau =2, \, c_1=2, \, d_1=1, \, c_2=0.3, \, d_2=1, a=1, \, b=-0.4, \, \kappa _1=2, \, \kappa _2=1, \, \alpha =1, \, \beta =2, \, \omega =1, \, \lambda =16, \, p_2=2, \, \Omega =1\). We plot the 2D graphs in Fig. 1c–f to investigate the effects of the parameters \(c_1\), \(c_2\), \(d_1\) and \(d_2\) to the behavior of the soliton. The 2D views of \(|\phi _{1,1}(x,1,1)|\) (continuous lines) and \(\psi _{1,1}(x,1,1)\) (dashed lines) at \(\tau =2, \, d_1=1, \, c_2=0.3, \, d_2=1, a=1, \, b=-0.4, \, \kappa _1=2, \, \kappa _2=1, \, \alpha =1, \, \beta =2, \, \omega =1, \, \lambda =16, \, p_2=2, \, \Omega =1\) for \(c_1=0.5,\, 0.75, \, 1.5\) is depicted in Fig. 1c. We demonstrate the 2D plots of \(|\phi _{1,1}(x,1,1)|\) (continuous lines) and \(\psi _{1,1}(x,1,1)\) (dashed lines) at \(\tau =2, \, d_1=1, \, c_1=2, \, d_2=1, a=1, \, b=-0.4, \, \kappa _1=2, \, \kappa _2=1, \, \alpha =1, \, \beta =2, \, \omega =1, \, \lambda =16, \, p_2=2, \, \Omega =1\) for \(c_2=0.25,\, 0.75, \, 1.5\) in Fig. 1d. The 2D views of \(|\phi _{1,1}(x,1,1)|\) (continuous lines) and \(\psi _{1,1}(x,1,1)\) (dashed lines) at \(\tau =2, \, c_1=2, \, c_2=0.3, \, d_2=1, a=1, \, b=-0.4, \, \kappa _1=2, \, \kappa _2=1, \, \alpha =1, \, \beta =2, \, \omega =1, \, \lambda =16, \, p_2=2, \, \Omega =1\) for \(d_1=1,\, 2, \, 3\) is plotted in Fig. 1e. We illustrate the 2D plots of \(|\phi _{1,1}(x,1,1)|\) (continuous lines) and \(\psi _{1,1}(x,1,1)\) (dashed lines) at \(\tau =2, \, d_1=1, \, c_1=2, \, c_2=0.3, a=1, \, b=-0.4, \, \kappa _1=2, \, \kappa _2=1, \, \alpha =1, \, \beta =2, \, \omega =1, \, \lambda =16, \, p_2=2, \, \Omega =1\) for \(d_2=0.25,\, 0.5, \, 1\) in Fig. 1f. We can observe that Fig. 1 represents the bright soliton for \(|\phi _{1,1}(x,1,t)|\) and the dark soliton for \(\psi _{1,1}(x,1,t)\). For increasing values of \(c_1\) in Fig. 1c, we can see that both the soliton represented with \(|\phi _{1,1}(x,1,1)|\) moves to the right and the amplitude of the soliton decreases. Depending on the increasing values of \(c_1\), the shape of the soliton turns into a more degenerate form, in a sense it gives a view whose apex approaches the horizontal axis. A similar view occurs for Fig. 1e but for decreasing values of \(d_1\). In Figs. 1d and f, the observation obtained with the previous examination is followed for increasing values of \(c_2\) and decreasing values of \(d_2\) without observing any horizontal movement of the soliton. However, the form of the soliton gives the view of more deformation in both graphs, that is, a view almost approaching the horizontal axis is formed. It is seen from Fig. 1c that the amplitude of the dark soliton decreases and moves to the right depending on the increasing values of \(c_1\) for \(\psi _{1,1}(x,1,1)\). A similar behavior occurs for decreasing values of \(d_1\) in Fig. 1e. On the other hand, the amplitude of the soliton increases depending on the increase in \(c_2\) without a horizontal position change in Fig. 1d. A similar view appears due to decreasing values of \(d_2\) in Fig. 1f.

Fig. 1
figure 1

The graphs of \(\phi _{1,1}(x,1,t)\) and \(\psi _{1,1}(x,1,t)\) in Eqs. (19),  (20) under the effects of \(c_1, \, c_2,\, d_1\) and \(d_2\)

Full size image

We demonstrate the 3D views of \(|\phi _{1,2}(x,1,t)|\) and \(\psi _{1,2}(x,1,t)\) for the parameter values \(\tau =2, \, c_1=2, \, d_1=1, \, c_2=0.3, \, d_2=1, a=1, \, b=-0.4, \, \kappa _1=2, \, \kappa _2=1, \, \alpha =1, \, \beta =2, \, \omega =1, \, \lambda =16, \, p_2=2, \, \Omega =1, \delta =2, \, \Lambda _1=1\) in Fig. 2a and b, respectively. We depict the 2D graphs for \(|\phi _{1,2}(x,1,1)|\) (continuous lines) and \(\psi _{1,2}(x,1,1)\) (dashed lines) with \(\tau =2, \, d_1=1, \, c_2=0.3, \, d_2=1, a=1, \, b=-0.4, \, \kappa _1=2, \, \kappa _2=1, \, \alpha =1, \, \beta =2, \, \omega =1, \, \lambda =16, \, p_2=2, \, \Omega =1, \delta =2, \, \Lambda _1=1\) at \(c_1=0.25, \, 0.75, \, 1.5\) in Fig. 2c. It can be observed from Fig. 1c that depending on the decrease in \(c_1\), the skirts of the soliton representation for \(|\phi _{1,2}(x,1,1)|\) open horizontally, and the bright soliton appearance gradually turns into a compacton-like appearance. Moreover, depending on the decrease in \(c_1\), the dark soliton view for \(\psi _{1,2}(x,1,1)\) deforms, gradually approaches the horizontal axis (decreases in amplitude), and the apex also shows a position change to the right. For \(c_2=0.25, \, 0.75, \, 1.5\), the 2D plots of \(|\phi _{1,2}(x,1,1)|\) (continuous lines) and \(\psi _{1,2}(x,1,1)\) (dashed lines) are illustrated in Fig. 2d at \(\tau =2, \, c_1=2, \, d_1=1, \, d_2=1, a=1, \, b=-0.4, \, \kappa _1=2, \, \kappa _2=1, \, \alpha =1, \, \beta =2, \, \omega =1, \, \lambda =16, \, p_2=2, \, \Omega =1, \delta =2, \, \Lambda _1=1\). From Fig. 2d we can see inverse effect from Fig. 2c because the skirts of the soliton for \(|\phi _{1,2}(x,1,1)|\) and \(\psi _{1,2}(x,1,1)\) open horizontally while \(c_2\) increases. We plot the 2D graphs for \(|\phi _{1,2}(x,1,1)|\) (continuous lines) and \(\psi _{1,2}(x,1,1)\) (dashed lines) at the values \(\tau =2, \, c_1=2, \, c_2=0.3, \, d_2=1,\, a=1, \, b=-0.4, \, \kappa _1=2, \, \kappa _2=1, \, \alpha =1, \, \beta =2, \, \omega =1, \, \lambda =16, \, p_2=2, \, \Omega =1, \delta =2, \, \Lambda _1=1\) for \(d_1=1, \, 2, \, 3\) in Fig. 2e. In Fig. 2e, as \(d_1\) increases, the width of the soliton acquired for \(|\phi _{1,2}(x,1,1)|\) increases horizontally and the bright soliton view gradually converts to the compacton-like shape. Furthermore, it can be examined from Fig. 2e that the amplitude of the soliton decreases and the apex of the soliton shifts to the right as \(d_1\) increases. Figure 2f shows the 2D views of \(|\phi _{1,2}(x,1,1)|\) (continuous lines) and \(\psi _{1,2}(x,1,1)\) (dashed lines) with \(\tau =2, \, c_1=2, \, d_1=1, \, c_2=0.3, \, a=1, \, b=-0.4, \, \kappa _1=2, \, \kappa _2=1, \, \alpha =1, \, \beta =2, \, \omega =1, \, \lambda =16, \, p_2=2, \, \Omega =1, \delta =2, \, \Lambda _1=1\) at \(d_2=0.25, \, 0.5, \, 1\). Depending on the decrease in \(d_2\), the width of the soliton for \(|\phi _{1,2}(x,1,1)|\) and \(\psi _{1,2}(x,1,1)\) increases horizontally in Fig. 2f; besides the amplitude of the soliton for \(\psi _{1,2}(x,1,1)\) (dashed lines) decreases. It can be seen from Fig. 2 that it represents the compacton-like shape.

Fig. 2
figure 2

The plots of \(\phi _{1,2}(x,1,t)\) and \(\psi _{1,2}(x,1,t)\) in Eqs. (21),  (22) under the influences of \(c_1, \, c_2, \, d_1\) and \(d_2\)

Full size image

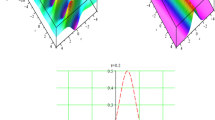
Figure 3a and b illustrate the 3D plots for \(|\phi _{2,1}(x,1,t)|\) and \(\psi _{2,1}(x,1,t)\) at \(\sigma _1=2, \, p_1=1, \, p_2=2, \, \kappa _1=0.2, \, \kappa _2=3, \, a=0.8,\, b=0.2, \, c_1=0.2, \, c_2=0.01, \,\alpha =1, \, \beta =0.2, \, \Omega =-1\), respectively. We depict the 2D plots in Fig. 3c–f so that we examine the effects of the parameters \(\kappa _1, \, \kappa _2, \, p_1, \, p_2\) to behavior of the soliton. The 2D views for \(|\phi _{2,1}(x,1,1)|\) (continuous lines) and \(\psi _{2,1}(x,1,1)\) (dashed lines) are illustrated in Fig. 3c using the values \(\sigma _1=2, \, p_1=1, \, p_2=2, \, \kappa _2=3, \, a=0.8,\, b=0.2, \, c_1=0.2, \, c_2=0.01, \,\alpha =1, \, \beta =0.2, \, \Omega =-1\) with \(\kappa _1=1,\, 2,\, 3\). We display the 2D plots of \(|\phi _{2,1}(x,1,1)|\) (continuous lines) and \(\psi _{2,1}(x,1,1)\) (dashed lines) in Fig. 3d at \(\sigma _1=2, \, p_1=1, \, p_2=2, \, \kappa _1=0.2, \, a=0.8,\, b=0.2, \, c_1=0.2, \, c_2=0.01, \,\alpha =1, \, \beta =0.2, \, \Omega =-1\) at \(\kappa _2=0.25, \, 0.5, \, 1\). We demonstrate the 2D views for \(|\phi _{2,1}(x,1,1)|\) (continuous lines) and \(\psi _{2,1}(x,1,1)\) (dashed lines) in Fig. 3e with the values \(\sigma _1=2, \, p_2=2, \, \kappa _1=0.2, \, \kappa _2=3, \, a=0.8,\, b=0.2, \, c_1=0.2, \, c_2=0.01, \,\alpha =1, \, \beta =0.2, \, \Omega =-1\) for \(p_1=1, \, 2, \, 3\). Moreover, the 2D visualizations of \(|\phi _{2,1}(x,1,1)|\) (continuous lines) and \(\psi _{2,1}(x,1,1)\) (dashed lines) are plotted in Fig. 3f at \(\sigma _1=2, \, p_1=1, \, \kappa _1=0.2, \, \kappa _2=3, \, a=0.8,\, b=0.2, \, c_1=0.2, \, c_2=0.01, \,\alpha =1, \, \beta =0.2, \, \Omega =-1\) for \(p_2 = 1,\,2,\,3\). It can be seen from Fig. 3c that depending on the increase in \(\kappa _1\), the soliton views for both \(|\phi _{2,1}(x,1,1)|\) and \(\psi _{2,1}(x,1,1)\) move to the left. The same effect is observed for \(\kappa _2\) in Fig. 3d and for \(p_2\) in Fig. 3f. We can examine the inverse effect for \(p_1\) in Fig. 3e because according to the increase in \(p_1\), the soliton views for both \(|\phi _{2,1}(x,1,1)|\) and \(\psi _{2,1}(x,1,1)\) move to the right. We can analyze from Fig. 3 that it shows the singular soliton.

Fig. 3
figure 3

The plots for \(\phi _{2,1}(x,1,t)\) and \(\psi _{2,1}(x,1,t)\) in Eqs. (36) and  (37) under the effects of \(\kappa _1, \, \kappa _2, \, p_1\) and \(p_2\)

Full size image

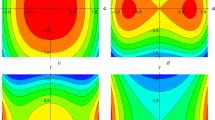
The 3D portraits of \(|\phi _{2,2}(x,1,t)|\) and \(\psi _{2,2}(x,1,t)\) are represented at the parameter values \(\sigma _1=2, \, p_1=1, \, p_2=2, \, \kappa _1=0.2, \, \kappa _2=3, \, a=0.8, \, \Omega =-1, \, b=0.2, \, c_1=0.2, \, c_2=0.01, \, \alpha =1, \, \beta =0.2\) in Fig. 4a and b, respectively. Figure 4a shows the kink soliton view as Fig. 4b represents the view of a combination of dark and kink soliton. We plot the 2D views of \(|\phi _{2,2}(x,1,1)|\) (continuous lines) and \(\psi _{2,2}(x,1,1)\) (dashed lines) at \(\sigma _1=2, \, p_1=1, \, p_2=2, \, \kappa _2=3, \, a=0.8, \, \Omega =-1, \, b=0.2, \, c_1=0.2, \, c_2=0.01, \, \alpha =1, \, \beta =0.2\) for \(\kappa _1=0.1, \, 0.2, \, 0.3\) in Fig. 4c. We can observe from Fig. 4c that depending on the increasing values of \(\kappa _1\) in the \(|\phi _{2,2}(x,1,1)|\) graph, the kink soliton view turns into a smoother form; besides, there is no change in the levels of the lower and upper skirts (flats) of the soliton, that is, in the amplitude of the soliton. For \(\psi _{2,2}(x,1,1)\), depending on the increase in \(\kappa _1\), the kink-dark soliton view does not change in general, but the lower peak (hole) point of the dark soliton shows a position change to the left. However, both the upper side (upper left flatness) and lower side (lower right flatness) of the kink soliton remain at the same level (amplitude) horizontally depending on the decreasing or increasing values of x. The 2D plots for \(|\phi _{2,2}(x,1,1)|\) (continuous lines) and \(\psi _{2,2}(x,1,1)\) (dashed lines) are depicted with the values \(\sigma _1=2, \, p_1=1, \, p_2=2, \, \kappa _1=0.2, \, a=0.8, \, \Omega =-1, \, b=0.2, \, c_1=0.2, \, c_2=0.01, \, \alpha =1, \, \beta =0.2\) for \(\kappa _2=0.25, \, 0.5, \, 1\) in Fig. 4d. It can be understood from Fig. 4d that the kink soliton view for \(|\phi _{2,2}(x,1,1)|\) is preserved, and the soliton for \(|\phi _{2,2}(x,1,1)|\) moves to the left depending on the increasing values of \(\kappa _2\). The same effect is observed for the soliton view of \(\psi _{2,2}(x,1,1)\) in Fig. 4d, that is, there is a movement to the left according to an increase in \(\kappa _2\). We represent the 2D views of \(|\phi _{2,2}(x,1,1)|\) (continuous lines) and \(\psi _{2,2}(x,1,1)\) (dashed lines) in Fig. 4e at the values \(\sigma _1=2, \, p_2=2, \, \kappa _1=0.2, \, \kappa _2=3, \, a=0.8, \, \Omega =-1, \, b=0.2, \, c_1=0.2, \, c_2=0.01, \, \alpha =1, \, \beta =0.2\) for \(p_1=1, \, 2, \, 3\). We can interpret from Fig. 4e that with the increase of \(p_1\), the soliton for \(|\phi _{2,2}(x,1,1)|\) (solid lines) changes position to the right, but this change is not proportional to the increase in \(p_1\) (red to green). At the same time, there is no change in the left and right flatness levels of the soliton for \(|\phi _{2,2}(x,1,1)|\). Moreover, for \(\psi _{2,2}(x,1,1)\), with the increase of \(p_1\), the soliton reflects both a rightward movement and a vertical amplitude increase. With a similar interpretation, we can not say that these increments are directly proportional to \(p_1\). The 2D graphs for \(|\phi _{2,2}(x,1,1)|\) (continuous lines) and \(\psi _{2,2}(x,1,1)\) (dashed lines) are displayed in Fig. 4f with \(\sigma _1=2, \, p_1=1, \, \kappa _1=0.2, \, \kappa _2=3, \, a=0.8, \, \Omega =-1, \, b=0.2, \, c_1=0.2, \, c_2=0.01, \, \alpha =1, \, \beta =0.2\) at \(p_2=1,\, 2,\, 3\). It can be analyzed from Fig. 4f that although the soliton for \(|\phi _{2,2}(x,1,1)|\) moves to the left, there is no change in the left and right flatness levels of the soliton for \(|\phi _{2,2}(x,1,1)|\) as in Fig. 4e while \(p_2\) increases. Contrary to Fig. 4e, the soliton for \(\psi _{2,2}(x,1,1)\) moves to the left with an increase of \(p_2\). Furthermore, Fig. 4f gives the view of amplitude increment vertically with increment in \(p_2\).

Fig. 4
figure 4

The plots for \(\phi _{2,2}(x,1,t)\), \(\psi _{2,2}(x,1,t)\) in Eqs. (38) and  (39) with the effects of \(\kappa _1, \, \kappa _2, \, p_1\) and \(p_2\)

Full size image

We represent the 3D portraits of \(|\phi _{2,5}(x,1,t)|\) and \(\psi _{2,5}(x,1,t)\) at \(\sigma _1=2, \Upsilon _1=1, \, p_1=1, \, p_2=2, \, \kappa _1=0.1, \, \kappa _2=3,\, a=0.8,\, b=0.2,\, \alpha =1, \, \beta =0.4, \, \Omega =-1\) in Fig. 5a and b, respectively. We can observe that Fig. 5a and b display the kink soliton. In Fig. 5c, the 2D views for \(|\phi _{2,5}(x,1,1)|\) (continuous lines) and \(\psi _{2,5}(x,1,1)\) (dashed lines) are depicted using \(\sigma _1=2, \Upsilon _1=1, \, p_1=1, \, p_2=2, \, \kappa _2=3,\, a=0.8,\, b=0.2,\, \alpha =1, \, \beta =0.4, \, \Omega =-1\) with \(\kappa _1=0.1, \, 0.2, \, 0.3\). It is seen from Fig. 5c that for both \(|\phi _{2,5}(x,1,1)|\) graph and \(\psi _{2,5}(x,1,1)\) graph, the lower and upper flatness levels of the soliton, that is, the amplitude of the soliton, do not change and there is a very small movement to the left with the increase of \(\kappa _1\). We illustrate the 2D plots of \(|\phi _{2,5}(x,1,1)|\) (continuous lines) and \(\psi _{2,5}(x,1,1)\) (dashed lines) via \(\sigma _1=2, \Upsilon _1=1, \, p_1=1, \, p_2=2, \, \kappa _1=0.1, \, a=0.8,\, b=0.2,\, \alpha =1, \, \beta =0.4, \, \Omega =-1\) for \(\kappa _2=0.25, \, 0.5, \, 1\) in Fig. 5d. Similar to the observation in Fig. 5c, it can be interpreted from Fig. 5d that the amplitude of the soliton does not change for both \(|\phi _{2,5}(x,1,1)|\) graph and \(\psi _{2,5}(x,1,1)\) graph, while the soliton moves to the left with the increase of \(\kappa _2\). Moreover, Fig. 5e demonstrates the 2D views of \(|\phi _{2,5}(x,1,1)|\) (continuous lines) and \(\psi _{2,5}(x,1,1)\) (dashed lines) with \(\sigma _1=2, \Upsilon _1=1, \, p_2=2, \, \kappa _1=0.1, \, \kappa _2=3,\, a=0.8,\, b=0.2,\, \alpha =1, \, \beta =0.4, \, \Omega =-1\) at \(p_1=1, \, 2, \,3\). Figure 5e shows that the solitons for both \(|\phi _{2,5}(x,1,1)|\) and \(\psi _{2,5}(x,1,1)\) move the the right with the increment of \(p_1\). Depending on the increase in \(p_1\), the amplitude of the soliton does not change for \(|\phi _{2,5}(x,1,1)|\) graph, while the amplitude of the soliton increases for \(\psi _{2,5}(x,1,1)\) graph according to Fig. 5e. The 2D plots of \(|\phi _{2,5}(x,1,1)|\) (continuous lines) and \(\psi _{2,5}(x,1,1)\) (dashed lines) at \(\sigma _1=2, \Upsilon _1=1, \, p_1=1, \, \kappa _1=0.1, \, \kappa _2=3,\, a=0.8,\, b=0.2,\, \alpha =1, \, \beta =0.4, \, \Omega =-1\) are depicted for \(p_2=1,\, 2, \, 3\) in Fig. 5f. Unlike Fig. 5e, in  5f, the movement of the soliton is to the left for both \(|\phi _{2,5}(x,1,1)|\) graph and \(\psi _{2,5}(x,1,1)\) graph depending on the \(p_2\) increment. Furthermore, with the increment of \(p_2\), while there is no change in the amplitude of the soliton for \(|\phi _{2,5}(x,1,1)|\) graph, the amplitude of the soliton decreases for \(\psi _{2,5}(x,1,1)\) graph in Fig. 5f.

Fig. 5
figure 5

The graphs of \(\phi _{2,5}(x,1,t)\), \(\psi _{2,5}(x,1,t)\) in Eqs. (44),  (45) under the effects of \(\kappa _1, \, \kappa _2, \, p_1\) and \(p_2\)

Full size image

In conclusion for this section, it should be noted that the graphs presented above and the examinations conducted pertain to the parabolic law nonlinearity form of the (2+1)-DSS model, which has been introduced for the first time in this study. In this regard, the results obtained have been presented for the first time in this study. Moreover, before proceeding to the graphic presentations of the conducted studies, it has been verified that all the solution functions obtained satisfy the main equation.

7 Conclusion

In this research article, the (2+1)-dimensional Davey-Stewartson system, which has a distinctive importance among NLPDEs and is the subject of many studies, has been investigated by adapting its parabolic law nonlinearity form. The examination was conducted using two effective methods, nKM and ShGEEM, and bright, dark, singular, and various kink-type soliton solutions were obtained. The 3D and 2D plots of some of the acquired solutions were depicted by using the appropriate parameter values. Moreover, the effect of parameters related to the parabolic law nonlinearity form has been investigated and interpreted with detailed graphical presentations. The acquired results provided us that the generated system is a model that produces different types of solitons and gives analytical solutions. The model that is worked on awaits the researchers’ interest to obtain different types of solitons using other methods, to study the fractional forms, to investigate multiple soliton solutions, to conduct bifurcation analysis, and to research its stochastic forms as open problems in this field.