1 Introduction

The propagation of electromagnetic waves in optical metamaterials is widely recognized to have several applications in real life (Cai and Shalaev 2010; Biswas et al. 2010; Shalaev 2007). In such real-world applications, metamaterials constitute a significant medium. Metamaterials are artificial synthetic materials that have numerous intriguing electromagnetic characteristics that regular materials do not have (Biswas et al. 2014; Hubert et al. 2019; Zhou et al. 2014, 2015; Kader et al. 2019; Xu et al. 2015). Victor Veselago, who concentrated on the purely theoretical conception of negative index materials, established the theoretical properties of metamaterials for the first time in the 1960s. Metamaterials are used in a wide range of applications, which would include smart solar power management, sensor detection and infrastructure monitoring, medical devices, optical filters, improving ultrasonic sensors, remote aerospace applications, high-frequency battlefield communication, and lenses for high-gain antennas, as well as earthquake shielding structures. (Valipour et al. 2021). The electric- and magnetic-field components contribute in the propagation of optical pulses through metamaterials (Hubert et al. 2019). It’s worth noting that some researchers recently demonstrated that the nonlinear dynamical model for explaining the propagation of ultrashort optical solitons in nonlinear metamaterials can be modeled by the perturbed nonlinear Schrödinger equation, which includes the Raman effect, parabolic law nonlinearity, third-order dispersion nonlinear dispersion, and self-steepening (Biswas et al. 2014; Hubert et al. 2019; Zhou et al. 2014, 2015; Kader et al. 2019; Xu et al. 2015). However, the fourth order dispersion term of the above models are missing. As a result, we take into account the nonlinear metamaterials model with cubic-quintic nonlinearity, self steepening effect, detuning multimodal dispersion, as well as nonlinear third and fourth order dispersion terms, which is given by Hubert et al. (2019):

$$\begin{aligned} \begin{aligned}&iu_t+au_{xx}+b|u|^2u+c|u|^4u+d\,u+i \lambda \,u_x+is(|u|^2u)_{x}+iv(|u|^2)_{x}u\\&\quad +i\theta |u|^2u_x+i\gamma \,u_{xxx}+\sigma \,u_{xxxx}\\&\quad +\theta _1(|u|^2u)_{xx}+\theta _2|u|^2u_{xx}+\theta _3u^2u^*_{xx}=0. \end{aligned} \end{aligned}$$
(1)

The complex-valued soliton profile is represented by u(x, t),  \(i=\sqrt{-1},\) whereas x and t are independent variables that represent spatial and temporal factors, respectively. The constants are a for the coefficients of the group velocity dispersion (GVD) term, b for the coefficients of the cubic, and quintic nonlinear terms, and c for the coefficients of the cubic and quintic nonlinear terms, respectively. The cubic and quintic nonlinearities, commonly known as the parabolic law nonlinearity, should be mentioned specifically here. In particular, \(\lambda \) represents intermodal dispersion, s and v represent detuning coefficients, as well as intermodal and nonlinear dispersion, correspondingly. The coefficients of third and fourth order dispersion, respectively, are \(\gamma \) and \(\sigma .\) Furthermore, \(\theta _{l},\,l=1,2,3\) denotes the perturbation terms typically arise in the context of metamaterials (Hubert et al. 2019).

In Hubert et al. (2019), the solitary ansatz and the Riccati equation techniques have recently been used to generate the bright, dark, combined dark-singular, and singular soliton solutions to Eq. (1). However, this present study also investigate novel soliton solutions to the governing Eq. (1) based on the extended sinh Gordon expansion method (EshGEM). In the past, many researchers applied the EshGEM to a variety of the nonlinear models (Yan 2003; Xie et al. 2002; Zhao 2006; Kumar et al. 2018, 2019; Seadawy et al. 2018). Except the EshGEM, analytic solutions are found to the variety of integer and fractal order models with the execution of other methods (Attia et al. 2020; Zafar et al. 2021, 2022; Kumar and Paul 2021; Kumar et al. 2021a, b; Akinyemi et al. 2021, 2022a, b; Khater et al. 2021; Nuruzzaman et al. 2021; Ghanbari 2021a, b; Ghanbari et al. 2020; Mathanaranjan 2020, 2021a, b; Ahmad et al. 2021; Korpinar et al. 2020; Hashemi et al. 2019; Cimpoiasu and Pauna 2018; Hosseini et al. 2021a, b). Notwithstanding, the prime intension of the study is to execute the EshGEM to Eq. (1). This suggested EshGEM can overcome the limitations of the solitary anstaz method (Hubert et al. 2019).

The rest of the paper is organized as follows: In Sect. 2, we provided the outline of EshGEM. The mathematical analysis of the model is discussed in Sect. 3. In Sects. 4 and 5, we described the implementation of the proposed method and physical explanation of the obtained solutions. Finally, Sect. 6 concludes the paper.

2 Outlines of EshGEM

The overall description of EshGEM is given in this section. To give an overview of the techniques, we consider the following sinh-Gordon equation (Yan 2003) where \(u=u(x,\,t)\) and \(\eta \in {\mathbb {R}}\setminus \{0\}\) as:

$$\begin{aligned} u_{xt}=\eta \sinh (u). \end{aligned}$$
(2)

The following nonlinear ordinary differential equation (NODE) is obtained by applying the wave transformation \(u=u(x,\,t)=U(\zeta ),\,\zeta =\alpha (x-ct)\) to Eq. (2):

$$\begin{aligned} U^{\prime \prime }=\frac{\eta }{\alpha ^{2}c}\sinh (U), \end{aligned}$$
(3)

where \(\alpha \) is the travelling wave’s amplitude and c is the travelling wave’s speed. Integrating Eq. (3), we obtain the following equation:

$$\begin{aligned} \left[ \left( \frac{U}{2}\right) ^{\prime }\right] ^{2}=\frac{\eta }{\alpha ^{2}c}\sinh ^{2}\left( \frac{U}{2}\right) +\kappa _1, \end{aligned}$$
(4)

where \(\kappa _1\) is the constant of integration. Substituting \(\displaystyle \frac{U}{2}=r(\zeta )\) and \(\displaystyle -\frac{\eta }{\alpha ^{2}c}=\kappa _2\) in Eq. (4), gives

$$\begin{aligned} r^{\prime }=\sqrt{\kappa _1+\kappa _2\sinh ^2(r)}, \end{aligned}$$
(5)

where \(\kappa _1\) and \(\kappa _2\) have distinct values. The following set of solutions are accessible to Eq. (5) [see Xie et al. (2002) for more detail].

Case 1

Taking \(\kappa _1=0\) and \(\kappa _1=1,\) Eq. (5) yields

$$\begin{aligned} r^{\prime }=\sinh (r). \end{aligned}$$
(6)

The sinh-Gordon equation is simplified in this way. When Eq. (6) is simplified, the following important equations result:

$$\begin{aligned} \sinh (r)=\pm {i}{{\,\mathrm{sech}\,}}(\zeta ),\quad \cosh (r)=-\tanh (\zeta ), \end{aligned}$$
(7)

and

$$\begin{aligned} \sinh (r)=\pm {{\,\mathrm{csch}\,}}(\zeta ),\quad \cosh (r)=-\coth (\zeta ). \end{aligned}$$
(8)

Case 2

Again, taking \(\kappa _1=1\) and \(\kappa _2=1,\) Eq. (5) becomes

$$\begin{aligned} r^{\prime }=\cosh (r). \end{aligned}$$
(9)

The sinh-Gordon equation is also simplified in this way. When \autoref{sng:55} is simplified, the following important equations result:

$$\begin{aligned} \sinh (r)=\tan (\zeta ),\quad \,\cosh (r)=\pm \sec (\zeta ), \end{aligned}$$
(10)

and

$$\begin{aligned} \sinh (r)=-\cot (\zeta ),\quad \,\cosh (r)=\pm \csc (\zeta ). \end{aligned}$$
(11)

To find various wave solutions to the nonlinear partial differential equations (NPDEs), we formulate the following form of equation:

$$\begin{aligned} P(u,\,uu_{x},\,u^{2}u_{t},\,u_{xx}\,\cdots ). \end{aligned}$$
(12)

Using the wave transformation \(u(x,t)=W(\zeta ),\,\zeta =\alpha (x-ct)\) on Eq. (12) results in the NODE:

$$\begin{aligned} G(W,\,WW^{\prime },\,W^{2}W^{\prime },\,W^{\prime \prime },\,\cdots ). \end{aligned}$$
(13)

Now, we assume the finite series solutions of the Eq. (13), as:

$$\begin{aligned} W(r)=\sum _{l=1}^{\Omega }\text {cosh}^{l-1}(r)\big [B_{l}\sinh (r)+A_{l}\cosh (r)\big ]+A_{0}. \end{aligned}$$
(14)

It is presumed that the solution \(W(\zeta )\) of the nonlinear Eq. (14), together with Eqs. (6), (7), and (8), may be stated as follows:

$$\begin{aligned} W(\zeta )=\sum _{l=1}^{\Omega }(-\tanh (\zeta ))^{^{l-1}}\big [\pm \,iB_{l}{{\,\mathrm{sech}\,}}(\zeta )-A_{l}\tanh (\zeta )\big ]+A_{0}, \end{aligned}$$
(15)

and

$$\begin{aligned} W(\zeta )=\sum _{l=1}^{\Omega }(-\coth (\zeta )^{^{l-1}}\big [\pm \,iB_{l}{{\,\mathrm{csch}\,}}(\zeta )-A_{l}\coth (\zeta )\big ]+A_{0}. \end{aligned}$$
(16)

Similarly, suppose that the solution \(W(\zeta )\) of the nonlinear Eq. (14), as well as Eqs. (9), (10), and (11), may be stated as follows:

$$\begin{aligned} W(\zeta )=\sum _{l=1}^{\Omega }(\pm \sec (\zeta ))^{^{l-1}}\big [B_{l}\tan (\zeta )\pm \,A_{l}\sec (\zeta )\big ]+A_{0}, \end{aligned}$$
(17)

and

$$\begin{aligned} W(\zeta )=\sum _{l=1}^{\Omega }(\pm \csc (\zeta )^{^{l-1}}\big [-B_{l}\cot (\zeta )\pm \,A_{l}\csc (\zeta )\big ]+A_{0}. \end{aligned}$$
(18)

We calculate \(\Omega \) by balancing the highest power nonlinear term with the highest derivative in the converted NODE. Setting each summation of the coefficients of \(\sinh ^{l}(r)\cosh ^{l}(r),\,0\le {l}\le {\Omega }\) to be zero results in a set of equations. Solving this set of equations yield the values of the coefficients \(A_{l},\,B_{l},\,\alpha \) and c. Finally, inserting the obtained values of these coefficients into Eq. (14) along with the value of \(\Omega \), gives the optical solutions to the Eq. (13).

3 Mathematical analysis of the model

To study Eq. (1), we consider the below wave transformation:

$$\begin{aligned} u(x,t)=\phi (\zeta )e^{i\theta (x,t)}, \quad \,\zeta =x+\nu {t},\quad \,\theta =-kx+g{t}, \end{aligned}$$
(19)

where \(g,\,k,\,\nu \) are the constants and \(i=\sqrt{-1}.\) Inserting Eq. (19) into Eq. (1) and splitting the real part and imaginary part, we have

$$\begin{aligned} \begin{aligned}&(d-ak^2-k^3\gamma +k\lambda +k^4\sigma -g)\phi (\zeta )\\&\quad +(b+ks+k\theta -k^2\theta _1-k^2\theta _2-k^2\theta _3)\phi (\zeta )^3\\&\quad +c\phi (\zeta )^5+6\theta _1\phi (\zeta )\phi ^{\prime }(\zeta )^2+(a+3k(\gamma -2k\sigma ))\phi ^{\prime \prime }(\zeta )\\&\quad +(3\theta _1+\theta _2+\theta _3)\phi (\zeta )^2\phi ^{\prime \prime }(\zeta )+\sigma \phi ^{(4)}(\zeta )=0. \end{aligned} \end{aligned}$$
(20)
$$\begin{aligned} \begin{aligned}&(-2 a k-3 k^2\gamma +\lambda +\nu +4k^3\sigma )\phi ^{\prime }(\zeta )+(3s+2v+\theta \\&\quad -6k\theta _1-2k\theta _2+2k\theta _3)\phi (\zeta )^2\phi ^{\prime }(\zeta )+(\gamma -4k\sigma )\phi ^{(3)}(\zeta )=0. \end{aligned} \end{aligned}$$
(21)

Differentiating Eq. (21) with regard to \(``\zeta "\) results:

$$\begin{aligned} \begin{aligned}&2(3s+2v+\theta -2k(3\theta _1+\theta _2-\theta _3))\phi (\zeta )\phi ^{\prime }(\zeta )^2\\&\quad +(-2ak-3k^2\gamma +\lambda +\nu +4k^3\sigma )\phi ^{\prime \prime }(\zeta )\\&\quad +(3s+2v+\theta -2k(3\theta _1+\theta _2-\theta _3))\phi (\zeta )^2\phi ^{\prime \prime }(\zeta )+(\gamma -4k\sigma )\phi ^{(4)}(\zeta )=0. \end{aligned} \end{aligned}$$
(22)

By eliminating \(\phi ^{(4)}(\zeta )\) from the Eqs. (20) and (22), we get

$$\begin{aligned} b_1 \phi (\zeta )^2 \phi ''(\zeta )+b_2 \phi ''(\zeta )+b_3 \phi (\zeta ) \phi '(\zeta )^2+b_4\phi (\zeta ) +b_5 \phi (\zeta )^3+b_6 \phi (\zeta )^5 =0, \end{aligned}$$
(23)

where

$$\begin{aligned} \begin{aligned} b_1&=(\gamma -2k\sigma )(3\theta _1+\theta _2)+(\gamma -6k\sigma )\theta _3-(3s+2v+\theta )\sigma ,\\ b_2&=\gamma (a+3k\gamma )-(2ak+15k^2\gamma +\lambda +\nu )\sigma +20k^3\sigma ^2,\\ b_3&=-2(-3(\gamma -2k\sigma )\theta _1+\sigma (3s+2v+\theta -2k\theta _2+2k\theta _3)),\\ b_4&=(\gamma -4k\sigma )(d+k(-k(a+k\gamma )+\lambda +k^3\sigma )-g),\\ b_5&=(\gamma -4k\sigma )(b+k(s+\theta )-k^2(\theta _1+\theta _2+\theta _3)),\\ b_6&=c(\gamma -4k\sigma ), \end{aligned} \end{aligned}$$
(24)

where \((\gamma -4k\sigma )\ne {0}.\) Our goal now is to solve Eq. (23), by using the expanded shGEEM.

4 Implementation of the described method

In the following subsections, we implement the extended shGEEM to solve the nonlinear meta-materials having third and fourth order dispersions. Applying the homogeneous balance principle between \(\phi (\zeta )^2\phi ^{\prime \prime }(\zeta )\) and \(\phi (\zeta )^5\) in Eq. (23), we have \(\Omega =1.\)

4.1 Case 1: For \(r^{\prime }=\sinh (r)\)

The expanded shGEEM has the solution in the form of Eq. (23) courtesy to Eqs. (14), (15), and (16) as:

$$\begin{aligned} W(\zeta )= & {} \pm {i}B_{1}{{\,\mathrm{sech}\,}}(\zeta )-A_{1}\tanh (\zeta )+A_{0}, \end{aligned}$$
(25)
$$\begin{aligned} W(\zeta )= & {} \pm {i}B_{1}{{\,\mathrm{csch}\,}}(\zeta )-A_{1}\coth (\zeta )+A_{0}, \end{aligned}$$
(26)

and

$$\begin{aligned} W(r)=B_{1}\sinh (r)+A_{1}\cosh (r)+A_{0}, \end{aligned}$$
(27)

where either \(A_1\) or \(B_1\) can be zero, but neither \(A_1\) nor \(B_1\) can be zero at the same time. After that, a polynomial in powers of hyperbolic functions is produced by putting the form of Eq. (27) together with its second derivative into Eq. (23). We obtain a collection of algebraic equations by putting the summation of the coefficients of the trigonometric identities with the same power to zero. The parameters value can be determined by simplifying these set of equations. By putting these values of the parameters into Eqs. (25) and (26), and then into Eq. (19), the following Eq. (1) solutions may be derived for each instance:

Result 1

$$\begin{aligned}&A_0= 0,\,\,\,A_1=\pm \sqrt{-\frac{2b_1+b_3}{b_6}},\,\,\,B_1= 0, \end{aligned}$$
(28)
$$ \begin{array}{*{20}l} {\nu = - (2ak + 15k^{2} \gamma + \lambda ) + 20k^{3} \sigma + \frac{{\gamma (a + 3k\gamma )}}{\sigma }} \hfill \\ {\;\;\; + \frac{{(2b_{1} + b_{3} )(2(b_{1} + b_{3} ) - b_{5} )}}{{2\sigma {\mkern 1mu} b_{6} }}} \hfill \\ \end{array} , $$
(29)

and

$$\begin{aligned} g=d+k(-k(a+k\gamma )+\lambda +k^3\sigma )+\frac{(2b_1+b_3)(2b_1+b_3-b_5)}{(\gamma -4k\sigma )b_6}. \end{aligned}$$
(30)

Putting the values of Result 1 into Eqs. (25) and (26), we obtain the dark and singular soliton solutions for the above model as follows:

$$\begin{aligned} u(x,t)=\pm \sqrt{-\frac{2b_1+b_3}{b_6}}\tanh (x+\nu {t})e^{i(-kx+g{t})}, \end{aligned}$$
(31)

and

$$\begin{aligned} u(x,t)=\pm \sqrt{-\frac{2b_1+b_3}{b_6}}\coth (x+\nu {t})e^{i(-k{x}+g{t})}, \end{aligned}$$
(32)

where \(b_l,\,l=1,\cdots ,6\) given in Eq. (24) and provided that \((2b_1+b_3)b_6<0.\)

Fig. 1
figure 1

The 3D plots of the solutions defined by Eqs. (31) and (32) that indicate a the dark soliton and b the singular soliton, respectively for \(\sigma =\gamma =k=\nu =\theta =\theta _1=\theta _2=\theta _3=s=v=1,\) and \(c=-1\)

Full size image

Result 2

$$\begin{aligned}&A_0=0,\,\,\,A_1=0,\,\,\,B_1=\pm \sqrt{-\frac{2b_1+b_3}{b_6}}, \end{aligned}$$
(33)
$$\begin{aligned}&\nu =-(2ak+15k^2\gamma +\lambda )+20k^3\sigma \nonumber \\&\quad +\frac{\gamma (a+3k\gamma )}{\sigma }-\frac{(2b_1+b_3)(b_1+b_3+b_5)}{2\sigma \,b_6}, \end{aligned}$$
(34)

and

$$\begin{aligned} g=d+k(-k(a+k\gamma )+\lambda +k^3\sigma )+\frac{(2b_1+b_3)(b_1+b_3+b_5)}{2 (\gamma -4k\sigma )b_6}. \end{aligned}$$
(35)

Inserting the values of Result 2 into Eqs. (25) and (26), we obtain the bright and singular soliton solutions for the above model as follows:

$$\begin{aligned} u(x,t)= \pm \sqrt{-\frac{2b_1+b_3}{b_6}}\,\,{{\,\mathrm{sech}\,}}(x+\nu {t})e^{i(-kx+g{t})}, \end{aligned}$$
(36)

and

$$\begin{aligned} u(x,t)=\pm \sqrt{-\frac{2b_1+b_3}{b_6}}\,\,\,{{\,\mathrm{csch}\,}}(x+\nu {t})e^{i(-kx+g{t})}, \end{aligned}$$
(37)

where \(b_l,\,l=1,\cdots ,6\) given in Eq. (24) and provided that \((2b_1+b_3)b_6<0.\)

Fig. 2
figure 2

The 3D plots of the solutions given by Eqs. (36) and (37) that indicate a the bright soliton and b the singular soliton, respectively, under taken the free parameters of \(\sigma =\gamma =k=\nu =\theta =\theta _1=\theta _2=\theta _3=s=v=1,\) and \(c=-1.\)

Full size image

Result 3.1

$$\begin{aligned}&A_0= 0,\,\,\,A_1=\pm \frac{1}{2}\sqrt{-\frac{2b_1+b_3}{b_6}},\,\,\,B_1=-\frac{1}{2}\sqrt{-\frac{2b_1+b_3}{b_6}}, \end{aligned}$$
(38)
$$\begin{aligned}&\nu =-(2ak+15k^2\gamma +\lambda )+20k^3\sigma +\frac{\gamma (a+3k\gamma )}{\sigma }\nonumber \\&\quad +\frac{(2b_1+b_3)(b_1+b_3-2b_5)}{4\sigma \,b_6}, \end{aligned}$$
(39)

and

$$\begin{aligned} g=d+k(-k(a+k\gamma )+\lambda +k^3\sigma )+\frac{(2b_1+b_3)(2b_1+b_3-4b_5)}{16(\gamma -4k\sigma )b_6}. \end{aligned}$$
(40)

Substituting the values of Result 3.1 into Eqs. (25) and (26), we obtain the mixed dark–bright and singular solitons of the considered nonlinear model as:

$$\begin{aligned} u(x,t)=\pm \frac{1}{2}\sqrt{-\frac{2b_1+b_3}{b_6}}\big (i{{\,\mathrm{sech}\,}}(x+\nu {t})+\tanh (x+\nu {t})\big )e^{i(-kx+g{t})}, \end{aligned}$$
(41)

and

$$\begin{aligned} u(x,t)=\pm \frac{1}{2}\sqrt{-\frac{2b_1+b_3}{b_6}}\big (i{{\,\mathrm{csch}\,}}(x+\nu {t})+\coth (x+\nu {t})\big )e^{i(-kx+g{t})}. \end{aligned}$$
(42)

Result 3.2

$$\begin{aligned}&A_0= 0,\,\,\,A_1=\pm \frac{1}{2}\sqrt{-\frac{2b_1+b_3}{b_6}},\,\,\,B_1=\frac{1}{2}\sqrt{-\frac{2b_1+b_3}{b_6}}, \end{aligned}$$
(43)
$$\begin{aligned}&\nu =-(2ak+15k^2\gamma +\lambda )+20k^3\sigma +\frac{\gamma (a+3k\gamma )}{\sigma }\nonumber \\&\quad +\frac{(2b_1+b_3)(b_1+b_3-2b_5)}{4\sigma \,b_6}, \end{aligned}$$
(44)

and

$$\begin{aligned} g=d+k(-k(a+k\gamma )+\lambda +k^3\sigma )+\frac{(2b_1+b_3)(2b_1+b_3-4b_5)}{16(\gamma -4k\sigma )b_6}. \end{aligned}$$
(45)

Putting the values of Result 3.2 into Eqs. (25) and (26), we acquire the mixed dark-bright and singular soliton solutions to the model as:

$$\begin{aligned} u(x,t)=\pm \frac{1}{2}\sqrt{-\frac{2b_1+b_3}{b_6}}\big (i{{\,\mathrm{sech}\,}}(x+\nu {t})-\tanh (x+\nu {t})\big )e^{i(-kx+g{t})}, \end{aligned}$$
(46)

and

$$\begin{aligned} u(x,t)=\pm \frac{1}{2}\sqrt{-\frac{2b_1+b_3}{b_6}}\big (i{{\,\mathrm{csch}\,}}(x+\nu {t})-\coth (x+\nu {t})\big )e^{i(-kx+g{t})}, \end{aligned}$$
(47)

where \(b_l,\,(l=1,\cdots ,6)\) given in Eq. (24) and provided that \((2b_1+b_3)b_6<0.\)

Fig. 3
figure 3

3D plots a for the combined dark-bright solution of the Eq. (46), and b for singular soliton solution of the Eq. (47) by taking the free parameter values as \(\sigma =\gamma =k=\nu =\theta =\theta _1=\theta _2=\theta _3=s=v=1,\) and \(c=-1.\)

Full size image

4.2 Case II: For \(r^{\prime }=\cosh (r)\)

The extended sinh-Gordon equation expansion method (EshGEEM) has the solution in the form of Eq. (23), according to Eqs. (14), (17), and (18) repectively.

$$\begin{aligned} W(\zeta )=B_{1}\tan (\zeta )\pm \,A_{1}\sec (\zeta )+A_{0}, \end{aligned}$$
(48)
$$\begin{aligned} W(\zeta )=-B_{1}\cot (\zeta )\pm \,A_{1}\csc (\zeta )+A_{0}, \end{aligned}$$
(49)

and

$$\begin{aligned} W(r)=B_{1}\sinh (r)+A_{1}\cosh (r)+A_{0}, \end{aligned}$$
(50)

where \(A_1\) or \(B_1\) may be zero, but neither \(A_1\) nor \(B_1\) may be zero at the same time. After that, a polynomial in powers of hyperbolic functions is produced by putting the form of Eq. (50) together with its second derivative into Eq. (23). We obtain a collection of algebraic equations by setting the summation of the coefficients of the trigonometric identities with the same power to zero. The parameter values can be determined after simplifying the equations. By putting the values of the parameters into Eqs. (48) and (49) and then into Eq. (19), the following solution of Eq. (1) may be determined for each instance.

Result 1

$$\begin{aligned}&A_0= 0,\,\,A_1=\pm \sqrt{-\frac{2b_1+b_3}{b_6}},\,\,\,B_1=0, \end{aligned}$$
(51)
$$\begin{aligned}&\nu =-(2ak+15k^2\gamma +\lambda )+20k^3\sigma +\frac{\gamma (a+3k\gamma )}{\sigma } +\frac{(2b_1+b_3)(b_1+b_3-b_5)}{2\sigma \,b_6}, \end{aligned}$$
(52)

and

$$\begin{aligned} g=d+k(-k(a+k\gamma )+\lambda +k^3\sigma )+\frac{(2b_1+b_3)(b_1+b_3-b_5)}{2 (\gamma -4k\sigma )b_6}. \end{aligned}$$
(53)

We derive the periodic and singular periodic solutions for the aforementioned model by plugging the values of Result 1 into Eqs. (48) and (49) accordingly:

$$\begin{aligned} u(x,t)= \pm \sqrt{-\frac{2b_1+b_3}{b_6}}\tan (x+\nu {t})e^{i(-kx+g{t})}, \end{aligned}$$
(54)

and

$$\begin{aligned} u(x,t)=\pm \sqrt{-\frac{2b_1+b_3}{b_6}}\cot (x+\nu {t})e^{i(-kx+g{t})}, \end{aligned}$$
(55)

where \(b_l,\,l=1,\cdots ,6\) given in Eq. (24) and provided that \((2b_1+b_3)b_6<0.\)

Result 2

$$\begin{aligned}&A_0= 0,\,\,\,A_1=0,\,\,\,B_1=\pm \sqrt{-\frac{2b_1+b_3}{b_6}}, \end{aligned}$$
(56)
$$\begin{aligned}&\nu =-(2ak+15k^2\gamma +\lambda )+20k^3\sigma \nonumber \\&\quad +\frac{\gamma (a+3k\gamma )}{\sigma } -\frac{(2b_1+b_3)(2(b_1+b_3)+b_5)}{2\sigma \,b_6}, \end{aligned}$$
(57)

and

$$\begin{aligned} g=d+k(-k(a+k\gamma )+\lambda +k^3\sigma )+\frac{(2b_1+b_3)(2b_1+b_3+b_5)}{(\gamma -4k\sigma )b_6}. \end{aligned}$$
(58)

We get the periodic and singular periodic solutions for the aforementioned model by plugging in the parameters from Result 2 into Eqs. (48) and (49):

$$\begin{aligned} u(x,t)=\pm \sqrt{-\frac{2b_1+b_3}{b_6}}\sec (x+\nu {t})e^{i(-kx+g{t})}, \end{aligned}$$
(59)

and

$$\begin{aligned} u(x,t)=\pm \sqrt{-\frac{2b_1+b_3}{b_6}}\csc (x+\nu {t})e^{i(-kx+g{t})}, \end{aligned}$$
(60)

where \(b_l,\,l=1,\cdots ,6\) given in Eq. (24) and provided that \((2b_1+b_3)b_6<0.\)

Result 3.1

$$\begin{aligned}&A_0= 0,\,\,\,A_1=\pm \frac{1}{2}\sqrt{-\frac{2b_1+b_3}{b_6}},\,\,\,B_1=-\frac{1}{2}\sqrt{-\frac{2b_1+b_3}{b_6}}, \end{aligned}$$
(61)
$$\begin{aligned}&\nu =-(2ak+15k^2\gamma +\lambda )+20k^3\sigma \nonumber \\&\quad +\frac{\gamma (a+3k\gamma )}{\sigma } -\frac{(2b_1+b_3)(b_1+b_3+2b_5)}{4\sigma \,b_6}, \end{aligned}$$
(62)

and

$$\begin{aligned} g=d+k(-k(a+k\gamma )+\lambda +k^3\sigma )+\frac{(2b_1+b_3)(2b_1+b_3+4b_5)}{16(\gamma -4k\sigma )b_6}. \end{aligned}$$
(63)

We acquire the mixed periodic-singular and singular periodic solutions to the aforementioned model by plugging the values from Result 3.1 into Eqs. (48) and (49), respectively:

$$\begin{aligned} u(x,t)=\pm \frac{1}{2}\sqrt{-\frac{2b_1+b_3}{b_6}}\big (i\sec (x+\nu {t})+\tan (x+\nu {t})\big )e^{i(-kx+g{t})}, \end{aligned}$$
(64)

and

$$\begin{aligned} u(x,t)=\pm \frac{1}{2}\sqrt{-\frac{2b_1+b_3}{b_6}}\big (i\csc (x+\nu {t})+\cot (x+\nu {t})\big )e^{i(-kx+g{t})}. \end{aligned}$$
(65)

Result 3.2

$$\begin{aligned}&A_0= 0,\,\,\,A_1=\pm \frac{1}{2}\sqrt{-\frac{2b_1+b_3}{b_6}},\,\,\,B_1=\frac{1}{2}\sqrt{-\frac{2b_1+b_3}{b_6}}, \end{aligned}$$
(66)
$$\begin{aligned}&\nu =-(2ak+15k^2\gamma +\lambda )+20k^3\sigma +\frac{\gamma (a+3k\gamma )}{\sigma }-\frac{(2b_1+b_3)(b_1+b_3+2b_5)}{4\sigma \,b_6}, \end{aligned}$$
(67)

and

$$\begin{aligned} g=d+k(-k(a+k\gamma )+\lambda +k^3\sigma )+\frac{(2b_1+b_3)(2b_1+b_3+4b_5)}{16(\gamma -4k\sigma )b_6}. \end{aligned}$$
(68)

Also, putting the values of Result 3.2 into Eqs. (48) and (49), we obtain the combined periodic-singular and singular periodic solutions to the proposed nonlinear model as follows:

$$\begin{aligned} u(x,t)=\pm \frac{1}{2}\sqrt{-\frac{2b_1+b_3}{b_6}}\big (i\sec (x+\nu {t})-\tan (x+\nu {t})\big )e^{i(-kx+g{t})}, \end{aligned}$$
(69)

and

$$\begin{aligned} u(x,t)=\pm \frac{1}{2}\sqrt{-\frac{2b_1+b_3}{b_6}}\big (i\csc (x+\nu {t})-\cot (x+\nu {t})\big )e^{i(-kx+g{t})}, \end{aligned}$$
(70)

where \(b_l,\,l=1,\,\cdots ,6\) given in Eq. (24) and provided that \((2b_1+b_3)b_6<0.\)

Fig. 4
figure 4

a 3D plot for combined periodic-singular solution of Eq. (69) b 3D plot for singular periodic solution of Eq. (70) for \(\sigma =\gamma =k=\nu =\theta =\theta _1=\theta _2=\theta _3=s=v=1,\) and \(c=-1.\)

Full size image

5 Physical explanation of the obtained solutions

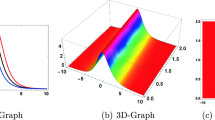
The EshGEM is executed to generate novel soliton solutions to the metamaterials model having the cubic-quintic nonlinearity, detuning intermodal dispersion, self steepening effect, nonlinear third and fourth order dispersion. It is mentioned in introduction section that the model has been solved though the ansatz and the Riccati equation methods. As in Hubert et al. (2019), bright, dark, combo dark–singular, and singular soliton solutions are reported. In this study, we determine some novel dark, bright, combined dark-bright, combined singular, and singular periodic soliton solutions of the governing equations for metamaterials via the EshGEM. To the best of our knowledge, all of the combined dark–bright, combined singular, and singular periodic soliton solutions have been reported here for the first time. It is point out that the accuracy of the received solutions are checked by substituting each analytic solutions back into model equation. All of the produced soliton solutions have some physical illustration. To display such phenomena, we have portrayed some 3D graphs among the generated dark, bright, mixed dark–bright, singular, and mixed periodic-singular soliton solutions under the selection of different values free parameters, which are mentioned in Figs. 1, 2, 3 and 4. Thus, the graphical outputs indicate that the EshGEM will contribute to secure novel soliton solutions for other related models.

6 Conclusions

In summary, the novel exact solutions in the form of dark, bright, combined dark–bright, singular, combined singular and other soliton solutions solitons are reported for the metamaterials model having third and fourth order dispersions with the aid of the EshGEM. The combined dark–bright, singular-periodic, and singular soliton solutions are reported first time for this model. The obtained result illustrates the wave propagation of ultrashort optical solitons in the nonlinear metamaterials. Furthermore, the results evidence that the proposed approach is highly reliable and provides novel solutions when compared to other techniques, as well as the power to produce a wide spectrum of soliton solutions.