1 Introduction

Nonlinear fractional differential equations(NFDEs) are mathematical equations that involve derivatives of fractional order. They combine the concepts of nonlinearity and fractional calculus, which extends the classical integer-order calculus to non-integer orders.

$$\begin{aligned} D^{\alpha } u(t) = f(t, u(t), D^{\beta } u(t)). \end{aligned}$$

where \(D^{\alpha }\) is the fractional derivative operator of order \(\alpha , u(t)\) represents the unknown function, \(f(t, u(t), D^{\beta } u(t))\) is a nonlinear function of t, y(t), and the fractional derivative \(D^{\beta } u(t)\) of order \(\beta \) is taken with respect to t. Because fractional derivatives introduce memory effects into the system, the state of the system at any given time depends on both its recent history and its current inputs.  Due to the nonlinear nature of the equations, solving nonlinear fractional differential equations is typically more difficult than solving linear fractional differential equations. To solve these equations, a number of numerical and analytical techniques have been developed, including the Laplace transform, the Adomian decomposition method, and the variational iteration method. Numerical techniques include finite difference methods, numerical approximation schemes, and spectral methods (Caputo 1969; Miller and Ross 1993; Clarkson et al. 1986; Saxton 1985; Prakash et al. 2021; Yan et al. 2022; WuFulai and Deng 2020; Baleanu et al. 2017; Veeresha et al. 2022; Akinyemi et al. 2022; Li et al. 2002; Gao et al. 2022; Seadawy et al. 2021; Renu et al. 2021; Zhang and Ma 1999; Kala et al. 2019; Li and Zhang 2002; Yan et al. 2021; Toprakseven 2021; Al-Smadi et al. 2021). Applications for nonlinear fractional differential equations can be found in a number of disciplines, such as physics, engineering, biology, finance, and control theory, where complex dynamics and memory effects are present but not well captured by integer-order models (Ali 2021; Wazwaz 2008; Mohebbi 2012; Hawagfeh and Kaya 2004; kumar et al. 2022; Achab 2019). The nonlinear fractional generalized Pochhammer-Chree equation is a mathematical equation that combines elements of nonlinear dynamics, fractional calculus, and the Pochhammer-Chree equation. It explains the behavior of specific physical phenomena or systems where nonlinearity and fractional order derivatives are important factors. Through the use of the homotopy perturbation transform method and the propagation of longitudinal deformation waves in an elastic rod, this paper aims to investigate new approximation solutions to the generalized Pochhammer-Chree equation (Seadawy et al. 2021).

$$\begin{aligned} u_{tt}-u_{ttxx}- \mu (u)_{xx}=0. \end{aligned}$$
(1)

where \(\mu (u)\) is a rational function of u. Eq. (1) describes how a longitudinal deformation wave moves through an elastic rod. for \(\mu (u)= u^q\) for the value \(q= 2, 3, 5\) respectively (Runzhang and Yacheng 2010), and numerically examined how two single wave solutions interacted.

$$\begin{aligned} \begin{aligned} \mu (u)&= a_1 u + a_2 u^2 + u^3,\\ \mu (u)&= a_1 u+ a_2 u^3 + a_3 u^5. \end{aligned} \end{aligned}$$
(2)

Runzhang and Yacheng (2010). I have offered some explicit solitary wave solutions to (1) using the method for solving algebraic equations.

In this work, we take into account the generalized PC equation.

$$\begin{aligned} \frac{\partial ^2 u}{\partial t^2}= \frac{\partial ^4 u}{\partial t^2 \partial x^2}+ \frac{\partial ^2 }{\partial x^2}\left( \beta _1 u(x,t)+ \beta _2u^q (x,t)+ \beta _3 u^{2q-1}(x,t)\right) .~~t>0, \end{aligned}$$
(3)

In this equation \(\beta _1,~ \beta _2,\) and \(\beta _3\) are arbitrary constant and \(q>0\).

Let’Considering the nonlinear fractional PC Equation

$$\begin{aligned} ^{CF}_0\;D_t^{2\alpha }\;u= \frac{\partial ^4 u}{\partial t^2 \partial x^2}+ \frac{\partial ^2 }{\partial x^2}\left( \beta _1 u(x,t)+ \beta _2u^q (x,t)+ \beta _3 u^{2q-1}(x,t)\right) . 1< \alpha \le 2,~~ q,t>0, \end{aligned}$$
(4)
$$\begin{aligned} u(x, 0)= \Phi (x),~~~~ u_t(x,0)= \Psi . \end{aligned}$$

where \(u= u(x, t)\) is the unknown functions x and \(t, u_t\) is the partial derivative of u with respect to \(t, u_x \) is the partial derivative of u with respect to x. The equation also involves fractional differentiation, represented by the Caputo-Fabrizio-fractional derivative operator \(^{CF}_0\;D^{\alpha }\) with \(\alpha \in (1, 2)\). The parameters \(\beta _2\) and \(\beta _3\) represent coefficients of nonlinear terms in the equation. The solution to this equation depends on the initial and boundary conditions specified for u(x, t) (Akinyemi et al. 2022; Li et al. 2002; Seadawy et al. 2021; Zhang and Ma 1999; Li and Zhang 2002; Wazwaz 2008; Mohebbi 2012), 224, Achab (2019); Ali et al. (2020); Runzhang and Yacheng (2010).

In general, it can be difficult to solve fractional partial differential equations analytically, so solutions are frequently approximated using numerical techniques. Different numerical techniques, such as finite difference methods, finite element methods, or spectral methods, may be used to solve the equation depending on the particular problem and circumstances (Baskonus et al. 2022; Veeresha et al. 2022, 2019; Chen et al. 2022; Veeresha 2021; Maraaba et al. 2008). In the areas of mathematical modeling and applied sciences, research on the nonlinear fractional generalized Pochhammer-Chree equation is highly relevant. It has uses in many different physical phenomena and can be used to comprehend complex dynamics that appear in a variety of systems, from fluid mechanics to nonlinear optics. Insights into the behavior of the solution are provided by numerical simulations and analysis of this equation, which also advance scientific understanding of fractional calculus and nonlinear dynamics (Prakash and Kaur 2022; Ciancio et al. 2022; Baskonus et al. 2022; He 1999; Veeresha et al. 2022). Nonlinear Partial differential equation research has important applications in many fields of science and engineering and plays a fundamental role in understanding and modeling complex systems (Malik et al. 2023; Asjad et al. 2023; Iyanda et al. 2023; Asghari et al. 2023a). To study the nonlinear partial differential equation (NLPDE) and its variations, researchers used fractional calculus (Asghari et al. 2023b; Akinyemi et al. 2021; Veeresha 2022; Deepika and Veeresha 2023; Ramapura et al. 2022; Lanre et al. 20222; Wei et al. 2022; Esin et al. 2021).

In this present study: In Sect. 2 the Preliminaries. In Sect. 3 depicts a thorough explanation of the suggested method and the model’s solutions. In Sect. 4 Analysis of the Existence and Uniqueness solution of the model. In Sect. 5 a few numerical examples. In Sect. 6 is devoted to graphs and their graphical representation of them. at the end. In sect. 7 gives the conclusion’s specifics.

2 Preliminaries

This section contains the detailed the used Laplace transform (LT), fractional differentiation (RD), and Riemann-Liouville (R-L) fractional differentiation are presented along with some basic definitions (Yan et al. 2022; Veeresha et al. 2022; Akinyemi et al. 2022; Li et al. 2002).

Definition 2.1

For \(\alpha >0\) left (R-L) order fractional integral of \(\alpha \) is defined as below (Wei et al. 2022; Esin et al. 2021).

$$\begin{aligned} ^{}_a\;I_t^\alpha \;u(t)= \frac{1}{\Gamma (\alpha )}\int _{a}^{t}(t-\xi )^{\alpha -1} u(\xi ) d\xi . \end{aligned}$$
(5)

Definition 2.2

For \(0<\alpha <1\)  left (R-L) order fractional integral of \(\alpha \)  is given as Esin et al. (2021).

$$\begin{aligned} (^{}_a\;D_t^\alpha \;u)(t)= \frac{d}{dt}(^{}_a\;I_t^\alpha \;u)(t)= \frac{\frac{d}{dt}}{\Gamma (1-\alpha )}\int _{a}^{t}(t-\xi )^{- \alpha } u(\xi ) d\xi . \end{aligned}$$
(6)

Definition 2.3

For Caputo fractional derivative is define for  \(\alpha \ge 0\)  &  \(n\in N\cup {0}\) is define as follows Esin et al. (2021).

$$\begin{aligned} ^{C}_a\;D_t^\alpha \;u(t)= \frac{1}{\Gamma (1-\alpha )}\int _{a}^{t}(t-\xi )^{n-\alpha -1} u^{n} d\xi . \end{aligned}$$
(7)

Definition 2.4

Consider u be a function \(u \in H^1(a_1,b_1),~ b_1>0,~0<\alpha <1.\) The fractional caputo-fabrizio factional operator is define as below (Esin et al. 2021).

$$\begin{aligned} ^{CF}_0\;D_t^\alpha \;u(t)= \frac{\lambda (\alpha )}{1-\alpha )}\int _{0}^{t}exp\left[-\frac{\alpha (1-\xi )}{1-\alpha }\right] u'(\xi )d\xi ,t\ge 0,~0<\alpha <1, \end{aligned}$$
(8)

with a normalize functions \(\lambda (\alpha )\) which is depend on \(\alpha \in \lambda (0)= \lambda (1)=1.\)

Definition 2.5

For CFD for integer order of \( 0<\alpha <1\).  is given by Esin et al. (2021).

$$\begin{aligned} ^{CF}_0\;D_t^\alpha \; u(t)= \frac{2(1-\alpha )}{\lambda (\alpha )(2-\alpha )}u(t)+ \frac{2\alpha }{\lambda (\alpha )(2-\alpha )} \int _{0}^{t} u(\xi )d\xi ,~t\ge 0, \end{aligned}$$
(9)

Definition 2.6

Laplace transform (LT) for the (CFD) of order \( 0<\alpha <1.\) and \(m\in N\) is given by Esin et al. (2021).

$$\begin{aligned} \begin{aligned} {\mathscr {L}}\left[ ^{CF}_0\;D_t^{(m+\alpha )}\; u(t)\right] (s)&= \frac{1}{1-\alpha } {\mathscr {L}}[u^{m+1}(t)] \mathscr {L}\left[ exp\left( \frac{-\alpha }{(1-\alpha )}t\right) \right] \\&= \frac{s^{m+1} {\mathscr {L}}[u(t)]- s^m u(0)-s^{m-1}u'(0) \ldots - u^m (0) }{s+\alpha (1-s)}. \end{aligned} \end{aligned}$$
(10)

we have, In particular

$$\begin{aligned} {\mathscr {L}} \left[ ^{CF}_0\;D_t^{(m+\alpha )}\;u(t)\right] (s)= \frac{s {\mathscr {L}}(u(t))}{s+ \alpha (1-s)},~~~~ m=0, \\ {\mathscr {L}}\left[ ^{CF}_0\;D_t^{(m+\alpha )}\;u(t)\right] (s)= \frac{s^2 {\mathscr {L}}(u(t))- su(o)-u'(0)}{s+ \alpha (1-s)},~~~ m=1. \end{aligned}$$

3 Methodology

Let’s consider the following NPDEs via the Caputo-Fabrizio derivative:

$$\begin{aligned} ^{CF}_0\;D^{m+\alpha }_t u(x,t) + \beta u(x,t) + \varphi u(x,t) = k(x,t),~~~~ n-1< \alpha +m \le n, \end{aligned}$$
(11)

for the initial conditions

$$\begin{aligned} \frac{\partial ^l u(x,0)}{\partial t^l} = f_l(x). ~~~~ l= 0,1,2, \ldots n-1. \end{aligned}$$
(12)

When we apply the Laplace transform’s derivative rule to equation Eqs. (11–12), we get

$$\begin{aligned} {\mathscr {L}}[u(x,t)]= \Theta (x,s) - \left( \frac{s+ \alpha (1- s)}{s^{n+1}} \right) {\mathscr {L}} [\beta u(x,t) + \varphi u(x,t)]. \end{aligned}$$
(13)

here

$$\begin{aligned} \Theta (x,s) = \frac{1}{s^{m+1}}[s^m f_0(x)+ s^{m-1}f_1(x)+ \ldots + f_m(x)]+ \frac{s+ \alpha (1-s)}{s^{m+1}} {\tilde{k}}(x,s). \end{aligned}$$
(14)

Utilizing the inverse Laplace transform on Eq. (13), we yield’s

$$\begin{aligned} u(x,t)= \Theta (x,s) - {\mathscr {L}}^{-1} \left[ \left( \frac{s+ \alpha (1-s)}{s^{n+1}} \right) {\mathscr {L}}[\beta u(x,t) + \varphi u(x,t)] \right] . \end{aligned}$$
(15)

as a result of an infinite series

$$\begin{aligned} u(x,t) = \sum _{n=0}^{\infty } p^n u_m(x,t). \end{aligned}$$
(16)

or nonlinear term is decomposable like

$$\begin{aligned} \varphi u(x,t) = \sum _{n=0}^{\infty } p^m H_m(x,t). \end{aligned}$$
(17)

\(H_n\) are He’s polynomials that can be evaluated using the formula below (He 1999).

$$\begin{aligned} H_m(u_0, u_1, u_2, \ldots u_n) = \frac{1}{n!}\frac{\partial ^m}{\partial p^m}\left[ \left( \sum _{m=0}^{\infty } p^i u_i \right) \right] _{p=0}. ~~~~ m = 0,1,2, \ldots ; \end{aligned}$$
(18)

For the Eqs. (16–17) into Eq. (15), we obtained

$$\begin{aligned} \sum _{m=0}^{\infty } u_m(x,t)= \Theta (x,s)- p {\mathscr {L}}^{-1} \left[ \left( \frac{s+ \alpha (1-s)}{s^{m+1}} \right) {\mathscr {L}} \left[ \beta \sum _{m=0}^{\infty }p^m u_m(x,t) + \sum _{n=0}^{\infty }p^m H_m \right] \right] . \end{aligned}$$
(19)

We obtained following approximations by equating the terms with similar powers in p in Eq. (19)

$$\begin{aligned} p^0: u_0(x,t)= &\, {} \Theta (x,s),\\ p^1: u_1(x,t)= & {} - {\mathscr {L}}^{-1} \left[ \left( \frac{s+ \alpha (1-s)}{s^{m+1}} \right) {\mathscr {L}} [\beta u_0(x,t) + H_0 (u) ] \right] \\ p^2: u_2(x,t)= & {} -{\mathscr {L}}^{-1} \left[ \left( \frac{s+ \alpha (1-s)}{s^{m+1}} \right) {\mathscr {L}} [\beta u_1(x,t) + H_1 (u) ] \right] \\ \vdots \\ p^{m+1}: u_{m+1}(x,t)= & {} -{\mathscr {L}}^{-1} \left[ \left( \frac{s+ \alpha (1-s)}{s^{m+1}} \right) {\mathscr {L}} [\beta u_{m+1}(x,t) + H_{m+1} (u) ] \right] . \end{aligned}$$

Finally, we derive the semi-analytic answer as a truncated series of approximations as

$$\begin{aligned} u(x,t) = \sum _{m=0}^{\infty } u_m(x,t). \end{aligned}$$
(20)

4 Analysis of existence and uniqueness for fractional generalized Pochhammer-Chree equation

In this section, We demonstrate the existence and uniqueness of the fractional GPC equation using a new CFD that lacks a singular kernel (Ali 2021).

Let’s consider the fractional generalized Pochhammer-Chree equation as:

$$\begin{aligned} ^{CF}_0\;D_t^{2\alpha }\;u= & {} \frac{\partial ^4 u}{\partial t^2 \partial x^2}+ \frac{\partial ^2 }{\partial x^2}\left( \beta _1 u(x,t)+ \beta _2u^q (x,t)+ \beta _3 u^{2q-1}(x,t)\right) ,\nonumber \\{} & {} 1< \alpha \le 2,~~ t>0. \end{aligned}$$
(21)
$$\begin{aligned} u(x, 0)= \Phi (x),~~~~ u_t(x,t)= \Psi (x). \end{aligned}$$

Eq. (21) is written as follows:

$$\begin{aligned} u(x,t)-u(x,0)-u_t(x,0)= I^\alpha [u_{ttxx}+ (\beta _1+ \beta _2 u^p + \beta _3 u^{2p-1})_{xx}]. \end{aligned}$$
(22)

Now, Eq. (22) is transformed into the Volterra integral equation as follows:

$$\begin{aligned} \begin{aligned} u(x,t)-u(x,0)-u_t(x,0)&= \frac{2(1-\alpha )}{(2-\alpha )M(\alpha )} \left[ u_{ttxx}+ (\beta _1+ \beta _2 u^p + \beta _3 u^{2p-1})_{xx}\right] \\&\quad + \frac{2\alpha }{(2-\alpha )M(\alpha )}\int ^t_0 \left[ u_{ttxx}+ (\beta _1+ \beta _2 u^p + \beta _3 u^{2p-1})_{xx}\right] d\tau . \end{aligned} \end{aligned}$$
(23)

4.1 Theorem

ref. Ali (2021) \(\Theta (x, t, u, \beta _1, \beta _2, \beta _3, p)\) If the following inequality exists, satisfy the Lipschitz condition and it is contractions.

$$\begin{aligned} 0<Q^4_1 + Q^2_2 (\beta _1+ \beta _2 p \eta ^{p-1}+ \beta _3 p\eta ^{2p-2})\le 1. \end{aligned}$$
(24)

where

$$\begin{aligned} \Theta (x,t,\beta _1, \beta _2, \beta _3, p)= \left[ u_{ttxx}+ (\beta _1+ \beta _2 u^p + \beta _3 u^{2p-1})_{xx}\right] . \end{aligned}$$
(25)

Proof

Let’s as u  &  v consist of two bounded functions. Using triangular inequality and Eq. (25). we determine

$$\begin{aligned}{} & {} \begin{aligned}&\parallel \Theta (x, t, u, \beta _1, \beta _2, \beta _3, p)-\Theta (x, t, v, \beta _1, \beta _2, \beta _3, p)\parallel \le \parallel u_{ttxx}- v_{ttxx}\parallel + \beta _1 \parallel u_{xx}- v_{xx}\parallel \\&\quad + \beta _2 \parallel u^p_{xx}- v^p_{xx}\parallel + \beta _3 \parallel u^{2p-1}_{xx}- v^{2p-1}_{xx}\parallel .\\ \end{aligned} \end{aligned}$$
(26)
$$\begin{aligned}{} & {} \begin{aligned}&\le \parallel \partial _{ttxx}(u-v)\parallel + \beta _1 \parallel \partial _{xx}(u-v)\parallel + \beta _2 \parallel \partial _{xx}(u^p-v^p)\parallel + \beta _3 \parallel \partial _{xx}(u^{2p-1}-v^{2p-1})\parallel . \end{aligned} \end{aligned}$$
(27)

since, u and v are positive, bounded, and constant \(\eta _1, \eta _2 >0\) s.t for all \((x, t), \Vert u\Vert \le \eta _1\)  and \(\Vert v\Vert \le \eta _2\).

Let \(\eta = max\{\eta _1, \eta _2 \}.\) The Lipschitz condition is met for the first order partial derivative function, \(\partial _x\)   &. there is a number \(Q_1, Q_2\ge 0\) s.t

$$\begin{aligned} \begin{aligned}&\parallel \Theta (x, t, u, \beta _1, \beta _2, \beta _3, p)-\Theta (x, t, v, \beta _1, \beta _2, \beta _3, p)\parallel \le Q^4_1\parallel (u-v)\parallel + \beta _1 Q^2_2\parallel (u-v)\parallel \\&\quad + p \eta ^{p-1} \beta _2 Q^2_2\parallel (u-v)\parallel + \beta _3 p Q^2_2 \eta ^{2p-2} \parallel (u-v)\parallel \\&\le Q^4_1 + Q^2_2 (\beta _1+ \beta _2 p \eta ^{p-1}+ \beta _3 p\eta ^{2p-2}) \Vert (u-v)\Vert . \end{aligned} \end{aligned}$$
(28)

Taking \(Q= Q^4_1 + Q^2_2 (\beta _1+ \beta _2 p \eta ^{p-1}+ \beta _3 p\eta ^{2p-2}) \), we get

$$\begin{aligned} \parallel \Theta (x, t, u, \beta _1, \beta _2, \beta _3, p)-\Theta (x, t, v, \beta _1, \beta _2, \beta _3, p)\parallel \le Q \Vert u-v\Vert . \end{aligned}$$
(29)

Hence, \(\Theta (x, t, u, \beta _1, \beta _2, \beta _3, p)\)  satisfies the Lipschitz condition, and if \(0< Q \le 1\), then the theorem is established because it is a contraction.

Now, the main outcome can be stated. \(\square \)

4.2 Theorem

The following bet is provided

$$\begin{aligned} \frac{2Q(1-\alpha )}{(2-\alpha ) M(\alpha )}+ \frac{2Q t \alpha }{(2-\alpha )M(\alpha )}<1. \end{aligned}$$
(30)

for, Eq. (4) the initial condition for the fractional generalised Pochhammer-Chree equation admits to the uniqueness and continuous solutions.

Proof

We take into consideration Eq. (23), using the expression (25).

$$\begin{aligned} \begin{aligned} u(x,t)-u(x,0)-u_t(x,0)&= \frac{2(1-\alpha )}{(2-\alpha )M(\alpha )} \left[ u_{ttxx}+ (\beta _1+ \beta _2 u^p + \beta _3 u^{2p-1})_{xx}\right] \\&\quad + \frac{2\alpha }{(2-\alpha )M(\alpha )}\int ^t_0 \left[ u_{ttxx}+ (\beta _1+ \beta _2 u^p + \beta _3 u^{2p-1})_{xx}\right] d\tau . \end{aligned} \end{aligned}$$
(31)

which implies the recurrence equation,

$$\begin{aligned} \begin{aligned} u_0(x,t)&= u(x,0)-u_t(x,0). \\ u_n(x, t)&= \frac{2(1-\alpha )}{(2-\alpha )M(\alpha )} \Theta (x, t, u_{n-1}, \beta _1, \beta _2, \beta _3, p)\\&\quad + \frac{2\alpha }{(2-\alpha )M(\alpha )}\int ^t_0 \Theta (x, t, u_{n-1}, \beta _1, \beta _2, \beta _3, p) d\tau . \end{aligned} \end{aligned}$$
(32)

Let

$$\begin{aligned} {\widetilde{u}}(x, t)= \lim _{n\rightarrow \infty } u_n(x, t ). \end{aligned}$$
(33)

Now we will demonstrate that the continuous \({\widetilde{u}}(x, t)= u(x, t)\)  solutions.

$$\begin{aligned} U_n(x,t)= u_n(x, t)-u_{n-1}(x, t). \end{aligned}$$
(34)

It is clear that

$$\begin{aligned} u_n(x,t)= \sum ^n_{m=0}U_m(x, t). \end{aligned}$$
(35)

Additionally, in a very thorough manner, we have

$$\begin{aligned} \begin{aligned} U_n(x, t)&= \frac{2(1-\alpha )}{(2-\alpha )M(\alpha )} \left[ \Theta (x, t, u_{n-1}, \beta _1, \beta _2, \beta _3, p)- \Theta (x, t, u_{n-2}, \beta _1, \beta _2, \beta _3, p)\right] \\&\quad + \frac{2\alpha }{(2-\alpha )M(\alpha )}\int ^t_0 \left[ \Theta (x, t, u_{n-1}, \beta _1, \beta _2, \beta _3, p)- \Theta (x, t, u_{n-2}, \beta _1, \beta _2, \beta _3, p)\right] d\tau . \end{aligned} \end{aligned}$$
(36)

Using the triangular inequality and the norm on both sides of Eq. (36) we obtain

$$\begin{aligned} \begin{aligned} \Vert U_n(x, t)\Vert&= \Vert u_n(x, t)-u_{n-1}(x, t)\Vert \\&\quad \le \frac{2(1-\alpha )}{(2-\alpha )M(\alpha )} \Vert \Theta (x, t, u_{n-1}, \beta _1, \beta _2, \beta _3, p)- \Theta (x, t, u_{n-2}, \beta _1, \beta _2, \beta _3, p)\Vert \\&\quad + \frac{2\alpha }{(2-\alpha )M(\alpha )}\ \Vert \int ^t_0 \left[ \Theta (x, t, u_{n-1}, \beta _1, \beta _2, \beta _3, p)- \Theta (x, t, u_{n-2}, \beta _1, \beta _2, \beta _3, p)\right] \Vert d\tau \\&\quad \le \frac{2(1-\alpha )}{(2-\alpha )M(\alpha )} \Vert \Theta (x, t, u_{n-1}, \beta _1, \beta _2, \beta _3, p)- \Theta (x, t, u_{n-2}, \beta _1, \beta _2, \beta _3, p)\Vert \\&\quad + \frac{2\alpha }{(2-\alpha )M(\alpha )}\ \int ^t_0 \Vert \Theta (x, t, u_{n-1}, \beta _1, \beta _2, \beta _3, p)- \Theta (x, t, u_{n-2}, \beta _1, \beta _2, \beta _3, p) d\tau \Vert . \end{aligned} \end{aligned}$$
(37)

applying Theorem 4.1 results

$$\begin{aligned} \begin{aligned} \Vert U_n(x, t)\Vert&\le \frac{2(1-\alpha )}{(2-\alpha )M(\alpha )} Q \Vert u_{n-1}-u_{n-2}\Vert + \frac{2 \alpha }{(2-\alpha )M(\alpha )} Q \int ^t_0 \Vert u_{n-1}-u_{n-2} \Vert d\tau . \end{aligned} \end{aligned}$$
(38)

which is comparable to

$$\begin{aligned} \Vert U_n(x, t)\Vert \le \frac{2(1-\alpha )}{(2-\alpha )M(\alpha )} Q \Vert U_{n-1}\Vert + \frac{2 \alpha }{(2-\alpha )M(\alpha )} Q \int ^t_0 \Vert U_{n-1} \Vert d \tau . \end{aligned}$$
(39)

Applying the recursive principle to Eq. (39), we obtain

$$\begin{aligned} \Vert U_n(x, t)\Vert \le \left[ \left( \frac{2(1-\alpha )}{(2-\alpha )M(\alpha )}\right) ^n + \left( \frac{2\alpha Q t}{(2-\alpha )M(\alpha )}\right) ^n\right] u(x,0). \end{aligned}$$
(40)

Shows that the problem has a solution and is being worked on.

It proves that

$$\begin{aligned} u(x, t)= \lim _{n\rightarrow \infty } u_n(x, t ). \end{aligned}$$
(41)

If Eq. (4) has solutions, then let’s

$$\begin{aligned} \Re _n(x, t)= {\widetilde{u}}(x, t)-u_n(x, t).~~for~~ n\in N \end{aligned}$$
(42)

Therefore, according to Eq. (35),the difference \(\Re _n(x, t)\) between \({\widetilde{u}}(x, t)\) and \(u_n(x, t)\) should tend to zero. as \(n\longrightarrow \infty \), as follows

$$\begin{aligned} \begin{aligned} {\widetilde{u}}(x, t)-u_n(x,t)&= \frac{2(1-\alpha )}{(2-\alpha )M(\alpha )} \left[ \Theta (x, t, u_, \beta _1, \beta _2, \beta _3, p)- \Theta (x, t, u_n, \beta _1, \beta _2, \beta _3, p)\right] \\&\quad + \frac{2\alpha }{(2-\alpha )M(\alpha )}\int ^t_0 \left[ \Theta (x, t, u, \beta _1, \beta _2, \beta _3, p)- \Theta (x, t, u_n, \beta _1, \beta _2, \beta _3, p)\right] d\tau . \end{aligned} \end{aligned}$$
(43)

We obtain this using Theorem 4.1

$$\begin{aligned} \begin{aligned} \Vert {\widetilde{u}}(x, t)-u_n(x,t)\Vert&= \frac{2(1-\alpha )}{(2-\alpha )M(\alpha )} \Vert \Theta (x, t, u, \beta _1, \beta _2, \beta _3, p)- \Theta (x, t, u_n, \beta _1, \beta _2, \beta _3, p)\Vert \\&\quad + \frac{2\alpha }{(2-\alpha )M(\alpha )}\int ^t_0 \Vert \Theta (x, t, u, \beta _1, \beta _2, \beta _3, p)- \Theta (x, t, u_n, \beta _1, \beta _2, \beta _3, p)\Vert d\tau ,\\&\quad \le \frac{2(1-\alpha )}{(2-\alpha )M(\alpha )} \Vert u- u_n\Vert + \frac{2\alpha }{(2-\alpha )M(\alpha )}\int ^t_0 \Vert u- u_n\Vert , \\&\quad \le \frac{2(1-\alpha )}{(2-\alpha )M(\alpha )} \Vert \Re _n\Vert + \frac{2\alpha }{(2-\alpha )M(\alpha )}\int ^t_0 \Vert \Re _n\Vert . \end{aligned} \end{aligned}$$
(44)

therefore, when \(n\longrightarrow \infty \) ,then \(\Re _n\longrightarrow 0\) and the RHS provides

$$\begin{aligned} \lim _{n\rightarrow \infty } u_n(x, t ) = {\widetilde{u}}(x, t). \end{aligned}$$
(45)

With the information above, we can use the equation \(u(x, t)= {\widetilde{u}}(x, t) \) as a solution to the continuous than Eq. (4)

$$\begin{aligned} \begin{aligned}&u(x,t)- \frac{2(1-\alpha )}{(2-\alpha )M(\alpha )} \Theta (x, t, u, \beta _1, \beta _2, \beta _3, p) + \frac{2\alpha }{(2-\alpha )M(\alpha )}\int ^t_0 \Theta (x, t, u, \beta _1, \beta _2, \beta _3, p) d \tau \\&\quad = \Re _n(x,t)+ \frac{2(1-\alpha )}{(2-\alpha )M(\alpha )}\left[ \Theta (x, t, u_{n-1}, \beta _1, \beta _2, \beta _3, p)- \Theta (x, t, u, \beta _1, \beta _2, \beta _3, p) \right] \\&\quad\,\, + \frac{2\alpha }{(2-\alpha )M(\alpha )}\int ^t_0 \left[ \Theta (x, t, u_{n-1}, \beta _1, \beta _2, \beta _3, p)- \Theta (x, t, u, \beta _1, \beta _2, \beta _3, p)\right] d \tau . \\ \end{aligned} \end{aligned}$$
(46)

Consequently, when we apply the Lipschitz condition to \(\Theta \), we get

$$\begin{aligned} \begin{aligned}&\Vert u(x,t)- \frac{2(1-\alpha )}{(2-\alpha )M(\alpha )} \Theta (x, t, u, \beta _1, \beta _2, \beta _3, p) + \frac{2\alpha }{(2-\alpha )M(\alpha )}\int ^t_0 \Theta (x, t, u, \beta _1, \beta _2, \beta _3, p) d \tau \Vert \\&\quad \le \Vert \Re _n(x, t)\Vert + \left[ \frac{2(1-\alpha ) Q}{(2-\alpha )M(\alpha )}+ \frac{2\alpha Q t}{(2-\alpha )M(\alpha )} \right] \Vert \Re _{n-1}(x, t) \Vert . \end{aligned} \end{aligned}$$
(47)

Considering the initial condition and the limit when \(n\longrightarrow \infty \), we obtain

$$\begin{aligned} \begin{aligned} u(x,t)&= u(x,0)+ \frac{2(1-\alpha )}{(2-\alpha )M(\alpha )} \Theta (x, t, u, \beta _1, \beta _2, \beta _3, p) \\&\quad + \frac{2\alpha }{(2-\alpha )M(\alpha )}\int ^t_0 \Theta (x, t, u, \beta _1, \beta _2, \beta _3, p) d\tau . \\ \end{aligned} \end{aligned}$$
(48)

Finally, we consider u and v to be two different solutions to Eq. (4) in order to ensure uniqueness. The Lipschitz condition for \(\Theta \) then yields.

$$\begin{aligned} \begin{aligned} \Vert u(x,t)- v(x,t)\Vert&\le \frac{2(1-\alpha )Q}{(2-\alpha )M(\alpha )} \Vert u(x,t)- v(x,t) \Vert \\&\,\,+ \frac{2\alpha Q t }{(2-\alpha )M(\alpha )}\Vert u(x,t)- v(x,t) \Vert . \\ \end{aligned} \end{aligned}$$
(49)

This results in

$$\begin{aligned} \Vert u(x,t)- v(x,t) \Vert \left( 1- \frac{2(1-\alpha )Q}{(2-\alpha )M(\alpha )}-\frac{2\alpha Q t}{(2-\alpha )M(\alpha )} \right) \le 0. \end{aligned}$$
(50)

Therefore, \( \Vert u(x,t)- v(x,t) \Vert =0\) if

$$\begin{aligned} \frac{2(1-\alpha )Q}{(2-\alpha )M(\alpha )}+\frac{2\alpha Q t}{(2-\alpha )M(\alpha )}<1. \end{aligned}$$
(51)

Hence proved. \(\square \)

5 Numerical Examples

Example 5.1

Consider the following Eq. (4) at \(\beta _1 \ne 0,~ \beta _2 \ne 0\) and \(\beta _3=0\)  Then, we have

$$\begin{aligned} ^{CF}_0\;D_t^{2\alpha }\;u= \frac{\partial ^4 u}{\partial t^2 \partial x^2}+ \frac{\partial ^2 }{\partial x^2}\left( \beta _1 u(x,t)+ \beta _2u^2 (x,t) \right) , \end{aligned}$$
(52)

than the initial conditions

$$\begin{aligned} u(x,0)= \frac{2\beta _1}{\beta _2} \sec h^2(x),~~ u_t(x,0)= \frac{4 \sqrt{-\beta _1 \beta _2 }}{\sqrt{3}\beta _2} \tanh (x) \sec h^2(x). \end{aligned}$$
(53)

With the aid of the anticipated algorithm, we have

$$\begin{aligned} \begin{aligned} \sum _{m=0}^{\infty } \phi _m(x,t)&= u_0(x, t)\\&\quad +p{\mathscr {L}}^{-1}\left[ \left( \frac{s+ \alpha (1-s)}{s^2} \right) {\mathscr {L}}\left[ \beta _1 (\sum _{m=0}^{\infty }p^m u_m(x,t))_{xx} + \beta _2\sum _{m=0}^{\infty }p^m H_m(\phi ) \right] \right] . \end{aligned} \end{aligned}$$
(54)

here

$$\begin{aligned} \sum _{m=0}^{\infty } p^m H_m(x,t)= (u^2_0)_x. \end{aligned}$$

The first few components of a homotopy polynomial are written as

$$\begin{aligned} \begin{aligned} H_0(u)&= (u^2_0)_x\\ H_1(u)&= (2u_0 u_1)_x\\ H_2(u)&= (2u_0 u_2 + 2u^2_1)_x\\ \vdots \\ \end{aligned} \end{aligned}$$
(55)

The result of comparing the coefficients of similar powers of p is

$$\begin{aligned} u_0(x,t)= \frac{-2\beta _1}{\beta _2} \sec h^2 x + \frac{4 \sqrt{-\beta _1 \beta _2 }}{-\sqrt{3}\beta _2} \tanh (x) \sec h^2(x). \end{aligned}$$
(56)

By carrying on in this manner, we can obtain the final element of the iteration formulas.

Consequently, the approximate answer is

$$\begin{aligned} u(x, t) = \sum _{m=0}^{\infty } u_m(x, t). \end{aligned}$$
(57)

Example 5.2

Consider Eq. (4) at \(\beta _1 \ne 0,~ \beta _2=0\) and \(\beta _3 \ne 0\)  Then, we have

$$\begin{aligned} ^{CF}_0\;D_t^{2\alpha }\;u= \frac{\partial ^4 u}{\partial t^2 \partial x^2}+ \frac{\partial ^2 }{\partial x^2}\left( \beta _1 u(x,t)+ \beta _3 u^3 (x,t) \right) , \end{aligned}$$
(58)

than the initial conditions

$$\begin{aligned} u(x,0)= \frac{\sqrt{2\beta _1}}{\sqrt{-\beta _3} (x+ \phi )},~~ u_t(x,0)= \frac{\sqrt{2}\beta _1}{\sqrt{-\beta _3}(x+\phi )^2}. \end{aligned}$$
(59)

With the aid of the anticipated algorithm, we have

$$\begin{aligned} \begin{aligned} \sum _{m=0}^{\infty } \phi _m(x,t)&= u_0(x, t)\\&\quad +p{\mathscr {L}}^{-1}\left[ \left( \frac{s+ \alpha (1-s)}{s^2} \right) {\mathscr {L}}\left[ \beta _1 \left(\sum _{m=0}^{\infty }p^m u_m(x,t)\right)_{xx} + \beta _3\sum _{m=0}^{\infty }p^m H_m(\phi ) \right] \right] . \end{aligned} \end{aligned}$$
(60)

here

$$\begin{aligned} \sum _{m=0}^{\infty } p^m H_m(x,t)= (u^3_0)_x. \end{aligned}$$

The first few components of a homotopy polynomial are written as

$$\begin{aligned} \begin{aligned} H_0(u)&= (u^3_0)_x\\ H_1(u)&= (3u^2_0 u_1)_x\\ H_2(u)&= (6u_0 u^2_1 + 3u^2_0 u_2)_x\\ \vdots \\ \end{aligned} \end{aligned}$$
(61)

The result of comparing the coefficients of similar powers of p is

$$\begin{aligned} u_0(x,t)= \frac{\sqrt{2\beta _1}}{\sqrt{-\beta _3} (x+ \phi )}+ t \frac{\sqrt{2}\beta _1}{\sqrt{-\beta _3}(x+\phi )^2}., \end{aligned}$$
(62)

By carrying on in this manner, we can obtain the final element of the iteration formulas.

Consequently, the approximate answer is

$$\begin{aligned} u(x, t) = \sum _{m=0}^{\infty } u_m(x, t). \end{aligned}$$
(63)

Example 5.3

Consider Eq. (4) at \(\beta _1 \ne 0,~ \beta _2 \ne 0\) and \(\beta _3 \ne 0\)  Then, we have

$$\begin{aligned} ^{CF}_0\;D_t^{2\alpha }\;u= \frac{\partial ^4 u}{\partial t^2 \partial x^2}+ \frac{\partial ^2 }{\partial x^2}\left( \beta _1 u(x,t)+ \beta _2 u^2(x,t) + \beta _3 u^3 (x,t) \right) , \end{aligned}$$
(64)

than the initial conditions

$$\begin{aligned} u(x,0)= & {} \frac{-\beta _2}{3 \beta _3} (1-\tanh \left( x\sqrt{\frac{\beta ^2_2}{2(2\beta ^2_2-9\beta _1 \beta _3)}}\right) ,~~ u_t(x,0)\nonumber \\= & {} \frac{\beta ^2_2}{9\sqrt{-2}\beta ^{\frac{3}{2}}_3} \sec h^2 \left( x\sqrt{\frac{\beta ^2_2}{2(2\beta ^2_2-9\beta _1 \beta _3)}}\right) . \end{aligned}$$
(65)

With the aid of the anticipated algorithm, we have

$$\begin{aligned} \begin{aligned} \sum _{m=0}^{\infty } \phi _m(x,t)&= u_0(x, t)\\&\quad +p{\mathscr {L}}^{-1}\left[ \left( \frac{s+ \alpha (1-s)}{s^2} \right) {\mathscr {L}}\right. \\&\qquad \left. \left[ \beta _1 (\sum _{m=0}^{\infty }p^m u_m(x,t))_{xx} + \beta _2\sum _{m=0}^{\infty }p^m H_m(\phi )+ \beta _3\sum _{m=0}^{\infty }p^m H_m(\phi ) \right] \right] . \end{aligned} \end{aligned}$$
(66)

here

$$\begin{aligned} \sum _{m=0}^{\infty } p^m H_m(x,t)= (u^2_0)_x + (u^3_0)_x. \end{aligned}$$

The first few components of a homotopy polynomial are written as

$$\begin{aligned} \begin{aligned} H_0(u)&= (u^2_0)_x + (u^3_0)_x \\ H_1(u)&= (2u_0 u_1)_x + (3u^2_0 u_1)_x\\ H_2(u)&= (2u_0 u_2 + 2u^2_1)_x + (6u_0 u^2_1 + 3u^2_0 u_2)_x\\ \vdots \\ \end{aligned} \end{aligned}$$
(67)

The result of comparing the coefficients of similar powers of p is

$$\begin{aligned} u_0(x,t)= \frac{-\beta _2}{3 \beta _3} (1-\tanh \left( x\sqrt{\frac{\beta ^2_2}{2(2\beta ^2_2-9\beta _1 \beta _3)}}\right) + t \frac{\beta ^2_2}{9\sqrt{-2}\beta ^{\frac{3}{2}}_3} \sec h^2 \left( x\sqrt{\frac{\beta ^2_2}{2(2\beta ^2_2-9\beta _1 \beta _3)}}\right) . \end{aligned}$$
(68)

By carrying on in this manner, we can obtain the final element of the iteration formulas (Tables 1, 2 and 3).

Consequently, the approximate answer is

$$\begin{aligned} u(x, t) = \sum _{m=0}^{\infty } u_m(x, t). \end{aligned}$$
(69)
Table 1 The numerical value 3-term FHPTM approximate solution for the different value of \(\alpha \) and \(\beta _1 = 1.5, \beta _2 = 1\) for Ex. 5.2
Full size table
Fig. 1
figure 1

(a) Plots of u(x, t) with respect to x for varying \(\alpha \), for Ex 5.1; and (b) exact solutions for Ex. 5.1

Full size image
Fig. 2
figure 2

The combined dark-bright soliton solution of u(x, t) in Ex.1

Full size image
Table 2 The numerical value 3-term FHPTM approximate solution for the different value of \(\alpha \) and \(\beta _1 = 1.5, \beta _2 = -0.5\) for Ex.\(-\)5.2
Full size table
Fig. 3
figure 3

(a) Plots of u(x, t) with respect to x for varying \(\alpha \), for Ex 5.2;  and (b) exact solutions for Ex. 5.2

Full size image
Fig. 4
figure 4

The rational function solution of u(x, t) in Ex.5.2

Full size image
Table 3 The numerical value 3-term FHPTM approximate solution for the different value of \(\alpha \)  and \(\beta _1 = 1.5, \beta _2 = 1, \beta _3= -0.1\) for Ex. 5.3
Full size table
Fig. 5
figure 5

(a) Plots of u(x, t) with respect to x for varying \(\alpha \), for Ex 5.3;  and (b) exact solutions for Ex. 5.3

Full size image
Fig. 6
figure 6

The dynamic behavior of 3D plot of u(x, t) solution in Ex.5.3

Full size image

6 Result and discussion

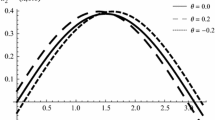
In this section, to analyze the solutions, we make use of graphical representations. We talk about the generalised Pochhammer-Chree equation with nonlinear fractions. For each of the solutions, a graph was made and a description of it was given. We ran some numerical calculations in Mathematica to demonstrate the dynamical behavior of the model and test the viability of our analysis regarding the existence of interior equilibrium and the corresponding initial conditions. we will display the graphical analysis of the model under consideration in this section. Fig. 1a the 2D graph fractional order of derivative value \(\alpha \) where \((\alpha = 1.25,~ 1.5,~ 1.75,~ 2),~ \beta _ 1= 1.5,~ \beta _2= 1\) and \(x=2,~~0\le t\le -5\).

(b) the display 3D analysis of the exact solutions u(x, t) with parametric value \(\beta _1= -1.5,~\beta _2= 1\) and \(-60\le x\le 75,~ -60\le t\le 75\).

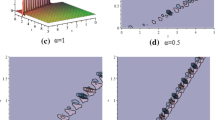
Figure 2a–d the display 3D graph to show the dynamical behavior of fractional order to of \(\alpha \) Ex.5.1. Figure 3a the 2D graph fractional order of derivative value \(\alpha \) where \((\alpha = 1.25,~ 1.5,~ 1.75,~ 2),~ \beta _ 1= 1.5,~ \beta _3= -0.5\) and \(x=1,~\lambda =1~~0\le t\le 2\).

(b) the display 3D analysis of the exact solutions u(x, t) with parametric value \(\beta _1= -1.5,~\beta _3= -0.5\),  &  \(\phi = 1\) and \(-15\le x\le 15,~ -15\le t\le 15\). Figure 4a–d the display 3D graph to show the dynamical behavior of fractional order to of \(\alpha \) Ex.5.2.

Figure 5a the 2D graph fractional order of derivative value \(\alpha \) where \((\alpha = 1.25,~ 1.5,~ 1.75,~ 2),~\beta _ 1= 1.5,~ \beta _2= 1,~\beta _3= -0.1\) and \(x=8,~~0\le t\le 1\).

(b) the display 3D analysis of the exact solutions u(x, t) with parametric value \(\beta _1= 1.5,~\beta _2= 1,~\beta _3= -0.1\) and \(-10\le x\le 15,~ -10\le t\le 15\).

Figure 6a–d the display 3D graph to show the dynamical behavior of fractional order to of \(\alpha \) Ex.5.3. It is apparent form these figures that as the value of \(\alpha \) increases, respectively. The technique employed is an effective mathematical tool for finding various types of solutions to numerous NGPCEs.

7 Conclusions

In this paper, We have developed a variety of new approximate solutions for the FGPC Eq. (4) using symbolic computation and the fractional homotopy perturbation transform method via the Caputo-Fabrizio fractional derivative(CFFD) of order \(\alpha \) where \(\alpha \in (1, 2].\) The FHATM provides a simple description for adjusting and controlling the convergence of the series solution by selecting appropriate auxiliary parameter \(\alpha \). We continued our research in Prakash et al. (2021); Toprakseven (2021), where we stated the existence and uniqueness results for fractional initial value problems of the form Eq. (4) with different three initial condition Eq. (4) and potential applications such as Fractional calculus enrichment, Nonlinearity, and soliton solutions, Numerical simulations, Applications in physics and beyond and Future research directions. There are a number of directions for additional research, even though we have made significant progress in comprehending the properties of the equation. Future research could focus on examining the stability of solitons, multi-dimensional extensions of the equation, and the effects of additional nonlinear terms. It should be noted that the proposed method could also be used to solve nonlinear GPCEs fractional differential equations involving the CFD of order \(\alpha \in (1, 2]\) , such as the FHPTM (He 1999). It is possible to conclude that the FHATM is simple to use and effective at finding approximate solutions to many fractional physical problems that arise in various fields of science and engineering. Furthermore, 2D and 3D graphs of some solutions were presented to demonstrate the physical characteristics of the acquired solutions. Additionally, real-world applications and experimental validation of the equation’s predictions can provide valuable insights.