Caputo–Riesz-Feller fractional wave equation: analytic and approximate solutions and their continuation

Abstract

In this article a time-space fractional wave equation is studied. In the new proposed fractional model, the second-order time derivative is replaced with a fractional derivative in Caputo sense, and the second-order space derivative is replaced with a Riesz-Feller derivative defined on infinite space domain. The fundamental solution of fractional wave equation is obtained in terms of Mittag-Leffler function in two parameters, that is by using the joint Laplace–Fourier transform method. We prove the continuation of the solution of the generalized Riesz wave equation as the skewness parameter tends to zero to the one of the corresponding fractional wave equation with classical Riesz derivative, this is accomplished by using the Lebesgue’s dominated convergence theorem. The optimal homotopy analysis method (OHAM) is employed to obtain semi-analytic solution of a newly proposed initial-value fractional wave problem, considering three numerical simulations. The continuation of the optimal solution and its dependence on the fractional derivative parameters are investigated. The study reveals that the OHAM is reliable and effective in case of fractional Riesz-Feller operator represents the fractional Laplacian operator.

1 Introduction

Fractional derivatives have been successfully applied in modeling numerous problems in different fields of applied science. This is because the hereditary properties of several types of materials and processes are perfectly described using fractional derivatives. The fractional derivative operators have been utilized to model processes that describe the dissipative attenuation in complex materials, such as anomalous diffusion [33], viscoelastic damping [23] and wave propagation [3]. Riesz and Riesz-Feller fractional derivatives are two of the fractional order operators that are utilized to model phenomena such as anomalous diffusion [24], discrete random walk models [15] , and continuous random walk models [13] in the form of fractional partial differential equations (FPDEs) .

The operators of fractional differentiation and integration are also used for extensions of the diffusion and wave equations, that results in the so called fractional diffusion-wave equations (FDWEs) [16, 24, 30]. Modeling of systems that support anomalous diffusion and subdiffusion and interaction of fractional diffusion and wave propagation motivates mathematicians and physicists to investigate the solutions of FDWEs. In these equations, the standard diffusion term is replaced by Riesz or Riesz-Feller derivative and/or the first-order time derivative is replaced by Caputo derivative of order $0<\beta \le 1$ which represents fractional diffusion equations (FDEs), while in case of fractional wave equations (FWEs) the second-order time derivative is replaced by Caputo derivative of order $1<\beta \le 2$ (see for example, [6, 14, 17, 22]), or by generalized Riemann-Liouville fractional operator [21, 29].

In the literature there are many analytical and numerical methods introduced to solve the time, space and space-time FDWEs. Among these methods the integral transform method [1, 12], Decomposition method [26] , variational iteration method [5, 25], differential transform method [31] and homotopy analysis method [4, 18] are used in case of the time FDEs and FWEs. Other methods are used in case of the fractional derivative in space and time, for example, the transform method [21, 22, 29], and similarity with transform methods [8].

Numerical methods and semi-analytic approaches have advantage over analytic methods when the nonlinear problems are studied. Hence, several numerical techniques are introduced in the literature to solve FDEs and FWEs considering Riesz fractional operator (see for example [2, 34]). Due to the difficulty in repeated application of Riesz-Feller fractional derivative to solution components, few articles dealt with applying iterative techniques, specially to Riesz and/or Riesz-Feller FPDEs. The motivation is to solve new proposed nonlinear space-time considering the generalized Riesz fractional operators in space and caputo derivative in time . Our work depends on the repetitive behavior for the complex exponential function, hence trigonometric sine and cosine functions, when subjected to the application of Riesz-Feller fractional derivative operators. In a recent work, the optimal homotopy analysis method (OHAM) was used successfully to solve different Riesz and/or Riesz-Feller FPDEs; Riesz fractional burger equation [9], Riesz FDEs in [10, 32] and Riesz-Feller FDE in [11]. In this article, we consider the nonlinear Caputo–Riesz-Feller FWE

$$\begin{aligned} \left\{ \begin{array}{l} ^{C}D_{t}^{\beta }u(x,t)=k(u)R_{x}^{{\alpha },{\theta }}u(x,t)+g(u),\quad x \in \mathbb {R},\quad t>0, \\ u(x,0)=f_{1}(x),\quad \frac{\partial }{\partial t}u(x,0)=f_{2}(x), \end{array} \right. \end{aligned}$$

(1)

where $^{C}D_{t}^{\beta }$ is the fractional time derivative of order $\beta$ in Caputo sense and $R_{x}^{\alpha ,\theta }$ denotes the Riesz-Feller fractional derivative (in space) of order $\alpha$ and skewness $\theta$. The parameters $\alpha ,$$\theta$ and $\beta$ are real numbers restricted to

$$\begin{aligned} 0<\alpha \le 2,\quad \alpha \ne 1,\quad \left| \theta \right| \le \min \{\alpha ,2-\alpha \}\quad \text {and}\quad 1<\beta \le 2. \end{aligned}$$

(2)

The functions k(u) and g(u) are continuous functions in u, and the two functions $f_{1}(x)$ and $f_{2}(x)$ belong to the space of integrable functions $L^{1}(-\infty ,\infty )$.

We aim to establish the continuation of the solution of Eq. (1) to the exact solution of the corresponding equation in Riesz fractional derivative as the skewness parameter approaches zero. This objective is carried out theoretically via proving two theorems concerning the fundamental solutions and numerically by using approximate series solution obtained iteratively by applying the OHAM. This paper is organized as follows. Basic definitions of fractional derivative operators involved are presented in Sect. 2. The fundamentals of the OHAM is illustrated in Sect. 3. Section 4 is devoted to the proof of two theorems; the first to find a fundamental solution using the transform method and the second theorem for the proof of continuation of solution using Lebesgue dominant convergence lemma. In Sect. 5, the results of some numerical experiments are presented, considering the time-space fractional sine-Gordan equation and introducing a problem in which a nonlinearity appears in the fractional lapacial term and the source term as well. We conclude the results in Sect. 6.

2 Fractional derivatives and integrals

Definition 1

A real function g(t), $t\in (0,\infty )$, is said to be in the space $C\rho$, $\rho \in \mathbb {R}$, if there exists a real number $p>\rho$, such that $g(t)=t^{p}f(t)$, where $f(t)\in$$C(0,\infty )$, and it is said to be in the space $C_{\rho }^{n}$ if $g^{n}\in C\rho ,$$n\in \mathbb {N} .$

Definition 2

The Riemann-Liouville fractional integral operator of order $\lambda \ge 0$ of a function $g(t)\in C_{\rho },$$\rho \ge -1$ is defined as

$$\begin{aligned} \left\{ \begin{array}{l} J^{\lambda }g(t)=\frac{1}{\varGamma (\lambda )}\int \limits _{0}^{t}(t-x)^{ \lambda -1}g(x)dx,\quad \lambda>0, t>0, \\ J^{0}g(t)=g(t). \end{array} \right. \end{aligned}$$

(3)

The operator $J^{\lambda }$ satisfies the following properties. For $g\in C_{\rho }$, $\rho \ge -1$, $\lambda ,\eta \ge 0$ and $\delta >-1$:

• 1. $J^{\lambda }J^{\eta }g(t)=J^{\lambda +\eta }g(t),$

• 2. $J^{\lambda }J^{\eta }g(t)=J^{\eta }J^{\lambda }g(t),$

• 3. $J^{\lambda }t^{\delta }=\frac{\varGamma (\delta +1)}{\varGamma (\delta +\lambda +1)}t^{\lambda +\delta }.$

Definition 3

The fractional derivative in Caputo sense of $g(t)\in C_{-1}^{n},$$n\in \mathbb {N} ,$$t>0$ is defined as

$$\begin{aligned} ^{C}D_{t}^{\eta }g(t)=\left\{ \begin{array}{ll} J^{n-\eta }\frac{d^{n}}{dt^{n}}g(t), &{} n-1<\eta <n, \\ \frac{d^{n}}{dt^{n}}g(t), &{} \eta =n. \end{array} \right. \end{aligned}$$

(4)

The Laplace transform formula for the Caputo time-fractional derivative of order $\eta (n-1<\eta <n, n\in \mathbb {N})$ is (see [27], p.106)

$$\begin{aligned} \pounds [^{C}D_{t}^{\eta }g(t);s]=s^\eta \tilde{g}(s)-\sum _{j=0}^{n-1} s^{\eta -1-j} g^{(j)}(0^{+}), \end{aligned}$$

(5)

where

$$\begin{aligned} \pounds [g(t);s]=\tilde{g}(s)=\int \limits _{0}^{\infty }e^{-st} g(t) dt. \end{aligned}$$

(6)

In the following lemma, basic properties of Caputo fractional derivative are listed

Lemma 1

If $n-1<\lambda \le n$, $n\in \mathbb {N}$ and $g\in C_{\rho }^{n}$ , $\rho \ge -1$, then:

$$\begin{aligned}&D^{\lambda }(k)=0,\ \ \ \ \ (k\ \ \text {is a constant}) \end{aligned}$$

(7)

$$\begin{aligned}&D^{\lambda }t^{\delta }=\left\{ \begin{array}{ll} \frac{\varGamma (\delta +1)}{\varGamma (\delta -\lambda +1)}t^{\delta -\lambda }, &{} \delta >\lambda -1, \\ 0,&{}\delta \le \lambda -1, \end{array} \right. \nonumber \\&D^{\lambda }J^{\lambda }g(t)=g(t), \end{aligned}$$

(8)

and

$$\begin{aligned} J^{\lambda }D^{\lambda }g(t)=g(t)-\sum \limits _{j=0}^{n-1}g^{(j)}(0)\frac{t\ ^{j}}{j\ !}, \quad t>0. \end{aligned}$$

(9)

Definition 4

The space Riesz-Feller partial fractional derivative $R_{x}^{\lambda ,\theta }$ is defined as [14]

$$\begin{aligned} R_{x}^{\lambda ,\theta }v(x)=-[a_{+}D_{+}^{\lambda }v(x)+a_{-}D_{-}^{\lambda }v(x)],0<\lambda <2, \quad \lambda \ne 1, \end{aligned}$$

(10)

where $D_{\pm }^{\lambda }v(x)$ denote the Weyl fractional-order derivatives defined by

$$\begin{aligned} D_{\pm }^{\lambda }v(x)=\left\{ \begin{array}{c} \pm \frac{d}{dx}W_{\pm }^{1-\lambda }v(x),0<\lambda<1, \\ \frac{d^{2}}{dx^{2}}W_{\pm }^{2-\lambda }v(x),1<\lambda <2, \end{array} \right. \end{aligned}$$

(11)

and $W_{\pm }^{\eta }$ are the Weyl fractional-order integrals of order $\eta >0$, defined by

$$\begin{aligned} \begin{array}{c} W_{+}^{\eta }v(x)=\frac{1}{\varGamma (\eta )}\int \limits _{-\infty }^{x}(x-y)^{\eta -1}v(y)dy, \\ W_{-}^{\eta }v(x)=\frac{1}{\varGamma (\eta )}\int \limits _{x}^{\infty }(y-x)^{\eta -1}v(y)dy. \end{array} \end{aligned}$$

(12)

The coefficients $a_{+}$ and $a_{-}$ have the following forms

$$\begin{aligned} a_{\pm }=\frac{\sin ((\lambda \mp \theta )\pi /2)}{\sin (\lambda \pi )}, \end{aligned}$$

(13)

where $\left| \theta \right| \le \min \{\lambda ,2-\lambda \}$.

When $\lambda =0$, the Weyl fractional-order derivative becomes the identity operator

$$\begin{aligned} D_{\pm }^{0}v(x)=Iv(x)=v(x). \end{aligned}$$

(14)

For continuity we get

$$\begin{aligned} D_{\pm }^{1}v(x)=\pm \frac{d}{dx}v(x), D_{\pm }^{2}v(x)=\frac{d^{2}}{ dx^{2}}v(x). \end{aligned}$$

(15)

Evidently, in case $\lambda =2$ and $\theta =0$, we define

$$\begin{aligned} R_{x}^{2 ,0}v(x)=\frac{d^{2}}{dx^{2}}v(x). \end{aligned}$$

(16)

For the case $\lambda =1$ and $\theta =0$ we have

$$\begin{aligned} R_{x}^{1,0}v(x)=\frac{d}{dx}Hv(x)=\frac{d}{dx}\frac{1}{\pi } \int \limits _{-\infty }^{\infty }\frac{v(y)}{y-x}dy, \end{aligned}$$

(17)

where H denotes the Hilbert transform and the integral is understood in the Cauchy principal value sense. For the case $\lambda =1$ and $\theta =\pm 1$ we obtain the first derivative

$$\begin{aligned} R_{x}^{1,\pm 1}v(x)=\pm \frac{d}{dx}v(x) \end{aligned}$$

(18)

The special case $\theta =0$ is known as Riesz fractional derivative.

Definition 5

Let

$$\begin{aligned} F(\omega )=\digamma [f(x);\omega ]=\int \limits _{-\infty }^{\infty }e^{i\omega x} f(x)dx, \omega \in \mathbb {R}, \end{aligned}$$

(19)

be the Fourier transform of a function $f(x) \in L^{1}(-\infty ,\infty )$, and let

$$\begin{aligned} f(x)=\digamma ^{-1}[F(\omega );x]=\int \limits _{-\infty }^{\infty }e^{-i\omega x} F(\omega )d\omega , x \in \mathbb {R}, \end{aligned}$$

(20)

be the inverse Fourier transform. For a sufficiently well-behaved function f(x), the Riesz-Feller space-fractional derivative of order $\lambda$ and skewness $\theta$, is defined as [22]

$$\begin{aligned} \digamma [ R_{x}^{\alpha ,\theta } f(x);\omega ]=-\varOmega _{\theta }^{\alpha }(\omega ) F(\omega ), \end{aligned}$$

(21)

where

$$\begin{aligned} \varOmega _{\theta }^{\alpha }(\omega )=|\omega |^\alpha e^{i (\text {sign}(\omega )) \theta \pi /2}, 0<\alpha \le 2, |\theta | \le \min {(\alpha ,2-\alpha )}. \end{aligned}$$

(22)

3 Optimal homotopy analysis method (OHAM)

The classical homotopy analysis method (HAM) was used to solve a nonlinear equation of the form

$$\begin{aligned} \aleph [v(x,t)]=0, \end{aligned}$$

(23)

where $\aleph$ denotes the considered nonlinear operator, v(x, t) is the unknown function in the two independent variables x and t. Liao [19] generalized the concept of homotopy method to present what is referred to as the zero-order deformation equation that takes the form

$$\begin{aligned} (1-q)\varUpsilon [ \psi (x,t;q)-v_{0}(x,t)]=q\hbar \aleph [\psi (x,t;q)], \end{aligned}$$

(24)

where $\psi (x,t;q)$ is an unknown function, q is a parameter that belongs to [0, 1], $\hbar$ is an auxiliary parameter in $\mathbb {R} -\{0\}$, $\varUpsilon$ denotes an auxiliary linear operator, and $v_{0}(x,t)$ is chosen as an initial guess of the unknown function v(x, t). As q increases from 0 to 1, the function $\psi (x,t;q)$ deforms from the initial guess $v_{0}(x,t)$ to the required solution v(x, t). The Taylor series of the function $\psi (x,t;q)$ with respect to parameter q takes the form

$$\begin{aligned} \psi (x,t;q)=v_{0}(x,t)+\sum \limits _{m=1}^{\infty }v_{m}(x,t)q^{m}, \end{aligned}$$

(25)

where

$$\begin{aligned} v_{m}(x,t)=\frac{1}{m!}\frac{\partial ^{m}\psi (x,t;q)}{\partial q^{m}}\mid _{q=0}. \end{aligned}$$

(26)

Liao [19] proved that for properly chosen auxiliary linear operator, initial guess and parameter $\hbar$, the series (25) converges at $q=1$ and we have

$$\begin{aligned} v(x,t)=v_{0}(x,t)+\sum \limits _{m=1}^{\infty }v_{m}(x,t), \end{aligned}$$

(27)

which, as proven by Liao [19], is one of solutions of problem (23). Consider the vector

$$\begin{aligned} \overrightarrow{v}_{n}=\{v_{0}(x,t),v_{1}(x,t),v_{2}(x,t),...,v_{n}(x,t)\}. \end{aligned}$$

(28)

From Eq. (24), the m th-order deformation equation is given by

$$\begin{aligned} \varUpsilon [v_{m}(x,t)-\sigma _{m}v_{m-1}(x,t)]=\hbar \mathfrak {R}_{m}[ \overrightarrow{v}_{m-1}(x,t)], \end{aligned}$$

(29)

where

$$\begin{aligned} \mathfrak {R}_{m}[\overrightarrow{v}_{m-1}]=\frac{1}{(m-1)!}\frac{\partial ^{m-1}\aleph [\psi (x,t;q)]}{\partial q^{m-1}}\mid _{q=0}, \end{aligned}$$

(30)

and

$$\begin{aligned} \sigma _{m}=\left\{ \begin{array}{c} 0,m\le 1, \\ 1,m>1. \end{array} \right. \end{aligned}$$

(31)

By applying the inverse operator $\varUpsilon ^{-1}$ to both sides of (29), $u_{m}(x,t)$ can be calculated by symbolic computations software.

It is obvious that $v_{m}(x,t)$ contains only one control parameter $\hbar$. Thus, by constructing a formula for the residual error, the OHAM solution is obtained by choosing the value for parameter $\hbar$ that minimizes the error. Here, the averaged residual error defined for ordinary differential equations in [20] is generalized to the case of two variable partial differential equations in the following form [10, 32]

$$\begin{aligned} E_{m}(\hbar )=\frac{1}{MK}\sum _{i=0}^{M}\sum _{j=0}^{K}\left[ \aleph \left( \sum _{n=0}^{m}v_{n}\left( \frac{i}{M},\frac{j}{K}\right) \right) \right] ^{2}. \end{aligned}$$

(32)

This is a nonlinear algebraic equation in the unknown $\hbar$. Thus, by minimizing $E_{m}$, the optimal value of $\hbar$ is obtained.

4 Continuation of the solution

In this section we derive the fundamental solution of the linear FWE using the Laplace and Fourier transforms. Then we use the convergence dominant lemma to prove the continuation of the solution of the proposed problem.

Theorem 1

If $f_1(x)~$ and $f_2(x)~$ are in $L^{1}(-\infty ,\infty )$, then the exact solution $u_{\beta }^{\alpha ,\theta }$ of the space-time FWE

$$\begin{aligned} \left\{ \begin{array}{l} ^{C}D_{t}^{\beta }u(x,t)=R_{x}^{\alpha ,\theta }u(x,t),\quad x \in \mathbb {R},\quad t>0, \\ u(x,0)=f_{1}(x),\quad u_{t}(x,0)=f_{2}(x), \end{array} \right. \end{aligned}$$

(33)

is given by

$$\begin{aligned} u_{\beta }^{\alpha ,\theta }(x,t)= & {} \frac{1}{2\pi }\int \limits _{-\infty }^{\infty }\int \limits _{-\infty }^{\infty }E_{\beta ,1}(-\varOmega _{\theta }^{\alpha }(\omega ))f_{1}(v)e^{i\omega (x-v)}d\omega dv \nonumber \\&+\frac{1}{2\pi }\int \limits _{-\infty }^{\infty }\int \limits _{-\infty }^{\infty }t~E_{\beta ,2}(-\varOmega _{\theta }^{\alpha }(\omega ))f_{2}(v)e^{i\omega (x-v)}d\omega dv, \end{aligned}$$

(34)

where the function $\varOmega _{\theta }^{\alpha }(\omega )$ is displayed in (22), $0<\alpha \le 2,$$\alpha \ne 1,$$\left| \theta \right| \le \min \{\alpha ,2-\alpha \},$$1<\beta \le 2$ and $E_{\eta ,\gamma }(z)$   is the two parameter Mittag-Leffler function defined as [27]

$$\begin{aligned} E_{\eta ,\gamma }(z)=\sum _{n=0}^{\infty }\frac{z^{n}}{\varGamma (\eta n+\gamma ) }. \end{aligned}$$

(35)

Proof

We use the joint Fourier–Laplace transform method. Refereing to the property shown in (5), and applying the Laplace transform $\pounds$ to both sides of (33) results in

$$\begin{aligned} s^\beta \tilde{u}(x,s)-s^{\beta -1} f_1(x)-s^{\beta -2} f_2(x)=R_{x}^{\alpha ,\theta }\tilde{u}(x,s), \end{aligned}$$

(36)

and when we continue by applying the Fourier transform $\digamma$ (see Definition 5) gives

$$\begin{aligned} s^\beta \tilde{U}(\omega ,s)-s^{\beta -1} F_1(\omega )-s^{\beta -2} F_2(\omega )=\digamma [R_{x}^{\alpha ,\theta }\tilde{u}(x,s)], \end{aligned}$$

(37)

and from the Riesz-Feller definition displayed in (21), we have

$$\begin{aligned} s^\beta \tilde{U}(\omega ,s)-s^{\beta -1} F_1(\omega )-s^{\beta -2} F_2(\omega )=-\varOmega _{\theta }^{\alpha }(\omega )\tilde{U}(\omega ,s). \end{aligned}$$

(38)

Thus the transformed solution is

$$\begin{aligned} \tilde{U}(\omega ,s)=\frac{s^{\beta -1} F_1(\omega )}{s^\beta +\varOmega _{\theta }^{\alpha }(\omega )}+\frac{s^{\beta -2} F_2(\omega )}{s^\beta +\varOmega _{\theta }^{\alpha }(\omega )}. \end{aligned}$$

(39)

Now, apply the inverse Laplace transform to (39) (refer to [27], p.29) to get

$$\begin{aligned} U(\omega ,t)= F_1(\omega ) E_{\beta ,1}(-\varOmega _{\theta }^{\alpha }(\omega ) t^\beta )+ t F_2(\omega ) E_{\beta ,2}(-\varOmega _{\theta }^{\alpha }(\omega ) t^\beta ), \end{aligned}$$

(40)

and then apply the inverse Fourier transform to have

$$\begin{aligned} u(x,t)=\frac{1}{2\pi }\int \limits _{-\infty }^{\infty }\left[ F_1(\omega ) E_{\beta ,1}(-\varOmega _{\theta }^{\alpha }(\omega ) t^\beta )+ t F_2(\omega ) E_{\beta ,2}(-\varOmega _{\theta }^{\alpha }(\omega ) t^\beta )\right] e^{-i \omega x}d\omega . \end{aligned}$$

(41)

At this point when substituting the two functions $F_1(\omega )$ and $F_2(\omega )$ (Fourier transforms to $f_1$ and $f_2$)

(42)

into the solution (41) and rearranging the integrals, we obtain the required form of the solution shown in (34). $\square$

Theorem 2

Let $\alpha \in (1,2),$$\beta \in (1,2),$$\left| \theta \right| \le \min (\alpha ,2-\alpha ),$$f_{1}(x)~$and $f_{2}(x)$ are functions in $L^{1}(-\infty ,\infty ),$ and $u_{\beta }^{\alpha ,\theta }$ be the solution (34) of the space-time fractional problem (33), then

$$\begin{aligned} \lim \limits _{\theta \rightarrow 0}u_{\beta }^{\alpha ,\theta }(x,t)=u_{\beta }^{\alpha }(x,t), \end{aligned}$$

where $u_{\beta }^{\alpha }(x,t)$ is the exact solution of Riesz fractional wave equation given by

$$\begin{aligned} \left\{ \begin{array}{l} ^{C}D_{t}^{\beta }u(x,t)=R_{x}^{\alpha }u(x,t),\, -\infty<x<\infty ,\, t>0, \\ u(x,0)=f_{1}(x),\ \ u_{t}(x,0)=f_{2}(x), \end{array} \right. \end{aligned}$$

(43)

with the same limits for parameters $\alpha$ and $\beta$.

Proof

Consider the two sets of functions $\varPhi _{n}(\omega )$ and $\varPsi _{n}(\omega )$ for $\omega \in (-\infty ,\infty ),$$n\in \mathbb {N}^{+}$, given by

$$\begin{aligned} \varPhi _{n}(\omega )= & {} \frac{1}{2\pi }E_{\beta ,1}(-\varOmega _{1/n}^{\alpha }(\omega )t^{\beta })\int \limits _{-\infty }^{\infty }f_1(v)e^{i\omega (x-v)}dv, \end{aligned}$$

(44)

$$\begin{aligned} \varPsi _{n}(\omega )= & {} \frac{1}{2\pi }t~E_{\beta ,2}(-\varOmega _{1/n}^{\alpha }(\omega )t^{\beta })\int \limits _{-\infty }^{\infty }f_2(v)e^{i\omega (x-v)}dv. \end{aligned}$$

(45)

These functions satisfy Lebesgue dominant convergence theorem and we prove that as follows. The absolute value to both sides of (44) leads to the inequality

$$\begin{aligned} \left| \varPhi _{n}(\omega )\right| \le \frac{1}{2\pi }\left| E_{\beta ,1}(-\varOmega _{1/n}^{\alpha }(\omega )t^{\beta })\right| \int \limits _{-\infty }^{\infty }\left| f_1(v)\right| \left| e^{i\omega (x-v)}\right| dv. \end{aligned}$$

(46)

As $\left| e^{i\omega (x-v)}\right| =1$, we obtain

$$\begin{aligned} \left| \varPhi _{n}(\omega )\right| \le \frac{1}{2\pi }\left| E_{\beta ,1}(\varOmega _{1/n}^{\alpha }(\omega )t^{\beta })\right| \int \limits _{-\infty }^{\infty }\left| f_1(v)\right| dv. \end{aligned}$$

(47)

Since $f_1(x)\in L^{1}(-\infty ,\infty ),$ there exists a constant $M_1>0$ such that

$$\begin{aligned} \left| \varPhi _{n}(\omega )\right| \le \frac{M_1}{2\pi }\left| E_{\beta ,1}(-\varOmega _{1/n}^{\alpha }(\omega )t^{\beta })\right| . \end{aligned}$$

(48)

From [27] (Theorem (1.6), p.35), there exists a constant $K_{1}>0$ such that

$$\begin{aligned} \left| E_{\beta ,1}(-z)\right| \le \frac{K_{1}}{1+\left| z\right| }. \end{aligned}$$

(49)

Then

$$\begin{aligned} \left| \varPhi _{n}(\omega )\right| \le \frac{1}{2\pi }\frac{M_1K_{1}}{ 1+\left| \varOmega _{1/n}^{\alpha }(\omega ) \right| t^{\beta }}, \omega \in (-\infty ,\infty ), n=1,2,...~, \end{aligned}$$

(50)

where $\varOmega _{1/n}^{\alpha }(\omega )$ which displayed in (22), and one can say

$$\begin{aligned} \left| \varOmega _{1/n}^{\alpha }(\omega )\right| =\left| - |\omega |^\alpha e^{i (\text {sign}(\omega )) \pi /2n}\right| =|\omega |^\alpha . \end{aligned}$$

(51)

For a bounded time interval $0<t<T<\infty ,\$there exists $Q_{1}>0$ such that

$$\begin{aligned} \left| \varPhi _{n}(\omega )\right| \le g_1(\omega )=\frac{Q_{1}}{ 1+\left| \omega \right| ^{\alpha }t^{\beta }},\quad \omega \in (-\infty ,\infty ),\, n=1,2,..., \end{aligned}$$

(52)

and $g_1(\omega )$$\in L^{1}(-\infty ,\infty )$ since

$$\begin{aligned} \int \limits _{-\infty }^{\infty }\left| g_1(\omega )\right| d\omega =2Q_{1}\int \limits _{0}^{\infty }\frac{d\omega }{1+\left| \omega \right| ^{\alpha }t^{\beta }}=\frac{2Q_{1}}{\alpha t^{\beta /\alpha }}\varGamma \left( \frac{1 }{\alpha }\right) \varGamma \left( 1-\frac{1}{\alpha }\right) ,\ \ \ \alpha >1. \end{aligned}$$

(53)

Thus the set of functions $\varPhi _{n}(\omega )$ satisfies Lebesgue dominated convergence theorem. Similarly, we can say that the set of functions $\varPsi _{n}(\omega )$ shown (45) satisfy the inequality

$$\begin{aligned} \left| \varPsi _{n}(\omega )\right| \le \frac{1}{2\pi }\left| t E_{\beta ,2}(-\varOmega _{1/n}^{\alpha }(\omega )t^{\beta })\right| \int \limits _{-\infty }^{\infty }\left| f_2(v)\right| dv. \end{aligned}$$

(54)

Also, as $f_2(x)\in L^{1}(-\infty ,\infty ),$ there exists a constant $M_2>0$ such that

$$\begin{aligned} \left| \varPsi _{n}(\omega )\right| \le \frac{M_2}{2\pi }\left| E_{\beta ,2}(-\varOmega _{1/n}^{\alpha }(\omega )t^{\beta })\right| , \end{aligned}$$

(55)

and From [27] (Theorem (1.6), p.35), there exists $K_{2}>0$ such that

$$\begin{aligned} \left| E_{\beta ,2}(-z)\right| \le \frac{K_{2}}{1+\left| z\right| }. \end{aligned}$$

(56)

Thus

$$\begin{aligned} \left| \varPsi _{n}(\omega )\right| \le \frac{M_2K_{2}}{2\pi }\frac{t}{ 1+\left| \varOmega _{1/n}^{\alpha }(\omega ) \right| t^{\beta }},\,\omega \in (-\infty ,\infty ),\, n=1,2,...~. \end{aligned}$$

(57)

Using the result displayed in (51), we can deduce the following. For a bounded time interval there exists $Q_{2}>0$ such that

$$\begin{aligned} \left| \varPsi _{n}(\omega )\right| \le g_2(\omega )=Q_2\frac{t}{ 1+\left| \omega \right| ^{\alpha }t^{\beta }},\, \omega \in (-\infty ,\infty ), \, n=1,2,..., \end{aligned}$$

(58)

and $g_2(\omega )$$\in L^{1}(-\infty ,\infty )$ since

$$\begin{aligned} \int \limits _{-\infty }^{\infty }\left| g_2(\omega )\right| d\omega =2Q_{2}\int \limits _{0}^{\infty }\frac{t d\omega }{1+\left| \omega \right| ^{\alpha }t^{\beta }}=\frac{2K_{2}}{\alpha t^{(\beta /\alpha )-1 }}\varGamma \left( \frac{1 }{\alpha }\right) \varGamma \left( 1-\frac{1}{\alpha }\right) ,\ \ \ \alpha >1 \end{aligned}$$

(59)

Thus the set of functions $\varPsi _{n}(\omega )$ satisfies Lebesgue dominated convergence theorem as well.

At this point, as

$$\begin{aligned} \lim _{n\rightarrow \infty }\varPhi _{n}(\omega )=\frac{1}{2\pi }E_{\beta ,1}(-\left| \omega \right| ^{\alpha }t^{\beta })\int \limits _{-\infty }^{\infty }f_{1}(v)e^{i\omega (x-v)}dv, \end{aligned}$$

(60)

and

$$\begin{aligned} \lim _{n\rightarrow \infty }\varPsi _{n}(\omega )=\frac{1}{2\pi }tE_{\beta ,2}(-\left| \omega \right| ^{\alpha }t^{\beta })\int \limits _{-\infty }^{\infty }f_{2}(v)e^{i\omega (x-v)}dv, \end{aligned}$$

(61)

then by Lebesgue dominated convergence theorem (setting $\theta =\frac{1}{ n}; \theta \rightarrow 0$ as $n\rightarrow \infty$) we have

$$\begin{aligned} \lim _{\theta \rightarrow 0}u_{\beta }^{\alpha ,\theta }(x,t)= & {} \lim _{n\rightarrow \infty }\int \limits _{-\infty }^{\infty }\left( \varPhi _{n}(\omega )+\varPsi _{n}(\omega )\right) d\omega \nonumber \\= & {} \int \limits _{-\infty }^{\infty }\lim _{n\rightarrow \infty }\left( \varPhi _{n}(\omega )+\varPsi _{n}(\omega )\right) d\omega \nonumber \\= & {} \frac{1}{2\pi }\int \limits _{-\infty }^{\infty }\int \limits _{-\infty }^{\infty }E_{\beta ,1}(-\left| \omega \right| ^{\alpha }t^{\beta })f_{1}(v)e^{i\omega (x-v)}d\omega dv \nonumber \\&+\frac{1}{2\pi }\int \limits _{-\infty }^{\infty }\int \limits _{-\infty }^{\infty }t~E_{\beta ,2}(-\left| \omega \right| ^{\alpha }t^{\beta })f_{2}(v)e^{i\omega (x-v)}d\omega dv \nonumber \\= & {} u_{\beta }^{\alpha }(x,t), \end{aligned}$$

(62)

which is the exact solution of the Riesz fractional Eq. (43). $\square$

5 The optimal homotopy solution

In this section, three different equations are considered to illustrate the efficiency of the OHAM to the proposed space-time fractional initial-value problem. Also, via these examples we illustrate the continuation of the solution as the fractional orders tends to their corresponding integer values (note that the exact solution of the integer order problem is known). It is crucial to know that when applying the recursive technique of OHAM to problem (1), a repeated evaluation of Riesz-Feller fractional derivative to solution components is needed. Fortunately to accomplish this task, we use a property of Riesz-Feller fractional derivative that is proved in the following lemma.

Lemma 2

Let $\alpha \in (0,2),$$\alpha \ne 1,$$\left| \theta \right| \le \min (\alpha ,2-\alpha ),$ and $\ \omega >0$. Then,

$$\begin{aligned} R_{x}^{\alpha ,\theta }(\sin (\omega x))= & {} -\omega ^{\alpha }\sin \left( \omega x-\theta \frac{\pi }{2}\right) , \end{aligned}$$

(63)

$$\begin{aligned} R_{x}^{\alpha ,\theta }(\cos (\omega x))= & {} -\omega ^{\alpha }\cos \left( \omega x-\theta \frac{\pi }{2}\right) . \end{aligned}$$

(64)

Proof

See [11]

Example 1

Consider problem (1) with $k(u)=1,~g(u)=a~u~$, $f_{1}(x)=~\sin (\pi x/a)$ and $f_{2}(x)=~-\sin (\pi x/a)$. That is we aim to find the OHAM series solution of the problem

$$\begin{aligned} \left\{ \begin{array}{l} ^{C}D_{t}^{\beta }u(x,t)=R_{x}^{\alpha ,\theta }u(x,t)+u,\quad x \in \mathbb {R},\quad t>0, \\ u(x,0)=~\sin (\pi x/a),\quad u_{t}(x,0)=-\sin (\pi x/a), \end{array} \right. \end{aligned}$$

(65)

where $a,~\epsilon ,~$and b are real constants.

By means of OHAM, let us consider the linear operator $\varUpsilon$ and nonlinear operator $\aleph$ as

$$\begin{aligned} \varUpsilon \left[ \psi \right] =^{C}D_{t}^{\beta }\psi ,\quad \aleph [\psi ]=^{C}D_{t}^{\beta }\psi -R_{x}^{\alpha ,\theta }\psi -\ \psi . \end{aligned}$$

(66)

Then one can write the mth deformation equation (refer to section 3, Eqs. (29), (30) and (31))

$$\begin{aligned} \varUpsilon [u_{m}(x,t)-\sigma _{m}u_{m-1}(x,t)]=\hbar \mathfrak {R}_{m}[u_{m-1}(x,t)], \end{aligned}$$

(67)

where

$$\begin{aligned} \mathfrak {R}_{m}[u_{m-1}]=^{C}D_{t}^{\beta }u_{m-1}-R_{x}^{\alpha ,\theta }u_{m-1}-u_{m-1}. \end{aligned}$$

(68)

Now, referring to lemma 1 (properties of Caputo fractional derivative) and when applying $\varUpsilon ^{-1}=J_{t}^{\mu }$ to both sides (67) one can find $u_{m}(x,t)$, the components of the homotopy series

$$\begin{aligned} u_{m}(x,t)= & {} (\sigma _{m}+\hbar )(u_{m-1}(x,t)-u_{m-1}(x,0)-t~\frac{ \partial }{\partial t}u_{m-1}(x,0))+u_{m}(x,0) \nonumber \\&+t~\frac{\partial }{\partial t}u_{m}(x,0)-\hbar J_{t}^{\beta }\left[ R_{x}^{\alpha ,\theta }u_{m-1}(x,t)+\ u_{m-1}(x,t)\right] , m\ge 1, \end{aligned}$$

(69)

where

$$\begin{aligned} u_{m}(x,0)=0,\ \ \ \frac{\partial }{\partial t}u_{m}(x,0)=0\ ,\ \ \ \ \ m\ge 1. \end{aligned}$$

(70)

If the initial approximation (the first term in the homotopy series) $u_{0}(x,t)$ is assumed as

$$\begin{aligned} u_{0}(x,t)=(1-t)\sin \left( \frac{\pi x}{a}\right) , \end{aligned}$$

(71)

one can obtain the second and third term in the series $u_{1}$ and $u_{2}$ as

$$\begin{aligned} u_{1}(x,t)=\frac{ht^{\beta }(t-\beta -1)}{\varGamma \left( 2+\beta \right) } \left( \sin \left( \frac{\pi x}{a}\right) -\left( \frac{\pi }{a}\right) ^{\alpha }\sin \left( \frac{\pi x}{a}-\frac{\pi \theta }{2}\right) \right) , \end{aligned}$$

and

$$\begin{aligned} u_{2}= & {} -\frac{h^{2}t^{2\beta }(t-2\beta -1)}{\varGamma \left( 2+2\beta \right) }\sin \left( \frac{\pi x}{a}\right) +\left( \frac{\pi }{a}\right) ^{\alpha }\left( \left( \frac{\pi }{a}\right) ^{\alpha }\sin \left( \frac{ \pi x}{a}-\pi \theta \right) \right) \\&+\frac{2h^{2}t^{2\beta }(t-2\beta -1)}{\varGamma \left( 2+2\beta \right) } \left( \left( \frac{\pi }{a}\right) ^{\alpha }\sin \left( \frac{\pi x}{a}- \frac{\pi \theta }{2}\right) \right) \\&+\frac{ht^{\beta }(1+h)(t-\beta -1)}{\varGamma \left( 2+2\beta \right) } \left( \sin \left( \frac{\pi x}{a}\right) -\left( \frac{\pi }{a}\right) ^{\alpha }\sin \left( \frac{\pi x}{a}-\frac{\pi \theta }{2}\right) \right) . \end{aligned}$$

It is important to note that, the exact solution of the corresponding equation of integer orders ($u_{tt}=u_{xx}+a u$) is gives by

$$\begin{aligned} u_{exact}=\sin (\pi x/a)\left[ \cos (\zeta t)-(1/\zeta )\sin (\zeta t)\right] ,\ \ \ \ \ \ \ \zeta =\sqrt{1-(\pi /a)^{2}}, \end{aligned}$$

(72)

We compare this exact solution with the obtained homotopy series solution as the fractional orders tend to their integer values, that proves the continuity of the solution numerically.

Fig. 1

The solution of (65) at $t=0.6,~0\le x\le \pi ,\$and the fractional parameters $\alpha =1.8\$and $\beta =2,~$ and the skewness $\theta =0,\ 0.2,\ -\,0.2.$

Fig. 2

The behavior of the OHAM solution of (65) at $t=0.8,~0\le x\le \pi ,\$ and the fractional parameters $\theta =0$, $\beta =2,~$and $\alpha =1.8,\ \ 1.9,\ 1.95~$ compared with the exact solution (the solution of the corresponding integer order problem) displayed in ( 72)

Fig. 3

The behavior of the OHAM solution of (65) at $t=0.8,~0\le x\le \pi ,\$and the fractional parameters $\theta =0$, $\alpha =2.0,~$and $\beta =1.8,\ 1.9,\ 1.95,\$compared with the exact solution (the solution of the corresponding integer order problem) displayed in (72)

Table 1 The estimated optimal convergence parameter $\hbar$ and the corresponding residual error $E_{m}$ at different fractional parameters used in Figs. 1, 2 and 3

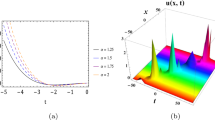
The solution (the first four terms in the OHAM series) behavior as the parameters $\theta ,$$\alpha$ and $\beta \$change at a fixed time and in the interval $0\le x\le \pi$ shown in Figs. 1–3. Figure 1 shows the effect of the skewness parameter $\theta$ on the behavior of the solution. At a fixed time, the plot represents the sum of the first four terms in the OHAM series when $a=3.0,~0<x<\pi ~$and the fractional parameters $\beta =2.0,$$\alpha =1.8,~$and $\theta =0,\ 0.2,\ -0.2.$ From Figs. 2 and 3, as $\alpha$ and $\beta$ reaches 2, the series solution approximately coincides with the exact solution of the corresponding integer order equation displayed in (72), which is represented by the solid lines. This numerical result supports the continuation of the optimal homotopy solution as the fractional orders converges to the value 2. The optimal convergence parameter $\hbar$ in each case is obtained by minimizing the residual error $E_{m}\$displayed in (32) in the interval $0\le x\le \pi$ and $0\le t\le 6.0$ , and the obtained results are shown in Table 1.

Example 2

In this example we consider the time-space Caputo–Riesz-Feller sine-Gordon problem

$$\begin{aligned} \left\{ \begin{array}{l} ^{C}D_{t}^{\beta }u(x,t)=R_{x}^{\alpha ,\theta }u(x,t)-\ \sin (u),\quad x \in \mathbb {R},\quad t>0,\\ u(x,0)=\pi +\varepsilon \cos (ax),\quad u_{t}(x,0)=0, \end{array} \right. \end{aligned}$$

(73)

where $\varepsilon ~$and a are real constants.

Here, the chosen auxiliary linear and nonlinear operators are operator is

$$\begin{aligned} \varUpsilon [\psi ]=^{C}D_{t}^{\beta }(\psi ), \quad \aleph [\psi ]=^{C}D_{t}^{\beta }\psi -R_{x}^{\alpha ,\theta }(\psi )+\sin (\psi ), \end{aligned}$$

(74)

then the deformation equation is

$$\begin{aligned} ^{C}D_{t}^{\beta }[u_{m}(x,t)-\sigma _{m}u_{m-1}(x,t)]=\hbar \mathfrak {R}_{m}[u_{m-1}(x,t)], \end{aligned}$$

(75)

where $\mathfrak {R}_{m}[u_{m-1}(x,t)]$ is given by

$$\begin{aligned} \mathfrak {R}_{m}[u_{m-1}(x,t)]=^{C}D_{t}^{\beta }u(x,t)(u_{m-1})-R_{x}^{\alpha ,\theta }(u_{m-1})+A_{m-1}, \end{aligned}$$

(76)

where the nonlinear term is replaced by its by Adomian polynomials $A_{k}$ [7]. For the function $\sin (u)$ the Adomian polynomials are

$$\begin{aligned} A_{0}=\sin (u_{0}),\ A_{1}=u_{1}\cos (u_{0}),\ A_{2}=1/2(-u_{1}^{2}\sin (u_{0})+2u_{2}\cos (u_{0})),... \end{aligned}$$

When we apply the operator $\varUpsilon ^{-1}=J_{t}^{\beta }$ to both sides of ( 75), one can obtain the mth term of the homotopy series in the form

$$\begin{aligned} u_{m}(x,t)= & {} (\sigma _{m}+\hbar )(u_{m-1}(x,t)-u_{m-1}(x,0)-t~\frac{ \partial }{\partial t}u_{m-1}(x,0))+u_{m}(x,0) \nonumber \\&+\,t~\frac{\partial }{\partial t}u_{m}(x,0)-\hbar J_{t}^{\beta }\left[ R_{x}^{\alpha ,\theta }u_{m-1}(x,t)-\sum \limits _{k=0}^{m-1}A_{k},\right] , \end{aligned}$$

(77)

where

$$\begin{aligned} u_{m}(x,0)=0,\ \ \ \frac{\partial }{\partial t}u_{m}(x,0)=0\ ,\ \ \ \ \ m>1. \end{aligned}$$

(78)

Thus, the first four terms of the series solution can be written as

$$\begin{aligned} u_{0}= & {} \pi , \\ u_{1}= & {} \varepsilon \cos (ax), \\ u_{2}= & {} \frac{\epsilon ht^{\beta }}{\varGamma \left( 1+\beta \right) }\left( -\cos \left( ax\right) +a^{\alpha }\cos \left( ax-\frac{\pi \theta }{2} \right) \right) , \\ u_{3}= & {} -\frac{2\epsilon h(1+h)t^{\beta }}{\varGamma \left( 1+\beta \right) } \left( \cos \left( ax\right) -a^{\alpha }\cos \left( ax-\frac{\pi \theta }{2} \right) \right) \\&+\frac{\epsilon h^{2}t^{2\beta }}{\varGamma \left( 1+2\beta \right) }\left( \cos \left( ax\right) +a^{\alpha }\left( a^{\alpha }\cos \left( ax-\pi \theta \right) -2\cos \left( ax-\frac{\pi \theta }{2}\right) \right) \right) , \end{aligned}$$

Fig. 4

The behavior of the OHAM solution of (73) at $t=1.0,~0\le x\le 2.0,\$and the fractional parameter $\alpha =1.5\$and $\beta =2,~$the skewness $\theta =0,\ 0.5,\ -\,0.5.$

Fig. 5

The behavior of the OHAM solution of (73) at $t=1.0,~0\le x\le 2,\$and the fractional parameter $\theta =0$, $\beta =2,~$and $\alpha =1.7,\ 1.8,\ 1.9~$and 2.0.

Fig. 6

The behavior of the OHAM solution of (73) at $t=1.0,~0\le x\le 2,\$and the fractional parameter $\theta =0$, $\alpha =2.0,~$and $\beta =1.7,\ 1.8,\ 1.9$ and 2.0.

In the interval $0\le x\le 2.0$ and at a fixed time, Figs. 4, 5 and 6 show the solution (the first five terms in the OHAM series) behavior as the parameters $\theta ,\ \alpha$ and $\beta \$ change at a fixed time. In the space domain $0\le x\le 2.0$ and the time interval $0\le t\le 2.0$, Table 2 shows the estimated values of the optimal convergence control parameter $\hbar$ and the corresponding residual error $E_{m}~$displayed in (32) for the problem (73) at different values of the fractional derivatives parameters $\theta ,\$$\alpha$ and $\beta$.

In this example, we obtained approximate solutions for the generalized Caputo–Riesz-Feller sine-Gordon equation using the OHAM. In [28], S.S. Ray solved the the sine-Gordon equation but in classical Riesz space fractional derivative operator by using transform method with the decomposition method.

Table 2 The estimated optimal convergence parameter $\hbar$ and the corresponding residual error $E_{m}$ at different fractional parameters used in Figs. 4, 5 and 6

Example 3

In this final example, we consider the nonlinear fractional problem (1) with $k(u)=u,~g(u)=u^{2}/4-u~,$$f_{1}(x)=\sin (2x)~$and $f_{2}(x)=0$

$$\begin{aligned} \left\{ \begin{array}{l} ^{C}D_{t}^{\beta }u(x,t)=u\ R_{x}^{\alpha ,\theta }u(x,t)+~u^{2}/4-u~,\quad x \in \mathbb {R},\quad t>0,\\ u(x,0)=~\sin (x/2),\quad ~u_{t}(x,0)=0. \end{array} \right. \end{aligned}$$

(79)

Here, the linear operator $\varUpsilon$ and the nonlinear operator $\aleph$ are

$$\begin{aligned} \varUpsilon [\psi ]=^{C}D_{t}^{\beta }(\psi ),\ \ \ \ \ \ \aleph [\psi ]=^{C}D_{t}^{\beta }\psi -\psi R_{x}^{\alpha ,\ \theta }(\psi )-\psi ^{2}/4+\psi , \end{aligned}$$

(80)

respectively. Thus the deformation equation is

$$\begin{aligned} ^{C}D_{t}^{\beta }[u_{m}(x,t)-\sigma _{m}u_{m-1}(x,t)]=\hbar \mathfrak {R}_{m}[u_{m-1}(x,t)], \end{aligned}$$

(81)

where $\mathfrak {R}_{m}[u_{m-1}(x,t)]$ is written as

$$\begin{aligned} \mathfrak {R}_{m}[u_{m-1}(x,t)]=^{C}D_{t}^{\beta }(u_{m-1})-\sum \limits _{k=0}^{m-1}u_{k}R_{x}^{\alpha ,\ \theta }(u_{m-1-k})- \frac{1}{4}\sum \limits _{k=0}^{m-1}u_{k}u_{m-1-k}+u_{m-1}, \end{aligned}$$

(82)

where the partial sums are the Adomian representation of the nonlinear terms.

Applying the inverse integral operator $\varUpsilon ^{-1}=J_{t}^{\beta }$ to both sides of (81) leads to

$$\begin{aligned} u_{m}(x,t)= & {} (\sigma _{m}+\hbar )(u_{m-1}(x,t)-u_{m-1}(x,0)) \nonumber \\&-\,\hbar J_{t}^{\beta }\left[ \sum \limits _{k=0}^{m-1}u_{k}R_{x}^{\alpha ,\ \theta }(u_{m-1-k})+\frac{1}{4}\sum \limits _{k=0}^{m-1}u_{k}u_{m-1-k}-u_{m-1} \right] , \end{aligned}$$

(83)

where

$$\begin{aligned} u_{m}(x,0)=0,\ \ \ \frac{\partial }{\partial t}u_{m}(x,0)\ ,\ \ \ \ \ m>0, \end{aligned}$$

(84)

and one can easily find that

$$\begin{aligned} u_{0}= & {} \sin (2x), \\ u_{1}= & {} \frac{ht^{\beta }\left( 2^{-\alpha }\cos \left( x-2\theta \right) - \frac{1}{4}\cos \left( x-\theta \right) -2^{1-\alpha }\sin \left( \frac{x}{2} -\theta \right) \right) }{2\varGamma (1+\beta )}. \end{aligned}$$

Fig. 7

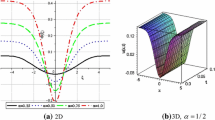
The behavior of the OHAM solution of (79) at $t=1.0,~0\le x\le 2\pi ,\$and the fractional parameter $\alpha =1.5\$and $\beta =2,~$the skewness $\theta =0,\ 0.5,\ -\,0.5$

Fig. 8

The behavior of the OHAM solution of (79) at $t=1.5,~0\le x\le 2\pi ,\$and the fractional parameter $\theta =0$, $\beta =1,~$and $\alpha =1.7,\ 1.8,\ 1.9,\$compared with the exact solution of the equation of integer order

Fig. 9

The behavior of the OHAM solution of (79) at $t=1.0,~0\le x\le 2\pi ,\$and the fractional parameter $\theta =0$, $\alpha =2.0,~$and $\beta =1.7,\ 1.8,\ 1.9,\$compared with the exact solution of the corresponding integer order equation

Figures 7–9 show the solution (the first five terms in the OHAM series) behavior as the parameters $\theta ,\$$\alpha$ and $\beta \$change at a fixed time and in the interval $0\le x\le 2\pi$. The effect of the skewness parameter $\theta$ on the behavior of the solution is depicted in Fig. 7. As $\alpha$ and/or $\beta \$increases to the integer limit 2, the amplitude of the solution increases. Also, the series solution approximately coincides with the exact solution ($u_{exact}=\cos (t)\sin (x/2)$) of the corresponding integer order equation ($u_{tt}=uu_{xx}+u^2/4-u$), which is represented by the solid line in the graphs, see Figs. 8 and 9. From these results, the continuation of thesolution is confirmed numerically. The series displayed in plots is the partial sum of the first five terms. The optimal convergence parameter $\hbar$ in each case is obtained by minimizing the residual error $E_{m}\$displayed in (32) in the interval $0\le x\le 2\pi$ and $0\le t\le 2.0$, and the obtained results shown in Table 3.

Table 3 The estimated optimal convergence parameter $\hbar$ and the corresponding residual error $E_{m}$ at different fractional parameters used in Figs. 7, 8 and 9

6 Conclusion

In this article, we proved the continuation of the solution of a fractional wave equation with Riesz-Feller spatial derivative to the corresponding fractional wave equation with Riesz definition. The iterative OHAM is applied successfully to obtain the approximate solution of the newly proposed time-space caputo–Riesz-Feller nonlinear fractional wave equation. The adopted optimal scheme has the ability to estimate the residual error that gives better approximate solution than classical homotopy methods. The results obtained illustrate graphically the continuation of the solution with the change in the fractional derivative parameters. From Lemma 3, the Riesz-Feller operator is applied only on sine and cosine and consequently complex exponential functions. Thus, we construct the OHAM solution efficiently for the considered initial value problem only when the initial conditions are in the form of sine and/or cosine functions. If the given initial condition is not a periodic function, one can use its Fourier series representation, and this can be found in a recent work [32]. We conclude that when approximating the solution of Riesz-Feller or Riesz fractional initial value problems, the OHAM iterative method works efficiently specially when the initial conditions are of the form of periodic function.