1 Introduction

The study of the exact solutions of nonlinear fractional partial differential equations (FPDEs) has become a wide area of research for many mathematicians. The nonlinear FPDEs have been used in the modeling of complex nonlinear aspects that defines some of our real-life problems in mathematical physics, engineering, distinct sciences, and other sciences including medical imaging, optical fiber, plasma physics, fluid dynamics, hydrodynamics, and many more. (Tarasov 2011; Das 2011; El-Nabulsi 2018, 2019; Hajipour et al. 2018; Zulfiqar et al. 2022; Aniqa and Ahmad 2021).

Closed-form analytical solutions make a substantial contribution to easily, more suitably and clearly expressing these phenomena. Different numerical and analytical methods have been applied to investigate the behavior of these models (Baleanu et al. 2021; Zulfiqar and Ahmad 2020; Zulfiqar et al. 2019; Zulfiqar and Ahmad 2021; Rani et al. 2021; Akbar et al. 2019; Goswami et al. 2019).

In an elastic rod, the longitudinal deformation wave propagation is modeled by the nonlinear partial differential equation known as Pochhammer-Chree (PC) equation and presented by Clarkson et al. as follows (Clarkson et al. 1986).

$$ u_{tt} - u_{ttxx} - \frac{1}{n}\left( {u^{n} } \right)_{xx} = 0, $$
(1)

where \(u(x,t)\) represents the longitudinal displacement at time t, of a material point originally lying at the point x. Clarkson et al. (Clarkson et al. 1986) resolve the Eq. (1) by considering n = 3 or 5 for studying the interactions of solitary waves in elastic rods. Soliton-type solutions have been obtained by Bogolubsky (Bogolubsky 1977) by considering n = 2, 3, 5. Exact solutions of Eq. (1) have been acquired by Triki et al. (Triki et al. 2015) for n = 6. The generalized Pochhammer-Chree equation is given by (Parand and Rad 2010; Yokus et al. 2021).

$$ u_{tt} - u_{ttxx} - \left( {\mu u + \beta u^{n + 1} + \nu u^{2n + 1} } \right)_{xx} = 0,\;\;n \ge 1, $$
(2)

where μ, β, and ν are constants. Many authors studied Eq. (2) for acquiring a variety of solutions by considering different analytical and numerical techniques. Explicit kink shape and bell shape solitary wave solutions of the GPC equation have been studied by Weiguo, and Wenxiu (Weiguo and Wenxiu 1999). The GPC equation has been studied for a class of nonlinear perturbation for obtaining blow-up solutions (Liu 1996). Different kinds of traveling wave solutions, namely kink shape, bell shape, and periodic solutions have been obtained by using two different analytical techniques (Wazwaz 2008). Li, & Zhang (Li and Zhang 2002) studied the bifurcation of kink wave and solitary wave for the GPC equation. Explicit power series solutions for the PC equation have been obtained by using the decomposition method (Shawagfeh and Kaya 2004). The first integral method has been utilized to get complex traveling wave solutions, complex rational function solutions, and complex periodic solutions for the GPC equation (El-Ganaini 2011). Mohebbi (Mohebbi 2012) resolves the GPC equation to get the solitary wave solutions by using the discrete Fourier transform. Exp-function method has been applied to acquire some exact solitary wave solutions for the GPC equation (Parand and Rad 2010). Exact solutions including singular, kink shape, and periodic solutions have been obtained by using different analytical techniques (Zuo 2010; Zhang 2005; Zhang et al. 2010).

This paper is concerned with the conformable space–time fractional order GPC equation given by

$$ D_{t}^{2\alpha } u - D_{ttxx}^{4\alpha } u - D_{x}^{2\alpha } \left( {\mu u + \beta u^{n + 1} + \nu u^{2n + 1} } \right) = 0,\,\,n \ge 1,\,\,0 < \alpha \le 1, $$
(3)

where the exponent is the power-law nonlinearity parameter. To the knowledge of the author, the fractional order GPC equation has not been studied before in the literature. The Exp-function method has been used before for the GPC equation but not for the non-integer order (Parand and Rad 2010). Therefore, the study of the fractional order GPC equation is very reasonable for describing the physical functioning of a longitudinal wave in elastic rods.

The Exp-function method was introduced by J. H. He and Wu (He and Wu 2006; He 2013). This technique is one of the competent techniques to resolve the nonlinear partial differential equations (PDEs). However, this technique performs an exceptional role in resolving the problems of fractional calculus. Many authors studied the FPDEs by utilizing this technique. Exp- function has been used to resolve fractional modified Camassa-Holm equation (Zulfiqar and Ahmad 2020), generalized KdV and the modified KdV equations (Heris and Bagheri 2010), the Calogero-Bogoyavlenskii-Schiff equation (Ayub et al. 2017), fractional order Boussinesq-like equations (Rahmatullah et al. 2018), fractional modified unstable Schrödinger equation (Zulfiqar and Ahmad 2020), modified Zakharov Kuznetsov equation (Mohyud-Din et al. 2010), improved Boussinesq equation (Abdou et al. 2007), nonlinear evolution equations (El-Wakil et al. 2007), and for many other nonlinear FPDs (Guner and Bekir 2017; Yaslan and Girgin 2019; Guner and Bekir 2017).

The objective of this article is to study the fractional order GPC equation with the n order term for constructing some new analytical solitary wave solutions by using a proficient Exp-function method in the sense of conformable fractional derivative. Khalil proposed a thrilling definition of derivative known as conformable spinoff (Khalil 2014) along with a set of properties. Moreover, the conformable by-product satisfies all the properties of the same old calculus, for example, the chain rule. The conformable derivative of \(g\) having order α for a function g(x) is defined by:

$$ \left( {D^{\alpha } g} \right)\left( x \right) = \mathop {\lim }\limits_{{\varepsilon \to 0}} \frac{{g\left( {x + \varepsilon x^{{1 - \alpha }} } \right) - g\left( x \right)}}{\varepsilon },x > 0,\;\alpha \in {\mkern 1mu} \left( {0,1} \right). $$
(4)

2 The summary of method

Consider the general nonlinear FPDE

$$ R\,\left( {u,u_{x} ,u_{t} ,D_{t}^{\alpha } ,...} \right) = 0,\;\;\;\;0 < \alpha \le 1. $$
(5)

The fractional traveling wave transformation is given by

$$ u(x,t) = U(\eta ),\;\;\;\;\eta = k\;\left( {\frac{{x^{\alpha } }}{\alpha } - r\frac{{t^{\alpha } }}{\alpha }} \right), $$
(6)

where and \(r\) are non-zero arbitrary constants. Inserting Eq. (6) into Eq. (5), yields

$$ P\,\left( {U,U^{\prime } ,U^{\prime \prime } ,U^{\prime \prime \prime } ...} \right) = 0. $$
(7)

Suppose the solitary wave solution as

$$ U(\eta ) = \frac{{\sum\nolimits_{m = - q}^{s} {a_{m} \exp \left[ {m\eta } \right]} }}{{\sum\nolimits_{l = - g}^{h} {b_{l} \exp \left[ {l\eta } \right]} }}, $$
(8)

where \(q,\;s,\;g\;and\;h\) are constants. To compare the specific terms which are further solved for the required set of parameters.

3 Solution of problem

Substituting the transformation in Eq. (6) into Eq. (3), we get

$$ k^{2} \left( {r^{2} - \mu } \right)\,\,U - k^{4} r^{2} U^{\prime\prime} - \beta k^{2} U^{n + 1} - \nu k^{2} U^{2n + 1} = 0. $$
(9)

By using the transformation

$$ U^{n} = V. $$
(10)
$$ k^{2} n^{2} \left( {r^{2} - \mu } \right)\,\,V^{2} - k^{4} r^{2} nVV^{\prime\prime} - k^{4} r^{2} \left( {1 - n} \right)V^{{\prime}{2}} - \beta k^{2} n^{2} V^{3} - \nu k^{2} n^{2} V^{4} = 0. $$
(11)

By using the homogeneous balance principle, we get \(r = s = g\, = \,h = 1\) and then Eq. (11) reduces to

$$ V\left( \eta \right) = U^{n} \left( \eta \right) = \frac{{a_{ - 1} \exp \left[ { - \eta } \right] + a_{0} + a_{1} \exp \left[ \eta \right]}}{{b_{ - 1} \exp \left[ { - \eta } \right] + b_{0} + b_{1} \exp \left[ \eta \right]}}. $$
(12)

By substituting Eq. (12) in Eq. (11) and equating the coefficients to zero with the help of symbolic computation, we have

$$ A_{0} = - a_{ - 1}^{2} n^{2} k^{2} \left( {a_{ - 1}^{2} \nu + \beta a_{ - 1} b_{ - 1} - b_{ - 1}^{2} \left( {r^{2} - \mu } \right)} \right) = 0, $$
$$ A_{1} = - nk^{2} a_{{ - 1}} \left( \begin{gathered} \left( {\left( {\beta b_{0} + 4\nu a_{0} } \right)a_{{ - 1}}^{2} - 2b_{{ - 1}} \left( { - \frac{{3\beta a_{0} }}{2} + b_{0} \left( {r^{2} - \mu } \right)} \right)a_{{ - 1}} - 2b_{{ - 1}}^{2} a_{0} \left( {r^{2} - \mu } \right)} \right)n \hfill \\ + k^{2} b_{{ - 1}} r^{2} \left( {a_{{ - 1}} b_{0} - a_{0} b_{{ - 1}} } \right) \hfill \\ \end{gathered} \right) = 0, $$
$$ A_{2} = - 4k^{2} a_{{ - 1}} \left( \begin{gathered} \left( \begin{gathered} \left( {\frac{{\beta b_{1} }}{4} + \nu a_{1} } \right)a_{{ - 1}}^{3} + \left( {\frac{{3\beta a_{1} b_{{ - 1}} }}{4} + \frac{{3\nu a_{0}^{2} }}{2} + \frac{{3\beta a_{0} b_{0} }}{4} - \frac{{\left( {r^{2} - \mu } \right)\left( {b_{{ - 1}} b_{1} + \frac{{b_{0}^{2} }}{2}} \right)}}{2}} \right)a_{{ - 1}}^{2} \hfill \\ - \frac{1}{2}\left( {b_{{ - 1}} \left( {b_{{ - 1}} \left( {r^{2} - \mu } \right)a_{1} + 2\left( { - \frac{{3\beta a_{0} }}{4} + b_{0} \left( {r^{2} - \mu } \right)} \right)a_{0} } \right)a_{{ - 1}} } \right) - \frac{{a_{0}^{2} b_{{ - 1}}^{2} \left( {r^{2} - \mu } \right)}}{4}n^{2} \hfill \\ \end{gathered} \right) \hfill \\ + k^{2} a_{{ - 1}} b_{{ - 1}} r^{2} \left( {a_{{ - 1}} b_{1} - a_{1} b_{{ - 1}} } \right)n - \frac{{k^{2} r^{2} \left( {a_{{ - 1}} b_{0} - a_{0} b_{{ - 1}} } \right)^{2} }}{4} \hfill \\ \end{gathered} \right) = 0, $$
$$ A_{3} = - 4k^{2} \left( \begin{gathered} \left( \begin{gathered} \left( {\left( {\frac{{3\beta b_{0} }}{4} + 3\nu a_{0} } \right)a_{1} - \frac{{\left( { - \frac{{3\beta a_{0} }}{2} + b_{0} \left( {r^{2} - \mu } \right)} \right)b_{1} }}{2}} \right)a_{{ - 1}}^{2} \hfill \\ + \left( { - b_{{ - 1}} \left( { - \frac{{3\beta a_{0} }}{2} + b_{0} \left( {r^{2} - \mu } \right)} \right)a_{1} } \right) - \left( { - \nu a_{0}^{2} - \frac{{3\beta a_{0} b_{0} }}{4} + \left( {r^{2} - \mu } \right)\left( {b_{{ - 1}} b_{1} + \frac{{b_{0}^{2} }}{2}} \right)a_{0} } \right)a_{{ - 1}} \hfill \\ - \frac{1}{2}\left( {b_{{ - 1}} a_{0} \left( {b_{{ - 1}} \left( {r^{2} - \mu } \right)a_{1} + a_{0} \left( { - \frac{{\beta a_{0} }}{2} + b_{0} \left( {r^{2} - \mu } \right)} \right)} \right)} \right)n^{2} \hfill \\ \end{gathered} \right) \hfill \\ + \frac{1}{4}k^{2} r^{2} \left( {a_{{ - 1}}^{2} b_{0} b_{1} + \left( { - 6a_{1} b_{{ - 1}} b_{0} + a_{0} \left( {6b_{{ - 1}} b_{1} - b_{0}^{2} } \right)} \right)a_{{ - 1}} - a_{0} a_{1} b_{{ - 1}}^{2} + a_{0}^{2} b_{{ - 1}} b_{0} } \right)n \hfill \\ - k^{2} r^{2} \left( {a_{{ - 1}} b_{0} - a_{0} b_{{ - 1}} } \right)\left( {a_{{ - 1}} b_{1} - a_{1} b_{{ - 1}} } \right) \hfill \\ \end{gathered} \right) = 0, $$
$$ A_{4} = 4k^{2} \left( \begin{gathered} \left( \begin{gathered} \left( {\frac{{3\nu a_{1}^{2} }}{2} + \frac{{3\beta a_{1} b_{1} }}{4} - \frac{{b_{1}^{2} \left( {r^{2} - \mu } \right)}}{4}} \right)a_{{ - 1}}^{2} \hfill \\ + \left( {\frac{{3\beta a_{1}^{2} b_{{ - 1}} }}{4} + a_{1} \left( \begin{gathered} 3\nu a_{0}^{2} + \frac{{3\beta a_{0} b_{0} }}{2} \hfill \\ - \left( {r^{2} - \mu } \right)\left( {b_{{ - 1}} b_{1} + \frac{{b_{0}^{2} }}{2}} \right) \hfill \\ \end{gathered} \right) - \left( { - \frac{{3\beta a_{0} }}{4} + b_{0} \left( {r^{2} - \mu } \right)} \right)a_{0} b_{1} } \right)a_{{ - 1}} \hfill \\ - \frac{{b_{{ - 1}}^{2} \left( {r^{2} - \mu } \right)a_{1}^{2} }}{4} - \left( { - \frac{{3\beta a_{0} }}{4} + b_{0} \left( {r^{2} - \mu } \right)} \right)b_{{ - 1}} a_{0} a_{1} \hfill \\ - \frac{1}{2}\left( { - \frac{{\nu a_{0}^{2} }}{2} - \frac{{\beta a_{0} b_{0} }}{2} + \left( {r^{2} - \mu } \right)} \right)\left( {b_{{ - 1}} b_{1} + \frac{{b_{0}^{2} }}{2}} \right)a_{0}^{2} \hfill \\ \end{gathered} \right)n^{2} - k^{2} r^{2} \left( \begin{gathered} a_{{ - 1}} a_{1} b_{0}^{2} \hfill \\ - b_{{ - 1}} b_{1} a_{0}^{2} \hfill \\ \end{gathered} \right)n \hfill \\ - \left( \begin{gathered} a_{{ - 1}}^{2} b_{1}^{2} + \left( {\left( { - 2b_{{ - 1}} b_{1} - \frac{{b_{0}^{2} }}{2}} \right)a_{1} + \frac{{b_{1} a_{0} b_{0} }}{2}} \right)a_{{ - 1}} + \hfill \\ b_{{ - 1}} \left( {a_{1}^{2} b_{{ - 1}} + \frac{1}{2}a_{0} a_{1} b_{0} - \frac{1}{2}b_{1} a_{0}^{2} } \right) \hfill \\ \end{gathered} \right)r^{2} k^{2} \hfill \\ \end{gathered} \right) = 0, $$
$$ \begin{gathered} A_{5} = - 4k^{2} \left( \begin{gathered} \left( \begin{gathered} \frac{1}{2}\left( {\left( {\frac{{3\beta b_{0} }}{4} + 3\nu a_{0} } \right)a_{1}^{2} - \left( { - \frac{{3\beta a_{0} }}{2} + b_{0} \left( {r^{2} - \mu } \right)} \right)b_{1} a_{1} - \frac{1}{2}\left( {a_{0} b_{1}^{2} \left( {r^{2} - \mu } \right)} \right)} \right)a_{{ - 1}} \hfill \\ - \left( {b_{{ - 1}} \left( { - \frac{{3\beta a_{0} }}{2} + b_{0} \left( {r^{2} - \mu } \right)} \right)} \right) - - \nu a_{0}^{2} - \frac{{3\beta a_{0} b_{0} }}{4} + \left( {r^{2} - \mu } \right)\left( {b_{{ - 1}} b_{1} + \frac{{b_{0}^{2} }}{2}} \right)a_{0} a_{1} \hfill \\ - \frac{1}{2}\left( {b_{1} a_{0}^{2} \left( { - \frac{{\beta a_{0} }}{2} + b_{0} \left( {r^{2} - \mu } \right)} \right)} \right) \hfill \\ \end{gathered} \right)n^{2} \hfill \\ + \frac{1}{2} - 3k^{2} r^{2} \left( {b_{1} \left( {a_{1} b_{0} + \frac{{a_{0} b_{1} }}{6}} \right)a_{{ - 1}} - \frac{{a_{1}^{2} b_{{ - 1}} b_{0} }}{6} - a_{0} \left( {b_{{ - 1}} b_{1} - \frac{{b_{0}^{2} }}{6}} \right)a_{1} - \frac{{a_{0}^{2} b_{0} b_{1} }}{6}} \right)n \hfill \\ + k^{2} r^{2} \left( { - a_{0} b_{1} + a_{1} b_{0} } \right)\left( {a_{{ - 1}} b_{1} - a_{1} b_{{ - 1}} } \right) = 0, \hfill \\ \end{gathered} \right) \hfill \\ \hfill \\ \end{gathered} $$
$$ A_{7} = - k^{2} \left( \begin{gathered} \left( {\left( {\beta b_{0} + 4\nu a_{0} } \right)a_{1}^{2} - 2\left( { - \frac{{3\beta a_{0} }}{2} + b_{0} \left( {r^{2} - \mu } \right)} \right)b_{1} a_{1} - 2a_{0} b_{1}^{2} \left( {r^{2} - \mu } \right)} \right)n \hfill \\ - nk^{2} a_{1} b_{1} r^{2} \left( { - a_{0} b_{1} + a_{1} b_{0} } \right) \hfill \\ \end{gathered} \right) = 0, $$
$$ A_{8} = - a_{1}^{2} n^{2} k^{2} \left( {a_{1}^{2} \nu + \beta a_{1} b_{1} - b_{1}^{2} \left( {r^{2} - \mu } \right)} \right) = 0. $$
(13)

By solving these equations we acquire the following form of solutions.

Case 1

$$ \begin{gathered} \,\beta = 0,\mu = - \frac{{r^{2} \left( {k^{2} - 2} \right)}}{2},n = 1,\,\nu = \frac{{b_{ - 1}^{2} k^{2} r^{2} }}{{2a_{ - 1}^{2} }},\,a_{ - 1} = a_{ - 1} ,\,a_{0} = a_{0} ,\,a_{1} = \frac{{a_{ - 1}^{2} b_{0}^{2} - a_{0}^{2} b_{ - 1}^{2} }}{{4a_{ - 1} b_{ - 1}^{2} }}, \hfill \\ b_{ - 1} = b_{ - 1} ,b_{0} = b_{0} ,b_{1} = \frac{{a_{ - 1}^{2} b_{0}^{2} - a_{0}^{2} b_{ - 1}^{2} }}{{4a_{ - 1} b_{ - 1}^{2} }}. \hfill \\ \end{gathered} $$
(14)
$$ u_{1} \left( {x,t} \right) = \left( {\frac{{a_{ - 1} \exp \left[ { - k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right] + a_{0} - \frac{{a_{ - 1}^{2} b_{0}^{2} - a_{0}^{2} b_{ - 1}^{2} }}{{4a_{ - 1} b_{ - 1}^{2} }}\exp \left[ {k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right]}}{{b_{ - 1} \exp \left[ { - k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right] + b_{0} + \frac{{a_{ - 1}^{2} b_{0}^{2} - a_{0}^{2} b_{ - 1}^{2} }}{{4a_{ - 1} b_{ - 1}^{2} }}\exp \left[ {k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right]}}} \right)^{\frac{1}{n}} . $$
(15)

Case 2

$$ \begin{gathered} \beta = 0,\,\mu = - \frac{{r^{2} \left( {k^{2} - 2} \right)}}{2},n = 1,\,\nu = \frac{{b_{1}^{2} k^{2} r^{2} }}{{2a_{1}^{2} }},\,a_{ - 1} = 0,\,a_{0} = a_{0} ,\,a_{1} = a_{1} , \hfill \\ b_{ - 1} = 0,b_{0} = - \frac{{a_{0} b_{1} }}{{a_{1} }},b_{1} = b_{1} . \hfill \\ \end{gathered} $$
(16)
$$ u_{2} \left( {x,t} \right) = \left( {\frac{{a_{0} + a_{1} \exp \left[ {k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right]}}{{ - \frac{{a_{0} b_{1} }}{{a_{1} }} + b_{1} \exp \left[ {k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right]}}} \right)^{\frac{1}{n}} . $$
(17)

Case 3

$$ \begin{gathered} \,\beta = 0,\mu = \frac{{r^{2} \left( {k^{2} + 4} \right)}}{4},n = 2,\,\nu = - \frac{{b_{1}^{2} k^{2} r^{2} }}{{4a_{1}^{2} }},\,a_{ - 1} = 0,\,a_{0} = a_{0} ,\,a_{1} = a_{1} , \hfill \\ b_{ - 1} = - \frac{{a_{0} \left( {a_{0} b_{1} - a_{1} b_{0} } \right)}}{{a_{1}^{2} }},b_{0} = b_{0} ,b_{1} = b_{1} . \hfill \\ \end{gathered} $$
(18)
$$ u_{3} \left( {x,t} \right) = \left( {\frac{{a_{0} + a_{1} \exp \left[ {k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right]}}{{ - \frac{{a_{0} \left( {a_{0} b_{1} - a_{1} b_{0} } \right)}}{{a_{1}^{2} }}\exp \left[ { - k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right] + b_{0} + b_{1} \exp \left[ {k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right]}}} \right)^{\frac{1}{n}} . $$
(19)

Case 4

$$ \begin{gathered} \,\beta = 0,\mu = \frac{{r^{2} \left( {k^{2} + 4} \right)}}{4},n = 2,\,\nu = 0,\,a_{ - 1} = \frac{{a_{0}^{2} }}{{4a_{1} }},\,a_{0} = a_{0} ,\,a_{1} = a_{1} , \hfill \\ b_{ - 1} = 0,b_{0} = b_{0} ,b_{1} = 0. \hfill \\ \end{gathered} $$
(20)
$$ u_{4} \left( {x,t} \right) = \left( {\frac{{\frac{{a_{0}^{2} }}{{4a_{1} }}\exp \left[ { - k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right] + a_{0} + a_{1} \exp \left[ {k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right]}}{{b_{0} }}} \right)^{\frac{1}{n}} . $$
(21)

Case 5

$$ \begin{gathered} \,\beta = 0,\mu = - r^{2} \left( {2k^{2} - 1} \right),n = 1,\,\nu = \frac{{2b_{1}^{2} k^{2} r^{2} }}{{a_{1}^{2} }},\,a_{ - 1} = a_{ - 1} ,\,a_{0} = 0,\,a_{1} = a_{1} , \hfill \\ b_{ - 1} = - \frac{{a_{ - 1} b_{1} }}{{a_{1} }},b_{0} = 0,b_{1} = b_{1} . \hfill \\ \end{gathered} $$
(22)
$$ u_{5} \left( {x,t} \right) = \left( {\frac{{a_{ - 1} \exp \left[ { - k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right] + a_{1} \exp \left[ {k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right]}}{{ - \frac{{a_{ - 1} b_{1} }}{{a_{1} }}\exp \left[ { - k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right] + b_{1} \exp \left[ {k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right]}}} \right)^{\frac{1}{n}} . $$
(23)

Case 6

$$ \,\beta = \beta ,\mu = \mu ,n = 1,\,\nu = \nu ,\,a_{ - 1} = a_{ - 1} ,\,a_{0} = a_{0} ,\,a_{1} = a_{1} ,b_{ - 1} = \frac{{a_{ - 1} b_{1} }}{{a_{1} }},b_{0} = \frac{{a_{0} b_{1} }}{{a_{1} }},b_{1} = b_{1} . $$
(24)
$$ u_{6} \left( {x,t} \right) = \left( {\frac{{a_{ - 1} \exp \left[ { - k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right] + a_{0} + a_{1} \exp \left[ {k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right]}}{{\frac{{a_{ - 1} b_{1} }}{{a_{1} }}\exp \left[ { - k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right] + \frac{{a_{0} b_{1} }}{{a_{1} }} + b_{1} \exp \left[ {k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right]}}} \right)^{\frac{1}{n}} . $$
(25)

Case 7

$$ \begin{gathered} \,\beta = \beta ,\mu = \mu ,n = n,\,\nu = - \frac{{b_{ - 1} \left( { - b_{ - 1} r^{2} + \beta a_{ - 1} + b_{ - 1} \mu } \right)}}{{a_{ - 1}^{2} }},\,a_{ - 1} = a_{ - 1} ,\,a_{0} = a_{0} ,\,a_{1} = 0, \hfill \\ b_{ - 1} = b_{ - 1} ,b_{0} = \frac{{a_{0} b_{ - 1} }}{{a_{ - 1} }},b_{1} = 0. \hfill \\ \end{gathered} $$
(26)
$$ u_{7} \left( {x,t} \right) = \left( {\frac{{a_{ - 1} \exp \left[ { - k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right] + a_{0} }}{{b_{ - 1} \exp \left[ { - k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right] + \frac{{a_{0} b_{ - 1} }}{{a_{ - 1} }}}}} \right)^{\frac{1}{n}} . $$
(27)

Case 8

$$ \begin{gathered} \,\beta = \beta ,\mu = \mu ,n = n,\,\nu = - \frac{{b_{1} \left( { - b_{1} r^{2} + \beta a_{1} + b_{1} \mu } \right)}}{{a_{1}^{2} }},\,a_{ - 1} = a_{ - 1} ,\,a_{0} = a_{0} ,\, \hfill \\ a_{1} = a_{1} ,b_{ - 1} = \frac{{a_{ - 1} b_{1} }}{{a_{1} }},b_{0} = \frac{{a_{0} b_{1} }}{{a_{1} }},b_{1} = b_{1} . \hfill \\ \end{gathered} $$
(28)
$$ u_{8} \left( {x,t} \right) = \left( {\frac{{a_{ - 1} \exp \left[ { - k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right] + a_{0} + a_{1} \exp \left[ {k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right]}}{{\frac{{a_{ - 1} b_{1} }}{{a_{1} }}\exp \left[ { - k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right] + \frac{{a_{0} b_{1} }}{{a_{1} }} + b_{1} \exp \left[ {k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right]}}} \right)^{\frac{1}{n}} . $$
(29)

Case 9

$$ \begin{gathered} \,\beta = \frac{{r^{2} k^{2} \left( {b_{1} a_{ - 1} n - b_{0} na_{0} + 2a_{ - 1} b_{1} - 2a_{0} b_{0} } \right)}}{{n^{2} a_{0}^{2} }},\mu = \frac{{r^{2} \left( {k^{2} + n^{2} } \right)}}{{n^{2} }},n = n,\, \hfill \\ \nu = - \frac{{\left( {a_{ - 1} b_{1} - a_{0} b_{0} } \right)r^{2} k^{2} \left( {b_{1} a_{ - 1} n - b_{0} na_{0} + a_{ - 1} b_{1} - a_{0} b_{0} } \right)}}{{a_{0}^{4} n^{2} }},\,a_{ - 1} = a_{ - 1} ,\,a_{0} = a_{0} ,\, \hfill \\ a_{1} = 0,b_{ - 1} = - \frac{{a_{ - 1} \left( {a_{ - 1} b_{1} - a_{0} b_{0} } \right)}}{{a_{0}^{2} }},b_{0} = b_{0} ,b_{1} = b_{1} . \hfill \\ \end{gathered} $$
(30)
$$ u_{9} \left( {x,t} \right) = \left( {\frac{{a_{ - 1} \exp \left[ { - k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right] + a_{0} }}{{ - \frac{{a_{ - 1} \left( {a_{ - 1} b_{1} - a_{0} b_{0} } \right)}}{{a_{0}^{2} }}\exp \left[ { - k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right] + b_{0} + b_{1} \exp \left[ {k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right]}}} \right)^{\frac{1}{n}} . $$
(31)

Case 10

$$ \begin{gathered} \beta = \frac{{\left( {r^{2} k^{2} - 2r^{2} + 2\mu } \right)b_{0} \left( {r^{2} k^{2} + r^{2} - \mu } \right)}}{{a_{0} \left( {r^{2} k^{2} - r^{2} + \mu } \right)}},\mu = \mu ,n = 1,\;\nu = \frac{\begin{gathered} \left( {r^{2} k^{2} - 2r^{2} + 2\mu } \right)\;b_{0}^{2} \hfill \\ \left( {r^{2} k^{2} + r^{2} - \mu } \right)^{2} \hfill \\ \end{gathered} }{{a_{0}^{2} \left( {r^{2} k^{2} - r^{2} + \mu } \right)^{2} }}, \hfill \\ a_{ - 1} = \frac{{b_{0} a_{0} \left( {r^{2} k^{2} - 2r^{2} + 2\mu } \right)}}{{8b_{1} \left( {2r^{2} k^{2} - r^{2} + \mu } \right)}},\,a_{0} = a_{0} ,\,a_{1} = - \frac{{b_{1} a_{0} \left( {2r^{2} k^{2} - r^{2} + \mu } \right)}}{{b_{0} \left( {r^{2} k^{2} + r^{2} - \mu } \right)}}, \hfill \\ b_{ - 1} = - \frac{{b_{0}^{2} \left( {r^{2} k^{2} - 2r^{2} + 2\mu } \right)\left( {r^{2} k^{2} - r^{2} + \mu } \right)}}{{8b_{1} \left( {2r^{2} k^{2} - r^{2} + \mu } \right)^{2} }},b_{0} = b_{0} ,b_{1} = b_{1} . \hfill \\ \end{gathered} $$
(32)
$$ u_{10} \left( {x,t} \right) = \left( {\frac{\begin{gathered} \frac{{b_{0} a_{0} \left( {r^{2} k^{2} - 2r^{2} + 2\mu } \right)}}{{8b_{1} \left( {2r^{2} k^{2} - r^{2} + \mu } \right)}}\exp \left[ { - k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right] + a_{0} \hfill \\ - \frac{{b_{1} a_{0} \left( {2r^{2} k^{2} - r^{2} + \mu } \right)}}{{b_{0} \left( {r^{2} k^{2} + r^{2} - \mu } \right)}}\exp \left[ { - k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right] \hfill \\ \end{gathered} }{\begin{gathered} - \frac{{b_{0}^{2} \left( {r^{2} k^{2} - 2r^{2} + 2\mu } \right)\left( {r^{2} k^{2} - r^{2} + \mu } \right)}}{{8b_{1} \left( {2r^{2} k^{2} - r^{2} + \mu } \right)^{2} }}\exp \left[ { - k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right] + b_{0} \hfill \\ + b_{1} \exp \left[ {k\left( {\frac{{x^{\alpha } }}{\alpha } - \frac{{rt^{\alpha } }}{\alpha }} \right)} \right] \hfill \\ \end{gathered} }} \right)^{\frac{1}{n}} . $$
(33)

4 Results and discussion

This article is about finding the solitary wave solutions for fractional order GPC equation with the n order term by the implementation of the Exp-function method with the help of a conformable derivative. Because of its wide range of applications, the fractional order GPC equation is the most extensively used nonlinear model in applied research. The presented model equation describes the longitudinal vibration of the material in a thin, straight cylindrical rod. In the literature, many authors studied the PC equation and GPC equation for integer order. Exp-function method has been applied to resolve the GPC equation for integer-order as given in Parand and Rad (2010) but this paper presents only numerical results no graphics of the problem have been discussed. For the comparison, we consider a recent article (Yokus et al. 2021) in which the GPC equation with n order term has been resolved by using an analytical technique. By comparing graphs for integer-order there exist similarity to some extent which shows that our results are correct and new for non-integer as well as integer order.

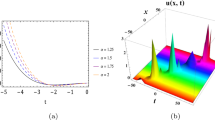
By considering the different parameter conditions, the existence of different kinds of solitary wave solutions are determined which are also presented in the form of 3D plots, contour plots, and 2D plots as given in Figs. (1–10) at \(\alpha = 0.5,\,\,\alpha = 0.7\) and \(\alpha = 1.\) Figure 1 indicates the solution of \(u_{1} \left( {x,t} \right)\) for \(a_{ - 1} = \frac{1}{2},a_{0} = \frac{2}{3},b_{ - 1} = \frac{1}{2},\,b_{0} = \frac{1}{3},k = 0.75.\) Figure 2 indicates the solution of \(u_{2} \left( {x,t} \right)\) at \(a_{1} = 1,a_{0} = \frac{2}{3},b_{1} = - \frac{1}{5},\,b_{0} = \frac{1}{3},k = 0.5.\) Figure 3 reveals the solution of \(u_{3} \left( {x,t} \right)\) for \(a_{1} = 1,a_{0} = \frac{2}{3},b_{1} = - \frac{1}{5},\,b_{0} = \frac{1}{3},k = 0.75,r = 1.25.\) Figure 4 indicates the solution of \(u_{4} \left( {x,t} \right)\) for \(a_{1} = 1,a_{0} = \frac{2}{3},\,b_{0} = \frac{2}{3},k = 0.75,r = 1.5.\) Figure 5 indicates the solution of \(u_{5} \left( {x,t} \right)\) for \(a_{1} = 1,a_{ - 1} = \frac{1}{2},b_{1} = - \frac{1}{5},\,k = 0.5,r = 1.25.\) Figure 6 indicates the solution of \(u_{6} \left( {x,t} \right)\) for \(a_{ - 1} = \frac{1}{2},a_{0} = - \frac{2}{3},a_{1} = 1,\,b_{1} = - \frac{1}{5},k = 0.5,r = 1.25.\) Figure 7 indicates the solution of \(u_{7} \left( {x,t} \right)\) for \(a_{ - 1} = \frac{1}{2},a_{0} = \frac{2}{3},b_{ - 1} = \frac{1}{2},\,k = 0.5,r = 1.25.\) Figure 8 indicates the solution of \(u_{8} \left( {x,t} \right)\) for \(a_{ - 1} = \frac{1}{2},a_{0} = \frac{2}{3},a_{1} = - 0.1,\,b_{1} = - \frac{1}{5},k = 0.5,r = 1.25,n = 1.\) Figure 9 indicates the solution of \(u_{9} \left( {x,t} \right)\) for \(a_{ - 1} = \frac{1}{2},a_{0} = \frac{2}{3},b_{1} = - \frac{1}{5},\,b_{0} = \frac{1}{3},k = 0.5,r = 1.25,n = 1.\) Figure 10 indicates the solution of \(u_{10} \left( {x,t} \right)\) for \(a_{0} = \frac{2}{3},b_{1} = - \frac{1}{5},\,b_{0} = \frac{1}{3},k = 0.5,r = 1.25,\mu = 1.2.\)

Fig. 1
figure 1

Associated graphs of \(u_{1} \left( {x,t} \right)\) in Eq. (15) obtained using the Exp-function method: a, b, c 3D plots: d, e, f demonstrate the contour comparison: g specifies the comparison in the form of a 2D plot

Full size image
Fig. 2
figure 2

Associated graph of \(u_{2} \left( {x,t} \right)\) in Eq. (17) obtained using the Exp-function method: a, b, c 3D plots: d, e, f illustrate the contour comparison: g indicates the comparison in the form of a 2D plot

Full size image
Fig. 3
figure 3

Associated grap of \(u_{3} \left( {x,t} \right)\) in Eq. (19) obtained using Exp-function method: a, b, c 3D plots: d, e, f illustrate the contour comparison: g indicates the comparison in the form of 2D plot

Full size image
Fig. 4
figure 4

Associated graphs in Eq. (21) obtained using the Exp-function method: a, b, c 3D plots: d, e, f illustrate the contour comparison: g indicates the comparison in the form of a 2D plot

Full size image
Fig. 5
figure 5

Associated graphs of \(u_{5} \left( {x,t} \right)\) in Eq. (23) obtained using the Exp-function method: a, b, c 3D plots: d, e, f illustrate the contour comparison: g indicates the comparison in the form of a 2D plot

Full size image
Fig. 6
figure 6

Associated graphs of \(u_{6} \left( {x,t} \right)\) in Eq. (25) obtained using the Exp-function method: a, b, c 3D plots: d, e, f illustrate the contour comparison: g indicates the comparison in the form of a 2D plot

Full size image
Fig. 7
figure 7

Associated graphs of \(u_{7} \left( {x,t} \right)\) in Eq. (27) obtained using the Exp-function method: a,b, c 3D plots: d, e, f illustrate the contour comparison: g indicates the comparison in the forma of 2D plot

Full size image
Fig. 8
figure 8

Associated graphs of \(u_{8} \left( {x,t} \right)\) in Eq. (29) obtained using the Exp-function method: a, b, c 3D plots: d, e, f illustrate the contour comparison: g indicates the comparison in the form of a 2D plot

Full size image
Fig. 9
figure 9

Associated graphs of \(u_{9} \left( {x,t} \right)\) in Eq. (31) obtained using the Exp-function method: a, b, c 3D plots: d, e, f illustrate the contour comparison: g indicates the comparison in the form of a 2D plot

Full size image
Fig. 10
figure 10

Associated graphs of \(u_{10} \left( {x,t} \right)\) in Eq. (32) obtained using the Exp-function method: a, b, c 3D plots: d, e, f illustrate the contour comparison: g indicates the comparison in the form of a 2D plot

Full size image

This section concludes that the results for solving the presented model are investigated for various values of α to prove the effectiveness and validity of the proposed algorithm. The attained results are more generic, novel, and have not been previously described in the literature.

5 Conclusion

The main concern of the presented article is to obtain the new analytical solutions in the form of solitary waves by considering the fractional order generalized Pochhammer-Chree equation. In this work, we efficaciously discover the solitary wave solutions of the fractional order GPC equation with the n order term by applying the Exp-function method with fractional traveling wave transform by the use of conformable fractional derivative. The fractional wave transformation is used for the conversion of the presented fractional order nonlinear partial differential equation into an ordinary differential equation. The obtained results are presented in the form of 3D plots, contour plots, and 2D plots. All the acquired results are new and have not been explored before in the literature. These new results have many applications in physics and many other areas of physical science. The obtained results also show the stability of the applied method and elucidate that this technique is direct, simple, competent, and maintains the exactness of the analytically computed results. Maple software is used for performing computational work.