Abstract
This paper studies various forms of analytical solutions for mixed derivative nonlinear Schrödinger equation (MD-NLSE) which is used extensively in optical fiber. Our aim is to obtain lump solution (which is analytic in all directions), lump with one kink, rogue waves, periodic waves and multi-wave solutions for our governing model. We also discuss the interaction between periodic and lump, breather wave (which is a localized periodic wave solution of either discrete lattice or continuous media mathematical models), generalized breather, Ma-breather, Kuznetsov-Ma-breather and their corresponding rogue waves. At the end, we also present the dynamical behaviour of our solutions in terms of graphs in various dimensions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
For the past few decades, the integrable nonlinear partial differential equations (INLPDEs) which posses the soliton solutions have gathered a lot of attention and interest due to their huge applications in so many areas of science(Yin and Chow 2021; Yin et al. 2022a, b, 2021). Soliton wave which firstly appeared in hydrodynamics and then extended to nonlinear optics, ocean engineering, medical physics, condensed matter, geo-chemistry, plasma physics, fluid mechanics and so on (Rehman et al. 2021; Seadawy et al. 2021b; Bilal et al. 2021; Akram et al. 2021). In soliton theory, some renowned equations are Korteweg-de Vries (KdV), nonlinear Schrödinger equations (NLSEs), sine Gordon, Sasa Sastuma equation, the mixed derivative NLSE and continuum Heisenberg spin equations. In recent years, so many integration schemes have been used to obtain soliton solutions for INLPDEs and the detailed investigation has generated some new concepts regarding integrability like dromions, conservation laws, Lax pair, Darboux transformation (DT), Painleve property, breathers etc., (Sulem and Sulem 2007; Ablowitz et al. 2004; Mylonas et al. 2017; Aly 2020; Ahmed et al. 2019; Aly 2019, 2020; Dianchen 2018).
In literature, different forms of soliton solutions have been studied for example lump solutions, rogue waves and breathers (Binder et al. 2000; Kibler et al. 2010; Chabchoub et al. 2012; Tao and He 2012; Zhang et al. 2015; Yua and Yan 2014). Lump solutions play an important role in describing certain complicated physical phenomena. Lump solution is just like a rational function solutions localized in all space directions. Rogue waves (RWs) are also known as killer wave or monster wave, their amplitude may be three to five times more than the surrounding waves (Li and Ma 2020). These waves appear in nonlinear optics and oceanics, so many approaches like Bäcklund transformation, dressing technique, bilinear, DT method, and so on have been utilized to obtain RWs. RWs suddenly appears from nowhere and disappears without any trace. The frequency of RWs must be higher than that of a classical Gaussian distribution. Breathers wave discusses about the nonlinear stages of the modulational instability, these waves affect the wave height distribution and probability density function of the surface elevation. Like RWs, breathers which are also localised waves have been observed in water waves. Rogue wave and breather have a closed relationship between them (Dudley et al. 2014; Zakharov and Gelash 2013). Some of the types of breathers are Ma-breather (Akhmediev et al. 1987), generalized breather (Guan and Li 2019), Kuznetsov-Ma breather (Kuznetsov and Li 1977). A lot of work has been done by various scientists to find lump, rogue wave and breather solutions like Tang et al. studied some NLPDEs for lump solitons. (Tang et al. 2016). Deng et al. obtained lump solitons and rogue waves for Melnikov system (Deng et al. 2019). Liu et al. studied Boiti-Leon-Manna-Pempinelli equation to obtain multi-wave, breather wave (Liu and Xiong 2020). Guan et al. retrieved some lump soliton and their interactions of KP equation Guan et al. (2020). Zhou et al. computed lump soliton solution for the Hirota-Satsuma model (Zhou et al. 2019). Kol et al. studied the rogue waves of Lugiato-Lefever model (Kol et al. 2014). Ren et al. worked on the NLPDE to get some lump soliton and its various types (Seadawy et al. 2021a). Hao et al. studied breather solitons for mixed NLSE (Hao et al. 2014). Rizvi et al. worked on time fractional NLSE to get rogue wave and lump solitons (Rizvi et al. 2021a). Younas et al. retrieved various types of exact solutions for (2+1)-dimensional NLSE (Khater et al. 2000). Ahmad et al. computed kinky-breathers, lump and multi-waves solitons solution for Dym equations Ahmad et al. (2021). Seadawy et al. retrieved lump, lump with one kink and breather solitons to the Hunter-Saxton equation Seadawy et al. (2021a). In this paper, we consider the following MD-NLSE for various forms of lump, rogue waves and breathers solutions (Bhrawy et al. 2014; Rizvi et al. 2021b; Ren et al. 2019b),
where P(x, t) is a complex valued wave profile, x and t are space and time co-ordinates respectively. Group velocity dispersion and spatio-temporal dispersion are represented by a and b respectively.
The rest of the paper is arranged in the following manner: In Sect. 2, we will provide mathematical analysis, In Sect. 3, we will study the lump soliton, in Sect. 4, we will discuss lump with one kink. In Sect. 5, we will attain the rogue wave. In Sect. 6, we will obtain periodic wave, in Sect. 7, we will retrieve periodic cross-lump wave. In Sect. 8, we will gain multi-wave solution. In sec. 9, we will discuss breather lump wave solutions. In Sect. 10, we will discuss Kuznetsov-Ma-breather solutions. In Sect. 11, we will discuss Ma-breather solutions. In Sect. 12, we will study generalized breather solutions. In Sect. 13, we will discuss our results in details and finally in Sect. 14, we will give concluding remarks.
2 Mathematical analysis
We use Kerr law, \(F(P) = P\), so Eq. (1) becomes,
Now we use following transformation,
After substituting Eq. (3) into Eq. (2), we get the real and imaginary parts given as;
Firstly, we will make bilinear form with the help of following ansatz transformation (Yang et al. 2018),
Now putting Eq. (3) into Eqs. (1) and (2), we get following bilinear form,
and
3 Lump soliton
For lump soliton, we consider the following function h (Tang et al. 2016):
where
However \(a_i (1\le i\le 7)\) are real parameters to be determined. Now Putting Eq. (9) into Eqs. (7) and (8) and taking the coefficient of the x, t to be zero, we get some algebraic equations which on solving give following values:
After Substituting Eq. (10) into Eq. (9) and then by using Eq. (6), we obtain lump solution of Eqs. (4) and (5),
Now, we study some graphical representation of the above solution.
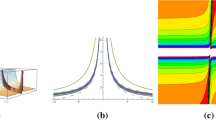
Plot 3D, Contour of q(x, t) in Eq. (11)
Plot 3D, Contour of q(x, t) in Eq. (11)
Plot 3D, Contour of q(x, t) in Eq. (11)
4 Lump with one kink soliton
In this section, we discuss the lump with one kink soliton in the form of the sum of quadratic function and one exponential function, we obtain the lump with one kink solution for Eqs. (4) and (5),
For lump with one kink soliton, we use the following function h (Ren et al. 2019a):
where
However \(a_i (1\le i\le 7)\) and \(b_1, b_2, m_1, \) are real parameters to be determined. Now putting Eq. (9) into Eqs. (7) and (8) and equating all the coefficient of the \(x, t, e^{b_2t+b_1x}, e^{2b_2t+2b_1x}, e^{3b_2t+3b_1x}, e^{4b_2t+4b_1x}, e^{5b_2t+5b_1x}, \) to be zero, we gain some algebraic expression which give values of coefficient given as:
Now substituting Eq. (13) into Eq. (12) and after using Eq. (6), we get lump with one kink solution of Eqs. (4) and (5),
Now we study some graphical representation of the above solutions.
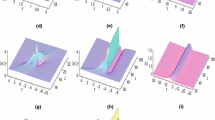
Plot 3D, Contour of q(x, t) in Eq. (14)
Plot 3D, Contour of q(x, t) in Eq. (14)
Plot 3D, Contour of q(x, t) in Eq. (14)
5 Rogue wave
In this section, we study RWs containing the hyperbolic trigonometry function and sum of quadratic function. For RWs, we consider the following function h (Rizvi et al. 2021a):
where
However \(b_i (1\le i\le 2)\), \(a_i (1\le i\le 7)\) and \(m_1\), are real parameters to be determined. By putting Eq. (15) in to Eqs. (4) and 5 and equating the coefficient of the \( \begin{gathered} x,t,\cosh (b_{2} t + b_{1} x),\cosh (b_{2} t + b_{1} x)^{2} ,\cosh (b_{2} t + b_{1} x)^{3} ,\cosh (b_{2} t + b_{1} x)^{4} , \hfill \\ \cosh (b_{2} t + b_{1} x)^{5} ,\cosh (b_{2} t + b_{1} x)^{6} ,\sinh (b_{2} t + b_{1} x), \hfill \\ \cosh (b2t + b1x)\sinh (b_{2} t + b_{1} x),\cosh (b_{2} t + b_{1} x)^{2} \sinh (b_{2} t + b_{1} x), \hfill \\ \cosh (b_{2} t + b_{1} x)^{3} \sinh (b_{2} t + b_{1} x),\cosh (b_{2} t + b_{1} x)^{4} \sinh (b_{2} t + b_{1} x), \hfill \\ \cosh (b_{2} t + b_{1} x)^{5} \sinh (b_{2} t + b_{1} x),\sinh (b_{2} t + b_{1} x)^{2} ,\cosh (b_{2} t + b_{1} x)\sinh (b_{2} t + b_{1} x)^{2} , \hfill \\ \cosh (b_{2} t + b_{1} x)^{2} \sinh (b_{2} t + b_{1} x)^{2} ,\cosh (b_{2} t + b_{1} x)^{3} \sinh (b_{2} t + b_{1} x)^{2} ,\sinh (b_{2} t + b_{1} x)^{3} , \hfill \\ \end{gathered} \) to be zero, we obtain some equations which give values of parameters such as:
After putting Eq. (16) into Eq. (15) and after using Eq. (6), we obtain RWs for Eqs. (4) and (5),
Here we present some graphical representation of the above solution.
Plot 3D, Contour of q(x, t) in Eq. (17)
Plot 3D, Contour of q(x, t) in Eq. (17)
Plot 3D, Contour of q(x, t) in Eq. (17)
6 Periodic wave
In this section, we discuss periodic wave for Eqs. (4) and (5) which contain quadratic functions as well as periodic function. We assume that (Ren et al. 2019a):
where
\(a_i (i= 1,2,...,7)\), \(b_i (i=1,2)\) and \(m_1\), are real constant to be determined. After using Eq. (18) into Eqs. (4) and (5). By equating the coefficient of \( \begin{gathered} x,t,\cos (b_{2} t + b_{1} x),\cos (b_{2} t + b_{1} x)^{2} ,\cos (b_{2} t + b_{1} x)^{3} ,\cos (b_{2} t + b_{1} x)^{4} , \hfill \\ \cos (b_{2} t + b_{1} x)^{5} ,\cos (b_{2} t + b_{1} x)^{6} ,\sin (b_{2} t + b_{1} x),\cos (b_{2} t + b_{1} x)\sin (b_{2} t + b_{1} x), \hfill \\ \cos (b_{2} t + b_{1} x)^{2} \sin (b_{2} t + b_{1} x),\cos (b_{2} t + b_{1} x)^{3} \sin (b_{2} t + b_{1} x),\cos (b_{2} t + b_{1} x)^{4} \sin (b_{2} t + b_{1} x), \hfill \\ \cos (b_{2} t + b_{1} x)^{5} \sin (b_{2} t + b_{1} x),\sin (b_{2} t + b_{1} x)^{2} ,\cos (b_{2} t + b_{1} x)\sin (b_{2} t + b_{1} x)^{2} , \hfill \\ \cos (b_{2} t + b_{1} x)^{2} \sin (b_{2} t + b_{1} x)^{2} ,\cos (b_{2} t + b_{1} x)^{3} \sin (b_{2} t + b_{1} x)^{2} ,\cos (b_{2} t + b_{1} x)^{4} \sin (b_{2} t + b_{1} x)^{2} , \hfill \\ \sin (b_{2} t + b_{1} x)^{3} ,\cos (b_{2} t + b_{1} x)\sin (b_{2} t + b_{1} x)^{3} ,\cos (b_{2} t + b_{1} x)^{2} \sin (b_{2} t + b_{1} x)^{3} ,\cos (b_{2} t + b_{1} x)^{3} \sin (b_{2} t + b_{1} x)^{3} , \hfill \\ \end{gathered} \) we retrieve values of the parameters given below:
Substituting Eq. (19) into Eq. (18) and using Eq. (6), we obtain periodic wave solution,
Here we discuss the dynamical behaviour of our solutions;
Plot 3D, Contour of q(x, t) in Eq. (20)
Plot 3D, Contour of q(x, t) in Eq. (20)
Plot 3D, Contour of q(x, t) in Eq. (20)
7 Periodic cross-lump wave
In this section, we study periodic cross-lump wave solution for Eqs. (4) and (5) containing quadratic functions as well as periodic function and hyperbolic periodic function. We assume that (Ren et al. 2019a):
where
\(a_i (i= 1, 2,..., 7)\), \(b_i (i=1, 2, 3, 4)\) and \(m_1, m_2\), are real coefficient to be determined. After putting Eq. (21) into Eqs. (7) and (8). By comparing the coefficient of \( \begin{gathered} x,t,\cos (b_{2} t + b_{1} x),\cos (b_{2} t + b_{1} x)^{2} ,\cos (b_{2} t + b_{1} x)^{3} ,\cos (b_{2} t + b_{1} x)^{4} , \hfill \\ \cos (b_{2} t + b_{1} x)^{5} ,\cos (b_{2} t + b_{1} x)^{6} ,\cosh (b_{2} t + b_{1} x),\cos (b_{2} t + b_{1} x)\cosh (b_{4} t + b_{3} x), \hfill \\ \cos (b_{2} t + b_{1} x)^{2} \cosh (b_{4} t + b_{3} x),\cos (b_{2} t + b_{1} x)^{3} \cosh (b_{4} t + b_{3} x), \hfill \\ \cos (b_{2} t + b_{1} x)^{4} \cosh (b_{4} t + b_{3} x),\cos (b_{2} t + b_{1} x)^{5} \cosh (b_{4} t + b_{3} x), \hfill \\ \cosh (b_{2} t + b_{1} x)^{2} ,\cos (b_{2} t + b_{1} x)\cosh (b_{4} t + b_{3} x)^{2} ,\cos (b_{2} t + b_{1} x)^{2} \cosh (b_{4} t + b_{3} x)^{2} , \hfill \\ \cos (b_{2} t + b_{1} x)^{3} \cosh (b_{4} t + b_{3} x)^{2} ,\sin (b_{2} t + b_{1} x),\cos (b2t + b1x)\sin (b_{2} t + b_{1} x), \hfill \\ \cos (b_{2} t + b_{1} x)^{2} \sin (b_{2} t + b_{1} x),\cos (b2t + b1x)^{3} \sin (b_{2} t + b_{1} x), \hfill \\ \cos (b2t + b1x)^{4} \sin (b_{2} t + b_{1} x),\cos (b2t + b1x)^{5} \sin (b_{2} t + b_{1} x), \hfill \\ \sin (b_{2} t + b_{1} x)^{2} ,\cos (b_{2} t + b_{1} x)\sin (b_{2} t + b_{1} x)^{2} ,\cos (b_{2} t + b_{1} x)^{2} \sin (b_{2} t + b_{1} x)^{2} , \hfill \\ \cos (b_{2} t + b_{1} x)^{3} \sin (b_{2} t + b_{1} x)^{2} ,\cos (b_{2} t + b_{1} x)^{4} \sin (b_{2} t + b_{1} x)^{2} ,\sin (b_{2} t + b_{1} x)^{3} , \hfill \\ \cos (b_{2} t + b_{1} x)\sin (b_{2} t + b_{1} x)^{3} ,\cos (b_{2} t + b_{1} x)^{2} \sin (b_{2} t + b_{1} x)^{3} ,\cos (b_{2} t + b_{1} x)^{3} \sin (b_{2} t + b_{1} x)^{3} , \hfill \\ \end{gathered} \) we retrieve values of the parameters given below:
Substituting Eq. (22) into Eq. (21) along with Eq. (6), we attain the periodic cross-lump wave solution of Eqs. (4) and (5),
Here we discuss graphical representation of the above solution.
Plot 3D, Contour of q(x, t) in Eq. (23)
Plot 3D, Contour of q(x, t) in Eq. (23)
Plot 3D, Contour of q(x, t) in Eq. (23)
8 Multiwave
In this section, we study multi-wave solution for Eqs. (4) and (5) possessing periodic function and hyperbolic periodic functions. We suppose that (Seadawy et al. 2021):
where
\(k_i (i=0, 1, 2)\), \(a_i (i= 1, 2,..., 10)\), \(b_i (i=0, 1, 2)\) are real constant to be determined. After putting Eq. (24) into Eqs. (7) and (8). and comparing the parameters of \( \begin{gathered} \cosh (a_{3} + a_{2} t + a_{1} x),\cosh (a_{3} + a_{2} t + a_{1} x)^{2} ,\cosh (a_{3} + a_{2} t + a_{1} x)^{3} , \hfill \\ \cosh (a_{3} + a_{2} t + a_{1} x)^{4} ,\sin (a_{6} + a_{5} t + a_{4} x),\cosh (a_{3} + a_{2} t + a_{1} x)\sin (a_{6} + a_{5} t + a_{4} x), \hfill \\ \cosh (a_{3} + a_{2} t + a_{1} x)^{2} \sin (a_{6} + a_{5} t + a_{4} x),\cosh (a_{3} + a_{2} t + a_{1} x)^{3} \sin (a_{6} + a_{5} t + a_{4} x), \hfill \\ \sin (a_{6} + a_{5} t + a_{4} x)^{2} ,\cosh (a_{3} + a_{2} t + a_{1} x)^{2} \sin (a_{6} + a_{5} t + a_{4} x)^{2} ,\sin (a_{6} + a_{5} t + a_{4} x)^{3} , \hfill \\ \cosh (a_{3} + a_{2} t + a_{1} x)\sin (a_{6} + a_{5} t + a_{4} x)^{3} ,\sinh (a_{3} + a_{2} t + a_{1} x), \hfill \\ \cosh (a_{3} + a_{2} t + a_{1} x)\sinh (a_{3} + a_{2} t + a_{1} x),\cosh (a_{3} + a_{2} t + a_{1} x)\sinh (a_{9} + a_{8} t + a_{7} x)^{3} , \hfill \\ \sinh (a_{9} + a_{8} t + a_{7} x)^{3} ,\cosh (a_{3} + a_{2} t + a_{1} x)\sinh (a_{3} + a_{2} t + a_{1} x)\sinh (a_{9} + a_{8} t + a_{7} x)^{2} , \hfill \\ \cosh (a_{3} + a_{2} t + a_{1} x)\sin (a_{6} + a_{5} t + a_{4} x)\sinh (a_{9} + a_{8} t + a_{7} x)^{2} , \hfill \\ \cosh (a_{3} + a_{2} t + a_{1} x)\sin (a_{6} + a_{5} t + a_{4} x)^{2} \sinh (a_{3} + a_{2} t + a_{1} x),\cosh (a_{3} + a_{2} t + a_{1} x)^{3} \sinh (a_{3} + a_{2} t + a_{1} x), \hfill \\ \end{gathered} \) we obtain values of the parameters which are given below:
Now putting Eq. (25) into Eq. (24) along with Eq. (6), we get the multi-wave solution of Eqs. (4) and (5),
Here we provide some graphical representation of the above solution.
Plot 3D, Contour of q(x, t) in Eq. (26)
Plot 3D, Contour of q(x, t) in Eq. (26)
Plot 3D, Contour of q(x, t) in Eq. (26)
9 Breather lump wave solutions
In this section, we discuss breather lump wave solutions for Eqs. (4) and (5) having periodic and exponential functions. We assume that (Seadawy et al. 2021):
where
However \( m_1, m_2, \) and \(a_i (1\le i\le 6)\) are real constant to be determined. Put Eq. (27) in to Eqs. (7) and (8). By putting all the coefficient of the \( \begin{gathered} e^{{ - 5q_{1} (a_{3} + a_{2} t + a_{1} x)}} ,e^{{ - 4q_{1} (a_{3} + a_{2} t + a_{1} x)}} ,e^{{ - 3q_{1} (a_{3} + a_{2} t + a_{1} x)}} ,e^{{ - 2q_{1} (a_{3} + a_{2} t + a_{1} x)}} , \hfill \\ e^{{ - q_{1} (a_{3} + a_{2} t + a_{1} x)}} ,e^{{q_{1} (a_{3} + a_{2} t + a_{1} x)}} ,e^{{2q_{1} (a_{3} + a_{2} t + a_{1} x)}} ,e^{{3q_{1} (a_{3} + a_{2} t + a_{1} x)}} ,e^{{4q_{1} (a_{3} + a_{2} t + a_{1} x)}} , \hfill \\ e^{{5q_{1} (a_{3} + a_{2} t + a_{1} x)}} ,e^{{ - 5q_{1} (a_{3} + a_{2} t + a_{1} x)}} \cos (q_{2} (a_{5} t + a_{4} x)),e^{{ - 4q_{1} (a_{3} + a_{2} t + a_{1} x)}} \cos (q_{2} (a_{5} t + a_{4} x)), \hfill \\ e^{{ - 3q_{1} (a_{3} + a_{2} t + a_{1} x)}} \cos (q_{2} (a_{5} t + a_{4} x)),e^{{ - 2q_{1} (a_{3} + a_{2} t + a_{1} x)}} \cos (q_{2} (a_{5} t + a_{4} x)), \hfill \\ e^{{ - q_{1} (a_{3} + a_{2} t + a_{1} x)}} \cos (q_{2} (a_{5} t + a_{4} x)),\cos (q_{2} (a_{5} t + a_{4} x)),e^{{q_{1} (a_{3} + a_{2} t + a_{1} x)}} \cos (q_{2} (a_{5} t + a_{4} x)), \hfill \\ e^{{2q_{1} (a_{3} + a_{2} t + a_{1} x)}} \cos (q_{2} (a_{5} t + a_{4} x)),e^{{3q_{1} (a_{3} + a_{2} t + a_{1} x)}} \cos (q_{2} (a_{5} t + a_{4} x)), \hfill \\ e^{{4q_{1} (a_{3} + a_{2} t + a_{1} x)}} \cos (q_{2} (a_{5} t + a_{4} x)),e^{{5q_{1} (a_{3} + a_{2} t + a_{1} x)}} \cos (q_{2} (a_{5} t + a_{4} x)), \hfill \\ \cos (q_{2} (a_{5} t + a_{4} x))^{2} \sin (q_{2} (a_{5} t + a_{4} x))^{4} ,e^{{q_{1} (a_{3} + a_{2} t + a_{1} x)}} \cos (q_{2} (a_{5} t + a_{4} x))\sin (q_{2} (a_{5} t + a_{4} x))^{4} , \hfill \\ e^{{ - q_{1} (a_{3} + a_{2} t + a_{1} x)}} \cos (q_{2} (a_{5} t + a_{4} x))\sin (q_{2} (a_{5} t + a_{4} x))^{4} , \hfill \\ \end{gathered} \) to be zero, we obtain some equations which give values of coefficient such as:
Substituting Eq. (28) into Eq. (27) along with Eq. (6), we obtain the breather lump wave solutions of Eqs. (4) and (5),
Now we provide some graphical representation of the above solution.
Plot 3D, Contour of q(x, t) in Eq. (29)
Plot 3D, Contour of q(x, t) in Eq. (29)
Plot 3D, Contour of q(x, t) in Eq. (29)
10 Kuznetsov-Ma-breather, generalized breather and their corresponding Rogue wave
Now we consider the following h function (Kuznetsov and Li 1977),
where \(\delta _1, \delta _2, \mu , \rho , q_1, z\) are real parameters. Inserting Eq. (30) into Eqs. (7) and (8), we gain values of the parameters.
Now inserting these values of parameters in to Eq. (31) and then substituting into Eq. (30) along with Eq. (6), we obtain the following solution of Eqs. (4) and (5).
Plot 3D, Contour of q(x, t) in Eq. (32)
Plot 3D, Contour of q(x, t) in Eq. (32)
11 Ma-Breather and its corresponding Rogue wave
Consider the following function h (Akhmediev et al. 1987),
where \(\mu , \lambda , \beta , \alpha , q_1\) are real coefficient. Inserting Eq. (33) into Eqs. (7) and (8), we get values of the parameters.
After putting Eq. (34) into Eq. (33) along with Eq. (6), we obtain the following solution;
Plot 3D, Contour of q(x, t) in Eq. (35)
Plot 3D, Contour of q(x, t) in Eq. (35)
12 Generalized breather
Consider the following function h (Guan and Li 2019),
where \(\sigma , c, z\) are real coefficient. Inserting Eq. (45) into Eq. (38), we get following values of the parameters.
Now inserting Eq. (37) into Eq. (36) along with Eq. (6), we attain the following solutions
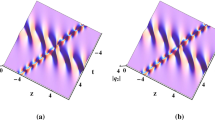
Plot 3D, Contour of q(x, t) in Eq. (38)
Plot 3D, Contour of q(x, t) in Eq. (38)
13 Results and discussion
In this section, we present a detailed comparison between our and previous results of our governing model. Yildrim et al. retrieved soliton solutions of MD-NLSE in Kerr and non-Kerr nonlinearities using Kudryashov technique (Yildirim et al. 2017). Zhang et al. used N-Fold DT to achieve the breather solitons for the MD-NLSE (Hao et al. 2014).
Equation (11) display the lump soliton of MD-NLSE. In Fig. 1, various bright lump faces appear. Equation (14) displays the lump with one kink solution for MD-NLSE. Figures 4 and 5, show one bright face, Fig. 6 show the one bright and one dark lump face. We change the graph by change the values of parameters. Equation (17) expose the rogue wave solutions for MD-NLSE. In Fig. 8, bright solitons occur. Figure 9 expresses the dark soliton. Equation (20) expresses the periodic wave solutions. Figure 11 represents many bright and dark faces with large amplitude. Equation (23) exposes the interaction between lump and periodic wave. Figure 13, displays the one bright face, Fig. 14 displays the dark and bright waves and Fig. 15 displays one bright wave with large amplitude. Equation (26) shows the multi-wave solution for MD-NLSE. Figure 16 expresses the multi-peak waves. Equation (29) explores the breather lump solitons. Figure 19, expresses many bright and dark waves with large amplitude. Equation (32) represents the Kuznetsov-Ma breather solutions for MD-NLSE. In Fig. 22, we explore the bright lump wave with large amplitude that depend on parameters. In Eq. (35), we gain the Ma-breather solitons for MD-NLSE. Figure 25 displays the first-order breather. In Eq. (38), we explore the generalized breather wave. Figure 26 explores the interaction between various parallel breather with fixed velocity and different periods. We have also studied the contour graphs of our solutions. All of these results may be useful in optical fiber industry.
14 Conclusion
We have obtained different analytical solutions for MD-NLSE such as lump soliton, lump with one kink, rogue wave, periodic wave, periodic cross-lump, multi-wave, breather lump wave solutions, generalized breather, Ma-breather, Kuznetsov-Ma-breather and its corresponding rogue wave. We also present the graphical representation of these solutions which contain 3D and contour plots. To the best of our knowledge, these results have never been obtained before for our governing model. At the end, we present the geometry of our solution in the result and discussion section.
References
Ablowitz, M.J., Prinari, B., Trubatch, A.D.: Discrete and continuous nonlinear Schrödinger systems, vol. 302. Cambridge University Press (2004)
Ahmad, S., Ashraf, R., Seadawy, A.R., Rizvi, S.T.R., Younis, M., Althobaiti, A., El-Shehawi, A.M.: Lump, multiwave, kinky breathers, interactional solutions and stability analysis for (2+1)-rth dispersionless Dym equation. Results in Physics 25, 104160 (2021)
Ahmed, Iftikhar, Seadawy, Aly R., Dianchen, Lu.: Kinky breathers, W-shaped and multi-peak solitons interaction in (2+1)-dimensional nonlinear Schrodinger’s equation with kerr law of nonlinearity. The European Physical Journal Plus 134(120), 1–11 (2019)
Akhmediev, N.N., Eleonskii, V.M., Kulagin, N.E.: Exact first-order solutions of the nonlinear Schrödinger equation. Theor. Math. Phys. 72, 809818 (1987)
Akram, U., Aly, R., Seadawy, S.T., Rizvi, R., Younis, M., Althobaiti, S., Sayed, S.: Traveling waves solutions for the fractional Wazwaz Benjamin Bona Mahony model in arising shallow water waves. Results Phys. 20, 103725 (2021)
Bhrawy, A.H., Alshaery, A.A., Hilal, E.M., Milovic, D., Moraru, L., Savescu, M., Biswas, A.: Optical solitons with polynomial and triple power law nonlinearities and spatio-temporal dispersion. Proc. Romanian Acad. 15, 235–240 (2014)
Bilal, M., Seadawy, A.R., Younis, M., Rizvi, S.T.R., Zahed, H.: Dispersive of propagation wave solution to unidirectional shallow water wave Dullin Gottwald Holm system and modulation instability analysis. Math. Methods Appl. Sci. 44, 40944104 (2021)
Binder, P., Abraimov, D., Ustinov, A.V.: Observation of breathers in josephson ladders. Phys. Rev. Lett. 84(4), 745 (2000)
Chabchoub, A., Hoffmann, N., Onorato, M., Akhmediev, N.: Super rogue waves: observation of a higher-order breather in water waves. Phys. Rev. X 2, 011015 (2012)
Deng, Yj., Jia, Ry., Lin, J.: Lump and mixed rogue-soliton solutions of the (2+1)-dimensional Mel’nikov system. Complexity 2019, 1–9 (2019)
Dianchen, Lu.: Bright-Dark optical soliton and dispersive elliptic function solutions of unstable nonlinear Schrodinger equation and its applications. Opt. Quant. Electron. 50(23), 1–10 (2018)
Dudley, J.M., Dias, F., Erkintalo, M., Genty, G.: Instabilities, breathers and rogue waves in optics. Nat. Photonics 8, 755764 (2014)
Guan, W.Y., Li, B.Q.: New observation on the breather for a generalized nonlinear Schrödinger system with two higher-order dispersion operators in inhomogeneous optical fiber. Optik 181, 853–861 (2019)
Guan, X., Liu, W., Zhou, Q., Biswas, A.: Some lump solutions for a generalized (3+1)-dimensional Kadomtsev-Petviashvili equation. Appl. Math. Comput. 366, 124757 (2020)
Hao, H.Q., Zhang, J.W., Guo, R.: Soliton and breather solutions for the mixed nonlinear Schrödinger equation via \(N\)-Fold Darboux transformation. J. Appl. Math. 2014, 7 (2014)
Khater, A.H., Helal, M.A., Seadawy, A.R.: General soliton solutions of n-dimensional nonlinear Schrödinger equation. IL Nuovo Cimento 115B, 1303–1312 (2000)
Kibler, B., Fatome, J., Finot, C., Millot, G., Dias, F., Genty, G., Akhmediev, N., Dudley, J.M.: The Peregrine soliton in nonlinear fibre optics. Nat. Phys. 6(10), 790–795 (2010)
Kol, G.R., Kingni, S.T., Woafo, P.: Rogue waves in Lugiato-Lefever equation with variable coefficients. Open Phys. 12(11), 767–772 (2014)
Kuznetsov, E.A., Li, B.Q.: Solitons in parametrically unstable plasma. Sov. Phys. Dokl. 22, 507–508 (1977)
Li, B.Q., Ma, Y.L.: Extended generalized Darboux transformation to hybrid rogue wave and breather solutions for a nonlinear Schrödinger equation. Appl. Math. Comput. 386, 125469 (2020)
Liu, J.G., Xiong, W.P.: Multi-wave, breather wave and lump solutions of the Boiti-Leon-Manna-Pempinelli equation with variable coefficients. Results in Physics 19, 103532 (2020)
Mylonas, I.K., Ward, C.B., Kevrekidis, P.G., Rothos, V.M., Frantzeskakis, D.J.: Asymptotic expansions and solitons of the Camassa-Holm-nonlinear Schrödinger equation. Phys. Lett. A 381(48), 3965–3971 (2017)
Peng, Y.Z.: Exact periodic wave solutions to the Melnikov equation. Zeitschrift Für Naturforschung A 60(5), 321–327 (2005)
Rehman, S.U., Aly, R., Seadawy, M., Younis, S.T., Rizvi, R.: On study of modulation instability and optical soliton solutions: the chiral nonlinear Schrödinger dynamical equation. Opt. Quant. Electron. 53, 411 (2021)
Ren, B., Lin, J., Lou, Z.M.: A new nonlinear equation with lump-soliton, lump-periodic, and lump-periodic-soliton solutions. Complexity 2019, 1–10 (2019a)
Ren, B., Lin, J., Lou, Z.-M.: A new nonlinear equation with lump-soliton, lump-periodic, and lump-periodic-soliton solutions. Complexity 2019, 4072754 (2019b)
Rizvi, S.T.R., Seadawy, A.R., Ahmed, S., Younis, M., Ali, K.: Study of multiple lump and rogue waves to the generalized unstable space time fractional nonlinear Schrödinger equation. Chaos Solitons Fractals 151, 111251 (2021a)
Rizvi, S.T.R., Seadawy, A. R., Younis, M., Ali, K., Iqbal, H.: Lump-soliton, lump-multi soliton and lump-periodic solutions of a generalized hyperelastic rod equation. Mod. Phys. Lett. B 35(11), 2150188 (2021b)
Seadawy, A. R., Cheemaa, N.: Some new families of spiky solitary waves of one-dimensional higher-order K-dV equation with power law nonlinearity in plasma physics, Indian Journal. Physics 94, 117–126 (2020)
Seadawy, A. R., Iqbal, M., Lu, D.: Applications of propagation of long-wave with dissipation and dispersion in nonlinear media via solitary wave solutions of generalized Kadomtsive-Petviashvili modified equal width dynamical equation. Comput. Math. Appl. 78, 3620–3632 (2019)
Seadawy, A. R., Arshad, M., Lu, D.: The weakly nonlinear wave propagation theory for the Kelvin-Helmholtz instability in magnetohydrodynamics flows. Chaos Solitons Fractals 139, 110141 (2020)
Seadawy, A. R., Rizvi, S.T.R., Ahmad, S., Younis, M., Baleanu, D.: Lump, lump-one stripe, multiwave and breather solutions for the Hunter-Saxton equation, Open. Physics 19(1), 1–10 (2021a)
Seadawy, A. R., Rehman, S.U., Younis, M., Rizvi, S.T.R., Althobaiti, S., Makhlouf, M.M.: Modulation instability analysis and longitudinal wave propagation in an elastic cylindrical rod modeled with Pochhammer-Chree equation and its modulation instability analysis. Phys. Scr. 96(4), 045202 (2021b)
Sulem, C., Sulem, P.L.: The nonlinear Schrödinger equation: self-focusing and wave collapse, vol. 139. Springer Science and Business Media (2007)
Tang, Y., Tao, S., Guan, Q.: Lump solitons and the interaction phenomena of them for two classes of nonlinear evolution equations. Comput. Math. Appl. 72(9), 2334–2342 (2016)
Tao, Y., He, J.: Multisolitons, breathers, and rogue waves for the HIROTA equation generated by Darboux transformation. Phys. Rev. E 85(2), 026601 (2012)
Wang, M., Zhou, Y., Li, Z.: Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics. Phys. Lett. A 216, 67–75 (1996)
Yang, J.Y., Ma, W.X., Qin, Z.: Lump and lump-soliton solutions to the (2+1)-dimensional Ito equation. Anal. Math. Phys. 8(3), 427–436 (2018)
Yildirim, Y., Celik, N., Yasar, E.: Nonlinear Schrödinger equations with spatio-temporal dispersion in Kerr, parabolic, power and dual power law media: A novel extended Kudryashov’s algorithm and soliton solutions. Results Phys. 7, 3116–3123 (2017)
Yin, H.M., Chow, K.W.: Breathers, cascading instabilities and Fermi-Pasta-Ulam-Tsingou recurrence of the derivative nonlinear Schrödinger equation: Effects of ‘self-steepening’ nonlinearity. Phys. D 428, 133033 (2021)
Yin, H.M., Pan, Q., Chow, K.W.: Four-wave mixing and coherently coupled Schrödinger equations: Cascading processes and Fermi-Pasta-Ulam-Tsingou recurrence. Chaos 31, 083117 (2021). https://doi.org/10.1063/5.0051584
Yin, H.M., Pan, Q., Chow, K.W.: The Fermi-Pasta-Ulam-Tsingou recurrence for discrete systems: Cascading mechanism and machine learning for the Ablowitz-Ladik equation. Commun. Nonlinear Sci. Numer. Simul. 114, 106664 (2022a)
Yin, H.M., Pan, Q., Chow, K.W.: Doubly periodic solutions and breathers of the Hirota equation: recurrence, cascading mechanism and spectral analysis. Nonlinear Dyn. (2022b). https://doi.org/10.1007/s11071-022-07799-4
Yua, F., Yan, Z.: New rogue waves and dark-bright soliton solutions for a coupled nonlinear Schrödinger equation with variable coefficients. Appl. Math. Comput. 233, 351–358 (2014)
Zakharov, V.E., Gelash, A.A.: Nonlinear stage of modulation instability. Phys. Rev. Lett. 111, 054101 (2013)
Zhang, W.: Generalized variational principle for long water-wave equation by He’s Semi-Inverse method. Math. Probl. Eng. 2009, 1–5 (2009)
Zhang, Y., Sun, Y., Xiang, W.: The rogue waves of the KP equation with self-consistent sources. Appl. Math. Comput. 263, 204–213 (2015)
Zhou, Y., Manukure, S., Ma, W.X.: Lump and lump-soliton solutions to the Hirota-Satsuma-Ito equation. Commun. Nonlinear Sci. Numer. Simulat. 68, 56–62 (2019)
Funding
The authors have not disclosed any funding.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have not disclosed any competing interests.
Ethical approval
I hereby declare that this manuscript is the result of my independent creation under the reviewers’ comments. Except for the quoted contents, this manuscript does not contain any research achievements that have been published or written by other individuals or groups.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Rizvi, S.T.R., Seadawy, A.R., Naqvi, S.K. et al. Study of mixed derivative nonlinear Schrödinger equation for rogue and lump waves, breathers and their interaction solutions with Kerr law. Opt Quant Electron 55, 177 (2023). https://doi.org/10.1007/s11082-022-04415-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11082-022-04415-y