Optical soliton solutions and various breathers lump interaction solutions with periodic wave for nonlinear Schrödinger equation with quadratic nonlinear susceptibility

Abstract

In this article, we cover some soliton solutions and breathers for nonlinear Schrödinger equation with quadratic nonlinear susceptibility like that Breather lump wave solutions, Interaction between lump periodic and kink wave, lump soliton solution, Lump one kink solution, Lump two kink solution, multiwave solution, periodic cross kink solution, periodic cross lump wave solution, periodic wave solution and rogue wave solution. We also explore some rational solution such as M-shaped rational solutions, M-shaped rational solutions with one and two kink, kink cross rational solution and periodic cross rational solution. Also, we acquire homoclinic breather solution, M-shaped interaction with rogue and kink and M-shaped interaction with periodic and kink. Furthermore we also study the stability of our solutions. we also represents our solutions graphically such as 3D, 2D, contour, density plot and stream plot.

1 Introduction

The nonlinear Schrödinger equation (NLSE) is essential for the improvement in optical communication system. From the mathematical perspective Schrödinger equation combines the characteristics of both parabolic and hyperbolic equations. The NLSE applied in many scientific fields to explain nonlinear physical characteristics also have applications in variety of fields including semiconductor manufacturing, biology, solid-state physics, condense matter physics, quantum chemistry, nonlinear optics, wave propagation, optical communication, protein folding and bending, nano-technology and industry (Ilhan et al. 2022; Li et al. 2022; Mohyaldeen et al. 2022; Yang et al. 2018). At the present time, the study of NLSE including analysis, numerics and applications becoming significant subject in computational and applied mathematics (Shen et al. 2021, 2022; Song et al. 2020; Guo et al. 2020). Some efficient ways for obtaining soliton solutions and optics have grabed the attention of many researchers because soliton theory is the fundamental and exciting topic in research (Rizvi et al. 2021, 2022a, b; Seadawy et al. 2021, 2022a, b, c, d; Batool et al. 2022; Ali et al. 2022; Ashraf et al. 2022).

In this paper, we will study NLSE-QNS given by Biswas et al. (2022):

$$\begin{aligned} iy_t+c_1y_{xx}+d_1y_{xt}+b_1y+\alpha _1y^*z=ia_1y_x, \end{aligned}$$

(1)

$$\begin{aligned} iz_t+c_2z_{xx}+d_2z_{xt}+b_2z+\alpha _2y^2=ia_2z_x. \end{aligned}$$

(2)

where x and t represents the spatial and temporal variables respectively. The coefficients $a_j$, $b_j$, $c_j$, $d_j$, $\alpha _j$ ($j=1,2$) are real valued constants. $a_j$ are the coefficients of inter-modal dispersion. $c_j$ depict the coefficient of chromatic dispersion, while $d_j$ stands for the coefficient of spatio-temporal dispersion. And $\alpha _j$ are the coefficient of QN. The function $y=y(x,t$ and $z=z(x,t)$ are complex valued function. The functions y represents the wave profile of the forward harmonic waves and z represents second harmonic waves. And $y^*=y^*(x,t)$ is the conjugate of $y=y(x,t)$.

2 LSS

By using following transformation, we obtain solution for LSS Biswas et al. (2022):

$$\begin{aligned} y(x,t) = 2s(ln g)_x, \quad z(x,t) =2(ln j)_{xx}. \end{aligned}$$

(3)

We have following bilinear form by putting Eq. (3) into Eq. (1),

$$\begin{aligned}{} & {} 2 b_1 s g^2 j^2 g_{x}-2isgj^2g_tg_x+2ia_1sgj^2g_{x}^{2}+4d_1sj^2g_tg_{x}^{2}+4c_1sj^2g_{x}^{3}-2\alpha _{1}g^3y^*j_{x}^{2}\nonumber \\ {}{} & {} \quad +2isg^2j^2g_{xt}-4d_1sgj^2g_xg_{xt} -2ia_1sg^2j^2g_{xx}-2d_1sgj^2g_tg_{xx}-6c_1sgj^2g_{x}g_{xx}\nonumber \\ {}{} & {} \quad +2\alpha _{1}g^3jy^*j_{xx}+2d_1sg^2j^2g_{xxt}+2c_1sg^2j^2g_{xxx}. \end{aligned}$$

(4)

For LS g and j are the following functions:

$$\begin{aligned}&g= \Lambda _1^2+\Lambda _2^2+k_7, \nonumber \\ {}&j= \Lambda _1^2+\Lambda _2^2+k_8, \end{aligned}$$

(5)

where

$$\begin{aligned}&\Lambda _1= k_1x+k_2t+k_3,\quad \Lambda _2= k_4x+k_5t+k_6, \end{aligned}$$

where $k_i (1\le i\le 8)$ are real parameters. Insert Eq. (5) in to Eq. (4). We find some equations that provide coefficient values, including:

$$\begin{aligned}&k_1=0, k_3=0, k_4=k_4, k_6=0, k_7=0, k_8=0, k_2=\frac{4}{3} i a_1 k_4, k_5=\frac{4 a_1 k_4}{3}, \end{aligned}$$

(6)

To obtain the LSS of Eq. (1), Insert Eq. (6) in to Eq. (5) and then in Eq. (3)

$$\begin{aligned} y(x,t)=\frac{4 k_4 s \left( \frac{4 a_1 k_4 t}{3}+k_4 x\right) }{\left( \frac{4 a_1 k_4 t}{3}+k_4 x\right) ^2-\frac{16}{9} a_1^2 k_4^2 t^2}. \end{aligned}$$

(7)

$$\begin{aligned} z(x,t)=\frac{2 \left( 2 k_4^2 \left( \left( \frac{4 a_1 k_4 t}{3}+k_4 x\right) ^2-\frac{16}{9}a_1^2 k_4^2 t^2\right) -4 k_4^2 \left( \frac{4 a_1 k_4 t}{3}+k_4 x\right) ^2\right) }{\left( \left( \frac{4 a_1 k_4 t}{3}+k_4 x\right) ^2-\frac{16}{9} a_1^2 k_4^2 t^2\right) ^2}. \end{aligned}$$

(8)

Now we represent some dynamical representation of solutions (Figs. 1 and 2):

Fig. 1

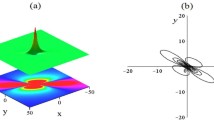
LS graphs of solution y(x, t) of Eq. (7) are shown as $k_4=0.5, s=4, a_1=-7.$ a 3D plot, b 2D plot, c contour plot

Fig. 2

LS graphs of solution z(x, t) of Eq. (8) are shown as $k_4=5, s=0.4, a_1=1.1.$

3 LOKS

The LOKS’s solution, which contains the sum of the quadratic functions and an exponential functions, is obtain in this section for Eq. (1) We use the following function g and j Ren et al. (2019):

$$\begin{aligned}&g= \Lambda _1^2+\Lambda 2^2+n_1e^{H_1}+k_7, \nonumber \\ {}&j= \Lambda _1^2+\Lambda _2^2+n_1e^{H_1}+k_8, \end{aligned}$$

(9)

where

$$\begin{aligned}&\Lambda _1= k_1x+k_2t+k_3, \quad \Lambda _2= k_4x+k_5t+k_6, \quad H_1=r_1x+r_2t, \end{aligned}$$

Inserting Eq. (9) in to Eq. (4). By inserting all the coefficient of the $x, t, e^{4 r_1 x+4 r_2 t},e^{3 r_1 x+3 r_2 t},e^{2 r_1 x+2 r_2 t}, e^{r_1 x+r_2 t},y^*(x,t),y^*(x,t) e^{4 r_1 x+4 r_2 t},y^*(x,t) e^{3 r_1 x+3 r_2 t},y^*(x,t) e^{2 r_1x+2 r_2 t},y^*(x,t) e^{r_1 x+r_2 t}$ to be zero, we get algebraic expression that provide coefficient values as:

$$\begin{aligned}{} & {} k_1=0, k_2=k_2, k_3 =0, k_4=-\frac{3 \left( k_2^2-2 k_5^2\right) }{2 (k_5 (3 a_1+2 b_1 d_1))}, \nonumber \\ {}{} & {} k_5=k_5, k_6=k_6, k_7=k_7, k_8=k_8, n_1=n_1, r_1=0, r_2=\frac{1}{3} (-(4 i))b_1, \end{aligned}$$

(10)

putting Eq. (10) in to Eq. (9) and then in Eq. (3) to get LOKS of Eq. (1),

$$\begin{aligned} y(x,t)=-\frac{6 s \left( k_2^2-2 k_5^2\right) \left( -\frac{3 x \left( k_2^2-2 k_5^2\right) }{2 k_5 (3 a_1+2 b_1 d_1)}+k_5 t+k_6\right) }{k_5 (3 a_1+2 b_1 d_1) \left( \left( -\frac{3 x \left( k_2^2-2 k_5^2\right) }{2 k_5 (3 a_1+2 b_1 d_1)}+k_5 t+k_6\right) ^2+n_1 e^{\frac{1}{3} (-4) i b_1 t}+k^2 t^2+k_7\right) }. \end{aligned}$$

(11)

$$\begin{aligned} z(x,t)=\frac{2 \left( -\frac{9 \left( k_2^2-2 k_5^2\right) ^2 \Psi ^2}{k_5^2 (3 a_1+2 b_1 d_1)^2}+\frac{9 \left( k_2^2-2 k_5^2\right) ^2 \left( \Psi ^2+n_1 e^{\frac{1}{3} (-4) i b_1 t}+k_2^2 t^2+k_8\right) }{2 k_5^2 (3 a_1+2 b_1 d_1)^2}\right) }{\left( \Psi ^2+n_1 e^{\frac{1}{3} (-4) i b_1 t}+k_2^2 t^2+k_8\right) ^2}, \end{aligned}$$

(12)

where $\Psi = -\frac{3 x \left( k_2^2-2 k_5^2\right) }{2 k_5 (3 a_1+2 b_1 d_1)}+k_5 t+k_6.$

Now we represent some graphical representation of solutions (Figs. 3 and 4):

Fig. 3

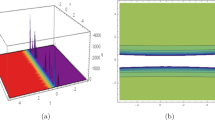
LOKS dynamical representation of solution y(x, t) of Eq. (11) are shown as $a_1=1.5, b_1=7, d_1=0.9, k_2=0.5, k_5=0.2, k_6=-4, k_7=-2, n_1=2.2, s=0.05$

Fig. 4

LOKS graphical representation of solution z(x, t) of Eq. (12) are shown as $a_1=1.5, b_1=7, d_1=0.9, k_2=0.5, k_5=0.2, k_6=-4, k_7=-2, k_8=-0.07, n_1=2.2, s=0.05$

4 LTKS

The LTKS’s solution, which contains the sum of the quadratic functions and an exponential functions, is obtain in this section for Eq. (1). We use the following function g and j:

$$\begin{aligned}&g= \Lambda _1^2+\Lambda _2^2+n_1e^{H_1}+n_2e^{H_2}+k_7, \nonumber \\&j= \Lambda _1^2+\Lambda _2^2+n_1e^{H_1}+n_2e^{H_2}+k_8, \end{aligned}$$

(13)

where

$$\begin{aligned}&\Lambda _1= k_1x+k_2t+k_3, \quad \Lambda _2= k_4x+k_5t+k_6, \quad H_1=r_1x+r_2t, \quad H_2=r_3x+r_4t, \end{aligned}$$

Putting Eq. (13) in to Eq. (4). By putting all the coefficient of the $x, t, e^{r_1 x+r_2 t},e^{2 r_1 x+2 r_2 t},e^{3 r_1 x+3 r_2 t},e^{4 r_1 x+4 r_2 t},e^{r_3 x+r_4 t},e^{2 r_3 x+2 r_4 t},e^{3 r_3 x+3 r_4 t},e^{r_1 x+r_2 t+r_3 x+r_4 t},e^{2 r_1 x+2 r_2 t+r_3 x+r_4 t},e^{3 r_1 x+3 r_2 t+r_3 x+r_4 t}, e^{r_1 x+r_2 t+2 r_3 x+2 r_4 t},e^{2 r_1 x+2 r_2 t+2 r_3 x+2 r_4 t},e^{r_1 x+r_2 t+3 r_3 x+3 r_4 t},y^*(x,t) e^{r_1 x+r_2 t},y^*(x,t) e^{2 r_1 x+2 r_2 t}, y^*(x,t) e^{3 r_1 x+3 r_2 t}, y^*(x,t) e^{4 r_1 x+4 r_2 t},y^*(x,t) e^{r_3 x+r_4 t},y^*(x,t) e^{2 r_3 x+2 r_4 t},y^*(x,t) e^{3 r_3x+3 r_4 t},y^*(x,t) e^{r_1 x+r_2 t+r_3 x+r_4 t}, y^*(x,t) e^{2 r_1 x+2 r_2 t+r_3 x+r_4 t},y^*(x,t) e^{3 r_1 x+3 r_2 t+r_3 x+r_4 t},y^*(x,t) e^{r_1 x+r_2 t+2 r_3 x+2 r_4 t}, y^*(x,t) e^{2 r_1 x+2 r_2t+2 r_3 x+2 r_4 t}, y^*(x,t) e^{r_1 x+r_2 t+3 r_3 x+3 r_4 t}$ to be zero, we get algebraic expression that provide coefficient values as:

$$\begin{aligned} k_1=k_1, k_2=0, k_3=k_3, k_4=k_4, k_5=-\frac{2 k_4 \left( 3 a_1 k_1^2+3 a_1 k_4^2+2 b_1 d_1 k_1^2+2 b_1 d_1 k_4^2\right) }{3 \left( k_1^2-2 k_4^2\right) },\nonumber \\ k_6=0, k_7=k_7, k_8=0, n_1=n_1, n_2=n_2, r_1=r_1, r_2=\frac{1}{2} i (-4 b_1+i r_4), r_3=0, r_4=r_4, \end{aligned}$$

(14)

Insert Eq. (14) in to Eq. (13) and then in Eq. (3) to get the LTKS solution of Eq. (1),

$$\begin{aligned} y(x,t)=\frac{2 s \left( 2 k_4 \left( k_4 x-\frac{2 k_4 t \left( 3 a_1 k_1^2+3 a_1 k_4^2+2 b_1 d_1 k_1^2+2 b_1 d_1 k_4^2\right) }{3 \left( k_1^2-2 k_4^2\right) }\right) +n_1 r_1 e^{r_1 x+\frac{1}{2} i t (-4 b_1+i r_4)}+2 k_1 (k_1 x+k_3)\right) }{\left( k_4 x-\frac{2 k_4 t \left( 3 a_1 k_1^2+3 a_1 k_4^2+2 b_1 d_1k_1^2+2 b_1 d_1 k_4^2\right) }{3 \left( k_1^2-2 k_4^2\right) }\right) ^2+n_1 e^{r_1 x+\frac{1}{2} i t (-4 b_1+i r_4)}+(k_1 x+k_3)^2+k_7+n_2 e^{r_4 t}}. \end{aligned}$$

(15)

$$\begin{aligned} z(x,t)=\frac{2 \left( \left( \Phi +2 k_1^2+2 k_4^2\right) \left( \Pi \right) -\left( 2 k_4 \left( \Pi \right) +\Phi +2 k_1 (k_1 x+k_3)\right) ^2\right) }{\left( \Pi \right) ^2}, \end{aligned}$$

(16)

where $\Phi =n_1 r_1^2 e^{r_1 x+\frac{1}{2} i t (-4 b_1+i r_4)},\; \Pi =\left( k_4 x-\frac{2 k_4 t \left( 3 a_1 k_1^2+3 a_1 k_4^2+2 b_1 d_1 k_1^2+2 b_1 d_1 k_4^2\right) }{3 \left( k_1^2-2 k_4^2\right) }\right) ^2+\Phi +(k_1 x+k_3)^2+n_2 e^{r_4 t}.$ and

Now we have shown some graphical representation of above solutions (Figs. 5 and 6):

Fig. 5

LTKS graphical representation of solution y(x, t) of Eq. (15) are shown as $k_1=0.1, k_3=-5, k_4=-0.4, k_7=3.9,r_1=-0.2, r_4=3, b_1=1.5, a_1=-4, n_1=2.5,n_2=0.2, d_1=3.1, s=-0.2$

Fig. 6

LTKS graphical representation of solution z(x, t) of Eq. (16) are shown as $k_1=1, k_3=5, k_4=0.4, k_7=3,r_1=0.2, r_4=0.3, b_1=5, a_1=4, n_1=2,n_2=0.6, d_1=3.5, s=2.$

5 RWS

The RWS’s solution, which contains the sum of the quadratic functions and an exponential functions, is obtain in this section for Eq. (1) We use the following function g and j Ren et al. (2019):

$$\begin{aligned}&g= \Lambda _1^2+\Lambda _2^2+n_1\cosh (\lambda )+k_7, \nonumber \\ {}&j= \Lambda _1^2+\Lambda _2^2+n_1\cosh (\lambda )+k_8, \end{aligned}$$

(17)

where

$$\begin{aligned}&\Lambda _1= k_1x+k_2t+k_3, \quad \Lambda _2= k_4x+k_5t+k_6, \quad \lambda =r_1x+r_2t, \end{aligned}$$

Insert Eq. (17) in to Eq. (4). Inserting all coefficient of $x, t, \cosh (r_1 x+r_2t),\cosh ^2(r_1 x+r_2t),\cosh ^3(r_1 x+r_2t),\cosh ^4(r_1 x+r_2t),\cosh ^5(r_1 x+r_2t),\cosh ^6(r_1 x+r_2t),\sinh (\text{( }r_1 x+r_2t),\sinh (r_1 x+r_2t) \cosh (r_1 x+r_2t),\sinh (r_1 x+r_2t) \cosh ^2(r_1 x+r_2t),\sinh (r_1 x+r_2t) \cosh ^3(r_1 x+r_2t),\sinh (r_1 x+r_2t) \cosh ^4(r_1 x+r_2t),\sinh (r_1 x+r_2t) \cosh ^5(r_1 x+r_2t),\sinh ^2(r_1 x+r_2t),\sinh ^2(r_1 x+r_2t) \cosh (r_1 x+r_2t),\sinh ^2(r_1 x+r_2t) \cosh ^2(r_1 x+r_2t),\sinh ^2(r_1 x+r_2t) \cosh ^3(r_1 x+r_2t),\sinh ^2(r_1 x+r_2t) \cosh ^4(r_1 x+r_2t),\sinh ^3(r_1 x+r_2t),\sinh ^3(r_1 x+r_2t) \cosh (r_1 x+r_2t),\sinh ^3(r_1 x+r_2t) \cosh ^2(r_1 x+r_2t),\sinh ^3(r_1 x+r_2t) \cosh ^3(r_1 x+r_2t),y^*(x,t),y^*(x,t) \cosh (r_1 x+r_2t),y^*(x,t) \cosh ^2(r_1 x+r_2t), y^*(x,t) \cosh ^3(r_1 x+r_2t),y^*(x,t) \cosh ^4(r_1 x+r_2t),y^*(x,t) \cosh ^5(r_1 x+r_2t),y^*(x,t) \cosh ^6(r_1 x+r_2t),y^*(x,t) \sinh (r_1 x+r_2t),y^*(x,t) \sinh (r_1 x+r_2t) \cosh (r_1 x+r_2t) t),y^*(x,t) \sinh (r_1 x+r_2t) \cosh ^2(r_1 x+r_2t),y^*(x,t) \sinh (r_1 x+r_2t) \cosh ^3(r_1 x+r_2t),y^*(x,t) \sinh (r_1 x+r_2t) \cosh ^4(r_1 x+r_2t),y^*(x,t) \sinh (r_1 x+r_2t) \cosh ^5(r_1 x+r_2t),y^*(x,t) \sinh ^2(r_1 x+r_2t),y^*(x,t) \sinh ^2(r_1 x+r_2t) \cosh (r_1 x+r_2t),y^*(x,t) \sinh ^2(r_1 x+r_2t) \cosh ^2(r_1 x+r_2t),y^*(x,t) \sinh ^2(r_1 x+r_2t) \cosh ^3(r_1 x+r_2t),y^*(x,t) \sinh ^2(r_1 x+r_2t) \cosh ^4(r_1 x+r_2t),y^*(x,t) \sinh ^3(r_1 x+r_2t),y^*(x,t) \sinh ^3(r_1 x+r_2t) \cosh (r_1 x+r_2t),y^*(x,t) \sinh ^3(r_1 x+r_2t) \cosh ^2(r_1 x+r_2t),y^*(x,t) \sinh ^3(r_1 x+r_2t) \cosh ^3(r_1 x+r_2t)$ to be zero, we get expression that provide coefficient values as:

$$\begin{aligned}&k_1=0, k_2=-\frac{(3 i) k_3 (2 a_1 d_1+3 c_1)}{4 d_1^2}, k_3=k_3, k_4=k_4, k_5=0, k_6=0, k_7=0,k_8=k_8, n_1=n_1, \nonumber \\ {}&r_1=-\frac{2 d_1 r_2}{3 c_1}, r_2=r_2, \end{aligned}$$

(18)

Insert Eq. (18) in to Eq. (17) and then in Eq. (3) to have the RWS solution of Eq. (1),

$$\begin{aligned} y(x,t)=\frac{2 s \left( 2 k_4^2 x-\frac{2 d_1 n_1 r_2 \sinh \left( r_2 t-\frac{2 d_1 r_2 x}{3 c_1}\right) }{3 c_1}\right) }{\left( k_3-\frac{3 i k_3 t (2 a_1 d_1+3 c_1)}{4 d_1^2}\right) ^2+n_1 \cosh \left( r_2 t-\frac{2 d_1 r_2 x}{3 c_1}\right) +k_4^2 x^2}. \end{aligned}$$

(19)

$$\begin{aligned} z(x,t)=\frac{2 \left( -\left( 2 k_4^2 x-\frac{2 d_1 n_1 r_2\sinh \left( \Omega \right) }{3 c_1}\right) ^2+\left( \frac{4 d_1^2 n_1 r_2^2 \cosh \left( \Omega \right) }{9 c_1^2}+2 k_4^2\right) \left( \Upsilon \right) \right) }{\left( \Upsilon \right) ^2}, \end{aligned}$$

(20)

where $\Omega =r_2 t-\frac{2 d_1 r_2 x}{3 c_1}$ and $\Upsilon =\left( k_3-\frac{3 i k_3 t (2a_1 d_1+3 c_1)}{4 d_1^2}\right) ^2+n_1 \cosh \left( \Omega \right) +k_4^2 x^2+k_8$.

Now we have given some graphical representation of these solutions (Figs. 7 and 8):

Fig. 7

RWS graphical representation of solution y(x, t) of Eq. (19) are shown as $k_3=0.5, k_4=7, r_2=0.1, c_1=5.5, a_1=0.06, n_1=4, d_1=1.3, s=2 .$

Fig. 8

RWS graphical representation of solution z(x, t) of Eq. (20) are shown as $k_3=-0.5, k_4=7, k_8=0.8, r_2=-0.1, c_1=-5.5, a_1=0.06, n_1=0.04, d_1=1.3, s=-2 .$

6 PWS

The PWS’s solution, which contains the sum of the quadratic functions and an exponential functions, is obtain in this section for Eq. (1). We use the following function g and j Ren et al. (2019):

$$\begin{aligned}&g= \Lambda _1^2+\Lambda _2^2+n_1\cos (\lambda )+k_7, \nonumber \\ {}&j= \Lambda _1^2+\Lambda _2^2+n_1\cos (\lambda )+k_8, \end{aligned}$$

(21)

Where

$$\begin{aligned}&\Lambda _1= k_1x+k_2t+k_3,\quad \Lambda _2= k_4x+k_5t+k_6,\quad \lambda =r_1x+r_2t, \end{aligned}$$

Put Eq. (21) into Eq. (4). The coefficient of $x, t, \cos (r_1x+r_2 t),\cos ^2(r_1x+r_2 t),\cos ^3(r_1x+r_2 t),\cos ^4(r_1x+r_2 t),\cos ^5(r_1x+r_2 t),\cos ^6(r_1x+r_2 t),\sin (r_1x+r_2 t),\sin (r_1x+r_2 t) \cos (r_1x+r_2 t),\sin (r_1x+r_2 t) \cos ^2(r_1x+r_2 t),\sin (r_1x+r_2 t) \cos ^3(r_1x+r_2 t),\sin (r_1x+r_2 t) \cos ^4(r_1x+r_2 t),\sin (r_1x+r_2 t) \cos ^5(r_1x+r_2 t),\sin ^2(r_1x+r_2 t),\sin ^2(r_1x+r_2 t) \cos (r_1x+r_2 t),\sin ^2(r_1x+r_2 t) \cos ^2(r_1x+r_2 t),\sin ^2(r_1x+r_2 t) \cos ^3(r_1x+r_2 t),\sin ^2(r_1x+r_2 t) \cos ^4(r_1x+r_2 t),\sin ^3(r_1x+r_2 t),\sin ^3(r_1x+r_2 t) \cos (r_1x+r_2 t),\sin ^3(r_1x+r_2 t) \cos ^2(r_1x+r_2 t),\sin ^3(r_1x+r_2 t) \cos ^3(r_1x+r_2 t),y^*(x,t),y^*(x,t) \cos (r_1x+r_2 t),y^*(x,t) \cos ^2(r_1x+r_2 t),y^*(x,t) \cos ^3(r_1x+r_2 t),y^*(x,t) \cos ^4(r_1x+r_2 t),y^*(x,t) \sin (r_1x+r_2 t),y^*(x,t) \sin (r_1x+r_2 t) \cos (r_1x+r_2 t),y^*(x,t) \sin (r_1x+r_2 t) \cos ^2(r_1x+r_2 t),y^*(x,t) \sin (r_1x+r_2 t) \cos ^3(r_1x+r_2 t),y^*(x,t) \sin ^2(r_1x+r_2 t), y^*(x,t) \sin ^2(r_1x+r_2 t) \cos (r_1x+r_2 t),y^*(x,t) \sin ^2(r_1x+r_2 t) \cos ^2(r_1x+r_2 t)$ values of the parameters which are given below:

$$\begin{aligned}&k_1=0, k_2=k_2, k_3=0, k_4=\frac{k_2^2+2 k_5^2}{2 (a_1 k_5)}, k_5=k_5, k_6=0, k_7=0, k_8=0, \nonumber \\&n_1=n_1, r_1=0, r_2=r_2, \end{aligned}$$

(22)

Insert Eq. (22) in to Eq. (21) and then in Eq. (3) to have the PWS solution of Eq. (1),

$$\begin{aligned} y(x,t)=\frac{2 s \left( k_2^2+2k_5^2\right) \left( \frac{x \left( k_2^2+2 k_5^2\right) }{2 a_1 k_5}+k_5 t\right) }{a_1 k_5 \left( \left( \frac{x \left( k_2^2+2 k_5^2\right) }{2 a_1 k_5}+k_5 t\right) ^2+k_2^2 t^2+n_1 \cos (r_2 t)\right) }. \end{aligned}$$

(23)

$$\begin{aligned} z(x,t)=\frac{2 \left( \frac{\left( k_2^2+2 k_5^2\right) ^2 \left( \left( \frac{x \left( k_2^2+2 k_5^2\right) }{2 a_1 k_5}+k_5 t\right) ^2+k_2^2 t^2+n_1 \cos (r_2 t)\right) }{2 a_1^2 k_5^2}-\frac{\left( k_2^2+2 k_5^2\right) ^2 \left( \frac{x \left( k_2^2+2 k_5^2\right) }{2 a_1 k_5}+k_5 t\right) ^2}{a_1^2 k_5^2}\right) }{\left( \left( \frac{x \left( k_2^2+2 k_5^2\right) }{2 a_1 k_5}+k_5 t\right) ^2+k_2^2 t^2+n_1 \cos (r_2 t)\right) ^2}. \end{aligned}$$

(24)

Now we have some graphical representation of these solutions (Figs. 9 and 10):

Fig. 9

PWS graphical representation of solution y(x, t) of Eq. (23) are shown as $k_2=1.3, k_5=0.5, r_2=0.05, n_1=6, a_1=1.5, s=0.1 .$

Fig. 10

PWS graphical representation of solution z(x, t) of Eq. (24) are shown as $k_2=1.5, k_5=2.5, r_2=5, n_1=-6, a_1=1.5, s=0.1 .$

7 PCKS

The PCKS’s solution, which contains the sum of the quadratic functions and an exponential functions, is obtain in this section for Eq. (1). We use the following function g and j:

$$\begin{aligned}&g= e^{-\Lambda _1}+r_1e^{\Lambda _1}+r_2\cos (\Lambda _2)+r_3\cosh (\Lambda _3)+k_{10}, \nonumber \\ {}&j= e^{-\Lambda _1}+\kappa _1e^{\Lambda _1}+\kappa _2\cos (\Lambda _2)+\kappa _3\cosh (\Lambda _3)+k_{11}, \end{aligned}$$

(25)

Where

$$\begin{aligned}&\Lambda _1= k_1x+k_2t+k_3,\quad \Lambda _2= k_4x+k_5t,\quad \Lambda _3 =k_6x+k_7t, \end{aligned}$$

Put Eq. (25) into Eq. (4). We have values of the parameters which are given below:

$$\begin{aligned}&k_1=0, k_2=k_2, k_3=0, k_4=k_4, k_5=-\frac{c_1 k_4}{d_1}, k_6=k_6, k_7=0, k_{10}=k_{10}, k_{11}=-\frac{\kappa _2 k_{10}}{r_2} \nonumber \\ {}&r_1=0, r_2=r_2, r_3=r_3, \kappa _1=0, \kappa _2=\kappa _2, \kappa _3=\kappa _3, \end{aligned}$$

(26)

Insert Eq. (26) into Eq. (25) and then in Eq. (3) to have the PCKS solution of Eq. (1),

$$\begin{aligned} y(x,t)=\frac{2 k_4r_2 s \sin \left( \frac{c_1 k_4 t}{d_1}-k_4 x\right) }{r_2 \cos \left( \frac{c_1k_4 t}{d_1}-k_4 x\right) +k_{10}+e^{-k_2 t}}. \end{aligned}$$

(27)

$$\begin{aligned} z(x,t)=\frac{2 \left( \left( \kappa _3 k_6^2 \cosh (k_6 x)-\kappa _2 k_4^2 \cos \left( \frac{c_1 k_4 t}{d_1}-k_4 x\right) \right) \left( \Delta \right) -\left( \Delta _1\right) ^2\right) }{\left( \Delta \right) ^2}, \end{aligned}$$

(28)

where $\Delta =\kappa _2 \cos \left( \frac{c_1k_4 t}{d_1}-k_4 x\right) -\frac{\kappa _2 k_{10}}{r_2}+e^{-k_2 t}+\kappa _3 \cosh (k_6 x),$ and $\Delta _1=\kappa _2 k_4 \sin \left( \frac{c_1 k_4 t}{d_1}-k_4 x\right) +\kappa _3 k_6 \sinh (k_6 x)$ .

Now we get some dynamical representation of our solutions (Figs. 11 and 12):

Fig. 11

PCKS graphical representation of solution y(x, t) of Eq. (27) are shown as $k_2=5, k_4=0.2, k_{10}=0.7 r_2=3, c_1=0.5, d_1=1.3, s=-2 .$

Fig. 12

PCKS graphical representation of solution z(x, t) of Eq. (28) are shown as $k_2=2, k_4=0.2, k_6=0.6, k_{10}=0.07, r_2=0.03, c_1=0.5, d_1=1.8, s=-5, \kappa _2=0.5, \kappa _3=4s .$

8 PCLWS

The PCLWS’s solution, which contains the sum of the quadratic functions and an exponential functions, is obtain in this section for Eq. (1). We use the following function g and j:

$$\begin{aligned}&g= \Lambda _1^2+\Lambda _2^2+n_1\cos (H_1)+n_2\cosh (H_2)+k_7, \nonumber \\ {}&j= \Lambda _1^2+\Lambda _2^2+n_1\cos (H_1)+n_2\cosh (H_2)+k_8, \end{aligned}$$

(29)

Where

$$\begin{aligned}&\Lambda _1= k_1x+k_2t+k_3,\quad \Lambda _2= k_4x+k_5t+k_6,\quad H_1 =r_1x+r_2t, \quad H_2 =r_3x+r_4t, \end{aligned}$$

Put Eq. (25) into Eq. (4). We have values of the parameters which are given below:

$$\begin{aligned}&k_1=k_1, k_2=0, k_3=k_3, k_4=k_4, k_5=k_5, k_6=k_6, k_7=k_7, k_8=0, \nonumber \\ {}&r_1=0, r_2=r_2, r_3=-\frac{d_1 r_4}{c_1}, r_4=r_4, \end{aligned}$$

(30)

Insert Eq. (30) into Eq. (29) and then in Eq. (3) to have the PCLWS solution of Eq. (1),

$$\begin{aligned} y(x,t)=\frac{2 s \left( -\frac{d_1 n_2 r_4 \sinh \left( r_4 t-\frac{d_1 r_4 x}{c_1}\right) }{c_1}+2 k_1 (k_1 x+k_3)+2 k_4 (k_4 x+k_5 t+\text {k6})\right) }{n_2 \cosh \left( r_4 t-\frac{d_1 r_4 x}{c_1}\right) +(k_1 x+k_3)^2+(k_4 x+k_5 t+k_6)^2+k_7+n_1 \cos (r_2 t)}. \end{aligned}$$

(31)

$$\begin{aligned} z(x,t)=\frac{2 \left( \left( \Sigma +2 k_1^2+2 k_4^2\right) \left( \Xi \right) -\left( -\Sigma +2 k_1 (k_1 x+k_3)+2 k_4 (k_4 x+k_5 t+k_6)\right) ^2\right) }{\left( \Xi \right) ^2}, \end{aligned}$$

(32)

where $\Xi =n_2 \cosh \left( r_4 t-\frac{d_1 r_4 x}{c_1}\right) +(k_1 x+k_3)^2+(k_4 x+k_5 t+k_6)^2+n_1 \cos (r_2 t)$ and $\Sigma =\frac{d_1^2 n_2 r_4^2 \cosh \left( r_4 t-\frac{d_1 r_4 x}{c_1}\right) }{c_1^2}$.

Now we get some dynamical representation of our solutions (Figs. 13 and 14):

Fig. 13

PCLWS graphical representation of solution y(x, t) of Eq. (31) are shown as $k_1=1.1, k_3=0.3, k_4=-0.4, k_5=0.5, k_6=6.5, k_7=0.1, n_1=4.4, n_2=2.9, r_2=1.2, r_4=1.05, c_1=8.5, d_1=1.5, s=5 .$

Fig. 14

PCLWS graphical representation of solution z(x, t) of Eq. (32) are shown as $k_1=-1, k_3=3.5, k_4=4, k_5=-5, k_6=0.6, k_7=-0.1, n_1=-4.4, n_2=2.9, r_2=-1.2, r_4=1, c_1=-5, d_1=1.5, s=5.$

9 MWS

The MWS’s solution, which contains the sum of the quadratic functions and an exponential functions, is obtain in this section for Eq. (1). We use the following function g and j Seadawy et al. (2021):

$$\begin{aligned}&g= \kappa _0\cosh (\lambda _1)+\kappa _1\cos (\lambda _2)+\kappa _2\cosh (\lambda _3)+k_{10}, \nonumber \\ {}&j= r_0\cosh (\lambda _1)+r_1\cos (\lambda _2)+r_2\cosh (\lambda _3)+k_{11}, \end{aligned}$$

(33)

Where

$$\begin{aligned}&\lambda _1= k_1x+k_2t+k_3,\quad \lambda _2= k_4x+k_5t+k_6,\quad \lambda _3 =k_7x+k_8t+k_9, \end{aligned}$$

Put Eq. (33) into Eq. (4). We have values of the parameters which are given below:

$$\begin{aligned}&k_1=0, k_2=0, k_3=0, k_4=k_4, k_5=k_5, k_6=0, k_7=0, k_8=0, k_9=k_9, k_{10}=k_{10},\nonumber \\ {}&k_{11}=0, r_0=0, r_1=-\frac{2 \kappa _1 r_2 \left( b_1+2 c_1 k_4^2+2 d_1 k_4 k_5\right) }{\kappa _2 \left( 2 b_1+c_1 k_4^2+d_1 k_4 k_5\right) }, r_2=r_2, \kappa _0=\kappa _0, \kappa _1=\kappa _1, \kappa _2=\kappa _2 \end{aligned}$$

(34)

Insert Eq. (34) into Eq. (33) and then in Eq. (3) to have the MWS solution of Eq. (1),

$$\begin{aligned} y(x,t)=-\frac{2 \kappa _1 k_4 s \sin (k_4 x+k_5 t)}{\kappa _0+k_{10}+\kappa _1 \cos (k_4 x+k_5 t)+\kappa _2 \cosh (k_9)}. \end{aligned}$$

(35)

$$\begin{aligned} z(x,t)=\frac{2 \left( \frac{2 \kappa _1k_4^2 r_2 \left( b_1+2 c_1k_4^2+2 d_1k_4 k_5\right) \cos (k_4 x+k_5 t) \left( \xi \right) }{\kappa _2 \left( 2 b_1+c_1k_4^2+d_1k_4 k_5\right) }-\frac{4 \kappa _1^2k_4^2 r_2^2 \left( b_1+2 c_1k_4^2+2 d_1k_4 k_5\right) ^2 \sin ^2(k_4 x+k_5 t)}{\kappa _2^2 \left( 2 b_1+c_1k_4^2+d_1k_4 k_5\right) ^2}\right) }{\left( \xi \right) ^2}, \end{aligned}$$

(36)

where $\xi =r_2 \cosh (k_9)-\frac{2 \kappa _1 r_2 \left( b_1+2 c_1k_4^2+2 d_1k_4 k_5\right) \cos (k_4 x+k_5 t)}{\kappa _2 \left( 2 b_1+c_1k_4^2+d_1k_4 k_5\right) }$.

Now we get some dynamical representation of our solutions (Figs. 15 and 16):

Fig. 15

MWS graphical representation of solution y(x, t) of Eq. (35) are shown as $k_4=-0.2, k_5=1.3, k_9=0.05, k_{10}=0.1, s=5, \kappa _0=2.5, \kappa _1=1.9, \kappa _2=3.5 .$

Fig. 16

MWS graphical representation of solution z(x, t) of Eq. (36) are shown as $k_4=-0.2, k_5=1.5, k_9=0.05, k_{10}=0.1, s=5, \kappa _0=2.5, \kappa _1=1.9, \kappa _2=3.5, b_1=5, d_1=4.5, c_1=3, r_2=2 .$

10 LPKW

The LPKW’s solution, which contains the sum of the quadratic functions and an exponential functions, is obtain in this section for Eq. (1). We use the following function g and j Ren et al. (2019):

$$\begin{aligned}&g= \Lambda _1^2+\Lambda _2^2+n_1e^{H_1}+n_2\cos (\lambda )+k_7, \nonumber \\ {}&j= \Lambda _1^2+\Lambda _2^2+n_1e^{H_1}+n_2\cos (\lambda )k_8, \end{aligned}$$

(37)

where

$$\begin{aligned}&\Lambda _1= k_1x+k_2t+k_3, \quad \Lambda _2= k_4x+k_5t+k_6, \quad H_1= r_1x+r_2t, \quad \lambda = m_1x+m_2t, \end{aligned}$$

Put Eq. (37) into Eq. (4). We have values of the parameters which are given below:

$$\begin{aligned}&k_1=0, k_2=0, k_3=k_3, k_4=k_4, k_5=k_5, k_6=0, k_7=\frac{1}{3} (-2) k_3^2, k_8=0, \end{aligned}$$

(38)

Insert Eq. (38) into Eq. (37) and then in Eq. (3) to have the LPKW solution of Eq. (1),

$$\begin{aligned} y(x,t)=\frac{2 s \left( 2 k_4 (k_4 x+k_5 t)-m_1 n_2 \sin (m_1 x+m_2 t)+\text {n1} r_1 e^{r_1 x+r_2 t}\right) }{\frac{k_3^2}{3}+(k_4 x+k_5 t)^2+n_2 \cos (m_1 x+m_2 t)+n_1 e^{r_1 x+r_2 t}}. \end{aligned}$$

(39)

$$\begin{aligned} z(x,t)=\frac{2 \left( \left( 2 k_4^2-m_1^2 n_2 \cos (\theta )+n_1 r_1^2 e^{r_1 x+r_2 t}\right) \left( \varrho \right) -\left( 2 k_4 (k_4 x+k_5 t)-m_1 n_2 \sin (\theta )+n_1 r_1 e^{r_1 x+r_2 t}\right) ^2\right) }{\left( \varrho \right) ^2}, \end{aligned}$$

(40)

where $\theta =m_1 x+m_2 t$ and $\varrho =k_3^2+(k_4 x+k_5 t)^2+n_2 \cos (\theta )+n_1 e^{r_1 x+r_2 t}$.

Now we get some dynamical representation of our solutions (Figs. 17 and 18):

Fig. 17

LPKW graphical representation of solution y(x, t) of Eq. (39) are shown as $k_3=-0.9, k_4=10, k_5=1.1, s=0.5, r_1=3, r_2=0.3, n_1=5, n_2=0.8, m_1=2.5, m_2=4 .$

Fig. 18

LPKW graphical representation of solution z(x, t) of Eq. (40) are shown as $k_3=-0.9, k_4=10, k_5=-1.1, s=0.5, r_1=3, r_2=-0.3, n_1=5, n_2=-0.8, m_1=2.5, m_2=-4 .$

11 BLWS

The BLWS’s solution, which contains the sum of the quadratic functions and an exponential functions, is obtain in this section for Eq. (1). We use the following function g and j Seadawy et al. (2021):

$$\begin{aligned}&g= e^{-h\Lambda _1}+m_1e^{h\Lambda _1}+n_2\cos (h_1\Lambda _2)+k_6, \nonumber \\ {}&j= e^{-h\Lambda _1}+n_1e^{h\Lambda _1}+n_2\cos (h_1\Lambda _2)+k_7, \end{aligned}$$

(41)

where

$$\begin{aligned}&\Lambda _1= k_1x+k_2t+k_3, \quad \Lambda _2= k_4x+k_5t, \end{aligned}$$

Put Eq. (41) into Eq. (4). We have values of the parameters which are given below:

$$\begin{aligned}&k_1=0, k_2=k_2, k_3=k_3, k_4=-\frac{d_1 k_5}{c_1}, k_5=k_5, k_6=k_6, n_1=n_1, n_2=n_2 \end{aligned}$$

(42)

Insert Eq. (42) into Eq. (41) and then in Eq. (3) to have the BLWS solution of Eq. (1),

$$\begin{aligned} y(x,t)=\frac{2 d_1 h_1 k_5 n_2 s \sin \left( h_1 \left( k_5 t-\frac{d_1 k_5 x}{\text {c1}}\right) \right) }{c_1 \left( n_2 \cos \left( h_1 \left( k_5 t-\frac{d_1 k_5 x}{c_1}\right) \right) +n_1 e^{h (k_2 t+k_3)}+e^{-h (k_2 t+k_3)}+k_6\right) }. \end{aligned}$$

(43)

$$\begin{aligned} z(x,t)=\frac{2 \left( -\frac{d_1^2 h_1^2 k_5^2 n_2 \cos \left( \varphi \right) \left( n_2 \cos \left( \varphi \right) +n_1 e^{h (k_2 t+k_3)}+e^{-h (k_2 t+k_3)}+\text {k7}\right) }{c_1^2}-\frac{d_1^2 h_1^2 k_5^2 n_2^2 \sin ^2\left( \varphi \right) }{c_1^2}\right) }{\left( n_2 \cos \left( \varphi \right) +n_1 e^{h (k_2 t+k_3)}+e^{-h (k_2 t+k_3)}+k_7\right) ^2}, \end{aligned}$$

(44)

where $\varphi =h_1 \left( k_5 t-\frac{d_1 k_5 x}{c_1}\right)$ .

Now we get some dynamical representation of our solutions (Figs. 19 and 20):

Fig. 19

BLWS graphical representation of solution y(x, t) of Eq. (43) are shown as $k_2=-0.5, k_3=7, k_5=0.05, k_6=0.7, s=0.2, d_1=5, h=0.1, h_1=0.3, n_1=2, n_2=3, c_1=0.5.$

Fig. 20

BLWS graphical representation of solution z(x, t) of Eq. (44) are shown as $k_2=0.7, k_3=0.7, k_5=5, k_6=7, k_7=-0.8, s=0.5, d_1=-3, h=0.01, h_1=0.5, n_1=0.2, n_2=0.03, c_1=6.$

12 Traveling wave transformation (TWT)

To solve Eqs. (1) and (2), the TWT are formed as Biswas et al. (2022),

$$\begin{aligned}&y(x,t)=Y_1(\nu )e^{i\xi _1(x,t)}, \end{aligned}$$

(45)

$$\begin{aligned}&z(x,t)=Y_2(\nu )e^{2i\xi _2(x,t)}. \end{aligned}$$

(46)

$Y_{j}(\nu )$ for j=1,2 are components of amplitude and wave variables is

$$\begin{aligned}&\nu =\psi (x-qt), \end{aligned}$$

(47)

where $\psi$ and q are the real-valued constants that symbolize the soliton width and velocity, and the phase components are given as

$$\begin{aligned}&\xi _j(x,t)=-px+vt+\phi , \end{aligned}$$

(48)

where p, v and $\phi$ are the real-valued constants that represents the soliton frequency, soliton wave number and phase constant respectively.

Next By putting Eqs. (45) and (46) in Eqs. (1) and (2) we have the real and imaginary parts are

$$\begin{aligned} \psi ^2(c_1-qd_1)Y_{1}^{''}+(b_1-v-p^2c_1+pvd_1-pa_1)Y_1+\alpha _1Y_1Y_2=0, \end{aligned}$$

(49)

$$\begin{aligned} pqd_1-2pc_1+vd_1-q-a_1=0, \end{aligned}$$

(50)

$$\begin{aligned} \psi ^2(c_2-qd_2)Y_{2}^{''}+(b_2-2v-4p^2c_2+4pvd_2-2pa_2)Y_2+\alpha _2Y_1^2=0, \end{aligned}$$

(51)

$$\begin{aligned} 2pqd_2-4pc_2+2vd_2-q-a_2=0, \end{aligned}$$

(52)

Equations (49)–(52) shorten to ordinary differential equation by using balancing rule

$$\begin{aligned} \psi ^2(c-qd)Y^{''}+(2cp^2-2dpv+ap+v)Y+\alpha Y^2=0, \end{aligned}$$

(53)

with velocity

$$\begin{aligned} q=\frac{4pc-2vd+\eta }{2pd-1}, \end{aligned}$$

(54)

and constraints are

$$\begin{aligned} Y_1=Y_2=Y, d_1=2d, d_2=d, c_1=2c, c_2=c, a_1=a_2=a,\nonumber \\ \alpha _1=2\alpha , \alpha _2=\alpha , b_1=b_2=b, b=6cp^2-6dpv+3ap+3v. \end{aligned}$$

(55)

Now we apply the transformation below for variety of rational solutions

$$\begin{aligned}&Y=2(log g)_\zeta , \end{aligned}$$

(56)

Eq. (56) is inserted into Eq. (51) to generate the following bilinear form,

$$\begin{aligned} 4 c d p \psi ^2 g^2 g^{'''}+2 c \psi ^2 g^2 g^{'''}-4 d^2 v \psi ^2 g^2 g^{'''}+2 d \eta \psi ^2 g^2 g^{'''}-4 a d p^2 g^2 g'+2 a p g^2 g'- 8 c d p^3 g^2 g'\nonumber \\ +8 c d p \psi ^2 g'^3 -12 c d p \psi ^2 g g' g''+4 c \psi ^2 g'^3+4 c p^2 g^2 g'-6 c \psi ^2 g g' g''+8 d^2 p^2 v g^2 g'-8 d^2 v \psi ^2 g'^3\nonumber \\ +12 d^2 v \psi ^2 g g' g''+4 d \eta \psi ^2 g'^3-8 \alpha d p g g'^2-8 d p v g^2 g'-6 d \eta \psi ^2 g g'g''+4 \alpha g g'^2+2 v g^2 g' \end{aligned}$$

(57)

The remaining part of the paper is structured as following:

13 MSRS

For solving MSRS we use the following transformation (Ashraf et al. 2022),

$$\begin{aligned}&g=\sigma _1^2+\sigma _2^2+u_5,\nonumber \\ {}&\sigma _1= u_1\zeta +u_2, \quad \sigma _2=u_3\zeta +u_4, \end{aligned}$$

(58)

inserting Eq. (58) into Eq. (57) and we have some values of parameters

$$\begin{aligned}&u_1=\frac{i \left( u_4^2+u_5\right) \left( a p+2 c p^2-2 d p v+v\right) }{2 (\alpha u_4)}, u_3=-\frac{a p u_4^2+a p u_5+2 c p^2 u_4^2+2 c p^2 u_5-2 d p u_4^2 v-2 d p u_5 v+u_4^2 v+u_5 v}{2 (\alpha u_4)},\nonumber \\ {}&u_2=0, u_4=u_4, u_5=u_5, \end{aligned}$$

(59)

For MSRS of Eqs. (45) and (46) substitute Eq. (59) into Eq. (58) and then put in Eq. (56),

$$\begin{aligned} y_{1}(x,t)=\frac{2 e^{i (-px+vt+\phi )} \left( -\frac{\psi \beta \left( \gamma \right) }{2 \alpha ^2 u_4^2}-\frac{\left( \delta \right) \left( \varpi \right) }{\alpha u_4}\right) }{-\frac{\psi ^2 \beta \left( \gamma \right) ^2}{4 \alpha ^2 u_4^2}+\left( \varpi \right) ^2+u_5}, \end{aligned}$$

(60)

$$\begin{aligned} z_{1}(x,t)=\frac{2 e^{2 i (-px+vt+\phi )} \left( -\frac{\psi \beta \tau }{2 \alpha ^2 u_4^2}-\frac{\left( \delta \right) \left( \varpi \right) }{\alpha u_4}\right) }{-\frac{\psi ^2 \beta \left( \tau \right) ^2}{4 \alpha ^2 u_4^2}+\left( \varpi \right) ^2+u_5}, \end{aligned}$$

(61)

where $\beta = \left( u_4^2+u_5\right) ^2 \left( a p+2 c p^2-2 d p v+v\right) ^2$, $\gamma =x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}$, $\delta =a p u_4^2+a p u_5+2 c p^2 u_4^2+2 c p^2 u_5-2 d p u_4^2 v-2 d p u_5 v+u_4^2 v+u_5 v$, $\tau =x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}$ and $\varpi =u_4-\frac{\psi \left( \delta \right) \tau }{2 \alpha u_4}$.

14 MSR1K

For solving MSR1K we use the following transformation (Ashraf et al. 2022),

$$\begin{aligned}&g=\sigma _1^2+\sigma _2^2+z_1e^{V_1}+u_5,\nonumber \\ {}&\sigma _1= u_1\zeta +u_2, \quad \sigma _2=u_3\zeta +u_4, \nonumber \\&V_1=w_1\zeta +w_2, \end{aligned}$$

(62)

inserting Eq. (62) into Eq. (57) and we have some values of parameters

$$\begin{aligned}&u_1=0, u_2=u_2, u_3=-\frac{3 u_4 \left( a p+2 c p^2-2 d p v+v\right) }{2 \alpha },\nonumber \\ {}&u_4=u_4, u_5=u_5, w_1=0, w_2=w_2, z_1=z_1, \end{aligned}$$

(63)

For MSR1K of Eqs. (45) and (46) substitute Eq. (63) into Eq. (62) and then put in Eq. (56),

$$\begin{aligned} y_{2}(x,t)=-\frac{6 u_4 e^{i (-px+vt+\phi )} \left( a p+2 c p^2-2 d p v+v\right) \left( u_4-\frac{3 u_4 \psi \left( a p+2 c p^2-2 d p v+v\right) \left( x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}\right) }{2 \alpha }\right) }{\alpha \left( \left( u_4-\frac{3 u_4 \psi \left( a p+2 c p^2-2 d p v+v\right) \left( x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}\right) }{2 \alpha }\right) ^2+u_2^2+u_5+e^{w_2} z_1\right) }. \end{aligned}$$

(64)

$$\begin{aligned} z_{2}(x,t)=-\frac{6 u_4 e^{2 i (-px+vt+\phi )} \left( a p+2 c p^2-2 d p v+v\right) \left( u_4-\frac{3 u_4 \psi \left( a p+2 c p^2-2 d p v+v\right) \left( x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}\right) }{2 \alpha }\right) }{\alpha \left( \left( u_4-\frac{3 u_4 \psi \left( a p+2 c p^2-2 d p v+v\right) \left( x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}\right) }{2 \alpha }\right) ^2+u_2^2+u_5+e^{w_2} z_1\right) }. \end{aligned}$$

(65)

15 MSR2K

For solving MSR2K we use the following transformation (Ashraf et al. 2022),

$$\begin{aligned}&g= \sigma _1^2+\sigma _2^2+r_1e^{V_1}+z_2e^{V_2}+u_5,\nonumber \\ {}&\sigma _1=u_1\zeta +u_2, \quad \sigma _2=u_3\zeta +u_4, \nonumber \\ {}&V_1=w_1\zeta +w_2, \quad V_2=w_3\zeta +u_4, \end{aligned}$$

(66)

inserting Eq. (66) into Eq. (57) and we have some values of parameters

$$\begin{aligned}&u_1=0, u_2=u_2, u_3=-\frac{3 u_4 \left( a p+2 c p^2-2 d p v+v\right) }{2 \alpha },\nonumber \\ {}&u_4=u_4, u_5=u_5, w_1=w_1, w_2=w_2, w_3=0, w_4=w_4, z_1=z_1, z_2=z_2, \end{aligned}$$

(67)

For MSR2K of Eqs. (45) and (46) substitute Eq. (66) into Eq. (67) and then put in Eq. (56),

$$\begin{aligned} y_{3}(x,t)=\frac{2 e^{i (-px+vt+\phi )} \left( w_1 z_1 e^{\left( w_1 \psi \left( x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}\right) +w_2\right) }-\frac{3 u_4 \left( a p+2 c p^2-2 d p v+v\right) \left( \varepsilon \right) }{\alpha }\right) }{\left( \varepsilon \right) ^2+z_1 e^{\left( w_1 \psi \left( x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}\right) +w_2\right) }+u_2^2+u_5+e^{w_4} z_2}, \end{aligned}$$

(68)

$$\begin{aligned} z_{3}(x,t)=\frac{2 e^{2 i (-px+vt+\phi )} \left( w_1 z_1 e^{\left( w_1 \psi \left( x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}\right) +w_2\right) }-\frac{3 u_4 \left( a p+2 c p^2-2 d p v+v\right) \left( \varepsilon \right) }{\alpha }\right) }{\left( \varepsilon \right) ^2+z_1 e^{\left( w_1 \psi \left( x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}\right) +w_2\right) }+u_2^2+u_5+e^{w_4} z_2}, \end{aligned}$$

(69)

where $\varepsilon =u_4-\frac{3 u_4 \psi \left( a p+2 c p^2-2 d p v+v\right) \left( x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}\right) }{2 \alpha }$.

16 HBS

For solving HBS we use the following transformation (Ahmed et al. 2019b),

$$\begin{aligned}&g=e^{-u(w_1\zeta +w_2)}+z_1e^{w(u_3\zeta +u_4)}+z_2\cos (u_1(w_5\zeta +w_6)), \end{aligned}$$

(70)

inserting Eq. (70) into Eq. (57) and we have some values of parameters

$$\begin{aligned}&u=\frac{a p+2 c p^2-2 d p v+v}{2 (m w_1)}, u_1=u_1, w_1=w_1, w_2=w_2, w_3=0, w_4=w_4, w_5=w_5, w_6=w_6,\nonumber \\ {}&z_1=0, z_2=0, \end{aligned}$$

(71)

For HBS of Eqs. (45) and (46) substitute Eq. (71) into Eq. (70) and then put in Eq. (56),

$$\begin{aligned} y_{4}(x,t)=-\frac{e^{i (-px+vt+\phi )} \left( a p+2 c p^2-2 d p v+v\right) }{\alpha }. \end{aligned}$$

(72)

$$\begin{aligned} z_{4}(x,t)=-\frac{e^{2 i (-px+vt+\phi )} \left( a p+2 c p^2-2 d p v+v\right) }{\alpha }. \end{aligned}$$

(73)

17 PCRS

For solving PCRS we use the following transformation (Ahmed et al. 2019a),

$$\begin{aligned}&g= \sigma _1^2+\sigma _2^2+z_1\cos (V_1)+z_2\cosh (V_2)+u_5,\nonumber \\ {}&\sigma _1=u_1\zeta +u_2, \quad \sigma _2=u_3\zeta +u_4,\nonumber \\ {}&V_1=w_1\zeta +w_2, \quad V_2=w_3\zeta +w_4, \end{aligned}$$

(74)

inserting Eq. (74) into Eq. (57) and we have some values of parameters:

$$\begin{aligned}&u_1=0, u_2=u_2, u_3=u_3, u_4=\frac{3 \left( \psi ^2 u_3 \left( 2 c d p+c-2 d^2 v+d \eta \right) \right) }{4 (\alpha (2 d p-1))}, u_5=u_5, z_1=0, z_2=0,\nonumber \\ {}&w_1=w_1, w_2=w_2, w_3=\frac{\sqrt{-\frac{-2 a d p^2+a p-4 c d p^3+2 c p^2+4 d^2 p^2 v-4 d p v+v}{2 c d p+c-2 d^2 v+d \eta }}}{\psi }, \end{aligned}$$

(75)

For PCRS of Eqs. (45) and (46) substitute Eq. (75) into Eq. (74) and then put in Eq. (56),

$$\begin{aligned} y_{5}(x,t)=\frac{2 e^{i (-px+vt+\phi )} \left( \frac{z_2 \sqrt{\frac{2 a d p^2-a p+4 c d p^3-2 c p^2-4 d^2 p^2 v+4 d p v-v}{2 c d p+c-2 d^2 v+d \eta }} \sinh \left( \theta \right) }{\psi }+2 u_3 \left( \rho \right) -w_1 z_1\sin \left( \Omega \right) \right) }{z_2 \cosh \left( \theta \right) +\left( \rho \right) ^2+z_1\cos \left( \Omega \right) +u_2^2+u_5}, \end{aligned}$$

(76)

$$\begin{aligned} z_{5}(x,t)=\frac{2 e^{2 i (-px+vt+\phi )} \left( \frac{z_2 \sqrt{\frac{2 a d p^2-a p+4 c d p^3-2 c p^2-4 d^2 p^2 v+4 d p v-v}{2 c d p+c-2 d^2 v+d \eta }} \sinh \left( \theta \right) }{\psi }+2 u_3 \left( \rho \right) -w_1 z_1\sin \left( \Omega \right) \right) }{z_2 \cosh \left( \theta \right) +\left( \rho \right) ^2+z_1\cos \left( \Omega \right) +u_2^2+u_5}, \end{aligned}$$

(77)

where $\theta =\sqrt{\frac{2 a d p^2-a p+4 c d p^3-2 c p^2-4 d^2 p^2 v+4 d p v-v}{2 c d p+c-2 d^2 v+d \eta }} \left( x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}\right) +w_4$ and $\rho =\frac{3 u_3 \psi ^2 \left( 2 c d p+c-2 d^2 v+d \eta \right) }{4 \alpha (2 d p-1)}+u_3 \psi \left( x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}\right)$ and $\Omega =w_1 \psi \left( x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}\right) +w_2$.

18 KCRS

For solving KCRS we use the following transformation (Ahmed et al. 2019a, b),

$$\begin{aligned}&g= e^{-V_1}+z_1e^{V_1}+\sigma _1^2+\sigma _2^2+u_5,\nonumber \\ {}&\sigma _1=u_1\zeta +u_2, \quad \sigma _2=u_3\zeta +u_4, \nonumber \\ {}&V_1=w_1\zeta +w_2, \end{aligned}$$

(78)

inserting Eq. (78) into Eq. (57) and we have some values of parameters

$$\begin{aligned}&u_1=0, u_2=u_2, u_3=-\frac{3 u_4 \left( a p+2 c p^2-2 d p v+v\right) }{2 \alpha }, u_4=u_4, u_5=u_5, z_1=z_1 \\ \nonumber&w_1=0, w_2=w_2, \end{aligned}$$

(79)

For KCRS of Eqs. (45) and (46) substitute Eq. (79) into Eq. (78) and then put in Eq. (56),

$$\begin{aligned} y_{6}(x,t)=-\frac{6 u_4 e^{i (-px+vt+\phi )} \left( a p+2 c p^2-2 d p v+v\right) \left( u_4-\frac{3 u_4 \psi \left( a p+2 c p^2-2 d p v+v\right) \left( x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}\right) }{2 \alpha }\right) }{\alpha \left( \left( u_4-\frac{3 u_4 \psi \left( a p+2 c p^2-2 d p v+v\right) \left( x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}\right) }{2 \alpha }\right) ^2+u+u_2^2+e^{w_2}z_1+e^{-w_2}\right) }. \end{aligned}$$

(80)

$$\begin{aligned} z_{6}(x,t)=-\frac{6 u_4 e^{2 i (-px+vt+\phi )} \left( a p+2 c p^2-2 d p v+v\right) \left( u_4-\frac{3 u_4 \psi \left( a p+2 c p^2-2 d p v+v\right) \left( x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}\right) }{2 \alpha }\right) }{\alpha \left( \left( u_4-\frac{3 u_4 \psi \left( a p+2 c p^2-2 d p v+v\right) \left( x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}\right) }{2 \alpha }\right) ^2+u+u_2^2+e^{w_2}z_1+e^{-w_2}\right) }. \end{aligned}$$

(81)

19 MSPK

For solving MSPK we use the following transformation (Ahmed et al. 2019b),

$$\begin{aligned}&g= \sigma _1^2+\sigma _2^2++z_1\cos (V_1)+z_2e^{V_2}+u_5,\nonumber \\&\sigma _1=u_1\zeta +u_2, \quad \sigma _2=u_3\zeta +u_4, \nonumber \\ {}&V_1=w_1\zeta +w_2,\quad V_2=w_3\zeta +w_4, \end{aligned}$$

(82)

inserting Eq. (82) into Eq. (57) and we have some values of parameters:

$$\begin{aligned}&u_1=0, u_2=u_2, u_3=u_3, u_4=\frac{3 \psi ^2 u_3 \left( 2 c d p+c-2 d^2 v+d \eta \right) }{4 (\alpha (2 d p-1))}, u_5=u_5, \nonumber \\ {}&w_1=\frac{\sqrt{-\frac{2 a d p^2-a p+4 c d p^3-2 c p^2-4 d^2 p^2 v+4 d p v-v}{2 c d p+c-2 d^2 v+d \eta }}}{\psi }, w_3=w_3, w_4=w_4, w_2=w_2 z_1=z_1, z_2=z_2, \end{aligned}$$

(83)

For MSPK of Eqs. (45) and (46) substitute Eq. (83) into Eq. (82) and then put in Eq. (56),

$$\begin{aligned} y_{7}(x,t)=\frac{2 e^{i (-px+vt+\phi )} \left( \Gamma +2u_3 \left( \frac{3u_3 \psi ^2 \left( 2 c d p+c-2 d^2 v+d \eta \right) }{4 \alpha (2 d p-1)}+u_3 \psi \left( x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}\right) \right) +w_3 z_2 e^\Theta \right) }{z_1 \cos \left( \xi \right) +\left( \frac{3u_3 \psi ^2 \left( 2 c d p+c-2 d^2 v+d \eta \right) }{4 \alpha (2 d p-1)}+u_3 \psi \left( x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}\right) \right) ^2+z_2 e^\Theta +u_2^2+u_5}, \end{aligned}$$

(84)

$$\begin{aligned} z_{7}(x,t)=\frac{2 e^{2 i (-px+vt+\phi )} \left( \Gamma +2u_3 \left( \frac{3u_3 \psi ^2 \left( 2 c d p+c-2 d^2 v+d \eta \right) }{4 \alpha (2 d p-1)}+u_3 \psi \left( x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}\right) \right) +w_3 z_2 e^\Theta \right) }{z_1 \cos \left( \xi \right) +\left( \frac{3u_3 \psi ^2 \left( 2 c d p+c-2 d^2 v+d \eta \right) }{4 \alpha (2 d p-1)}+u_3 \psi \left( x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}\right) \right) ^2+z_2 e^\Theta +u_2^2+u_5}, \end{aligned}$$

(85)

where $\xi =\sqrt{\frac{-2 a d p^2+a p-4 c d p^3+2 c p^2+4 d^2 p^2 v-4 d p v+v}{2 c d p+c-2 d^2 v+d \eta }} \left( x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}\right) +w_2$ and

$\Gamma =-\frac{z_1 \sqrt{\frac{-2 a d p^2+a p-4 c d p^3+2 c p^2+4 d^2 p^2 v-4 d p v+v}{2 c d p+c-2 d^2 v+d \eta }} \sin \left( \xi \right) }{\psi }$ and $\Theta =w_3 \psi \left( x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}\right) +w_4+u_2^2+u_5$.

20 MSRK

For solving MSRK we use the following transformation (Seadawy et al. 2021; Manafian et al. 2020),

$$\begin{aligned}&g= \sigma _1^2+\sigma _2^2++z_1\cosh (V_1)+z_2e^{V_2}+u_5,\nonumber \\ {}&\sigma _1=u_1\zeta +u_2, \quad \sigma _2=u_3\zeta +u_4, \nonumber \\ {}&V_1=w_1\zeta +w_2,\quad V_2=w_3\zeta +w_4, \end{aligned}$$

(86)

inserting Eq. (86) into Eq. (57) and we have some values of parameters:

$$\begin{aligned}&u_1=0, u_2=u_2, u_3=u_3, u_4=\frac{3 \left( \psi ^2 u_3 \left( 2 c d p+c-2 d^2 v+d \eta \right) \right) }{4 (\alpha (2 d p-1))}, u_5=u_5, \\ \nonumber&w_1=\frac{\sqrt{-\frac{-2 a d p^2+a p-4 c d p^3+2 c p^2+4 d^2 p^2 v-4 d p v+v}{2 c d p+c-2 d^2 v+d \eta }}}{\psi }, w_3=w_3, w_4=w_4, w_2=w_2 z_1=z_1, z_2=z_2, \end{aligned}$$

(87)

For MSRK of Eqs. (45) and (46) insert Eq. (87) into Eq. (86) and then put in Eq. (56),

$$\begin{aligned} y_{8}(x,t)=\frac{2 e^{i (-px+vt+\phi )} \left( \frac{z_1 \sqrt{\frac{2 a d p^2-a p+4 c d p^3-2 c p^2-4 d^2 p^2 v+4 d p v-v}{2 c d p+c-2 d^2 v+d \eta }} \sinh \left( \Phi \right) }{\psi }+2 u_3 \left( \Delta \right) +w_3 z_2 e^{\omega }\right) }{z_1 \cosh \left( \Phi \right) +\left( \Delta \right) ^2+z_2 e^{\omega }+u_2^2+u_5}, \end{aligned}$$

(88)

$$\begin{aligned} z_{8}(x,t)=\frac{2 e^{2 i (-px+vt+\phi )} \left( \frac{z_1 \sqrt{\frac{2 a d p^2-a p+4 c d p^3-2 c p^2-4 d^2 p^2 v+4 d p v-v}{2 c d p+c-2 d^2 v+d \eta }} \sinh \left( \Phi \right) }{\psi }+2 u_3 \left( \Delta \right) +w_3 z_2 e^{\omega }\right) }{z_1 \cosh \left( \Phi \right) +\left( \Delta \right) ^2+z_2 e^{\omega }+u_2^2+u_5}, \end{aligned}$$

(89)

where $\Phi =\sqrt{\frac{2 a d p^2-a p+4 c d p^3-2 c p^2-4 d^2 p^2 v+4 d p v-v}{2 c d p+c-2 d^2 v+d \eta }} \left( x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}\right) +w_2$, $\Delta =\frac{3 u_3 \psi ^2 \left( 2 c d p+c-2 d^2 v+d \eta \right) }{4 \alpha (2 d p-1)}+u_3 \psi \left( x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}\right)$ and $\omega =w_3 \psi \left( x-\frac{t (4 c p-2 d v+\eta )}{2 d p-1}\right) +w_4$.

21 Stability

Now using Hamiltonian method $\Gamma$ framework, we examine the stability (Khater 2019),

$$\begin{aligned} \Gamma _1 =\frac{1}{2} \int \limits _{ - p}^p {{y^2}\left( x \right) dx} \quad \Gamma _2 =\frac{1}{2} \int \limits _{ - p}^p {{z^2}\left( x \right) dx}, \end{aligned}$$

(90)

Now we verify the stability as

$$\begin{aligned} \frac{{\partial \Gamma _{j}}}{{\partial c}} > 0 \end{aligned}$$

(91)

where $\Gamma _j$ (j=1,2) and c represented as momentum and velocity respectively (Figs. 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31,32, 33,34, 35 and 36). Hamiltonian system provides the stability condition, all solutions we got through this condition is given by (Table 1), ,

Table 1 Stability $y_{i}(x,t)$ and $z_{i}(x,t)$ where $(i = 1, 2, 3, ..., 8.)$

Fig. 21

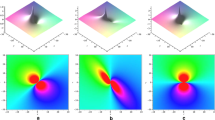
Graphical representation of solution $y_{1}(x,t)$ in Eq. (60) are presented via $a=2, \alpha =0.8, c=0.01, d=-4, \eta =2, p=5, u=2, u_2=0.06, u_3=-0.03, u_4=-0.9, u_5=5, v=0.3, w_2=5, w_3=3, w_4=-7, \psi =8, z_1=0.9, z_2=-5, \phi =0.5$, (a) 3D plot (b) 2D plot (c) density plot and (d) stream plot respectively

Fig. 22

Graphical representation of solution $z_{1}(x,t)$ in Eq. (61) are presented via $a=2, \alpha =0.8, c=0.01, d=-4, \eta =2, p=5, u=2, u_2=0.06, u_3=-0.03, u_4=-0.9, u_5=5, v=0.3, w_2=5, w_3=3, w_4=-7, \psi =8, z_1=0.9, z_2=-5, \phi =0.5$

Fig. 23

Graphical representation of solution $y_{2}(x,t)$ in Eq. (64) are presented via $a=-2, \alpha =-0.2, c=10, d=0.4, \eta =5, p=1.5, u=-2, u_2=0.6, u_3=-3, u_4=1.9, u_5=-0.5, v=-3, w_2=1.5, w_3=0.03, w_4=-0.7, \psi =-0.8, z_1=-0.1, z_2=5, \phi =15$

Fig. 24

Graphical representation of solution $z_{2}(x,t)$ in Eq. (65) are presented via $a=-2, \alpha =-0.2, c=10, d=0.4, \eta =5, p=1.5, u=-2, u_2=0.6, u_3=-3, u_4=1.9, u_5=-0.5, v=-3, w_2=1.5, w_3=0.03, w_4=-0.7, \psi =-0.8, z_1=-0.1, z_2=5, \phi =15$

Fig. 25

Graphical representation of solution $y_{3}(x,t)$ in Eq. (68) are presented via $a=-2.4, \alpha =-0.2, c=1.7, d=2.4, \eta =5.5, p=6.5, u=2.5, u_2=-0.6, u_3=-0.03, u_4=-1.9, u_5=0.5, v=-3.9, w_1=0.4, w_2=1.05, w_3=3.7, w_4=0.7, \psi =0.08, z_1=0.01, z_2=-3, \phi =1.05$

Fig. 26

Graphical representation of solution $z_{3}(x,t)$ in Eq. (69) are presented via $a=-2.4, \alpha =-0.2, c=1.7, d=2.4, \eta =5.5, p=6.5, u=2.5, u_2=-0.6, u_3=-0.03, u_4=-1.9, u_5=0.5, v=-3.9, w_1=0.4, w_2=1.05, w_3=3.7, w_4=0.7, \psi =0.08, z_1=0.01, z_2=-3, \phi =1.05$

Fig. 27

Graphical representation of solution $y_{4}(x,t)$ in Eq. (72) are presented via $a=5, \alpha =-0.5, c=0.3, d=2, p=3, v=0.5, \phi =0.2$

Fig. 28

Graphical representation of solution $z_{4}(x,t)$ in Eq. (73) are presented via $a=5, \alpha =-0.5, c=0.3, d=2, p=3, v=0.5, \phi =0.2$

Fig. 29

Graphical representation of solution $y_{5}(x,t)$ in Eq. (77) are presented via $u_5=7.5, a=4, \alpha =-0.2, c=-6.7, d=2.5, \eta =-5.5, p=-5, u=2, u_2=-0.06, u_3=-3, u_4=-1, v=0.09, w_1=4, w_2=7, w_3=3.7, w_4=-0.7, \psi =8, z_1=-1, z_2=3, \phi =5$

Fig. 30

Graphical representation of solution $z_{5}(x,t)$ in Eq. (77) are presented via $u_5=7.5, a=4, \alpha =-0.2, c=-6.7, d=2.5, \eta =-5.5, p=-5, u=2, u_2=-0.06, u_3=-3, u_4=-1, v=0.09, w_1=4, w_2=7, w_3=3.7, w_4=-0.7, \psi =8, z_1=-1, z_2=3, \phi =5$

Fig. 31

Graphical representation of solution $y_{6}(x,t)$ in Eq. (80) are presented via $a=0.5, alpha =0.08, c=0.2, d=-0.4, \eta =0.2, p=0.5, u=-2, u_2=0.6, u_4=-0.4, v=-0.3, w_2=7, \psi =-0.5, z_1=0.9, \phi =3$

Fig. 32

Graphical representation of solution $z_{6}(x,t)$ in Eq. (81) are presented via $a=0.5, alpha =0.08, c=0.2, d=-0.4, \eta =0.2, p=0.5, u=-2, u_2=0.6, u_4=-0.4, v=-0.3, w_2=7, \psi =-0.5, z_1=0.9, \phi =3$

Fig. 33

Graphical representation of solution $y_{7}(x,t)$ in Eq. (84) are presented via $a=0.5, \alpha =8, c=0.2, d=0.4, \eta =-2, p=-3, u=-2, u_2=-0.6, u_3=-0.3, u_4=0.7, u_5=-8, v=-3, w_2=5, w_3=-0.3, w_4=-7, \psi =-0.5, z_1=-0.9, z_2=-5, \phi =5$

Fig. 34

Graphical representation of solution $z_{7}(x,t)$ in Eq. (85) are presented via $a=0.5, \alpha =8, c=0.2, d=0.4, \eta =-2, p=-3, u=-2, u_2=-0.6, u_3=-0.3, u_4=0.7, u_5=-8, v=-3, w_2=5, w_3=-0.3, w_4=-7, \psi =-0.5, z_1=-0.9, z_2=-5, \phi =5$

Fig. 35

Graphical representation of solution $y_{8}(x,t)$ in Eq. (88) are presented via $a=-0.5, \alpha =8, c=0.2, d=0.4, \eta =-2, p=5, u=-2, u_2=0.6, u_3=-0.3, u_4=0.4, u_5=8, v=0.3, w_2=5, w_3=0.3, w_4=7, \psi =-0.5, z_1=-0.9, z_2=-5, \phi =3$

Fig. 36

Graphical representation of solution $z_{8}(x,t)$ in Eq. (89) are presented via $a=-0.5, \alpha =8, c=0.2, d=0.4, \eta =-2, p=5, u=-2, u_2=0.6, u_3=-0.3, u_4=0.4, u_5=8, v=0.3, w_2=5, w_3=0.3, w_4=7, \psi =-0.5, z_1=-0.9, z_2=-5, \phi =3$

22 Results and discussion

By establishing the proper values for the parameters, we were able to successfully generate the desired type of solutions which express wave discrepancy. Take note of Figs. 1 and 2 which presents bright soliton solution for Eq. (7–8) by using appropriate values for parameters. In Figs. (a) 3D plot (b) 2D plot and (c) contour plot respectively. We get some multiple bright soliton graph for Eq. (11-12) by using the values $a_1=1.5, b_1=7, d_1=0.9, k_2=0.5, k_5=0.2, k_6=-4, k_7=-2, n_1=2.2, s=0.05$ in Figs. 3 and 4. The geometrical structures of lump wave soliton solutions are presented in Figs. 4, 5, 6, 7, 8, 9 and 10 for various values for parameters. Figures 13, 14, 15, 16, 17, 18, 19 and 20 shows kink type LSS for different values of parameters. We have computed M-shaped graphs for $y_1(x,t)$ and $z_1(x,t)$ with values $a=2, \alpha =0.8, c=0.01, d=-4, \eta =2, p=5, u=2, u_2=0.06, u_3=-0.03, u_4=-0.9, u_5=5, v=0.3, w_2=5, w_3=3, w_4=-7, \psi =8, z_1=0.9, z_2=-5, \phi =0.5$ in Figs. 21 and 22, (a) 3D plot (b) 2D plot (c) density plot and (d) stream plot respectively. Figures 23 and 24 represented graph of M-shaped with one and two kinks. We have attained the breather for $y_4(x,t)$ and $z_4(x,t)$ with values $a=5, \alpha =-0.5, c=0.3, d=2, p=3, v=0.5, \phi =0.2$ in Figs. 27 and 28. We also obtained some M-shaped interaction with periodic, rogue and kink profiles are presented in Figs. 29, 30, 31, 32, 33, 34, 35 and 36.

23 Conclusion

In this paper, we explored distinct solutions for NLSE-QNS such as multi, rogue and periodic waves. we have investigated lump with kink, lump periodic and kink, breather lump, homoclinic breather. We also categorised MSRS, MSRS with one and two kink, HBS, PCRS, KCRS, MSPK and MSRK. Additionally, we also manipulated their stability. We discovered by HS properties that $y_i(x,y)$, $z_j(x,y)$ where ($i=2,4,7$) and ($j=1,2$) to be stable solutions.