1 Introduction

The mathematical models of the nonlinear physical phenomena are illustrated explicitly by the nonlinear evaluation equations (NLEEs) that have a significant influence on the investigation of nonlinear sciences. So, recently, obtaining exact soliton solutions to NLEEs with the help of computer programs that make repetitious and monotonous mathematical computations easier, has been a marvelous field for analysts and researchers. NLEEs play out an extraordinary part in depicting the actual behavior of real phenomena and dynamical processes in fluid mechanics, optical fibers, material science, geochemistry, ocean engineering, geophysics, mathematical physics, plasma physical science, and numerous other logical regions. Nonlinear science is one of the best astonishing fields for investigators in this bleeding-edge season of science. To track down the analytically or exact results has been the focal point of researchers because of its fundamental commitment to examine the genuine element of the frameworks. As we all know, scholars have devised several methodologies and mathematical tools to aid in the discovery of exact solutions to NLEEs, and each method is tailored to a certain sort of solution (Al-Ghafri 2018; Lu et al. 2019; Ali et al. 2018; Younis et al. 2020; Bulut et al. 2017; Arshad et al. 2020; Sulaiman and Bulut 2019, 2020; Aslan and Inc 2017a, b; Aslan et al. 2017; Inc 2017; Inc et al. 2016; Barman et al. 2021; Hosseini et al. 2020; Kumar et al. 2021; Ding et al. 2019; Chen et al. 2021; Raza et al. 2020; Bilal et al. 2021b).

Moreover, solitons are stable, efficient, self-restricted, and persistent solitary waves that do not disperse and retain their individuality as they pass through a medium. The fundamental perception about a soliton was shaped by Russell in 1844, attributable to a serendipitous idea in 1834 on the Edinburgh–Glasgow Canal. He named it the “wave of translation”. In acknowledgment of its single pulse form, this phenomenon was later named as a solitary wave. In this way, Boussinesq and Rayleigh, were between the preeminent specialists who executed hypothetical contemplation of a solitary wave. From that point forward, the Solitary wave’s examination has mounted to a prime field of examinations of solitary waves. The stable, powerful, self-restricted and enduring solitary waves which do not scatter and maintain their uniqueness as they travel in a medium- are ubiquitous in nature are refereed to solitons and nonlinear wave excitation. Solitons in fact the result of non-linearity (a tendency to increase the wave slope) and dispersion (the wave attentive tendency). They emerge in numerous crucial areas of technology and physics from high-piece rate media communications and controllable soliton super-continuum generation in ultra-fast photonics, condensed matter, and plasma physical science to elementary particle physics, cosmology, and oceanic monster (rogue) waves as well as Bose–Einstein condensates. Due to its Galilean symmetry the soliton is characterized by its own de Broglie wavelength analogue as the self-localized wave entity. On the other hand, the soliton as an extended particle-like entity, due to nonlinear self-interaction, becomes a bound state in its own self-induced trapping potential and as a result, possesses negative self-interaction (binding) energy. Ones may obtain the information about the form and the shape of the solitons. The structural stability of the solitons and in the same way as nuclear binding energy, the degree to which the quasi particles that make up the soliton are tightly bound together can be considered (Russell 1844; Nguepjouo et al. 2014). Furthermore, different authors studied via various schemes to search the exact traveling wave solution of the NLEEs. In published work various computational techniques have been applied to discuss the exact solutions such as, the \((G^{\prime }/G\))-expansion method (Kazi Sazzad Hossain et al. 2017), the anstaz approach (Shi and Zhang 2020), the trial equation technique (Yildirim 2019), the adomian decomposition method (Malaikah 2020), the variation iteration method (VIM) (Anjum and He 2019), the modified \(\exp (-\varPhi (\zeta ))\)-expansion method (Baskonus et al. 2016), the direct algebraic method (Seadawy al. 2019), the extended Fan sub-equation method (Osman et al. 2020), the F-expansion technique (Seadawy et al. 2020), the generalized exponential rational function method (Ghanbari et al. 2019), new \(\varPhi ^{6}\)-model expansion method (Seadawy et al. 2021) and several others (Mahak and Akram 2019; Gaber et al. 2019; Chen et al. 2020; Dusunceli et al. 2021; Younis et al. 2017; Tian 2020; Ilie et al. 2018; Bilal et al. 2021d; Younas and Ren 2021; Inc and Kilic 2017; Kilic and Inc 2017; Tchier et al. 2016a, b, 2017a, b, c; Osman and Ali 2020; Malik et al. 2021; Tahir et al. 2021; Kayum et al. 2021; Ali et al. 2020; Osman 2017; Osman et al. 2018).

The key idea of this study is to conceive a variety of soliton solutions in the (2 + 1)-dimensional soliton equation by employing three analytical methods. In this article we will consider the (2 + 1)-dimensional soliton equation given by Chowdhury et al. (2021)

$$\begin{aligned}&i \varPsi _{t}+\varPsi _{xx}+\varPsi \varPhi =0, \nonumber \\&\varPhi _{t}+\varPhi _{y}+\left( \varPsi \varPsi ^{*}\right) _{x}=0, \end{aligned}$$
(1)

where \(*\) represents the complex conjugate. The real and imaginary functions are \(\varPhi =\varPhi (x,y,t)\), and \(\varPsi =\varPsi (x,y,t)\) respectively. Here x, y and t represent the spatial domains and time respectively. The governing equation is similar to integrable Zakharov equation in plasma physics which shows the significant role in several physical applications and governs the behavior of weakly nonlinear ion-acoustic waves in a plasma. The physically most important example involves the interaction between the Langmuir and ion-acoustic waves in plasmas. So far many studies for the (2 + 1)-dimensional soliton have been done in literature, for detail see refrences Ye and Zhang (2011), Maccari (1996), Porsezian (1997), Yan (2002) and Darvishi et al. (2016). The authors attained a few solutions of the above equation. The more effective, novel solitary wave solutions of the given model will be achieved via three proposed methods. The discovered solutions are novel and have potential applications in nonlinear sciences.

The content of this manuscript is summarized as follows: Extraction of soliton solutions is given in Sect. 2. The results and discussion along with the graphical representation are presented in Sect. 3. The conclusion is revealed in Sect. 4.

2 Extraction of soliton solutions

In this section, the application of the proposed methods are utilized for Eq. (1) to establish the new soliton solutions. Suppose the following traveling wave transformation:

$$\begin{aligned} \begin{aligned} \varPsi (x,y,t)=H(\zeta )e^{i\theta },\, \,\varPhi (x,y,t)=G(\zeta ) \,\, \theta =lx+py+ct, \, \, \zeta =L(x+Py - 2lt), \end{aligned} \end{aligned}$$
(2)

where l, p, c, L and P are constants; \(H(\zeta )\) and \(G(\zeta )\) represent real functions. By inserting Eq. (2) into Eq. (1), we attain,

$$\begin{aligned}&L^{2} H^{\prime \prime }(\zeta )-(c+l^{2}) H(\zeta )+H(\zeta ) G(\zeta )=0. \end{aligned}$$
(3)
$$\begin{aligned}&(P-2l) G'(\zeta )+ (H^{2}(\zeta ))' =0. \end{aligned}$$
(4)

By integrating Eq. (4), we obtain

$$\begin{aligned} \begin{aligned} G(\zeta )= \frac{H^{2}(\zeta )}{(P-2l)}+a, \end{aligned} \end{aligned}$$
(5)

where a is the constant of the integration and \(P\ne 2l\). Substituting Eq. (5) into Eq. (4), we get

$$\begin{aligned} \begin{aligned} \frac{ \left( a-c-l^{2}\right) }{L^{2}}H(\zeta )-\frac{1}{L^{2} (P-2 l)}H^{3}(\zeta )+H^{\prime \prime }(\zeta )=0. \end{aligned} \end{aligned}$$
(6)

2.1 Solutions via extended ShGEEM

In this subsection, extended ShGEEM (Bilal et al. 2021a) is employed. The homogeneous balance between the linear term \(H^{\prime \prime }\) and the non-linear term \(H^{3}\) to determine the value of m in Eq. (6), yields \(m=1\). The solution of Eq. (6), becomes

$$\begin{aligned} H(\varpi )= \,& {} \delta _{1}\sinh (\varpi )+\beta _{1}\cosh (\varpi )+\beta _{0}, \end{aligned}$$
(7)
$$\begin{aligned} H(\zeta )=\, & {} \pm \, \delta _{1}\;i\;{\text{sech}}(\zeta )\pm \, \beta _{1}\tanh (\zeta )+\beta _{0}, \end{aligned}$$
(8)
$$\begin{aligned} H(\zeta )=\, & {} \pm \, \delta _{1}\;{\text{csch}}(\zeta )\pm \, \beta _{1}\coth (\zeta )+\beta _{0}. \end{aligned}$$
(9)

Substituting Eq. (7) and its second derivative along with \(\varpi ^{\prime }=\sinh (\varpi )\) and/or \(\varpi ^{\prime }=\cosh (\varpi )\) into Eq. (6), formulate a polynomial in terms of hyperbolic functions. A system of strategic equations is attained by collecting the coefficients of same power of the hyperbolic function and equating each summation to zero. Furthermore, by using Mathematica, solving the system of strategic equations for the values of the coefficients involved. Yields the solution sets as follows.

$$\begin{aligned}&{\mathbf{Set-1}}:\quad \beta _{0}=0,\;\beta _{1}=0,\;\delta _{1}=\sqrt{2 L^{2} (P-2 l)},\;c=a-l^{2}+L^{2}.\\&{\mathbf{Set-2}}:\quad \beta _{0}=0,\;\beta _{1}=\frac{\sqrt{L^{2} (P-2 l)}}{\sqrt{2}},\;\delta _{1}=\frac{\sqrt{L^{2} (P-2 l)}}{\sqrt{2}},\;c=a-l^{2}-\frac{L^{2}}{2}.\\&{\mathbf{Set-3}}:\quad \beta _{0}=0,\; \beta _{1}=\sqrt{2 L^{2} (P-2 l)},\; \delta _{1}=0,\; c=a-l^{2}-2 L^{2}.\\&{\mathbf{Set-4}} :\quad \beta _{0}=0,\; \beta _{1}=-\frac{\sqrt{L^{2} (P-2 l)}}{\sqrt{2}},\;\delta _{1}=\frac{\sqrt{L^{2} (P-2 l)}}{\sqrt{2}},\;c=a-l^{2}-\frac{L^{2}}{2}. \end{aligned}$$

For Set-1:

$$\begin{aligned} \beta _{0}=0,\;\beta _{1}=0,\;\delta _{1}=\sqrt{2 L^{2} (P-2 l)},\;c=a-l^{2}+L^{2}. \end{aligned}$$

Bright and singular solitons can be constructed as

$$\begin{aligned} \varPsi _{1}(x,y, t)= &\, {} \left( i \sqrt{2} \sqrt{L^{2} (P-2 l)} {\text{sech}}(L (-2 l t+P y+x))\right) \times e^{i(lx+py+ct)}. \end{aligned}$$
(10)
$$\begin{aligned} \varPhi _{1}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( i \sqrt{2} \sqrt{L^{2} (P-2 l)} {\text{sech}}(L (-2 l t+P y+x))\right) ^{2}+a. \end{aligned}$$
(11)
$$\begin{aligned} \varPsi _{2}(x,y, t)= \, & {} \left( \sqrt{2} \sqrt{L^{2} (P-2 l)} {\text{csch}}(L (-2 l t+P y+x))\right) \times e^{i(lx+py+ct)}. \end{aligned}$$
(12)
$$\begin{aligned} \varPhi _{2}(x,y,t)= \, & {} \frac{1}{(2 l-P)}\left( \sqrt{2} \sqrt{L^{2} (P-2 l)} {\text{csch}}(L (-2 l t+P y+x))\right) ^{2}+a. \end{aligned}$$
(13)

For Set-2:

$$\begin{aligned} \beta _{0}=0,\;\beta _{1}=\frac{\sqrt{L^{2} (P-2 l)}}{\sqrt{2}},\;\delta _{1}=\frac{\sqrt{L^{2} (P-2 l)}}{\sqrt{2}},\;c=a-l^{2}-\frac{L^{2}}{2}. \end{aligned}$$

We formulate bell shaped-shock wave and combo singular soliton, respectively.

$$\begin{aligned} \varPsi _{3}(x,y, t)= \, & {} \left( \frac{\sqrt{L^{2} (P-2 l)} \tanh (L (-2 l t+P y+x))}{\sqrt{2}}+\frac{i \sqrt{L^{2} (P-2 l)} {\text{sech}}(L (-2 l t+P y+x))}{\sqrt{2}}\right) \times e^{i(lx+py+ct)}. \end{aligned}$$
(14)
$$\begin{aligned} \varPhi _{3}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( \frac{\sqrt{L^{2} (P-2 l)} \tanh (L (-2 l t+P y+x))}{\sqrt{2}}+\frac{i \sqrt{L^{2} (P-2 l)} {\text{sech}}(L (-2 l t+P y+x))}{\sqrt{2}}\right) ^{2}+a. \end{aligned}$$
(15)
$$\begin{aligned} \varPsi _{4}(x,y, t)=\, & {} \left( \frac{\sqrt{L^{2} (P-2 l)} \coth (L (-2 l t+P y+x))}{\sqrt{2}}+\frac{\sqrt{L^{2} (P-2 l)} {\text{csch}}(L (-2 l t+P y+x))}{\sqrt{2}}\right) \times e^{i(lx+py+ct)}. \end{aligned}$$
(16)
$$\begin{aligned} \varPhi _{4}(x,y,t)= \, & {} \frac{1}{(2 l-P)}\left( \frac{\sqrt{L^{2} (P-2 l)} \coth (L (-2 l t+P y+x))}{\sqrt{2}}+\frac{\sqrt{L^{2} (P-2 l)} {\text{csch}}(L (-2 l t+P y+x))}{\sqrt{2}}\right) ^{2}+a. \end{aligned}$$
(17)

For Set-3:

$$\begin{aligned} \beta _{0}=0,\;\beta _{1}=\sqrt{2 L^{2} (P-2 l)},\;\delta _{1}=0,\;c=a-l^{2}-2 L^{2}. \end{aligned}$$

We attain shock wave and singular soliton, respectively.

$$\begin{aligned} \varPsi _{5}(x,y,t)=\, & {} \left( -\sqrt{2} \sqrt{L^{2} (P-2 l)} \tanh (L (-2 l t+P y+x))\right) \times e^{i(lx+py+ct)}. \end{aligned}$$
(18)
$$\begin{aligned} \varPhi _{5}(x,y,t)= & {} \frac{1}{(2 l-P)}\left( -\sqrt{2} \sqrt{L^{2} (P-2 l)} \tanh (L (-2 l t+P y+x))\right) ^{2}+a. \end{aligned}$$
(19)
$$\begin{aligned} \varPsi _{6}(x,y, t)=\, & {} \left( \sqrt{2} \sqrt{L^{2} (P-2 l)} \coth (L (-2 l t+P y+x))\right) \times e^{i(lx+py+ct)}. \end{aligned}$$
(20)
$$\begin{aligned} \varPhi _{6}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( \sqrt{2} \sqrt{L^{2} (P-2 l)} \coth (L (-2 l t+P y+x))\right) ^{2}+a. \end{aligned}$$
(21)

For Set-4:

$$\begin{aligned} \beta _{0}=0,\;\beta _{1}=-\frac{\sqrt{L^{2} (P-2 l)}}{\sqrt{2}},\;\delta _{1}=\frac{\sqrt{L^{2} (P-2 l)}}{\sqrt{2}},\;c=a-l^{2}-\frac{L^{2}}{2}. \end{aligned}$$

We formulate bell shaped-shock wave and combo singular soliton, respectively.

$$\begin{aligned} \varPsi _{7}(x,y, t)=\, & {} \left( -\frac{\sqrt{L^{2} (P-2 l)} \tanh (L (-2 l t+P y+x))}{\sqrt{2}}+\frac{i \sqrt{L^{2} (P-2 l)} {\text{sech}}(L (-2 l t+P y+x))}{\sqrt{2}}\right) \nonumber \\&\times e^{i(lx+py+ct)}. \end{aligned}$$
(22)
$$\begin{aligned} \varPhi _{7}(x,y,t)= \,& {} \frac{1}{(2 l-P)}\left( -\frac{\sqrt{L^{2} (P-2 l)} \tanh (L (-2 l t+P y+x))}{\sqrt{2}}+\frac{i \sqrt{L^{2} (P-2 l)} {\text{sech}}(L (-2 l t+P y+x))}{\sqrt{2}}\right) ^{2}+a. \end{aligned}$$
(23)
$$\begin{aligned} \varPsi _{8}(x,y, t)= \,& {} \left( \frac{\sqrt{L^{2} (P-2 l)} {\text{csch}}(L (-2 l t+P y+x))}{\sqrt{2}}-\frac{\sqrt{L^{2} (P-2 l)} \coth (L (-2 l t+P y+x))}{\sqrt{2}}\right) \times e^{i(lx+py+ct)}. \end{aligned}$$
(24)
$$\begin{aligned} \varPhi _{8}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( \frac{\sqrt{L^{2} (P-2 l)} {\text{csch}}(L (-2 l t+P y+x))}{\sqrt{2}}-\frac{\sqrt{L^{2} (P-2 l)} \coth (L (-2 l t+P y+x))}{\sqrt{2}}\right) ^{2}+a. \end{aligned}$$
(25)

2.2 Solutions via extended rational sine–cosine method (Rehman et al. 2020)

By applying balance rule in above Eq. (6), we have n = 1, the proposed method has the solution to Eq. (6) as follows:

$$\begin{aligned} H(\zeta )=\frac{\alpha _{0}\sin (\rho \zeta )}{\alpha _{2}+\alpha _{1}\cos (\rho \zeta )}. \end{aligned}$$
(26)

Plugging Eq. (26) along its derivative into Eq. (6) and by equating the coefficients of each powers of \(\cos (\rho \zeta )^{m}\) to 0, we seek the following nonlinear equations. On the above system of equations through symbolic equation solver Mathematica, we secure the solution sets as follows:

$$\begin{aligned}&{\mathbf{Set-1}}:\quad \rho =\frac{\sqrt{-a+c+l^{2}}}{\sqrt{2} L},\;\alpha _{0}=\pm \, \alpha _{1} \sqrt{2 l-P} \sqrt{a-c-l^{2}},\; \alpha _{1}=\alpha _{1},\; \alpha _{2}=0. \\&{\mathbf{Set-2}}:\quad \rho =\frac{\sqrt{2} \sqrt{-a+c+l^{2}}}{L},\; \alpha _{0}=\pm \, \alpha _{1} \sqrt{2 l-P} \sqrt{a-c-l^{2}},\; \alpha _{1}=\alpha _{1},\; \alpha _{2}=\pm \, \alpha _{1}. \end{aligned}$$

Periodic solutions for the Eq. (1) corresponding to set 1 can be formulated as:

$$\begin{aligned} \varPsi _{1,1}(x,y,t)=\, & {} \sqrt{2 l-P} \sqrt{a-c-l^{2}} \tan \left( \frac{\sqrt{-a+c+l^{2}} (-2 l t+P y+x)}{\sqrt{2}}\right) \times e^{i(lx+py+ct)}. \end{aligned}$$
(27)
$$\begin{aligned} \varPhi _{1,1}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( \sqrt{2 l-P} \sqrt{a-c-l^{2}} \tan \left( \frac{\sqrt{-a+c+l^{2}} (-2 l t+P y+x)}{\sqrt{2}}\right) \right) ^{2}+a. \end{aligned}$$
(28)
$$\begin{aligned} \varPsi _{1,2}(x,y,t)=\, & {} -\sqrt{2 l-P} \left( \sqrt{a-c-l^{2}}\right) \tan \left( \frac{\sqrt{-a+c+l^{2}} (-2 l t+P y+x)}{\sqrt{2}}\right) \times e^{i(lx+py+ct)}. \end{aligned}$$
(29)
$$\begin{aligned} \varPhi _{1,2}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( -\sqrt{2 l-P} \left( \sqrt{a-c-l^{2}}\right) \tan \left( \frac{\sqrt{-a+c+l^{2}} (-2 l t+P y+x)}{\sqrt{2}}\right) \right) ^{2}+a. \end{aligned}$$
(30)

Similarly, mixed periodic solutions for Eq. (1) corresponding to set 2 can be constructed as:

$$\begin{aligned} \varPsi _{2,1}(x,y,t)=\, & {} \frac{\sqrt{2 l-P} \sqrt{a-c-l^{2}} \sin \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) }{\cos \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) +1}\times e^{i(lx+py+ct)}. \end{aligned}$$
(31)
$$\begin{aligned} \varPhi _{2,1}(x,y,t)= & {} \frac{1}{(2 l-P)}\left( \frac{\sqrt{2 l-P} \sqrt{a-c-l^{2}} \sin \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) }{\cos \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) +1}\right) ^{2}+a. \end{aligned}$$
(32)
$$\begin{aligned} \varPsi _{2,2}(x,y,t)=\, & {} \frac{\sqrt{2 l-P} \sqrt{a-c-l^{2}} \sin \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) }{\cos \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) -1}\times e^{i(lx+py+ct)}. \end{aligned}$$
(33)
$$\begin{aligned} \varPhi _{2,2}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( \frac{\sqrt{2 l-P} \sqrt{a-c-l^{2}} \sin \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) }{\cos \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) -1}\right) ^{2}+a. \end{aligned}$$
(34)
$$\begin{aligned} \varPsi _{2,3}(x,y,t)=\, & {} -\frac{\sqrt{2 l-P} \sqrt{a-c-l^{2}} \sin \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) }{\cos \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) +1}\times e^{i(lx+py+ct)}. \end{aligned}$$
(35)
$$\begin{aligned} \varPhi _{2,3}(x,y,t)= \,& {} \frac{1}{(2 l-P)}\left( -\frac{\sqrt{2 l-P} \sqrt{a-c-l^{2}} \sin \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) }{\cos \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) +1}\right) ^{2}+a. \end{aligned}$$
(36)
$$\begin{aligned} \varPsi _{2,4}(x,y,z,t)=\, & {} -\frac{\sqrt{2 l-P} \sqrt{a-c-l^{2}} \sin \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) }{\cos \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) -1}\times e^{i(lx+py+ct)}. \end{aligned}$$
(37)
$$\begin{aligned} \varPhi _{2,4}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( -\frac{\sqrt{2 l-P} \sqrt{a-c-l^{2}} \sin \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) }{\cos \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) -1}\right) ^{2}+a. \end{aligned}$$
(38)

OR

Suppose that Eq. (6) has solutions of the form

$$\begin{aligned} H(\zeta )=\frac{\alpha _{0}\cos (\rho \zeta )}{\alpha _{2}+\alpha _{1}\sin (\rho \zeta )}. \end{aligned}$$
(39)

Inserting Eq. (39) along its derivative into Eq. (6) and by equating the coefficients of each powers of \(\sin (\rho \zeta )^{m}\) to 0, we secure the following nonlinear equations. On simplifying the above set of equations with the assistance of Mathematica, we secure the following solution sets:

$$\begin{aligned}&{\mathbf{Set-3}}:\quad \rho =\frac{\sqrt{-a+c+l^{2}}}{\sqrt{2} L},\; \alpha _{0}=\pm \, \alpha _{1} \sqrt{2 l-P} \sqrt{a-c-l^{2}},\; \alpha _{1}=\alpha _{1},\; \alpha _{2}=0. \\&{\mathbf{Set-4}}:\quad \rho =\frac{\sqrt{2} \sqrt{-a+c+l^{2}}}{L},\; \alpha _{0}=\pm \, \alpha _{1} \sqrt{2 l-P} \sqrt{a-c-l^{2}},\; \alpha _{1}=\alpha _{1},\; \alpha _{2}=\pm \, \alpha _{1}. \end{aligned}$$

Singular periodic solutions for Eq. (1) corresponding to set 3 can be derived as :

$$\begin{aligned} \varPsi _{3,1}(x,y,t)=\, & {} \sqrt{2 l-P} \sqrt{a-c-l^{2}} \cot \left( \frac{\sqrt{-a+c+l^{2}} (-2 l t+P y+x)}{\sqrt{2}}\right) \times e^{i(lx+py+ct)}. \end{aligned}$$
(40)
$$\begin{aligned} \varPhi _{3,1}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( \sqrt{2 l-P} \sqrt{a-c-l^{2}} \cot \left( \frac{\sqrt{-a+c+l^{2}} (-2 l t+P y+x)}{\sqrt{2}}\right) \right) ^{2}+a. \end{aligned}$$
(41)
$$\begin{aligned} \varPsi _{3,2}(x,y,t)=\, & {} \sqrt{2 l-P} \left( -\sqrt{a-c-l^{2}}\right) \cot \left( \frac{\sqrt{-a+c+l^{2}} (-2 l t+P y+x)}{\sqrt{2}}\right) \times e^{i(lx+py+ct)}. \end{aligned}$$
(42)
$$\begin{aligned} \varPhi _{3,2}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( \sqrt{2 l-P} \left( -\sqrt{a-c-l^{2}}\right) \cot \left( \frac{\sqrt{-a+c+l^{2}} (-2 l t+P y+x)}{\sqrt{2}}\right) \right) ^{2}+a. \end{aligned}$$
(43)

Similarly, combo singular periodic solutions for Eq. (1) corresponding to set 4 are :

$$\begin{aligned} \varPsi _{4,1}(x,y,t)= & {} \frac{\sqrt{2 l-P} \sqrt{a-c-l^{2}} \cos \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) }{\sin \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) +1}\times e^{i(lx+py+ct)}. \end{aligned}$$
(44)
$$\begin{aligned} \varPhi _{4,1}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( \frac{\sqrt{2 l-P} \sqrt{a-c-l^{2}} \cos \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) }{\sin \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) +1}\right) ^{2}+a. \end{aligned}$$
(45)
$$\begin{aligned} \varPsi _{4,2}(x,y,t)= \,& {} \frac{\sqrt{2 l-P} \sqrt{a-c-l^{2}} \cos \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) }{\sin \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) -1}\times e^{i(lx+py+ct)}. \end{aligned}$$
(46)
$$\begin{aligned} \varPhi _{4,2}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( \frac{\sqrt{2 l-P} \sqrt{a-c-l^{2}} \cos \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) }{\sin \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) -1}\right) ^{2}+a. \end{aligned}$$
(47)
$$\begin{aligned} \varPsi _{4,3}(x,y,t)=\, & {} -\frac{\sqrt{2 l-P} \sqrt{a-c-l^{2}} \cos \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) }{\sin \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) +1}\times e^{i(lx+py+ct)}. \end{aligned}$$
(48)
$$\begin{aligned} \varPhi _{4,3}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( -\frac{\sqrt{2 l-P} \sqrt{a-c-l^{2}} \cos \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) }{\sin \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) +1}\right) ^{2}+a. \end{aligned}$$
(49)
$$\begin{aligned} \varPsi _{4,4}(x,y,t)=\, & {} -\frac{\sqrt{2 l-P} \sqrt{a-c-l^{2}} \cos \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) }{\sin \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) -1}\times e^{i(lx+py+ct)}. \end{aligned}$$
(50)
$$\begin{aligned} \varPhi _{4,4}(x,y,t)= \,& {} \frac{1}{(2 l-P)}\left( -\frac{\sqrt{2 l-P} \sqrt{a-c-l^{2}} \cos \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) }{\sin \left( \sqrt{2} \sqrt{-a+c+l^{2}} (-2 l t+P y+x)\right) -1}\right) ^{2}+a. \end{aligned}$$
(51)

2.3 Solutions via extended rational sinh-cosh method (Rehman et al. 2020)

Suppose that the Eq. (6) has the following.

$$\begin{aligned} H(\zeta )=\frac{\alpha _{0}\sinh (\rho \zeta )}{\alpha _{2}+\alpha _{1}\cosh (\rho \zeta )}. \end{aligned}$$
(52)

Switching Eq. (52) along with its derivative into Eq. (6) and by equating the coefficients of each powers of \(\cosh (\rho \zeta )^{m}\) to 0, we get collect the following algebraic equation. On solving these equations with assistance of Mathematica, we gain the following solution sets:

$$\begin{aligned}&{\mathbf{Set-5}}:\quad \rho =\frac{\sqrt{a-c-l^{2}}}{\sqrt{2} L},\; \alpha _{0}=\pm \,\alpha _{1} \sqrt{2 l-P} \sqrt{-a+c+l^{2}},\; \alpha _{1}=\alpha _{1},\; \alpha _{2}=0. \\&{\mathbf{Set-6}}:\quad \rho =\frac{\sqrt{2} \sqrt{a-c-l^{2}}}{L},\; \alpha _{0}=\pm \, \alpha _{1} \sqrt{2 l-P} \sqrt{-a+c+l^{2}},\; \alpha _{1}=\alpha _{1},\; \alpha _{2}=\pm \, \alpha _{1}. \end{aligned}$$

Dark optical soliton solutions for Eq. (1) corresponding to set 5 can be written as:

$$\begin{aligned} \varPsi _{5,1}(x,y,t)=\, & {} \sqrt{2 l-P} \sqrt{-a+c+l^{2}} \tanh \left( \frac{\sqrt{a-c-l^{2}} (-2 l t+P y+x)}{\sqrt{2}}\right) \times e^{i(lx+py+ct)}. \end{aligned}$$
(53)
$$\begin{aligned} \varPhi _{5,1}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( \sqrt{2 l-P} \sqrt{-a+c+l^{2}} \tanh \left( \frac{\sqrt{a-c-l^{2}} (-2 l t+P y+x)}{\sqrt{2}}\right) \right) ^{2}+a. \end{aligned}$$
(54)
$$\begin{aligned} \varPsi _{5,2}(x,y,t)=\, & {} \sqrt{2 l-P} \left( -\sqrt{-a+c+l^{2}}\right) \tanh \left( \frac{\sqrt{a-c-l^{2}} (-2 l t+P y+x)}{\sqrt{2}}\right) \times e^{i(lx+py+ct)}. \end{aligned}$$
(55)
$$\begin{aligned} \varPhi _{5,2}(x,y,t)= \,& {} \frac{1}{(2 l-P)}\left( \sqrt{2 l-P} \left( -\sqrt{-a+c+l^{2}}\right) \tanh \left( \frac{\sqrt{a-c-l^{2}} (-2 l t+P y+x)}{\sqrt{2}}\right) \right) ^{2}+a. \end{aligned}$$
(56)

Similarly, mixed optical soliton for Eq. (1) corresponding to set 6 can be acquired as:

$$\begin{aligned} \varPsi _{6,1}(x,y,t)=\, & {} \frac{\sqrt{2 l-P} \sqrt{-a+c+l^{2}} \sinh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) }{\cosh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) +1}\times e^{i(lx+py+ct)}. \end{aligned}$$
(57)
$$\begin{aligned} \varPhi _{6,1}(x,y,t)= \,& {} \frac{1}{(2 l-P)}\left( \frac{\sqrt{2 l-P} \sqrt{-a+c+l^{2}} \sinh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) }{\cosh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) +1}\right) ^{2}+a. \end{aligned}$$
(58)
$$\begin{aligned} \varPsi _{6,2}(x,y,t)=\, & {} \frac{\sqrt{2 l-P} \sqrt{-a+c+l^{2}} \sinh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) }{\cosh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) -1}\times e^{i(lx+py+ct)}. \end{aligned}$$
(59)
$$\begin{aligned} \varPhi _{6,2}(x,y,t)= & {} \frac{1}{(2 l-P)}\left( \frac{\sqrt{2 l-P} \sqrt{-a+c+l^{2}} \sinh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) }{\cosh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) -1}\right) ^{2}+a. \end{aligned}$$
(60)
$$\begin{aligned} \varPsi _{6,3}(x,y,t)=\, & {} -\frac{\sqrt{2 l-P} \sqrt{-a+c+l^{2}} \sinh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) }{\cosh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) +1}\times e^{i(lx+py+ct)}. \end{aligned}$$
(61)
$$\begin{aligned} \varPhi _{6,3}(x,y,t)= & {} \frac{1}{(2 l-P)}\left( -\frac{\sqrt{2 l-P} \sqrt{-a+c+l^{2}} \sinh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) }{\cosh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) +1}\right) ^{2}+a. \end{aligned}$$
(62)
$$\begin{aligned} \varPsi _{6,4}(x,yt)=\, & {} -\frac{\sqrt{2 l-P} \sqrt{-a+c+l^{2}} \sinh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) }{\cosh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) -1}\times e^{i(lx+py+ct)}. \end{aligned}$$
(63)
$$\begin{aligned} \varPhi _{6,4}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( -\frac{\sqrt{2 l-P} \sqrt{-a+c+l^{2}} \sinh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) }{\cosh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) -1}\right) ^{2}+a. \end{aligned}$$
(64)

OR

Suppose the Eq. (6) has the following solutions

$$\begin{aligned} H(\zeta )=\frac{\alpha _{0}\cosh (\rho \zeta )}{\alpha _{2}+\alpha _{1}\sinh (\rho \zeta )} \end{aligned}$$
(65)

Imposing Eq. (65) along with its derivative into Eq. (6) and by equating the coefficients of each powers of \(\sinh (\rho \zeta )^{m}\) to 0, we achieve the following strategic equations. On simplifying above equations through Mathematica, we obtain the following solution sets:

$$\begin{aligned}&{\mathbf{Set-7}}:\quad \rho =\frac{\sqrt{a-c-l^{2}}}{\sqrt{2} L},\; \alpha _{0}=\pm \, \alpha _{1} \sqrt{2 l-P} \sqrt{-a+c+l^{2}},\; \alpha _{1}=\alpha _{1},\; \alpha _{2}=0.\\&{\mathbf{Set-8}}:\quad \rho =\frac{\sqrt{2} \sqrt{a-c-l^{2}}}{L},\; \alpha _{0}=\pm \, \alpha _{1} \sqrt{2 l-P} \sqrt{-a+c+l^{2}},\; \alpha _{1}=\alpha _{1},\; \alpha _{2}=\pm \, \alpha _{1}. \end{aligned}$$

Singular optical soliton for Eq. (1) corresponding to set 7 can be compiled as:

$$\begin{aligned} \varPsi _{7,1}(x,y,t)= \,& {} \sqrt{2 l-P} \sqrt{-a+c+l^{2}} \coth \left( \frac{\sqrt{a-c-l^{2}} (-2 l t+P y+x)}{\sqrt{2}}\right) \times e^{i(lx+py+ct)}. \end{aligned}$$
(66)
$$\begin{aligned} \varPhi _{7,1}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( \sqrt{2 l-P} \sqrt{-a+c+l^{2}} \coth \left( \frac{\sqrt{a-c-l^{2}} (-2 l t+P y+x)}{\sqrt{2}}\right) \right) ^{2}+a. \end{aligned}$$
(67)
$$\begin{aligned} \varPsi _{7,2}(x,y,t)=\, & {} \sqrt{2 l-P} \left( -\sqrt{-a+c+l^{2}}\right) \coth \left( \frac{\sqrt{a-c-l^{2}} (-2 l t+P y+x)}{\sqrt{2}}\right) \times e^{i(lx+py+ct)}. \end{aligned}$$
(68)
$$\begin{aligned} \varPhi _{7,2}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( \sqrt{2 l-P} \left( -\sqrt{-a+c+l^{2}}\right) \coth \left( \frac{\sqrt{a-c-l^{2}} (-2 l t+P y+x)}{\sqrt{2}}\right) \right) ^{2}+a. \end{aligned}$$
(69)

Similarly,complex soliton solutions for Eq.(1) corresponding to set 8 can be extracted as:

$$\begin{aligned} \varPsi _{8,1}(x,y,t)=\, & {} \frac{\sqrt{2 l-P} \sqrt{-a+c+l^{2}} \cosh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) }{\sinh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) +i}\times e^{i(lx+py+ct)}. \end{aligned}$$
(70)
$$\begin{aligned} \varPhi _{8,1}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( \frac{\sqrt{2 l-P} \sqrt{-a+c+l^{2}} \cosh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) }{\sinh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) +i}\right) ^{2}+a. \end{aligned}$$
(71)
$$\begin{aligned} \varPsi _{8,2}(x,y,t)=\, & {} \frac{\sqrt{2 l-P} \sqrt{-a+c+l^{2}} \cosh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) }{\sinh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) -i}\times e^{i(lx+py+ct)}. \end{aligned}$$
(72)
$$\begin{aligned} \varPhi _{8,2}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( \frac{\sqrt{2 l-P} \sqrt{-a+c+l^{2}} \cosh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) }{\sinh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) -i}\right) ^{2}+a. \end{aligned}$$
(73)
$$\begin{aligned} \varPsi _{8,3}(x,y,t)=\, & {} -\frac{\sqrt{2 l-P} \sqrt{-a+c+l^{2}} \cosh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) }{\sinh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) +i}\times e^{i(lx+py+ct)}. \end{aligned}$$
(74)
$$\begin{aligned} \varPhi _{8,3}(x,y,t)= & {} \frac{1}{(2 l-P)}\left( -\frac{\sqrt{2 l-P} \sqrt{-a+c+l^{2}} \cosh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) }{\sinh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) +i}\right) ^{2}+a. \end{aligned}$$
(75)
$$\begin{aligned} \varPsi _{8,4}(x,y,t)=\, & {} -\frac{\sqrt{2 l-P} \sqrt{-a+c+l^{2}} \cosh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) }{\sinh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) -i}\times e^{i(lx+py+ct)}. \end{aligned}$$
(76)
$$\begin{aligned} \varPhi _{8,4}(x,y,t)= & {} \frac{1}{(2 l-P)}\left( -\frac{\sqrt{2 l-P} \sqrt{-a+c+l^{2}} \cosh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) }{\sinh \left( \sqrt{2} \sqrt{a-c-l^{2}} (-2 l t+P y+x)\right) -i}\right) ^{2}+a. \end{aligned}$$
(77)

2.4 Solutions via MDAM (Bilal et al. 2021c)

The solution of Eq. (6) as follows

$$\begin{aligned} H(\zeta )=a_{0}+a_{1}Z+b_{1}Z^{-1}, \end{aligned}$$
(78)

where \(a_{0}, a_{1}\) and \(b_{1}\) are parameters. Solving Eq. (78) along with \((Z'=\vartheta +Z^{2})\) into Eq. (6), and taking coefficients of Z to zero with similar powers and hence on proceeding with Mathematica, we get solution sets as follows

$$\begin{aligned}&{\mathbf{Set-1}}:\quad a_{0}=0,\; a_{1}=\sqrt{2 L^{2} (P-2 l)},\; b_{1}=0,\; c=a-l^{2}+2 \vartheta L^{2}.\\&{\mathbf{Set-2}}:\quad a_{0}=0,\; a_{1}=0,\; b_{1}=-\sqrt{2} \sqrt{\vartheta ^{2} L^{2} (P-2 l)},\; c=a-l^{2}+2 \vartheta L^{2}.\\&{\mathbf{Set-3}}:\quad a_{0}=0,\; a_{1}=-\sqrt{2} \sqrt{L^{2} (P-2 l)},\; b_{1}=\sqrt{ 2 L^{2} (P-2 l)}\vartheta ,\; c=a-l^{2}+\frac{6 \vartheta ^{2} L^{2} \sqrt{L^{2} (P-2 l)}}{\sqrt{\vartheta ^{2} L^{2} (P-2 l)}}+2 \vartheta L^{2}. \end{aligned}$$

For Set-1

  • \(\vartheta <0\), we get the following form of solutions

    Dark wave structure

    $$\begin{aligned} \varPsi _{1}(x,y,t)=\, & {} -\sqrt{2} \sqrt{-\vartheta } \sqrt{L^{2} (P-2 l)} \tanh \left( \sqrt{-\vartheta } L (-2 l t+P y+x)\right) \times e^{i(lx+py+ct)}. \end{aligned}$$
    (79)
    $$\begin{aligned} \varPhi _{1}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( -\sqrt{2} \sqrt{-\vartheta } \sqrt{L^{2} (P-2 l)} \tanh \left( \sqrt{-\vartheta } L (-2 l t+P y+x)\right) \right) ^{2}+a. \end{aligned}$$
    (80)

    Singular wave structure

    $$\begin{aligned} \varPsi _{2}(x,y,t)=\, & {} -\sqrt{2} \sqrt{-\vartheta } \sqrt{L^{2} (P-2 l)} \coth \left( \sqrt{-\vartheta } L (-2 l t+P y+x)\right) \times e^{i(lx+py+ct)}. \end{aligned}$$
    (81)
    $$\begin{aligned} \varPhi _{2}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( -\sqrt{2} \sqrt{-\vartheta } \sqrt{L^{2} (P-2 l)} \coth \left( \sqrt{-\vartheta } L (-2 l t+P y+x)\right) \right) ^{2}+a. \end{aligned}$$
    (82)

    It is noted that above results converge to particular solutions for some constant values of coefficients of hyperbolic functions. For instance, if \(\sqrt{*}\rightarrow 2\) then \(\varPhi _{1}\rightarrow \) sech\(^{2}(.)\) which is solitary wave type structure and also \(\varPhi _{2}\rightarrow \) csch\(^{2}(.)\) which is singular wave type-II structure.

  • \(\vartheta >0\), the periodic solutions of following forms are obtained

    $$\begin{aligned} \varPsi _{3}(x,y,t)=\, & {} \sqrt{2} \sqrt{\vartheta } \sqrt{L^{2} (P-2 l)} \tan \left( \sqrt{\vartheta } L (-2 l t+P y+x)\right) \times e^{i(lx+py+ct)}. \end{aligned}$$
    (83)
    $$\begin{aligned} \varPhi _{3}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( \sqrt{2} \sqrt{\vartheta } \sqrt{L^{2} (P-2 l)} \tan \left( \sqrt{\vartheta } L (-2 l t+P y+x)\right) \right) ^{2}+a. \end{aligned}$$
    (84)

    And

    $$\begin{aligned} \varPsi _{4}(x,y,t)=\, & {} -\sqrt{2} \sqrt{\vartheta } \sqrt{L^{2} (P-2 l)} \cot \left( \sqrt{\vartheta } L (-2 l t+P y+x)\right) \times e^{i(lx+py+ct)}. \end{aligned}$$
    (85)
    $$\begin{aligned} \varPhi _{4}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( -\sqrt{2} \sqrt{\vartheta } \sqrt{L^{2} (P-2 l)} \cot \left( \sqrt{\vartheta } L (-2 l t+P y+x)\right) \right) ^{2}+a. \end{aligned}$$
    (86)

    For Set-2

  • \(\vartheta <0\), we get the singular and dark wave structures respectively

    $$\begin{aligned} \varPsi _{5}(x,y,t)=\, & {} \frac{\sqrt{2} \sqrt{\vartheta ^{2} L^{2} (P-2 l)} \coth \left( \sqrt{-\vartheta } L (-2 l t+P y+x)\right) }{\sqrt{-\vartheta }}\times e^{i(lx+py+ct)}. \end{aligned}$$
    (87)
    $$\begin{aligned} \varPhi _{5}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( \frac{\sqrt{2} \sqrt{\vartheta ^{2} L^{2} (P-2 l)} \coth \left( \sqrt{-\vartheta } L (-2 l t+P y+x)\right) }{\sqrt{-\vartheta }}\right) ^{2}+a. \end{aligned}$$
    (88)

    And

    $$\begin{aligned} \varPsi _{6}(x,y,t)= \,& {} \frac{\sqrt{2} \sqrt{\vartheta ^{2} L^{2} (P-2 l)} \tanh \left( \sqrt{-\vartheta } L (-2 l t+P y+x)\right) }{\sqrt{-\vartheta }}\times e^{i(lx+py+ct)}. \end{aligned}$$
    (89)
    $$\begin{aligned} \varPhi _{6}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( \frac{\sqrt{2} \sqrt{\vartheta ^{2} L^{2} (P-2 l)} \tanh \left( \sqrt{-\vartheta } L (-2 l t+P y+x)\right) }{\sqrt{-\vartheta }}\right) ^{2}+a. \end{aligned}$$
    (90)

  • \(\vartheta >0,\) the periodic solutions are retrieved

    $$\begin{aligned} \varPsi _{7}(x,y,t)=\, & {} -\frac{\sqrt{2} \sqrt{\vartheta ^{2} L^{2} (P-2 l)} \cot \left( \sqrt{\vartheta } L (-2 l t+P y+x)\right) }{\sqrt{\vartheta }}\times e^{i(lx+py+ct)}. \end{aligned}$$
    (91)
    $$\begin{aligned} \varPhi _{7}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( -\frac{\sqrt{2} \sqrt{\vartheta ^{2} L^{2} (P-2 l)} \cot \left( \sqrt{\vartheta } L (-2 l t+P y+x)\right) }{\sqrt{\vartheta }}\right) ^{2}+a. \end{aligned}$$
    (92)

    And

    $$\begin{aligned} \varPsi _{8}(x,y,t)= \,& {} \frac{\sqrt{2} \sqrt{\vartheta ^{2} L^{2} (P-2 l)} \tan \left( \sqrt{\vartheta } L (-2 l t+P y+x)\right) }{\sqrt{\vartheta }}\times e^{i(lx+py+ct)}. \end{aligned}$$
    (93)
    $$\begin{aligned} \varPhi _{8}(x,y,t)=\, & {} \frac{1}{(2 l-P)}\left( \frac{\sqrt{2} \sqrt{\vartheta ^{2} L^{2} (P-2 l)} \tan \left( \sqrt{\vartheta } L (-2 l t+P y+x)\right) }{\sqrt{\vartheta }}\right) ^{2}+a. \end{aligned}$$
    (94)

    For Set-3

  • \(\vartheta <0\), we get the following mixed hyperbolic solution

    $$\begin{aligned} \varPsi _{9}(x,y,t)=\, & {} \sqrt{2} \sqrt{-\vartheta } \sqrt{L^{2} (P-2 l)} \tanh \left( \sqrt{-\vartheta } L (-2 l t+P y+x)\right) \nonumber \\&-\frac{\sqrt{2} \sqrt{\vartheta ^{2} L^{2} (P-2 l)} \coth \left( \sqrt{-\vartheta } L (-2 l t+P y+x)\right) }{\sqrt{-\vartheta }}\times e^{i(lx+py+ct)}. \end{aligned}$$
    (95)
    $$\begin{aligned} \varPhi _{9}(x,y,t)= \,& {} \frac{1}{(2 l-P)}\left( sqrt{2} \sqrt{-\vartheta } \sqrt{L^{2} (P-2 l)} \tanh \left( \sqrt{-\vartheta } L (-2 l t+P y+x)\right) \right. \nonumber \\&\left. -\frac{\sqrt{2} \sqrt{\vartheta ^{2} L^{2} (P-2 l)} \coth \left( \sqrt{-\vartheta } L (-2 l t+P y+x)\right) }{\sqrt{-\vartheta }}\right) ^{2}+a. \end{aligned}$$
    (96)

  • \(\vartheta >0,\) the periodic solutions are expressed as

    $$\begin{aligned} \varPsi _{10}(x,y,t)=\, & {} \frac{\sqrt{2} \sqrt{\vartheta ^{2} L^{2} (P-2 l)} \cot \left( \sqrt{\vartheta } L (-2 l t+P y+x)\right) }{\sqrt{\vartheta }}\nonumber \\&-\sqrt{2} \sqrt{\vartheta } \sqrt{L^{2} (P-2 l)} \tan \left( \sqrt{\vartheta } L (-2 l t+P y+x)\right) \times e^{i(lx+py+ct)}. \end{aligned}$$
    (97)
    $$\begin{aligned} \varPhi _{10}(x,y,t)= \,& {} \frac{1}{(2 l-P)}\left( \frac{\sqrt{2} \sqrt{\vartheta ^{2} L^{2} (P-2 l)} \cot \left( \sqrt{\vartheta } L (-2 l t+P y+x)\right) }{\sqrt{\vartheta }}\right. \nonumber \\&\left. -\sqrt{2} \sqrt{\vartheta } \sqrt{L^{2} (P-2 l)} \tan \left( \sqrt{\vartheta } L (-2 l t+P y+x)\right) \right) ^{2}+a. \end{aligned}$$
    (98)

3 Rseults and discussion

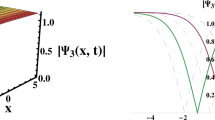
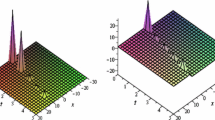
After the successful implementation of three proposed analytical methods to the given model, we will compare our results with other results in the existing research literature. Chowdhury et al. (2021) examine the explicit and periodic solutions by utilizing the double \(( \frac{G}{G}\), \(\frac{1}{G})\)-expansion method. Besides, in these references (Ye and Zhang 2011; Maccari 1996; Porsezian 1997; Yan 2002; Darvishi et al. 2016), they (authors) attained a few solutions to the (2 + 1)-dimensional soliton equation. However, in this study, we extract a variety of soliton solutions in the form of bright, dark, singular, and their combined forms by the proposed methods and also gain rational function and singular periodic solutions. We observe that the retrieved solutions are new and to the best of our knowledge the applications of these techniques to the (2 + 1)-dimensional soliton equation have not been reported in the literature beforehand. We analyzed that the outcomes introduced in this article could be useful in clarifying the actual significance of different nonlinear applications especially mathematical physics. By substituting the diverse values to the parameters, variants wave results are discovered from the exact peregrinating wave solution. The bright, combo, periodic, singular and dark soliton solutions, which are provided in Eqs. (10), (22), (44), (81) and (89) as exhibited in Figs. 1, 2, 3, 4 and 5 respectively. The physically description of some solutions are given below. Hence physically description of some solutions and discussion of the results segment, we conclude that our present modifed mathematical methods are fruitful tools for investigate the further results for nonlinear wave problems in applied science.

Fig. 1
figure 1

The 3D, 2D and their contour wave profiles are presented for Eq. (10)

Full size image
Fig. 2
figure 2

The 3D, 2D and their contour wave profiles are presented for Eq. (22)

Full size image
Fig. 3
figure 3

The 3D, 2D and their contour wave profiles are presented for Eq. (44)

Full size image
Fig. 4
figure 4

The 3D, 2D and their contour wave profiles are presented for Eq. (81)

Full size image
Fig. 5
figure 5

The 3D, 2D and their contour wave profiles are presented for Eq. (89)

Full size image

4 Conclusion

The exploration of this novel effort is to investigate solitary wave structures in different shapes like hyperbolic, trigonometric, and rational function solutions including some special known solitary wave solutions such as bright dark, singular, and multiple solitons by three analytical mathematical methods. The achieved results are extraordinary and new from the existing outcomes in the already published literature. For example, hyperbolic functions shows up in various regions like, in the computation and speed of special relativity, in the Langevin function for attractive polarization, in the gravitational capability of a chamber and the estimation of as far as possible, in the profile of a laminar jet. Moreover, the bright soliton solutions will be a big asset in controlling the soliton clutter as mentioned in the introduction section. This means that the solitons can be converted to a state of separation from a state of attraction which would mean clearing the clutter. The bright soliton solutions will be a major resource in controlling the soliton mess as referenced in the presentation area (Weisstein 2002). Furthermore, 3D, 2D, and contour profiles are plotted under the choice of appropriate parameters for getting the physical behavior of secured solutions. The reported outcomes will be valuable for a comprehensive insight of the dynamics of the mentioned model, and more, the analysis can be enhanced to other nonlinear models. The scrutinized wave’s results are loyal to the researchers and also have imperious applications in mathematical physics. Finally, our solutions have been verified using the Mathematica by substituting them back into the original equation. We will extend the proposed methods for some fractional models in a future work.