1 Introduction

This world has many complicated natural phenomena with a broad scope of mathematical applications. The mathematical models of the nonlinear physical phenomena are illustrated explicitly by the nonlinear evolution equations (NLEEs) that have a significant influence on the investigation of nonlinear sciences. So, recently, obtaining exact soliton solutions to NLEEs with the help of computer programs that make repetitious and monotonous mathematical computations easier, has been a marvelous field for analysts and researchers. NLEEs play out an extraordinary part in depicting the actual behavior of real phenomena and dynamical processes in fluid mechanics, optical fibers, material science, geochemistry, ocean engineering, geophysics, mathematical physics, plasma physical science, and numerous other logical regions. Nonlinear science is one of the best astonishing fields for investigators in this bleeding-edge season of science. To track down the analytically or exact results has been the focal point of researchers because of its fundamental commitment to examine the genuine element of the frameworks. As we all know, scholars have devised several methodologies and mathematical tools to aid in the discovery of exact solutions to NLEEs, and each method is tailored to a certain sort of solution [1,2,3,4,5,6,7,8].

Moreover, the concept of soliton or solitary waves is a phenomenon that has attracted the attention of people of all ages. When there is a disturbance in the phenomenon, waves are formed. Soliton interactions occur when two or moresolitons come near enough to interact. Soliton waves have risen to prominence among all the waves found in nature due to their fundamental properties that are rarely found in other waves. Due to dispersive effects, the velocity of soliton waves varies with wavelength and is significantly different from the velocity of energy propagation. Moreover, linear effects of soliton waves can be shown dominantly in breaking roll waves on the seashore. Wave spreading effects, also known as dispersive effects, and wave focusing effects, also known as nonlinear effects, have shown a moderate balance in generating waves with a permanent shape. Furthermore, the optical solitons are one of the most significant domains of research in the branch of nonlinear optics. Particularly, the investigation of dispersive optical solitons is getting a lot of consideration in the present days. This tendency is actually continuing, there are numerous new outcomes that are constantly being published in the context of given model. Besides, the exact solutions are necessary for observing the physical properties of mathematical modeled problems. Mathematical techniques are being established in a variety of ways. In previous findings, several analytical schemes have been used to observe the analytic solutions such as the \((G^{\prime }/G\))-expansion method [9], the anstaz approach [10, 11], the trial equation technique [12], the adomian decomposition method [13], the variation iteration method (VIM) [14], the modified \(\exp (-\varPhi (\zeta ))\)-expansion method [15], the direct algebraic method [16], the extended Fan sub-equation method [17], the F-expansion technique [18], the generalized exponential rational function method [19], new \(\varPhi ^{6}\)-model expansion method [20] and several others [21,22,23,24,25,26].

The key idea of this study is to conceive a variety of soliton solutions in the (2+1)-dimensional soliton equation by employing three analytical methods. In this article we will consider the (2+1)-dimensional soliton equation given by [27]

$$\begin{aligned}&i \varPsi _{t}+\varPsi _{xx}+\varPsi \varPhi =0,~~~\nonumber \\&\varPhi _{t}+\varPhi _{y}+(\varPsi \varPsi ^{*})_x=0, \end{aligned}$$
(1)

where \(*\) represents the complex conjugate. The \(\varPhi =\varPhi (x,y,t)\) is real and \(\varPsi =\varPsi (x,y,t)\) is imaginary function. Here x, y and t represent the spatial domains and time respectively. The governing equation is similar to the integrable Zakharov equation in plasma physics which shows a significant role in several physical applications and governs the behavior of weakly nonlinear ion-acoustic waves in a plasma. The physically most important example involves the interaction between the Langmuir and ion-acoustic waves in plasmas. So far many studies for the (2 + 1)-dimensional soliton have been done in literature, for detail see references [28,29,30,31,32]. The authors attained a few solutions to the above equation. The more effective, novel solitary wave solutions of the given model will be achieved via three proposed methods.

The layout of this manuscript is arranged as follows: The description of GERFM, (\(\frac{G^{\prime }}{G^2}\))-expansion function method and the generalized Kudryashov method, is discussed in Sec. 2. Extraction of solitary wave solutions is given in Sec. 2. The Sec. 3 consist of results and discussion along with the graphical representation. The conclusion is revealed in Sec. 4.

2 Description of the methods

We present brief description of the proposed methods in this section.

Suppose a NLPDE,

$$\begin{aligned} \varDelta (\varTheta , \varTheta _{t}, \varTheta _{x}, \varTheta _y, \varTheta _{xx}, \varTheta _{yy}, \varTheta _{xt}, \cdots )=0, \end{aligned}$$
(2)

where \(\varDelta \) is a polynomial in its arguments. We start with hypothesis as:

$$\begin{aligned} \varTheta (x,y,t)=\phi (\zeta )~~~\text{ and }~~~ \zeta = x+\eta y-\mu t, \end{aligned}$$

putting the traveling wave transformation into Eq. (2), yields NODE as,

$$\begin{aligned} \chi (\phi , \phi ^{\prime }, \phi ^{\prime \prime }, \phi ^{\prime \prime \prime }, \cdots )=0, \end{aligned}$$
(3)

where \(\chi \) is a polynomial function of its arguments and \(^\prime \) expresses the derivative w.r.t \(\zeta \).

2.1 GERFM

First we give a detail description of GERFM [33]. This technique incorporates the following steps.

Step 1. The solution of Eq. (3) is written as

$$\begin{aligned} \phi (\zeta )=\delta _{0}+\sum _{k=1}^n \delta _k\sigma (\zeta )^{k}+\sum _{k=1}^n \rho _k \sigma (\zeta )^{-k},~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(4)

where

$$\begin{aligned} \sigma (\zeta )=\frac{p_1 e^{q_1 \zeta }+p_2 e^{q_2 \zeta }}{p_3 e^{q_3 \zeta }+p_4 e^{q_4 \zeta }}. \end{aligned}$$
(5)

The unknown coefficients \(\delta _{0}\), \(\delta _{k}\), \(\rho _{k}\) \((1\le k \le n)\) and constants \(p_{i}\), \(q_{i}\) \((1\le i\le 4)\) are determined. We use homogeneous balance principle [34] in order to determine the positive integer n by balancing the nonlinear term and linear term with the highest order in Eq. (3). More precisely, if degree of \(\phi (\zeta )\) is \(deg\big [\phi (\zeta )\big ]=n\) then other terms will have degree may be obtained as follows:

$$\begin{aligned} deg\big [\phi ^k(\zeta )\big ]=n+k,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\nonumber \end{aligned}$$
$$\begin{aligned} deg\big [(\phi (\zeta ))^p\big (\phi ^k(\zeta )\big )^s\big ]=np+s(n+k).~~~~~~~~~~~~~~~ \end{aligned}$$
(6)

From above equation we get

$$\begin{aligned} n + k = np + s(n + k). \end{aligned}$$
(7)

Step 2. We get a cluster of algebraic equations on putting Eq. (4) together with (5) into Eq. (3).

Step 3. On solving the cluster of equations, we get the unknown terms and consequently, the required solutions are achieved.

2.2 (\(\frac{G^{\prime }}{G^2}\))-expansion function method

Here, we discuss in detail the general property of the proposed method [35].

Step 1. Suppose that Eq. (3) has the following form of solution

$$\begin{aligned} \phi (\zeta )=a_{0}+\sum _{k=1}^n\Bigg ( \alpha _k\bigg (\frac{G^{\prime }}{G^2}\bigg )^k+ \beta _k\bigg (\frac{G^{\prime }}{G^2}\bigg )^{-k}\Bigg ),~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(8)

where \(G = G(\zeta )\) holds

$$\begin{aligned} \bigg (\frac{G^{\prime }}{G^2}\bigg )^{\prime }=\varUpsilon +\varOmega \bigg (\frac{G^{\prime }}{G^2}\bigg )^{2},~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(9)

with \(\varOmega \ne 0\), \(\varUpsilon \ne 1\) are integers. The unknown constants \( a_{0}, \alpha _{k}, \beta _{k} ~( k=1, 2, 3, \cdots , n)\) to be calculated latter.

Step 2. Thus \((\frac{G^{\prime }}{G^2})\)-expansion method provides three types of solutions:

  • Trigonometric solution:

    If \(\varUpsilon ~\varOmega > 0\),

    $$\begin{aligned} \bigg (\frac{G^\prime }{G^2}\bigg )=\sqrt{\frac{\varUpsilon }{\varOmega }}\bigg (\frac{\zeta _1\cos (\sqrt{\varUpsilon \varOmega }~\zeta )+\zeta _2\sin (\sqrt{\varUpsilon \varOmega }~\zeta )}{{\zeta _2\cos (\sqrt{\varUpsilon \varOmega }~\zeta )-\zeta _1\sin (\sqrt{\varUpsilon \varOmega }~\zeta )}}\bigg ).~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (10)

  • Hyperbolic solution:

    If \(\varUpsilon ~\varOmega < 0\),

    $$\begin{aligned} ~~~ \bigg (\frac{G^\prime }{G^2}\bigg )=-\frac{\sqrt{|\varUpsilon \varOmega |}}{\varOmega }\bigg (\frac{\zeta _1\sinh (2\sqrt{|\varUpsilon \varOmega |}\zeta )+\zeta _1\cosh (2\sqrt{|\varUpsilon \varOmega |}\zeta )+\zeta _2}{{\zeta _1\sinh (2\sqrt{|\varUpsilon \varOmega |}\zeta )+\zeta _1\cosh (2\sqrt{|\varUpsilon \varOmega |}\zeta )-\zeta _2}}\bigg ),\end{aligned}$$
    (11)

  • Rational solution:

    If \(\varUpsilon =0\), \(\varOmega \ne 0\),

    $$\begin{aligned} \bigg (\frac{G^\prime }{G^2}\bigg )=\bigg (-\frac{\zeta _1}{\varOmega (\zeta _1~\zeta +\zeta _2)}\bigg ),~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (12)

    where \(\zeta _1\) and \(\zeta _2\) are constants.

Step 3. On the utilization of Eq. (7) for the homogeneous balance principle the value of n in Eq. (3) is calculated.

Step 4. After putting Eq. (8) together with (9) into Eq. (3) and a set of algebraic system is extracted on the comparison of specific terms.

Step 5. The required set of parameters will be obtained after solving the system of algebraic equations through soft computations.

2.3 The general properties of generalized Kudryashov method

Here, we discuss in detail the general property of the proposed method [36].

Step 1: Suppose that Eq. (3) has the following form of solution

$$\begin{aligned} \phi (\zeta )=\frac{\sum _{i=0}^{n} a_{i} ~G^{i}(\zeta )}{\sum _{j=0}^{m}b_{j} ~G^{j}(\zeta )}, \end{aligned}$$
(13)

where, \(a_{i}(i=0,1, 2, 3,\cdots , n)\) and \(b_{j}(j=0,1, 2, 3,\cdots , m)\) are constants to be determined after ward such that \( a_{n}\ne 0\) and \( b_{m}\ne 0\),

where \(G = G(\zeta )\) holds

$$\begin{aligned} G'(\zeta )=G^2(\zeta )-G(\zeta ). \end{aligned}$$
(14)

Moreover,the solution of Eq. (14) has the structure like

$$\begin{aligned} G(\zeta )=\frac{1}{1+S e^\zeta }. \end{aligned}$$
(15)

Here, S is constant of integration.

Step 2: The values of n and m are evaluated by using homogeneous balance principle in Eq. (3).

Step 3: We obtain a polynomial in \(G(\zeta )\), after putting Eqs. (13) and (14) into Eq. (3). We get a cluster of an algebraic equations on equating the same powers of \(G(\zeta )\) to zero, and we secure the values of \(a_{i}(i=0, 1, 2, 3,\cdots , n)\) and \(b_{{j}}(j=0, 1, 2, 3,\cdots , m)\). On the utilization of the obtained values in Eq. (13) with the usage of Eq. (15), we finally find the exact solutions of Eq. (1).

3 Extraction of solitary wave solutions

In this section, the application of the proposed methods are utilized for establishing the new soliton solutions to Eq.(1). Suppose the following traveling wave transformation :

$$\begin{aligned} \begin{aligned} \varPsi (x,y,t)=H(\zeta )e^{i\theta },\,~\,\varPhi (x,y,t)={R(\zeta )}~\,\,~\theta =lx+py+ct,~\,~\,~\zeta =L(x+Py - 2lt), \end{aligned} \end{aligned}$$
(16)

where l, p, c, L and P are constants; \(H(\zeta )\) and \({R(\zeta )}\) represent real functions. By inserting Eq. (16) into Eq. (1), we attain,

$$\begin{aligned}&\begin{aligned} L^2 H^{\prime \prime }(\zeta )-(c+l^2) H(\zeta )+H(\zeta ) {R(\zeta )}=0. \end{aligned} \end{aligned}$$
(17)
$$\begin{aligned}&\begin{aligned} (P-2l) {R'(\zeta )}+ (H^2(\zeta ))' =0. \end{aligned} \end{aligned}$$
(18)

By integrating Eq. (18), we obtain

$$\begin{aligned} \begin{aligned} {R(\zeta )=- \frac{H^2(\zeta )}{(P-2l)}+a}. \end{aligned} \end{aligned}$$
(19)

where a is the constant of the integration and \(P\ne 2l\). Substituting Eq. (19) into Eq. (18), we get

$$\begin{aligned} \begin{aligned} \frac{ \left( a-c-l^2\right) }{L^2}H(\zeta )-\frac{1}{L^2 (P-2 l)}H^3(\zeta )+H^{\prime \prime }(\zeta )=0. \end{aligned} \end{aligned}$$
(20)

3.1 Solutions via GERFM

By using the homogeneous balance rule, the highest order derivative \(H^{\prime \prime }(\zeta )\) and the nonlinear term of the highest order \(H^3(\zeta )\) are balanced via the Eq. (7) in Eq. (20), and from Eq. (20), we get

$$\begin{aligned} deg\big [H^{\prime \prime }(\zeta )\big ]=n+2= deg\big [H^3(\zeta )\big (H^{\prime \prime }(\zeta )\big )^s\big ]=3n+0(n+2) \end{aligned}$$
(21)

which leads to \(n=1\). The solution of (20), becomes

$$\begin{aligned} H(\zeta )=\delta _{0}+\delta _{1}\sigma (\zeta )+\rho _{1}\sigma (\zeta )^{-1}. \end{aligned}$$
(22)

Family-1: For \(p=[-1,-1,1,-1]\) and \(q=[1,-1,1,-1]\), the Eq. (5) gives

$$\begin{aligned} \sigma (\zeta )=-\frac{\cosh (\zeta )}{\sinh (\zeta )}. \end{aligned}$$
(23)

Plugging Eq. (22) and Eq. (23) in Eq. (20), we secure solution sets as follows:

Set-1:

$$\begin{aligned} \delta _0= 0,~ \delta _{1}=\sqrt{2} \sqrt{L^2 (P-2 l)},~ \rho _{1}=\sqrt{2} \sqrt{L^2 (P-2 l)},~ c =a-l^2-8 L^2. \end{aligned}$$

  • Combo solitons are obtained

    $$\begin{aligned} \varPsi _{1}(x,y,t)= & {} \bigg (- \sqrt{2 L^2 (P-2 l)} \tanh (L (-2 l t+P y+x))~~~~~~~~~~~~~~~~~~~~~\nonumber \\&- \sqrt{2 L^2 (P-2 l)} \coth (L (-2 l t+P y+x))\bigg )\times e^{i(lx+py+ct)}. \end{aligned}$$
    (24)

    Set-2:

    $$\begin{aligned} \delta _0=0,~\delta _1= \sqrt{2} \sqrt{L^2 (P-2 l)},~\rho _{1}=0,~ c =a-l^2-2 L^2.~~ \end{aligned}$$

  • Singular solitons are obtained

    $$\begin{aligned} \varPsi _{2}(x,y,t)=-\sqrt{2} \sqrt{L^2 (P-2 l)} \coth (L (-2 l t+P y+x))\times e^{i(lx+py+ct)}.~~~~~~~ \end{aligned}$$
    (25)

    Set-3:

    $$\begin{aligned} \delta _{0}=0,~\delta _{1}=0,~\rho _{1}=\sqrt{2} \sqrt{L^2 (P-2 l)},~ c =a-l^2-2 L^2. \end{aligned}$$

  • Dark solitons are obtained

    $$\begin{aligned} \varPsi _{3}(x,y,t)=-\sqrt{2} \sqrt{L^2 (P-2 l)} \tanh (L (-2 l t+P y+x))\times e^{i(lx+py+ct)}.~~~~~~~~ \end{aligned}$$
    (26)

    Family-2: For \(p=[-i, i, 1, 1]\) and \(q=[i,-i,i,-i]\), the Eq. (5) provides

    $$\begin{aligned} \sigma (\zeta )=-\frac{\sin (\zeta )}{\cos (\zeta )}. \end{aligned}$$
    (27)

    Putting Eq. (22) and Eq. (27) in Eq. (20), we retrieves the solution sets as follows:

    Set-1:

    $$\begin{aligned} \delta _{0}=0,~\delta _{1}=i L \sqrt{4 l-2 P},~\rho _{1}=i L \sqrt{4 l-2 P},~ c =a-l^2-4 L^2. \end{aligned}$$

  • Trigonometric solutions are obtained

    $$\begin{aligned} \varPsi _{4}(x,y,t)=-2 i L \sqrt{4 l-2 P} \csc (2 L (-2 l t+P y+x))\times e^{i(lx+py+ct)}.~~~~~~~ \end{aligned}$$
    (28)

    Set-2:

    $$\begin{aligned} \delta _{0}=0,~\delta _{1}=\sqrt{2 L^2 \left( P-2 \sqrt{a-c-4 L^2}\right) },~\rho _{1}=\sqrt{2 L^2 \left( P-2 \sqrt{a-c-4 L^2}\right) },~\\ l =\sqrt{a-c-4 L^2}. \end{aligned}$$

  • Periodic solutions are obtained

    $$\begin{aligned} \varPsi _{5}(x,y,t)=-2 \sqrt{2} \sqrt{L^2 \left( P-2 \sqrt{a-c-4 L^2}\right) } \csc \left( 2 L \left( -2 t \sqrt{a-c-4 L^2}+P y+x\right) \right) \times e^{i(lx+py+ct)}. \end{aligned}$$
    (29)

    Family-3: For \(p=[1,0,1,1]\) and \(q=[1,0,1,0]\), the Eq. (5) gives

    $$\begin{aligned} \sigma (\zeta )=\frac{e^{\zeta }}{e^{\zeta }+1}. \end{aligned}$$
    (30)

    Substituting Eq. (22) and Eq. (30) in Eq. (20), we achieves the solution set as follows:

    Set-1:

    $$\begin{aligned} \delta _0=i \sqrt{2 l-P} \sqrt{a-c-l^2},~\delta _1=-2 i \sqrt{2 l-P} \sqrt{a-c-l^2},~\rho _1=0,~L=\sqrt{2} \sqrt{a-c-l^2}. \end{aligned}$$

  • Exponential function solutions are obtained

    $$\begin{aligned} \varPsi _{6}(x,y,t)=-\frac{i \sqrt{2 l-P} \sqrt{a-c-l^2} \left( e^{\sqrt{2} \sqrt{a-c-l^2} (-2 l t+P y+x)}-1\right) }{e^{\sqrt{2} \sqrt{a-c-l^2} (-2 l t+P y+x)}+1}\times e^{i(lx+py+ct)}.~~~~~~~ \end{aligned}$$
    (31)

    Family-4: For \(p=[1-i, 1+i, 1, 1]\) and \(q=[i,-i,i,-i]\), the Eq. (5) provides

    $$\begin{aligned} \sigma (\zeta )=\frac{\cos (\zeta )+\sin (\zeta )}{\cos (\zeta )}. \end{aligned}$$
    (32)

    Imposing Eq. (22) and Eq. (32) in Eq. (20), we get solution set as follows:

    Set-1:

    $$\begin{aligned} \delta _0=\sqrt{2 L^2 (P-2 l)},~\delta _1=0,~\rho _1=-2\sqrt{2 L^2 (P-2 l)},~c=a-l^2+2 L^2. \end{aligned}$$

  • Trigonometric solutions are obtained

    $$\begin{aligned} \varPsi _{7}(x,y,t)=\frac{\sqrt{2} \sqrt{L^2 (P-2 l)} (\sin (L (-2 l t+P y+x))-\cos (L (-2 l t+P y+x)))}{\sin (L (-2 l t+P y+x))+\cos (L (-2 l t+P y+x))}\times e^{i(lx+py+ct)}. \end{aligned}$$
    (33)

    Family-5: For \(p=[-3, -1, 1, 1]\) and \(q=[1,-1,1,-1]\), the Eq. (5) provides

    $$\begin{aligned} \sigma (\zeta )=\frac{-2\cosh (\zeta )-\sinh (\zeta )}{\cosh (\zeta )}. \end{aligned}$$
    (34)

    Inserting Eq. (22) and Eq. (34) in Eq. (20), we obtain the solution sets as follows:

    Set-1:

    $$\begin{aligned} \delta _0=2\sqrt{2 L^2 (P-2 l)},~\delta _1=\sqrt{L^2 (P-2 l)},~\rho _1=0,~c=a-l^2-2 L^2. \end{aligned}$$

  • Dark solitons are obtained

    $$\begin{aligned} \varPsi _{8}(x,y,t)=-\sqrt{2} \sqrt{L^2 (P-2 l)} \tanh (L (-2 l t+P y+x))\times e^{i(lx+py+ct)}.~~~~~~~~~ \end{aligned}$$
    (35)

    Set-2:

    $$\begin{aligned} \delta _0=2 \sqrt{2 L^2 (P-2 l)},~\delta _1=0,~\rho _1=3\sqrt{2 L^2 (P-2 l)},~c=a-l^2-2 L^2. \end{aligned}$$

  • Combo solitons are obtained

    $$\begin{aligned} \varPsi _{9}(x,y,t)=\frac{\sqrt{2} \sqrt{L^2 (P-2 l)} (2 \sinh (L (-2 l t+P y+x))+\cosh (L (-2 l t+P y+x)))}{\sinh (L (-2 l t+P y+x))+2 \cosh (L (-2 l t+P y+x))}\times e^{i(lx+py+ct)}. \end{aligned}$$
    (36)

    Family-6: For \(p=[-1, 0, 1, 1]\) and \(q=[0, 1, 0, 1]\), the Eq. (5) gives

    $$\begin{aligned} \sigma (\zeta )=-\frac{1}{e^{\zeta }+1}. \end{aligned}$$
    (37)

    Switching Eq. (22) and Eq. (37) in Eq. (20), we recover solution sets as follows:

    Set-1:

    $$\begin{aligned} \delta _0=\frac{\sqrt{L^2 \left( P-\sqrt{4 a-2 \left( 2 c+L^2\right) }\right) }}{\sqrt{2}},~\delta _1=\sqrt{2 L^2 \left( P-\sqrt{4 a-2 \left( 2 c+L^2\right) }\right) },~\rho _1=0,~l=\sqrt{a-c-\frac{L^2}{2}}. \end{aligned}$$

  • Exponential function solutions are obtained as

    $$\begin{aligned} \varPsi _{10}(x,y,t)=\frac{\sqrt{-L^2 \left( \sqrt{4 a-2 \left( 2 c+L^2\right) }-P\right) } \left( \exp \left( L \left( t \left( -\sqrt{4 a-4 c-2 L^2}\right) +P y+x\right) \right) -1\right) }{\sqrt{2} \left( \exp \left( L \left( t \left( -\sqrt{4 a-4 c-2 L^2}\right) +P y+x\right) \right) +1\right) }\times e^{i(lx+py+ct)}. \end{aligned}$$
    (38)

    Set-2:

    $$\begin{aligned} \delta _0=i \sqrt{2 l-P} \sqrt{a-c-l^2},~\delta _1=2 i \sqrt{2 l-P} \sqrt{a-c-l^2},~\rho _1=0,~L=\sqrt{2} \sqrt{a-c-l^2}. \end{aligned}$$

  • Exponential function solutions are obtained

    $$\begin{aligned} \varPsi _{11}(x,y,t)=i \sqrt{2 l-P} \sqrt{a-c-l^2} \left( 1-\frac{2}{e^{\sqrt{2} \sqrt{a-c-l^2} (-2 l t+P y+x)}+1}\right) \times e^{i(lx+py+ct)}.~~~~~~~~ \end{aligned}$$
    (39)

    Family-7: For \(p=[-1, 1, 1, 1]\) and \(q=[1, -1, 1,-1]\), the Eq. (5) provides

    $$\begin{aligned} \sigma (\zeta )=-\frac{\sinh (\zeta )}{\cosh (\zeta )}. \end{aligned}$$
    (40)

    Putting Eq. (22) and Eq. (40) in Eq. (20), we get the solution sets as follows:

    Set-1:

    $$\begin{aligned} \delta _0=0,~\delta _1=\frac{\sqrt{2 l-P} \sqrt{a-c-l^2}}{\sqrt{2}},~\rho _1=-\frac{\sqrt{2 l-P} \sqrt{a-c-l^2}}{\sqrt{2}},~L=\frac{1}{2} \sqrt{-a+c+l^2}. \end{aligned}$$

  • Mixed solitons are obtained

    $$\begin{aligned} \varPsi _{12}(x,y,t)= & {} \bigg (\frac{\sqrt{2 l-P} \sqrt{a-c-l^2} \coth \left( \frac{1}{2} \sqrt{-a+c+l^2} (-2 l t+P y+x)\right) }{\sqrt{2}}~~~~~~~~~~~~~~~~~~~\nonumber \\&-\frac{\sqrt{2 l-P} \sqrt{a-c-l^2} \tanh \left( \frac{1}{2} \sqrt{-a+c+l^2} (-2 l t+P y+x)\right) }{\sqrt{2}}\bigg )\times e^{i(lx+py+ct)}. \end{aligned}$$
    (41)

    Set-2:

    $$\begin{aligned} \delta _0=0,~\delta _1=-i L \sqrt{4 l-2 P},~\rho _1=i L \sqrt{4 l-2 P},~c=a-l^2+4 L^2. \end{aligned}$$

  • The soliton solutions are obtained

    $$\begin{aligned} \varPsi _{13}(x,y,t)=\i L \sqrt{4 l-2 P} \tanh (L (-2 l t+P y+x))-i L \sqrt{4 l-2 P} \coth (L (-2 l t+P y+x))\times e^{i(lx+py+ct)}.~~~~~~~ \end{aligned}$$
    (42)

    Family-8: For \(p=[2-i, 2+i, 1, 1]\) and \(q=[i, -i, i, -i]\), the Eq. (5) provides

    $$\begin{aligned} \sigma (\zeta )=\frac{\sin (\zeta )+2\cos (\zeta )}{\cos (\zeta )}. \end{aligned}$$
    (43)

    Placing Eq. (22) and Eq. (43) in Eq. (20), we retrieve the solution sets as follows:

    Set-1:

    $$\begin{aligned} \delta _{0}=2\sqrt{2 L^2 (P-2 l)},~\delta _{1}=-\sqrt{2 L^2 (P-2 l)},~\rho _{1}=0,~c=a-l^2+2 L^2. \end{aligned}$$

  • Singular periodic solutions are obtained

    $$\begin{aligned} \varPsi _{14}(x,y,t)=-\sqrt{2} \sqrt{L^2 (P-2 l)} \tan (L (-2 l t+P y+x))\times e^{i(lx+py+ct)}.~~~~~ \end{aligned}$$
    (44)

    Set-2:

    $$\begin{aligned} \delta _{0}=-2\sqrt{2 L^2 (P-2 l)},~\delta _{1}=0,~\rho _{1}=5\sqrt{2 L^2 (P-2 l)},~c=a-l^2+2 L^2. \end{aligned}$$

  • Singular periodic solutions are obtained

    $$\begin{aligned} \varPsi _{15}(x,y,t)=\frac{\sqrt{2} \sqrt{L^2 (P-2 l)} (1-2 \tan (L (-2 l t+P y+x)))}{\tan (L (-2 l t+P y+x))+2}\times e^{i(lx+py+ct)}.~~~~ \end{aligned}$$
    (45)

    Family-9: For \(p=[1, 2, 1, 1]\) and \(q=[1, 0, 1, 0]\), the Eq. (5) recovers

    $$\begin{aligned} \sigma (\zeta )=\frac{e^{\zeta }+2}{e^{\zeta }+1}. \end{aligned}$$
    (46)

    Imposing Eq. (22) and Eq. (46) in Eq. (20), we get the solution sets as follows:

    Set-1:

    $$\begin{aligned} \delta _0=-\frac{3 \sqrt{L^2 (P-2 l)}}{\sqrt{2}},~\delta _1=0,~\rho _1=2\sqrt{2 L^2 (P-2 l)},~c=a-l^2-\frac{L^2}{2}. \end{aligned}$$

  • Exponential function solutions are obtained

    $$\begin{aligned} \varPsi _{16}(x,y,t)=\frac{\sqrt{L^2 (P-2 l)} \left( e^{L (-2 l t+P y+x)}-2\right) }{\sqrt{2} \left( e^{L (-2 l t+P y+x)}+2\right) }\times e^{i(lx+py+ct)}.~~~~~~~ \end{aligned}$$
    (47)

    Set-2:

    $$\begin{aligned} \delta _0=-\frac{3 \sqrt{L^2 (P-2 l)}}{\sqrt{2}},~\delta _1=\sqrt{2 L^2 (P-2 l)},~\rho _1=0,~c=a-l^2-\frac{L^2}{2}. \end{aligned}$$

  • Exponential function solutions are obtained

    $$\begin{aligned} \varPsi _{17}(x,y,t)=-\frac{\sqrt{L^2 (P-2 l)} \left( e^{L (-2 l t+P y+x)}-1\right) }{\sqrt{2} \left( e^{L (-2 l t+P y+x)}+1\right) }\times e^{i(lx+py+ct)}.~~~~~~~ \end{aligned}$$
    (48)

    Family-10: For \(p=[2, 1, 1, 1]\) and \(q=[1, 0, 1, 0]\), the Eq. (5) retrieves

    $$\begin{aligned} \sigma (\zeta )=\frac{2e^{\zeta }+1}{e^{\zeta }+1}. \end{aligned}$$
    (49)

    Switching Eq. (22) and Eq. (49) in Eq. (20), we obtain the solution sets as follows:

    Set-1:

    $$\begin{aligned} \delta _0=-\frac{3 \sqrt{L^2 (P-2 l)}}{\sqrt{2}},~\delta _1=0,~\rho _1=2\sqrt{2 L^2 (P-2 l)},~c=a-l^2-\frac{L^2}{2}. \end{aligned}$$

  • Exponential function solutions are obtained

    $$\begin{aligned} \varPsi _{18}(x,y,t)=\frac{\sqrt{L^2 (P-2 l)} \left( 1-2 e^{L (-2 l t+P y+x)}\right) }{\sqrt{2} \left( 2 e^{L (-2 l t+P y+x)}+1\right) }\times e^{i(lx+py+ct)}.~~~~~~~ \end{aligned}$$
    (50)

    Set-2:

    $$\begin{aligned} \delta _0=-\frac{3 \sqrt{L^2 (P-2 l)}}{\sqrt{2}},~\delta _1=\sqrt{2 L^2 (P-2 l)},~\rho _1=0,~c=a-l^2-\frac{L^2}{2}. \end{aligned}$$

  • Exponential function solutions are obtained

    $$\begin{aligned} \varPsi _{19}(x,y,t)=\frac{\sqrt{L^2 (P-2 l)} \left( e^{L (-2 l t+P y+x)}-1\right) }{\sqrt{2} \left( e^{L (-2 l t+P y+x)}+1\right) }\times e^{i(lx+py+ct)}.~~~~~~~ \end{aligned}$$
    (51)

    Family-11: For \(p=[1, 1, 1, 1]\) and \(q=[0, 0, 1, -1]\), the Eq. (5) provides

    $$\begin{aligned} \sigma (\zeta )=\frac{2}{e^{\zeta }+e^{-\zeta }}. \end{aligned}$$
    (52)

    Putting Eq. (22) and Eq. (49) in Eq. (20), we get the solution set as follows:

    Set-1:

    $$\begin{aligned} \delta _0=0,~\delta _1=\sqrt{2 L^2 (2 l-P)},~\rho _1=0,~c=a-l^2+L^2. \end{aligned}$$

  • Bright solitons are obtained

    $$\begin{aligned} \varPsi _{20}(x,y,t)=\sqrt{2 L^2 (2 l-P)} \text {sech}(L (2 l t-P y-x))\times e^{i(lx+py+ct)}.~~~~~ \end{aligned}$$
    (53)

3.2 Solutions via (\(\frac{G^{\prime }}{G^2}\))-expansion method

By applying balance rule via Eq. (21), in Eq. (20) yields, \(n=1\). The solution of Eq. (20) as follows:

$$\begin{aligned} H(\zeta )=\beta _{0}+\sum _{j=1}^n\Bigg ( \beta _j\bigg (\frac{G^{\prime }}{G^2}\bigg )^j+ \delta _j\bigg (\frac{G^{\prime }}{G^2}\bigg )^{-j}\Bigg ), \end{aligned}$$
$$\begin{aligned} H(\zeta )=\beta _{0}+\beta _{1} \bigg (\frac{G^{\prime }}{G^{2}}\bigg )+\delta _{1} \bigg (\frac{G^{\prime }}{G^{2}}\bigg )^{-1}.~~~~ \end{aligned}$$
(54)

Inserting Eq. (54) into Eq. (20) together with Eq. (9) and by equating the coefficients of each powers of \(\bigg (\frac{G^{\prime }}{G^{2}}\bigg )\) to zero. On solving the system of algebraic equations through Mathematica, we obtain the following solution sets:

$$\begin{aligned} {\mathbf{Set-1}}&:&~~\beta _0=0,~~\beta _1=\sqrt{2 L^2 \varOmega ^2 (P-2 l)},~~\delta _1=0,~~c=a-l^2+2 L^2 \varUpsilon \varOmega .~~~~~~~~~~~~~~~~~~~~~ \\ {\mathbf{Set-2}}&:&~~\beta _0=0,~~\beta _1=0,~~\delta _1=\sqrt{2 L^2 \varUpsilon ^2 (P-2 l)},~~c=a-l^2+2 L^2 \varUpsilon \varOmega .~~~~~~~~~~~~~~~~~~~~~ \\ {\mathbf{Set-3}}&:&~~\beta _0=0,~~\beta _1=\sqrt{2 L^2 \varOmega ^2 (P-2 l)},~~\delta _1=\sqrt{2 L^2 \varUpsilon ^2 (P-2 l)},\\&c&=a-l^2-\frac{6 L^2 \varUpsilon ^2 \sqrt{L^2 \varOmega ^2 (P-2 l)}}{\sqrt{L^2 \varUpsilon ^2 (P-2 l)}}+2 L^2 \varUpsilon \varOmega . \end{aligned}$$

For Set-1,

  •  Trigonometric solutions:

    If \(\varUpsilon \varOmega >0\),

    $$\begin{aligned} \varPsi _{1,1}(x, y, t)=\frac{\sqrt{2} \sqrt{\varUpsilon } \sqrt{L^2 \varOmega ^2 (P-2 l)} \left( \zeta _1 \sin \left( \zeta \sqrt{\varUpsilon \varOmega }\right) +\zeta _2 \cos \left( \zeta \sqrt{\varUpsilon \varOmega }\right) \right) }{\sqrt{\varOmega } \left( \zeta _2 \cos \left( \zeta \sqrt{\varUpsilon \varOmega }\right) -\zeta _1 \sin \left( \zeta \sqrt{\varUpsilon \varOmega }\right) \right) }\times e^{i(lx+py+ct)}.~~~~~~~~ \end{aligned}$$
    (55)

  •  Hyperbolic solution:

    If \(\varUpsilon \varOmega <0\),

    $$\begin{aligned} \varPsi _{1,2}(x, y, t)=-\frac{ \sqrt{\big | \varUpsilon \varOmega \big | } \sqrt{-2 L^2 \varOmega ^2 (2 l-P)} \big (\zeta _1 \big (\sinh \big (2 \zeta \sqrt{\big | \varUpsilon \varOmega \big | }\big )+\cosh \big (2 \zeta \sqrt{\big | \varUpsilon \varOmega \big | }\big )\big )+\zeta _2\big )}{\varOmega \big (\zeta _1 \big (\sinh \big (2 \zeta \sqrt{\big | \varUpsilon \varOmega \big | }\big )+\cosh \big (2 \zeta \sqrt{\big | \varUpsilon \varOmega \big | }\big )\big )-\zeta _2\big )}\times e^{i(lx+py+ct)}.~~~~~~~ \end{aligned}$$
    (56)

  •  For soliton solution, take \(\zeta _1=\zeta _2\), we get singular wave solution as:

    $$\begin{aligned} \varPsi _{1,2}(x, y, t)=-\frac{\sqrt{2} \sqrt{\big | \varUpsilon \varOmega \big | } \sqrt{-L^2 \varOmega ^2 (2 l-P)} \coth \left( \zeta \sqrt{\big | \varUpsilon \varOmega \big | }\right) }{\varOmega }\times e^{i(lx+py+ct)}. \end{aligned}$$
    (57)

  •  Rational solutions:

    If \(\varUpsilon =0, \varOmega \ne 0\),

    $$\begin{aligned} \varPsi _{1,3}(x, y, t)= -\frac{\sqrt{2} \zeta _1 \sqrt{L^2 \varOmega ^2 (P-2 l)}}{\varOmega \left( \zeta \zeta _1+\zeta _2\right) }\times e^{i(lx+py+ct)}.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (58)

    If we take \(\zeta _1=\zeta _2\), a rational function solution is obtained

    $$\begin{aligned} \varPsi _{1,3}(x, y, t)= -\frac{\sqrt{2} \sqrt{-L^2 \varOmega ^2 (2 l-P)}}{\zeta \varOmega +\varOmega }\times e^{i(lx+py+ct)}.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (59)

    For Set-2,

  •  Trigonometric solutions:

    If \(\varUpsilon \varOmega >0\),

    $$\begin{aligned} \varPsi _{2,1}(x, y, t)=\frac{\sqrt{2} \sqrt{\varOmega } \sqrt{L^2 \varUpsilon ^2 (P-2 l)} \left( \zeta _2 \cos \left( \zeta \sqrt{\varUpsilon \varOmega }\right) -\zeta _1 \sin \left( \zeta \sqrt{\varUpsilon \varOmega }\right) \right) }{\sqrt{\varUpsilon } \left( \zeta _1 \sin \left( \zeta \sqrt{\varUpsilon \varOmega }\right) +\zeta _2 \cos \left( \zeta \sqrt{\varUpsilon \varOmega }\right) \right) }\times e^{i(lx+py+ct)}. \end{aligned}$$
    (60)

  •  Hyperbolic solution:

    If \(\varUpsilon \varOmega <0\),

    $$\begin{aligned} \varPsi _{2,2}(x, y, t)=-\frac{\sqrt{2} \varOmega \sqrt{-L^2 \varUpsilon ^2 (2 l-P)} \left( \zeta _1 \left( \sinh \left( 2 \zeta \sqrt{\big | \varUpsilon \varOmega \big | }\right) +\cosh \left( 2 \zeta \sqrt{\big | \varUpsilon \varOmega \big | }\right) \right) -\zeta _2\right) }{\sqrt{\big | \varUpsilon \varOmega \big | } \left( \zeta _1 \left( \sinh \left( 2 \zeta \sqrt{\big | \varUpsilon \varOmega \big | }\right) +\cosh \left( 2 \zeta \sqrt{\big | \varUpsilon \varOmega \big | }\right) \right) +\zeta _2\right) }\times e^{i(lx+py+ct)}.~~~~ \end{aligned}$$
    (61)

  •  For soliton solution, take \(\zeta _1=\zeta _2\), we get dark soliton solution as:

    $$\begin{aligned} \varPsi _{2,2}(x, y, t)=-\frac{\sqrt{2} \varOmega \sqrt{-L^2 \varUpsilon ^2 (2 l-P)} \tanh \left( \zeta \sqrt{\big | \varUpsilon \varOmega \big | }\right) }{\sqrt{\big | \varUpsilon \varOmega \big | }}\times e^{i(lx+py+ct)}.~~~~~~~~ \end{aligned}$$
    (62)

    For Set-3,

  •  Trigonometric solutions:

    If \(\varUpsilon \varOmega >0\),

    $$\begin{aligned} \varPsi _{3,1}(x, y, t)= & {} \frac{\sqrt{2} \sqrt{\varOmega } \sqrt{L^2 \varUpsilon ^2 (P-2 l)} \left( \zeta _2 \cos \left( \zeta \sqrt{\varUpsilon \varOmega }\right) -\zeta _1 \sin \left( \zeta \sqrt{\varUpsilon \varOmega }\right) \right) }{\sqrt{\varUpsilon } \left( \zeta _1 \sin \left( \zeta \sqrt{\varUpsilon \varOmega }\right) +\zeta _2 \cos \left( \zeta \sqrt{\varUpsilon \varOmega }\right) \right) }\nonumber \\&+\frac{\sqrt{2} \sqrt{\varUpsilon } \sqrt{L^2 \varOmega ^2 (P-2 l)} \left( \zeta _1 \sin \left( \zeta \sqrt{\varUpsilon \varOmega }\right) +\zeta _2 \cos \left( \zeta \sqrt{\varUpsilon \varOmega }\right) \right) }{\sqrt{\varOmega } \left( \zeta _2 \cos \left( \zeta \sqrt{\varUpsilon \varOmega }\right) -\zeta _1 \sin \left( \zeta \sqrt{\varUpsilon \varOmega }\right) \right) }\times e^{i(lx+py+ct)}. \end{aligned}$$
    (63)

  •   For soliton solution, take \(\zeta _1=\zeta _2\), we get periodic wave solution as:

    $$\begin{aligned} \varPsi _{3,1}(x, y, t)= & {} \frac{1}{\sqrt{\varUpsilon } \sqrt{\varOmega }}\times \sqrt{2}\sec \left( 2 \zeta \sqrt{\varUpsilon \varOmega }\right) \left( \varOmega \sqrt{-L^2 \varUpsilon ^2 (2 l-P)}+\varUpsilon \sqrt{-L^2 \varOmega ^2 (2 l-P)}\right. ~~~~~~~~~~~~\nonumber \\&\left. +\left( \varUpsilon \sqrt{-L^2 \varOmega ^2 (2 l-P)}-\varOmega \sqrt{-L^2 \varUpsilon ^2 (2 l-P)}\right) \sin \left( 2 \zeta \sqrt{\varUpsilon \varOmega }\right) \right) \times e^{i(lx+py+ct)}. \end{aligned}$$
    (64)

  •  Hyperbolic solution:

    If \(\varUpsilon \varOmega <0\),

    $$\begin{aligned} \varPsi _{3,2}(x, y, t)= & {} \frac{\varOmega ^2 \left( -\sqrt{2 L^2 \varUpsilon ^2 (P-2 l)}\right) \left( \zeta _2-\zeta _1 e^{2 \zeta \sqrt{\big | \varUpsilon \varOmega \big | }}\right) {}^2}{\left. \varOmega \sqrt{\big | \varUpsilon \varOmega \big | } \left( \zeta _1^2 e^{4 \zeta \sqrt{\big | \varUpsilon \varOmega \big | }}-\zeta _2^2\right) \right) }~~~~~~~~~~~~~~~~\nonumber \\&-\frac{\big | \varUpsilon \varOmega \big | \sqrt{2L^2 \varOmega ^2 (P-2 l)} \left( \zeta _1 e^{2 \zeta \sqrt{\big | \varUpsilon \varOmega \big | }}+\zeta _2\right) {}^2}{\left. \varOmega \sqrt{\big | \varUpsilon \varOmega \big | } \left( \zeta _1^2 e^{4 \zeta \sqrt{\big | \varUpsilon \varOmega \big | }}-\zeta _2^2\right) \right) }\times e^{i(lx+py+ct)}. \end{aligned}$$
    (65)

  •   For soliton solution, take \(\zeta _1=\zeta _2\), we get combo dark-singular wave solution as:

    $$\begin{aligned} \varPsi _{3,2}(x, y, t)=-\frac{ \tanh \left( \zeta \sqrt{\big | \varUpsilon \varOmega \big | }\right) \left( \big | \varUpsilon \varOmega \big | \sqrt{2L^2 \varOmega ^2 (P-2 l)} \coth ^2\left( \zeta \sqrt{\big | \varUpsilon \varOmega \big | }\right) +\varOmega ^2 \sqrt{L^2 \varUpsilon ^2 (P-2 l)}\right) }{\varOmega \sqrt{\big | \varUpsilon \varOmega \big | }}\times e^{i(lx+py+ct)}.\nonumber \\ \end{aligned}$$
    (66)

    For all the above set (1, 2, 3)    \(\zeta =L(x+Py - 2lt)\).

3.3 Solutions via generalized Kudryashov method

By using the homogeneous balance rule, the highest order derivative \(H^{\prime \prime }(\zeta )\) and the nonlinear term of the highest order \(H^3(\zeta )\) are balanced via the Eq. (7) in Eq. (20), and from Eq. (20), for this method we have

$$\begin{aligned} deg\big [H^{\prime \prime }(\zeta )\big ]=(n-m)+2\end{aligned}$$
(67)
$$\begin{aligned} deg\big [H^3(\zeta )\big (H^{\prime \prime }(\zeta )\big )^s\big ]=3(n-m)+s(n-m+k). \end{aligned}$$
(68)

From above two equations we have

$$\begin{aligned} (n-m)+2=3(n-m)+0(n-m+k). \end{aligned}$$
(69)

which leads to

$$\begin{aligned} n=m+1. \end{aligned}$$
(70)

Particularly, if we assigning \(m=1\), we get \(n=2\). The proposed method has the solution to Eq. (20) as follows

$$\begin{aligned} H(\zeta )=\frac{a_0+a_1G(\zeta )+a_2G^2(\zeta )}{b_0+b_1G(\zeta )},~~~~~~~~~~~~~~ \end{aligned}$$
(71)

where \( a_0, a_1, a_2, b_0 \) and \(b_1\) are to be determined. Now, solving Eqs. (20) and (71), and following the step 3 of the method, we get the system of equations is obtained. With the assistance of computational software like Mathematica, we solve the system of algebraic expression, and a variety of solution sets is obtained as

Set-1:

$$\begin{aligned} a_1=-i \left( 2 b_0-b_1\right) L \sqrt{l-\frac{P}{2}},~a_0=i b_0 L \sqrt{l-\frac{P}{2}},~c=a-l^2-\frac{L^2}{2},~a_2=-i b_1 L \sqrt{4 l-2 P}.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$

On substituting the above values of parameters in Eq. (71) and with the assistance of Eq. (15), and on setting \(S=1 \), the hyperbolic functions are obtained

$$\begin{aligned} \varPsi _1(x,y, t)=-i L \sqrt{l-\frac{P}{2}} \tanh \left( \frac{1}{2} L (2 l t-P y-x)\right) \times e^{i(lx+py+ct)}.~~~~~~~~~~~~~~ \end{aligned}$$
(72)

Set-2:

$$\begin{aligned} a_1=-i \left( 2 b_0+b_1\right) L \sqrt{l-\frac{P}{2}},~a_0=-\frac{\sqrt{b_0^2 \left( b_0+b_1\right) {}^2 \left( -L^2\right) (2 l-P)}+i b_0^2 L \sqrt{2 l-P}}{\sqrt{2} b_1},~\\c=\frac{1}{2} \left( 2 a+\frac{2 L \left( b_0 \left( b_0+b_1\right) (-L)+\frac{i \sqrt{b_0^2 \left( b_0+b_1\right) {}^2 \left( -L^2\right) (2 l-P)}}{\sqrt{2 l-P}}\right) }{b_1^2}-2 l^2-L^2\right) ,~a_2=0.~ \end{aligned}$$

By taking \(S=1\) and solving Eqs. (71) and (15) together, we get exponential function solution as follows

$$\begin{aligned} \varPsi _2(x,y, t)=-\frac{\frac{\sqrt{b_0^2 \left( b_0+b_1\right) {}^2 \left( -L^2\right) (2 l-P)}+i b_0^2 L \sqrt{2 l-P}}{\sqrt{2} b_1}+\frac{i \left( 2 b_0+b_1\right) L \sqrt{l-\frac{P}{2}}}{e^{L (-2 l t+P y+x)}+1}}{\frac{b_1}{e^{L (-2 l t+P y+x)}+1}+b_0}\times e^{i(lx+py+ct)}.~~~~~~~~~~~ \end{aligned}$$
(73)

Set-3:

$$\begin{aligned} a_1=-2 i b_0 L \sqrt{4 l-2 P},~b_1=-2 b_0;a_0=\frac{-\sqrt{b_0^2 L^2 (P-2 l)}+3 i b_0 L \sqrt{2 l-P}}{2 \sqrt{2}},~\\c=a-\frac{3 i L \sqrt{b_0^2 L^2 (P-2 l)}}{4 b_0 \sqrt{2 l-P}}-l^2-\frac{5 L^2}{4},~a_2=2 i b_0 L \sqrt{4 l-2 P}.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$

On selecting \(S=1\) and solving Eqs. (71) and (15) together, we get soliton solution as

$$\begin{aligned} \varPsi _3(x,y, t)= & {} \frac{1}{b_0-\frac{2 b_0}{-\sinh (2 l L t-L P y-L x)+\cosh (2 l L t-L P y-L x)+1}}\times \nonumber \\&\times \bigg (\frac{2 i b_0 L \sqrt{4 l-2 P}}{(-\sinh (2 l L t-L P y-L x)+\cosh (2 l L t-L P y-L x)+1)^2}+\frac{3 i b_0 L \sqrt{2 l-P}}{2 \sqrt{2}}~~~~~~~~~~~~~~~~~\nonumber \\&-\frac{\sqrt{b_0^2 L^2 (P-2 l)}}{2 \sqrt{2}}-\frac{2 i b_0 L \sqrt{4 l-2 P}}{-\sinh (2 l L t-L P y-L x)+\cosh (2 l L t-L P y-L x)+1}\bigg )\times e^{i(lx+py+ct)}. \end{aligned}$$
(74)

Set-4:

$$\begin{aligned} a_1=i b_0 L \sqrt{4 l-2 P},~b_1=0,~a_0=-i b_0 L \sqrt{l-\frac{P}{2}},~c=a-l^2-\frac{L^2}{2},~a_2=0.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$

For \(S=1\) and solving Eqs. (71) and (15) together, we get the singular wave solution as

$$\begin{aligned} \varPsi _4(x,y, t)=i L \sqrt{l-\frac{P}{2}} \coth \left( \frac{1}{2} L (2 l t-P y-x)\right) \times e^{i(lx+py+ct)}.~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(75)

Set-5:

$$\begin{aligned} a_1= & {} 2 i b_0 L \sqrt{4 l-2 P},~b_1=-2 b_0,~a_0=\frac{\sqrt{b_0^2 L^2 (P-2 l)}-3 i b_0 L \sqrt{2 l-P}}{2 \sqrt{2}}\\ c= & {} a-\frac{3 i L \sqrt{b_0^2 L^2 (P-2 l)}}{4 b_0 \sqrt{2 l-P}}-l^2-\frac{5 L^2}{4},~a_2=-2 i b_0 L \sqrt{4 l-2 P}. \end{aligned}$$

In particular, on \(S=-1\) and solving Eqs. (71) and (15) together, the hyperbolic function solution can be expressed as

$$\begin{aligned} \varPsi _5(x,y, t)= & {} \frac{1}{\sqrt{2} b_0 \left( e^{2 L (-2 l t+P y+x)}-1\right) } \times \bigg (-i b_0 L \sqrt{2 l-P} (3 \cosh (L (2 l t-P y-x))+1)\nonumber \\&\sqrt{b_0^2 L^2 (P-2 l)} +(\cosh (L (2 l t-P y-x))-1)\bigg )\times e^{i(lx+py+ct)}. \end{aligned}$$
(76)

Set-6:

$$\begin{aligned} a_1=-i b_1 L \sqrt{4 l-2 P},~a_0=0,~b_0=-\frac{b_1}{2},~c=a-l^2+L^2,~a_2=i b_1 L \sqrt{4 l-2 P}.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$

If we select \(S=1\) and solving Eqs. (71) and (15) together, then we obtain singular wave solution as

$$\begin{aligned} \varPsi _6(x,y, t)=-i L \sqrt{4 l-2 P} \text {csch}(L (2 l t-P y-x))\times e^{i(lx+py+ct)}.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(77)

4 Results and discussion

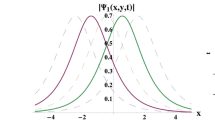
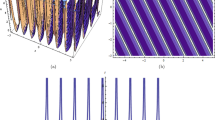
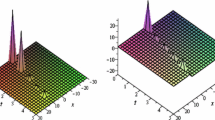
In this section, we will compare our results with other results in the existing research literature after successful utilization of three proposed computational methods to the given dynamical model. Akhtar Chowdhury et al. [27] examine the explicit and periodic solutions by utilizing the double \(( \frac{G'}{G}\), \(\frac{1}{G})\)-expansion method. Besides, in these references [28,29,30,31,32], the authors attained a few solutions to the (2+1)-dimensional soliton equation. However, in this manuscript, our main objective is to extract a variety of solitons in bright, dark, singular, and combo forms along with exponential function, rational and singular periodic solutions. We observe that the retrieved solutions are new and to the best of our knowledge the applications of these techniques to the dynamical soliton equation have not been reported in the literature beforehand. The accomplished outcomes are remarkable and new from the current results in available writing. We encountered that the results presented in this article could help explain the genuine meaning of various nonlinear advancement conditions arising in the many fields of nonlinear sciences especially in mathematical physics. Moreover, these results have some other physical meanings, for instance; the hyperbolic sine function appears in the gravitational potential of a cylinder and the calculation of the Roche limit, the hyperbolic cosine function appears in the shape of a hanging cable (the so-called CATENARY), the hyperbolic tangent appears in the calculation of magnetic moment and special relativity rapidity, and the hyperbolic cotangent appears in the Langevin function for magnetic porosity [37]. By substituting the diverse values to the parameters, variants wave results are discovered from the exact peregrinating wave solution. The dark, periodic and bright soliton solutions, which are provided in Eqs.  (26, 62, 72),  44 and (53) as exhibited in figs (1,4, 5), (2) and (3) respectively. The physically description of some solutions are given below.

Fig. 1
figure 1

The 3D, and 2D graphs are presented for Eq. (26)

Full size image
Fig. 2
figure 2

The 3D, and 2D graphs are presented for Eq. (44)

Full size image
Fig. 3
figure 3

The 3D, and 2D graphs are presented for Eq. (53)

Full size image
Fig. 4
figure 4

The 3D, and 2D graphs are presented for Eq. (62)

Full size image
Fig. 5
figure 5

The 3D, and 2D graphs are presented for Eq. (72)

Full size image

5 Conclusions

The exploration of this novel effort is to investigate solitary wave solutions in diverse forms as hyperbolic, trigonometric, exponential, and rational function solutions along with well-known soliton solutions in the shapes of bright dark, singular, and multiple solitons by three analytical mathematical methods. The accomplished outcomes are remarkable and new from the current results in available writing. Furthermore, 3D, and 2D graphs have been plotted under the choice of appropriate parameters for getting the physical behavior of some secured solutions. The reported outcomes will be valuable for a comprehensive insight of the dynamics of the mentioned model, and more, the analysis can be enhanced to other nonlinear models. The scrutinized wave’s results are loyal to the researchers and also have imperious applications in mathematical physics. Finally, our solutions have been verified using the Mathematica by substituting them back into the original equation. We can assert from the obtained results that the applied techniques are simple, vibrant, and quite well, and will be helpful tool for addressing more highly nonlinear issues in various of fields, especially in physical sciences. Furthermore, our findings are first step toward understanding the structure and physical behavior of complicated structures. We anticipate that our results will be highly valuable in better understanding the waves that occur in the diverse area of physics. We feel that this work is timely and will be of interest to a wide spectrum of experts working on physical and engineering models.