1 Introduction

The dynamics of optical solitons is one of the most important areas of research in the field of nonlinear optics [1–15]. There are many new results that have been produced in this field. Many long-distance communications around the world are put into practice under favour of this technology.

The governing equation for the propagation of optical solitons is the NLSE. There are many mathematical features of the NLSE that interest the nonlinear optics community. We consider the CNLSE with spatiotemporal dispersion (STD) and group velocity dispersion (GVD) in this study. There are four nonlinear forms of the optical couplers that will be studied in this paper. These are Kerr law, power law, parabolic law and dual-power law. Jacobi elliptic functions are going to be used to get exact solutions of the CNLSE.

The paper is arranged as follows: In Sect. 2, we present the mathematical analysis for the CNLSE with Kerr, power, parabolic and dual-power laws. In last Section, we give some conclusions.

2 Mathematical analysis

The CNLSE is going to be studied in this paper which is given by [3, 4]

$$\begin{aligned} iq_t +a_1 q_{xx} +b_1 q_{xt} +c_1 F\left( {\left| q \right| ^{2}} \right) q= & {} k_1 r, \end{aligned}$$
(1)
$$\begin{aligned} ir_t +a_2 r_{xx} +b_2 r_{xt} +c_2 F\left( {\left| r \right| ^{2}} \right) r= & {} k_2 q. \end{aligned}$$
(2)

Equations (1) and (2) are the governing equation for twin-core couplers. Here, q and r represent dimensionless forms of the optical fields in the respective cores of the optical fibres. \(a_\ell \) and \(b_\ell \) represent, respectively, the coefficients of GVD and STD for \(\ell =1,2\). Also, \(c_\ell \) represents the coefficients of nonlinearity and \(k_\ell \) describes the coupling coefficients for \(\ell =1,2\). The function F gives the type of nonlinearity that will be studied. Considering the complex plane C as a two-dimensional linear space \(R^{2}\), the function \(F\left( {\left| q \right| ^{2}} \right) q:C\rightarrow C\) is k times continuously differentiable, so that \(F\left( {q^{2}} \right) q\in \cup _{m,n=1}^\infty C^{k}\left( {\left( {-n,n} \right) \times \left( {-m,m} \right) ;R^{2}} \right) \). Since q and r are complex-valued function, the solution for the CNLSE can be written in the form

$$\begin{aligned} q(x,t)= & {} P_1(x,t)e^{i\phi }, \end{aligned}$$
(3)
$$\begin{aligned} r(x,t)= & {} P_2(x,t)e^{i\phi }, \end{aligned}$$
(4)

where \(P\ell (x,t)\) represents the amplitude component of the soliton, while the phase component \(\phi \) is defined as

$$\begin{aligned} \phi (\hbox {x},\hbox {t})=-\kappa \hbox {x}+\hbox {wt}+\theta , \end{aligned}$$
(5)

where \(\kappa \) represents the soliton frequency, w is the soliton wave number and \(\theta \) is the phase constant. Substituting (3) and (4) into (1) and (2) and then decomposing into real and imaginary parts gives

$$\begin{aligned}&a_\ell \frac{\partial ^{2}P_\ell }{\partial x^{2}} +b_\ell \frac{\partial ^{2}P_\ell }{\partial x\partial t} +P_\ell \left( {b_\ell wk-w-a_\ell \kappa ^{2}} \right) \nonumber \\&\quad +c_\ell F\left( {P_\ell ^2 } \right) P_\ell -k_\ell P_{\ell ^{{*}}} =0, \end{aligned}$$
(6)

and

$$\begin{aligned} \left( {1-b_\ell k} \right) \frac{\partial P_\ell }{\partial t}+\left( {b_\ell w-2a_\ell \kappa } \right) \frac{\partial P_\ell }{\partial x}=0, \end{aligned}$$
(7)

respectively. Here, \(\ell =1,2\) and \(\ell ^{{*}}=3-\ell . \quad P_\ell \) is written of the following form of travelling wave type

$$\begin{aligned}&P_1 \left( {x,t} \right) =U_1 \left( \xi \right) ,\quad P_2 \left( {x,t} \right) =U_2 \left( \xi \right) ,\nonumber \\&\quad \xi =B\left( {x-vt} \right) \end{aligned}$$
(8)

where B represent the inverse width and v is the velocity of the soliton. So, it can be written

$$\begin{aligned}&\left( {a_\ell -b_\ell v} \right) B^{2}\frac{\partial ^{2}U_\ell }{\partial \xi ^{2}}+U_\ell \left( {b_\ell wk-w-a_\ell \kappa ^{2}} \right) \nonumber \\&\quad +c_\ell F\left( {U_\ell ^2 } \right) U_\ell -k_\ell U_{\ell ^{{*}}} =0, \end{aligned}$$
(9)

and

$$\begin{aligned} \left\{ {-v\left( {1-b_\ell \kappa } \right) +b_\ell w-2a_\ell \kappa } \right\} B\frac{\partial U_\ell }{\partial \xi }=0. \end{aligned}$$
(10)

Equation (10) leads to

$$\begin{aligned} v=\frac{b_\ell w-2a_\ell \kappa }{1-b_\ell \kappa }. \end{aligned}$$
(11)

Equating the two expressions for the soliton velocity leads to

$$\begin{aligned} a_1 =a_2 ,b_1 =b_2 \end{aligned}$$
(12)

So, Eq. (9) reduces to

$$\begin{aligned} v=\frac{bw-2a\kappa }{1-b\kappa }. \end{aligned}$$
(13)

In this way, the CNLSE for twin-core couplers given by (1) and (2) can be written

$$\begin{aligned} iq_t +aq_{xx} +bq_{xt} +c_1 F\left( {\left| q \right| ^{2}} \right) q= & {} k_1 r, \end{aligned}$$
(14)
$$\begin{aligned} ir_t +ar_{xx} +br_{xt} +c_2 F\left( {\left| r \right| ^{2}} \right) r= & {} k_2 q, \end{aligned}$$
(15)

where \(a_1 =a_2 =a\) and \(b_1 =b_2 =b.\) Hence, the Eq. (9) modifies to

$$\begin{aligned}&\left( {a-bv} \right) B^{2}\frac{\partial ^{2}U_\ell }{\partial \xi ^{2}}+U_\ell \left( {bwk-w-a\kappa ^{2}} \right) \nonumber \\&\quad +c_\ell F\left( {U_\ell ^2 } \right) U_\ell -k_\ell U_{\ell ^{{*}}} =0. \end{aligned}$$
(16)

We note that the result for the velocity of the soliton, given by (13), is true for all types of nonlinearity in question.

The CNLSE will be studied with the following four nonlinear forms.

2.1 Kerr law

The Kerr law nonlinearity is the case when \(F(s)=s\). For Kerr law nonlinearity, the considered CNLSE is given by

$$\begin{aligned} iq_t +aq_{xx} +bq_{xt} +c_1 \left| q \right| ^{2}q= & {} k_1 r, \end{aligned}$$
(17)
$$\begin{aligned} ir_t +ar_{xx} +br_{xt} +c_2 \left| r \right| ^{2}r= & {} k_2 q. \end{aligned}$$
(18)

Real part (16) is reduces

$$\begin{aligned}&\left( {a-bv} \right) B^{2}\frac{\partial ^{2}U_\ell }{\partial \xi ^{2}}+U_\ell \left( {bwk-w-a\kappa ^{2}} \right) \nonumber \\&\quad +c_\ell U_\ell ^3 -k_\ell U_{\ell ^{{*}}} =0. \end{aligned}$$
(19)

We assume that U is in the form

$$\begin{aligned} U_\ell \left( \xi \right) =\lambda _\ell sn^{p}\left( {\mu \xi ,m} \right) , \end{aligned}$$
(20)

where \(\lambda \) represents the amplitude and m is the modulus of Jacobi elliptic function \(0<m<1\). The unknown index p will be determined. The second-order derivative of Eq. (20) is as follows:

$$\begin{aligned} \left( {U_\ell } \right) _{\xi \xi }= & {} \left( {p-1} \right) p\lambda _\ell \mu ^{2}sn^{p-2}\left( {\mu \xi ,m} \right) \nonumber \\&-p\left[ {m+m^{2}\left( {p-1} \right) +p} \right] \nonumber \\&\times \lambda _\ell \mu ^{2}sn^{p}\left( {\mu \xi ,m} \right) \nonumber \\&+mp\left( {mp+1} \right) \lambda _\ell \mu ^{2}sn^{p+2}\left( {\mu \xi ,m} \right) \end{aligned}$$
(21)

Substituting (20) and (21) into (19) gives

$$\begin{aligned}&\left( {a-bv} \right) B^{2}\left( {p-1} \right) p\lambda _\ell \mu ^{2}sn^{p-2}\left( {\mu \xi ,m} \right) \nonumber \\&\quad -\left( {a-bv} \right) B^{2}p\left[ {m+m^{2}\left( {p-1} \right) +p} \right] \nonumber \\&\quad \lambda _\ell \mu ^{2}sn^{p} \left( {\mu \xi ,m} \right) +\left( {a-bv} \right) B^{2}mp\nonumber \\&\quad \left( {mp+1} \right) \lambda _\ell \mu ^{2}sn^{p+2}\left( {\mu \xi ,m} \right) \nonumber \\&\quad +\lambda _\ell \left( {bwk-w-a\kappa ^{2}} \right) sn^{p} \left( {\mu \xi ,m} \right) \nonumber \\&\quad +c_\ell \lambda _\ell ^3 sn^{3p}\left( {\mu \xi ,m} \right) -k_\ell \lambda _{\ell ^{{*}}} sn^{p}\left( {\mu \xi ,m} \right) =0.\nonumber \\ \end{aligned}$$
(22)

From (22), matching the exponents \(sn^{p+2}\left( {\mu \xi ,m} \right) \) and \(sn^{3p}\left( {\mu \xi ,m} \right) \) yields

$$\begin{aligned} p+2=3p, \end{aligned}$$
(23)

which gives

$$\begin{aligned} p=1. \end{aligned}$$
(24)

Now, setting the coefficients of \(sn^{p+j}\left( {\mu \xi ,m} \right) \), for \(\hbox {j}=-2,0\), to zero in (22) as these are linearly independent functions yields

$$\begin{aligned} w=\frac{m\left( {a\kappa ^{2}\lambda _\ell +k_\ell \lambda _\ell ^{*} } \right) -c_\ell \lambda _\ell ^3 }{m\lambda _\ell \left( {b\kappa -1} \right) }, \end{aligned}$$
(25)

and

$$\begin{aligned} v=\frac{c_\ell \lambda _\ell ^2 +m\left( {m+1} \right) aB^{2}\mu ^{2}}{m\left( {m+1} \right) bB^{2}\mu ^{2}}. \end{aligned}$$
(26)

Now, equating the two values of the soliton wave number from (25) for \(\ell =1,2\), we get

$$\begin{aligned} \lambda _1 \lambda _2 \left( {c_2 \lambda _2^2 -c_1 \lambda _1^2 } \right) =m\left( {k_2 \lambda _1^2 -k_1 \lambda _2^2 } \right) . \end{aligned}$$
(27)

Similarly, equating the two values of the soliton velocity from (26) gives

$$\begin{aligned} \frac{\lambda _1 }{\lambda _2 }=\sqrt{\frac{c_2 }{c_1 }},\quad c_1 c_2 >0. \end{aligned}$$
(28)

Finally, equating the two expressions for inverse width of the soliton from (13) and (26), we obtain

$$\begin{aligned} B=\pm \sqrt{\frac{\left( {1-b\kappa } \right) c_\ell }{m\left( {m+1} \right) \mu ^{2}\left( {b^{2}w-ab\kappa -a} \right) }}\lambda _\ell , \end{aligned}$$
(29)

which requires the constraint condition

$$\begin{aligned} \left( {1-b\kappa } \right) c_\ell \left( {b^{2}w-ab\kappa -a} \right) >0. \end{aligned}$$
(30)

Hence, for Kerr law nonlinearity, Jacobi elliptic function solutions are obtained as follows,

$$\begin{aligned} q= & {} \lambda _1 sn\left[ {\sqrt{\frac{\left( {1-b\kappa } \right) c_1 }{m\left( {m+1} \right) \left( {b^{2}w-ab\kappa -a} \right) }} \lambda _1 } \right. \nonumber \\&\left. {\left\{ {x-\left( {\frac{bw-2a\kappa }{1-b\kappa }} \right) t,m} \right\} } \right] e^{i\left( {-\kappa x+wt+\theta } \right) }, \end{aligned}$$
(31)
$$\begin{aligned} r= & {} \lambda _2 sn\left[ {\sqrt{\frac{\left( {1-b\kappa } \right) c_2 }{m\left( {m+1} \right) \left( {b^{2}w-ab\kappa -a} \right) }} \lambda _2 } \right. \nonumber \\&\left. {\left\{ {x-\left( {\frac{bw-2a\kappa }{1-b\kappa }} \right) t,m} \right\} } \right] e^{i\left( {-\kappa x+wt+\theta } \right) }, \end{aligned}$$
(32)

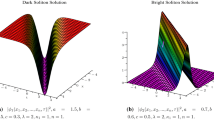
where the soliton wave number w is given by (25). When the modulus \(m\rightarrow 1\) in (31) and (32), we obtain following new dark optical soliton solutions

$$\begin{aligned} q\left( {x,t} \right)= & {} \lambda _1 \tanh \left[ {\sqrt{\frac{\left( {1-b\kappa } \right) c_1 }{2\left( {b^{2}w_1 -ab\kappa -a} \right) }}\lambda _1 } \right. \nonumber \\&\left. {\left\{ {x-\left( {\frac{bw_1 -2a\kappa }{1-b\kappa }} \right) t} \right\} } \right] e^{i\left( {-\kappa x+w_1 t+\theta } \right) }, \nonumber \\\end{aligned}$$
(33)
$$\begin{aligned} r\left( {x,t} \right)= & {} \lambda _2 \tanh \left[ {\sqrt{\frac{\left( {1-b\kappa } \right) c_2 }{2\left( {b^{2}w_1 -ab\kappa -a} \right) }}\lambda _2 } \right. \nonumber \\&\left. {\left\{ {x-\left( {\frac{bw_1 -2a\kappa }{1-b\kappa }} \right) t} \right\} } \right] e^{i\left( {-\kappa x+w_1 t+\theta } \right) }.\nonumber \\ \end{aligned}$$
(34)

Here, \(w_1 \) is in the form

$$\begin{aligned} w_1 =\frac{\left( {a\kappa ^{2}\lambda _\ell +k_\ell \lambda _\ell ^{*} } \right) -c_\ell \lambda _\ell ^3 }{\lambda _\ell \left( {b\kappa -1} \right) }. \end{aligned}$$
(35)

To get another pair of Jacobi elliptic function solution of CNLSE with Kerr law nonlinearity, we use the following function

$$\begin{aligned} U_\ell \left( \xi \right) =\lambda _\ell cn^{p}\left( {\mu \xi ,m} \right) . \end{aligned}$$
(36)

For (36), one obtains

$$\begin{aligned} \left( {U_\ell } \right) _{\xi \xi }= & {} \left( {1-m^{2}} \right) \left( {p-1} \right) p\lambda _\ell \mu ^{2}cn^{p-2}\left( {\mu \xi ,m} \right) \nonumber \\&+p\left[ {m+m^{2}\left( {2p-1} \right) -p} \right] \nonumber \\&\times \lambda _\ell \mu ^{2}cn^{p}\left( {\mu \xi ,m} \right) -mp\left( {mp+1} \right) \nonumber \\&\times \,\lambda _\ell \mu ^{2}cn^{p+2}\left( {\mu \xi ,m} \right) \end{aligned}$$
(37)

Thus, Eq. (19) reduces

$$\begin{aligned}&\left( {a-bv} \right) B^{2}\left( {1-m^{2}} \right) \left( {p-1} \right) p\lambda _\ell \mu ^{2}cn^{p-2}\nonumber \\&\quad \left( {\mu \xi ,m} \right) +\left( {a-bv} \right) B^{2}p \nonumber \\&\quad \times \left[ {m+m^{2}\left( {2p-1} \right) ]-p} \right] \lambda _\ell \mu ^{2}cn^{p}\left( {\mu \xi ,m} \right) \nonumber \\&\quad -\left( {a-bv} \right) B^{2}mp\left( {mp+1} \right) \nonumber \\&\quad \times \lambda _\ell \mu ^{2}cn^{p+2}\left( {\mu \xi ,m} \right) +\lambda _\ell \left( {bwk-w-a\kappa ^{2}} \right) cn^{p}\nonumber \\&\quad \times \,\left( {\mu \xi ,m} \right) +c_\ell \lambda _\ell ^3 cn^{3p}\left( {\mu \xi ,m} \right) \nonumber \\&\quad -k_\ell \lambda _{\ell ^{{*}}} cn^{p}\left( {\mu \xi ,m} \right) =0. \end{aligned}$$
(38)

From (38), setting the coefficients \(p+2\) and 3p equal to one another gives the same value of p which is in (24). The functions \(cn^{p+j}\left( {\mu \xi ,m} \right) \), for \(j=-2,0\) are linearly independent, and this yields

$$\begin{aligned} w= & {} \frac{m\left( {m+1} \right) \left( {a\kappa ^{2}\lambda _\ell +k_\ell \lambda _\ell ^{*} } \right) -\left( {m^{2}+m-1} \right) c_\ell \lambda _\ell ^3 }{m\left( {m+1} \right) \lambda _\ell \left( {b\kappa -1} \right) }, \nonumber \\\end{aligned}$$
(39)
$$\begin{aligned} v= & {} \frac{m\left( {m+1} \right) aB^{2}\mu ^{2}-c_\ell \lambda _\ell ^2 }{m\left( {m+1} \right) bB^{2}\mu ^{2}}. \end{aligned}$$
(40)

Equating the two values of soliton wave number from (39) and also two values of soliton velocity from (40), for \(\ell =1,2\), gives

$$\begin{aligned}&\left( {m^{2}+m-1} \right) \lambda _1 \lambda _2 \left( {c_2 \lambda _2^2 -c_1 \lambda _1^2 } \right) \nonumber \\&\quad =m\left( {m+1} \right) \left( {k_2 \lambda _1^2 -k_1 \lambda _2^2 } \right) , \end{aligned}$$
(41)

and

$$\begin{aligned} \frac{\lambda _1 }{\lambda _2 }=\sqrt{\frac{c_2 }{c_1 }},\quad c_1 c_2 >0 \end{aligned}$$

respectively. Next, matching the two expressions for inverse width of the soliton from (13) and (40), we get

$$\begin{aligned} B=\pm \sqrt{\frac{\left( {b\kappa -1} \right) c_\ell }{m\left( {m+1} \right) \mu ^{2}\left( {b^{2}w-ab\kappa -a} \right) }}\lambda _\ell , \end{aligned}$$
(42)

which requires the constraint

$$\begin{aligned} \left( {b\kappa -1} \right) c_\ell \left( {b^{2}w-ab\kappa -a} \right) >0. \end{aligned}$$
(43)

So, for Kerr law nonlinearity, another Jacobi elliptic function solution of the CNLSE is given by

$$\begin{aligned} q= & {} \lambda _1 cn\left[ {\sqrt{\frac{\left( {b\kappa -1} \right) c_1 }{m\left( {m+1} \right) \left( {b^{2}w-ab\kappa -a} \right) }}\lambda _1 } \right. \nonumber \\&\left. \times \,{\left\{ {x-\left( {\frac{bw-2a\kappa }{1-b\kappa }} \right) t,m} \right\} } \right] e^{i\left( {-\kappa x+wt+\theta } \right) }, \nonumber \\ \end{aligned}$$
(44)
$$\begin{aligned} r= & {} \lambda _2 cn\left[ {\sqrt{\frac{\left( {b\kappa -1} \right) c_2 }{m\left( {m+1} \right) \left( {b^{2}w-ab\kappa -a} \right) }}\lambda _2 } \right. \nonumber \\&\left. \times \,{\left\{ {x-\left( {\frac{bw-2a\kappa }{1-b\kappa }} \right) t,m} \right\} } \right] e^{i\left( {-\kappa x+wt+\theta } \right) },\nonumber \\ \end{aligned}$$
(45)

where the w is given by (39). If the modulus \(m\rightarrow 1,\) (44) and (45) solutions become following new bright optical soliton solutions.

$$\begin{aligned} q\left( {x,t} \right)= & {} \lambda _1 \sec h\left[ {\sqrt{\frac{\left( {b\kappa -1} \right) c_1 }{2\left( {b^{2}w_1 -ab\kappa -a} \right) }}\lambda _1 } \right. \nonumber \\&\left. {\left\{ {x-\left( {\frac{bw_1 -2a\kappa }{1-b\kappa }} \right) t} \right\} } \right] e^{i\left( {-\kappa x+w_1 t+\theta } \right) }, \nonumber \\ \end{aligned}$$
(46)
$$\begin{aligned} r\left( {x,t} \right)= & {} \lambda _2 \sec h\left[ {\sqrt{\frac{\left( {b\kappa -1} \right) c_2 }{2\left( {b^{2}w_1 -ab\kappa -a} \right) }}\lambda _2 } \right. \nonumber \\&\left. {\left\{ {x-\left( {\frac{bw_1 -2a\kappa }{1-b\kappa }} \right) t} \right\} } \right] e^{i\left( {-\kappa x+w_1 t+\theta } \right) },\nonumber \\ \end{aligned}$$
(47)

where \(w_1 \) is in the form

$$\begin{aligned} w_1 =\frac{2\left( {a\kappa ^{2}\lambda _\ell +k_\ell \lambda _\ell ^{*} } \right) -c_\ell \lambda _\ell ^3 }{2\lambda _\ell \left( {b\kappa -1} \right) }. \end{aligned}$$
(48)

Remark 1

Bright optical soliton solutions (46) and (47) are identical to solutions in [4] obtained by using the sine–cosine function method.

2.2 Power law

For the case of power law nonlinearity, where \(F(s)=s^{n},\) the CNLSE reduces to

$$\begin{aligned} iq_t +aq_{xx} +bq_{xt} +c_1 \left| q \right| ^{2n}q= & {} k_1 r, \end{aligned}$$
(49)
$$\begin{aligned} ir_t +ar_{xx} +br_{xt} +c_2 \left| r \right| ^{2n}r= & {} k_2 q. \end{aligned}$$
(50)

It is worth considering that \(0<n<2\) for stability of solitons. Furthermore, \(n\ne 2\) to avoid self-focusing singularity. For this law of nonlinearity, real part Eq. (16) is written as follows

$$\begin{aligned}&\left( {a-bv} \right) B^{2}\frac{\partial ^{2}U_\ell }{\partial \xi ^{2}}+U_\ell \left( {bwk-w-a\kappa ^{2}} \right) \nonumber \\&\quad +c_\ell U_\ell ^{2n+1} -k_\ell U_{\ell ^{{*}}} =0. \end{aligned}$$
(51)

To obtain the solutions of this equation, the starting assumption for the form of U stays the same as in (20). So, substituting (20) and (21) into (51), then matching the exponents \(\left( {2n+1} \right) p\) and \(p+2\) in the obtained equation

$$\begin{aligned} \left( {2n+1} \right) p=p+2, \end{aligned}$$
(52)

that gives

$$\begin{aligned} p=\frac{1}{n}. \end{aligned}$$
(53)

Again from this obtained equation, setting the coefficients of \(sn^{p+j}\left( {\mu \xi ,m} \right) \) to zero, where \(j=-2,0\), yields

$$\begin{aligned} w= & {} \frac{\left\{ {m\left( {m+n} \right) \left( {a\kappa ^{2}\lambda _\ell -k_\ell \lambda _\ell ^{*} } \right) -c_\ell \lambda _\ell ^3 \left( {m^{2}\left( {1-n} \right) +mn+1} \right) } \right\} }{m\left( {m+n} \right) \lambda _\ell \left( {b\kappa -1} \right) },\nonumber \\ \end{aligned}$$
(54)
$$\begin{aligned} v= & {} \frac{m\left( {m+n} \right) aB^{2}\mu ^{2}+n^{2}c_\ell \lambda _\ell ^{2n} }{m\left( {m+n} \right) bB^{2}\mu ^{2}}. \end{aligned}$$
(55)

Equating the two expressions for wave number from (54) and also two expressions for the soliton velocity from (55) gives

$$\begin{aligned}&\left( {m^{2}\left( {1-n} \right) +mn+1} \right) \lambda _1 \lambda _2 \left( {c_2 \lambda _2^{2n} -c_1 \lambda _1^{2n} } \right) \nonumber \\&\quad =m\left( {m+n} \right) \left( {k_1 \lambda _2^2 -k_2 \lambda _1^2 } \right) . \end{aligned}$$
(56)
$$\begin{aligned}&\quad \frac{\lambda _1 }{\lambda _2 }=\left( {\frac{c_2 }{c_1 }} \right) ^{\frac{1}{2n}},\quad c_1 c_2 >0 \end{aligned}$$
(57)

respectively. Finally, matching the (11) and (55) implies

$$\begin{aligned} B=\pm \sqrt{\frac{\left( {1-b\kappa } \right) c_\ell }{m\left( {m+n} \right) \mu ^{2}\left( {b^{2}w-ab\kappa -a} \right) }}n\lambda _\ell ^n , \end{aligned}$$
(58)

where

$$\begin{aligned} \left( {1-b\kappa } \right) c_\ell \left( {b^{2}w-ab\kappa -a} \right) >0. \end{aligned}$$

Thus, for power law nonlinearity, we obtain the Jacobi elliptic function solutions of Eqs. (49) and (50) as

$$\begin{aligned} q= & {} \lambda _1 sn^{\frac{1}{n}}\left[ {\sqrt{\frac{\left( {1-b\kappa } \right) c_1 }{m\left( {m+n} \right) \left( {b^{2}w-ab\kappa -a} \right) }}n\lambda _1^n } \right. \nonumber&\left. \times \,{\left\{ {x-\left( {\frac{bw-2a\kappa }{1-b\kappa }} \right) t,m} \right\} } \right] e^{i\left( {-\kappa x+wt+\theta } \right) }, \end{aligned}$$
(59)
$$\begin{aligned} r= & {} \lambda _2 sn^{\frac{1}{n}}\left[ {\sqrt{\frac{\left( {1-b\kappa } \right) c_2 }{m\left( {m+n} \right) \left( {b^{2}w-ab\kappa -a} \right) }}n\lambda _2^n } \right. \nonumber&\left. \times \, {\left\{ {x-\left( {\frac{bw-2a\kappa }{1-b\kappa }} \right) t,m} \right\} } \right] e^{i\left( {-\kappa x+wt+\theta } \right) }. \end{aligned}$$
(60)

Here, the wave number is given by (54). When the modulus \(m\rightarrow 1\) in (59) and (60), we get following new dark optical soliton solutions

$$\begin{aligned} q= & {} \lambda _1 \tanh ^{\frac{1}{n}}\left[ {\sqrt{\frac{\left( {1-b\kappa } \right) c_1 }{\left( {n+1} \right) \left( {b^{2}w_1 -ab\kappa -a} \right) }}n\lambda _1^n } \right. \nonumber&\left. \times \, {\left\{ {x-\left( {\frac{bw_1 -2a\kappa }{1-b\kappa }} \right) t} \right\} } \right] e^{i\left( {-\kappa x+w_1 t+\theta } \right) }, \end{aligned}$$
(61)
$$\begin{aligned} r= & {} \lambda _2 \tanh ^{\frac{1}{n}}\left[ {\sqrt{\frac{\left( {1-b\kappa } \right) c_2 }{\left( {n+1} \right) \left( {b^{2}w_1 -ab\kappa -a} \right) }}n\lambda _2^n } \right. \nonumber&\left. \times \, {\left\{ {x-\left( {\frac{bw_1 -2a\kappa }{1-b\kappa }} \right) t} \right\} } \right] e^{i\left( {-\kappa x+w_1 t+\theta } \right) }, \end{aligned}$$
(62)

where

$$\begin{aligned} w_1 =\frac{\left( {n+1} \right) \left( {a\kappa ^{2}\lambda _\ell -k_\ell \lambda _\ell ^{*} } \right) -2c_\ell \lambda _\ell ^3 }{\left( {n+1} \right) \lambda _\ell \left( {b\kappa -1} \right) }. \end{aligned}$$
(63)

Now, to look for other solutions of the coupled NLSE with power law nonlinearity, we use the starting assumption for the form of U the same as in (36). Substituting (36) and (37) into (51), then setting the coefficients \(\left( {2n+1} \right) p\) and \(p+2\) equal to one another in the obtained equation, gives the same value of p which is in (53). Next, setting the coefficients of the linearly independent functions \(cn^{p+j}\left( {\mu \xi ,m} \right) \), for \(j=-2,0\) to zero yields

$$\begin{aligned} w= & {} \frac{\left\{ {m\left( {m+n} \right) \left( {a\kappa ^{2}\lambda _\ell +k_\ell \lambda _\ell ^{*} } \right) -c_\ell \lambda _\ell ^{2n+1} \left( {m^{2}\left( {2-n} \right) +mn-1} \right) } \right\} }{m\left( {m+n} \right) \lambda _\ell \left( {b\kappa -1} \right) }, \end{aligned}$$
(64)
$$\begin{aligned} v= & {} \frac{m\left( {m+n} \right) aB^{2}\mu ^{2}-n^{2}c_\ell \lambda _\ell ^{2n} }{m\left( {m+n} \right) bB^{2}\mu ^{2}}. \end{aligned}$$
(65)

Equating the components gives the following relations, respectively.

$$\begin{aligned}&\left( {m^{2}\left( {2-n} \right) +mn-1} \right) \lambda _1 \lambda _2 \left( {c_2 \lambda _2^{2n} -c_1 \lambda _1^{2n} } \right) \nonumber&\quad =m\left( {m+n} \right) \left( {k_2 \lambda _1^2 -k_1 \lambda _2^2 } \right) , \nonumber&\quad \frac{\lambda _1 }{\lambda _2 }=\left( {\frac{c_2 }{c_1 }} \right) ^{\frac{1}{2n}},\quad c_1 c_2 >0 \end{aligned}$$
(66)

Again, equating (13) and (65) gives

$$\begin{aligned} B=\pm \sqrt{\frac{\left( {b\kappa -1} \right) c_\ell }{m\left( {m+n} \right) \mu ^{2}\left( {b^{2}w-ab\kappa -a} \right) }}n\lambda _\ell ^n , \end{aligned}$$
(67)

where

$$\begin{aligned} \left( {b\kappa -1} \right) c_\ell \left( {b^{2}w-ab\kappa -a} \right) >0. \end{aligned}$$

Hence, for power law nonlinearity, solutions of CNLSE are given by

$$\begin{aligned} q= & {} \lambda _1 cn^{\frac{1}{n}}\left[ {\sqrt{\frac{\left( {b\kappa -1} \right) c_1 }{m\left( {m+n} \right) \left( {b^{2}w-ab\kappa -a} \right) }}n\lambda _1^n } \right. \nonumber&\left. \times \,{\left\{ {x\!-\!\left( \! {\frac{bw\!-\!2a\kappa }{1\!-\!b\kappa }} \!\right) t,m} \right\} } \right] e^{i\left( {-\kappa x\!+\!wt\!+\!\theta } \right) }, \end{aligned}$$
(68)
$$\begin{aligned} r= & {} \lambda _2 cn^{\frac{1}{n}}\left[ {\sqrt{\frac{\left( {b\kappa -1} \right) c_2 }{m\left( {m+n} \right) \left( {b^{2}w-ab\kappa -a} \right) }}n\lambda _2^n } \right. \nonumber&\left. \times \, {\left\{ {x\!-\!\left( {\frac{bw\!-\!2a\kappa }{1\!-\!b\kappa }} \right) t,m} \right\} } \right] e^{i\left( {-\kappa x\!+\!wt\!+\!\theta } \right) }, \end{aligned}$$
(69)

where the wave number is given by (64). When the modulus \(m\rightarrow 1\) in (68) and (69), we obtain following bright optical soliton solutions as

$$\begin{aligned} q= & {} \lambda _1 \sec h^{\frac{1}{n}}\left[ {\sqrt{\frac{\left( {b\kappa -1} \right) c_1 }{\left( {n+1} \right) \left( {b^{2}w_1 -ab\kappa -a} \right) }}n\lambda _1^n } \right. \nonumber&\left. \times \,{\left\{ {x-\left( {\frac{bw_1 -2a\kappa }{1-b\kappa }} \right) t} \right\} } \right] e^{i\left( {-\kappa x+w_1 t+\theta } \right) }, \end{aligned}$$
(70)
$$\begin{aligned} r= & {} \lambda _2 \sec h^{\frac{1}{n}}\left[ {\sqrt{\frac{\left( {b\kappa -1} \right) c_2 }{\left( {n+1} \right) \left( {b^{2}w_1 -ab\kappa -a} \right) }}n\lambda _2^n } \right. \nonumber&\left. \times \, {\left\{ {x-\left( {\frac{bw_1 -2a\kappa }{1-b\kappa }} \right) t} \right\} } \right] e^{i\left( {-\kappa x+w_1 t+\theta } \right) }, \end{aligned}$$
(71)

where

$$\begin{aligned} w_1 =\frac{\left( {n+1} \right) \left( {a\kappa ^{2}\lambda _\ell +k_\ell \lambda _\ell ^{*} } \right) -c_\ell \lambda _\ell ^{2n+1} }{\left( {n+1} \right) \lambda _\ell \left( {b\kappa -1} \right) }. \end{aligned}$$
(72)

Remark 2

Bright optical solutions (70) and (71) are identical to solutions in [4] obtained by using the sine–cosine function method.

2.3 Parabolic law

For this kind of nonlinearity, \(F\left( s \right) =s+k_1 s^{2}.\) In this case, the CNLSE is

$$\begin{aligned} iq_t +aq_{xx} +bq_{xt} +\left( {\tau _1 \left| q \right| ^{2}+\eta _1 \left| q \right| ^{4}} \right) q= & {} k_1 r, \nonumber \\\end{aligned}$$
(73)
$$\begin{aligned} ir_t +ar_{xx} +br_{xt} +\left( {\tau _2 \left| r \right| ^{2}+\eta _2 \left| r \right| ^{4}} \right) r= & {} k_2 q.\nonumber \\ \end{aligned}$$
(74)

Here the constants \(\tau \) and \(\eta \) for \(\ell =1,2\) represent the coefficients of cubic and quintic nonlinear terms. In this case, Eq. (16) reduces to

$$\begin{aligned}&\left( {a-bv} \right) B^{2}\frac{\partial ^{2}U_\ell }{\partial \xi ^{2}}+U_\ell \left( {bwk-w-a\kappa ^{2}} \right) \nonumber \\&\quad +\tau _\ell U_\ell ^3 +\eta _\ell U_\ell ^5 -k_\ell U_{\ell ^{{*}}} =0. \end{aligned}$$
(75)

We assume that U is in the form

$$\begin{aligned} U_\ell \left( \xi \right) =\lambda _\ell \left[ {D_1 +sn\left( {\mu \xi ,m} \right) } \right] ^{p}, \end{aligned}$$
(76)

where the constant \(D_1 \) and the unknown index p will be determined. The second-order derivative of (76) is obtained as follows

$$\begin{aligned} \left( {U_\ell } \right) _{\xi \xi }= & {} \left( {p-1} \right) p \lambda _\ell \mu ^{2}\left( {1-D_1^2 } \right) \left( {1-m^{2}D_1^2 } \right) \nonumber \\&\left[ D_1 +sn\left( {\mu \xi ,m} \right) \right] ^{p-2} \nonumber \\&+p\left\{ 2p\left( 1-m^{2}D_1^2 \right) +m\left( {1-D_1^2 } \right) \right. \nonumber \\&\left. + m^{2}\left( {3D_1^2 -2} \right) -1 \right\} \lambda _\ell \mu ^{2}D_1 \nonumber \\&\left[ D_1 +sn \left( {\mu \xi ,m} \right) \right] ^{p-1}\nonumber \\&+p\left\{ mD_1^2 \left( 6mp-4mD_1 +m+2 \right) \right. \nonumber \\&\left. +m^{2}\left( {1-2D_1 -p} \right) -m-p \right\} \nonumber \\&\times \lambda _\ell \mu ^{2}\left[ {D_1 +sn\left( {\mu \xi ,m} \right) } \right] ^{p} \nonumber \\&+mp\left( {-4mp+3m-3} \right) \lambda _\ell \mu ^{2}D_1\nonumber \\&\left[ {D_1 +sn\left( {\mu \xi ,m} \right) } \right] ^{p+1} \nonumber \\&+mp\left( {mp+1} \right) \lambda _\ell \mu ^{2}\nonumber \\&\times \left[ {D_1 +sn\left( {\mu \xi ,m} \right) } \right] ^{p+2}. \end{aligned}$$
(77)

Substituting (76) and (77) into the Eq. (75) and then setting the exponents \(p+1\) and 3p equal to one another give

$$\begin{aligned} p+1=3p \end{aligned}$$
(78)

so that

$$\begin{aligned} p=\frac{1}{2} \end{aligned}$$
(79)

which is also obtained the exponents \(p+2\) and 5p are equated. The functions \(\left[ {D_1 +sn\left( {\mu \xi ,m} \right) } \right] ^{p+j}\) for \(j=-2,-1,0\) are linearly independent, and this yields,

$$\begin{aligned} w= & {} \frac{\left\{ \begin{array}{l} 2m\left( {m-3} \right) D_1 \left( {a\kappa ^{2}\lambda _\ell + k_\ell \lambda _\ell ^{*} } \right) \\ -\tau _\ell \lambda _\ell ^3 \left[ 4mD_1^2 \left( {2m-2mD_1 +1} \right) \right. \\ \left. +m^{2}\left( {1-2D_1 } \right) -2m+1 \right] \\ \end{array} \right\} }{2m\left( {m-3} \right) D_1 \lambda _\ell \left( {b\kappa -1} \right) }, \end{aligned}$$
(80)
$$\begin{aligned} v= & {} \frac{m\left( {m-3} \right) aB^{2}\mu ^{2}D_1 +2\tau _\ell \lambda _\ell ^2 }{m\left( {m-3} \right) bB^{2}\mu ^{2}D_1 }, \end{aligned}$$
(81)

and

$$\begin{aligned} D_1 =\frac{\left( {m+2} \right) \tau _\ell }{2\left( {3-m} \right) \eta _\ell \lambda _\ell ^2 }. \end{aligned}$$
(82)

Equating the wave number of the solitons from the two components and also velocity of the soliton from the two components gives the following relations, respectively

$$\begin{aligned}&\left[ {4mD_1^2 \left( {2m-2mD_1 +1} \right) +m^{2}\left( {1-2D_1 } \right) -2m+1} \right] \nonumber \\&\quad \times \lambda _1 \lambda _2 \left( {\tau _1 \lambda _1^2 -\tau _2 \lambda _2^2 } \right) \nonumber \\&\quad =2m\left( {m-3} \right) D_1 \left( {k_2 \lambda _1^2 -k_1 \lambda _2^2 } \right) , \end{aligned}$$
(83)
$$\begin{aligned}&\quad \frac{\lambda _1 }{\lambda _2 }=\sqrt{\frac{\tau _2 }{\tau _1 }},\quad \tau _1 \tau _2 >0 \end{aligned}$$
(84)

Finally, matching (13) and (81) implies

$$\begin{aligned} B=\pm \sqrt{\frac{\left( {b\kappa -1} \right) \eta _\ell }{m\left( {m+2} \right) \mu ^{2}\left( {b^{2}w-ab\kappa -a} \right) }}2\lambda _\ell ^2 , \end{aligned}$$
(85)

where

$$\begin{aligned} \left( {b\kappa -1} \right) \eta _\ell \left( {b^{2}w-ab\kappa -a} \right) >0. \end{aligned}$$
(86)

Thus, the Jacobi elliptic function solutions for the CNLSE with parabolic law nonlinearity are given by

$$\begin{aligned} q\left( {x,t} \right)= & {} \lambda _1 \left\{ {\frac{\left( {m+2} \right) \tau _1 }{2\left( {3-m} \right) \eta _1 \lambda _1^2 }} \right. \nonumber \\&+sn\left[ {\sqrt{\frac{\left( {b\kappa -1} \right) \eta _1 }{m\left( {m+2} \right) \left( {b^{2}w-ab\kappa -a} \right) }}2\lambda _1^2 } \right. \nonumber \\&\left. {\left. {\times \left\{ {x-\left( {\frac{bw-2a\kappa }{1-b\kappa }} \right) t,m} \right\} } \right] } \right\} ^{\frac{1}{2}}\nonumber \\&e^{i\left( {-\kappa x+wt+\theta } \right) }, \end{aligned}$$
(87)
$$\begin{aligned} r\left( {x,t} \right)= & {} \lambda _2 \left\{ {\frac{\left( {m+2} \right) \tau _2 }{2\left( {3-m} \right) \eta _2 \lambda _2^2 }} \right. \nonumber \\&+sn\left[ {\sqrt{\frac{\left( {b\kappa -1} \right) \eta _2 }{m\left( {m+2} \right) \left( {b^{2}w-ab\kappa -a} \right) }}2\lambda _2^2 } \right. \nonumber \\&\left. {\left. {\times \left\{ {x-\left( {\frac{bw-2a\kappa }{1-b\kappa }} \right) t,m} \right\} } \right] } \right\} ^{\frac{1}{2}}\nonumber \\&\times \,e^{i\left( {-\kappa x+wt+\theta } \right) }, \end{aligned}$$
(88)

where the wave number is given by (80). When the modulus \(m\rightarrow 1\) in (87) and (88), we obtain following dark optical soliton solutions

$$\begin{aligned} q\left( {x,t} \right)= & {} \lambda _1 \left\{ {\frac{3\tau _1 }{4\eta _1 \lambda _1^2 }} \right. \nonumber \\&+\tanh \left[ {\sqrt{\frac{\left( {b\kappa -1} \right) \eta _1 }{3\left( {b^{2}w_1 -ab\kappa -a} \right) }}2\lambda _1^2 } \right. \nonumber \\&\left. {\left. {\times \left\{ {x-\left( {\frac{bw_1 -2a\kappa }{1-b\kappa }} \right) t} \right\} } \right] } \right\} ^{\frac{1}{2}}\nonumber \\&\times \,e^{i\left( {-\kappa x+w_1 t+\theta } \right) }, \end{aligned}$$
(89)
$$\begin{aligned} r\left( {x,t} \right)= & {} \lambda _2 \left\{ {\frac{3\tau _2 }{4\eta _2 \lambda _2^2 }} \right. \nonumber \\&+\tanh \left[ {\sqrt{\frac{\left( {b\kappa -1} \right) \eta _2 }{3\left( {b^{2}w_1 -ab\kappa -a} \right) }}2\lambda _2^2 } \right. \nonumber \\&\left. {\left. {\times \left\{ {x-\left( {\frac{bw_1 -2a\kappa }{1-b\kappa }} \right) t} \right\} } \right] } \right\} ^{\frac{1}{2}}\nonumber \\&\times \,e^{i\left( {-\kappa x+w_1 t+\theta } \right) }, \end{aligned}$$
(90)

where

$$\begin{aligned} w_1 =\frac{\left\{ {-4D_1 \left( {a\kappa ^{2}\lambda _\ell +k_\ell \lambda _\ell ^{*} } \right) -\tau _\ell \lambda _\ell ^3 \left[ {4D_1^2 \left( {3-2D_1 } \right) -2D_1 } \right] } \right\} }{-4D_1 \lambda _\ell \left( {b\kappa -1} \right) }. \end{aligned}$$
(91)

Now, we use the starting assumption as

$$\begin{aligned} U_\ell \left( \xi \right) =\lambda _\ell \left[ {D_1 +cn\left( {\mu \xi ,m} \right) } \right] ^{p}, \end{aligned}$$
(92)

The second-order derivativeof (92) is obtained as follows.

$$\begin{aligned} \left( {U_\ell } \right) _{\xi \xi }= & {} \left( {p-1} \right) p\lambda _\ell \mu ^{2}\left( {1-D_1^2 } \right) \left( {m^{2}+1} \right) \nonumber \\&\times \,\left[ {D_1 +cn\left( {\mu \xi ,m} \right) } \right] ^{p-2}\nonumber \\&+p\left\{ {\left[ {m^{2}\left( {4p-3} \right) +m} \right] } \right. \nonumber \\&\left. \times \, {\left( {D_1^2 -1} \right) +2p-1} \right\} \lambda _\ell \mu ^{2}D_1 \nonumber \\&\times \,\left[ {D_1 +cn\left( {\mu \xi ,m} \right) } \right] ^{p-1} \nonumber \\&+p\left\{ {\left( {1-3D_1^2 } \right) \left( {2m^{2}p-m^{2}+m} \right) -p} \right\} \nonumber \\&\times \,\lambda _\ell \mu ^{2}\left[ {D_1 +cn\left( {\mu \xi ,m} \right) } \right] ^{p} \nonumber \\&+mp\left( {4mp-m+3} \right) \lambda _\ell \mu ^{2}D_1 \nonumber \\&\left[ {D_1 +cn\left( {\mu \xi ,m} \right) } \right] ^{p+1} \nonumber \\&-mp\left( {mp+1} \right) \lambda _\ell \mu ^{2}\nonumber \\&\times \,\left[ {D_1 +cn\left( {\mu \xi ,m} \right) } \right] ^{p+2} \end{aligned}$$
(93)

Substituting (92) and (93) into the Eq. (75) and then setting the exponents \(p+1\) and 3p equal to one another give the same value of p which is in (79). The same value of the exponent p is also yielded when the exponents \(p+2\) and 5p are equated. The functions \(\left[ {D_1 +cn\left( {\mu \xi ,m} \right) } \right] ^{p+j},\) for \(j=-2,-1,0\), are linearly independent, and this yields,

$$\begin{aligned}&w=\frac{\left\{ {2m\left( {m+3} \right) D_1 \left( {a\kappa ^{2}\lambda _\ell +k_\ell \lambda _\ell ^{*} } \right) +\tau _\ell \lambda _\ell ^3 \left[ {2m\left( {1-3D_1^2 } \right) -1} \right] } \right\} }{2m\left( {m+3} \right) D_1 \lambda _\ell \left( {b\kappa -1} \right) },\nonumber \\ \end{aligned}$$
(94)
$$\begin{aligned}&v=\frac{m\left( {m+3} \right) aB^{2}\mu ^{2}D_1 +2\tau _\ell \lambda _\ell ^2 }{m\left( {m+3} \right) bB^{2}\mu ^{2}D_1 }, \end{aligned}$$
(95)
$$\begin{aligned}&D_1 =\frac{-\left( {m+2} \right) \tau _\ell }{2\left( {m+3} \right) \eta _\ell \lambda _\ell ^2 }. \end{aligned}$$
(96)

Equating the components, we obtain the same value in (85) with the condition (86) and also we get the same relation in(84) and following relation

$$\begin{aligned}&\left[ {2m\left( {1-3D_1^2 } \right) -1} \right] \lambda _1 \lambda _2 \left( {\tau _1 \lambda _1^2 -\tau _2 \lambda _2^2 } \right) \nonumber \\&\quad =2m\left( {m+3} \right) D_1 \left( {k_2 \lambda _1^2 -k_1 \lambda _2^2 } \right) , \end{aligned}$$
(97)

So, another pair of Jacobi elliptic function solution in a parabolic law media for the CNLSE is given by

$$\begin{aligned} q\left( {x,t} \right)= & {} \lambda _1 \left\{ {\frac{-\left( {m+2} \right) \tau _1 }{2\left( {m+3} \right) \eta _1 \lambda _1^2 }} \right. \nonumber \\&+cn\left[ {\sqrt{\frac{\left( {b\kappa -1} \right) \eta _1 }{m\left( {m+2} \right) \left( {b^{2}w-ab\kappa -a} \right) }}2\lambda _1^2 } \right. \nonumber \\&\left. {\left. {\times \left\{ {x-\left( {\frac{bw-2a\kappa }{1-b\kappa }} \right) t,m} \right\} } \right] } \right\} ^{\frac{1}{2}}\nonumber \\&\times \,e^{i\left( {-\kappa x+wt+\theta } \right) }, \end{aligned}$$
(98)
$$\begin{aligned} r\left( {x,t} \right)= & {} \lambda _2 \left\{ {\frac{-\left( {m+2} \right) \tau _2 }{2\left( {m+3} \right) \eta _2 \lambda _2^2 }} \right. \nonumber \\&+cn\left[ {\sqrt{\frac{\left( {b\kappa -1} \right) \eta _2 }{m\left( {m+2} \right) \left( {b^{2}w-ab\kappa -a} \right) }}2\lambda _2^2 } \right. \nonumber \\&\left. {\left. {\times \left\{ {x-\left( {\frac{bw-2a\kappa }{1-b\kappa }} \right) t,m} \right\} } \right] } \right\} ^{\frac{1}{2}}\nonumber \\&\times \,e^{i\left( {-\kappa x+wt+\theta } \right) }, \end{aligned}$$
(99)

where the wave number is given by (94). When the modulus \(m\rightarrow 1\) in (98) and (99), we obtain following bright optical soliton solutions

$$\begin{aligned} q\left( {x,t} \right)= & {} \lambda _1 \left\{ {\frac{-3\tau _1 }{8\eta _1 \lambda _1^2 }} \right. \nonumber \\&+\sec h\left[ {\sqrt{\frac{\left( {b\kappa -1} \right) \eta _1 }{3\left( {b^{2}w_1 -ab\kappa -a} \right) }}2\lambda _1^2 } \right. \nonumber \\&\left. {\left. {\times \left\{ {x-\left( {\frac{bw_1 -2a\kappa }{1-b\kappa }} \right) t} \right\} } \right] } \right\} ^{\frac{1}{2}}\nonumber \\&\times \,e^{i\left( {-\kappa x+w_1 t+\theta } \right) }, \end{aligned}$$
(100)
$$\begin{aligned} r\left( {x,t} \right)= & {} \lambda _2 \left\{ {\frac{-3\tau _2 }{8\eta _2 \lambda _2^2 }} \right. \nonumber \\&+\sec h\left[ {\sqrt{\frac{\left( {b\kappa -1} \right) \eta _2 }{3\left( {b^{2}w_1 -ab\kappa -a} \right) }}2\lambda _2^2 } \right. \nonumber \\&\left. {\left. {\times \left\{ {x-\left( {\frac{bw_1 -2a\kappa }{1-b\kappa }} \right) t} \right\} } \right] } \right\} ^{\frac{1}{2}}\nonumber \\&\times \,e^{i\left( {-\kappa x+w_1 t+\theta } \right) }, \end{aligned}$$
(101)

where

$$\begin{aligned} w_1 =\frac{8D_1 \left( {a\kappa ^{2}\lambda _\ell +k_\ell \lambda _\ell ^{*} } \right) +\tau _\ell \lambda _\ell ^3 \left( {1-6D_1^2 } \right) }{8D_1 \lambda _\ell \left( {b\kappa -1} \right) }. \end{aligned}$$
(102)

2.4 Dual-power law

The dual-power law nonlinearity is formulated as \(F\left( s \right) =s^{n}+k_2 s^{2n}\). If \(n=1\), this law reduces to parabolic law nonlinearity. The CNLSE with dual-power law nonlinearity is given by

$$\begin{aligned}&iq_t +aq_{xx} +bq_{xt} \nonumber \\&\quad +\left( {\tau _1 \left| q \right| ^{2n}+\eta _1 \left| q \right| ^{4n}} \right) q=k_1 r, \end{aligned}$$
(103)
$$\begin{aligned}&\quad ir_t +ar_{xx} +br_{xt} \nonumber \\&\quad +\left( {\tau _2 \left| r \right| ^{2n}+\eta _2 \left| r \right| ^{4n}} \right) r=k_2 q. \end{aligned}$$
(104)

In this case Eq. (16) reduces to

$$\begin{aligned}&\left( {a-bv} \right) B^{2}\frac{\partial ^{2}U_\ell }{\partial \xi ^{2}}+U_\ell \left( {bwk-w-a\kappa ^{2}} \right) \nonumber \\&\quad +\tau _\ell U_\ell ^{2n+1} +\eta _\ell U_\ell ^{4n+1} -k_\ell U_{\ell ^{{*}}} =0. \end{aligned}$$
(105)

For dual-power law nonlinearity, the starting hypothesis for U is given by

$$\begin{aligned} U_\ell \left( \xi \right) =\lambda _\ell \left[ {D_2 +sn\left( {\mu \xi ,m} \right) } \right] ^{p}, \end{aligned}$$
(106)

Here the constant \(D_2 \) and the unknown index p will be determined. Substituting the required derivatives in the Eq. (105) and then equating the coefficients \(\left( {2n+1} \right) p\) and \(p+1\) give

$$\begin{aligned} \left( {2n+1} \right) p= & {} p+1, \end{aligned}$$
(107)
$$\begin{aligned} p= & {} \frac{1}{2n}. \end{aligned}$$
(108)

The above value of the exponent p is yielded when the exponents \(\left( {4n+1} \right) p\) and \(p+2\) are equated. Now, setting the coefficients of \(\left[ {D_2 +sn\left( {\mu \xi ,m} \right) } \right] ^{p+j}\) to zero, for \(j=-2,-1,0\), gives

$$\begin{aligned} w= & {} \frac{\left\{ {\begin{array}{l} 2m\left[ {3n\left( {m-1} \right) -2m} \right] D_2 \left( {a\kappa ^{2}\lambda _\ell +k_\ell \lambda _\ell ^{*} } \right) \\ +\tau _\ell \lambda _\ell ^{2n+1} \left[ {mD_2^2 \left\{ {6m+2n\left( {-4mD_2 +m+2} \right) } \right\} } \right. \\ \left. {+m^{2}\left( {-4nD_2 +2n-1} \right) -2mn-1} \right] \\ \end{array}} \right\} }{2m\left[ {3n\left( {m-1} \right) -2m} \right] D_2 \lambda _\ell \left( {b\kappa -1} \right) }, \nonumber \\\end{aligned}$$
(109)
$$\begin{aligned} v= & {} \frac{m\left[ {3n\left( {m-1} \right) -2m} \right] aB^{2}\mu ^{2}D_2 +2n^{2}\tau _\ell \lambda _\ell ^{2n} }{m\left[ {3n\left( {m-1} \right) -2m} \right] bB^{2}\mu ^{2}D_2 }, \end{aligned}$$
(110)

and

$$\begin{aligned} D_2 =\frac{-\left( {m+2n} \right) \tau _\ell }{2\left[ {3n\left( {m-1} \right) -2m} \right] \eta _\ell \lambda _\ell ^{2n} }. \end{aligned}$$
(111)

Equating the components, we obtain following relations

$$\begin{aligned}&\left[ {mD_2^2 \left( {6m+2n\left( {-4mD_2 +m+2} \right) } \right) } \right. \nonumber \\&\quad \left. +m^{2} {\left( {2n-4nD_2 -1} \right) -2mn-1} \right] \nonumber \\&\quad \times \lambda _1 \lambda _2 \left( {\tau _1 \lambda _1^{2n} -\tau _2 \lambda _2^{2n} } \right) \nonumber \\&\quad =2m\left[ {3n\left( {m-1} \right) -2m} \right] D_2 \left( {k_2 \lambda _1^2 -k_1 \lambda _2^2 } \right) ,\nonumber \\ \end{aligned}$$
(112)
$$\begin{aligned}&\quad \frac{\lambda _1 }{\lambda _2 }=\left( {\frac{\tau _2 }{\tau _1 }} \right) ^{\frac{1}{2n}},\quad \tau _1 .\tau _2 >0 \end{aligned}$$
(113)

and

$$\begin{aligned} B=\pm \sqrt{\frac{\left( {b\kappa -1} \right) \eta _\ell }{m\left( {m+2n} \right) \mu ^{2}\left( {b^{2}w-ab\kappa -a} \right) }}2n\lambda _\ell ^{2n} , \end{aligned}$$
(114)

with the condition

$$\begin{aligned} \left( {b\kappa -1} \right) \eta _\ell \left( {b^{2}w-ab\kappa -a} \right) >0. \end{aligned}$$

Thus, the Jacobi elliptic function solutions for the coupled NLSE with dual-power law nonlinearity are given by

$$\begin{aligned} q\left( {x,t} \right)= & {} \lambda _1 \left\{ {\frac{-\left( {m+2n} \right) \tau _1 }{2\left[ {3n\left( {m-1} \right) -2m} \right] \eta _1 \lambda _1^{2n} }} \right. \nonumber \\&+sn\left[ {\sqrt{\frac{\left( {b\kappa -1} \right) \eta _1 }{m\left( {m+2n} \right) \left( {b^{2}w-ab\kappa -a} \right) }}2n\lambda _1^{2n} } \right. \nonumber \\&\left. {\left. {\times \left\{ {x-\left( {\frac{bw-2a\kappa }{1-b\kappa }} \right) t,m} \right\} } \right] } \right\} ^{\frac{1}{2n}}\nonumber \\&\times \,e^{i\left( {-\kappa x+wt+\theta } \right) }, \end{aligned}$$
(115)
$$\begin{aligned} r\left( {x,t} \right)= & {} \lambda _2 \left\{ {\frac{-\left( {m+2n} \right) \tau _2 }{2\left[ {3n\left( {m-1} \right) -2m} \right] \eta _2 \lambda _2^{2n} }} \right. \nonumber \\&+sn\left[ {\sqrt{\frac{\left( {b\kappa -1} \right) \eta _2 }{m\left( {m+2n} \right) \left( {b^{2}w-ab\kappa -a} \right) }}2n\lambda _2^{2n} } \right. \nonumber \\&\left. {\times \left\{ {x-\left( {\frac{bw-2a\kappa }{1-b\kappa }} \right) t,m} \right\} } \right] ^{\frac{1}{2n}}\nonumber \\&\times \,e^{i\left( {-\kappa x+wt+\theta } \right) }, \end{aligned}$$
(116)

where the wave number is given by (109). If the modulus \(m\rightarrow 1\) in (115) and (116), we obtain following dark optical soliton solutions

$$\begin{aligned} q\left( {x,t} \right)= & {} \lambda _1 \left\{ {\frac{\left( {2n+1} \right) \tau _1 }{4\eta _1 \lambda _1^{2n} }} \right. \nonumber \\&+\tanh \left[ {\sqrt{\frac{\left( {b\kappa -1} \right) \eta _1 }{\left( {2n+1} \right) \left( {b^{2}w_1 -ab\kappa -a} \right) }}2n\lambda _1^{2n} } \right. \nonumber \\&\left. {\left. {\times \left\{ {x-\left( {\frac{bw_1 -2a\kappa }{1-b\kappa }} \right) t} \right\} } \right] } \right\} ^{\frac{1}{2n}}\nonumber \\&\times \,e^{i\left( {-\kappa x+w_1 t+\theta } \right) }, \end{aligned}$$
(117)
$$\begin{aligned} r\left( {x,t} \right)= & {} \lambda _2 \left\{ {\frac{\left( {2n+1} \right) \tau _2 }{4\eta _2 \lambda _2^{2n} }} \right. \nonumber \\&+\tanh \left[ {\sqrt{\frac{\left( {b\kappa -1} \right) \eta _2 }{\left( {2n+1} \right) \left( {b^{2}w_1 -ab\kappa -a} \right) }}2n\lambda _2^{2n} } \right. \nonumber \\&\left. {\left. {\times \left\{ {x-\left( {\frac{bw_1 -2a\kappa }{1-b\kappa }} \right) t} \right\} } \right] } \right\} ^{\frac{1}{2n}}\nonumber \\&\times \,e^{i\left( {-\kappa x+w_1 t+\theta } \right) }, \end{aligned}$$
(118)

where

$$\begin{aligned} w_1 =\frac{\left\{ {\begin{array}{l} -4D_2 \left( {a\kappa ^{2}\lambda _\ell +k_\ell \lambda _\ell ^{*} } \right) +\tau _\ell \lambda _\ell ^{2n+1} \left[ {D_2^2 } \right. \\ \times \left. {\left\{ {6+2n\left( {-4D_2 +3} \right) } \right\} +-4nD_2 -2} \right] \\ \end{array}} \right\} }{-4D_2 \lambda _\ell \left( {b\kappa -1} \right) }. \end{aligned}$$
(119)

Now, to look for the solutions of CNLSE with dual-power nonlinearity, the starting hypothesis is given by

$$\begin{aligned} U_\ell \left( \xi \right) =\lambda _\ell \left[ {D_2 +cn\left( {\mu \xi ,m} \right) } \right] ^{p}, \end{aligned}$$
(120)

Substituting the hypothesis into (105) and then equating the coefficients \(\left( {2n+1} \right) p\) and \(p+1\) give the same value of p which is in (108). The same value of p is obtained on equating \(\left( {4n+1} \right) p\) and \(p+2\). Then, setting the coefficients of \(\left[ {D_2 +cn\left( {\mu \xi ,m} \right) } \right] ^{p+j}\) to zero, for \(j=-2,-1,0,\) gives

$$\begin{aligned} w= & {} \frac{\left\{ {\begin{array}{l} 2m\left[ {m\left( {2-n} \right) +3} \right] D_2 \left( {a\kappa ^{2}\lambda _\ell +k_\ell \lambda _\ell ^{*} } \right) \\ +\tau _\ell \lambda _\ell ^{2n+1} \left[ {2m\left( {1-3D_2^2 } \right) \left[ {m+n\left( {1-m} \right) } \right] -1} \right] \\ \end{array}} \right\} }{2m\left[ {m\left( {2-n} \right) +3} \right] D_2 \lambda _\ell \left( {b\kappa -1} \right) }, \nonumber \\\end{aligned}$$
(121)
$$\begin{aligned} v= & {} \frac{m\left[ {m\left( {2-n} \right) +3} \right] aB^{2}\mu ^{2}D_2 +2n^{2}\tau _\ell \lambda _\ell ^{2n} }{m\left[ {m\left( {2-n} \right) +3} \right] bB^{2}\mu ^{2}D_2 }, \end{aligned}$$
(122)

and

$$\begin{aligned} D_2 =\frac{-\left( {m+2n} \right) \tau _\ell }{2\left[ {m\left( {2-n} \right) +3} \right] \eta _\ell \lambda _\ell ^{2n} }. \end{aligned}$$
(123)

Equating the components, we obtain the same value in (114) and also we get the same relation in (113) and following relation

$$\begin{aligned}&\left[ {2m\left( {1-3D_2^2 } \right) \left[ {m+n\left( {1-m} \right) } \right] -1} \right] \nonumber \\&\quad \lambda _1 \lambda _2 \left( {\tau _1 \lambda _1^{2n} -\tau _2 \lambda _2^{2n} } \right) \nonumber \\&\quad =2m\left[ {m\left( {2-n} \right) +3} \right] D_2 \left( {k_2 \lambda _1^2 -k_1 \lambda _2^2 } \right) . \end{aligned}$$
(124)

Thus, finally, another pair of Jacobi elliptic function solution for the coupled NLSE with dual-power law nonlinearity is given by

$$\begin{aligned} q\left( {x,t} \right)= & {} \lambda _1 \left\{ {\frac{-\left( {m+2n} \right) \tau _1 }{2\left[ {m\left( {2-n} \right) +3} \right] \eta _1 \lambda _1^{2n} }} \right. \nonumber \\&+cn\left[ {\sqrt{\frac{\left( {b\kappa -1} \right) \eta _1 }{m\left( {m+2n} \right) \left( {b^{2}w-ab\kappa -a} \right) }}2n\lambda _1^{2n} } \right. \nonumber \\&\left. {\left. {\times \left\{ {x-\left( {\frac{bw-2a\kappa }{1-b\kappa }} \right) t,m} \right\} } \right] } \right\} ^{\frac{1}{2n}}\nonumber \\&\times \,e^{i\left( {-\kappa x+wt+\theta } \right) }, \end{aligned}$$
(125)
$$\begin{aligned} r\left( {x,t} \right)= & {} \lambda _2 \left\{ {\frac{-\left( {m+2n} \right) \tau _2 }{2\left[ {m\left( {2-n} \right) +3} \right] \eta _2 \lambda _2^{2n} }} \right. \nonumber \\&+cn\left[ {\sqrt{\frac{\left( {b\kappa -1} \right) \eta _2 }{m\left( {m+2n} \right) \left( {b^{2}w-ab\kappa -a} \right) }}2n\lambda _2^{2n} } \right. \nonumber \\&\left. {\left. {\times \left\{ {x-\left( {\frac{bw-2a\kappa }{1-b\kappa }} \right) t,m} \right\} } \right] } \right\} ^{\frac{1}{2n}}\nonumber \\&\times \,e^{i\left( {-\kappa x+wt+\theta } \right) }, \end{aligned}$$
(126)

where the wave number is given by (121). When the modulus \(m\rightarrow 1\) in (125) and (126), we obtain following bright optical soliton solutions

$$\begin{aligned} q\left( {x,t} \right)= & {} \lambda _1 \left\{ {\frac{\left( {2n+1} \right) \tau _1 }{2\left( {n-5} \right) \eta _1 \lambda _1^{2n} }} \right. \nonumber \\&+\sec h\left[ {\sqrt{\frac{\left( {b\kappa -1} \right) \eta _1 }{\left( {2n+1} \right) \left( {b^{2}w_1 -ab\kappa -a} \right) }}2n\lambda _1^{2n} } \right. \nonumber \\&\left. {\left. {\times \left\{ {x-\left( {\frac{bw_1 -2a\kappa }{1-b\kappa }} \right) t} \right\} } \right] } \right\} ^{\frac{1}{2n}}\nonumber \\&\times \,e^{i\left( {-\kappa x+w_1 t+\theta } \right) }, \end{aligned}$$
(127)
$$\begin{aligned} r\left( {x,t} \right)= & {} \lambda _2 \left\{ {\frac{\left( {2n+1} \right) \tau _2 }{2\left( {n-5} \right) \eta _2 \lambda _2^{2n} }} \right. \nonumber \\&+\sec h\left[ {\sqrt{\frac{\left( {b\kappa -1} \right) \eta _2 }{\left( {2n+1} \right) \left( {b^{2}w_1 -ab\kappa -a} \right) }}2n\lambda _2^{2n} } \right. \nonumber \\&\left. {\left. {\times \left\{ {x-\left( {\frac{bw_1 -2a\kappa }{1-b\kappa }} \right) t} \right\} } \right] } \right\} ^{\frac{1}{2n}}\nonumber \\&\times \,e^{i\left( {-\kappa x+w_1 t+\theta } \right) }, \end{aligned}$$
(128)

where

$$\begin{aligned} w_1 =\frac{\left\{ {2D_2 \left( {5-n} \right) \left( {a\kappa ^{2}\lambda _\ell +k_\ell \lambda _\ell ^{*} } \right) +\tau _\ell \lambda _\ell ^{2n+1} \left( {1-6D_2^2 } \right) } \right\} }{2D_2 \left( {5-n} \right) \lambda _\ell \left( {b\kappa -1} \right) }. \end{aligned}$$
(129)

3 Conclusions

This study focuses on exact solutions in a type of nonlinear directional optical couplers. The Jacobi elliptic functions are used to obtain dark and bright optical soliton solutions of this couplers with four forms of nonlinearity.

The sn and cn Jacobi elliptic functions have been the focus in this study. Other Jacobi elliptic functions can also be used to get different solutions of the coupled NLSE. Similarly, these functions can also be used to get exact solutions of other nonlinear equations and systems.

The conclusions of this work provide a lot of support to future work. In the future, different soliton solutions and conservation laws will be examined with Lie symmetry of this system.