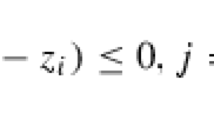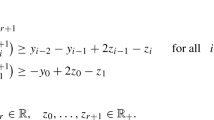Extension of the LP-Newton method to conic programming problems via semi-infinite representation

Abstract

The LP-Newton method solves linear programming (LP) problems by repeatedly projecting a current point onto a certain relevant polytope. In this paper, we extend the algorithmic framework of the LP-Newton method to conic programming (CP) problems via a linear semi-infinite programming (LSIP) reformulation. In this extension, we produce a sequence by projection onto polyhedral cones constructed from LP problems obtained by finitely relaxing the LSIP problem equivalent to the CP problem. We show global convergence of the proposed algorithm under mild assumptions. To investigate its efficiency, we apply our proposed algorithm and a primal-dual interior-point method to second-order cone programming problems and compare the obtained results.

1 Introduction

In this paper, we consider the following conic programming problem (CP):

$$ \begin{array}{@{}rcl@{}} &&\text{minimize} \quad c^{\top} x\\ &&\text{subject to}\quad A x = b,\\ && \qquad\qquad\quad x \in \mathcal{K}, \end{array} $$

(1)

where $A \in \mathbb {R}^{m \times n}, b \in \mathbb {R}^{m}$, and $c \in \mathbb {R}^{n}$ are a given matrix and vectors, respectively, and ${\mathcal{K}} := {\prod }_{i = 1}^{p} {\mathcal{K}}_{i} \subseteq \mathbb {R}^{n}$ is the Cartesian product of nonempty closed convex cones ${\mathcal{K}}_{i}$ for $i = 1, \dots , p$. In what follows, we denote n_i by the dimension of ${\mathcal{K}}_{i}$, i.e., ${\mathcal{K}}_{i} \subseteq \mathbb {R}^{n_{i}}$. If ${\mathcal{K}} = \mathbb {R}_{+}^{n}$ (nonnegative orthant), then the CP problem (1) reduces to the linear programming (LP) problem of the standard form:

$$ \begin{array}{@{}rcl@{}} &&\text{minimize} \quad c^{\top} x\\ &&\text{subject to} \quad A x = b,\\ && \qquad\qquad\quad x \ge 0. \end{array} $$

(2)

More generally, if ${\mathcal{K}}$ is a symmetric cone, the CP problem (1) is called a symmetric cone programming (SCP) problem. The SCP problem includes the second-order cone programming (SOCP) problems and the semidefinite programming (SDP) problems. The CP problem (1) is a very important optimization model because it has many practical applications in fields such as synthesis of filter and antennae arrays, structural design, stability analysis of mechanics, robust optimization, and relaxation of combinatorial optimization [1, 2, 13, 20, 21].

To solve the CP problem (1), many researchers have developed algorithms exploiting the geometrical or algebraic structure of the cone ${\mathcal{K}}$. For instance, we can find Newton-type methods such as primal-dual interior-point methods [16, 18, 20] and non-interior continuous methods along with complementarity functions [3, 7, 9], Chubanov-type algorithms [12, 15], and simplex-type algorithms [6, 17, 25]. These algorithms were originally carried over from LP. One popular extension from LP to SCP is based on the Jordan algebra [4], by which the LP and SCP problems can be handled in the same algebraic framework. Another approach is based on a semi-infinite reformulation of the conic constraint $x \in {\mathcal{K}}$. This approach can be applied to the CP problem (1) with ${\mathcal{K}}$ being possibly nonsymmetric cone. By representing the conic constraint as the intersection of an infinite number of half-spaces, the CP problem (1) can be reformulated as the following linear semi-infinite programming (LSIP) problem with infinitely many linear inequality constraints as we mention below. To derive the semi-infinite reformulation of the CP problem (1), we define the dual cone ${\mathcal{K}}_{i}^{\ast }$ of ${\mathcal{K}}_{i}$ by ${\mathcal{K}}_{i}^{\ast } := \{s \in \mathbb {R}^{n}: x^{\top } s \ge 0\ (x \in {\mathcal{K}}_{i})\}$. In addition, we call a compact subset S of $\mathbb {R}^{n_{i}}$ a base of ${\mathcal{K}}_{i}^{\ast }$ when it satisfies

$$ \{\alpha v: \alpha \in \mathbb{R}_{+}, v \in S\} = \mathcal{K}_{i}^{\ast}. $$

Note that for each cone, a base is not unique. In this paper, we denote a fixed base of ${\mathcal{K}}_{i}^{\ast }$ by $\text {base}({\mathcal{K}}_{i}^{\ast })$. Using these notations, we can derive the following LSIP problem equivalent to the CP problem (1):

$$ \begin{array}{@{}rcl@{}} &&\text{minimize} \quad c^{\top} x\\ &&\text{subject to} \quad A x = b,\\ && \qquad\qquad (v^{i})^{\top} x^{i} \ge 0\ (v^{i} \in \text{base}(\mathcal{K}_{i}^{\ast});\ i = 1, \dots, p), \end{array} $$

(3)

where $x^{i} \in \mathbb {R}^{n_{i}}$ denotes the i-th block of x partitioned so that it matches the Cartesian structure of ${\mathcal{K}}$, i.e., $x = ((x^{1})^{\top }, (x^{2})^{\top }, \dots , (x^{p})^{\top })^{\top } \in {\prod }_{i = 1}^{p} \mathbb {R}^{n_{i}}$. For example, if we take a base of a second-order cone appropriately, this semi-infinite constraint can be simplified to $(1, (\bar {v}^{i})^{\top }) x^{i} \ge 0\ (\bar {v}^{i} \in \mathbb {R}^{n_{i} - 1}: \|\bar {v}^{i}\| \le 1;\ i = 1, \dots , p)$ as we mention later. Hayashi et al. [6] tailored the dual-simplex method for LP problems to dual SOCP problems via their LSIP representation. For an overview of semi-infinite programming problems, we refer readers to the survey articles [8, 14].

Algorithms for solving LP problems include the simplex method, ellipsoid method, and interior-point method. Although the ellipsoid and interior-point methods are polynomial-time algorithms, the existence of a strongly polynomial-time algorithm for solving LPs remains an open problem. In an attempt to devise a strongly polynomial-time algorithm for LPs, Fujishige et al. [5] proposed the LP-Newton method for box-constrained LP problems, which have a box constraint l ≤ x ≤ u instead of the nonnegativity constraint x ≥ 0 in the LP problem (2). Kitahara et al. [10] extended it to the LP problem (2). This algorithm repeats projecting a current point onto a polytope arising from the feasible region and the computation of a supporting hyperplane. Numerical results in [5] suggest that the algorithm is promising. In addition, Kitahara and Sukegawa [11] proposed a simple projection algorithm for the box-constrained LP problems based on the LP-Newton method.

Recently, Silvestri and Reinelt [19] developed an LP-Newton method for SCP problems. To the best of our knowledge, this is the first extension of the LP-Newton method to SCP problems. In [19], the authors considered conic-box-constrained SCP problems, i.e., the CP problem (1) with $x \in {\mathcal{K}}$ replaced by a conic-box constraint l ≼ x ≼ u, which denotes $x - l, u - x \in {\mathcal{K}}$ with a symmetric cone ${\mathcal{K}}$. Their algorithm computes a projection onto a conic zonotope at each iteration, and they proposed a Frank–Wolfe-based inner algorithm for this computation. Nevertheless, the computation of the projection still appears to be difficult. In fact, their numerical results showed that the inner algorithm for obtaining the projection required a number of iterations, although the outer loop was repeated relatively few times.

In this paper, we propose a different type of LP-Newton method for the CP problem (1) with ${\mathcal{K}}$ being possibly a nonsymmetric cone, which is based on the semi-infinite reformulation (3). In our approach, we construct a sequence of LPs by adaptively selecting finitely many constraints from the infinitely many constraints of the LSIP problem (3). To produce an iteration point, we compute a projection onto a polytope arising from a polyhedral approximation of ${\mathcal{K}}$, which can be realized by solving a convex quadratic programming (QP) problem.

The remainder of this paper is organized as follows. In Section 2, we describe our proposed LP-Newton method for the CP problem (1). In Section 3, we establish global convergence of the proposed algorithm under the boundedness assumption of the optimal set of the CP problem (1). In Section 4, we propose a primal-dual algorithm that generates a sequence in the dual space of the CP problem (1). We also show its global convergence to a pair of optimums of the CP problem (1) and its dual problem under Slater’s constraint qualification. In Section 5, we report numerical results of applying the proposed method to SOCPs to investigate its validity and effectiveness.

2 Primal algorithm

In this section, we extend the LP-Newton method for the LP problem (2) proposed by Kitahara et al. [10] to the CP problem (1). For simplicity, we use the following notation:

$$ \bar{A} := \left( \begin{array}{ll} c^{\top}\\ A \end{array}\right) \in \mathbb{R}^{(1 + m) \times n},\ L := \left\{ \left( \begin{array}{ll} \gamma\\ b \end{array}\right): \gamma \in \mathbb{R}\right\} \subseteq \mathbb{R}^{1 + m}, $$

(4)

and for some $V_{i} \subseteq \text {base}({\mathcal{K}}_{i}^{\ast })\ (i = 1, \dots , p)$,

$$ V := \prod\limits_{i = 1}^{p} V_{i},\ \text{cone}(V)^{\ast} := \{x \in \mathbb{R}^{n}: (v^{i})^{\top} x^{i} \ge 0\ (v^{i} \in V_{i};\ i = 1, \dots, p)\}. $$

Note that cone(V )^∗ defined above is the dual cone of the conic hull of V, denoted by cone(V ), and hence especially $\text {cone}(\text {base}({\mathcal{K}}_{i}^{\ast }))^{\ast } = ({\mathcal{K}}^{\ast })^{\ast } = {\mathcal{K}}_{i}$ for each i. Moreover, we often use a MATLAB notation for a partitioned vector, i.e., we denote (u^⊤,v^⊤)^⊤ by (u;v) for any vectors u and v. In addition, we denote m-dimensional zero vector $(0; \dots ; 0) \in \mathbb {R}^{m}$ by 0_m.

In the proposed algorithm, we construct sequences $\{x^{(k)}\} \subseteq \mathbb {R}^{n}$ and $\{V^{(k)}\} \subseteq {\prod }_{i = 1}^{p} \text {base}({\mathcal{K}}_{i}^{\ast })$ such that $V^{(k)} := {\prod }_{i = 1}^{p} V_{i}^{(k)}$ and $|V_{i}^{(k)}| < \infty \ (i = 1, \dots , p)$ for each k ≥ 1. As more specifically described shortly, the sequence {x^(k)} is produced by performing one iteration of the LP-Newton method for the following LP problem, which is obtained by replacing $\text {base}({\mathcal{K}}^{\ast })$ in the LSIP problem (3) by the finite set $V_{i}^{(k)}$ for $i = 1, \dots , p$:

$$ \begin{array}{@{}rcl@{}} &&\text{minimize} \quad c^{\top} x\\ &&\text{subject to} \quad A x = b,\\ &&\qquad\qquad\quad (v^{i})^{\top} x^{i} \ge 0 (v^{i} \in V_{i}^{(k)};\ i = 1, \dots, p). \end{array} $$

(5)

Note that the finite number of linear inequality constraints of the LP problem (5) form an outer polyhedral approximation of ${\mathcal{K}}$. Thus, the LP problem (5) is a relaxation problem of the LSIP problem (3) or the CP problem (1). As will be proved later, if x^(k) is feasible to the CP problem (1), it is nothing but an optimum of the CP problem (1).

Otherwise, for each i such that $x^{i, (k)} \notin {\mathcal{K}}_{i}$, we update $V_{i}^{(k)}$ by adding $v^{i, (k)} \in \mathop {\text {argmin}}_{v^{i} \in \text {base}({\mathcal{K}}_{i}^{\ast })} (v^{i})^{\top } x^{i, (k)}$, which is one of the indices most violating the i-th conic constraint $x^{i} \in {\mathcal{K}}^{(i)}$ at x^(k).

We name the proposed algorithm the adaptive LP-Newton (ALPN) method for the CP problem (1) and formally describe it in Algorithm 1. This algorithm generates sequences $\{w^{(k - 1 / 2)}\}_{k \ge 1}$ on the line L and {w^(k)} on the outside of $\bar {A} {\mathcal{K}}$ (recall the definition by (4)). For illustration, we give a schematic diagram in Fig. 1. At the k-th iteration of Algorithm 1, we first compute w^(k) and w^(k+ 1/2) from w^(k− 1/2) by applying one iteration of the existing LP-Newton method [10] developed for LPs to the LP problem (5). Specifically, we set the projection of w^(k− 1/2) onto $\bar {A} {\mathcal{K}}$ as w^(k). Subsequently, we update an outer approximation $\bar {A} \text {cone}(V_{i}^{(k)})^{\ast }$ of $\bar {A} {\mathcal{K}}_{i}$ for each i by updating V^(k) in the way explained in the previous paragraph. After that, we construct the support hyperplane H^(k) of $\bar {A} {\mathcal{K}}$ at w^(k) and set the intersection of the plane H^(k) and the line L as w^(k+ 1/2). A sequence $\{\gamma ^{(k - 1 / 2)}\} \cup \{\gamma ^{(k)}\} = \{\gamma ^{(1 / 2)}, \gamma ^{(1)}, \gamma ^{(3 / 2)}, \gamma ^{(2)}, \dots \}$ is nondecreasing and bounded above by the optimal value 𝜃^∗ of the CP problem (1) as we show in Lemma 2. Moreover, it converges to 𝜃^∗ under mild assumptions. Another sequence {β^(k)} converges to b as we show in Lemma 3. In conjunction with these two sequences, a sequence {x^(k)} converges to an optimal solution (Theorem 1).

Fig. 1

A schematic diagram of the k-th iteration of Algorithm 1. The horizontal line depicts L, which is parallel to the γ-axis associated with the objective function. The circular cone (shown in blue) and the square pyramid (whose four ridges are shown in solid lines) depict $\bar {A} {\mathcal{K}}$ and $\bar {A} \text {cone}(V^{(k)})^{\ast }$, respectively. The line segment from w^(k− 1/2) to w^(k) (shown in dotted line) is orthogonal to a supporting hyperplane H^(k) (shown in green) of $\bar {A} \text {cone}(V^{(k)})^{\ast }$ at w^(k). Note that H^(k) touches $\bar {A} \text {cone}(V^{(k)})^{\ast }$ on a ridge. The intersecting point of L and H^(k) is w^(k+ 1/2)

In Algorithm 1, it is easy to compute γ^(k+ 1/2) as follows:

$$ \gamma^{(k + 1 / 2)} = \gamma^{(k)} - \frac{\|{\upbeta}^{(k)} - b\|^{2}}{\gamma^{(k - 1 / 2)} - \gamma^{(k)}}. $$

In addition, it is also easy to compute

$$ v^{i, (k)} \in \mathop{\text{argmin}}_{v^{i} \in \text{base}(\mathcal{K}_{i}^{\ast})} (v^{i})^{\top} x^{i, (k)} $$

(6)

for some particular cones as illustrated below.

Example 1 (Second-order cone)

For the n-dimensional second-order cone ${\mathcal{K}}_{\text {SOC}}^{n} \subset \mathbb {R}^{n}$ defined by ${\mathcal{K}}_{\text {SOC}}^{n} := \{x \in \mathbb {R}_{+} \times \mathbb {R}^{n - 1}: x_{1} \ge \|\bar {x}\|\}$, where $\bar {x} \in \mathbb {R}^{n - 1}$ denotes the subvector of x without the first element, that is, $x = (x_{1}; \bar {x}) \in \mathbb {R} \times \mathbb {R}^{n - 1}$, we can take $\{(s_{1}; \bar {s}) \in {\mathcal{K}}_{\text {SOC}}^{n}: s_{1} = 1\}$ as $\text {base}(({\mathcal{K}}_{\text {SOC}}^{n})^{\ast }) = \text {base}({\mathcal{K}}_{\text {SOC}}^{n})$. In addition, $(1; -\bar {x}^{i, (k)} / \|\bar {x}^{i, (k)}\|)$ is an optimal solution to the subproblem (6) with ${\mathcal{K}}_{i}^{\ast } = {\mathcal{K}}_{\text {SOC}}^{n}$ if $\bar {x}^{i, (k)} \ne 0_{n - 1}$; otherwise, (1;0_n− 1) is optimal.

Example 2 (Positive semidefinite cone)

The set of all n-dimensional positive semidefinite matrices forms a cone. The cone is called the n-dimensional positive semidefinite cone and denoted by ${\mathcal{K}}_{\text {PSD}}^{n}$. For ${\mathcal{K}}_{\text {PSD}}^{n}$, we can take $\{S \in {\mathcal{K}}_{\text {PSD}}^{n}: \text {trace}(S) = 1\}$ as $\text {base}(({\mathcal{K}}_{\text {PSD}}^{n})^{\ast }) = \text {base}({\mathcal{K}}_{\text {PSD}}^{n})$. In addition, it holds that $\xi ^{\ast } (\xi ^{\ast })^{\top } \in \mathop {\text {argmin}}_{V^{i} \in \text {base}({\mathcal{K}}_{i}^{\ast })} \text {trace}(V^{i} X^{i, (k)})$, which is the matrix version of the subproblem (6), where ξ^∗ is a normalized eigenvector of X^i,(k) corresponding to the minimum eigenvalue.

Example 3 (ℓ _p-norm cone)

For p ≥ 1, the n-dimensional ℓ_p-norm cone ${\mathcal{K}}_{\ell _{p}}^{n} \subset \mathbb {R}^{n}$ is defined by ${\mathcal{K}}_{\ell _{p}}^{n} := \{x \in \mathbb {R}_{+} \times \mathbb {R}^{n - 1}: x_{1} \ge \|\bar {x}\|_{p}\}$. The ℓ_p-norm cone is a generalization of the second-order cone. In fact, ${\mathcal{K}}_{\ell _{2}}^{n} = {\mathcal{K}}_{\text {SOC}}^{n}$. In addition, it holds that ${\mathcal{K}}_{\ell _{p}}^{\ast } = {\mathcal{K}}_{\ell _{q}}$, where q := (1 − p^− 1)^− 1. For this cone, we can take $\{(s_{1}; \bar {s}) \in {\mathcal{K}}_{\ell _{q}}^{n}: s_{1} = 1\}$ as $\text {base}({\mathcal{K}}_{\ell _{q}}^{n})$ and an optimal solution to the subproblem (6) with ${\mathcal{K}}_{i}^{\ast } = {\mathcal{K}}_{\mathrm {\ell _{q}}}^{n}$ can be written as $(1; -\text {sign}(\bar {x}^{i, (k)}) \circ (|\bar {x}^{i, (k)}| / \|\bar {x}^{i, (k)}\|_{p})^{p / q})$ if $\bar {x}^{i, (k)} \ne 0_{n - 1}$, where ∘ denotes the Hadamard product and $(\text {sign}(\bar {x}^{i, (k)}))_{j} := 1\ (\bar {x}_{j}^{i, (k)} > 0), 0\ (\bar {x}_{j}^{i, (k)} = 0), -1\ (\bar {x}_{j}^{i, (k)} < 0)$ and $(|\bar {x}^{i, (k)}|)_{j} = |\bar {x}_{j}^{i, (k)}|$ for each j; otherwise, (1;0_n− 1) is optimal.

Remark 1

Cones ${\mathcal{K}}_{\text {SOC}}^{n}, {\mathcal{K}}_{\text {PSD}}^{n}, {\mathcal{K}}_{\ell _{p}}^{n}$ in Examples 1–3 have nonempty interior. Such cones are called solid. For a solid cone ${\mathcal{K}}$, we can take $\{s \in {\mathcal{K}}^{\ast }: \tilde {x}^{\top } s = 1\}$ as $\text {base}({\mathcal{K}}^{\ast })$ for any $\tilde {x} \in \text {int}\ {\mathcal{K}}$, where $\text {int}\ {\mathcal{K}}$ denotes the interior of ${\mathcal{K}}$. Bases given in Examples 1–3 are constructed by this procedure.

Drawbacks of Algorithm 1 are the construction of V⁽¹⁾, which corresponds to initial cutting hyperplanes, and the computation of w^(k) and x^(k), that is, the projection onto $\bar {A} \text {cone}(V^{(k)})^{\ast }$. In general, it is not easy to construct an initial finite set V⁽¹⁾ such that the following LP problem is lower-bounded:

$$ \begin{array}{ll} \text{minimize}& c^{\top} x\\ \text{subject to}& A x = b,\\ & x \in \text{cone}(V^{(1)})^{\ast}. \end{array} $$

(7)

However, if a feasible solution $\hat {y}$ to the dual of the CP problem (1)

$$ \begin{array}{ll} \text{maximize}& b^{\top} y\\ \text{subject to}& c - A^{\top} y \in \mathcal{K}^{\ast} \end{array} $$

(8)

is available, we can take $\{c - A^{\top } \hat {y}\}$ as V⁽¹⁾. In fact, if we take $V^{(1)} := \{c - A^{\top } \hat {y}\}$, x ∈cone(V⁽¹⁾)^∗ is equivalent to $(c - A^{\top } \hat {y})^{\top } x \ge 0$, which implies $c^{\top } x \ge b^{\top } \hat {y}$ for any feasible solution x of the LP problem (7). If there are no dual feasible solutions available, we may construct V⁽¹⁾ heuristically. In the computation of w^(k) and x^(k) in Algorithm 1, we may solve the following convex quadratic programming (QP) problem for $i = 1, \dots , p$:

$$ \begin{array}{lll} \text{minimize}& \|\bar{A} x - w^{(k - 1 / 2)}\|^{2}\\ \text{subject to}& (v^{i})^{\top} x^{i} \ge 0 &(v^{i} \in V_{i}^{(k)};\ i = 1, \dots, p), \end{array} $$

(9)

and use an optimal solution of the QP problem (9) as x^(k), and set $w^{(k)} = \bar {A} x^{(k)}$. The number of constraints in the QP problem (9) increases as iterations progress. This drawback can be mitigated by using warm-start techniques or exchange methods [8, 14]. For example, if we solve the QP problem (9) using the active set method, we can set (w^(k),x^(k)) as an initial point of the active method in the (k + 1)-th iteration. The use of initial points often accelerates the active set method. Moreover, like exchange methods, by dropping constraints, we may refrain the number of constraints of the QP problem (9) at every iteration. But, it is nontrivial how to select constraints to be dropped, while preserving the global convergence. Even though warm-start techniques or exchange methods are utilized, solving QP problems is still computationally expensive. Hence, a more sophisticated subroutine is required. The LP-Newton method [5] for a box-constrained LP problem employs Wolfe’s algorithm [24] to find the nearest point in a zonotope to a given point, and the LP-Newton method [10] for the standard form LP problem (2) uses Wilhelmsen’s algorithm [23] to find the nearest point in a polyhedral cone to a given point. The subroutines are conjectured to be polynomial-time algorithms, and thus the LP-Newton methods for LPs have the potential to be strongly polynomial-time algorithms. Although these subroutines are powerful, it may be difficult to use them in Algorithm 1. In these subroutines, extreme directions or points of the zonotope or polyhedral cone are explicitly required. In our case, unfortunately, we do not have such explicit formulas.

Remark 2

Algorithm 1 is able to detect infeasibility of the LP problem (5), and hence of the CP problem (1), if β^(k)≠b and γ^(k− 1/2) = γ^(k) hold. It can be proved in a manner similar to [10, Lemma 3.3].

3 Convergence analysis

In this section, we prove that a sequence generated by Algorithm 1 converges globally to an optimum of the CP problem (1). We first state the following technical lemmas.

Lemma 1

Let {α^(k)} be a sequence of nonnegative scalars and {z^(k)} be defined by z^(k) := α^(k)x^(k) for each k. If Algorithm 1 generates an infinite sequence {x^(k)} and there exists an accumulation point of {z^(k)}, then it belongs to ${\mathcal{K}}$.

Proof 1

Let us express z^(k) as $z^{(k)} := (z^{1, (k)}, \dots ,z^{p, (k)}) = \alpha ^{(k)} (x^{1, (k)}, \dots , x^{p, (k)})$ and let $z^{\ast } := (z^{1, \ast }, \dots ,z^{p, \ast })$ be an arbitrarily chosen accumulation point of {z^(k)}. Because of the compactness of $\text {base}({\mathcal{K}}_{i}^{\ast })$ for every $i = 1, \dots , p$, $\{v^{(k)}\} \subseteq \text {base}({\mathcal{K}}^{\ast }) = {\prod }_{i = 1}^{p} \text {base}({\mathcal{K}}_{i}^{\ast })$ has at least one accumulation point in $\text {base}({\mathcal{K}}^{\ast })$. Denote this point by v^∗ and express it as $(v^{1,\ast }, v^{2, \ast }, \dots , v^{p, \ast }) \in {\prod }_{i = 1}^{p} \text {base}({\mathcal{K}}_{i}^{\ast })$. Taking an appropriate subsequence $\{v^{(k)}\}_{k \in K}$, we can assume that (v^(k),z^(k)) converges to (v^∗,z^∗) as $k \in K \to \infty$.

Note that $v^{i, (k)} \in {\text {argmin}}_{v^{i} \in \text {base}({\mathcal{K}}_{i}^{\ast })} (v^{i})^{\top } z^{i, (k)}$ holds because $v^{i, (k)} \in {\text {argmin}}_{v^{i} \in \text {base}({\mathcal{K}}_{i}^{\ast })} (v^{i})^{\top } x^{i, (k)}$ and α^(k) ≥ 0. Here, by letting $k \in K \to \infty$, we obtain $v^{i, \ast } \in \mathop {\text {argmin}}_{v^{i} \in \text {base}({\mathcal{K}}_{i}^{\ast })} (v^{i})^{\top } z^{i, \ast }$. Thus, to show $z^{\ast } \in {\mathcal{K}}$, it suffices to prove that (v^i,∗) ^⊤z^i,∗≥ 0 for each i. To this end, let us fix i and prove (v^i,(k))^⊤z^i,∗≥ 0 for any k ∈ K. Choosing some arbitrary $\hat {k} \in K$, it follows that $(v^{i, (\hat {k})})^{\top } z^{i, (k)} \ge 0$ for any $k > \hat {k}$ in K, because z^i,(k) = α^(k)x^i,(k) ∈cone(V^(k))^∗ and $v^{i, (\hat {k})} \in V_{i}^{(k)}$ for any $k > \hat {k}$. Then, by letting $k \in K \to \infty$, we obtain $(v^{i, (\hat {k})})^{\top } z^{i, \ast } \ge 0$. As $\hat {k}$ was arbitrarily chosen from K, we conclude that (v^i,(k))^⊤z^i,∗≥ 0 (k ∈ K) holds. Finally, by forcing $k \in K \to \infty$, we conclude that (v^i,∗)^⊤z^i,∗≥ 0 for any i. Therefore, $z^{\ast } \in {\mathcal{K}}$. □

Lemma 2

Assume that the optimal value of the CP problem (1) is finite and 𝜃^∗ be the optimal value. If Algorithm 1 does not stop at the k-th iteration, we have

$$ \gamma^{(k - 1 / 2)} \le \gamma^{(k)} \le \gamma^{(k + 1 / 2)} \le \theta^{\ast}. $$

Proof 2

Let $\theta ^{(k)} \in \mathbb {R}$ be the optimal value of the LSIP problem (3) with $\text {base}({\mathcal{K}}_{i}^{\ast })$ replaced by $V_{i}^{(k)}$ for $i = 1, \dots , p$, which is a relaxation problem for the CP problem (1). Therefore, 𝜃^(k) ≤ 𝜃^∗ holds. In a similar manner to [10, Lemma 3.1], it can be verified that

$$ \gamma^{(k - 1 / 2)} \le \gamma^{(k)} \le \gamma^{(k + 1 / 2)} \le \theta^{(k)}. $$

Hence, we have the desired result.

□

Lemma 3

Assume that the optimal value of the CP problem (1) is finite. If Algorithm 1 generates an infinite sequence {β^(k)}, then $\lim _{k \to \infty } {\upbeta }^{(k)} = b$ holds.

Proof 3

To show the desired result, we prove $\lim _{k \to \infty } \|{\upbeta }^{(k)} - b\| = 0$. Note that {γ^(k− 1/2)} and {γ^(k)} converge to the same point by Lemma 2. In fact, the joint sequence $\{\gamma ^{(k - 1 / 2)}\} \cup \{\gamma ^{(k)}\} = \{\gamma ^{(1 / 2)}, \gamma ^{(1)}, \gamma ^{(1 + 1 / 2)}, \gamma ^{(2)}, \dots \}$ is a nondecreasing sequence bounded above and thus convergent. Since {γ^(k− 1/2)} and {γ^(k)} are both convergent subsequences of the joint sequence, they must share the same limit point. Thus, |γ^(k+ 1/2) − γ^(k− 1/2)|→ 0 and |γ^(k) − γ^(k− 1/2)|→ 0 as $k \to \infty$. Moreover, as w^(k) is the projection of w^(k− 1/2) onto the supporting hyperplane H^(k) and w^(k+ 1/2) ∈ H^(k), we have

$$ |\gamma^{(k + 1 / 2)} - \gamma^{(k - 1 / 2)}| = \|w^{(k + 1 / 2)} - w^{(k - 1 / 2)}\| \ge \|w^{(k)} - w^{(k - 1 / 2)}\| = \left\| \left( \begin{array}{ll} \gamma^{(k)} - \gamma^{(k - 1 / 2)}\\ {\upbeta}^{(k)} - b \end{array}\right) \right\|. $$

From these facts, it follows that $\lim _{k \to \infty } \|{\upbeta }^{(k)} - b\| = 0$.

□

In what follows, we prove the boundedness of {x^(k)} and its global convergence to an optimal solution. To this end, let us make the following assumption.

Assumption 1

The optimal solution set ${\mathcal{S}}_{\mathrm {P}}$ of the CP problem (1) is nonempty and compact.

Remark 3

Assumption 1 holds if the dual CP problem (8) has an optimum and strictly feasible solution, i.e., there exists some $\hat {y} \in \mathbb {R}^{m}$ such that $c - A^{\top } \hat {y}\in \text {int}\ {\mathcal{K}}^{\ast }$.

Proposition 1

If Algorithm 1 generates an infinite sequence {x^(k)} and Assumption 1 holds, then the generated sequence {x^(k)} is bounded.

Proof 4

Denote the feasible domain of the CP problem (1) by ${\mathcal{F}}_{\mathrm {P}}$. To show the boundedness of {x^(k)}, we assume to the contrary for a contradiction. Thus, there exists some subsequence $\{x^{(k)}\}_{k \in K} \subseteq \{x^{(k)}\}$ such that $\lim _{k \in K \to \infty } \|x^{(k)}\| = \infty$ and ∥x^(k)∥≠ 0 for any k ∈ K. Then, we have

$$ \frac{A x^{(k)}}{\|x^{(k)}\|} = \frac{{\upbeta}^{(k)}}{\|x^{(k)}\|},\ \frac{x^{(k)}}{\|x^{(k)}\|} \in \text{cone}(V^{(k)})^{\ast},\ \frac{c^{\top} x^{(k)}}{\|x^{(k)}\|} \le \frac{\theta^{\ast}}{\|x^{(k)}\|}, $$

where the second relation is derived from the fact that x^(k) ∈cone(V^(k))^∗ and cone(V^(k))^∗ is a cone. Letting $k\in K \to \infty$ in the above and choosing an arbitrary accumulation point of {x^(k)/∥x^(k)∥}, denoted by d^∗, implies that

$$ A d^{\ast} = 0_{m},\ d^{\ast} \in \mathcal{K},\ c^{\top} d^{\ast} \le 0,\ \|d^{\ast}\| = 1, $$

(10)

where the first relation follows from the boundedness of {β^(k)} implied by Lemma 3 and the second one follows from Lemma 1 with z^(k) = x^(k)/∥x^(k)∥ and α^(k) = 1/∥x^(k)∥. Choose $x^{\ast } \in {\mathcal{S}}_{\mathrm {P}}$ arbitrarily and define Ω := {x^∗ + αd^∗ : α ≥ 0}. We then deduce that ${\Omega } \subseteq {\mathcal{S}}_{\mathrm {P}}$ from (10), because

$$ A (x^{\ast} + \alpha d^{\ast}) = b,\ x^{\ast} + \alpha d^{\ast} \in \mathcal{K},\ c^{\top} (x^{\ast} + \alpha d^{\ast}) \le c^{\top} x^{\ast} $$

for any α ≥ 0, where the second statement follows from the facts that $x^{\ast } \in {\mathcal{K}}$, $\alpha d^{\ast } \in {\mathcal{K}}$, and ${\mathcal{K}}$ is a convex cone. Note that Ω is unbounded because ∥d^∗∥ = 1, which implies the unboundedness of ${\mathcal{S}}_{\mathrm {P}}$. However, this contradicts Assumption 1. As a consequence, {x^(k)} is bounded. □

Theorem 1

Under Assumption 1, Algorithm 1 stops in a finite number of iterations and returns an optimal solution, or it generates an infinite sequence {x^(k)} such that any accumulation point of {x^(k)} is an optimal solution of the CP problem (1).

Proof 5

First, we assume Algorithm 1 terminates at the k-th iteration. Since we are assuming the feasibility of the CP problem (1) here, it terminates because conditions β^(k) = b and V^(k+ 1) = V^(k) are simultaneously satisfied. Because β^(k) = b and $x^{(k)} \in \bar {A} \text {cone}(V^{(k)})$, we have Ax^(k) = β^(k) = b and $(v^{i})^{\top } x^{i, (k)} \ge 0\ (v^{i} \in V_{i}^{(k)})$. This means the feasibility of x^(k) for the LP problem (5). In addition, from V^(k+ 1) = V^(k), we can deduce $(v^{i})^{\top } x^{i, (k)} \ge 0\ (v^{i} \in \text {base}({\mathcal{K}}_{i}^{\ast }))$ for each i. Therefore, x^(k) is feasible for the LSIP problem (3) and the CP problem (1), and hence c^⊤x^(k) ≥ 𝜃^∗ follows, where 𝜃^∗ denotes the optimal value of the CP problem (1). On the other hand, from Lemma 2, we have c^⊤x^(k) = γ^(k) ≤ 𝜃^∗. Therefore, we obtain c^⊤x^(k) = 𝜃^∗ and conclude that x^(k) is optimal for the CP problem (1).

Hereinafter, we assume {x^(k)} is an infinite sequence. From Proposition 1, {x^(k)} is bounded and has an accumulation point. Choose an arbitrary accumulation point and denote it by x^∗. Without loss of generality, we may assume that $\lim _{k \to \infty } x^{(k)} = x^{\ast }$ by taking a subsequence if necessary. Now, let us recall that Ax^(k) = β^(k) and x^(k) ∈cone(V^(k))^∗ hold for any k. Together with Lemmas 1 and 3, this implies that Ax^∗ = b and $x^{\ast } \in {\mathcal{K}}$, that is, x^∗ is feasible for the CP problem (1). Hence, c^⊤x^∗≥ 𝜃^∗ follows. On the other hand, by Lemma 2, it holds that c^⊤x^(k) = γ^(k) ≤ 𝜃^∗ for each k, and by taking the limit therein, we obtain c^⊤x^∗≤ 𝜃^∗. Therefore, we have c^⊤x^∗ = 𝜃^∗. Thus, we conclude that x^∗ is optimal for the CP problem (1). □

Remark 4

According to [10, Theorem 3.1], for the case with ${\mathcal{K}} = \mathbb {R}_{+}^{n}$, the number of iterations of the algorithm is, at most, the number of faces of the cone $\bar {A} {\mathcal{K}}$.

4 Primal-dual algorithm

4.1 Description of the algorithm

In Section 3, we proposed the ALPN method for solving the CP problem (1). In this section, we consider a primal-dual algorithm for the ALPN method, which solves the CP problem (1) and the dual problem (8) simultaneously.

Our primal-dual algorithm is described in Algorithm 2, where {x^(k)}, {γ^(k− 1/2)}, {γ^(k)}, and {β^(k)} represent sequences generated by Algorithm 1. Since Algorithm 2 uses sequences generated by Algorithm 1, they are executed jointly. Note that (1;−y^(k)) is the normal vector of the supporting hyperplane H^(k) of $\bar {A} {\mathcal{K}}$ at $\bar {A} x$. Supporting hyperplanes of $\bar {A} {\mathcal{K}}$ play a crucial role as the following property.

Proposition 2

Let $x^{\ast } \in {\mathcal{K}}$ be an optimum of the CP problem (1) and H^∗ be a supporting hyperplane of $\bar {A} {\mathcal{K}}$ at $\bar {A} x^{\ast } \in \bar {A} {\mathcal{K}}$. Suppose that (1;−y^∗) is a normal vector to H^∗. Then, together with x^∗, y^∗, and s^∗ := c − A^⊤y^∗ satisfy the Karush–Kuhn–Tucker (KKT) conditions of the CP problem (1):

$$ A x^{\ast} = b,\ A^{\top} y^{\ast} + s = c,\ x^{\ast} \in \mathcal{K},\ s^{\ast} \in \mathcal{K}^{\ast},\ (s^{\ast})^{\top} x^{\ast} = 0. $$

(11)

In particular, y^∗ is an optimum of the dual CP problem (8).

Proof 6

As H^∗ is a supporting hyperplane of $\bar {A} {\mathcal{K}}$ at $\bar {A} x^{\ast } = (c^{\top } x^{\ast }; A x^{\ast })$ and x^∗ solves the CP problem (1), we have

$$ \bar{A} x^{\ast} \in \mathop{\text{argmin}}_{w \in \bar{A} \mathcal{K}} (1, -(y^{\ast})^{\top}) w. $$

Hence, it holds that

$$ x^{\ast} \in \mathop{\text{argmin}}_{x \in \mathcal{K}} (c - A^{\top} y^{\ast})^{\top} x. $$

(12)

By the KKT conditions of the problem (12), there exists some $s^{\ast } \in \mathbb {R}^{n}$ such that

$$ s^{\ast} = c - A^{\top} y^{\ast},\ x^{\ast} \in \mathcal{K},\ s^{\ast} \in \mathcal{K}^{\ast},\ (s^{\ast})^{\top} x^{\ast} = 0, $$

which, together with Ax^∗ = b, implies the system (11). The optimality of y^∗ for the dual CP problem (8) is obvious. □

4.2 Convergence analysis

In our analysis of the primal-dual algorithm, we make the following assumption:

Assumption 2

Slater’s constraint qualification holds for the CP problem (1), i.e., there exists some $\hat {x} \in \mathbb {R}^{n}$ such that $\hat {x} \in \text {int}\ {\mathcal{K}}$ and $A \hat {x} = b$, and the matrix A is of full row rank.

Under Assumptions 1 and 2, it is guaranteed that the optimal set of the dual CP problem (8) is nonempty and compact.

Remark 5

In Proposition 2, by assuming the existence of a supporting hyperplane H^∗ of $\bar {A} {\mathcal{K}}$ at $\bar {A} x^{\ast } \in \bar {A} {\mathcal{K}}$ that is not parallel to L, we proved the existence of a KKT point. We can derive the assumption of such a supporting hyperplane from Assumption 2 (details are omitted here) but the converse is not true. Hence, we can regard the assumption of the existence of such a supporting hyperplane as a weaker constraint qualification than Slater’s one and the full rank assumption.

Here, we prove the global convergence of Algorithm 2 under Assumptions 1 and 2.

Theorem 2

Under Assumptions 1 and 2, Algorithm 2 stops in a finite number of iterations and returns an optimal solution, or it generates an infinite sequence {y^(k)} such that {y^(k)} is bounded and any accumulation point of {y^(k)} solves the dual CP problem (8).

Proof 7

Since the case of the finite termination is obvious, we assume {y^(k)} is an infinite sequence in what follows. We first show the boundedness of {y^(k)}. To derive a contradiction, suppose that {y^(k)} is unbounded, and hence there exists some subsequence $\{y^{(k)}\}_{k \in K}$ such that $\|y^{(k)}\| \to \infty$ and y^(k)≠ 0_m for any k ∈ K. Note that H^(k) is a supporting hyperplane of $\bar {A} \text {cone}(V^{(k)})^{\ast }$ at $\bar {A} x^{(k)}$ that has the normal vector (1;−y^(k)). Then, by the definition of x^(k), we find that

$$ \bar{A} x^{(k)} \in \mathop{\text{argmin}}_{w \in \bar{A} \text{cone}(V^{(k)})^{\ast}} (1, -(y^{(k)})^{\top}) w, $$

and thus

$$ x^{(k)} \in \mathop{\text{argmin}}_{x \in \text{cone}(V^{(k)})^{\ast}} (c - A^{\top} y^{(k)})^{\top} x. $$

Using the KKT conditions and the definition of x^(k) again, we have

$$ x^{(k)} \in \text{cone}(V^{(k)})^{\ast},\ c - \!\!A^{\top} y^{(k)} \in \text{cone}(V^{(k)}),\ (c -\!\! A^{\top} y^{(k)})^{\top} x^{(k)} = 0,\ A x^{(k)} = {\upbeta}^{(k)}. $$

(13)

As $\text {cone}(V^{(k)}) \subseteq {\mathcal{K}}^{\ast }$ follows from ${\mathcal{K}} \subseteq \text {cone}(V^{(k)})^{\ast }$, we find that $c - A^{\top } y^{(k)} \in {\mathcal{K}}^{\ast }$. Divide $c - A^{\top } y^{(k)} \in {\mathcal{K}}^{\ast }$ and (c − A^⊤y^(k))^⊤x^(k) = 0 by ∥y^(k)∥ and let $k \in K \to \infty$ in (13). Choose an accumulation point of {y^(k)/∥y^(k)∥} and denote it by d^∗. Let x^∗ be an accumulation point of {x^(k)} (recall Theorem 1). Without loss of generality, we may assume that $\lim _{k \in K \to \infty } (x^{(k)}, y^{(k)} / \|y^{(k)}\|) = (x^{\ast }, d^{\ast })$. Then, noting that $(c - A^{\top } y^{(k)}) / \|y^{(k)}\| \in {\mathcal{K}}^{\ast }$ for any k ∈ K and $\lim _{k \to \infty } {\upbeta }^{(k)} = b$ by Lemma 3, it holds that

$$ x^{\ast} \in \mathcal{K},\ -A^{\top} d^{\ast} \in \mathcal{K}^{\ast},\ (A x^{\ast})^{\top} d^{\ast} = 0,\ A x^{\ast} = b. $$

(14)

Here, let y^∗ be an arbitrary optimum of the dual CP problem (8). Then, the set Ω := {y^∗ + αd^∗ : α ≥ 0} is contained in the optimal solution set of the dual CP problem (8), denoted by ${\mathcal{S}}_{\mathrm {D}}$. This is shown as follows. Fix an arbitrary value of α ≥ 0. Using the second relation in (14) and $c - A^{\top } y^{\ast } \in {\mathcal{K}}^{\ast }$ together with the fact that ${\mathcal{K}}^{\ast }$ is a closed convex cone, we have $c - A^{\top } (y^{\ast } + \alpha d^{\ast }) \in {\mathcal{K}}^{\ast }$, and so y^∗ + αd^∗ is feasible for the dual CP problem (8). Moreover, we can deduce from (14) that

$$ b^{\top} (y^{\ast} + \alpha d^{\ast}) = b^{\top} y^{\ast} + \alpha (A x^{\ast})^{\top} d^{\ast} = b^{\top} y^{\ast}, $$

which indicates that the optimal value of the dual CP problem (8) is also attained at y^∗ + αd^∗. Therefore, ${\Omega } \subseteq {\mathcal{S}}_{\mathrm {D}}$. Note that Ω is unbounded because ∥d^∗∥≠ 0, which implies the unboundedness of ${\mathcal{S}}_{\mathrm {D}}$. However, this contradicts the boundedness of ${\mathcal{S}}_{\mathrm {D}}$ derived from Assumptions 1 and 2. Hence, {y^(k)} is bounded.

The remaining part of the claim is easy to prove by taking the limit in (13) with the second relation replaced by $c - A^{\top } y^{(k)} \in {\mathcal{K}}$ using $\text {cone}(V^{(k)}) \subseteq {\mathcal{K}}^{\ast }$. □

5 Numerical results

We conducted numerical experiments to verify the performance of our proposed algorithm for SOCP problems. We implemented the ALPN method with MATLAB R2018a (9.4.0.813654) on a workstation running CentOS release 6.10 with eight Intel Xeon CPUs (E3-1276 v3 3.60 GHz) and 32 GB RAM.

In our experiments, we solved the CP problem (1) with ${\mathcal{K}}_{i} := {\mathcal{K}}_{\text {SOC}}^{n_{i}}$ for each i, which is SOCP. We used an initial polyhedral approximation of the i-th block ${\mathcal{K}}_{\text {SOC}}^{n_{i}}$ of ${\mathcal{K}}$ with n_i ≥ 2 given by $V_{i}^{(1)} := \bigcup _{j = 1}^{n_{i} - 1} \{e_{j}, -e_{j}\}$, where e_j denotes the j-th column of the identity matrix of appropriate size. Note that $V_{i}^{(1)}$ defined above exactly represents ${\mathcal{K}}_{\text {SOC}}^{n_{i}}$ if n_i = 1,2. In the projection step, we solved Problem (9) using the MATLAB function lsqlin. We stopped the algorithm when an approximate primal optimal solution was found, namely, a primal solution x^(k) at the k-th iteration satisfies

$$ \max\{\|A x^{(k)} - b\|, \max_{i = 1}^{p} \|\bar{x}^{i, (k)}\| - x_{1}^{i, (k)}\} \le 10^{-4}. $$

We randomly generated the following instances of the SOCP problem. First, we set m, p, and $(n_{1}, n_{2}, \dots , n_{p})$ and randomly generated each element of A from the standard Gaussian distribution. Next, we set $b = A \tilde {x}$ and $c = A^{\top } e - \tilde {s}$, where e is the vector whose elements are all ones and $\tilde {x}^{i} = \tilde {s}^{i} := e_{1}$ for each i. Note that the two points $\tilde {x}$ and $\tilde {s}$ are interior feasible solutions of the primal and dual problems, respectively.

5.1 Performance of the adaptive LP-Newton method

For the ALPN method, Table 1 presents the average runtime, number of iterations, and number of hyperplanes in the initial and final approximations of the second-order cone over ten executions. From this table, we can make the following observations:

• When ${\mathcal{K}} = {\prod }_{i = 1}^{p} {\mathcal{K}}_{\text {SOC}}^{n_{i}}$ is polyhedral-like, i.e., p ≈ n and n_i ≈ 1 for all $i = 1, \dots , p$, the ALPN method works well. The algorithm gives a good polyhedral approximation of ${\mathcal{K}}$ with a small number of hyperplanes. As a result, there are few iterations and the computation time is short.

  Table 1 Performance of the adaptive LP-Newton method

• When ${\mathcal{K}} = {\prod }_{i = 1}^{p} {\mathcal{K}}_{\text {SOC}}^{n_{i}}$ is medium-dimensional, i.e., 1 ≪ p ≪ n and 1 ≪ n_i ≪ n for all $i = 1, \dots , p$, the ALPN method becomes slow, although it gets better when ${\mathcal{K}} = {\prod }_{i = 1}^{p} {\mathcal{K}}_{\text {SOC}}^{n_{i}}$ is high-dimensional, i.e., p ≈ 1 and n_i ≈ n for all $i = 1, \dots , p$. The medium-dimensional ${\mathcal{K}}$ requires many hyperplanes to obtain a good polyhedral approximation.

• The total dimension n of the variables seems to be positively correlated with the runtime, although the runtime of the original LP-Newton method for LP is almost independent of n [5]. This difference arises from the solution methods of the minimum norm point step. In our implementation, we solve the QP problem (9) using the MATLAB function lsqlin, for which the computation time depends on n.

• Surprisingly, the number m of linear constraints is negatively correlated with the runtime. This might be because the dimension of the feasible region is low for large values of m, and this region can then be approximated by a small number of hyperplanes.

5.2 Comparison with a primal-dual interior-point method

We also compared our proposed ALPN method with a primal-dual interior-point method. In this experiment, we solved the randomly generated instances using our implementation of ALPN and SDPT3 [22], which is a MATLAB implementation of the primal-dual interior-point method. Basically, SDPT3 was found to be faster than the ALPN method. However, the computation time of SDPT3 increases with m, whereas that of ALPN decreases as m and p increase. For instances with large values of m and p, ALPN outperformed SDPT3. The results are presented in Table 2, which shows the average runtime of the ALPN and SDPT3 methods over ten runs.

Table 2 Comparison with SDPT3

6 Conclusions

In this paper, we have developed an LP-Newton method for the CP problem (1) through a transformation into an LSIP problem with an infinite number of linear inequality constraints. The proposed ALPN algorithm produces a sequence by sequentially projecting a current point onto a polyhedral cone arising from finitely many linear inequality constraints chosen from the constraints of the LSIP problem. We have also proposed a dual algorithm for the ALPN method for solving the dual of the CP problem. Under some mild assumptions, we have proved that an arbitrary accumulation point of a couple of sequences generated by the two proposed algorithms are optima of the CP problem and its dual. Finally, we have conducted some numerical experiments for SOCP problems and compared the performance of our algorithms with that of the primal-dual interior-point method. Our future work includes analysis under weaker assumptions, for example, in the absence of Slater’s constraint qualification, or infeasible cases.