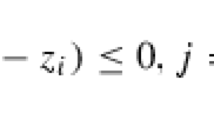1 Introduction

Polynomial optimization problems (POPs) are those for which we want to optimize a polynomial objective function over a feasible set defined by a set of polynomial inequalities (we call such a feasible set a basic semi-algebraic set). Several NP-hard problems can be formulated in this way. We provide a short list of some examples of such problems: (i) optimizing a homogeneous quadratic polynomial over the non-negative orthant, which is equivalent to testing the matrix copositivity [7, 32]; (ii) 0–1 linear optimization problems [48, 49, 55]; (iii) quadratic optimization problems including, for example, the Quadratic assignment problem, the Graph partitioning problem and the MAX-CUT problem [9, 27, 40,41,42, 45, 46]. Polynomial optimization is also a strong tool in control, see [10]. A good overview of the possible applications of polynomial optimization can also be found in [2].

Polynomial optimization problems attract a lot of attention in theoretical and applied mathematics. Real algebraic geometry and semi-algebraic geometry are sub-fields in algebra that are strongly related to polynomial optimization problems. Since these problems are, in general, very difficult, it is a natural choice to look for tractable relaxations. These relaxations are often based on some variant of a “Positivstellensatz” for given semi-algebraic sets [43, 44, 47]. Many researchers have proposed hierarchies of such relaxations that are based on moment and sums-of-squares (SOS) approximations of the original problem, and give semi-definite optimization/programming (SDP) problems. Lasserre [21] proposed a hierarchy of semi-definite optimization problems that, under certain conditions, converge with their optimal values to the optimal value of the original polynomial optimization problem, see also [38, 50]. We refer the reader to a 2010 book by Lasserre [22] and a 2008 chapter by Laurent [26] for beautiful and comprehensive overviews of the results from this area.

In polynomial optimization we have inequality constraints, and a natural extension to this is to consider other conic constraints, giving us, for example, polynomial semi-definite optimization (PSDP) and polynomial second-order cone optimization (PSOCP). The feasible set in the first case is primarily defined by the constraint that a given matrix polynomial (i.e., a matrix whose entries are polynomials) is positive semi-definite. In the second case the feasible set is primarily determined by the constraint that a given polynomial vector must belong to the second-order cone.

In the papers [13,14,15, 19] the authors considered how to extend the SOS approach to obtain good relaxations for PSDP problems, see also [10, 18]. The hierarchy of relaxations, which contain SOS polynomials and matrix SOS polynomials, is recaptured in Sect. 4.2.

The PSOCPs can be simply rewritten as classic POPs and later approached using tools from this area. The authors of the paper [20] proposed a general lift-and-project and reformulation-linearization technique that can also be efficiently applied to this family of problems.

If the feasible set for a POP is contained in the non-negative orthant then the existing approaches still work and the sign constraints can be modelled explicitly, i.e., by adding constraints \(x_i\ge 0\) to the set of polynomial constraints. The same idea works for PSDP and PSOCP. In [8, Theorem 2.4] a new Positivstellensatz was presented that is tailored for the non-negativity case and can be used to develop new, linear, conic optimization approximation hierarchies for POPs over the non-negative semi-algebraic sets.

The main contributions of this paper are:

  • Based on [8, Theorem 2.4], we propose a new hierarchy of linear conic optimization relaxations that can be uniformly applied to general polynomial conic optimization problems (over the non-negative orthant), including the special cases listed above.

  • We prove that under conditions closely related to the compactness of the feasible set and non-redundancy in its description, the optimal values of the proposed hierarchy are monotonic and asymptotically convergent to the optimal value of the original problem.

  • Numerical evaluations are considered for POPs, and it is found that in these examples, our method performs poorly in comparison with the classic SOS method. However, by adding an additional (redundant) positive semi-definite constraint to the original problem, our new method then performs reasonably well in comparison to the classic SOS approach.

  • We also provide numerical evaluations for PSDPs and PSOCPs, which demonstrate that in these examples our new method performs very well in comparison to the classic SOS approach. This performance is further improved by adding a (redundant) positive semi-definite constraint to the original problem, which implies SOS-like semi-definite programming constraints in our hierarchy. The enhanced hierarchy often outperforms the classic SOS approach also on POP problems.

Our work is also inline with recent results from Ahmadi and Majumdar [1] and Lasserre et al. [24], who developed new approximation hierarchies that would overcome the complexity drawbacks of the existing SOS hierarchies. New linear optimization/programming (LP) and second-order cone (SOC) hierarchies are presented in [1]. In [24] the authors proposed an LP-SDP hierarchy, but with only one SDP constraint with which they can control the dimension. They also provided proof of convergence for the hierarchy and numerical results, which together with the numerical results from [30] show that these approaches have a strong potential. A sparse version of this hierarchy is provided in [53] and can solve much larger problem instances. Another provably convergent hierarchy, called the mismatch hierarchy, is proposed in [16], which solves complex polynomial optimization problems with several thousand variables and constraints arising in electrical engineering.

Throughout the paper we will use \(\mathbb {N}\) to denote the set of non-negative integers \(\{0,1,2,\ldots \}\) and use \(\mathbb {R}_+\) to denote the set of non-negative real numbers.

2 Polynomial conic optimization

We define a polynomial conic optimization problem to be one with the following form

$$\begin{aligned} \begin{aligned} \min _{\mathbf {x}} \quad&f(\mathbf {x}) \\ \text {s.t.}\quad&\mathbf {g}_i(\mathbf {x})\in \mathcal {K}_i^*\qquad \text {for all}\quad i=1,\ldots ,p,\\&\mathbf {x}\in \mathbb {R}_+^n, \end{aligned} \end{aligned}$$
(1)

where

i:

\(f:\mathbb {R}^n\rightarrow \mathbb {R}\) is a polynomial of degree \(d_0\ge 1\),

ii:

For \(i=1,\ldots ,p\), we have that \(\mathbf {g}_i:\mathbb {R}^n\rightarrow \mathbb {R}^{m_i}\) is a polynomial vector of degree \(d_i\ge 1\), i.e., \(d_i\) is the maximum degree of the polynomials \(\big (\mathbf {g}_i(\mathbf {x})\big )_j\) for \(j\in \{1,\ldots ,m_i\}\),

iii:

For \(i=1,\ldots ,p\), we have that \(\mathcal {K}_i^*\subseteq \mathbb {R}^{m_i}\) is a nonempty closed convex cone.

For \(i=1,\ldots ,p\) we will in fact consider the cone \(\mathcal {K}_i^*\) to be the dual cone to a nonempty convex cone \(\mathcal {K}_i\), i.e., \(\mathcal {K}_i^*= \{\mathbf {u}\in \mathbb {R}^{m_i}\mid \langle \mathbf {u},\mathbf {w}\rangle \ge 0 \text { for all } \mathbf {w}\in \mathcal {K}_i\}\) where \(\langle \mathbf {u},\mathbf {w}\rangle := \mathbf {u}^\mathsf {T}\mathbf {w}= \sum _{j=1}^{m_i} u_jw_j\). For a nonempty closed convex cone \(\mathcal {K}_i^*\) in Euclidean space, there always exists such a cone \(\mathcal {K}_i\), for example, the dual cone to \(\mathcal {K}_i^*\). For the theory in this paper, the cones \(\mathcal {K}_i\) need not be closed, whereas dual cones in Euclidean space are always closed, and it is for this reason that we have denoted our cones in this unusual manner (i.e., the dual cone being in the problem). Note that the sets \(\mathcal {K}_i\) and \(\mathcal {K}_i^*\) are convex cones in Euclidean space, i.e.,

$$\begin{aligned} \mathbf {y},\mathbf {z}\in \mathcal {K}_i,\quad \varphi ,\theta \in \mathbb {R}_+\qquad \Rightarrow \qquad \varphi \mathbf {y}+\theta \mathbf {z}\in \mathcal {K}_i, \end{aligned}$$

and likewise for \(\mathcal {K}_i^*\). They should not be confused with polynomial cones, which are often discussed in relation to polynomial optimization.

Problems such as (1) include as special cases (i) POPs over the non-negative orthant (for \(m_i=1\) and \(\mathcal {K}_i=\mathcal {K}_i^*=\mathbb {R}_+\) for all i), (ii) PSDPs over the non-negative orthant (for \(\mathcal {K}_i^*\) being linearly isomorphic to a positive semi-definite cone for all i) and (iii) PSOCPs over the non-negative orthant (here we take \(\mathcal {K}_i^*\) to be linearly isomorphic to a second-order cone for all i). This will be discussed further in Sect. 4, where examples of such problems will also be looked at.

Note that polynomial equality constraints can be included through the cones \(\mathcal {K}_i=\mathbb {R}\), \(\mathcal {K}_i^*=\{0\}\). Also note that if we have a polynomial conic optimization problem, similar to the form (1), with a compact feasible set but without the sign constraint \(\mathbf {x}\in \mathbb {R}_+^n\), then through a change of coordinates we can move the feasible set into the non-negative orthant and can then add the (redundant) sign constraint (see Example 4.3). For the main results in this paper we need a compactness-like assumption (Assumption 2.2), therefore having \(\mathbf {x}\in \mathbb {R}_+^n\) explicitly in the problem is not very restrictive.

For ease of notation, throughout the paper we will let \(\mathcal {F}\) be the feasible set of (1), i.e.

$$\begin{aligned} \mathcal {F}=\{\mathbf {x}\in \mathbb {R}_+^n \mid \mathbf {g}_i(\mathbf {x})\in \mathcal {K}_i^*\quad \text {for}\; i=1,\ldots ,p \}. \end{aligned}$$
(2)

We will make the following two assumptions about the problem (1):

Assumption 2.1

For all i we assume that \(\mathcal {K}_i\) has a nonempty interior.

Assumption 2.2

We assume that one of the constraints in the problem (1) is of the form \(R-\mathbf {a}^\mathsf {T}\mathbf {x}\in \mathbb {R}_+\), where \(\mathbf {a}\in \mathbb {R}^n\) is a vector with all entries being strictly positive.

These assumptions guarantee asymptotic convergence of the hierarchy of lower bounds introduced in the following section. Without these assumptions we would still have valid lower bounds, but we would not be able to guarantee their convergence.

The first assumption is equivalent to having \(\mathcal {K}_i^*\cap (-\mathcal {K}_i^*)=\{\varvec{0}\}\) for all i, see, e.g., [3, Theorem 2.3]. Within the conic optimization literature, this property is referred to as \(\mathcal {K}_i^*\) being pointed; however, we shall avoid this term due to the confusion with alternative meanings of the term pointed. If we have a cone \(\mathcal {K}_i^*\) such that \(\mathcal {K}_i^*\cap (-\mathcal {K}_i^*)\ne \{\varvec{0}\}\) then it is possible to project this constraint into a smaller subspace with the cone having the required property in this subspaceFootnote 1. We thus see that for simple cones Assumption 2.1 is relatively mild. However, it should be noted that for cones with a complicated definition it might be more difficult to ensure that this holds.

Also note that if the feasible set of problem (1) is bounded, then we can always add a redundant constraint to the problem of the form required in Assumption 2.2. This assumption holding means that provided \(\mathcal {F}\ne \emptyset \) then \(\mathcal {F}\) is compact and the optimal solution to problem (1) is obtained. Further discussion of these assumptions will be provided in Sect. 3.3.

3 Approximation

3.1 New hierarchy

For an optimization problem (P), we let \({{\,\mathrm{val}\,}}(P)\) denote its optimal value. From the definition of the infimum, we have that \({{\,\mathrm{val}\,}}\)(1) is equal to the optimal value of the following problem:

$$\begin{aligned} \begin{aligned} \max _\lambda \quad&\lambda \\ \text {s.t.}\quad&f(\mathbf {x})-\lambda \ge 0 \qquad \text {for all}\quad \mathbf {x}\in \mathcal {F}\end{aligned} \end{aligned}$$
(3)

Letting \(D=\max _i\{d_i \mid i=0,\ldots ,p\}\) and \(\mathbf {e}\) be the all ones vector, we now introduce the following problems for \(r\in \mathbb {N}:=\{0,1,2,\ldots \}\):

$$\begin{aligned} \max _{\lambda ,\mathbf {y}} \quad&\lambda \\ \text {s.t.}\quad&(1+\mathbf {e}^\mathsf {T}\mathbf {x})^{D-d_0+r}(f(\mathbf {x})-\lambda ) \ge _c \sum _{i=1}^p \sum _{\begin{array}{c} \varvec{\alpha }\in \mathbb {N}^n: \\ \mathbf {e}^\mathsf {T}\varvec{\alpha }\le D-d_i+r \end{array}} \mathbf {x}^{\varvec{\alpha }} \langle {\mathbf {y}_{i,\varvec{\alpha }}}, {\mathbf {g}_i(\mathbf {x})} \rangle \\&\mathbf {y}_{i,\varvec{\alpha }}\in \mathcal {K}_i \qquad \text {for all}\quad i=1,\ldots ,p,\quad \varvec{\alpha }\in \mathbb {N}^n: \mathbf {e}^\mathsf {T}\varvec{\alpha }\le D-d_i+r. \end{aligned}$$
($4_r$)

The “\(\ge _c\)” means that we are comparing the coefficients of the polynomials, for example, \(a x_1^3 + bx_1x_2 \ge _c c x_1^3 + dx_2^2\) iff \(a\ge c\) and \(b\ge 0\) and \(0 \ge d\) (see also Example 3.1 below). This should not be confused with the NP-hard problem of checking whether one polynomial is greater than or equal to another for all \(\mathbf {x}\). It is, however, a simple sufficient condition for one polynomial being greater than or equal to another for all \(\mathbf {x}\in \mathbb {R}_+^n\). In Sect. 3.2 we will see that

$$\begin{aligned} {{\,\mathrm{val}\,}}({4}_{0}) \le {{\,\mathrm{val}\,}}({4}_{1}) \le {{\,\mathrm{val}\,}}({4}_{2}) \le \cdots \le \lim _{r\rightarrow \infty }{{\,\mathrm{val}\,}}({4}_{r})\le {{\,\mathrm{val}\,}}{(1)}, \end{aligned}$$
(5)

and in Sect. 3.4 we will see that if Assumptions 2.1 and 2.2 hold then we have

$$\begin{aligned} \lim _{r\rightarrow \infty }{{\,\mathrm{val}\,}}({4}_{r})={{\,\mathrm{val}\,}}{(1)}. \end{aligned}$$
(6)

Written out explicitly, the problem \(({4}_{r})\) is a linear conic optimization problem over the cones \(\mathcal {K}_i\). Therefore, if we can optimize over combinations of these cones then we can solve \(({4}_{r})\). The problem \(({4}_{r})\) is in fact a linear conic optimization problem with

  • \(\left( {\begin{array}{c}n+D-d_i+r\\ n\end{array}}\right) \) cone constraints of being in \(\mathcal {K}_i\), for \(i\in \{1,\ldots ,p\}\),

  • \(\left( {\begin{array}{c}n+D+r\\ n\end{array}}\right) \) inequality constraints,

  • \(1+\sum _{i=1}^p m_i \left( {\begin{array}{c}n+D-d_i+r\\ n\end{array}}\right) \) variables.

This compares favourably with other standard approximation hierarchies for polynomial optimization. One of the advantages of our new approach is that although as r increases, the number of cones we have to optimize over increases dramatically, the cones themselves remain the same. This is in contrast to the sum-of-squares approach for polynomial matrix problems, as will be discussed in Sect. 4.

Another advantage of our new approach is that we are not dependent on the form of \(\mathcal {K}_i\), we only require that it is a convex cone that we can optimize over. This increases the range of possible future applications.

Before discussing the theory behind this new approach, we will first consider an illustrative example. This example is purposely picked to be a simple example for which the convergence of our method is slow. In Sect. 4 we will consider more representative examples, which fully demonstrate the strength of our new method.

Example 3.1

Let us consider the following polynomial optimization problem:

$$\begin{aligned} \min _x \quad&x \\ \text {s.t.}\quad&x^2 = x \\&2x \ge 1. \end{aligned}$$

Trivially, \(x=1\) is the only feasible point for this problem and thus the optimal value is equal to 1. This problem is in the form required with

$$\begin{aligned} f(x)&= x,&g_1(x)&= x^2-x,&\mathcal {K}_1^*&= \{0\},&\mathcal {K}_1&= \mathbb {R},\\&g_2(x)&= 2x-1,&\mathcal {K}_2^*&= \mathbb {R}_+,&\mathcal {K}_2&= \mathbb {R}_+. \end{aligned}$$

The rth level of our new hierarchy is given by

$$\begin{aligned} \max _{\lambda ,\mathbf {y},\mathbf {z}} \quad&\lambda \\ \text {s.t.}\quad&(1+x)^{r+1}(x-\lambda ) \ge _c \sum _{i=0}^r y_i x^i (x^2-x) + \sum _{i=0}^{r+1} z_i x^i (2x-1)\\&\lambda ,y_0,\ldots ,y_r\in \mathbb {R},\qquad z_0,\ldots ,z_{r+1}\in \mathbb {R}_+. \end{aligned}$$

We have

$$\begin{aligned} (1+x)^{r+1}(x-\lambda )&= x^{r+2} + \sum _{i=1}^{r+1}x^i\left( \left( {\begin{array}{c}r+1\\ i-1\end{array}}\right) - \lambda \left( {\begin{array}{c}r+1\\ i\end{array}}\right) \right) - \lambda ,\\ \sum _{i=0}^r y_i x^i (x^2-x)&= x^{r+2}y_r + \sum _{i=2}^{r+1} x^i (y_{i-2}-y_{i-1}) - xy_0,\\ \sum _{i=0}^{r+1} z_i x^i (2x-1)&= 2x^{r+2}z_{r+1} + \sum _{i=1}^{r+1} x^i (2z_{i-1}-z_i) - z_0 \end{aligned}$$

Therefore, the rth level of the hierarchy is equivalent to the following, where after the vertical line we show which monomial term this constraint corresponds to:

figure a

By first eliminating the \(\mathbf {y}\) variable, this problem can be solved analytically to give an optimal value of \(1-(1+2^{r+1})^{-1}\), which tends towards 1, the optimal value of the original problem, as r tends to infinity.

3.2 Monotonically increasing lower bounds

In this subsection we will prove the inequality relations from (5).

Proposition 3.2

We have \({{\,\mathrm{val}\,}}({4}_{r})\le {{\,\mathrm{val}\,}}\)(3)\(={{\,\mathrm{val}\,}}\)(1) for all \(r\in \mathbb {N}\).

Proof

From the definition of the infimum it is trivial to see that \({{\,\mathrm{val}\,}}\)(3)\(={{\,\mathrm{val}\,}}\)(1). It is also trivial to see that if \((\lambda ,\mathbf {y})\) is feasible for \(({4}_{r})\) then \(\lambda \) is feasible for (3). \(\square \)

Proposition 3.3

We have \({{\,\mathrm{val}\,}}({4}_{r})\le {{\,\mathrm{val}\,}}({4}_{r+1})\) for all \(r\in \mathbb {N}\).

Proof

We will show that if \((\lambda ,\mathbf {y})\in \mathbb {R}\times \left( \mathcal {K}_i^{\left| \{\varvec{\alpha }\in \mathbb {N}^n\mid \mathbf {e}^\mathsf {T}\varvec{\alpha }\le D-d_i+r\}\right| }\right) _{i\in \{1,\ldots ,p\}}\) is feasible for \(({4}_{r})\) then there exists \({\widetilde{\mathbf {y}}}\in \left( \mathcal {K}_i^{\left| \{\varvec{\alpha }\in \mathbb {N}^n\mid \mathbf {e}^\mathsf {T}\varvec{\alpha }\le D-d_i+r+1\}\right| }\right) _{i\in \{1,\ldots ,p\}}\) such that \((\lambda ,{\widetilde{\mathbf {y}}})\) is feasible for \(({4}_{r+1})\).

Such a \({\widetilde{\mathbf {y}}}\) is constructed by letting

$$\begin{aligned} {\widetilde{\mathbf {y}}}_{i,\varvec{\alpha }}&= \mathbf {y}_{i,\varvec{\alpha }} + \sum _{\begin{array}{c} j=1,\ldots ,n:\\ \alpha _j\ge 1 \end{array}}\mathbf {y}_{i,\varvec{\alpha }-\mathbf {e}_j} \in \mathcal {K}_i \qquad \text {for all}\quad \begin{aligned}&i=1,\ldots ,p,\\&\varvec{\alpha }\in \mathbb {N}^n: \mathbf {e}^\mathsf {T}\varvec{\alpha }< D-d_i+(r+1), \end{aligned}\\ {\widetilde{\mathbf {y}}}_{i,\varvec{\alpha }}&= \sum _{\begin{array}{c} j=1,\ldots ,n:\\ \alpha _j\ge 1 \end{array}} \mathbf {y}_{i,\varvec{\alpha }-\mathbf {e}_j} \in \mathcal {K}_i \text {for all}\quad \begin{aligned}&i=1,\ldots ,p,\\&\varvec{\alpha }\in \mathbb {N}^n: \mathbf {e}^\mathsf {T}\varvec{\alpha }= D-d_i+(r + 1), \end{aligned} \end{aligned}$$

where \(\mathbf {e}_j\in \mathbb {R}^n\) is the unit vector with the jth entry equal to one and all the other entries equal to zero, with membership of \(\mathcal {K}_i\) following from this being a convex cone.

This construction implies that

$$\begin{aligned} \sum _{i=1}^p \sum _{\begin{array}{c} \varvec{\alpha }\in \mathbb {N}^n \\ \mathbf {e}^\mathsf {T}\varvec{\alpha }\le D-d_i+(r+1) \end{array}} \mathbf {x}^{\varvec{\alpha }} \left\langle {\widetilde{\mathbf {y}}}_{i,\varvec{\alpha }}, \mathbf {g}_i(\mathbf {x}) \right\rangle =_c (1+\mathbf {e}^\mathsf {T}\mathbf {x}) \sum _{i=1}^p \sum _{\begin{array}{c} \varvec{\alpha }\in \mathbb {N}^n \\ \mathbf {e}^\mathsf {T}\varvec{\alpha }\le D-d_i+r \end{array}} \mathbf {x}^{\varvec{\alpha }} \left\langle \mathbf {y}_{i,\varvec{\alpha }}, \mathbf {g}_i(\mathbf {x}) \right\rangle . \end{aligned}$$

Having \((\lambda ,\mathbf {y})\) feasible for \(({4}_{r})\), and \((1+\mathbf {e}^\mathsf {T}\mathbf {x})\) with all the coefficients non-negative, this implies that

$$\begin{aligned} (1+\mathbf {e}^\mathsf {T}\mathbf {x}) \sum _{i=1}^p \sum _{\begin{array}{c} \varvec{\alpha }\in \mathbb {N}^n \\ \mathbf {e}^\mathsf {T}\varvec{\alpha }\le D-d_i+r \end{array}} \mathbf {x}^{\varvec{\alpha }} \left\langle \mathbf {y}_{i,\varvec{\alpha }}, \mathbf {g}_i(\mathbf {x}) \right\rangle&\le _c (1+\mathbf {e}^\mathsf {T}\mathbf {x})^{D-d_0+(r+1)}(f(\mathbf {x})-\lambda ). \end{aligned}$$

\(\square \)

3.3 Analysis of the assumptions

Before we look at the convergence of our new approximation hierarchy, we will first need to analyse the assumptions we made about problem (1). We will show that Assumptions  2.1 and 2.2 imply two properties, introduced below. The presence of these properties simplifies the workings in Sect. 3.4. We could have in fact assumed that these properties are held in place of Assumptions 2.1 and 2.2. This would have had the advantage of encapsulating a larger class of problems. However, we chose not to do this as these properties are somewhat more complicated than Assumptions 2.1 , 2.2.

Before defining these properties, we first need to introduce some new notation. For \(i\in \{1,\ldots ,p\}\) and \(\mathbf {w}\in \mathbb {R}^{m_i}\) we define the polynomial \(g_{i,\mathbf {w}}(\mathbf {x}):=_c \langle \mathbf {w}, \mathbf {g}_i(\mathbf {x}) \rangle \), and note that \({{\,\mathrm{deg}\,}}(g_{i,\mathbf {w}})\le d_i\). The first property is then as follows:

Proposition 3.4

For all \(i\in \{1,\ldots ,p\}\) there exists \(\varvec{\gamma }\in \mathcal {K}_i\) such that \({{\,\mathrm{deg}\,}}(g_{i,\varvec{\gamma }})=d_i\).

An intuitive justification for Property 3.4 is that it ensures that none of the highest-degree terms are trivially redundant. If Property 3.4 does not hold for some i then we can remove all the degree \(d_i\) terms from \(\mathbf {g}_i\) without affecting the feasible set \(\mathcal {F}\).

For \(i\in \{1,\ldots ,p\}\), we now let \(\widetilde{\mathbf {g}_i}(\mathbf {x})\) be the highest-order homogeneous part of \(\mathbf {g}_i(\mathbf {x})\), i.e., the homogeneous polynomial vector \(\mathbf {g}_i(\mathbf {x})\) with all the terms of degree strictly less than \(d_i\) removed (and similarly for \(\widetilde{f}\)). For example, if

$$\begin{aligned} \mathbf {g}_1(\mathbf {x}) = \begin{pmatrix} x_1x_2^2+ x_1 \\ x_2 - 1 \\ 16 - 4x_1^2 - 2x_2^3\end{pmatrix}, \qquad \text {then}\qquad \widetilde{\mathbf {g}_1}(\mathbf {x}) = \begin{pmatrix} x_1x_2^2 \\ 0 \\ -2x_2^3\end{pmatrix}. \end{aligned}$$

We also let \({\widetilde{\mathcal {F}}}=\{\mathbf {x}\in \mathbb {R}_+^n \mid \widetilde{\mathbf {g}_i}(\mathbf {x})\in \mathcal {K}_i^*\text { for } i=1,\ldots ,p \}\). The second property is then as follows:

Proposition 3.5

We have \(\widetilde{f}(\mathbf {x})>0\) for all \(\mathbf {x}\in {\widetilde{\mathcal {F}}}\setminus \{\varvec{0}\}\).

An intuitive justification for Property 3.5 is that it ensures that the problem is well behaved at infinity.

From the following two results it immediately follows that Assumptions 2.1 and 2.2 imply Properties 3.4 and 3.5, respectively.

Proposition 3.6

For \(i\in \{1,\ldots ,p\}\) let \(\widehat{\mathcal {K}_i} = \{\mathbf {w}\in \mathcal {K}_i \mid {{\,\mathrm{deg}\,}}(g_{i,\mathbf {w}})=d_i \}\), where \(\mathcal {K}_i\subseteq \mathbb {R}^{m_i}\), \(g_{i,\mathbf {w}}\in \mathbb {R}[\mathbf {x}]\) and \(d_i\in {\mathbb {N}}\) are as given earlier in the paper. Now, consider the following statements:

  1. i

    \({{\,\mathrm{int}\,}}\mathcal {K}_i\ne \emptyset \);

  2. ii

    \(\widehat{\mathcal {K}_i}\ne \emptyset \);

  3. iii

    \(\widehat{\mathcal {K}_i}\) is a dense subset of \(\mathcal {K}_i\);

  4. iv

    \(\widehat{\mathcal {K}_i}^*=\mathcal {K}_i^*\).

We then have

$$\begin{aligned} \mathrm{(i)}\quad \Rightarrow \quad \mathrm{(ii)} \quad \Leftrightarrow \quad \mathrm{(iii)} \quad \Rightarrow \quad \mathrm{(iv)}. \end{aligned}$$

Proof

We begin by noting that \({{\,\mathrm{deg}\,}}(g_{i,\mathbf {w}})\le d_i\) for all \(\mathbf {w}\in \mathbb {R}^{m_i}\) and \(\widehat{\mathcal {K}_i}\subseteq \mathcal {K}_i\). We split the remainder of the proof into the following parts:

\((i)\Rightarrow (ii)\)::

Consider an arbitrary \(\mathbf {w}\in {{\,\mathrm{int}\,}}\mathcal {K}_i\). If \(\mathbf {w}\in \widehat{\mathcal {K}_i}\) then we are done, and from now on in this part of the proof we will assume that \(\mathbf {w}\notin \widehat{\mathcal {K}_i}\), i.e. \({{\,\mathrm{deg}\,}}(g_{i,\mathbf {w}})<d_i\).

There exists \(j\in \{1,\ldots ,m_i\}\) such that \(d_i={{\,\mathrm{deg}\,}}((\mathbf {g}_i(\mathbf {x}))_j)={{\,\mathrm{deg}\,}}(g_{i,\mathbf {e}_j})\), where \(\mathbf {e}_j\in \mathbb {R}^{m_i}\) is the unit vector with the jth entry equal to one and all the other entries equal to zero. For all \(\varepsilon \ne 0\) we then have \({{\,\mathrm{deg}\,}}(g_{i,\mathbf {w}+\varepsilon \mathbf {e}_j}) = {{\,\mathrm{deg}\,}}(g_{i,\mathbf {w}}+\varepsilon g_{i,\mathbf {e}_j}) = d_i.\) The proof of this part is then completed by noting that as \(\mathbf {w}\in {{\,\mathrm{int}\,}}\mathcal {K}_i\) there exists \(\varepsilon \ne 0\) such that \(\mathbf {w}+\varepsilon \mathbf {e}_j\in \mathcal {K}_i\).

\((ii)\Rightarrow (iii)\)::

Suppose that \(\exists \varvec{\gamma }\in \widehat{\mathcal {K}_i}\) and consider an arbitrary \(\mathbf {w}\in \mathcal {K}_i\setminus \widehat{\mathcal {K}_i}\). Then \({{\,\mathrm{deg}\,}}(g_{i,\varvec{\gamma }})=d_i>{{\,\mathrm{deg}\,}}(g_{i,\mathbf {w}})\), and thus for all \(\varepsilon \ne 0\) we have

$$\begin{aligned} {{\,\mathrm{deg}\,}}(g_{i,\mathbf {w}+\varepsilon \varvec{\gamma }}) = {{\,\mathrm{deg}\,}}(g_{i,\mathbf {w}}+\varepsilon g_{i,\varvec{\gamma }}) = d_i. \end{aligned}$$

The proof of this part is then completed by noting that as \(\mathcal {K}_i\) is a convex cone we have \(\mathbf {w}+\varepsilon \varvec{\gamma }\in \mathcal {K}_i\) for all \(\varepsilon >0\).

\((ii)\Leftarrow (iii)\)::

This trivially follows from the fact that \(\mathcal {K}_i\ne \emptyset \).

\((iii) \Rightarrow (iv)\)::

If \(\widehat{\mathcal {K}_i}\) is a dense subset of \(\mathcal {K}_i\) then \({{\,\mathrm{cl}\,}}\widehat{\mathcal {K}_i}={{\,\mathrm{cl}\,}}\mathcal {K}_i\) and from a well-known result for sets in Euclidean space we have \(\mathcal {K}_i^*= ({{\,\mathrm{cl}\,}}\mathcal {K}_i)^*= ({{\,\mathrm{cl}\,}}\widehat{\mathcal {K}_i})^*= \widehat{\mathcal {K}_i}^*\), e.g., [3, Theorem 2.1].

\(\square \)

Proposition 3.7

If Assumption 2.2 holds for the problem (1) then \({\widetilde{\mathcal {F}}}=\{\varvec{0}\}\).

Proof

First, note that \(\varvec{0}\in {\widetilde{\mathcal {F}}}\) follows from \(\widetilde{\mathbf {g}_i}(\mathbf {x})\) being homogeneous and \(\mathcal {K}_i^*\) being a nonempty closed cone for all i. We then complete the proof by noting that if Assumption 2.2 holds for the problem (1) then

$$\begin{aligned}&{\widetilde{\mathcal {F}}} =\{\mathbf {x}\in \mathbb {R}_+^n \mid \widetilde{\mathbf {g}_i}(\mathbf {x})\in \mathcal {K}_i^*\text { for } i=1,\ldots ,p \} {\subseteq }\{\mathbf {x}\in \mathbb {R}_+^n \mid {-}\mathbf {a}^\mathsf {T}\mathbf {x}\in \mathbb {R}_+\} {=} \{\varvec{0}\}.\qquad \qquad \end{aligned}$$

\(\square \)

3.4 Asymptotic convergence

In this subsection we look at the theory behind how our new hierarchy converges. In Sect. 4 we will then look at some numerical examples to see how it performs in practice.

In order to prove the convergence we need to begin by considering the following Positivstellensatz:

Theorem 3.8

[8, Theorems 2.4 and 4.1] Consider the homogeneous polynomials \(f_i:\mathbb {R}^{n+1}\rightarrow \mathbb {R}\) for \(i\in \{0\}\cup \mathcal {I}\) such that \(f_0(\mathbf {x})>0\) for all \(\mathbf {x}\in \mathbb {R}_+^{n+1}\setminus \{\varvec{0}\}:\, f_i(\mathbf {x})\ge 0 \,\forall i\in \mathcal {I}\). Then for some \(R\in \mathbb {N}{}\) there exists a subset \(\mathcal {J}\subseteq \mathcal {I}\) of finite cardinality and homogeneous polynomials \(q_j:\mathbb {R}^{n+1}\rightarrow \mathbb {R}\) for \(j\in \mathcal {J}\), with all of their coefficients non-negative and \({{\,\mathrm{deg}\,}}(q_j)+{{\,\mathrm{deg}\,}}(f_j)=R+{{\,\mathrm{deg}\,}}(f_0)\), such that \((\mathbf {e}^\mathsf {T}\mathbf {x})^R f_0(\mathbf {x}) \ge _c \sum _{j\in \mathcal {J}} f_j(\mathbf {x})q_j(\mathbf {x})\).

The restriction on the degrees was not in the original theorems, but can be added as all of the polynomials are homogeneous. There are no limitations on the set \(\mathcal {I}\), it could in fact index uncountably many polynomials \(f_i\).

Before we can use this Positivstellensatz, we first need to adapt it to apply for nonhomogeneous polynomials. In order to do this we use the notation from Property 3.5, i.e., \(\widetilde{g}(\mathbf {x})\) is the polynomial \(g(\mathbf {x})\) with all terms of degree strictly less than \({{\,\mathrm{deg}\,}}(g)\) removed. We then obtain the following Positivstellensatz:

Theorem 3.9

Consider polynomials \(f_i:\mathbb {R}^n\rightarrow \mathbb {R}\) for \(i\in \{0\}\cup \mathcal {I}\) such that

  1. i

    \(f_0(\mathbf {x})>0\) for all \(\mathbf {x}\in \mathbb {R}_+^n:\, f_i(\mathbf {x})\ge 0 \,\forall i\in \mathcal {I}\), and

  2. ii

    \(\widetilde{f_0}(\mathbf {x})>0\) for all \(\mathbf {x}\in \mathbb {R}_+^n\setminus \{\varvec{0}\}:\, \widetilde{f_i}(\mathbf {x})\ge 0 \,\forall i\in \mathcal {I}\).

Then for some \(R\in \mathbb {N}{}\) there exists a subset \(\mathcal {J}\subseteq \mathcal {I}\) of finite cardinality and polynomials \(q_j:\mathbb {R}^n\rightarrow \mathbb {R}\) for \(j\in \mathcal {J}\), with all of their coefficients non-negative and \({{\,\mathrm{deg}\,}}(q_j)+{{\,\mathrm{deg}\,}}(f_j)\le R+{{\,\mathrm{deg}\,}}(f_0)\), such that \((1+\mathbf {e}^\mathsf {T}\mathbf {x})^R f_0(\mathbf {x}) \ge _c \sum _{j\in \mathcal {J}} f_j(\mathbf {x})q_j(\mathbf {x})\).

Proof

For a polynomial \(g:\mathbb {R}^n\rightarrow \mathbb {R}\) of degree d, we define \(g^H(\mathbf {x},x_{n+1}):\mathbb {R}^{n+1}\rightarrow \mathbb {R}\) to be the unique homogeneous polynomial of degree d such that \(g(\mathbf {x})=g^H(\mathbf {x},1)\). We then have \(\widetilde{g}(\mathbf {x})=g^H(\mathbf {x},0)\), e.g., for \(g(x_1,x_2)=x_1x_2^2+x_1\) we have

$$\begin{aligned} g^H(x_1,x_2,x_3)&=x_1x_2^2+x_1x_3^2,\\ g^H(x_1,x_2,1)&=x_1x_2^2+x_1 = g(x_1,x_2),\\ g^H(x_1,x_2,0)&=x_1x_2^2 = \widetilde{g}(x_1,x_2). \end{aligned}$$

Using this notation, for \(f_0\) given in the theorem we have

  1. i

    \(f_0^H(\mathbf {x},1)>0\) for all \(\mathbf {x}\in \mathbb {R}_+^n:\, f_i^H(\mathbf {x},1)\ge 0 \,\forall i\in \mathcal {I}\), and

  2. ii

    \(f_0^H(\mathbf {x},0)>0\) for all \(\mathbf {x}\in \mathbb {R}_+^n\setminus \{\varvec{0}\}:\, f_i^H(\mathbf {x},0)\ge 0 \,\forall i\in \mathcal {I}\).

As all the polynomials are homogeneous, this is equivalent to

$$\begin{aligned} f_0^H(\mathbf {x},x_{n+1})>0 \text { for all } (\mathbf {x},x_{n+1})\in \mathbb {R}_+^{n+1}\setminus \{(\varvec{0},0)\}:\, f_i^H(\mathbf {x},x_{n+1})\ge 0 \,\forall i\in \mathcal {I}. \end{aligned}$$

From Theorem 3.8 we find that for some \(R\in \mathbb {N}{}\) there exists a subset \(\mathcal {J}\subseteq \mathcal {I}\) of finite cardinality and homogeneous polynomials \(q_j:(\mathbb {R}^n\times \mathbb {R})\rightarrow \mathbb {R}\) for \(j\in \mathcal {J}\), with all of their coefficients non-negative and \({{\,\mathrm{deg}\,}}(q_j)+{{\,\mathrm{deg}\,}}(f_j)=R+{{\,\mathrm{deg}\,}}(f_0)\), such that \((\mathbf {e}^\mathsf {T}\mathbf {x}+x_{n+1})^R f_0^H(\mathbf {x},x_{n+1}) \ge _c \sum _{j\in \mathcal {J}} f_j^H(\mathbf {x},x_{n+1})q_j(\mathbf {x},x_{n+1})\). Letting \(x_{n+1}=1\), we then obtain the required result. \(\square \)

We are now ready to apply this result for our case:

Theorem 3.10

Let \(\mathcal {F}\) be as given in (2) with Properties 3.4 and 3.5 holding, and consider a polynomial f of degree \(d_0\) and \(\lambda \in \mathbb {R}\) such that \(f(\mathbf {x})-\lambda >0\) for all \(\mathbf {x}\in \mathcal {F}\). Then there exists \(r\in \mathbb {N}\) and \(\mathbf {y}_{i,\varvec{\alpha }}\in \mathcal {K}_i\) for \(i=1,\ldots ,p\), \(\varvec{\alpha }\in \mathbb {N}^n: \mathbf {e}^\mathsf {T}\varvec{\alpha }\le D-d_i+r\) such that

$$\begin{aligned} (1+\mathbf {e}^\mathsf {T}\mathbf {x})^{D-d_0+r} (f(\mathbf {x})-\lambda ) \ge _c \sum _{i=1}^p \sum _{\begin{array}{c} \varvec{\alpha }\in \mathbb {N}^n \\ \mathbf {e}^\mathsf {T}\varvec{\alpha }\le D-d_i+r \end{array}} \mathbf {x}^{\varvec{\alpha }} \langle \mathbf {y}_{i,\varvec{\alpha }}, \mathbf {g}_i(\mathbf {x}) \rangle \end{aligned}$$

Proof

In order to apply Theorem 3.9 we let \(f_0(\mathbf {x})=f(\mathbf {x})-\lambda \) and \(f_i\in \mathbb {R}[\mathbf {x}]\) for i in some set \(\mathcal {I}\) be such that

$$\begin{aligned} \{f_i\mid i\in \mathcal {I}\} = \{ g_{i,\mathbf {w}} : i=1,\ldots ,p,\quad \mathbf {w}\in \widehat{\mathcal {K}_i} \}, \end{aligned}$$

where \(\widehat{\mathcal {K}_i}\) is as given in Proposition 3.6 and recall from this proposition that Property 3.4 implies that \(\widehat{\mathcal {K}_i}^*=\mathcal {K}_i^*\). We then have

$$\begin{aligned} \widetilde{f_0}(\mathbf {x})&=\widetilde{f}(\mathbf {x}),\\ \{ \mathbf {x}\in \mathbb {R}_+^n \mid f_i(\mathbf {x})\ge 0 \,\forall i\in \mathcal {I}\}&= \{ \mathbf {x}\in \mathbb {R}_+^n \mid \langle \mathbf {w}, \mathbf {g}_i(\mathbf {x}) \rangle \ge 0 \,\forall i=1,\ldots ,p,\; \mathbf {w}\in \widehat{\mathcal {K}_i} \} \\&= \{ \mathbf {x}\in \mathbb {R}_+^n \mid \mathbf {g}_i(\mathbf {x})\in \widehat{\mathcal {K}_i}^*\,\forall i=1,\ldots ,p\} \\&= \{ \mathbf {x}\in \mathbb {R}_+^n \mid \mathbf {g}_i(\mathbf {x})\in \mathcal {K}_i^*\,\forall i=1,\ldots ,p\} = \mathcal {F},\\ \{ \mathbf {x}\in \mathbb {R}_+^n \mid \widetilde{f_i}(\mathbf {x})\ge 0 \,\forall i\in \mathcal {I}\}&= \{ \mathbf {x}\in \mathbb {R}_+^n \mid \langle \mathbf {w}, \widetilde{\mathbf {g}_i}(\mathbf {x}) \rangle \ge 0 \,\forall i=1,\ldots ,p,\; \mathbf {w}\in \widehat{\mathcal {K}_i} \} \\&= \{ \mathbf {x}\in \mathbb {R}_+^n \mid \widetilde{\mathbf {g}_i}(\mathbf {x})\in \widehat{\mathcal {K}_i}^*\,\forall i=1,\ldots ,p \} \\&= \{ \mathbf {x}\in \mathbb {R}_+^n \mid \widetilde{\mathbf {g}_i}(\mathbf {x})\in \mathcal {K}_i^*\,\forall i=1,\ldots ,p \} = {\widetilde{\mathcal {F}}}. \end{aligned}$$

This, in addition to Property 3.5 holding, implies that the requirements of \(f_0\) for Theorem 3.9 hold, and thus for some \(R\in \mathbb {N}\) there exists a finite set

$$\begin{aligned} \mathcal {J}\subseteq \{ (i,\mathbf {w}) \mid i\in \{1,\ldots ,p\},\; \mathbf {w}\in \widehat{\mathcal {K}_i} \} \end{aligned}$$

and polynomials \(q_{i,\mathbf {w}}:\mathbb {R}^n\rightarrow \mathbb {R}\) for \((i,\mathbf {w})\in \mathcal {J}\), with non-negative coefficients and \({{\,\mathrm{deg}\,}}(q_{i,\mathbf {w}})+d_i\le R+d_0\), such that

$$\begin{aligned} (1+\mathbf {e}^\mathsf {T}\mathbf {x})^R (f(\mathbf {x})-\lambda ) \ge _c \sum _{(i,\mathbf {w})\in \mathcal {J}} \langle \mathbf {w}, \mathbf {g}_i(\mathbf {x}) \rangle q_{i,\mathbf {w}}(\mathbf {x}). \end{aligned}$$

We can write \(q_{i,\mathbf {w}}\) in the form

$$\begin{aligned} q_{i,\mathbf {w}} = \sum _{\begin{array}{c} \varvec{\alpha }\in \mathbb {N}^n:\\ \mathbf {e}^\mathsf {T}\varvec{\alpha }\le R+d_0-d_i \end{array}} q_{i,\mathbf {w},\varvec{\alpha }} \mathbf {x}^{\varvec{\alpha }}, \end{aligned}$$

where \(q_{i,\mathbf {w},\varvec{\alpha }}\) are non-negative scalars for all \(i,\mathbf {w},\varvec{\alpha }\). Using this notation we have

$$\begin{aligned} (1+\mathbf {e}^\mathsf {T}\mathbf {x})^R (f(\mathbf {x})-\lambda )&\ge _c \sum _{i=1}^p \sum _{\begin{array}{c} \varvec{\alpha }\in \mathbb {N}^n: \\ \mathbf {e}^\mathsf {T}\varvec{\alpha }\le R+d_0-d_i \end{array}} \mathbf {x}^{\varvec{\alpha }} \left\langle \mathbf {y}_{i,\varvec{\alpha }}, \mathbf {g}_i(\mathbf {x}) \right\rangle ,\\ \text {where } \mathbf {y}_{i,\varvec{\alpha }}&= \sum _{\begin{array}{c} \mathbf {w}\in \mathcal {K}_i:\\ (i,\mathbf {w})\in \mathcal {J} \end{array}} q_{i,\mathbf {w},\varvec{\alpha }}\mathbf {w}\in \mathcal {K}_i. \end{aligned}$$

Now letting \(r=\max \{0,R+d_0-D\}\) and considering Proposition 3.3 we obtain the required result. \(\square \)

Remark 3.11

Suppose that the polynomial f and the polynomial vectors \(\mathbf {g}_i\) are in fact homogeneous, i.e., \((\mathbf {g}_i(\mathbf {x}))_j\) is a homogeneous polynomial of degree \(d_i\) for all \(j=1,\ldots ,m_i\). Then from Theorem  3.8 (using the techniques from Theorem 3.10), we find that if \(f(\mathbf {x})>0\) for all \(\mathbf {x}\in \mathcal {F}\setminus \{\varvec{0}\}\), then there exist \(r\in \mathbb {N}\) and \(\mathbf {y}_{i,\varvec{\alpha }}\in \mathcal {K}_i\) for \(i=1,\ldots ,p\), \(\varvec{\alpha }\in \mathbb {N}:\mathbf {e}^\mathsf {T}\varvec{\alpha }= D-d_i+r\) such that

$$\begin{aligned} \begin{aligned} (\mathbf {e}^\mathsf {T}\mathbf {x})^{D-d_0+r} f(\mathbf {x}) \ge _c \sum _{i=1}^p \sum _{\begin{array}{c} \varvec{\alpha }\in \mathbb {N}^n: \\ \mathbf {e}^\mathsf {T}\varvec{\alpha }= D-d_i+r \end{array}} \mathbf {x}^{\varvec{\alpha }} \langle \mathbf {y}_{i,\varvec{\alpha }}, \mathbf {g}_i(\mathbf {x}) \rangle \end{aligned} \end{aligned}$$
(7)

3.5 Enhancing the convergence

The main characteristic of our hierarchy, the conic linearity, has an affect on the tightness of the bounds it provides. The bounds improve if we increase r, but sometimes we would like to improve these bounds already for the beginning members of the hierarchy. One way to make such improvements and stay tractable is to add to the original problem the redundant constraint

$$\begin{aligned} \begin{pmatrix} 1 &{} \mathbf {x}^\mathsf {T}\\ \mathbf {x}&{} \mathbf {x}\mathbf {x}^\mathsf {T}\end{pmatrix}\in \mathcal {PSD}^{n+1}, \end{aligned}$$
(8)

and then apply our hierarchy, where \(\mathcal {PSD}^{n+1}\) denotes the set of positive semi-definite matrices of the order \(n+1\). This gives us (extra) positive semi-definite variables in the hierarchy, but these positive semi-definite variables would be limited to having the order \(n+1\), unlike in the classic SOS approach, where the order of the positive semi-definite constraints quickly grows to an intractable level. This approach is closely related to that taken by Peña, Vera and Zuluaga [39], which has been demonstrated to be very effective, and it was its effectiveness in this paper that provided the inspiration for us to consider it. It is also aligned with a recent hierarchy of Lasserre et al. [24], where each member of the hierarchy is an SDP with a bounded size and some linear constraints. Considered on the dual side, this approach is closely related to considering truncated moment matrices, but with subtle differences caused by the multiplication with \(\mathbf {x}^{\varvec{\alpha }}\) [see problem (12)].

We tested this approach on several examples in Sect. 4, and the numerical results show that it improves the bounds significantly.

Another approach to improve our hierarchy would be to add optimality conditions to the original problem, similar to was previously done for Lasserre’s hierarchy [6, 34, 37]. If the cones \(\mathcal {K}_i^*\) from (1) are semi-algebraic, then we can write out the polynomial inequalities for the cones explicitly, and then apply the SOS or linear optimization approach from this subsection. However, this could result in a lot of terms with a very high degree, and thus large semi-definite or linear optimization instances. We have not tested this approach.

3.6 Further discussion on convergence

One advantage of the moment and sums-of-squares-based hierarchies is the occurrence of a finite convergence [11, 12, 25, 35]. Recently Nie has provided in [33, 36] an extensive and clear study of the convergence of Lasserre’s hierarchy. He showed that under some generic assumptions, the so-called flat truncation is a necessary and sufficient condition for finite convergence. A similar property also holds for non-commutative polynomials [4, 17].

We do not yet have results of this type for our hierarchy - neither for the original nor for the enhanced version. Actually, we hope that this paper will motivate other researchers to pursue this direction.

We know that for our new hierarchy (without enhancement) we would not generally expect to get finite convergence, and in Example  3.1 we saw an example with an asymptotic but not finite convergenceFootnote 2. If \(\mathcal {K}_1,\ldots ,\mathcal {K}_m\) are all polyhedral cones, then the optimization problems in our hierarchy would all be linear ones and thus we cannot expect them to encapsulate the nonlinearity in the problem. However, after adding (8) the resulting hierarchy converges in practice much better and we believe a variant of Nie’s results can be obtained.

While the convergence results for Lasserre’s hierarchy are beautiful results, they are limited by the fact that in practice the finite convergence can be at a level of the hierarchy that is intractable. The main advantage of our new hierarchy is that much higher levels of the hierarchy remain tractable, as will be seen in Sect. 4.

4 Applications of the new hierarchy

In this section we will consider generalized classes of polynomial conic optimization problems from the literature, and consider how the application of our new approach to these problems compares with previous approaches. In particular we consider:

  • POP over the non-negative orthant, where we found that our hierarchy in its standard form performs poorly compared to state-of-the-art methods, but performs comparatively well when we added the redundant SDP constraint (8) to the original problem before applying our hierarchy.

  • PSDP over the non-negative orthant, where we found that our hierarchy (in its standard form) performs comparatively well in comparison to state-of-the-art methods, and performs even better when adding the redundant SDP constraint (8) to the original problem.

  • PSOCP over the non-negative orthant, where we found that our hierarchy outperforms state-of-the-art methods in its standard form.

For all the examples in this section, for ease of implementation we used YALMIP [28] within MATLAB [29], which can handle polynomials directly. This converted the optimization problems from our hierarchy (and state-of-the-art hierarchies) into LP, SOC and SDP optimization problems, which were then in almost all cases solved by SeDuMi [52]. We also used MOSEK [31] to compute the values for (11) in Table 2 and the SOS bounds in Table 9.

Although using YALMIP made the implementations easier, it meant that most of the computation times were spent in constructing the problems, rather than in solving them. These total computation times can be reduced through better, more direct implementations, and thus are not representative measures of the performance. For this reason no computation times have been included. Instead, we consider whether the optimization problems can be solved, or if there are memory problems, along with comparing the size of these problems.

All the computations were carried out on a laptop with two 2.30-GHz CPU cores and 4.0 GB of RAM. The code for these examples is available from the authors on request.

4.1 Constrained polynomial optimization over the non-negative orthant

In this subsection we will apply our method to POPs over the non-negative orthant. We will see that our method performs poorly in comparison to the classic SOS approach. If, however, we add the constraint (8) to the original problem before applying our method then the performance is drastically improved, even occasionally outperforming the classic SOS approach. We are, however, of the opinion that the classic SOS approach is currently still superior to our new method for these problems and instead this subsection should be thought of as an illustration of how our new method works, in preparation for the subsequent subsections where we apply our (enhanced) method to the more complicated cases of PSDPs and PSOCPs.

A polynomial \(f:\mathbb {R}^n\rightarrow \mathbb {R}\) is defined to be a sum-of-squares (SOS) polynomial if there exists a polynomial vector \(\mathbf {h}:\mathbb {R}^n\rightarrow \mathbb {R}^q\) such that \(f(\mathbf {x})=_c \mathbf {h}(\mathbf {x})^\mathsf {T}\mathbf {h}(\mathbf {x})=_c \sum _{i=1}^q h_i(\mathbf {x})^2\), and we then trivially have that \(f(\mathbf {x})\ge 0\) for all \(\mathbf {x}\in \mathbb {R}^n\).

Letting \(\mathbf {v}_{d}(\mathbf {x}):\mathbb {R}^n\rightarrow \mathbb {R}^{\left( {\begin{array}{c}n+d\\ n\end{array}}\right) }\) be such that \(\mathbf {v}_{d}(\mathbf {x})=_c (\mathbf {x}^{\varvec{\alpha }})_{\varvec{\alpha }\in \mathbb {N},\; \mathbf {e}^\mathsf {T}\varvec{\alpha }\le d}\), it is well known that a polynomial \(f:\mathbb {R}^n\rightarrow \mathbb {R}\) of degree at most 2d is SOS if and only if there exists an order \(\left( {\begin{array}{c}n+d\\ n\end{array}}\right) \) positive semi-definite matrix A, denoted \(A\in \mathcal {PSD}^{\left( {\begin{array}{c}n+d\\ n\end{array}}\right) }\), such that \(f(\mathbf {x})=_c \mathbf {v}_{d}(\mathbf {x})^\mathsf {T}A \mathbf {v}_{d}(\mathbf {x})\), and there is a linear relationship between the elements of A and the coefficients of f. This allows us to optimize over the set of SOS polynomials using positive semi-definite optimization [22, 26].

Let us consider a constrained polynomial optimization problem over the non-negative orthant:

$$\begin{aligned} \begin{aligned} \min _{\mathbf {x}} \quad&f(\mathbf {x}) \\ \text {s.t.}\quad&g_i(\mathbf {x})\ge 0 \qquad \text {for all}\quad i=1,\ldots ,p,\\&x_i\ge 0 \qquad \text {for all}\quad i=1,\ldots ,n. \end{aligned} \end{aligned}$$
(9)

Note that this is a special instance of (1) with \(\mathcal {K}_i^*=\mathbb {R}_+\) for all i.

If the sign constraints \(x_i\ge 0\) are considered as the usual polynomial inequalities then (9) is a special instance of a classic constrained polynomial optimization problem, formulated in [22, problem (5.2)].

Due to the hardness of (9), several approximation hierarchies are proposed in the literature. Probably one of the most well-known and tight is the SOS hierarchy, which consists of the following approximation problems (for each \(r\in \mathbb {N}\)):

$$\begin{aligned} \begin{aligned} \max _{\lambda ,\{a_i\}} \quad&\lambda \\ \text {s.t.}\quad&f(\mathbf {x})-\lambda =_c a_0(\mathbf {x}) + \sum _{i=1}^n x_i\, a_i(\mathbf {x}) + \sum _{i=1}^p g_i(\mathbf {x})\, a_{n+i}(\mathbf {x})\\&a_0(\mathbf {x}) \text { is SOS of degree at most } 2\lfloor \tfrac{1}{2}(D+r) \rfloor \\&a_i(\mathbf {x}) \text { is SOS of degree at most } 2\lfloor \tfrac{1}{2}(D+r-1) \rfloor \quad \text { for } \quad i=1,\ldots ,n\\&a_{n+i}(\mathbf {x}) \text { is SOS of degree at most } 2\lfloor \tfrac{1}{2}(D+r-d_i) \rfloor \quad \text {for all}\quad i=1,\ldots ,p. \end{aligned} \end{aligned}$$
(10)

In practice this method provides very good approximations. If we know some constant N such that the feasible set for (9) is contained in the Euclidean ball centred at the origin with the radius N (note that this is essentially our Assumption 2.2) then we can add this ball constraint to the problem (9) and then the solutions of the dual problems (10) converge to the optimal value of (9), when \(r\rightarrow \infty \) (see [21, Theorem 4.2], [22, Theorem 5.6]). However, as r (and/or D) increase, the hierarchy members contain increasingly larger positive semi-definite constraints that are more and more difficult to handle. The problem from the hierarchy corresponding to fixed r has:

  • One positive semi-definite constraint of the order \(\left( {\begin{array}{c}n+\lfloor \tfrac{1}{2}(D+r) \rfloor \\ n\end{array}}\right) \),

  • n positive semi-definite constraints of the order \(\left( {\begin{array}{c}n+\lfloor \tfrac{1}{2}(D+r-1) \rfloor \\ n\end{array}}\right) \),

  • a positive semi-definite constraint of the order \(\left( {\begin{array}{c}n+\lfloor \tfrac{1}{2}(D+r-d_i) \rfloor \\ n\end{array}}\right) \) for each \(i\in \{1,\ldots ,p\}\),

  • \(\left( {\begin{array}{c}n+D+r\\ n\end{array}}\right) \) equality constraints,

  • \(1+\tfrac{1}{2} \left( {\begin{array}{c}n+\lfloor \tfrac{1}{2}(D+r) \rfloor \\ n\end{array}}\right) \left[ \left( {\begin{array}{c}n+\lfloor \tfrac{1}{2}(D+r) \rfloor \\ n\end{array}}\right) +1\right] +\tfrac{1}{2}n \left( {\begin{array}{c}n+\lfloor \tfrac{1}{2}(D+r-1) \rfloor \\ n\end{array}}\right) \left[ \left( {\begin{array}{c}n{+}\lfloor \tfrac{1}{2}(D+r-1) \rfloor \\ n\end{array}}\right) {+}1\right] + +\sum _{i=1}^p\tfrac{1}{2} \left( {\begin{array}{c}n+\lfloor \tfrac{1}{2}(D+r-d_i) \rfloor \\ n\end{array}}\right) \left[ \left( {\begin{array}{c}n+\lfloor \tfrac{1}{2}(D+r-d_i) \rfloor \\ n\end{array}}\right) +1\right] \) variables.

Our hierarchy from Sect. 3 applied to (9) can be simplified to

$$\begin{aligned} \begin{aligned} \max _{\lambda ,\{y_{i,\varvec{\alpha }}\}} \quad&\lambda \\ \text {s.t.}\quad&(1+\mathbf {e}^\mathsf {T}\mathbf {x})^{D-d_0+r}(f(\mathbf {x})-\lambda ) \ge _c \sum _{i=1}^p g_i(\mathbf {x})\sum _{\begin{array}{c} \varvec{\alpha }\in \mathbb {N}^n: \\ \mathbf {e}^\mathsf {T}\varvec{\alpha }\le D-d_i+r \end{array}} y_{i,\varvec{\alpha }}\mathbf {x}^{\varvec{\alpha }} \\&y_{i,\varvec{\alpha }}\ge 0\qquad \text {for all } i,\varvec{\alpha }\end{aligned} \end{aligned}$$
(11)

This hierarchy is usually weaker, but on the other hand contains problems that are easier to solve. It contains

  • \(\left( {\begin{array}{c}n+D+r\\ n\end{array}}\right) +\sum _{i=1}^p \left( {\begin{array}{c}n+D-d_i+r\\ n\end{array}}\right) \) inequality constraints,

  • \(1+\sum _{i=1}^p \left( {\begin{array}{c}n+D-d_i+r\\ n\end{array}}\right) \) variables.

By adding the redundant PSD constraint (8) to the original problem and then applying our hierarchy to give the following problem adds additional \(\left( {\begin{array}{c}n+D+r-2\\ n\end{array}}\right) \) PSD constraints of the order \(n+1\) and an additional \(\tfrac{1}{2}\left[ \left( {\begin{array}{c}n+D+r-2\\ n\end{array}}\right) \right] \left[ \left( {\begin{array}{c}n+D+r-2\\ n\end{array}}\right) +1\right] \) variables:

$$\begin{aligned} \begin{aligned} \max _{\lambda ,\{y_{i,\varvec{\alpha }}\},\{Z_{\varvec{\beta }}\}} \quad&\lambda \\ \text {s.t.}\quad&(1+\mathbf {e}^\mathsf {T}\mathbf {x})^{D-d_0+r}(f(\mathbf {x})-\lambda ) \ge _c \sum _{i=1}^p g_i(\mathbf {x})\sum _{\begin{array}{c} \varvec{\alpha }\in \mathbb {N}^n: \\ \mathbf {e}^\mathsf {T}\varvec{\alpha }\le D-d_i+r \end{array}} y_{i,\varvec{\alpha }}\mathbf {x}^{\varvec{\alpha }} +\ldots \\&\ldots + \sum _{\begin{array}{c} \varvec{\beta }\in \mathbb {N}^n:\\ \mathbf {e}^\mathsf {T}\varvec{\beta }\le D+r-2 \end{array}} \mathbf {x}^{\varvec{\beta }}\, \mathbf {v}_{1}(\mathbf {x})^\mathsf {T}Z_{\varvec{\beta }}\mathbf {v}_{1}(\mathbf {x})\\&y_{i,\varvec{\alpha }}\ge 0\qquad \text {for all}\quad i,\varvec{\alpha }\\&Z_{\varvec{\beta }}\in \mathcal {PSD}^{n+1} \qquad \text {for all}\quad \varvec{\beta }\end{aligned} \end{aligned}$$
(12)

Remark 4.1

Suppose we have \(d_0=d_1=\cdots =d_p=2\). For \(r=0\) the SOS relaxation (10) is equivalent to the enhanced relaxation (12), since every feasible solution for the first problem yields a feasible solution with the same objective value for the second problem and vice versa.

In Table 1 we consider the explicit problem sizes that this would give for an instance with \(r=4~,n=d_0=8,~p=d_1=d_2=2\). As we see, the SOS problem, (10), is on the boundary or even beyond the reach of state-of-the-art SDP solvers that are based on the interior point methods, but are still solvable with some other SDP solvers, like SDPNAL [57], while our new LP approximation (11) is solvable with most LP solvers. The new SDP hierarchy (12) contains a lot of SDP variables of small size and is solvable with SDP solvers that enable parallelization, see ,e.g., [51, 56].

Table 1 Considering a polynomial optimization problem with \(n=d_0=8,~p=d_1=d_2=2\) the table below gives the size of the approximation problems (10), (11) and (12) for \(r=4\)
Full size table

Example 4.2

In the paper [24], in particular instances C4_2, C4_4, C4_6, C6_2, C6_4, C6_6, C8_2, C8_4, C10_4, C20_2, the authors considered some polynomial optimization problems of the form (9) such that for all feasible points of this problem and all \(i\in \{1,\ldots ,m\}\) we have \(g_i(\mathbf {x})\le 1\).Footnote 3 For these problems the authors compared the standard SOS approach, a bounded SOS approach [23] and an LP approach based on Krivine-Stengle’s Positivstellensatz to compute the lower bounds on these problems.

For these instances we computed the lower bounds provided by our new LP hierarchy, (11), and SDP hierarchy, (12). The new LP hierarchy was computed for all r for which we did not get “out of memory” warnings, while the new SDP hierarchy was computed for \(r=1\). The results for this are in Table 2.

Table 2 The results of Example 4.2 are presented, considering instances from the paper [24]
Full size table

As we can see, our new LP approximation, (11), does not perform very well in comparison to the other methods, but our new SDP approximation, (12), does perform extremely well, always giving the tightest lower bound of all the approximations in the instances considered. It is even strictly better than all of the other bounds for instances C4_6 and C6_6.

In order to compare the sizes of these problems, in Table 3 we consider the size of the hierarchies for the case C6_6. For \(r=1\) we see that not only does our new SDP hierarchy, (12), provide a better lower bound than the (bounded) SOS approach, but the size of the problem, in terms of the order of the largest PSD constraints, is also significantly smaller.

Table 3 Comparing the size of the approximation hierarchies for the case C6_6 in Example 4.2
Full size table

4.2 Polynomial semi-definite optimization over the non-negative orthant

In this subsection we will apply our method to PSDPs over the non-negative orthant. We will see that our method performs very well on these problems, especially after adding the redundant constraint (8) to the original problem, but the method does not suffer as severely from memory problems as the classic SOS approach.

In [13,14,15, 19] the authors considered PSDPs, and how the SOS approach could be extended for positive semi-definite constraints using the concept of matrix SOS.

Let us consider a (scalar) polynomial f and the matrix polynomials \(G_i:\mathbb {R}^n\rightarrow \mathcal {S}^{m_i}\) (i.e., (\((G_i)_{k\ell }=(G_i)_{\ell k}\) is a polynomial for all \(k,\ell =1,\ldots ,m_i\)). We define

$$\begin{aligned} d_0={{\,\mathrm{deg}\,}}(f),~~d_i={{\,\mathrm{deg}\,}}(G_i)=\max _{k,\ell }{{\,\mathrm{deg}\,}}(G_i)_{k\ell }. \end{aligned}$$

Following [13, 14] we define a PSDP over the non-negative orthant as

$$\begin{aligned} \begin{aligned} \min _{\mathbf {x}} \quad&f(\mathbf {x}) \\ \text {s.t.}\quad&G_i(\mathbf {x})\in \mathcal {PSD}^{m_i}&\text {for all}\quad i=1,\ldots ,p,\\&x_i\ge 0&\text {for all }\quad i=1,\ldots ,n.\\ \end{aligned} \end{aligned}$$
(13)

This is again a very hard problem, so tractable relaxations are very desirable. The standard SOS approach to (13) is based on using matrix SOS constraints.

A polynomial matrix \(G:\mathbb {R}^n\rightarrow \mathcal {S}^{m}\) is matrix SOS if there exists a matrix polynomial \(H:\mathbb {R}^n\rightarrow \mathbb {R}^{q\times m}\) such that \(G(\mathbf {x})=_c H(\mathbf {x})^\mathsf {T}H(\mathbf {x})\), and we then trivially have that \(G(\mathbf {x})\in \mathcal {PSD}^{m}\) for all \(\mathbf {x}\in \mathbb {R}^n\). Similar to the standard SOS case (see, e.g., [14, 19]), we have that \(G(\mathbf {x}):\mathbb {R}^n\rightarrow \mathcal {S}^{m}\) is a matrix SOS of degree at most 2d if and only if there exists \(A\in \mathcal {PSD}^{m \left( {\begin{array}{c}n+d\\ n\end{array}}\right) }\) such that

$$\begin{aligned} G(\mathbf {x})&=_c (I_m \otimes \mathbf {v}_{d}(\mathbf {x}))^\mathsf {T}A (I_m \otimes \mathbf {v}_{d}(\mathbf {x})), \end{aligned}$$

where “\(\otimes \)” denotes the Kronecker product and \(I_m\) denotes the identity matrix of the order m. Also, similar to before, there is a linear relationship between the elements of A and the coefficients of the elements of \(G(\mathbf {x})\), and thus we can optimize over the set of matrix SOS polynomials using positive semi-definite optimization. We can also construct the SOS relaxation hierarchy for (13) for each \(r\in \mathbb {N}\) [13, 14]:

$$\begin{aligned} \begin{aligned} \max _{\lambda ,\{a_i,A_i\}} \quad&\lambda \\ \text {s.t.}\quad&f(\mathbf {x})-\lambda =_c a_0(\mathbf {x}) + \sum _{i=1}^n x_i\, a_i(\mathbf {x}) + \sum _{i=1}^p \langle G_i(\mathbf {x}),\, A_{i}(\mathbf {x})\rangle \\&a_0(\mathbf {x}) \text { is SOS of degree at most } 2\lfloor \tfrac{1}{2}(D+r) \rfloor \\&a_i(\mathbf {x}) \text { is SOS of degree at most } 2\lfloor \tfrac{1}{2}(D+r-1) \rfloor \quad \text { for }\quad i=1,\ldots ,n\\&A_{i}(\mathbf {x}) \text { is matrix SOS}, {{\,\mathrm{deg}\,}}(A_{i})\le 2\lfloor \tfrac{1}{2}(D+r-d_i) \rfloor \quad \text { for all }\quad i{=}1,\ldots ,p. \end{aligned} \end{aligned}$$
(14)

where \(D=\max \{d_i:i=0,1,\ldots ,p\}\). Under some conditions related to the compactness of the feasibility set for (13), the optimal values of this hierarchy converge to the optimal value of (13) [13, Theorem 2.2].

Similar to before, the order of the PSD constraints in this problem grows very quickly with r. In fact for each \(i\in \{1,\ldots ,p\}\), the SOS constraint for \(A_i(\mathbf {x})\) is equivalent to a PSD constraint of the order \(m_i\left( {\begin{array}{c}n+\lfloor (D+r-d_i)/2\rfloor \\ n\end{array}}\right) \).

Alternatively, by taking \(\mathcal {K}_i = \mathcal {PSD}^{m_i} = \mathcal {K}_i^*\) for all i, we can apply our hierarchy from Sect. 3 to problem (13), both with and without the additional PSD constraint (8) in the original problem, to give the following problems, respectively:

$$\begin{aligned} \max _{\lambda ,\{Y_{i,\varvec{\alpha }}\}} \quad&\lambda \nonumber \\ \text {s.t.}\quad&(1+\mathbf {e}^\mathsf {T}\mathbf {x})^{D-d_0+r}(f(\mathbf {x})-\lambda ) \ge _c \sum _{i=1}^p \sum _{\begin{array}{c} \varvec{\alpha }\in \mathbb {N}^n: \\ \mathbf {e}^\mathsf {T}\varvec{\alpha }\le D-d_i+r \end{array}} \mathbf {x}^{\varvec{\alpha }} \langle Y_{i,\varvec{\alpha }},G_i(\mathbf {x})\rangle \nonumber \\&Y_{i,\varvec{\alpha }}\in \mathcal {PSD}^{m_i}\qquad \text {for all }\quad i,\varvec{\alpha }, \end{aligned}$$
(15)
$$\begin{aligned} \max _{\lambda ,\{Y_{i,\varvec{\alpha }}\},\{Z_{\varvec{\beta }}\}} \quad&\lambda \nonumber \\ \text {s.t.}\quad&(1+\mathbf {e}^\mathsf {T}\mathbf {x})^{D-d_0+r}(f(\mathbf {x})-\lambda ) \ge _c \sum _{i=1}^p \sum _{\begin{array}{c} \varvec{\alpha }\in \mathbb {N}^n: \\ \mathbf {e}^\mathsf {T}\varvec{\alpha }\le D-d_i+r \end{array}} \mathbf {x}^{\varvec{\alpha }} \langle Y_{i,\varvec{\alpha }},G_i(\mathbf {x})\rangle +\ldots \nonumber \\&\quad \ldots + \sum _{\begin{array}{c} \varvec{\beta }\in \mathbb {N}^n:\\ \mathbf {e}^\mathsf {T}\varvec{\beta }\le D+r-2 \end{array}} \mathbf {x}^{\varvec{\beta }}\, \mathbf {v}_{1}(\mathbf {x})^\mathsf {T}Z_{\varvec{\beta }} \mathbf {v}_{1}(\mathbf {x})\nonumber \\&Y_{i,\varvec{\alpha }}\in \mathcal {PSD}^{m_i}\qquad \text {for all }\quad i,\varvec{\alpha },\nonumber \\&Z_{\varvec{\beta }}\in \mathcal {PSD}^{n+1} \qquad \text {for all }\quad \varvec{\beta }. \end{aligned}$$
(16)

Here, in comparison to the matrix SOS approach, we have many more SDP constraints, but the order of the positive semi-definite constraints is fixed.

In Table 4 we consider the sizes of these approximation problems for \(r=4\) with \(n=8\) variables and \(p=5\) matrix SDP constraints of the order 10 with degrees \(d_0=4\) and \(d_i=2,~i=1,\ldots ,5\).

Table 4 Complexity of the \(r=4\) member of matrix SOS hierarchy (14) and our new hierarchies (15) and (16), for \(n=8,~p=5, d_0=4\) and \(d_i=2,~m_i=10,~i=1,\ldots ,5\)
Full size table

The difference is significant. While the Matrix SOS problem is already out of reach for most of the SDP solvers, our new hierarchies are manageable by at least those SDP solvers that can explore parallelization, like [51, 56].

Example 4.3

Let us consider the example from [13, Sect. II E]:

$$\begin{aligned} \begin{aligned} \min _{\mathbf {x}} \quad&f(\mathbf {x}) = -x_1^2-x_2^2 \quad \text {s.t.}\quad G(\mathbf {x}) = \left[ \begin{array}{cc} 1-4x_1x_2 &{} x_1\\ x_1 &{} 4-x_1^2-x_2^2 \end{array} \right] \in \mathcal {PSD}^{2}. \end{aligned} \end{aligned}$$

This has the optimal solutions (0, 2) and \((0,-2)\) with the optimal value \(-4\).

As reported in [13, Table II], the SOS approximation hierarchy (14) applied to this problem reduces for \(r=0\) to semi-definite optimization problems with 2 PSD constraints of the orders 3 and 2, giving an optimal value of \(-4\), which is already the optimal value of the original problem.

We can transform the semi-definite constraint from (17) into two (scalar) polynomial constraints and apply the approach from Sect. 4.1. However, in [13, Table I] it is reported that only the 7th member of the hierarchy (10) yields the optimal value of \(-4\). This member of the hierarchy has 3 PSD constraints of the orders 36, 28 and 21.

To apply our hierarchy to this problem, we first need to translate its feasible set into the non-negative orthant. To do this we substitute \(x_1\) by \(x_1-2\) and \(x_2\) by \(x_2-2\) to give the following problem.

$$\begin{aligned} \begin{aligned} \min _{\mathbf {x}} \quad&f(\mathbf {x}) = -(x_1-2)^2-(x_2-2)^2 \\ \text {s.t.}\quad&G(\mathbf {x}) = \left[ \begin{array}{cc} 1-4(x_1-2)(x_2-2) &{} x_1-2\\ x_1-2 &{} 4-(x_1-2)^2-(x_2-2)^2 \end{array} \right] \in \mathcal {PSD}^{2}. \end{aligned} \end{aligned}$$

Note that the semi-definite constraint implies that \(4-(x_1-2)^2-(x_2-2)^2\ge 0\); therefore, \(x_1,x_2\ge 0\), i.e., after the substitution the sign constraint is redundant and we can add it without affecting the feasible region.

Our hierarchy (15) for this problem reduces for \(r=1\) to

$$\begin{aligned} \begin{aligned} \max _{\lambda ,\{Y\}} \quad&\lambda \\ \text {s.t.}\quad&(1+x_1+x_2)(-(x_1-2)^2-(x_2-2)^2-\lambda ) \\&\quad \ge _c \langle Y_{(0,0)} +x_1 Y_{(1,0)}+x_2 Y_{(0,1)},G(\mathbf {x})\rangle \\&Y_{(0,0)},Y_{(1,0)},Y_{(0,1)}\in \mathcal {PSD}^{2} \end{aligned} \end{aligned}$$
(17)

The optimal value for this is also equal to \(-4\), i.e., the member of the hierarchy corresponding to \(r=1\) is already giving the optimal value of the original problem. Note that the problem from our hierarchy has only 3 PSD constraints, all being of the order 2.

Example 4.4

Let us consider the following family of PSDPs:

$$\begin{aligned} \begin{aligned} \min _{\mathbf {x}} \quad&\mathrm {trace}~G(\mathbf {x}) \\ \text {s.t.}\quad&G(\mathbf {x}) \in \mathcal {PSD}^{n} \\&\mathbf {x}\in \mathbb {R}_+^n, \end{aligned} \end{aligned}$$
(18)

where

$$\begin{aligned} G(\mathbf {x})=\left[ \begin{matrix} (1+x_1/2)^2 &{}\quad 0 &{}\quad \ldots &{} 0\\ 0 &{}\quad (1+x_2/2)^2 &{}\quad \ldots &{}\quad 0\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ 0 &{}\quad 0 &{}\quad \ldots &{}\quad (1+x_n/2)^2 \end{matrix}\right] - \left[ \begin{matrix} x_1\\ x_2\\ \vdots \\ x_n \end{matrix}\right] \cdot \left[ \begin{matrix} x_1\\ x_2\\ \vdots \\ x_n \end{matrix}\right] ^\mathsf {T}. \end{aligned}$$

It is shown in Appendix A that for the problem (18) we have:

  • The optimal value is equal to \(n-1\);

  • The matrix SOS hierarchy, (14), for \(r\in \{0,1\}\) has an optimal value of zero;

  • Our new hierarchy, (15), for \(r\in \{0,1\}\) has an optimal value of zero;

  • Our new hierarchy, (16), for \(r=0\) has an optimal value of zero.

In Table 5 we report on the numerical results for higher levels of these hierarchies, and in Table 6 we compare how large these problems are for \(n=21\). From these results we see that, in terms of optimal values, our new hierarchies perform very competitively in comparison with the matrix SOS approach. Moreover, in Table 6, we see that the sizes of our hierarchies, in terms of the order of the largest PSD constraint, are much smaller than the matrix SOS approach. We also see that adding the redundant constraint (8) to the original problem before applying our hierarchy to give the problem (16), significantly improves the lower bound in comparison to the problem (15).

Table 5 Numerical results for polynomial SDP problem (18), computed for different approximation hierarchies
Full size table
Table 6 Comparing the size of some instances of approximation hierarchies, in terms of order and number of PSD constraints, of the problem in Example 4.4 for \(n=21\)
Full size table

4.3 Polynomial second-order cone optimization over the non-negative orthant

In this subsection we will apply our method to PSOCPs over the non-negative orthant. We will see that our method performs very well on these problems, especially after adding the redundant constraint (8) to the original problem, convincingly outperforming the classic SOS approach.

Suppose that the cones \(\mathcal {K}_i^*\) in (1) are the second-order cones (SOC):

$$\begin{aligned} \mathcal {SOC}^{m_i}:=\{ (z_1,\mathbf {z})\in \mathbb {R}\times \mathbb {R}^{m_i-1} : \Vert \mathbf {z}\Vert _2\le z_1 \}. \end{aligned}$$

Note that \((z_1,\mathbf {z})\in \mathbb {R}\times \mathbb {R}^{m_i-1}\) belongs to \(\mathcal {SOC}^{m_i}\) iff \(z_1\ge 0\) and \(z_1^2-\sum _{i=2}^{m_i}z_i^2\ge 0\).

For \(\mathbf {g}:\mathbb {R}^n\rightarrow \mathbb {R}^{m_i}\) being a polynomial vector of degree d, we call \(\mathbf {g}(\mathbf {x})\in \mathcal {SOC}^{m_i}\) a polynomial second-order cone constraint (PSOC). It can be transformed into two polynomial inequalities, one of the order d and one of the order 2d. Therefore, we can handle PSOCPs as classic polynomial optimization problems and use approaches from Sect. 4.1.

Since SOCs are tractable, i.e., we can solve linear conic optimization problems over these cones numerically efficiently, it is a natural idea to approximate PSOCPs also using the new hierarchy from Sect. 3 directly. We demonstrate this with the following two examples.

Example 4.5

Let us consider the following simple PSOC optimization problem:

$$\begin{aligned} \begin{aligned} \min _{x_1,x_2} \quad&x_1^2+x_2^2\\ \text {s.t.}\quad&\mathbf {g}(\mathbf {x})=\left[ \begin{array}{c} x_1^2-x_2^2\\ x_1x_2\\ x_1+x_2+1 \end{array} \right] \in \mathcal {SOC}^{3}\\&x_1,x_2\in \mathbb {R}_+. \end{aligned} \end{aligned}$$
(19)
Table 7 The optimal values of our hierarchy (20) (without (8)) compared to SOS hierarchy (10), obtained by replacing the PSOC constraint with two polynomial constraints. We also consider adding the additional redundant constraint (8) to the problem (19) before applying our hierarchy
Full size table
Table 8 We compare the sizes of the optimization problems, in terms of the size and the number of PSD and \(\mathcal {SOC}^{3}\) constraints, for some approximation hierarchies for the problem in Example 4.5
Full size table

Its minimum, obtained by Mathematica [54], is attained at \(\mathbf {x}^*=(1.6180, 0)^\mathsf {T}\) and is equal to 2.6180. Our hierarchy reduces for fixed r to

$$\begin{aligned} \begin{aligned} \max _{\lambda ,\{\mathbf {y}_{\varvec{\alpha }}\}} \quad&\lambda \\ \text {s.t.}\quad&(1+x_1+x_2)^r( x_1^2+x_2^2-\lambda ) \ge _c \sum _{\mathbf {e}^\mathsf {T}\varvec{\alpha }\le r}x^{\varvec{\alpha }}\langle \mathbf {y}_{\varvec{\alpha }},\mathbf {g}(\mathbf {x})\rangle \\&\mathbf {y}_{\varvec{\alpha }}~\in ~\mathcal {SOC}^{3}~~ \forall \mathbf {e}^\mathsf {T}\varvec{\alpha }\le r. \end{aligned} \end{aligned}$$
(20)

The optimal values of (20) for \(r\in \{0,\ldots ,5\}\) are reported in the second row of Table 7.

We can replace the PSOC constraint \(\mathbf {g}(\mathbf {x})\in \mathcal {SOC}^{3}\) by two equivalent polynomial constraints:

$$\begin{aligned} x_1^2-x_2^2~\ge ~ 0, ~~ (x_1^2-x_2^2 )^2- (x_1x_2)^2-( x_1+x_2+1)^2~\ge ~ 0 \end{aligned}$$

and apply the SOS hierarchy (10). The lower bounds provided by the SOS hierarchy are shown in the fourth row of Table 7. We can see that in this example our hierarchy outperforms the SOS hierarchy. This is especially apparent when we consider the sizes of the problems in Table 8. We also consider adding the redundant PSD constraint (8) to the original problem and then applying our hierarchy, and when doing this the \(r=1\) member of the hierarchy gives the exact optimal value (within numerical errors) using a very small optimisation problem, as is also shown in Tables 7 and 8.

Table 9 This table contains the results for eight randomly generated polynomial second-order cone-optimization problems
Full size table

Example 4.6

We have also evaluated our hierarchy on seven randomly generated polynomial second-order cone-optimization problems in three variables. Each such problem has two polynomial SOC constraints of degree two and dimension four. More precisely, for \(i=1,2\) we generated polynomials \(g^i_1(\mathbf {x}),\ldots ,g^i_4(\mathbf {x})\), which have all possible monomials in three variables of the degree two with coefficients generated randomly from \([-0.3,\,0.7]\) following the uniform distribution. We then replaced \(g^i_1\) with \({\tilde{g}}^i_1 = \sum _{k=1}^4g^i_k\) and set the PSOC \(\mathbf {g}^i=(\tilde{g}^i_1,g^i_2,g^i_3,g^i_4)^\mathsf {T}\in \mathcal {SOC}^{4}\). When we have generated both PSOCs, we set the objective function \(f(\mathbf {x}) = \tilde{g}^1_1(\mathbf {x})+\tilde{g}^2_1(\mathbf {x})+h(\mathbf {x})\), where h is polynomials of the degree two with random uniform coefficients from \([-0.5,\,0.5]\).

For each random polynomial second-order cone optimization problem we computed the optimum value using Mathematica [54] and the optimal values of the first three members of our hierarchy (with and without adding the additional SDP constraint (8) to the original problem) and of the standard SOS hierarchy. Recall that the SOS hierarchy is applied after reformulating each polynomial SOC constraint into two polynomial inequalities, as described at the beginning of this subsection. The results are in Table 9.

As we can see, for these examples our new hierarchy [without (8)] provides better bounds through solving smaller optimization problems in comparison to the standard SOS method. If we add (8) to the original problem, then the hierarchy is even better.

5 Conclusion

In this paper we considered polynomial conic optimization over the non-negative orthant. We proposed a hierarchy of relaxations that are in the form of conic linear optimization problems. We demonstrated that when the feasible set is contained in the non-negative orthant we can successfully apply the proposed hierarchy to constrained polynomial optimization problems (POPs), polynomial semi-definite optimization problems (PSDPs) and polynomial second-order cone-optimization problems (PSOCPs). We proved that the hierarchy is monotonic and gives bounds that converge asymptotically to the optimum value of the original problem, if some classic assumptions are satisfied. Through the addition of a redundant PSD constraint in the original problem, the proposed hierarchy performs reasonably well for POPs, in comparison to the classic SOS approach, and outperforms the classic SOS approach for PSDPs and PSOCPs, while also being cheaper to compute. The preliminary numerical evaluation confirms that this hierarchy deserves a deeper theoretical/numerical study and efficient code development. In particular, it would be of interest to consider the dual problems of our hierarchy, investigating whether similar results to that for the SOS/moment hierarchies hold with regards to the flat extension conditions [5], flat truncations [33] and extracting optimal solutions [12, Sect. 2].