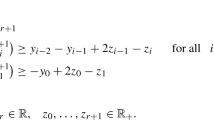Exact Conic Programming Relaxations for a Class of Convex Polynomial Cone Programs

Abstract

In this paper, under a suitable regularity condition, we establish a broad class of conic convex polynomial optimization problems, called conic sum-of-squares convex polynomial programs, exhibiting exact conic programming relaxation, which can be solved by various numerical methods such as interior point methods. By considering a general convex cone program, we give unified results that apply to many classes of important cone programs, such as the second-order cone programs, semidefinite programs, and polyhedral cone programs. When the cones involved in the programs are polyhedral cones, we present a regularity-free exact semidefinite programming relaxation. We do this by establishing a sum-of-squares polynomial representation of positivity of a real sum-of-squares convex polynomial over a conic sum-of-squares convex system. In many cases, the sum-of-squares representation can be numerically checked via solving a conic programming problem. Consequently, we also show that a convex set, described by a conic sum-of-squares convex polynomial, is (lifted) conic linear representable in the sense that it can be expressed as (a projection of) the set of solutions to some conic linear systems.

1 Introduction

The class of conic convex polynomial optimization problems is an important subclass of conic convex programming problems. It covers broad classes of convex programs such as inequality constrained convex polynomial programs [1], the SOS-convex polynomial programs [1–3], convex semidefinite programs [4, 5], second-order cone programs as well as p-order cone programs [6, 7]. It frequently appears in robust optimization [8]. For instance, a robust counterpart of a convex quadratic programming problem with a second-order cone constraint under (unstructured) norm-bounded uncertainty can equivalently be written as a conic convex quadratic optimization problem with the positive semidefinite cone (see Theorem 6.3.2 [8]).

Moreover, many basic control problems are modeled as conic polynomial optimization problems. In particular, static output feedback design problems [9] are formulated as polynomial matrix inequality optimization problems. These conic polynomial problems are solved by approximating them with the Lasserre hierarchy of conic programming relaxation problems such as semidefinite linear programming (SDP) relaxation problems [2, 9], which can efficiently be solved by interior point methods.

In particular, for an inequality constrained convex polynomial programs, the Lasserre hierarchy of SDP relaxations is known to converge finitely [10–12] under suitable assumptions. An exact SDP relaxation has been shown to hold for the special class of SOS-convex programs [2, 3] and for some other classes of robust SOS-convex programs [1]. Due to the importance of exact SDP relaxations to conic convex programs, it has recently been shown that SOS-convex programs with semidefinite linear constraints [4] exhibit exact SDP relaxations under appropriate regularity conditions.

The purpose of this piece of work is to show that a broad class of conic convex polynomial programming problems exhibits exact conic programming relaxations under suitable conditions. As an outcome, we give the following key unified results that apply to many classes of important convex cone programs, such as the second-order cone programs, p-order cone programs, semidefinite programs, and polyhedral cone programs.

• (i) By generalizing the notion of sum-of-squares convexity (SOS-convexity) of real polynomials [4, 13–20] to conic SOS-convexity of vector-valued polynomial mappings, we show that the class of conic SOS-convex polynomials includes various classes of conic convex polynomials such as the matrix SOS-convex polynomials [21] and conic convex quadratic maps. We establish that the positivity of an SOS-convex polynomial over a conic SOS-convex system can be characterized in terms of a sum-of-squares polynomial representation under a regularity condition. Related recent results for SOS-convex inequality systems with applications to robust optimization can be found in [1, 16]. In many cases, the sum-of-squares representation can be numerically checked via solving a conic, such as semidefinite linear program. This representation also paves the way for deriving exact conic programming relaxation results.

• (ii) We prove that the class of SOS-convex cone programs enjoys exact conic programming relaxations under suitable regularity conditions. In the case, where the cone involved in the program is a convex polyhedral cone, we show that our exact relaxation result collapses to an exact semidefinite linear programming relaxation without any regularity condition. We further show that the relaxation problem attains its maximum under a generalized Slater condition.

• (iii) Consequently, we also show that a convex set, described by a conic SOS-convex polynomial, is (lifted) conic linear representable in the sense that it can be expressed as (a projection of) the set of solutions to some conic linear systems.

The outline of the paper is as follows. Section 2 introduces the notion of conic SOS-convexity and provides various dual characterizations of solvability of conic SOS-convex systems, including a sum-of-squares representation result on positivity of polynomials. Section 3 presents exact conic programming relaxation results. Section 4 present results on conic linear representability of some convex sets.

2 Conic SOS-Convexity and Positivstellensatz

In this section we introduce the notion of conic SOS-convexity for polynomial mappings and present various first- and second-order characterizations of conic SOS-convexity. Consequently, we establish characterizations of positivity and nonnegativity of SOS-convex polynomials over conic SOS-convex polynomial systems.

We begin with some preliminaries on polynomials. We say that a real polynomial f is sum-of-squares [11, 22] if there exist real polynomials $f_j$, $j=1,\ldots ,r$, such that $f=\sum _{j=1}^rf_j^2$. The set consisting of all sum-of-squares real polynomials is denoted by $\varSigma ^2[x]$. Moreover, the set consisting of all sum-of-squares real polynomials with degree at most d is denoted by $\varSigma ^2_d[x]$. If each $G_i, i=1,2,\ldots ,m$, is a polynomial on ${\mathbb {R}}^n$, then the degree of the polynomial map G, defined by $G(x)=(G_1(x),\ldots , G_m)$, is denoted by $\mathrm{deg}\,G$. It is defined as the maximum degree of each $G_i$, $i=1,\ldots ,m$.

In this paper, ${\mathbb {R}}^m$ denotes the Euclidean space with dimension m. For any $x,y \in {\mathbb {R}}^m$, the inner product between x, y is denoted by $\langle x, y \rangle$ and the norm induced by the inner product is defined by $\Vert x\Vert =\sqrt{\langle x, x\rangle }$. We also use $\overline{{\mathbb {B}}}$ (resp. ${\mathbb {B}}$) to denote the closed (resp. open) unit ball of ${\mathbb {R}}^m$. Throughout the paper, we assume that K is a closed and convex cone in ${\mathbb {R}}^m$. Its dual cone of K, denoted by $K^{\oplus }$, is given by $K^{\oplus }=\{y \in {\mathbb {R}}^m: \langle y, k \rangle \ge 0 \hbox { for all } k \in K\}$.

The set $S^{n}$ denotes the space of symmetric $(n\times n)$ matrices with the trace inner product and $\succeq$ denotes the Löwner partial order of $S^{n}$, that is, for $M,N\in S^{n},$ $M\succeq N$ if and only if $(M-N)$ is positive semidefinite. Let $S^{n}_+:=\{M\in S_{n}: M\succeq 0\}$ be the closed and convex cone of positive semidefinite $(n\times n)$ matrices. Note that for $M,N\in S^{n}_+$, the inner product, $(M,N):=\mathrm {Tr}[MN]$, where $\mathrm {Tr}\ [.]$ refers to the trace operation. Note also that $M\succ 0$ means that M is positive definite.

Positive semidefinite cones, second-order cones, and polyhedral cones are some important closed and convex cones K that arise in numerous applications of optimization.

Recall that a real polynomial f on ${\mathbb {R}}^n$ is called SOS-convex [13] if for any $\alpha \in [0,1]$, $h(x,y):= \alpha f(x)+(1-\alpha ) f(y)- f(\alpha x+(1-\alpha )y)$ is a sum-of-squares polynomial on ${\mathbb {R}}^n\times {\mathbb {R}}^n$. An equivalent notion of SOS-convexity was first introduced in [15]. Clearly, a SOS-convex polynomial is convex. However, the converse is not true, that is, there exists a convex polynomial which is not SOS-convex [13]. It is known that any convex quadratic function and any convex separable polynomial is a SOS-convex polynomial. Moreover, the class of SOS-convex polynomials is much larger than the convex quadratic functions and convex separable polynomials. For instance, $f(x)=x_1^8+x_1^2+x_1x_2+x_2^2$ is a SOS-convex polynomial (see [15]) which is nonquadratic and nonseparable.

We now introduce the new notion of conic SOS-convexity of a polynomial map, extending the notion of the scalar SOS-convex polynomial.

Definition 2.1

(Conic SOS-convexity) Let K be a closed and convex cone in ${\mathbb {R}}^m$. Let $G:{\mathbb {R}}^n \rightarrow {\mathbb {R}}^m$ be a polynomial vector-valued mapping, that is, $G(x)=(G_1(x),\ldots ,G_m(x))$ where each $G_i$ is a polynomial on ${\mathbb {R}}^n$. We say $G: {\mathbb {R}}^n \rightarrow {\mathbb {R}}^m$ is a K -SOS-convex polynomial if and only if, for any $\alpha \in [0,1]$ and for any $\lambda \in K^{\oplus }$

$$\begin{aligned} h(x,y)=\langle \lambda , \alpha G(x)+(1-\alpha ) G(y)-G(\alpha x+(1-\alpha )y) \rangle \end{aligned}$$

is a sum-of-squares polynomial on ${\mathbb {R}}^n \times {\mathbb {R}}^n$.

The following equivalent characterization for scalar SOS-convex polynomial from [13] will be useful for us.

Lemma 2.1

[13] Let f be a real polynomial on ${\mathbb {R}}^n$. Then, the following statements are equivalent:

• (a) f is a SOS-convex polynomial on ${\mathbb {R}}^n$;

• (b) $(x,y) \mapsto \frac{1}{2} f(x)+ \frac{1}{2} f(y)-f(\frac{x+y}{2})$ is a sum-of-squares polynomial on ${\mathbb {R}}^n \times {\mathbb {R}}^n$;

• (c) $(x,y) \mapsto f(x)- f(y) -\nabla f(y)(x-y)$ is a sum-of-squares polynomial on ${\mathbb {R}}^n \times {\mathbb {R}}^n$;

• (d) $(x,y) \mapsto y^T\nabla ^2_{xx} f(x) y$ is a sum-of-squares polynomial on ${\mathbb {R}}^n \times {\mathbb {R}}^n$;

It is easy to see that, if $K={\mathbb {R}}_+^m$, then G is ${\mathbb {R}}_+^m$-SOS-convex if and only if $G_i$ is SOS-convex for each $i=1,2,\ldots , m$. In particular, if $m=1$ and $K={\mathbb {R}}_+$, then our notion of conic SOS-convexity collapses to the definition of an SOS-convex polynomial [13].

We now present simple first- and second-order characterizations of conic SOS-convexity.

Lemma 2.2

(First- & second-order characterizations of conic SOS-convexity) Let K be a closed and convex cone in ${\mathbb {R}}^m$; let $G_i:{\mathbb {R}}^n \rightarrow {\mathbb {R}}$, $i=1,\ldots ,m$, be polynomials. Let $G: {\mathbb {R}}^n \rightarrow {\mathbb {R}}^m$ be a polynomial mapping, given by $G(x)=(G_1(x),\ldots ,G_m(x))$. Then, the following statements are equivalent:

• (i) G is a K-SOS-convex polynomial;

• (ii) for any $\lambda \in K^{\oplus }$,

  $$\begin{aligned} h(x,y)=\left\langle \lambda , \frac{1}{2} (G(x)+ G(y))-G\left( \frac{x+y}{2}\right) \right\rangle \end{aligned}$$

  is a sum-of-squares polynomial on ${\mathbb {R}}^n \times {\mathbb {R}}^n$.

• (iii) for any $\lambda \in K^{\oplus }$, $(x,y) \mapsto \langle \lambda , G(x)- G(y) -\nabla G(y)(x-y) \rangle$ is a sum-of-squares polynomial on ${\mathbb {R}}^n \times {\mathbb {R}}^n$;

• (iv) for any $\lambda \in K^{\oplus }$, $(x,y) \mapsto y^T\nabla ^2_{xx}(\langle \lambda , G(x)\rangle )y$ is a sum-of-squares polynomial on ${\mathbb {R}}^n \times {\mathbb {R}}^n$;

• (v) for any $\lambda \in K^{\oplus }$, $(x,y) \mapsto \langle \lambda , (\nabla G(x)-\nabla G(y))(x-y)\rangle$ is a sum-of-squares polynomial on ${\mathbb {R}}^n \times {\mathbb {R}}^n$.

Proof

From the definition, we see that G is a K-SOS-convex polynomial if and only if for any $\alpha \in [0,1]$ and for any $\lambda \in K^{\oplus }$,

$$\begin{aligned} h(x,y)=\langle \lambda , \alpha G(x)+(1-\alpha ) G(y)-G(\alpha x+(1-\alpha )y) \rangle \end{aligned}$$

is a sum-of-squares polynomial on ${\mathbb {R}}^n \times {\mathbb {R}}^n$, which is further equivalent to $x \mapsto \langle \lambda , G(x)\rangle$ is a scalar SOS-convex polynomial for any $\lambda \in K^{\oplus }$. Thus, the equivalences between (i), (ii) (iii) and (iv) follow immediately from Lemma 2.1.

$[\mathrm{(iii)} \Rightarrow \mathrm{(v)}]$ Assume that (iii) holds. Fix an arbitrary $\lambda \in K^{\oplus }$. Then, $h_1(x,y)=\langle \lambda , G(x)- G(y) -\nabla G(y)(x-y) \rangle$ is a sum-of-squares polynomial on ${\mathbb {R}}^n \times {\mathbb {R}}^n$. Then,

$$\begin{aligned}&\langle \lambda , (\nabla G(x)-\nabla G(y))(x-y)\rangle \\&\quad =\, \langle \lambda , G(x)- G(y) -\nabla G(y)(x-y) \rangle +\langle \lambda , G(y)- G(x) -\nabla G(x)(y-x) \rangle \\&\quad =\, h_1(x,y)+h_1(y,x), \end{aligned}$$

is a sum-of-squares polynomial. Thus, (v) follows.

$[\mathrm{(v)} \Rightarrow \mathrm{(iv)}]$ Assume that (v) holds. Fix an arbitrary $\lambda \in K^{\oplus }$. Let d be the degree of G. Then, $h_2(x,y):=\langle \lambda , (\nabla G(x)-\nabla G(y))(x-y) \rangle$ is a sum-of-squares polynomial on ${\mathbb {R}}^n \times {\mathbb {R}}^n$ with degree at most d. It follows that, for any $\epsilon >0$

$$\begin{aligned} \langle \lambda , (\nabla G(x+\epsilon y)-\nabla G(x)) (\epsilon y) \rangle =h_2(x+\epsilon y,x) \end{aligned}$$

is also a sum-of-squares polynomial with degree at most d on ${\mathbb {R}}^n \times {\mathbb {R}}^n$. Since

$$\begin{aligned} y^T\nabla ^2_{xx}\big (\langle \lambda , G(x)\rangle \big )y=\lim _{\epsilon \rightarrow 0} \frac{\langle \lambda , (\nabla G(x+\epsilon y)-\nabla G(x)) (\epsilon y) \rangle }{\epsilon ^2} \end{aligned}$$

is a polynomial with degree at most d, it follows from the closedness of the cone consisting of all sum-of-squares polynomials with degree at most d (see [10]) that the function $(x,y) \mapsto y^T\nabla ^2_{xx}(\langle \lambda , G(x)\rangle )y$ is also a sum-of-squares polynomial with degree at most d. $\square$

In the special case where K is the positive semidefinite cone in the space of symmetric matrices, by exploiting the structure of the positive semidefinite cone, we obtain a simplified characterizations in terms of vectors (instead of semidefinite matrices). This also allows us to compare the known notion of matrix SOS-convexity introduced in [15] with our notions in the following corollary. We note that the equivalence between (ii) and (iii) of the following corollary has been established in [23]. For the sake of convenience of a reader and for completeness, we provide a simple proof here.

Corollary 2.1

(Conic SOS-convexity and matrix SOS-convexity) Let $G: {\mathbb {R}}^n \rightarrow S^q$ be a matrix polynomial, and let $S^q_+$ be the positive semidefinite matrix cone. Then, the following statements are equivalent

• (i) G is a $S^q_+$-SOS-convex polynomial;

• (ii) for any $z \in {\mathbb {R}}^q$, $(x,y) \mapsto y^T\nabla ^2_{xx}(z^TG(x)z)y$ is a sum-of-squares polynomial on ${\mathbb {R}}^n \times {\mathbb {R}}^n$;

• (iii) G is matrix SOS-convex in the sense that, for any $z \in {\mathbb {R}}^m$, there exist $l \in {\mathbb {N}}$ and a matrix polynomial $F_z:{\mathbb {R}}^n \rightarrow {\mathbb {R}}^{l \times n}$ such that, for all $x \in {\mathbb {R}}^n$, $\nabla ^2_{xx}(z^TG(x)z)=F_z(x)^TF_z(x)$.

Proof

As $S^q$ and ${\mathbb {R}}^{q(q+1)/2}$ have the same dimensions, there exists an invertible linear map $L:S^q \rightarrow {\mathbb {R}}^{q(q+1)/2}$ such that

$$\begin{aligned} L(M_1)^T L(M_2)= \mathrm{Tr}(M_1M_2) \quad \hbox { for all }\quad M_1,M_2 \in S^q. \end{aligned}$$

We now identify $S^q$, that is equipped with the trace inner product, as ${\mathbb {R}}^{q(q+1)/2}$ with the usual Euclidean inner product by associating each symmetric matrix M to L(M). Let $K=S^q_+$. Note that any positive semidefinite matrix can be written as sum of rank-one matrices and $\mathrm{Tr}((zz^T) G(x))=z^T(G(x))z$ for any $x \in {\mathbb {R}}^n$ and $z \in {\mathbb {R}}^q$. Then, for any $\Lambda \in S^q_+$, $(x,y) \mapsto y^T\nabla ^2_{xx}(\mathrm{Tr}(\Lambda G(x))y$ is a sum-of-squares polynomial is equivalent to the condition that, for any $z \in {\mathbb {R}}^q$, $(x,y) \mapsto y^T\nabla ^2_{xx} (z^TG(x)z)y$ is a sum-of-squares polynomial. Then, the equivalence of (i) and (ii) follows from the preceding lemma with $K=S^q_+$.

To finish the proof, we only need to show the equivalence of (ii) and (iii). Suppose that (iii) holds. Then, for any $y \in {\mathbb {R}}^n$,

$$\begin{aligned} y^T\nabla ^2_{xx}(z^TG(x)z)y=y^T(F_z(x)^TF_z(x))y=\Vert F_z(x)y\Vert ^2=\sum _{j=1}^l (F_z(x) y)_j^2, \end{aligned}$$

which is a sum-of-squares polynomial. So, (ii) holds. Conversely, if (ii) holds, then for any $z \in {\mathbb {R}}^m$, there exist $l \in {\mathbb {N}}$ and polynomials $f^j_z:{\mathbb {R}}^n \times {\mathbb {R}}^n \rightarrow {\mathbb {R}}$, $j=1,\ldots ,l$, such that

$$\begin{aligned} y^T\nabla ^2_{xx}(z^TG(x)z)y=\sum _{j=1}^l f_z^j(x,y)^2. \end{aligned}$$

As, for each fixed $z \in {\mathbb {R}}^m$ and $x \in {\mathbb {R}}^n$, $y^T\nabla ^2_{xx}(z^TG(x)z)y$ is a homogeneous quadratic function with respect to the variable y, we can assume that $f_z^j(x,y)$ is linear with respect to y for each $j=1,\ldots ,l$. Let

$$\begin{aligned}(f_z^1(x,y),\ldots , f_z^l(x,y))=F_z(x)y,\end{aligned}$$

where $F_z:{\mathbb {R}}^n \rightarrow {\mathbb {R}}^{l \times n}$ is a matrix polynomial. It follows that

$$\begin{aligned}y^T\nabla ^2_{xx}(z^TG(x)z) y=y^T(F_z(x)^TF_z(x))y \quad \hbox { for all }\quad y \in {\mathbb {R}}^n.\end{aligned}$$

This shows that (iii) holds. $\square$

Example 2.1

(Classes of conic SOS-convex polynomials) We now provide some simple examples of conic SOS-convex polynomials.

• (a) Let $K={\mathbb {R}}_+^m$. Then, $K^{\oplus }=K$, and so a polynomial vector-valued mapping $G=(G_1,\ldots ,G_m)$ is a K-SOS-convex polynomial if and only if each $G_i$ is a scalar SOS-convex polynomial.

• (b) Let $K=\{x \in {\mathbb {R}}^m:a_j^Tx \ge 0, j=1,\ldots ,s\}$ be a convex polyhedral cone where $a_j=(a_{j1},\ldots ,a_{jm}) \in {\mathbb {R}}^m$, $j=1,\ldots ,s$. Then, we see that $K^{\oplus }:=\{\sum _{j=1}^s \mu _j a_j: \mu _j \ge 0\}$ and a polynomial vector-valued mapping $G=(G_1,\ldots ,G_m)$ is K-SOS-convex if and only if $h_j(x):=\sum _{i=1}^{m} a_{ji}G_i(x)$ is a scalar SOS-convex polynomial for all $j=1,\ldots ,s$.

  In particular, if each $G_i$ is a quadratic function of the form

  $$\begin{aligned} G_i(x)= \alpha _i+v_i^Tx + x^TA_ix, \end{aligned}$$

  where $\alpha _i \in {\mathbb {R}}$, $v_i \in {\mathbb {R}}^n$ and $A_i \in S^n$, then $G=(G_1,\ldots ,G_m)$ is K-SOS-convex if and only if $\sum _{i=1}^{m} a_{ji}A_i \succeq 0$ for all $j=1,\ldots ,s$.

• (c) Let $K=S^q_+$ be the cone consisting of all the $(q \times q)$ positive semidefinite matrices. Then, by corollary 2.1, $G: {\mathbb {R}}^n \rightarrow S^q$ is a matrix SOS-convex polynomial [21] if and only if G is K-SOS-convex polynomial.

• (d) Let $K=\mathrm{SOC}_m:=\{x \in {\mathbb {R}}^{m}: x_1 \ge \sqrt{\sum _{i=2}^{m}|x_i|^2}\}$ be the second-order cone in ${\mathbb {R}}^m$. Then, the dual cone $K^{\oplus }=K$. Let $G_i(x)$, for $i=1,2,\ldots ,m$, be defined by

  $$\begin{aligned} G_i(x)=\left\{ \begin{array}{lll} \alpha _1+\mathop {\sum }\nolimits _{j=1}^na_{1j}x_j+ \mathop {\sum }\nolimits _{j=1}^n \beta _{j} x_j^d, &{}\quad \hbox { if } &{} i=1,\\ \alpha _i+\mathop {\sum }\nolimits _{j=1}^n a_{ij}x_j, &{}\quad \hbox { if } &{} i \ge 2, \end{array}\right. \end{aligned}$$

  where $\alpha _i,a_{ij} \in {\mathbb {R}}$, $\beta _{j} \ge 0$ and d is an even number. Then it can easily be checked that the map G, defined by $G(x)=(G_1(x),\ldots ,G_m(x))$, is a K-SOS-convex polynomial because for any $\lambda =(\lambda _1,\ldots ,\lambda _m) \in K^{\oplus }=K$, $\lambda _1 \ge 0$ and

  $$\begin{aligned} y^T\nabla ^2_{xx}\big (\langle \lambda , G(x)\rangle \big )y= \lambda _1 d(d-1) \left( \sum _{j=1}^n \beta _j x_j^{d-2}y_j^2\right) , \end{aligned}$$

  which is a sum-of-squares polynomial.

  For instance, the map G, defined by

  $$\begin{aligned} G(x)=(1+2x_1-x_2+x_1^8+3x_2^8,x_1+x_2), \end{aligned}$$

  satisfies the condition above and so is an $\mathrm{SOC}_2$-SOS-convex polynomial.

Remark 2.1

(Conic SOS-convexity vs conic convexity) Let $G_i$ be real polynomials with degree d on ${\mathbb {R}}^n$ and let $G=(G_1,\ldots ,G_m)$.

• In the case where $K={\mathbb {R}}^m_+$, $G=(G_1,\ldots ,G_m)$ is a K-SOS-convex polynomial if and only if each $G_i$ is a scalar SOS-convex polynomial. So, the recent characterization of scalar SOS-convexity [13] implies that ${\mathbb {R}}^m_+$-SOS-convexity is equivalent to ${\mathbb {R}}^m_+$-convexity if and only if either one of the following holds (1) $n=1$; (2) $d=2$; (3) $(n,d)=(2,4)$.

• Let $m=q(q+1)/2$ and identify $S^q$ with ${\mathbb {R}}^{q(q+1)/2}$. We now consider the case where $K=S^q_+$. Note that any bivariate quartic nonnegative polynomial is sum-of-squares, and G is a $S^q_+$-SOS-convex polynomial if and only if for any $z \in {\mathbb {R}}^q$, $(x,y) \mapsto y^T\nabla ^2_{xx}(z^TG(x)z)y$ is a sum-of-squares polynomial on ${\mathbb {R}}^n \times {\mathbb {R}}^n$. This shows that, if $(n,d)=(1,2)$, G is $S^q_+$-SOS-convex if and only if G is $S^q_+$-convex.

In the case where the cone K has specific structure, we obtain new tractable class for conic SOS-convexity. To do this, let $\circ$ be a bilinear operation from ${\mathbb {R}}^m \times {\mathbb {R}}^m \rightarrow {\mathbb {R}}^m$ satisfying $a \circ b = b \circ a \hbox { for all } a,b \in {\mathbb {R}}^q$. Let K be a closed and convex cone which is self-dual in the sense that $K^{\oplus }=K$. We say K is generated by the bilinear operation $\circ$ if and only if

$$\begin{aligned} K=\{a \circ a : a \in {\mathbb {R}}^m\}. \end{aligned}$$

We note that many important and widely used closed and convex cones can be generated in this way. For example,

• The nonnegative orthant $K={\mathbb {R}}^m_+=\{a \circ a: a \in {\mathbb {R}}^m\},$ where the bilinear operation is defined by $a \circ b= (a_1b_1,\ldots ,a_mb_m)^T$ for all $a,b \in {\mathbb {R}}^m$.

• In the case where K is the second-order cone, that is,

  $$\begin{aligned}K=\{(r,z) \in {\mathbb {R}} \times {\mathbb {R}}^{m-1} : r \ge \Vert (z_1,\ldots ,z_{m-1})\Vert _2\},\end{aligned}$$

  we see that $K =\{a \circ a: a \in {\mathbb {R}}^m\}$ where bilinear operation is defined by $(\alpha ,u) \circ (\beta ,v)=(\alpha \beta +u^Tv, \alpha v+ \beta u) \in {\mathbb {R}} \times {\mathbb {R}}^{m-1}$ for all $(\alpha ,u)$ and $(\beta ,v) \in {\mathbb {R}} \times {\mathbb {R}}^{m-1}$.

• As $S^q$ and ${\mathbb {R}}^{q(q+1)/2}$ have the same dimensions, there exists an invertible linear map $L:S^q \rightarrow {\mathbb {R}}^{q(q+1)/2}$ such that

  $$\begin{aligned} L(M_1)^T L(M_2)= \mathrm{Tr}(M_1M_2) \hbox { for all } M_1,M_2 \in S^q. \end{aligned}$$

  We now identify $S^q$, that is equipped with the trace inner product, as ${\mathbb {R}}^{q(q+1)/2}$ with the usual Euclidean inner product by associating each symmetric matrix M to L(M). Then, the cone of positive semidefinite matrix satisfies $S^q_+ = \{a \circ a: a \in {\mathbb {R}}^{q(q+1)/2}\}$ where bilinear operation is defined by $a \circ b= \frac{1}{2}(L^{-1}(a) L^{-1}(b)+L^{-1}(b) L^{-1}(a))$ for all $a,b \in {\mathbb {R}}^{q(q+1)/2}$.

Definition 2.2

(SDP tractable class of conic SOS-convex mappings: uniformly K -SOS-convex) Let K be a closed and convex self-dual cone which is generated by the bilinear operation $\circ$, that is, $K=\{a \circ a : a \in {\mathbb {R}}^m\}$. We say G is uniformly K-SOS-convex whenever

$$\begin{aligned} (x,y,a) \mapsto y^T\nabla ^2_{xx}\big (\langle a \circ a, G(x)\rangle \big )y \end{aligned}$$

is a sum-of-squares polynomial on ${\mathbb {R}}^n \times {\mathbb {R}}^n \times {\mathbb {R}}^m$.

Now, it follows from the definition that, uniformly K-SOS-convex mappings must be K-SOS-convex for any closed and convex self-dual cone K generated by a bilinear operation $\circ$. Moreover, an important feature of the uniformly K-SOS-convexity is that checking whether a mapping G is uniformly K-SOS-convex or not is equivalent to solving a semidefinite programming problem.

Example 2.2

(Classes of uniform conic SOS-convex polynomials)

• Let $K={\mathbb {R}}^m_+$. Then, any K-SOS-convex polynomial is uniformly K-SOS-convex. To see this, note that $K={\mathbb {R}}^m_+=\{a \circ a: a \in {\mathbb {R}}^m\}$ where bilinear operation is defined by $a \circ b= (a_1b_1,\ldots ,a_mb_m)^T$ for all $a,b \in {\mathbb {R}}^m$, and any polynomial mapping $G=(G_1,\ldots ,G_m)$ is ${\mathbb {R}}^m_+$-SOS-convex if and only if each $G_i$, $i=1,\ldots ,m$, is a scalar SOS-convex polynomial. Then,

  $$\begin{aligned} y^T\nabla ^2_{xx}\big (\langle a \circ a, G(x)\rangle \big )y = \sum _{i=1}^m a_i^2 \big (y^T \nabla ^2 G_i(x) y \big ) \end{aligned}$$

  is a sum-of-squares polynomial.

• Let $K=S^q_+$ be the cone consisting of all the $(q \times q)$ positive semidefinite matrices. By identifying $S^q$ as ${\mathbb {R}}^{q(q+1)/2}$, we define $G:{\mathbb {R}}^n \rightarrow S^q$ as

  $$\begin{aligned} G(x)= A_0+\sum _{i=1}^n x_i A_i + \sum _{l=1}^p f_l(x) B_l, \end{aligned}$$

  where for each $l=1,\ldots ,p$, $f_l(x)$ is an SOS-convex scalar polynomial, $A_0,A_1,\ldots ,A_n \in S^q$ and $B_l \succeq 0$. Recall that the positive semidefinite cone can be written as $S^q_+ = \{a \circ a: a \in {\mathbb {R}}^{q(q+1)/2}\}$ where bilinear operation is defined by $a \circ b= \frac{1}{2}(L^{-1}(a) L^{-1}(b)+L^{-1}(b) L^{-1}(a))$ for all $a,b \in {\mathbb {R}}^{q(q+1)/2}$. Then, G is a uniform K-SOS-convex polynomial. To see this, we note that, for any $a \in {\mathbb {R}}^{q(q+1)/2}$,

  $$\begin{aligned} y^T\nabla ^2_{xx}\big (\langle a \circ a, G(x)\rangle \big )y=\sum _{l=1}^p \mathrm{Tr}([L^{-1}(a)]^2 B_l) y^T \nabla ^2_{xx} f_l(x) y. \end{aligned}$$

  As each $f_l$ is an SOS-convex scalar polynomial, $(x,y) \mapsto y^T\nabla ^2_{xx} f_l(x)y$ is a sum-of-squares polynomial. Moreover, note that $B_l \succeq 0$ and $[L^{-1}(a)]^2 \succeq 0$. So, $a \mapsto \mathrm{Tr}([L^{-1}(a)]^2 B_l)$ is a nonnegative quadratic function and so is also a sum-of-squares polynomial. This implies that

  $$\begin{aligned} (x,y,a) \mapsto y^T\nabla ^2_{xx}\big (\langle a \circ a, G(x)\rangle \big )y \end{aligned}$$

  is also a sum-of-squares polynomial. Thus, G is a uniform K-SOS-convex polynomial. As a simple example, consider the map G, defined by

  $$\begin{aligned} G(x)= & {} \left( \begin{array}{cc} 1+x_2+x_1^8+(x_1+x_2)^4 &{}\quad -1+x_1+x_2 \\ -1+x_1+x_2 &{}\quad x_2+x_1^8+(x_1+x_2)^4 \end{array}\right) \\= & {} \left( \begin{array}{cc} 1 &{}\quad -1 \\ -1 &{}\quad 0 \end{array}\right) + x_1 \left( \begin{array}{cc} 0 &{}\quad 1 \\ 1 &{}\quad 0 \end{array}\right) +x_2 \left( \begin{array}{cc} 1 &{}\quad 1 \\ 1 &{}\quad 1 \end{array}\right) + (x_1^8+(x_1+x_2)^4)\left( \begin{array}{cc} 1 &{}\quad 0 \\ 0 &{}\quad 1 \end{array}\right) . \end{aligned}$$

  Then, G satisfies the condition above and so is a uniform $S^2_+$-SOS-convex polynomial. $\square$

2.1 Solvability of Conic SOS-Convex Systems

We now establish characterizations of positivity or nonnegativity of SOS-convex polynomials over sets described by conic SOS-convex polynomial systems. To do this, for $\lambda \in {\mathbb {R}}^{m}$ and $G: {\mathbb {R}}^n \rightarrow {\mathbb {R}}^m$, we define the function $\langle \lambda , G\rangle$ by

$$\begin{aligned} \langle \lambda , G\rangle (x):=\langle \lambda , G(x) \rangle \hbox { for all } x \in {\mathbb {R}}^n. \end{aligned}$$

Moreover, the following existence result for solutions of a convex polynomial optimization problem will also be useful for our later analysis.

Lemma 2.3

[24, Theorem 3] Let $f_0,f_1,\ldots ,f_m$ be convex polynomials on ${\mathbb {R}}^n$. Suppose that $\displaystyle \inf _{x\in C}f_0(x)>-\infty$ where $C=\left\{ x \in {\mathbb {R}}^n : f_i(x) \le 0, i=1,\ldots ,m\right\}$. Then, $\displaystyle \mathrm{argmin}_{x\in C}f_0(x) \ne \emptyset .$

Proposition 2.1

(Strict solvability) Let K be a closed and convex cone in ${\mathbb {R}}^m$ with nonempty interior. Let $G: {\mathbb {R}}^n \rightarrow {\mathbb {R}}^m$ be a K-SOS-convex polynomial. Then, exactly one of the following statements holds:

• (i) there exists $x_0 \in {\mathbb {R}}^n$ such that $G(x_0) \in -\mathrm{int} K$;

• (ii) there exists $\lambda \in K^{\oplus } \backslash \{0\}$ such that $\langle \lambda , G\rangle \in \varSigma ^2[x]$.

Proof

$[\mathrm{(ii)} \Rightarrow \mathrm{Not \ }\mathrm{(i)}]$ Suppose (ii) holds. Then,

$$\begin{aligned} \langle \lambda , G\rangle \ge 0. \end{aligned}$$

(1)

By construction and by the definition of $K^{\oplus }$, both systems (i) and (1) cannot have solutions simultaneously.

$[\mathrm{Not }\mathrm{(i)} \Rightarrow \mathrm{(ii)}]$ Suppose that (i) fails. Then, $0 \notin \mathrm{int} \big (\{G(x): x \in {\mathbb {R}}^n\}+K\big )$, where $\{G(x): x \in {\mathbb {R}}^n\}+K$ is a convex set. Now, it follows by a convex separation theorem that $\lambda \in K^{\oplus } \backslash \{0\}$ and $\langle \lambda , G(x) \rangle \ge 0 \hbox { for all } x \in {\mathbb {R}}^n.$ As G is a K-SOS-convex polynomial, we see that $H(x):=\langle \lambda , G(x)\rangle$ is a convex polynomial. From Lemma 2.3, we obtain that $\mathrm{argmin}_{x \in {\mathbb {R}}^n}\{H(x)\} \ne \emptyset$. Now, let $\displaystyle x^* \in \mathrm{argmin}_{x \in {\mathbb {R}}^n}\{H(x)\}$. Then, $H(x^*) \ge 0$ and $\nabla H(x^*)=0$. This implies that for any $h \in {\mathbb {R}}^n$, $\langle \lambda , \nabla G(x^*) h\rangle =0$. Moreover, from Lemma 2.2, we see that $h(x,y):=\langle \lambda , G(x)- G(y) -\nabla G(y)(x-y) \rangle$ is a sum-of-squares polynomial on ${\mathbb {R}}^n \times {\mathbb {R}}^n$. It follows that

$$\begin{aligned} h(x,x^*)=\langle \lambda , G(x)- G(x^*) -\nabla G(x^*)(x-x^*) \rangle = \langle \lambda , G(x) \rangle - H(x^*) \end{aligned}$$

is an SOS-convex polynomial. It follows that $\langle \lambda , G(x) \rangle = h(x,x^*)+H(x^*)$ is also a sum-of-squares polynomial. $\square$

We now provide a characterization of positivity of an SOS-convex polynomial over a set described by conic SOS-convex systems, under the condition that the set

$$\begin{aligned} \varOmega:= & {} (f, G)({\mathbb {R}}^n)+({\mathbb {R}}_+ \times K)\\= & {} \{(s,y) \in {\mathbb {R}} \times {\mathbb {R}}^m: \exists x \in {\mathbb {R}}^n, \; s \ge f(x) , y \in G(x)+K \}, \end{aligned}$$

is closed. It is easy to check that $\varOmega$ is a closed set if; for instance, f is coercive in the sense that $\lim _{\Vert x\Vert \rightarrow \infty } f(x)=+\infty$. The set of the form $\varOmega$ has played an important role in the study of duality in convex optimization [25].

Theorem 2.1

(Positivstellensatz for conic SOS-convex systems) Let K be a closed and convex cone in ${\mathbb {R}}^m$. Let f be an SOS-convex real polynomial and let G be a K-SOS-convex polynomial. Let $\{x: G(x) \in -K\} \ne \emptyset$. If the convex set $(f, G)({\mathbb {R}}^n)+({\mathbb {R}}_+ \times K)$ is closed, then the following statements are equivalent

• (i) $G(x) \in -K \ \Rightarrow \ f(x) > 0$;

• (ii) $(\exists \ \lambda \in K^{\oplus }, \ \delta _0 > 0)$ $(\exists \sigma _0\in \varSigma ^2[x])$ $(\forall x\in {\mathbb {R}}^n)$ $f(x)+ \langle \lambda , G(x) \rangle =\delta _0 +\sigma _0(x)$.

Proof

$[\mathrm{(ii)}\Rightarrow \mathrm{(i)}]$ Suppose that there exist a sum-of-squares polynomial $\sigma _0$, $\lambda \in K^{\oplus }$ and $\delta _0>0$ such that $f=\delta _0+\sigma _0 - \langle \lambda , G\rangle .$ Then, for each x with $G(x) \in -K$, $f(x)=\delta _0+\sigma _0(x)- \langle \lambda , G(x)\rangle \ge \delta _0>0$.

$[\mathrm{(i)} \Rightarrow \mathrm{(ii)}]$ Suppose that f is positive on $F:=\{x: G(x) \in -K\}$. Then, we see that

$$\begin{aligned} 0_{m+1} \notin \varOmega :=(f, G)({\mathbb {R}}^n)+({\mathbb {R}}_+ \times K). \end{aligned}$$

Thus, strict separation theorem (cf. [26]) shows that there exist $\alpha \in {\mathbb {R}}$, $\epsilon >0$ and $(\mu _0,\mu _1,\ldots ,\mu _m) \ne (0,0,\ldots ,0)$ such that, for all $y= (y_0,y_1,\ldots ,y_m) \in \varOmega$,

$$\begin{aligned} 0 \le \alpha < \alpha +\epsilon \le \langle (y_0,y_1,\ldots ,y_m), (\mu _0,\mu _1,\ldots ,\mu _m)\rangle \ . \end{aligned}$$

As $\varOmega +\big ({\mathbb {R}}_+ \times K\big ) \subseteq \varOmega$, we see that $(r,\mu ) \in \big ({\mathbb {R}}_+ \times K^{\oplus }\big )\backslash \{0\}$. Since, for each $x \in {\mathbb {R}}^n$, $(f(x),G(x)) \in \varOmega$, it follows that

$$\begin{aligned} r f(x)+ \langle \mu , G(x)\rangle \ge \alpha +\epsilon \ge \epsilon , \quad \hbox { for all }\quad x \in {\mathbb {R}}^n. \end{aligned}$$

As $F \ne \emptyset$, we see that $r \ne 0$, and so $r>0$. So, we obtain that

$$\begin{aligned} f(x)+ \langle \lambda , G(x)\rangle \ge \delta _0, \quad \hbox { for all }\quad x \in {\mathbb {R}}^n, \end{aligned}$$

where $\lambda =\frac{\mu }{r} \in K^{\oplus }$ and $\delta _0=\frac{\epsilon }{r}>0$. This implies that

$$\begin{aligned} r:=\inf _{x \in {\mathbb {R}}^n}\{f(x)+ \langle \lambda , G(x)\rangle \} \ge \delta _0. \end{aligned}$$

Now, by Lemma 2.3, we can find $x^*$ such that $f(x^*)+ \langle \lambda , G(x^*)\rangle =r$. Let

$$\begin{aligned} h(x):= f(x)+ \langle \lambda , G(x)\rangle -r, \quad \hbox { for each }\quad x\in {\mathbb {R}}^n. \end{aligned}$$

Then h is a SOS-convex polynomial with $h(x^*)=0$ and $\nabla h(x^*)=0$. The SOS-convexity of f and K-SOS-convexity of G together with Lemma 2.2 give us that $f(x) - f(x^*) - \nabla f(x^*)(x - x^*) = \theta _0(x)$ for some sum-of-squares polynomial $\theta _0$ and $\langle \lambda , G(x) - G(x^*) - \nabla G(x^*)(x - x^*) \rangle = \theta _i(x)$ for some sum-of-squares polynomial $\theta _i$. So, we see that, for all $x \in {\mathbb {R}}^n$

$$\begin{aligned} f(x)+ \langle \lambda , G(x)\rangle - (f(x^*)+ \langle \lambda , G(x^*)\rangle )=\theta _0(x)+\sum _{i=1}^m\lambda _i\theta _i(x). \end{aligned}$$

As $f(x^*)+ \langle \lambda , G(x^*)\rangle =h(x^*)+r=r$, we see that

$$\begin{aligned} h(x)=f(x)+ \langle \lambda , G(x)\rangle -r=\theta _0(x)+\sum _{i=1}^m\lambda _i\theta _i(x) \end{aligned}$$

which is a sum-of-squares polynomial. Hence,

$$\begin{aligned} f(x)+ \langle \lambda , G(x)\rangle =h(x)+r=(h(x)+r-\delta _0)+\delta _0= \sigma _0(x)+\delta _0, \end{aligned}$$

where $r - \delta _0 >0$ and $\sigma _0(x):=h(x)+(r-\delta _0)$ is a sum-of-squares polynomial. Thus, the conclusion follows. $\square$

In passing, we note that the sum-of-squares representation (ii) of Theorem 2.1 can, in many cases, be numerically checked by solving a related conic, such as a semidefinite linear program. Now, as a consequence, we obtain a characterization for nonnegativity of an SOS-convex polynomial over a set described by a conic SOS-convex system.

Corollary 2.2

(Nonnegativity characterization) Let f be an SOS-convex scalar polynomial. Let K be a closed and convex cone, and let $G: {\mathbb {R}}^n \rightarrow {\mathbb {R}}^m$ be a K-SOS-convex polynomial with $\{x: G(x) \in -K\} \ne \emptyset$. If the convex set $(f, G)({\mathbb {R}}^n)+({\mathbb {R}}_+\times K)$ is closed, then the following statements are equivalent:

• (i) $G(x) \in -K \ \Rightarrow \ f(x) \ge 0$;

• (ii) $(\forall \epsilon > 0)$ $(\exists \ \lambda \in K^{\oplus })$ $(\exists \sigma _0\in \varSigma ^2[x])$ $(\forall x\in {\mathbb {R}}^n)$ $f(x)+ \langle \lambda , G(x) \rangle + \epsilon =\sigma _0(x)$.

Proof

$[\mathrm{(ii)}\Rightarrow \mathrm{(i)}]$. Suppose that for each $\epsilon >0$ there exist a sum-of-squares polynomial $\sigma _0$, $\lambda \in K^{\oplus }$ such that $f+\epsilon =\sigma _0- \langle \lambda , G \rangle$. Let x be such that $G(x)\in -K$. Then, $f(x)+\epsilon =\sigma _0(x)- \langle \lambda , G(x) \rangle \ge 0$. Letting $\epsilon \rightarrow 0$, we see that $f(x) \ge 0$ for all x with $G(x) \in -K$.

$[\mathrm{(i)}\Rightarrow \mathrm{(ii)}]$ Assume that (i) holds. Then, for any $\epsilon >0$, $f+\epsilon$ is positive on F. So, Theorem 2.1 implies that there exist a sum-of-square polynomial $\sigma _0$, $\lambda \in K^{\oplus }$ and $\delta _0>0$ such that, for all $x \in {\mathbb {R}}^n$, $f(x)+ \langle \lambda , G(x)\rangle +\epsilon =\delta _0+\sigma _0$. Hence, the conclusion follows. $\square$

3 Exact Conic Programming Relaxations

In this section, we present exact conic relaxations for a class of conic convex nonlinear programming problems. We consider the problem

$$\begin{aligned} \inf _{x \in {\mathbb {R}}^n}\{f(x): G(x) \in -K\}, \end{aligned}$$

(P)

where f is a SOS-convex polynomial with degree $d_0$ on ${\mathbb {R}}^n$ and $G:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^m$ is a K-SOS-convex polynomial with degree $d_1$. Let d be the smallest even number such that $d \ge \max \{d_0,d_1\}$. We assume throughout that the feasible set $F:=\{x: G(x) \in -K\} \ne \emptyset$.

It is easy to see that the program (P) is equivalent to the program

$$\begin{aligned} \displaystyle \sup _{\mu \in {\mathbb {R}}}\{\mu \ : \ f(x) - \mu \ge 0, \; \forall x\in F\}. \end{aligned}$$

The conic programming relaxation of (P) based on certificate of nonnegativity on F (see Corollary 2.2) is given by

$$\begin{aligned} \displaystyle \sup _{\mu \in {\mathbb {R}}, \lambda \in {\mathbb {R}}^m} \{\mu : f + \langle \lambda , G\rangle -\mu \in \varSigma _d^2[x], \; \lambda \in K^{\oplus }\}, \end{aligned}$$

(RP)

where $\varSigma _d^2[x]$ denotes the sum-of-squares polynomial with degree no larger than d. Note that the sum-of-squares condition, $f + \langle \lambda , G \rangle -\mu \in \varSigma _d^2[x]$, can equivalently be reformulated as a linear matrix inequality [10]. In particular, if $K=S_+^m$ is the positive semidefinite matrix cone (or more generally, if K is a linear matrix inequality representable closed and convex cone), then (RP) can equivalently be written as a semidefinite linear programming problem. Moreover, if K is the p-order cone, then (RP) can also be equivalently reformulated as a tractable conic involving semidefinite constraints and norm constraints.

Theorem 3.1

(Exact conic programming relaxation) For problem (P), let f be a SOS-convex polynomial with degree $d_0$ and let G be a K-SOS-convex polynomial with degree $d_1$. Let $F:=\{x: G(x) \in -K\} \ne \emptyset$. If the set $(f, G)({\mathbb {R}}^n)+({\mathbb {R}}_+\times K)$ is closed, then

$$\begin{aligned} \inf (P)=\displaystyle \sup _{\mu \in {\mathbb {R}}, \lambda \in {\mathbb {R}}^m} \{\mu : f + \langle \lambda , G \rangle -\mu \in \varSigma _d^2[x], \; \lambda \in K^{\oplus }\}, \end{aligned}$$

where d is the smallest even number such that $d \ge \max \{d_0,d_1\}$.

Proof

Clearly, for any $x \in F$, $\mu \in {\mathbb {R}}$ and $\lambda \in K^{\oplus }$, with $f + \langle \lambda , G \rangle -\mu \in \varSigma _d^2[x]$,

$$\begin{aligned} f(x)-\mu \ge f(x)+ \langle \lambda , G(x) \rangle -\mu \ge 0. \end{aligned}$$

So, $\inf _{x \in F}f(x) \ge \sup _{\mu \in {\mathbb {R}}, \lambda \in K^{\oplus }} \{\mu : f + \langle \lambda , G \rangle -\mu \in \varSigma _d^2[x]\}.$

To see the reverse inequality, we assume without loss of generality that $\inf _{x \in F}f(x)>-\infty$; otherwise, the conclusion trivially holds. As $F \ne \emptyset$, we have $r:=\inf _{x \in F}f(x) \in {\mathbb {R}}$. Then, for any $\epsilon >0$, $f-r+\epsilon$ is positive on F. So, our Theorem 3.1 implies that there exists a sum-of-squares polynomial $\sigma _0$, $\lambda \in K^{\oplus }$ and $\delta _0>0$ such that

$$\begin{aligned} f + \langle \lambda , G \rangle -(r-\epsilon )=\delta _0+\sigma _0 \end{aligned}$$

is a sum-of-squares polynomial. Note that any sum-of-squares polynomial must have even degree, f is of degree $d_0$ and G is of degree $d_1$. It follows that $f + \langle \lambda , G \rangle -(r-\epsilon )$ is of degree at most d. This shows that, for any $\epsilon >0$,

$$\begin{aligned} \sup _{\mu \in {\mathbb {R}}, \lambda \in K^{\oplus }} \{\mu : f + \langle \lambda , G \rangle -\mu \in \varSigma _d^2[x]\} \ge r-\epsilon . \end{aligned}$$

Letting $\epsilon \rightarrow 0$, we see that $\sup _{\mu \in {\mathbb {R}}, \lambda \in K^{\oplus }} \{\mu : f + \langle \lambda , G \rangle -\mu \in \varSigma _d^2[x]\} \ge r$ and so the conclusion follows. $\square$

As an easy consequence, we obtain the following exact SDP relaxation for SOS-convex polynomial optimization problem over a SOS-convex polynomial matrix inequality problem under the closedness condition.

Corollary 3.1

For problem (P), let f be a SOS-convex polynomial with degree $d_0$ and let $G:{\mathbb {R}}^n \rightarrow S^q$ be a matrix SOS-convex polynomial with degree $d_1$. Let $F:=\{x: G(x) \in -S^q_+\} \ne \emptyset$. If $(f, G)({\mathbb {R}}^n)+({\mathbb {R}}_+\times S^q_+)$ is closed, then

$$\begin{aligned} \inf (P)=\displaystyle \sup _{\mu \in {\mathbb {R}}, \lambda \in S^q} \{\mu : f + \mathrm{Tr}(\lambda G)-\mu \in \varSigma _d^2[x], \; \lambda \in S^q_+\}, \end{aligned}$$

where, for $\lambda \in S^q$, $\mathrm{Tr}(\lambda G)(x):=\mathrm{Tr}(\lambda G(x))$ for all $x \in {\mathbb {R}}^n$ and d is the smallest even number such that $d \ge \max \{d_0,d_1\}$.

Proof

By identifying $S^q$ as ${\mathbb {R}}^{q(q+1)/2}$, Corollary 2.1 implies that G is indeed an $S^q_+$-SOS-convex polynomial. Thus the conclusion follows from Theorem 3.1 with $K=S^q_+$. $\square$

Now, we consider a conic SOS-convex polynomial optimization with quadratic constraints involving the p-order cone:

$$\begin{aligned} \min _{x \in {\mathbb {R}}^n} \{f(x): G(x) \in -\mathrm{POC}_m\}, \end{aligned}$$

(PP)

where f is an SOS-convex polynomial and $G=(G_1,\ldots ,G_m)$ where each $G_i$ is a quadratic function given by

$$\begin{aligned} G_i(x)= \alpha _i+a_i^Tx + x^TA_ix, \end{aligned}$$

(2)

with $\alpha _i \in {\mathbb {R}}$, $a_i \in {\mathbb {R}}^n$ and $A_{i} \in S^n$, $i=1,\ldots ,m$ and $\mathrm{POC}_m$ is the p-order cone given by $\mathrm{POC}_m=\{(x_1,\ldots ,x_m) \in {\mathbb {R}}^m:x_1 \ge \root p \of {\sum _{i=2}^m |x_i|^p}\}$. We now show that problem (PP) admits an exact conic relaxation under easily verifiable conditions.

Recall that, for a symmetric matrix A, the minimum eigenvalue of A is denoted by $\lambda _{\min }(A)$ and $\Vert A\Vert _2=\sup \{\Vert Ay\Vert _2: \Vert y\Vert _2=1\}=\sqrt{\lambda _{\max }(A^TA)}$ is known as the matrix 2-norm of A.

Corollary 3.2

(Exact relaxation with quadratic constraints and p-order cone) For problem (PP), let f be a SOS-convex polynomial with degree $d_0$ and let $G=(G_1,\ldots ,G_m)$ be a quadratic vector-valued mapping where each $G_i$ is given as in (2). Let $F:=\{x: G(x) \in -\mathrm{POC}_m\} \ne \emptyset$. If $\nabla ^2_{xx} f(x_0) \succ 0$ for some $x_0 \in {\mathbb {R}}^n$ and

$$\begin{aligned} \lambda _{\min }(A_1) \ge \root p \of {\sum _{i=2}^m \Vert A_i\Vert _2^p}, \end{aligned}$$

(3)

then

$$\begin{aligned} \inf (PP)=\displaystyle \sup _{\mu \in {\mathbb {R}}, (\lambda _1,\ldots ,\lambda _m)\in {\mathbb {R}}^m} \left\{ \mu : f + \langle \lambda , G \rangle -\mu \in \varSigma _d^2[x], \ \lambda _1 \ge \root p^* \of {\sum _{i=2}^m|\lambda _i|^{p^*}}\right\} , \end{aligned}$$

where $p^*$ is a real number satisfies $\frac{1}{p}+\frac{1}{p^*}=1$ and d is the smallest even number such that $d \ge \max \{d_0,2\}$.

Proof

Let $K=\mathrm{POC}_m$. Then, the dual cone $K^{\oplus }$ is the $p^*$-order cone where $p^*$ satisfies $\frac{1}{p}+\frac{1}{p^*}=1$. Let $G(x)=(G_1(x),\ldots ,G_m(x))$ be a quadratic vector function where each $G_i$ is defined as in (2).

We first verify that G is a ${POC}_m$-SOS-convex polynomial. To see this, fix any $\lambda =(\lambda _1,\ldots ,\lambda _m) \in K^{\oplus }$. Then, $\lambda _1 \ge \root p^* \of {\sum _{i=2}^m |\lambda _i|^{p^*}}$ and

$$\begin{aligned} y^T\nabla ^2_{xx}\big (\langle \lambda , G(x)\rangle \big )y= & {} \left( \sum _{i=1}^m \lambda _i y^TA_i y \right) \end{aligned}$$

which is a quadratic function of y only. As any nonnegative quadratic function is a sum-of-squares polynomial, to show $(x,y) \mapsto y^T\nabla ^2_{xx}\big (\langle \lambda , G(x)\rangle \big )y$ is a sum-of-squares polynomial, we only need to prove that $\sum _{i=1}^m \lambda _i y^TA_i y \ge 0$ for all $y \in {\mathbb {R}}^n$. To verify this, note from (3) that, for all $y \in {\mathbb {R}}^n$,

$$\begin{aligned} y^TA_1y \ge \lambda _{\min }(A_1) \Vert y\Vert ^2 \ge \root p \of {\left( \sum _{i=2}^m \Vert A_i\Vert _2 \, \Vert y\Vert _2^2\right) ^p} \ge \root p \of {\sum _{i=2}^m |y^TA_i y| ^p}. \end{aligned}$$

It now follows that

$$\begin{aligned} \sum _{i=1}^m \lambda _i y^TA_i y= & {} \lambda _1 y^TA_1 y +\sum _{i=2}^m \lambda _i y^TA_iy \\\ge & {} \lambda _1 y^TA_1 y - \root p^* \of {\sum _{i=2}^m |\lambda _i|^{p^*}} \ \root p \of {\sum _{i=2}^m |y^TA_iy|^p} \\\ge & {} \left( \lambda _1-\root p^* \of {\sum _{i=2}^m |\lambda _i|^{p^*}}\right) y^TA_1y \ge 0, \end{aligned}$$

where the first inequality follows by the Hölder inequality and the last inequality follows from $A_1 \succeq 0$ [thanks to (3)] and $\lambda _1 \ge \root p^* \of {\sum _{i=2}^m |\lambda _i|^{p^*}}$. Thus, G is a $\mathrm{POC}_m$-SOS-convex polynomial.

Finally, as f is a convex polynomial with $\nabla ^2_{xx} f(x_0) \succ 0$ for some $x_0 \in {\mathbb {R}}^n$, [12, Lemma 3.1] implies that f is coercive. This shows that $(f,G)({\mathbb {R}}^n)+ ({\mathbb {R}}_+\times K)$ is closed. Then, the conclusion follows from Theorem 3.1 with $K=\mathrm{POC}_m$. $\square$

Corollary 3.3

(Qualification-free exact SDP relaxation and polyhedral cones K) For the problem (P), let $K=\{x \in {\mathbb {R}}^m: a_j^Tx \ge 0, j=1,\ldots ,s\}$ be the polyhedral cone where $a_j \in {\mathbb {R}}^m$. Let f be a SOS-convex polynomial with degree $d_0$ and let $G=(G_1,\ldots ,G_m)$ be a K-SOS-convex polynomials with degree $d_1$. Let $F=\{x: G(x) \in -K\} \ne \emptyset$. Then,

$$\begin{aligned} \inf _{x \in F}f(x)=\displaystyle \sup _{\mu \in {\mathbb {R}}, \lambda \in {\mathbb {R}}^m, \mu _j \in {\mathbb {R}}} \left\{ \mu : f + \sum _{i=1}^m \sum _{j=1}^s\mu _ja_{ji} G_i -\mu \in \varSigma _d^2[x], \; \mu _j \ge 0\right\} , \end{aligned}$$

where $a_j=(a_{j1},\ldots ,a_{jm})^T \in {\mathbb {R}}^{m}$ and d is the smallest even number larger than $\max \{d_0,d_1\}$.

Proof

Let $G(x)=(G_1(x), \dots , G_m(x))$ and denote $a_j=\big (a_{j1},\ldots ,a_{jm}\big ) \in {\mathbb {R}}^m$, $j=1,\ldots ,s$. Then, the set $\varOmega :=(f, G)({\mathbb {R}}^n)+({\mathbb {R}}_+\times K)$ becomes

$$\begin{aligned} \varOmega= & {} \left\{ (y_0,y_1,\ldots ,y_m): \exists \, x \in {\mathbb {R}}^n\quad \hbox {s.t.}\quad f(x) \le y_0, \right. \\&\left. \sum _{i=1}^ma_{ji}(G_i(x)-y_i) \le 0, j=1,\ldots ,s\right\} . \end{aligned}$$

We now show that the set $\varOmega$ is closed. To see this, take any $(y_0^k,y_1^k,\ldots ,y_m^k) \in \varOmega$ be such that $(y_0^k,y_1^k,\ldots ,y_m^k) \rightarrow (y_0,y_1,\ldots ,y_m).$ By the definition of $\varOmega$, for each k, there exists $x^k \in {\mathbb {R}}^n$ such that $f(x^k) \le y_0^k$ and $\sum \nolimits _{i=1}^ma_{ji}(G_i(x^k)-y_i) \le 0$, $j=1,\ldots ,s$. Now, consider the optimization problem

For each $j=1,\ldots ,s$, let $h_j(x,z):=\sum _{i=1}^ma_{ji}(G_i(x)-z_i)$. Note that, for each $j=1,\ldots ,s$, $a_j \in K^{\oplus }$. As G is a K-SOS-convex polynomial, it follows that $\sum _{i=1}^m a_{ji} G_i(x)=\langle a_j, G(x) \rangle$ is an SOS-convex polynomial. This implies that each $h_j$ is an SOS-convex polynomial, and so ($\mathrm{P}_0$) is a convex polynomial optimization problem and

$$\begin{aligned} 0 \le \inf (P_0) \le \sum _{i=0}^m (y_i^k-y_i)^2 \rightarrow 0. \end{aligned}$$

So, $\inf (P_0)=0$. Moreover, Lemma 2.3 implies that $\inf (P_0)$ is attained, and so there exists $x^* \in {\mathbb {R}}^n$ such that and $f_0(x^*) \le y_0$ and $\sum _{i=1}^ma_{ji}(G_i(x^*)-y_i)\le 0$, $j=1,\ldots ,s$. So, $(y_0,y_1,\ldots ,y_m) \in \varOmega .$ Therefore, $\varOmega$ is closed.

Then, Theorem 3.1 gives us that

$$\begin{aligned} \inf (P)=\displaystyle \sup _{\mu \in {\mathbb {R}}, \lambda \in {\mathbb {R}}^m} \{\mu : f + \langle \lambda , G \rangle -\mu \in \varSigma _d^2[x], \; \lambda \in K^{\oplus }\}. \end{aligned}$$

As K is a polyhedral cone with the form $\{x:a_j^Tx \ge 0\}$, one has

$$\begin{aligned} K^{\oplus }=\left\{ \sum _{j=1}^s \mu _j a_j: \mu _j \ge 0\right\} . \end{aligned}$$

So, $\lambda \in K^{\oplus }$ if and only if $\lambda =\sum _{j=1}^s \mu _j a_j$ for some $\mu _j \ge 0$, and for all $x \in {\mathbb {R}}^n$,

$$\begin{aligned} \langle \lambda , G(x)\rangle = \sum _{j=1}^s\mu _j \sum _{i=1}^m a_{ji} G_i(x)=\sum _{i=1}^m \sum _{j=1}^s\mu _j a_{ji} G_i(x). \end{aligned}$$

Therefore, the conclusion follows. $\square$

Corollary 3.4

Let f be a SOS-convex polynomial and let $g_i$, $i=1,\ldots ,m$, be SOS-convex polynomials with $F=\{x: g_i(x) \le 0, i=1,\ldots ,m\} \ne \emptyset$. Then,

$$\begin{aligned} \inf _{x \in F}f(x)=\sup _{\mu \in {\mathbb {R}}, \lambda _i\in {\mathbb {R}}}\left\{ \mu : f+\sum _{i=1}^m \lambda _i g_i-\mu \in \varSigma ^2_d[x], \; \lambda _i\ge 0, i=1,2,\ldots ,m\right\} , \end{aligned}$$

where d is the smallest even number larger than $\max \{\mathrm{deg}\,f, \max _{1 \le i \le m}\mathrm{deg}\,g_i\}$.

Proof

Let $a_j=e_j$, $j=1,\ldots ,m$, where $e_j$ is the vector whose jth coordinate is one, and zero otherwise. Then, $\{x: a_j^Tx \ge 0, j=1,\ldots ,m\}={\mathbb {R}}^m_+$ and $G=(g_1,\ldots ,g_m)$ is ${\mathbb {R}}^m_+$-SOS-convex. Thus, the conclusion follows immediately from the preceding corollary. $\square$

We finish this section by establishing an exact conic relaxation with the solution attainment under a strict feasibility condition. In the special case when G is an affine function and $K=S^m_+$, this exact conic relaxation result collapses to the exact SDP relaxation result for nonlinear semidefinite programming problems with SOS-convex polynomial objective functions, established in [4].

Theorem 3.2

(Relaxation with attainment) Let K be a closed and convex cone with nonempty interior. For the problem (P), f be a SOS-convex polynomial with degree $d_0$ and G be a K-SOS-convex polynomial with degree $d_1$. Suppose that there exists $x_0\in {\mathbb {R}}^n$ such that $G(x_0) \in -\mathrm{int} K$. Then

$$\begin{aligned} \inf (P)=\displaystyle \max _{\mu \in {\mathbb {R}}, \lambda \in {\mathbb {R}}^m} \{\mu : f + \langle \lambda , G \rangle -\mu \in \varSigma _d^2[x], \; \lambda \in K^{\oplus }\}, \end{aligned}$$

where d is the smallest even number such that $d \ge \max \{d_0,d_1\}$.

Proof

Without loss of generality, let $r:=\inf _{x \in F}f(x) \in {\mathbb {R}}$ be finite. Then, the system

$$\begin{aligned} x\in {\mathbb {R}}^n, G(x)\in -K, \ f(x) -r < 0 \end{aligned}$$

has no solution. So the following system

$$\begin{aligned} x\in {\mathbb {R}}^n, G(x)\in -\mathrm{int} K, \ f(x) -r < 0 \end{aligned}$$

has no solution. Now, by Proposition 2.1, there exists $0_{m+1}\ne (\tau , \lambda )\in {\mathbb {R}}_+ \times K^{\oplus }$ such that

$$\begin{aligned} \tau (f -r) + \langle \lambda , G \rangle \in \varSigma _d^2[x]. \end{aligned}$$

If $\tau =0$, then $\lambda \ne 0$ and $\langle \lambda , G \rangle \in \varSigma _d^2[x]$. This gives us a contradiction, by Proposition 2.1, to the hypothesis that $G(x_0) \in -\mathrm{int} K$ for some $x_0\in {\mathbb {R}}^n$. Hence, $\tau > 0$ and so we get that $f + \langle {\bar{\lambda }}, G \rangle - r \in \varSigma _d^2[x]$, where ${\bar{\lambda }}=\frac{\lambda }{\tau }$. Thus, $\max _{\mu \in {\mathbb {R}}, \lambda \in K^{\oplus }} \{\mu : f + \langle \lambda , G \rangle -\mu \in \varSigma _d^2[x]\} \ge r$. The conclusion now holds as the opposite inequality always holds by construction. $\square$

4 Conic Representations of Some Convex Sets

In this section, we show that the sets described by conic SOS-convex polynomials admit lifted conic representations. Let $G:{\mathbb {R}}^n \rightarrow {\mathbb {R}}^m$ be a K-SOS-convex polynomial with degree d. Its epigraph is given by

$$\begin{aligned} \mathrm{epi}\, G=\{(x,y) \in {\mathbb {R}}^{n} \times {\mathbb {R}}^{m}: y \in G(x)+K\}. \end{aligned}$$

It is easy to verify that $\mathrm{epi}\, G$ is a convex set.

Next, we show that the epigraph is lifted conic representable in the sense that it can be rewritten as a projection of a convex set described by a conic linear system. If the degree $d=1$, then $\mathrm{epi}\, G$ can be trivially described by a conic linear system. Thus, without loss of generality, we only consider the case where $d \ge 2$. To do this, let ${\mathbb {R}}_d[x_1,\ldots ,x_n]$ be the space consisting of all real polynomials on ${\mathbb {R}}^n$ with degree d and let C(d, n) be the dimension of ${\mathbb {R}}_d[x_1,\ldots ,x_n]$. Write the canonical basis of ${\mathbb {R}}_d[x_1,\ldots ,x_n]$ by

$$\begin{aligned} x^{(d)}:=\left( 1,x_1,x_2,\ldots ,x_n,x_1^2,x_1x_2,\ldots ,x_2^2,\ldots ,x_n^2,\ldots ,x_1^{d},\ldots ,x_n^d\right) ^T \end{aligned}$$

and let $x^{(d)}_{\alpha }$ be the $\alpha$-th coordinate of $x^{(d)}$, $1 \le \alpha \le C(d,n)$. Then, we can write $f(x)= \sum _{\alpha =1}^{C(d,n)} f_{\alpha }x^{(d)}_{\alpha }$. Let $G:{\mathbb {R}}^n \rightarrow {\mathbb {R}}^m$ be a polynomial mapping with degree d. Then $G=(G_1,\ldots ,G_m)$ and

$$\begin{aligned} \displaystyle G(x)=\sum _{1 \le \alpha \le C(n,d)}G_{\alpha }x^{(d)}_{\alpha } =\left( \sum _{1 \le \alpha \le C(n,d)}(G_1)_{\alpha }x^{(d)}_{\alpha },\ldots , \sum _{1 \le \alpha \le C(n,d)}(G_m)_{\alpha }x^{(d)}_{\alpha }\right) , \end{aligned}$$

where

$$\begin{aligned} G_{\alpha }=\left( (G_1)_{\alpha },\ldots ,(G_m)_{\alpha }\right) . \end{aligned}$$

(4)

It is easy to see that $[x^{(d/2)}][x^{(d/2)}]^T$ is a matrix whose entries are real polynomials on ${\mathbb {R}}^n$ with degree d. We then define $A_{\alpha }^{(d)}$, $1 \le \alpha \le C(n,d)$, to be symmetric matrices such that

$$\begin{aligned}{}[x^{(d/2)}][x^{(d/2)}]^T=\sum _{1 \le \alpha \le C(n,d)}A_{\alpha }^{(d)}x_{\alpha }^{(d)}. \end{aligned}$$

(5)

Theorem 4.1

Let K be a closed and convex cone in ${\mathbb {R}}^m$. Let $G:{\mathbb {R}}^n \rightarrow {\mathbb {R}}^m$ be a K-SOS-convex polynomial with degree $d \ge 2$. Suppose that either K is a polyhedral cone or K has a nonempty interior and $G(x_0) \in \mathrm{int}K$ for some $x_0 \in {\mathbb {R}}^n$. Then,

$$\begin{aligned} \mathrm{epi}\, G= & {} \left\{ (x,y) \in {\mathbb {R}}^{n} \times {\mathbb {R}}^{m}: \exists z=(z_{\alpha }) \in {\mathbb {R}}^{C(d,n)}, \; y-\sum _{1 \le \alpha \le C(d,n)}G_{\alpha }z_{\alpha } \in K, \right. \\&\left. \sum _{1 \le \alpha \le C(n,d)}A_{\alpha }^{(d)}z_{\alpha } \succeq 0,\ z_1=1, z_{2}=x_1,\ldots , z_{n+1}=x_n\right\} . \end{aligned}$$

In particular,

$$\begin{aligned} \{x\in {\mathbb {R}}^n :G(x) \in -K\}= & {} \left\{ x \in {\mathbb {R}}^{n} : \exists z=(z_{\alpha })_{1 \le \alpha \le C(d,n)}, \; \sum _{1 \le \alpha \le C(d,n)}G_{\alpha }z_{\alpha } \in -K, \right. \\&\left. \sum _{1 \le \alpha \le C(n,d)}A_{\alpha }^{(d)}z_{\alpha } \succeq 0,\ z_1=1, z_{2}=x_1,\ldots , z_{n+1}=x_n\right\} , \end{aligned}$$

where $G_{\alpha }$ and $A_{\alpha }^d$ are defined as in (4) and (5) respectively.

Proof

Denote the degree of G be $d \ge 2$. Clearly d must be an even number. It follows that

$$\begin{aligned} \mathrm{epi}\, G= & {} \left\{ (x,y): y-\sum _{1 \le \alpha \le C(n,d)}G_{\alpha }z_{\alpha } \in K, z_{\alpha }=x^{(d)}_{\alpha } \right\} \\= & {} \left\{ (x,y): y-\sum _{1 \le \alpha \le C(n,d)}G_{\alpha }z_{\alpha } \in K, z_{\alpha }=x^{(d)}_{\alpha }, [x^{(d/2)}][x^{(d/2)}]^T \succeq 0\right\} \\= & {} \left\{ (x,y): y-\sum _{1 \le \alpha \le C(n,d)}G_{\alpha }z_{\alpha } \in K, z_{\alpha }=x^{(d)}_{\alpha }, \sum _{1 \le \alpha \le C(n,d)}A_{\alpha }^{(d)}z_{\alpha } \succeq 0\right\} , \end{aligned}$$

where the last equality follows from the definitions of $A_{\alpha }^{(d)}$. This shows that $\mathrm{epi}\, G \subseteq S$ where

$$\begin{aligned} S= & {} \left\{ (x,y) \in {\mathbb {R}}^{n} \times {\mathbb {R}}^{m}: \exists z_{\alpha } \, \hbox {such that} \ y-\sum _{1 \le \alpha \le C(n,d)}G_{\alpha }z_{\alpha } \in K, \right. \\&\left. \sum _{1 \le \alpha \le C(n,d)}A_{\alpha }^{(d)}z_{\alpha } \succeq 0,\, z_1=1, z_{2}=x_1,\ldots , z_{n+1}=x_n\right\} . \end{aligned}$$

To see the converse inclusion, we proceed by the method of contradiction and suppose there exists $({\overline{x}},{\overline{y}}) \in S$ but $({\overline{x}},{\overline{y}}) \notin \mathrm{epi}\, G$. Then, by the strict separation theorem, there exist $(a,b) \in ({\mathbb {R}}^n \times {\mathbb {R}}^m) \backslash \{0_{n+m}\}$, $r \in {\mathbb {R}}$ and $\delta >0$ such that

$$\begin{aligned} a^T{\overline{x}} + b^T{\overline{y}} \le r <r+2\delta \le a^Tx+b^Ty \hbox { for all } y \in G(x)+K. \end{aligned}$$

Now, consider the following optimization problem

where $\mathrm{val}({{\bar{P}}}):= \inf _{(x,y) \in {\mathbb {R}}^n \times {\mathbb {R}}^m}\{a^Tx+b^Ty-(r+\delta ) \; : \; G(x)-y \in -K\}.$ Then, we see that $\mathrm{val}({{\bar{P}}}) \ge \delta >0$. From our assumption, either K is a polyhedral or K has a nonempty interior and $G(x_0) \in \mathrm{int}K$ for some $x_0 \in {\mathbb {R}}^n$. We now claim that under this assumption, one can find $\lambda \in K^{\oplus }$ and $\sigma \in \varSigma ^2[x,y]$ such that, for all $(x,y) \in {\mathbb {R}}^n \times {\mathbb {R}}^m$,

$$\begin{aligned} a^Tx+b^Ty+\langle \lambda , G(x)-y \rangle -(r+\delta )=\sigma (x,y). \end{aligned}$$

(6)

Granting this, note that $a^Tx+b^Ty+\langle \lambda , G(x)-y \rangle -(r+\delta )+\epsilon$ is affine and any sum-of-squares polynomial must be of even order. This implies that $b=\lambda \in K^{\oplus }$, and so

$$\begin{aligned} a^Tx+\langle \lambda , G(x)\rangle -(r+\delta )=\sigma (x) \hbox { and } \sigma \in \varSigma ^2[x]. \end{aligned}$$

So, by the positive semidefinite representation of a sum-of-squares polynomial, there exists $W \succeq 0$ such that for all $x \in {\mathbb {R}}^n$

$$\begin{aligned} a^Tx+\langle \lambda , G(x) \rangle -(r+\delta )= & {} (x^{(d/2)})^TW x^{(d/2)} \nonumber \\= & {} \sum _{1 \le \alpha \le C(n,d)}x_{\alpha }^{(d)}\mathrm{Tr}\left( W A_{\alpha }^{(d)} \right) . \end{aligned}$$

(7)

Let $a \in {\mathbb {R}}^{C(n,d)}$. Define a linear map $L_a:{\mathbb {R}}_d[x] \rightarrow {\mathbb {R}}$ by

$$\begin{aligned} L_u(f)=\sum _{\alpha } f_{\alpha }u_{\alpha } \hbox { for all } f(x)=\sum _{\alpha }f_{\alpha }x^{(d)}_{\alpha }. \end{aligned}$$

Note that $({\overline{x}},{\overline{y}}) \in S$. There exists ${\overline{z}} \in {\mathbb {R}}^{C(m+n,d)}$ such that

$$\begin{aligned} {{\overline{y}}}-\sum _{1 \le \alpha \le C(n,d)}G_{\alpha }\overline{z}_{\alpha } \in K, \ \ \ \sum _{1 \le \alpha \le C(n,d)}A_{\alpha }^{(d)}{{\overline{z}}}_{\alpha } \succeq 0 \end{aligned}$$

and ${{\overline{z}}}_1=1, {{\overline{z}}}_{2}={{\overline{x}}}_1,\ldots , {{\overline{z}}}_{n+1}={{\overline{x}}}_n$.

Applying the linear map $L_{{\overline{z}}}$ to (7), we obtain that

$$\begin{aligned} a^T{{\bar{x}}}+ \left\langle \lambda , \sum _{1 \le \alpha \le C(n,d)}G_{\alpha }{{\overline{z}}}_{\alpha } \right\rangle -(r+\delta )=\sum _{1 \le \alpha \le C(n,d)}{\overline{z}}_{\alpha }\mathrm{Tr}\left( W A_{\alpha }^{(d)} \right) \ge 0. \end{aligned}$$

where the last inequality follows from the fact $\sum _{1 \le \alpha \le C(n,d)}A_{\alpha }^{(d)}{{\overline{z}}}_{\alpha } \succeq 0$ and $W \succeq 0$. Recall that $\lambda =b \in K^{\oplus }$. It follows that

$$\begin{aligned} a^T{{\bar{x}}}+ b^T{{\bar{y}}}+ \left\langle \lambda , \sum _{1 \le \alpha \le C(n,d)}G_{\alpha }{{\overline{z}}}_{\alpha }-{{\bar{y}}} \right\rangle -(r+\delta ) \ge 0. \end{aligned}$$

This together with $a^T{{\bar{x}}}+ b^T{{\bar{y}}} \le r$ and $\overline{y}-\sum _{1 \le \alpha \le C(n,d)}G_{\alpha }{{\overline{z}}}_{\alpha } \in K$ gives us that $-\delta =r-(r+\delta ) \ge 0,$ which is impossible.

To see our claim (6), we first consider the case where K is polyhedral. Note that $\mathrm{val}({{\bar{P}}})\ge \delta >0$. Thus, Corollary 3.3 implies that

$$\begin{aligned} \sup _{\mu \in {\mathbb {R}}, \lambda \in K^{\oplus }}\{\mu : a^Tx+b^Ty+\langle \lambda , G(x)-y \rangle -(r+\delta )-\mu \in \varSigma ^2_d\} \ge \delta >0. \end{aligned}$$

Thus, there exist $\lambda \in K^{\oplus }$ and $\sigma \in \varSigma ^2[x,y]$ such that, for all $(x,y) \in {\mathbb {R}}^n \times {\mathbb {R}}^m$, $a^Tx+b^Ty+\langle \lambda , G(x)-y \rangle -(r+\delta )=\sigma (x,y)+\delta _0$, for some $\delta _0>0$. Thus, the claim (6) holds.

In the case where $G(x_0) \in \mathrm{int}K$ for some $x_0 \in {\mathbb {R}}^n$, then strict feasibility condition holds for problem $(\bar{P})$ with $(x_0,0)$. So, Theorem 3.2 implies that there exist $\lambda \in K^{\oplus }$ and $\sigma \in \varSigma ^2[x,y]$ such that, for all $(x,y) \in {\mathbb {R}}^n \times {\mathbb {R}}^m$,

$$\begin{aligned} a^Tx+b^Ty+\langle \lambda , G(x)-y \rangle -(r+\delta )=\sigma (x,y)+\mathrm{val}({{\bar{P}}}). \end{aligned}$$

(8)

Thus, claim (6) also holds.

The conic linear representation of the set $S:=\{x\in {\mathbb {R}}^n : G(x) \in -K\}$ follows as $\{x\in {\mathbb {R}}^n : G(x) \in -K\}=\{x \in {\mathbb {R}}^n: (x,0) \in \mathrm{epi} \, G\}$. $\square$

5 Conclusions

In this paper, we extended the notion of SOS-convexity of a real-valued polynomial to a more general notion of conic SOS-convexity for polynomial mappings. We then established that conic sum-of-squares convex (SOS-convex) polynomial programs exhibit exact conic programming relaxations under suitable regularity assumptions, and so they can be solved by various numerical methods such as interior point methods. As conic convexity and conic programming have found many applications in other branches of mathematics, economics and engineering [7], our results point a way to obtaining further computational tractable classes of conic convex programs and their associated applications. This is a topic of further research and will be examined in a forthcoming study.