Nonlinear forced vibration analysis of doubly curved shells via the parameterization method for invariant manifold

Abstract

In this work, the nonlinear forced vibrations of doubly curved shells are studied. For this, the Forced Resonance Curves of four different shells were determined: a shallow cylindrical panel, a shallow spherical panel, a non-shallow spherical panel, and a hyperbolic paraboloid. To model the shells, the Koiter’s nonlinear shell theory, for both shallow and non-shallow shells, was applied. The forced resonance curves were determined using an adaptive harmonic balance method and through a reduced-order model (ROM) via parameterization method for invariant manifolds. The findings of this study reveal the complex dynamic behavior exhibited by doubly curved shells, with various types of bifurcations such as Saddle–Node, Neimark–Sacker, and Period Doubling bifurcations. Thanks to the general treatment of the forcing term implemented in the parameterization method, the results highlight how complex high-order resonances can be retrieved by the ROM, up to a comfortable range of vibration and forcing amplitudes tested. Finally, it clearly demonstrates how the Nonlinear Normal Modes as invariant manifolds provide accurate and efficient ROMs for nonlinear vibrations of shells.

1 Introduction

Thin walled doubly curved shells exhibit exceptional load capacities under transversal and in-plane loads, making them structurally advantageous systems, which are extensively utilized across various engineering domains. To accurately analyze the vibration characteristics of these shells, it is imperative to incorporate geometrical nonlinearities into their mathematical models due to their inherent slenderness.

Extensive researches have been focused on diverse applications of the nonlinear behavior of thin shells. These studies involve examining how thin shells perform under different types of loads, boundary conditions, geometric imperfections, and constitutive laws, as summarized in review studies [1,2,3,4]. Amabili [5] explored forced vibrations with geometrical nonlinearities in laminated circular cylindrical shells using the Amabili-Reddy theory. Du et al. [6] investigated the nonlinear forced vibrations, including chaotic behavior, in infinitely long, functionally graded cylindrical shells using the Lagrangian theory and the multi-scale method. Xie et al. [7] analyzed free and forced vibrations of stepped conical shells with general boundary conditions using a unified analytical method combining Flügge shell theory with power series method. Wang et al. [8] analysed free and forced vibrations of open and closed cylindrical shells in thermal environments, considering thermal effects and material property changes. Amabili and Balasubramanian [9] investigated the nonlinear forced vibrations in laminated composite conical shells using higher-order shear deformation theory. Ye and Wang [10] analyzes the nonlinear forced vibration of graphene platelet-reinforced metal foam shells with 1:1:1:2 internal resonances, considering various porosity and graphene distributions, demonstrating their influence on vibration behavior and weakening the nonlinear coupling effect. Yadav et al. [11] analyzed the geometrically nonlinear forced vibrations in circular cylindrical sandwich shells with cellular core using higher-order theories. Liu et al. [12] studied the nonlinear forced vibrations magneto-electro-elastic smart composite cylindrical shells using the Galerkin scheme and the pseudo-arclength continuation method.

Despite significant research on shell applications, studies on non-shallow doubly curved shells remain scarce. Applying the Koiter’s theory, Pinho et al. [13] compared the free vibrations of shallow and non-shallow shells of various geometries. This study showed that Marguerre’s shallow shell theory yiels less accurate results, highlighting the importance of tensor formulation for non-orthogonal geometries. To further explore both types of shells, Pinho et al. [14] combined two approximations of Koiter’s theory with the Proper Orthogonal Decomposition (POD) for efficient nonlinear static analysis. This approach significantly reduced the number of degrees of freedom when compared to the Finite Element Method (FEM) while maintaining accuracy. Later, Pinho et al. [15] applied the same approach to analyze nonlinear free vibrations of shells. They employed a combination of multiple shooting and continuation methods to determine the backbones for various shell geometries, revealing the presence of internal resonances and complex modal interactions. Due to the complex interactions between different vibration modes, many studies focus on analyzing internal resonances in shells of different geometries. Chin and Nayfeh [16] examined the nonlinear response of an infinitely long cylindrical shell under primary resonance excitation, involving internal two-to-one and one-to-one resonances among flexural and breathing modes. Amabili et al. [17] investigated the response-frequency relationship, traveling wave response, and internal resonances in simply supported circular cylindrical shells using Donnell’s nonlinear shallow-shell theory, revealing complex modal interactions in a water-filled shell with 1:1:1:2 internal resonances. Pellicano et al. [18] expanded the analysis using a second-order perturbation approach and direct simulations, finding strong modal interactions when the structure is excited with small resonant loads. Thomas et al. [19] analyzed the vibrations of shallow spherical shells under large amplitude transverse displacement using von Kármán’s theory, predicting energy exchanges between modes for various internal resonances and specifically examining mode coupling due to a 1:1:2 internal resonance.

High-order numerical models, requiring a large number of degrees of freedom (dof), are typically used to capture the nonlinear response in shells, which are very costly in terms of memory and processing time. To address this challenge, several reduced order models (ROMs) have been employed, including the application of Proper Orthogonal Decomposition (POD) to analyze large amplitude vibrations of shells [20,21,22,23]. A comprehensive review of order reduction techniques for geometrically nonlinear structures can be found in [24]. Several ROMs have been developed based on the concept of Nonlinear Normal Modes (NNMs), initially introduced by Rosenberg [25] as unison vibrations characterized by periodic orbits with coordinates reaching their maximum amplitude simultaneously. This concept was later expanded by Shaw and Pierre [26] who described NNMs as invariant manifolds in the phase space, a definition that naturally facilitates the derivation of ROMs. Cabré et al. [27,28,29] presented a method to find the invariant manifold while simultaneously obtaining a polynomial mapping that is conjugate to the reduced dynamics on the invariant manifold, resulting in an accurate representation of both the manifold and the dynamics on it. An extensive investigation of the parameterization method for invariant manifolds, including different parameterization styles such as the normal form and graph style, was made by [30]. The parameterization method has been applied to study micro-electromechanical systems (MEMS) [31, 32], rotor-foundation systems [33] and resonant piezoelectric micro-actuators [34]. Early works on the subject dealt only with the determination of two-dimensional invariant manifold from dynamic models described in modal coordinates [35,36,37,38], then progressed to automatic computation and applied to high-dimensional systems [39, 40]. An important advancement has been the development of methods enabling the direct handling of invariant manifolds of arbitrary dimension in physical coordinates. This capability allows for the computation of high-order invariant manifolds for finite element models [41,42,43,44,45,46,47]. However, only recently have some studies implemented higher-order approximations of terms involving the non-autonomous part of the invariance equation, highlighting the importance of considering these terms to accurately estimate the maximum vibration amplitude experienced by structures [48, 49].

This study presents an analysis of forced vibrations of thin shells, with particular emphasis on non-shallow doubly curved shells, using Koiter’s nonlinear theory in tensor form. Four distinct geometries were investigated: the spherical cylindrical panel, the shallow spherical panel, the non-shallow spherical panel, and the hyperbolic paraboloid panel. The resonant behavior of these shells under a concentrated harmonic load was examined through the determination of forced resonance curves (FRCs). To capture the dynamic response, a combination of the continuation method and the Adaptive Harmonic Balance Method (AHBM) [50, 51] was employed to establish frequency-response relationships. Subsequently, the FRCs were re-determined using a ROM via the parameterization method for invariant manifolds. The findings of this study reveal the complex dynamic behavior exhibited by doubly curved shells, with various types of bifurcations observed, including Saddle-Node, Neimark-Sacker, and Period Doubling bifurcations. These results contribute to the understanding of nonlinear vibrations in non-shallow doubly curved shells, and the applied methodology can be further extended to the study of other geometries. This work also helps in understanding the application of the parameterization method for invariant manifolds, especially to shells that exhibit internal resonances without necessarily having an integer ratio between their natural frequencies.

2 Mathematical formulation

This section provides a brief presentation of Koiter’s theory regarding thin shells, while a more comprehensive explanation can be found in the existing literature [13,14,15, 52]. Greek indices span from 1 to 2, whereas Latin indices span from 1 to 3, unless explicitly stated otherwise. The summation convention for repeated indices is also employed.

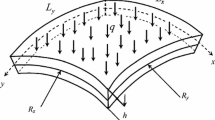
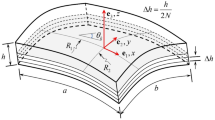
Consider a thin double curved shell with thickness h, made of an elastic isotropic material characterized by a Young’s modulus E, Poisson ratio $\nu$, density $\rho$ and damping constant c. The motion from reference and current configurations of the shell is illustrated in Fig. 1. The shell is oriented in Cartesian directions $x^1$, $x^2$ and $x^3$ with unit vectors ${\textbf{e}}_1$, ${\textbf{e}}_2$ and ${\textbf{e}}_3$, and its mid-surface is parameterized by vectors ${\textbf{R}}$ and ${\textbf{r}}$, in reference and current configurations, respectively. The mid-surface of the shell in reference configuration is described by vector ${\textbf{R}}(\xi ^1, \xi ^2)=\xi ^1{\textbf{e}}_1+ \xi ^2{\textbf{e}}_2+Z(\xi ^1, \xi ^2){\textbf{e}}_3$, where $\xi ^1$ and $\xi ^2$ are the curvilinear coordinates and function $Z(\xi ^1, \xi ^2)$ provides the elevation of the mid-surface. The domain $\Omega$ bounds the mid-surface and is defined as $0\le \xi ^1\le a$ and $0\le \xi ^2\le b$, where a and b correspond to the dimensions of the rectangular projection of the mid-surface onto the horizontal plane. The triads vectors ${\textbf{M}}_i$ and ${\textbf{m}}_i$ are the natural basis of the mid-surface, respectively, in both reference and current configuration, meanwhile ${\textbf{M}}^i$ and ${\textbf{m}}^i$ are the reciprocal basis in reference and current configuration, respectively. The vector ${\textbf{u}}=u_i(\xi ^1, \xi ^2, t){\textbf{M}}^i$ represents the displacement of the mid-surface, such as $u_i(\xi ^1, \xi ^2, t)$ are the displacement fields of the shell’s mid-surface. Vectors ${\textbf{X}}$ and ${\textbf{x}}$ are the positions of any point of the shell in reference and current configuration, respectively, and depend on the correspondent position of the mid-surface according to Kirchhoff hypothesis.

Fig. 1

Motion of the shell

According to Koiter’s theory, the components of the stretching and bending components of the strain tensor are defined by Eqs. (1a) and (1b), respectively:

$$\begin{aligned}&\gamma _{\alpha \beta }=\frac{1}{2}\left( g_{\alpha \beta }-G_{\alpha \beta }\right) \end{aligned}$$

(1a)

$$\begin{aligned}&\rho _{\alpha \beta }=\kappa _{\alpha \beta }-K_{\alpha \beta } \end{aligned}$$

(1b)

where $g_{\alpha \beta }$ and $G_{\alpha \beta }$ represent the components of the metric tensor in the current and reference configurations, respectively. Similarly, $\kappa _{\alpha \beta }$ and $K_{\alpha \beta }$ correspond to the components of the curvature tensor in the current and reference configurations, respectively. The components $G_{\alpha \beta }$ and $K_{\alpha \beta }$ are functions of vector ${\textbf{R}}$, meanwhile $g_{\alpha \beta }$ and $\kappa _{\alpha \beta }$ also depend on the displacement fields $u_k(\xi ^1, \xi ^2, t)$. In this study, two approximations of $\gamma _{\alpha \beta }$ and $\rho _{\alpha \beta }$ were employed, one for shallow shells and another for non-shallow shells, which have been previously investigated [14, 15], and are presented in Appendix A.

2.1 Lagrange equations of motion

The strain energy, according to Koiter’s shell theory, is given by

$$\begin{aligned} U\!=\!\iint _{\Omega }C^{\alpha \beta \theta \lambda }\left( \frac{h}{2}\gamma _{\alpha \beta }\gamma _{\theta \lambda }\!+\!\frac{h^3}{24}\rho _{\alpha \beta }\rho _{\theta \lambda }\right) \sqrt{G}\textrm{d}\xi ^1\textrm{d}\xi ^2\nonumber \\ \end{aligned}$$

(2)

where $C^{\alpha \beta \lambda \theta }=\frac{E}{2(1-\nu ^2)}((G^{\alpha \theta }G^{\beta \lambda }+G^{\alpha \lambda }G^{\beta \theta })(1-\nu )+2\nu G^{\alpha \beta }G^{\lambda \theta })$ are the components of the fourth order constitutive tensor of a linear elastic material considering plane stress state; G is the determinant of the matrix composed by the components $G_{\alpha \beta }$ of the metric tensor.

The kinetic energy, by neglecting rotary inertia, is given by

$$\begin{aligned} T=\iint _{\Omega }\rho \frac{h}{2}G^{ij}{\dot{u}}_i{\dot{u}}_j\sqrt{G}\textrm{d}\xi ^1\textrm{d}\xi ^2 \end{aligned}$$

(3)

where ${\dot{u}}_i$ is the time derivative of the displacement field $u_i$.

The Rayleigh dissipation function F is given by:

$$\begin{aligned} F=\iint _{\Omega }c\frac{h}{2}G^{ij}{\dot{u}}_i{\dot{u}}_j\sqrt{G}\textrm{d}\xi ^1\textrm{d}\xi ^2 \end{aligned}$$

(4)

The work done by the external forces considering a harmonic vertical load ${\textbf{F}}=\epsilon f\cos (\omega t){\textbf{e}}_3$ applied at the point $(\xi ^1_F, \xi ^2_F)$ is given by:

$$\begin{aligned} W={\textbf{F}}\cdot {\textbf{u}}(\xi ^1_F, \xi ^2_F,t) \end{aligned}$$

(5)

where $\epsilon f$ represents the maximum amplitude of the load, and $\omega$ is the excitation frequency.

In order to reduce the system to a finite number of degrees of freedom, the displacement fields $u_i\left( \xi ^1,\xi ^2,t\right)$ can be expanded using the following approximate functions:

$$\begin{aligned} u_k\left( \xi ^1,\xi ^2,t\right) \approx \sum _{i=1}^{m_k}\sum _{j=1}^{n_k}{{u_{k_{ij}}}\left( t\right) {\phi _{k_{ij}}}\left( \xi ^1,\xi ^2\right) } \end{aligned}$$

(6)

where $m_k$ and $n_k$ represent the number of functions for each curvilinear coordinate, ${u_{k_{ij}}}\left( t\right)$ are the unknown time-dependent generalized coordinates, and $\phi _{k_{ij}}\left( \xi ^1,\xi ^2\right)$ are the selected shape functions chosen to satisfy the geometric boundary conditions.

After substituting the field displacement (6) into Eqs. (2), (3), (4) and (5), the equilibrium condition can be determined using the Lagrange equations:

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}\left( \frac{\partial L}{\partial {{{{\dot{u}}}_{k_{ij}}}}}\right) -\frac{\partial L}{\partial {u_{k_{ij}}}}+\frac{\partial F}{\partial {{\dot{u}}_{k_{ij}}}}=0 \end{aligned}$$

(7)

where $L=T-\Pi$ represents the Lagrangian function of the shell, such as $\Pi =U-W$ denotes the total potential energy, and F is the Rayleigh dissipation given by Eq. (4).

The Eq. (7) can be rewritten in matrix form as

$$\begin{aligned} {\textbf{M}}\ddot{{\textbf{U}}}+{\textbf{C}}\dot{{\textbf{U}}}+{\textbf{K}}{\textbf{U}}+{\textbf{f}}({\textbf{U}})-\epsilon \mathbf {f_e}\cos (\omega t)={\textbf{0}} \end{aligned}$$

(8)

where ${\textbf{M}}$ is the mass matrix; ${\textbf{K}}$ is the linear stiffness matrix; Eq. (4) results in a damping matrix in the form of ${\textbf{C}}=\alpha {\textbf{M}}$ where $\alpha =c/\rho$, but the proportional damping matrix ${\textbf{C}}=\alpha {\textbf{M}}+\beta {\textbf{K}}$ was also considered; ${\textbf{U}}=[u_{k_{ij}}]$ is a vector of dimension $n=m_k n_k$ containing all generalized coordinates $u_{k_{ij}}$, for $k=1\dots 3$, $i=1\dots m_k$ and $j=1\dots n_k$; and $\dot{{\textbf{U}}}$ and $\ddot{{\textbf{U}}}$ denote the first and second time derivative of the vector ${\textbf{U}}$; $\epsilon \mathbf {f_e}\cos (\omega t)$ represents the external harmonic load, where $\epsilon$ is a non-dimensional value that represents the load magnitude. The vector function ${\textbf{f}}$ contains all quadratic and cubic nonlinear stiffness terms which components can be written as

$$\begin{aligned} f_i=\sum _{j=1}^{n}\sum _{k=1}^{n}f^2_{ijk} U_j U_k+\sum _{j=1}^{n}\sum _{k=1}^{n}\sum _{l=1}^{n}f^3_{ijkl} U_jU_kU_l \end{aligned}$$

(9)

This work employs an Adaptive Harmonic Balance Method (AHBM) to solve Eq. (8). This method aims to determine the periodic orbits of the Forced Response Curve, defined by ${\textbf{U}}(t) = {\textbf{U}}(t+T)$. Here, $T = 2\pi /\omega$ represents the period of the orbit, and $\omega$ denotes the circular frequency. Refer to [50] for a detailed explanation of both the HBM and the Alternating Frequency-Time (ATF) scheme employed. Additionally, to improve computational efficiency, an adaptive procedure based on simple magnitude comparisons is applied, selecting dominant harmonics and eliminating unnecessary ones [51].

The solution ${\textbf{U}}(t)$ may exhibit internal resonances without requiring commensurate linear natural frequencies due to the coupling between the vibration modes during the system’s general motion (combination internal resonances, see Eq. (3.79) in [53]) [15, 54]. In order to analyze these interactions, the time response of each displacement field in modal coordinates can be expressed as:

$$\begin{aligned} u_k\left( \xi ^1,\xi ^2,t\right) =\sum _{m=1}^{n}{\mu _m\left( t\right) {\psi _k^m\left( \xi ^1,\xi ^2\right) }} \end{aligned}$$

(10)

where $\mu _m(t)$ is the modal coordinate amplitude of the correspondent eigenfunction $\psi _k^m\left( \xi ^1,\xi ^2\right)$, which is determined by:

$$\begin{aligned} \psi _k^m\left( \xi ^1,\xi ^2\right) =\sum _{i=1}^{m_k}\sum _{j=1}^{n_k}{{y^m_{k_{ij}}}{\phi _{k_{ij}}}\left( \xi ^1,\xi ^2\right) } \end{aligned}$$

(11)

The values of ${y^m_{k_{ij}}}$ are the elements of the eigenvector ${\textbf{y}}^m=[y^m_{k_{ij}}]$, determined by the eigenvalue/eigenvector problem resulted by the linearization of the Eq. (8) considering $\epsilon =0$:

$$\begin{aligned} \begin{aligned} ({\textbf{K}}-\omega _m^2{\textbf{M}}){\textbf{y}}^m=0 \\ {\textbf{y}}^m\cdot {\textbf{M}}{\textbf{y}}^n=\delta _{mn} \end{aligned} \end{aligned}$$

(12)

where $\omega _m$ is the correspondent linear natural frequency of the vibration mode ${\textbf{y}}^m$, which is normalized by the mass matrix.

The modal response is determined projecting the displacement vector ${\textbf{U}}$ onto the orthogonal vector space of the linear vibration modes, according to

$$\begin{aligned} \varvec{\mu }(t)={\textbf{Y}}^{\textsf{T}}{\textbf{M}}{\textbf{U}}(t) \end{aligned}$$

(13)

where ${\textbf{Y}}=[{\textbf{y}}^1 \dots {\textbf{y}}^N]$ is a matrix formed by all eigenvectors ${\textbf{y}}^m$ and $\varvec{\mu }$ is a vector which elements are the modal coordinate responses $\mu _m(t)$. The vibration modes and eigenfunctions are sorted according to their linear natural frequencies.

2.2 Reduced-order model using the parameterization method for invariant manifold

The study of non-shallow doubly curved shells typically requires many degrees of freedom for accurate numerical results [15]. Therefore, ROMs are frequently used for both continuous and discrete systems, whether of moderate or large dimension. In this work, the direct parameterization for invariant manifolds is applied to solve the non-autonomous system of Eq. (8), which is transformed into its first-order equivalent system of dimension $N=2n$:

$$\begin{aligned} \begin{aligned} {\textbf{B}}\dot{{\textbf{z}}}={\textbf{A}}{\textbf{z}}+{\textbf{F}}\left( {\textbf{z}}\right) +{\textbf{E}}^+\exp (+\textrm{i}\omega t)+{\textbf{E}}^-\exp (-\textrm{i}\omega t) \end{aligned} \end{aligned}$$

(14)

where ${\textbf{z}}=[{\textbf{U}}^{\textsf{T}}, \dot{{\textbf{U}}}^{\textsf{T}}]^{\textsf{T}} \in {\mathbb {R}}^N$ contains the system’s state variables. The equivalent coefficients of this system are shown in Eq. (15):

$$\begin{aligned}&{\textbf{A}}=\begin{bmatrix} {\textbf{0}} & -{\textbf{K}} \\ -{\textbf{K}} & -{\textbf{C}} \end{bmatrix}, \nonumber \\&{\textbf{B}}=\begin{bmatrix} -{\textbf{K}} & {\textbf{0}} \\ {\textbf{0}} & {\textbf{M}} \end{bmatrix},\nonumber \\&{\textbf{F}}\left( {\textbf{z}}\right) =\begin{bmatrix} {\textbf{0}} \\ -{\textbf{f}} \end{bmatrix},\nonumber \\&\mathbf {E^+}=\mathbf {E^-}=\begin{bmatrix} {\textbf{0}} \\ \mathbf {f_e}/2 \end{bmatrix} \end{aligned}$$

(15)

Vizzaccaro et al. [49] proposed a parameterization method for the invariant manifold in which the non-autonomous system (14) is transformed into an equivalent augmented autonomous system:

$$\begin{aligned} \begin{aligned} {\textbf{B}}\dot{{\textbf{z}}}={\textbf{A}}{\textbf{z}}+{\textbf{F}}\left( {\textbf{z}}\right) +{\textbf{E}}^+{\tilde{p}}_++{\textbf{E}}^-{\tilde{p}}_- \\ \dot{{\tilde{p}}}_+=+\textrm{i}\omega {\tilde{p}}_+ \\ \dot{{\tilde{p}}}_-=-\textrm{i}\omega {\tilde{p}}_- \end{aligned} \end{aligned}$$

(16)

where $p_+$ and $p_-$ are dummy variables introduced to represent the harmonic load, such that ${\tilde{p}}_+(t)=\epsilon \exp (+\textrm{i}\omega t)$ and ${\tilde{p}}_-(t)=\epsilon \exp (-\textrm{i}\omega t)$ are the solutions of the last two equations of (16), considering the initial conditions ${\tilde{p}}_+(0) = {\tilde{p}}_-(0) = \epsilon$. By applying the parameterization method, it is possible to determine the following ROM:

$$\begin{aligned} \dot{{\textbf{p}}}(t)={\textbf{R}}({\textbf{p}}(t)) \end{aligned}$$

(17)

where ${\textbf{p}} = [p_1, \dots , p_M]^{\textsf{T}} =[{\bar{p}}_1, \dots , {\bar{p}}_d, {\tilde{p}}_+, {\tilde{p}}_-]^{\textsf{T}} \in {\mathbb {C}}^M$ is a augmented vector that contains the normal coordinates, with the first $d \ll N$ variables, being the normal coordinates of the master modes, which span the spectral subspace E. The spectral analysis of the linear autonomous part of the system (16) and the determination of E are shown in Appendix B. The function ${\textbf{R}}:{\mathbb {C}}^M \rightarrow {\mathbb {C}}^M$ represents the reduced dynamics, such that the parameterization function ${\textbf{W}}:{\mathbb {C}}^M \rightarrow {\mathbb {R}}^N$ maps the trajectory ${\textbf{p}}(t)$ of the reduced model to a trajectory of the full model contained in the invariant manifold:

$$\begin{aligned} {\textbf{z}}(t)={\textbf{W}}({\textbf{p}}(t)) \end{aligned}$$

(18)

Given that the trajectories of the dummy variables are already known, the least two equations of the system (17) are equal to the last two equation of (16), and its dynamics cannot be altered by the method. Additionally, the parameterization method is applied by selecting only the physical coordinates ${\textbf{z}}$ from the augmented system (16), as shown in left-hand side of the nonlinear mapping equation (18), as proposed by Vizzaccaro et al. [49]. Substituting Eqs. (17) and (18) into Eq. (16), the following invariance equations is determined:

$$\begin{aligned} {\textbf{B}}\frac{\textrm{d}{\textbf{W}}}{\textrm{d}{\textbf{p}}}{\textbf{R}}({\textbf{p}})={\textbf{A}}{\textbf{W}}({\textbf{p}})+{\textbf{F}}({\textbf{W}}({\textbf{p}}))+{\textbf{E}}^+{\tilde{p}}_++{\textbf{E}}^-{\tilde{p}}_- \end{aligned}$$

(19)

where the time-dependency is embedded into the dummy variables.

The parameterization method assumes that the vector functions ${\textbf{R}}$ and ${\textbf{W}}$ are polynomial expansions of ${\textbf{p}}$, truncated to the order ${\mathcal {O}}(p^o)$, where o represents the maximum degree of the polynomial expansion and $p=\left\Vert {\textbf{p}} \right\Vert$. By treating the dummy variables (${\tilde{p}}_+$ and ${\tilde{p}}_-$) in the same manner as the remaining normal coordinates (${\bar{p}}_i$ for $i=1,\dots ,d$), this method facilitates the fully automated solution for any arbitrary order of $\epsilon$. Additionally, one can set the maximum order of ${\tilde{p}}_+$ and ${\tilde{p}}_-$ to be smaller than o by removing specific monomials from the polynomial expansions of ${\textbf{W}}$ and ${\textbf{R}}$. For instance, one could consider a case where the maximum order of the polynomial expansion is ${\mathcal {O}}(p^5, \epsilon ^3)$. In this scenario, all coordinates are expanded up to the fifth order, but the non-autonomous variables are limited up to the power 3 in the expansion. The particular case ${\mathcal {O}}(p^o, \epsilon ^1)$ coincides with the formulation presented in [43]. This notation was introduced by Vizzaccaro et al. [49], who also provide an interesting discussion about which terms should be included in the expansion based on the magnitudes of the normal coordinates of the master modes and the dummy variables. Appendix C presents a succinct overview of the methodology behind determining the invariant manifold and their ensuing reduced-order models using a bordering technique [41, 49], which allows the computation of the invariant manifold and its reduced model directly from the equilibrium system (16), presented in physical coordinates. The methodology described in Appendix C was implemented in Matlab, and the code is available in the repository [55]. For an in-depth insight, the reader is directed to the detailed works in the literature [41, 43, 44, 48, 49].

In the literature, the solution to Eq. (17) of the ROM is often achieved by parameterizing the variables ${\textbf{p}}$ in polar or cartesian coordinates, which results in a system where finding the fixed points corresponds to a finding the periodic orbit of the ROM [43, 44]. In this work, we chose to solve Eq. (17) in its presented form, using the AHBM.

3 Numerical results

3.1 Shallow cylindrical panel

In this section, the FRC of a shallow cylindrical panel has been determined. This particular shell has been previously examined in the literature [43, 44], where the FRC was established using a finite element model with 1320 dof. The shell is depicted in Fig. 2, and its physical and geometric properties are detailed as follows: horizontal projection dimensions of $a=2~\textrm{m}$ and $b=1~\textrm{m}$, thickness $h=0.01~\textrm{m}$, Young’s modulus $E=70~\textrm{GPa}$, Poisson’s ratio $\nu =0.33$, density $\rho =2700~\mathrm {kg/m}^3$, along with damping coefficients $\alpha =0.004\omega _1\omega _2/(\omega _1+\omega _2)$ and $\beta =0.004/(\omega _1+\omega _2)$. In this case, a force is applied at the point with curvilinear coordinates $\xi ^1_F=a/4$ and $\xi ^2_F=b/2$, with a maximum magnitude of $\epsilon f=10~\textrm{N}$. The numerical results presented in this section have been performed using the AHBM with a maximum number of 20 harmonics.

Fig. 2

Shallow cylindrical panel

The boundary conditions on the edges of the shell are:

$$\begin{aligned}&u_1=u_2=u_3=M_1=0 \text { at }\xi ^1=0,a \end{aligned}$$

(20a)

$$\begin{aligned}&V_1=N_1=M_1=V_2=N_2=M_2=0 \text { at }\xi ^2=0,b \end{aligned}$$

(20b)

where the shape functions $\phi _{k_{ij}}(\xi ^1,\xi ^2)$ that satisfy the geometric boundary conditions (20) are given by Eqs. (D46) presented in Appendix D.

The first two natural frequencies of the shell are $\omega _1=23.99 \times 2\pi ~\mathrm {rad/s}$ and $\omega _2=47.93 \times 2\pi ~\mathrm {rad/s}$, calculated for a model with 147 dof ($m_k=n_k=7$ in Eq. (6)). These findings closely align with those reported in the literature [44], i. e. $\omega _1=23.75 \times 2\pi ~\mathrm {rad/s}$ and $\omega _2=47.55 \times 2\pi ~\mathrm {rad/s}$. Notably, the examination reveals an inherent 1:2 internal resonance between the initial two modes, depicted in Fig. 12 in Appendix E. This resonance arises from the integer ratio between the frequencies, i. e., $\omega _2=2\omega _1$.

Figure 3 compares the FRC obtained via FEM [44] with the FRCs obtained using the methodology presented in this work, showing a high degree of similarity, validating the strain–displacement relations, the displacement expansion with 147 dof and AHBM formulation used. The FEM solution [44] presented in the figure was determined for a model with 1320 dof using the shooting method to extract the FRC of the full nonlinear system. The Newmark algorithm was used to perform numerical integration during the shooting process, with 100 integration steps per excitation period. The FRCs display two different families of periodic orbits corresponding to two different parabolic NNMs of the underlying conservative problem. Such a phenomenon of internal resonance between the first two modes was also observed in the analysis of an arch MEMS resonator [31], resulting in a very similar forced resonance curve. The FRCs of the shallow cylindrical panel were also determined using the ROM via parameterization of the invariant manifold. With the inclusion of the first two modes in the master subspace ($E=E_1\oplus E_2$), and adopting the normal form style of parameterization, allows the ROM to accurately capture near resonances, achieving convergence up to fifth order ${\mathcal {O}}(p^5, \epsilon ^1)$. Given the very small magnitude of the forcing, a linear approximation is sufficient to properly describe the harmonic load.

Fig. 3

Displacement amplitude $u_{3}(a/4, b/2, t)$ of the shallow cylindrical panel as a function of the excitation frequency, considering a load of magnitude $\epsilon f=10~\textrm{N}$. SN, Saddle–Node bifurcations; NS, Neimark–Sacker bifurcation

Figure 4 compare the time responses at four points (a-d) along the FRC, indicated by bullet points in Fig. 3 for both the full model (dashed lines) and the ROM (solid lines). The close agreement between the results also demonstrates the effectiveness of the ROM.

Fig. 4

Time responses in modal coordinates for the periodic orbits of points a-d on the FRCs of the shallow cylindrical panel.  Mode 1;  Mode 2. The solid lines represent the responses of the reduced model considering an SSM with $E=E_1\oplus E_2$ and ${\mathcal {O}}(p^5,\epsilon ^1)$. The dashed lines represent the response of the full model with 147 dof

3.2 Doubly curved shells

Results of forced vibration analyses of three doubly curved shells are presented in this section. The shells are depicted in Fig. 5: (a) Shallow spherical panel, (b) Non-shallow spherical panel, and (c) Hyperbolic paraboloid. The shells have the following geometric and physical properties: horizontal projection dimensions $a=b=0.1~\text {m}$, thickness $h=0.001~\text {m}$, Young’s modulus $E=206~\text {GPa}$, Poisson’s ratio $\nu =0.3$, density $\rho =7850~\text {kg/m}^3$, and damping coefficients $\alpha =2\zeta \omega _1$ with $\zeta =0.004$ and $\beta =0$. These shells were previously analyzed by Pinho et al. [15], who determined the backbone curves of the shells in a nonlinear free vibration analysis. The nonlinear free vibration analysis helps determine which modes are essential to include in the master subspace. Again, all the numerical results presented in this section have been performed using the AHBM with a maximum number of 20 harmonics.

In this section, all investigated geometries will be subjected to a concentrated load applied symmetrically at shell boundaries, i. e., all shells are subjected to a vertical harmonic force ${\textbf{F}}=\epsilon f\cos (\omega t){\textbf{e}}_3$, acting at its center $(\xi ^1_F=a/2,\xi ^2_F=b/2)$, where $\epsilon f$ represents the maximum amplitude of the load, and $\omega$ is the excitation frequency. It is noteworthy that the presence of any initial geometric imperfection in shell’s geometry and/or asymmetric applied load can break the symmetry of the vibration, leading a modal coupling of the asymmetric vibration modes. In this work, the numerical results do not consider any kind of asymmetry. Also, it is important to state that some of the investigated geometries can display snap-through buckling, leading the structures to a new stable potential-well after inverting the concavity. This work investigates only the resonance curves in the potential-well around the initial configuration.

Fig. 5

Shell’s geometry: a shallow spherical panel; b non-shallow spherical panel and c hyperbolic paraboloid. $Z(\xi ^1, \xi ^2)$ represents the elevation of the mid-surface. The axes of the graphs are uniformly scaled and measured in meters

3.2.1 Shallow spherical panel

This section focuses on the nonlinear vibration analysis of a simply supported with movable edges shallow spherical panel with radius $R=1~\text {m}$, shown in Fig. 5a. This shell was previously examined in the literature [56, 57], the movable edges allow membrane displacement in the direction orthogonal to the edge while restricting membrane displacement tangential to the edge and transverse displacement. The essential geometric and natural boundary conditions on the four edges are given as follows:

$$\begin{aligned}&u_2=u_3=N_1=M_1=0 \text { at }\xi ^1=0,a \end{aligned}$$

(21a)

$$\begin{aligned}&u_1=u_3=N_2=M_2=0 \text { at }\xi ^2=0,b \end{aligned}$$

(21b)

where $N_\alpha$ is the normal force and $M_\alpha$ is the bending moment per unit of length in the direction of ${\textbf{m}}^\alpha$. The shape functions $\phi _{k_{ij}}(\xi ^1,\xi ^2)$, which satisfy the boundary conditions (21), are given by Eqs. (D47) presented in Appendix D.

The fundamental natural frequency of this shell is $\omega _1=952.2\times 2\pi ~\text {rad/s}$. Previous studies considered a harmonic load with a maximum magnitude of $\epsilon f=31.2~\text {N}$ and analyzed the shell using Donnell’s theory [57] with two different displacement field expansions with 9 ($m_1=n_1=m_2=n_2=2$ and $m_3=n_3=1$) and 22 dof ($m_1=n_1=m_2=n_2=3$ and $m_3=n_3=2$). Here, two expansions with 22 dof ($m_1=n_1=m_2=n_2=3$ and $m_3=n_3=2$) and 27 dof ($m_k=n_k=3$) were considered to investigate the solution’s convergence.

Figure 6a–c depict the FRCs of the shallow spherical panel. The FRC for the 22 dof model aligns with the FRC determined by Amabili [57], who employed the same expansion of the displacement field. Generally, the FRC indicates a transition from softening to hardening behavior for vibration amplitudes around 1.2h. Figure 6b provides a zoomed-in view, highlighting the emergence of a complex curve within the frequency range $0.9<\omega /\omega _1<0.95$. The complex shape of the FRC is directly linked to the intricate internal resonances that arise in this shell, as also verified in the free vibration analysis [15] The solutions with 22 and 27 dof exhibit very similar results, with slight differences in the curves observed for amplitudes greater than 1.4h, as highlighted in Fig. 6c. Furthermore, the figure also presents the backbone curve determined by Pinho et al. [15], using the same displacement expansion with 22 dof, demonstrating that the FRC underlines the results of the conservative problem.

Figure 6a–c also display the FRC for the shallow spherical panel using ROM via parameterization of the invariant manifold. The ROM was built using the master subspace $E=E_1\oplus E_2\oplus E_3\oplus E_4$, with these modes – depicted in Fig. 13 in Appendix E – identified as crucial for internal resonances in the analysis of nonlinear free vibrations [15]. Given the non-integer frequency ratios of these modes ($\omega _2=2.7\omega _1$, $\omega _3=2.7\omega _1$, and $\omega _4=4.7\omega _1$), a graph style parameterization was adopted. Initially, an order of ${\mathcal {O}}(p^{15}, \epsilon ^{1})$ was considered, involving only linear terms of the forcing dummy variables in the expansion of the normal coordinates. However, this approach did not fully capture the response, particularly struggled to accurately represent the complex behavior within the frequency range $0.9<\omega /\omega _{1}<0.95$. Notably, the model fails to determine displacement amplitudes larger than 1h, demonstrating the inadequacy of the linear approximation of the dummy variables. However, when the nonlinear terms of the dummy variables are included in the polynomials expansion, the ROM with order ${\mathcal {O}}(p^5, \epsilon ^5)$ precisely captured the entire FRC, emphasizing the importance of nonlinear forcing terms in the parameterization of the invariant manifold in this case. The graph style of parameterization is effective in this case, as there are no folding points presented in the manifold.

Fig. 6

Results of the FRC for the shallow spherical panel obtained using the full model with 22 and 27 dof and the results obtained using the ROM. NS, Neimark–Sacker bifurcations; SN, Saddle–Node bifurcations; PD period doubling bifurcations

To determine whether the reduced model responses closely match those of the full model, the time responses in modal coordinates for four points (a-d) on the FRC of Fig. 6a–c are presented in Fig. 7. The dashed lines represent the responses of the full model, while the solid lines represent the responses of the ROM considering $E=E_1\oplus E_2\oplus E_3\oplus E_4$ and ${\mathcal {O}}(p^5, \epsilon ^5)$. All points exhibit responses identical to those of the full model. In summary, the reduced model accurately identified the internal resonances. At point b, there is a significant 1:3 internal resonance between modes 1 and 2. The other points (a, c and d) also exhibit internal resonances, although less pronounced, with the displacement predominantly characterized by the first mode.

Fig. 7

Time responses in modal coordinates for the periodic orbits of points a–d on the FRC of the shallow spherical panel for $\epsilon f=31.2~\textrm{N}$.  mode 1;  mode 2;  mode 4. The solid lines represent the responses of the reduced-order model considering an SSM with $E=E_1\oplus E_2\oplus E_3\oplus E_4$ and ${\mathcal {O}}(p^5,\epsilon ^5)$. The dashed lines represent the response of the full model with 22 dof

Fig. 8

Maximum amplitude of the displacement field $u_3$ at the center of the non-shallow spherical panel as a function of excitation frequency considering a load of $\epsilon f=200~\textrm{N}$. In a results for models with 48, 75, and 108 dof. In b a comparison between the results obtained using the full model with 108 dof and the reduced-order models via parameterization method for invariant manifolds. In c a zoom of the shaded area in figure (b). NS Neimark–Sacker bifurcations; SN Saddle–Node bifurcations

3.2.2 Non-shallow spherical panel

In this section, an non-shallow spherical panel with a radius of $R=0.1~\textrm{m}$ will be analyzed, subjected to a concentrated harmonic load of maximum magnitude $\epsilon f=200~\textrm{N}$, as shown in Fig. 5b. The fundamental natural frequency is $\omega _1=8,271.6\times 2\pi ~\text {rad/s}$. The shell is simply supported with immovable edges, which means the following boundary conditions apply:

$$\begin{aligned}&u_1=u_2=u_3=M_1=0 \text { for }\xi ^1=0,a \end{aligned}$$

(22a)

$$\begin{aligned}&u_1=u_2=u_3=M_2=0 \text { for }\xi ^2=0,b \end{aligned}$$

(22b)

where the shape functions $\phi _{k_{ij}}(\xi ^1,\xi ^2)$, satisfying the boundary conditions (22), are defined by Eqs. (D48). Similar to the previous example, these functions were chosen to account for symmetric vibrations along the $\xi ^1=a/2$ and $\xi ^2=b/2$ axes.

Fig. 9

Time responses in modal coordinates for the periodic orbits of points a–c on the resonance curve of the non-shallow spherical panel.  Mode 1;  Mode 3;  Mode 13. The solid lines represent the responses of the reduced model considering an SSM with $E=E_1 \oplus E_3 \oplus E_{13}$ and O(9). The dashed lines represent the response of the full model with 108 dof

Fig. 10

Maximum displacement of $u_3$ at the center of the hyperbolic paraboloid for a load of $\epsilon f=200~\textrm{N}$. a Results for models with 48, 75, and 108 dof. b Comparison between the FRCs for the hyperbolic paraboloid obtained by the full model with 108 dof and by the reduced-order models via parameterization method for invariant manifolds. SN, Saddle–Node bifurcations

To ensure convergence, three expansions were analyzed with 48 ($m_k=n_k=4$), 75 ($m_k=n_k=5$), and 108 dof ($m_k=n_k=6$). Figure 8a illustrates the maximum amplitude of the periodic orbit for the displacement $u_3$ at the center of the shell as a function of excitation frequency. In general, all models exhibit an initial softening behavior, with vibrations becoming unstable for amplitudes larger than 1h. Figure 8b presents the results of the FRCs calculated by the reduced-order models. When only the first mode is considered in the master subspace ($E=E_1$), the reduced-order model diverges from the full model for vibration amplitudes greater than 0.8h, considering the order ${\mathcal {O}}(p^7, \epsilon ^7)$.Adding the resonant modes increases the accuracy of the reduced-order model. When considering the master subspace $E=E_1 \oplus E_3 \oplus E_{13}$, the model captures part of the unstable region. Moreover, for the order ${\mathcal {O}}(p^7, \epsilon ^7)$, it more precisely captures the position of the Neimark-Sacker bifurcation compared to other models. However, the unstable part of the solution does not exhibit the complexities present in the full model, specially in the region highlighted in Fig. 8c. It is crucial to include nonlinear terms in the expansion of the variables representing the loading. This necessity becomes clear when comparing results obtained using the same master subspace ($E=E_1 \oplus E_3 \oplus E_{13}$) with an expansion that considers only the linear terms of the loading, specifically ${\mathcal {O}}(p^7, \epsilon ^1)$.

To characterize the internal resonances, the time responses in modal coordinates for three points (a-c) on the FRC of Fig. 8b are displayed in Fig. 9. The solid lines represent the responses of the reduced-order model considering $E=E_1\oplus E_3\oplus E_{13}$ and ${\mathcal {O}}(p^7,\epsilon ^7)$, while the dashed lines represent the responses of the full model with 108 dof. The influence of modes 1 and 3 at these three points can be observed. It is noteworthy that a model with only 3 degrees of freedom accurately describes the internal resonances. Point b exhibits more complex vibrations, with a coupling between modes 1, 3, and 13 in a 1:1:2 internal resonance scenario. This modes are depicted in Fig. 14 in  Appendix E.

3.2.3 Hyperbolic paraboloid

The third example features a hyperbolic paraboloid, as illustrated in Fig. 5c. A concentrated harmonic load with a maximum magnitude of $\epsilon f=200~\textrm{N}$ is applied at the center of the shell. The shell is simply supported with immovable edges, as described in Eq. (22). The shape functions are given by Eqs. (D48), the same as in the previous example.

Once again, three expansions were used, with 48 ($m_k=n_k=4$), 75 ($m_k=n_k=5$), and 108 dof ($m_k=n_k=6$). The fundamental natural frequency of the shell is $\omega _1=6{,}421.1\times 2\pi ~\text {rad/s}$. The FRCs for these three expansions are shown in Fig. 10a, representing the maximum value of the displacement field $u_3$ at the center of the shell as a function of excitation frequency. The maximum amplitude value decreases as more degrees of freedom are added, maintaining a hardening behavior. However, convergence of the solution is observed starting from 75 dof. The behavior of the shell is similar to that of a simple Duffing oscillator.

Figure 10b displays the FRC results for a hyperbolic paraboloid using a reduced-order model. When considering only the first mode as the master subspace ($E=E_1$), the reduced-order model accurately captures most of the response. Adding modes 4 and 10 brings the solution even closer to the full model, indicating a complex internal resonance that changes the curvature of the FRC near the peak, given the difference between the solutions with one NNM and three NNMs. This case clearly illustrates the need to include nonlinear terms in the expansion of the forcing. The solution using the order ${\mathcal {O}}(p^9, \epsilon ^1)$ is unable to capture the FRC accurately. However, when considering ${\mathcal {O}}(p^9, \epsilon ^5)$, the solution closely aligns with that of the full model. It is evident that the high-order forcing terms have significant effects on the reduced dynamics, given the substantial differences between the solutions considering only linear forcing terms and those including nonlinear forcing terms.

Once again, some points (a-c) on the FRC in Fig. 10b were selected to evaluate the time responses in modal coordinates, presented in Figs. 11. There is a significant influence of mode 10 on the shell’s response as the displacements increase, in a 1:2 internal resonance scenario. The accuracy of the reduced-order model results can also be observed in the time responses in modal coordinates, where results with $E=E_1\oplus E_4 \oplus E_{10}$ and ${\mathcal {O}}(p^9,\epsilon ^5)$ are very close to those of the full model.

Fig. 11

Time responses in modal coordinates for the periodic orbits of points a-c on the FRC of the hyperbolic paraboloid.  Mode 1;  Mode 4;  Mode 10. The solid lines represent the responses of the reduced-order model considering $E=E_1\oplus E_4\oplus E_{10}$ and ${\mathcal {O}}(p^9,\epsilon ^5)$. The dashed lines represent the response of the full model with 108 dof

4 Conclusion

In this study, the nonlinear vibrations of doubly curved shells were investigated. Koiter’s nonlinear shell theory was employed to determine the forced resonance curves of shells with four different geometries: shallow cylindrical panel, shallow spherical panel, non-shallow spherical panel, and hyperbolic paraboloid. The methodology applied in this study allows for the analysis of non-shallow shells parameterized by non-orthogonal curvilinear coordinates. The analysis of forced vibrations of these structures described by non-orthogonal curvilinear coordinates represents a novel contribution to this research field. The Forced Resonance Curves exhibit complex behavior even for moderate displacements, on the same order of magnitude as the shell thickness. The parameterization method for invariant manifolds has proven effective in reducing the system’s dimension, even for highly complex solutions. While low-order approximations of non-autonomous terms can lead to inaccurate results, the methodology presented here is easily adaptable and capable of considering high-order approximations of these non-autonomous forcing terms. These shells exhibit internal resonances without the frequencies having integer ratios. In this context, determining the backbone curves was a good initial step for determining the master modes and, consequently, the forced resonance curves.

Appendices

Strain–displacement relations

This appendix presents two approximations of the strain–displacement relations of the Koiter’s nonlinear shell theory. In cases where the displacement of the shell is of the order of magnitude of the shell thickness or less, the nonlinear terms of the bending tensor can be neglected. Furthermore, the membrane components of the displacement are small compared to the transversal components, and hence the nonlinear terms involving $u_\alpha$ can be removed [14, 15]. Combining these simplifications, the components of the stretching and bending tensors can be written as:

$$\begin{aligned}&\gamma _{\alpha \beta }=\frac{1}{2}\left( u_{\alpha |\beta }+u_{\beta |\alpha }+G^{\sigma \lambda }K_{\alpha \sigma } K_{\beta \lambda }u_3^2+u_{3,\alpha }u_{3,\beta }\right) \end{aligned}$$

(A1a)

$$\begin{aligned}&\rho _{\alpha \beta }=\Gamma ^{\gamma }_{\alpha \beta }u_{3|\gamma }-u_{3|\alpha \beta } \end{aligned}$$

(A1b)

Additionally, if the shell is geometrically shallow, then the curvature is small and terms involving the components $K_{\alpha \beta }$ can also be neglected [14, 15], resulting in:

$$\begin{aligned}&\gamma _{\alpha \beta }=\frac{1}{2}\left( u_{\alpha |\beta }+u_{\beta |\alpha }+u_{3,\alpha }u_{3,\beta }\right) \end{aligned}$$

(A2a)

$$\begin{aligned}&\rho _{\alpha \beta }=\Gamma ^{\gamma }_{\alpha \beta }u_{3,\gamma }-u_{3,\alpha \beta } \end{aligned}$$

(A2b)

where the values of $u_{\sigma |\alpha }$, $u_{3|\alpha }$, $u_{\sigma |\alpha \beta }$ and $u_{3|\alpha \beta }$ are the covariant derivatives of the displacement vector ${\textbf{u}}$, given by:

$$\begin{aligned} \begin{aligned}&u_{\sigma |\alpha }=u_{\sigma ,\alpha }-\Gamma ^\tau _{\sigma \alpha }u_\tau +K_{\alpha \sigma }u_3\\&u_{3|\alpha }=u_{3,\alpha }-K^\tau _\alpha u_\tau \\&u_{\sigma |\alpha \beta }=(u_{\sigma |\alpha })_{,\beta } -\Gamma ^\tau _{\beta \sigma }u_{\tau |\alpha }+K_{\sigma \beta }u_{3|\alpha } \\&u_{3|\alpha \beta }=(u_{3|\alpha })_{,\beta }-K^\tau _\beta u_{\tau |\alpha } \end{aligned} \end{aligned}$$

(A3)

$K_{\alpha \beta }$ and $K_\beta ^\alpha$ are, respectively, the covariant and mixed components of the curvature tensor given by Eq. (A4a) and Eq. (A4b).

$$\begin{aligned} & K_{\alpha \beta }={\textbf{M}}_\alpha \cdot \frac{\partial {\textbf{M}}_3}{\partial \xi ^\beta }=-{\textbf{M}}_3\cdot \frac{\partial {\textbf{M}}_\alpha }{\partial \xi ^\beta }=-{\textbf{M}}_3\cdot \frac{\partial {\textbf{M}}_\beta }{\partial \xi ^\alpha } \nonumber \\\end{aligned}$$

(A4a)

$$\begin{aligned} & K_\beta ^\alpha ={\textbf{M}}^\alpha \cdot \frac{\partial {\textbf{M}}_3}{\partial \xi ^\beta }=-{\textbf{M}}_3\cdot \frac{\partial {\textbf{M}}^\alpha }{\partial \xi ^\beta } \end{aligned}$$

(A4b)

$\Gamma _{\beta \gamma }^\alpha$ are the Christoffel symbols determined by:

$$\begin{aligned} \Gamma _{\beta \gamma }^\alpha ={\textbf{M}}^\alpha \cdot \frac{\partial {\textbf{M}}_\beta }{\partial \xi ^\gamma } \end{aligned}$$

(A5)

The triad of vectors ${\textbf{M}}_i$ ($i=1,2,3$) compose the natural basis of the mid-surface in the reference configuration and are described in Eqs. (A6) as a function of vector ${\textbf{R}}$ and the curvilinear coordinates $\xi ^1$ and $\xi ^2$

$$\begin{aligned} {\textbf{M}}_1=\frac{\partial {\textbf{R}}}{\partial \xi ^1} \end{aligned}$$

(A6a)

$$\begin{aligned} {\textbf{M}}_2=\frac{\partial {\textbf{R}}}{\partial \xi ^2} \end{aligned}$$

(A6b)

$$\begin{aligned} {\textbf{M}}_3=\frac{{\textbf{M}}_1\times {\textbf{M}}_2}{\sqrt{G}} \end{aligned}$$

(A6c)

where vectors ${\textbf{M}}_1$ and ${\textbf{M}}_2$, defined in Eq. (A6a) and Eq. (A6b), are tangent to the coordinate lines $\xi ^\alpha$ ($\alpha =1,2$); ${\textbf{M}}_3$, defined in Eq. (A6c), is a unit vector perpendicular to the mid-surface of the shell; and $\sqrt{G}=|{\textbf{M}}_1\times {\textbf{M}}_2|$.

The reciprocal basis is composed by vectors ${\textbf{M}}^i$ ($i=1,2,3$) and can be determined by

$$\begin{aligned} {\textbf{M}}_i\cdot {\textbf{M}}^j=\delta _i^j \end{aligned}$$

(A7)

where $\delta _i^j$ is the Kronecker’s delta. It can be demonstrated by Eqs. (A6) and (A7) that ${\textbf{M}}^3={\textbf{M}}_3$.

Linear spectral analysis

Consider the autonomous case of Eq. (16) and its subsequent linearization at ${\textbf{z}}={\textbf{0}}$:

$$\begin{aligned} \begin{aligned} {\textbf{B}}\dot{{\textbf{z}}}={\textbf{A}}{\textbf{z}} \end{aligned} \end{aligned}$$

(B8)

The linear system’s motion can be obtained by the superposition of the Linear Normal Modes (LNM), given by the left and right eigenvectors ${\textbf{u}}_i$ and ${\textbf{v}}_i$, determined by the following eigenproblem:

$$\begin{aligned} \begin{aligned} {\textbf{A}}{\textbf{v}}_j&=\lambda _j{\textbf{B}}{\textbf{v}}_j \\ {\textbf{u}}^*_j{\textbf{A}}&=\lambda _j{\textbf{u}}^*_j{\textbf{B}} \end{aligned} \end{aligned}$$

(B9)

where $[\quad ]^*$ denotes the conjugate transpose. The eigenvalues $\lambda _j$ and eigenvectors ${\textbf{u}}_j$ and ${\textbf{v}}_j$ can be written in terms of the natural frequencies $\omega _i$ and vibration modes ${\textbf{y}}_i$ as

$$\begin{aligned} \begin{aligned}&\lambda _{2i-1,2i}=-\frac{\alpha +\beta \omega _i^2}{2}\\&\quad \pm \textrm{i}\omega _i\sqrt{1-\left( \frac{\alpha }{2\omega _i}+\frac{\beta \omega _i}{2}\right) ^2}, \quad i=1\dots n \\&{\textbf{v}}_{2i-1}= \begin{bmatrix} {\textbf{y}}^i \\ \lambda _{2i-1}{\textbf{y}}^i \end{bmatrix}, \quad {\textbf{v}}_{2i}= \begin{bmatrix} {\textbf{y}}^i \\ \lambda _{2i}{\textbf{y}}^i \end{bmatrix}, \quad i=1\dots n \\&{\textbf{u}}_{2i-1}= \begin{bmatrix} {\textbf{y}}^i \\ {\bar{\lambda }}_{2i-1}{\textbf{y}}^i \end{bmatrix}, \quad {\textbf{u}}_{2i}= \begin{bmatrix} {\textbf{y}}^i \\ {\bar{\lambda }}_{2i}{\textbf{y}}^i \end{bmatrix}, \quad i=1\dots n \\ \end{aligned} \end{aligned}$$

(B10)

where $0<\alpha \ll \omega _i$ and $0<\beta \ll 1$ (lightly damped assumption); $\lambda _{2i-1}={\bar{\lambda }}_{2i}$ and ${\textbf{v}}_i=\bar{{\textbf{u}}}_i$ (the bar denotes the complex conjugate operation). Furthermore, the eigenvectors are normalized so ${\textbf{u}}^*_i{\textbf{B}}{\textbf{v}}_j=\delta _{ij}$.

The LNM are invariant, which means that once a trajectory initiates within the vector space defined by an LNM, it will perpetually stay within this space. These trajectories are contained within the eigenspace $E_i$ that can be expressed as:

$$\begin{aligned} \begin{aligned} E_i=\textrm{span}\{{\textbf{v}}_{2i-1}, {\textbf{v}}_{2i}\} \end{aligned} \end{aligned}$$

(B11)

Since the eigenspaces are generated by the LNM, they are also invariant for the linear system (B8), and any subspace generated by the linear combination of the eigenspaces is also invariant. The LNM are commonly used to reduce the dimension of linear systems when the focus of the analysis is limited to specific frequency ranges. In these cases, modes whose frequencies are far from the frequency range of interest contribute very little to the system response and can be removed from the analysis. The LNM used in the analysis constitute the master spectral subspace $E\subset {\mathbb {C}}^N$ which contains all the approximate trajectories of the reduced system, such that:

$$\begin{aligned} \begin{aligned} E=E_{j_1}\oplus \dots \oplus E_{j_m} \end{aligned} \end{aligned}$$

(B12)

where $m\ll n$, $\textrm{dim}(E)=d\ll N$ and $d=2\,m$, such as the frequencies $\omega _{j_1}\dots \omega _{j_m}$ are in the range of interest; $\oplus$ represents the sum of the vector spaces.

The matrices ${\textbf{V}}_E$, ${\textbf{U}}_E$ and $\varvec{\Lambda }_E$ respectively contain the right eigenvectors, the left eigenvectors, and the eigenvalues of the master spectral subspace E, such that:

$$\begin{aligned} {\textbf{V}}_E&=[{\textbf{v}}^E_1,\dots ,{\textbf{v}}^E_d]=[{\textbf{v}}_{2j_1-1},{\textbf{v}}_{2j_1}, \dots , {\textbf{v}}_{2j_m-1},{\textbf{v}}_{2j_m}] \nonumber \\ {\textbf{U}}_E&=[{\textbf{u}}^E_1,\dots ,{\textbf{u}}^E_d]=[{\textbf{u}}_{2j_1-1},{\textbf{u}}_{2j_1}, \dots , {\textbf{u}}_{2j_m-1},{\textbf{u}}_{2j_m}]\nonumber \\ \varvec{\Lambda }_E&=\textrm{diag}\left( \lambda _{1}^E, \dots , \lambda ^E_{d}\right) \nonumber \\&=\textrm{diag}\left( \lambda _{2j_1-1},\lambda _{2j_1}, \dots , \lambda _{2j_m-1},\lambda _{2j_m}\right) \end{aligned}$$

(B13)

which are also solution to the following eigenproblem:

$$\begin{aligned} {\textbf{A}}{\textbf{V}}_E={\textbf{B}}{\textbf{V}}_E\varvec{\Lambda }_E \end{aligned}$$

(B14a)

$$\begin{aligned} {\textbf{U}}_E^*{\textbf{A}}=\varvec{\Lambda }_E{\textbf{U}}_E^*{\textbf{B}} \end{aligned}$$

(B14b)

Solution of invariance equation

This appendix presents a succinct overview of the methodology behind determining the invariant manifold and their ensuing reduced-order model. For an in-depth insight, the reader is directed to the detailed works in the literature [43, 44, 48, 49]. The described methodology was implemented in the invariant_manifold_and_rom_forced function in Matlab, available from the repository [55].

Expanding the Eq. (19), we obtain the following form in indexed notation:

$$\begin{aligned} \sum _{j=1}^N B_{ij}{\dot{z}}_j= & \sum _{j=1}^N A_{ij}z_j+\sum _{j=1}^N \sum _{k=1}^N F^2_{ijk}z_j z_k\nonumber \\ & +\sum _{j=1}^N \sum _{k=1}^N \sum _{l=1}^N F^3_{ijkl}z_j z_k z_l\nonumber \\ & +E^+_i{\tilde{p}}_++E^-_i{\tilde{p}}_- \end{aligned}$$

(C15)

In practice, the summations present in the equation are not computed explicitly. Instead, we use the Tensor Toolbox for Matlab library [58], which stores matrices and tensors in sparse structures, optimizing computational performance. The parameterization method proposed by Cabré et al. [27] assumes that the functions ${\textbf{W}}({\textbf{p}})$ and ${\textbf{R}}({\textbf{p}})$ are polynomial expansions of the normal coordinates. Using multi-index notation, these functions are written as:

$$\begin{aligned} \begin{aligned} z_j=\sum _{r=1}^o \sum _{i=1}^{N_r} W^r_{jm}p^{\varvec{\alpha }^r_m} \qquad {\dot{p}}_a=\sum _{s=1}^o \sum _{k=1}^{N_s} R^s_{ak}p^{\varvec{\alpha }^s_k} \end{aligned} \end{aligned}$$

(C16)

where ${\textbf{W}}^r\in {\mathbb {C}}^{N\times N_r}$ and ${\textbf{R}}^r\in {\mathbb {C}}^{M\times N_r}$ are matrices whose elements $W^r_{jm}$ and $R^r_{ak}$ contain the coefficients of the polynomial expansion. The symbol $p^{\varvec{\alpha }^s_k}$ is used to represent the monomials of the expansion in multi-index notation:

$$\begin{aligned} p^{\varvec{\alpha }^r_j}=\prod _{a=1}^M p^{{\alpha }^r_{ja}}_a \end{aligned}$$

(C17)

Here, $\varvec{\alpha }^r$ is a matrix with elements that are non-negative integers, given by ${\alpha }^r_{ja}$, for $a=1,\dots ,M$ and $j=1,\dots ,N_r$. The sum of the elements of any row $\varvec{\alpha }^r_j$ is always equal to the degree of the monomial:

$$\begin{aligned} \sum _{a=1}^M {\alpha }^r_{ja}=r \end{aligned}$$

(C18)

For each degree r, there are $N_r=\frac{(r+M-1)!}{r!(M-1)!}$ distinct monomials, which must be stored in a consistent order indexed by j. The indexing starts with the monomials where the first variable has the highest exponent and proceeds methodically, decreasing the exponent of the first variable while increasing the exponents of subsequent variables. This process continues until the last monomial, where the last variable has the highest exponent. Equation (C19) can be written in matrix form as

$$\begin{aligned} \begin{aligned} {\textbf{z}}=\sum _{r=1}^o {\textbf{W}}^r{\textbf{p}}^{\varvec{\alpha }^r} \\ {\textbf{p}}=\sum _{r=1}^o {\textbf{R}}^r{\textbf{p}}^{\varvec{\alpha }^r} \end{aligned} \end{aligned}$$

(C19)

where ${\textbf{p}}^{\varvec{\alpha }^r}=[p^{\varvec{\alpha }^r_1}, \dots , p^{\varvec{\alpha }^r_{N_r}}]^{\textsf{T}}$ is a vector containing all $N_r$ monomials of order r.

The multiplication of two polynomial expansions results in a new polynomial expansion that can also be written in multi-index notation. This process is illustrated in the following example:

$$\begin{aligned} \sum _{q=1}^{N_t} C^t_{iaq} p^{\varvec{\alpha }^t_q}=\sum _{j} \sum _{k=1}^{N_r} \sum _{l=1}^{N_s} A^r_{ijk} p^{\varvec{\alpha }^r_k} B^s_{jal} p^{\varvec{\alpha }^s_l} \end{aligned}$$

(C20)

In this example, the coefficients of the polynomials are stored in tensors ${\textbf{A}}^r$ and ${\textbf{B}}^s$, whose tensor contraction results in the tensor ${\textbf{C}}^t$. The resulting monomials, represented by $p^{\varvec{\alpha }^t_q}$, have the order $t = r + s$. The indices $k$ and $l$ are combined to form the new index $q$, such that $\varvec{\alpha }^r_k + \varvec{\alpha }^s_l = \varvec{\alpha }^t_q$. This approach allows for efficient computation and manipulation of polynomial expansions in high-dimensional spaces, leveraging the power of sparse matrix and tensor representations.

Additionally, the derivative of the monomial $p^{\varvec{\alpha }^r_j}$ with respect to the normal coordinate $p_a$ can also be written in multi-index notation, where the resulting monomial is of order $r-1$. The coefficients resulting from the derivative can be rearranged in the tensor ${\textbf{D}}^{r-1}\in {\mathbb {Z}}^{N_r\times M\times N_{r-1}}$, as shown in the following equation:

$$\begin{aligned} \frac{\partial p^{\varvec{\alpha }^r_j}}{\partial p_a}={\alpha }^r_{ja}\prod _{k=1}^M p^{\varvec{\alpha }^r_{jk}-\delta _{ka}}_k=\sum _{l=1}^{N_{r-1}}D^{r-1}_{jal}p^{\varvec{\alpha }^{r-1}_l} \end{aligned}$$

(C21)

The tensor ${\textbf{D}}^{r-1}$ can be used as an operator to determine the components of the gradient $\textrm{d}{\textbf{W}}/\textrm{d}{\textbf{p}}$:

$$\begin{aligned} \frac{\partial {z}_j}{\partial {p}_a} = \sum _{r=1}^o \sum _{m=1}^{N_r} \sum _{l=1}^{N_{r-1}} W^r_{jm} D^{r-1}_{mal}p^{\varvec{\alpha }^{r-1}_l} \end{aligned}$$

(C22)

The Matlab class MultiIndexFixedOrder was developed for the manipulation and algebra of polynomial expansions using multi-index notation. This class is also available from the repository [55].

The goal of the parameterization method is to find the values $W^p_{ji}$ and $R^p_{ji}$, starting with the first order and incrementally determining the values for higher orders. The solution to the invariance equation is found by writing it at each order, giving rise to the homological equation of order p that can be derived from Eq. (19) as:

$$\begin{aligned} \left[ {\textbf{B}}\frac{\textrm{d}{\textbf{W}}}{\textrm{d}{\textbf{p}}}{\textbf{R}}({\textbf{p}})\right] _p= & \left[ {\textbf{A}}{\textbf{W}}({\textbf{p}})+{\textbf{F}}({\textbf{W}}({\textbf{p}}))\right. \nonumber \\ & \left. +{\textbf{E}}^+{\tilde{p}}_++{\textbf{E}}^-{\tilde{p}}_- \right] _p \end{aligned}$$

(C23)

where the operator $[\ \ ]p$ is used to return only the monomials of degree p from the invariance equation.

1.1 Order-1 Solution

At first-order order, Eq. (C23) can be simplified to:

$$\begin{aligned} \begin{aligned} {\textbf{B}} {\textbf{W}}^1 {\textbf{R}}^1 {\textbf{p}} = {\textbf{A}} {\textbf{W}}^1 {\textbf{p}} + {\textbf{E}}^+{\tilde{p}}_+ {\textbf{E}}^-{\tilde{p}}_-\\ \end{aligned} \end{aligned}$$

(C24)

Vizzaccaro et al. [49] proposed the following solution for Eq. (C24):

$$\begin{aligned} {\textbf{R}}^1= \begin{bmatrix} \mathbf {\Lambda }_E & {\textbf{r}}^+ & {\textbf{r}}^-\\ {\textbf{0}} & +\textrm{i}\omega & 0 \\ {\textbf{0}} & 0 & -\textrm{i}\omega \end{bmatrix},\ \ {\textbf{W}}^1= \begin{bmatrix} {\textbf{V}}_E&{\textbf{w}}^+&{\textbf{w}}^- \end{bmatrix} \end{aligned}$$

(C25)

where the vectors ${\textbf{r}}^+$, ${\textbf{r}}^-$, ${\textbf{w}}^+$, and ${\textbf{w}}^-$ are determined by solving the following linear system:

(C26)

Here, $r$ can take the values $+$ or $-$ and denotes the indices that are not part of ${\mathcal {R}}^r$. In the normal form style of parameterization, ${\mathcal {R}}^r$ represents the indices of the eigenvectors of the master subspace $E$ that are resonant with the excitation frequency $\omega$, defined as:

$$\begin{aligned} {\mathcal {R}}^r=\{i\in \{1, \dots , d\}: \lambda ^E_i\approx r\omega \} \end{aligned}$$

(C27)

In the graph style of parameterization, the indices ${\mathcal {R}}^r$ are given by:

$$\begin{aligned} {\mathcal {R}}^r=\{1, \dots , d\} \end{aligned}$$

(C28)

1.2 Order-p solution

This section addresses the calculation of terms of order $p > 1$, which are more complex due to the involvement of nonlinear internal forces. The elements of $\dot{{\textbf{z}}}$ can be expressed as follows:

$$\begin{aligned} {\dot{z}}_j=\frac{\partial {z}_j}{\partial {p}_a} {\dot{p}}_a \end{aligned}$$

(C29)

By substituting Eqs. (C19) and (C22) into Eq. (C29), the following expression is obtained:

$$\begin{aligned} {\dot{z}}_j\!=\!\sum _{r=1}^o \sum _{i=1}^{N_r} \!\sum _{a=1}^M\sum _{l=1}^{N_{r-1}} \!\sum _{s=1}^o \sum _{k=1}^{N_s} W^r_{ji} D^{r-1}_{ial}p^{\varvec{\alpha }^{r-1}_l} R^s_{ak}p^{\varvec{\alpha }^s_k}\nonumber \\ \end{aligned}$$

(C30)

Considering only the terms of order $p$, the result for ${\dot{z}}_j$ can be divided into three parts:

$$\begin{aligned} \left[ {\dot{z}}_j\right] _p=\left[ {\dot{z}}_j\right] _p^1+\left[ {\dot{z}}_j\right] _p^2+\left[ {\dot{z}}_j\right] _p^3 \end{aligned}$$

(C31)

The first part, $\left[ {\dot{z}}_j\right] ^1_p$, retains only the terms with $r = p$ and $s = 1$ in the summations of Eq. (C30), resulting in:

$$\begin{aligned} \left[ {\dot{z}}_j\right] _p^1=\sum _{i=1}^{N_p} \sum _{q=1}^{N_{p}} W^p_{ji} G^{p}_{iq}p^{\varvec{\alpha }^{p}_q} \end{aligned}$$

(C32)

where the matrix ${\textbf{G}}^p$ is introduced to simplify the expression and can be determined as:

$$\begin{aligned} \sum _{q=1}^{N_{p}} G^{p}_{iq}p^{\varvec{\alpha }^{p}_q}=\sum _{a=1}^M\sum _{l=1}^{N_{p-1}} \sum _{k=1}^{N_1}D^{p-1}_{ial}\ R^1_{ak}\ p^{\varvec{\alpha }^{p-1}_l}p^{\varvec{\alpha }^1_k} \end{aligned}$$

(C33)

The term $\left[ {\dot{z}}_j\right] _p^2$ considers only the terms with $r = 1$ and $s = p$ in the summations of Eq. (C30), resulting in:

$$\begin{aligned} \left[ {\dot{z}}_j\right] _p^2=\sum _{a=1}^M \sum _{k=1}^{N_p} W^1_{ja}R^p_{ak}p^{\varvec{\alpha }(p,k)} \end{aligned}$$

(C34)

The remaining terms of order-p in the summation of Eq. (C30) are given by:

$$\begin{aligned} \begin{aligned} \left[ {\dot{z}}_j\right] _p^3&=\sum _{r=2}^{p-1} \sum _{a=1}^M \sum _{i=1}^{N_r} \sum _{l=1}^{N_{r-1}} \sum _{k=1}^{N_{p+1-r}} \\&\quad W^r_{ji} D^{r-1}_{ial}\ R^{p+1-r}_{ak} p^{\varvec{\alpha }^{r-1}_l} p^{\varvec{\alpha }^{p+1-r}_k} \\&=\sum _{r=2}^{p-1}\sum _{q=1}^{N_{p}} H^{rp}_{jq} p^{\varvec{\alpha }^p_q} \end{aligned} \end{aligned}$$

(C35)

where the components of ${\textbf{H}}$ are determined as:

$$\begin{aligned} \begin{aligned} \sum _{q=1}^{N_{p}} H^{rp}_{jq} p^{\varvec{\alpha }^p_q}&= \sum _{a=1}^M\sum _{i=1}^{N_r}\sum _{l=1}^{N_{r-1}} \sum _{k=1}^{N_{p+1-r}} \\&\quad W^r_{ji}D^{r-1}_{ial}\ R^{p+1-r}_{ak} p^{\varvec{\alpha }^{r-1}_l} p^{\varvec{\alpha }^{p+1-r}_k} \end{aligned} \end{aligned}$$

(C36)

Finally, the nonlinear terms should be formulated in terms of normal coordinates. By substituting Eq. (C19), the nonlinear terms in Eq. (C15) are given by:

$$\begin{aligned} \begin{aligned} F^2_{ijk}z_j z_k&=F^2_{ijk} \sum _{r=1}^o \sum _{n=1}^{N_r} W^r_{jn}p^{\varvec{\alpha }^r_n} \sum _{s=1}^o \sum _{m=1}^{N_s} W^s_{km}p^{\varvec{\alpha }^s_m} \\ F^3_{ijkl}z_j z_k z_l&= F^3_{ijkl} \sum _{r=1}^o \sum _{n=1}^{N_r} W^r_{jn}p^{\varvec{\alpha }^r_n} \sum _{s=1}^o \sum _{m=1}^{N_s} \\&\quad W^s_{km}p^{\varvec{\alpha }^s_m} \sum _{t=1}^o \sum _{p=1}^{N_t} W^t_{lp}p^{\varvec{\alpha }^t_p} \end{aligned} \end{aligned}$$

(C37)

Multiplying tensors ${\textbf{F}}^2$ and ${\textbf{F}}^3$ by ${\textbf{W}}^r$, and contracting the dummy indices in Eqs. (C37), results in the tensor $\bar{{\textbf{F}}}$. Furthermore, through the combination of monomials from polynomial expansions, the nonlinear terms can be simplified as follows:

$$\begin{aligned} \begin{aligned} \sum _{j=1}^N \sum _{k=1}^N F^2_{ijk}z_j z_k=&\sum _{u=1}^{2o} {\bar{F}}_{iq}^{(2,u)}p^{\varvec{\alpha }^u_q} \\ \sum _{j=1}^N \sum _{k=1}^N \sum _{l=1}^N F^3_{ijkl}z_j z_k z_l=&\sum _{v=1}^{3o}{\bar{F}}_{iq}^{(3,v)}p^{\varvec{\alpha }^v_q} \end{aligned} \end{aligned}$$

(C38)

Finally, by substituting (C32), (C34), (C35), and (C38) into Eq. (C23) and collecting only the monomials of order $p$, we obtain:

$$\begin{aligned} \begin{aligned}&\sum _{j=1}^N \sum _{q=1}^{N_{p}} \left[ \sum _{n=1}^{N_p} B_{ij} W^p_{jn} G^{p}_{nq}-A_{ij}W^p_{jq}\right] p^{\varvec{\alpha }^p_q}\\&= \sum _{j=1}^N \sum _{q=1}^{N_p} \left[ \sum _{a=1}^M -B_{ij} W^1_{ja}R^p_{aq}+C^p_{iq}\right] p^{\varvec{\alpha }^p_q} \end{aligned} \end{aligned}$$

(C39)

where the matrix ${\textbf{C}}^p$, whose components are given by $C^p_{iq}$, represents the components of the Eq. (C39) that are independent of ${\textbf{W}}^p$ and ${\textbf{R}}^p$:

$$\begin{aligned} \begin{aligned}&C^p_{iq}p^{\varvec{\alpha }(p,q)}\\&\quad =\sum _{q=1}^{N_{p}}\left[ {\bar{F}}_{iq}^{(2,p)}\!+\!{\bar{F}}_{iq}^{(3,p)}\!-\!\sum _{j=1}^N \sum _{r=2}^{p-1} B_{ij}H^{rp}_{jq}\right] p^{\varvec{\alpha }(p,q)} \end{aligned}\nonumber \\ \end{aligned}$$

(C40)

For a given order $p$, the matrix ${\textbf{C}}^p$ can be computed based only on the results of the previous orders.

From Eq. (C39), the following homological equation in matrix notation is derived:

$$\begin{aligned} {\textbf{B}}{\textbf{W}}^p{\textbf{G}}^p-{\textbf{A}}{\textbf{W}}^p+{\textbf{B}}{\textbf{W}}^1{\textbf{R}}^p={\textbf{C}}^p \end{aligned}$$

(C41)

Given that the matrix ${\textbf{R}}^1$ is upper triangular, ${\textbf{G}}^p$ also results in an upper triangular matrix. Consequently, the system (C41) can be solved iteratively for each index j:

$$\begin{aligned} ({\textbf{B}}G^p_{jj}-{\textbf{A}}){\textbf{W}}^p_{\cdot j}+{\textbf{B}}{\textbf{W}}^1{\textbf{R}}^p_{\cdot j}={\textbf{C}}^p_{\cdot j}-\sum _{k=1}^{j-1}G^p_{kj}{\textbf{B}}{\textbf{W}}^p_{\cdot k}\nonumber \\ \end{aligned}$$

(C42)

where ${\textbf{W}}^p_{\cdot j}$ denotes the $j$-th column of ${\textbf{W}}^p$. To calculate ${\textbf{W}}^p_{\cdot j}$, one must first determine ${\textbf{W}}^p_{\cdot k}$ for all $k < j$.

Following the solution proposed by Vizzaccaro et al. [49], the values of ${\textbf{W}}^p_{\cdot j}$ and ${\textbf{R}}^p_{\cdot j}$ can be computed iteratively by solving the following linear system:

(C43)

Fig. 12

Vibration modes of the shallow cylindrical panel. The function $\psi _i^k$ represents the $i{\text {th}}$ component of the shape function for mode k

In the normal form style of parameterization, ${\mathcal {R}}$ represents the indices of the master modes of the subspace $E$ that are internally resonant:

$$\begin{aligned} {\mathcal {R}}=\{ k\in \{1, \dots , d\}: \lambda ^E_k\approx G^p_{jj}\} \end{aligned}$$

(C44)

In the graph style of parameterization, the indices ${\mathcal {R}}$ are given by:

$$\begin{aligned} {\mathcal {R}}=\{1, \dots , d\} \end{aligned}$$

(C45)

Trigonometric expansions of the displacement field

This appendix presents the displacement field expansions used in the analysis of the shells studied in this paper.

Shallow cylindrical panel:

$$\begin{aligned}&{\phi _1}_{ij}=\sin {\left( \frac{i\pi \xi ^1}{a}\right) }\left\{ \frac{1+(-1)^j}{2}\sin {\left( \frac{j\pi \xi ^2}{2b}\right) }\right. \nonumber \\&\quad \left. +\frac{1+(-1)^{j+1}}{2}\cos {\left( \frac{(j-1)\pi \xi ^2}{2b}\right) }\right\} \nonumber \\&{\phi _2}_{ij}=\sin {\left( \frac{i\pi \xi ^1}{a}\right) }\left\{ \frac{1+(-1)^j}{2}\sin {\left( \frac{j\pi \xi ^2}{2b}\right) }\right. \nonumber \\&\quad \left. +\frac{1+(-1)^{j+1}}{2}\cos {\left( \frac{(j-1)\pi \xi ^2}{2b}\right) }\right\} \nonumber \\&{\phi _3}_{ij}=\sin {\left( \frac{i\pi \xi ^1}{a}\right) }\left\{ \frac{1+(-1)^j}{2}\sin {\left( \frac{j\pi \xi ^2}{2b}\right) }\right. \nonumber \\&\quad \left. +\frac{1+(-1)^{j+1}}{2}\cos {\left( \frac{(j-1)\pi \xi ^2}{2b}\right) }\right\} \end{aligned}$$

(D46)

Shallow spherical panel:

$$\begin{aligned}&{\phi _1}_{ij}=\left\{ \frac{1+(-1)^i}{2}\sin {\left( \frac{i\pi \xi ^1}{a}\right) }\right. \nonumber \\&\quad \left. +\frac{1+(-1)^{i+1}}{2}\cos {\left( \frac{i\pi \xi ^1}{a}\right) }\right\} \sin {\left( \frac{(2j-1)\pi \xi ^2}{b}\right) } \nonumber \\&{\phi _2}_{ij}=\sin {\left( \frac{(2i-1)\pi \xi ^1}{a}\right) }\left\{ \frac{1+(-1)^j}{2}\sin {\left( \frac{j\pi \xi ^2}{b}\right) }\right. \nonumber \\&\quad \left. +\frac{1+(-1)^{j+1}}{2}\cos {\left( \frac{j\pi \xi ^2}{b}\right) }\right\} \nonumber \\&{\phi _3}_{ij}=\sin {\left( \frac{(2i-1)\pi \xi ^1}{a}\right) }\sin {\left( \frac{(2j-1)\pi \xi ^2}{b}\right) } \end{aligned}$$

(D47)

Non-shallow spherical panel and hyperbolic paraboloid:

$$\begin{aligned} \begin{aligned}&{\phi _1}_{ij}=\sin {\left( \frac{(2i)\pi \xi ^1}{a}\right) }\sin {\left( \frac{(2j-1)\pi \xi ^2}{b}\right) } \\&{\phi _2}_{ij}=\sin {\left( \frac{(2i-1)\pi \xi ^1}{a}\right) }\sin {\left( \frac{(2j)\pi \xi ^2}{b}\right) } \\&{\phi _3}_{ij}=\sin {\left( \frac{(2i-1)\pi \xi ^1}{a}\right) }\sin {\left( \frac{(2j-1)\pi \xi ^2}{b}\right) } \end{aligned} \end{aligned}$$

(D48)

Vibration modes

This section presents the vibration modes included in the master subspaces of the ROMs.

Fig. 13

Vibration modes of the shallow spherical panel. The function $\psi _i^k$ represents the $i{\text {th}}$ component of the shape function for mode k

Fig. 14

Vibration modes of the non-shallow spherical panel. The function $\psi _i^k$ represents the $i{\text {th}}$ component of the shape function for mode k

Fig. 15

Vibration modes of the hyperbolic paraboloid. The function $\psi _i^k$ represents the $i{\text {th}}$ component of the shape function for mode k