1 Introduction

Metal foams, as a kind of lightweight materials, possess many excellent properties such as light weight, low density, low cost, and high energy absorption [1, 2]. Therefore, metal foams can be applied in aerospace, electromagnetic shielding, and construction, which has attracted much attention in recent years [3,4,5,6,7].

Graphene platelets (GPLs) are considered to be two-dimensional thin plates composed of several graphene sheets [8]. As a new kind of reinforcing materials, GPLs can be added to matrix materials to enhance their mechanical properties [8,9,10]. Due to the high specific surface area, GPLs can closely combine with the matrix materials. Thus, GPL enhanced structures have better mechanical properties and more stable chemical properties [11, 12].

In order to combine the outstanding properties of the two materials mentioned above, graphene platelet-reinforced metal foam (GPLRMF) structures are synthesized [13,14,15]. GPLRMF structures possess the advantages of high stiffness, high strength, and high thermal conductivity. Additionally, the mass of GPLs added is very small, which does not affect the original lightweight and designability of the metal foams [11, 16]. Because of the above excellent characteristics, GPLRMF structures have great potential in engineering fields such as construction, aerospace, and automotive [13, 14, 17, 18].

In the application, GPLs can be artificially distributed in metal foams to achieve various functionally graded distributions, i.e., functionally graded GPLRMF (FG-GPLRMF) [17]. Therefore, understanding the mechanical behavior of FG-GPLRMF structures is very meaningful. Because FG-GPLRMF structures are a new kind of nanocomposite structures, there are few studies in the literature that concentrates on the mechanical characteristics of them. In the framework of the first-order shear deformation theory, Yang and co-authors investigated the free vibration of rectangular FG-GPLRMF plates [19] and spinning FG-GPLRMF cylindrical shells [20]. Further, they analyzed nonlinear free vibration of FG-GPLRMF beams and plates [21, 22]. Based on the nonlinear refined beam theory, Barati and Zenkour [23] investigated nonlinear post-buckling of imperfect FG-GPLRMF beams. Wang et al. [24] conducted the nonlinear free vibration investigation of FG-GPLRMF cylindrical shells using the improved Donnell theory.

Internal resonance phenomenon produces the energy transfer between different modes of a nonlinear system and directly influences the dynamical response of structures, which makes it an unneglected phenomenon in nonlinear vibration of engineering structures. So many researchers are devoted to the investigation of internal resonance of structures. Through the Runge–Kutta method, the nonlinear response with 1:3 internal resonance of carbon fiber-reinforced composite sandwich plates was investigated by Chen et al. [25]. The nonlinear periodic response of a cantilever beam with 3:1 internal resonance was studied by Shaw et al. [26]. In the case of 3:1 internal resonance, Tang et al. [27] presented the investigation of nonlinear vibration of a moving viscoelastic beam embedded in the elastic media. Using the multiple-scale method, Yi and Stanciulescu [28] studied the 2:1 internal resonance of a shallow arch with elastic boundary constraints. Wang and Yang [29] conducted the analysis of internal resonance of a moving porous functionally graded plate contacting with fluid. The nonlinear vibration of water-filled cylindrical shells with 1:1 internal resonance was investigated by Amabili et al. [30] via the experiment and arclength continuation method. The investigation of 1:2 internal resonance of laminated cylindrical shells was conducted by Chen and Li [31]. Liu et al. [32] presented the nonlinear dynamic analysis of laminated cylindrical shells under internal resonance and subharmonic resonance. The research on nonlinear vibration of the laminated cylindrical shell including chaos phenomenon and 1:1 internal resonance was conducted by Zhang et al. [33]. Considering subharmonic resonance and internal resonance, Yang et al. [34] conducted the investigation on nonlinear vibration of truncated composite conical shells. Considering primary, subharmonic, and internal resonances, chaos and bifurcations phenomena of laminated cylindrical shells were investigated by Bian et al. [35].

The FG-GPLRMF shells are one type of porous structures that is prone to large-deflection vibration under external dynamical excitation. Through the literature review, however, no research on nonlinear forced vibration of FG-GPLRMF cylindrical shells is found. In the present study, the nonlinear dynamics of FG-GPLRMF cylindrical shells with internal resonances is investigated. By employing Donnell’s nonlinear shell theory and the stress function, we deduce the equations of motion and the compatibility equation. By using the Galerkin method, a set of nonlinear ODEs is obtained. The pseudo-arclength continuation technique is used to numerically analyze the 1:1:1:2 internal resonances behavior. Moreover, the effects of key parameters on the nonlinear dynamic characteristics of FG-GPLRMF cylindrical shells are discussed in detail.

2 Material properties

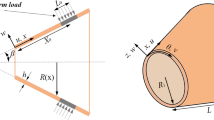
An FG-GPLRMF cylindrical shell under consideration is demonstrated in Fig. 1. A coordinate system (x, θ, z) is established at the midplane of the shell. u, v and w are the axial, circumferential, and radial displacements of a point of the shell’s middle plane, respectively. The shell’s length, thickness, and middle radius are L, h and R, respectively. Also, three types of porosity distribution, i.e., P-1, P-2, and P-3, are shown in Fig. 1. Pores of P-1 and P-2 disperse symmetrically in the z-direction; the size of pores is the largest at the shell’s midplane for P-1, while it is the smallest for P-2. P-3 shows a uniform porosity distribution.

Fig. 1
figure 1

An FG-GPLRMF cylindrical shell [24]

Full size image

The effective elastic modulus E, mass density ρ, and Poisson’s ratio µ of FG-GPLRMF shells are given by [19, 24]

$$ E\left( z \right) = \left\{ \begin{gathered} E^{*} \left[ {1 - e_{1} \cos \left( {\pi z/h} \right)} \right]{\text{ P}}- 1 \hfill \\ E^{*} \left\{ {1 - e_{2} \left[ {1 - \cos \left( {\pi z/h} \right)} \right]} \right\}{\text{ P}}- 2 \hfill \\ E^{*} e_{3} {\text{ P}}- 3 \hfill \\ \end{gathered} \right. $$
(1)
$$ \rho \left( z \right) = \left\{ \begin{gathered} \rho^{*} \left[ {1 - e_{{{{\rm m}}1}} \cos \left( {\pi z/h} \right)} \right]{\text{ P}}- 1 \hfill \\ \rho^{*} \left\{ {1 - e_{{{{\rm m}}2}}^{{}} \left[ {1 - \cos \left( {\pi z/h} \right)} \right]} \right\}{\text{ P}}- 2 \hfill \\ \rho^{*} e_{{{{\rm m}}3}} {\text{ P}}- 3 \hfill \\ \end{gathered} \right. $$
(2)
$$ \mu \left( z \right) = \mu^{*} $$
(3)

where E*, ρ*, and µ* denote Young’s modulus, the mass density, and Poisson’s ratio of GPL-reinforced solid metal, respectively; e1, e2, and e3 are porosity coefficients; em1, em2, and em3 are mass density coefficients.

E*, ρ*, and µ * are determined by [11, 24, 36, 37]:

$$ E^{*} = \frac{3}{8}\left[ {\frac{{1 + \frac{{2l_{{{\text{GPL}}}} }}{{t_{{{\text{GPL}}}} }}\frac{{E_{{{\text{GPL}}}} - E{}_{{{\rm m}}}}}{{E_{{{\text{GPL}}}} + \frac{{2l_{{{\text{GPL}}}} }}{{t_{{{\text{GPL}}}} }}E{}_{{{\rm m}}}}}V_{{{\text{GPL}}}} \left( z \right)}}{{1 - \frac{{E_{{{\text{GPL}}}} - E{}_{{{\rm m}}}}}{{E_{{{\text{GPL}}}} + \frac{{2l_{{{\text{GPL}}}} }}{{t_{{{\text{GPL}}}} }}E{}_{{{\rm m}}}}}V_{GPL} \left( z \right)}}} \right]E_{{{\rm m}}} + \frac{5}{8}\left[ {\frac{{1 + \frac{{2w_{{{\text{GPL}}}} }}{{t_{{{\text{GPL}}}} }}\frac{{E_{{{\text{GPL}}}} - E{}_{{{\rm m}}}}}{{E_{{{\text{GPL}}}} + \frac{{2w_{{{\text{GPL}}}} }}{{t_{{{\text{GPL}}}} }}E{}_{{{\rm m}}}}}V_{{{\text{GPL}}}} \left( z \right)}}{{1 - \frac{{E_{{{\text{GPL}}}} - E{}_{{{\rm m}}}}}{{E_{{{\text{GPL}}}} + \frac{{2w_{GPL} }}{{t_{{{\text{GPL}}}} }}E{}_{{{\rm m}}}}}V_{{{\text{GPL}}}} \left( z \right)}}} \right]E_{{{\rm m}}} $$
(4)
$$ \rho^{*} = \rho_{{{\rm m}}} \left[ {1 - V_{{{\text{GPL}}}} \left( z \right)} \right] + \rho_{{{\text{GPL}}}} V_{{{\text{GPL}}}} \left( z \right) $$
(5)
$$ \mu^{*} = \mu_{{{\rm m}}} \left[ {1 - V_{{{\text{GPL}}}} \left( z \right)} \right] + \mu_{{{\text{GPL}}}} V_{{{\text{GPL}}}} \left( z \right) $$
(6)

In the above equations, E, ρ, and µ with subscript “GPL,” respectively, denote GPLs’ Young’s modulus, mass density, and Poisson’s ratio, while E, ρ, and µ with subscript “m” denote those of the matrix material, respectively; the length lGPL, width wGPL, and thickness tGPL are the geometric parameters of GPLs; VGPL is GPL volume fraction.

Without loss of generality, the masses of FG-GPLRMF shells for all kinds of GPL distribution and porosity distribution are set to be equal. For details, readers can refer to Ref. [24].

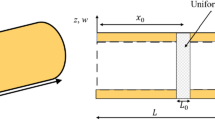
Figure 2 demonstrates different kinds of GPL reinforcement in the z-direction. The GPLs of GPL-I and GPL-II are non-uniform distribution. The largest GPL volume fraction appears at the surfaces of GPL-I shells, but at the midplane of GPL-II shells. GPL-III is a uniform distribution of GPLs. GPL volume fraction VGPL for the three types of GPL distribution is given by [19, 24]

$$ V_{{{\text{GPL}}}} \left( z \right) = \left\{ {\begin{array}{*{20}c} {s_{i1} \left[ {1 - \cos \left( {\pi z/h} \right)} \right]} & {\text{GPL - I}} \\ {s_{i2} \cos \left( {\pi z/h} \right)} & {\text{GPL - II}} \\ {s_{i3} } & {\text{GPL - II}} \\ \end{array} } \right. $$
(7)
Fig. 2
figure 2

Different types of GPL distribution [24]

Full size image

Note that VGPL also relates to GPL weight fraction WGPL. For details of material properties, readers can refer to the authors’ previous investigation [24].

3 Theory and solution procedure

According to the Donnell nonlinear shell theory, the axial, circumferential, and radial displacements (u1, u2, u3) of an arbitrary point of the shell are [38]

$$ \begin{gathered} u_{1} \left( {x,\theta ,z,t} \right) = u\left( {x,\theta ,t} \right) - z\frac{{\partial w\left( {x,\theta ,t} \right)}}{\partial x} \hfill \\ u_{2} \left( {x,\theta ,z,t} \right) = v\left( {x,\theta ,t} \right) - z\frac{{\partial w\left( {x,\theta ,t} \right)}}{R\partial \theta } \hfill \\ u_{3} \left( {x,\theta ,z,t} \right) = w\left( {x,\theta ,t} \right) \hfill \\ \end{gathered} $$
(8)

The constitutive relation of the FG-GPLRMF shell is:

$$ \left\{ {\sigma_{x} ,\sigma_{\theta } ,\tau_{x\theta } } \right\} = \left\{ {Q_{11} \varepsilon_{x} + Q_{12} \varepsilon_{\theta } ,Q_{12} \varepsilon_{x} + Q_{22} \varepsilon_{\theta } ,Q_{66} \gamma_{x\theta } } \right\} $$
(9)

where σx, σθ and τxθ are stress components; εx, εθ, and γxθ are strain components; Qij are the reduced stiffnesses [24].

Strain relations are given by [39]:

$$ \left\{ \begin{gathered} \varepsilon_{x} \hfill \\ \varepsilon_{\theta } \hfill \\ \gamma_{x\theta } \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} \varepsilon_{x}^{0} \hfill \\ \varepsilon_{\theta }^{0} \hfill \\ \gamma_{x\theta }^{0} \hfill \\ \end{gathered} \right\} + z\left\{ \begin{gathered} \varphi_{x} \hfill \\ \varphi_{\theta } \hfill \\ 2\varphi_{x\theta } \hfill \\ \end{gathered} \right\} $$
(10)

where \({\varepsilon }_{{x}}^{0}\), \(\varepsilon_{\theta }^{0}\), and \({\gamma}_{{x\,\theta}}^{0}\) are midplane strains; φx, φθ, and φxθ are surface curvatures.

The strain–displacement relationship according to the Donnell nonlinear shell theory is given as [38]

$$ \left\{ {\varepsilon_{x}^{0} ,\varepsilon_{\theta }^{0} ,\gamma_{x\theta }^{0} } \right\} = \left\{ {\frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} ,\frac{1}{R}\left( {\frac{\partial v}{{\partial \theta }} + w} \right){ + }\frac{1}{2}\left( {\frac{\partial w}{{R\partial \theta }}} \right)^{2} ,\frac{\partial v}{{\partial x}} + \frac{1}{R}\frac{\partial u}{{\partial \theta }} + \frac{1}{R}\frac{\partial w}{{\partial \theta }}\frac{\partial w}{{\partial x}}} \right\} $$
(11)
$$ \left\{ {\varphi_{x} ,\varphi_{\theta } ,\varphi_{x\theta } } \right\} = \left\{ { - \frac{{\partial^{2} w}}{{\partial x^{2} }}, - \frac{1}{{R^{2} }}\frac{{\partial^{2} w}}{{\partial \theta^{2} }}, - \frac{1}{R}\frac{{\partial^{2} w}}{\partial x\partial \theta }} \right\} $$
(12)

The internal moments and forces can be expressed as:

$$ \begin{gathered} \left\{ {\begin{array}{*{20}c} {M_{x} } \\ {M_{\theta } } \\ {M_{x\theta } } \\ \end{array} } \right\} = \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\left\{ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{\theta } } \\ {\tau_{x\theta } } \\ \end{array} } \right\}z{\text{ d}}z} , \hfill \\ \left\{ {\begin{array}{*{20}c} {N_{x} } \\ {N_{\theta } } \\ {N_{x\theta } } \\ \end{array} } \right\} = \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\left\{ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{\theta } } \\ {\tau_{x\theta } } \\ \end{array} } \right\}{\text{ d}}z} \hfill \\ \end{gathered} $$
(13)

Inserting Eqs. (9) and (10) in Eq. (13) yields

$$ {\mathbf{\rm N}} = {\mathbf{S}} \cdot {{\varvec{\upvarepsilon}}} $$
(14)

in which ε and N are stated as

$$ \begin{gathered} {{\varvec{\upvarepsilon}}}_{{}}^{{\text{T}}} = \left\{ {\varepsilon_{x}^{0} ,\varepsilon_{\theta }^{0} ,\gamma_{x\theta }^{0} ,\varphi_{x} ,\varphi_{\theta } ,2\varphi_{x\theta } } \right\}, \\ {\mathbf{\rm N}}_{{}}^{{\text{T}}} = \left\{ {N_{x} ,N_{\theta } ,N_{x\theta } ,M_{x} ,M_{\theta } ,M_{x\theta } } \right\}, \\ \end{gathered} $$
(15)

and S is

$$ {\mathbf{S}} = \left[ {\begin{array}{*{20}c} {\mathbf{A}} & {\mathbf{B}} \\ {\mathbf{B}} & {\mathbf{D}} \\ \end{array} } \right] $$
(16)

In Eq. (16), A, B and D are, respectively, the coefficient matrixes of bending, coupling, and stretching stiffnesses:

$$ {\mathbf{A}} = \left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & 0 \\ {A_{12} } & {A_{22} } & 0 \\ 0 & 0 & {A_{66} } \\ \end{array} } \right], \, {\mathbf{B}} = \left[ {\begin{array}{*{20}c} {B_{11} } & {B_{12} } & 0 \\ {B_{12} } & {B_{22} } & 0 \\ 0 & 0 & {B_{66} } \\ \end{array} } \right], \, {\mathbf{D}} = \left[ {\begin{array}{*{20}c} {D_{11} } & {D_{12} } & 0 \\ {D_{12} } & {D_{22} } & 0 \\ 0 & 0 & {D_{66} } \\ \end{array} } \right], $$
(17)

In particular, the following relation can be found

$$ \begin{gathered} A_{11} = A_{22} , \, A_{66} = \left( {A_{11} - A_{12} } \right)/2, \\ B_{11} = B_{22} , \, B_{66} = \left( {B_{11} - B_{12} } \right)/2, \\ D_{11} = D_{22} , \, D_{66} = \left( {D_{11} - D_{12} } \right)/2. \\ \end{gathered} $$
(18)

Substituting Eqs. (11) and (12) into Eq. (14), we can obtain

$$ \begin{gathered} N_{x} = \frac{{A_{12} w}}{R} + \frac{{A_{12} }}{R}\frac{\partial v}{{\partial \theta }} + \frac{{A_{12} }}{{2R^{2} }}\left( {\frac{\partial w}{{\partial \theta }}} \right)^{2} - \frac{{B_{12} }}{{R^{2} }}\frac{{\partial^{2} w}}{{\partial \theta^{2} }} + A_{11} \frac{\partial u}{{\partial x}} + \frac{1}{2}A_{11} \left( {\frac{\partial w}{{\partial x}}} \right)^{2} - B_{11} \frac{{\partial^{2} w}}{{\partial x^{2} }}, \hfill \\ N_{\theta } = \frac{{A_{11} w}}{R} + \frac{{A_{11} }}{R}\frac{\partial v}{{\partial \theta }} + \frac{{A_{11} }}{{2R^{2} }}\left( {\frac{\partial w}{{\partial \theta }}} \right)^{2} - \frac{{B_{11} }}{{R^{2} }}\frac{{\partial^{2} w}}{{\partial \theta^{2} }} + A_{12} \frac{\partial u}{{\partial x}} + \frac{1}{2}A_{12} \left( {\frac{\partial w}{{\partial x}}} \right)^{2} - B_{12} \frac{{\partial^{2} w}}{{\partial x^{2} }}, \hfill \\ N_{x\theta } = \frac{{A_{11} - A_{12} }}{2R}\frac{\partial u}{{\partial \theta }} + \frac{{A_{11} - A_{12} }}{2}\frac{\partial v}{{\partial \theta }} + \frac{{A_{11} - A_{12} }}{2R}\frac{\partial w}{{\partial x}}\frac{\partial w}{{\partial \theta }} - \frac{{B_{11} - B_{12} }}{R}\frac{{\partial^{2} w}}{\partial x\partial \theta }, \hfill \\ \end{gathered} $$
(19)
$$ \begin{gathered} M_{x} = \frac{{B_{12} w}}{R} + \frac{{B_{12} }}{R}\frac{\partial v}{{\partial \theta }} + \frac{{B_{12} }}{{2R^{2} }}\left( {\frac{\partial w}{{\partial \theta }}} \right)^{2} - \frac{{D_{12} }}{{R^{2} }}\frac{{\partial^{2} w}}{{\partial \theta^{2} }} + B_{11} \frac{\partial u}{{\partial x}} + \frac{1}{2}B_{11} \left( {\frac{\partial w}{{\partial x}}} \right)^{2} - D_{11} \frac{{\partial^{2} w}}{{\partial x^{2} }}, \hfill \\ M_{\theta } = \frac{{B_{11} w}}{R} + \frac{{B_{11} }}{R}\frac{\partial v}{{\partial \theta }} + \frac{{B_{11} }}{{2R^{2} }}\left( {\frac{\partial w}{{\partial \theta }}} \right)^{2} - \frac{{D_{11} }}{{R^{2} }}\frac{{\partial^{2} w}}{{\partial \theta^{2} }} + B_{12} \frac{\partial u}{{\partial x}} + \frac{1}{2}B_{12} \left( {\frac{\partial w}{{\partial x}}} \right)^{2} - D_{12} \frac{{\partial^{2} w}}{{\partial x^{2} }}, \hfill \\ M_{x\theta } = \frac{{B_{11} - B_{12} }}{2R}\frac{\partial u}{{\partial \theta }} + \frac{{B_{11} - B_{12} }}{2}\frac{\partial v}{{\partial x}} + \frac{{B_{11} - B_{12} }}{2R}\frac{\partial w}{{\partial \theta }}\frac{\partial w}{{\partial x}} - \frac{{D_{11} - D_{12} }}{R}\frac{{\partial^{2} w}}{\partial x\partial \theta }. \hfill \\ \end{gathered} $$
(20)

The radial excitation force − f (positive outward) is

$$ - f = - f_{0} \cos \left( {n\theta } \right)\sin \left( {\frac{\pi x}{L}} \right)\cos \left( {{\varvec{\varOmega}}t} \right) $$
(21)

The Hamilton principle is used as follows

$$ \delta \int_{{t_{1} }}^{{t_{2} }} {\left( {T - U - W} \right){\text{ d}}t = 0} $$
(22)

where the kinetic energy T, the strain energy U, and the work W done by the excitation force are given as follows

$$ \begin{gathered} T = \frac{1}{2}\int_{0}^{L} {\int_{0}^{2\pi } {\int_{ - h/2}^{h/2} \rho \left( {\dot{u}_{1}^{2} + \dot{u}_{2}^{2} + \dot{u}_{3}^{2} } \right) \, R{\text{ d}}z{\text{d}}\theta {\text{d}}x} } \\ { = }\frac{1}{2}\int_{0}^{L} {\int_{0}^{2\pi } {\left[ {I_{0} \left( {\dot{u}^{2} + \dot{v}^{2} + \dot{w}^{2} } \right) - I_{1} \left( {2\dot{u}\frac{{\partial \dot{w}}}{\partial x} + 2\dot{v}\frac{{\partial \dot{w}}}{R\partial \theta }} \right) + I_{2} \left( {\frac{{\partial \dot{w}}}{\partial x}} \right)^{{2}} + I_{2} \left( {\frac{{\partial \dot{w}}}{R\partial \theta }} \right)^{{2}} } \right] \, R{\text{ d}}\theta {\text{d}}x} } \\ \end{gathered} $$
(23)
$$ \begin{gathered} U = \frac{1}{2}\int_{0}^{L} {\int_{0}^{2\pi } {\int_{ - h/2}^{h/2} {\left( {\sigma_{x} \varepsilon_{x} + \sigma_{\theta } \varepsilon_{\theta } + \tau_{x\theta } \gamma_{x\theta } } \right)} \, R{\text{ d}}z{\text{d}}\theta {\text{d}}x} } \\ { = }\frac{1}{2}\int_{0}^{L} {\int_{0}^{2\pi } {{{\varvec{\upvarepsilon}}}^{{\text{T}}} \cdot {\mathbf{N}} \, R{\text{ d}}\theta {\text{d}}x} } \\ \end{gathered} $$
(24)
$$ W = \int_{0}^{L} {\int_{0}^{2\pi } {\left( { - fw} \right) \, R{\text{ d}}\theta {\text{d}}x} } $$
(25)

where “\(\cdot{}\)” denotes the time derivative of a function; I0, I1, I2 are expressed as

$$ I_{0} = \int_{ - h/2}^{h/2} \rho {\text{ d}}z, \, I_{1} = \int_{ - h/2}^{h/2} {\rho \, z} {\text{ d}}z = 0, \, I_{2} = \int_{ - h/2}^{h/2} {\rho \, z^{2} } {\text{ d}}z. $$
(26)

By using Eq. (22), one can obtain the nonlinear governing equations:

$$ \frac{{\partial N_{x\theta } }}{R\partial \theta } + \frac{{\partial N_{x} }}{\partial x} = I_{0} \ddot{u} - I_{1} \frac{{\partial \ddot{w}}}{\partial x} $$
(27)
$$ \frac{{\partial N_{\theta } }}{R\partial \theta } + \frac{{\partial N_{x\theta } }}{\partial x} = I_{0} \ddot{v} - I_{1} \frac{{\partial \ddot{w}}}{R\partial \theta } $$
(28)
$$ \begin{gathered} - \frac{{N_{\theta } }}{R} + \frac{1}{{R^{2} }}\frac{{\partial N_{\theta } }}{\partial \theta }\frac{\partial w}{{\partial \theta }} + \frac{1}{{R^{2} }}\frac{{\partial^{2} M_{\theta } }}{{\partial \theta^{2} }} + \frac{{N_{\theta } }}{{R^{2} }}\frac{{\partial^{2} w}}{{\partial \theta^{2} }} + \frac{{\partial N_{x\theta } }}{\partial x}\frac{\partial w}{{R\partial \theta }} + \frac{{\partial N_{x\theta } }}{R\partial \theta }\frac{\partial w}{{\partial x}} + \frac{{\partial N_{x} }}{\partial x}\frac{\partial w}{{\partial x}} + 2\frac{{\partial^{2} M_{x\theta } }}{R\partial x\partial \theta } \hfill \\ + 2N_{x\theta } \frac{{\partial^{2} w}}{R\partial x\partial \theta } + \frac{{\partial^{2} M_{x} }}{{\partial x^{2} }} + N_{x} \frac{{\partial^{2} w}}{{\partial x^{2} }} = I_{0} \ddot{w} + I_{1} \left( {\frac{{\partial \ddot{u}}}{\partial x} + \frac{{\partial \ddot{v}}}{R\partial \theta }} \right) - I_{2} \left( {\frac{{\partial^{2} \ddot{w}}}{{\partial x^{2} }} + \frac{{\partial^{2} \ddot{w}}}{{R^{2} \partial \theta^{2} }}} \right) - f \hfill \\ \end{gathered} $$
(29)

The following simply supported boundary condition is considered:

$$ v = w = N_{x} = M_{x} = 0{ (}x = 0,L{)} $$
(30)

where Nx and Mx represent the axial force and bending moment per unit length, respectively.

After applying Donnell’s assumption in Eqs. (27–29), i.e., neglecting the rotary and in-plane inertia, the Airy stress function F is introduced to express the axial force, circumferential force, and shear force: [38, 40,41,42]

$$ N_{x} = \frac{1}{{R^{2} }}\frac{{\partial^{2} F}}{{\partial \theta^{2} }}, \, N_{\theta } = \frac{{\partial^{2} F}}{{\partial x^{2} }}, \, N_{x\theta } = - \frac{1}{R}\frac{{\partial^{2} F}}{\partial x\partial \theta }. $$
(31)

It can be noted that Eq. (31) automatically satisfies Eqs. (27) and (28).

The compatibility conditions can be written as

$$ \frac{{\partial^{2} \varepsilon_{\theta }^{0} }}{{\partial x^{2} }} + \frac{{\partial^{2} \varepsilon_{x}^{0} }}{{R^{2} \partial \theta^{2} }} - \frac{{\partial^{2} \gamma_{x\theta }^{0} }}{R\partial x\partial \theta } = \left( {\frac{{\partial^{2} w}}{\partial x\partial \theta R}} \right)^{2} - \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{2} w}}{{R^{2} \partial \theta^{2} }} + \frac{{\partial^{2} w}}{{R\partial x^{2} }} $$
(32)

Let us reconsider Eq. (14), which can be transformed to

$$ \left\{ \begin{gathered} \varepsilon_{x}^{0} \hfill \\ \varepsilon_{\theta }^{0} \hfill \\ \gamma_{x\theta }^{0} \hfill \\ \end{gathered} \right\} = {\mathbf{A}}^{ - 1} \left\{ {\begin{array}{*{20}c} {N_{x} } \\ {N_{\theta } } \\ {N_{x\theta } } \\ \end{array} } \right\} + \left( { - {\mathbf{A}}^{ - 1} {\mathbf{B}}} \right)\left\{ \begin{gathered} \varphi_{x} \\ \varphi_{\theta } \\ 2\varphi_{x\theta } \\ \end{gathered} \right\} $$
(33)
$$ \left\{ {\begin{array}{*{20}c} {M_{x} } \\ {M_{\theta } } \\ {M_{x\theta } } \\ \end{array} } \right\} = {\mathbf{BA}}^{ - 1} \left\{ {\begin{array}{*{20}c} {N_{x} } \\ {N_{\theta } } \\ {N_{x\theta } } \\ \end{array} } \right\} + \left( {{\mathbf{D}} - {\mathbf{BA}}^{ - 1} {\mathbf{B}}} \right)\left\{ \begin{gathered} \varphi_{x} \\ \varphi_{\theta } \\ 2\varphi_{x\theta } \\ \end{gathered} \right\} $$
(34)

with

$$ \begin{gathered} {\mathbf{A}}^{ - 1} = \left[ {\begin{array}{*{20}c} {l_{1} } & {l_{2} } & 0 \\ {l_{2} } & {l_{1} } & 0 \\ 0 & 0 & {2\left( {l_{1} - l_{2} } \right)} \\ \end{array} } \right], \, - {\mathbf{A}}^{ - 1} {\mathbf{B}} = \left[ {\begin{array}{*{20}c} {k_{1} } & {k_{2} } & 0 \\ {k_{2} } & {k_{1} } & 0 \\ 0 & 0 & {\left( {k_{1} - k_{2} } \right)} \\ \end{array} } \right], \\ {\mathbf{BA}}^{ - 1} = \left[ {\begin{array}{*{20}c} {m_{1} } & {m_{2} } & 0 \\ {m_{2} } & {m_{1} } & 0 \\ 0 & 0 & {\left( {m_{1} - m_{2} } \right)} \\ \end{array} } \right], \, {\mathbf{D}} - {\mathbf{BA}}^{ - 1} {\mathbf{B}} = \left[ {\begin{array}{*{20}c} {n_{1} } & {n_{2} } & 0 \\ {n_{2} } & {n_{1} } & 0 \\ 0 & 0 & {\left( {n_{1} - n_{2} } \right)/2} \\ \end{array} } \right], \\ \end{gathered} $$
(35)

and

$$ \begin{gathered} \varepsilon_{x}^{0} = l_{1} N_{x} + l_{2} N_{\theta } + k_{1} \varphi_{x} + k_{2} \varphi_{\theta } , \hfill \\ \varepsilon_{\theta }^{0} = l_{2} N_{x} + l_{1} N_{\theta } + k_{2} \varphi_{x} + k_{1} \varphi_{\theta } , \hfill \\ \gamma_{x\theta }^{0} = 2\left( {l_{1} - l_{2} } \right)N_{x\theta } + 2\left( {k_{1} - k_{2} } \right)\varphi_{x\theta } , \hfill \\ \end{gathered} $$
(36)
$$ \begin{gathered} M_{x} = m_{1} N_{x} + m_{2} N_{\theta } + n_{1} \varphi_{x} + n_{2} \varphi_{\theta } , \hfill \\ M_{\theta } = m_{2} N_{x} + m_{1} N_{\theta } + n_{2} \varphi_{x} + n_{1} \varphi_{\theta } , \hfill \\ M_{x\theta } = \left( {m_{1} - m_{2} } \right)N_{x\theta } + \left( {n_{1} - n_{2} } \right)\varphi_{x\theta } , \hfill \\ \end{gathered} $$
(37)

where

$$ \begin{gathered} l_{1} = \frac{{A_{11} }}{{ - A_{12}^{2} + A_{11}^{2} }}, \, l_{2} = - \frac{{A_{12} }}{{ - A_{12}^{2} + A_{11}^{2} }}, \, \hfill \\ k_{1} = \frac{{A_{11} B_{11} - A_{12} B_{12} }}{{A_{12}^{2} - A_{11}^{2} }}, \, k_{2} = \frac{{A_{11} B_{12} - A_{12} B_{11} }}{{A_{12}^{2} - A_{11}^{2} }}, \hfill \\ m_{1} = \frac{{ - A_{11} B_{11} + A_{12} B_{12} }}{{A_{12}^{2} - A_{11}^{2} }}, \, m_{2} = \frac{{A_{12} B_{11} - A_{11} B_{12} }}{{A_{12}^{2} - A_{11}^{2} }}, \hfill \\ n_{1} = \frac{{A_{11} B_{11}^{2} - 2A_{12} B_{11} B_{12} + A_{11} B_{12}^{2} + A_{12}^{2} D_{11} - A_{11}^{2} D_{11} }}{{A_{12}^{2} - A_{11}^{2} }}, \hfill \\ n_{2} = \frac{{A_{11} B_{12} B_{11} - A_{12} \left( {B_{12}^{2} + B_{11}^{2} } \right) + A_{12}^{2} D_{12} + A_{11} \left( {B_{11} B_{12} - A_{11} D_{12} } \right)}}{{A_{12}^{2} - A_{11}^{2} }}. \hfill \\ \end{gathered} $$
(38)

By introducing Eqs. (12), (31) and (33) into Eq. (32), the compatibility equation is obtained as

$$ \begin{gathered} l_{1} \left( {\frac{1}{{R^{4} }}\frac{{\partial^{4} F}}{{\partial \theta^{4} }} + \frac{2}{{R^{2} }}\frac{{\partial^{4} F}}{{\partial x^{2} \partial \theta^{2} }} + \frac{{\partial^{4} F}}{{\partial x^{4} }}} \right) - k_{2} \left( {\frac{1}{{R^{4} }}\frac{{\partial^{4} w}}{{\partial \theta^{4} }} + \frac{2}{{R^{2} }}\frac{{\partial^{4} w}}{{\partial x^{2} \partial \theta^{2} }} + \frac{{\partial^{4} w}}{{\partial x^{4} }}} \right) \hfill \\ { = } - \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{2} w}}{{R^{2} \partial \theta^{2} }} + \frac{{\partial^{2} w}}{{R\partial x^{2} }} + \left( {\frac{{\partial^{2} w}}{\partial x\partial \theta R}} \right)^{2} \hfill \\ \end{gathered} $$
(39)

Inserting Eqs. (12), (31) and (37) in Eq. (29) and considering the damping effect, the motion equation is obtained as

$$ \begin{gathered} m_{2} \nabla^{4} F - n_{1} \nabla^{4} w - \frac{2}{{R^{2} }}\frac{{\partial^{2} F}}{\partial x\partial \theta }\frac{{\partial^{2} w}}{\partial x\partial \theta } - \frac{1}{R}\frac{{\partial^{2} F}}{{\partial x^{2} }} + \frac{1}{{R^{2} }}\frac{{\partial^{2} F}}{{\partial x^{2} }}\frac{{\partial^{2} w}}{{\partial \theta^{2} }} + \frac{1}{{R^{2} }}\frac{{\partial^{2} F}}{{\partial \theta^{2} }}\frac{{\partial^{2} w}}{{\partial x^{2} }} \hfill \\ = I_{0} \ddot{w} + I_{1} \left( {\frac{{\partial \ddot{u}}}{\partial x} + \frac{{\partial \ddot{v}}}{R\partial \theta }} \right) - I_{2} \left( {\frac{{\partial^{2} \ddot{w}}}{{\partial x^{2} }} + \frac{{\partial^{2} \ddot{w}}}{{R^{2} \partial \theta^{2} }}} \right) - f + ch\dot{w} \hfill \\ \end{gathered} $$
(40)

where \(\nabla^{4}\)\(={\left[{\partial}^{2}{/}\left({\partial}{{x}}^{2}\right){+}{\partial}^{2}{/}\left({{R}}{\partial}{\theta}^{2}\right)\right]}^{2}\); c is the damping coefficient.

Now, we have obtain two governing equations, i.e., the compatibility equation (39) and the equation of motion (40), which contain two functions F and w. The displacement function w can be written as

$$ \begin{gathered} w\left( {x,\theta ,t} \right) = \sum\limits_{n = 1}^{ + \infty } {\sum\limits_{m = 1}^{{M_{1} }} {\left[ {A_{m,n} \cos \left( {n\theta } \right)\sin \left( {m\pi x/L} \right) + B_{m,n} \sin \left( {n\theta } \right)\sin \left( {m\pi x/L} \right)} \right]} } \\ + \sum\limits_{m = 1}^{{M_{2} }} {A_{2m - 1,0} } \sin \left[ {\left( {2m - 1} \right)\pi x/L} \right] \\ \end{gathered} $$
(41)

where t represents time; driven mode Am,n, companion mode Bm,n and axisymmetric mode A2m-1,0 are unknown functions of t; the axisymmetric modes A2,0, A4,0, …, etc. are eliminated here because their effects on average shell deflection are zero [38, 41]; n denotes the circumferential wave number and m denotes the axial half-wave number.

The solution of compatibility equation is given by

$$ F = F_{p} + F_{h} $$
(42)

where Fp and Fh are the particular solution and homogeneous solution, respectively.

By introducing Eq. (41) into Eq. (39), the particular solution Fp for (M1 = 1, M2 = 2) can be given as [41]

$$ \begin{gathered} F_{p} = c_{1} \left( t \right)\sin \left( {\pi x/L} \right) + c_{2} \left( t \right)\cos \left( {2\pi x/L} \right) + c_{3} \left( t \right)\sin \left( {3\pi x/L} \right) + c_{4} \left( t \right)\sin \left( {n\theta } \right) \\ + c_{5} \left( t \right)\cos \left( {n\theta } \right) + c_{6} \left( t \right)\sin \left( {2n\theta } \right) + c_{7} \left( t \right)\cos \left( {2n\theta } \right) + c_{8} \left( t \right)\cos \left( {n\theta } \right)\sin \left( {\pi x/L} \right) \\ + c_{9} \left( t \right)\sin \left( {n\theta } \right)\sin \left( {\pi x/L} \right) + c_{10} \left( t \right)\cos \left( {n\theta } \right)\cos \left( {2\pi x/L} \right) \\ + c_{11} \left( t \right)\cos \left( {n\theta } \right)\cos \left( {4\pi x/L} \right) + c_{12} \left( t \right)\sin \left( {n\theta } \right)\cos \left( {2\pi x/L} \right) \\ + c_{13} \left( t \right)\sin \left( {n\theta } \right)\cos \left( {4\pi x/L} \right) \\ \end{gathered} $$
(43)

in which ci(t) are the functions of A1,n, B1,n, A1,0, and A3,0.

The homogeneous solution Fh in Eq. (42) is given by [40]

$$ F_{h} = \frac{1}{2}\widetilde{N}_{x} R^{2} \theta^{2} + \frac{1}{2}\widetilde{N}_{\theta } x^{2} - \widetilde{N}_{x\theta } xR\theta $$
(44)

where \(\widetilde{N}_{x}\), \(\widetilde{N}_{\theta}\) and \(\widetilde{N}_{x\theta}\) are the in-plane restraint stress resultants.

Consider that the displacement u is “on the average” zero at both ends of the shell (x = 0, L); the displacement v is continuous in the θ-direction “on the average,” i.e.,

$$ \begin{gathered} \int_{0}^{L} {\int_{0}^{2\pi } {\frac{\partial u}{{\partial x}} \, R{\text{d}}\theta {\text{d}}x} } = \int_{0}^{2\pi } {\left[ {u\left( {L,\theta } \right) - u\left( {0,\theta } \right)} \right] \, R{\text{d}}\theta } = 0, \hfill \\ \int_{0}^{L} {\int_{0}^{2\pi } {\frac{\partial v}{{\partial \theta }} \, R{\text{d}}\theta {\text{d}}x} } = \int_{0}^{L} {R\left[ {v\left( {x,2\pi } \right) - v\left( {x,0} \right)} \right]{\text{ d}}x} = 0. \hfill \\ \end{gathered} $$
(45)

Additionally, u and w are continuous in the circumferential coordinate “on the average,” and v is zero “on the average” at x = 0, L; thus, we have

$$ \int_{0}^{L} {\int_{0}^{2\pi } {N_{x\theta } \, R{\text{d}}\theta {\text{d}}x} } = 0 $$
(46)

By substituting Eqs. (19), (31), (42), (45), (46) into Eq. (30), it yields

$$ \left\{ \begin{gathered} \widetilde{N}_{x} = 0, \\ \widetilde{N}_{\theta } = \frac{{2A_{1,0} A_{11} }}{\pi R} + \frac{{n^{2} A_{1,n}^{2} A_{11} }}{{8R^{2} }} - \frac{{2A_{3,0} A_{11} }}{3\pi R} + \frac{{n^{2} B_{1,n}^{2} A_{11} }}{{8R^{2} }} \\ + \frac{{\pi^{2} A_{1,0}^{2} A_{12} }}{{4L^{2} }} + \frac{{\pi^{2} A_{1,n}^{2} A_{12} }}{{8L^{2} }} + \frac{{9\pi^{2} A_{3,0}^{2} A_{12} }}{{4L^{2} }} + \frac{{\pi^{2} B_{1,n}^{2} A_{12} }}{{8L^{2} }} \\ + \frac{{6\pi A_{3,0} B_{12} }}{{L^{2} }} + \frac{{2\pi A_{1,0} B_{12} }}{{L^{2} }} - \frac{{2A_{1,0} }}{{\pi Rl_{1} }} - \frac{{2A_{3,0} }}{{3\pi Rl_{1} }} + \frac{{2\pi A_{1,0} k_{2} }}{{L^{2} l_{1} }} \\ + \frac{{6\pi A_{3,0} k_{2} }}{{L^{2} l_{1} }}, \\ \widetilde{N}_{x\theta } = 0. \\ \end{gathered} \right. $$
(47)

Therefore, the Airy stress function F is obtained based on Eqs. (42–47).

Finally, substituting the Airy stress function F and Eq. (41) into Eq. (40), afterwards employing the Galerkin method, 2M1 + M2 second-order nonlinear coupled ODEs with respect to the generalized coordinates Am,n(t), Bm,n(t) and A2m-1,0(t) are obtained as follows

$$ \ddot{A}_{1,n} + 2\xi_{1,n} \omega_{1,n} \dot{A}_{1,n} + \omega_{1,n}^{2} A_{1,n} + {\text{Function}}_{1} \left[ {A_{1,n} ,B_{1,n}^{{}} ,A_{1,0} ,A_{3,0} } \right] = \frac{{f_{0} }}{{I_{{{f}}} }}\cos \left( {\Omega t} \right) $$
(48)
$$ \ddot{B}_{1,n} + 2\xi_{1,n} \omega_{1,n} \dot{B}_{1,n} + \omega_{1,n}^{2} B_{1,n} + {\text{Function}}_{2} \left[ {A_{1,n} ,B_{1,n}^{{}} ,A_{1,0} ,A_{3,0} } \right] = 0 $$
(49)
$$ \ddot{A}_{1,0} + 2\xi_{1,0} \omega_{1,0} \dot{A}_{1,0} + \omega_{1,0}^{2} A_{1,0} + {\text{Function}}_{3} \left[ {A_{1,n} ,B_{1,n}^{{}} ,A_{1,0} ,A_{3,0} } \right] = 0 $$
(50)
$$ \ddot{A}_{3,0} + 2\xi_{3,0} \omega_{3,0} \dot{A}_{3,0} + \omega_{3,0}^{2} A_{3,0} + {\text{Function}}_{4} \left[ {A_{1,n} ,B_{1,n}^{{}} ,A_{1,0} ,A_{3,0} } \right] = 0 $$
(51)

where Functioni (i = 1, 2, 3, 4) is listed in Appendix and If = I0 + I2(n2/R2 + π2/L2), ξ1,n = ch/(2Ifω1,n), M1 = 1, M2 = 2.

Here we employ the pseudo-arclength continuation method by using Matcont [43] to solve ODEs (48)–(51) numerically.

4 Results and discussion

At first, a simply supported isotropic cylindrical shell is considered for the validation analysis. The adopted parameters are: L = 0.2 m, R = 0.1 m, h = 0.247 × 10−3 m, ρ = 2796 kg/m3, µ  = 0.31, E = 71.02 × 109 Pa. Our results are compared with those given by Ref. [44], as shown in Table. 1. The comparison shows good agreement between them.

Table 1 Comparison of natural frequencies ω (Hz) of a simply supported isotropic circular cylindrical shell (m = 1)
Full size table

For further comparing the present model, a simply supported metal foam cylindrical shell is considered and its dimensionless natural frequencies are calculated. The parameters are: L/R = 0.2, h/R = 0.01, ρ* = 7850 kg/m3, µ  = 0.3, E* = 200 × 109 Pa. The results are compared with those in Ref. [45], as shown in Table 2. One can see that good agreement has been achieved between them.

Table 2 Comparison of dimensionless natural frequencies ωd = ωR(ρ*/E*)1/2 of a simply supported metal foam cylindrical shell (P-1, m = 1)
Full size table

At last, the nonlinear vibration of a simply supported homogeneous circular cylindrical shell is considered to prove the validity of the present derivation and method. The system parameters are: L = 0.2 m, R = 0.1 m, h = 0.247 × 10−3 m, ρ = 2796 kg/m3, µ  = 0.31, E = 71.02 × 109 Pa, f0 = 0.0012I0hω1,n2, ξ1,n = 0.0005, ξ1,0 = (ω1,0/ω1,n) ξ1,n, ξ3,0 = (ω3,0/ω1,n) ξ1,n, n = 6. It should be noted that w is defined positive outward in the present study, which is contrary to that defined in Ref. [41]. The comparison between the results from this paper and those given by Amabili et al. [41] is shown in Fig. 3. The result shows a quite excellent agreement between them, which verify the present analysis.

Fig. 3
figure 3

Comparison of frequency response of a simply supported homogeneous cylindrical shell: a driven mode; b companion mode; c first axisymmetric mode; d third axisymmetric mode

Full size image

In the following, the nonlinear forced vibration of the FG-GPLRMF cylindrical shell is investigated. Unless otherwise stated, the parameters are:

Em = 210GPa, µm = 0.3, ρm = 7850 kg/m3, L = 0.39 m, R = 0.5 m, h = 0.019 m, EGPL = 1010GPa, µ GPL = 0.186, ρGPL = 1060 kg/m3, tGPL = 1.5 × 10−9 m, lGPL = 2.5 × 10−6 m, wGPL = 1.5 × 10−6 m, f0 = 0.05I0hω1,n2, ξ1,n = 0.025, ξ1,0 = (ω1,0/ω1,n) ξ1,n, ξ3,0 = (ω3,0/ω1,n) ξ1,n.

The mode studied here is m = 1 and n = 8. When e1 = 0.3, WGPL = 1.0%, the natural frequencies of the FG-GPLRMF cylindrical shell are obtained as ω1,8 = 1903.44 Hz, ω1,0 = 1.01101ω1,8, ω3,0 = 2.01791ω1,8. This relation gives rise to the 1:1:1:2 internal resonances. Moreover, calculations show that within the range of e1 ∈ [0,0.5] and WGPL ∈ [0,0.01], the 1:1:1:2 internal resonance relation always exists.

The frequency–response curves of the FG-GPLRMF cylindrical shell are shown in Fig. 4. Here, Fig. 4b is a partially enlarged image of Fig. 4a. The maximum absolute value of the dimensionless amplitude of the generalized coordinates is shown hereafter. It can be seen that the response of the system is much more complicated than that in Fig. 3, which is due to the interaction of different modes in 1:1:1:2 internal resonances. Softening and hardening characteristics of nonlinearity coexist in the FG-GPLRMF cylindrical shell. It should be mentioned that there is no stable solution in internal resonance responses when Ω/ω1,8 ∈ (1.041, 1.083) ∪ (0.961, 0.978). Two stable solutions exist when Ω/ω1,8 ∈ (0.978, 0.986) ∪ (1.107, 1.121), while three stable solutions exist when Ω/ω1,8 ∈ (0.945, 0.956). In Fig. 4a, the driven mode produces a peak on branch “2.” Analysis shows that the generation of this peak is because of the participation of companion mode B1,8. The companion mode shows two nonzero branches: for branch “2” in the region of Ω/ω1,8 ∈ (0.978, 1.115), the companion mode appears through the pitchfork bifurcation (BPC) at Ω/ω1,8 = 1.115 of “zero” branch “1”; for branch “3” in the region of Ω/ω1,8 ∈ (0.947, 0.986), the companion mode appears through the pitchfork bifurcation (BPC) at Ω/ω1,8 = 0.947 of “zero” branch “4.” It should be noted that the travelling wave solution is produced as the companion mode appears. Besides, the amplitude-modulated (quasi-periodic) response appears in the interval Ω/ω1,8 ∈ (0.956, 0.979) ∪ (1.041, 1.107), which was bracketed by two Neimark–Sacker bifurcation points on branch “3” and branch “2.” Moreover, the present results are compared to those excluding the axisymmetric modes A1,0 and A3,0. The conclusion is that the emergence of additional branches “3” and “4” is due to the participation of these axisymmetric modes. If the axisymmetric modes are not considered, branches “3” and “4” in all the subfigures will disappear.

Fig. 4
figure 4

Frequency response of FG-GPLRMF cylindrical shell, case of 1:1:1:2 internal resonances (------, unstable solution; –––, stable solution; BPC, pitchfork bifurcation; NS, Neimark–Sacker bifurcation; e1 = 0.3; WGPL = 1.0%; P-1; GPL-I): a driven mode; b partially enlarged image of (a); c companion mode; d first axisymmetric mode; e third axisymmetric mode

Full size image

The variation of response with force amplitude of the FG-GPLRMF cylindrical shell for Ω/ω1,8 = 1.115 is shown in Fig. 5. It is seen that when the force amplitude reaches f0/(I0hω1,82) = 0.05, branch ‘‘2′’ appears from branch “1” through the pitchfork bifurcation (BPC). After this point, all the branches “1” of driven mode and axisymmetric modes increase with the force amplitude, while the branch “1” of the companion mode is always zero after branch “2” appears. It is clear that the emergence of the branch “2” of companion mode is due to the 1:1 internal resonance with the driven mode. Moreover, the stable solution on branch “2” is found to occur when f0/(I0hω1,82) ∈ (0.244, 0.274) for all the modes.

Fig. 5
figure 5

Force amplitude response of FG-GPLRMF cylindrical shell (------, unstable solution; –––, stable solution; BPC, pitchfork bifurcation; NS, Neimark–Sacker bifurcation; e1 = 0.3; WGPL = 1.0%; Ω/ω1,8 = 1.115; P-1; GPL-I): a driven mode; b companion mode; c first axisymmetric mode; d Third axisymmetric mode

Full size image

Figure 6 illustrates the time–response curves of the FG-GPLRMF cylindrical shell for Ω/ω1,8 = 1.115 and f0/(I0hω1,82) = 0.244 (the NS point in Fig. 5). One can see that the phase difference between the responses of driven mode and companion mode is π/2. Also, it is observed that the vibration period of non-axisymmetric modes is twice that of the axisymmetric modes.

Fig. 6
figure 6

Time response of FG-GPLRMF cylindrical shell (e1 = 0.3; WGPL = 1.0%; P-1; GPL-I): a driven mode; b companion mode; c first axisymmetric mode; d third axisymmetric mode

Full size image

Figure 7 shows frequency–response curves of the FG-GPLRMF cylindrical shell for different porosity coefficients, where only driven and companion modes are shown for brevity. Here, P-1 and GPL-I are chosen as the representative to discuss the effect of the porosity coefficient. As can be seen, the FG-GPLRMF cylindrical shell with no pores (e1 = 0) has the most branches of stable solution. There are two additional branches “5” and “6” in the driven and companion modes when e1 = 0 (Fig. 7a). These two branches disappear as the porosity coefficient increases, as can be seen in Fig. 7b. In addition, branches “3” and “4”, which are related to the axisymmetric modes, shrink obviously with the increasing porosity coefficient, indicating that the porosity coefficient plays a significant role on the mode interaction of FG-GPLRMF shells. Results show that the lower porosity coefficient leads to more obvious softening spring characteristics of the FG-GPLRMF shell.

Fig. 7
figure 7

Frequency response of FG-GPLRMF cylindrical shell with various e1 (------, unstable solution; ––– stable solution; WGPL = 1.0%; P-1; GPL-I): a e1 = 0; b e1 = 0.3; c e1 = 0.5

Full size image

Frequency–response curves of the FG-GPLRMF cylindrical shell for various kinds of porosity distribution are demonstrated in Figs. 8 and 7c. Figure 7c is the case of the P-1 shell. One can see that the porosity distribution influences significantly the frequency response of the FG-GPLRMF cylindrical shell. It is found that branches “3” and “4” of the P-2 shell separate into two parts, respectively. Comparing the driven modes of different porosity distribution, it is noted that for the P-1 shell, the region of branches “3” and “4” is the smallest; for the P-2 shell, branches “3” and “4” separate into two parts and move to the high-frequency region, and the branch “1” shrinks obviously compared with the other two types; for the P-3 shell, the region of branches “3” and “4” is the largest. Moreover, additional branches “5” and “6” are produced in P-3 shell, showing that evenly distributed pores make the shell exhibit the strongest modal interaction.

Fig. 8
figure 8

Frequency response of FG-GPLRMF cylindrical shell for different kinds of porosity distribution (------, unstable solution; stable solution; –––, e1 = 0.5; WGPL = 1.0%; GPL-I): a P-2; b P-3

Full size image

Figures 9 and 7c show frequency–response curves of FG-GPLRMF cylindrical shells with various GPL weight fractions. Figure 7c corresponds to the case of WGPL = 1%. Here, GPL-I and P-1 are chosen as the representative to analyze the influence of GPL weight fraction. Obviously, as the GPL weight fraction increases, branches “3” and “4” in both driven and companion modes reduce. Because these two branches are produced by the axisymmetric modes, this result demonstrates that the lager weight fraction weakens the modal interaction of the FG-GPLRMF cylindrical shell. This can be explained that the inclusion of GPLs enhances the structural stiffness, thereby weakening the nonlinear coupling caused by the large deformation of the shell.

Fig. 9
figure 9

Frequency response of FG-GPLRMF cylindrical shell for different GPL weight fractions (-------, unstable solution; –––, stable solution; e1 = 0.5; P-1; GPL-I): a WGPL = 0; b WGPL = 0.5%

Full size image

Figures 10 and 7c illustrate frequency–response curves of the FG-GPLRMF cylindrical shell with different types of GPL distribution. Figure 7c is the case of the GPL-I shell. It is found that the branch “4” of the GPL-II shell separates into two parts. Comparing the driven modes of different GPL distribution, one can see that branches “3” and “4” of the GPL-II shell are the largest, while branch “4” of the GPL-I shell is the smallest. Moreover, additional branches “5” and “6” appear in the GPL-II shell. The above phenomenon indicates that the GPL-II distribution makes the shell have the strongest modal interaction compared to the other two types of GPL distribution.

Fig. 10
figure 10

Frequency response of FG-GPLRMF cylindrical shell for different kinds of GPL distribution (------, unstable solution; –––, stable solution; e1 = 0.5; WGPL = 1%; P-1): a GPL-II; b GPL-III

Full size image

5 Conclusions

The 1:1:1:2 internal resonances are found to exist in nonlinear vibration of FG-GPLRMF cylindrical shells, and detailed analysis on this complex phenomenon is carried out. Donnell’s nonlinear shell theory and the Airy stress function are employed to derive the equation of motion and compatibility equation. Afterward, the Galerkin method and the pseudo-arclength continuation technique are used to numerically analyze the present nonlinear problem. The results show that in the case of 1:1:1:2 internal resonances, the frequency response of the FG-GPLRMF cylindrical shell is very complex; the traveling wave occurs; and the system exhibits both softening and hardening spring characteristics. In certain frequency regions, the response does not have a stable solution at all, while in certain frequency regions there are two or even three stable solutions at the same time. The effects of the GPL weight fraction and porosity coefficient on the frequency response are strongly related to the types of GPL distribution and porosity distribution, respectively. Different types of GPL distribution and porosity distribution influence obviously the modal interaction. Moreover, it is found that the inclusion of GPLs can weaken the nonlinear modal coupling of the FG-GPLRMF shells.