Nonlinear free vibration analysis of doubly curved shells

Abstract

In this work, Sanders–Koiter’s nonlinear shell theory is applied to study the nonlinear moderate-amplitude vibrations of doubly curved shells using two different approximations of the strain–displacement relations for shallow and non-shallow shells. The nonlinear equations of motion are determined by Lagrange equations. The displacement fields are approximated using an expansion of trigonometric functions that satisfy geometric (essential) and nonlinear natural boundary conditions. Therefore, the backbone curves are determined using multiple shooting method and an Euler–Newtonian predictor–corrector continuation algorithm; the Floquet theory is applied to determine the stability of the periodic solutions. The obtained backbone curves show multiple internal resonances due to the coupling between normal modes. The mode influence of some selected points on the backbone curves is depicted to analyze the internal resonances, which can represent loss of stability and sudden changes in the dynamic behavior of shells undergoing moderate-amplitude vibrations. Saddle–node, Newmark–Sacker and period-doubling bifurcations are observed.

1 Introduction

Due to their structural efficiency, thin shells are widely used structural elements in several engineering branches and are mainly conceived with a relatively small thickness when compared to their span. In many cases, shells are subjected to dynamic loads that can induce large-amplitude vibrations; then, a geometric nonlinear model considering large displacements should be considered in analysis. The literature on shell vibrations is vast, and detailed review studies of this subject were presented by [1,2,3] and [4].

Nonlinear systems can exhibit extremely complex behavior, and phenomena include jumps, bifurcations, saturation, subharmonic and superharmonic vibrations, internal resonances and chaos [5]. One of the main characteristics of nonlinear free vibrations is its dependence between frequency and amplitude/energy of vibration. This dependence can be characterized by the determination of the frequency–amplitude plots (FAPs) or frequency–energy plots (FEPs), which are curves that relate the maximum amplitude (for a given generalized coordinate) or energy of a periodic orbit with its frequency. These curves, named backbone curves, represent the nonlinear normal modes (NNMs) of the structure and describe, among other things, the degree of nonlinearity of the dynamic system, whether there is hardening or softening (typically turning to hardening for larger amplitudes) behavior of the system when subjected to large-amplitude vibrations. [5] describe several applications where NNMs represent a useful framework for the structural dynamicist: (a) the representation of NNMs in a FEP is a robust and accurate tool to decide whether or not the linear framework is still applicable and to determine which modes are sensitive to the nonlinearity; (b) forced resonances in nonlinear systems occur in their neighborhoods and therefore provide valuable insight into the structure of the resonances; (c) damped dynamics closely follows the NNMs of the underlying undamped system; (d) NNMs provide effective bases for constructing reduced-order models; (e) the fact that NNMs spatially confine vibrational energy can find applications in vibration mitigation of mechanical systems.

The determination of the backbone curves of shells is the object of study in several works. [6] investigated the nonlinear free vibration of functionally graded orthotropic cylindrical shells considering the shear stresses. Nonlinear frequencies depending on the amplitude of vibration are investigated through a parametric study. [7] analyzed the nonlinear free vibrations of shells based on the six-parameter shell theory. The frequency–response curves of cylindrical and spherical shells were obtained by applying time periodic discretization and pseudo arc-length continuation techniques. [8] investigated the geometrically nonlinear free vibration analysis of doubly curved composite spherical shell panels using the nonlinear finite element analysis (FEA). The frequency–amplitude relations for the nonlinear free vibrations of spherical shell panel were computed. The effects of curvature, thickness, vibration amplitude, modular ratio, stacking sequence, lamination scheme and different support conditions on the frequency ratio were examined. [9] studied nonlinear free vibrations of heterogeneous orthotropic shallow shells using a generalized first-order shear deformation theory. They applied this theory to study several types of shells such as circular cylindrical panels, spherical panels and hyperbolic paraboloidal panels. [10] studied the linear and geometrically nonlinear vibrations of the three-layered functionally graded shallow shells. Effects of different material distributions, lamination schemes, curvatures, boundary conditions, and geometrical parameters on natural frequencies and backbone curves were analyzed.

Internal resonance is essentially a nonlinear vibration phenomenon and occurs when energy is transferred between several modes, causing NNMs to interact during a general motion of the system. Several works describe the presence of internal resonances in the analysis of free and forced vibrations of shells. [11] investigated the internal resonance of a thin-walled hyperelastic cylindrical shell composed of incompressible Mooney–Rivlin material under radial harmonic excitation, and the condition of 2:1 internal resonance of the shell was studied. [12] studied the geometrically nonlinear forced vibration response of truncated thin conical shells using the Novozhilov shell theory. They detected different types of complex nonlinear behavior such as pitchfork, Newmark–Sacker and period-doubling bifurcations of the forced vibration responses arising from internal resonances. [13] investigated the energy transfer of rectangular plates when 1:3 internal resonance is obtained between different modes due to transversal and in-plane harmonic excitation. [14] studied the dynamics of elastic circular cylindrical shells subjected to multi-harmonic excitation. The shells exhibit many kinds of nonlinear behavior such as simple periodic vibration, quasi-periodic oscillations, subharmonic response, period-doubling bifurcations and chaos. It was found that the presence of a 1:1:2:2 internal resonance is the reason for the complexity of the response. [15] studied the nonlinear response of an imperfect circular cylindrical shell, simply supported at the edges, to harmonic excitation and analyzed the 1:1:1:1 internal resonance considering four vibration modes with the same natural frequency. [16] studied resonant response of an imperfect cylindrical shell using Donnell’s nonlinear shallow shell theory and the nonlinear modal interactions and couplings between two asymmetric vibration modes with near commensurable natural frequencies in a 1:2 ratio. As a result of the circumferential symmetry, each mode exhibits a 1:1 internal resonance, leading to a possible 1:1:2:2 multiple internal resonance. Different problems of internal resonances were studied for circular cylindrical and doubly curved shells in references [17,18,19,20,21]. Many studies explore the phenomenon of internal resonances occurring between modes of a system with linear natural frequencies having integer ratios. They often determine solutions using perturbation techniques that exploit this property [11, 15, 19]. However, internal resonances may occur without commensurate linear natural frequencies [13], highlighting the possibility of missing important nonlinear phenomena when using perturbation techniques limited to small-amplitude motions [5].

Experimental analyses have been conducted that demonstrate how damped dynamics closely follow the NNMs of the underlying undamped system. This relationship is exemplified by experiments conducted on planar cantilever beams, employing a continuous wavelet transformation to trace the temporal evolution of instantaneous frequencies [5]. Experiments have also been conducted on an aluminum cylindrical panel to identify the nonlinear response of the fundamental mode [22]. Additionally, linear free vibration analyses have been carried out for polymeric and composite cylindrical shells [23, 24]. Similar analyses were performed for cylindrical shells, considering thermal and hygrothermal effects [25, 26]. Moreover, internal resonances, specifically the 1:1:2 internal resonance, have been examined using a perturbation method in the context of harmonic forced excitation of spherical shells [27], and these findings were subsequently validated through experiments [28].

Despite several works on nonlinear dynamic behavior of shells, some shell geometries have not been studied yet, especially doubly curved non-shallow shells. Recently, [29] applied Sanders–Koiter’s shell theory to obtain the natural vibration modes and natural frequencies of thin shallow and non-shallow elliptic paraboloids, hyperbolic paraboloids and parabolic conoids; the obtained results showed good agreement with FEA.

In this study, the nonlinear free vibrations of shells are studied through the determination of backbone curves. For this, the Sanders–Koiter’s nonlinear shell theory is applied using two different approximations: one for shallow and the other for non-shallow shells. The nonlinear equilibrium equations are derived through Lagrange equations using an expansion that satisfies the geometric (essential) and nonlinear natural boundary conditions. The FAP and FEP are obtained by applying a combination of multiple shooting method and numerical continuation. First, the backbone curves of a shallow spherical panel is obtained; numerical results are compared with the literature and finite element method, showing a good agreement. Next, the backbone curves of three non-shallow shell geometries—spherical panel, hyperbolic paraboloid and parabolic conoid—are determined, again showing good agreement with the FEA. The percentage influence of each mode in the time response is determined to characterize internal resonances. Finally, the stability of the backbone curves is determined by using Floquet’s theory. Saddle–node, Newmark–Sacker and period-doubling bifurcations are observed.

2 Mathematical formulation

Consider a generic thin shell, with constant thickness h, made of an isotropic homogeneous elastic material with Young’s module E, Poisson ratio $\nu$ and density $\rho$. In this section, Koiter’s theory of thin shells will be briefly presented. Regarding index notation, Greek indices take values 1 and 2 and Latin indices take values 1, 2 and 3, unless another definition is presented. Summation convention with respect to repeated indices is also adopted. A description of the differential geometry relations of the mid-surface of the shell used in this work is presented in Appendix A.

According to Koiter’s theory [30,31,32], the Green–Lagrange strain tensor of the shell can be approximated by:

$$\begin{aligned} {\textbf{E}}\approx \gamma _{\alpha \beta }{\textbf{M}}^\alpha \otimes {\textbf{M}}^\beta +\xi ^3\rho _{\alpha \beta }{\textbf{M}}^\alpha \otimes {\textbf{M}}^\beta \end{aligned}$$

(1)

where the triad of vectors ${\textbf{M}}^i$ are the contravariant basis of the mid-surface (see in Appendix A); the symbol $\otimes$ denotes the dyadic product; $\gamma _{\alpha \beta }$ and $\rho _{\alpha \beta }$ are, respectively, and the components of the stretching and bending tensors given by Eqs. (2a) and (2b).

$$\begin{aligned}&\gamma _{\alpha \beta }=\frac{1}{2}\left( g_{\alpha \beta }-G_{\alpha \beta }\right) \end{aligned}$$

(2a)

$$\begin{aligned}&\rho _{\alpha \beta }=\kappa _{\alpha \beta }-K_{\alpha \beta } \end{aligned}$$

(2b)

where $g_{\alpha \beta }$ and $G_{\alpha \beta }$ are, respectively, the components of the metric tensor in the current and reference configurations; $\kappa _{\alpha \beta }$ and $K_{\alpha \beta }$ are, respectively, the components of the curvature tensor in the current and reference configurations. The values of $g_{\alpha \beta }$ and $\kappa _{\alpha \beta }$ depend on the position vector ${\textbf{r}}$, while $G_{\alpha \beta }$ and $K_{\alpha \beta }$ depend on ${\textbf{R}}$, as presented in Appendix A.

Equation (2) is highly nonlinear, and some approximations can be considered to reduce the coupling level between the nonlinear terms in the resultant equilibrium equations. In cases where the displacement of the shell is of the order of magnitude of the shell thickness or less, the nonlinear terms of the bending tensor can be neglected [3, 12, 29, 33,34,35]. Furthermore, in most cases, the membrane components of the displacement are small compared to the transversal components, and hence, the nonlinear terms involving $u_\alpha$ can be removed [35]. Combining these simplifications, the components of the stretching and bending tensors can be written as:

$$\begin{aligned}&\gamma _{\alpha \beta }=\frac{1}{2}\left( u_{\alpha |\beta } +u_{\beta |\alpha }+G^{\sigma \lambda }K_{\alpha \sigma } K_{\beta \lambda }u_3^2+u_{3,\alpha }u_{3,\beta }\right) \end{aligned}$$

(3a)

$$\begin{aligned}&\rho _{\alpha \beta }=\Gamma ^{\gamma }_{\alpha \beta }u_{3|\gamma }-u_{3|\alpha \beta } \end{aligned}$$

(3b)

Moreover, if the shell is geometrically shallow, then the curvature is small and terms involving the components $K_{\alpha \beta }$ can also be neglected [35, 36], resulting in:

$$\begin{aligned}&\gamma _{\alpha \beta }=\frac{1}{2}\left( u_{\alpha |\beta }+u_{\beta |\alpha }+u_{3,\alpha }u_{3,\beta }\right) \end{aligned}$$

(4a)

$$\begin{aligned}&\rho _{\alpha \beta }=\Gamma ^{\gamma }_{\alpha \beta }u_{3,\gamma }-u_{3,\alpha \beta } \end{aligned}$$

(4b)

The strain energy, according to Koiter’s shell theory, is given by:

$$\begin{aligned} U= & {} \iint _{\Omega }C^{\alpha \beta \theta \lambda }\left( \frac{h}{2}\gamma _{\alpha \beta } \gamma _{\theta \lambda }+\frac{h^3}{24}\rho _{\alpha \beta }\rho _{\theta \lambda }\right) \nonumber \\{} & {} \sqrt{G}\textrm{d}\xi ^1\textrm{d}\xi ^2 \end{aligned}$$

(5)

where $C^{\alpha \beta \lambda \theta }=\frac{E}{2(1-\nu ^2)}\left( \left( G^{\alpha \theta }G^ {\beta \lambda }+G^{\alpha \lambda }G^{\beta \theta }\right) \right.$$\left. (1-\nu )+2\nu G^{\alpha \beta }G^{\lambda \theta }\right)$ are the components of the fourth-order constitutive tensor of a linear elastic material considering plane stress state; G is the determinant of the matrix composed by the components $G_{\alpha \beta }$ of the metric tensor. Finally, the kinetic energy, by neglecting rotary inertia, is given by:

$$\begin{aligned} T=\iint _{\Omega }\rho \frac{h}{2}G^{ij}\dot{u}_i\dot{u}_j\sqrt{G}\textrm{d}\xi ^1\textrm{d}\xi ^2 \end{aligned}$$

(6)

In order to reduce the system to a finite number of degrees of freedom, the displacements fields $u_i$ are expanded using the approximate functions given by:

$$\begin{aligned} u_k\left( \xi ^1,\xi ^2,t\right) \approx \sum _{i=1}^{m_k}\sum _{j=1}^{n_k}{{u_{k_{ij}}} \left( t\right) {\phi _{k_{ij}}}\left( \xi ^1,\xi ^2\right) } \end{aligned}$$

(7)

where $m_k$ and $n_k$ are the number of functions for each curvilinear coordinate; ${u_{k_{ij}}}\left( t\right)$ are the unknown time-dependent generalized coordinates; and $\phi _{k_{ij}}\left( \xi ^1,\xi ^2\right)$ are the shape functions properly chosen to satisfy the boundary conditions.

The system of nonlinear equilibrium equations of motion, for the free vibration problem of shells, can be determined via Euler–Lagrange equations as:

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}\left( \frac{\partial L}{\partial {{{\dot{u}}_{k_{ij}}}}}\right) -\frac{\partial L}{\partial {u_{k_{ij}}}}=0 \end{aligned}$$

(8)

where $L=K-U$ is the Lagrange functional of the shell. The resulting system can be rewritten in the matrix form as:

$$\begin{aligned} \begin{gathered} {\textbf{M}}\ddot{{\textbf{U}}}+{\textbf{K}} {\textbf{U}}+{\textbf{F}}({\textbf{U}})={\textbf{0}} \end{gathered} \end{aligned}$$

(9)

where ${\textbf{M}}$ is the mass matrix; ${\textbf{K}}$ is the linear stiffness matrix; ${\textbf{U}}=[u_{k_{ij}}]$ is a vector of dimension $N=m_k n_k$ containing all generalized coordinates $u_{k_{ij}}$, for $k=1\dots 3$, $i=1\dots m_k$ and $j=1\dots n_k$; and $\ddot{{\textbf{U}}}$ denotes the second time derivative of the vector ${\textbf{U}}$. N represents the number of degrees of freedom of the approximation. The vector function ${\textbf{F}}$ contains all quadratic and cubic nonlinear stiffness terms and can be written as:

(10)

where ${\textbf{F}}_k$ is a sparse matrix of dimension $N\times N^k$ due to approximations (3) and (4) of the strain–displacement relations; is equal to the product (k times) where the symbol represents the Kronecker product.

The system described by equation (9) is investigated using a combination of the multiple shooting method [37] and an Euler–Newtonian predictor-corrector continuation algorithm [38] to determine periodic solutions (see Appendix B). This methodology is used to extract the backbone curves, i.e., the FAP and FEP, which represent of the NNMs of the shells. Finally, the stability of the periodic solutions is evaluated via the Floquet theory. Since the system (9) is autonomous and conservative, at least one of the Floquet multipliers is always 1 and is not considered in the stability checks. A classical case is to obtain periodic solutions which are marginally stable; therefore, the tolerance for the stability check has to be chosen carefully as the multipliers often lies exactly on the unit cycle [39]. Hence, a circle slightly larger than the unit (1.00001) was considered in the determination of stability via Floquet theory.

2.1 Modal decomposition

There are NNMs that can be internally resonant without necessarily having commensurate linear natural frequencies due to the coupling between them during a general motion of the system [40]. In order to analyze these interactions, it is convenient to decompose the time response of the shell in the vector space of the linear vibration modes [41]. For this, the time response of each displacement field is rewritten in modal coordinates as:

$$\begin{aligned} u_k\left( \xi ^1,\xi ^2,t\right) =\sum _{m=1}^{N}{\mu _m\left( t\right) {\psi _k^m\left( \xi ^1,\xi ^2\right) }} \end{aligned}$$

(11)

where $\mu _m(t)$ is the modal coordinate amplitude of the correspondent eigenfunction $\psi _k^m\left( \xi ^1,\xi ^2\right)$, which is determined by:

$$\begin{aligned} \psi _k^m\left( \xi ^1,\xi ^2\right) =\sum _{i=1}^{m_k}\sum _{j=1}^{n_k}{{z^m_{k_{ij}}} {\phi _{k_{ij}}}\left( \xi ^1,\xi ^2\right) } \end{aligned}$$

(12)

The values of ${z^m_{k_{ij}}}$ are the elements of the eigenvector ${\textbf{z}}^m=[z^m_{k_{ij}}]$, determined by the eigenvalue/eigenvector problem resulted by the linearization of the Eq. (9):

$$\begin{aligned} \begin{aligned} ({\textbf{K}}-\omega _m^2{\textbf{M}}){\textbf{z}}^m=0 \\ {\textbf{z}}^m\cdot {\textbf{M}}{\textbf{z}}^n=\delta _{mn} \end{aligned} \end{aligned}$$

(13)

where $\omega _m$ is the correspondent linear natural frequency of the vibration mode ${\textbf{z}}^m$, which is normalized by the mass matrix.

The modal response is determined projecting the displacement vector ${\textbf{U}}$ onto the orthogonal vector space of the linear vibration modes, according to

$$\begin{aligned} \varvec{\mu }(t)={\textbf{Z}}^{\textsf{T}}{\textbf{M}}{\textbf{U}}(t) \end{aligned}$$

(14)

where ${\textbf{Z}}=[{\textbf{z}}^1 \dots {\textbf{z}}^N]$ is a matrix formed by all eigenvectors ${\textbf{z}}^m$ and $\varvec{\mu }$ is a vector which elements are the modal coordinate responses $\mu _m(t)$. The vibration modes and eigenfunctions are sorted according to their linear natural frequencies.

In order to evaluate the percentage influence of each mode for a given periodic steady-state response of the shell, one can determine the average of the projection of each modal response onto the displacement vector along the time response curve, according to:

$$\begin{aligned} \text {Mode influence}=\int _0^1{\frac{\mu _m(\tau ){\textbf{z}}^m\cdot {\textbf{U}}(\tau )}{{\textbf{U}}(\tau )\cdot {\textbf{U}}(\tau )}\textrm{d}\tau } \end{aligned}$$

(15)

where $\tau =\omega t/(2\pi )$ is the normalized time and $\omega$ is the angular frequency of the periodic orbit.

3 Numerical results

In the present work, the backbone curves are obtained for shells with three different mid-surfaces, as illustrated in Fig. 1: (a) spherical panel; (b) parabolic conoid; and (c) hyperbolic paraboloid. These figures also display the equations of $Z(\xi ^1,\xi ^2)$ that mathematically define the mid-surface as a function of curvilinear coordinates together with the other functions $X(\xi ^1,\xi ^2)=\xi ^1$ and $Y(\xi ^1,\xi ^2)=\xi ^2$. In all cases, the domain $\Omega$ is composed by the set $0\le \xi ^1\le a$ and $0\le \xi ^2\le b$, which also represents the projection of the shell’s mid-surface on the horizontal plane.

Fig. 1

Mid-surface geometry: a spherical panel; b parabolic conoid and c hyperbolic paraboloid

In order to validate the present formulation, a numerical approximation of the backbone curve for the finite element problem is also presented. This solution was obtained using the commercial software Abaqus with a $50 \times 50$ mesh and S4 elements, which is a quadrilateral fully integrated, general-purpose, finite-membrane-strain shell element with 4 nodes with 3 translations and 3 rotations per node [42]. This mesh is large enough to guarantee numerical convergence. The backbone curves are determined from a nonlinear time domain solution with a small damping and the initial conditions corresponding to displacement with the shape of the first mode and zero velocity. The vibration frequency is determined by calculating the period between two consecutive points of maximum kinetic energy.

3.1 Shallow spherical panel

The first example is a simply supported movable (i.e. in-plane displacement orthogonal to the edge is allowed, while the out-of-plane displacement and the one tangent to the edge are restrained) spherical shallow shell with radius $R=1~\text {m}$, horizontal projections with dimensions $a=b=0.1~\text {m}$, thickness $h=0.001~\text {m}$, Young’s module $E=206~\text {GPa}$, Poisson ratio $\nu =0.3$ and density $\rho =7850~\mathrm {kg/m^3}$. The geometric (essential) and natural boundary conditions at the four edges are given by:

$$\begin{aligned} u_2&=u_3=N_1=M_1=0 \text { at }\xi ^1=0,a \end{aligned}$$

(16a)

$$\begin{aligned} u_1&=u_3=N_2=M_2=0 \text { at }\xi ^2=0,b \end{aligned}$$

(16b)

where $N_\alpha$ is the normal force and $M_\alpha$ is the bending moment per unit of length in the direction of ${\textbf{m}}^\alpha$. The shape functions $\phi _{k_{ij}}(\xi ^1,\xi ^2)$, which satisfy the boundary conditions (16), were adopted as:

$$\begin{aligned} {\phi _1}_{ij}= & {} \left\{ \frac{1+(-1)^i}{2}\sin {\left( \frac{i\pi \xi ^1}{a}\right) } +\frac{1+(-1)^{i+1}}{2}\right. \nonumber \\{} & {} \quad \times \left. \cos {\left( \frac{i\pi \xi ^1}{a}\right) }\right\} \sin {\left( \frac{(2j-1)\pi \xi ^2}{b}\right) } \nonumber \\ \quad {\phi _2}_{ij}= & {} \sin {\left( \frac{(2i-1)\pi \xi ^1}{a}\right) }\left\{ \frac{1+(-1)^j}{2} \sin {\left( \frac{j\pi \xi ^2}{b}\right) }\right. \nonumber \\{} & {} \quad \left. +\frac{1+(-1)^{j+1}}{2}\cos {\left( \frac{j\pi \xi ^2}{b}\right) }\right\} \nonumber \\ \quad {\phi _3}_{ij}= & {} \sin {\left( \frac{(2i-1)\pi \xi ^1}{a}\right) }\sin {\left( \frac{(2j-1)\pi \xi ^2}{b}\right) } \end{aligned}$$

(17)

Fig. 2

Maximum amplitude vibration of the generalized coordinate $u_{3_{11}}(t)$ versus normalized frequency $\omega /\omega _1$ of the backbone curve of the fundamental mode for a shallow spherical panel—in a for the model with 9 dof and in b for the model with 22 dof and 27 dof ; NS, Newmark–Sacker bifurcations. The dashed curves represent unstable solutions; meanwhile, the solid curves represent stable solutions. NS, Newmark–Sacker bifurcations; SN, saddle–node bifurcations; PD, period-doubling bifurcations. (Color figure online)

By adopting expansions of Eq. (17), only vibrations that are symmetrical along the axis $\xi ^1=a/2$ and $\xi ^2=b/2$ are considered. The shape functions $\phi _{1_{ij}}$ and $\phi _{2_{ij}}$ present both $\sin (i\pi \xi ^1/a)\sin (j\pi \xi ^2/b)$ (for even i and odd j) and $\cos (i\pi \xi ^1/a)\sin (j\pi \xi ^2/b)$ (for odd i and j) terms. Term $\cos (i\pi \xi ^1/a)\sin (j\pi \xi ^2/b)$ guarantees that the displacement $u_1$ is allowed at $\xi ^1=0,a$. Although term $\sin (i\pi \xi ^1/a)\sin (j\pi \xi ^2/b)$ does not change the displacement $u_1$ at $\xi ^1=0,a$, without the inclusion of this term, the natural boundary condition on the in-plane normal force $N_1$, which is essentially nonlinear, is not satisfied at the edge; therefore, it is also necessary in the expansion [43].

Fig. 3

Total energy versus normalized frequency $\omega /\omega _1$ of the backbone curve of the fundamental mode for a shallow spherical panel; , stable periodic orbit of the model with 9 dof; , stable periodic orbit of the model with 22 dof; , unstable solution of the model with 22 dof; , stable periodic orbit of the model with 27 dof; , unstable solution of the model with 27 dof;, Abaqus’ backbone curve; NS, Newmark–Sacker bifurcations; SN, saddle–node bifurcations; PD, period-doubling bifurcations. (Color figure online)

This shell was previously studied by [44], who determined the backbone curve using a model with 9 dof, and [34], who determined the forced vibration response curves for models with 9 and 22 dof considering an harmonic vertical concentrated load applied at the center of the shell. Similar expansions were also adopted in the present work—with 9 dof ($m_1=n_1=m_2=n_2=2$ and $m_3=n_3=1$) and 22 dof ($m_1=n_1=m_2=n_2=3$ and $m_3=n_3=2$). In order to seek convergence, a model with 27 dof ($m_k=n_k=3$) was also employed. The natural fundamental frequency of the shell is $\omega _1=952.2\times 2\pi ~\text {rad/s}$. The comparison between the results from the literature with the results of the present work is depicted in Fig. 2a, b.

Fig. 4

Time responses in modal coordinates of the periodic solutions a-d of the shallow spherical panel. , mode 1; ; mode 2; , mode 3; , mode 4. (Color figure online)

Table 1 Percentage mode influence of the first two most influential modes determined by the periodic orbits at the points a-d of the backbone curve of the shallow spherical panel for the model with 22 dof in Fig. 3

As illustrated by Fig. 2a, the backbone curve of the model with 9 dof shows an initial softening behavior followed by a hardening behavior as the vibration amplitude reaches the value of about 1.3h, which corresponds to a normalized frequency $\omega /\omega _1=0.75$. This response is in good agreement with the curves found in the literature. The model with 22 dof shows a more complex curve, as illustrated in Fig. 2b. The model with 27 dof shows very similar behavior to the model with 22 dof, with the stable part being almost identical between the two models. Due to the internal resonances between multiple vibration modes, multiple branches arise from the fundamental response curve. This nonlinear behavior is also depicted in Fig. 3, which shows the relation between the total energy versus the frequency of the periodic orbits of the shell. As shown in the figure, internal resonances are also characterized by a sudden increase in the shell’s total energy. Furthermore, the response of FEA aligns consistently with the analytical solution for the main branch of the backbone. The points with energy levels higher than $0.6~\textrm{J}$ depict aperiodic solutions, after which, as the energy decreases, the solution converges to the main branch of the backbone. As the FEA solution is derived from a damped free vibration analysis, considering the first linear vibration mode as the initial condition, the FEA solution fails to capture new internal resonance branches, which manifest as an energy increase that cannot occur in a scenario of free damped vibration.

To better understand the nonlinear behavior of the shell, the time response curves in modal coordinates of four points of the backbone curve of the model with 22 dof in Fig. 3 are displayed in the graphs of Fig. 4a–d. The mode influence at each of these four points is determined using Eq. (15). The percentage of mode influence of the first two most influential modes at each point is presented in Table 1. To characterize the internal resonances, the table also presents the dominant frequency of each modal response, which is a multiple of the frequency of the periodic orbit $\omega$. Only the responses of the most influential modes (1-4) were highlighted in the graphs of Fig. 4, and their correspondent eigenfunctions $\psi ^m_{k}(\xi ^1,\xi ^2)$ are depicted in Fig. 5, which also presents the linear natural frequencies of these modes. Despite being internally resonant, the linear frequencies of the resonant modes do not exhibit an integer ratio, i.e., $\omega _2/\omega _1=2.7$, $\omega _3/\omega _1=2.7$, $\omega _4/\omega _1=4.7$.

In the 108 dof model, four periodic orbits (a–d) taken from the backbone curve in Fig. 6a were analyzed to characterize the different branches along the curve. Therefore, the percentage mode influences at these points are determined by using Eq. (15), and results are presented in Table 2.

Fig. 5

Modal shape functions of the shallow spherical panel

Fig. 6

Backbone curves of the non-shallow spherical panel for the models with 48 dof , 75 dof , 108 dof and 147 dof . , Abaqus’ backbone curve. In a total energy versus normalized frequency, and, in b maximum amplitude of the generalized coordinate $u_{3_{11}}$ versus normalized frequency are given. The dashed curves represent unstable solutions; meanwhile, the solid curves represent stable solutions. NS, Newmark–Sacker bifurcation. (Color figure online)

The main branch (points a and d) presents a stable solution mostly represented by the first vibration mode (Fig. 5a), as shown in the time response of Fig. 4a. However, the influence of mode 2 (Fig. 5b) increases, as shown in the response curve of Fig. 4d for point (d). The second branch (b) presents a 5:1 internal resonance due to the interaction between modes 1 and 4 (Fig. 5d), as depicted in the time response of Fig. 4b. This branch presents an unstable solution delimited by saddle–node bifurcations. The branch (c) contains multiple changes of the stability due to saddle–node bifurcations, and it is mostly characterized by a 3:1 internal resonance between modes 1 and 3 (Fig. 5c), as illustrated by the time response of Fig. 4c. After a Newmark–Sacker bifurcation near the energy level of $1~\textrm{J}$ and frequency $\omega =0.75\omega _1$, the solution becomes unstable.

3.2 Non-shallow spherical panel

Now, the present formulation will be applied for the study of non-shallow shells. For this, a non-shallow spherical panel with the following geometric and physical properties was studied (see Fig. 1a): $R=0.1~\text {m}$, $a=b=0.1~\text {m}$, $h=0.001~\text {m}$, $E=206~\text {GPa}$, $\nu =0.3$ and $\rho =7850~\mathrm {kg/m^3}$. The shell is simply supported with immovable edges, i.e.,

$$\begin{aligned}&u_1=u_2=u_3=M_1=0 \text { at }\xi ^1=0,a \end{aligned}$$

(18a)

$$\begin{aligned}&u_1=u_2=u_3=M_2=0 \text { at }\xi ^2=0,b \end{aligned}$$

(18b)

The shape functions $\phi _{k_{ij}}(\xi ^1,\xi ^2)$, which satisfy the boundary conditions (18), are defined by Eqs. (19). Similar to the previous example, these functions were chosen considering only the symmetrical effects along the axes $\xi ^1=a/2$ and $\xi ^2=b/2$.

$$\begin{aligned} \begin{aligned}&{\phi _1}_{ij}=\sin {\left( \frac{(2i)\pi \xi ^1}{a}\right) }\sin {\left( \frac{(2j-1)\pi \xi ^2}{b}\right) } \\&{\phi _2}_{ij}=\sin {\left( \frac{(2i-1)\pi \xi ^1}{a}\right) }\sin {\left( \frac{(2j)\pi \xi ^2}{b}\right) } \\&{\phi _3}_{ij}=\sin {\left( \frac{(2i-1)\pi \xi ^1}{a}\right) }\sin {\left( \frac{(2j-1)\pi \xi ^2}{b}\right) } \end{aligned} \end{aligned}$$

(19)

Table 2 Percentage mode influence of the first two most influential modes determined by the periodic orbits at the points a–d of the backbone curve of the non-shallow spherical panel for the model with 108 dof in Fig. 6a

In order to check the convergence of the solution, four models with 48 dof ($m_k=n_k=4$), 75 dof ($m_k=n_k=5$), 108 dof ($m_k=n_k=6$) and 147 dof ($m_k=n_k=7$) were built. The fundamental natural frequency is $\omega _1=8{,}271.6\times 2\pi ~\text {rad/s}$. Figure 6a, b shows the backbone curves of these four models. Convergence is observed in the stable segments of the backbones and at the beginning of the unstable segments in models with 108 and 147 dof. In both models, the solution becomes unstable around $\omega =0.985\omega _1$. Consequently, the shell displays aperiodic vibrations due to a Newmark–Sacker bifurcation, which cannot be evaluated using the shooting method. The same behavior could also be detected using FEA. Close to the bifurcation point, the Abaqus’ solution approaches the analytical backbone. Notably, for energy levels below $2~\textrm{J}$, both solutions exhibit highly similar results.

The main branch (points a and b) of the backbone is predominantly characterized by mode 1 (Fig. 10a) with increasing influence of mode 3 (Fig. 10b). The internal resonances of the non-shallow spherical panel have a fundamental difference when compared to the shallow spherical panel. Notably, the branches of internal resonances activate in-plane modes and are unstable. In point (c), there is a 9:1 internal resonance between modes 1 and 40 (Fig. 10c). At point (d), there is a 13:1 internal resonance between modes 1 and 44 (Fig. 10d). These internal resonances, although mathematically determined, do not represent real vibrations of the structure and may vanish with the addition of new modes in the model.

3.3 Hyperbolic paraboloid

The third example is a non-shallow hyperbolic paraboloid with the following geometric and physical properties (see Fig. 1b): $f_1=0.02~\text {m}$, $f_2=0.02~\text {m}$, $a=b=0.1~\text {m}$, $h=0.001~\text {m}$, $E=206~\text {GPa}$, $\nu =0.3$ and $\rho =7850~\mathrm {kg/ m^3}$. The boundary conditions are the same as the previous example: simply supported with immovable edges (see Eq. (18)). As the shell is symmetric along $\xi ^1=a/2$ and $\xi ^2=b/2$, the shape functions from Eq. (19) were also adopted in this case. Therefore, only symmetric vibrations along these two axes were considered. Figure 7a, b shows the backbone curve for the hyperbolic paraboloid for models considering 48 dof ($m_k=n_k=4$), 75 dof ($m_k=n_k=5$) and 108 dof ($m_k=n_k=6$). Figure 7a displays the total energy versus the normalized frequency, while Fig. 7b shows the maximum amplitude of the generalized coordinate $u_{3_{33}}$ versus the normalized frequency. The fundamental natural frequency of the shell is $\omega _1=6{,}391.1\times 2\pi ~\text {rad/s}$. Among the structures examined, the hyperbolic paraboloid is the only one that exhibits initial stiffness gain. While the models with 75 and 108 degrees of freedom converge in the stable segments of the backbone, the model with 48 degrees of freedom does not exhibit any internal resonances. However, as additional degrees of freedom are introduced to the system, new internal resonances arise. The FEP determined via the finite element analysis exhibits the same behavior as the analytical solution. The FEA solution closely resembles the analytical one for energy levels below $10~\textrm{J}$ and becomes nearly identical for energy levels below $1~\textrm{J}$.

Again, some points (a-c) along the backbone curve of the model with 75 dof were selected and are displayed in Fig. 7a to characterize the modal coupling in the response. Therefore, the modal influences of the most dominant modes, determined by Eq. (15), are displayed in Table 3; for each point—the modes with more influence are depicted in Fig. 11. The table also presents the dominant frequency of each modal response.

In the main branch, the free vibrations are most characterized by the first mode (Fig. 11a), with the increasing presence of mode 12 (Fig. 11b) exhibiting a 3:1 internal resonance, as illustrated by the points (a) and (c). The ratio between the linear natural frequencies of these two modes is $\omega _{12}/\omega _1=2.3$, demonstrating once again that internal resonances can occur without having commensurable linear frequencies. At point (b), there is an 7:1 internal resonance with the interaction between modes 1 and 26. Similar to the previous example, the branches of internal resonances that activate in-plane modes (e.g., mode 26 depicted in Fig. 11) are unstable, thus not physically realizable, and may vanish with the addition of new modes to the model.

Fig. 7

Backbone curves of the hyperbolic paraboloid for the models with 48 dof , 75 dof and 108 dof . , Abaqus’ backbone curve. In a total energy versus normalized frequency, and, in b maximum amplitude of the generalized coordinate $u_{3_{33}}$ versus normalized frequency are given. The dashed curves represent unstable solutions; meanwhile, the solid curves represent stable solutions. NS, Newmark–Sacker bifurcation; SN, saddle–node bifurcation. (Color figure online)

3.4 Parabolic conoid

Now, the results of the parabolic conoid are presented, which has the following geometric and physical properties (see Fig. 1c): $f_1=0.03~\text {m}$, $f_2=0.02~\text {m}$, $a=b=0.1~\text {m}$, $h=0.001~\text {m}$, $E=206~\text {GPa}$, $\nu =0.3$ and $\rho =7850~\mathrm {kg/m^3}$. The shell is simply supported with immovable edges, according to Eq. (18). Unlike the other shells, this one presents symmetry only along the axis $\xi ^2=b/2$, so the shape functions ${\phi _1}_{ij}$ were chosen considering symmetric vibrations along this axes as

$$\begin{aligned} {\phi _1}_{ij}= & {} \sin {\left( \frac{i\pi \xi ^1}{a}\right) }\sin {\left( \frac{(2j-1)\pi \xi ^2}{b}\right) }\nonumber \\ {\phi _2}_{ij}= & {} \sin {\left( \frac{i\pi \xi ^1}{a}\right) }\sin {\left( \frac{2j\pi \xi ^2}{b}\right) } \nonumber \\ {\phi _3}_{ij}= & {} \sin {\left( \frac{i\pi \xi ^1}{a}\right) }\sin {\left( \frac{(2j-1)\pi \xi ^2}{b}\right) } \end{aligned}$$

(20)

In order to check convergence, four models with 48 dof ($m_k=n_k=4$), 75 dof ($m_k=n_k=5$), 108 dof ($m_k=n_k=6$) and 147 dof ($m_k=n_k=7$) were built. The fundamental natural frequency of the shell is $\omega _1=3{,}623.9\times 2\pi ~\text {rad/s}$. The backbone curves for these models are depicted in Figs. 8a, b. At the beginning of the curve, the four models show the same softening behavior, but the model with 48 dof starts to display hardening behavior for a frequency value around $\omega =0.994\omega _1$. Overall, the model with 75 dof presents a behavior similar to the models with 108 and 147 but without the unstable internal resonances. The models with 108 and 147 dof exhibit internal resonances with the activation of in-plane modes in unstable branches of the backbone that do not represent real vibrations of the structure. In the model with 147 dof, after a Newmark–Sacker bifurcation the solution becomes unstable. The backbone determined via FEA exhibits the same behavior as the backbone determined by the model with 147 dof, once again confirming the efficiency of the present formulation in the analysis of free vibrations under moderate-amplitude conditions.

Table 3 Percentage mode influence of the first two most influential modes determined by the periodic orbits of the points a–c at the backbone curve of the non-shallow hyperbolic paraboloid for the model with 75 dof in Fig. 7a

4 Conclusion

This study explored the fundamental nonlinear normal mode of doubly curved shells using two different approximations of the Sanders–Koiter shell theory—one for shallow shells and the other for non-shallow shells. The existing literature on semianalytical solutions of shells was limited to specific geometries due to the constraints of orthogonal theories. A tensor formulation was applied to study shells with four different geometries, including shallow and non-shallow spherical panels, a hyperbolic paraboloid, and a parabolic conoid.

The frequency–energy relations of the shells were compared with results obtained with a finite element method using Abaqus, demonstrating good agreement. These results can serve as a benchmark for future researchers working in the field of non-shallow doubly curved shells. For future works, due to its reliability and generality, the tensor formulation can be further applied to analyze shells with different geometries. Also, the determined backbone curves offer valuable insights into the energy levels at which linear theories are applicable or not.

Table 4 shows the results of mode influence (Eq. 15) of the periodic orbits of points a-c on the backbone curve for the model with 147 dof depicted in Fig. 8a—the modes with more influence are depicted in Fig. 12. The response is majorly influenced by the first mode (Fig. 12a) with increasing influence of modes 2 (Fig. 12b) and 4 (Fig. 12c), exhibiting 2:1 internal resonances.

To analyze internal resonances, time responses of periodic orbits in modal coordinates were used to determine the mode influence of each mode, highlighting that some modes can be internally resonant without having an integer ratio between their linear natural frequencies. Thus, significant internal resonances have been characterized in the backbone curves of the shells. Particularly, in the case of the shallow spherical panel, these internal resonances represent abrupt changes in the shell’s vibrations, accompanied by a sudden increase in the total energy. For non-shallow shells, certain branches exhibit non-persistent unstable internal resonances with the activation of in-plane vibration modes. However, the main branch of the backbones displays stable internal resonances, and the activated modes exert an increasing influence with rising energy levels.

Appendices

Appendix A Differential geometric relations of the shell’s mid-surface

Fig. 8

Backbone curves of the parabolic conoid for the models with 48 dof , 75 dof , 108 dof and 147 dof . , Abaqus’ backbone curve. In a total energy versus normalized frequency, and, in b maximum amplitude of the generalized coordinate $u_{3_{13}}$ versus normalized frequency are given. The dashed curves represent unstable solutions; meanwhile, the solid curves represent stable solutions. NS, Newmark–Sacker bifurcation. (Color figure online)

In this Appendix, the differential relations of the mid-surface are briefly presented; a detailed description of the tensor formulations can be found in the literature [31, 32]. The shell is oriented in Cartesian directions $x^1$, $x^2$ and $x^3$ with unit vectors ${\textbf{e}}_1$, ${\textbf{e}}_2$ and ${\textbf{e}}_3$, and its mid-surface is parameterized by vectors ${\textbf{R}}$ and ${\textbf{r}}$, in reference and current configurations. Vectors ${\textbf{R}}$ and ${\textbf{r}}$ are function of curvilinear coordinates $\xi ^1$ and $\xi ^2$, respectively, and are given by:

$$\begin{aligned}&{\textbf{R}}\!=\!X(\xi ^1,\xi ^2){\textbf{e}}_1\!+\!Y(\xi ^1,\xi ^2){\textbf{e}}_2\!+\!Z(\xi ^1,\xi ^2){\textbf{e}}_3 \end{aligned}$$

(A1a)

$$\begin{aligned}&{\textbf{r}}={\textbf{R}}+{\textbf{u}} \end{aligned}$$

(A1b)

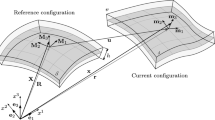
where $\xi ^1$ and $\xi ^2$ are the curvilinear coordinates of the mid-surface, which can be interpreted as Cartesian coordinates taking values in some planar domain $\Omega$, according to $\left( \xi _1,\xi _2\right) \in \Omega$; functions X, Y and Z mathematically describe the mid-surface in reference configuration and ${\textbf{u}}$ is the field vector that describes the displacement of the shell’s mid-surface. Figure 9 displays the shells coordinates in reference and current configuration.

Vectors ${\textbf{X}}$ and ${\textbf{x}}$ describe the position of any point of the shell in both reference and current configurations. The kinematics of the shell follows the Kirchhoff–Love hypotheses, so vectors ${\textbf{X}}$ and ${\textbf{x}}$ are defined as:

$$\begin{aligned} {\textbf{X}}\,&={\textbf{R}}+\xi ^3{\textbf{M}}^3 \end{aligned}$$

(A2a)

$$\begin{aligned} {\textbf{x}}\,&={\textbf{r}}+\xi ^3{\textbf{m}}^3 \end{aligned}$$

(A2b)

where $-h/2\le \xi ^3\le h/2$ is the coordinate that defines the position of a point of the shell perpendicular to the mid-surface. The triad of vectors ${\textbf{M}}_i$ ($i=1,2,3$) compose the covariant basis of the mid-surface in the reference configuration and are described in Eqs. (A3) as a function of vector ${\textbf{R}}$ and the curvilinear coordinates $\xi ^1$ and $\xi ^2$

$$\begin{aligned}{} & {} {\textbf{M}}_1=\frac{\partial {\textbf{R}}}{\partial \xi ^1}=X_{,1}{\textbf{e}}_1+Y_{,1}{\textbf{e}}_2 +Z_{,1}{\textbf{e}}_3 \end{aligned}$$

(A3a)

$$\begin{aligned}{} & {} {\textbf{M}}_2=\frac{\partial {\textbf{R}}}{\partial \xi ^2}=X_{,2}{\textbf{e}}_1+Y_{,2}{\textbf{e}}_2 +Z_{,2}{\textbf{e}}_3 \end{aligned}$$

(A3b)

$$\begin{aligned}{} & {} {\textbf{M}}_3=\frac{{\textbf{M}}_1\times {\textbf{M}}_2}{\sqrt{G}} \end{aligned}$$

(A3c)

where vectors ${\textbf{M}}_1$ and ${\textbf{M}}_2$, defined in Eqs. (A3a) and (A3b), are tangent to the coordinate lines $\xi ^\alpha$ ($\alpha =1,2$); ${\textbf{M}}_3$, defined in Eq. (A3c), is a unit vector perpendicular to the mid-surface of the shell; and $\sqrt{G}=|{\textbf{M}}_1\times {\textbf{M}}_2|$. Notation $Z_{,\alpha }$ represents the derivative of Z with respect to $\xi ^\alpha$ where $\alpha =1,2$.

The contravariant basis is composed by vectors ${\textbf{M}}^i$ ($i=1,2,3$) and can be determined by

$$\begin{aligned} {\textbf{M}}_i\cdot {\textbf{M}}^j=\delta _i^j \end{aligned}$$

(A4)

where $\delta _i^j$ is the Kronecker’s delta. It can be demonstrated by Eqs. (A3) and (A4) that ${\textbf{M}}^3={\textbf{M}}_3$ and both ${\textbf{M}}_i$ and ${\textbf{M}}^i$ bases are necessary in the analysis of shells when the orthogonal condition ${\textbf{M}}_1\cdot {\textbf{M}}_2=0$ is not satisfied.

Table 4 Percentage mode influence of the first two most influential modes determined by the periodic orbits at the points a–c of the backbone curve of the non-shallow parabolic conoid for the model with 147 dof in Fig. 8a

Fig. 9

Shell’s motion description

The metric tensor ${\textbf{G}}={\textbf{M}}_i\otimes {\textbf{M}}^i$ is used to measure the length of a curve along the surface, and its components in both covariant and contravariant bases are given by Eqs. (A5a) and (A5b), respectively, as:

$$\begin{aligned}{} & {} G_{ij}={\textbf{M}}_i\cdot {\textbf{M}}_j \end{aligned}$$

(A5a)

$$\begin{aligned}{} & {} G^{ij}={\textbf{M}}^i\cdot {\textbf{M}}^j \end{aligned}$$

(A5b)

An infinitesimal vector $\textrm{d}{\textbf{R}}$ located on the mid-surface of the shell can be expressed in terms of the tangent vectors ${\textbf{M}}_\alpha$ and the infinitesimals $\textrm{d}\xi ^\alpha$, according to:

$$\begin{aligned} \textrm{d}{\textbf{R}}={\textbf{M}}_\alpha \textrm{d}\xi ^\alpha \end{aligned}$$

(A6)

The curvature tensor ${\textbf{K}}$ relates both the infinitesimal vectors $\textrm{d}{\textbf{M}}_3$ and $\textrm{d}{\textbf{R}}$, according to Eq. (A7a) and can be expanded in Eq. (A7b) as a function of vectors ${\textbf{M}}^\alpha$ (contravariant basis) and ${\textbf{M}}_\alpha$ (covariant basis) and the infinitesimals $\textrm{d}\xi ^\beta$

$$\begin{aligned}{} & {} \textrm{d}{\textbf{M}}_3={\textbf{K}}\cdot \textrm{d}{\textbf{R}} \end{aligned}$$

(A7a)

$$\begin{aligned}{} & {} \textrm{d}{\textbf{M}}_3=K_{\alpha \beta }{\textbf{M}}^\alpha \textrm{d}\xi ^\beta =K_\beta ^\alpha {\textbf{M}}_\alpha \textrm{d}\xi ^\beta \end{aligned}$$

(A7b)

where $K_{\alpha \beta }$ and $K_\beta ^\alpha$ are, respectively, the covariant and mixed components of ${\textbf{K}}$ given by Eqs. (A8a) and (A8b).

$$\begin{aligned}{} & {} K_{\alpha \beta }={\textbf{M}}_\alpha \cdot \frac{\partial {\textbf{M}}_3}{\partial \xi ^\beta } =-{\textbf{M}}_3\cdot \frac{\partial {\textbf{M}}_\alpha }{\partial \xi ^\beta }= -{\textbf{M}}_3\cdot \frac{\partial {\textbf{M}}_\beta }{\partial \xi ^\alpha } \nonumber \\ \end{aligned}$$

(A8a)

$$\begin{aligned}{} & {} K_\beta ^\alpha ={\textbf{M}}^\alpha \cdot \frac{\partial {\textbf{M}}_3}{\partial \xi ^\beta } =-{\textbf{M}}_3\cdot \frac{\partial {\textbf{M}}^\alpha }{\partial \xi ^\beta } \end{aligned}$$

(A8b)

The infinitesimal vectors $\textrm{d}\mathbf {M_\alpha }$ and $\textrm{d}\mathbf {M^\alpha }$ can also be written as a function of $\mathbf {M_\beta }$ and $\mathbf {M^\beta }$, according to Eqs. (A9a) and  (A9b), such as:

$$\begin{aligned}{} & {} \textrm{d}{\textbf{M}}_\alpha =\Gamma _{\alpha \gamma }^\beta {\textbf{M}}_\beta \textrm{d}\xi ^\gamma \end{aligned}$$

(A9a)

$$\begin{aligned}{} & {} \textrm{d}{\textbf{M}}^\alpha =-\Gamma _{\beta \gamma }^\alpha {\textbf{M}}^\beta \textrm{d}\xi ^\gamma \end{aligned}$$

(A9b)

where $\Gamma _{\beta \gamma }^\alpha$ are the well-known Christoffel symbols determined by:

$$\begin{aligned} \Gamma _{\beta \gamma }^\alpha ={\textbf{M}}^\alpha \cdot \frac{\partial {\textbf{M}}_\beta }{\partial \xi ^\gamma } \end{aligned}$$

(A10)

By combining Eqs. (A7), (A8), (A9) and (A10), the Gauss and Weingarten equations of the mid-surface can be obtained and are given by:

$$\begin{aligned} \begin{aligned}&\frac{\partial {\textbf{M}}_3}{\partial \xi ^\alpha }=K_{\alpha \beta }{\textbf{M}}^\beta \\&\frac{\partial {\textbf{M}}_3}{\partial \xi ^\alpha }=K_\beta ^\alpha {\textbf{M}}_\beta \\&\frac{\partial {\textbf{M}}_\beta }{\partial \xi ^\alpha }=\Gamma _{\alpha \beta }^\gamma {\textbf{M}}_\gamma -K_{\alpha \beta }{\textbf{M}}_3 \\&\frac{\partial {\textbf{M}}^\beta }{\partial \xi ^\alpha }=-\Gamma _{\alpha \gamma }^\beta {\textbf{M}}^\beta -K_\alpha ^\beta {\textbf{M}}_3 \end{aligned} \end{aligned}$$

(A11)

Any vector field acting on the mid-surface, e.g., the displacement vector ${\textbf{u}}$, can be decomposed in contravariant basis as ${\textbf{u}}=u_i{\textbf{M}}^i$. Therefore, its derivatives with respect to $\xi ^\alpha$ are given by:

$$\begin{aligned} {\textbf{u}}_{,\alpha }=u_{i|\alpha }{\textbf{M}}^i \end{aligned}$$

(A12)

where the values of $u_{i|\alpha }$ are the covariant derivatives of the displacement vector ${\textbf{u}}$, given by:

$$\begin{aligned} \begin{aligned}&u_{\sigma |\alpha }=u_{\sigma ,\alpha }-\Gamma ^\tau _{\sigma \alpha } u_\tau +K_{\alpha \sigma }u_3\\&u_{3|\alpha }=u_{3,\alpha }-K^\tau _\alpha u_\tau \\\end{aligned} \end{aligned}$$

(A13)

The second derivative of displacement vector ${\textbf{u}}$ is given by:

$$\begin{aligned} {\textbf{u}}_{,\alpha \beta }=u_{\sigma |\alpha \beta }{\textbf{M}} ^\sigma +u_{3|\alpha \beta }{\textbf{M}}^3 \end{aligned}$$

(A14)

where $u_{\sigma |\alpha \beta }$ and $u_{3|\alpha \beta }$ are given by:

$$\begin{aligned} \begin{aligned}&u_{\sigma |\alpha \beta }=(u_{\sigma |\alpha })_{,\beta } -\Gamma ^\tau _{\beta \sigma }u_{\tau |\alpha }+K_{\sigma \beta }u_{3|\alpha } \\&u_{3|\alpha \beta }=(u_{3|\alpha })_{,\beta }-K^\tau _\beta u_{\tau |\alpha } \end{aligned} \end{aligned}$$

(A15)

In this Appendix, the differential geometric properties of the mid-surface ${\mathcal {S}}$ in reference configuration were shown. Although the same properties (covariant and contravariant basis vector, metric and curvature tensors and Gauss–Weingarten equations) can also be obtained in the current configuration. Therefore, in the current configuration, vectors ${\textbf{m}}_i$ and ${\textbf{m}}^i$ are, respectively, the covariant and contravariant basis vectors and tensors ${\textbf{g}}$ and $\varvec{\kappa }$ are, respectively, the metric and curvature tensors of the mid-surface ${\mathcal {s}}$.

Appendix B Numerical determination of periodic orbits

To the determination of the periodic orbits, the nonlinear system of second-order differential equations (9) is transformed into a first-order differential system consisting of $2\times N$ equations:

$$\begin{aligned}{} & {} {\textbf{y}}'(\tau )=\varvec{f}({\textbf{y}}(\tau ), \omega ,\alpha )\nonumber \\{} & {} \quad =\frac{2\pi }{\omega } \begin{bmatrix} {\textbf{U}}' \\ {\textbf{M}}^{-1}(-{\textbf{K}}{\textbf{U}}-\alpha {\textbf{M}}{\textbf{U}}'-{\textbf{F}}({\textbf{U}})) \end{bmatrix}, \end{aligned}$$

(B16)

where $\omega$ represents the angular frequency of the periodic orbit; $\tau$ is the dimensionless time variable scaled by $T=(2\pi )/\omega$ to ensure a period of 1 for the orbits; ${\textbf{y}}'=\textrm{d}{\textbf{y}}/(\textrm{d}\tau )$ represents the derivative with respect to $\tau$; and ${\textbf{y}}=[[{\textbf{U}}]^{\textsf{T}}, [{\textbf{U}}']^{\textsf{T}}]^{\textsf{T}}$ denotes the vector of state variables. The term $\alpha {\textbf{M}}{\textbf{U}}'$ has been introduced to account for system damping, with the damping coefficient $\alpha$ approaching zero as the continuation algorithm converges to a periodic orbit.

The integration interval is divided into $N_t$ segments, i.e., $0=\tau _0<\tau _1<\dots <\tau _{N_t}=1$. To find the values of the shooting points ${\textbf{y}}(\tau _k)$ for a given initial condition ${\textbf{y}}(\tau _{k-1})$, $N_t$ systems of ordinary differential equations are solved, following the structure defined by the initial value problem:

$$\begin{aligned} \begin{aligned} {\textbf{y}}'(\tau )=\varvec{f}\left( {{\textbf{y}}(\tau )},\omega ,\alpha \right) \\ {\textbf{y}}(\tau _{k-1})={\textbf{y}}_{k} \\ \tau _{k-1}\le \tau \le \tau _{k} \end{aligned} \end{aligned}$$

(B17)

where $k = 1, \dots , N_t$, and the values of ${\textbf{y}}_k$ represent the initial conditions at the time points. In this work, we adopted $N_t = 40$, and the ordinary differential equations (ODE) are solved in parallel using the $\textsf{ode45}$ function in Matlab.

The goal of the multiple shooting method is to find the vector ${\textbf{Y}}=[[{\textbf{y}}_1]^{\textsf{T}},\dots , [{\textbf{y}}_{N_t}]^{\textsf{T}}]^{\textsf{T}}$—that storages the initial conditions ${\textbf{y}}_{k}$—the damping coefficient $\alpha$ and the frequency $\omega$ that represent a periodic orbit ${\textbf{y}}(\tau )$ such that ${\textbf{y}}(\tau )={\textbf{y}}(\tau +1)$. In other words, the objective of the continuation algorithm is to find the root of the residue equation (B18)

$$\begin{aligned} {\textbf{r}}\left( {{\textbf{Y}}},\omega ,\alpha \right) = \begin{bmatrix} {\textbf{y}}(\tau _{N_t})-{{\textbf{y}}_1} \\ {\textbf{y}}(\tau _{1})-{{\textbf{y}}_2} \\ \vdots \\ {\textbf{y}}(\tau _{N_t-1})-{{\textbf{y}}_{N_t}} \\ \end{bmatrix} \end{aligned}$$

(B18)

which means that all initial conditions ${\textbf{y}}_k$ and the correspondent shooting points ${\textbf{y}}(\tau _{k})$ lie in the same periodic orbit ${\textbf{y}}(\tau )$.

In this work, the phase constraint of Eq. (B19) was adopted [37].

$$\begin{aligned} r_{\textsf{ph}}\left( {{\textbf{Y}}},\omega ,\alpha \right) =\sum \limits _{k=1}^{N_t}\left\{ \left( {\textbf{y}}_{k}-[{\textbf{y}}_k]^{0}\right) \cdot [{\textbf{y}}'(\tau _{k-1})]^{0}\right\} \nonumber \\ \end{aligned}$$

(B19)

where $[\ ]^0$ represents the previous iteration of the continuation method, such that $[{\textbf{Y}}]^0$ is a solution to Eq. (B18). From a geometric perspective, the phase constraint in equation (B19) aims to find a new periodic orbit ${\textbf{y}}(\tau )$ whose values of $[{\textbf{y}}_k]^0$ and ${\textbf{y}}_k$ lie in the same Poincaré section, which is perpendicular to the orbit $[{\textbf{y}}(\tau )]^0$ at $\tau =\tau _{k-1}$. The expanded problem adding the phase constraint (B19) is given by:

$$\begin{aligned} {\textbf{R}}({\textbf{x}})= \begin{bmatrix} {\textbf{r}}({\textbf{x}}) \\ r_{\textsf{ph}}({\textbf{x}}) \end{bmatrix} \end{aligned}$$

(B20)

where the vector ${\textbf{x}}=[{\textbf{Y}}^{\textsf{T}},\omega ,\alpha ]^{\textsf{T}}$ represents the variables of the continuation algorithm.

The continuation method begins by using a known solution $[{\textbf{x}}]^0$ to calculate an approximate solution ${\textbf{w}}$. This initial step is referred to as the predictor.

$$\begin{aligned} {\textbf{w}}:=[{\textbf{x}}]^0+\delta [{\textbf{t}}]^0 \end{aligned}$$

(B21)

Here, the tangent vector ${\textbf{t}}={\textbf{t}}(\partial _{{\textbf{x}}}{\textbf{R}})$ is a function of the Jacobian of the residue at the previous iteration [38], and $\delta$ represents the step size of the predictor. Throughout the continuation steps, various adaptation schemes can be applied to modify the value of $\delta$ [38]. The solution ${\textbf{w}}$ is then improved through iterative correction steps until convergence is achieved using equation (B22)

$$\begin{aligned} \begin{aligned} {\textbf{w}}:={\textbf{w}}-\textrm{pinv}(\partial _{{\textbf{x}}}{\textbf{R}}({\textbf{w}})) {\textbf{R}}({\textbf{w}}) \end{aligned} \end{aligned}$$

(B22)

The process continues for a new solution ${\textbf{x}}:={\textbf{w}}$, and subsequently applying the next fstep of the continuation algorithm.

Appendix C Modal shapes

In this appendix, the vibration modes and natural frequencies of the non-shallow spherical panel, the hyperbolic paraboloid, and the parabolic conoid are depicted in Figs.10, 11 and 12, respectively.

Fig. 10

Modal shape functions of the non-shallow spherical panel

Fig. 11

Modal shape functions of the hyperbolic paraboloid

Fig. 12

Modal shape functions of the parabolic conoid