1 Introduction

In stable mechanical systems, elastic bodies subject to external disturbances often exhibit vibrations or oscillations. These interactions can exacerbate into more severe collision phenomena due to clearances between the bodies. Factors such as damping can dissipate the energy from these collisions and vibrations, restoring the system to a stable state. However, collisions and oscillations significantly affect the contact state between elastic bodies, potentially leading to noise, fatigue, and wear, thereby endangering the system’s stability. Consequently, extensive research [1,2,3,4,5,6] has been dedicated to addressing contact issues under such unstable conditions.

As a common contact type in mechanical systems, collision involves two elastic bodies meeting at a specific initial relative velocity to undergo compression and restitution deformation. The force generated during collision contact is vital for analyzing the dynamic response of collisions, prompting the development of numerous models for simulating collision dynamics. Among them, models based on spring-damping element are widely used. A simple one is the Kelvin-Voigt model which was employed by Khulief and Shabana [7] for impact analysis in multibody system. However, this linear model has short in representing the overall nonlinear nature of contact. In contrast, Hunt and Crossley [8] established a nonlinear contact force model combining Hertzian contact force and damping force. This had spurred a series of improved models tailored by researchers for specific purposes, like the Lee and Wang model [9], the Lankarani and Nikravesh model [10], and other models [11,12,13,14,15,16] up to the Zhang et al. model [17]. These models primarily focus on accurately representing energy loss during collision through damping forces, typically using Newton’s restitution coefficient to derive the key parameter of hysteresis damping factor. However, reference [18] argues that Newton’s restitution coefficient is not suitable for collision processes under external forces, and recommending the use of the energy restitution coefficient [19] to model forces in such scenarios. Moreover, this reference also believes that external forces and collision energy loss are the key factors that cause collision state to end, and applies the established quantitative judgment to identify two collision end states—separation and non-separation.

When non-separation occurs, the elastic bodies continue their compression and restitution deformation under cyclic external forces. In other words, there exists a special collision contact state between elastic bodies when there is no initial relative velocity, termed here as NIRV-collision contact. Although some studies, like gear meshing forces [20,21,22], utilize the Kelvin-Voigt model for NIRV-collision scenarios, significant simulation errors are evident when collision models are improperly applied. For instance, Warzecha [23] used Michalczyk model [24] and Zhang model [17] to simulate the multi-zone collisions of a collinear system consisting of six particles, resulting in frequently changing and incomprehensible NIRV-collision contact forces. It should be noted that it is difficulty to clearly express energy dissipation for NIRV-collision contact, thus, Carretero-González et al. [25] have made strides in this area by using experimental data to establish a dissipation coefficient for NIRV-collision force models in multi-particle collision systems. Therefore, the contact force model required for non-stationary dynamic analysis considering both collision and NIRV-collision needs further research.

The purpose of this article is to establish a contact force calculation approach applicable to collision and NIRV-collision dynamic analysis. It begins by elaborating the overarching issue of modeling contact forces under external influences. Then, examines the collision process with only the initial relative velocity considered, and establishes a model for collision contact without external forces. Building on this foundation, it develops a method for calculating collision and NIRV-collision contact forces under varying external conditions and proposes a corresponding numerical process. The effectiveness of this approach is demonstrated through dynamic analysis of simultaneous and multiple continuous collisions, underscoring the model’s practical relevance.

2 General issues of contact force model

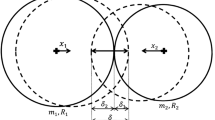
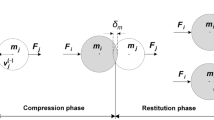
The one-dimensional direct central frictionless contact between two elastic spheres is utilized to analyze the collision and NIRV-collision, as illustrated in Fig. 1, where the masses of the two elastic spheres are represented as mi and mj, respectively. When subjected to variable external forces Fi(t) and Fj(t), the two elastic spheres start to contact at velocities \(\dot{v}_{i}^{\left( - \right)}\) and \(\dot{v}_{j}^{\left( - \right)}\), respectively, then deformation takes place in the local contact area, and this denotes the start of compression phase. According to Hertz force and damping force, the contact force between these two spheres can be expressed

$$F_{n} = k\delta^{\frac{3}{2}} + \mu \delta^{\frac{3}{2}} \dot{\delta }$$
(1)

where δ is the local deformation, k denotes the contact stiffness, \(\dot{\delta }\) represents the deformation velocity, and μ is the hysteresis damping factor which plays a crucial role in modeling contact force.

Fig. 1
figure 1

Collision process between two elastic spheres under external forces

Full size image

At this point, the external forces begin to do work, and along with the initial relative kinetic energy, are converted into elastic deformation potential energy, relative kinetic energy, and work done by the damping force, as shown

$$\frac{1}{2}m_{e} \left( {\dot{\delta }^{\left( - \right)} } \right)^{2} + \mathop \smallint \limits_{0}^{\delta } F_{e} \left( t \right)d\delta = \frac{2}{5}k\delta^{\frac{5}{2}} + \frac{1}{2}m_{e} \dot{\delta }^{2} + \mathop \smallint \limits_{0}^{\delta } \mu \delta^{\frac{3}{2}} \dot{\delta }d\delta$$
(2)

where Fe(t) = Fi(t) − Fj(t) is the equivalent external force, \(\mathop \smallint \limits_{0}^{\delta } F_{e} \left( t \right)d\delta\) denotes the work done by equivalent external force, \(\dot{\delta }^{\left( - \right)} = \dot{v}_{i}^{\left( - \right)} - \dot{v}_{j}^{\left( - \right)}\) and \(m_{e} \left( {\dot{\delta }^{\left( - \right)} } \right)^{2} /2\) represent the initial relative velocity and the initial relative kinetic energy, respectively, whereas \(2k\delta^{5/2} /5\), \(m_{e} \dot{\delta }^{2} /2\) and \(\mathop \smallint \limits_{0}^{\delta } \mu \delta^{3/2} \dot{\delta }d\delta\) are the elastic deformation potential energy, the relative kinetic energy, and the work done by damping force, respectively.

As the deformation peaks, the deformation velocity reaches zero, and the accumulated potential and kinetic energies alongside the work done by the damping force reach their respective maxima. Thus, the energy balance at the end of the compression phase is

$$\frac{1}{2}m_{e} \left( {\dot{\delta }^{\left( - \right)} } \right)^{2} + \mathop \smallint \limits_{0}^{{\delta_{m} }} F_{e} \left( t \right)d\delta = \frac{2}{5}k\delta_{m}^{\frac{5}{2}} + \mathop \smallint \limits_{0}^{{\delta_{m} }} \mu \delta^{\frac{3}{2}} \dot{\delta }d\delta$$
(3)

where \(2k\delta_{m}^{5/2} /5\) is the maximum elastic deformation potential energy, \(\mathop \smallint \limits_{0}^{{\delta_{m} }} \mu \delta^{3/2} \dot{\delta }d\delta\) and \(\mathop \smallint \limits_{0}^{{\delta_{m} }} F_{e} \left( t \right)d\delta\) denote the work done by damping force and the work done by equivalent external force during the compression phase, respectively.

Subsequently, the deformation begins to diminish, indicating the start of the restitution phase. The energy balances during and at the end of this phase can be respectively expressed as

$$\frac{2}{5}k\delta_{m}^{\frac{5}{2}} = \frac{2}{5}k\delta^{\frac{5}{2}} + \mathop \smallint \limits_{\delta }^{{\delta_{m} }} \mu \delta^{\frac{3}{2}} \left| {\dot{\delta }} \right|d\delta + \mathop \smallint \limits_{\delta }^{{\delta_{m} }} F_{e} \left( t \right)d\delta + \frac{1}{2}m_{e} \dot{\delta }^{2}$$
(4)
$$\frac{2}{5}k\delta_{m}^{\frac{5}{2}} = \mathop \smallint \limits_{0}^{{\delta_{m} }} \mu \delta^{\frac{3}{2}} \left| {\dot{\delta }} \right|d\delta + \mathop \smallint \limits_{0}^{{\delta_{m} }} F_{e} \left( t \right)d\delta + \frac{1}{2}m_{e} \left( {\dot{\delta }^{\left( + \right)} } \right)^{2}$$
(5)

where \(\dot{\delta }^{\left( + \right)}\) is the separation velocity, \(m_{e} \left( {\dot{\delta }^{\left( + \right)} } \right)^{2} /2\) denotes the relative separation kinetic energy, and \(\mathop \smallint \limits_{0}^{{\delta_{m} }} \mu \delta^{3/2} \left| {\dot{\delta }} \right|d\delta\) represents the work done by damping force in restitution phase.

Substituting Eq. (5) into Eq. (3) yields

$$\frac{1}{2}m_{e} \left( {\dot{\delta }^{\left( - \right)} } \right)^{2} + \mathop \smallint \limits_{0}^{{\delta_{m} }} F_{e} \left( t \right)d\delta = \mathop \smallint \limits_{0}^{{\delta_{m} }} F_{e} \left( t \right)d\delta + \frac{1}{2}m_{e} \left( {\dot{\delta }^{\left( + \right)} } \right)^{2} + \oint {\mu \delta^{\frac{3}{2}} \dot{\delta }d\delta }$$
(6)

where \(\oint {\mu \delta^{3/2} \dot{\delta }d\delta }\) is the work done by damping force throughout the entire contact process, which is also considered as the energy loss during a compression and restitution cycle, and how to calculate this energy loss is important to deriving contact force model.

It is crucial to acknowledge that the energy balance shown in Eq. (6) can manifest in three distinct situations: ① Ignoring the work done by the equivalent external force; ② Considering cases where the initial relative kinetic energy is zero; ③ Accounting these two energies simultaneously. In the following sections, the contact forces for these three situations will be analyzed respectively.

3 Collision contact hysteresis damping factor without external forces

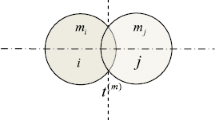
The collision system that ignores external forces is a commonly used system for modeling collision force, as shown in Fig. 2. Based on this system, Flores et al. [26], Hu and Guo [27] constructed typical collision contact force models, with key steps including derivations of deformation velocity and hysteresis damping factor.

Fig. 2
figure 2

Collision system without external forces

Full size image

For the deformation velocity, the energy balance shown in Eqs. (2) and (3) can be rewritten as

$$\frac{1}{2}m_{e} \left( {\dot{\delta }^{\left( - \right)} } \right)^{2} = \frac{2}{5}k\delta^{\frac{5}{2}} + \frac{1}{2}m_{e} \dot{\delta }^{2} + \mathop \smallint \limits_{0}^{\delta } \mu \delta^{\frac{3}{2}} \dot{\delta }d\delta$$
(7)
$$\frac{1}{2}m_{e} \left( {\dot{\delta }^{\left( - \right)} } \right)^{2} = \frac{2}{5}k\delta_{m}^{\frac{5}{2}} + \mathop \smallint \limits_{0}^{{\delta_{m} }} \mu \delta^{\frac{3}{2}} \dot{\delta }d\delta$$
(8)

Ignoring the work done by damping force, yields

$$\frac{1}{2}m_{e} \left( {\dot{\delta }^{\left( - \right)} } \right)^{2} = \frac{2}{5}k\delta^{\frac{5}{2}} + \frac{1}{2}m_{e} \dot{\delta }^{2}$$
(9)
$$\frac{1}{2}m_{e} \left( {\dot{\delta }^{\left( - \right)} } \right)^{2} = \frac{2}{5}k\delta_{m}^{\frac{5}{2}}$$
(10)

Multiplying both sides of Eq. (9) by Eq. (10) results in

$$\dot{\delta } = \dot{\delta }^{\left( - \right)} \sqrt {1 - \left( {\frac{\delta }{{\delta_{m} }}} \right)^{\frac{5}{2}} }$$
(11)

Substituting Eq. (11) into the damping force work term of Eq. (8) to obtain

$$\Delta E_{c} = \mathop \smallint \limits_{0}^{{\delta_{m} }} \mu \dot{\delta }^{\left( - \right)} \sqrt {1 - \left( {\frac{\delta }{{\delta_{m} }}} \right)^{\frac{5}{2}} } \delta^{\frac{3}{2}} d\delta$$
(12)

where ΔEc is the work done by damping force during compression phase.

Setting x = δ/δm, then Eq. (12) is transformed into

$$\Delta E_{c} = \frac{2}{5}\mu \dot{\delta }^{\left( - \right)} \delta_{m}^{\frac{5}{2}} \mathop \smallint \limits_{0}^{1} \sqrt {1 - x^{\frac{5}{2}} } dx^{\frac{5}{2}}$$
(13)

Calculating the integral term of the above equation to obtain

$$\Delta E_{c} = \frac{4}{15}\mu \dot{\delta }^{\left( - \right)} \delta_{m}^{\frac{5}{2}}$$
(14)

In addition, the collision restitution coefficient can be used to estimate the energy loss of collision, and the Stronge’s model [19] shown in Eq. (15), which is also called energy model, is used here.

$$\varepsilon^{2} = - \frac{{W_{r} }}{{W_{c} }}$$
(15)

where ε denotes the restitution coefficient, Wr and Wc are the work done by contact force in compression and restitution phases, respectively, given by

$$W_{r} = \mathop \smallint \limits_{{\delta_{m} }}^{0} F_{n} d\delta = - \frac{2}{5}k\delta_{m}^{\frac{5}{2}} + \mathop \smallint \limits_{{\delta_{m} }}^{0} \mu \delta^{\frac{3}{2}} \dot{\delta }d\delta$$
(16)
$$W_{c} = \mathop \smallint \limits_{0}^{{\delta_{m} }} F_{n} d\delta = \frac{2}{5}k\delta_{m}^{\frac{5}{2}} + \mathop \smallint \limits_{0}^{{\delta_{m} }} \mu \delta^{\frac{3}{2}} \dot{\delta }d\delta$$
(17)

Substituting Eqs. (16) and (17) into Eq. (15), yields

$$\varepsilon^{2} \Delta E_{c} + \Delta E_{r} = \frac{2}{5}\left( {1 - \varepsilon^{2} } \right)k\delta_{m}^{\frac{5}{2}}$$
(18)

where ΔEr is the work done by damping force in restitution phase. For ΔEr, considering the similarity in deformation velocity between the compression and restitution phases, and the Newtonian restitution coefficient, references [26, 27] assume ΔEr = εΔEc to derive the expression of the hysteresis damping factor μ.

However, the disparities in deformation velocity between compression and restitution phases is increasing as the reduction of the restitution coefficient, as shown in Fig. 3. In turn, this difference leads to an increase in the error of the damping factor model, as shown in Fig. 4 where post- restitution coefficients are calculated by these damping factor models shown in Table 1, including Hunt and Crossley model, Lankarani and Nikravesh model, Flores et al. model, and Hu and Guo model. It should be noted that the smaller the error, the better the model accuracy.

Fig. 3
figure 3

Deformation velocity

Full size image
Fig. 4
figure 4

Post-restitution versus pre-restitution coefficients

Full size image
Table 1 Hysteresis damping factor model
Full size table

To reduce this error, we assume that the relationship between the work done by the damping force during the restitution and compression phases is

$$\Delta E_{r} = \varepsilon^{a} \Delta E_{c}$$
(19)

where a is the constant index of restitution coefficient.

Substituting Eqs. (14) and (19) into Eq. (18) yields

$$\mu = \alpha \frac{k}{{\dot{\delta }^{\left( - \right)} }}$$
(20)
$$\alpha = \frac{3}{2}\frac{{\left( {1 - \varepsilon^{2} } \right)}}{{\left( {\varepsilon^{2} + \varepsilon^{a} } \right)}}$$
(21)

where α is the hysteresis damping factor coefficient. It should be noted that Eq. (21) represents the Hu and Guo model when a is taken as 1, which means that the hysteresis damping factor μ is too high when the restitution coefficient is small. Since ε generally ranges between 0 and 1, a should be adjusted below 1 to reduce the hysteresis damping factor μ.

For a more precise μ estimation, Eq. (22) is utilized to perform iterative calculation with a step size decrement of 0.01.

$$m_{e} \,\ddot{\delta } + \frac{3}{2}\frac{{\left( {1 - \varepsilon^{2} } \right)}}{{\left( {\varepsilon^{2} + \varepsilon^{a} } \right)}}\frac{k}{{\dot{\delta }^{\left( - \right)} }}\delta^{\frac{3}{2}} \dot{\delta } + k\delta^{\frac{3}{2}} = 0$$
(22)

here, me is equal to 0.5 kg and \(\dot{\delta }^{\left( - \right)}\) is 0.5 m/s, whereas the value of k is 2.41 × 1010N/m3/2, and the restitution coefficient ε is calculated by Eq. (15). The result shows that the post-restitution coefficient is nearly identical to the pre-restitution coefficient at a = 0.87, as indicated by the dashed line in Fig. 4 where the discrepancy in the post-restitution coefficient is within 2.9% and 1.1% when the pre-restitution coefficient ranges from 0.05 to 0.3, with others error being less than 0.8%. Equation (23) presents the corresponding hysteresis damping factor, and Fig. 5 illustrates the comparative curves of the hysteresis damping factor between the Hu and Guo model and the model discussed herein.

$$\mu = \frac{3}{2}\frac{{\left( {1 - \varepsilon^{2} } \right)}}{{\left( {\varepsilon^{2} + \varepsilon^{0.87} } \right)}}\frac{k}{{\dot{\delta }^{\left( - \right)} }}$$
(23)
Fig. 5
figure 5

Factor α versus restitution coefficient

Full size image

4 Collision contact hysteresis damping factor considering only external forces

The collision contact considering only external forces is a special collision contact, which is described by Fig. 6. Compared to Fig. 1, the two elastic spheres start to contact with no initial relative velocity. It should be noted that there may be initial compression δs between the two elastic spheres. In addition, the spheres might not fully separate at the end of a contact cycle, resulting in an inseparable state, as shown Fig. 6 where δo denotes incomplete separation compression.

Fig. 6
figure 6

Elastic contact process under external force

Full size image

Combined Eqs. (16) to (17), and Eq. (6) that ignoring the initial relative velocity, yields

$$\Delta E = \left( {1 - \varepsilon^{2} } \right)\mathop \smallint \limits_{0}^{{\delta_{m} }} F_{e} \left( t \right)d\delta$$
(24)

where ΔE denotes the energy loss of the NIRV-collision contact.

It can be drawn from above equation that this energy loss is hard to calculate due to the influence of variable external forces. Additionally, the relationship between ΔEr and ΔEc described in Eq. (19) is difficult to derive, as is deducing the deformation velocity model. To address these complexities, we propose a calculation approach using bisection method to iteratively determine the hysteresis damping factor. The main mentality is to apply the energy restitution coefficient shown in Eq. (15) to construct a function f(μ) with hysteresis damping factor as a variable, as shown in Eq. (25). Next, determine the value range for the function variable μ through Eq. (26), which is [a, b]. It should be noted that Wcn and Wrn in the function are obtained from simulations of the contact process with Eqs. (17) and (16). Then, calculate the next iteration value of μ according to Eq. (27).

$$f\left( {\mu_{n} } \right) = \frac{{W_{rn} }}{{W_{cn} }} + \varepsilon^{2}$$
(25)
$$\left\{ {\begin{array}{*{20}c} {a = \mu_{n} } & {f\left( {\mu_{n} } \right) < 0} \\ {b = \mu_{n} } & {f\left( {\mu_{n} } \right) > 0} \\ \end{array} } \right.$$
(26)
$$\mu_{n + 1} = \frac{a + b}{2}$$
(27)

The primary challenges in this iterative process includes setting the initial value of μ and the iteration value before [a, b] is determined. The initial μ value could either be μn-1 from the previous collision or μ0 calculated from Eq. (28).

$$\mu_{0} = \frac{3}{2}\frac{{\left( {1 - \varepsilon^{2} } \right)}}{{\left( {\varepsilon^{2} + \varepsilon^{0.87} } \right)}}k$$
(28)

For the second challenge, Eq. (29) can be employed for the iteration value, which is obtained according to the Newton method. However, this method is sensitive to the selection of initial value and there is a possibility of too many iterations. In this case, other methods can be used, such as the approach shown in Eq. (31).

$$\mu_{n + 1} = \mu_{n} - \frac{{f\left( {\mu_{n} } \right)}}{{f^{\prime } \left( {\mu_{n} } \right)}}$$
(29)

where

$$\begin{gathered} \left\{ {\begin{array}{*{20}l} {f^{\prime } \left( {\mu_{n} } \right) = \frac{{W_{cn} S_{rn} - W_{rn} S_{cn} }}{{W_{cn}^{2} }}} \hfill \\ {S_{cn} = \mathop \smallint \limits_{{\delta_{s} }}^{{\delta_{m} }} \delta^{\frac{3}{2}} \dot{\delta }d\delta } \hfill \\ {S_{rn} = \mathop \smallint \limits_{{\delta_{m} }}^{{\delta_{o} }} \delta^{\frac{3}{2}} \dot{\delta }d\delta } \hfill \\ \end{array} } \right. \hfill \\ \hfill \\ \end{gathered}$$
(30)

Equation (31) mainly considers that if the post-restitution coefficient εoutn calculated by Eq. (15) is too larger, it indicates that μn is too small, conversely, μn tends to larger. Therefore, when εoutn is greater than pre- restitution coefficient εin, then εoutn/εin is greater than 1. Multiplying it by μn to obtaine the increased iteration value of μn+1, and on the contrary, decreased μn+1 can be obtained.

$$\mu_{n + 1} = \mu_{n} \frac{{\varepsilon_{outn} }}{{\varepsilon_{in} }}$$
(31)

It’s crucial to highlight that at the end of NIRV-collision contact, two potential states emerge: separation and non-separation. The criteria for these states during the restitution phase are discussed in reference [18], where it is noted that during the restitution phase, separation occurs when δ = 0 and \(\dot{\delta }^{\left( + \right)}\) ≥ 0, and non-separation occurs when δ > 0 and \(\dot{\delta }^{\left( + \right)}\) = 0.

5 Calculation process for collision contact forces under external forces

In the contact system shown in Fig. 1, collisions undergo several transitions between their initiation and cessation. Due to energy loss and external forces, the strength of collision contact may gradually decrease until NIRV-collision contact occurs, and the influence of external forces on the contact process increases accordingly. This means that it is necessary to separately calculate collision contact force and NIRV-collision contact force when analyzing the dynamics of the contact system, and both need to consider the influence of external forces.

The energy loss of a collision influenced by external forces, as derived from Eqs. (6), (15) and (17), indicates multiple contributing factors, complicating the prediction of collision energy loss.

$$\Delta E = \left( {1 - \varepsilon^{2} } \right)\left[ {\frac{1}{2}m_{e} \left( {\dot{\delta }^{\left( - \right)} } \right)^{2} + \mathop \smallint \limits_{0}^{{\delta_{m} }} F_{e} \left( t \right)d\delta } \right]$$
(32)
Fig. 7
figure 7

Numerical calculation process

Full size image

Therefore, similar to NIRV-collision contact, the hysteresis damping factor of this contact is calculated by Eqs. (25) to (31), then substituting into Eq. (1) to determine the corresponding contact forces. The corresponding calculation process for these two contact forces is proposed here, as shown in Fig. 7.

During each compression and restitution cycle, it is important to note the following points:

  1. 1.

    Collision occurs when the deformation changes from δ ≤ 0 to δ > 0 and the initial relative velocity \(\dot{\delta }^{ - }\) is greater than zero, and the initial value of the collision hysteresis damping factor μ0 can be calculated by Eq. (23).

  2. 2.

    NIRV-collision occurs when the deformation changes from δ ≤ 0 to δ > 0 and the initial relative velocity \(\dot{\delta }^{ - }\) is zero, and the initial value of the collision hysteresis damping factor μ0 can be calculated by Eq. (28) or the hysteresis damping factor from the last collision.

  3. 3.

    During the initialization process, both the values of a and b are set to zero, and the existing values of a and b need to be maintained during reinitialization.

  4. 4.

    The post- restitution coefficient εoutn calculated by Eq. (15), and ξε is the accuracy of εoutn.

  5. 5.

    The formula for calculating the iteration value μn+1 of the hydrogenation damping factor can be selected based on the principle of fewer iterations.

  6. 6.

    In the collision restitution phase, when δ ≤ 0, or δ > 0 and \(\dot{\delta } = 0\), the collision is end.

  7. 7.

    The integrations in the dynamic equations can be performed by the Runge–Kutta method of order 4 with a time step equal 10−6 s.

6 Application to collision under external force

To enhance understanding of the proposed contact force calculation approach, we explore applications involving simultaneous collisions and multiple continuous collisions under externa forces. Here are examples for application.

6.1 Collinear collision of triple ball chain

The collinear collision system shown in Fig. 8 demonstrates simultaneous collisions. The three balls, B1, B2 and B3, each have the same mass m = 0.5 kg and radius R = 0.05 m, and the contact stiffness k between B1 and B2, as well as between B2 and B3, is equal to 1 × 108 N/m3/2. The ball B1 impacts B2 along the collinear direction at an initial velocity of \(\dot{x}_{1}^{\left( - \right)}\) = 0.2 m/s, while B2 and B3 are in contact before the initial collision. Using x1, x2 and x3 to represent the displacements of B1, B2 and B3, with initial values of 0 m, 0.1 m and 0.2 m, respectively.

Fig. 8
figure 8

Collinear collision system of triple ball chain

Full size image

The dynamic equations of this system can be written as follows

$$\left\{ {\begin{array}{*{20}l} {m\ddot{x}_{1} = - F_{n1} } \hfill \\ {m\ddot{x}_{2} = F_{n1} - F_{n2} } \hfill \\ {m\ddot{x}_{3} = F_{n2} } \hfill \\ \end{array} } \right.$$
(33)

with

$$\left\{ {\begin{array}{*{20}l} {F_{n1} = k\delta_{12}^{\frac{3}{2}} + \mu_{12} \delta_{12}^{\frac{3}{2}} \dot{\delta }_{12} } \hfill \\ {F_{n2} = k\delta_{23}^{\frac{3}{2}} + \mu_{23} \delta_{23}^{\frac{3}{2}} \dot{\delta }_{23} } \hfill \\ {\delta_{12} = 2R - \left( {x_{2} - x_{1} } \right)} \hfill \\ {\delta_{23} = 2R - \left( {x_{3} - x_{2} } \right)} \hfill \\ {\dot{\delta }_{12} = \dot{x}_{1} - \dot{x}_{2} } \hfill \\ {\dot{\delta }_{23} = \dot{x}_{2} - \dot{x}_{3} } \hfill \\ \end{array} } \right.$$
(34)

where Fn1 and Fn2 represent the contact forces between B1 and B2, as well as between B2 and B2, respectively, whereas δ12 and δ23 are the corresponding deformations, \(\dot{\delta }_{12}\) and \(\dot{\delta }_{23}\) denote the corresponding deformation velocities, μ12 and μ23 are the corresponding hysteresis damping factors, and the pre- restitution coefficients used to calculate the initial values of μ12 and μ23 are set to εin12 and εin23, respectively.

The computation process in Fig. 7 is utilized to simulate the dynamic responses of the three ball, and the initial parameters of X0, V0, εin12 and εin23 are [0, 0.1, 0.2]T, [0.2, 0, 0]T, 0.8 and 0.7, respectively. The initial values of μ12 and μ23 are calculated by Eq. (23) with the initial velocity 0.2 m/s, with each factor requiring independent and simultaneous iteration in each cycle of calculation. After six cycles, μ12 and μ23 meet the required precision (ξε = 1%). The Hunt and Crossley model, as well as Flores et al. model are also applied to simulate the same simultaneous collisions. In this simulation, μ12 and μ23 are equal and calculated based on the initial velocity. Then, we get the simulation results, as shown in Figs. 9, 10, 11, 12.

Fig. 9
figure 9

Velocities of the balls

Full size image
Fig. 10
figure 10

Collision contact forces of the two collision

Full size image
Fig. 11
figure 11

Deformation velocities of the two collision

Full size image
Fig. 12
figure 12

Hysteresis loops of the two collisions

Full size image

Figure 9 represents the velocity developments of B1, B2 and B3, corresponding to solid, dashed, and dotted lines, respectively. Under the collision contact force Fn1 shown in Fig. 10, the velocity of B1 continues to decrease from 0.2 m/s until it separates from B2, while the velocity of B3 continues to accelerate from zero until it separates from B2 under the contact force Fn2. Unlike B1 and B3, B2 is simultaneously influenced by Fn1 and Fn2. Initially, Fn1 exceeds Fn2, causing B2’s velocity to increase until it reaches its peak, then it diminishes as Fn1 becomes less than Fn2, until it separates from B1 and B3.

The velocities shown Fig. 9 are obtained based on the proposed method, and similar results can also be obtained by applying Hunt and Crossley model, and Flores et al. model. However, there are differences in the influence of different contact force models on the dynamic response of simultaneous collisions, as shown in Figs. 10, 11, 12. From Fig. 10, it can be observed that the differences in the collision contact forces Fn1 calculated by the Hunt and Crossley model, the Flores et al. model, and the proposed method are relatively small during the compression phase, whereas the difference is relatively obvious in the restitution phase. The reasons are the different effect in μ12 values and the influence of the external force Fn2 during the restitution phase. Compared to Fn1, there is a significant difference in the NIRV-collision contact force Fn2, and the main reason is the different values of μ23. The above differences are also clearly reflected in the deformation velocity shown in Fig. 11.

Figure 12 shows the hysteresis loops of the collisions between B1 and B2, and between B2 and B3, respectively, denoted as the hysteresis loops B12 and B23. This figure reveals that the B12 loops generated by the Flores et al. model and the proposed method are relatively similar, indicating minor differences in energy loss between these two models. Additionally, the post-restitution coefficients εout12 differ from the pre-restitution coefficients εin12 by less than 1%, as illustrated in Table 2. In contrast, the hysteresis loop produced by the Hunt and Crossley model shows marked differences, with a deviation of 5.7% from the pre-restitution coefficients. For the hysteresis loops of B23, the discrepancies among the Hunt and Crossley model, Flores et al. model, and the proposed method are significant, with errors in the post-and pre-restitution coefficients of 23.7%, 18.7%, and 0.8%, respectively.

Table 2 Pre- and post- restitution coefficients
Full size table

It is important to note that the number of iterations required in the calculation process, as demonstrated in Fig. 7, correlates with the pre-restitution coefficient and the initial relative velocity, as shown in Table 3 which is calculated with the condition of εin12 = εin23. When the values of μ12 and μ23 computed by Eq. (23) both meet the accuracy requirements, only one cycle calculation is required, such as εin is 0.85; otherwise, several cycles of calculation are needed. Due to the mutual influence of the two collisions, the simultaneous iteration of μ12 and μ23 may result in more cycles and even inability to converge marked by “–”, as shown in Table 3. In this case, it is necessary to reduce the accuracy requirements or adopt other methods.

Table 3 Number of cycle calculations under different conditions
Full size table

6.2 Elastic ball collision under spring support and external force

When simulating multiple consecutive collisions using the computation process shown in Fig. 7, attention should be paid to initializing parameters for each collision. The system setup for this simulation involves a ball supported by a spring and external forces as depicted in Fig. 13. The ball, with a mass m of 0.5 kg, a radius R = 0.05 m, and an equivalent stiffness k equal to 1.8 × 107 N/m3/2, impacts on a rigid wall under the action of a periodic force F (t) and spring damping force. When the spring is inactive, the original coordinate system is centered at the ball, with a distance b from the ball to the wall set at 0.048 m.

Fig. 13
figure 13

Collision system with periodic external force and spring damping force

Full size image

The following is the dynamic equivalent equation of the contact system shown in Fig. 13.

$$m\ddot{\delta } + \mu \delta^{\frac{3}{2}} \dot{\delta } + k\delta^{\frac{3}{2}} = F\left( t \right) - \left( {k_{e} x + c_{e} \dot{x}} \right)$$
(35)

where x denotes the position of the ball and its initial value x0 is − 0.01 m, δ represents the deformation between the ball and wall and it is evaluated by Eq. (36), ke = 10.6N/m and ce = 100 N·s/m are the support spring stiffness and damping, respectively, and F(t) is the sinusoidal external force shown in Eq. (37)

$$\delta = x + R - b$$
(36)
$$F\left( t \right) = 500 + 250{\text{sin}}\left( {2000t} \right)$$
(37)

Assuming here that the restitution coefficient of each contact process is 0.9 and setting ξε = 0.5%, the simulation for each collision is initialized as per the process shown in Fig. 7. For collisions starting with initial velocity, V0 is determined at the point of collision occurs, whereas for those without initial velocity = 0 while X0 is calculated based on the timing of collision occurrence. Additionally, the iterative value of μn+1 is calculated by the Newton’s iterative formula (29), or Eq. (27) based on bisection method, and the number of iterations for the first 10 collisions is shown in the Table 4. Correspondingly, the iteration times of the method used in Sect. 6.1 are listed in the third row of this table. It can be drawn from the table that in this case, it is more optimal to apply Newton’s iterative method to calculate μn+1 before the range [a, b] is determined.

Table 4 Comparison of iteration times
Full size table

Then, we get the simulation results, as shown in Figs. 14, 15, 16, 17. Figure 14 represents the development of the ball position, including solid line acquired by the described approach, and the straight line illustrates the position of the ball at the instant of contact occurs. From this figure, it can be drawn that after several collisions, the ball adheres closely to the wall, and its distance from the center to the wall gradually decreases until it changes in a cycle since the collision consuming the elastic potential energy at the initial position. The symbols “o” and “ × ” which denote the start mark and the end mark of contact cycle have also evolved from separation to overlap.

Fig. 14
figure 14

Position of the ball

Full size image
Fig. 15
figure 15

Contact force and equivalent external force

Full size image
Fig. 16
figure 16

Velocity of the ball

Full size image
Fig. 17
figure 17

Hysteresis loop during contact process

Full size image

Figure 15 shows the variation curves of contact force and equivalent external force, where the solid line represents the contact force and the dashed line is the equivalent external force formed by the combination of spring support force and sinusoidal external force, respectively. Corresponding to Fig. 14, the contact force decreases significantly until it undergoes a constant amplitude cyclic change. It should be noted that the first 5 cycles are collision contact, and the following are NIRV-collision contact. Moreover, the equivalent external force during these collisions and NIRV-collisions also decreases, and its influence on the contact process gradually increases until basically under the influence of the equivalent external force. This figure also shows that hysteresis damping factor coefficient α for each contact process increases as the contact strength weakens, until to a constant value. For this constant value, the constant amplitude and variation frequency of the contact cycle are the reasons.

The plots of the ball velocity are exhibit the same trend, as shown in Fig. 16. In addition, due to the influence of the equivalent external force, the difference between the initial approach velocity and the maximum approach velocity during contact process is increased as the initial approach velocity decreases. When the initial approach velocity is equal to zero, the approach velocity changes with the variation of the equivalent external force.

It can be observed from Figs. 14, 15, 16, 17 that the area of hysteresis loop is decreased with the reduction of the distance between the ball and the wall. The sources of the energy loss represented by the hysteresis loop of the first 5 collision contact are the initial relative kinetic energy and the work done by the equivalent external force, whereas other contact processes are only come from the work done by the equivalent external force. It should be highlight that the first four collision hysteresis loops are closed curves that change from the origin to the origin, and the fifth collision hysteresis loop changes from the origin to a non-origin, whereas the subsequent hysteresis loops change from a non-origin to a non-origin.

7 Conclusion

For unstable mechanical systems, the calculation for collision and NIRV-collision contact forces between elastic spheres was studied. Initially, brief issues of the continuous contact force models associated with the fundamental contact mechanics and energy conversion during contact process were illustrated. Next, the collision process without external forces was studied, and a corresponding hysteresis damping factor model was established combining with energy restitution coefficient and numerical computation. On these bases, the bisection method, Newton’s method and energy restitution coefficient were applied to construct an iterative formula for the hysteresis damping factor, and then a collision and NIRV-collision contact force calculation approach was established, whereas corresponding numerical calculation process was also proposed. Finally, the proposed approach was applied to simulate the collision and NIRV-collision contact dynamics of simultaneous collisions and multiple continuous collisions, and the characteristics of the elastic balls in these systems were analyzed, including displacement, contact force, equivalent external force, velocity, and hysteresis loop. The results indicate:

  1. (1)

    The proposed collision hysteresis damping factor without external forces can achieve high accuracy even with low recovery coefficients.

  2. (2)

    The calculation approach established in this article can be well applied to collision and NIRV-collision dynamic analysis.

  3. (3)

    The energy loss law of periodic NIRV-collision contact can be described by the Strong’s energy model.