1 Introduction

A collision between two bodies is a usual phenomenon in many engineering applications such as mechanisms [1, 2], robotics [3], biomechanics [4], railway dynamics [5], and impact dampers [6]. The state of mechanical system is changed abruptly in the contact events. The velocities and accelerations of colliding bodies are discontinuous in these problems. This discontinuity causes the nonlinearity of the dynamic behavior of multibody systems. When the two bodies impact each other, the contact force relationship between them must be satisfied. Therefore the contact force model is an important issue in the contact–impact process.

The first work on the collision between two bodies was done by Hertz, who developed the theory now bearing his name [7]. In this theory, a perfectly nonlinear elastic element is considered as the contact force model between the two colliding bodies. The Hertz model is not representing the energy dissipation in the collision process. For this reason, a damping element is added to the Hertz model to account for energy dissipation during the impact of colliding bodies. The combination of the stiffness and the damping element is called the viscoelastic constitutive model. The first viscoelastic impact model is the Kelvin–Voigt model, which consists of a linear spring and a linear damper element connected in parallel configuration [7]. This model is not very accurate because it does not consider nonlinearity of the impact process. Also the contact force at the beginning of contact is not continuous, because of the existence of the damping element in this model. To solve this problem, Hunt and Crossley proposed a nonlinear viscoelastic model for the contact problems [8].

The most important problem in the nonlinear viscoelastic model is determining the hysteresis damping factor. Many researchers have worked on this matter. Their studies can be divided into four categories. In the first category, the hysteresis damping factor is determined by the experimental tests, as done by Ristow [9], Lee and Herrmann [10], Schäfer et al. [11], Bordbar and Hyppänen [12], as well as Zhang and Sharf [13]. In the second category, an exact equation is proposed for determining the hysteresis damping factor, as done by Herbert and McWhannell [14], Gonthier et al. [15], as well as Zhang and Sharf [16]. The exact equation is a nonlinear function between the hysteresis damping factor and the physical parameters of the contact process. This equation doesn’t have an explicit solution, but can be solved numerically. In the third category, a simple assumption is considered and an explicit expression for the hysteresis damping factor is obtained, as done by Hunt and Crossley [8], Lee and Wang [17], Kuwabara and Kono [18], Lankarani and Nikravesh [19], Tsuji et al. [20], Brilliantov et al. [21], Marhefka and Orin [3], as well as Gharib and Hurmuzlu [22]. In the fourth category, the researchers considered an expression for the relation between the deformation and its velocity; an explicit expression between the hysteresis damping factor and the coefficient of restitution was obtained as in Flores et al. [23] and Hu and Guo [24].

Further comparative and review studies of contact force models for solid colliding bodies can be found in [25,26,27,28,29,30].

In this paper, a new model for contact force between two colliding bodies is derived. For this purpose, the mathematical modeling of a contact process is presented in Sect. 2. The kinetic energy and the work done by the Hertz contact force in the process are obtained in Sects. 3 and 4, respectively. In Sect. 5, the exact expression for the maximum deformation of the contact process is obtained. The energy loss due to the damping force is calculated in Sect. 6. In Sect. 7, the new model for contact force is derived. Finally, three numerical examples of two colliding bodies, the classic bouncing ball problem, the resilient impact damper, and a planar slider–crank mechanism, are presented and analyzed in Sects. 8, 9, and 10, respectively.

2 Mathematical modeling

The Hertz model is the base of most contact force models in the engineering applications. This model relates the contact force and the normal deformation with a nonlinear power function and is expressed as [7, 19, 31, 32]

$$ F=K \delta ^{n} $$
(1)

where \(K\) represents the generalized stiffness parameter and \(\delta \) is the relative normal deformation between the two contacting bodies. For the two contacting spheres, the generalized parameter \(K\) is a function of the radii of the spheres and the material properties. Under this condition, the generalized parameter \(K\) can be expressed as [7, 19, 31, 32]

$$ K= \frac{4}{3\pi ( \sigma _{1} + \sigma _{2} )} \sqrt{\frac{R_{1} R_{2}}{R_{1} + R_{2}}} $$
(2)

where \(R_{1}\) and \(R_{2}\) are the radii of the spheres, and the material parameters of the spheres are given by

$$ \sigma _{i} = \frac{1- v_{i}^{2}}{\pi E_{i}}\quad i=1,2 $$
(3)

where the variables \(v_{i}\) and \(E_{i}\) are the Poisson’s ratios and the Young moduli of the spheres, respectively. For a contact between sphere 1 and a plane surface of body 2, the generalized stiffness parameter \(K\) is expressed as

$$ K= \frac{4}{3\pi ( \sigma _{1} + \sigma _{2} )} \sqrt{R_{1}}. $$
(4)

It is well known that the Hertz model cannot represent the dissipative energy during the contact process.

Hunt and Crossley presented a nonlinear viscoelastic contact force model which can be expressed as [8]

$$ F=K \delta ^{n} +D \dot{\delta } $$
(5)

where the exponent \(n\) is usually set to \(3/2\) in the Hertz model [19]. Hunt and Crossley proposed that the damping coefficient \(D\) be expressed as [8]

$$ D=C \delta ^{n} $$
(6)

where \(C\) is the hysteresis damping factor. So the contact force between the two colliding spheres is expressed as

$$ F=K \delta ^{3/2} +C \delta ^{3/2} \dot{\delta }. $$
(7)

The relations between the hysteresis damping factor and the coefficient of restitution in some earlier contact force models are listed in Table 1.

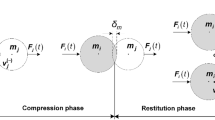
Table 1 The hysteresis damping factor in some earlier contact force models
Full size table

Each contact process consists of two phases. The first is named compression, the approaching or loading period, while the other is restitution, the separating or unloading period [7]. The two spheres come in contact and reach their maximum deformation during the compression period. In this period, the deformation velocity is reduced from its initial value to zero. The two spheres separate from each other during the restitution period, in which the deformation velocity is increased to its maximum value.

Figure 1 shows the contact between the two spheres. In this figure, \(x_{1}\), \(x_{2}\), \(\delta _{1}\) and \(\delta _{2}\) represent the displacements of the center of mass and the deformations of both spheres, respectively, just like the parameters \(m_{1}\), \(m_{2}\), \(R_{1}\), and \(R_{2}\) that represent the masses and the radii of both spheres.

Fig. 1
figure 1

The contact between two spheres

Full size image

In Fig. 1, the total deformation \(\delta \) is the sum of both spheres, i.e., \(\delta = \delta _{1} + \delta _{2}\). The total deformation is also equal to the relative motion between the two spheres and can be expressed as [33]

$$ \delta = x_{1} + x_{2}. $$
(8)

It is be noted that the deformation of each sphere in not equal to the displacement of the center of mass, i.e., \(\delta _{1} \neq x_{1}\) and \(\delta _{2} \neq x_{2}\).

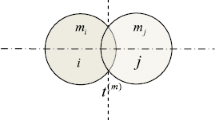
The free diagram of two spheres in contact is shown in Fig. 2. In this figure, \(F\) represents the contact force between the two colliding spheres and expressed by (7).

Fig. 2
figure 2

Free diagrams of two spheres

Full size image

Using the Newton’s second law, the acceleration of the center of mass of each sphere can be obtained as:

$$\begin{aligned} \ddot{x}_{1} =&- \frac{F}{m_{1}}, \end{aligned}$$
(9)
$$\begin{aligned} \ddot{x}_{2} =&- \frac{F}{m_{2}}. \end{aligned}$$
(10)

By double differentiation of (8) and combining with (9) and (10), the mathematical representation of the dynamical equivalent system can be expressed as

$$ m \ddot{\delta } +F=0 $$
(11)

where \(\ddot{\delta }\) represents the acceleration of the equivalent system and the equivalent mass, \(m\), is given by

$$ m= \frac{m_{1} m_{2}}{m_{1} + m_{2}}. $$
(12)

Using (7) and (11), the mathematical model of the dynamical system can be expressed as

$$ m \ddot{\delta } +C \delta ^{3/2} \dot{\delta } +K \delta ^{3/2} =0. $$
(13)

The mathematical model (13) is a second-order ordinary differential equation with variable coefficients. This equation doesn’t have an analytical solution.

3 The kinetic energy

The balance of the linear momentum for the two spheres between the initial instant and the maximum deformation instant of the contact can be expressed as [34]

$$ m_{1} V_{1}^{-} + m_{2} V_{2}^{-} = ( m_{1} + m_{2} ) V_{12} $$
(14)

where \(V_{1}^{-}\) and \(V_{2}^{-}\) are velocities of the two spheres in the initial instant of contact. So, the common velocity of both spheres in the maximum deformation instant of the contact can be obtained as

$$ V_{12} = \frac{m_{1} V_{1}^{-} + m_{2} V_{2}^{-}}{m_{1} + m_{2}}. $$
(15)

The coefficient of restitution is defined as the ratio between the deformation velocity at the separation and the deformation velocity at the initial contact of the two spheres and can be expressed as

$$ c_{r} =- \frac{\dot{\delta }^{+}}{\dot{\delta }^{-}} $$
(16)

where \(\dot{\delta }^{-}\) and \(\dot{\delta }^{+}\) represent the impacting and the separating velocities, respectively.

The change in the kinetic energy in the compression period of the contact process can be expressed as

$$ \Delta T_{\mathrm{com}} = \frac{1}{2} ( m_{1} + m_{2} ) V_{12}^{2} - \biggl( \frac{1}{2} m_{1} \bigl( V_{1}^{-} \bigr)^{2} + \frac{1}{2} m_{2} \bigl( V_{2}^{-} \bigr)^{2} \biggr). $$
(17)

Using \(V_{1}^{-} = \dot{\delta }_{1}^{-}\), \(V_{2}^{-} =- \dot{\delta}_{2}^{-}\), \(\dot{\delta }^{-} = \dot{\delta }_{1}^{-} + \dot{\delta}_{2}^{-}\) and combining with (15), (16), and (17), the change in the kinetic energy in the compression period is obtained as

$$ \Delta T_{\mathrm{com}} =- \frac{1}{2} m \bigl( \dot{\delta }^{-} \bigr)^{2} $$
(18)

where \(m\) is the equivalent mass as given by (12).

Similarly, the change in the kinetic energy in the restitution period can be expressed as

$$ \Delta T_{\mathrm{res}} =+ \frac{1}{2} m \bigl( \dot{\delta }^{+} \bigr)^{2}. $$
(19)

The total change in the kinetic energy in the contact process of the two solid spheres is the sum of the changes in the kinetic energy in the compression and the restitution periods. The total change in the kinetic energy can be obtained as

$$ \Delta T=- \frac{1}{2} m \bigl( \dot{\delta }^{-} \bigr)^{2} \bigl( 1- c_{r}^{2} \bigr). $$
(20)

Equation (20) represents the kinetic energy loss in the contact process of the two solid spheres in terms of the initial deformation velocity and the coefficient of restitution. For a fully elastic contact, the coefficient of restitution is equal to one, so the change in the kinetic energy in this contact is zero. For a fully plastic contact, the coefficient of restitution is null, so the change in the kinetic energy in this contact is maximized.

4 The work done by the Hertz contact force

The work done by the Hertz contact force in the compression period of the contact process can be expressed as

$$ \Delta W_{\mathrm{com}} = \int _{0}^{\delta _{\max }} \bigl( -K \delta ^{3/2} \bigr) d\delta $$
(21)

which can be obtained as

$$ \Delta W_{\mathrm{com}} =- \frac{2}{5} K \delta _{\max }^{5/2}. $$
(22)

Similarly, the work done by the Hertz contact force in the restitution period can be obtained as

$$ \Delta W_{\mathrm{res}} = \frac{2}{5} K \delta _{\max }^{5/2}. $$
(23)

So, the total work done by the Hertz contact force in the contact process can be obtained as

$$ \Delta W= \Delta W_{\mathrm{com}} + \Delta W_{\mathrm{res}} =0. $$
(24)

5 The maximum deformation

The relation between the deformation and its velocity can be expressed as [34]

$$ \dot{\delta } d \dot{\delta } = \ddot{\delta } d\delta . $$
(25)

This equation is a relation between distance, velocity, and acceleration in 1 DOF motion of a particle.

Using (13), the acceleration of the equivalent 1-DOF system can be obtained as

$$ \ddot{\delta } =- \frac{C \delta ^{3/2} \dot{\delta } +K \delta ^{3/2}}{m}. $$
(26)

Combining (25) and (26) gives

$$ \dot{\delta } d \dot{\delta } =- \frac{C \delta ^{3/2} \dot{\delta } +K \delta ^{3/2}}{m} d\delta . $$
(27)

Equation (27) can be represented as

$$ \frac{\dot{\delta }}{K+C \dot{\delta }} d \dot{\delta } =- \frac{\delta ^{3/2}}{m} d\delta . $$
(28)

Integrating (28) from \(\dot{\delta }^{-}\) to 0 for \(\dot{\delta }\) and from 0 to \(\delta _{\max } \) for \(\delta \), the maximum deformation of the contact process can be obtained as

$$ \delta _{\max } = \biggl( \frac{5m}{2C} \biggl( \dot{\delta }^{-} - \frac{K}{C} \ln \biggl( \frac{K+C \dot{\delta }^{-}}{K} \biggr) \biggr) \biggr)^{2/5}. $$
(29)

Equation (29) is an exact expression for the maximum deformation of the contact process.

6 The energy loss due to the damping force

The energy loss due to the damping force in the compression period can be expressed as

$$ \Delta E_{\mathrm{com}} = \int _{0}^{\delta _{\max }} \bigl( -C \delta ^{3/2} \dot{\delta } \bigr) d\delta . $$
(30)

This energy is dissipated in the thermal form and the plastic deformation in the colliding bodies.

For evaluation of Eq. (30), the relation between the deformation and its velocity must be specified.

Integrating (28) from \(\dot{\delta }^{-}\) to \(\dot{\delta }_{\mathrm{com}}\) for \(\dot{\delta }\) and from 0 to \(\delta _{\mathrm{com}}\) for \(\delta \), the relation between the deformation and its velocity in the compression period can be obtained as

$$ \delta _{\mathrm{com}} = \biggl( \frac{5m}{2C} \biggl( \bigl( \dot{ \delta }^{-} - \dot{\delta }_{\mathrm{com}} \bigr) - \frac{K}{C} \ln \biggl( \frac{K+C \dot{\delta }^{-}}{K+C \dot{\delta }_{\mathrm{com}}} \biggr) \biggr) \biggr)^{2/5}. $$
(31)

Combining (31) with (30), the energy loss due to the damping force in the compression period can be obtained as

$$ \Delta E_{\mathrm{com}} =m \biggl( \frac{- ( \dot{\delta }^{-} )^{2}}{2} + \frac{K}{C} \dot{\delta }^{-} + \biggl( \frac{K}{C} \biggr)^{2} \ln \biggl( \frac{K}{K+C \dot{\delta }^{-}} \biggr) \biggr). $$
(32)

Similarly, the energy loss due to the damping force in the restitution period can be obtained as

$$ \Delta E_{\mathrm{res}} =m \biggl( \frac{ ( \dot{\delta }^{+} )^{2}}{2} - \frac{K}{C} \dot{\delta }^{+} + \biggl( \frac{K}{C} \biggr)^{2} \ln \biggl( \frac{K+C \dot{\delta }^{+}}{K} \biggr) \biggr). $$
(33)

The total energy loss due to the damping force in the contact process of the two solid spheres is the sum of the energy losses in the compression and the restitution periods. So, the total energy loss due to the damping force can be calculated as

$$\begin{aligned} \Delta E&=- \frac{1}{2} \bigl( \bigl( \dot{\delta }^{-} \bigr)^{2} - \bigl( \dot{\delta }^{+} \bigr)^{2} \bigr) + \frac{mK}{C} \bigl( \dot{\delta }^{-} - \dot{\delta }^{+} \bigr) \\ &\quad{}+m \biggl( \frac{K}{C} \biggr)^{2} \biggl( \ln \biggl( \frac{K}{K+C \dot{\delta }^{-}} \biggr) + \ln \biggl( \frac{K+C \dot{\delta }^{+}}{K} \biggr) \biggr). \end{aligned}$$
(34)

Combining (16) and (34) gives

$$ \Delta E=- \frac{1}{2} \bigl( \dot{\delta }^{-} \bigr)^{2} \bigl( 1- c_{r}^{2} \bigr) + \frac{mK}{C} \dot{\delta }^{-} ( 1+ c_{r} ) +m \biggl( \frac{K}{C} \biggr)^{2} \ln \biggl( \frac{K-C c_{r} \dot{\delta }^{-}}{K+C \dot{\delta }^{-}} \biggr). $$
(35)

The balance of the energy in the contact process can be expressed as

$$ \Delta W+\Delta E=\Delta T. $$
(36)

Combining (20), (24), and (35) with (36) gives

$$ \dot{\delta }^{-} ( 1+ c_{r} ) + \frac{K}{C} \ln \biggl( \frac{K-C c_{r} \dot{\delta }^{-}}{K+C \dot{\delta }^{-}} \biggr) =0. $$
(37)

For simplicity, the hysteresis damping ratio is defined as

$$ h_{r} = \frac{C \dot{\delta }^{-}}{K}. $$
(38)

So, the relation between the hysteresis damping ratio and the coefficient of restitution can be expressed as

$$ h_{r} ( 1+ c_{r} ) = \ln \biggl( \frac{1+ h_{r}}{1- c_{r} h_{r}} \biggr). $$
(39)

This relation is the exact equation between the hysteresis damping ratio and the coefficient of restitution as obtained by Zhang and Sharf [16]. This equation has no explicit solution, but can be solved numerically. In this paper, this numerical solution is called the numerical model. To derive an explicit expression for the relation between the hysteresis damping ratio and the coefficient of restitution, a simpler relation between the deformation and its velocity can be considered instead of (31).

The relation between the hysteresis damping ratio and the coefficient of restitution in the numerical model and the earlier models are shown in Fig. 3.

Fig. 3
figure 3

The hysteresis damping ratio versus the coefficient of restitution in the numerical model and earlier models

Full size image

All the models presented in Fig. 3, except the Gharib and Hurmuzlu model [22], have a similar response when the value of the coefficient of restitution is higher than 0.8. The contact force approaches by Flores et al. [23], Gharib and Hurmuzlu [22], Hu and Guo [24], and the numerical model have a similar behavior for moderate and low values of the coefficient of restitution. Indeed, when the coefficient of restitution is equal to zero, the hysteresis damping ratio and the hysteresis damping factor in these models become infinite, which is logical from the physical view of the contact process.

The numerical model is nearly equivalent to the real contact force model. So for the low values of coefficient of restitution, Gharib and Hurmuzlu model is closer to reality but this model is originally not proper for the high values of coefficient of restitution. For such values, Flores et al. and Hu and Guo models are closer to reality.

It can be observed that the behavior of Flores et al. [23] and Hu and Guo [24] models is very similar to the numerical model in the whole range of the coefficient of restitution.

Flores et al. used the solution of the Kelvin–Voigt model and considered the relation between the deformation and its velocity as [23]

$$ \frac{\dot{\delta }}{\dot{\delta }^{-}} = \biggl( 1- \biggl( \frac{\delta }{\delta _{\max }} \biggr)^{2} \biggr)^{\frac{1}{2}}. $$
(40)

Hu and Guo used the solution of the Hertz model and considered the relation between the deformation and its velocity as [24]

$$ \frac{\dot{\delta }}{\dot{\delta }^{-}} = \biggl( 1- \biggl( \frac{\delta }{\delta _{\max }} \biggr)^{\frac{5}{2}} \biggr)^{\frac{1}{2}}. $$
(41)

Similarly, in this paper, a parametric expression is considered for the relation between the deformation and its velocity in the compression period given by

$$ \frac{\dot{\delta }}{\dot{\delta }^{-}} = \biggl( 1- \biggl( \frac{\delta }{\delta _{\max }} \biggr)^{a} \biggr)^{\frac{1}{b}} $$
(42)

where \(a\) and \(b\) are two unknown constants.

Combining (30) and (42) gives

$$ \Delta E_{\mathrm{com}} = \int _{0}^{\delta _{\max }} \biggl( -C \delta ^{3/2} \dot{\delta }^{-} \biggl( 1- \biggl( \frac{\delta }{\delta _{\max }} \biggr)^{a} \biggr)^{\frac{1}{b}} \biggr) d\delta . $$
(43)

Considering \(\delta / \delta _{\max } = y\) gives

$$ \Delta E_{\mathrm{com}} =-C \delta _{\max }^{5/2} \dot{ \delta }^{-} \int _{0}^{1} y^{3/2} \bigl( 1- y^{a} \bigr)^{\frac{1}{b}} dy. $$
(44)

Introducing \(I = \int _{0}^{1} y^{3/2} ( 1- y^{a} )^{\frac{1}{b}} dy\) gives

$$ \Delta E_{\mathrm{com}} =-IC \delta _{\max }^{5/2} \dot{ \delta }^{-}. $$
(45)

Similarly, the energy loss due to the damping force in the restitution period can be obtained as

$$ \Delta E_{\mathrm{res}} =IC \delta _{\max }^{5/2} \dot{ \delta }^{+}. $$
(46)

So, the total energy loss due to the damping force in the contact process of two solid spheres can be calculated as

$$ \Delta E=-IC \delta _{\max }^{5/2} \bigl( \dot{\delta }^{-} - \dot{\delta }^{+} \bigr). $$
(47)

Combining (16) with (47) gives

$$ \Delta E=-IC \delta _{\max }^{5/2} \dot{\delta }^{-} ( 1+ c_{r} ). $$
(48)

As shown in (28), the relation between the deformation and the deformation velocity is related to \(K\), \(C\), and \(m\). Using (2), (3), and (12), it is clear that the relation between the deformation and deformation velocity is related to the modulus of elasticity, Poisson’s ratio, radius, and mass of two colliding bodies. Equation (42) show a combination of parameters \(a\) and \(b\) that determine the relation between the deformation and the deformation velocity. An integral combination of these two parameters is equal to parameter \(I\). So parameters \(a\), \(b\) and \(I\) are related to the modulus of elasticity, Poisson’s ratio, radius, and mass of two colliding bodies.

7 The new contact force model

The energy balance in the compression period of the contact process can be expressed as [34]

$$ \Delta E_{\mathrm{com}} + \Delta W_{\mathrm{com}} = \Delta T_{\mathrm{com}}. $$
(49)

Combining (18), (22), and (46) with (49) gives

$$ -IC \delta _{\max }^{5/2} \dot{\delta }^{-} - \frac{2}{5} K \delta _{\max }^{5/2} =- \frac{1}{2} m \bigl( \dot{\delta }^{-} \bigr)^{2}. $$
(50)

Solving Eq. (50) gives

$$ \delta _{\max }^{5/2} = \frac{\frac{1}{2} m ( \dot{\delta }^{-} )^{2}}{\frac{2}{5} K+IC \dot{\delta }^{-}}. $$
(51)

So, the maximum deformation in the contact process can be obtained by

$$ \delta _{\max } = \biggl( \frac{\frac{1}{2} m ( \dot{\delta }^{-} )^{2}}{\frac{2}{5} K+IC \dot{\delta }^{-}} \biggr)^{2/5}. $$
(52)

Combining (20), (24), (48), and (51) with (36) gives

$$ -IC \biggl( \frac{\frac{1}{2} m ( \dot{\delta }^{-} )^{2}}{\frac{2}{5} K+IC \dot{\delta }^{-}} \biggr) \dot{\delta }^{-} ( 1+ c_{r} ) +0=- \frac{1}{2} m \bigl( \dot{\delta }^{-} \bigr)^{2} \bigl( 1- c_{r}^{2} \bigr). $$
(53)

Solving (53), the hysteresis damping factor can be obtained as

$$ C= \frac{2}{5I} \frac{ ( 1- c_{r} )}{c_{r}} \frac{K}{\dot{\delta }^{-}}. $$
(54)

So, the hysteresis damping ratio in the new model can be expressed as

$$ h_{r} = \frac{2}{5I} \frac{ ( 1- c_{r} )}{c_{r}} $$
(55)

where \(I\) is a function of two unknown constants \(a\) and \(b\). To determine \(a\) and \(b\), the RMS of the percentage error of the hysteresis damping ratio of the new model with respect to the numerical model is minimized. The RMS of the percentage error of the hysteresis damping ratio of the new model with respect to the numerical model for various values of \(a\) and \(b\) is listed in Table 2.

Table 2 The RMS of the percentage error of the hysteresis damping ratio of the new model with respect to the numerical model
Full size table

It is clear that the RMS of the percentage error is minimized at \(a =1.5\) and \(b =5.5\). This minimized value is 12.596. So, the relation between the deformation and its velocity can be expressed as

$$ \frac{\dot{\delta }}{\dot{\delta }^{-}} = \biggl( 1- \biggl( \frac{\delta }{\delta _{\max }} \biggr)^{\frac{3}{2}} \biggr)^{\frac{2}{11}}. $$
(56)

Thus, parameter \(I\) can be expressed as

$$ I= \int _{0}^{1} \bigl( y^{3/2} \bigl( 1- y^{3/2} \bigr)^{2/11} \bigr) dy $$
(57)

which can be evaluated as

$$ I=0.3180\approx 0.3200= \frac{8}{25}. $$
(58)

It is being noted that the RMS of the percentage error of Flores et al. and Hu and Guo models is 29.438 and 22.566, respectively. These values are much greater than the RMS of the minimized value, which is 12.596.

Combining (55) with (58), the hysteresis damping ratio can be obtained as

$$ h_{r} = \frac{5}{4} \frac{ ( 1- c_{r} )}{c_{r}}. $$
(59)

The relation (59) is called the new model. The relation between the hysteresis damping ratio and the coefficient of restitution in the new model, the numerical model, as well as Flores et al. [23] and Hue and Guo [24] models are shown in Fig. 4.

Fig. 4
figure 4

The hysteresis damping ratio versus the coefficient of restitution in the contact force models

Full size image

Although Flores et al. and Hu and Guo models have similar behavior as the numerical model, they are not completely consistent with the numerical model for the low values of the coefficient of restitution.

Analyzing Fig. 4, it is clear that the new model is completely consistent with the numerical model in the whole range of the coefficient of restitution. So, the new model can be selected as the best contact force model for the collision between the two solid spheres in the whole range of the coefficient of restitution. Thus, this new model can be used in the hard and soft impact problems.

The same result can be obtained by another way. The contact force model is performed by using the input coefficient of restitution (\(c_{r,\text{in}}\)). Then the deformation velocity at separation time (\(\dot{\delta }^{+}\)) is obtained by using the new contact force model. Thus, the output coefficient of restitution is obtained as

$$ c_{r,\text{out}} =- \frac{\dot{\delta }^{+}}{\dot{\delta }^{-}}. $$
(60)

It can be found that the output coefficient of restitution differs from the input coefficient of restitution, but they should be the same value theoretically. The plots of the output coefficient of restitution versus the input coefficient of restitution for different contact force models are shown in Fig. 5. The error of the output coefficient of restitution with respect to the input coefficient of restitution for various contact force models are plotted in Fig. 6.

Fig. 5
figure 5

The relation between the output and the input coefficients of restitution

Full size image
Fig. 6
figure 6

The error of output coefficients of restitutions respect to the input coefficients of restitution

Full size image

Analyzing Figs. 5 and 6 shows that the error of the new model for low values of the coefficient of restitution (e.g., less than 0.4) is less than the error of Flores et al. and Hu and Guo models. So the new model is closer to reality for low values of the coefficient of restitution.

Analyzing Figs. 3, 4, 5, and 6 shows that the contact force models can be divided into four groups. In the first group, the contact force models are suitable for the high values of the coefficient of restitution. All of the models, except for Gharib and Hurmuzlu model, are placed in this group. In the second group, the contact force models are suitable for the low and moderate values of the coefficient of restitution, such as Flores et al. model, Gharib and Hurmuzlu model, Hu and Guo model, and the new model derived in this paper. In the third group, the contact force models are nearly suitable for the whole range of the coefficient of restitution and include Flores et al. and Hu and Guo models. In the fourth group, the contact force models are completely suitable for the whole range of the coefficient of restitution. The new model is placed in this group.

The hysteresis damping factor in the new model can be obtained as

$$ C= \frac{5}{4} \frac{ ( 1- c_{r} )}{c_{r}} \frac{K}{\dot{\delta }^{-}}. $$
(61)

Thus, the new model of the contact force can be expressed as

$$ F=K \delta ^{3/2} \biggl( 1+ \frac{5}{4} \frac{ ( 1- c_{r} )}{c_{r}} \frac{\dot{\delta }}{\dot{\delta }^{-}} \biggr). $$
(62)

It is important to point out that the new model is valid for the direct central and frictionless impacts. In perfectly elastic contacts when the coefficient of restitution is equal to one, the hysteresis damping factor is zero and the new model is equivalent to the Hertz model. When the coefficient of restitution is equal to zero, the hysteresis damping factor become infinite, which is logical from the physical view of the contact process.

8 Example 1: the bouncing ball problem

A numerical example, the classic bouncing problem, which is a simple example for analyzing the contact process, is considered here to compare the new model with the earlier contact force models listed in Table 1. The model of this problem is shown in Fig. 7. The numerical values of this example are listed in Table 3 [24].

Fig. 7
figure 7

The bouncing ball

Full size image
Table 3 Numerical values for the bouncing ball problem [24]
Full size table

The bouncing ball falls down and collides with the ground. The ground is assumed to be rigid and stationary. The initial velocity of the ball when it collides with the ground can be expressed as [34]

$$ \dot{\delta }^{-} = \sqrt{2g ( H_{0} -R )} $$
(63)

where \(g\) represents gravity acceleration. In relation (63), \(H_{0}\) and \(R\) are the initial height of the center of mass and the radius of the ball, respectively.

The new model, the Hertz model, and the earlier contact force models are used to calculate the contact force, deformation, and time of the contact during the contact process between the ball and the ground. Analyzing this problem is done by using Matlab codes. The contact force versus the deformation for four values of the coefficient of restitution (0.2, 0.4, 0.6, and 0.8) is plotted in Figs. 8, 9, 10, and 11, respectively.

Fig. 8
figure 8

The contact force versus the deformation for \(c_{r} =0.2\)

Full size image
Fig. 9
figure 9

The contact force versus the deformation for \(c_{r} =0.4\)

Full size image
Fig. 10
figure 10

The contact force versus the deformation for \(c_{r} =0.6\)

Full size image
Fig. 11
figure 11

The contact force versus the deformation for \(c_{r} =0.8\)

Full size image

By analyzing Figs. 8–11, the following results are obtained:

  1. 1.

    When the coefficient of restitution is high, i.e., 0.8, all of the models, except for Gharib and Hurmuzlu model, have a similar behavior and become very similar to Hertz model.

  2. 2.

    When the coefficient of restitution is low, i.e., 0.2, Flores et al. model, Gharib and Hurmuzlu model, Hu and Guo model, and the new model have a similar behavior.

  3. 3.

    When the coefficient of restitution is increasing (from Fig. 8 to Fig. 11), the maximum deformation increases while the maximum contact force is reduced. These results are expected because of decreasing in energy loss due to damping force while the coefficient of restitution is increasing.

9 Example 2: the resilient impact damper

The impact damper is a passive device composed of one or more cavities that are filled with dry granular particles such as granules of steel, aluminum, lead, tungsten carbide, or ceramic [35]. The impact damper consists of one or several small masses which are mounted on top or inside the vibrating system. When the primary system vibrates, the impact mass moves and collides with fixed stops of the mounting system. These collisions lead to the momentum transfer from the primary system to the impact mass. The kinetic energy of the vibrating system equipped with the impact damper gets dissipated due to impact between impact and primary masses, friction and sound radiation. So the kinetic energy of the primary system is reduced and the vibrating motion gets damped.

The impact dampers can be classified into rigid and resilient. For low contact velocity and high modulus of elasticity, the impact damper can be considered as rigid. While for high contact velocity and low modulus of elasticity, the impact damper is resilient. In the rigid impact damper, the contact time is very small. Thus the changes in the positions of the primary and impact masses can be neglected. So the positions after contact can be considered equal to those before contact. In the resilient impact damper, the contact time is not negligible. So the changes in the positions of the primary and impact masses must be considered.

Figure 12 shows a schematic of a 1-DOF system equipped with the resilient single-unit impact damper.

Fig. 12
figure 12

The 1-DOF system equipped with resilient impact damper

Full size image

When there is no contact between the impact and primary masses, the equations of motion of the system can be written as

$$ \begin{aligned} &-C \dot{x}_{M} -K x_{M} -\mu m g \operatorname{sgn} ( \dot{x}_{M} - \dot{x}_{m} ) =M \ddot{x}_{M} \\ &\mu m g \operatorname{sgn} ( \dot{x}_{M} - \dot{x}_{m} ) =m \ddot{x}_{m} \end{aligned} $$
(64)

where \(x_{M}\) and \(x_{m}\) are the positions of the primary and the impact masses, respectively; \(\mu \) is the kinetic friction coefficient between these two masses. Dot and double dot denote the first and second derivatives with respect to time, respectively. These equations are a system of two nonhomogeneous coupled second-order ordinary differential equations with constant coefficients and so can be solved analytically as

$$ \begin{aligned} x_{M} ( t ) &= e^{-\xi \omega _{n} t} \bigl\{ A \sin \bigl( \sqrt{1- \xi ^{2}} t \bigr) +B \cos \bigl( \sqrt{1- \xi ^{2}} t \bigr) \bigr\} -\mu \frac{m}{K} g \operatorname{sgn} ( \dot{x}_{M} - \dot{x}_{m} ), \\ x_{m} ( t ) &= \frac{1}{2} \mu g \operatorname{sgn} ( \dot{x}_{M} - \dot{x}_{m} ) t^{2} +C t+D \end{aligned} $$
(65)

where \(\omega _{n}\), \(\xi \), and \(t\) represent the natural frequency, damping ratio, and time, respectively. The initial conditions are considered parametrically as

$$ \begin{aligned} x_{M} ( t_{0} ) &= x_{M,0}, \qquad \dot{x}_{M} ( t_{0} ) = V_{M,0}, \\ x_{m} ( t_{0} ) &= x_{m,0},\qquad \dot{x}_{m} ( t_{0} ) = V_{m,0}. \end{aligned} $$
(66)

Using these initial conditions, the general solution of the equations of motion can be determined. The contact situation between main mass and impact mass can be determined using the following relations:

$$ \begin{aligned} x_{m} - ( x_{M} -d/2 ) &=0\quad (\text{Contact between impact mass and left side}), \\ ( x_{M} +d/2 ) - x_{m} &=0\quad (\text{Contact between impact mass and right side}) \end{aligned} $$
(67)

where \(d\) is the gap size.

When contact occurs between impact mass and two end stoppers, the contact force between them must be added to the equations of motion. In this situation, the equations of motions can be written as

$$ \begin{aligned} &M \ddot{x}_{M} +C \dot{x}_{M} +K x_{M} +\mu m g \operatorname{sgn} ( \dot{x}_{M} - \dot{x}_{m} ) + F_{\mathrm{contact}} =0 \\ &m \ddot{x}_{m} -\mu m g \operatorname{sgn} ( \dot{x}_{M} - \dot{x}_{m} ) - F_{\mathrm{contact}} =0 \end{aligned} $$
(68)

where \(F_{\mathrm{contact}}\) is the contact force between the impact and main masses. By defining the deformation between impact mass and the left side of main mass container as \(\delta = ( x_{M} -d/2 ) - x_{m}\) and also using the new contact force model described in this article, the equations of motion can be obtained as

$$ \begin{aligned} &M \ddot{x}_{M} +C \dot{x}_{M} +K x_{M} +\mu m g \operatorname{sgn} ( \dot{x}_{M} - \dot{x}_{m} ) \\ &\quad{}+ K_{\text{Hz}} \bigl\langle ( x_{M} -d/2 ) - x_{m} \bigr\rangle ^{\frac{3}{2}} \biggl( 1+ \frac{5}{4} \frac{1- c_{r}}{c_{r} \dot{\delta }^{-}} ( \dot{x}_{M} - \dot{x}_{m} ) \biggr) =0 \\ &m \ddot{x}_{m} -\mu m g \operatorname{sgn} ( \dot{x}_{M} - \dot{x}_{m} ) \\ &\quad{}- K_{\text{Hz}} \bigl\langle ( x_{M} -d/2 ) - x_{m} \bigr\rangle ^{\frac{3}{2}} \biggl( 1+ \frac{5}{4} \frac{1- c_{r}}{c_{r} \dot{\delta }^{-}} ( \dot{x}_{M} - \dot{x}_{m} ) \biggr) =0 \end{aligned} $$
(69)

where \(K_{\text{Hz}}\) is the generalized stiffness parameter which can be determined using Eq. (2) or (4). These equations form a system of two coupled nonlinear differential equations. They cannot be solved analytically but can be solved numerically.

The numerical values of this example are listed in Table 4.

Table 4 Numerical values for the impact damper problem
Full size table

Figure 13 shows the time response of the positions of the impact mass and two end stoppers in the impact damper with 20 mm gap size. As shown in this figure, the behavior of this damper can be classified into three zones. In the first zone, from 0 to 30 seconds, the impact mass has effective collisions with two end stoppers. This zone is named the impact zone. The effect of friction and structural damping is insignificant in the impact zone. In this zone, the decreasing rate of the amplitude of the position of the primary mass is nearly linear. In the second zone, from 30 to 45 seconds, the collisions between the impact mass and two end stoppers is not so effective. The reason for the movement of the impact mass in this zone is mainly the friction between the impact mass and the guiding bars. This zone is named the friction zone. In the third zone, after 45 seconds, the movement of impact mass relative to the end stoppers is nearly insignificant. In this zone, the dynamic behavior of this system is similar to the behavior of the system without an impact damper. This zone is named the no-impact zone.

Fig. 13
figure 13

Time response of impact mass and left and right sides of the container (the impact damper with 10 mm gap size)

Full size image

For simplifying response graphs, the amplitude of the position of the 1-DOF system can be displayed. Figures 14, 15, 16 and 17 show the amplitude of the position response in the 1-DOF system equipped with an impact damper with 20, 30, 40, and 50 mm gap size, respectively.

Fig. 14
figure 14

Amplitude of position of 1-DOF system equipped with impact damper with 20 mm gap size

Full size image
Fig. 15
figure 15

Amplitude of position of 1-DOF system equipped with impact damper with 30 mm gap size

Full size image
Fig. 16
figure 16

Amplitude of position of 1-DOF system equipped with impact damper with 40 mm gap size

Full size image
Fig. 17
figure 17

Amplitude of position of 1-DOF system equipped with impact damper with 50 mm gap size

Full size image

As shown in these figures, while the gap size increased, the impact damper effect in free vibration reduction improved. When the gap size is very small, the effect of the impact damper is insignificant. For the zero gap size, the impact damper has no effect on the free vibration reduction. In this situation, the system is equivalent to a 1-DOF system without impact damper. When the gap size is very large, greater than twice the initial displacement of 1-DOF system theoretically, the impact mass cannot collide with the end stoppers. Thus the impact damper has no effect on the free vibration reduction. In this situation, the system is equivalent to a 1-DOF system without an impact damper, which is similar to the zero gap size situation.

10 Example 3: a planar slider–crank mechanism

A planar slider–crank mechanism is a classical contact–impact problem in multibody system dynamics. This system consists of five solid bodies representing the slider–crank mechanism and the free sliding block as shown in Fig. 18 [36]. When the slider moves to the right, it collides with the free block and the contact problem occurs. This system represents a multibody model with a total of two degrees of freedom (2-DOF). The geometrical and inertial properties of solid bodies and the initial conditions and simulation configurations of this multibody system are listed in Tables 5 and 6, respectively.

Fig. 18
figure 18

A slider–crank mechanism and a free sliding block [36]

Full size image
Table 5 Geometrical and inertial propertied of multibody system
Full size table
Table 6 Initial conditions and simulation configurations of multibody system
Full size table

The relative deformation of the slider with respect to the free block can be determined using the following geometrical condition [36]:

$$ \delta = x_{5} - x_{4} -2a. $$
(70)

The crank and the connecting rod are aligned in the \(x\) direction at the start of dynamic analysis. Using the constraint equation between the crank and slider, the position and velocity of the slider can be calculated. When the slider and free block collide, the difference in their velocities can be obtained using the new contact force model described in this article.

The time response of positions and velocities of the slider and free block are shown in Figs. 19 and 20, respectively.

Fig. 19
figure 19

The time response of positions of the slider and free block

Full size image
Fig. 20
figure 20

The time response of velocities of the slider and free block

Full size image

At the start of dynamic analysis, the crack rotates counterclockwise and the slider moves to the left. At this time, the free block moves to the left. When time is close to 0.28, the slider moves to the right and collides with the free block. After collision, the slider moves to the left and the free block moves to the right. As shown in Fig. 19, two collisions between slider and free block occur. After each collision, the velocity of the slider decreased while the velocity of the free block increased.

As shown in this example, the new contact force model described in this article can be used in multibody system dynamics problems.

11 Conclusions

The new model of the contact of the collision between the two solid bodies has been derived in this paper. This model can be used directly for the impact analysis of the multibody dynamics. This model has been developed by using the energy balance during the contact process. The change in the kinetic energy is obtained by using the classical kinetic energy principle. Furthermore, a parametric relation between the deformation and its velocity is considered. Then the dissipated energy due to the damping force has been calculated. Equating the change in the kinetic energy with the energy loss due to the damping force, an explicit parametric expression between the hysteresis damping factor and the coefficient of restitution is obtained. For determining the unknown constants, the RMS of the percentage error of this expression with respect to the numerical model is minimized. This expression is called the new model which can be used directly for the impact analysis of the multibody dynamic systems.

To sum up, this new model is completely suitable for analyzing the contact process for the whole range of the coefficient of restitution (0–1). So this model is valid for the hard and soft contact problems. Also this model, as an independent formula, can be used directly for impact analysis of the multibody dynamic systems.

Funding This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sector.