Introduction

In our ecological environment, the interaction between prey and predator is a common occurrence that exists everywhere. This environmentally friendly scheme is one of the key areas for mathematical ecology. Some mathematicians and ecologists have shown a considerable interest in researching prey deprivation in population dynamics during the past couple of decades [4, 5, 31, 32, 41]. The first to present a model of prey predator in the area was one of its pioneers in population ecology [8, 9], and it identified differences between observation and projections of the Lotka–Volterra model [23] of prey predators. The Gause concept was revamped [2011] by Krivan [20] and the ill-presented model defined.

The prey refuge impact is a phenomenon triggered by environmental heterogeneity. It alludes to the idea that certain prey may be protected from predators or be unavailable to them. McNair [28] (1986) did a lot of research on the refuge effect; Jana [17] did a lot of research on it as well (2013).

The revisiting influence exercises being an impact with regard to prey development, thereby also pronouncing an effect that is inimical to predators. If one were to go by the experiments, the part played by the prey’s refuge is indeed highly impactful, determine the rationale for coexistence of prey and predator, given that it enhances the equilibrium density of one community prey and brings about assured stability around the positive fixed point. Any species belonging to the prey category that comes with a massive population is sure to locate safe places to preserve themselves. A case in point would be rats, which thrive under adverse conditions once they identify ways and means to find threats from natural predators [21]. The availability of a prey refuge signals the higher populations of both prey and predators [28, 34]. Plenty of research has gone into looking at prey refuges with a fine tooth-comb [10, 39, 43]. Ghosh et al. [10] examined a prey-predator arrangement involving prey refuge and the availability of food in plenty for the predator. Their calculations revealed that to enable the co-existence of species, one pre-condition was the assurance of high values of prey refuge. At the same time, the presence of a very safe shelter for prey implied the near or total annihilation of the predator. Kar [19] came up with numerous puzzling findings in relation to the existence of a single global asymptotical stable limit cycle. Despite such discoveries, only a few researchers [11, 25, 27] have demonstrated that prey refuge is influenced by prey and predator population density. The often made assumption that prey refuge and predator bio-mass are directly correlated permits a fair degree of realistic understanding of prey-predator symbiosis. It needs to be said that there are biological environments where prey refuge is significantly impacted by predator biomass.

Intra-specific rivalry for prey among predators begins the moment the predator-to-prey ratio is high enough, resulting in individuals in the predator community losing fitness due to a lack of food [29]. Severe rivalry occurs in blue crab colonies, which exhibit brutal behaviour as a result of a shortage, resulting in bloodied wounds [6]. Owing to a lack of alternative food sources, more intense intra-specific rivalry has been observed in a number of predator species [7]. Finally, in a deterministic setting, rivalry within the predator community may be favorable for predator species in some conditions.

In general, predator reproduction is not instantaneous in response to prey consequences; rather, there is a discrete time lag required for gestation. As a result, the proposed model has a continuous time lag. Time delay causes complex dynamical behaviour in biological processes, which may lead to limited period oscillations and instability [24]. Specific population growth fluctuates when the gestation time delay increases and the mechanism becomes unpredictable. Jana et al. [18] brought to light a prey-predator mechanism involving prey refuge and Holling type-II functional response that carried a time delay. Ko and Ryu [40] examined the asymptotic activity that was spatially non-uniform in nature and that involved the presence of a periodic result below the uniform Neumann boundary state. The spatiotemporal dynamics that put in the picture a 2D prey-predator model was actually a restricted version of a variant of the Leslie–Gower model involving a prey refuge [13].

Researchers have zeroed in on the direction as well as the stability of Hopf bifurcation drawing on delay-induced ecological systems for quite some time now [3,12, 14, 35, 42]. The primary aim is to look at the manner in which gestational delay is instrumental in determining crucial aspects of the prey-predator relationship. Some researchers [22, 26] have displayed a keen interest in embedding white noise as a causal factor vis-à-vis environmental variations to examine how noise impacts population dynamics. May [26] view a biological system comprising both white noise and stochastic fluctuation to show that any movement of the population from the equilibrium point sets up the system for instability? Ripa et al. [30] researched the influence of noise on populations in general and drew up a general hypothesis that would account for ambient noise in any biological food chain. Upadhyay et al. [38] also took up exciting research on how noise impacted an ecological model in real-time with a top predator, and in the course of research, it came through that the magnitude, trophic levels, and sensitivity of the community to environmental noise were each paramount as factors exercising a major impact. Attempts to deploy models of actively interacting populations became very popular because these models were used to supplement evolutionary mechanism models from injecting stochasticity at many stages of interactions, the major factor behind stochasticity in a population [33, 36]. May [26] came to discover that all the parameters concerning a working model can be manipulated suitably to decrease the values in such a manner as to stimulate repeated fluctuations.

In order to be more consistent with the actual development of biological populations, many researchers combine the fractional-order derivative with the time delay in the model to describe and explore diverse complex systems, such as predator–prey interactions with memory effect. Because of its memory effects, fractional-order systems have been investigated for modeling realistic phenomena throughout the last few decades. In comparison to the standard integer-order models with ordinary time derivatives [47,48,49,50], this feature makes fractional-order models more useful for representing real-world processes.

We're looking at a prey-predator model that includes prey refuge and intra-specific predator rivalry in this study. We're interested in merging these subjects and studying the consequences because many scholars have focused on them separately. According to earlier study, delay destabilises the mechanism in general, and Hopf-bifurcation causes equilibrium loss of stability. We show that the delay parameters have a critical value below which the coexistence equilibrium is stable and an unstable value above which it is unstable. Hopf bifurcation occurs when the latency parameters reach their essential levels. This work expected that stochastic perturbations would be white noise-based, and that these perturbations would be absorbed into prey and predator groups as described in our study. In the vicinity of the interior equilibrium point, stochastic differential equations were used to investigate the various characteristics. We also propose a modified functional response that might be appropriate for predator–prey interactions in complex habitats. It would be more ideal for laboratory setup in general, for example, in the Luckinbill experiment [44]. The primary goal of this research is to look into the impact of prey refuge as well as intra-specific predator rivalry on the dynamics of the prey-predator system. We've shown that predators' intra-specific rivalries, as well as the refuge level of prey, have a key influence in influencing dynamics.

This paper assumed that perturbations involving stochasticity would be white noise based which would be incorporated into prey and predator communities invoked in our study. The various aspects were looked into through stochastic differential equations in proximity to interior equilibrium point. The model in question draws from the predator–prey system:

$$ \begin{gathered} \frac{dx}{{dt}} = rx\left( {1 - \frac{x}{K}} \right) - \frac{\beta xy}{{1 + \alpha x}}, \hfill \\ \frac{dy}{{dt}} = \frac{c\beta xy}{{1 + \alpha x}} - \gamma y. \hfill \\ \end{gathered} $$
(1.1)

In the nonappearance of predator species \(y(t)\), the prey population \(x(t)\) is expected to expand logistically to its carrying ability \(K\) at an inherent growth rate \(r\).\(\alpha\) is the predator's maximum per capita prey intake rate, \(a\) is the amount of prey required for the predator's relative biomass growth rate to be half of its maximum, \(c\) is a calculation of the food quality content provided by the prey, which is translated to predator birth, and \(\gamma\) is the predator's death rate. The term \({{\beta x} \mathord{\left/ {\vphantom {{\beta x} {1 + \alpha x}}} \right. \kern-\nulldelimiterspace} {1 + \alpha x}}\) refers to the predator's practical reaction. Holling type II response function [15] is the name given to this response function.

The model above is gradually extended in the present study from making use of the relation \(m \in \left[ {0,1} \right)\). This equation is a measure of the degree or extent of prey refuge to reckon with, when one assumes that the refuge is defending \(mx\) of the prey while leaving \(\left( {1 - m} \right)x\) of the same prey vulnerable to the predator. \(\theta\) represents values in terms of prey-predator intra-specific rivalry. The moment all such assumptions are factored in the equation; it is easy to see that the reworked system from (1) can now be cast as

$$ \begin{gathered} \frac{dx}{{dt}} = rx\left( {1 - \frac{x}{K}} \right) - \frac{{\beta \left( {1 - m} \right)xy}}{{1 + \alpha \left( {1 - m} \right)x}}, \hfill \\ \frac{dy}{{dt}} = \frac{{c\beta \left( {1 - m} \right)xy}}{{1 + \alpha \left( {1 - m} \right)x}} - \gamma y - \theta y^{2} . \hfill \\ \end{gathered} $$
(1.2)

\(x(t) > 0,y(t) > 0\,\forall t \ge 0.\)

Existence and Boundedness of the System

Existence

Theorem 1

Every solution of the system Eq. (1.2) with initial conditions exists in the interval \(\left( {0,\infty } \right)\) and \(x(t) > 0,y(t) > 0\,\forall t \ge 0\).

Proof

Let

$$ \frac{dx}{{dt}} = \psi_{1} \left( {x,y} \right),\,\frac{dy}{{dt}} = \psi_{2} \left( {x,y} \right). $$
(2.1)

Integrating then we obtain \(x(t) = x(0)\,e^{{\int\limits_{0}^{t} {\psi_{1} \left( {x,y} \right)ds} }} ,\,\,y(t) = y(0)\,e^{{\int\limits_{0}^{t} {\psi_{2} \left( {x,y} \right)ds} }}\) where \(x(0),y(0)\) initial conditions which are positive. Hence the solution is exist and which is unique on \(\left( {0,\varsigma } \right)\,\,{\text{where}}\,\,0 < \varsigma < \infty\) since \(\psi_{1} ,\,\,\psi_{2}\) are continuous functions and locally Lipschitzian.

Boundedness

Theorem 2

The solutions of the system Eq. (1.2) with initial conditions \(x(0) = y(0) > 0\) are uniformly bounded in \(\Re_{ + }^{2}\).

Proof

Let

$$ \rho = x + \frac{1}{c}y\,, $$
(2.2)
$$ \frac{d\rho }{{dt}} = \frac{dx}{{dt}} + \frac{1}{c}\frac{dy}{{dt}}\,\,, $$
$$ \frac{d\rho }{{dt}} = rx\left( {1 - \frac{x}{K}} \right) - \frac{\gamma }{c}y - \frac{\theta }{c}y^{2} \,, $$
$$ \frac{d\rho }{{dt}} \le 2rx - \frac{{rx^{2} }}{K} - rx - \frac{\gamma }{c}y\,, $$
$$ \le - \frac{r}{K}\left( {x - K} \right)^{2} + rK - rx - \frac{\gamma }{c}y\,, $$

\(\le rK - \upsilon \left( {x + \frac{1}{c}y} \right)\), where \(\upsilon = \min \{ r,\gamma \}\)

$$ \frac{d\rho }{{dt}} \le x\left( {r + 1} \right) - \upsilon \rho . $$

On using the theorem in differential inequalities Birkhoff et al., [2], we obtain.

\(0 \le \rho (x,y) \le \frac{rK}{\upsilon } + \left( {\rho (x(0),y(0)) - \frac{rK}{\upsilon }} \right)/e^{\upsilon t}\) and if \(t \to \infty ,\,\,0 \le \rho \le \frac{rK}{\upsilon }.\)

Thus, the solutions of the model Eq. (1.1) are exist in the region

$$ \Omega = \left\{ {\left( {x,y} \right) \in \Re_{ + }^{2} :0 < \rho \le \frac{rK}{\upsilon }} \right\}\,, $$

Hence the system Eq. (1.2) is uniformly bounded.

System Behavior at Positive Equilibrium Point

In ecology, emphasis is always on the stability of co-existing equilibrium. This leads to one to examine in some detail the local stability in so far as the positive equilibrium of the system, show in Eq. (1.2), which is given by \(\left( {x^{*} ,y^{*} } \right)\), where \(y^{*} = \frac{1}{\theta }\left( {\frac{{c\beta \left( {1 - m} \right)x^{*} }}{{1 + \alpha \left( {1 - m} \right)x^{*} }} - \gamma } \right)\) and \(x^{*}\) is the positive root of the following cubic equation.

$$ A_{1} x^{3} + A_{2} x^{2} + A_{3} x + A_{4} = 0 $$
(3.1)

where \(A_{1} = r\theta \alpha^{2} \left( {1 - m} \right)^{2}\), \(A_{2} = 2r\theta \alpha \left( {1 - m} \right) - Kr\theta \alpha^{2} \left( {1 - m} \right)^{2}\),

\(A_{3} = r\theta + Kc\beta^{2} \left( {1 - m} \right)^{2} - 2Kr\theta \alpha \left( {1 - m} \right) - K\alpha \beta \gamma \left( {1 - m} \right)^{2}\), \(A_{4} = - Kr\theta - K\gamma \beta \left( {1 - m} \right)\).

To assure the presence of a positive equilibrium point, we adapt two conditions \(c\beta > \alpha \gamma\) and

$$ 1 - \frac{2}{K\alpha } < m < 1 - \frac{2r\theta \alpha }{{\beta \left( {c\beta - \alpha \gamma } \right)}} $$
(3.2)

Local Stability

On using the equations of Eq. (1.2) at positive equilibrium, we can obtain the Jacobian matrix as

$$ J = \left[ {\begin{array}{*{20}c} {\frac{{ - rx^{*} }}{K} + \frac{{\alpha \beta \left( {1 - m} \right)^{2} x^{*} y^{*} }}{{\left[ {1 + \alpha \left( {1 - m} \right)x^{*} } \right]^{2} }}} & {\frac{{ - \beta \left( {1 - m} \right)x^{*} }}{{1 + \alpha \left( {1 - m} \right)x^{*} }}} \\ {\frac{{c\beta \left( {1 - m} \right)y^{*} }}{{\left[ {1 + \alpha \left( {1 - m} \right)x^{*} } \right]^{2} }}} & { - \theta y^{*} } \\ \end{array} } \right], $$
(3.3)

The Latent equation can be obtained from a Jacobian matrix (3.3) is

$$ \lambda^{2} + U_{1} \lambda + U_{2} = 0 $$
(3.4)

where \(U_{1} = \frac{{ - rx^{*} }}{K} + \frac{{\alpha \beta \left( {1 - m} \right)^{2} x^{*} y^{*} }}{{\left[ {1 + \alpha \left( {1 - m} \right)x^{*} } \right]^{2} }} - \theta y^{*} ,\) and \(U_{2} = \frac{{r\theta x^{*} y^{*} }}{K} - \frac{{\alpha \beta \theta \left( {1 - m} \right)^{2} x^{*} y^{*2} }}{{\left[ {1 + \alpha \left( {1 - m} \right)x^{*} } \right]^{2} }} + \frac{{c\beta^{2} \left( {1 - m} \right)^{2} x^{*} y^{*} }}{{\left[ {1 + \alpha \left( {1 - m} \right)x^{*} } \right]^{3} }}.\)

The non delayed approach is stable for the situations supplied by the theorem-3 hold.

Theorem 3

The system Eq. (1.2) is said to be locally asymptotically stable if \(U_{1} < 0\,,\,\,{\text{and}}\,\,U_{2} > 0\).The positive equilibrium of the system discussed above, namely, (1.2) is deemed stable only if the characteristic roots of the Eq. (3.4) are negative or have negative real parts. This is only feasible if the conditions of Theorem 3 apply.

Global Stability

Theorem 4

The system (1.2) is globally asymptotically stable if \(S_{11} > 0\,,\,\,{\text{and}}\,\,S_{11} S_{22} - \left( {S_{12} } \right)^{2} > 0.\)

Proof

Let the Lyapunov’s function is

$$ L(x,y) = x - x^{*} - x^{*} \ln \frac{x}{{x^{*} }} + y - y^{*} - y^{*} \ln \frac{y}{{y^{*} }} $$
(3.5)
$$ \frac{dL}{{dt}} = \left( {x - x^{*} } \right)\left[ {r\left( {1 - \frac{x}{K}} \right) - \frac{{\beta \left( {1 - m} \right)y}}{{1 + \alpha \left( {1 - m} \right)x}}} \right] + \left( {y - y^{*} } \right)\left[ {\frac{{c\beta \left( {1 - m} \right)x}}{{1 + \alpha \left( {1 - m} \right)x}} - \gamma - \theta y} \right], $$
$$ \begin{gathered} \frac{dL}{{dt}} = \left( {x - x^{*} } \right)\left[ { - \frac{r}{K}\left( {x - x^{*} } \right) - \left( {\frac{{\beta \left( {1 - m} \right)y}}{{1 + \alpha \left( {1 - m} \right)x}} - \frac{{\beta \left( {1 - m} \right)y^{*} }}{{1 + \alpha \left( {1 - m} \right)x^{*} }}} \right)} \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \left( {y - y^{*} } \right)\left[ {\frac{{c\beta \left( {1 - m} \right)x}}{{1 + \alpha \left( {1 - m} \right)x}} - \theta y - \frac{{c\beta \left( {1 - m} \right)x^{*} }}{{1 + \alpha \left( {1 - m} \right)x^{*} }} + \theta y^{*} } \right], \hfill \\ \end{gathered} $$
$$ \begin{gathered} \frac{dL}{{dt}} = - \left[ {\frac{r}{K} - \frac{{\alpha \beta \left( {1 - m} \right)^{2} }}{AB}y^{*} } \right]\left( {x - x^{*} } \right)^{2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{{\beta \left( {1 - m} \right)}}{AB}\left( {1 + \alpha \left( {1 - m} \right)x^{*} } \right)\left( {x - x^{*} } \right)\left( {y - y^{*} } \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \theta \left( {y - y^{*} } \right)^{2} + \frac{{c\beta \left( {1 - m} \right)}}{AB}\left( {x - x^{*} } \right)\left( {y - y^{*} } \right). \hfill \\ \end{gathered} $$

where \(A = \left( {1 + \alpha \left( {1 - m} \right)x} \right);B = \left( {1 + \alpha \left( {1 - m} \right)x^{*} } \right).\)

We consider

$$ \frac{dL}{{dt}} = - S_{11} \left( {x - x^{*} } \right)^{2} - S_{22} \left( {y - y^{*} } \right)^{2} + 2S_{12} \left( {x - x^{*} } \right)\left( {y - y^{*} } \right), $$

\(\frac{dL}{{dt}} = - Q^{T} SQ,\,\,\,\,{\text{where}}\,Q = \,\left( {\left( {x - x^{*} } \right),\left( {y - y^{*} } \right)} \right)^{T} ,\) \(S\) denotes a symmetric matrix and is given by \(S = \left[ {\begin{array}{*{20}c} {S_{11} } & {S_{12} } \\ {S_{21} } & {S_{22} } \\ \end{array} } \right].\) where \(S_{11} = \frac{r}{K} - \frac{{\alpha \beta \left( {1 - m} \right)^{2} }}{AB}y^{*} ,\,\,S_{22} = \theta ,\,\,S_{12} = \frac{1}{2}\frac{{\beta \left( {1 - m} \right)}}{AB}\left[ {\left( {1 + \alpha \left( {1 - m} \right)x^{*} } \right) - c} \right].\)Here \(\frac{dL}{{dt}} < 0\) when the symmetric matrix \(S\) is positive definite, and this is true if \(S_{11} > 0\,\,{\text{and}}\,\,S_{11} S_{22} - \left( {S_{12} } \right)^{2} > 0\).

Consequently, if the above two requirements are satisfied, the structure in question is asymptotically stable.

Time Delay Analysis

In a prey-predator symbiosis, delay is employed as an instrument to make the model highly accurate and reliable biologically. Predator reproduction is apparently not possible soon after prey consumption. Time lag is predictably de rigeur for gestation. Naturally, the delay with regard to capturing prey and the increase in prey numbers so as to meet the demands of any predator is a vital parameter in conceiving a workable model. Model Eq. (1.2) involving a gestational delay \(\left( \tau \right)\) may then be illustrated like given below:

$$ \begin{gathered} \frac{dx}{{dt}} = rx\left( {1 - \frac{x}{K}} \right) - \frac{{\beta \left( {1 - m} \right)xy}}{{1 + \alpha \left( {1 - m} \right)x}}, \hfill \\ \frac{dy}{{dt}} = \frac{{c\beta \left( {1 - m} \right)x\left( {t - \tau } \right)y}}{{1 + \alpha \left( {1 - m} \right)x\left( {t - \tau } \right)}} - \gamma y - \theta y^{2} . \hfill \\ \end{gathered} $$
(4.1)

Hopf bifurcation will then be injected into the system Eq. (4.1).

Theorem 5

The next logical step is to show that Eq. (4.1) experiences Hopf bifurcation on undergoing endemic equilibrium point when \(\tau = \tau_{0}\).

Proof

The above system's Eq. (4.1) Jacobian matrix is.

$$ J^{*} = \left[ {\begin{array}{*{20}c} { - \frac{rx}{K} + \frac{{\alpha \beta \left( {1 - m} \right)^{2} xy}}{{\left[ {1 + \alpha \left( {1 - m} \right)x} \right]^{2} }}} & {\frac{{ - \beta \left( {1 - m} \right)xy}}{{1 + \alpha \left( {1 - m} \right)x}}} \\ {\frac{{c\beta \left( {1 - m} \right)^{2} e^{ - \lambda \tau } y}}{{\left[ {1 + \alpha \left( {1 - m} \right)x} \right]^{2} }}} & { - \theta y} \\ \end{array} } \right], $$

The Jacobian matrix's characteristic equation is as follows:

$$ \lambda^{2} + E_{1} \lambda + E_{2} + e^{ - \lambda \tau } F_{1} = 0 $$
(4.2)

where \(E_{1} = \frac{rx}{K} + \theta y - \frac{{\alpha \beta \left( {1 - m} \right)^{2} xy}}{{\left[ {1 + \alpha \left( {1 - m} \right)x} \right]^{2} }},\,\,E_{2} = \frac{r\theta xy}{K} - \frac{{\theta \alpha \beta \left( {1 - m} \right)^{2} xy^{2} }}{{\left[ {1 + \alpha \left( {1 - m} \right)x} \right]^{2} }},\) and

$$ \,\,F_{1} = \frac{{c\beta^{2} \left( {1 - m} \right)^{2} xy}}{{\left[ {1 + \alpha \left( {1 - m} \right)x} \right]^{3} }}. $$

For a critical value of \(\tau > 0\), whenever a latent root of the Eq. (4.2) reaches the imaginary axis, instability exists.

Substituting \(\lambda = i\omega\) into Eq. (4.2) gives

$$ - \omega^{2} + E_{2} + F_{1} \cos \omega \tau + i\left( {E_{1} \omega - F_{1} \sin \omega \tau } \right) = 0. $$
(4.3)

The following equations can be obtained on comparing real and imaginary parts,

$$ \begin{gathered} F_{1} \cos \omega \tau - \omega^{2} + E_{2} = 0, \hfill \\ E_{1} \omega - F_{1} \sin \omega \tau = 0. \hfill \\ \end{gathered} $$
(4.4)

Squaring and adding above two equations

$$ \omega^{4} + B_{1} \omega^{2} + B_{2} = 0 $$
(4.5)

where \(B_{1} = E_{1}^{2} - 2E_{2} ,\,and\,B_{2} = E_{2}^{2} - F_{1}^{2} .\)

The criteria for at most one positive solution to above equation are \(B_{1}\) positive and \(B_{2}\) negative.

If the criteria mentioned above are met, the Eq. (4.5) has a single positive origin, and we have \(\tau_{z} = \frac{1}{{\omega_{0} }}\cos^{ - 1} \left[ {\frac{{\omega^{2} - E_{2} }}{{F_{1} }}} \right] + \frac{2z\pi }{{\omega_{0} }},\,z = 0,1,2,......\)

Next, we have to show that the system Eq. (4.1) go through Hopf bifurcation at endemic equilibrium when \(\tau = \tau_{0}\).

DifferentiatingEq. (4.2) with respect to \(\tau\), we get

$$ \left( {\frac{d\lambda }{{d\tau }}} \right)^{ - 1} = \frac{{\left( {2\lambda + E_{1} } \right) - F_{1} \tau e^{ - \lambda \tau } }}{{F_{1} \lambda e^{ - \lambda \tau } }}, $$
$$ \left( {\frac{d\lambda }{{d\tau }}} \right)^{ - 1} = \frac{{\left( {2\lambda + E_{1} } \right) - F_{1} \tau e^{ - \lambda \tau } }}{{F_{1} \lambda e^{ - \lambda \tau } }} - \frac{\tau }{\lambda }. $$

Substituting \(\lambda = i\omega_{0}\) and from Eq. (4.4), we get

\(\left. {{\text{Re}} \left( {\frac{d\lambda }{{d\tau }}} \right)^{ - 1} } \right|_{{\lambda = i\omega_{0} }} = \frac{{2\omega_{0}^{2} + \left( {E_{1}^{2} - 2E_{2} } \right)}}{{E_{1} \omega_{0}^{2} + \left( {\omega_{0}^{2} - E_{2} } \right)^{2} }}\) > 0 if \(E_{1}^{2} - 2E_{2} > 0.\)

Hence the system Eq. (4.1) go through the Hopf bifurcation at endemic equilibrium when \(\tau = \tau_{0}\).

The direction and stability of Hopf bifurcation

The last section saw the formulation of conditions under which Eq. (4.1) samples Hopf bifurcation at positive equilibrium point, where \(\tau = \tau_{0}\). This is followed up with determining the orientation and phase of bifurcating periodic solutions. By using the normal form and central manifold theory [43], we can be interpreted the results.

Let \(\tau = \tau_{0} + \mu ,\,\mu \in {\mathbb{R}}\), \(x_{1} = x - x^{*} ,\,x_{2} = y - y^{*}\), \(x_{i} = x_{i} (\tau t)\) then the system Eq. (4.1) transformed into FDE and \(\phi = \left( {\phi_{1} ,\,\,\phi_{2} } \right)^{T} \in C\left( {\left[ { - 1,0} \right],\,\,R^{2} } \right)\) as

$$ \dot{x}\left( t \right) = L_{\mu } \left( {x_{t} } \right) + f\left( {\mu ,x_{t} } \right), $$
(5.1)

where

$$ \begin{aligned} L_{\mu } \left( \phi \right) = & & \left( {\tau_{0} + \mu } \right)\left( {\begin{array}{*{20}c} { - \frac{{rx^{*} \left[ {K\alpha \left( {1 - m} \right) - 1 - 2x^{*} \alpha \left( {1 - m} \right)} \right]}}{{K\left[ {1 + \alpha \left( {1 - m} \right)x^{*} } \right]}}} & {\frac{{ - \left[ {\gamma + \theta y^{*} } \right]}}{c}} \\ 0 & { - \theta y^{*} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\phi_{1} \left( 0 \right)} \\ {\phi_{2} \left( 0 \right)} \\ \end{array} } \right) \\ & & + \left( {\tau_{0} + \mu } \right)\left( {\begin{array}{*{20}c} 0 & 0 \\ {\frac{{cr\left( {K - x^{*} } \right)}}{{K\left[ {1 + \alpha \left( {1 - m} \right)x^{*} } \right]}}} & 0 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\phi_{1} \left( { - 1} \right)} \\ {\phi_{2} \left( { - 1} \right)} \\ \end{array} } \right), \\ \end{aligned} $$
(5.2)

and

$$ f\left( {\mu ,x_{t} } \right) = \left( {\tau _{0} + \mu } \right)\left( {\begin{array}{*{20}c} { - \frac{{r\phi _{1}^{2} \left( 0 \right)}}{K} - \frac{{\beta \left( {1 - m} \right)\phi _{1} \left( 0 \right)\phi _{2} \left( 0 \right)}}{{1 + \alpha \left( {1 - m} \right)\phi _{1} \left( 0 \right)}}} \\ {\frac{{c\beta \left( {1 - m} \right)\phi _{1} \left( { - 1} \right)\phi _{2} \left( 0 \right)}}{{1 + \alpha \left( {1 - m} \right)\phi _{1} \left( { - 1} \right)}} - \theta \phi _{{_{2} }}^{2} \left( 0 \right)} \\ \end{array} } \right). $$
(5.3)

Using Riesz representation theorem, it can be shown that there exists a function \(\eta \left( {\vartheta ,\mu } \right)\) of bounded variation for \(\vartheta \in \left[ { - 1,0} \right],\) such that \(L_{\mu } \left( \phi \right) = \int\limits_{ - 1}^{0} {d\eta \left( {\vartheta ,0} \right)\phi \left( \vartheta \right)}\) for \(\phi \in C.\)

As a matter of fact, it is up to choose.

\(\begin{aligned} \eta \left( {\vartheta ,\mu } \right) = & \left( {\tau + \mu } \right)\left( {\begin{array}{*{20}c} { - \frac{{rx^{*} \left[ {K\alpha \left( {1 - m} \right) - 1 - 2x^{*} \alpha \left( {1 - m} \right)} \right]}}{{K\left[ {1 + \alpha \left( {1 - m} \right)x^{*} } \right]}}} & {\frac{{ - \left[ {\gamma + \theta y^{*} } \right]}}{c}} \\ 0 & { - \theta y^{*} } \\ \end{array} } \right)\delta \left( \vartheta \right) \\ & - \left( {\overline{\tau } + \mu } \right)\left( {\begin{array}{*{20}c} 0 & 0 \\ {\frac{{cr\left( {K - x^{*} } \right)}}{{K\left[ {1 + \alpha \left( {1 - m} \right)x^{*} } \right]}}} & 0 \\ \end{array} } \right)\delta \left( {\vartheta + 1} \right). \\ \end{aligned}\) where \(\delta\) is the Dirac delta function. For \(\phi \in C^{\prime}\left( {\left[ { - 1\,,0} \right],\,R^{2} } \right),\) define

$$ A\left( \mu \right)\phi = \left\{ \begin{gathered} \phi^{\prime}\left( \vartheta \right);\,\,\vartheta \in \left[ { - 1,0} \right) \hfill \\ \int\limits_{ - 1}^{0} {d\eta \,\phi \left( s \right);\,\,\vartheta = 0} , \hfill \\ \end{gathered} \right. $$
(5.4)

And

$$ R\left( \mu \right)\phi = \left\{ \begin{gathered} 0\,;\,\,\,\vartheta \in \left[ { - 1,0} \right) \hfill \\ f\left( {\mu ,\phi } \right);\,\,\vartheta = 0. \hfill \\ \end{gathered} \right. $$
(5.5)

Then the system Eq. (5.1) can be modifies as operator equation given below

$$ \dot{x}\left( t \right) = A\left( \mu \right)X_{t} + R\left( \mu \right)X_{t} $$
(5.6)

Define

$$ A^{ * } \left( \psi \right) = \left\{ \begin{gathered} \frac{ - d\psi \left( s \right)}{{ds}},\,s \in \left( {0,1} \right] \hfill \\ \int\limits_{ - 1}^{0} {d\eta^{T} \left( {t,0} \right)\psi \left( { - t} \right),\,s = 0} \hfill \\ \end{gathered} \right. $$
(5.7)

and a bilinear form is given by

$$ \left\langle {\psi \left( s \right),\,\,\phi \left( \vartheta \right)} \right\rangle = \overline{\psi } \left( 0 \right)\phi \left( 0 \right) - \int\limits_{ - 1}^{0} {\int\limits_{\xi = 0}^{\vartheta } {\overline{\psi } \left( {\xi - \vartheta } \right)d\eta \,\phi \,d\xi } } $$
(5.8)

where \(x\left( \vartheta \right) = \eta \left( {\vartheta ,0} \right).\) Then \(A\left( 0 \right)\) and \(A^{ * }\) are adjoint operators. We initial require to figure the eigen vectors of \(A\left( 0 \right)\) and \(A^{ * }\) relating to \(i\overline{\omega } \overline{\tau }\) and \(- i\overline{\omega } \overline{\tau } ,\) individually. Let \(q = \left( {1,h} \right)^{T} e^{{i\overline{w} \overline{\tau } \vartheta }}\) is the eigen vector of \(A\left( 0 \right)\) corresponding to \(i\overline{\omega } \overline{\tau }\), then \(A\left( 0 \right)q = i\overline{w} \overline{\tau } q.\) Then from \(A\left( 0 \right)\), Eq. (5.2) and Eq. (5.5)

$$ \tau \left( {\begin{array}{*{20}c} {i\overline{\omega } + \frac{{rx^{*} \left[ {K\alpha \left( {1 - m} \right) - 1 - 2x^{*} \alpha \left( {1 - m} \right)} \right]}}{{K\left[ {1 + \alpha \left( {1 - m} \right)x^{*} } \right]}}} & {\frac{{\left[ {\gamma + \theta y^{*} } \right]}}{c}} \\ { - \frac{{cr\left( {K - x^{*} } \right)}}{{K\left[ {1 + \alpha \left( {1 - m} \right)x^{*} } \right]}}e^{{ - i\overline{\omega } \overline{\tau } }} } & {i\overline{\omega } + \theta y^{*} } \\ \end{array} } \right)q\left( 0 \right) = \left( {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right). $$

Therefore, we are able to get \(q\left( 0 \right) = \left( {1,h} \right)^{T}\), where \(h = \frac{{ - cr\left( {K - x^{ * } } \right)e^{{ - i\overline{\omega } \overline{\tau } }} }}{{K\left[ {1 + \alpha \left( {1 - m} \right)x^{ * } } \right]\left( {i\overline{\omega } + \theta y^{ * } } \right)}}.\)

Likewise, let \(q^{ * } \left( s \right) = D\left( {1,h^{ * } } \right)^{T} e^{{i\overline{\omega } \overline{\tau } s}}\) be the characteristic vector of \(A^{ * }\) relating to \(- i\overline{\omega } \overline{\tau } \,\,.\)

Employing the definition of \(A^{ * }\) and Eq. (5.2), (5.3), (5.4) and (5.5), computing becomes easy

$$ q^{ * } \left( s \right) = D\left( {1,h^{ * } } \right)^{T} e^{{i\overline{\omega } \overline{\tau } s}} = D\left( {1,\,\frac{{\left[ {\vartheta + \theta y^{ * } } \right)}}{{c\left\{ {i\overline{\omega } + \theta y^{ * } } \right\}}}} \right)e^{i\omega \tau s} $$

In order to ensure \(\left\langle {q^{ * } ,q} \right\rangle = 1,\) we require computing the value of \(D\) from (5.7) we have

$$ \begin{gathered} \left\langle {q^{ * } \left( s \right),\,\,q\left( \vartheta \right)} \right\rangle = \overline{D} \left( {1,\,\overline{\,h}^{ * } } \right)\left( {1,\,\,h} \right)^{T} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \int\limits_{ - 1}^{0} {\int\limits_{\xi = 0}^{\vartheta } {\overline{D} \left( {1,\,\,\overline{h}^{ * } } \right)e^{{ - i\omega \tau \left( {\xi - \vartheta } \right)}} } } d\eta \left( \vartheta \right)\left( {1,\,\,h} \right)^{T} e^{i\omega \tau \xi } d\xi \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \overline{D} \left\{ {1 + h\overline{h}^{ * } - \int\limits_{ - 1}^{0} {\left( {1,\,\,\overline{h}^{ * } } \right)\vartheta e^{{i\overline{\omega } \overline{\tau } \vartheta }} d\eta \left( \vartheta \right)\left( {1,\,\,h} \right)^{T} } } \right\} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \overline{D} \left\{ {1 + h\overline{h}^{ * } + \overline{h}^{ * } \overline{\tau } \left( {\frac{{cr\left( {k - x^{ * } } \right)}}{{k\left[ {1 + \alpha \left( {1 - m} \right)x^{ * } } \right]}}} \right)e^{{ - i\overline{\omega } \overline{\tau } }} } \right\}. \hfill \\ \end{gathered} $$

Thus, we can choose \(D\) as \(\overline{D} = \frac{1}{{1 + h\overline{h}^{ * } + \overline{h}^{ * } \overline{\tau } \left( {\frac{{cr\left( {k - x^{ * } } \right)}}{{k\left[ {1 + \alpha \left( {1 - m} \right)x^{ * } } \right]}}} \right)e^{{ - i\overline{\omega } \overline{\tau } }} }}.\)

The notations used in Gopal swamy and He [16] are made use of in the section to follow. The main job is computing the coordinates of the centre manifold \(C_{0}\) at \(\mu = 0.\)

Let us consider,

$$ z = \left\langle {q^{ * } ,X_{\tau } } \right\rangle ,\,\,W\left( {t,\,\vartheta } \right) = X_{\tau } - 2{\text{Re}} \left\{ {z\,q} \right\}. $$
(5.9)

On the center manifold \(C_{0} ,\) we have

$$ W\left( {t,\,\vartheta } \right) = W\left( {z,\overline{z} ,\,\vartheta } \right),\, $$

where

$$ W\left( {z,\,\overline{z} ,\,\vartheta } \right) = W_{20} \frac{{z^{2} }}{2} + W_{11} z\overline{z} + W_{02} \frac{{\overline{z}^{2} }}{2} + ... $$
(5.10)

\(z\) and \(\overline{z}\) are local coordinates for center manifold \(C_{0}\) in the direction of \(q^{ * }\) and \(\overline{q}^{ * }\).

For solution \(X_{t} \in C_{0}\) of Eq. (5.6), since \(\mu = 0\), we have.

\(\frac{dz}{{dt}}\left( t \right) = i\overline{\omega } \overline{\tau } z + \overline{q}^{ * } \left( 0 \right)f\left( {0,W\left( {z,\overline{z} ,0} \right) + 2{\text{Re}} \left\{ {z\,q} \right\}} \right)\mathop \equiv \limits^{def} \,i\overline{\omega } \overline{\tau } z + \overline{q}^{ * } \left( 0 \right)f_{0} \left( {z,\overline{z} } \right).\) We rewrite this equation as

$$ \dot{z}\left( t \right) = i\overline{\omega } \overline{\tau } z\left( t \right) + g\left( {z,\overline{z} } \right), $$

where

$$ g\left( {z,\overline{z} } \right) = \overline{q}^{ * } \left( 0 \right)f_{0} \left( {z,\overline{z} } \right) = g_{20} \frac{{z^{2} }}{2} + g_{11} z\overline{z} + g_{02} \frac{{\overline{z}^{2} }}{2} + g_{21} \frac{{z^{2} \overline{z} }}{2} + ... $$
(5.11)

It follows from Eqs. (5.9) and (5.10) that

$$ \begin{gathered} X_{t} \left( \vartheta \right) = W\left( {t,\vartheta } \right) + 2{\text{Re}} \left\{ {z\left( t \right)q\left( t \right)} \right\} = W_{20} \left( \vartheta \right)\frac{{z^{2} }}{2} + W_{11} \left( \vartheta \right)z\overline{z} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + W_{02} \left( \vartheta \right)\frac{{\overline{z}^{2} }}{2} + \left( {1,h} \right)^{T} e^{{i\overline{\omega } \overline{\tau } \vartheta }} z + \left( {1,\overline{h} } \right)^{T} e^{{ - i\overline{\omega } \overline{\tau } \vartheta }} \overline{z} + ... \hfill \\ \end{gathered} $$
(5.12)

It follows together with Eq. (5.3) that

$$ \begin{gathered} g\left( {z,\overline{z} } \right) = \overline{q}^{ * } \left( 0 \right)f\left( {0,X_{t} } \right) = \overline{\tau } \overline{D} \left( {1,\overline{h}^{ * } } \right)\left( {\begin{array}{*{20}c} { - \frac{r}{k}X_{1t}^{2} \left( 0 \right) - \frac{{\beta \left( {1 - m} \right)X_{1t} \left( 0 \right)X_{2t} \left( 0 \right)}}{{1 + \alpha \left( {1 - m} \right)X_{1t} \left( 0 \right)}}} \\ {\frac{{c\beta \left( {1 - m} \right)X_{1t} \left( { - 1} \right)X_{2t} \left( 0 \right)}}{{1 + \alpha \left( {1 - m} \right)X_{1t} \left( 0 \right)}}} \\ \end{array} } \right) \hfill \\ \,\, = - \overline{\tau } \overline{D} \left\{ {z + \overline{z} + W_{20}^{\left( 1 \right)} \left( 0 \right)\frac{{z^{2} }}{2} + W_{11}^{\left( 1 \right)} \left( 0 \right)z\overline{z} + W_{02}^{\left( 1 \right)} \left( 0 \right)\frac{{\overline{z}^{2} }}{2} + ...} \right\} \hfill \\ \, \times \left[ {\frac{r}{k}\left( {z + \overline{z} + W_{20}^{\left( 1 \right)} \left( 0 \right)\frac{{z^{2} }}{2} + W_{11}^{\left( 1 \right)} \left( 0 \right)z\overline{z} + W_{02}^{\left( 1 \right)} \left( 0 \right)\frac{{\overline{z}^{2} }}{2} + ...} \right)} \right. \hfill \\ + \beta \left( {1 - m} \right)\left( {hz + \overline{h} \overline{z} + W_{20}^{\left( 2 \right)} \left( 0 \right)\frac{{z^{2} }}{2} + W_{11}^{\left( 2 \right)} \left( 0 \right)z\overline{z} + W_{02}^{\left( 2 \right)} \left( 0 \right)\frac{{\overline{z}^{2} }}{2} + ...} \right) \hfill \\ \times \left\{ {1 - \alpha \left( {1 - m} \right)\left( {z + \overline{z} + W_{20}^{\left( 1 \right)} \left( 0 \right)\frac{{z^{2} }}{2} + W_{11}^{\left( 1 \right)} \left( 0 \right)z\overline{z} + W_{02}^{\left( 1 \right)} \left( 0 \right)\frac{{\overline{z}^{2} }}{2} + ...} \right)} \right. \hfill \\ \left. {\left. { + \alpha^{2} \left( {1 - m} \right)^{2} \times \left( {z^{2} + \overline{z}^{2} + 2z\overline{z} + 2W_{11}^{\left( 1 \right)} \left( 0 \right)z^{2} \overline{z} + 2W_{20}^{\left( 1 \right)} \left( 0 \right)\frac{{z^{2} \overline{z}}}{2} + ...} \right) - ...} \right\}} \right] \hfill \\ + \overline{\tau } \overline{D} \overline{h}^{ * } c\beta \left( {1 - m} \right) \hfill \\ \left[ {\left( {ze^{{ - i\overline{\omega } \overline{\tau } }} + \overline{z} e^{{i\overline{\omega } \overline{\tau } }} + W_{20}^{\left( 1 \right)} \left( { - 1} \right)\frac{{z^{2} }}{2} + W_{11}^{\left( 1 \right)} \left( { - 1} \right)z\overline{z} + W_{02}^{\left( 1 \right)} \left( { - 1} \right)\frac{{\overline{z}^{2} }}{2} + ...} \right)} \right. \hfill \\ \times \left( {hz + \overline{h} \overline{z} + W_{20}^{\left( 2 \right)} \left( 0 \right)\frac{{z^{2} }}{2} + W_{11}^{\left( 2 \right)} \left( 0 \right)z\overline{z} + W_{02}^{\left( 2 \right)} \left( 0 \right)\frac{{\overline{z}^{2} }}{2} + ...} \right) \hfill \\ \times \left\{ {1 - \alpha \left( {1 - m} \right)\left( {ze^{{ - i\overline{\omega } \overline{\tau } }} + \overline{z} e^{{i\overline{\omega } \overline{\tau } }} + W_{20}^{\left( 1 \right)} \left( { - 1} \right)\frac{{z^{2} }}{2} + W_{11}^{\left( 1 \right)} \left( { - 1} \right)z\overline{z} + W_{02}^{\left( 1 \right)} \left( { - 1} \right)\frac{{\overline{z}^{2} }}{2} + ...} \right)} \right. \hfill \\ \left. { \times \alpha^{2} \left( {1 - m} \right)^{2} \left( {z^{2} e^{{ - 2i\overline{\omega } \overline{\tau } }} + \overline{z}^{2} e^{{2i\overline{\omega } \overline{\tau } }} + 2z\overline{z} + \frac{{z^{2} \overline{z}}}{2}\left( {4W_{11}^{\left( 1 \right)} \left( { - 1} \right)e^{{ - i\overline{\omega } \overline{\tau } }} + 2W_{20}^{\left( 1 \right)} \left( { - 1} \right)e^{{ki\overline{\omega } \overline{\tau } }} } \right)} \right) - ...} \right\} \hfill \\ \left. { - \theta \left\{ {hz + \overline{h} \overline{z} + W_{20}^{\left( 2 \right)} \left( 0 \right)\frac{{z^{2} }}{2} + W_{11}^{\left( 2 \right)} \left( 0 \right)z\overline{z} + W_{02}^{\left( 2 \right)} \left( 0 \right)\frac{{\overline{z}^{2} }}{2} + ...} \right\}^{2} } \right]. \hfill \\ \end{gathered} $$
(5.13)

We obtain the following on comparing the coefficients with (4.10),

$$ g_{20} = 2\overline{\tau } \overline{D} \left\{ { - \left( {\frac{r}{k} + \left( {1 - m} \right)\beta } \right) + h\overline{h}^{ * } \left[ {c\beta \left( {1 - m} \right)e^{{ - i\overline{\omega } \overline{\tau } }} - \theta h} \right]} \right\}, $$
$$ g_{11} = 2\overline{\tau } \overline{D} \left\{ { - \left( {\frac{r}{k} + \beta \left( {1 - m} \right){\text{Re}} \left\{ h \right\} + \overline{h}^{ * } \left[ {c\beta \left( {1 - m} \right){\text{Re}} \left\{ h \right\} - \theta h\overline{h}} \right]} \right)} \right\}, $$
$$ g_{02} = 2\overline{\tau } \overline{D} \left\{ { - \left( {\frac{r}{k} + \beta \left( {1 - m} \right)\overline{h} } \right) + \overline{h} \overline{h}^{ * } \left[ {c\beta \left( {1 - m} \right)e^{{i\overline{\omega } \overline{\tau } }} - \theta \overline{h} } \right]} \right\}, $$
$$ \begin{gathered} g_{21} = \overline{\tau } \overline{D} \left[ { - \frac{r}{k}\left( {4W_{11}^{1} \left( 0 \right) + 2W_{20}^{1} \left( 0 \right)} \right) - \beta \left( {1 - m} \right)} \right.\left\{ {2W_{11}^{2} \left( 0 \right) + W_{20}^{2} \left( 0 \right) + \overline{h} W_{20}^{1} \left( 0 \right)} \right. \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left. {\,\,\, + 2hW_{11}^{1} \left( 0 \right) - 2\alpha \left( {1 - m} \right)\left( {h + 2\overline{h} } \right)} \right\} + \overline{h}^{ * } \left\{ {c\beta \left( {1 - m} \right)\left( {W_{20}^{2} \left( 0 \right)e^{{i\overline{\omega } \overline{\tau } }} } \right.} \right. \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + W_{20}^{1} \left( { - 1} \right)\overline{h} + 2W_{20}^{1} \left( { - 1} \right)h - 2h\alpha \left( {1 - m} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - 2\left. {\overline{h}\alpha \left( {1 - m} \right)e^{{ - 2i\overline{\omega } \overline{\tau } }} - 2h\alpha \left( {1 - m} \right)} \right)\left. {\,\,\left. { - 4\theta hW_{11}^{2} \left( 0 \right) - 2\theta \overline{h} W_{20}^{2} \left( 0 \right)} \right\}} \right]. \hfill \\ \end{gathered} $$
(5.14)

However, we require to solve \(W_{20} \left( \vartheta \right)\) and \(W_{11} \left( \vartheta \right)\) in Eq. (5.14). From Eq. (5.6) and Eq. (5.9), we have

$$ \begin{gathered} \dot{W} = \dot{X}_{t} - \dot{z} - \dot{\overline{z}}\,\overline{q} = AW - 2{\text{Re}} \left\{ {\overline{q}^{ * } \left( 0 \right)f_{0q} \left( \vartheta \right)} \right\},\,\,\vartheta \in \left[ { - 1,0} \right), \hfill \\ = AW - 2{\text{Re}} \left\{ {\overline{q}^{ * } \left( 0 \right)f_{0q} \left( \vartheta \right)} \right\} + f_{0} ,\,\,\,\vartheta = 0, \hfill \\ \underline{\underline{def}} \,AW + H\left( {z,\,\overline{z},\theta } \right). \hfill \\ \end{gathered} $$
(5.15)

where

$$ \left( {z,\,\overline{z},\vartheta } \right) = H_{20} \left( \vartheta \right)\frac{{z^{2} }}{2} + H_{11} \left( \vartheta \right)z\overline{z} + H_{02} \left( \vartheta \right)\frac{{\overline{z}^{2} }}{2} + ... $$
(5.16)

Substituting the series concerned into Eq. (5.15) and making a comparison of coefficients leads to the following equations

$$ \left( {A - 2i\overline{\omega }\,\overline{\tau }} \right)W_{20} \left( \vartheta \right) = - H_{20} \left( \vartheta \right),\,\,AW_{11} \left( \vartheta \right) = - H_{11} \left( \vartheta \right)... $$
(5.17)

From (4.14), we know that for \(\theta \in \left[ { - 1,0} \right)\),

$$ H\left( {z,\,\overline{z},\vartheta } \right) = - \overline{q}^{ * } \left( 0 \right)f_{0} q\left( \vartheta \right) - q^{ * } \left( 0 \right)\overline{f}_{0} \left( \vartheta \right) = - g\left( {z,\,\overline{z}} \right)q\left( \vartheta \right) - \overline{g}\left( {z,\,\overline{z}} \right)\overline{q}\left( \vartheta \right). $$
(5.18)

Comparing the coefficients with Eq. (5.16), yields

$$ H_{20} \left( \vartheta \right) = - g_{20} q\left( \vartheta \right) - \overline{g}_{02} \overline{q}\left( \vartheta \right), $$
(5.19)

and

$$ H_{11} \left( \vartheta \right) = - g_{11} q\left( \vartheta \right) - \overline{g}_{11} \overline{q}\left( \vartheta \right). $$
(5.20)

From (5.17) and (5.19)

$$ \dot{W}_{20} = 2i\overline{\omega }\,\overline{\tau }\,W_{20} + g_{20} q + \overline{g}_{02} \overline{q}. $$

and \(q = \left( {1,\,h} \right)e^{{i\overline{\omega }\,\overline{\tau }\,\theta }} \,,\) therefore

$$ W_{20} = \frac{{ig_{20} }}{{\overline{\omega }\,\overline{\tau }}}qe^{{i\overline{\omega }\,\overline{\tau }\,\theta }} + \frac{{i\,\overline{g}_{02} }}{{3\overline{\omega }\,\overline{\tau }}}\overline{q}e^{{ - i\overline{\omega }\,\overline{\tau }\,\theta }} + E_{1} e^{{2i\overline{\omega }\,\overline{\tau }\,\theta }} , $$
(5.21)

where \(E_{1} = \left( {E_{1}^{\left( 1 \right)} ,\,E_{1}^{\left( 2 \right)} } \right)\) represents an invariant vector in 2-dim plane. Also, from (5.15) and (5.20), we get

$$ W_{11} = - \frac{{ig_{11} }}{{\overline{\omega }\,\overline{\tau }}}qe^{{i\overline{\omega }\,\overline{\tau }\,\theta }} + \frac{{i\,\overline{g}_{11} }}{{\overline{\omega }\,\overline{\tau }}}\overline{q}e^{{ - i\overline{\omega }\,\overline{\tau }\,\theta }} + E_{2} , $$
(5.22)

where \(E_{2} = \left( {E_{2}^{\left( 1 \right)} ,\,E_{2}^{\left( 2 \right)} } \right)\) represents an invariant vector in 2-dim plane. We shall try to find suitable \(E_{1}\) and \(E_{2}\) in the below. From the definition of \(A\) and (5.17), we get

$$ \int\limits_{ - 1}^{0} {d\eta } \,W_{20} = 2i\overline{\omega }\,\overline{\tau }W_{20} - H_{20} , $$
(5.23)

and

$$ \int\limits_{ - 1}^{0} {d\eta } \,W_{11} = - H_{11} $$
(5.24)

where \(\eta \left( \vartheta \right) = \eta \left( 0 \right)\). By (5.15), we have

$$ H_{20} \left( 0 \right) = - g_{20} q\left( 0 \right) - \overline{g}_{02} \overline{q}\left( 0 \right) + 2\overline{\tau }\left( {\begin{array}{*{20}c} { - \left( {\frac{r}{k} + \left( {1 - m} \right)\beta } \right)} \\ {h\left( {c\beta \left( {1 - m} \right)e^{{ - i\overline{\omega } \overline{\tau } }} - \theta h} \right)} \\ \end{array} } \right), $$
(5.25)

and

$$ H_{11} \left( 0 \right) = - g_{11} q\left( 0 \right) - \overline{g}_{11} \overline{q}\left( 0 \right) + 2\overline{\tau }\left( {\begin{array}{*{20}c} { - \left( {\frac{r}{k} + \beta \left( {1 - m} \right){\text{Re}} \left\{ h \right\}} \right)} \\ {c\beta \left( {1 - m} \right){\text{Re}} \left\{ h \right\} - \theta h\overline{h}} \\ \end{array} } \right). $$
(5.26)

Substituting (5.21) and (5.25) into (5.23) and noticing that.

\(\left( {i\overline{\omega }\,\overline{\tau }I - \int\limits_{ - 1}^{0} {e^{{i\overline{\omega }\,\overline{\tau }\vartheta }} d\eta } \left( \vartheta \right)} \right)q\left( 0 \right) = 0,\) and

$$ \left( { - i\overline{\omega }\,\overline{\tau }I - \int\limits_{ - 1}^{0} {e^{{ - i\overline{\omega }\,\overline{\tau }\vartheta }} d\eta } \left( \vartheta \right)} \right)\overline{q}\left( 0 \right) = 0. $$

we get

$$ \left( {2i\overline{\omega }\,\overline{\tau }I - \int\limits_{ - 1}^{0} {e^{{2i\overline{\omega }\,\overline{\tau }\vartheta }} d\eta } \left( \vartheta \right)} \right)E_{1} = 2\overline{\tau }\left( {\begin{array}{*{20}c} { - \left( {\frac{r}{k} + \left( {1 - m} \right)\beta } \right)} \\ {h\left( {c\beta \left( {1 - m} \right)e^{{ - i\overline{\omega } \overline{\tau } }} - \theta h} \right)} \\ \end{array} } \right). $$

This leads to

$$ \begin{gathered} \left( {\begin{array}{*{20}c} {2i\overline{\omega } + \frac{{rx^{*} \left[ {K\alpha \left( {1 - m} \right) - 1 - 2x^{*} \alpha \left( {1 - m} \right)} \right]}}{{K\left[ {1 + \alpha \left( {1 - m} \right)x^{*} } \right]}}} & {\frac{{\left[ {\gamma + \theta y^{*} } \right]}}{c}} \\ { - \frac{{cr\left( {K - x^{*} } \right)}}{{K\left[ {1 + \alpha \left( {1 - m} \right)x^{*} } \right]}}e^{{ - 2i\overline{\omega } \overline{\tau } }} } & {2i\overline{\omega } + \theta y^{*} } \\ \end{array} } \right)E_{1} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2\left( {\begin{array}{*{20}c} { - \left( {\frac{r}{k} + \left( {1 - m} \right)\beta } \right)} \\ {h\left( {c\beta \left( {1 - m} \right)e^{{ - i\overline{\omega } \overline{\tau } }} - \theta h} \right)} \\ \end{array} } \right). \hfill \\ \end{gathered} $$

It follows that

$$ E_{1}^{(1)} = \frac{2}{A}\left| {\begin{array}{*{20}c} { - \left( {\frac{r}{k} + \left( {1 - m} \right)\beta } \right)} & {\frac{{\left[ {\gamma + \theta y^{*} } \right]}}{c}} \\ {h\left( {c\beta \left( {1 - m} \right)e^{{ - i\overline{\omega } \overline{\tau } }} - \theta h} \right)} & {2i\overline{\omega } + \theta y^{*} } \\ \end{array} } \right|, $$

and

$$E_{1}^{(2)} = \frac{2}{A}\left| {\begin{array}{*{20}c} {2i\overline{\omega } + \frac{{rx^{*} \left[ {K\alpha \left( {1 - m} \right) - 1 - 2x^{*} \alpha \left( {1 - m} \right)} \right]}}{{K\left[ {1 + \alpha \left( {1 - m} \right)x^{*} } \right]}}} & { - \left( {\frac{r}{k} + \left( {1 - m} \right)\beta } \right)} \\ { - \frac{{cr\left( {K - x^{*} } \right)}}{{K\left[ {1 + \alpha \left( {1 - m} \right)x^{*} } \right]}}e^{{ - 2i\overline{\omega } \overline{\tau } }} } & {c\beta \left( {1 - m} \right)e^{{ - i\overline{\omega } \overline{\tau } }} - \theta h} \\ \end{array} } \right|.$$

where

$$ A = \left| {\begin{array}{*{20}c} {2i\overline{\omega } + \frac{{rx^{*} \left[ {K\alpha \left( {1 - m} \right) - 1 - 2x^{*} \alpha \left( {1 - m} \right)} \right]}}{{K\left[ {1 + \alpha \left( {1 - m} \right)x^{*} } \right]}}} & {\frac{{\left[ {\gamma + \theta y^{*} } \right]}}{c}} \\ { - \frac{{cr\left( {K - x^{*} } \right)}}{{K\left[ {1 + \alpha \left( {1 - m} \right)x^{*} } \right]}}e^{{ - 2i\overline{\omega } \overline{\tau } }} } & {2i\overline{\omega } + \theta y^{*} } \\ \end{array} } \right| $$

Similarly, substituting (5.22) and (5.26) into (5.24)

$$ \begin{gathered} \left( {\begin{array}{*{20}c} {\frac{{rx^{*} \left[ {K\alpha \left( {1 - m} \right) - 1 - 2x^{*} \alpha \left( {1 - m} \right)} \right]}}{{K\left[ {1 + \alpha \left( {1 - m} \right)x^{*} } \right]}}} & {\frac{{\left[ {\gamma + \theta y^{*} } \right]}}{c}} \\ { - \frac{{cr\left( {K - x^{*} } \right)}}{{K\left[ {1 + \alpha \left( {1 - m} \right)x^{*} } \right]}}e^{{ - 2i\overline{\omega } \overline{\tau } }} } & {\theta y^{*} } \\ \end{array} } \right)E_{1} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2\left( {\begin{array}{*{20}c} { - \left( {\frac{r}{k} + \beta \left( {1 - m} \right){\text{Re}} \left\{ h \right\}} \right)} \\ {c\beta \left( {1 - m} \right){\text{Re}} \left\{ h \right\} - \theta h\overline{h}} \\ \end{array} } \right) \hfill \\ \end{gathered} $$

It follows that

$$ E_{2}^{(1)} = \frac{2}{B}\left| {\begin{array}{*{20}c} { - \left( {\frac{r}{k} + \beta \left( {1 - m} \right){\text{Re}} \left\{ h \right\}} \right)} & {\frac{{\left[ {\gamma + \theta y^{*} } \right]}}{c}} \\ {c\beta \left( {1 - m} \right){\text{Re}} \left\{ h \right\} - \theta h\overline{h}} & {2i\overline{\omega } + \theta y^{*} } \\ \end{array} } \right| $$

and

\(E_{2}^{(2)} = \frac{2}{B}\left| {\begin{array}{*{20}c} {2i\overline{\omega } + \frac{{rx^{*} \left[ {K\alpha \left( {1 - m} \right) - 1 - 2x^{*} \alpha \left( {1 - m} \right)} \right]}}{{K\left[ {1 + \alpha \left( {1 - m} \right)x^{*} } \right]}}} & { - \left( {\frac{r}{k} + \beta \left( {1 - m} \right){\text{Re}} \left\{ h \right\}} \right)} \\ { - \frac{{cr\left( {K - x^{*} } \right)}}{{K\left[ {1 + \alpha \left( {1 - m} \right)x^{*} } \right]}}e^{{ - 2i\overline{\omega } \overline{\tau } }} } & {c\beta \left( {1 - m} \right){\text{Re}} \left\{ h \right\} - \theta h\overline{h}} \\ \end{array} } \right|\)

where

$$ B = \left| {\begin{array}{*{20}c} {\frac{{rx^{*} \left[ {K\alpha \left( {1 - m} \right) - 1 - 2x^{*} \alpha \left( {1 - m} \right)} \right]}}{{K\left[ {1 + \alpha \left( {1 - m} \right)x^{*} } \right]}}} & {\frac{{\left[ {\gamma + \theta y^{*} } \right]}}{c}} \\ { - \frac{{cr\left( {K - x^{*} } \right)}}{{K\left[ {1 + \alpha \left( {1 - m} \right)x^{*} } \right]}}e^{{ - 2i\overline{\omega } \overline{\tau } }} } & {\theta y^{*} } \\ \end{array} } \right| $$

This enables determination of \(W_{20} \left( \vartheta \right)\,\,{\text{and}}\,W_{11} \left( \vartheta \right)\) from what is available in (5.21) and (5.22). Additionally,\(g_{21}\) in (5.14) may be expressed in the form of delay and other related parameters.\(C_{1} \left( 0 \right) = \frac{i}{{2\overline{\omega }\,\overline{\tau }}}\left( {g_{20} g_{11} - 2\left| {g_{11} } \right|^{2} - \frac{{\left| {g_{02} } \right|^{2} }}{3}} \right) + \frac{{g_{21} }}{2},\)

$$ \mu_{2} = - \frac{{{\text{Re}} \left\{ {C_{1} (0)} \right\}}}{{{\text{Re}} \left\{ {\lambda^{\prime}(\tau )} \right\}}}, $$
$$ \beta_{2} = 2{\text{Re}} \left\{ {C_{1} (0)} \right\}, $$
$$ T_{2} = - \frac{{{\text{Im}} \left\{ {C_{1} (0)} \right\} + \mu_{2} {\text{Im}} \left\{ {\lambda^{\prime}(\overline{\tau })} \right\}}}{{\overline{\omega }\overline{\tau }}}. $$

The concomitant values which measure the characteristics of a bifurcating periodic solution in the center manifold at the critical value \(\overline{\tau }\).

Theorem 6

The parameter \(\mu_{2}\) is used to identify the direction of the Hopf bifurcation. The Hopf bifurcation is supercritical (subcritical) when \(\mu_{2}\) positive (negative) and bifurcating periodic solutions arise if \(\tau > \overline{\tau } \left( {\tau < \overline{\tau } } \right)\).

Stability Analysis of Stochastic Model

In ecology, deterministic models seldom provide biological variation which is normally explained by the tacit belief that stochastic variations in broad populations are minor enough to be overlooked. Only if the dynamical structures shown by deterministic models remained after stochastic effects were applied would they be ecologically beneficial. Since the environmental variability in a terrestrial system is high over both short and long time periods, it is likely that the system will evolve internal structures to deal with short-term variability while minimising the impact of long-term variability, resulting in improved outcomes when the system is analysed with white noise. Temperature, humidity, pests and viruses, air contamination, and other conditions all play a role in species reproduction [37]. Since populations' physical and biological conditions are unpredictable, population growth can be seen as a stochastic rather than a deterministic mechanism [38]. The following stochastic differential equations will be used to describe the model method (1) in this case: It may be then safe to conclude that the perturbations which are stochastic in characteristics (Model 1) show an indubitably high tendency to white noise. Also, the perturbations are proportional to the distance from the origin and are susceptible to environmental fluctuations. The stochastic differential system of Eq. (1.2) is seen below, and it has the same equilibria as the system before it Eq. (1.2).

$$ \frac{dx}{{dt}} = rx\left( {1 - \frac{x}{K}} \right) - \frac{{\beta \left( {1 - m} \right)xy}}{{1 + \alpha \left( {1 - m} \right)x}} + \Upsilon_{1} \left( {x - x^{*} } \right)d\xi_{t}^{1} , $$
$$ \frac{dy}{{dt}} = \frac{{c\beta \left( {1 - m} \right)xy}}{{1 + \alpha \left( {1 - m} \right)x}} - \gamma y - \theta y^{2} + \Upsilon_{2} \left( {y - y^{*} } \right)d\xi_{t}^{1} . $$
(6.1)

The linearized Stochastic Differential Equations corresponding to the positive equilibrium \(V_{2}\) is given by

$$ dp\left( t \right) = f\left( {p\left( t \right)} \right)dt + g\left( {p\left( t \right)} \right)d\xi \left( t \right) $$
(6.2)

where \(p\left( t \right) = \left( {p_{1} \left( t \right),\,\,p_{2} \left( t \right)} \right)^{T}\) and \(f(p(t))\) is the variation matrix \(J\left( {\overline{x},\overline{y}} \right)\)

$$ g\left( p \right) = \left[ {\begin{array}{*{20}c} {\Upsilon_{1} p_{1} } & 0 \\ 0 & {\Upsilon_{2} p_{2} } \\ \end{array} } \right] $$

Let \(C^{1,2} \left( {\left[ {0, + \infty } \right) \times \Re^{2} ,\Re^{{^{ + } }} } \right)\) be the family of nonnegative functions. \(W\left( {t,p} \right)\) defined on \(\left[ {0, + \infty } \right) \times \Re^{2}\) is a continuously differentiable function with respect to t and twice with respect to \(p\).

The differential operator \(L\) is first defined for a \(L\), function \(W\left( {t,p} \right)\) given by the equation below:

$$ LW(t,p) = \frac{{\partial W\left( {t,p} \right)}}{\partial t} + f^{T} \left( p \right)\frac{{\partial W\left( {t,p} \right)}}{\partial p} + \frac{1}{2}Tr\left[ {g^{T} \left( p \right)\frac{{\partial^{2} W\left( {t,p} \right)}}{{\partial p^{2} }}g\left( p \right)} \right], $$
(6.3)

\(\frac{\partial W}{{\partial p}} = col\left( {\frac{\partial W}{{\partial p_{1} }},\frac{\partial W}{{\partial p_{2} }},\frac{\partial W}{{\partial p_{3} }}} \right),\) and \(\frac{{\partial^{2} W\left( {t,p} \right)}}{{\partial p^{2} }} = \left( {\frac{{\partial^{2} W}}{{\partial p_{j} \partial p_{i} }}} \right).\,\,\,\,\,\,\,\,\,\,i,j = 1,2\),\(T\) denotes transpose.

The trivial solution marked for (6.2) must be proven to be globally asymptotically stable through probability [1, 39].

Theorem 7

Suppose that \(\Upsilon_{1}^{2} \le 2\left( {\frac{{rx^{*} }}{K} - \frac{{\alpha \beta \left( {1 - m} \right)^{2} x^{*} y^{*} }}{{\left( {1 + \alpha \left( {1 - m} \right)x^{*} } \right)^{2} }}} \right),\,\,\Upsilon_{2}^{2} \le 2\left( {\theta y^{*} } \right)\) hold. Then, the trivial solution of (6.2) is asymptotically mean square stable.

Proof

Let us consider the Lyapunov function

$$ W\left( p \right) = \frac{1}{2}\left[ {w_{1} p_{1}^{2} + w_{2} p_{2}^{2} } \right] $$
(6.4)

here \(w_{1} ,\,w_{2}\) are nonnegative constants are to be taken as in the given below.

$$ \begin{gathered} LW\left( u \right) = w_{1} \left[ {\left( { - \frac{{rx^{*} }}{K} + \frac{{\alpha \beta \left( {1 - m} \right)^{2} x^{*} y^{*} }}{{\left( {1 + \alpha \left( {1 - m} \right)x^{*} } \right)^{2} }}} \right)p_{1} + \left( {\frac{{ - \beta \left( {1 - m} \right)x^{*} }}{{1 + \alpha \left( {1 - m} \right)x^{*} }}} \right)p_{2} } \right]p_{1} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + w_{2} \left[ {\frac{{c\beta \left( {1 - m} \right)y^{*} }}{{\left( {1 + \alpha \left( {1 - m} \right)x^{*} } \right)^{2} }}p_{1} - \theta y^{*} p_{2} } \right]p_{2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{1}{2}Tr\left[ {g^{T} \left( p \right)\frac{{\partial^{2} W\left( {t,p} \right)}}{{\partial p^{2} }}g\left( p \right)} \right]. \hfill \\ \end{gathered} $$
(6.5)

with \(\frac{1}{2}Tr\left[ {g^{T} \left( p \right)\frac{{\partial^{2} W\left( {t,p} \right)}}{{\partial p^{2} }}g\left( p \right)} \right] = \frac{1}{2}\left[ {w_{1} \Upsilon_{1}^{2} p_{1}^{2} + w_{2} \Upsilon_{2}^{2} p_{2}^{2} } \right]\).

If in (6.5) we choose \(\frac{{ - \beta \left( {1 - m} \right)x^{*} }}{{1 + \alpha \left( {1 - m} \right)x^{*} }}w_{1} = \frac{{c\beta \left( {1 - m} \right)y^{*} }}{{\left( {1 + \alpha \left( {1 - m} \right)x^{*} } \right)^{2} }}w_{2}\), then

$$ LW\left( p \right) = - \left( {\frac{{rx^{*} }}{K} - \frac{{\alpha \beta \left( {1 - m} \right)^{2} x^{*} y^{*} }}{{\left( {1 + \alpha \left( {1 - m} \right)x^{*} } \right)^{2} }} - \frac{1}{2}\Upsilon_{1}^{2} } \right)w_{1} p_{1}^{2} - \left( {\theta y^{*} - \frac{1}{2}\Upsilon_{2}^{2} } \right)w_{2} p_{2}^{2} $$

Based on theorem (7), it is surmised that the trivial solution of (6.1) is indeed globally asymptotically stable.

Numerical Simulations

We offer numerical examples in this part to corroborate the theoretical analysis presented in the previous sections.

Example 1

Taking the various estimates as \(r = 0.207;K = 52.1;\beta = 0.948;m = 0.047;\alpha = 0.955;\)

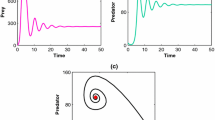
\(c = 0.631;\gamma = 0.081;\theta = 0.218\) and we examine time series and phase portraits under different -time delays. Figure 1 and Fig. 2 confirm how the variation of time delay impacts the dynamical behavior of the model. If \(\tau = 0.6\) then positive equilibrium is asymptotically stable (Fig. 1) and if \(\tau = 0.8\) then positive equilibrium loses its stability and a family of periodic solutions bifurcates from positive equilibrium and a Hopf bifurcation exist.

Fig. 1
figure 1

The directions and phase portrait of the system Eq. (3.4) taking the time delay \(\tau = 0.6\)

Full size image
Fig. 2
figure 2

The direction and phase portrait of the model Eq. (3.4) taking the time delay \(\tau = 0.8\)

Full size image

Example 2

We got the following graphs by taking the various estimates as \(r = 0.26;K = 52;\beta = 0.08;m = 0.01;\alpha = 0.05;c = 0.8;\gamma = 0.31;\theta = 0.218.\) with various values of white noise intensities and the method satisfy the Theorem (7) conditions for these parameter values. The Figures (Fig. 3, Fig. 4, and Fig. 5) clearly demonstrate that when the white noise strength increases, the populations begin to converge at a point of equilibrium with wildly arbitrary oscillations.

Fig. 3
figure 3

The stochastic directions of the model (6.1) taking the white noise intensities \(\Upsilon_{1} = 0.05\,\& \,\Upsilon_{2} = 0.07\) and \(\Upsilon_{1}^{2} < 0.3007\,\& \,\Upsilon_{2}^{2} = 1.0630\) (Theorem (7))

Full size image
Fig. 4
figure 4

The stochastic directions of the model (6.1) taking the white noise intensities \(\Upsilon_{1} = 0.2\,\& \,\Upsilon_{2} = 0.4\) and \(\Upsilon_{1}^{2} < 0.3007\,\& \,\Upsilon_{2}^{2} = 1.0630\)(Theorem (7))

Full size image
Fig. 5
figure 5

The stochastic directions of the model (6.1) taking the white noise intensities \(\Upsilon_{1} = 0.4\,\& \,\Upsilon_{2} = 0.6\) and \(\Upsilon_{1}^{2} < 0.3007\,\& \,\Upsilon_{2}^{2} = 1.0630\)(Theorem (7))

Full size image

Example 3

In Figs. 6 and 7, we look at time series diagrams of various estimates of \(m\) and \(\theta\) the same other constraints as in Example 1. We observe when the minimal value of \(\theta = 0.1\) and increasing refuge values then the scheme interchanged the oscillatory bearing by a stable equilibrium. If \(\theta = 0.5\) and varying refuge, we see that the present system does not change its stable behavior. This remark enables us that for a larger intra-specific competition in predators, the prey refuge does not affect the system behavior.

Fig. 6
figure 6

The time series trajectories of the system Eq. (1.2) for fixed \(\theta = 0.1\) with two various values of \(m = 0.2,\,0.5\) respectively

Full size image
Fig. 7
figure 7

The time series trajectories of the system Eq. (1.2) for fixed \(\theta = 0.5\) with two various values of \(m = 0,\,0.5\) respectively

Full size image

Conclusions

The paper concerned itself with a prey-predator relationship, with a prey refuge in the picture, and rivalry between predators. It was further assumed that the mechanism with regard to predator reaction obeyed the Holling type II format. While there can be little argument that a refuge is essential for biological management of pests, increasing the rate of refuge can lead to a tragic increase in prey density and a swift outbreak of population growth. The paper commenced with an elaboration on the boundedness of the system and then dealt with the local stability around the positive equilibrium point. The equations essential to proving with a high degree of certainty the nature of the stability of the system and the direction it takes were formulated with the help of normal form theory and the centre manifold theorem. The main effect of white noise on stochastic differential systems was a foregone conclusion from the equations. Under conditions of environmental fluctuations; equations were derived and solved to reveal parameters requisite for achieving global asymptotic stabilization.

The study's key finding is that time delay and environmental fluctuations are two essential features of real-time equation applications that cannot be overlooked. This research also shows that the prey refuge has no effect on predator behavior when there is more intra-specific competition.

The term "refuge" refers to a critical component in the biological management of prey predator populations. Increased refuge levels, on the other hand, can result in an increase in prey individuals and, as a result, prey population outbreaks. Hotspots of high spider mite densities in almond orchards, according to Hoy [45], can initiate orchard-wide outbreaks. These hotspots are places where the predator is having difficulty controlling the prey, and thus can be classified as prey refugia. In a variety of predator–prey settings, our model can also be utilised to explain real-world population dynamics. For example, in an aquatic system with patchy habitat, the model can be used to depict the dynamics of predator–prey interaction. Conservation biologists may find the theoretical results valuable in preserving species in real-world ecological systems.

Many topics for further research are open based on the stated findings. Spice dispersion can be accounted for using spatial diffusion terms, and diffusion-induced instabilities can be studied. The impact of geographical diffusion in the model using the Valenti et al. [46] technique is another promising subject for further research.