Bifurcation analysis in a predator–prey system with a functional response increasing in both predator and prey densities

Abstract

This paper presents a qualitative study of a predator–prey interaction system with the functional response proposed by Cosner et al. (Theor Popul Biol 56:65–75, 1999). The response describes a behavioral mechanism which a group of predators foraging in linear formation searches, contacts and then hunts a school of prey. On account of the response, strong Allee effects are induced in predators. In the system, we determine the existence of all feasible nonnegative equilibria; further, we investigate the stabilities and types of the equilibria. We observe the bistability and paradoxical phenomena induced by the behavior of a parameter. Moreover, we mathematically prove that the saddle-node, Hopf and Bogdanov–Takens types of bifurcations can take place at some positive equilibrium. We also provide numerical simulations to support the obtained results.

1 Introduction

Numerous systems of differential equations have been formulated and studied to explain the dynamics and interactions observed in population biology. An increasing number of studies are being conducted on this topic because it has helped understand the dynamics and interactions of organisms. In the last half-century, one of the dominant themes in the discipline has been studying dynamic interactions between the predators and their preys. Consequently, a substantial number of various predator–prey interaction systems have been proposed and qualitatively analyzed to determine the underlying dynamics taking place in real ecological systems.

Traditionally, a prototypical predator–prey model has the following structure:

$$\begin{aligned} \left\{ \begin{array}{ll}\displaystyle \displaystyle \frac{\mathrm{d} x}{\mathrm{d} t} = f(x)x-g(x,y)y, \ \ \ &{} \ \ x(0)>0\text{, }\\ \displaystyle \frac{\mathrm{d} y}{\mathrm{d} t} = \epsilon g(x,y)y -\mu y, &{} \ \ y(0)>0, \end{array} \right. \end{aligned}$$

(1.1)

where x and y are the respective population densities of the prey and predator; f(x) is the net growth rate of the prey in the absence of predators; g(x, y) is the prey consumption rate of a predator to prey; and $\mu$ and $\epsilon$ are positive constants representing the predator death rate and the conversion rate of the captured prey into the predator, respectively. To demonstrate the crowding effect, the prey growth rate f(x) is typically negative in (1.1) when the prey is large. The most well-known example of f(x) is the logistic form

$$\begin{aligned} f(x) =r \left( 1-\frac{x}{K}\right) , \end{aligned}$$

where the positive constants r and K refer to the prey intrinsic growth rate and the carrying capacity of the environment for the prey population, respectively. Thus, in this paper, we assume that f(x) has the logistic form given above. The behavioral characteristic of the predator species can be reflected using the key element g(x, y) called the functional response or the trophic function. Eventually, the functional response plays an important role in determining the different dynamical behaviors, namely, the steady states, the oscillations, the chaos and the bifurcation phenomena [14]. The functional response g(x, y) in the population dynamics (and in other disciplines) has several traditional and interesting forms:

• (i) Monotonic $g(x,y)=g(x)$ depending on x only: mx (Lotka–Volterra type), $\frac{mx}{a+x}$ (Holling type II), $\frac{mx^2}{a+x^2}$ (Holling type III).

• (ii) Nonmonotonic $g(x,y)=g(x)$ depending on x only: $\frac{mx}{a+x^2}$ (Monod-Haldane), $mxe^{-ax}$.

• (iii) Monotonic g(x, y) depending on x and y: $\frac{mx}{x+ay}$ (Ratio-dependent), $\frac{mx}{a+bx+cy}$ (Beddington–DeAngelis).

Here m, a, b and c used above are positive constants, and they have appropriate biological meanings in each response function [see [8, 16] for (i), [12, 22, 29] for (ii), [3, 5, 11, 14, 27] for (iii)].

Asymptotic behavior of solutions to the biological systems [including (1.1)] has the simplest type, equilibrium points (i.e., nonnegative constant solutions of the systems). Moreover, in predator–prey interactions, there is another asymptotic type: periodic. This is supported by Hudson company lynx-hare data. Studying the periodic asymptotic behavior (further, limit cycle and homoclinic loop) is one of the popular research topics in biological models. In system (1.1) with the functional responses above, interesting topics such as permanence, the stability of equilibria, the existence and nonexistence of a limit cycle, and various kinds of bifurcations have been extensively studied by many researchers. For reference, besides ecology, bifurcation has been studied in various fields (e.g., see [1, 23, 24, 30]). In recent years, numerous mathematical studies have been performed on the bifurcation of multiple parameters [18, 20] in predator–prey systems, because they determine all feasible types of bifurcations according to variations in some parameters (e.g., see [7, 13, 17, 19, 22, 26, 28, 29]). In (1.1), when the functional response is nonmonotonic as in (ii) above, a variety of interesting bifurcations, such as saddle-node, Hopf and codimension-2 cusp (i.e., Bogdanov–Takens [18, 20]), can occur with variations in some parameters [22, 29]. However, if the functional response is monotonic as in (i) or (iii), the cusp bifurcation of the codimension 2 (further, multiple parameters bifurcation) cannot occur in (1.1). From this viewpoint, we can see that the nonmonotonicity of the functional responses plays an important role in inducing the multiple parameters bifurcation. Of course, in system (1.1) if we introduce a prey growth rate f(x) with an Allee effect or introduce a prey or a predator harvesting rate when the functional response is monotonic, we can observe the bifurcation phenomenon (e.g., see [13, 26, 28]).

Even when a harvest rate or Allee effect (on f(x)) is not considered in reaction terms, several functional responses induce the bifurcation of multiple parameters (at least, of the codimension 2). One response is introduced in [2] (see also [6]); this response was obtained by adding a cooperation effect to the predation rate. This response ($g(x,y)=(\lambda +a v)u$ with some positive constants $\lambda$ and a) has the monotonicity property; it increases in both the prey and predator densities. As a result, the hunting cooperation in the predator–prey interactions mechanically induces Allee effects in predators. Therefore, the above-mentioned bifurcation takes place in the predator–prey system described by (1.1) with the functional response reflecting the hunting cooperation effects. In fact, in [2], in addition to the two-parameter bifurcation, the equilibrium stability and Hopf bifurcation were investigated numerically based on the cooperation rate and the predator basic reproduction number. Further, the numerical results obtained were biologically interpreted. To date, there have been very few studies on the monotonic functional responses with the hunting cooperation [2, 6]. In this paper, we briefly introduce another functional response reflecting the cooperation effects proposed by Cosner et al. [9], and we investigate the dynamics of the response mathematically.

In [9], to propose a functional response for demonstrating a mechanism of how a group of predators (e.g., a school of tuna) searches, contacts and then hunts a school or a herd of prey, several biological assumptions were made. Based on these assumptions and the logic of Holling [15], the Cosner et al. [9] proposed the following functional response:

$$\begin{aligned} g(x,y) = \frac{C e_0 xy}{1+hCe_0 xy}. \end{aligned}$$

Here, the given coefficients C, h and $e_0$ are all positive constants. In particular, these coefficients have the following biological meanings: C is the amount of prey captured by a predator per encounter; h is the handling time per prey; $e_0$ is the total encounter coefficient between the predator and the prey. Unlike the conventional responses [e.g., (i), (ii) and (iii)], the functional response has a monotonicity for both x and y, and the response even increases in y. We may understand the monotonicity and the (upper) boundedness of this predation function as follows. When the size of the predators’ population is large, the predators’ hunting becomes more efficient. However, when the size of the predators’ population becomes too large, the predation efficiency is not as good because if the predators’ foraging line formation becomes too long, then the signal transmission between them is not smooth; this happens because of the assumptions in [9].

The primary purpose of this study is to investigate mathematically what interesting dynamical behaviors the above functional response gives to system (1.1); in particular, we investigate the occurrence of the two-parameter bifurcation. This functional response has been proposed many years back [9]; however, to the best of our knowledge, our proposed study is the first mathematical investigation of the response. By substituting the above-derived functional response and the logistic prey growth rate in ordinary differential equations (1.1), we eventually have the following predator–prey system:

$$\begin{aligned} \left\{ \begin{array}{ll}\displaystyle \frac{\mathrm{d} x}{\mathrm{d} t} = rx \left( 1- \frac{x}{K} \right) - \frac{Ce_0 xy}{1+hCe_0 xy}y, \ \ \ &{} \ \ {x(0)>0,}\\ \displaystyle \frac{\mathrm{d} y}{\mathrm{d} t} = \frac{\epsilon Ce_0 xy}{1+hCe_0 xy} y -\mu y, &{} \ \ {y(0)>0}. \end{array} \right. \end{aligned}$$

Recall that the given parameters r, K, C, $e_0$, h, $\epsilon$ and $\mu$ are positive constants. For simplicity in studying the above ODEs, after defining the scaling:

$$\begin{aligned}&r t=\overline{t}, \ \ \frac{x}{K}= \overline{x}, \ \ hCe_0 Ky =\overline{y}, \ \ \frac{1}{Ce_0 (hK)^2 r}=\alpha , \\ \ \&\frac{\epsilon }{rh}=\beta , \ \ \frac{\mu }{r}=\gamma , \end{aligned}$$

and then dropping the upper bars, we can rewrite the simplified system in the form:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\mathrm{d} x}{\mathrm{d} t} = x (1-x) -\frac{\alpha xy^2 }{1+xy} , &{}\;\; x(0)>0,\\ \displaystyle \frac{\mathrm{d} y}{\mathrm{d} t} = \frac{\beta xy^2 }{1+ xy} -\gamma y , &{}\;\; y(0)>0. \end{array} \right. \end{aligned}$$

(1.2)

With the previous background on bifurcations, we study whether system (1.2) exhibits the saddle-node, Hopf and Bogdanov–Takens types of bifurcations. To this end, we choose $\alpha$ (with $\beta$ if necessary in studying the cusp bifurcation) as the main parameter. Before studying the bifurcations, we investigate the stabilities of all nonnegative equilibrium points of system (1.2) with variations in the parameter $\alpha$. As well known, the stabilities are determined by the eigenvalues of Jacobian matrix corresponding system (1.2). From these results, we can find some critical values of $\alpha$ (and $\beta$), which would provide a guide to the study of the above-mentioned bifurcations. Further, we expect system (1.2) to provide distinct and much richer dynamics. First, we investigate a rather well-known bistability phenomenon in the system. This phenomenon in the one-predator one-prey interaction model is usually observed when an Allee effect is present. The functional response in (1.2) indeed yields a strong Allee effect in predators, as in [2]. Second, we obtain the global stability of the predator-extinction equilibrium point when $\alpha$ is greater than the threshold value. We thereby observe an interesting paradoxical phenomenon (in the sense of Remark 3.3). Along with the occurrence of the Bogdanov–Takens bifurcation, the two features discussed above differentiate system (1.2) from other systems, that is, system (1.1) with g(x, y) in (i) or (iii) (including the Rosenzweig–MacArthur model). To emphasize again, the novelty of this paper is the first analytical study of the predator–prey model with a (first) proposed functional response that reflects the cooperation effect in predation rates. More specifically, three interesting results are obtained for predator–prey system (1.2) with the functional response that is biologically and structurally different from the existing functional responses: Bogdanov–Takens bifurcation, a paradoxical biological phenomenon and bistability. These will allow us to understand the full dynamics of system (1.2).

The rest of this paper is organized as follows. In Sect. 2, we obtain all the conditions for system (1.2) to possess nonnegative equilibria. In Sect. 3, we provide a general phase portrait analysis of the system. Moreover, we study the stabilities and types of all equilibria found in the previous section. In Sect. 4, we discuss the bifurcations that can occur in the system. We show that the system undergoes the saddle-node, (supercritical) Hopf and Bogdanov–Takens (codimension 2) types of bifurcations. Finally, in Sect. 5, we provide a discussion.

2 Equilibria

In this section, we investigate the existence of all nonnegative equilibria in system (1.2).

The origin (0, 0) is apparently the total extinction equilibrium of (1.2), and (1, 0) is the predator-extinction equilibrium. If the system has a positive equilibrium, say (x, y), then the following two algebraic equations hold true:

$$\begin{aligned} (1-x)=\frac{\alpha y^2}{1+xy} \ \ \text{ and } \ \ \frac{\beta xy}{1+xy} =\gamma , \end{aligned}$$

which is equivalent to

$$\begin{aligned} x^3 -x^2 +\frac{\alpha \gamma ^2}{\beta (\beta -\gamma )}=0\ \ \text{ and } \ \ y=\frac{\gamma }{(\beta -\gamma )x}. \end{aligned}$$

(2.1)

Thus, investigating the existence of the root $x\in (0,1)$ of the cubic polynomial, we obtain the following results. Note that the function on the left-hand side of the first equation in (2.1) has critical points 0 and 2 / 3. Thus we need to check the sign at 2 / 3 of the function.

Lemma 2.1

In system (1.2), the following positive equilibriums hold:

• (i) There is no positive equilibrium if

  $$\begin{aligned} \alpha >\alpha _{bt}(\beta , \gamma ):=\frac{4}{27}\frac{\beta (\beta -\gamma )}{\gamma ^2}. \end{aligned}$$

• (ii) There is a unique positive equilibrium $(x_0,y_0):=(\frac{2}{3}, \frac{3\gamma }{2(\beta -\gamma )})$ if $\alpha =\alpha _{bt}$ and $\beta >\gamma$.

• (iii) There are two distinct positive equilibria $(x_1,y_1)$ and $(x_2, y_2)$, satisfying (2.1) and $x_1<\frac{2}{3}<x_2$, if $\alpha <\alpha _{bt}$ and $\beta >\gamma$.

Note that using the trigonometric method, we can also find explicit but very complex forms of $(x_1,y_1)$ and $(x_2, y_2)$.

3 Phase portrait and stability analysis

In this section, we mainly present all the results on the stabilities and types of all nonnegative equilibria of the system. Moreover, we perform a simple phase portrait analysis of system (1.2).

We first point out that the standard and simple arguments show that solutions of (1.2) always exist positively. Moreover, for the system, we have the boundedness property below.

Theorem 3.1

For the solution (x(t), y(t)) of system (1.2),

$$\begin{aligned} \limsup _{t \rightarrow \infty } x(t) \le 1 \ \ \text{ and } \ \ \limsup _{t \rightarrow \infty } y(t) \le \frac{\beta }{\alpha } \frac{M(\gamma )}{\gamma }, \end{aligned}$$

where $M(\gamma ) = \frac{(\gamma +1)^2}{4}$ if $\gamma \le 1$; $M(\gamma )=\gamma$ if $\gamma > 1$.

Proof

The first assertion easily holds from a simple comparison argument. To obtain the second result, we define $w(t)=x(t)+ \frac{\alpha }{\beta } y(t)$. Then we easily see that along the solution of (1.2),

$$\begin{aligned} w_t= x_t +\frac{\alpha }{\beta } y_t =x(1-x)-\frac{\alpha }{\beta }\gamma y. \end{aligned}$$

Thus using the first result, we see that for all large $t>0$,

$$\begin{aligned} w_t +\gamma w =x(1+\gamma -x) \le M(\gamma ). \end{aligned}$$

Hence the standard comparison argument shows that

$$\begin{aligned} \limsup _{t \rightarrow \infty } \left( x(t)+ \frac{\alpha }{\beta } y(t) \right) \le \frac{M(\gamma )}{\gamma }, \end{aligned}$$

which implies that the second assertion holds. $\square$

Therefore we have shown that system (1.2) has a compact global attractor.

We notice that if system (1.2) has a positive equilibrium point (x, y), then the corresponding Jacobian matrix becomes

$$\begin{aligned} J(x,y):= {\begin{pmatrix} \displaystyle 1-x-\frac{\alpha y^2}{1+xy}+x \left( -1+\frac{\alpha y^3}{(1+xy )^2} \right) &{} \displaystyle -\frac{\alpha xy (2 +xy )}{(1+xy )^2}\\ \displaystyle \frac{\beta y ^2}{(1+xy )^2} &{} \displaystyle -\gamma +\frac{\beta xy}{1+xy}+\frac{\beta xy }{(1+xy )^2} \end{pmatrix}}. \end{aligned}$$

In particular, system (1.2), given by (0, 0) and (1, 0), has the corresponding Jacobian

$$\begin{aligned} J(0,0)= {\begin{pmatrix} 1 &{}\quad 0\\ 0&{}\quad -\gamma \end{pmatrix}} \ \ \text{ and } \ \ J(1,0)= {\begin{pmatrix} -1 &{}\quad 0\\ 0&{} \quad -\gamma \end{pmatrix}}. \end{aligned}$$

Thus we know that (0, 0) is a hyperbolic saddle (whose stable manifold is the y-axis), and (1, 0) is a stable node. Moreover, because the positive equilibrium $(x_i, y_i)$ satisfies (2.1), a simple calculation gives

$$\begin{aligned} J(x_i ,y_i )= {\begin{pmatrix} \displaystyle \frac{\gamma }{\beta } -\frac{\beta +\gamma }{\beta }x_i &{} \displaystyle -\frac{\alpha \gamma (2\beta -\gamma )}{\beta ^2}\\ \displaystyle \frac{\beta -\gamma }{\alpha }(1-x_i) &{} \displaystyle \frac{\gamma (\beta -\gamma )}{\beta } \end{pmatrix}} \end{aligned}$$

for $i=0,1,2$. Then, the characteristic polynomial corresponding to the Jacobian matrix above is $\lambda ^2 -\text{ trace }(J(x_i , y_i)) \lambda +\det (J(x_i , y_i))$ with

$$\begin{aligned}&\text{ trace }(J(x_i , y_i))=\frac{\beta +\gamma }{\beta } \left( \frac{\gamma (1+\beta -\gamma )}{\beta +\gamma }-x_i \right) \ \\&\quad \text{ and } \ \det (J(x_i, y_i))=\frac{\gamma (\beta -\gamma )}{\beta }(2-3x_i). \end{aligned}$$

From Lemma 2.1(iii), it is obvious that $\det (J(x_1, y_1))>0$ and $\det (J(x_2, y_2))<0$. Thus, $(x_1, y_1 )$ is an anti-saddle. However, $(x_2 , y_2 )$ is always a saddle with its stable and unstable manifolds denoted by $\Gamma _s$ and $\Gamma _u$, respectively. From our calculations, the tangential direction of $\Gamma _s$ at $(x_2 ,y_2)$ is found to be negative and greater than the tangential direction of the nullcline of y at $(x_2 ,y_2)$; the tangential direction of $\Gamma _u$ at $(x_2 ,y_2)$ is negative and less than the tangential direction of the nullcline of x at $(x_2 ,y_2)$. Further, we denote the orbit approaching from the left of $(x_2 , y_2 )$ as $\Gamma _s^l$, and we denote the orbits leaving the point in the up and down directions as $\Gamma _u^u$ and $\Gamma _u^d$, respectively. From the vector field analysis in (1.2), we have the following information and introduce some notations:

• (i) $\Gamma _u^d \rightarrow (1,0)$ as $t\rightarrow \infty$;

• (ii) the orbit $\Gamma _u^u$ first meets the line $\{(x,y): x=x_1 ,\ y>0\}$ at a point, say $(x_1 , y_u)$; $y_u \ge y_1$ holds, in particular if $(x_1 , y_1)$ is unstable, then $y_u >y_1$;

• (iii) there is a point, say $(x_1 , y_s)$ at which the orbit $\Gamma _s^l$ first meets the line $\{(x,y): x=x_1 ,\ y \ge y_1 \}$; if $(x_1 , y_1)$ is stable, then $y_s >y_1$.

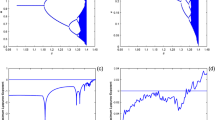
Based on these observations, there are three possibilities (see Fig. 1) in (1.2) when $\alpha <\alpha _{bt}$.

• (1) Case of $y_s >y_u$. Here, $\Gamma _s^l$ has to cross the line $\{(x,y): x=x_2 , \ y>y_2 \}$. In the region bounded by $\Gamma _s$ and the line $x=x_2$, either there is no periodic orbit surrounding the stable $(x_1 , y_1)$ or there are one or more periodic orbits. Obviously, the outermost periodic orbit is stable from the outside. If the periodic orbit is unique, and $(x_1 , y_1 )$ is unstable, then the orbit is stable; (1, 0) is globally asymptotically stable with respect to the exterior (not on $\Gamma _s$) of the region bounded by $\Gamma _s$.

• (2) Case of $y_s =y_u$. Since $(x_1 , y_1)$ is an anti-saddle, we know $y_s =y_u >0$. $\Gamma _s^l$ and $\Gamma _u^u$ make one homoclinic orbit (surrounding $(x_1 , y_1)$), which tends to $(x_2 , y_2 )$ as $t \rightarrow \pm \,\infty$. In the region bounded by the orbit, if $(x_1 , y_1 )$ is unstable, there exists at least one periodic orbit (surrounding $(x_1 , y_1)$). (1, 0) is globally asymptotically stable with respect to the exterior (not on $\Gamma _s$) of the region above.

• (3) Case of $y_s <y_u$. The orbit $\Gamma _s^l$ lies in the region bounded by $\Gamma _u^u$ and $\Gamma _u^d$. In this region, either there is no periodic orbit surrounding the unstable $(x_1 ,y_1)$, or there are one or more periodic orbits. Obviously, the outermost periodic orbit is unstable. There are two distinct heteroclinic orbits $\Gamma _u^u$ and $\Gamma _u^d$ connecting $(x_2 , y_2)$ and (1, 0), and (1, 0) is globally asymptotically stable with respect to at least the exterior (not on $\Gamma _s$) of the region.

Fig. 1

Three possible phase portraits of system (1.2) a $y_s >y_u$, b $y_s =y_u$, c $y_s <y_u$

At (1, 0), we can obtain the global stability if the system does not have a positive equilibrium.

Theorem 3.2

If $\alpha >\alpha _{bt}$, then (1, 0) is globally asymptotically stable.

Proof

We first notice from Theorem 3.1 that system (1.2) has a bounded positively invariant region. Furthermore, according to Lemma 2.1, the system has no positive equilibrium in the region; $x_t >0$ holds for a small $x>0$ and $y>0$. As mentioned earlier, the origin is a hyperbolic saddle, and (1, 0) is a stable node. Thus, according to the Poincaré–Bendixson theorem, there are no periodic and heteroclinic orbits. Hence, because of the local stability of (1, 0), all solutions with positive initial values approach (1, 0), which is globally asymptotically stable. $\square$

The above result is confirmed by the phase plane for system (1.2) with $\alpha =0.00362$, $\beta =4.70883$ and $\gamma =4.6$, as in Fig. 6b. We observe that all the orbits converge to the predator-free equilibrium (1, 0), when $\alpha >\alpha _{bt}$. The red and green lines in the phase portrait are, respectively, the x and y nullclines of (1.2).

Remark 3.3

The given variable $\alpha$ is the food consumption rate of the predator. If this is large, we may expect either growth of the predator or the total extinction of both the predator and the prey due to overfishing by the predators (i.e., overexploitation [21, 25]). In any situation, it is a bad environment for the prey species. Paradoxically, according to the above theorem, a large consumption rate causes the extinction of only the predators. If we recall the rescaling of $\alpha$ given in introduction, we can see that only the predators will become extinct in the system if the carrying capacity K is small.

Obviously, from the above theorem, we can see that (1.2) has no limit cycle in the first quadrant, if $\alpha >\alpha _{bt}$. We now consider the nonexistence of limit cycles in the system when $\alpha \le \alpha _{bt}$. First of all, we note that when $\gamma <\frac{1}{3}$, the quadratic equation

$$\begin{aligned}&\frac{4}{27}\left( \frac{4}{27}- \gamma M(\gamma ) \right) \beta ^2 -\gamma \left( 2 \left( \frac{4}{{27}}\right) ^2 +(M(\gamma ))^3 \right. \\&\left. -\frac{4}{27}\gamma M(\gamma ) \right) \beta +\left( \frac{4 }{{27}}\right) ^2 \gamma ^2 \end{aligned}$$

has only one zero, say $\beta _*$, in $(\gamma , \infty )$.

Theorem 3.4

Assume that $\gamma <\frac{1}{3}$ and $\beta >\beta _*$. Then system (1.2) has no limit cycle in the positive quadrant of the phase plane, provided that

$$\begin{aligned} \alpha > \alpha _* := \frac{M(\gamma ) \beta ^2}{2\gamma }\left( 1+\sqrt{1+\frac{4M(\gamma )}{\gamma \beta }}\right) . \end{aligned}$$

Proof

We know from Theorem 3.1 that the positive solution of system (1.2) eventually enters and stays in

$$\begin{aligned} G:=\left\{ (x,y): 0<x\le 1 , \ 0<y \le \frac{\beta }{\alpha } \frac{M(\gamma )}{\gamma } \right\} . \end{aligned}$$

Thus, if a limit cycle exists, it is in the region G. We employ a Dulac function $F(x,y) =\frac{1}{xy}$. Then

$$\begin{aligned}&\frac{\partial }{\partial x} \left( F(x,y) \left( x(1-x) -\frac{\alpha xy^2}{1+xy}\right) \right) \\&\qquad +\frac{\partial }{\partial y} \left( F(x,y) \left( -\gamma y +\frac{\beta xy^2}{1+xy}\right) \right) \\&\ \ \ =\frac{1}{y(1+xy)^2}(\alpha y^3 +\beta y-(1+xy)^2 ), \end{aligned}$$

which is negative in G if

$$\begin{aligned} \alpha \left( \frac{\beta }{\alpha }\frac{M(\gamma )}{\gamma }\right) ^3 +\beta \left( \frac{\beta }{\alpha }\frac{M(\gamma )}{\gamma }\right) -1 <0. \end{aligned}$$

(3.1)

It is easy to see that (3.1) holds if $\alpha >\alpha _*$; moreover, $\alpha _{bt} >\alpha _*$ if and only if $\beta$($>\gamma$) and $\gamma$ satisfy $\beta >\beta _*$ and $\gamma < 1/3$. Hence, from the Dulac criterion, a limit cycle does not exist. $\square$

We now focus on the type and stability of $(x_1 ,y_1)$ found in the previous section. To do this, we need to investigate the signs of $\text{ trace }(J(x_1 , y_1))$ and $\det (J(x_1, y_1))$ as well as

$$\begin{aligned} \Phi (x_1):= & {} (\text{ trace }(J(x_1 , y_1)))^2 -4 \det (J(x_1, y_1)) \\ {}= & {} \left( \frac{\beta +\gamma }{\beta }\right) ^2 (x_1^2 +2A(\beta , \gamma ) x_1 +B(\beta , \gamma )), \end{aligned}$$

where

$$\begin{aligned} A(\beta , \gamma )&:=\frac{6\beta \gamma (\beta -\gamma )}{(\beta +\gamma )^2}-\frac{\gamma (1+\beta -\gamma )}{\beta +\gamma }\\ {}&=\frac{\gamma \left( 5(\beta -\gamma )^2+(4\gamma -1)(\beta -\gamma )-2\gamma \right) }{(\beta +\gamma )^2},\\ B(\beta , \gamma )&:= \left( \frac{\gamma (1+\beta -\gamma )}{\beta +\gamma }\right) ^2 -\frac{8\beta \gamma (\beta -\gamma )}{(\beta +\gamma )^2}\\ {}&= \frac{\gamma \left( (\gamma -8)(\beta -\gamma )^2 -6\gamma (\beta -\gamma )+\gamma \right) }{(\beta +\gamma )^2}. \end{aligned}$$

When $\beta >\gamma$, $(A(\beta , \gamma ))^2 -B(\beta , \gamma )>0$, and so $\Phi (x)$ always has two roots, say $\phi _l (\beta , \gamma )$ and $\phi _r (\beta , \gamma )$ (with $\phi _l <\phi _r$). Moreover, $\phi _l <\phi _r \le \frac{2}{3}$ holds when $\beta >\gamma$, since $-A(\beta , \gamma )<\frac{2}{3}$ and $\Phi (\frac{2}{3})=(\frac{\beta +\gamma }{\beta })^2 ( \frac{\gamma (1+\beta -\gamma )}{\beta +\gamma } -\frac{2}{3})^2$.

For convenience, we denote

$$\begin{aligned} \phi _m (\beta , \gamma ):=\frac{\gamma (1+\beta -\gamma )}{\beta +\gamma }, \end{aligned}$$

and

$$\begin{aligned}&\alpha _1 (\beta , \gamma ):=\frac{\beta (\beta -\gamma )}{\gamma ^2}\phi _l^2 (1-\phi _l) \ (\hbox { only when } \phi _l>0\text{) } ,\\&\alpha _2 (\beta , \gamma ):=\frac{\beta (\beta -\gamma )}{\gamma ^2}\phi _m^2 \left( 1- \phi _m \right) \ (\hbox {only when } \phi _m <\frac{2}{3}),\\&\alpha _3 (\beta , \gamma ) :=\frac{\beta (\beta -\gamma )}{\gamma ^2}\phi _r^2 (1-\phi _r) \ (\hbox {only when } \phi _r>0),\\&\beta _{bt} (\gamma ) := \gamma +\frac{\gamma }{3\gamma -2} \;\; (\hbox {only when } \gamma>\frac{2}{3}), \\&\beta _1 (\gamma ):=\left\{ \begin{array}{ll} \gamma +\frac{1}{6} \;\; \hbox {if } \gamma =8, \\ &{}\gamma +\frac{3\gamma -\sqrt{8\gamma (\gamma +1)}}{\gamma -8} \;\; \hbox {if } \gamma \ne 8, \end{array} \right. \\&\beta _2 (\gamma ) :=\gamma +\frac{3\gamma +\sqrt{8\gamma (\gamma +1)}}{\gamma -8} \;\; (\hbox {only when } \gamma >8),\\&\beta _a (\gamma ):=\gamma + \frac{1}{10}(-(4\gamma -1) +\sqrt{(4\gamma -1)^2 +40\gamma }). \end{aligned}$$

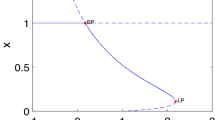
Moreover, the introduced notations (their graphs are in Fig. 2) satisfy the following properties when $\beta >\gamma$:

• (i) $\phi _m <\frac{2}{3}$ if and only if either $\gamma \le \frac{2}{3}$ and $\gamma < \beta$ or $\gamma >\frac{2}{3}$ and $\gamma<\beta <\beta _{bt}$ holds; in particular, $\phi _m = \frac{2}{3}$ if and only if $\gamma >\frac{2}{3}$ and $\beta =\beta _{bt}$;

• (ii) $\Phi (\phi _m )=4\frac{(\beta -\gamma )\gamma }{\beta } (3\phi _m-2)<0$ if and only if $\phi _m <\frac{2}{3}$;

• (iii) only $\beta _i (\gamma )$ (for $i=1,2$) satisfies $B(\cdot , \gamma )=0$;

• (iv) if $\frac{2}{3} <\gamma$, then $0<\beta _1 <\beta _{bt}$; if $8< \gamma$, then $\beta _2$ exists and $\beta _{bt} <\beta _2$;

• (v) if either $\gamma<\beta <\beta _1$ or $\beta _2 <\beta$ and $8< \gamma$, then $B(\beta , \gamma )>0$; if either $\beta _1 <\beta$ and $\gamma \le 8$ or $\beta _1<\beta <\beta _2$ and $8< \gamma$, then $B(\beta , \gamma )<0$;

• (vi) $A(\beta , \gamma )<0$ if and only if $\gamma<\beta <\beta _a (\gamma )$; in particular, if $\gamma <\beta \le \beta _1$, then $A(\beta , \gamma )<0$, and if $8<\gamma$ and $\beta _2 \le \beta$, then $A(\beta , \gamma )>0$.

The process of obtaining the above properties is quite simple and tedious. The obtained stability results are summarized in Fig. 2.

Theorem 3.5

• (i) Assume that $\gamma<\beta <\beta _1$. Then, $(x_1, y_1)$ is an unstable node if $\alpha \le \alpha _1$; an unstable focus if $\alpha _1<\alpha < \alpha _2$; a weak focus or center if $\alpha = \alpha _2$; a stable focus if $\alpha _2<\alpha < \alpha _3$; and a stable node if $\alpha _3 \le \alpha < \alpha _{bt}$.

• (ii) Assume that either $\gamma \le \frac{2}{3}$ and $\beta _1 \le \beta$ or $\frac{2}{3} <\gamma$ and $\beta _1 \le \beta <\beta _{bt}$. Then, $(x_1, y_1)$ is an unstable focus if $\alpha < \alpha _2$; a weak focus or center if $\alpha = \alpha _2$; a stable focus if $\alpha _2<\alpha < \alpha _3$; and a stable node if $\alpha _3 \le \alpha < \alpha _{bt}$.

• (iii) Assume that $\frac{2}{3} <\gamma$ and $\beta = \beta _{bt}$. Then, $(x_1, y_1)$ is an unstable focus if $\alpha < \alpha _{bt}$.

• (iv) Assume that either $\frac{2}{3}<\gamma \le 8$ and $\beta _{bt} <\beta$ or $8<\gamma$ and $\beta _{bt}<\beta <\beta _2$. Then, $(x_1, y_1)$ is an unstable focus if $\alpha < \alpha _3$; and an unstable node if $\alpha _3 \le \alpha <\alpha _{bt}$.

• (v) Assume that $8<\gamma$ and $\beta _2 \le \beta$. Then, $(x_1, y_1)$ is an unstable node if $\alpha < \alpha _{bt}$.

Fig. 2

Summary of Theorem 3.5, a $\beta$-$\gamma$ regions in Theorem 3.5 (i)–(v), b stability of $(x_1, y_1)$ when $\gamma \le \frac{2}{3}$, c stability of $(x_1, y_1)$ when $\frac{2}{3} <\gamma \le 8$, d stability of $(x_1, y_1)$ when $8 <\gamma$

Proof

For each case, the existence of the interior equilibrium $(x_1, y_1)$ follows from Lemma 2.1. Moreover, $\det (J(x_1 , y_1))>0$ holds. From now on, we determine the signs of $\text{ trace }(J(x_1 ,y_1))$ and $\Phi (x_1 )$.

• (i) If $\gamma<\beta <\beta _1$, then it follows from the previous arguments ((i)–(vi)) that $\phi _m <\frac{2}{3}$ (and so $\Phi (\phi _m )<0$ and $\Phi (\frac{2}{3})>0$), $A(\beta , \gamma )<0$ and $B(\beta , \gamma )>0$. These leads to $0<\phi _l<\phi _m<\phi _r <\frac{2}{3}$, so that $\alpha _1<\alpha _2<\alpha _3 <\alpha _{bt}$ holds since $\frac{d}{dx} (x^2 (1-x) )>0$ for $0<x<\frac{2}{3}$. According to the fact that $x_1$ satisfies the first equation in (2.1), if $\alpha \le \alpha _1$, then $x_1 \le \phi _l$, which gives $\text{ trace }(J(x_1 ,y_1))>0$ and $\Phi (x_1 ) \ge 0$; if $\alpha _1< \alpha < \alpha _2$, then $\phi _l< x_1 < \phi _m$, which gives $\text{ trace }(J(x_1 ,y_1))>0$ and $\Phi (x_1 ) < 0$; if $\alpha = \alpha _2$, then $x_1 = \phi _m$, which gives $\text{ trace }(J(x_1 ,y_1))=0$ and $\Phi (x_1 ) < 0$; if $\alpha _2< \alpha < \alpha _3$, then $\phi _m< x_1 < \phi _r$, which gives $\text{ trace }(J(x_1 ,y_1))<0$ and $\Phi (x_1 ) < 0$; if $\alpha _3 \le \alpha < \alpha _{bt}$, then $\phi _r \le x_1 < \frac{2}{3}$, which gives $\text{ trace }(J(x_1 ,y_1))<0$ and $\Phi (x_1 ) \ge 0$. Hence, the desired results hold.

• (ii) The given assumptions yield $\phi _m <\frac{2}{3}$ (and further $\Phi (\phi _m )<0$ and $\Phi (\frac{2}{3})>0$) and $B(\beta , \gamma )\le 0$. In particular, when $B(\beta , \gamma )= 0$ (i.e., $\beta =\beta _1$), $A(\beta , \gamma )<0$. Thus $\phi _l \le 0<\phi _m<\phi _r <\frac{2}{3}$. In this case, $\alpha _1 (\beta , \gamma )$ is not defined. If $\alpha < \alpha _2$, then $x_1 < \phi _m$, so that $\text{ trace }(J(x_1 ,y_1))>0$ and $\Phi (x_1 ) < 0$. The remaining parts are the same as in (i) above.

• (iii) In this case, $\phi _m =\frac{2}{3}$ (and so $\Phi (\frac{2}{3})=0$) and $B(\beta , \gamma )< 0$. Thus $\phi _l <0$, $\phi _r =\phi _m =\frac{2}{3}$ and further $\alpha _2 =\alpha _3 =\alpha _{bt}$. If $\alpha <\alpha _{bt}$, then $\text{ trace }(J(x_1 ,y_1))=0$ and $\Phi (x_1 ) < 0$; therefore, the assertion holds.

• (iv) It is easy to see that $\phi _m >\frac{2}{3}$ (and so $\Phi (\frac{2}{3})>0$) and $B(\beta , \gamma ) < 0$, which gives $\phi _l<0<\phi _r<\frac{2}{3} <\phi _m$. The defined $\alpha _3$ and $\alpha _{bt}$ satisfy $\alpha _3 <\alpha _{bt}$. If $\alpha <\alpha _3$, then $x_1 <\phi _r$, and so $\text{ trace }(J(x_1 ,y_1))>0$ and $\Phi (x_1 ) < 0$. If $\alpha _3 \le \alpha <\alpha _{bt}$, then $\phi _r \le x_1 <\frac{2}{3}$, and thus $\text{ trace }(J(x_1 ,y_1))>0$ and $\Phi (x_1 ) \ge 0$. Hence the result holds.

• (v) From the given assumptions, it follows that $\phi _m >\frac{2}{3}$ (and so $\Phi (\frac{2}{3})>0$), $A(\beta , \gamma ) > 0$ and $B(\beta , \gamma ) \ge 0$, which gives $\phi _l<\phi _r \le 0<\frac{2}{3} <\phi _m$. Thus if $\alpha <\alpha _{bt}$, then $x_1 <\frac{2}{3}$, and so $\text{ trace }(J(x_1 ,y_1))>0$ and $\Phi (x_1 ) > 0$. Hence $(x_1, y_1)$ is an unstable node.

$\square$

Remark 3.6

According to Theorem 3.5(i), (ii) and the argument after Theorem 3.1, (1, 0) and $(x_1 ,y_1)$ are simultaneously stable if $\alpha _2<\alpha <\alpha _{bt}$ and either $\gamma \le \frac{2}{3}$ and $\gamma <\beta$ or $\frac{2}{3}<\gamma$ and $\gamma< \beta < \beta _{bt}$. That is to say, system (1.2) admits the bistability of a boundary equilibrium point of predator extinction and one of positive equilibrium points. Figure 6c shows the bistability of the system for the parameter values $\alpha =0.00362$, $\beta =4.71733$ and $\gamma =4.6$.

As in [7, 17, 27, 31], using classical qualitative methods, we study the dynamical types of the equilibrium $(x_0 , y_0)$. Hereinafter, for brevity, we denote by $O_k (X,Y)$ various smooth functions with degree k or greater in (X, Y).

Theorem 3.7

Assume that $\gamma < \beta$ and $\alpha =\alpha _{bt}$. Then $(x_0, y_0)$ is degenerate. Moreover,

• (i) if either $\gamma \le \frac{2}{3}$ or $\frac{2}{3}<\gamma$ and $\beta \ne \beta _{bt}$, then $(x_0 , y_0)$ is a saddle-node;

• (ii) if $\frac{2}{3}<\gamma$ and $\beta =\beta _{bt}$, then $(x_0 , y_0)$ is a cusp.

Proof

Obviously,

$$\begin{aligned} J(x_0 ,y_0 )= {\begin{pmatrix} \displaystyle -\frac{2\beta -\gamma }{3\beta } &{} \displaystyle -\frac{\alpha \gamma (2\beta -\gamma )}{\beta ^2}\\ \displaystyle \frac{\beta -\gamma }{3\alpha } &{} \displaystyle \frac{\gamma (\beta -\gamma )}{\beta } \end{pmatrix}}, \end{aligned}$$

therefore $\det (J(x_0 , y_0)) =0$. Thus, $(x_0 , y_0)$ is degenerate (i.e., nonhyperbolic).

• (i) We first notice that $\text{ trace }(J(x_0 , y_0))= \frac{(3\gamma -2)\beta - \gamma (3\gamma -1)}{3\beta }\ne 0$ under the given assumptions. Using the simple translation from $(x_0 , y_0)$ to (0, 0) and a series expansion around (0, 0), and denoting $X=x-x_0$ and $Y=y-y_0$, system (1.2) becomes

  $$\begin{aligned} \displaystyle \displaystyle X_t= & {} \displaystyle -\frac{2\beta -\gamma }{3\beta }X-\frac{\alpha \gamma (2\beta -\gamma )}{\beta ^2}Y \nonumber \\&+ \left( -1+\frac{\gamma (\beta -\gamma )}{2\beta ^2} \right) X^2 \displaystyle -\frac{3\alpha \gamma (\beta -\gamma )^2}{\beta ^3}XY \nonumber \\&-\frac{2\alpha (\beta -\gamma )^3}{3\beta ^3}Y^2+O_3 (X,Y),\nonumber \\ Y_t= & {} \displaystyle \frac{\beta -\gamma }{3\alpha } X +\frac{\gamma (\beta -\gamma )}{\beta } Y-\frac{\gamma (\beta -\gamma ) }{2\alpha \beta } X^2 \nonumber \\&\displaystyle + \frac{3\gamma (\beta -\gamma )^2}{\beta ^2} XY +\frac{2(\beta -\gamma )^3}{3\beta ^2} Y^2 \nonumber \\&+O_3 (X,Y). \end{aligned}$$

  (3.2)

We next use the substitutions in system (3.2):

$$\begin{aligned} \displaystyle X_1= & {} \displaystyle \frac{\beta (\beta -\gamma )}{ \alpha (\gamma (3\gamma -1)-(3\gamma -2)\beta ) } \nonumber \\&\quad \left( X+\frac{\alpha (2\beta -\gamma )}{\beta (\beta -\gamma )}Y \right) ,\nonumber \\ \displaystyle Y_1= & {} \displaystyle \frac{\beta (\beta -\gamma )}{ \alpha ((3\gamma -2)\beta -\gamma (3\gamma -1)) } \left( X+\frac{3\alpha \gamma }{\beta }Y \right) \end{aligned}$$

and

$$\begin{aligned} t=\displaystyle \frac{3 \beta }{ (3\gamma -2)\beta -\gamma (3\gamma -1) } \ \tau . \end{aligned}$$

Then, we obtain

$$\begin{aligned} \displaystyle {X_1}_{\tau }= & {} \displaystyle \frac{6\beta (\beta -\gamma )^2}{ ((3\gamma -2)\beta -\gamma (3\gamma -1))^2}X_1^2 +P (X_1 , Y_1 ),\\ \displaystyle {Y_1}_{\tau }= & {} \displaystyle Y_1 +O_2 (X_1 , Y_1), \end{aligned}$$

where $P (X_1 , Y_1 )$ is a smooth function of degree 2 or greater in $(X_1 , Y_1 )$; in particular, $P (X_1 , 0)$ is a smooth function of degree 3 or greater in $X_1$.

By the implicit function theorem, there is a small neighborhood at the origin such that $Y_1 +O_2 (X_1 , Y_1 )=0$ has the solution $Y_1 =\psi (X_1 )$, which is analytic in the neighborhood and $\psi (0)=\psi ^{\prime } (0) =0$. Moreover, the chain rule implies that $P (X_1 , \psi (X_1 ))$ is equal to the sum of the terms with orders (with respect to $X_1$) not less than 3. Therefore, by Theorem 7.1 in [31] (or Chap 2 of [20]), the desired assertion holds.

• (ii) By the given assumptions, we have a more specific Jacobian matrix

  $$\begin{aligned} J(x_0 ,y_0 )= {\begin{pmatrix} \displaystyle -\frac{\gamma }{3\gamma -1} &{} \displaystyle -\frac{4 \gamma }{ 9(3\gamma -1)(3\gamma -2)}\\ \displaystyle \frac{9 \gamma (3\gamma -2)}{4(3\gamma -1)} &{} \displaystyle \frac{\gamma }{3\gamma -1} \end{pmatrix}}, \end{aligned}$$

  which satisfies $\det (J(x_0 , y_0)) =0$ and $\text{ trace }(J(x_0 , y_0))= 0$.

Let

$$\begin{aligned} X_1= & {} -\frac{9(3\gamma -1)(3\gamma -2)}{4\gamma }X \ \text{ and } \\ Y_1= & {} \frac{9(3\gamma -2)}{4}X+Y. \end{aligned}$$

Then system (3.2) with $\alpha =\alpha _{bt}(\beta _{bt}(\gamma ), \gamma )$ and $\beta =\beta _{bt}(\gamma )$ is transformed into

$$\begin{aligned} \displaystyle \displaystyle {X_1}_t= & {} \displaystyle Y_1 +\frac{2 \gamma (2\gamma -1)}{3(3\gamma -1)^2 (3\gamma -2)}X_1^2 \\&+\frac{2}{9\gamma (3\gamma -1)(3\gamma -2)}Y_1^2 +O_3 (X_1 ,Y_1 ),\\ {Y_1}_t= & {} \displaystyle -\frac{2 \gamma ^2}{3(3\gamma -1)^2 (3\gamma -2)} X_1^2 \\&+\frac{2}{9(3\gamma -1)(3\gamma -2)}Y_1^2 +O_3 (X_1 ,Y_1 ). \end{aligned}$$

Next, by following the normal formulas in [20], we can consider and introduce the substitutions in a small neighborhood of the origin:

$$\begin{aligned} X_2= & {} X_1 -\frac{2}{9\gamma (3\gamma -1)(3\gamma -2)}X_1 Y_1 \ \text{ and } \\ Y_2= & {} Y_1 +\frac{2\gamma (2\gamma -1)}{3(3\gamma -1)^2 (3\gamma -2)}Y_1^2 . \end{aligned}$$

Then we obtain

$$\begin{aligned} \displaystyle \displaystyle {X_2}_t= & {} \displaystyle Y_2 + O_3 (X_2 ,Y_2 ),\\ {Y_2}_t= & {} \displaystyle -\frac{2 \gamma ^2}{3(3\gamma -1)^2 (3\gamma -2)} X_2^2 \\&+\frac{4\gamma (2\gamma -1)}{3(3\gamma -1)^2 (3\gamma -2)}X_2 Y_2 +O_3 (X_2 ,Y_2 ). \end{aligned}$$

We finally take $X_3 =X_2$ and $Y_3 =Y_2 +P_4 (X_2 , Y_2 )$ so that we have

$$\begin{aligned} \displaystyle \displaystyle {X_3}_t= & {} \displaystyle Y_3,\\ {Y_3}_t= & {} \displaystyle -\frac{2 \gamma ^2}{3(3\gamma -1)^2 (3\gamma -2)} X_3^2 \\&+\frac{4\gamma (2\gamma -1)}{3(3\gamma -1)^2 (3\gamma -2)}X_3 Y_3 +O_3 (X_3 ,Y_3 ). \end{aligned}$$

Since $\gamma >\frac{2}{3}$,

$$\begin{aligned}&-\frac{2 \gamma ^2}{3(3\gamma -1)^2 (3\gamma -2)} \ne 0 \ \text{ and } \\&\quad \frac{4\gamma (2\gamma -1)}{3(3\gamma -1)^2 (3\gamma -2)} \ne 0. \end{aligned}$$

Hence from [20, 31], the assertion holds true. $\square$

According to the theorem above, when $\alpha =0.889 \ (=\alpha _{bt})$, $\beta =0.3$ and $\gamma =0.1$, the unique positive equilibrium $(x_0 , y_0)$ of system (1.2) is a saddle-node, and when $\alpha =0.01362 \ (=\alpha _{bt})$, $\beta =4.98983 \ (=\beta _{bt})$ and $\gamma =4.6$, it is a cusp. The phase portraits for the saddle-node and cusp are given in Figs. 3a and 6a, respectively.

4 Bifurcations

In this section, we discuss the bifurcations (e.g., saddle-node, Hopf and Bogdanov–Takens) that can occur in system (1.2).

We first see from the previously obtained results that system (1.2) may undergo a saddle-node bifurcation.

Theorem 4.1

Assume that either $\gamma \le \frac{2}{3}$ and $\gamma <\beta$ or $\frac{2}{3}<\gamma$ and $\gamma < \beta \ne \beta _{bt}$. Then, system (1.2) experiences a saddle-node bifurcation at $(x_0, y_0)$ as $\alpha$ passes through $\alpha _{bt}$.

Proof

We know from Lemma 2.1 that if $\alpha >\alpha _{bt}$, then system (1.2) has no positive equilibria. Moreover, as $\alpha$ decreasingly crosses $\alpha _{bt}$, the system possesses two positive equilibria (the saddle and anti-saddle). Thus, according to Sotomayor’s theorem [20], Theorem 3.7(i) yields the desired assertion. $\square$

For example, in system (1.2) with $\beta =0.3$ and $\gamma =0.1$, the saddle-node bifurcation at $(x_0 ,y_0)$ occurs when $\alpha =0.889 \ (=\alpha _{bt})$. Correspondingly, the phase portrait and bifurcation diagram are given in Figs. 3a and 4.

Fig. 3

Phase portraits of system (1.2) with $\beta =0.3$ and $\gamma =0.1$. a Saddle-node of $(x_0 ,y_0)$ when $\alpha =0.889 \ (=\alpha _{bt})$, b a stable limit cycle when $\alpha =0.378 \ (=\alpha _2)$

Fig. 4

Hopf and saddle-node bifurcation diagrams with respect to $\alpha$, for $\beta =0.3$ and $\gamma =0.1$. The solid green circle denotes stable periodic orbits, and the open blue circles are unstable; the red line is stable, and the black line unstable. These show that the supercritical Hopf bifurcation occurs at $\alpha =0.378 \ (=\alpha _2)$, and the saddle-node one occurs at $\alpha =0.889 (=\alpha _{bt})$. a Prey, b predator

In the generic case, a Hopf bifurcation occurs (i.e., a periodic orbit is created) as the stability of an equilibrium point changes. Thus, according to Theorem 3.5, we may expect the occurrence of the positive equilibrium $(x_1 , y_1 )$.

Theorem 4.2

Assume that $\alpha <\alpha _2$, $|\alpha -\alpha _2 |\ll 1$ and

$$\begin{aligned} (\beta , \gamma ) \in HB:= & {} \left\{ (\beta , \gamma ) \ | \ \hbox { either } \gamma \le \frac{2}{3} \hbox { and } \gamma \right. \\ {}< & {} \left. \beta , \hbox { or } \frac{2}{3}<\gamma \hbox { and } \gamma< \beta < \beta _\mathrm{bt} \right\} . \end{aligned}$$

Then, there is at least one stable limit cycle in system (1.2).

Proof

Note that Theorem 3.5(i) and (ii) indicates that $(x_1 , y_1)$ is a weak focus or a center, if $\alpha =\alpha _2$ and $(\beta ,\gamma ) \in HB$. Thus, we know that a Hopf bifurcation occurs at $(x_1 , y_1)$.

To figure out the kind of Hopf bifurcation, we compute the well-known first Lyapunov coefficient of the normal form of the system. Using $X=x-x_1$ and $Y=y-y_1$, system (1.2) with $\alpha =\alpha _2$ becomes

$$\begin{aligned} \displaystyle \displaystyle X_t= & {} \displaystyle a_{10}X+a_{01} Y+a_{20}X^2 +a_{11}XY +a_{02}Y^2 +a_{30}X^3 \nonumber \\&\displaystyle +\,a_{21}X^2 Y +a_{12}XY^2 +a_{03}Y^3 +O_4 (X,Y),\nonumber \\ Y_t= & {} \displaystyle b_{10}X+b_{01} Y+b_{20}X^2 +b_{11}XY +b_{02}Y^2 +b_{30}X^3 \nonumber \\&\displaystyle +\,b_{21}X^2 Y +b_{12}XY^2 +b_{03}Y^3 +O_4 (X,Y), \end{aligned}$$

(4.1)

where $a_{ij}$ and $b_{ij}$ are coefficients involved in the series expansions of the given growth rates $x (1-x) -\frac{\alpha xy^2}{1+xy}$ and $-\gamma y +\frac{\beta xy^2}{1+ xy}$ at $(x_1 , y_1)$, respectively. Obviously, when $(\beta ,\gamma ) \in HB$,

$$\begin{aligned} \Delta:= & {} a_{10} b_{01} -a_{01} b_{10}\\ {}= & {} \frac{\gamma (\beta -\gamma )(\gamma (3\gamma -1)-(3\gamma -2)\beta )}{\beta (\beta +\gamma )}>0 \end{aligned}$$

and $a_{10}+b_{01}=-\frac{\gamma (\beta -\gamma )}{\beta }+\frac{\gamma (\beta -\gamma )}{\beta }=0$. Then, from the formula of the first Lyapunov number $\sigma$ [20] of system (4.1) at the origin, we obtain

$$\begin{aligned} \sigma =-\frac{3\pi }{2 \frac{\alpha _2 \gamma }{\beta ^2} (2\beta -\gamma ) \Delta ^{3/2}} \frac{(\beta -\gamma )^2 \gamma ^2}{(\beta +\gamma )^6 \beta ^6} \ Q(\beta , \gamma ), \end{aligned}$$

where $Q(\beta , \gamma )$ is a degree 16 polynomial in $\beta$ and $\gamma$. We have to determine the sign of $Q(\beta , \gamma )$ when $(\beta , \gamma )\in HB$. For convenience, we investigate the sign of $Q( s +\gamma , \gamma ):= \widetilde{Q} ( s , \gamma )$ when either $\gamma \le \frac{2}{3}$ and $0 < s$ or $\frac{2}{3}<\gamma$ and $0< s < \frac{\gamma }{3\gamma -2}$. With the help of mathematical packages (such as Maple), we obtain

$$\begin{aligned} \widetilde{Q} ( s , \gamma )&= 4\gamma (\gamma -1)^2 s^{13} +2\gamma (\gamma -1)(\gamma ^2 +3\gamma -8)s^{12} \\&\quad +(4 \gamma ^4 -16 \gamma ^3 -8\gamma ^2 +21 \gamma +3)s^{11}\\&\quad -(2\gamma ^4 +24 \gamma ^3 -8\gamma ^2 -25 \gamma -15)s^{10} \\&\quad -2(4\gamma ^4 +17 \gamma ^3+21 \gamma ^2 -78 \gamma -4) s^9 \\&\quad +\gamma (20\gamma ^3 -480 \gamma ^2 +661 \gamma +90)s^8 \\&\quad +\gamma ^2 (167 \gamma ^3 -1271 \gamma ^2 +1543 \gamma +441) s^7 \\&\quad +\gamma ^3 (218 \gamma ^3 -1733 \gamma ^2 +2178 \gamma +1237) s^6 \\&\quad +\gamma ^4 (116 \gamma ^3 -1370 \gamma ^2 +1901 \gamma +2193)s^5 \\&\quad +\gamma ^5 (24 \gamma ^3 -660 \gamma ^2 +1006 \gamma +2553) s^4 \\&\quad -2 \gamma ^6 (100 \gamma ^2 -150 \gamma -977)s^3 \\&\quad -4 \gamma ^7 (8\gamma ^2 -10 \gamma -237) s^2 +264 \gamma ^8 s \\&\quad + 32 \gamma ^9 . \end{aligned}$$

Moreover, $\widetilde{Q}$ satisfies the following properties:

• (i) $\widetilde{Q} (0,\gamma )=32 \gamma ^9 >0$ and $\frac{\partial \widetilde{Q}}{\partial s}>0$ for $\gamma \le 1$ and $s>0$;

• (ii) $\widetilde{Q} (s,1)$ is a degree 11 polynomial in s with positive coefficients for $0<s<\frac{1}{3\cdot 1 -2}$, and $\frac{\partial \widetilde{Q}}{\partial \gamma }>0$ for $0<s<\frac{\gamma }{3\gamma -2}$ and $\gamma \ge 1$. Thus $\widetilde{Q}(s,\gamma )>0$ when either $\gamma \le \frac{2}{3}$ and $0 < s$ or $\frac{2}{3}<\gamma$ and $0< s < \frac{\gamma }{3\gamma -2}$; therefore $\sigma <0$ when $(\beta , \gamma ) \in HB$. This means that the equilibrium point $(x_1 , y_1)$ of system (1.2) is a weak focus (with the multiplicity one); also, it is stable.

Together with Theorem 3.5, the result above implies that $(x_1 , y_1)$ is an unstable focus if $\alpha <\alpha _2$ and $(\beta , \gamma ) \in HB$; $(x_1 , y_1)$ is a stable focus if $\alpha \ge \alpha _2$ and $(\beta , \gamma ) \in HB$. Hence from the theory of Hopf bifurcation [20, 31], a stable limit cycle is bifurcated from the positive equilibrium $(x_1 , y_1)$ when $\alpha$ passes through $\alpha _2$ decreasingly so that system (1.2) undergoes a supercritical Hopf bifurcation. $\square$

We choose $\alpha$ as the main bifurcation parameter. Then, consider system (1.2) with $\alpha =\alpha _2 -\lambda$, $\beta =0.3$ and $\gamma =0.1$, where $\lambda >0$ is a small constant. Here $\alpha _2 =0.378$. Then from the above theorem, we can see that as $\lambda$ increases from zero, a supercritical Hopf bifurcation occurs in the system so that a stable limit cycle is created. The phase portrait and bifurcation diagram are given in Figs. 3b and 4. In Fig. 4b, the black curve y goes to $\infty$ as $\alpha \rightarrow 0^{+}$; therefore, this part is inevitably excluded.

We finally study the Bogdanov–Takens bifurcation in system (1.2). From Theorem 3.7(ii), we already know that $(x_0 , y_0)$ is a codimension-2 cusp, if $\alpha =\alpha _{bt}$, $\beta = \beta _{bt}$ and $\gamma >\frac{2}{3}$. In showing the following theorem, $\alpha$ and $\beta$ are used as the bifurcation parameters.

Theorem 4.3

Assume that $0<|\alpha -\alpha _{bt}| \ll 1$, $0<|\beta -\beta _{bt}| \ll 1$ and $\gamma >\frac{2}{3}$. Then system (1.2) undergoes the Bogdanov–Takens bifurcation.

Proof

For convenience, we start by introducing new parameters $\lambda _1$ and $\lambda _2$, which are as small as necessary. Then, using $\alpha =\alpha _{bt} -\lambda _1$ and $\beta = \beta _{bt} -\lambda _2$ in system (1.2), we have

$$\begin{aligned} \begin{array}{ll} \displaystyle \displaystyle &{} x_t = \displaystyle x(1-x) -(\alpha _{bt}-\lambda _1) \frac{xy^2}{1+xy} ,\\ &{} y_t = \displaystyle (\beta _{bt} -\lambda _2) \frac{xy^2}{1+xy} -\gamma y. \end{array} \end{aligned}$$

(4.2)

As mentioned earlier, when $\lambda _1 =\lambda _2 =0$, (4.2) has a unique positive equilibrium $(x_0 , y_0)$ that is a codimension-2 cusp.

To attain the versal unfolding for system (4.2), we will consecutively perform $C^{\infty }$ transforms of the variables. Hereafter, we denote by $O_k (X,Y, \lambda _1, \lambda _2 )$ the various smooth functions (having coefficients depending on $\lambda _1$ and $\lambda _2$) of the degree k or greater in (X, Y). First, using the substitution $X=x-x_0$ and $Y=y-y_0$, (4.2) becomes

$$\begin{aligned} \displaystyle \displaystyle X_t= & {} \displaystyle a_{00} + a_{10}X+a_{01} Y+a_{20}X^2 \nonumber \\&+\,a_{11}XY +a_{02}Y^2 +O_3 (X,Y,\lambda _1 ),\nonumber \\ Y_t= & {} \displaystyle b_{00} + b_{10}X+b_{01} Y+b_{20}X^2 \nonumber \\&+\,b_{11}XY +b_{02}Y^2 +O_3 (X,Y, \lambda _2 ), \end{aligned}$$

(4.3)

where

$$\begin{aligned} a_{00}&=\frac{3(3\gamma -2)^2}{2(3\gamma -1)}\lambda _1 , \\ a_{10}&=-\frac{\gamma }{3\gamma -1} +\frac{9(3\gamma -2)^2}{4(3\gamma -1)^2}\lambda _1 ,\\ a_{01}&= -\frac{4\gamma }{9(3\gamma -1)(3\gamma -2)}+\frac{3\gamma (3\gamma -2)}{(3\gamma -1)^2}\lambda _1 , \\ a_{20}&=-1 +\frac{3\gamma -2}{2(3\gamma -1)^2} -\frac{27 (3\gamma -2)^3}{8(3\gamma -1)^3}\lambda _1 , \\ a_{11}&= -\frac{4}{9(3\gamma -1)^2 (3\gamma -2)}+ \frac{ 3(3\gamma -2)}{(3\gamma -1)^3}\lambda _1 , \\ a_{02}&= -\frac{8}{81(3\gamma -1)^2 (3\gamma -2)^2} +\frac{ 2}{(3\gamma -1)^3}\lambda _1 , \\ b_{00}&=-\frac{3(3\gamma -2)^2}{2(3\gamma -1)}\lambda _2 , \\ b_{10}&=\frac{9\gamma (3\gamma -2)}{4(3\gamma -1)} -\frac{9(3\gamma -2)^2}{4(3\gamma -1)^2}\lambda _2 ,\\ b_{01}&= \frac{ \gamma }{ 3\gamma -1 } - \frac{3\gamma (3\gamma -2)}{(3\gamma -1)^2}\lambda _2 ,\\ b_{20}&=- \frac{27 \gamma (3\gamma -2)^2}{8(3\gamma -1)^2} +\frac{27 (3\gamma -2)^3}{8(3\gamma -1)^3}\lambda _2 ,\\ b_{11}&= \frac{3\gamma }{ (3\gamma -1)^2 } - \frac{ 3(3\gamma -2)}{(3\gamma -1)^3}\lambda _2 ,\\ b_{02}&= \frac{2\gamma }{3(3\gamma -1)^2 (3\gamma -2)} - \frac{ 2}{3(3\gamma -1)^3}\lambda _2 .\\ \end{aligned}$$

We next carry out the following variable changes in sequence:

$$\begin{aligned} \text{(i) } \ X_1&=X , \ Y_1 =a_{10} X +a_{01} Y ;\\ \text{(ii) } \ X_2&=X_1 -\frac{(a_{11}+b_{02})a_{01} -a_{02}a_{10}}{2a_{01}^2}X_1^2 \nonumber \\&\quad -\frac{a_{02}}{a_{01}^2}X_1 Y_1 , \\ Y_2&=Y_1 +\left( a_{20}-\frac{a_{11}a_{10}}{a_{01}}+\frac{a_{02}a_{10}^2}{a_{01}^2} \right) X_1^2 \\ {}&-\left( \frac{a_{02}a_{10}}{a_{01}^2}+\frac{b_{02}}{a_{01}} \right) X_1 Y_1 ;\end{aligned}$$

$$\begin{aligned} \text{(iii) } \ X_3&=X_2 -\left[ \frac{a_{02}}{a_{01}^2} \left\{ a_{00} \left( \frac{a_{11}}{a_{01}}-\frac{3a_{02}a_{10}}{a_{01}^2}\right) \right. \right. \\ {}&\left. \left. -\frac{a_{02}a_{01}b_{00}}{a_{01}^2}-a_{10}-b_{01} \right\} \right] \frac{X_2^2}{2}, \\ Y_3&=Y_2 +\left[ -a_{00} \left( \frac{a_{11}+b_{02}}{a_{01}}-\frac{a_{02} a_{10}}{a_{01}^2} \right) ^2 \right. \\&\left. -\frac{a_{02}}{a_{01}^2} \left\{ 2 a_{00} \left( \frac{a_{11}a_{10}}{a_{01}}-\frac{a_{20} a_{01}^2+a_{02} a_{10}^2}{a_{01}^2} \right) \right. \right. \\&+\,(a_{10} a_{00} +a_{01} b_{00} )\left( \frac{a_{11}+b_{02}}{a_{01}}-\frac{a_{02}a_{10}}{a_{01}^2} \right) \\&\left. \left. +\,2(a_{01} b_{10}-b_{01}a_{10})\right\} \right] \frac{X_2^2}{2}. \end{aligned}$$

Then (4.3) becomes

$$\begin{aligned} \displaystyle \displaystyle {X_3}_t= & {} \displaystyle a_0 +a_1 X_3 +a_2 Y_3 +O_3 (X_3 , Y_3 , \lambda _1 , \lambda _2 ) ,\nonumber \\ \displaystyle {Y_3}_t= & {} \displaystyle b_0 +b_1 X_3 +b_2 Y_3 +b_3 X_3^2 +b_4 X_3 Y_3 \nonumber \\&+O_3 (X_3 , Y_3 , \lambda _1 , \lambda _2), \end{aligned}$$

(4.4)

where

$$\begin{aligned} a_0&=\frac{3(3\gamma -2)^2}{2(3\gamma -1)}\lambda _1 , \\ a_1&=\frac{3 (3\gamma -2)^3}{4\gamma (3\gamma -1)^2}\lambda _1 +\frac{3\gamma -2}{3\gamma (3\gamma -1)^2}\lambda _2 \nonumber \\&\quad +O_2 (\lambda _1, \lambda _2),\\ a_2&= 1+\frac{3 (3\gamma -2)^3}{4\gamma ^2 (3\gamma -1)}\lambda _1 +O_2 (\lambda _1, \lambda _2),\\ b_0&=-\frac{3\gamma (3\gamma -2)^2}{2 (3\gamma -1)^2}\lambda _1 +\frac{2\gamma (3\gamma -2)}{3 (3\gamma -1)^2}\lambda _2 \\ {}&\quad +O_2 (\lambda _1, \lambda _2),\\ b_1&=-\frac{3(21 \gamma -11)(3\gamma -2)^2}{4(3\gamma -1)^2}\lambda _1 -\frac{3\gamma -2}{3(3\gamma -1)}\lambda _2 \\ {}&\quad +O_2 (\lambda _1 , s\lambda _2),\\ b_2&=\frac{3 (6\gamma -1)(3\gamma -2)^2}{4 \gamma (3\gamma -1)^2}\lambda _1-\frac{3\gamma (3\gamma -2)}{(3\gamma -1)^2} \lambda _2 \\ {}&\quad +O_2 (\lambda _1 , \lambda _2),\\ b_3&=\frac{3\gamma }{2(3\gamma -1)}\\ {}&\quad -\,\frac{3(54\gamma ^3 -27 \gamma ^2 -24 \gamma +13)(3\gamma -2)^2}{16 \gamma (3\gamma -1)^3}\lambda _1 \\&\quad -\,\frac{(108\gamma ^3 -27 \gamma ^2 +24 \gamma -13)(3\gamma -2)}{12 \gamma (3\gamma -1)^3}\lambda _2 \\ {}&\quad +O_2 (\lambda _1 , \lambda _2),\\ b_4&= -\frac{6(2\gamma -1)}{3\gamma -1}-\frac{3 (27\gamma ^2 -1)(3\gamma -2)^2}{4 \gamma ^2 (3\gamma -1)^2}\lambda _1 \\ {}&\quad +\frac{3\gamma -2}{6\gamma ^2 (3\gamma -1)}\lambda _2 +O_2 (\lambda _1 , \lambda _2 ). \end{aligned}$$

Let $u=X_3$ and $v=a_0 +a_1 X_3 +a_2 Y_3 +O_3 (X_3 , Y_3 , \lambda _1 , \lambda _2)$. Then system (4.4) becomes

$$\begin{aligned} \displaystyle {u}_t= & {} \displaystyle v ,\\ \displaystyle {v}_t= & {} \displaystyle c_0 +c_1 u +c_2 v + c_3 u^2 + c_4 u v \\&+O_3 (u,v , \lambda _1 , \lambda _2), \end{aligned}$$

where

$$\begin{aligned} c_0&= a_2 b_0 -a_0 b_2 =- \frac{3 \gamma (3\gamma -2)^2}{2(3\gamma -1)^2 }\lambda _1 +\frac{2 \gamma (3\gamma -2)}{3(3\gamma -1)^2} \lambda _2 \\ {}&\quad +O_2 (\lambda _1 , \lambda _2),\\ c_1&=a_2 b_1 -a_1 b_2 -a_0 b_4 =\frac{3 \gamma (3\gamma -2)^2}{4(3\gamma -1) }\lambda _1 \\ {}&\quad +\frac{ 3\gamma -2}{3(3\gamma -1)^2} \lambda _2 +O_2 (\lambda _1 , \lambda _2),\\ c_2&=a_1 +b_2 =\frac{9 (3\gamma -2)^2}{4 \gamma (3\gamma -1) }\lambda _1 - \frac{ (3\gamma +1)(3\gamma -2)}{3\gamma (3\gamma -1)} \lambda _2 \\ {}&\quad +O_2 (\lambda _1 , \lambda _2),\\ c_3&= a_2 b_3 -a_1 b_4 =\frac{3\gamma }{2(3\gamma -1)}+O_1 (\lambda _1 , \lambda _2),\\ c_4&=b_4 =-\frac{6(2\gamma -1)}{3\gamma -1}+O_1 (\lambda _1 , \lambda _2). \end{aligned}$$

Note that $c_3 >0$ for small $\lambda _1$ and $\lambda _2$; therefore, we can introduce new variables:

$$\begin{aligned} w=u,\ z=\frac{v}{\sqrt{c_3}},\ \tau =\sqrt{c_3}t. \end{aligned}$$

Then, we obtain

$$\begin{aligned} \displaystyle {w}_{\tau }= & {} \displaystyle z ,\nonumber \\ \displaystyle {z}_{\tau }= & {} \displaystyle \frac{c_0}{c_3} +\frac{c_1}{c_3} w + \frac{c_2}{\sqrt{c_3}} z + w^2 + \frac{c_4}{\sqrt{c_3}} w z \nonumber \\&+O_3 (w,z , \lambda _1 , \lambda _2). \end{aligned}$$

(4.5)

To complete our assertion, we follow the steps similar to those in [7, 17, 18]. Substituting $x=w+\frac{c_1}{2c_3}$ and $y=z$ into system (4.5), and renaming $\tau$ as t, we have

$$\begin{aligned} \displaystyle {x}_{t}= & {} \displaystyle y ,\\ \displaystyle {y}_{t}= & {} \displaystyle \left( \frac{c_0}{c_3}-\frac{c_1^2}{4c_3^2} \right) +\left( \frac{c_2}{\sqrt{c_3}}-\frac{c_1 c_4}{2 c_3 \sqrt{c_3}} \right) y +x^2 \\&+\frac{c_4}{\sqrt{c_3}} xy +O_3 (x,y , \lambda _1 , \lambda _2). \end{aligned}$$

Note that $c_4 <0$ when $\lambda _1$ and $\lambda _2$ are small. We denote

$$\begin{aligned} \eta _1 =\frac{c_4^2}{c_3} x , \ \eta _2 =-\frac{c_4^3}{c_3 \sqrt{c_3}} y, \ \tau =-\frac{\sqrt{c_3}}{c_4} t, \end{aligned}$$

and rename $\tau$ by t again (for simplicity). This allow us to have the final versal unfolding of system (4.2):

$$\begin{aligned} \displaystyle {\eta _1 }_{t}= & {} \displaystyle \eta _2 ,\\ \displaystyle {\eta _2 }_{t}= & {} \displaystyle \mu _1 (\lambda _1 , \lambda _2) +\mu _2 (\lambda _1 , \lambda _2) \eta _2 +\eta _1^2 -\eta _1 \eta _2 \\&+O_3 (\eta _1 ,\eta _2 , \lambda _1 , \lambda _2), \end{aligned}$$

where (expanding $\mu _i$ in a power series of $(\lambda _1 , \lambda _2)$ up to the second order)

$$\begin{aligned} \mu _1 (\lambda _1 ,\lambda _2)&:=\left( \frac{c_0}{c_3}-\frac{c_1^2}{4c_3^2} \right) \frac{c_4^4}{c_3^2} =-\frac{576(2\gamma -1)^4 (3\gamma -2)^2}{(3\gamma -1)^3 \gamma ^2} \lambda _1 +\frac{256 (2 \gamma -1)^4 (3\gamma -2)}{(3\gamma -1)^3 \gamma ^2} \lambda _2 \\&\qquad -\frac{36 (3 \gamma -2)^4 (2\gamma -1)^3 (702 \gamma ^4-1593 \gamma ^3 +2187 \gamma ^2 -1103 \gamma +183)}{(3\gamma -1)^5 \gamma ^4}\lambda _1^2 \\&\qquad -\frac{32 (3 \gamma -2)^3 (2\gamma -1)^3 (270 \gamma ^4 +459 \gamma ^3 -1323 \gamma ^2 +755\gamma -133)}{(3\gamma -1)^5 \gamma ^4} \lambda _1 \lambda _2 \\&\qquad +\frac{64 (3 \gamma -2)^2 (2\gamma -1)^3 (1242 \gamma ^4 -891 \gamma ^3 -207\gamma ^2 +311\gamma -71)}{9 (3\gamma -1)^5 \gamma ^4} \lambda _2^2+O_3 (\lambda _1 , \lambda _2) , \end{aligned}$$

$$\begin{aligned} \mu _2 (\lambda _1 , \lambda _2)&:=\left( \frac{c_1 c_4}{2c_3}-c_2 \right) \frac{c_4}{c_3} = \frac{3 (3\gamma -2)^2 (4 \gamma +1) (2 \gamma -1)}{(3\gamma -1) \gamma ^2} \lambda _1 -\frac{4 (3 \gamma -2) (7\gamma -1) (2\gamma -1)}{3(3\gamma -1) \gamma ^2} \lambda _2 \\&\qquad +\,\frac{3 (3\gamma -2)^4 (864 \gamma ^5-1548\gamma ^4+1467\gamma ^3+22\gamma ^2-461\gamma +120) }{8(3\gamma -1)^3 \gamma ^4}\lambda _1^2 \\&\qquad +\,\frac{(3\gamma -2)^3 (1080\gamma ^5 +5418 \gamma ^4 -12342 \gamma ^3 +8321 \gamma ^2 -2280 \gamma +215) }{12 (3\gamma -1)^3 \gamma ^4} \lambda _1 \lambda _2 \\&\qquad - \frac{(11\gamma -3) (3 \gamma -2)^2 (432 \gamma ^4 -324 \gamma ^3-51 \gamma ^2 +98\gamma -23)}{27(3 \gamma -1)^3 \gamma ^4} \lambda _2^2 +\,O_3 (\lambda _1 , \lambda _2) . \end{aligned}$$

After some computations, we obtain

$$\begin{aligned}&\left| \frac{\partial (\mu _1 , \mu _2 )}{\partial (\lambda _1 ,\lambda _2)}\right| _{(\lambda _1 , \lambda _2 )=(0,0)} \\&\quad = \frac{768 (3\gamma -2)^4 (2\gamma -1)^5 }{\gamma ^4 (3\gamma -1)^4}>0, \end{aligned}$$

because $\gamma >\frac{2}{3}$. Thus, the above transformation from $(\lambda _1 , \lambda _2)$ to $(\mu _1 , \mu _2)$ is nonsingular for small $\lambda _1$ and $\lambda _2$. Therefore, from theorems of Bogdanov and Takens [18, 20], the proof is complete. $\square$

From the above proof, we see that in system (1.2), a stable limit cycle is generated for some parameter values $(\alpha , \beta , \gamma )$ and a stable homoclinic loop is generated for other values as well.

Remark 4.4

When $|\lambda _1|$ and $|\lambda _2|$ are small, we define the curves in the $(\lambda _1 , \lambda _2 )$-plane as

$$\begin{aligned} SN&=\left\{ (\lambda _1 , \lambda _2 ) : \mu _1 (\lambda _1 , \lambda _2 )=0, \ \mu _2 (\lambda _1 , \lambda _2 ) \ne 0 \right\} ,\\ H&=\left\{ (\lambda _1 , \lambda _2 ) : \mu _2 (\lambda _1 , \lambda _2 )\right. \\&\quad = \left. -\sqrt{ -\mu _1 (\lambda _1 , \lambda _2 )}, \ \mu _1 (\lambda _1 , \lambda _2 )<0 \right\} ,\\ HL&=\left\{ (\lambda _1 , \lambda _2 ) : \mu _2 (\lambda _1 , \lambda _2 )\right. \\&\quad =\left. -\frac{5}{7}\sqrt{ -\mu _1 (\lambda _1 , \lambda _2 )}, \ \mu _1 (\lambda _1 , \lambda _2 )<0 \right\} . \end{aligned}$$

When $\gamma >\frac{2}{3}$, the above curves in the $(\lambda _1 , \lambda _2 )$-plane can be rewritten as the curves in the $(\alpha , \beta )$-plane by $\alpha =\alpha _{bt} -\lambda _1$ and $\beta =\beta _{bt} -\lambda _2$. For convenience, we still use the same notations for the rewritten curves. Then, according to [18, 20], we see from the Bogdanov–Takens bifurcation above that there is a neighborhood of $(\alpha _{bt}, \beta _{bt})$ such that system (1.2) undergoes a saddle-node bifurcation near $(x_0 , y_0)$ as $(\alpha , \beta )$ crossing SN; the system undergoes a Hopf bifurcation near $(x_0 , y_0)$ as $(\alpha , \beta )$ crossing H and a homoclinic bifurcation near $(x_0 , y_0)$ as $(\alpha , \beta )$ crossing HL. Moreover, the occurrence of the stable homoclinic loop in system (1.2) can be understood as follows. There is a bounded (x, y)-region where the densities of both the predator and prey species are controlled (for the coexistence).

For example, we consider system (4.2) with $\alpha _{bt} =0.01362$, $\beta _{bt}=4.98983$ and $\gamma =4.6$. From the theorem and remark above, we see that in the $(\lambda _1 , \lambda _2)$-plane, the small neighborhood of (0, 0) is divided into several regions by the three bifurcation curves. The bifurcation diagram is given in Fig. 5.

Fig. 5

The Bogdanov–Takens bifurcation diagram

The corresponding phase portraits are given in Fig. 6.

• (a) At $(\lambda _1 , \lambda _2 )=(0,0)$, the unique positive equilibrium $(x_0, y_0)$ of (4.2) is a cusp of codimension 2. This phase portrait is not similar to the one in Fig. 3a, in that there is no separatrix to the left of the point $(x_0, y_0)$.

• (b) System (4.2) with $(\lambda _1 , \lambda _2 ) \in I$ does not have any positive equilibria. All solutions go to the axial equilibrium (1, 0).

• (c) When $(\lambda _1 , \lambda _2 )$ moves from the region I into II, there exists a stable focus positive equilibrium and a saddle positive equilibrium. The bistability is observed because (1, 0) is always stable.

• (d) When $(\lambda _1 , \lambda _2 )$ moves from the region II into III, (4.2) undergoes supercritical Hopf bifurcation and a stable limit cycle is created. At this time, $(x_1 , y_1 )$ is an unstable focus.

• (e) When $(\lambda _1 , \lambda _2 )$ on HL, the homoclinic bifurcation creates a stable homoclinic cycle.

• (f) When $(\lambda _1 , \lambda _2 )$ crosses HL into the region IV, there exist two positive equilibria, which are an unstable focus and a saddle.

Fig. 6

Phase portraits of system (4.2) with $\alpha _{bt} =0.01362$, $\beta _{bt}=4.98983$ and $\gamma =4.6$. a $(\lambda _1, \lambda _2)=(0,0)$. b $(\lambda _1, \lambda _2)=(0.01,0.281)$ in region I. c $(\lambda _1, \lambda _2)=(0.01, 0.2725)$ in region II. d $(\lambda _1, \lambda _2)=(0.01, 0.27)$ in region III. e $(\lambda _1, \lambda _2)=(0.01, 0.26541)$ on curve HL. f $(\lambda _1, \lambda _2)=(0.01, 0.265)$ in region IV

5 Discussion

In this paper, we presented a qualitative study on a predator–prey model with the newly proposed functional response in [9]. In deriving this type of functional response, the influence of the spatial grouping of predators on the encounter rate between the predators and the prey was considered to explain a situation of hunting cooperation in which a group of predators searches (in line formation), contacts and then hunts a school or herd of prey. We studied the existence of all positive equilibria, local stability at the equilibria and the occurrence of bifurcations, in system (1.2). To this end, we chose the consumption rate $\alpha$ by predators as the main parameter. The details are as follows.

We showed that the predators’ population go extinct (i.e., the global stability of the axial equilibrium (1, 0)) if the consumption rate by a predator is greater than the critical value. Ecologically, we may understand this situation as follows. The large consumption rate by the predators reduces the density of the prey so much that the predators are unable to search any prey and eventually become extinct. By a thorough stability analysis of all the equilibria of system (1.2), we observed the bistability of the system around its two equilibrium points (1, 0) and $(x_1 ,y_1)$ depending on the initial conditions of the system. The local stability of (1, 0) comes from the strong Allee effect in predators because predators can go to extinction for low initial predator densities. Moreover, in system (1.2), we observed various kinds of bifurcation phenomena. The stability analysis of the equilibria of the system presents a complete analysis of the local bifurcation behavior, such as the saddle-node, Hopf and Bogdanov–Takens. Moreover, to determine the type of Hopf bifurcation undergone by the system, we computed the first Lyapunov coefficient. As a result, we found that only a stable limit cycle was created. This gives that the predator and prey coexist with an oscillatory behavior. The limit cycle disappeared due to the homoclinic bifurcation. The occurrence of a homoclinic loop indicates that there is a (x, y)-region that the predator and prey densities can be controlled.

The functional response in [9] derived by considering the grouping (i.e., the cooperation) effect has the monotonically increasing property in both the predator and prey populations; this response gives a strong Allee effect in predators, which allows system (1.2) to have interesting and rich dynamics as predator–prey systems with a harvesting rate or a nonmonotonic functional response.