Modeling and analysis of the fractional-order epidemic model to investigate mutual influence in HIV/HCV co-infection

Abstract

Based on the Caputo fractional-order derivative, this work investigates the dynamics of a newly developed co-infection model of Human immunodeficiency virus (HIV) and Hepatitis C virus (HCV). Due to their ability to take into account memory history and heritability, Caputo fractional-order derivatives are a natural candidate to study the HIV/HCV co-infection where these two properties are critical to study how infections spread. Furthermore, applying the Caputo fractional-derivative to the co-infection model helps forecast disease progression and offers optimal treatment strategies for understanding complex HIV/HCV interactions and co-evolutionary dynamics. Mathematical analysis of the co-infection model reveals two equilibria, one without sickness and the other with sickness. The next-generation matrix approach is employed to calculate the basic reproduction number for the cases of HIV and HCV only respectively, and the co-infection model of HIV and HCV, jointly that demonstrates the mutual influence of the two diseases. Using the reproduction numbers, the Lyapunov functional method, and the Routh-Hurwitz criterion, we establish the global dynamics of the model. To validate theoretical predictions, the fractional Adams Method (FAM), a popular numerical technique with a predictor-corrector structure, is utilized to compute the model’s numerical solutions. Finally, numerical simulations confirm the theoretical findings, elucidating the high degree of agreement between the theoretical analysis and the numerical results. Different from the existing literature using the L1 scheme, we incorporated a memory trace (MT) procedure in our paper that captures and amalgamates the historical dynamics of the system to evoke the memory effect in detail. One of the novel results obtained from this study is that the memory trace starts to come into existence once fractional power $\zeta$ starts to increase from 0 to 1 and completely disappears when $\zeta$ becomes 1. Upon increasing the fractional-order $\zeta$ from 0, the memory effect exploits a nonlinear proliferation starting from zero. This observed memory effect emphasizes the difference between the integer and non-integer order derivatives and thus claims the existence of memory effects of fractional-order derivatives. The findings of the paper will contribute to a better understanding of the disease outbreak, as well as aid in the development of future predictions and control strategies.

1 Introduction

Hepatitis virus infections are a public health issue affecting millions of people, causing death, disability, and considerable expenditure [1]. Hepatitis that causes liver inflammation may be self-limited or progress to fibrosis (scarring), cirrhosis, or hepatocellular carcinoma. Hepatitis virus is the most prevalent source of hepatitis in the world, however other infections, toxic substances (such as alcohol, and certain drugs), and autoimmune diseases can also cause hepatitis. Its morbidity and mortality increase in case of Human immunodeficiency virus (HIV) co-infection. There are five major hepatitis viruses, called A, B, C, D, and E [2, 3]. These five types are of the most concern because of the burden of illness and death they cause as well as being a leading driver for the likelihood of outbreaks and epidemic spread. It is estimated that there are 2 billion people worldwide who have evidence of previous or current HBV infection [4].

Hepatitis B (known as HBV) and C (HCV) infections are the most common causes of liver disease, and they lead to more than 380,000 cancer-related deaths in China each year [5, 6]. There are 87 million in China, who are chronic hepatitis B virus carriers accounting for about one-third of the world’s chronic carriers of hepatitis B virus. It is estimated that about 7.6 million people are living with chronic hepatitis C virus in China [7]. Chronic infection with hepatitis B virus (HBV) or hepatitis C virus (HCV) can cause severe public health problems because of their high prevalence and poor long-term clinical outcomes in many parts of the world, including cirrhosis, premature death from hepatic decompensation, and liver cancer. This is especially true in China, where the prevalence of HBV and HCV infection is quite high. People can get the hepatitis B virus through infected blood, perinatal infection, or sexual contact [8].

The complex serological and natural history associated with HBV infection poses challenges in assessing the prevalence of HBV and providing comparable global estimates. This is due to the availability of multiple hepatitis B laboratory markers for the infection. Hepatitis B viral surface antigen (HBsAg) is the primary clinical marker suggestive of acute or chronic infection, and the prevalence and endemism of HBV infection is defined by the presence of HBsAg [9]. About 240 million are chronic carriers of HBsAg worldwide, with a prevalence that varies according to geographical areas ranging from less than 2 percent in regions with low endemicity to more than 8 percent in highly endemic areas, particularly in developing countries of sub-Saharan Africa and South-East Asia [10].

Fractional calculus includes derivatives of non-local and non-integer order, which greatly complicates analytical solutions to fractional-order differential equations (FODE) problems and hence limits their applicability [11]. Numerous studies have demonstrated that fractional-order derivatives provide the most accurate and reliable models for real-life problems including many contagious diseases such as tuberculosis (TB) disease [12], Dengue flu [13, 14], HIV [15], COVID-19 [16, 17]. In a study by Khan et al., [18], the influence of convex incidence rate and various control measures on the transmission dynamics of HBV disease was investigated using a fractional-order epidemic model in the Caputo-type sense. Also, the sensitivity analysis was performed to verify the impact of various parameters on the dynamic behavior of the system. Fractional calculus includes derivatives of non-local and non-integer order, which greatly complicates analytical solutions to fractional-order differential equation problems and hence limits their applicability [19, 20]. Fractional calculus offers the advantage of non-locality and memory effects, meaning that the state of the system depends not only on time and position but also on its previous states. The Caputo type fractional derivative operator is particularly useful as it includes initial boundary conditions, unlike other types of fractional-order derivatives, such as the Riemann-Liouville operator [21].

The memory effects refer to the phenomenon in fractional calculus where a system’s response or behavior at a given point in time is influenced by both its previous and present inputs, with the influence gradually decreasing but never quite disappearing. Non-integer order derivatives and integrals are taken into consideration in fractional calculus. Because these non-integer orders account for prior data or previous system states, they introduce memory effects [22]. Fractional-order derivatives and integrals take into account the complete history of the input signal, in contrast to integer-order derivatives and integrals, which only take into account the instantaneous effect. This behavior can be described as memory-like, in which the system’s response at any given time is dependent upon the information received in the past [23, 24].

When analytical solutions become unattainable, this adaptability becomes very valuable. The development of increasingly sophisticated computer tools and algorithms has made it possible to obtain accurate and trustworthy outcomes. Researchers can get insight into the behavior of the temporal dynamics of FODE systems by simulating and analyzing these systems with these methods [25]. Due to the occurrence of non-local and non-integer-order derivatives, numerical instability is a common feature of FODE systems. Stability and the prevention of error Propagation can be designed into numerical methods. When simulating FODE systems, it is possible to preserve stability and accuracy by employing various numerical techniques, such as implicit schemes and stabilizing algorithms. Results from FODE systems can be verified using experimental data with numerical techniques, which allow for experimental validation. The system’s complexity often makes it so that direct experimental measurements are either unavailable or impractical.

The mathematical models help compare various infection control treatments and promote a deeper knowledge of their epidemiology. For decades, scholars have conducted extensive research based on the classical as well as fractional-order cases [26,27,28]. Recently, Tang et al. [29] conducted an epidemiological mathematical study aiming to incorporate the intricate phenomena of the immune system into chronic myelogenous leukemia in the frame of fractional calculus. Their approach utilized a Matlab-based model with numerical simulations to explore the dynamical patterns of chronic myelogenous leukemia to inform policymakers and health authorities about the systems essential for control and treatment. Mathematical modeling and simulation do not find application only in the field of mathematical epidemiology such as disease modeling [30, 31], but are widely used to derive dynamic process models in the other fields of Science and Technology [32,33,34,35,36,37].

Researchers continuously work in the field of fractional-order modeling of disease dynamics [38]. Naik and co-workers [39] studied the chaotic behavior of a fractional-order HIV-1 model incorporating AIDS-related cancer cells. They visualized the impact of memory on disease transmission and the effect of various biological parameters including the fractional power of the derivative with the help of numerical simulations. Qureshi and Jan [40] investigated a new epidemiological measles model in integer- and fractional-order derivatives along with their comparison. The sensitivity of the biological parameters involved in the model was carried out in their study to observe the impact of these parameters on disease transmission. They suggested that the memory of the fractional derivative plays a significant role in the transmission process.

Recently, the COVID-19 and tuberculosis (TB) co-infection model was studied by Joshi and Yavuz [41] in the frame of fractional calculus. They discussed the local and global stability of the COVID-19 and tuberculosis (TB) sub-models separately. They obtained the conditions that guarantee the local asymptotic stability of the equilibria of their co-infection model. Through their results, they provided the impact of COVID-19 on TB and TB on COVID-19. Although researchers studied many fractional-order epidemic disease models there is still a need to develop or modify these models for a better understanding of the transmission dynamic process of various infectious diseases.

Despite existing treatment and control measures, HIV and HCV continue to challenge healthcare systems, especially in developing nations [42,43,44]. This paper introduces a fractional-order epidemic model to elucidate the dynamic behavior of the HIV-HCV co-infection model. This research marks a pioneering contribution to the field of infectious disease modeling, particularly in the specific context of HIV and HCV infections causing challenges for the scientists and healthcare system for their control. What sets this study apart is its groundbreaking application of a fractional-order model, a sophisticated mathematical framework that delves into the nuanced intricacies of infection dynamics. By incorporating varying $\zeta$ values, we not only enhance the model’s adaptability but also emphasize the crucial role of fractional calculus principles in providing a more accurate representation of infectious disease dynamics. The introduction of fractional calculus adds a layer of complexity that aligns more closely with the intricate and often non-linear nature of biological systems. Unlike traditional integer-order models, fractional-order models capture subtle temporal dependencies and fractional differentiation, offering a refined tool for exploring the dynamic behaviors of infections and treatment responses. This choice in methodology reflects a commitment to capturing the real-world complexity of pathogen-host interactions, making this research a pivotal step towards a more biologically faithful representation of infectious diseases. In essence, the novel combination of fractional calculus, real-world applications, and meticulous simulations positions this research as a trailblazer in infectious disease modeling. By offering a more profound biological understanding of HIV-HCV co-infection, our findings underscore the importance of considering the fractional nature of infectious disease dynamics, propelling the scientific community toward more nuanced and effective approaches in combating emerging infectious threats.

In view of the above discussion, a non-linear system of differential equations is constructed to examine the co-infection model of HIV and HCV in this article. The assumptions concerning the HCV and HIV co-infection model are as follows: sexual activities are responsible for transmission, involving sexually active individuals aged 16 or older. It is assumed that simultaneous transmission of HIV and HCV is not possible. The reinfection of acute HCV-cleared individuals is possible because past infection does not stipulate immunity. People with advanced HCV or full-blown AIDS are unable to be involved in sexual activities, thereby reducing the transmission of HIV and advanced HCV. Our model differs from other studies in the literature in that it addresses the relationship between HIV and HCV infections along with stability analysis and is created with fractional-order differential equations (FODE). Additionally, in our proposed FODE model we have included memory traces (MT), unlike studies in the literature [45,46,47,48]. Besides we obtained the convergence of the applied numerical technique as there are very few studies in the literature that did it before.

Fig. 1

Compartmental HIV-HCV co-infection model

The remaining body of the paper is designed as follows: after the introduction in Sect. 1, Sect. 2 gives some basics that we required for the modeling purposes. Section 3, provides the memory-dependent model formulation. Section 4 studies the equilibrium points and their stability results. Also in this section, the threshold quantity is calculated through the next-generation matrix method. Further, this section details the local and global dynamics of the obtained equilibria. Section 5 discusses the numerical scheme for the solution of the proposed fractional-order co-infection system along with its convergence analysis. In Sect. 6, we provided the effect of memory traces (MT) of the factional-order derivatives on the dynamic process. Section 7 gives the numerical results and a detailed discussion of these results. In Sect. 8, a summary in terms of the conclusion of the study is provided. Finally, some potential future directions are discussed in Sect. 9.

2 Preliminaries

Definition 1

Suppose $\zeta > 0$ and $\eta (t) \in L^{1}([0,a],R)$ where $[0,a] \subset R_{+}$. Then fractional integral of order $\zeta$ for a function $\eta (t)$ in the sense of Riemann-Liouville is defined as [49,50,51]

$$\begin{aligned} I_{0^{+}}^{\zeta } \eta (t) = \frac{1}{{\Gamma }(\zeta )} {\int }_{0}^{t} (t-{\tau })^{\zeta -1} \eta (\tau ) d\tau , \ \ t>0, \end{aligned}$$

(1)

where ${\Gamma }(*)$ is the classical gamma function defined by

$$\begin{aligned} {\Gamma }(v) = {\int }_{0}^{\infty } {\tau }^{v-1} e^{-\tau } d\tau . \end{aligned}$$

(2)

Definition 2

Let $n-1< \zeta < n, n \in N$, and $\eta (t) \in C^{n}[0,a]$. The Caputo fractional derivative of order $\zeta$ for a function $\eta (t)$ is defined as [49,50,51],

$$\begin{aligned} {}^C_0 {\Omega }^{\zeta }_t \eta (t) = \frac{1}{\Gamma (n-\zeta )} {\int }_{0}^{t} (t-{\tau })^{\zeta -1} \eta (\tau ) d\tau , \ \ t>0. \end{aligned}$$

(3)

Lemma 1

Let $Re(\zeta ) > 0, n= [Re(\zeta )] + 1$ and $\eta (t) \in AC^{n} (0,a)$. Then [49,50,51]

$$\begin{aligned} ({J^v_{0^{+^c}}{\Omega }^{\zeta }_t}\eta )(t) = \eta (t) - \mathop {\sum }\limits _{j=1^m} \frac{(\omega ^j_{0^+}\eta )(0^{+})}{j!}t^{j}. \end{aligned}$$

(4)

In particular, if $0 < \zeta \le 1$, then

$$\begin{aligned} (J^{\zeta }_{0^{+}}{\Omega }^{\zeta }_t \eta )(t) = \eta (t)-\eta _{0}. \end{aligned}$$

(5)

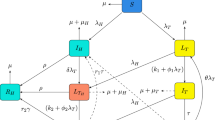
The transmission of HIV-HCV co-infection in various compartments is presented in the following Fig 1.

The mathematical model for HIV-HCV co-infection is derived using the notations provided in Table 1.

Table 1 Parametric values and notations used in the HIV-HCV co-infection model

3 HIV-HCV mathematical model formulation

In this model, a constant recruitment rate B is considered for individuals entering the susceptible class S(t), while a constant natural mortality rate $\mu$ for every compartment. The average number of sexual partners per year (k), the likelihood of HIV transmission during each sexual interaction, and the percentage of people who are HIV-positive all affect the infection rate of $\beta _h$ per capita. Similar to this, those who are vulnerable contract HCV at a per capita rate of $\beta _c$, where $\gamma _2$ denotes the likelihood of HCV transmission during each sexual encounter. Therefore, (6) and (7) respectively represent the forces of infection linked to HIV and HCV infections:

$$\begin{aligned} {{\beta _h}}=\frac{k{{\gamma }_{1}}({{I}_{HIV}}+{{\text {k}}_{1}}({{I}_{HA}}+{{I}_{HL}})}{N}, \end{aligned}$$

(6)

and

$$\begin{aligned} {{\beta }_{c}}=\frac{k{{\gamma }_{2}}({{\text {A}}_{HCV}}+{{L}_{HCV}}+ {{\text {k}}_{2}}({{I}_{HA}}+{{I}_{HL}})}{N}. \end{aligned}$$

(7)

The risk of infection for both viruses rises when HIV and HCV are present in the same person. The parameter $k_2 > 1$ denotes the increased risk of contracting HCV by a person co-infected with HIV and HCV, while the improvement factor $k_1 > 1$ denotes the increased risk of contracting HIV by a dually infected individual. Co-infected people are more likely to become infected with HIV and HCV than people with only one virus, which increases the risk of spreading both infections. Additionally, co-infected individuals tend to be more infectious than those with a single infection.

Once susceptible individuals become infected with HIV, they enter the $I_{HIV}$ class, representing individuals infected with HIV only. Individuals in the $I_{HIV}$ class progress to the AIDS class at a rate of $\eta$. Similarly, once susceptible individuals become infected with HCV, they enter the $A_{HCV}$ class, which consists of individuals with acute HCV infection. While some members of the $A_{HCV}$ class spontaneously recover from acute HCV infection at a rate of $c_r$, others move on to develop latent HCV at a rate of $c_1$. HIV-positive people are more likely to contract HCV than HIV-negative people, making them more susceptible to the disease. HIV compromises the immune system, leaving the body susceptible to other diseases and infections. In addition, those with HIV are more likely to contract HCV than those without HIV because the two diseases are spread similarly. Propagation parameters have been added for people who have already contracted HIV or HCV, respectively, to account for this elevated risk, as detailed below:

When individuals in the $I_{HIV}$ and $A_{HCV}$ classes engage in sexual contact, they are likely to become dually infected with both HIV and acute HCV. Individuals infected with HIV only (not yet in the AIDS class) become infected with acute HCV at a rate of $h_2\beta _c$, entering the class of individuals co-infected with HIV and acute HCV, denoted as $I_{HA}$. Conversely, individuals infected with acute HCV become co-infected with HIV at a rate of $c_2\beta _h$. Similarly, when individuals in the latent HCV class $L_{HCV}$ and the infected HIV class $I_{HIV}$ engage in sexual encounters, individuals in the latent HCV class are projected to become co-infected with HIV at a rate of $c_3\beta _h$, entering the class of individuals dually infected with HIV and latent HCV, denoted as $I_{HCL}$.

The nonlinear dynamical system of the HIV-HCV co-infection model is formulated with the system of ordinary differential equations under the parameter details discussed in the introduction section above. Therefore, we get the classical co-infection model of HIV-HCV epidemics as [53,54,55,56,57,58]

$$\begin{aligned} \left\{ \begin{array}{lll} \frac{\textrm{d}S}{\textrm{d}t} &{}=&{} B-{{\beta _h}}S-{{\beta _c}}S+{{c_r}}{A_{HCV}}-\mu S, \\ \frac{\textrm{d}{{I}_{HIV}}}{\textrm{d}t} &{}=&{} {{\beta }_{h}}S+{{c}_{r}}\varepsilon {{I}_{HA}}-{{h}_{2}}{{\beta }_{c}}{{I}_{HIV}}-{{h}_{1}}{{I}_{HIV}}\\ &{}&{} \quad -\mu {{I}_{HIV}}, \\ \frac{\textrm{d}{{A}_{HIV}}}{\textrm{d}t} &{}=&{} {{h}_{1}}{{I}_{HIV}}-\mu {{A}_{HIV}}, \\ \frac{\textrm{d}{{A}_{HCV}}}{\textrm{d}t} &{}=&{} {{\beta }_{c}}S-{{c}_{r}}{{A}_{HCV}}-{{c}_{2}}{{\beta }_{h}}{{A}_{HCV}}-{{c}_{1}}{{A}_{HCV}}\\ &{}&{}-\mu {{A}_{HCV}}, \\ \frac{\textrm{d}{{L}_{HCV}}}{\textrm{d}t} &{}=&{} {{c}_{1}}{{A}_{HCV}}-{{c}_{3}}{{\beta }_{h}}{{L}_{HCV}}-\mu {{L}_{HCV}}, \\ \frac{\textrm{d}{{I}_{HA}}}{\textrm{d}t} &{}=&{} {{h}_{2}}{{\beta }_{c}}{{I}_{HIV}}+{{c}_{2}}{{\beta }_{h}}{{A}_{HCV}}-{{c}_{r}}\varepsilon {{I}_{HA}}\\ &{}&{}-\eta {{I}_{HA}}-\mu {{I}_{HA}}, \\ \frac{\textrm{d}{{I_{HCL}}}}{\textrm{d}t} &{}=&{} \eta {{I}_{HA}}+{c_3}{{\beta }_{h}}{L_{HCV}}-\mu {I_{HCL}}. \\ \end{array}\right. \end{aligned}$$

(8)

By employing the Caputo-type fractional derivative, we can investigate the impact of memory effect and hereditary effect on the transmission dynamics of the HIV-HCV co-infection model. Traditional models assume instantaneous reactions, while fractional-order models account for the history of the system. Fractional-order derivatives are non-local, meaning they consider information from a range of past times rather than just the immediate past. The HIV-HCV disease model may exhibit different fractional-order behaviors, and adjusting the order allows for a more accurate representation. Caputo fractional derivatives in the co-infection models of disease dynamics give a more accurate and nuanced picture of how infections spread because they can take into account biological systems’ memory and heritability [59,60,61,62]. This innovative mathematical technique helps forecast disease progression and optimize treatment strategies by understanding complex HIV-HCV interactions and co-evolutionary dynamics. Generalizing the classical model (8) to the fractional-order scenario, we obtain the memory-dependent model as follows [39,40,41, 50]

$$\begin{aligned} \left\{ \begin{array}{ll} {{}^C_0\Omega }^{\zeta }_t S &{}= B^{\zeta }-{{\beta _h} }S-{{\beta _c}}S+{{c_r}^{\zeta }}{A_{HCV}}-\mu ^{\zeta } S, \\ {{}^C_0\Omega }^{\zeta }_t I_{HIV} &{}= {{\beta }_{h}}S+{{c}_{r}^{\zeta }}\varepsilon ^{\zeta } {{I}_{HA}}-{{h}_{2}^{\zeta }}{{\beta }_{c}}{{I}_{HIV}}\\ &{}\quad \quad -{{h}_{1}^{\zeta }}{{I}_{HIV}}-\mu ^{\zeta }{{I}_{HIV}}, \\ {{}^C_0\Omega }^{\zeta }_t A_{HIV} &{}= {{h}_{1}^{\zeta }}{{I}_{HIV}}-\mu ^{\zeta } {{A}_{HIV}}, \\ {{}^C_0\Omega }^{\zeta }_t A_{HCV} &{}= {{\beta }_{c}}S-{{c}_{r}^{\zeta }}{{A}_{HCV}}-{{c}_{2}^{\zeta }}{{\beta }_{h}}{{A}_{HCV}}\\ &{}\quad -{{c}_{1}^{\zeta }}{{A}_{HCV}} -\mu ^{\zeta } {{A}_{HCV}}, \\ {{}^C_0\Omega }^{\zeta }_t L_{HCV} &{}= {{c}_{1}^{\zeta }}{{A}_{HCV}}-{{c}_{3}^{\zeta }}{{\beta }_{h}}{{L}_{HCV}}-\mu ^{\zeta }{{L}_{HCV}}, \\ {{}^C_0\Omega }^{\zeta }_t I_{HA} &{}= {{h}_{2}^{\zeta }}{{\beta }_{c}}{{I}_{HIV}}+{{c}_{2}^{\zeta }}{{\beta }_{h}}{{A}_{HCV}}-{{c}_{r}^{\zeta }}\varepsilon ^{\zeta } {{I}_{HA}}\\ &{}\quad -\eta ^{\zeta }{{I}_{HA}} -\mu ^{\zeta }{{I}_{HA}}, \\ {{}^C_0\Omega }^{\zeta }_t I_{HCL} &{}= \eta ^{\zeta } {{I}_{HA}}+{c_3^{\zeta }}{{\beta }_{h}}{L_{HCV}}-\mu ^{\zeta } {I_{HCL}}. \\ \end{array}\right. \end{aligned}$$

(9)

where,

$$\begin{aligned} {{\beta _h}}=\frac{k^{\zeta }{{\gamma }_{1}^{\zeta }}({{I}_{HIV}}+{{\text {k}}_{1}^{\zeta }}({{I}_{HA}}+{{I}_{HL}})}{N}, \end{aligned}$$

and

$$\begin{aligned} {{\beta }_{c}}=\frac{k^{\zeta }{{\gamma }_{2}^{\zeta }}({{\text {A}}_{HCV}}+{{L}_{HCV}}+ {{\text {k}}_{2}^{\zeta }}({{I}_{HA}}+{{I}_{HL}})}{N}, \end{aligned}$$

where $\zeta$, $(0<\zeta \le 1,)$ represents the order of the Caputo fractional derivative $_0^C\Omega _t^{\zeta }$ in (9) with non-negative and appropriate initial conditions given by

$$\begin{aligned}{} & {} S(0)=S^0,\ I_{HIV}(0)=I_{HIV}^0, \ A_{HIV}(0)=A_{HIV}^0, \\{} & {} A_{HCV}(0)=A_{HCV}^0, L_{HCV} (0)=L_{HCV}^0,\\{} & {} I_{HA}(0)=I_{HA}^0, \ I_{HCL}(0)=I_{HCL}^0. \end{aligned}$$

4 Fixed points and their stability analysis

In this section, we find the positivity and boundedness of the model and also find out HIV-HCV co-infection free equilibrium (HFE) and HIV-HCV co-infection exist equilibrium point (HEE).

4.1 Positivity and finiteness

Let us denote $\mathbb {R}_{+}^{7}=\left\{ X \left( \tau \right) \in \mathbb {R}^{7}:X \left( \tau \right) \ge 0\right\}$ and let

$X\left( \tau \right) =\Big [S(t),I_{HIV}(t),A_{HIV}(t),A_{HCV}(t), L_{HCV}(t), I_{HA}(t),I_{HCL}(t)\Big ]^{T}$.

Theorem 1

The solution to system HIV-HCV co-infection is unique and in $\mathbb {R}_{+}^{7}$ are bounded.

Proof

Here, we find the solution to the HIV-HCV co-infection system

$$\begin{aligned}{} & {} \big (S(t), I_{HIV}(t), A_{HIV}(t), A_{HCV}(t), L_{HCV}(t), \\{} & {} \quad I_{HA}(t), I_{HCL}(t)\big ), \end{aligned}$$

and find that the domain $\mathbb {R}_{+}^{7}$ is a positive invariant region with initial conditions. From the HIV-HCV co-infection model, we first

$$\begin{aligned}{} & {} {{}^C_0\Omega }^{\zeta }_t S(\tau )|_{S=0}=\frac{B^{\zeta }}{\mu ^{\zeta }} >0,\\{} & {} {{}^C_0\Omega }^{\zeta }_t I_{HIV}(\tau )|_{I_{HIV}=0}=\left( \beta _{h}S\left( \tau \right) +c_r^{\zeta }\epsilon ^{\zeta } I_{HA}\left( \tau \right) \right) \ge 0,\\{} & {} {{}^C_0\Omega }^{\zeta }_tA_{HIV}(\tau )|_{A_{HIV}=0} = h_1 ^{\zeta } I_{HIV}(\tau ) \ge 0,\\{} & {} {{}^C_0\Omega }^{\zeta }_t A_{HCV}(\tau )|_{A_{HCV}=0}=\beta _{c} \ge 0,\\{} & {} {{}^C_0\Omega }^{\zeta }_tL_{HCV}(\tau )|_{L_{HCV}=0}= c_1^{\zeta }(A_{HCV}\left( \tau \right) \ge 0,\\{} & {} {{}^C_0\Omega }^{\zeta }_t I_{HA}(\tau )|_{I_{HA}=0}= h_2 ^{\zeta } \beta _c (I_{HIV} \left( \tau \right) \\{} & {} + c_2 ^{\zeta } \beta _h (A_{HCV} \left( \tau \right) \ge 0,\\{} & {} {{}^C_0\Omega }^{\zeta }_t I_{HCL}(\tau )|_{I_{HCL}=0}= \eta ^{\zeta } (I_{HA}\left( \tau \right) )\\{} & {} + c_3 ^{\zeta } \beta _h (L_{HCV}\left( \tau \right) \ge 0. \end{aligned}$$

The above equations hold for all points of the HIV-HCV co-infection model and along with theorem 1, we proved that the set X is positive invariant with respect to the initial conditions. Next, we derived the boundedness of the HIV-HCV co-infection system. For the total population, we add all the HIV-HCV system equations of the model, we get

$$\begin{aligned} \left. {{{}^C_0\Omega }^{\zeta }_t}N(\tau ) = B ^{\zeta }- \mu ^{\zeta } N\left( \tau \right) . \right. \end{aligned}$$

For, $t \ge 0$

$$\begin{aligned} \left. {{}^C_0\Omega }^{\zeta }_t N(\tau )+\mu ^{\zeta } N\left( \tau \right) \le B ^{\zeta }, \right. \end{aligned}$$

and

$$\begin{aligned} \left. N\left( \tau \right) \le \frac{B^{\zeta }}{\mu ^{\zeta }} + \left( N_{0} - \frac{B^{\zeta }}{\mu ^{\zeta }}\right) e^{\left( -\mu ^{\zeta }t\right) }.\right. \end{aligned}$$

Therefore, for co-infection HIV-HCV model, $N(\tau )$, that is, the sub-populations $S\left( \tau \right) ,I_{HIV}\left( \tau \right) ,$ $A_{HIV}\left( \tau \right) ,A_{HCV}\left( \tau \right) ,$ $L_{HCV}\left( \tau \right) , I_{HA}\left( \tau \right) ,I_{HCL}\left( \tau \right)$ are delimited.

Therefore, the biologically feasible area for the model (9) is

$$\begin{aligned} X= & {} \Bigl \{ \big (S\left( \tau \right) ,I_{HIV}\left( \tau \right) ,A_{HIV}\left( \tau \right) ,A_{HCV}\left( \tau \right) ,\\{} & {} \left. L_{HCV}\left( \tau \right) , I_{HA}\left( \tau \right) ,I_{HCL}\left( \tau \right) \right) \in \mathbb {R} _{+}^{7}\big | 0 \\{} & {} <S\left( \tau \right) +I_{HIV}\left( \tau \right) +A_{HIV}\left( \tau \right) +A_{HCV}\left( \tau \right) \\{} & {} +L_{HIV}\left( \tau \right) +I_{HA}\left( \tau \right) +I_{HCL}\left( \tau \right) \le \frac{B}{\mu }\Big \}. \end{aligned}$$

$\square$

4.2 HIV-AIDS only model

Here, we are interested in the persistence of HIV and AIDS, we take only HIV-AIDS-infected compartments as

$$\begin{aligned} \left\{ \begin{array}{rcl} {{}^C_0\Omega }^{\zeta }_t S_{HIV} &{}=&{} B^{\zeta }-{{\beta _h} }S_{HIV}-\mu ^{\zeta } S_{HIV}, \\ {{}^C_0\Omega }^{\zeta }_t I_{HIV} &{}=&{} {{c}_{r}^{\zeta }}\varepsilon ^{\zeta }{{I}_{HA}}-{{h}_{2}^{\zeta }}{{\beta }_{c}}{{I}_{HIV}}\\ &{}&{}-{{h}_{1}^{\zeta }}{{I}_{HIV}}-\mu ^{\zeta }{{I}_{HIV}}, \\ {{}^C_0\Omega }^{\zeta }_t A_{HIV} &{}=&{} {{h}_{1}^{\zeta }}{{I}_{HIV}}-\mu ^{\zeta } {{A}_{HIV}}. \\ \end{array}\right. \end{aligned}$$

(10)

where,

$$\begin{aligned} {{\beta _h}}=\frac{k^{\zeta }{\gamma _1^{\zeta }}{I_{HIV}}}{N_{HIV}}, \end{aligned}$$

(11)

where, $N_{HIV}=S_{HIV}+I_{HIV}+A_{HIV}$.

Now, calculate the threshold of the HIV model.

Consider the following equations for finding the disease-free equilibrium point of the HIV-only sub-model,

$$\begin{aligned} \left\{ \begin{array}{lll} B^{\zeta }-{{\beta _h}}S_{HIV}-\mu ^{\zeta } S_{HIV} &{}=&{} 0,\\ {{\beta }_{h}}S_{HIV}-{{h}_{2}^{\zeta }}{{\beta }_{c}}{{I}_{HIV}}-{{h}_{1}^{\zeta }}{{I}_{HIV}}-\mu ^{\zeta } {{I}_{HIV}} &{}=&{} 0, \\ {{h}_{1} ^{\zeta }}{{I}_{HIV}}-\mu ^{\zeta } {{A}_{HIV}} &{}=&{} 0, \\ \end{array}\right. \end{aligned}$$

(12)

when $I_{HIV}=0, A_{HIV}=0$. Thus, the HIV-AIDS free equilibrium point is given by $H_{HIV}^0=\left( S_{HIV}^0,I_{HIV}^0,A_{HIV}^0\right) =\left( \frac{B^{\zeta }}{\mu ^{\zeta }},0,0\right) .$

and the unique endemic equilibrium point is

$H_{HIV}^*=\left( S_{HIV}^*,\ I_{HIV}^*,A_{HIV}^*\right)$ where

$$\begin{aligned} \left\{ \begin{array}{lll} S_{HIV}^*=\frac{B^{\zeta }}{f_{HIV}^*+\mu ^{\zeta }}, \\ I_{HIV}^*=\frac{B^{\zeta } f_{HIV}^*}{(f_{HIV}^*+\mu ^{\zeta })\left( h_1^{\zeta }+\mu ^{\zeta }\right) }, \\ A_{HIV}^*=\frac{B^{\zeta } f_{HIV}^*h_1 ^{\zeta }}{\mu ^{\zeta }(f_{HIV}^*+\mu ^{\zeta })\left( h_1^{\zeta }+\mu ^{\zeta } \right) }. \end{array}\right. \end{aligned}$$

(13)

with $f_{HIV}^*=\frac{k ^{\zeta }\gamma _1 ^{\zeta }I_{HIV}^*}{N_{HIV}}$.

4.3 Basic reproduction number $\mathcal {R}_0^{H}$

Here, we need to derive the reproduction number $\mathcal {R}_0^{H}$ of the HIV-AIDS-only sub-model. The reproductive number is a threshold variable that indicates the total number of subsequent diseases caused by an infected individual in a fully susceptible population during the infection period. For this, we use the next-generation matrix approach. Consider the matrices let $H^{^{\prime }}=\left( S_{HIV},I_{HIV},A_{HIV}\right) ^{T}$, the system (10) can be written as $\left. X^{^{\prime }}=\mathcal {F}\left( X\right) -\mathcal {V}\left( X\right) \right.$

here, $\left. \mathcal {F}\left( X\right) =\left[ \begin{array}{c} \left( -\beta _{h}S_{HIV}) \right. \\ \left( \beta _{h}S_{HIV}) \right. \\ 0 \end{array} \right] \right.$,

and $\left. \mathcal {V}\left( X\right) =\left[ \begin{array}{c} B^{\zeta } -\mu ^{\zeta } S_{HIV} \\ -h_1^{\zeta } I_{HIV}-\mu ^{\zeta } I_{HIV} \\ h_1 ^{\zeta }I_{HIV}-\mu ^{\zeta } A_{HIV} \end{array} \right] \right.$.

The threshold of HIV-AIDS-only model is the spectral radius of $FV^{-1}$, which is

$\mathcal {R}_0^{H}=\frac{k^{\zeta } \gamma _1^{\zeta }\ }{N_{HIV}}\left( \frac{B^{\zeta }}{\mu ^{\zeta }\left( \mu ^{\zeta }+h_1^{\zeta }\right) }\right)$.

4.4 Stability analysis of HIV-AIDS sub-model

Theorem 2

The HIV-AIDS free equilibrium point $H_{HIV}^0$ of the HIV-AIDS sub-model is locally asymptotically stable if $\mathcal {R}_0^{H}<1$.

Proof

The Jacobian matrix of the HIV-AIDS sub-model (10) is obtained as follows

$$\begin{aligned}&J_{HIV} \nonumber \\&\quad =\left[ \begin{array}{ccc} -\frac{k ^{\zeta }\gamma _1 ^{\zeta }I_{HIV}\ }{N_{HIV}}-\mu ^{\zeta } &{}-\frac{k\gamma _1^{\zeta }\ }{N_{HIV}}S&{}0\\ \frac{k^{\zeta }\gamma _1 ^{\zeta }I_{HIV}\ }{N_{HIV}}&{}\left( \frac{k ^{\zeta }\gamma _1 ^{\zeta }}{N_{HIV}}\right) S-h_1 ^{\zeta }-\mu ^{\zeta }&{}0\\ 0&{}h_1^{\zeta }&{}-\mu ^{\zeta }\\ \end{array}\right] .\ \end{aligned}$$

(14)

The Jacobian matrix of the HIV-AIDS sub-model at $H_{HIV}^0$ is

$$\begin{aligned}&J_{HIV}\left( H_{HIV}^0\right) \nonumber \\&\quad =\left[ \begin{array}{ccc} -\mu ^{\zeta }&{}-\frac{k ^{\zeta }\gamma _1^{\zeta }\ }{N_{HIV}}\left( \frac{B ^{\zeta }}{\mu ^{\zeta }}\right) &{}0\\ 0&{}\frac{B ^{\zeta }k ^{\zeta }\gamma _1 ^{\zeta }}{N_{HIV}\mu ^{\zeta }}-{h_{1}^{\zeta }}-\mu ^{\zeta }&{}0\\ 0&{}h_1 ^{\zeta } &{}-\mu ^{\zeta } \end{array}\right] . \end{aligned}$$

(15)

The characteristic equation of $J_{HIV}\left( H_{HIV}^0\right) is$

$\det {\left( J_{HIV}\left( H_{HIV}^0\right) -\lambda I\right) }=0$, where $\lambda$ is the root of the equation.

The root $\lambda _1=-\mu ^{\zeta }$ is trivial eigenvalue and the other two eigenvalues are obtained from the submatrix $J_1\left( H_{HIV}^0\right) =\left[ \begin{array}{cc}\frac{B ^{\zeta } k ^{\zeta } \gamma _1^{\zeta }}{N_{HIV}\mu ^{\zeta }}-h_1 ^{\zeta }-\mu ^{\zeta }&{}0\\ h_1 ^{\zeta }&{}-\mu ^{\zeta }\\ \end{array}\right] .$

To get the local stability at the HIV-AIDS free equilibrium $H_{HIV}^0$, it is sufficient to prove that $trace\left( J_1\left( H_{HIV}^0\right) \right) <0$ and the $\det {\left( J_1\left( H_{HIV}^0\right) \right) }>0.$

Now,

$$\begin{aligned} trace\left( \ J_1\left( E_{HIV}^0\right) \right) =\frac{Bk\gamma _1\ }{N_{HIV}\mu }-h_1-2\mu <0, \end{aligned}$$

(16)

provided

$$\begin{aligned} \frac{B^{\zeta }k\gamma _1 ^{\zeta } -\left( \mu ^{\zeta }+h_1^{\zeta }\right) {\mu ^{\zeta } N}_{HIV}\ }{N_{HIV}\mu ^{\zeta }}<\mu ^{\zeta }, \end{aligned}$$

(17)

and $\det {\left( \ J_1\left( H_{HIV}^0\right) \right) }>0=\frac{\left( \mu ^{\zeta }+h_1^{\zeta }\right) {\mu ^{\zeta } N}_{HIV}-B^{\zeta }\gamma _1^{\zeta }k^{\zeta }\ }{N_{HIV}}>0\$ if

$$\begin{aligned} \frac{B^{\zeta }\gamma _1^{\zeta }k^{\zeta }}{\left( \mu ^{\zeta }+h_1^{\zeta }\right) {\mu ^{\zeta } N}_{HIV}}<1\Rightarrow \mathcal {R}_0^{H}<1. \end{aligned}$$

Hence by the Routh-Hurwitz criteria of stability, the HIV-AIDS sub-model is locally asymptotically stable at the HIV-AIDS free equilibrium point $H_{HIV}^0$ if $\mathcal {R}_0^{H}<1$ otherwise unstable. $\square$

Theorem 3

The HIV-AIDS sub-model (10) possesses a unique endemic equilibrium point $H_{HIV}^*=\Big (S_{HIV}^*,\ I_{HIV}^*,A_{HIV}^*\Big )$ if $\mathcal {R}_0^{H}>1$ where, $S_{HIV}^*=\frac{B^{\zeta }}{f_{HIV}^*+\mu ^{\zeta }}, I_{HIV}^*=\frac{B^{\zeta }f_{HIV}^*}{(f_{HIV}^*+\mu ^{\zeta })\left( h_1+\mu \right) }$, $A_{HIV}^*\,{=}\,\frac{B^{\zeta }f_{HIV}^*h_1^{\zeta }}{\mu ^{\zeta }(f_{HIV}^*{+}\mu ^{\zeta })\left( h_1^{\zeta }+\mu ^{\zeta }\right) },$ with $f_{HIV}^*=\frac{k^{\zeta }\gamma _1^{\zeta }I_{HIV}^*}{N_{HIV}}$.

Proof

To find the endemic equilibrium point of the HIV-AIDS sub-model (10), we have solved the following system of equations $\frac{\textrm{d}S_{HIV}^*}{\textrm{d}t}=0$,$\frac{\textrm{d}I_{HIV}^*}{\textrm{d}t}=0$,$\frac{\textrm{d}A_{HIV}^*}{\textrm{d}t}=0$.

Hence we have the following algebraic equations

$$\begin{aligned}{} & {} B^{\zeta }-\left( \frac{k^{\zeta }\gamma _1^{\zeta } {I_{HIV}^*}\ }{N_{HIV}^*}\right) {S_{HIV}^*}-\mu ^{\zeta } {S_{HIV}^*} = 0, \nonumber \\{} & {} \left( \frac{k^{\zeta } \gamma _1^{\zeta } {I_{HIV}^*}\ }{N_{\ HIV}^*}\right) {S_{HIV}^*}-h_1^{\zeta } {I_{HIV}^*}-\mu ^{\zeta } {I_{HIV}^*} = 0, \nonumber \\{} & {} h_1^{\zeta }I_{HIV^*}-\mu ^{\zeta } {A_{HIV}^*} = 0.\nonumber \\ \end{aligned}$$

(18)

By solving, the above simultaneously of equations with consideration $f_{HIV}^*=\frac{k^{\zeta }\gamma _1^{\zeta } I_{HIV}^*}{N_{HIV}}$, gives us the unique endemic equilibrium point

$$\begin{aligned} S_{HIV}^*= & {} \frac{B^{\zeta }}{f_{HIV}^*+\mu ^{\zeta }},\\ I_{HIV}^*= & {} \frac{B^{\zeta } f_{HIV}^*}{(f_{HIV}^*+\mu ^{\zeta })\left( h_1^{\zeta }+\mu ^{\zeta }\right) }, \\ A_{HIV}^*= & {} \frac{B^{\zeta }f_{HIV}^*h_1^{\zeta }}{\mu ^{\zeta }(f_{HIV}^*+\mu ^{\zeta })\left( h_1^{\zeta }+\mu ^{\zeta }\right) }. \end{aligned}$$

After substituting above values in the expression of $f_{HIV}^*=\frac{k^{\zeta }\gamma _1^{\zeta }I_{HIV}^*}{N_{HIV}}$, and after simplification, we have $f_{HIV}^*=\frac{k^{\zeta }\gamma _1^{\zeta }B^{\zeta }}{N_{HIV}\left( h_1^{\zeta }+\mu ^{\zeta }\right) }{-\mu ^{\zeta }}$.

Thus the force of infection for HIV-AIDS in terms of $\mathcal {R}_0^{H}$ is expressed as

$f_{HIV}^*=\mathcal {R}_0^{H}\mu ^{\zeta }-\mu ^{\zeta }=\left( \mathcal {R}_0^{H}-1\right) \mu ^{\zeta }$.

Hence, the force of infection for the HIV-AIDS sub-model i.e., $f_{HIV}^*$ is positive if $\mathcal {R}_0^{H}>1$. $\square$

Theorem 4

The equilibrium $H_{HIV}^*$ of HIV-AIDS only model is GAS, if $\mathcal {R}_0^{H}<1$ and unstable when $\mathcal {R}_0^{H}>1$.

Proof

Let a Lyapunov function $L _{1}\left( \tau \right)$ given by

$$\begin{aligned} L_{1}\left( \tau \right)= & {} V_1 \left( S_{HIV}-S_{HIV}^*-S_{HIV}^*ln \left( \frac{S_{HIV}}{S_{HIV}^*}\right) \right) \nonumber \\{} & {} + V_2 \left( I_{HIV}-I_{HIV}^*-I_{HIV}^*ln \left( \frac{I_{HIV}}{I_{HIV}^*}\right) \right) \nonumber \\{} & {} +V_3 \left( A_{HIV}-A_{HIV}^*-A_{HIV}^*ln \left( \frac{A_{HIV}}{A_{HIV}^*}\right) \right) ,\nonumber \\ \end{aligned}$$

(19)

where, $V_1=\frac{1}{\mu ^\zeta },\ V_2=\frac{\ \mathcal {R}_0^H}{h_1^\zeta +\mu ^\zeta },\ \mathcal {R}_0^H>1, and \ V_3=\frac{1}{\mu ^\zeta }$.

Therefore, $L_{1}\left( \tau \right)$ is continuous and non-negative for all $\tau \ge 0$. The caputo derivative of $L_1(t)$ along with HIV-AIDS sub model is,

$$\begin{aligned}{} & {} {{}^C_0\Omega }^{\zeta }L_1\left( t\right) \le V_1\left( 1-\frac{S^*_{HIV}}{S_{HIV}}\right) {{}^C_0\Omega }^{\zeta }S_{HIV^*}\nonumber \\{} & {} \qquad +\ V_2\ \left( 1-\frac{I^*_{HIV}}{I_{HIV}}\right) {_0^c}\Omega _t^\zeta \ I_{HIV^*}\nonumber \\{} & {} \qquad +\ V_3\ \left( 1-\frac{A^*_{HIV}}{A_{HIV}}\right) \ {{}^C_0\Omega }^{\zeta } A^*_{HIV} \nonumber \\{} & {} \quad \le \frac{1}{\mu ^\zeta }\left( 1-\frac{S^*}{S}\right) \left( B^{\zeta }-\left( \frac{k^\zeta \gamma _1^\zeta I_{HIV}}{N_{HIV}}\right) S-\ \mu ^\zeta S\right) \nonumber \\{} & {} \qquad +\frac{\ \mathcal {R}_0^H}{h_1^\zeta +\mu ^\zeta }\ \left( 1-\frac{I_{HIV}^*}{I_{HIV}}\right) \left( \left( \frac{k^\zeta \gamma _1^\zeta I_{HIV}}{N_{HIV}}\right) S\right. \nonumber \\{} & {} \qquad \left. -h_1^\zeta I_{HIV}-{\mu }_{HIV}^\zeta \right) \nonumber \\{} & {} \qquad +\frac{1}{\mu ^\zeta }\ \left( 1-\frac{A_{HIV}^*}{A_{HIV}}\right) (h_1I_{HIV}-\mu ^\zeta A_{HIV}). \end{aligned}$$

(20)

We have,

$$\begin{aligned} B^{\zeta }= & {} \left( \frac{k^\zeta \gamma _1^{\zeta }{I_{HIV}^*}}{N_{HIV}}\right) S^{*}\nonumber \\{} & {} +\mu ^{\zeta } S^{*}_{HIV}, \left( \frac{k^\zeta \gamma _1^\zeta {I_{HIV}^*}\ }{N_{HIV}}\right) \frac{S^*_{HIV}}{{I_{HIV}^*}}\nonumber \\= & {} h_1^\zeta +\mu ^\zeta , h_1^\zeta {I_{HIV}^*}=\mu ^\zeta {A_{HIV}^*}. \end{aligned}$$

(21)

Substituting the values of equation (21) in equation (20), we have,

$$\begin{aligned} {{_0^C}D}_t^\zeta \left( L\left( t\right) \right)\le & {} -\left\{ \frac{\left( S_{HIV}-S_{HIV}^*\right) ^2}{S_{HIV}}\right. \\{} & {} \qquad +\frac{\left( I_{HIV}-I_{HIV}^*\right) ^2}{I_{HIV}}\left( \mathcal {R}_0^{HIV}-1\right) \\{} & {} \qquad \left. +\frac{\left( A_{HIV}-A_{HIV}^*\right) ^2}{A_{HIV}}\right\} . \end{aligned}$$

It proves that if $\mathcal {R}_0^{H}>1$, then we get, ${{_0^C}\Omega }_t^\zeta \left( L\left( t\right) \right) \le 0$. Moreover, ${{}^C_0\Omega }^{\zeta }_t\left( L\left( t\right) \right) =0$ at $S=S_{HIV}^*$, $I_{HIV}=I_{HIV}^*$, $A_{HIV}=A_{HIV}^*$.

Hence, by LaSalle’s invariant extension to Lyapunov’s principles, the endemic equilibrium point $H_{HIV}^*$ of the HIV-AIDS sub-model is globally asymptotically stable if $\mathcal {R}_0^{H}>1$, otherwise unstable. $\square$

4.5 HCV only sub-model

In this section, we discuss the HCV model without the impact of HIV-AIDS on the HCV population.

$$\begin{aligned} \left\{ \begin{array}{rcl} {{}^C_0\Omega }^{\zeta }_t S_{HCV} &{}=&{} B^{\zeta }-{{\beta _c}}S_{HCV}+{{c_r}^{\zeta }}{A_{HCV}}\\ &{}&{}-\mu ^{\zeta } S_{HCV}, \\ {{}^C_0\Omega }^{\zeta }_t A_{HCV} &{}=&{} {{\beta }_{c}}S_{HCV}-{c_r^{\zeta }}{A_{HCV}^{\zeta }}-{{c}_{1}^{\zeta }}{{A}_{HCV}}\\ &{}&{}-\mu ^{\zeta } {A_{HCV}}, \\ {{}^C_0\Omega }^{\zeta }_tL_{HCV} &{}=&{} {{c_1}^{\zeta }}{{A}_{HCV}}-\mu ^{\zeta } {L_{HCV}}. \end{array} \right. \end{aligned}$$

(22)

where, $\beta _c=\frac{k^{\zeta }\gamma _2^{\zeta } \left( A_{HCV}+L_{HCV}\right) }{N_{HCV}}$, with, $N_{HCV}=S_{HCV}+I_{HCV}+A_{HCV}$.

By using the same method as done for the HIV-AIDS sub-model (10), we obtained the disease-free equilibrium point of the HCV sub-model (22) as $H_{HCV}^0=\left( S_{HCV}^0, A_{HCV}^0, L_{HCV}^0\right) =\left( \frac{B^{\zeta }}{\mu ^{\zeta }},0,0\right)$ and the basic reproduction number $\mathcal {R}_0^{C}=\frac{B^{\zeta }k^{\zeta }\gamma _2^{\zeta }(\mu +c_1)}{N_{HCV}\mu ^{2\zeta }\left( c_1^{\zeta }+c_r^{\zeta }+\mu ^{\zeta }\right) }$.

Theorem 5

The disease-free equilibrium point $H_{HCV}^0$ of the HCV sub model (22) is locally asymptotically stable if $\frac{B^{\zeta }k^{\zeta }\gamma _2^{\zeta }\ }{\mu ^{\zeta }}<c_r^{\zeta }+c_1^{\zeta }+2\mu ^{\zeta }$ and $\mathcal {R}_0^{C}<1$.

Proof

The Jocobian matrix of the HCV sub-model (22) is obtained as follows

$$\begin{aligned}{} & {} J_{HCV} =\left[ \begin{array}{ccc} -\frac{k^{\zeta }\gamma _2^{\zeta }\left( A_{HCV}+L_{HCV}\right) }{N_{HCV}}-\mu ^{\zeta }&{}-\frac{k^{\zeta }\gamma _2^{\zeta }\ }{N_{HCV}}S_{HCV}+c_r^{\zeta }&{}-\frac{k^{\zeta }\gamma _2^{\zeta }\ }{N_{HCV}}S_{HCV}\\ \frac{k^{\zeta }\gamma _2^{\zeta }\left( A_{HCV}+L_{HCV}\right) }{N_{HCV}}&{}\frac{k\gamma _2\ }{N_{HCV}}S_{HCV}-c_r^{\zeta }-c_1^{\zeta }-\mu ^{\zeta }&{}\frac{k\gamma _2\ }{N_{HCV}}S_{HCV}\\ 0&{}c_1^{\zeta }&{}-\mu ^{\zeta }\\ \end{array}\right] . \end{aligned}$$

The Jacobian matrix of HCV sub-model at $H_{HCV}^0$ is

$$\begin{aligned}{} & {} J_{HCV}\left( H_{HCV}^0\right) \\{} & {} \quad =\left[ \begin{array}{ccc} -\mu ^{\zeta }&{}-\frac{B^{\zeta }k^{\zeta }\gamma _2^{\zeta }\ }{N_{HCV}\mu ^{\zeta }}+c_r^{\zeta }&{}-\frac{B^{\zeta }k^{\zeta }\gamma _2^{\zeta }\ }{N_{HCV}\mu ^{\zeta }}\\ 0&{}\frac{B^{\zeta }k^{\zeta }\gamma _2^{\zeta }\ }{N_{HCV}\mu ^{\zeta }}-c_r^{\zeta }-c_1^{\zeta }-\mu ^{\zeta }&{}\frac{B^{\zeta }k^{\zeta }\gamma _2^{\zeta }\ }{N_{HCV}\mu ^{\zeta }}\\ 0&{}c_1^{\zeta }&{}-\mu ^{\zeta }\\ \end{array}\right] . \end{aligned}$$

The characteristic equation of the $J_{HCV}$ at $H^0_{HCV}$ is

$\det {\left( J_{HCV}\left( H_{HCV}^0\right) -\lambda I\right) }=0$, where $\lambda$ is the root of the equation.

The root $\lambda _1={-\mu ^{\zeta }}$ is the trivial eigenvalue and the other two eigenvalues are obtained from the sub matrix

$$\begin{aligned}{} & {} J_HCV\left( H_{HCV}^0\right) \\{} & {} \quad =\left[ \begin{array}{cc} \frac{B^{\zeta }k^{\zeta }\gamma _2^{\zeta }\ }{N_{HCV}\mu ^{\zeta }}-c_r^{\zeta }-c_1^{\zeta }-\mu ^{\zeta }&{}\frac{B^{\zeta }k^{\zeta }\gamma _2^{\zeta }\ }{N_{HCV}\mu ^{\zeta }}\\ c_1^{\zeta }&{}-\mu ^{\zeta }\\ \end{array}\right] . \end{aligned}$$

To get the local stability of HCV sub-model (22) at the disease-free equilibrium $H_{HCV}^0,$ it is sufficient to prove that

$trace \left( J_{HCV}\left( H_{HCV}^0\right) \right) <0$ and $\det {\left( \ J_{HCV}\left( H_{HCV}^0\right) \right) }>0.$

Now, $trace\left( \ J_{HCV}\left( H_{HCV}^0\right) \right) =\frac{B^{\zeta }k^{\zeta }\gamma _2^{\zeta }\ }{\mu ^{\zeta }}-c_r^{\zeta }-c_1^{\zeta }-2\mu ^{\zeta }<0$,

with the condition, $\frac{B^{\zeta }k^{\zeta }\gamma _2^{\zeta }\ }{\mu ^{\zeta }}<c_r^{\zeta }+c_1^{\zeta }+2\mu ^{\zeta }$,

and $det{\left( J_1\left( H_{HCV}^0\right) \right) }>0\Rightarrow -\frac{B^{\zeta }k^{\zeta }\gamma _2^{\zeta }\left( \mu ^{\zeta }+c_1^{\zeta }\right) \ }{\mu ^{\zeta }}+\mu ^{\zeta }(c_r^{\zeta }+c_1^{\zeta }+\mu ^{\zeta })>0$, if $\frac{B^{\zeta }k^{\zeta }\gamma _2^{\zeta }(\mu ^{\zeta }+c_1^{\zeta })}{\mu ^{2\zeta }\left( c_1^{\zeta }+c_r^{\zeta }+\mu ^{\zeta }\right) }<1\Rightarrow \mathcal {R}_0^{C}<1$.

Hence by the Routh-Hurwitz criteria of stability, the HCV sub-model is locally asymptotically stable at the disease-free equilibrium point $H_{HCV}^0$ if $\mathcal {R}_0^{C}<1$ and $\frac{B^{\zeta }k^{\zeta }\gamma _2^{\zeta }\ }{\mu ^{\zeta }}<c_r^{\zeta }+c_1^{\zeta }+2\mu ^{\zeta }$ otherwise unstable. $\square$

Theorem 6

The HCV sub-model (22) possesses a unique endemic equilibrium point

${H_{HCV}^*}=(S_{HCV}^*,I_{HCV}^*,A_{HCV}^*)$ if $\mathcal {R}_0^C>1$

where

$$\begin{aligned} S_{HCV}^*= & {} \frac{B^{\zeta }\left( c_1^{\zeta } + c_r ^{\zeta }+\mu ^{\zeta } \right) }{f_{HCV}^*{(c}_1^{\zeta } +\mu ^{\zeta })\ +\mu ^{\zeta }{(c}_1^{\zeta }+ c_r^{\zeta } +\mu ^{\zeta }) },\\ A_{HCV}^*= & {} \frac{B^{\zeta }f_{HCV}^*}{f_{HCV}^*{(c}_1^{\zeta } +\mu ^{\zeta })\ +\mu ^{\zeta }{(c}_1^{\zeta } + c_r^{\zeta } +\mu ^{\zeta })}, \end{aligned}$$

and

$$\begin{aligned} L_{HCV}^*=\frac{c_1^{\zeta }B^{\zeta } f_{HCV}^*}{\mu ^{\zeta } \left( f_{HCV}^*{(c}_1 ^{\zeta } + \mu ^{\zeta }) +\mu ^{\zeta }{(c}_1^{\zeta } + c_r^{\zeta } + \mu ^{\zeta })\right) }, \end{aligned}$$

with

$$\begin{aligned}{} & {} f_{HCV}^*=\frac{1}{{\mu ^{\zeta } N}_{HCV}}\\{} & {} \quad \left( -\frac{N_{HCV}\mu ^{2\zeta }\left( \mu ^{\zeta }+c_1^{\zeta }+c_r^{\zeta } \right) - B\gamma _2^{\zeta }k^{\zeta }{(c}_1^{\zeta }+\mu ^{\zeta })}{\left( c_1^{\zeta } + \mu ^{\zeta }\right) }\right) . \end{aligned}$$

Proof

To find the endemic equilibrium point of the HCV sub-model (22), we have solved the following system of equations

$$\begin{aligned} {{}^C_0\Omega }^{\zeta }_t S_{HCV}= & {} 0,\\ {{}^C_0\Omega }^{\zeta }_t A_{HCV}= & {} 0,\\ {{}^C_0\Omega }^{\zeta }_t L_{HCV}= & {} 0. \end{aligned}$$

Hence, we have the following algebraic equations

$$\begin{aligned}{} & {} B^{\zeta }-\frac{k^{\zeta }\gamma _2^{\zeta }\left( A_{HCV}+L_{HCV}\right) }{{N_{HCV}}S_{HCV}+c_r^{\zeta }A_{HCV}-\mu ^{\zeta } S_{HCV}} = 0, \nonumber \\{} & {} \frac{k^{\zeta }\gamma _2^{\zeta }\left( A_{HCV}+L_{HCV}\right) }{N_{HCV}}S_{HCV}-c_r^{\zeta } A_{HCV}\nonumber \\{} & {} \quad -c_1^{\zeta } A_{HCV}-\mu ^{\zeta } A_{HCV}=0, \nonumber \\{} & {} c_1^{\zeta } A_{HCV} -\mu ^{\zeta } L_{HCV}=0. \end{aligned}$$

(23)

By solving, the above simultaneously equations with consideration

$$\begin{aligned} f_{HCV}^*=\frac{k^{\zeta }\gamma _2^{\zeta }\left( A_{HCV}^*+L_{HCV}^*\right) }{N_{HCV}^*}, \end{aligned}$$

gives us the unique endemic equilibrium point

$$\begin{aligned} S_{HCV}^*= & {} \frac{B^{\zeta }\left( c_1^{\zeta } + c_r ^{\zeta }+\mu ^{\zeta } \right) }{f_{HCV}^*{(c}_1^{\zeta } +\mu ^{\zeta })\ +\mu ^{\zeta }{(c}_1^{\zeta }+ c_r^{\zeta } +\mu ^{\zeta }) },\\ A_{HCV}^*= & {} \frac{B^{\zeta }f_{HCV}^*}{f_{HCV}^*{(c}_1^{\zeta } +\mu ^{\zeta })\ +\mu ^{\zeta }{(c}_1^{\zeta } + c_r^{\zeta } +\mu ^{\zeta })},\\ L_{HCV}^*= & {} \frac{c_1^{\zeta }B^{\zeta } f_{HCV}^*}{\mu ^{\zeta } \left( f_{HCV}^*{(c}_1 ^{\zeta } + \mu ^{\zeta }) +\mu ^{\zeta }{(c}_1^{\zeta } + c_r^{\zeta } + \mu ^{\zeta })\right) }. \end{aligned}$$

After substituting above values in the expression of

$$\begin{aligned} f_{HCV}^*=\frac{k\gamma _2\left( A_{HCV}^*+L_{HCV}^*\right) }{N_{HCV}^*}, \end{aligned}$$

and after simplification, we have

$$\begin{aligned}{} & {} f_{HCV}^*=\frac{1}{{\mu ^{\zeta } N}_{HCV}}\\{} & {} \quad \left( -\frac{N_{HCV}\mu ^{2\zeta }\left( \mu ^{\zeta }+c_1^{\zeta }+c_r^{\zeta } \right) - B\gamma _2^{\zeta }k^{\zeta }{(c}_1^{\zeta }+\mu ^{\zeta })}{\left( c_1^{\zeta } + \mu ^{\zeta }\right) }\right) . \end{aligned}$$

Thus, the force of infection for HCV in terms of $\mathcal {R}_0^{C}$ is expressed as

$f_{HCV}^*=\frac{\mu ^{\zeta }\left( \mu ^{\zeta }+ c_1^{\zeta } +c_r^{\zeta } \right) }{\ \left( c_1^{\zeta } +\mu ^{\zeta }\right) }\left( \mathcal {R}_0^{C}-1\right)$.

Hence, the force of infection for HCV i.e., $f_{HCV}^*$ is positive if $\mathcal {R}_0^{C}>1$. $\square$

Theorem 7

The endemic equilibrium point $H_{HCV}^*$ of HCV only sub-model (22) is globally asymptotically stable if $\mathcal {R}_0^{C}>1$.

Proof

Consider the positive definite Lyapunov function $L_2 \left( S_{HCV}\,A_{HCV},L_{HCV}\right) :\Omega _{HCV}\rightarrow R^+$ defined as

$$\begin{aligned} L_2\left( t\right)= & {} v_1\left( S_{HCV}-S_{HCV}^*-S_{HCV}^*\ln {\left( \frac{S_{HCV}}{S_{HCV}^*}\right) }\right) \nonumber \\{} & {} +v_2\left( A_{HCV}-A_{HCV}^*-A_{HCV}^*\ln {\left( \frac{A_{HCV}}{A_{HCV}^*}\right) }\right) \nonumber \\{} & {} +v_3\left( L_{HCV}-L_{HCV}^*-L_{HCV}^*\right. \nonumber \\{} & {} \quad \left. -L_{HCV}^*\ln {\left( \frac{L_{HCV}}{L_{HCV}^*}\right) }\right) , \end{aligned}$$

(24)

where $v_1=\frac{1}{\mu ^\zeta }$,$v_2=\frac{\mathcal {R}_0^{C}}{c_r^\zeta +c_1^\zeta +\mu ^\zeta }$,$\mathcal {R}_0^{C}>1$, and $v_3=\frac{1}{\mu ^\zeta }$.

Now, by applying the Caputo fractional derivative to the above Lyapunov function

$$\begin{aligned} {{_0^C}\Omega }_t^\zeta \left( L\left( t\right) \right)\le & {} \frac{1}{\mu ^\zeta }\left( 1-\frac{S_{HCV}^*}{S_{HCV}}\right) {{_0^C}\Omega }_t^\zeta S_{HCV}\nonumber \\{} & {} +\frac{\ \mathcal {R}_0^C}{c_r^\zeta +c_1^\zeta +\mu ^\zeta }\left( 1-\frac{A_{HCV}^*}{A_{HCV}}\right) {{_0^C}\Omega }_t^\zeta A_{HCV} \nonumber \\{} & {} +\frac{1}{\mu ^\zeta }\left( 1-\frac{L_{HCV}^*}{L_{HCV}}\right) {{_0^C}D}_t^\zeta L_{HCV}. \end{aligned}$$

(25)

From equation (24), we have,

$$\begin{aligned}{} & {} {{_0^C}\Omega }_t^\zeta \left( L_2\left( t\right) \right) \nonumber \\{} & {} \quad \le \frac{1}{\mu ^\zeta }\left( 1-\frac{S_{HCV}^*}{S_{HCV}}\right) \nonumber \\{} & {} \qquad \left( B^\zeta -\frac{k^\zeta \gamma _2^\zeta \left( A_{HCV}+L_{HCV}\right) }{N_{HCV}}S_{HCV}\right. \nonumber \\{} & {} \qquad \left. +c_rA_{HCV}-\mu S_{HCV}\right) \nonumber \\{} & {} \qquad +\frac{\ \mathcal {R}_0^{C}}{c_r^\zeta +c_1^\zeta +\mu ^\zeta }\left( 1-\frac{A_{HCV}^*}{A_{HCV}}\right) \nonumber \\{} & {} \qquad \left( \frac{k\gamma _2\left( A_{HCV}+L_{HCV}\right) }{N_{HCV}}S\right. \nonumber \\{} & {} \qquad \left. -c_rA_{HCV}-c_1A_{HCV}-\mu A_{HCV}\right) \nonumber \\{} & {} \qquad +\frac{\ 1}{\mu ^\zeta }\left( 1-\frac{L_{HCV}^*}{L_{HCV}}\right) \left( c_1A_{HCV}-\mu L_{HCV}\right) . \end{aligned}$$

(26)

At the HCV endemic equilibrium from equation (23), we have,

$$\begin{aligned}{} & {} B^\zeta =\frac{k^\zeta \gamma _2^\zeta \left( {A_{HCV}^*}+{L_{HCV}^*}\right) }{N_{HCV}}S_{HCV}^*\nonumber \\{} & {} \quad +c_r^\zeta {A_{HCV}^*}-\mu ^\zeta S_{HCV}^*, \nonumber \\{} & {} \frac{k^\zeta \gamma _2^\zeta \left( {A^*}_{HCV}+{L^*}_{HCV}\right) }{N_{HCV}}\frac{S_{HCV}^*}{{A^*}_{HCV}}=c_r^\zeta +c_1^\zeta +\mu ^\zeta , \nonumber \\{} & {} {A^*}_{HCV}=\mu ^\zeta {L^*}_{HCV}. \end{aligned}$$

(27)

Substituting the values of equation (27) in equation (26), we get,

$$\begin{aligned}{} & {} {{_0^C}\Omega }_t^\zeta \left( L_2\left( t\right) \right) \nonumber \\{} & {} \quad \le -\left\{ \frac{\left( S_{HCV}-S_{HCV}^*\right) ^2}{S_{HCV}}\right. \nonumber \\{} & {} \qquad +\frac{\left( I_{HCV}-I_{HCV}^*\right) ^2}{I_{HCV}}\left( \mathcal {R}_0^{C}-1\right) \nonumber \\{} & {} \qquad \left. +\frac{\left( L_{HCV}-L_{HCV}^*\right) ^2}{L_{HCV}}\right\} . \end{aligned}$$

(28)

It shows that if $\mathcal {R}_0^{C}>1$, ${{_0^C}\Omega }_t^\zeta \left( L_2\left( t\right) \right) \le 0$. Moreover, ${{_0^C}\Omega }_t^\zeta \left( L_2\left( t\right) \right) =0$ at $S=S_{HCV}^*$, $I_{HCV}=I_{HCV}^*$, $L_{HCV}=L_{HCV}^*$.

Hence by LaSalle’s invariant extension to Lyapunov’s principles, the endemic equilibrium point $H_{HCV}^*$ of the HCV sub-model is globally asymptotically stable if $\mathcal {R}_0^{C}>1$, otherwise unstable. $\square$

4.6 Equilibrium points for HIV-HCV co-infection model

The disease-free equilibrium of the HIV-HCV co-infection model is given by $H^0_{HC}=\Big (S^0, I_{HIV}^0, A_{HIV}^0, A_{HCV}^0, L_{HCV}^0, I_{HA}^0, I_{HCL}^0\Big )=\left( \frac{B^\zeta }{\mu ^\zeta },0,0,0,0,0,0\right)$.

Theorem 8

The basic reproduction number for HIV-HCV co-infection model $\mathcal {R}_0^{HC}=\max {\left\{ \mathcal {R}_0^{H},\mathcal {R}_0^{C}\right\} }$.

Proof

Using the next-generation matrix method, the Jacobian infection matrix of the co-infection model and the matrix from transfer from one compartment to another compartment in the co-infection model at the disease-free equilibrium $H^0_{HC}=\left( \frac{B^\zeta }{\mu ^\zeta },0,0,0,0,0,0\right)$ are as follows:

$$\begin{aligned} J_{FHC}=\left[ \begin{array}{cccccc} \frac{k^\zeta \gamma _1^\zeta B^\zeta }{\mu ^\zeta }&{}0&{}0&{}0 &{}\frac{k^ \zeta k_1^{\zeta } \gamma _1^\zeta B^\zeta }{\mu ^\zeta }&{}\frac{k^{\zeta } k_1^{\zeta }\gamma _1^\zeta B^\zeta }{\mu ^\zeta }\\ 0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}\frac{k^\zeta \gamma _2^\zeta B^\zeta }{\mu ^\zeta } &{}\frac{k^\zeta \gamma _2^\zeta B^\zeta }{\mu ^\zeta } &{} \frac{k^\zeta k_2^\zeta \gamma _2^\zeta B^\zeta }{\mu ^\zeta }&{} \frac{k^\zeta k_2^\zeta \gamma _2^\zeta B^\zeta }{\mu ^\zeta }\\ 0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0\\ \end{array} \right] , \end{aligned}$$

and,

$$\begin{aligned}{} & {} J_{VHC}\\{} & {} =\left[ \begin{array}{cccccc} h_1^\zeta +\mu ^\zeta &{}0&{}0&{}0&{}{-c_r}^\zeta \varepsilon ^\zeta &{}0\\ {-h_1}^\zeta &{}\mu ^\zeta &{}0&{}0&{}0&{}0\\ 0&{}0&{}c_r^\zeta +c_1^\zeta +\mu ^\zeta &{}0&{}0\\ &{}0&{}0{-c_1}^\zeta &{}\mu ^\zeta &{} 0&{}0\\ 0&{}0&{}0&{}c_r^\zeta \varepsilon ^\zeta +\eta ^\zeta +\mu ^\zeta &{}0\\ 0&{}0&{}0&{}0&{}-\eta ^\zeta &{}\mu ^\zeta \\ \end{array} \right] . \end{aligned}$$

The basic reproduction number, $\mathcal {R}_0^{HC}$ for the co-infection model HIV-HCV is the maximum of eigenvalues of the next generation matrix $J_{FHC}({J_{VHC})}^{-1}$, that is

$$\begin{aligned}{} & {} \mathcal {R}_0^{HC}\\{} & {} \quad =\max \left\{ \frac{B^\zeta \gamma _2^\zeta k^\zeta \left( \mu ^\zeta +c_1^\zeta \right) }{\mu ^{2\zeta }\left( c_1^\zeta +c_r^\zeta +\mu ^\zeta \right) },\right. \\{} & {} \qquad \left. \frac{B^\zeta \gamma _1^\zeta k^\zeta }{\mu ^\zeta \left( h_1^\zeta +\mu ^\zeta \right) },0,0,0,0\right\} \\{} & {} \quad =\max {\left\{ \mathcal {R}_0^{H},\mathcal {R}_0^{C}\right\} }, \end{aligned}$$

where, $\mathcal {R}_0^{H}$ and $\mathcal {R}_0^{C}$ are the basic reproduction number of sub-models HIV-AIDS only and HCV only respectively. $\square$

Theorem 9

The co-infection (HIV and HCV)-free equilibrium, $H_{HC}^0$, of the model is locally asymptotically stable if $\mathcal {R}_{0}^{HC}<1$ and unstable otherwise.

Proof

The Jacobian matrix of the HIV-HCV co-infection model at the disease-free equilibrium $H_{HC}^0$ is

$$\begin{aligned}{} & {} J_{HC}^0 =\left[ \begin{array}{ccccccc}{-\mu ^\zeta }&{}-\frac{B^\zeta \gamma _1^\zeta k^\zeta }{\mu ^\zeta }&{}{c_r}^\zeta &{}\frac{-B^\zeta \gamma _2^\zeta k^\zeta }{\mu ^\zeta }&{}\frac{-B^\zeta \gamma _2^\zeta k^\zeta }{\mu ^\zeta }&{} \frac{B^\zeta \gamma _1^\zeta k^\zeta }{\mu }&{}\frac{B^\zeta \gamma _1^\zeta k^\zeta }{\mu ^\zeta }\\ 0&{}\frac{B^\zeta {\gamma _1^\zeta }{k^\zeta }}{\mu ^\zeta }-{\mu ^\zeta -h_1^\zeta }&{}0&{}0&{}0&{}{c_r^\zeta }{\varepsilon ^\zeta }+\frac{B^\zeta \{\gamma _1^\zeta }{k^\zeta }{k_1^\zeta }{\mu ^\zeta }&{}{c_r^\zeta }{\varepsilon ^\zeta } +\frac{B^\zeta \gamma _1^\zeta k^\zeta k_1^\zeta }{\mu ^\zeta }\\ 0&{}0&{}0&{} c_r^\zeta \varepsilon ^\zeta +\frac{B^\zeta \gamma _1^\zeta k^\zeta k_1^\zeta }{\mu ^\zeta }&{}c_r^\zeta \varepsilon ^\zeta +\frac{B^\zeta \gamma _1^\zeta k^\zeta k_1^\zeta }{\mu ^\zeta } &{}\frac{B^\zeta \gamma _2^\zeta k^\zeta k_2^\zeta }{\mu ^\zeta }&{}\frac{B^\zeta \gamma _2^\zeta k^\zeta k_2}{\mu ^\zeta }\\ 0&{}0&{}0&{}{c_1^\zeta }&{}-\mu ^\zeta &{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}\frac{B^\zeta \gamma _2^\zeta k^\zeta k_2^\zeta }{\mu ^\zeta }+\eta ^\zeta + \mu ^\zeta &{}0\\ 0&{}0&{}0&{}0&{}0&{}\eta ^\zeta &{}-\mu ^\zeta \\ \end{array} \right] . \end{aligned}$$

Rewriting the $J_{HC}^0$ as

$J_{HC}^0=\left[ \begin{array}{cc}J_{11}&{}J_{12}\\ J_{21}&{}J_{22}\\ \end{array}\right] .$

Where,

$$\begin{aligned} J_{11}= & {} \left[ \begin{array}{cccc} -\mu ^\zeta &{}-\frac{B^\zeta \gamma _1^\zeta k^\zeta }{\mu ^\zeta }&{}c_r^\zeta &{}-\frac{B^\zeta \gamma _2^\zeta k^\zeta }{\mu ^\zeta }\\ 0&{}\frac{B^\zeta \gamma _1^\zeta k^\zeta }{\mu ^\zeta }-\mu ^\zeta -h_1^\zeta &{}0&{}0\\ 0&{}h_1^\zeta &{}{\mu ^\zeta }&{}0\\ 0&{}0&{}0&{} -\frac{B^\zeta \gamma _2^\zeta k^\zeta }{\mu ^\zeta }-c_r^\zeta -\mu ^\zeta -c_1^\zeta \\ \end{array}\right] , \\ J_{12}= & {} \left[ \begin{array}{ccc} \frac{B^\zeta \gamma _2^\zeta k^\zeta }{\mu ^\zeta } &{} \frac{B^\zeta \gamma _2^\zeta k^\zeta }{\mu ^\zeta }&{}\frac{B^\zeta \gamma _2^\zeta k^\zeta }{\mu ^\zeta }\\ 0&{}\frac{B^\zeta \gamma _2^\zeta k^\zeta }{\mu ^\zeta }&{}-\frac{B^\zeta \gamma _1^\zeta k^\zeta k_1^\zeta }{\mu ^\zeta }\\ 0&{}0&{}0\\ -\frac{B^\zeta \gamma _2^\zeta k^\zeta }{\mu ^\zeta }&{}-\frac{B^\zeta \gamma _2^\zeta k^\zeta k_2^\zeta }{\mu ^\zeta }&{}-\frac{B^\zeta \gamma _2^\zeta k^\zeta k_2^\zeta }{\mu ^\zeta } \\ \end{array}\right] , \\ J_{21}= & {} \left[ \begin{array}{cccc} 0&{}0&{}0&{}c_1^\zeta \\ 0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0 \\ \end{array}\right] ,\\ J_{22}= & {} \left[ \begin{array}{ccc} -\mu ^\zeta &{}0&{}0\\ 0&{}-\eta ^\zeta -\mu ^\zeta -c_r^\zeta \varepsilon ^\zeta &{}0\\ 0&{}\eta ^\zeta &{}-\mu ^\zeta \\ \end{array}\right] . \end{aligned}$$

The co-infection (HIV and HCV)-free equilibrium is locally asymptotically stable if and only if the roots of $J_{11}$ and $J_{22}$ have all negative eigenvalues. The eigenvalues of $J_{22}$ are $-\mu ^\zeta$,$-\mu ^\zeta$,$-(\eta ^\zeta +\mu ^\zeta +c_r^\zeta \varepsilon ^\zeta )$ which are negative. The eigenvalues of $J_{11}$ are $-\mu ^\zeta$, $-\mu ^\zeta$,$-\frac{\mu ^{2\zeta } +h_1^\zeta \mu ^\zeta -B^\zeta \gamma _1^\zeta k^\zeta }{\mu ^\zeta }$, $-\frac{\mu ^{2\zeta } -B^\zeta \gamma _2^\zeta k^\zeta +c_1^\zeta \mu ^\zeta + c_r^\zeta \mu ^\zeta }{\mu ^\zeta }$. However, all the eigenvalues of $J_{11}$ are negative when

$$\begin{aligned}{} & {} \frac{\mu ^{2 \zeta }+h_1^\zeta \mu ^\zeta -B^\zeta \gamma _1^\zeta k^\zeta }{\mu ^\zeta }>0\Rightarrow \frac{B^\zeta \gamma _1^\zeta k^\zeta }{\mu ^\zeta \left( \mu ^\zeta +h_1^\zeta \right) }<1\nonumber \\{} & {} \quad \Rightarrow \mathcal {R}_0^{H}<1, \end{aligned}$$

(29)

and

$$\begin{aligned}{} & {} \frac{\mu ^{2\zeta } - B^\zeta \gamma _2^\zeta k^\zeta + c_1^\zeta \mu ^\zeta +c_r^\zeta \mu ^\zeta }{\mu ^\zeta }>0\nonumber \\{} & {} \quad \Rightarrow \frac{B^\zeta \gamma _2^\zeta k^\zeta }{\mu ^\zeta \left( c_1^\zeta +c_r^\zeta +\mu ^\zeta \right) }<1\Rightarrow \frac{\mu ^\zeta }{(\mu ^\zeta +c_1^\zeta )}\mathcal {R}_0^{C}<1.\nonumber \\ \end{aligned}$$

(30)

Therefore, if inequality in (29) and (30) is satisfied, then $\mathcal {R}_{0}^{HC}<1$. $\square$

5 Numerical scheme for the solution

Numerous compelling arguments support the use of numerical techniques for the solution of systems of fractional-order differential equations (FODEs) [63,64,65,66]. Closed-form solutions are either not available or highly difficult to develop in many situations. When approximating the solutions of fractional-order differential equation (FODE) systems, numerical techniques offer an alternate method. Complex FODE systems can be modeled with greater ease using numerical techniques. They allow for the precise study of a wide variety of physical processes and systems by accommodating a wide variety of boundary conditions, initial conditions, and nonlinearities.

When analytical methods fail to yield useful results, this adaptability becomes very valuable [67]. Solutions to FODE problems can be efficiently and accurately provided by numerical techniques. The development of increasingly sophisticated computer tools and algorithms has made it possible to obtain accurate and trustworthy solutions. Researchers can get insight into the behavior and dynamics of FODE systems by simulating and analyzing these systems with these methods [68]. Due to the occurrence of non-local and non-integer-order derivatives, numerical instability is a common feature of FODE systems. Stability and the prevention of error Propagation can be designed into numerical methods. When simulating FODE systems, it is possible to preserve stability and accuracy by employing a variety of numerical techniques, such as implicit schemes and stabilizing algorithms. Results from FODE systems can be verified using experimental data using numerical techniques, which allow for experimental validation. The complexity of the system often makes it so that direct experimental measurements are either unavailable or impractical.

Researchers can validate their numerical predictions with relevant tests by simulating the system using numerical techniques. Because of this, the numerical models may be checked and double-checked for accuracy. Optimization using numerical methods FODE systems can be optimized using numerical methods. Scientists can get the system to behave how they want it to be defining an optimization problem and then using numerical optimization techniques to find the optimal solution. This allows for the optimization and exploration of parameter spaces for systems that would be difficult to analyze analytically. In conclusion, when analytical solutions are scarce or nonexistent, numerical schemes provide a practical and effective method for solving FODE systems [69]. In researching and analyzing complex FODE systems, their malleability, efficiency, precision, stability, and ability to validate against experimental data make them valuable tools.

In the light of the above discussion, we have attempted to solve the Caputo system in (9) with the help of a most commonly used numerical method known as the fractional Adams method (FAM) that uses predictor-corrector type structure as explained in [70,71,72]. It is worthwhile to be noted that the Adams-Bashforth-Moulton (ABM) fractional numerical method combines explicit and implicit procedures to efficiently solve FODE. Numerical simulations incorporating fractional derivatives can benefit from their increased accuracy, stability, and ability to handle stiff equations. To approximate the solution of Caputo model (9) by ABM, we take the system of nonlinear fractional-order differential equation (FODE) as given in [70,71,72]:

$$\begin{aligned}{} & {} {}^C_0\Omega _{t}^{\zeta }\psi (t)=F(t, \psi (t)), 0\le t \le T, \psi ^{(j)}(0)\nonumber \\{} & {} \quad =\psi _{0}^{j}, j=0, 1, 2,..., m-1, \end{aligned}$$

(31)

where, $\zeta >0$ and $m=\lceil \zeta \rceil$ is the integer greater than or equal to $\zeta$. The $\zeta$ order fractional derivative of $\psi (t)$ in Caputo sense denoted by $^C_0\Omega _{t}^{\zeta }\psi (t)$ is defined by

$$\begin{aligned}{} & {} {}^C_0\Omega _{t}^{\zeta }\psi (t)=\dfrac{1}{\Gamma (n-\zeta )}\\{} & {} \int _{0}^{t}(t-r)^{n-\zeta -1}\psi ^{(n)}(r)dr, n-1\\{} & {} \quad<\zeta <n, n\in Z^{+}. \end{aligned}$$

Note that the notation $\psi ^{(n)}(r)$ denotes the $n^{th}$ integer order derivative of $\psi (r)$. It is worth mentioning that the theorems of existence and uniqueness for the fractional IVP in (31) can be found in [70,71,72]. The fractional differential equation (31) is also equivalent to the Volterra integral equation given by

$$\begin{aligned} \psi (t)= & {} \sum _{j=0}^{m-1}\psi _{0}^{(j)}\dfrac{t^{j}}{j!}+\dfrac{1}{\Gamma (\zeta )} \int _{0}^{t}(t-r)^{\zeta -1}F(r, \psi (r))dr \nonumber \\= & {} \sum _{j=0}^{m-1}\psi _{0}^{(j)}\dfrac{t^{j}}{j!}+^C_0\Omega _{t}^{-\zeta }F(t,\psi (t)). \end{aligned}$$

(32)

The predictor-corrector type method (FAM) is used in several existing research works such as [73,74,75,76,77] for integrating equations of the type (32). Each equation in the Caputo fractional-order model (9) can be discretized in the following way:

$$\begin{aligned} \psi _{n+1}^P&= \psi _0+\sum _{j=0}^{n} b_{j,n+1}F(t_j,\psi _j),\nonumber \\ \psi _{n+1}&= \psi _0+\sum _{j=0}^{n} a_{j,n+1}F(t_j,\psi _j)\nonumber \\&\quad + a_{n+1,n+1}F(t_{n+1},\psi _{n+1}^P), \end{aligned}$$

(33)

where,

$$\begin{aligned}{} & {} a_{j,n+1}=\dfrac{\Delta t^{\zeta }}{\Gamma (\zeta +2)}\nonumber \\{} & {} \quad {\left\{ \begin{array}{ll} n^{\zeta +1}-(n-\zeta )(n+1)^{\zeta }, \quad \text {if}, j=0, \\ (n-j+2)^{\zeta +1}-2(n-j+1)^{\zeta +1}\\ \quad +(n-j)^{\zeta +1}, \quad \text {if}, 1\le j \le n, \\ 1, \quad \text {if}, j=n+1. \end{array}\right. } \end{aligned}$$

(34)

The above-discussed fractional Adams method is employed to simulate the Caputo model given in (9). We have used MATLAB software to run the required simulations.

5.1 Convergence analysis

In this part, we derive criteria for boundedness and convergence on system signals, and we study the case of systems defined by fractional-order nonlinear differential equations [78]

$$\begin{aligned} \left\{ \begin{array}{rcl} {{}^C_0\Omega }^{\zeta }\phi &{}=&{} g(t,\phi ), \\ \end{array}\right. \end{aligned}$$

(35)

where, $\phi (t)$ and $g(t, \phi (t)) \in \Re ^n$ with initial condition $\phi (0) \in \Re ^n$. Here we assumed that g(t,0) = 0 for all t positive.

Theorem 10

For the system (35), If there exists a scalar function $\Im = \Im (\phi )$, a scalar class-K function $Z_1$ and, for any $\phi$ (or at origin $\phi = 0$) and a bounded continuous differentiable function h($\cdot$, $\phi$) such that [78]

(i) $\Im \ge Z_1(\phi )$ (ii) ${{}^C_0\Omega }^{\zeta }\Im \le -|h(\phi , t)|^2Z_1(\phi )$ (iii) $I^\zeta [\left\| h(\phi , t)\right\| ^2] \rightarrow \infty$ for any fixed $\phi$ as $t\rightarrow \infty$. Then, $\Vert \phi (t)\Vert \rightarrow 0$ as $\hbox {t} \rightarrow \infty$.

Theorem 11

For the system (35), there exists a positive-definite function $\Im = \Im (\phi ) \in \Re$, such that ${{}^C_0\Omega }^{\zeta }\Im = h(\Im )$ locally (globally) holds with the concave function h($\cdot$) such that $h(\phi ) = 0 \Rightarrow \phi = 0$ and $h'(0) < 0$. Then the trajectories of (35) are locally (globally) asymptotically stable and converges to zero.

Remark

For $\zeta =1$, the above theorem can be simplified by stating that since ${{}^C_0\Omega }^{\zeta }\Im \le 0$ in $\omega ^k$ (with $\omega$ in a compact neighborhood around the origin $\phi = 0$) which is not necessarily true for any kind of fractional derivative and $\Im$ cannot increase and therefore $\phi (t)$ is finite.

6 Exploration of memory effect

This section is devoted to exploring the impact of memory traces on the transmission dynamics of the HIV-HCV co-infection epidemic model under the Caputo-type fractional-order derivative. To study the effect of memory trace on the fractional-order HIV-HCV co-infection epidemic model described in (9), the Caputo operator is used as discussed in definition 2. Now for the fractional-order $\zeta$, $0<\zeta \le 1$, the fractional derivation of function $\eta (t)$ is given as

$$\begin{aligned} {{}^C_0\Omega }^{\zeta }_t\eta (t)=\mathcal {G}(\eta (t),t). \end{aligned}$$

(36)

The Caputo operator for the function $\eta (t)$ as discussed in definition 2 is given by

$$\begin{aligned} {{}^C_0\Omega }^{\zeta }_t\eta (t)=\frac{1}{{\Gamma }(1-\zeta )}\int ^t_0{\frac{\eta '(x)}{(t-x)^{\zeta }}}dx. \end{aligned}$$

(37)

Now, we define the numerical L1 scheme that involves memory traces under the properties of fractional-order derivative by applying the Caputo fractional derivative to the method. The fractional derivative of $\eta (t)$ using L1 scheme is numerically approximated as [79, 80]

$$\begin{aligned}{} & {} {{}^C_0\Omega }^{\zeta }_t\eta (t) \nonumber \\{} & {} \approx \frac{(dt)^{-\zeta }}{{\Gamma }(2-\zeta )}\left[ \sum ^{H-1}_{m=0}\big [\eta (t_{m+1})-\eta (t_m)][(H-m)^{1-\zeta }\right. \nonumber \\{} & {} \left. -(H-1-m)^{1-\zeta }\big ]\right] . \end{aligned}$$

(38)

By combining Eq.(36) and Eq.(38), we get the numerical solution for the Eq.(36) as given by

$$\begin{aligned} \eta (t_H)\approx & {} {{}^C_0\Omega }^{\zeta }_t{\Gamma }(2-\zeta )\mathcal {G}(\eta (t),t)+\eta (t_{H-1})\nonumber \\{} & {} -\left[ \sum ^{H-2}_{m=0}\big [\eta (t_{m+1})-\eta (t_m)][(H-m)^{1-\zeta }\right. \nonumber \\{} & {} \left. -(H-1-m)^{1-\zeta }\big ]\right] . \end{aligned}$$

(39)

Therefore, using the L1 numerical scheme for the solution of the model (9), we define the Markov term weighted by the Gamma function and the $\eta$-memory trace respectively as

$$\begin{aligned} \hbox {Markov term}= {{}^C_0\Omega }^{\zeta }_t{\Gamma }(2-\zeta )\mathcal {G}(\eta (t),t)+\eta (t_{H-1}). \end{aligned}$$

(40)

and

$$\begin{aligned} \hbox {Memory trace}= & {} \sum ^{H-2}_{m=0}\big [\eta (t_{m+1})-\eta (t_m)][(H-m)^{1-\zeta }\nonumber \\{} & {} -(H-1-m)^{1-\zeta }\big ]. \end{aligned}$$

(41)

6.1 Memory trace using L1 scheme for the proposed model

Now following the similar procedure discussed in Sect. 6, the numerical approximation for each class in system (9) along with Markov term and memory trace is obtained. Therefore, the numerical approximation for susceptible class S(t) is given by

$$\begin{aligned} {{}^C_0\Omega }^{\zeta }_t S(t)\approx & {} \frac{(dt)^{-\zeta }}{{\Gamma }(2-\zeta )}\left[ \sum ^{H-1}_{m=0}\big [S(t_{m+1})-S(t_m)][(H-m)^{1-\zeta }\right. \nonumber \\{} & {} \left. -(H-1-m)^{1-\zeta }\big ]\right] . \end{aligned}$$

(42)

By combining (42) and first equation of model (9), the numerical solution of susceptible class S(t) is finally given by

$$\begin{aligned} S (t_{H})\approx \big [\hbox {Markov term} \ S(t)-\hbox {Memory trace} \ S(t)\big ], \end{aligned}$$

(43)

with

$$\begin{aligned} \hbox {Markov term}= {{}^C_0\Omega }^{\zeta }_t{\Gamma }(2-\zeta )\mathcal {G}(S(t),t)+S(t_{H-1}), \end{aligned}$$

(44)

and

$$\begin{aligned} \hbox {Memory trace}= & {} \sum ^{H-2}_{m=0}\big [S(t_{m+1})-S(t_m)][(H-m)^{1-\zeta }\nonumber \\{} & {} -(H-1-m)^{1-\zeta }\big ]. \end{aligned}$$

(45)

By a similar process, the numerical approximation for the HIV infected class $I_{HIV}(t)$ is given by

$$\begin{aligned} {{}^C_0\Omega }^{\zeta }_t I_{HIV}(t)\approx & {} \frac{(dt)^{-\zeta }}{{\Gamma }(2-\zeta )}\left[ \sum ^{H-1}_{m=0}\big [I_{HIV}(t_{m+1})\right. \nonumber \\{} & {} -I_{HIV}(t_m)][(H-m)^{1-\zeta }\nonumber \\{} & {} \left. -(H-1-m)^{1-\zeta }\big ]\right] . \end{aligned}$$

(46)

By combining (46) and second equation of model (9), the numerical solution of HIV infected class $I_{HIV}(t)$ is finally given by

$$\begin{aligned}&I_{HIV} (t_{H})\approx \big [\hbox {Markov term} \ I_{HIV}(t)\nonumber \\&\quad -\hbox {Memory trace} \ I_{HIV}(t)\big ], \end{aligned}$$

(47)

with

$$\begin{aligned} \hbox {Markov term}&= {{}^C_0\Omega }^{\zeta }_t{\Gamma }(2-\zeta )\mathcal {G}(I_{HIV}(t),t)+I_{HIV}(t_{H-1}), \end{aligned}$$

(48)

and

$$\begin{aligned} \hbox {Memory trace}= & {} \sum ^{H-2}_{m=0}\big [I_{HIV}(t_{m+1})\nonumber \\{} & {} -I_{HIV}(t_m)][(H-m)^{1-\zeta }\nonumber \\{} & {} -(H-1-m)^{1-\zeta }\big ]. \end{aligned}$$

(49)

Similarly, we can obtain the numerical solutions for acute HIV-AIDS class $A_{HIV}(t)$, acute HCV class $A_{HCV}(t)$, latent HCV class $L_{HCV}(t)$, acute HIV-HCV co-infection class $I_{HA}(t)$, infected HIV and latent HCV co-infection class $I_{HCL}(t)$, respectively.

7 Results and discussion

Numerical results have been computed using the data of parameters given in Table 1. The co-infection model of HIV and HCV (8) is a deterministic, classical epidemic model in which a population is partitioned into seven subsets. The classical form of the HIV-HCV model describes the movement of individuals between these regions using ordinary differential equations (ODEs). However, the model transforms into a FODE system when the Caputo operator is used with varying values of the fractional-order $\zeta$ as shown in (9). The Caputo operator, which extends the idea of differentiation to orders other than 1, is a fractional derivative operator. Systems with memory or long-range dependencies are often described using fractional calculus. The HIV-HCV epidemic dynamics can be extended to include fractional-order effects by using the Caputo operator. Changing the HIV-HCV model’s fractional-order $\zeta$ has several effects on the epidemic’s dynamics as depicted in Fig. 2 and stated below:

• Inhibiting or promoting the spread of the pandemic The system’s memory and long-range reliance are both controlled by the fractional-order $\zeta$. For $\zeta$ values below 1, the epidemic spreads more quickly than the standard integer-order HIV-HCV model predicted. For $\zeta$ levels above 1, however, the epidemic progresses at a slower rate.

• The decline of infected people is not exponential In the classical HIV-HCV model, the number of infected people decreases exponentially as they get immune and enter the recovered compartment. However, the decay of infected people becomes non-exponential when the Caputo operator is utilized with fractional orders. The decay rate is proportional to the fractional-order $\zeta$, with slower decay rates corresponding to lower values of $\zeta$.

• Erratic dispersion The fractional-order $\zeta$ modifies the epidemic’s spreading dynamics. The classical HIV-HCV model predicts that the virus will spread through the population as though by normal diffusion. However, when fractional orders are included, the spreading behavior no longer follows the rules of classical diffusion, and the process is deemed abnormal. The velocity and shape of the spread are both determined by the value of $\zeta$.

• Implications for Long-Term Memory Because of the long-term memory effects seen in fractional-order systems, the course of the pandemic will be affected by its prior behavior. The depth and breadth of the system’s memory are set by the fractional-order $\zeta$. As $\zeta$ decreases, the memory effects become more significant, and the past states have a greater impact on the epidemic’s future development.

It is worth noting that the HIV-HCV model with the Caputo operator and fractional orders can exhibit highly nuanced and value-dependent behavior. Since closed-form solutions are rarely, if ever, attainable, analyzing the dynamics of such systems typically entails the use of numerical methods and simulations. Numerical methods like fractional integration and fractional differential equations are used to investigate the dynamics of fractional-order epidemic models.

Fig. 2

Behavior of each state variable in the Caputo model (9) for different values of $\zeta$ while using the parameters’ values from Table 1

The HIV-HCV model with the Caputo operator (9) and various biological parameters can display nonlinear behavior, which should be taken into account. The dynamics of the model as a whole may be affected by a change in a single parameter. Therefore, it is necessary to conduct an in-depth analysis to comprehend the impacts of varying parameter values; this is typically done by numerical simulations or mathematical approaches specifically designed for fractional differential equations, such as numerical integration methods or stability analysis. It is also possible to calibrate the model’s parameters and evaluate their impact on epidemic behavior using real-world data and empirical observations. To better understand the impact of these changes, we have attempted to mimic the Caputo model by holding the fractional parameter $\zeta$ constant while changing other key biological factors. For instance, in Fig. 3, the dynamics of the state variable shift when the value of parameter $h_1$ is reduced. Notably, and in fair agreement with real-world facts, the vulnerable population falls as the progression rate from HIV to AIDS drops. Similarly, in Fig. 4, the number of infected HIV and acute HCV co-infected individuals starts dwindling as the propagation factor for the individuals $h_2$ is reduced. Effects in other compartments are also depicted in the same Figure. The influence of $\beta _h$ and $\beta _c$ in the class $I_{HIV}(t)$ is shown in Fig. 5 wherein the number of HIV-infected people reduces when a force of infection associated with HIV ($\beta _h$) is halved every time while the number of HIV-infected people starts increasing when a force of infection associated with HCV is reduced. The pace of infection-induced deterioration of healthy T-cells slows down as infection intensity drops. Because of this, the curve showing infected T-cells would increase more slowly. This scenario is also in good alignment with reality. The number of infected HIV and acute HCV co-infected individuals starts declining when both $\beta _h$ and $\beta _c$ are reduced since the people have co-infection, as shown in Fig. 6. Finally, when both of these biological parameters ($\beta _h$ and $\beta _c$) are reduced, the number of infected HIV and latent HCV co-infected individuals start decreasing speedily as evident in Fig. 7. The modulation of these behaviors by Caputo fractional derivative, which result in memory effects and non-local dynamics, produces complex and frequently counterintuitive system responses. This complexity, which is a defining feature of such systems, emphasizes the rich dynamics that can emerge from fractional-order models.

Fig. 3

Behavior of each state variable in the Caputo model (9) for $\zeta = 0.95$ while using the parameters’ values from Table 1 with decreasing $h_1$ values

Fig. 4

Behavior of each state variable in the Caputo model (9) for $\zeta = 0.95$ while using the parameters’ values from Table 1 with decreasing $h_2$ values

Fig. 5

Behavior of $I_{HIV}(t)$ in the Caputo model (9) for $\zeta = 0.95$ while using the parameters’ values from Table 1 with decreasing $\beta _h$ and $\beta _c$ values

Fig. 6

Behavior of $I_{HA}(t)$ in the Caputo model (9) for $\zeta = 0.95$ while using the parameters’ values from Table 1 with decreasing a $\beta _h$ and b $\beta _c$ values

Fig. 7

Behavior of $I_{HCL}(t)$ in the Caputo model (9) for $\zeta = 0.95$ while using the parameters’ values from Table 1 with decreasing a $\beta _h$ and b $\beta _c$ values

In epidemiology, the measure of a disease’s spreadability is the Basic Reproductive Number, abbreviated as $\mathcal {R}_0$. It is the number of further cases that can be expected from a single initial case in a population where everyone is at risk of contracting the disease. To better grasp how $\mathcal {R}_0$ responds to changes in two external variables, we will use a three-dimensional graph (with the two external variables along the x and y axes and $\mathcal {R}_0$ along the z-axis) to visualize the relationship between the three values. Additionally, a contour plot is also shown side by side. Statistics and mathematics use contour plots to visualize three-dimensional data in two dimensions. Contours cut across the three-dimensional graph as level curves or isolines. The contour’s level indicates the function’s “height” or “depth” at each point in the graph. Closely spaced contour lines indicate a steep graph, while farther apart lines indicate a gentler slope. Contour plots depict gradients, peaks, valleys, and complex variable interactions in complex data.

Figure 8 shows the dynamical behavior of $\mathcal {R}_0^{H}$ based on variations carried out in $\mu$ (natural mortality rate) and $\gamma _1$ (HIV transmission rate per sexual contact). It shows that with increasing values of $\gamma _1$, the rate of $\mathcal {R}_0^{H}$ starts increasing while $\mu$ does not cause many effects. This analysis is in agreement with the theoretical observations wherein disease can spread if the HIV transmission rate increases. The results of changing $h_1$ (progression rate from HIV to AIDS) and $\gamma _1$ (HIV transmission rate per sexual contact) on $\mathcal {R}_0^{H}$ are shown in Fig. 9. Consistent with the theoretical results, it has been found that when $h_1$ and $\gamma _1$ are both active, $\mathcal {R}_0^{H}$ increases. Compared to Fig. 8, the basic reproduction number for Fig. 9 is higher. Parameters $h_1$ and $\gamma _1$ are responsible. The value of $\mathcal {R}_0^{H}$ is profoundly impacted by these parameters. The results in $\mathcal {R}_0^{H}$, when k and $h_1$ (progression rate from HIV to AIDS) are changed, are shown in Fig. 10. $\mathcal {R}_0^{H}$ is seen to increase as k grows, corroborated by theoretical predictions given that the likelihood of simultaneous infection grows with the number of sexual partners. The value of $\mathcal {R}_0^{H}$ is sensitive to the k parameter.

It may be noted that the major goal of these plots is to visually depict the dynamic behavior of $\mathcal {R}_0$ about variations in particular model parameters. Understanding the sensitivity of the epidemic model and identifying important elements that can influence the propagation of the disease is of utmost importance. Although the changes in $\mathcal {R}_0$ may seem minor, these variances are crucial in epidemiological modeling. They assist in forecasting the critical values for disease management and in comprehending how minor modifications in parameters can profoundly impact disease dynamics.

Fig. 8

Behavior of $\mathcal {R}_0^{H}$ under $(\mu , \gamma _1)$ via a surface and b contour plots

Fig. 9

Behavior of $\mathcal {R}_0^{H}$ under $(h_1, \gamma _1)$ via a surface and b contour plots

Fig. 10

Behavior of $\mathcal {R}_0^{H}$ under $(k, h_1)$ via a surface and b contour plots

Changing the values of k (average number of sexual partners required per year) and $\mu$ (natural mortality rate) is depicted in Fig. 11 to show how $\mathcal {R}_0^{C}$ behaves dynamically. It has been noted that as k increases and $\mu$ decreases, $\mathcal {R}_0^{C}$ also rises. This is because an increase in the average number of sexual partners exposes more people to the disease when the natural mortality rate is low. The dynamical behavior of $\mathcal {R}_0^{C}$ is seen in Fig. 12 as k and $c_1$ (progression rate from acute to latent HCV) are varied. Increases in $\mathcal {R}_0^{C}$ are seen to occur as k grows and decreases in $c_1$. The reason is that if people increase their average number of sexual partners while the progression rate from acute to latent HCV is low, then there will inevitably be more people infected. The dynamical behavior of $\mathcal {R}_0^{C}$ is seen in Fig. 13 as k and $c_r$ ( Rate of spontaneous removal of acute HCV) are varied. The observed relationship between $c_r$ and $\mathcal {R}_0^{C}$ is a decrease in $\mathcal {R}_0^{C}$ with increasing $c_r$. This is because an increase in the average number of sexual partners is not adequate to counteract the large drop in $\mathcal {R}_0^{C}$ that occurs when the rate of spontaneous removal of acute HCV rises.

Fig. 11

Behavior of $\mathcal {R}_0^{C}$ under $(k,\mu )$ via a surface and b contour plots

Fig. 12

Behavior of $\mathcal {R}_0^{C}$ under $(k, c_1)$ via a surface and b contour plots

Fig. 13

Behavior of $\mathcal {R}_0^{C}$ under $(k, c_r)$ via a surface and b contour plots

Changing the values of k and $\mu$ (natural mortality rate) is depicted in Fig. 14 to show how $\mathcal {R}_0^{HC}$ behaves dynamically. It has been noted that as k increases and $\mu$ is small, $\mathcal {R}_0^{HC}$ rises drastically. This is because an increase in the average number of sexual partners exposes more people to the disease when the natural mortality rate is a bit low. However, when $\mu$ is high then for sure there are not many people to have sex with, and $\mathcal {R}_0^{HC}$ shows a small value thereby showing compatibility with real-world scenarios. Similarly, the values of k and $h_1$ (progression rate from HIV to AIDS) play a vital role in the dynamics of $\mathcal {R}_0^{HC}$ as depicted in Fig. 15. A little larger k brings $\mathcal {R}_0^{HC}$ to a peak level no matter if $h_1$ is small. $\mathcal {R}_0^{HC}$ can be reduced by controlling k parameter. Finally, when the HIV transmission rate per sexual contact ($\gamma _1$) moves to a smaller value then it gets credit to reduce $\mathcal {R}_0^{HC}$ as shown in Fig. 16.

Fig. 14

Behavior of $\mathcal {R}_0^{HC}$ under $(k, \mu )$ via a surface and b contour plots

Fig. 15

Behavior of $\mathcal {R}_0^{HC}$ under $(k, h_1)$ via a surface and b contour plots

Fig. 16

Behavior of $\mathcal {R}_0^{HC}$ under $(\gamma _1, h_1)$ via a surface and b contour plots

Exploring fractional-order epidemic models in the context of HIV/HCV co-infection has diverse applications for public health departments, which are crucial in managing and reducing the impact of both diseases [81, 82]. These models offer a detailed comprehension of the intricacies of co-infection dynamics, improving the capacity to forecast outbreaks and transmission, hence enabling more prompt and focused responses. They play a crucial role in devising optimum treatment methods, taking into account the distinctive interactions between HIV and HCV, resulting in enhanced patient care outcomes. Moreover, these models facilitate the effective distribution of healthcare resources, especially in regions with elevated co-infection risks. The knowledge acquired from these studies is essential for developing efficient public health strategies, customizing educational and awareness initiatives for vulnerable populations, and promoting a cooperative, interdisciplinary approach to disease control. Furthermore, they play a crucial role in determining immunization tactics and have far-reaching implications for global health, given that both HIV and HCV are significant public health issues on a global scale. In conclusion, the use of these models guarantees a more customized and efficient public health intervention, leading to a notable enhancement in disease management and improved health results for those impacted by both HIV and HCV.

Fig. 17

The impact of memory trace on a S(t) class b $I_{HIV}(t)$ class c $A_{HIV}(t)$ class and d $A_{HCV}(t)$ class for different values of $\zeta$

Fig. 18

The impact of memory trace on a $L_{HCV}(t)$ class b $I_{HA}(t)$ class and $I_{HCL}(t)$ class for different values of $\zeta$

In Figs. 17, 18, we have shown how the memory trace (MT) changes for various $\zeta$ values. The absence of MT in the system is shown graphically when $\zeta =1$ denotes the integer-order situation. Nevertheless, the MT is considered as the fractional-order $\zeta$ begins to move from 0 to 1. Consistently, the measured MT displays an upward trend as $\zeta$ declines from 1 to 0.75. Incorporating this behavior is crucial for building a highly accurate mathematical model, given the inherent MT in the structure of the co-infection system. As shown in Figs. 17, 18, the intrinsic MT in each system population is revealed by our mathematical model’s use of fractional derivatives. In the initial interaction with the disease, susceptible individuals’ immune systems swiftly activate the memory effect in their immune cells, attempting to eradicate any foreign cells that they perceive as a danger. Some memory immune cells, however, gradually die off as they battle abnormal cells from the acute to chronic phase, which happens as a consequence of co-infection. As the communication network of dying immune cells fades away, the memory impact of immune cells diminishes, and foreign cells entering the body now act similarly to bodily cells [83,84,85]. The memory trace graphs (Figs. 17, 18) that accompany our suggested model corroborate this biological phenomenon. In particular, beginning at around 0 days and continuing onwards, a declining tendency in the memory trace may be observed in Figs. 17, 18. Figures 17, 18 show that although some subpopulations see a positive shift in the memory trace, others see a negative change. By combining the data from Figs. 2, 3 with Figs. 17, 18, we can observe that the memory trace is positive during intervals when populations are on the rise and negative during intervals when populations are on the decline. Put simply, memory trace graphs allow us to foretell whether population densities will rise or fall. The numerical simulation findings confirm without a doubt that fractional-order differential equations have been quite successful in capturing the system’s memory trace.

8 Conclusion

The main task of the current study was to model and analyze a fractional-order co-infection model of HIV and HCV epidemics. The nonlinear form of the co-infection epidemic model was divided into seven dynamic classes namely susceptible, HIV-infected individuals, acute HIV-AIDs individuals, acute HCV individuals, latent HCV individuals, infected HIV and acute HCV co-infected individuals, and infected HIV and latent HCV co-infected individuals. The basic reproduction number was determined using the Next-generation matrix method. The model was analyzed through the determination of the model’s steady states. The stabilities of steady states were analyzed based on reproduction number using: signs of the Jacobi matrix evaluated at steady states, Lyapunov functional approach, and Routh-Hurwitz criteria.

The local and global stability analyses were analyzed for disease-free and endemic equilibrium. The numerical results of the nonlinear HIV-HCV co-infection epidemic system applying the fractional ordinary differential equations were presented. Those models which involve nonlinearity are always difficult to solve analytically. Therefore, numerical methods are alternate authentic methods to solve such stiff models. For the proposed fractional-order system the Adams-Bashforth-Moulton fractional numerical method was employed to obtain the numerical results as it combines explicit and implicit procedures to efficiently solve fractional ordinary differential equations. At the end of the article, we demonstrated the numerical simulations for the state variables and different parameters including reproduction numbers of the fractional-order HIV-HCV co-infection model. We concluded that the elimination or prevalence of the co-infection of HIV and HCV is closely related to the basic reproduction number $\mathcal {R}_0^{HC}$ of the co-infection model and the parameters involved in the model. Furthermore, it is concluded based on the obtained results that both diseases have a significant effect on the transmission dynamics of each other during epidemics.

Graphical representations identified the impact of memory effect in the fractional-order co-infection model (9) that is not visible in the classical model to observe the dynamical process of the disease and also the impact of vector compartments. We discovered that the fractional-order proposed HIV-HCV co-infection model has greater stages of freedom in comparison to ordinary derivatives. The components of the proposed model display first-rate feedback whilst non-integer values $\zeta$ of the fractional parameter were used, and in small fractional orders, the growth or lower interest actions were quicker than in large fractional orders. Fractional-order derivations, which might be the most outstanding and dependable compared to classical order, were more efficient in explaining bodily approaches. In addition, numerical simulations have been conducted to provide a clearer illustration of MT utilizing the L1 scheme. This scheme incorporates an MT mechanism that effectively captures and integrates the historical dynamics of the system. The study’s findings show that the L1 scheme used is powerful and useful in studying fractional-order differential equations that arise in the context of disease dynamics. The findings reveal that the fractional derivative’s order exerts a considerable impact on the dynamics of the model. Based on these results, it is clear that the MT becomes zero when $\zeta$ is equal to 1. When the fractional-order $\zeta$ is reduced from 1, the MT undergoes a nonlinear increase, starting at zero. This observed mathematical theory highlights the contrast between fractional and integer-order derivatives. Our findings indicate that as the damping ratio ($\zeta$) falls from 1, the cells take longer to reach equilibrium positions.

The outcome of the current approach enables a substantially better understanding of the mechanism of HCV transmission in a population, which leads to important insights into its spread and control for example, better treatment dosage for different age groups, identifying the best control measure, improves health, prolongs life, reduces the risk of HCV transmission, effectively increases the quality of life of HCV patients and reduces the number of HCV patients during the whole epidemic.

Our research emphasizes the importance of considering the fractional nature of infectious disease dynamics and suggests a promising direction for future studies to refine and optimize treatment approaches based on these insights. This research not only advances our understanding of infection dynamics but also highlights the imperative to consider fractional calculus principles in infectious disease modeling.

9 Future directions

This work opens up a lot of possibilities for future investigation. Improving the model to account for other variables, such as patient age, gender, and concomitant diseases, that impact the dynamics of HIV and HCV co-infection is one possible avenue to explore. Alternatively, one might model the effect of various treatment approaches on the dynamics of co-infection using the Caputo fractional-order derivative. Among these options are antiviral medications for hepatitis C and HIV. To see how well, accurately, and steadily different numerical approaches work compared to the fractional Adams method (FAM), researchers may also try using these approaches on the model. To better understand the best numerical methods for these complicated biological models, this comparative study could be very helpful. Additionally, to have a better grasp of fractional calculus in biological systems, it could be instructive to investigate how changing the derivative’s fractional order affects the model’s dynamics. Lastly, to gain a more complete picture of the worldwide effects of HIV and HCV co-infections, it would be helpful to broaden the model to include dynamics in other demographics or geographic areas.