Two strains and drug adherence: An HIV model in the paradigm of community transmission

Abstract

A two-strain model, comprising of drug-sensitive and drug-resistant strains, is proposed for the dynamics of Human Immunodeficiency Virus (HIV) spread in a community. A treatment model is introduced by taking drug adherence into account. The treatment-free model is analyzed for the effect of treatment availability and drug adherence on disease dynamics. The analysis revealed that for the treatment-free model, at least one strain faces competitive exclusion, and co-existence of both strains is not possible. On the contrary, both strains may co-exist in presence of treatment. The analysis carried out was both local, as well as global. A comprehensive bifurcation analysis showed periodic behaviour and all solutions approached a stable limit cycle for a wide range of parametric values. Overall, we concluded that the treatment availability and drug adherence play a significant role in determining the dynamics of HIV spread. Numerical simulations are performed to validate the analytical results using MATLAB.

1 Introduction

From the epidemiological perspective, Human Immunodeficiency Virus (HIV) is a RNA retrovirus that progressively weakens the hosts’ immune system by targeting the helper CD4$^+$ T cells [1, 2]. The entry of HIV into CD4$^+$ T cells happens through the translation of RNA into DNA, using a viral enzyme called reverse transcriptase. The level of severity of HIV infection can be measured by the viral load or the CD4$^+$ T cell count. In particular, an HIV-infected patient is classified as having Acquired Immunodeficiency Syndrome (AIDS), if the CD4$^+$ T cell count decreases from the normal level (of around 1000 $\hbox {mm}^{-3}$) to 200 $\hbox {mm}^{-3}$ or below [2]. In the absence of any treatment, HIV infection is almost certainly fatal, leading to the death of an infected person within 5–10 years [3]. Despite the continuous progress in the field of treatment and prevention, there is no cure or vaccine for HIV infection yet. However, there are therapeutic interventions like antiretroviral therapy (ART), which reduces the replication of HIV significantly, thereby improving the prognosis for the infected person [4]. Clinical trials and observational studies have shown a substantial reduction in mortality and morbidity, leading to increased life expectancy in HIV-infected patients treated with ART [4,5,6,7]. With the enhanced accessibility to medical facilities, around $73\%$ of individuals living with HIV had started ART by the end of 2020 [8].

Drug adherence usually refers to the degree to which a patient adheres to the prescribed medications, and plays a vital role in the control of chronic diseases, in general. The viral suppression of HIV replication is significantly associated with the adherence to ART regimens [9]. Optimal adherence to ART helps in preventing onward HIV transmission to others [10, 11], minimizing the emergence of drug resistance [12, 13] and brings down the HIV related mortality [14]. There are several factors, namely, personal attributes, institutional management, treatment related factors and psychological factors that lead to ART non-adherence, in developing as well as developed countries [15]. The fear of disclosure of HIV diagnosis and subsequent stigma in the society [16,17,18], low self-efficacy and reading ability [19], as well as mental illness [17, 20] are some major concerning factors related to ART adherence. The situation gets exacerbated when two major diseases collide. In this context, the COVID-19 pandemic has severely affected the ART adherence in HIV patients. On one hand, COVID-19 has interrupted the ART drug supply due to transportation difficulties (as most cities have implemented some form of lockdown), while on the other hand, overstretched healthcare system under COVID-19 resulted in lower quality of clinical care for HIV patients, in addition to suspension of HIV testing [21,22,23]. It has also increased the cases of mental health issues such as depression and anxiety [24]. In July 2020, WHO announced that 73 countries have warned of being at risk of stock of ART medicines running out because of the COVID-19 pandemic, and 24 countries reported having either an extremely low stock of ARTs or disruptions in the supply of these vital medicines [25]. Therefore, it becomes very crucial to study the impact of drug adherence on the dynamics of HIV infection in a population.

The phenomenon of HIV drug resistance (HIVDR) continuously remains a major clinical and public health issue, because resistant HIV not only increases the vulnerability of the infected patients, but also the likelihood of transmission to others [26, 27]. The drug-resistant mutant generally develops via inadequate drug concentration during the treatment. There are lot of reasons of inadequate drug level such as poor adherence, treatment interruptions, host genetics, or use of sub-optimal drug combinations [13]. HIVDR can be classified as primary (transmitted) and secondary (acquired). Primary HIVDR exists even before the initiation of ART. This type of resistance is usually transmitted from other drug-resistant infected person or acquired during previous treatment to eliminate vertical transmission of HIV [28]. This leads to the failure of first-line regimens, especially when not identified at the time of ART initiation [29]. On the other hand, secondary HIVDR evolves through selection process between virus mutants under sub-optimal drug adherence [13]. The development of drug resistance can be easily represented by the following schematic diagram.

Among people failing ART, the levels of resistance reached up to $97\%$ [30]. ART is highly exposed to poor or sub-optimal drug adherence due to the above discussed factors. As a result, the risk of emergence of drug resistance is increasing, concurrently, with the improvement in the coverage of ART. To control the development of HIVDR, it is extremely important to study the impact of ART and its adherence to the dynamics of drug resistance in HIV infected population.

Table 1 Comparison between present work and previously existed studies based on various factors

Mathematical modelling has been useful in epidemiology over the years to determine the major contributing factors to the disease dynamics. Several researchers have analyzed the within-host [2, 31,32,33] and between-host [3, 34,35,36,37,38,39,40] dynamics of HIV spread. The initial efforts towards modelling the HIV dynamics in a community were carried out in [34, 35] and subsequently various refinements have been added to the modelling frameworks. In [3], Cai et al. considered an HIV/AIDS treatment model by dividing the period of infection into the asymptomatic and the symptomatic phases and showed the dependency of disease status on different treatment levels. Naresh et al. [37] proposed a mathematical model for the spread of HIV/AIDS in a population of varying size with immigration of infectives and deduced that the restriction on a direct inflow of infective population can slow down the spread of infection. A different HIV/AIDS epidemic treatment model with nonlinear incidence rate showed that appreciable change in the susceptible individual’s sexual habits reduces both incidence and prevalence of the disease [39]. Recent studies [36, 41,42,43] have shown the dynamics of multiple pathogen strains of various infectious diseases including HIV. Sharomi et al. [36] developed a two-strain HIV model of six compartments with the inclusion of drug-sensitive and drug-resistant HIV-infected populations. In this study, the authors analyzed the impact of ART on HIV dynamics and concluded that the widespread use of ART, despite the risk of the development and transmission of drug-resistant strain, can lead to a significant reduction in disease burden or even eradicate the HIV infection from a community, under certain conditions. Further, Kuddus et al. [43] investigated a two-strain model for general infectious diseases that have a protracted infectious period with treatment. They suggested that the emergence of drug resistance could be reduced if the treatment rate is sufficient to eliminate the drug-sensitive strain from the population. We note that none of the related prior studies have explored the role of drug adherence in the presence of treatment. Also, the effect of drug adherence on the drug-resistant infected population has not been studied yet. In this study, we develop a novel mathematical model that includes two separate compartments for the infected population, namely, the drug-sensitive and the drug-resistant, and analyze the impact of treatment, and its adherence on the community transmission of HIV. In particular, we focus on the role of treatment availability and its adherence, in the control of transmission and emergence of drug-resistant strain in a community. The key features of relevant models in literature along with the novelty of the model proposed here are summarized in Table 1.

To the best of the knowledge of the authors, a rigorous study of the dynamics of HIV spread under treatment in presence of drug-sensitive and drug-resistant infected population has not be conducted using mathematical modelling. Keeping all these facts in mind, we presented a mathematical model in Sect. 2 and rest of this article is organized as follows. In Sect. 3, we analyzed the treatment-free model, followed by the treatment model. In this section, we discussed non-negativity and boundedness of the solutions, existence of equilibrium points and their local and global stability followed by bifurcation analysis. Section 4 is devoted to the estimation of all the parameters and interpretation of all analytic results with the help of numerical simulations. Finally, in Sect. 5, we concluded this article by discussing various possible biological interpretations of obtained results.

Fig. 1

Schematic representation of the model (2.1)

2 Formulation of mathematical model

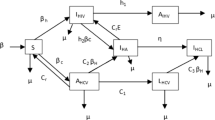
The model divides the total sexually active population into four mutually exclusive groups, namely, susceptible (S), infected individuals with the drug-sensitive strain ($I_S$), infected individuals under treatment (T) and infected individuals with the drug-resistant strain ($I_R$). We assume that the individuals are homogeneously distributed in the given population. The susceptible population increases through the process of recruitment of individuals, who enter into the sexually active class, at a constant rate $\lambda$. The susceptibles become infected after an effective contact either with the drug-sensitive infected or the drug-resistant infected individuals with the incidence rates of $\alpha I_S S$ and $\beta I_R S$, respectively. Here $\alpha$ and $\beta$ represent the effective contact rates of susceptible with the drug-sensitive infected and the drug-resistant infected individuals, respectively. Generally, $\alpha$ is larger than $\beta$, since most mutant strains are less fit than the wild-type strains. We assume that an effective contact transmits the same type of strain in the newly infected person. The primary reason for the drug resistance in the infected population is its acquisition from the failure of treatment, and not the transmission [44]. Therefore, we do not consider the transmission of resistance from drug-sensitive infected population. Further, individuals in each of the groups die naturally at the rate $\mu$. The poor economic condition of infected patients, in addition to limited medical infrastructure, restricts the reach of treatment to only a fraction ($\eta$) of the whole drug-sensitive infected population. Moreover, we assume that only a fraction ($\epsilon$) of total population under treatment adheres to it, as directed. The remaining fraction $(1-\epsilon )$ of the treatment class is non-adherent to the prescribed drugs, which causes this population to develop a drug-resistant strain of the virus. As a result, individuals of the treatment class will transfer to the drug-resistant infected class at the rate of $(1-\epsilon )T$. Also, these remaining fraction of the population in the drug-sensitive infected $(1-\eta )$ and treatment $(1-\epsilon )$ compartments die with disease induced death rate of $\mu _S$. This population also develops drug resistance because of the sub-optimal adherence to the treatment. Here we are considering only the sub-optimal adherence to the treatment as the reason for the development of drug resistance. The drug-resistant infected population dies with the disease induced death rate of $\mu _R$. We also assume that a drug-resistant infected individual is at $100\%$ drug resistance level. In other words, the treatment does not work at all on drug-resistant infected population. A schematic representation for this type of HIV spread is presented in Fig. 1.

Taking into account the aforementioned assumptions, the population in each group is determined by the following deterministic system of coupled nonlinear ordinary differential equations:

$$\begin{aligned} S^{\prime }= & {} \lambda -\alpha I_{S}S-\beta I_{R}S-\mu S, \nonumber \\ I_{S}^{\prime }= & {} \alpha I_{S}S-\eta I_{S}-\mu _{S}(1-\eta )I_{S}-\mu I_{S}, \nonumber \\ T^{\prime }= & {} \eta I_{S}-(1-\epsilon )T-\mu _{S}(1-\epsilon )T-\mu T, \nonumber \\ I_{R}^{\prime }= & {} \beta I_{R}S+(1-\epsilon )T-\mu _{R}I_{R}-\mu I_{R}. \end{aligned}$$

(2.1)

where all the parameters are as defined in the preceding description. For simplicity, we define,

$$\begin{aligned} a:= & {} \eta +\mu _{S}(1-\eta )+\mu , \\ b:= & {} (1-\epsilon )+\mu _{S}(1-\epsilon )+\mu ~\text {and}\\ c:= & {} \mu +\mu _{R}. \end{aligned}$$

3 Model analysis

Since the state variables of the model represents the human population, the solution of system (2.1) needs to be non-negative (for all non-negative initial conditions) and bounded. We begin with the non-negativity part. Let $t_{1}$ denote the time at which the susceptible population S becomes extinct. Then $S(t_{1})=0$ and $S^{\prime }(t_{1})=\lambda >0$. Therefore $\not \exists$ any $\epsilon >0$ such that $S(t_{1})=0$ and $S(t_{1}+\epsilon )<0$. Hence $S(t_{1})\ge 0,~\forall t_{1}>0$ and $S(0)\ge 0$. Now, from the second equation of (2.1), we have, $\displaystyle {I_{S}(t)=I_{S}(0)\exp \left[ \int _{0}^{t} \left( \alpha S(\tau )-a \right) d\tau \right] \ge 0}$ for $I_{S}(0)\ge 0$. In an analogous manner, from the third and fourth equation of (2.1), we have, $\displaystyle T(t)\ge T(0)\exp \left[ \int _{0}^{t}(-b)d\tau \right] \ge 0$ and $\displaystyle I_{R}(t)=I_{R}(0)\exp \Big [\int _{0}^{t}\big (\beta S(\tau )-c \big )d\tau \Big ] \ge 0$, respectively.

For the boundedness part, we define $W=S+I_{S}+T+I_{R}$. Then,

$$\begin{aligned} W^{\prime }= & {} S^{\prime }+I_{S}^{\prime }+T^{\prime }+I_{R}^{\prime }\\= & {} \lambda -\mu W-\mu _{S}(1-\eta )I_{S}-\mu _{S}(1-\epsilon )T-\mu _{R}I_{R} \\\le & {} \lambda -\mu W, \end{aligned}$$

which implies that $\displaystyle {W\le \frac{\lambda }{\mu }:=M_{1}~(\text {say})}$. This shows that W is bounded by $M_{1}$. Therefore S, $I_{S}$, T and $I_{R}$ are also bounded by $M_{1}$. From these results, we can now state the following Theorem (Fig. 2).

Theorem 1

The biologically feasible region ${\mathcal {R}}$ defined by:

$$\begin{aligned} {\mathcal {R}}=\left\{ (S,I_{S},T,I_{R})\in {\mathbb {R}}_{+}^{4}:0\le S+I_{S}+T+I_{R}\le \frac{\lambda }{\mu }\right\} \end{aligned}$$

where ${\mathbb {R}}_{+}^{4}$ denotes the non-negative cone and its lower dimensional faces, is positively invariant for the system (2.1) with non-negative initial conditions.

Fig. 2

Schematic representation of the model (3.1)

3.1 Treatment-free model

We choose $\eta =0,\epsilon =0$ and $T=0$ in model (2.1) to analyze the dynamics of HIV spread in the absence of the treatment. Accordingly, the resultant model is given by:

$$\begin{aligned} S^{\prime }= & {} \lambda -\alpha I_{S}S-\beta I_{R}S-\mu S, \nonumber \\ I_{S}^{\prime }= & {} \alpha I_{S}S -(\mu +\mu _S) I_{S}, \nonumber \\ I_{R}^{\prime }= & {} \beta I_{R}S-(\mu +\mu _{R}) I_{R}. \end{aligned}$$

(3.1)

where all the parameters have same meaning as in system (2.1). From Theorem 1, we can conclude that for the treatment-free model (3.1), the feasible region ${\mathcal {R}}_1$ defined by:

$$\begin{aligned} {\mathcal {R}}_1=\left\{ (S,I_{S},I_{R})\in {\mathbb {R}}_{+}^{3}:0\le S+I_{S}+I_{R}\le \frac{\lambda }{\mu }\right\} \end{aligned}$$

is positively invariant with non-negative initial conditions. Therefore, it is sufficient to consider the dynamics of model system (3.1) in the region ${\mathcal {R}}_1$.

3.1.1 Equilibrium points and local stability analysis

For the system given by equation (3.1), there exists three equilibrium points, as enumerated below.

• (A) Disease-free equilibrium point: $\displaystyle {E_{0}^{(1)}\left( \frac{\lambda }{\mu },0,0\right) }$.

• (B) Drug-sensitive equilibrium point: $\displaystyle E_{1}^{(1)}=\Big (S_{1},I_{S_{1}},0\Big ) =\Big (\frac{\mu +\mu _{S}}{\alpha }, \frac{\lambda \alpha -\mu (\mu +\mu _{S})}{\alpha (\mu +\mu _{S})},0\Big )$, which exists provided $\displaystyle {\frac{\lambda }{\mu }>\frac{\mu +\mu _{S}}{\alpha }}$.

• (C) Drug-resistant equilibrium point: $\displaystyle E_{2}^{(1)}=\Big (S_{2},0,I_{R_{2}}\Big ) =\Big (\frac{\mu +\mu _{R}}{\beta },0, \frac{\lambda \beta -\mu (\mu +\mu _{R})}{\beta (\mu +\mu _{R})}\Big )$, which exists provided $\displaystyle {\frac{\lambda }{\mu }>\frac{\mu +\mu _{R}}{\beta }}$.

Note that the interior equilibrium point $E_{*}^{(1)}= (S_{*},{I_{S}}_{*},{I_{R}}_{*})$ does not exists, unless $\displaystyle \frac{\mu +\mu _{R}}{\beta }=\frac{\mu +\mu _{S}}{\alpha }$, in which case there are infinitely many solutions for different initial conditions.

Table 2 Existence and stability conditions for different equilibrium points

Now, in order to determine the “Basic Reproduction Number”, for system (3.1), we consider, the next generation matrix as,

$$\begin{aligned} FV^{-1}=\begin{pmatrix} \frac{\alpha \lambda }{\mu (\mu +\mu _{S})}&{}0\\ 0&{}\frac{\beta \lambda }{\mu (\mu +\mu _{R})} \end{pmatrix}. \end{aligned}$$

Hence the “Basic Reproduction Number” for the drug-sensitive strain and the drug-resistant strain are given by $\displaystyle {R_{0}^{(S)}=\frac{\alpha \lambda }{\mu (\mu +\mu _{S})}}$ and $\displaystyle {R_{0}^{(R)}=\frac{\beta \lambda }{\mu (\mu +\mu _{R})}}$, respectively. We denote the ratio of $\displaystyle {R_{0}^{(S)}}$ and $\displaystyle {R_{0}^{(R)}}$, as $\displaystyle {R_{0}^{(SR)}} := \displaystyle {\frac{\alpha (\mu +\mu _R)}{\beta (\mu +\mu _S)}}$.

Finally, we present the stability analysis for system (3.1), for which we consider the following Jacobian,

$$\begin{aligned} J_{1}=\begin{bmatrix} -\alpha I_{S}-\beta I_{R}-\mu &{} -\alpha S &{} -\beta S\\ \alpha I_{S} &{} \alpha I_{S}-\mu -\mu _{S} &{} 0 \\ \beta I_{R} &{} 0 &{} \beta S-\mu -\mu _{R} \end{bmatrix}. \end{aligned}$$

• (A) The eigenvalues of the Jacobin matrix, evaluated at $E_{0}^{(1)}$ are $-\mu$, $\displaystyle {\frac{\alpha \lambda -\mu ^{2}-\mu \mu _{S}}{\mu }}$ and $\displaystyle {\frac{\beta \lambda -\mu ^{2}-\mu \mu _{R}}{\mu }}$. So the disease-free equilibrium $E_{0}^{(1)}$ is locally stable if, $\alpha \lambda -\mu ^{2}-\mu \mu _{S}<0$ and $\beta \lambda -\mu ^{2}-\mu \mu _{R}<0$, i.e, $R_{0}^{(S)}<1$ and $R_{0}^{(R)}<1$, respectively. This is equivalent to the condition $\displaystyle {\max \left( R_0^{(S)},R_0^{(R)}\right) <1}$. Note that under these conditions $E_{1}^{(1)}$ and $E_{2}^{(1)}$ do not exist.

• (B) One of the eigenvalues of the Jacobin matrix, evaluated at $E_{1}^{(1)}$ is given by $\displaystyle {-\mu -\mu _{R}+\frac{\beta (\mu +\mu _{S})}{\alpha }}$. The remaining two eigenvalues are the solutions of the characteristic equation $\displaystyle x^{2}+\frac{\alpha \lambda }{\mu +\mu _{S}}x-\mu (\mu +\mu _{S})+\alpha \lambda =0$, which have negative real parts provided $\alpha \lambda> \mu (\mu +\mu _{S})\iff R_{0}^{(S)}>1$ (this condition is already satisfied from the existential condition of $E_{1}^{(1)}$). Note that the first eigenvalue is negative, provided,

  $\displaystyle {\frac{\mu +\mu _{S}}{\alpha }< \frac{\mu +\mu _{R}}{\beta } \iff R_{0}^{(SR)}>1}$. Therefore the equilibrium point $E_{1}^{(1)}$ is locally stable if and only if $\displaystyle {R_{0}^{(SR)}>1}$.

• (C) One of the eigenvalues of the Jacobin matrix, evaluated at $E_{2}^{(1)}$ is given by $\displaystyle {-\mu -\mu _{S}+\frac{\alpha (\mu +\mu _{R})}{\beta }}$. The remaining two eigenvalues are the solution of the characteristic equation $\displaystyle x^{2}+\frac{\beta \lambda }{\mu +\mu _{R}}x-\mu (\mu +\mu _{R})+\beta \lambda =0$, which have negative real parts provided $\beta \lambda> \mu (\mu +\mu _{R})\iff R_{0}^{(R)}>1$ (this condition is already satisfied from the existential condition of $E_{2}^{(1)}$). Note that the first eigenvalue is negative, provided,

  $\displaystyle {\frac{\mu +\mu _{R}}{\beta }< \frac{\mu +\mu _{S}}{\alpha } \iff R_{0}^{(SR)}<1}$. Therefore the equilibrium point $E_{2}^{(1)}$ is locally stable if and only if $\displaystyle {R_{0}^{(SR)}<1}$.

Fig. 3

Two-parameter bifurcation diagram showing existence and stability regions for different equilibrium points of model (3.1). The dashed boxes contain total existing equilibrium point while solid boxes contain only stable equilibrium points. The dashed blue line represents $R_{0}^{(S)}=R_{0}^{(R)}$

Table 3 Existent equilibrium points and their stability in different cases

The summary of existence and stability conditions for different equilibrium points are presented in Table 2 and Fig. 3.

Existent equilibrium points and their stability in different cases are presented in Table 3, for which we define $\displaystyle {P_{1}:=\frac{\mu +\mu _{S}}{\alpha }}$, $\displaystyle {P_{2}:=\frac{\mu +\mu _{R}}{\beta }}$ and $\displaystyle {P_{3}:=\frac{\lambda }{\mu }}$

3.1.2 Global stability analysis

Theorem 2

The equilibrium point $\displaystyle {E_{0}^{(1)}}$ is globally asymptotically stable with $\displaystyle {R_{0} < 1}.$ $\Big (\text {where}~ \displaystyle R_{0}=\max \left\{ {R_{0}^{(S)}},R_{0}^{(R)}\right\} \Big )$

Proof

We define the Lyapunov function as:

$$\begin{aligned} L_1(t)= & {} L_1(S(t),I_S(t),I_R(t))\\= & {} \left( 1-R_{0}^{(R)}\right) I_S+\left( 1-R_{0}^{(S)}\right) I_R \end{aligned}$$

Then $\displaystyle {L_1\left( E_{0}^{(1)}\right) =0}$ and $\displaystyle {L_1(x)>0,x\ne E_{0}^{(1)}}.$ The derivative of $\displaystyle {L_1(t)}$ along the solution of system (3.1) gives

$$\begin{aligned} \dfrac{dL_1}{dt}= & {} \left( 1-R_{0}^{(R)}\right) I'_S+\left( 1-R_{0}^{(S)}\right) I'_R \\= & {} \left( 1-R_{0}^{(R)}\right) \left( \alpha I_{S}S -(\mu +\mu _S) I_{S}\right) \\&+\left( 1-R_{0}^{(S)}\right) \left( \beta I_{R}S-(\mu +\mu _{R}) I_{R}\right) \\\le & {} \left( 1-R_{0}^{(R)}\right) \left( \frac{\alpha \lambda }{\mu } I_{S} -(\mu +\mu _S) I_{S}\right) \\&+\left( 1-R_{0}^{(S)}\right) \left( \frac{\beta \lambda }{\mu } I_{R}-\left( \mu +\mu _{R}\right) I_{R}\right) \\= & {} -(I_S(\mu +\mu _S)+I_R(\mu +\mu _R))\\&\left( R_{0}^{(S)}-1\right) \left( R_{0}^{(R)}-1\right) \\\le & {} 0,~~~~\text {if }\displaystyle {R_{0}< 1}. \end{aligned}$$

Therefore, by LaSalle invariance principle, $\displaystyle {E_{0}^{(1)}}$ is globally asymptotically stable if $\displaystyle {R_{0}< 1}.$ $\square$

Theorem 3

The equilibrium point $\displaystyle {E_{1}^{(1)}}$ is globally asymptotically stable whenever it exists if $\displaystyle {R_{0}^{(SR)}}> 1$.

Proof

We consider the Lyapunov function as:

$$\begin{aligned} L_2(t)= & {} L_2(S(t),I_S(t),I_R(t))\\= & {} S-S_1-S_1\ln \left( \frac{S}{S_1}\right) +I_{S}-I_{S_{1}}\\&-I_{S_{1}}\ln \left( \frac{I_{S}}{I_{S_{1}}}\right) +I_{R} \end{aligned}$$

The derivative of $\displaystyle {L_2(t)}$ along the solution of system (3.1) gives

$$\begin{aligned} \dfrac{dL_2}{dt}= & {} \left( 1-\frac{S_1}{S}\right) S'+\left( 1-\frac{I_{S_{1}}}{I_S}\right) I'_S+I'_R\\= & {} \left( 1-\frac{S_1}{S}\right) \left( \lambda -\alpha I_S S-\beta I_R S-\mu S\right) \\&+I_S \left( 1-\frac{I_{S_{1}}}{I_S}\right) \left( \alpha S-\mu -\mu _{S}\right) \\&+I_R \left( \beta S-\mu -\mu _{R}\right) \\= & {} \lambda -\mu S-\frac{\lambda S_1}{S}+I_R \left( \frac{\beta (\mu +\mu _S)(\mu +\mu _R)}{\alpha (\mu +\mu _R)}\right) \\&-I_R(\mu +\mu _R)-\alpha I_{S_{1}}S+I_{S_{1}}(\mu +\mu _S)\\&+\frac{\mu (\mu +\mu _S)}{\alpha }\\= & {} -\mu S-\frac{\lambda S_1}{S}+\frac{\lambda \alpha +\mu (\mu +\mu _S)}{\alpha }\\&+I_R(\mu +\mu _R)\left( \frac{R_{0}^{R}}{R_{0}^{S}}-1\right) \\&-\alpha I_{S_{1}}S+I_{S_{1}}(\mu +\mu _S)\\= & {} -\frac{(\lambda -\mu S R_{0}^{S})^2}{\mu S R_{0}^{S}}+I_R(\mu +\mu _R)\left( \frac{R_{0}^{R}}{R_{0}^{S}}-1\right) \\\le & {} 0,~~~~\text {if }\displaystyle {R_{0}^{(SR)}> 1}. \end{aligned}$$

Therefore, by LaSalle invariance principle, $\displaystyle {E_{1}^{(1)}}$ is globally asymptotically stable if $\displaystyle {R_{0}^{(SR)}> 1}.$ $\square$

Theorem 4

The equilibrium point $\displaystyle {E_{2}^{(1)}}$ is globally asymptotically stable whenever it exists if $\displaystyle {R_{0}^{(SR)}}< 1$.

Proof

We define the Lyapunov function as

$$\begin{aligned} L_3(t)= & {} L_3(S(t),I_S(t),I_R(t))\\= & {} S-S_2-S_2\ln \left( \frac{S}{S_2}\right) +I_{S}+I_{R}-I_{R_{2}}\\&-I_{R_{2}}\ln \left( \frac{I_{R}}{I_{R_{2}}}\right) \end{aligned}$$

The remaining proof is similar to the proof in Theorem 3. $\square$

3.1.3 Bifurcation analysis

Theorem 5

The system (3.1) undergoes through transcritical bifurcation at $\displaystyle {\alpha =\alpha _{*}^{(1)}=\frac{\mu (\mu +\mu _S)}{\lambda }}$ if $\displaystyle \beta \lambda -\mu ^2-\mu \mu _R < 0$ $(R_0^{(R)}<1)$. Here, equilibrium points $\displaystyle {E_{0}^{(1)}}$ and $\displaystyle {E_{1}^{(1)}}$ exchange their stability at $\displaystyle {\alpha =\alpha _{*}^{(1)}~(\text {or }R_0^{(S)}=1)}$.

Proof

Let $\displaystyle {\alpha =\alpha _{*}^{(1)}=\frac{\mu (\mu +\mu _S)}{\lambda }}$, then

$$\begin{aligned}&J_{1}(E_{0}^{(1)})\bigm |_{\alpha =\alpha _{*}^{(1)}}\\&\quad = \begin{bmatrix} -\mu &{} -(\mu +\mu _S) &{} \displaystyle {-\frac{\beta \lambda }{\mu }}\\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} \displaystyle {\frac{\beta \lambda -\mu ^2-\mu \mu _R}{\mu }} \end{bmatrix}, \end{aligned}$$

and

$$\begin{aligned} J_{1}^T(E_{0}^{(1)})\bigm |_{\alpha =\alpha _{*}^{(1)}}= \begin{bmatrix} -\mu &{} 0 &{} 0\\ -(\mu +\mu _S) &{} 0 &{} 0 \\ \displaystyle {-\frac{\beta \lambda }{\mu }} &{} 0 &{} \displaystyle {\frac{\beta \lambda -\mu ^2-\mu \mu _R}{\mu }} \end{bmatrix}. \end{aligned}$$

Notice that one eigenvalue of matrix $\displaystyle {J_{1}(E_{0}^{(1)})\bigm |_{\alpha =\alpha _{*}^{(1)}}}$ become zero at $\alpha =\alpha _{*}^{(1)}$ and remaining two eigenvalues are negative only if $\displaystyle {\beta \lambda -\mu ^2-\mu \mu _R < 0}$. Now, we choose $v=\left[ \begin{array}{c} -\left( \displaystyle {\frac{\mu +\mu _S}{\mu }}\right) \\ 1 \\ 0\\ \end{array} \right]$ and $w=\left[ \begin{array}{c} 0 \\ 1 \\ 0 \\ \end{array} \right]$ as the eigenvectors corresponding to the zero eigenvalues of the matrices $J_{1}(E_{0}^{(1)})\bigm |_{\alpha =\alpha _{*}^{(1)}}$ and $J_{1}^T(E_{0}^{(1)})\bigm |_{\alpha =\alpha _{*}^{(1)}}$, respectively. We rewrite the system (3.1) as $\dfrac{dX}{dt}=\left[ \begin{array}{c} f(S,I_S,I_R) \\ g(S,I_S,I_R) \\ h(S,I_S,I_R) \\ \end{array} \right] =F(E^{(1)}(S,I_S,I_R))$ and $v=\left[ \begin{array}{c} v_1 \\ v_2 \\ v_3 \\ \end{array} \right]$. Then,

$$\begin{aligned} F_\alpha (E_{0}^{(1)},\alpha _{*}^{(1)})= \left[ \begin{array}{c} 0 \\ 0 \\ 0 \\ \end{array} \right] , \end{aligned}$$

(3.2)

and

$$\begin{aligned} DF_\alpha (E_{0}^{(1)},\alpha _{*}^{(1)})\cdot v= \left[ \begin{array}{c} -\frac{\lambda }{\mu } \\ \frac{\lambda }{\mu } \\ 0 \\ \end{array} \right] . \end{aligned}$$

(3.3)

Also, $D^2F(E^{(1)},\alpha )\cdot (v,v)=$

$$\begin{aligned} \left[ \begin{array}{c} f_{SS} v_1 v_1 + f_{SI_S} v_1 v_2 + f_{SI_R} v_1 v_3 + f_{I_S S} v_2 v_1 + f_{I_S I_S} v_2 v_2 + f_{I_S I_R} v_2 v_3 + f_{I_R S} v_3 v_1 + f_{I_R I_S} v_3 v_2 + f_{I_R I_R} v_3 v_3 \\ g_{SS} v_1 v_1 + g_{SI_S} v_1 v_2 + g_{SI_R} v_1 v_3 + g_{I_S S} v_2 v_1 + g_{I_S I_S} v_2 v_2 + g_{I_S I_R} v_2 v_3 + g_{I_R S} v_3 v_1 + g_{I_R I_S} v_3 v_2 + g_{I_R I_R} v_3 v_3 \\ h_{SS} v_1 v_1 + h_{SI_S} v_1 v_2 + h_{SI_R} v_1 v_3 + h_{I_S S} v_2 v_1 + h_{I_S I_S} v_2 v_2 + h_{I_S I_R} v_2 v_3 + h_{I_R S} v_3 v_1 + h_{I_R I_S} v_3 v_2 + h_{I_R I_R} v_3 v_3 \\ \end{array} \right] \end{aligned}$$

So,

$$\begin{aligned} D^2F(E_{0}^{(1)},\alpha _{*}^{(1)})\cdot (v,v)= \left[ \begin{array}{c} \displaystyle {\frac{2(\mu +\mu _S)^2}{\lambda }} \\ \displaystyle {-\frac{2(\mu +\mu _S)^2}{\lambda }} \\ 0 \\ \end{array} \right] . \end{aligned}$$

(3.4)

Now, from equations (3.2), (3.3) and (3.4), we can conclude that,

• 1. $w^T F_\alpha (E_{0}^{(1)},\alpha _{*}^{(1)})=0$,

• 2. $w^T [DF_\alpha (E_{0}^{(1)},\alpha _{*}^{(1)})\cdot v]=\displaystyle {\frac{\lambda }{\mu }}\ne 0$,

• 3. $w^T [D^2F(E_{0}^{(1)},\alpha _{*}^{(1)})\cdot (v,v)]=\displaystyle {-\frac{2(\mu +\mu _S)^2}{\lambda }}\ne 0.$

Therefore, F satisfies all the transversality conditions (from Sotomayor’s theorem) for transcritical bifurcation at $\displaystyle {\alpha =\alpha _{*}^{(1)}=\frac{\mu (\mu +\mu _S)}{\lambda }}$. $\square$

Theorem 6

The system (3.1) undergoes through transcritical bifurcation at $\displaystyle {\beta =\beta _{*}^{(1)}=\frac{\mu (\mu +\mu _R)}{\lambda }}$ if $\displaystyle \alpha \lambda -\mu ^2-\mu \mu _S < 0$ $(R_0^{(S)}<1)$. Here, equilibrium points $\displaystyle {E_{0}^{(1)}}$ and $\displaystyle {E_{2}^{(1)}}$ exchange their stability at $\displaystyle {\beta =\beta _{*}^{(1)}}~(\text {or }R_0^{(R)}=1)$.

Proof

The proof of this theorem is similar to the proof in Theorem 5. $\square$

In the absence of treatment, there is no development of drug resistance. The only way of getting drug resistance is transmission from already drug-resistant infected population. There is a strong competition between both strains as they share their common resource, namely, the susceptible population. The strongest and the fittest one will win this battle and survive for long time. The basic reproduction number is a good indicator of the overall fitness of a strain. Co-existence of both the mutants is not possible, due to the competitive selection process. This model lacks a range of biological scenarios due to its apparent simplicity. By excluding the possibility of development of drug resistance, only three scenarios of competitive exclusion are possible: (a) both the types of infected population die out, (b) only the drug-sensitive infected population survives and, (c) only the drug-resistant infected population survives, which makes co-existence impossible. But, there are more possible outcomes between the two strains, beyond the competitive exclusion. Thus, it becomes extremely important to study the model system (2.1) that considers the fact that the drug-resistant infected population increases as a result of development of drug resistance, due to sub-optimal drug adherence, along with the transmission from the already existent drug-resistant infected population.

3.2 Treatment model

Recall that the model system (2.1) shows the dynamics of HIV spread with treatment. We analyze this mathematical model by determining the equilibrium states, and their stability, followed by the bifurcation analysis.

3.2.1 Equilibrium points and local stability analysis

For the system given by equation (2.1), there exist three equilibrium points as enumerated below:

• (A) Disease-free equilibrium point: $\displaystyle {E_{0}^{(2)}\left( \frac{\lambda }{\mu },0,0,0\right) }$.

• (B) Planar equilibrium point: $\displaystyle E_{1}^{(2)}\left( {\bar{S}}_{1},0,0,{\bar{I}}_{R_{1}}\right) = \left( \frac{c}{\beta },0,0,\frac{\beta \lambda -\mu c}{c}\right)$

• (C) Interior equilibrium point: $\displaystyle E_{*}^{(2)}{=}(S_{*},I_{{S}_{*}},T_{*},I_{{R}_{*}})$, where, $\displaystyle {S_{*}{=}\frac{a}{\alpha }}$, $\displaystyle I_{{S}_{*}}{=} \frac{b(c\alpha {-}a\beta )(\lambda \alpha {-}a\mu )}{a\alpha (bc\alpha {-}ab\beta {+}(1{-}\epsilon )\beta \eta )}$, $\displaystyle T_{*}=\frac{\eta (c\alpha -a\beta )(\alpha \lambda -a\mu )}{a\alpha (bc\alpha -ab\beta +(1-\epsilon )\beta \eta )}$ and $\displaystyle I_{{R}_{*}}=\frac{\eta (1-\epsilon )(\alpha \lambda -a\mu )}{a(bc\alpha -ab\beta +(1-\epsilon )\beta \eta )}$,

where the parameters a, b and c are as defined in Sect. 2.

Now, we determine the “Basic Reproduction Number”, for system (2.1), by considering the next generation matrix as,

$$\begin{aligned} FV^{-1}=\begin{pmatrix} \frac{\alpha \lambda }{a\mu }&{}0\\ 0&{}\frac{\beta \lambda }{c\mu } \end{pmatrix}. \end{aligned}$$

Hence the “Basic Reproduction Number” for the sensitive strain and the drug-resistant strain are given by $\displaystyle {{\bar{R}}_{0}^{(S)}=\frac{\alpha \lambda }{a\mu }}$ and $\displaystyle {{\bar{R}}_{0}^{(R)}=\frac{\beta \lambda }{c\mu }}$, respectively. In particular, the “Basic Reproduction Number” for the system (2.1) is $\displaystyle {{\bar{R}}_{0}=\max \{{\bar{R}}_{0}^{(S)},{\bar{R}}_{0}^{(R)}\}}$. We denote the ratio of $\displaystyle {{\bar{R}}_{0}^{(S)}}$ and $\displaystyle {{\bar{R}}_{0}^{(R)}}$, as $\displaystyle {{\bar{R}}_{0}^{(SR)}} := \displaystyle {\frac{\alpha c}{\beta a}}$.

For the presentation of the stability analysis, we consider the following Jacobian,

$$\begin{aligned} J_{2}=\begin{bmatrix} -\alpha I_{S}-\beta I_{R}-\mu &{} -\alpha S &{} 0 &{} -\beta S\\ \alpha I_{S} &{} \alpha S-a &{} 0 &{} 0\\ 0 &{} \eta &{} -b &{} 0 \\ \beta I_{R} &{} 0 &{} 1-\epsilon &{} \beta S-c \end{bmatrix}. \end{aligned}$$

The stability analysis for each of the equilibria is enumerated below:

• (A) The eigenvalues of the Jacobin matrix, evaluated at $E_{0}^{(2)}$ are $-b$, $-\mu$, $\displaystyle {\frac{\alpha \lambda -a\mu }{\mu }}$ and $\displaystyle {\frac{\beta \lambda -c\mu }{\mu }}$. Therefore, the disease-free equilibrium $E_{0}^{(2)}$ is locally stable, provided, $\alpha \lambda -a\mu <0$ and $\beta \lambda -c\mu <0$, i.e, ${\bar{R}}_{0}^{(S)}<1$ and ${\bar{R}}_{0}^{(R)}<1$, respectively.

• (B) The eigenvalues of the Jacobin matrix, evaluated at $E_{1}^{(2)}$ are given by $-b$, $\alpha {\bar{S}}_{1}-a$ and $\displaystyle \frac{A_{1}\pm \sqrt{A_{1}^{2}-4B_{1}}}{2}$, where $\displaystyle A_{1}:=c-\beta {\bar{S}}_{1}+\frac{\lambda }{{\bar{S}}_{1}}$ and $\displaystyle B_{1}:=\beta ^{2}{\bar{I}}_{R_{1}}{\bar{S}}_{1}+\frac{\lambda c}{{\bar{S}}_{1}}-\beta \lambda$. All the eigenvalues are either negative or have negative real part provided $\displaystyle {{\bar{S}}_{1}<\frac{a}{\alpha }}$ and $A_{1}>0$, which are equivalent to $\displaystyle {{\bar{R}}_{0}^{(SR)}<1}$, and the existential condition for $E_{1}^{(2)}$, namely ${\bar{R}}_{0}^{(R)}>1$. Thus, the equilibrium point $E_{1}^{(2)}$ is stable, provided ${\bar{R}}_{0}^{(S)}<{\bar{R}}_{0}^{(R)}$.

• (C) Finally, the eigenvalues of the interior equilibrium point $E_{*}^{(2)}$ are given by the roots of the following characteristic equation of the Jacobian matrix, evaluated at $E_{*}^{(2)}$:

  $$\begin{aligned} x^{4}+A_{*}x^{3}+B_{*}x^{2}+C_{*}x+D_{*}=0, \end{aligned}$$

  (3.5)

  where

  $$\begin{aligned} A_{*}= & {} b+c-\beta S_{*}+\frac{\lambda }{S^{*}},\\ B_{*}= & {} bc+\alpha ^{2}I_{S_{*}}S_{*}-b\beta S_{*}+\beta ^{2}I_{R_{*}}S_{*}\\&+\frac{b\lambda }{S_{*}}+ \frac{c\lambda }{S_{*}}-\beta \lambda ,\\ C_{*}= & {} I_{S_{*}}S_{*}(b\alpha ^{2}+c\alpha ^{2}-S_{*}\alpha ^{2}\beta )\\&+b\beta ^{2}I_{R_{*}}S_{*}+\frac{bc\lambda }{S_{*}}-b\beta \lambda ,\\ D_{*}= & {} bc\alpha ^{2}I_{S_{*}}S_{*}-b\alpha ^{2}\beta I_{S_{*}}S_{*}^{2}\\&+(1-\epsilon ) \alpha \beta \eta I_{S_{*}}S_{*}. \end{aligned}$$

  By the Routh-Hurwitz criterion, all the eigenvalues will have negative real part if,

  • (A) $A_{*}>0, B_{*}>0, C_{*}>0, D_{*}>0$,

  • (B) $A_{*}B_{*}-C_{*}>0$,

  • (C) $A_{*}B_{*}C_{*}-A_{*}^{2}D_{*}-C_{*}^{2}>0$.

  The coefficients of the characteristic equation, in terms of the Basic Reproduction Numbers are given by,

  $$\begin{aligned} A_{*}:= & {} \frac{\alpha (ab+\alpha \lambda )+a^{2}\beta \left( {\bar{R}}_{0}^{(SR)}-1\right) }{a\alpha }, \\ B_{*}:= & {} \frac{a\beta (ab+\alpha \lambda )\left( {\bar{R}}_{0}^{(SR)}-1\right) +b\alpha ^{2}\lambda }{a\alpha }\\&+\frac{a^{2}b\mu \left( {\bar{R}}_{0}^{(S)}-1\right) \left( {\bar{R}}_{0}^{(SR)}-1\right) }{ab\left( {\bar{R}}_{0}^{(SR)}-1\right) +\eta (1-\epsilon )}\\&+\frac{a(1-\epsilon )\left( {\bar{R}}_{0}^{(S)}-1\right) \beta \eta \mu }{\alpha \left( ab\left( {\bar{R}}_{0}^{(SR)}-1\right) +\eta (1-\epsilon )\right) }, \\ C_{*}:= & {} b\lambda \beta \left( {\bar{R}}_{0}^{(SR)}-1\right) \\&+\frac{a^{2}b^{2}\mu \left( {\bar{R}}_{0}^{(S)}-1\right) \left( {\bar{R}}_{0}^{(SR)}-1\right) }{ab\left( {\bar{R}}_{0}^{(SR)}-1\right) +\eta (1-\epsilon )}\\&+\frac{a^{3}b\beta \mu \left( {\bar{R}}_{0}^{(S)}-1\right) \left( {\bar{R}}_{0}^{(SR)}-1\right) ^{2}}{\alpha \left( ab\left( {\bar{R}}_{0}^{(SR)}-1\right) +\eta (1-\epsilon )\right) }\\&+\frac{ab(1-\epsilon )\left( {\bar{R}}_{0}^{(S)}-1\right) \beta \eta \mu }{\alpha \left( ab\left( {\bar{R}}_{0}^{(SR)}-1\right) +\eta (1-\epsilon )\right) }, \\ D_{*}:= & {} \frac{a^{2}b\beta \mu \left( {\bar{R}}_{0}^{(S)}-1\right) \left( {\bar{R}}_{0}^{(SR)}-1\right) }{\alpha }\\ \end{aligned}$$

  The condition (A) has already been satisfied since the interior equilibrium point $E_{*}^{(2)}$ exists if and only if $\displaystyle {{\bar{R}}_{0}^{(S)}>1}$ and $\displaystyle {{\bar{R}}_{0}^{(SR)}>1}$. For condition (B), we have

  $$\begin{aligned}&A_{*}B_{*}-C_{*} =\frac{(b \alpha +a \beta ({\bar{R}}_{0}^{(SR)}-1))(a b({\bar{R}}_{0}^{(SR)}-1)+ \eta (1-\epsilon ))(a b+\alpha \lambda )(a^2 \beta ({\bar{R}}_{0}^{(SR)}-1)+\alpha ^2 \lambda )}{\alpha ^2 a^2 (a b({\bar{R}}_{0}^{(SR)}-1)+\eta (1-\epsilon ))}\\&\qquad +\frac{a^2 \mu ({\bar{R}}_{0}^{(S)}-1)(a^2 \beta ^2 \eta (1-\epsilon ) ({\bar{R}}_{0}^{(SR)}-1)+\alpha ^2(a b \alpha ({\bar{R}}_{0}^{(SR)}-1)+ \beta \eta (1-\epsilon ))\lambda )}{\alpha ^2 a^2 (a b({\bar{R}}_{0}^{(SR)}-1)+\eta (1-\epsilon ))} >0, \end{aligned}$$

  which shows that condition (B) also holds whenever $\displaystyle {E_{*}^{(2)}}$ exists. So, we are left only with condition (C) to obtain a locally stable interior equilibrium point.

The summary of existence and stability conditions for different equilibrium points of model (2.1) are presented in Table 4 and Fig. 4.

Table 4 Existence and stability conditions for different equilibrium points of model (2.1)

Fig. 4

Two-parameter bifurcation diagram showing existence and stability regions for different equilibrium points of model (2.1). The dashed boxes contain total existing equilibrium point while solid boxes contain only stable equilibrium points. The dashed blue line represents ${\bar{R}}_{0}^{(S)}={\bar{R}}_{0}^{(R)}$. The interior equilibrium point is not stable in the whole region showed in above figure, instead it is stable only in a sub-region of above stability region where condition (C) holds

3.2.2 Global stability analysis

Theorem 7

The equilibrium point $E_{0}^{(2)}$ is globally asymptotically stable with ${\bar{R}}_{0}<1$, where ${\bar{R}}_{0}=\max {\left( {\bar{R}}_{0}^{(S)},{\bar{R}}_{0}^{(R)}\right) }$.

Proof

From the system (2.1), we have

$$\begin{aligned} I_{S}^{\prime }=\left( \alpha S-a\right) I_{S} \end{aligned}$$

which can be integrated to give

$$\begin{aligned} I_S(t)=I_S (0)\exp {\left[ \int _{0}^{t}\alpha S(\tau )d\tau -at\right] },\qquad \forall ~ t\ge 0. \end{aligned}$$

After using the upper bound of S(t), which is $\frac{\lambda }{\mu }$, we obtain

$$\begin{aligned} I_S(t)\le & {} I_S (0)\exp {\left[ \left( \frac{\alpha \lambda }{\mu }-a \right) t \right] } \\= & {} I_S (0)\exp {\left[ a \left( {\bar{R}}_{0}^{(S)}-1 \right) t \right] } \end{aligned}$$

It follows then that $I_S(t)\rightarrow 0$ as $t\rightarrow \infty$, if ${\bar{R}}_{0}^{(S)}<1.$ Therefore, the hyperplane $I_S=0$ attracts all solutions of the system (2.1) originating in domain ${\mathcal {R}}$.

Since $I_S(t)\rightarrow 0$ as $t\rightarrow \infty$ for ${\bar{R}}_{0}^{(S)}<1$, from the system (2.1), we have

$$\begin{aligned} T^{\prime }=-bT \implies T(t)=T(0)\exp (-bt) \end{aligned}$$

It follows then that $T(t)\rightarrow 0$ as $t\rightarrow \infty$, if ${\bar{R}}_{0}^{(S)}<1$ and the hyperplane $T=0$ attracts all solution of the system (2.1) originating in domain ${\mathcal {R}}$. Similarly, if ${\bar{R}}_{0}^{(R)}<1$, $I_R(t)\rightarrow 0$ as $t\rightarrow \infty$, since $I_S(t)\rightarrow 0 \text { and } T(t)\rightarrow 0$ as $t\rightarrow \infty$ and the hyperplane $I_R=0$ attracts all solution of the system (2.1) originating in domain ${\mathcal {R}}$. Now, it is simple to show that if $I_S\rightarrow 0 \text { and } I_R\rightarrow 0$, then $S\rightarrow \frac{\lambda }{\mu }$. Therefore, the equilibrium point $E_{0}^{(2)}$ is globally asymptotically stable when ${\bar{R}}_{0}<1$. $\square$

Theorem 8

The equilibrium point $E_1^{(2)}$ is globally asymptotically stable whenever it exists if ${\bar{R}}_{0}^{(SR)}<1.$

Proof

From the second and last equations of the system (2.1), we have:

$$\begin{aligned} I_{S}^{\prime }= & {} \left( \alpha S-a\right) I_{S} \end{aligned}$$

(3.6)

$$\begin{aligned} I_{R}^{\prime }= & {} \left( \beta S-c\right) I_{R}+(1-\epsilon ) T \end{aligned}$$

(3.7)

Now, we divide equations (3.6) and (3.7) by $I_S$ and $I_R$, respectively, and obtain

$$\begin{aligned} \dfrac{d(logI_S)}{dt}=\alpha S-a, \end{aligned}$$

(3.8)

$$\begin{aligned} \dfrac{d(logI_R)}{dt}=\beta S-c+(1-\epsilon )\frac{T}{I_R} \end{aligned}$$

(3.9)

Here, equations (3.8) and (3.9) leads to the following relation:

$$\begin{aligned}&S=\frac{1}{\alpha } \dfrac{d(logI_S)}{dt}+\frac{a}{\alpha }=\frac{1}{\beta }\dfrac{d(logI_R)}{dt}+\frac{c}{\beta }-\frac{(1-\epsilon )T}{\beta I_R}, \end{aligned}$$

and immediately obtain the following inequality:

$$\begin{aligned} \frac{1}{\alpha } \dfrac{d(logI_S)}{dt}+\frac{a}{\alpha } \le \frac{1}{\beta }\dfrac{d(logI_R)}{dt}+\frac{c}{\beta } \end{aligned}$$

Now, integrating both sides of the above inequality yields

$$\begin{aligned} \left( \frac{I_S(t)}{I_S(0)}\right) ^{\frac{1}{\alpha }} \exp {\left( \frac{at}{\alpha }\right) }\le \left( \frac{I_R(t)}{I_R(0)}\right) ^{\frac{1}{\beta }} \exp {\left( \frac{ct}{\beta }\right) } \end{aligned}$$

which we rearrange in the following form

$$\begin{aligned} \left( \frac{I_S(t)}{I_S(0)}\right) ^{\frac{1}{\alpha }}\le & {} \left( \frac{I_R(t)}{I_R(0)}\right) ^{\frac{1}{\beta }} \exp {\left( \left( \frac{c}{\beta }-\frac{a}{\alpha }\right) t\right) } \\= & {} \left( \frac{I_R(t)}{I_R(0)}\right) ^{\frac{1}{\beta }} \exp {\left( \frac{c}{\beta }\left( 1-\frac{1}{{\bar{R}}_{0}^{(SR)}}\right) t\right) } \end{aligned}$$

Finally, as we take the limit as $t\rightarrow \infty$, since both $I_S(t)$ and $I_R(t)$ are bounded, we get:

$$\begin{aligned}&\lim _{t\rightarrow \infty } \left( \frac{I_S(t)}{I_S(0)}\right) ^{\frac{1}{\alpha }} \le \lim _{t\rightarrow \infty } \left( \frac{I_R(t)}{I_R(0)}\right) ^{\frac{1}{\beta }}\\&\quad \exp {\left( \frac{c}{\beta }\left( 1-\frac{1}{{\bar{R}}_{0}^{(SR)}}\right) t\right) } \rightarrow 0,~~~\text {if } {\bar{R}}_{0}^{(SR)}<1. \end{aligned}$$

Therefore, all solutions of the system (2.1) converge to the hyperplane $I_S=0$ when ${\bar{R}}_{0}^{(SR)}<1$. Consequently, all solutions of this system converge to the hyperplane $T=0$ also, as proved in Theorem 7.

Next, we construct the Lyapunov function to show the globally asymptotically stable behaviour of the equilibrium point $E_1^{(2)}$ on the hyperplanes $I_S=0$ and $T=0$. We consider the Lyapunov function as

$$\begin{aligned} L_4(t)= & {} L_4(S(t),I_S(t),T(t),I_R(t))\\= & {} S-\bar{S_1}-\bar{S_1}\log \left( \frac{S}{\bar{S_1}}\right) \\&+I_R-{\bar{I}}_{R_1}-{\bar{I}}_{R_1}ln\left( \frac{{I}_{R_1}}{{\bar{I}}_{R_1}}\right) \end{aligned}$$

Then $L_4(E_1^{(2)})=0$ and $L_4(x)>0,x\ne E_1^{(2)}.$ The derivative of $L_4(t)$ along the solution of system (2.1) gives

$$\begin{aligned} \dfrac{dL_4}{dt}= & {} \left( 1-\frac{\bar{S_1}}{S}\right) (\lambda -\beta I_R S-\mu S)\nonumber \\&+\left( 1-\frac{{\bar{I}}_{R_1}}{I_R}\right) (\beta I_R S-c I_R) \end{aligned}$$

(3.10)

Now, at the equilibrium point $E_1^{(2)}$, we have

$$\begin{aligned} \lambda =\beta {\bar{I}}_{R_1} \bar{S_1}+\mu \bar{S_1} \end{aligned}$$

Replacing this $\lambda$ in equation (3.10), we obtain

$$\begin{aligned} \dfrac{dL_4}{dt}&= \mu \bar{S_1}\left( 2-\frac{\bar{S_1}}{S}-\frac{S}{\bar{S_1}}\right) +c {\bar{I}}_{R_1} \left( 2-\frac{\bar{S_1}}{S}-\frac{S}{\bar{S_1}}\right) \\&= \left( 2-\frac{\bar{S_1}}{S}-\frac{S}{\bar{S_1}}\right) (\mu S_1+c {\bar{I}}_{R_1}) \end{aligned}$$

Since the arithmetic mean is always greater than or equal to the geometric mean, we obtain $\dfrac{dL_4}{dt}\le 0$. Therefore, by LaSalle invariance principle, it follows that the equilibrium point $E_1^{(2)}$ is globally asymptotically stable whenever it exists if ${\bar{R}}_{0}^{(SR)}<1.$ $\square$

Remark

The global behaviour of the interior equilibrium point $E_*^{(2)}$ is uncertain, since we are unable to construct any suitable Lyapunov function for it. However, we have numerically shown that for a given set of parametric values, this equilibrium point is an attractor for solutions starting from a wide range of initial conditions (see Fig. 8).

3.2.3 Bifurcation analysis

Theorem 9

The system (2.1) undergoes through transcritical bifurcation at $\displaystyle {\beta =\beta _*^{(2)}=\frac{\mu c}{\lambda }}~ (\text {or }{\bar{R}}_0^{(R)}=1)$ if $\displaystyle {{\bar{R}}_0^{(S)}<1}$. Here, equilibrium points $\displaystyle {E_0^{(2)}}$ and $\displaystyle {E_1^{(2)}}$ exchange their stability at $\displaystyle {\beta =\beta _*^{(2)}}$.

Proof

Since the equilibrium point $\displaystyle {E_0^{(2)}}$ becomes non-hyperbolic at $\displaystyle {\beta =\beta _*^{(2)}}$, therefore linearization is inconclusive. We use the center manifold theory to study the local behaviour of this non-hyperbolic equilibrium point at $\displaystyle {\beta =\beta _*^{(2)}}$. It also describes the existence of another equilibrium point $\displaystyle {E_1^{(2)}}$, which is bifurcated from the non-hyperbolic equilibrium. The Jacobian matrix of model system (2.1) around the equilibrium $\displaystyle {E_0^{(2)}}$ evaluated at $\beta =\beta _*^{(2)}$, represented by $J_{2} {\left( E_{0}^{(2)}\right) }\Bigm |_{\beta =\beta _{*}^{(2)}}$, gives one simple zero eigenvalue and all the other eigenvalues have negative real parts if $\displaystyle {{\bar{R}}_0^{S}<1}$. Therefore, we can apply center manifold theory. We calculate the right eigenvector u and left eigenvector v corresponding to the zero eigenvalue of the matrix $J_{2} {\left( E_{0}^{(2)}\right) }\Bigm |_{\beta =\beta _{*}^{(2)}}$, which are given by $u=\left[ -\frac{c}{\mu },0,0,1\right] ^T$ and $v=\left[ 0,\frac{(1-\epsilon )\eta \mu }{b(a\mu -\alpha \lambda )},\frac{(1-\epsilon )}{b},1\right] ^T$. Now, we rewrite the system (2.1) as $\displaystyle \dfrac{dX}{dt}=F(X,\beta ),\quad F:{\mathbb {R}}^4 \times {\mathbb {R}} \rightarrow {\mathbb {R}}^4$ and $\displaystyle F\in {\mathbb {C}}^2 ({\mathbb {R}}^4\times {\mathbb {R}})$, where $\displaystyle X=\left[ x_1,x_2,x_3,x_4\right] ^T=\left[ S,I_S,T,I_R\right] ^T$ and $\displaystyle F=\left[ f_1,f_2,f_3,f_4\right] ^T$. Let

$$\begin{aligned} f&=\sum _{k,i,j=1}^{4} u_k v_i v_j \dfrac{\partial ^2 f_k}{\partial x_i \partial x_j}\left( E_0^{(2)},\beta _*^{(2)}\right) , \\ g&=\sum _{k,i=1}^{4} u_k v_i \dfrac{\partial ^2 f_k}{\partial x_i \partial \beta }\left( E_0^{(2)},\beta _*^{(2)}\right) . \end{aligned}$$

Further, by calculating the partial derivatives of the functions associated with model system (2.1) at equilibrium point $\displaystyle {E_0^{(2)}}$ and $\displaystyle {\beta =\beta _*^{(2)}}$, we get $\displaystyle {f=-\frac{2c^2}{\lambda }<0}$ and $\displaystyle {g=\frac{\lambda }{\mu }>0}$. Therefore, from Theorem 4.1(iv) of [45], we conclude that the model system (2.1) undergoes transcritical bifurcation at $\beta =\beta _*^{(2)}$. $\square$

Theorem 10

The equilibrium point $\displaystyle {E_*^{(2)}}$ changes its stability through Hopf-bifurcation when the real part of eigenvalues of $\displaystyle {J_2(E_*^{(2)})}$ intersects the imaginary axis at $\displaystyle {\eta =\eta _{H}^{(2)}}$, where $\displaystyle {\eta _{H}^{(2)}}$ is a root of the equation $\displaystyle {A_* B_* C_*-A_{*}^2 D_*-C_{*}^2=0}$.

Proof

The characteristic equation of the matrix $\displaystyle {J_2(E_*^{(2)})}$ has purely imaginary roots if:

• (A) $A_{*}>0, B_{*}>0, C_{*}>0, D_{*}>0$,

• (B) $A_{*}B_{*}-C_{*}>0$,

• (C) $A_{*}B_{*}C_{*}-A_{*}^{2}D_{*}-C_{*}^{2}=0$

and the system becomes structurally unstable in the neighborhood of the equilibrium point $\displaystyle {E_*^{(2)}}$, at $\eta =\eta _{H}^{(2)}$ where $\eta _{H}^{(2)}\in [0,1]$ is a root of equation $A_{*}B_{*}C_{*}-A_{*}^{2}D_{*}-C_{*}^{2}=0$. Further, this equilibrium point will change its stability at $\eta =\eta _{H}^{(2)}$ through Hopf-bifurcation if conditions (A), (B) and (C) are satisfied along with the transversality condition $\displaystyle {{\mathcal {R}}\Bigl \{\dfrac{d}{d\eta }\left[ x(\eta )\right] \Bigm |_{\eta =\eta _{H}^{(2)}}\Bigr \}\ne 0}$ [46], where x is the root of characteristic equation (3.5). Now differentiating equation (3.5) with respect to $\eta$, we have:

$$\begin{aligned}&4x^3 \dfrac{dx}{d\eta }+x^3 \dfrac{dA_*}{d\eta }+3A_*x^2 \dfrac{dx}{d\eta }{+}x^2\dfrac{dB_*}{d\eta }{+}2B_* x \dfrac{dx}{d\eta }\\&\quad +x\dfrac{dC_*}{d\eta }+C_*\dfrac{dx}{d\eta }+\dfrac{dD_*}{d\eta }=0 \end{aligned}$$

Therefore,

$$\begin{aligned} \dfrac{dx}{d\eta }=-\frac{x^3 \dfrac{dA_*}{d\eta }+x^2\dfrac{dB_*}{d\eta }+x\dfrac{dC_*}{d\eta }+\dfrac{dD_*}{d\eta }}{4x^3+3A_*x^2+2B_* x+C_*} \end{aligned}$$

Since x is purely imaginary at $\eta =\eta _{H}^{(2)}$ (say $x=\pm i \omega$), we get:

$$\begin{aligned}&{\mathcal {R}}\Bigl \{\dfrac{d}{d\eta }\left[ x(\eta )\right] \Bigm |_{\{x=\pm i \omega ,\eta =\eta _{H}^{(2)}\}}\Bigr \}\nonumber \\&\quad =\frac{\left( \dfrac{dD_*}{d\eta }-\omega ^2 \dfrac{dB_*}{d\eta }\right) \left( C_*-3\omega ^2 A_* \right) +\left( \omega \dfrac{dC_*}{d\eta }-\omega ^3 \dfrac{dA_*}{d\eta }\right) \left( 2\omega B_*-4\omega ^3\right) }{(C_*-3\omega ^2 A_*)^2+(2\omega B_*-4\omega ^3)^2} \end{aligned}$$

(3.11)

where $A_*, B_*, C_*$ and $D_*$ are as defined in previous section. In order to satisfy the transversality condition, the numerator (say $N(\eta )$) must be non-zero at $\eta =\eta _{H}^{(2)}$. It is extremely difficult to simplify this expression furthermore, therefore we choose a set of parametric values and then investigate the existence of the Hopf-bifurcation numerically. This analysis has been done in the next section. $\square$

4 Parameter estimation and numerical simulation

In this Section, we shall estimate the parametric values for the models (3.1) and (2.1) based on the real data from the Indian population. Further, we will also verify the analytic results on existence and stability of the equilibrium points and different bifurcations, through several numerical illustrations, in case of both the models.

The recruitment rate ($\lambda$) can be estimated as the sum of new individuals, who enter in the sexually active class and number of net migrated individuals, during the whole year, at the initial time. In India, we assume that most of the adults become sexually active during the age interval of 18–30 years. We set the base year to be 2019, for the purpose of our simulation. The number of individuals recruited in the susceptible class during base year is equal to the average net births during the period 1989–2001, in addition to the net migration in the base year. The net births are total number of births adjusted with the infant deaths in a year. According to United Nations- World Population Prospectus [47], the average birth rate and average infant mortality rate in India during time period 1989–2001 was 29.38 per thousand population per year and 78.87 per thousand live births per year, respectively. Further, the average total population of India during this time period was 955.29 million. Also, the net migration into India in 2019 was $-0.54$ million.

Therefore, the constant recruitment rate $(\lambda )$ can be estimated as follows:

$$\begin{aligned} \lambda= & {} \text {(avg. population)} \times \text {(avg. birth rate)} \\&\times \text {(1 - avg. infant mortality rate)}\\&+ \text {(net migration rate)}\\= & {} (955.29 \times 0.02938 \times (1-0.07887))-0.54\\= & {} 25.31 \text { million per year} \end{aligned}$$

According to United Nations- World Population Prospectus [47], in India, around 7.2 persons died for every 1000 individuals during 2019. Therefore, the natural death rate $(\mu )$ is 0.007 per year in 2019. The disease induced death rates can be estimated by using the life expectancy of an HIV-infected person. In [48], the authors have concluded that the life expectancy of an HIV-infected patient reduces about 38 years from the general population at the exact age of 20. In India, the life expectancy from birth was 69.50 years in 2019 [47]. From this we can conclude that the life expectancy of an HIV infected person without any treatment would be around 11 years. Therefore, 1 in every 11 HIV-infected person will die every year. Thus, we estimate that, $\displaystyle {\mu _S=\frac{1}{11}=0.0909}$ per year.

The transmission rate $\alpha$ represents the rate of change of drug-sensitive infected population in presence of unit susceptible and unit drug-sensitive infected population. According to India HIV Estimate 2019 Report, NACO [49], there were 69200 new HIV cases reported with total 2.35 million cases. The population in age group 20–50 can be considered as total susceptible population since it includes most of the sexually active people. According to [47], in 2019, India had 625.19 million people in the age group of 20–50. Therefore, the transmission rate is given by,

$$\begin{aligned} \alpha =\frac{0.06922}{625.19 \times 2.35}= 0.000047134 {\text { million}}^{-1}{\text {year}^{-1}}. \end{aligned}$$

We have seen that due to the enhanced accessibility to medical facilities, around $73\%$ of individuals living with HIV had started ART by the end of 2020 [8]. Therefore, we assume $\eta =0.7$ for most of the numerical simulations carried out. Further, we assume that $75\%$ of the population in the treatment class follows the prescribed treatment properly. The remaining parameters related to the drug-resistant infected class would be varied within a suitable range, considering the corresponding parametric values associated with the drug-sensitive infected class. For each of the parameters, the unit, estimated value and range of variation has been included in Table 5.

Table 5 Units and values (estimate and range) of various parameters

For numerical representation of all previous discussed analytic results, we fix $\lambda =25.31, \mu =0.007, \mu _S=0.0909, \mu _R=0.06$ for model (3.1) and $\lambda =25.31, \mu _S=0.0909, \epsilon =0.75, \eta =0.7$ for model (2.1) and vary other parameters to illustrate all the possible existence and stability scenarios for both models. We choose the initial population as 625 million for susceptible, 2.2 million for drug-sensitive infected, 1.5 million for under treatment and 1 million (assumption) for drug-resistant infected individuals, $ic_1=(625,2.2,1.5,1)$, which is based on the number of individuals in different classes in the base year. We also choose two other initial conditions to validate the global stability results: $ic_2=(300,30,20)$ and $ic_3=(1000,80,100)$ for the model (3.1) and $ic_2=(300,30,20,20)$ and $ic_3=(1000,80,50,100)$ for the model (2.1).

Fig. 5

Time series plot for each population of the model system (3.1) with other parametric values as $\lambda =25.31, \mu =0.007, \mu _S=0.0909, \mu _R=0.06$ and initial condition [625, 2.2, 1]

Fig. 6

Phase portrait for model (3.1) with various initial conditions assuring the global stability of each existing equilibrium point. Other parametric values as $\lambda =25.31, \mu =0.007, \mu _S=0.0909, \mu _R=0.06$

For model (3.1), first we consider $\alpha =0.000025$ and $\beta =0.000015$ for which $R_0^{(S)}=0.92$ and $R_0^{(R)}=0.81$. The solutions are represented in Fig. 5a which points out the local asymptotic stable behaviour of the disease-free equilibrium point $E_0^{(1)}(3615.7,0,0)$, as expected, since $R_0^{(S)}<1$ and $R_0^{(R)}<1$. The population level of susceptible individuals for different initial values converges to $\displaystyle {\frac{\lambda }{\mu }(=3615.7)}$ while the drug-sensitive and drug-resistant population decrease continuously and eventually get extinct (see Fig. 6a). This ensures the global asymptotic stability of equilibrium point $E_0^{(1)}$ and supports the theoretical result in Theorem 2. In order to illustrate the case $R_0^{(S)}>1$ and $R_0^{(SR)}>1$, we choose $\alpha =0.000047$ and $\beta =0.00002$ which results in $R_0^{(S)}=1.74$ and $R_0^{(R)}=1.08$. The dynamics for these parametric values is represented in Fig. 5b which indicates the persistence of susceptible and drug-sensitive infected population and extinction of drug-resistant infected population after a certain time. It is seen from Fig. 6b, that the population levels of susceptible and drug-sensitive infected individuals for different initial conditions exhibit oscillatory behaviour before stabilizing at the level 2082.98 and 109.59, respectively, while the drug-resistant infected population becomes extinct in a very short period of time. This also suggests the global asymptotic stability of drug-sensitive mutant dominant equilibrium point $E_1^{(1)}$ and is in agreement with the theoretical result of Theorem 3. Note that the basic reproduction number of drug-resistant infected population is greater than 1 but still this population gets wiped out from the system. This is because of a higher basic reproduction number of drug-sensitive mutant which makes it dominant in comparison to the drug-resistant mutant. Further, in order to illustrate the case $R_0^{(R)}>1$ and $R_0^{(SR)}<1$, we choose $\alpha =0.000047$ and $\beta =0.00006$ which leads to $R_0^{(S)}=1.74$ and $R_0^{(R)}=3.24$. The solution trajectories are drawn in Fig. 5c which shows that the susceptible and drug-resistant infected population saturate to a positive level and the drug-sensitive infected population dies out after some time. The global stability of drug-resistant mutant dominant equilibrium point $E_2^{(1)}(1116.67,0,261.09)$, as already obtained theoretically in Theorem 4, can be confirmed from Fig. 6c which also depicts an oscillatory behaviour of the susceptible and drug-resistant infected population before progressing to a steady state. The drug-resistant infected population dominates the drug-sensitive infected population due to its higher basic reproduction number. However, the basic reproduction number for both infected populations is greater than one. This analysis indicates that both the infected populations can be controlled by their transmission rate and disease induced death rate. A higher transmission rate of an infected population is in favor of its persistence at a higher level, while a higher disease induced death rate can cause its extinction from the system. We also observed that the coexistence of both infected populations is not possible because they share the only resource available to them, that is, the susceptible population.

Fig. 7

Time series plot for each population of the model system (2.1) with other parametric values as $\lambda =25.31, \mu _S=0.0909, \epsilon =0.75, \eta =0.7$ and initial condition [625, 2.2, 1.5, 1].

Fig. 8

Phase portrait for model (2.1) with various initial conditions assuring the global stability of existing equilibrium points (except $E_{*}^{(2)}$). Other parametric values are $\lambda =25.31, \mu _S=0.0909, \epsilon =0.75, \eta =0.7$

On the other hand, we vary the parameters $\alpha , \beta , \mu \text {and } \mu _R$ to investigate the dynamics of model (2.1). We consider $\alpha =0.000047, \beta =0.000015, \mu =0.007$ and $\mu _R=0.06$ and get the corresponding basic reproduction numbers as ${\bar{R}}_0^{(S)}=0.23~(<1)$ and ${\bar{R}}_0^{(R)}=0.81~(<1)$. The dynamics for these parametric values is represented in Fig. 7a. Clearly, the compartment of infected and under treatment individuals become empty at a very early stage, while the susceptible population increase continuously and eventually reach to its highest level $\displaystyle {\frac{\lambda }{\mu }(=3615.7)}$. The phase portraits in Fig. 8a and b confirms the global stability of disease-free equilibrium point $E_0^{(2)}$. Next, we choose $\alpha =0.0003, \beta =0.00003, \mu =0.007$ and $\mu _R=0.06$ to illustrate the case when $R_0^{(R)}(=1.62)>1$ and $R_0^{(SR)}(=0.91)<1$. In this case, the drug-resistant mutant dominant equilibrium point behaves like a sink and only the susceptible and drug-resistant infected populations are able to survive for long run. The dynamics for this case is illustrated in Fig. 7b and the global stability of $E_1^{(2)}(2233.33,0,0,144.43)$ is shown in Fig. 8c, d. Note that the drug-sensitive infected population is wiped out from the system after some time, although it has basic reproduction number greater than one. This happens since the drug-resistant infected population has a higher basic reproduction number than drug-sensitive infected population. In other words we can say that the transmission rate of drug-sensitive infected population is not enough for its survival. Finally, we choose $\alpha =0.00015, \beta =0.00001, \mu =0.004$ and $\mu _R=0.18$. This set of parametric values results in ${\bar{R}}_0^{(S)}(=1.29)>1$, ${\bar{R}}_0^{(SR)}(=3.77)>1$ and $\displaystyle {A_{*}B_{*}C_{*}-A_{*}^{2}D_{*}-C_{*}^{2}(=2.02\times 10^{-6})>0}$. Figure 7c represents the long time dynamics of the model (2.1) and suggests that each population converges to the interior equilibrium point $E_*^{(2)}(4875.13,6.06,15.32,28.32)$ after some initial oscillations. Further, the phase portraits in Fig. 8e, f show that the phase point converges to the interior equilibrium point for various initial conditions. It also indicates that the equilibrium point $E_*^{(2)}$ is an attractor for a large region around it.

Fig. 9

Transcritical bifurcation diagrams with respect to parameters a $\alpha (\text {or }\beta )$ and b $\displaystyle {R_0^{(S)}~ \left( \text {or } R_0^{(R)}\right) }$

Fig. 10

a Time series plot for each population of the model system (2.1) showing periodic nature of solutions. b Phase portrait for the model system (2.1) with two different initial conditions assuring the existence of a stable limit cycle for the parametric values: $\lambda =25.31, \alpha =0.00025, \beta =0.000025, \mu =0.005, \mu _S=0.0909, \mu _R=0.08, \eta =0.37$ and $\epsilon =0.75$

Fig. 11

The bifurcation diagram of each population of the model system (2.1) with respect to the Hopf-bifurcation parameter $\eta$. The other parameters are $\lambda =25.31,\alpha =0.00025, \beta =0.000025, \mu =0.005, \mu _S=0.0909, \mu _R=0.08, \epsilon =0.75$

Fig. 12

The existence of limit cycle for the model system (2.1) corresponding to variation in Hopf-bifurcation parameter $\eta$. The other parameters are $\lambda =25.31,\alpha =0.00025, \beta =0.000025, \mu =0.005, \mu _S=0.0909, \mu _R=0.08, \epsilon =0.75$

Fig. 13

Density Plot for a S, b $I_S$, c T, d T and e $I_R$ on $\epsilon \eta -$plane. The other parameters are $\lambda =25.31,\alpha =0.0003, \beta =0.00007, \mu =0.007, \mu _S=0.0909, \mu _R=0.2$

Now we choose the parameters as $\lambda =25.31, \mu =0.007$ and $\mu _S=\mu _R=0.0909$ to illustrate the transcritical bifurcation when equilibrium point $\displaystyle {E_0^{(1)}}$ exchanges its stability with equilibrium point $\displaystyle {E_1^{(1)}~ \left( \text {or } E_2^{(1)}\right) }$. Also, we vary the parameter $\mu _S~\text {(or }\mu _R)$ to show the exchange of stability between equilibrium point $\displaystyle {E_0^{(1)}}$ and $\displaystyle E_1^{(1)}~ \left( \text {or } E_2^{(1)}\right)$, we vary the parameter $\mu _S~\text {(or }\mu _R)$. In Fig. 9a, we observe that the equilibrium point $\displaystyle {E_0^{(1)}}$ bifurcates and losses its stability at $\displaystyle \alpha =\alpha _*^{(1)}~\text {(or }\beta =\beta _*^{(1)})=2.71\times 10^{-5}$ and a new stable equilibrium point $\displaystyle {E_1^{(1)}~ \left( \text {or } E_2^{(1)}\right) }$ comes into the picture. We also demonstrated this bifurcation behaviour between these equilibrium points with respect to basic reproduction number $\displaystyle {R_0^{(S)}~ \left( \text {or } R_0^{(R)}\right) }$. For this, we fix $\alpha =\beta =0.000047$ and vary the basic reproduction number $\displaystyle {R_0^{(S)}}$ and $\displaystyle {R_0^{(S)}}$ by changing common parameters $\lambda$ and $\mu$. Figure 9b depicts that if $\displaystyle {R_0^{(S)}~ \left( \text {or } R_0^{(R)}\right) }<1$, only one equilibrium point exists, that is $\displaystyle {E_0^{(1)}}$, which is locally asymptotically stable. On $\displaystyle {R_0^{(S)}~ \left( \text {or } R_0^{(R)}\right) }=1$, a new equilibrium point $\displaystyle {E_1^{(1)}~ \left( \text {or } E_2^{(1)}\right) }$ emerges and $\displaystyle {E_0^{(1)}}$ exchanges its stability with this new equilibrium point provided that $\displaystyle {R_0^{(R)}~ \left( \text {or } R_0^{(S)}\right) }<1$. We find similar figures of the transcritical bifurcation for model system (2.1) with same parametric values as discussed above, when disease-free equilibrium point $\displaystyle {E_0^{(2)}}$ changes its stability with axial equilibrium point $\displaystyle {E_1^{(2)}}$. These numerical results support Theorems 5, 6 and 9.

For the set of parametric values: $\lambda =25.31, \alpha =0.00025, \beta =0.000025, \mu =0.005, \mu _S=0.0909, \mu _R=0.08, \eta =0.37$ and $\epsilon =0.75$, we observe that condition $\displaystyle A_{*}B_{*}C_{*}-A_{*}^{2}D_{*}-C_{*}^{2}>0$ is not satisfied. Therefore, the interior equilibrium point $\displaystyle {E_*^{(2)}}$ of model system (2.1) is not locally asymptotically stable for this set of parametric values. Our numerical simulation shows that the solution curves of this system admits periodic behaviour and converge to a stable limit cycle. The time series plot of each population for the above set of parametric values is shown in Fig. 10a, which assures the existence of the periodic nature of the solutions and predicts that the interior equilibrium point $E^{(2)}_{*}$ is unstable. In Fig. 10b, solutions starting from different initial values are converging to a stable limit cycle.

Considering $\eta$ as a bifurcation parameter, we note that the solutions of equation $A_{*}B_{*}C_{*}-A_{*}^{2}D_{*}-C_{*}^{2}=0$ for $\eta$ are $\displaystyle {\eta _{H1}^{(2)}=0.3422}$ and $\displaystyle {\eta _{H2}^{(2)}=0.8191}$, which lies in the interval [0, 1]. The set of eigenvalues for these parametric values corresponding to Jacobian matrices $\displaystyle {J_2(E_*^{(2)})\bigm |_{\eta = \eta _{H1}^{(2)}}}$ and $\displaystyle {J_2(E_*^{(2)})\bigm |_{\eta = \eta _{H2}^{(2)}}}$ are $(-0.2765,-0.0611,2.2551\times 10^{-17}\pm 0.0559 i)$ and $(-0.2777,-0.0085,-2.7322\times 10^{-17}\pm 0.0154)$, respectively. These sets consist only either negative real or almost pure imaginary eigenvalues. Further, we have $\displaystyle {N\left( \eta _{H1}^{(2)}\right) =-2.18682\times 10^{-7}\ne 0}$ and $\displaystyle {N\left( \eta _{H2}^{(2)}\right) =5.4698\times 10^{-9}\ne 0}$, which is in agreement with the transversality condition (3.11). Here $N(\eta )$ is as discussed in Theorem 10. So, the equilibrium point $E_*^{(2)}$ changes its stability through Hopf-bifurcation at bifurcation points $\displaystyle {\eta _{H1}^{(2)}=0.3422}$ and $\displaystyle {\eta _{H2}^{(2)}=0.8191}$. Geometrically, Figs. 11 and 12 confirm the occurrence of Hopf-bifurcation at points $\displaystyle {\eta _{H1}^{(2)}}$ and $\displaystyle {\eta _{H2}^{(2)}}$. In Fig. 11, the curves before the bifurcation point $\eta _{H1}^{(2)}$ and after the bifurcation point $\eta _{H2}^{(2)}$ show the population levels for different values of the parameter $\eta$. The limit cycles occur between these two bifurcation points and the red coloured dots represent the lowest population level, while the blue coloured dots represent the highest population level, at a specific value of the parameter $\eta$. In addition, Fig. 12 shows the periodic nature of solutions of system (2.1) for different values of parameter $\eta$. We can conclude from Fig. 10b, 12 and stability of coexistence equilibrium point $E_*^{(2)}$ that solutions of model system (2.1) achieve steady state at $E_*^{(2)}$ for $\eta <\eta _{H1}^{(2)}$ and $\eta >\eta _{H2}^{(2)}$ while converge to a stable limit cycle for $\eta \in [\eta _{H1}^{(2)},\eta _{H2}^{(2)}]$. This confirms that Hopf-bifurcation is supercritical in nature.

Further, we have plotted density plots for each population on the $\epsilon \eta -$plane to know the best possible scenario to minimize the infected populations and maximize the under treatment population. We used parametric values: $\lambda =25.31,\alpha =0.0003, \beta =0.00007, \mu =0.007, \mu _S=0.0909, \mu _R=0.2$ for these density plots. Figure 13a suggests that lower treatment rate will minimize the susceptible population. This happens because lower treatment levels lead to a major increase in total infected population which we can observe in Fig. 13b. It is observed from Fig. 13c, d that perfect adherence with medium treatment rate is an optimal scenario for maximizing the population under treatment. On the other hand, Fig. 13e depicts that a medium treatment rate with imperfect adherence lead to a greater risk of emergence of drug resistance, while extremely low or high treatment rate minimizes this risk. In addition, a perfect drug adherence can also hold the drug-resistant infected population at lower levels.

5 Conclusion

In this study, we formulated a mathematical model to understand the dynamics of HIV spread under treatment in presence of drug-sensitive and drug-resistant infected population. We considered that the drug resistance transmits from drug-resistant infected population to susceptible via direct contact. Also, drug resistance can develop through improper drug adherence. Therefore, transmission is the only source for the newly drug-resistant infected population, in the absence of treatment. For the treatment-free model, we obtained the basic reproduction number for drug-sensitive $\displaystyle {(R_0^{(S)})}$ and drug-resistant $\displaystyle {(R_0^{(R)})}$ strains with the help of the next generation matrix. The existence of equilibrium points and their stability is totally controlled by these basic reproduction numbers. The stability analysis of equilibrium points provides us with three possible scenarios:

• (a) Both type of infected population dies out when $\displaystyle {R_0^{(S)}<1}$ and $\displaystyle {R_0^{(R)}<1}$.

• (b) Only drug-sensitive infected population survives when $\displaystyle {R_0^{(S)}>1}$ and $\displaystyle {R_0^{(SR)}>1}$.

• (c) Only drug-resistant infected population survives when $\displaystyle {R_0^{(R)}>1}$ and $\displaystyle {R_0^{(SR)}<1}$.

In all of the above cases, we observe that the co-existence of all populations is impossible. This happens because both infected populations with drug-sensitive and drug-resistant strains share their common source (susceptible population) of growth. The bifurcation analysis shows that the transmission rate and disease induced death rate of both strains are the determining factors for the elimination of the disease from the system. The lower transmission rate or higher disease induced death rate from certain threshold values makes the system disease free after some time. On the other hand, a greater transmission rate or a lower disease induced death rate of a strain from these threshold values is directly related to the increased fitness of that strain.

In presence of treatment to the infected population, however, we expect some more potential outcomes between two strains, beyond the competitive exclusion. We calculated the basic reproduction number for drug-sensitive $\displaystyle {{\bar{R}}_0^{(S)}}$ and drug-resistant $\displaystyle {{\bar{R}}_0^{(R)}}$ strains for treatment model to analyze it. We analyzed all existing equilibrium points and their stability. The treatment model also shows three different possible scenarios for infected population:

• (a) Both type of infected population dies out when $\displaystyle {{\bar{R}}_0^{(S)}<1}$ and $\displaystyle {{\bar{R}}_0^{(R)}<1}$.

• (b) Only drug-resistant infected population survives when $\displaystyle {{\bar{R}}_0^{(R)}>1}$ and $\displaystyle {{\bar{R}}_0^{(SR)}<1}$.

• (c) drug-sensitive and drug-resistant infected population co-exist in the system when $\displaystyle {{\bar{R}}_0^{(S)}>1}$ and $\displaystyle {{\bar{R}}_0^{(SR)}>1}$.

From this, we can conclude that the system becomes disease free at lower reproductive capacities of both the strains. At the same time, a higher basic reproduction number is not enough for the survival of the drug-sensitive infected population, since the drug-resistant infected population out-competes the former, if $\displaystyle {{\bar{R}}_0^{(SR)}<1}$. This could be a result of high transmission rate or low disease induced death rate of drug-resistant infected class and a higher number of infected individuals in treatment class. These results are consistent with observations in a prior two-strain disease model [43]. We also found that the population in the drug-resistant infected class faces survival risk only at their lower reproductive capacity, in the absence of drug-sensitive infected population. We observed that the drug resistance infected population remains in the system, even at its lower reproductive capacity, if the number of individuals in drug-sensitive infected and treatment class are at a positive level. This shows that a better treatment availability is responsible for the emergence of drug resistance. Therefore, one could question the sustainability of the treatment of the drug-sensitive infected population at the expense of an increment in the drug-resistant individuals in the community [50]. However, during the initial phase, such resistant strains have low fitness levels and are less transmissible than their drug-susceptible counterparts [51]. So an early awareness campaign in non-adherent patients may reduce the risk of emergence of the drug-resistant strain. From the existence condition of the interior equilibrium point, we conclude that the co-existence of both the infected populations, under better treatment availability, demands a high transmission rate in drug-sensitive infected population compare to the other one.

Finally, we have performed an extensive analysis of possible bifurcations for treatment model. We found that the system undergoes a transcritical bifurcation at a critical transmission rate of drug-resistant infected population. The system remains at disease-free state if the transmission rate remains below this threshold value, without which the system goes to the only drug-resistant strain endemic equilibrium point. A lower disease induced death rate of drug-resistant infected population also contributes in this transformation from disease-free to endemic state of the system. We also found that the co-existence endemic equilibrium point changes its stability through Hopf-bifurcation at a critical value of parameter $\eta$ and the system shows periodic behaviour. Numerical simulation suggests that all solutions converge to a stable limit cycle for a range of parametric values of $\eta$. Extremely low or high treatment availability makes the co-existence endemic equilibrium point stable. On the other hand, a large range of medium treatment availability forces the system to show a periodic behaviour, eventually approaching to a limit cycle. In this case, it is extremely difficult for policy makers to reach any concluding strategy to control the spread of the disease if the ratio of number of individuals in each class changes continuously. Therefore, a medium range of treatment availability is not an efficient way to control the disease. We also observed that both basic reproduction numbers are independent of the proportion of population which properly adheres to the treatment, but the stability condition of co-existence endemic equilibrium point depends on it. Sharomi et al. [36] concluded that the widespread use of ART could significantly reduce the disease burden, despite the risk of the development and transmission of drug-resistant strain. But, our study suggests that the drug-adherence to the treatment also plays a vital role in determining the dynamics and is responsible for periodic behavior. The density plot for treatment model shows that a medium level of treatment availability with sub-optimal drug adherence is suitable template for emergence of the drug resistance. This result can be a stepping stone for public health debates [50] regarding the potential benefits and dangers of providing ART to the infected population at risk for the emergence of drug-resistance in patients.

In summary, the present study shows that without treatment, there is no emergence of drug resistance which results in competitive exclusion of one of the infected population. Co-existence of both type of infected population is impossible. On the contrary, when treatment is provided to the infected population, the drug-sensitive infected population either face competitive exclusion or co-exist with drug-resistant infected population. The number of infected patients under treatment and patients who follow the treatment properly are the main determining factors of the dynamics of disease spread. Also, a higher transmission rate of drug-sensitive strain with enough treatment availability and its improper adherence ultimately supports the growth of the drug-resistant infected population. Our analysis shows that policy makers should focus on providing better conditions to the patients to adhere their treatment properly. Otherwise, a higher treatment availability with sub-optimal drug adherence could lead us to a danger of increased number of drug-resistant infected population, or an endemic of drug-resistant infection in the worst of conditions.