Combination resonances of a dual-rotor-bearing-casing system

Abstract

In this paper, the combination resonance characteristics of a high-dimensional dual-rotor-bearing-casing system with bearing nonlinearities are presented. All the periodic solution branches, including the unstable solutions of the system, are obtained by the semi-analytical harmonic balance method. Two primary and two combination resonance regions are found in the amplitude–frequency responses, with the vibration jump and multiple solutions phenomena being observed. Furthermore, the amplitude–frequency responses with separated frequencies are analyzed; it is shown that the vibration responses of the combination resonance regions are dominated by the combination frequencies of the rotating speeds of the high- and low-pressure rotors. Moreover, parametric analysis shows that the combination resonances are sensitive to the change in the inter-shaft bearing clearance. With the increase in clearance, the combination resonance regions are widened. The results in this paper provide a better understanding of the combination resonances in high-dimensional dual-rotor-bearing-casing systems.

1 Introduction

The dual-rotor system is widely used in modern aero-engine due to its high thrust-weight ratio and significant advantage in stability. In a dual-rotor system, the back end of the high-pressure (HP) rotor is supported on the rotating shaft of the low-pressure (LP) rotor by the inter-shaft bearing. Thus, the rear fulcrum of the HP rotor no longer requires a bearing seat, reducing the weight of the system. However, on the one hand, the use of the inter-shaft bearing will cause the vibration coupling between two rotors. On the other hand, the nonlinear restoring force of the inter-shaft bearing contains many coupling nonlinearities including fractional exponential function, radial clearance, and variable stiffness excitations; this induces a series of nonlinear vibration behaviors [1], such as vibration jump, resonance hysteresis, multiple solutions and combination resonance. Studying the nonlinear dynamic characteristics of the dual-rotor system is significant to the health and parametric optimization of aero-engines.

The dynamic characteristics of dual-rotor systems have been studied widely using numerical simulations and experiments, where the effect of nonlinearities of bearing and faults was analyzed in detail. First of all, the basic dynamic characteristics [2] of dual-rotor systems are discussed, including critical speed, mode and the sense of the whirl, etc. The modeling [3] and model reduction methods are studied, and simplified models of dual-rotor systems with several degrees of freedom are established, in which the nonlinearities of the bearings and the coupling effect of the two rotors are considered. Studies on the local defect of the inter-shaft bearing [4] and the thermo-mechanical coupled characteristics [5] are analyzed, revealing that the radial clearance has a great effect on the nonlinear responses of the system. Ma et al. [6] investigated the effects of squeeze film damper and showed that the oil film clearance affects the damping performance of the squeeze film damper. Unbalanced vibration characteristics, the effects of dual-frequency excitations [7], base excitation [8] and the coupling effect of bending-torsional [9] were analyzed in detail. It was found that the vibration response of the dual-rotor system is related to the unbalanced position and the unbalanced phase. The nonlinear characteristics of dual-rotor system with nonlinear faults [10], including the non-concentricity faults [11], the rubbing fault [12], and the inter-shaft rub-impact [13], were also studied; the results show that the faults will cause complicated responses of the system, which contain complex frequency components. The above studies have obtained many nonlinear vibration properties of the dual-rotor system and revealed the effect of bearing nonlinearities and nonlinear faults. However, there are insufficient investigations on the nonlinear vibration mechanism.

In order to get a further understanding of the nonlinear vibration mechanism, the harmonic balance-alternating frequency/time domain (HB-AFT) method has been widely applied in the analysis of rotor systems. The basic idea of the HB-AFT method [14, 15] is to convert the differential equations of the system into algebraic equations using the harmonic balance (HB) program. The Newton–Raphson iterative procedure is then employed to obtain the periodic solution, in which the Jacobian matrix of the nonlinear parts needed in the process is obtained by the alternating frequency/time domain (AFT) procedure. HB-AFT method is a semi-analytical method; it is able to handle a variety of nonlinear problems [16, 17], including fractional exponential function [18], clearance [19], time-varying stiffness [20], self-excited vibration [21] and so on. Furthermore, by combining with the numerical continuation procedure [22,23,24,25], HB-AFT is able to obtain the different solution branches for nonlinear systems. Compared with numerical methods [26], it is not only highly efficiency, but also able to obtain all periodic solution branches (including the unstable solutions) [27, 28]. Based on the HB-AFT method, much work has been carried out in the nonlinear dynamics analysis of rotor systems. A series of nonlinear characteristics, including quasi-periodic response [29, 30], the primary resonant [31], the combination resonance [32], the super-harmonic resonance [33], the internal resonance [34], bifurcation and stability [35], are analyzed in detail. The effects of the bearing’s nonlinearities on rotor system [18, 36] and the mechanism of the varying compliance parametric resonances [37, 38] were revealed; it was found that the nonlinearities of the bearing would introduce instability to the system. The HB-AFT method was also modified to deal with the nonlinear stochastic dynamics problems [39,40,41] of rotor system; the results show that the modified HB-AFT method is high-efficiency and high-precision. In addition, the nonlinear dynamic characteristics of rotor systems with nonlinear faults, including misalignment [42], rub-impact [43,44,45], synchronous impact [46], are detected by HB-AFT method, showing that nonlinear faults would make more complex frequency components in the responses of the system and even cause abnormal resonances in some cases. The above studies provide in-depth understanding of the mechanism of nonlinear behaviors such as vibration jump, multiple solutions and bifurcation of rotor system. However, most of these studies focused on the Jeffcott rotor model or simple dual-rotor model with several degrees of freedom, and there is insufficient research on high-dimensional complex rotor systems.

The motivation of this paper is to detect the combination resonances of a dual-rotor-bearing-casing system with 284 degrees of freedom. Wherein the Hertz contact model of the nonlinear restoring force of the inter-shaft bearing is utilized, in which the fractional exponential function, the radial clearance and the variable stiffness excitation are considered. The semi-analytical harmonic balance (SAHB) method is employed to obtain all the periodic solution branches of the high-dimensional nonlinear system, providing an overall understanding of the nonlinear dynamic characteristics of the system. Two distinct combination resonance regions are found, wherein the vibration jump, multiple solutions and circular phenomena are observed. Moreover, the dominant frequency components of the combination resonances are determined, the nonlinear force of the inter-shaft bearing is calculated, providing a further understanding of the combination resonance mechanisms.

2 Dynamic model of the dual-rotor-bearing-casing system

The dynamic model of the dual-rotor-bearing-casing system (Ref [1]) is established in this section, in which the characteristics of the system are introduced and the motion equations of the system are given.

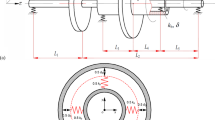
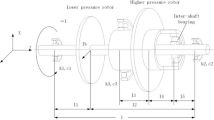
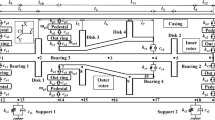
Figure 1 shows the schematic diagram of the dual-rotor-bearing-casing system, which consists of four parts, i.e., the low-pressure rotor (LP rotor), the high-pressure rotor (HP rotor), the inner casing and the outer casing. The LP rotor and the HP rotor are connected by the inter-shaft bearing. Furthermore, the LP rotor is composed of a flexible rotating shaft and three rigid disks with gyroscopic effect consolidated on it. The HP rotor contains a flexible rotating shaft and eight rigid disks with gyroscopic effect consolidated on it. The rotating speeds of the LP rotor and HP rotors are $\omega_{1}$ and $\omega_{2}$, respectively, and the rotating speed ratio of the two rotors is defined as $\lambda = \omega_{2} /\omega_{1}$.The finite element method is employed to establish the dynamic model of the system, in which the LP rotor is divided into nodes 1–20, the HP rotor is divided into nodes 21–35, the inner casing is divided into nodes 36–44 and the outer casing is divided into nodes 45–71. The motion of each node is described in four degrees of freedom, i.e., the horizontal displacement x and the vertical displacement y, and the corresponding rotating angle is denoted as $\theta_{x}$ and $\theta_{y}$. Therefore, the total degrees of freedom of the system’s dynamic model are 284. In addition, the nonlinear restoring force of the inter-shaft bearing is modeled by the Hertz contact model [47], where the fractional exponential function, the radial clearance and the variable stiffness excitation are considered. Interested readers may refer to Ref [1] for more details about the dynamic model of the system.

Fig. 1

Schematic diagram of the dual-rotor-bearing-casing system, which contains four parts, i.e., the low-pressure rotor (LP rotor), the high-pressure rotor (HP rotor), the inner casing and the outer casing. The LP rotor contains a flexible rotating shaft and three rigid disks, is divided with nodes 1–20; the HP rotor contains a flexible rotating shaft and eight rigid disks, is divided with nodes 21–35; the inner casing is divided with nodes 36–44 and the outer casing is divided with nodes 45–71. The LP rotor and the HP rotor are connected by the inter-shaft bearing. $k_{i} \, (i = 1 - 9)$ and $c_{i} \, (i = 1 - 9)$ are the stiffness and the damping coefficients for support 1–9

According to the finite element method [48], based on the dynamic equation of the rigid disks, flexible shaft segments and the casings, the nonlinear force of the inter-shaft bearing, the dynamic equation of the whole rotor system can be expressed as follows:

$$ {\mathbf{M}\ddot{\mathbf{X}}} + {\mathbf{C}\dot{\mathbf{X}}} + {\mathbf{KX}} = {\mathbf{F}}({\mathbf{X}},t) $$

(1)

where M, C and K are the mass matrix, damping matrix and stiffness matrix, respectively. In addition, the gyroscopic effect matrix is integrated into the matrix C. F denotes external force on the system, including the LP rotor unbalanced excitation, HP rotor unbalanced excitation and the nonlinear force of the inter-shaft bearing. X, ${\dot{\mathbf{X}}}$ and ${\mathbf{\ddot{X}}}$ denote the displacement, velocity and acceleration of the system, respectively.

3 Methodology formulation

According to the characteristics of the system’s dynamics equation, a (SAHB) method is proposed in this section, which is able to obtain the periodic solutions (including the unstable solutions) of the system efficiently.

As Eq. (1) shows, the motion equation of the system is not only highly dimensional, i.e., contains 284 degrees of freedom, but also contains nonlinearities from the inter-shaft bearing, including the fractional exponential function, the radial clearance and the variable stiffness excitation. As such, neither the traditional analytical method nor the numerical method can give its periodic solution efficiently and comprehensively. Thus, the SAHB method is proposed to handle it. In the SAHB method, the periodic solution of the system is set as a truncated Fourier series, and the residual of the equations obtained by the harmonic balance method is generated by the discrete Fourier transform (DFT) procedure; both the periodic solution and the residual are written as the product of the harmonic basis matrix and the harmonic expending coefficients matrix. Then, the harmonic expending coefficients matrix of the residuals is generated by the inverse discrete Fourier transform (IDFT) procedure in the time domain. Thereafter, the Jacobian matrix of the residuals can be calculated programmatically and efficiently by the chain derivative rule. Consequently, the harmonic expending coefficients matrix of the periodic solution can be updated efficiently by the Newton–Raphson iterative procedure until the norm of the residual is less than the preset error. In addition, the different solution branches of the system can be obtained by combining the SAHB method with the arc length continuation procedure [25], and the stabilities of the different solution branches can be analyzed by the Floquet theory [49].

In the procedure of the SAHB method, first of all, a time-scale normalization is performed in the equation of motion (1) of the system, set $\tau = \omega_{1} t$, then

$$ {\dot{\mathbf{X}}} = \frac{{{\text{d}}{\mathbf{X}}}}{{{\text{d}}\tau }}\frac{{{\text{d}}\tau }}{{{\text{d}}t}} = \omega_{1} {\mathbf{X}}^{\prime } ,\;{\mathbf{\ddot{X}}} = \frac{{{\text{d}}{\dot{\mathbf{X}}}}}{{{\text{d}}\tau }}\frac{{{\text{d}}\tau }}{{{\text{d}}t}} = \omega_{1}^{2} {\mathbf{X}}^{\prime \prime } $$

(2)

in which $( \bullet )^{\prime }$ denotes the first-order derivative and $( \bullet )^{\prime \prime }$ represents the second-order derivative with respect to $\tau$, substituting Eq. (2) into Eq. (1), then

$$ \omega_{1}^{2} {\mathbf{M}}{\mathbf{X}}^{\prime \prime } + \omega_{1} {\mathbf{C}}{\mathbf{X}}^{\prime } + {\mathbf{KX}} = {\mathbf{F}}({\mathbf{X}},\tau ). $$

(3)

For the equation of motion (3), the periodic solution of each freedom of the system is set as a truncated Fourier series, i.e.,

$$ {\mathbf{X}} = \left[ {\begin{array}{*{20}c} {a_{0 - 1} + \sum\limits_{p = 1}^{s} {(a_{p - 1} \cos p\tau + b_{p - 1} \sin p\tau } )} \\ {\begin{array}{*{20}c} \vdots \\ {\begin{array}{*{20}c} {a_{0 - i} + \sum\limits_{p = 1}^{s} {(a_{p - i} \cos p\tau + b_{p - i} \sin p\tau } )} \\ \vdots \\ {a_{0 - 284} + \sum\limits_{p = 1}^{s} {(a_{p - 284} \cos p\tau + b_{p - 284} \sin p\tau } )} \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]^{T} $$

(4)

in which s denotes the number of the truncated Fourier series order, i denotes the number of degrees of freedom, p stands for harmonic order.$a_{0 - i}$ denotes the direct component of the response in the ith degree of freedom, $a_{p - i}$ denotes the coefficient of the cosine component in the ith degree of freedom, $b_{p - i}$ denotes the coefficient of the sinusoidal component in the ith degree of freedom. The periodic solution of the system in Eq. (4) can be rewritten as the product of the harmonic basis matrix H and the harmonic expending coefficients matrix A.

$$ {\mathbf{X}} = {\mathbf{HA}} $$

(5)

The detailed expressions of H and A are as follows:

$$ {\mathbf{H}} = \left( {\begin{array}{*{20}c} 1 & {\cos \tau } & \cdots & {\cos s\tau } & {\sin \tau } & \cdots & {\sin s\tau } \\ \end{array} } \right) $$

(6)

$$ {\mathbf{A}} = \left( {\begin{array}{*{20}c} {a_{0 - 1} } & {a_{1 - 1} } & \cdots & {a_{s - 1} } & {b_{1 - 1} } & \cdots & {b_{s - 1} } \\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ {a_{0 - 284} } & {a_{1 - 284} } & \cdots & {a_{s - 284} } & {b_{1 - 284} } & \cdots & {b_{s - 284} } \\ \end{array} } \right)^{T} . $$

(7)

Defining the residual of the dynamic Eq. (3) of the system as R, i.e.,

$$ {\mathbf{R}}(\tau ,{\tilde{\mathbf{X}}}^{\prime \prime } ,{\tilde{\mathbf{X}}}^{\prime } ,{\tilde{\mathbf{X}}}) = {\mathbf{F}}({\tilde{\mathbf{X}}},\tau ) - \omega_{1}^{2} {\mathbf{M\tilde{X}}}^{\prime \prime } - \omega_{1} {\mathbf{C\tilde{X}}}^{\prime } - {\mathbf{K\tilde{X}}} = 0. $$

(8)

Since the external force ${\mathbf{F}}({\mathbf{X}},\tau )$ of the system, i.e., the unbalanced excitation of the LP rotor and HP rotor, and the nonlinear force of the inter-shaft bearing, can be expressed by a truncated Fourier series, R also can be expressed as a truncated Fourier series, i.e., R = HB, where H is the harmonic basis matrix, as shown in Eq. (6), and B is the corresponding harmonic expending coefficients matrix; the detailed expression of B is as follows:

$$ {\mathbf{B}} = \left[ {\begin{array}{*{20}c} {c_{0 - 1} } & {c_{1 - 1} } & \cdots & {c_{s - 1} } & {d_{1 - 1} } & \cdots & {d_{s - 1} } \\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ {c_{0 - 284} } & {c_{1 - 284} } & \cdots & {c_{s - 284} } & {d_{1 - 284} } & \cdots & {d_{s - 284} } \\ \end{array} } \right]^{T} $$

(9)

Therefore, after a harmonic balance procedure, the differential Eq. (3) of the system is equivalent to the following algebraic equation:

$$ {\mathbf{B}}\left( {\mathbf{A}} \right) = {\mathbf{0}}. $$

(10)

The Newton–Raphson iterative procedure is then employed to find the fixed point of Eq. (10), i.e.,

$$ {\mathbf{A}}^{(k + 1)} = {\mathbf{\rm A}}^{(k)} - {\mathbf{J}}^{ - 1} {\mathbf{B}} $$

(11)

in which J is the Jacobian matrix, defined as

$$ {\mathbf{J}} = \frac{{\partial {\mathbf{B}}}}{{\partial {\mathbf{A}}}}. $$

(12)

Because the harmonic expending coefficients matrix B contains the Fourier expansion coefficient of the inter-shaft bearing nonlinear forces, $\partial {\mathbf{B}}/\partial {\mathbf{A}}$ cannot be calculated directly. For this, the procedure that combines the inverse discrete Fourier transform (IDFT) with the chain derivative rule is employed to construct the relationship between B and A; the details are as follows.

3.1 Discrete sampling

At the beginning, the period T is equally divided into N points, noting that N must satisfy Nyquist–Shannon sampling theorem. Then, one can define the sampling time series as follows:

$$ \tau_{k} = \frac{T}{N}k,\;k = 0,1,2, \ldots , \, N - 1 $$

(13)

3.2 Calculate B by the IDFT procedure

Using the IDFT procedure, one can obtain the components of B in the time domain, i.e.,

$$ {\text{c}}_{0 - i} = \frac{1}{N}\sum\limits_{k = 0}^{N - 1} {R_{i} \left( {\tau_{k} } \right)} ,{\text{c}}_{j - i} = \frac{2}{N}\sum\limits_{k = 0}^{N - 1} {R_{i} \left( {\tau_{k} } \right)\cos j\tau_{k} } ,\;\;{\text{d}}_{j - i} = \frac{2}{N}\sum\limits_{n = 0}^{N - 1} {R_{i} \left( {\tau_{k} } \right)\sin j\tau_{k} } $$

(14)

where $R_{i}$ is the ith row of the residual matrix R, corresponding to the residual of the ith degree of freedom of the system.

3.3 Calculate the Jacobian matrix J

After constructing the relationship between B and A, the Jacobian matrix J can also be calculated in the time domain by the chain derivation rule, i.e.,

$$ {\mathbf{J}} = \left[ {\begin{array}{*{20}c} {\partial {\mathbf{B}}_{1} /\partial {\mathbf{A}}_{1} } & \cdots & {\partial {\mathbf{B}}_{1} /\partial {\mathbf{A}}_{i} } & \cdots & {\partial {\mathbf{B}}_{1} /\partial {\mathbf{A}}_{284} } \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ {\partial {\mathbf{B}}_{i} /\partial {\mathbf{A}}_{1} } & \cdots & {\partial {\mathbf{B}}_{i} /\partial {\mathbf{A}}_{i} } & \cdots & {\partial {\mathbf{B}}_{i} /\partial {\mathbf{A}}_{284} } \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ {\partial {\mathbf{B}}_{284} /\partial {\mathbf{A}}_{1} } & \cdots & {\partial {\mathbf{B}}_{284} /\partial {\mathbf{A}}_{i} } & \cdots & {\partial {\mathbf{B}}_{284} /\partial {\mathbf{A}}_{284} } \\ \end{array} } \right] $$

(15)

in which ${\mathbf{B}}_{i} = \left( {\begin{array}{*{20}c} {c_{0 - i} } & {c_{1 - i} } & \cdots & {c_{s - i} } & {d_{1 - i} } & \cdots & {d_{s - i} } \\ \end{array} } \right)^{T}$ corresponds to the ith row of matrix B, and then, the chain derivation rule is employed to calculate $\partial {\mathbf{B}}_{i} /\partial {\mathbf{A}}_{i}$, and the specific expressions of $\partial {\mathbf{B}}_{i} /\partial {\mathbf{A}}_{i}$ are shown in “Appendix”.

Substituting the Jacobian matrix J into Eq. (11), the Newton–Raphson iterative procedure is performed. A is updated until the norm of B is less than an allowed error tolerance, and then, the result is deemed to have converged, as the periodic solution of the system is X = HA. In addition, Fig. 2 shows the schematic diagram of the SAHB method proposed in this paper. The harmonic balance procedure is performed first, with both the periodic solutions and the residuals of the dynamic equations expressed as Fourier series. Subsequently, the nonlinear algebraic equation obtained by the harmonic balance procedure is solved by utilizing the Newton–Raphson iterative procedure, in which the Jacobian matrix J is acquired by combining the IDFT with the chain derivative rule. Finally, the harmonic coefficients of the periodic vibration response of the system are obtained when the Newton–Raphson iteration converges.

Fig. 2

Schematic diagram of the SAHB method

4 Results and discussion

In this section, the nonlinear vibration responses of the system are obtained by employing the SAHB method, the combination resonance characteristics are analyzed in detail by utilizing the amplitude–frequency responses, orbits of the LP rotor and HP rotor. Furthermore, the combination resonance mechanism is revealed by the separated amplitude–frequency responses and the analysis of the inter-shaft bearing nonlinear restoring force. Finally, the effect of the inter-shaft bearing clearance is detected.

The Campbell diagram of the dual-rotor-bearing-casing system is shown in Fig. 3. Setting the rotating speed ratio as $\lambda = 1.2$, the first-order critical speed of the system is determined to be $\omega_{1} = 163\;{\text{rad/s}}\;(\omega_{{2}} = 193\;{\text{rad/s)}}$, and the second-order critical speed of the system is $\omega_{1} = 376\;{\text{rad/s}}\;(\omega_{2} = 462\;{\text{rad/s)}}$. In order to analyze the nonlinear vibration characteristics near the first-order critical speed of the system, the sweep frequency range is set to be $\omega_{1} \in [140,220]\;{\text{rad/s}}[140,220]$$\;{\text{rad/s}}$. Thus, in addition to the two rotors excitation frequencies, other combination frequencies may be closed to the first- or second-order critical speed of the rotor system.

Fig. 3

Campbell diagram of the system, the blue lines represent the critical speed of the system under HP rotor excitation, and the cyan lines represent the critical speed of the system under LP rotor excitation. The points marked in black represent the critical speed of the system at the speed ratio equal to 1.2

The SAHB method presented before is employed to analyze the system's dynamic characteristics near the first-order critical rotating speed. In order to get the combination resonance responses of the system, through several tests, set the response X as a truncated Fourier series with 27 frequency components, i.e., $\omega_{1} /2$, $\omega_{2} /2$, $\omega_{2} - \omega_{1} /2$, $2\omega_{1} - \omega_{2}$, $\omega_{1} /2 + \omega_{2} /3$, $\omega_{1}$, $(\omega_{1} + \omega_{2} )/2$, $\omega_{2}$, $3\omega_{2} /2 - \omega_{1} /2$, $2\omega_{2} - \omega_{1}$, $3\omega_{1} /2$, $3\omega_{2} - 2\omega_{1}$, $\omega_{2} + \omega_{1} /2$, $3\omega_{1} - \omega_{2}$, $3\omega_{1} /2 + \omega_{2} /3$, $2\omega_{1}$, $3\omega_{1} /2 + \omega_{2} /2$, $\omega_{1} + \omega_{2}$, $3\omega_{2} /2 + \omega_{1} /2$, $2\omega_{2}$, $5\omega_{1} /2$, $3\omega_{2} - \omega_{1}$, $3\omega_{1} /2 + \omega_{2}$, $4\omega_{2} - 2\omega_{1}$, $2\omega_{2} + \omega_{1} /2$, $3\omega_{1}$, $5\omega_{1} /2 + \omega_{2} /2$, which adequately reflect the vibration response of the system after several tests. Substituting the above frequency components into Eqs. (6) and (7), the harmonic basis matrix H and the harmonic expending coefficients matrix A can be expressed as follows:

$$ {\mathbf{H}} = \left( {\begin{array}{*{20}c} {1} & {\cos \frac{{\omega_{1} }}{2}\tau } & {\cos \frac{{\omega_{2} }}{2}\tau } & \cdots & {\cos \left( {\frac{{5\omega_{1} }}{2} + \frac{{\omega_{2} }}{2}} \right)\tau } & {\sin \tau } & {\sin \omega_{2} \tau } & \cdots & {\sin \left( {\frac{{5\omega_{1} }}{2} + \frac{{\omega_{2} }}{2}} \right)\tau } \\ \end{array} } \right) $$

(16)

$$ {\mathbf{A}} = \left[ {\begin{array}{*{20}c} {a_{0 - 1} } & {a_{1 - 1} } & {a_{2 - 1} } & \cdots & {a_{27 - 1} } & {b_{1 - 1} } & {b_{2 - 1} } & \cdots & {b_{27 - 1} } \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {a_{0 - 284} } & {a_{1 - 284} } & {a_{2 - 284} } & \cdots & {a_{27 - 284} } & {b_{1 - 284} } & {b_{2 - 284} } & \cdots & {b_{27 - 284} } \\ \end{array} } \right]^{T} . $$

(17)

The response amplitudes for any node of the system can be calculated as follows:

$$ {\text{A}}_{mp} = \sqrt {\sum\limits_{k = 1}^{{\hat{N}}} {\left( {\left( {x\left( k \right) - \overline{x}} \right)^{2} + \left( {y\left( k \right) - \overline{y}} \right)^{2} } \right)/\hat{N}} } $$

(18)

where $\hat{N}$ represents the discrete sampling number. x denotes the horizontal displacement response, y is the vertical displacement response, $\overline{x}$ and $\overline{y}$ are the averages displacement response corresponding to x and y. The vibration response of each node in the x and y directions is considered in Eq. (18), which could accurately reflect the vibration status of the system.

4.1 The overall vibration responses of the system

The periodic responses of the system with different rotating speeds (near the first critical speed) of the system are obtained by employing the SAHB method. Figure 4 shows the three-dimensional amplitude–frequency response of each part of the system, in which the three axes represent the rotating speed of the rotor, the z coordinate of different nodes and the vibration amplitudes of each node, which are calculated by Eq. (18). Furthermore, the amplitude–frequency response curves of each node are plotted in Fig. 4, in which the orange–red lines represent the stable solution branches, and the magenta lines denote the unstable solution branches of the system.

Fig. 4

Three-dimensional amplitude–frequency response of the system. a LP rotor, b HP rotor, c inner casing, d outer casing. The solid lines represent the amplitude–frequency responses curves of each node. P1 and P2 represent the primary resonance regions; C1, C2 represent the combination resonance regions

As shown in Fig. 4, there are two obvious primary resonance regions marked as P1 and P2, the first primary resonance peak located at $\omega_{1} {\text{ = 160 rad/s (}}\omega_{2} {\text{ = 192 rad/s)}}$, which is aroused by the HP rotor passing through the critical rotating speed of the system; the other one is located at $\omega_{1} {\text{ = 190 rad/s (}}\omega_{2} {\text{ = 228 rad/s)}}$, which is excited by the LP rotor passing through the critical rotating speed of the system. The relative position of the two primary resonance peaks is determined by the rotational speed ratio. Due to the influence of the nonlinear factors of the inter-shaft bearing, the amplitude–frequency response curves of the system bend to the right in the primary resonance region, which makes the system show obvious hardening characteristics. Meanwhile, the vibration jump and bistable phenomenon emerge here, and there are two stable periodic solutions and one unstable periodic solution in the bistable regions. Furthermore, there is a small resonance peak in the bottom of the primary resonance region P2, which gives that there are five solutions in this region. The reason for these nonlinear phenomena is the nonlinear force of the inter-shaft bearing that contains fractional exponential function, radial clearance and variable stiffness excitation, which are essentially nonlinear. Note that the primary resonances have been analyzed in detail in our previous work Ref [1] and will not be discussed in detail here.

Besides, as shown in Fig. 4, there are two small resonance peaks near the primary resonance peaks: the first one is marked as C1, the second one is marked as C2. The resonance peaks C1, C2 are excited by the combination frequencies close to the system's first-order critical speed. In addition, it is worth noting that the vibration amplitudes of the combination resonances C1 and C2 are smaller than that of the primary resonance, but it is much more violent than that of non-resonance points. On the other hand, the amplitude–frequency responses also bend to the right at the combination resonance regions. As a result, the vibration jump and multiple solutions phenomena also emerge in these regions, which are harmful to the healthy operation of the system. Furthermore, the combination resonances are also synchronized in each part of the system.

In addition, the dynamic mode of the LP rotor, the HP rotor, the inner casing, the outer casing with respect to the primary resonance regions and the combination resonance regions are shown in Fig. 5.

Fig. 5

Dynamic mode of the system. a primary resonance region P1 ($\omega_{1} = 160\;{\text{rad/s}}$); b combination resonance region C1 ($\omega_{1} = 165.1\;{\text{rad/s}}$); c primary resonance region P2 ($\omega_{1} = 190\;{\text{rad/s}}$); d combination resonance region C3 ($\omega_{1} = 205.7\;{\text{rad/s}}$)

As shown in Fig. 5, the dynamic modes of the LP and HP rotor are the same in different resonance regions, but the modes of the casings in combination resonance region C2 are different from that in the primary resonance regions and combination resonance C1. As for the inner casing, the vibration amplitude increases gradually from left to right in region P1, P2 and C1. However, in region C2, the vibration amplitude decreases first and then increases. As for the outer casing, the vibration amplitude is larger in the middle and tail, but smaller in the front in the resonance regions P1, P2 and C1. However, the vibration amplitude of the front and tail is larger, while that of the middle is smaller in resonance region C2. In general, the combination resonance C2 would change the dynamic modes on the system’s casing, but has little effect on the rotors’ mode.

4.2 The nonlinear resonances of the system

In order to give an insight into the nonlinear resonances of the system, the amplitude–frequency responses curve of the LPT rotor disk (Node 19) is shown in Fig. 6. (As shown in Fig. 4, the vibration characteristics of each node of the system are similar, so selecting one node of that to display in detail is enough.) The solid line represents the stable periodic solutions, and the dotted line represents the unstable periodic solutions obtained by the SAHB method. The primary resonance regions marked as P1 and P2, and the combination resonance regions marked as C1 and C2 correspond to the resonance regions shown in Fig. 4. It is found that the amplitude–frequency response curves of the system behave like the hardening characteristic both in the primary resonance regions and the combination resonance regions. In the resonance region C1, there are three periodic solutions, in which the solutions with smaller and larger amplitude are stable, and the solution in the middle is unstable. In the resonance region C2, there is a circle phenomenon, which makes the multiple solutions phenomena emerge in this region, i.e., there are three periodic solutions, in which the biggest one is unstable.

Fig. 6

Amplitude–frequency responses curve of the LPT rotor disk, in which the solid lines represent the stable periodic solutions, the dotted lines represent the unstable periodic solutions obtained by the SAHB method, and the lines marked with asterisks represent the periodic solutions obtained by the Newmark method. A1, A3 are points in the primary regions, A2, A4 are points in the combination resonance regions

In addition, the periodic solutions of the system obtained by the Newmark method are also shown in Fig. 6, marked with asterisks. It is found that the amplitude–frequency response curves of the system obtained by the two methods are basically consistent. The difference is that the SAHB method can obtain the unstable periodic solution of the system, so as to give the whole picture of the system solution, which is very important for the in-depth analysis of the nonlinear resonance characteristics of the system. Therefore, the SAHB method has more advantages than the Newmark method in analyzing combination resonances.

In order to further detect the vibration response characteristics of the system, point A1 ($\omega_{1} = 160\;{\text{rad/s}}$, $\omega_{2} = 192\;{\text{rad/s}}$) in the primary resonance P1, point A2 ($\omega_{1} = 165.1\;{\text{rad/s}}$,$\omega_{2} = 198.1\;{\text{rad/s}}$) in the combination resonance region C1, point A3 ($\omega_{1} = {\text{190 rad/s}}$,$\omega_{2} = 228\;{\text{rad/s}}$) in the primary resonance P2, point A4 ($\omega_{1} = 205.7\;{\text{rad/s}}$, $\omega_{2} = 246.8\;{\text{rad/s}}$) in the combination resonance region C2 are taken out from the amplitude–frequency response curves shown in Fig. 6, and the orbits of the LP rotor and HP rotor are given, as shown in Fig. 7, in which z represents the position of the nodes, x, y denotes the horizontal displacement and vertical displacement, respectively. The curves in different colors represent the orbits of different nodes.

Fig. 7

orbits of the LP rotor and HP rotor. a, c, e, g, are for the LP rotor; b, d, f, h are for the HP rotor; a, b are for point A1: $\omega_{1} = {160}\;{\text{rad/s}}$,$\omega_{2} = 192{\text{ rad/s}}$; c, d are for point A2: $\omega_{1} = {165}{\text{.1 rad/s}}$, $\omega_{2} = 198.1{\text{ rad/s}}$; e, f are for point A3: $\omega_{1} = {\text{190 rad/s}}$,$\omega_{2} = 228{\text{ rad/s}}$; g, h are for point A4: $\omega_{1} = 205.7{\text{ rad/s}}$, $\omega_{2} = 246.8{\text{ rad/s}}$). The curves in different colors represent the orbits of different nodes, and the black curves represent the dynamic mode of the rotors

As shown in Fig. 7, the orbits of each node of the LP rotor and the HP rotor are regular circles in the primary resonance region P1 and P2; however, the orbits of each node of the two rotors become chaotic and are no longer regular circles in the combination resonance region C1, C2. This is because in the primary resonance regions, the vibration responses of the system are mainly dominated by the excitation frequency of the HP rotor or the LP rotor, while in the combination resonance regions, there are numerous frequency components. More details about these will be analyzed later. Furthermore, the black curves represent the dynamic mode of the rotors, and they are consistent with Fig. 5; it is found that the closer to the inter-shaft bearing, the more intense the vibration of the node, which makes the operating environment of the bearing more severe and harmful to its health.

4.3 The combination resonance analysis of the system

In the procedure of the SAHB method, as shown in Sect. 3, the periodic responses of the system are expressed as the truncated Fourier series, i.e., X = HA, so the exact expressions of the responses corresponding to each frequency component of the solution X could be obtained. One can define the vibration responses of a separated frequency component at a wanted degree of freedom as follows:

$$ x_{{\omega_{i} }} = a_{{\omega_{i} }} \cos (\omega_{i} t) + b_{\omega i} \sin (\omega_{i} t) $$

(19)

where $a_{{\omega_{i} }}$ and $b_{\omega i}$ is the Fourier expansion coefficients corresponding to the ith frequency component of X. The effective values of response amplitudes for each node in a separated frequency component are also calculated by Eq. (18); then, one can obtain the separated amplitude–frequency responses of each node of the system. In order to further analyze the combination resonance characteristics, the separated amplitude–frequency responses of the LPT rotor disk (Node 19) corresponding to Fig. 6 are shown in Fig. 8.

Fig. 8

Separated amplitude–frequency responses of the LPT rotor disk, in which the different colored lines represent separated amplitude–frequency responses curve corresponding to different frequency components, the frequency components that are notable are circled by dotted boxes in the legend

As shown in Fig. 8, the amplitude–frequency responses curve corresponding to the excitation frequency $\omega_{1}$ of the LP rotor is the largest one in the primary resonance region P1, and the amplitude–frequency responses curve corresponding to the excitation frequency $\omega_{2}$ of the HP rotor is the largest one in the primary resonance P2, which proves that the first formant is excited by the HP rotor passing through the critical rotation speed and the second formant is excited by the LP rotor passing through the critical rotation speed. Furthermore, in the combination resonance regions, the amplitude–frequency responses curve corresponding to the frequency components $(\omega_{1} + \omega_{2} )/2$, $\omega_{1} /2 + \omega_{2} /3$, $2\omega_{1} - \omega_{2}$ are notable; meanwhile, other combination frequencies such as $\omega_{1} /2$, $\omega_{2} /2$,$3\omega_{2} /2 - \omega_{1} /2$, $2\omega_{1}$, $2\omega_{2}$, $2\omega_{2} - \omega_{1}$, $3\omega_{2} - 2\omega_{1}$ also have some contribution to the combination resonances. It is worth noting that the amplitude–frequency responses curve of the system shown in Fig. 6 is just the integration of the separated amplitude–frequency responses corresponding to each frequency shown in Fig. 8. Thus, based on the SAHB method, one can accurately obtain the contribution of each frequency component to the vibration of the system, which is of great significance for understanding the nonlinear vibration mechanism and vibration control of the system.

In order to give an insight into the nonlinear vibration characteristics of the combination resonance, the separated amplitude–frequency responses curves of the system in regions C1, C2 are obtained, as shown in Figs. 9 and 10.

Fig. 9

Separated amplitude–frequency responses of the LPT rotor disk in region C1, in which the different colored lines represent separated amplitude–frequency responses curve corresponding to different frequency components, the frequency components that are notable are circled by dotted boxes in the legend

Fig. 10

Separated amplitude–frequency responses of the LPT rotor disk in region C2, in which the different colored lines represent separated amplitude–frequency responses curves corresponding to different frequency components, the frequency components that are notable are circled by dotted boxes in the legend

4.3.1 Combination resonance in region C1

Figure 9 shows the separated amplitude–frequency responses of the LPT rotor disk in region C1. As shown in the figure, the amplitude–frequency response curve corresponding to the combination frequency $(\omega_{1} + \omega_{2} )/2$ is the most notable one. It is indicated that the vibration responses of the system in region C1 are mainly composed of the combination frequency $(\omega_{1} + \omega_{2} )/2$, the excitation frequency of the LP rotor $\omega_{1}$ and the excitation frequency of the HP rotor $\omega_{2}$. Meanwhile, combination frequencies $3\omega_{2} /2 - \omega_{1} /2$, $\omega_{1} /2 + \omega_{2} /3$ also take a prominent role in the responses of the system, while other combination frequencies have little contribution. It is worth noting that the response amplitude of the combination frequency $\omega_{1} /2 + \omega_{2} /3$ exceeds that of the system’s excitation frequency $\omega_{1}$ and $\omega_{2}$, and the shape of the amplitude–frequency response curves of the system (as shown in Fig. 6) in this region is consistent with that of the frequency $\omega_{1} /2 + \omega_{2} /3$, which indicates that the combination resonance region C1 is dominated by $\omega_{1} /2 + \omega_{2} /3$. The resonance in region C1 illustrates that when the combination frequency $\omega_{1} /2 + \omega_{2} /3$ is close to the critical speed of the system, it will also arouse resonance.

4.3.2 Combination resonance in region C2

Figure 10 shows the separated amplitude–frequency responses of the LPT rotor disk (node 19) in the combination resonance region C2. It is observed that the amplitude–frequency response curve corresponding to the combination frequency $2\omega_{1} - \omega_{2}$ is the most notable one, which indicates that the vibration responses of the system in region C2 are mainly composed of the combination frequency $2\omega_{1} - \omega_{2}$ and the excitation frequency $\omega_{1}$, $\omega_{2}$; meanwhile, the frequency components $\omega_{2} /2$, $2\omega_{2} - \omega_{1}$, $3\omega_{2} - 2\omega_{1}$, $3\omega_{1} - \omega_{2}$, $\omega_{1} + \omega_{2}$, $2\omega_{2}$ are also have significant contributions to the responses. Furthermore, the separated amplitude–frequency responses of the frequency $2\omega_{1} - \omega_{2}$ are the most notable one in Fig. 10, and the shape of the amplitude–frequency response curves of the system (as shown in Fig. 6) in this region is consistent with that of the combination frequency $2\omega_{1} - \omega_{2}$, which indicates that the combination resonance region C3 is dominated by $2\omega_{1} - \omega_{2}$.

4.3.3 Discussion

Through detailed analysis, it is found that the vibration responses of the combination resonance regions of the system are jointly determined by the excitation frequency and the combination frequencies of them. The combination resonance region C1 is dominated by the frequency $(\omega_{1} + \omega_{2} )/2$; the separated amplitude–frequency responses of the combination frequency $2\omega_{1} - \omega_{2}$ are the most notable in the combination resonance region C2. The reason for the combination resonance is the combination frequencies closing to the critical speed of the system. Furthermore, the emergence of the combination frequencies is originated from the nonlinear restoring force of the inter-shaft bearing, which contains three nonlinear factors, namely fractional exponential function, the clearance and time-variable stiffness, and intrinsic nonlinear characteristics.

4.4 The nonlinear restoring force of inter-shaft bearing

As shown in Ref [1], the nonlinear restoring force of the inter-shaft bearing contains three kinds of nonlinear factors, i.e., the fractional exponential function, the radial clearance and the variable stiffness excitation. The nonlinear restoring force of the inter-shaft bearing has intrinsic nonlinear characteristics, which is the inducement of nonlinear vibration phenomena of the system. In order to further analyze the characteristics and mechanism of the combination resonances of the system, corresponding to the amplitude–frequency responses of the system (as shown in Fig. 6), the effective values of the nonlinear restoring forces of the inter-shaft bearing are calculated by Eq. (20), in which $F_{x}$ and $F_{y}$ are the component of the force in the x and y directions, $\overline{F}_{x}$ and $\overline{F}_{y}$ denote the averages corresponding to them, N represents the discrete sampling number.

$$ F_{b} = \sqrt {\frac{{\sum\nolimits_{i = 1}^{N} {\left( {\left( {F_{x} (i) - \overline{F}_{x} } \right)^{2} + \left( {F_{y} (i) - \overline{F}_{y} } \right)^{2} } \right)} }}{N}} $$

(20)

The nonlinear restoring force–frequency responses curve is shown in Fig. 11, in which the solid lines represent the nonlinear restoring force corresponding to the stable periodic solution of the system, and the dotted lines represent the restoring force corresponding to the unstable periodic solution. It is found that there are also two primary resonance regions (P1 and P2) and two combination resonance regions (C1, C2 and C3) corresponding to Fig. 6. The vibration jump phenomenon also occurs in the nonlinear restoring force–frequency responses of the inter-shaft bearing; the maximum jump amplitudes of the force at each resonance regions are shown in Table 1. In the primary resonance region A1 and A2, the maximum jump amplitude of the force is 1610N and 1769N, respectively. It is worth noting that the maximum jump amplitude of the force is 228N and 124N in regions C1, C2. The vibration jump phenomenon would cause a bad load environment to the inter-shaft bearing, which is detrimental to its health.

Fig. 11

Nonlinear restoring force–frequency responses of the inter-shaft bearing, the solid lines represent the nonlinear restoring force corresponding to the stable periodic solution of the system, and the dotted lines represent the restoring force corresponding to the unstable periodic solution

Table 1 Maximum jump amplitude of the inter-shaft nonlinear restoring force $F_{b}$ in each resonance region

Furthermore, corresponding to the rotors’ orbits of the LP rotor and HP rotor in Fig. 7, the nonlinear restoring force responses (including the time history and the frequency spectrum) of the inter-shaft bearing at point A1 ($\omega_{1} = 160\;{\text{rad/s}}$, $\omega_{2} = 192\;{\text{rad/s}}$) in the primary resonance P1, point A2 ($\omega_{1} = 165.1\;{\text{rad/s}}$, $\omega_{2} = 198.1\;{\text{rad/s}}$) in the combination resonance region C1, point A3 ($\omega_{1} = {\text{190 rad/s}}$, $\omega_{2} = 228\;{\text{rad/s}}$) in the primary resonance P2, point A4 ($\omega_{1} = 205.7\;{\text{rad/s}}$, $\omega_{2} = 246.8\;{\text{rad/s}}$) in the combination resonance region C2 are shown in Fig. 12.

Fig. 12

Time history and frequency spectrum of the nonlinear restoring force. a, b for point A1:$\omega_{1} = {\text{160 rad/s}}$, $\omega_{2} = 192{\text{ rad/s}}$; c, d for point A2: $\omega_{1} = {165}{\text{.1 rad/s}}$, $\omega_{2} = 198.1{\text{ rad/s}}$; e, f for point A3: $\omega_{1} = {\text{190 rad/s}}$, $\omega_{2} = 228{\text{ rad/s}}$; g, h for piont A4: $\omega_{1} = 205.7{\text{ rad/s}}$, $\omega_{2} = 246.8{\text{ rad/s}}$

As shown in Fig. 12a, b, in the primary resonance P1, the time history of the inter-shaft bearing nonlinear force is a regular periodic response curve, and there are only two frequency components in the frequency spectrum, the excitation frequency $\omega_{2}$ of the HP rotor is dominant. Meanwhile, corresponding to Fig. 7a, b, the rotors’ orbits of the LP rotor and HP rotor are regular circles.

As shown in Fig. 12c, d, in the combination resonance region C1, the time history of the inter-shaft bearing nonlinear force is a periodic response curve and there are four distinct peaks, but there are more frequency components in the frequency spectrum, the frequency of inter-shaft bearing cage $(\omega_{1} + \omega_{2} )/2$ plays a dominant role in the response; meanwhile, the $\omega_{2}$, $\omega_{1}$, $\omega_{1} /2 + \omega_{2} /3$ and $3\omega_{2} /2 - \omega_{1} /2$ are also notable; this is consistent with the performance of the system responses in combination resonance region C1 shown in Fig. 9.

As shown in Fig. 12e, f, in the primary resonance P2, the time history of the inter-shaft bearing nonlinear force is a regular periodic response curve similar to that of A1. Furthermore, there are only two frequency components in the frequency spectrum; the excitation frequency $\omega_{1}$ of the LP rotor is dominant. Meanwhile, corresponding to Fig. 7e, f, the rotors’ orbits of the LP rotor and HP rotor are regular circles.

As shown in Fig. 12g, h, in the combination resonance region C2, the time history of the inter-shaft bearing nonlinear force is a periodic response curve and there are eight distinct peaks. Meanwhile, there are many frequency components in the frequency spectrum, in which the frequency $\omega_{1}$ and $2\omega_{1} - \omega_{2}$ play a dominant role in the response, and the frequency components $\omega_{2}$, $\omega_{2} /2$, $2\omega_{1}$, $\omega_{1} + \omega_{2}$, $2\omega_{2}$ are also notable; this is consistent with the performance of the system responses in combination resonance region C2 shown in Fig. 10. It is worth noting that the frequency division, frequency doubling and frequency combination of the excitation frequency are obvious.

In summary, in the primary resonance regions, the response of the nonlinear force of the inter-shaft bearing only contains the HP and LP rotor excitation frequencies, but in the combination resonance regions, due to the effect of nonlinearities, there will be more frequency components in the response of the inter-shaft bearing force, one of these frequency components will be close to the critical rotating speed of the system in the combination resonance region, which is the reason for the combination resonance of the system.

4.5 Effect of the inter-shaft bearing clearance

The inter-shaft bearing clearance is one of the main inducements of nonlinear dynamic behaviors such as combination resonance, vibration jump and multiple solutions of the system. It is significant for the health and vibration control of the system to study the influence of the clearance. Figure 13 shows the amplitude–frequency responses of the LP rotor (node 19) with different clearance ($\delta_{0} = 0\;\upmu {\text{m}}$, $\delta_{0} = 2\;\upmu {\text{m}}$,$\delta_{0} = 4\;\upmu {\text{m}}$,$\delta_{0} = 6\;\upmu {\text{m}}$,$\delta_{0} = 8\;\upmu {\text{m}}$), in which the dotted lines represent the unstable periodic solution of the system. It is worth noting that the vibration of each node in the system is synchronous, and the shape of the amplitude–frequency response of each node is similar, as shown in Fig. 4, so it is enough to take one node as an example to illustrate the effect of the inter-shaft bearing clearance.

Fig. 13

Amplitude–frequency responses of the LP rotor (node 19) with different clearances, P1, P2 represent the two primary resonance regions, C1, C2 represent the two combination primary resonance regions. The two subgraphs are local magnifications of the two combination resonance regions

As shown in Fig. 13, in appearance, the change of the clearance of the inter-shaft bearing would hardly affect the response amplitude of the system. However, the change of the clearance of the inter-shaft bearing will shift the amplitude–frequency response curves (including the primary resonance regions and the combination resonance regions) to the left. Furthermore, increasing the clearance will make the position of the bifurcation points under the primary resonance of the system shift to the left, but the bifurcation points with small amplitude shift to the left more, resulting in a wider width of the bistable region under the primary resonance of the system. As for the combination resonance regions C1, C2, they also shift to the left as the increasing of the clearance.

As for the combination resonance region C1, when the clearance of the inter-shaft-bearing is $\delta_{0} = 0\;\upmu {\text{m}}$, the combination resonance does not occur in the region. When the clearance is $\delta_{0} = 2\;\upmu {\text{m}}$, $\delta_{0} = 4\;\upmu {\text{m}}$, $\delta_{0} = 6\;\upmu {\text{m}}$, $\delta_{0} = 8\;\upmu {\text{m}}$, the system shows obvious combination resonance in this area, marked in red, green, blue and black, respectively. It is found that the positions of the combination resonance regions move to the left gradually and the amplitudes corresponding to the combination resonance regions increase gradually as the increasing of the clearance. Furthermore, the increase of the clearance will widen the width of the combination resonance region C1, which means the multi-solution regions of the system also widen.

For the combination resonance region C2, even if the clearance of the inter-shaft bearing is zero, there are still obvious combination resonance in this area, which suggests that the existence of the combination resonance in this region is not determined by the clearance. Similar to region C1, increasing the clearance will hardly affect the amplitudes of the combination region C2, but the positions will move to the left with the increase of the clearance. In addition, the widths of the combination regions gradually widen with the increase of the clearance.

In summary, the inter-shaft bearing clearance is one of the determining factors for the appearance of the combination resonance region C1. The increase of the inter-shaft bearing clearance will widen the width of the combination resonance regions, and at the same time shifts the position of to the left, the reason is that the clearance will change the contact state of the inter-shaft bearing rollers, resulting in the change of its dynamic stiffness.

5 Conclusions

In this paper, the combination resonances of a high-dimensional dual-rotor-bearing-casing system has been investigated in detail by employing the SAHB method. The results show that the SAHB method has more advantages than the Newmark method, since the SAHB method can obtain all the periodic solutions (including the unstable periodic solution) of the system, thus providing a more comprehensive understanding of the combination resonance characteristics of the system.

The characteristics of the combination resonances have been analyzed in detail by employing the SAHB method. Four obvious resonance regions have been found in the amplitude–frequency responses, of which the two primary resonance regions are excited by the two rotors passing through the critical speed, and the two combination resonance regions are dominated by the combination frequencies $(\omega_{1} + \omega_{2} )/2$, $2\omega_{1} - \omega_{2}$, respectively. In addition, the vibration jump and multiple solutions phenomena have been observed in all resonance regions.

More in-depth studies show that the inter-shaft bearing forces emerge various combination frequency components under the action of nonlinearities, leading to the appearance of combination resonances. Through parametric analysis, it has been shown that the combination resonances may change the dynamic modes of the casing. The combination resonances are very sensitive to the change of the inter-shaft bearing clearance; the increase of the clearance will widen the combination resonance regions.

The study undertaken in this work is of great significance in parameter optimization design and vibration control for the dual-rotor-bearing-casing system. In addition, the SAHB method proposed here is a generalized method; it is an advantageous tool to analyze the nonlinear dynamic characteristics of high-dimensional engineering systems with complex nonlinearities. Future works will focus on analyzing the nonlinear resonances of the high-dimensional rotor system with complex coupling nonlinearities and carrying out the relevant experimental study.

Appendix

$$ \frac{{\partial {\mathbf{B}}_{i} }}{{\partial {\mathbf{A}}_{i} }} = \left[ {\begin{array}{*{20}c} {\partial c_{0 - i} /\partial a_{0 - i} } & {\partial c_{0 - i} /\partial a_{1 - i} } & \cdots & {\partial c_{0 - i} /\partial a_{s - i} } & {\partial c_{0 - i} /\partial b_{1 - i} } & \cdots & {\partial c_{0 - i} /\partial b_{s - i} } \\ {\partial c_{1 - i} /\partial a_{0 - i} } & {\partial c_{1 - i} /\partial a_{1 - i} } & \cdots & {\partial c_{1 - i} /\partial a_{s - i} } & {\partial c_{1 - i} /\partial b_{1 - i} } & \cdots & {\partial c_{1 - i} /\partial b_{s - i} } \\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ {\partial c_{s - i} /\partial a_{0 - i} } & {\partial c_{s - i} /\partial a_{1 - i} } & \cdots & {\partial c_{s - i} /\partial a_{s - i} } & {\partial c_{s - i} /\partial b_{1 - i} } & \cdots & {\partial c_{s - i} /\partial b_{s - i} } \\ {\partial d_{1 - i} /\partial a_{0 - i} } & {\partial d_{1 - i} /\partial a_{1 - i} } & \cdots & {\partial d_{1 - i} /\partial a_{s - i} } & {\partial d_{1 - i} /\partial b_{1 - i} } & \cdots & {\partial d_{1 - i} /\partial b_{s - i} } \\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ {\partial d_{s - i} /\partial a_{0 - i} } & {\partial d_{s - i} /\partial a_{1 - i} } & \cdots & {\partial d_{s - i} /\partial a_{s - i} } & {\partial d_{s - i} /\partial b_{1 - i} } & \cdots & {\partial d_{s - i} /\partial b_{s - i} } \\ \end{array} } \right] $$

(21)

in which

$$ \frac{{\partial c_{0 - i} }}{{\partial a_{j - i} }} = \frac{1}{N}\sum\limits_{k = 0}^{N - 1} {\left( {\left( {\frac{{\partial R_{i} \left( {\tau_{k} } \right)}}{{\partial u_{i} }} - j^{2} \frac{{\partial R_{i} \left( {\tau_{k} } \right)}}{{\partial u_{i}^{\prime \prime } }}} \right)\cos j\tau_{k} - j\frac{{\partial R_{i} \left( {\tau_{k} } \right)}}{{\partial u_{i}^{\prime } }}\sin j\tau_{k} } \right)} $$

(22)

$$ \frac{{\partial c_{m - i} }}{{\partial a_{j - i} }} = \frac{2}{N}\sum\limits_{k = 0}^{N - 1} {\left( {\left( {\left( {\frac{{\partial R_{i} \left( {\tau_{k} } \right)}}{{\partial u_{i} }} - j^{2} \frac{{\partial R_{i} \left( {\tau_{k} } \right)}}{{\partial u_{i}^{\prime \prime } }}} \right)\cos j\tau_{n} - j\frac{{\partial R_{i} \left( {\tau_{k} } \right)}}{{\partial u_{i}^{\prime } }}\sin j\tau_{k} } \right)\cos m\tau_{k} } \right)} $$

(23)

$$ \frac{{\partial c_{m - i} }}{{\partial b_{j - i} }} = \frac{2}{N}\sum\limits_{k = 0}^{N - 1} {\left( {\left( {\left( {\frac{{\partial R_{i} \left( {\tau_{k} } \right)}}{{\partial u_{i} }} - j^{2} \frac{{\partial R_{i} \left( {\tau_{k} } \right)}}{{\partial u_{i}^{\prime \prime } }}} \right)\sin j\tau_{k} + j\frac{{\partial R_{i} \left( {\tau_{n} } \right)}}{{\partial u_{i}^{\prime } }}\cos j\tau_{k} } \right)\cos m\tau_{k} } \right)} $$

(24)

$$ \frac{{\partial d_{m - i} }}{{\partial a_{j - i} }} = \frac{2}{N}\sum\limits_{k = 0}^{N - 1} {\left( {\left( {\left( {\frac{{\partial R_{i} \left( {\tau_{k} } \right)}}{{\partial u_{i} }} - j^{2} \frac{{\partial R_{i} \left( {\tau_{k} } \right)}}{{\partial u_{i}^{\prime \prime } }}} \right)\cos j\tau_{k} - j\frac{{\partial R_{i} \left( {\tau_{k} } \right)}}{{\partial u_{i}^{\prime } }}\sin j\tau_{k} } \right)\sin m\tau_{k} } \right)} $$

(25)

$$ \frac{{\partial d_{m - i} }}{{\partial b_{j - i} }} = \frac{2}{N}\sum\limits_{k = 0}^{N - 1} {\left( {\left( {\left( {\frac{{\partial R_{i} \left( {\tau_{k} } \right)}}{{\partial u_{i} }} - j^{2} \frac{{\partial R_{i} \left( {\tau_{k} } \right)}}{{\partial u_{i}^{\prime \prime } }}} \right)\sin j\tau_{k} + j\frac{{\partial R_{i} \left( {\tau_{k} } \right)}}{{\partial u_{i}^{\prime } }}\cos j\tau_{k} } \right)\sin m\tau_{k} } \right)} $$

(26)

where $u_{i}$ corresponds to the ith row of the solution X, it represents the displacement response of the system in ith degrees of freedom. In addition, $u_{i}^{\prime }$ and $u_{i}^{\prime \prime }$ are corresponding to the first and second derivatives of $u_{i}$, they denote the velocity response and acceleration response of the system in ith degrees of freedom, respectively.