1 Introduction

Aeroengine with the dual-rotor system has been widely used in the aviation industry [1], because of the great advantage in high thrust–weight ratio, high aerodynamic stability and not prone of surging, etc. Dual-rotor system [2] is one of the core components of aeroengine, in which the high-pressure rotor and the low-pressure rotor are connected by the inter-shaft bearing [3], which could reduce the bearing casing of the high-pressure rotor and shorten the length of engine, thus reducing the weight and improving the thrust–weight ratio of the aeroengine. But on the other hand, the nonlinearities of the inter-shaft bearing are always one of the main inducements of the nonlinear dynamic behavior of the dual-rotor system, such as jump, bi-stable, combination resonance and so on. It is of great significance to analyze the influence of the inter-shaft bearing nonlinearities on the dual-rotor system dynamics for the parameter optimization and healthy operation of aeroengine [4].

Much work has been carried out to analyze the dynamic characteristics of dual-rotor systems based on numerical method simulations, including the Runge–Kutta method, the Newmark method and the shooting method. Gupta et al. [5] performed some dynamic calculation and experiments on a dual-rotor test rig, the conclusions showed that there is cross-excitation between the inner and outer rotor. Ferraris et al. [6] analyzed the mass unbalance responses of a dual-rotor system, it is indicated that the symmetry of the system will affect the critical speed. Zhang et al. [7] proposed a method to sense the unbalance of the rotors for a dual-rotor system, in which the trial weigh is just added on the outer rotor. Hu et al. [8] developed a five degrees of freedom model for a dual-rotor system, the simulation results indicated that the nonlinearities of bearings have great effect on the dynamic characteristics of the system. Wang et al. [9] analyzed the influence of squeeze film damper (SFD) on a dual-rotor system, the conclusions showed that the SFD would induce complex motion of the system under the conditions of small unbalance and high speed. Chen et al. [10] studied the combined effect of base motions, unbalanced excitations and gravity on the dynamic characteristics of a dual-rotor system; it is found that the base motions would influence the vibration modes of the system. Gao et al. [11] presented a force model for the inter-shaft bearing, in which a local defect and nonlinearities of the bearing are taken into consideration; the results showed that the defect will increase the clearance and induce some abnormal resonances. Gao et al. [12] analyzed the paroxysmal impulse vibrations of a dual-rotor system based on the inter-shaft bearing model with an outer raceway defect; the results obtained by the Runge–Kutta method show that the intermittently antiphase of the loading and defect position is the inducement of the paroxysmal impulse vibrations. Ma et al. [13] analyzed the dynamic characteristics of a dual-rotor system with coupling effect of the inter-shaft bearing and rub-impact fault; it is indicated that increasing the rub-impact stiffness would induce complex motion of the system. Wang et al. [14] analyzed the dynamic characteristics of dual-rotor system with rubbing fault and unbalance-misalignment coupling faults, the conclusions showed that the coupling between the two rotors is very strong due to the inter-shaft bearing. Yu et al. [15] employed the Newmark method combined with the model order reduction technique to obtain the responses of a dual-rotor system with consideration of the inter-shaft rub-impact, the results showed that the inter-shaft rub-impact will induce new resonance peaks of the system. Liu et al. [16] proposed dual-rotor dynamic coupling model with nonlinear restoring forces of the two rotors, the results obtained by the shooting method showed that nonlinear dynamic phenomenon such as multiple solutions, double period motions and even chaotic motions emerged. Bavi et al. [17] analyzed the simultaneous resonance and stability for the unbalanced asymmetric thin-walled composite shafts; the effects of key parameters on the stability of the system were examined. The above studies revealed many valuable dynamic properties of dual-rotor system such as multiple solutions, vibration jump and complex motion, etc., but the mechanism investigations are insufficient.

HB-AFT method (harmonic balance-alternating frequency/time domain method) has been widely applied to analyze the nonlinear dynamic characteristics and the mechanism of rotor systems. It has great advantages in dealing with nonlinear problems such as piecewise linearity [18, 19], clearance [20], fractional exponents [21], strong nonlinearity [22, 23] and so on. Meanwhile, HB-AFT method is a semi-analytical solution method which can grasp all solutions, including the unstable solutions for rotor system. Therefore, although the HB-AFT method could only obtain the steady-state response of the rotor system, it is more suitable than numerical method for the study of nonlinear dynamic behavior mechanism of rotor system with complex nonlinearities such as clearance, piecewise linearity, nonlinear faults, etc. In the HB-AFT method, both the vibration responses and nonlinear terms of the system are expressed by Fourier series, then the nonlinear differential equations of the system are transformed into algebraic equations by the Harmonic Balance procedure, a Newton–Raphson iterative procedure is employed to solve these algebraic equations, the Jacobian matrix needed in which is calculated by using the inverse discrete Fourier transform (IDFT) procedure to construct the relationship between the Fourier coefficients of responses and nonlinear terms. Kim et al. [24, 25] analyzed the nonlinear dynamic characteristics for a Jeffcott rotor with piecewise linearity and clearance, quasi-periodic response and internal resonant vibration are obtained. By combining the HB-AFT method with an arc length continuation procedure, Guskov et al. [26, 27] obtained all the solution branches (including unstable solutions) for a Jeffcott rotor system with piecewise-linear pedestal. Zhang et al. [28, 29] modified the HB-AFT method to deal with the rotor system with bearing nonlinearities and analyzed the varying compliance resonances of a ball bearing-rotor system with clearance. The results show that period-doubling bifurcation and chaos are found in the system. By using the HB-AFT method, Li et al. [30] found there are two ways toward instability, i.e., the period-doubling bifurcation and the secondary Hopf bifurcation for an offset-disk rotor system with nonlinear restoring force of support. Yang et al. [31] employed the HB-AFT method to obtain the responses of a bearing-rotor with local defect on the outer raceway of the bearing; the results showed that the defect would induce super-harmonic resonances. Hou et al. [32] extended the application of the HB-AFT method to nonlinear dynamic analysis of dual-rotor system with inter-shaft bearing and dual-frequencies excitations, bi-stable, resonance hysteresis, and quasi-periodic behaviors are found in the system. In order to improve the computing efficiency of the Jacobi matrix needed in the HB-AFT method, Gupta et al. [33,34,35,36] showed that the advanced version of DFT and chaos analysis may be a helpful tool in the future scope. Rahman et.al [37] proposed a modified multi-level residue harmonic balance method, which could handle the nonlinear vibration problem of beam resting on nonlinear elastic foundation. The above studies give a comprehensive analysis of the nonlinear dynamic characteristics for rotor system, however, most of dynamic model of which are Jeffcott rotor system, the dynamic characteristics and mechanism investigations for the dual-rotor system with nonlinearities of the inter-shaft bearing are insufficient.

The motivation of this paper is to detect the combination resonances of a dual-rotor system with inter-shaft bearing clearance and subjected to dual-frequencies unbalanced excitations. Herein, the HB-AFT method combined with an arc length continuation procedure is employed to obtain all the periodic solutions branches including the unstable solutions of the system, hence one can get a comprehensive understanding of the nonlinear dynamic characteristics of the system. Wherein, three combination resonance regions in the frequency response curves of the system are found, in which the jump and bi-stable phenomena are observed. By using the separated frequency responses based on the HB-AFT method, the contribution of each frequency component to the combination resonances and the effect of the inter-shaft bearing clearance is revealed, providing a better understanding of the combination resonances mechanism of the dual-rotor system. The results obtained in this paper are of great significance to understand the combination resonances mechanism of the dual-rotor system so as to avoid harmful vibration.

2 Mechanical model

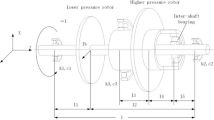
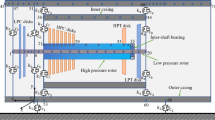
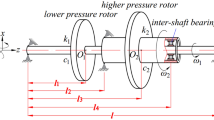
The schematic diagram of the dual-rotor system is shown in Fig. 1a, where the inner rotor is the low-pressure rotor supported by two rigid supports, while the outer rotor is the high-pressure rotor supported by a rigid support and an inter-shaft bearing. The inter-shaft bearing model is shown in Fig. 1b. Assume that the rotational shafts are rigid shafts, all the supports are linearly elastic except the inter-shaft bearing, all dampings are linear damping. Besides, the torsional vibration of the rotors is ignored since the torsional vibration is much smaller than the bending vibration and will hardly affect the performance of the rotor system when there is no lateral-torsional coupled vibration in the system. This model [38] is obtained from an actual dual-rotor system based on the modal synthesis method. Although it is a simplified model, it is able to reflect the vibration characteristics of the system, including critical speed, resonances and some nonlinear dynamics.

Fig. 1
figure 1

Schematic diagram of a dual-rotor system with inter-shaft bearing. a for the dual-rotor system model, b for the inter-shaft bearing model

Full size image

In the model, \(m_{1}\) and \(e_{1}\) are the mass and the eccentricity of the inner rotor, \(m_{2}\) and \(e_{2}\) are the mass and the eccentricity of the outer rotor, \(k_{1}\) and \(c_{1}\) are the stiffness coefficient and the damping coefficient of the left support of the inner rotor, \(k_{2}\) and \(c_{2}\) are the stiffness coefficient and the damping coefficient of the right support of the inner rotor, \(k_{3}\) and \(c_{3}\) are the stiffness coefficient and the damping coefficient of the left support of the outer rotor, \(J_{{{\text{d}}1}}\) and \(J_{{{\text{p}}1}}\) are the diameter and the polar rotational inertias of the inner rotor, \(J_{{{\text{d2}}}}\) and \(J_{{{\text{p2}}}}\) are the diameter and the polar rotational inertias of the outer rotor, \(\omega_{1}\) and \(\omega_{2}\) are the rotation speeds of the inner rotor and the outer rotor, and \(k_{{\text{b}}}\) and \(\delta\) are the stiffness and the clearance of the inter-shaft bearing. Besides, \(L_{1} = \frac{1}{3}L\), \(L_{2} = \frac{2}{3}L\), \(L_{3} = L_{4} = \frac{2}{15}L\), \(L_{5} = \frac{1}{3}L\) are the length of the rotational shafts. The motion of the system is described by eight degrees of freedom, where \(x_{1}\) and \(y_{1}\) are the horizontal and the vertical displacements of the inner rotor, \(\theta_{1}\) and \(\psi_{1}\) represent the rotation angles of the inner rotor with respect to x-axis and y-axis, \(x_{2}\) and \(y_{2}\) are the horizontal and the vertical displacements of the outer rotor, and \(\theta_{2}\) and \(\psi_{2}\) refer to the rotating angles of the outer rotor with respect to x-axis and y-axis. The motion of the system can be formulated by using the Lagrange equation.

The kinetic energy [39] of the rotor consists of the kinetic energy of the rotor translation and the kinetic energy of the rotor rotation, in which the kinetic energy of the inner rotor and rotor translation is \(\frac{1}{2}m_{1} \left( {\dot{x}_{1}^{2} + \dot{y}_{1}^{2} } \right)\), \(\frac{1}{2}m_{2} \left( {\dot{x}_{2}^{2} + \dot{y}_{2}^{2} } \right)\), respectively, and the kinetic energy of the inner rotor and rotor rotation is \(\frac{1}{2}J_{{{\text{d}}1}} \left( {\dot{\theta }_{1}^{2} + \dot{\psi }_{1}^{2} } \right) + \frac{1}{2}J_{{{\text{p}}1}} \omega_{1}^{2} - J_{{{\text{p}}1}} \omega_{1} \dot{\psi }_{1} \theta_{1}\) and \(\frac{1}{2}J_{{{\text{d2}}}} \left( {\dot{\theta }_{2}^{2} + \dot{\psi }_{2}^{2} } \right) + \frac{1}{2}J_{{{\text{p2}}}} \omega_{2}^{2} + J_{{{\text{p2}}}} \omega_{2} \dot{\psi }_{2} \theta_{2}\), respectively. Thus, the kinetic energy of the inner rotor and the outer rotor can be obtained as follows

$$ T_{1} = \frac{1}{2}m_{1} \left( {\dot{x}_{1}^{2} + \dot{y}_{1}^{2} } \right) + \frac{1}{2}J_{d1} \left( {\dot{\theta }_{1}^{2} + \dot{\psi }_{1}^{2} } \right) + \frac{1}{2}J_{p1} \omega_{1}^{2} - J_{p1} \omega_{1} \dot{\psi }_{1} \theta_{1} $$
(1a)
$$ T_{{2}} = \frac{1}{2}m_{2} \left( {\dot{x}_{2}^{2} + \dot{y}_{2}^{2} } \right) + \frac{1}{2}J_{{{\text{d2}}}} \left( {\dot{\theta }_{2}^{2} + \dot{\psi }_{2}^{2} } \right) + \frac{1}{2}J_{{{\text{p2}}}} \omega_{2}^{2} + J_{{{\text{p2}}}} \omega_{2} \dot{\psi }_{2} \theta_{2} $$
(1b)

The elastic potential energy of the inner and outer rotors is denoted as follows

$$ V_{{1}} = \frac{1}{2}k_{1} \left( {\left( {x_{1} + L_{1} \psi_{1} } \right)^{2} + \left( {y_{1} - L_{1} \theta_{1} } \right)^{2} } \right) $$
(2a)
$$ V_{{2}} = \frac{1}{2}k_{2} \left( {\left( {x_{1} - L_{2} \psi_{1} } \right)^{2} + \left( {y_{1} + L_{2} \theta_{1} } \right)^{2} } \right) $$
(2b)
$$ V_{{3}} = \frac{1}{2}k_{3} \left( {\left( {x_{2} + L_{3} \psi_{2} } \right)^{2} + \left( {y_{2} - L_{3} \theta_{2} } \right)^{2} } \right) $$
(2c)

The dissipated energy of the inner and outer rotors is denoted as follows

$$ D_{{1}} = \frac{1}{2}c_{1} \left( {\left( {\dot{x}_{1} + L_{1} \dot{\psi }_{1} } \right)^{2} + \left( {\dot{y}_{1} - L_{1} \dot{\theta }_{1} } \right)^{2} } \right) $$
(3a)
$$ D_{{2}} = \frac{1}{2}c_{2} \left( {\left( {\dot{x}_{1} - L_{2} \dot{\psi }_{1} } \right)^{2} + \left( {\dot{y}_{1} + L_{2} \dot{\theta }_{1} } \right)^{2} } \right) $$
(3b)
$$ D_{{3}} = \frac{1}{2}c_{3} \left( {\left( {\dot{x}_{2} + L_{3} \dot{\psi }_{2} } \right)^{2} + \left( {\dot{y}_{2} - L_{3} \dot{\theta }_{2} } \right)^{2} } \right) $$
(3c)

The inter-shaft bearing is considered as a linear spring model with a clearance \(\delta\); the bearing force can be denoted as

$$ F_{b} = \left\{ \begin{gathered} k_{b} \left( {e - \delta } \right)\;{\text{for}}\;e > \delta \hfill \\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;{\text{for}}\;e \le \delta \hfill \\ \end{gathered} \right. $$
(4)

where \(e = \sqrt {x_{{\text{b}}}^{2} + y_{{\text{b}}}^{2} }\) is the radial displacement, \(x_{{\text{b}}} = \left( {x_{1} - \left( {L_{2} - L_{5} } \right)\psi_{1} } \right) - \left( {x_{2} - L_{4} \psi_{2} } \right)\) is the horizontal displacement, \(y_{{\text{b}}} = \left( {y_{1} + \left( {L_{2} - L_{5} } \right)\theta_{1} } \right) - \left( {y_{2} + L_{4} \theta_{2} } \right)\) is the vertical displacement.

The component forces with respect to x-axis and y-axis are as follows

$$ \left[ {\begin{array}{*{20}c} {F_{x} } \\ {F_{y} } \\ \end{array} } \right] = \frac{{F_{{\text{b}}} }}{e}\left[ {\begin{array}{*{20}c} {y_{{\text{b}}} } \\ {z_{{\text{b}}} } \\ \end{array} } \right] = H\left( {e - \delta } \right)k_{{\text{b}}} \left( {1 - \frac{\delta }{e}} \right)\left[ {\begin{array}{*{20}c} {x_{{\text{b}}} } \\ {y_{{\text{b}}} } \\ \end{array} } \right] $$
(5)

where \(H\left( x \right) = \left\{ {\begin{array}{*{20}c} {1, \, x > 0} \\ {0, \, x \le 0} \\ \end{array} } \right.\) is the Heaviside function.

Finally, according to Eq. (1–5), and by using the Lagrange equation

$$ \frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{{\partial L_{{\text{T}}} }}{{\partial \dot{q}}}} \right) - \frac{{\partial L_{{\text{T}}} }}{\partial q} + \frac{{\partial D_{{\text{T}}} }}{{\partial \dot{q}}} = F\left( t \right) $$
(6)

where

$$ L_{{\text{T}}} = T_{1} + T_{{2}} - \left( {V_{{1}} + V_{{2}} + V_{{3}} } \right) $$
(7a)
$$ D_{{\text{T}}} = D_{{1}} + D_{{2}} + D_{{3}} $$
(7b)

the equations of motion of the system can be obtained as follows

$$ m_{1} \ddot{x}_{1} + \left( {c_{1} + c_{2} } \right)\dot{x}_{1} + \left( {L_{1} c_{1} - L_{2} c_{2} } \right)\dot{\psi }_{1} + \left( {k_{1} + k_{2} } \right)x_{1} + \left( {L_{1} k_{1} - L_{2} k_{2} } \right)\psi_{1} = m_{1} e_{1} \omega_{1}^{2} \cos \omega_{1} t - F_{x} $$
(8a)
$$ m_{1} \ddot{y}_{1} + \left( {c_{1} + c_{2} } \right)\dot{y}_{1} - \left( {L_{1} c_{1} - L_{2} c_{2} } \right)\dot{\theta }_{1} + \left( {k_{1} + k_{2} } \right)y_{1} - \left( {L_{1} k_{1} - L_{2} k_{2} } \right)\theta_{1} = m_{1} e_{1} \omega_{1}^{2} \sin \omega_{1} t - F_{y} $$
(8b)
$$ J_{{{\text{d}}1}} \ddot{\theta }_{1} + \left( {L_{1}^{2} c_{1} + L_{2}^{2} c_{2} } \right)\dot{\theta }_{1} - \left( {L_{1} c_{1} - L_{2} c_{2} } \right)\dot{y}_{1} + J_{{{\text{p}}1}} \omega_{1} \dot{\psi }_{1} + \left( {L_{1}^{2} k_{1} + L_{2}^{2} k_{2} } \right)\theta_{1} - \left( {L_{1} k_{1} - L_{2} k_{2} } \right)y_{1} = \left( {L_{2} - L_{5} } \right)F_{y} $$
(8c)
$$ J_{{{\text{d}}1}} \ddot{\psi }_{1} + \left( {L_{1}^{2} c_{1} + L_{2}^{2} c_{2} } \right)\dot{\psi }_{1} + \left( {L_{1} c_{1} - L_{2} c_{2} } \right)\dot{x}_{1} - J_{{{\text{p}}1}} \omega_{1} \dot{\theta }_{1} + \left( {L_{1}^{2} k_{1} + L_{2}^{2} k_{2} } \right)\psi_{1} + \left( {L_{1} k_{1} - L_{2} k_{2} } \right)x_{1} = - \left( {L_{2} - L_{5} } \right)F_{x} $$
(8d)
$$ m_{2} \ddot{x}_{2} + c_{3} \dot{x}_{2} + L_{3} c_{3} \dot{\psi }_{2} + k_{3} x_{2} + L_{3} k_{3} \psi_{2} = m_{2} e_{2} \omega_{2}^{2} \cos \omega_{2} t + F_{x} $$
(8e)
$$ m_{2} \ddot{y}_{2} + c_{3} \dot{y}_{2} - L_{3} c_{3} \dot{\theta }_{2} + k_{3} y_{2} - L_{3} k_{3} \theta_{2} = m_{2} e_{2} \omega_{2}^{2} \sin \omega_{2} t + F_{y} $$
(8f)
$$ J_{{{\text{d2}}}} \ddot{\theta }_{2} + L_{3}^{2} c_{3} \dot{\theta }_{2} - L_{3} c_{3} \dot{y}_{2} - J_{{{\text{p}}2}} \omega_{2} \dot{\psi }_{2} + L_{3}^{2} k_{3} \theta_{2} - L_{3} k_{3} y_{2} = - \left( {L_{2} - L_{5} } \right)F_{y} $$
(8g)
$$ J_{{{\text{d2}}}} \ddot{\psi }_{2} + L_{3}^{2} c_{3} \dot{\psi }_{2} + L_{3} c_{3} \dot{x}_{2} + J_{{{\text{p}}2}} \omega_{2} \dot{\theta }_{2} + L_{3}^{2} k_{3} \psi_{2} + L_{3} k_{3} x_{2} = \left( {L_{2} - L_{5} } \right)F_{x} $$
(8h)

Letting \(q_{1} = \frac{{x_{1} }}{{\delta_{0} }}\), \(q_{2} = \frac{{y_{1} }}{{\delta_{0} }}\), \(q_{3} = \frac{{L\theta_{1} }}{{\delta_{0} }}\), \(q_{4} = \frac{{L\psi_{1} }}{{\delta_{0} }}\), \(q_{5} = \frac{{x_{2} }}{{\delta_{0} }}\), \(q_{6} = \frac{{y_{2} }}{{\delta_{0} }}\), \(q_{7} = \frac{{L\theta_{2} }}{{\delta_{0} }}\), \(q_{8} = \frac{{L\psi_{2} }}{{\delta_{0} }}\), \(\tau = \omega_{1} t\), where \(\delta_{0}\) is the initial clearance of the inter-shaft bearing, the dimensionless equations of Eq. (8) can be obtained as follows

$$ q^{\prime\prime}_{1} + \alpha_{1} q^{\prime}_{1} + \alpha_{2} q^{\prime}_{4} + \alpha_{3} q_{1} + \alpha_{4} q_{4} = \alpha_{5} \cos \Omega_{1} \tau - \alpha_{6} F_{X} $$
(9a)
$$ q^{\prime\prime}_{2} + \alpha_{1} q^{\prime}_{2} - \alpha_{2} q^{\prime}_{3} + \alpha_{3} q_{2} - \alpha_{4} q_{3} = \alpha_{5} \sin \Omega_{1} \tau - \alpha_{6} F_{Y} $$
(9b)
$$ q^{\prime\prime}_{3} + \alpha_{8} q^{\prime}_{3} - \alpha_{9} q^{\prime}_{2} + \alpha_{10} q^{\prime}_{4} + \alpha_{11} q_{3} - \alpha_{12} q_{2} = \alpha_{13} F_{Y} $$
(9c)
$$ q^{\prime\prime}_{4} + \alpha_{8} q^{\prime}_{4} + \alpha_{9} q^{\prime}_{1} - \alpha_{10} q^{\prime}_{3} + \alpha_{11} q_{4} + \alpha_{12} q_{1} = - \alpha_{13} F_{X} $$
(9d)
$$ q^{\prime\prime}_{5} + \beta_{1} q^{\prime}_{5} + \beta_{2} q^{\prime}_{8} + \beta_{3} q_{5} + \beta_{4} q_{8} = \beta_{5} \cos \Omega_{2} \tau + \beta_{6} F_{X} $$
(9e)
$$ q^{\prime\prime}_{6} + \beta_{1} q^{\prime}_{6} - \beta_{2} q^{\prime}_{7} + \beta_{3} q_{6} - \beta_{4} q_{7} = \beta_{5} \sin \Omega_{2} \tau + \beta_{6} F_{Y} $$
(9f)
$$ q^{\prime\prime}_{7} + \beta_{8} q^{\prime}_{7} - \beta_{9} q^{\prime}_{6} - \beta_{10} q^{\prime}_{8} + \beta_{11} q_{7} - \beta_{12} q_{6} = - \beta_{13} F_{Y} $$
(9g)
$$ q^{\prime\prime}_{8} + \beta_{8} q^{\prime}_{8} + \beta_{9} q^{\prime}_{5} + \beta_{10} q^{\prime}_{7} + \beta_{11} q_{8} + \beta_{12} q_{5} = \beta_{13} F_{X} $$
(9h)

in which, \(\Omega_{1} = \frac{{\omega_{1} }}{{\omega_{1} }} = 1\), \(\Omega_{2} = \frac{{\omega_{2} }}{{\omega_{1} }} = \lambda\) where \(\lambda\) is the rotating speed ratio, \(\alpha_{1} = \frac{{\left( {c_{1} + c_{2} } \right)}}{{m_{1} \omega_{1} }}\), \(\alpha_{2} = \frac{{L_{1} c_{1} - L_{2} c_{2} }}{{Lm_{1} \omega_{1} }}\), \(\alpha_{3} = \frac{{\left( {k_{1} + k_{2} } \right)}}{{m_{1} \omega_{1}^{2} }}\), \(\alpha_{4} = \frac{{L_{1} k_{1} - L_{2} k_{2} }}{{Lm_{1} \omega_{1}^{2} }}\), \(\alpha_{5} = \frac{{e_{1} }}{{\delta_{0} }}\), \(\alpha_{6} = \frac{1}{{m_{1} \omega_{1}^{2} \delta_{0} }}\), \(\alpha_{8} = \frac{{L_{1}^{2} c_{1} + L_{2}^{2} c_{2} }}{{J_{{{\text{d}}1}} \omega_{1} }}\), \(\alpha_{9} = \frac{{L\left( {L_{1} c_{1} - L_{2} c_{2} } \right)}}{{J_{{{\text{d}}1}} \omega_{1} }}\), \(\alpha_{10} = \frac{{J_{{{\text{p}}1}} }}{{J_{{{\text{d}}1}} }}\), \(\alpha_{11} = \frac{{\left( {L_{1}^{2} k_{1} + \left( {L - L_{1} } \right)^{2} k_{2} } \right)}}{{J_{{{\text{d}}1}} \omega_{1}^{2} }}\), \(\alpha_{12} = \frac{{L\left( {L_{1} k_{1} - L_{2} k_{2} } \right)}}{{J_{{{\text{d}}1}} \omega_{1}^{2} }}\), \(\alpha_{13} = \frac{{L\left( {L_{2} - L_{5} } \right)}}{{J_{{{\text{d}}1}} \omega_{1}^{2} }}\), \(\beta_{1} = \frac{{c_{3} }}{{m_{2} \omega_{1} }}\), \(\beta_{2} = \frac{{L_{3} c_{3} }}{{Lm_{2} \omega_{1} }}\), \(\beta_{3} = \frac{{k_{3} }}{{m_{2} \omega_{1}^{2} }}\), \(\beta_{4} = \frac{{L_{3} k_{3} }}{{Lm_{2} \omega_{1}^{2} }}\), \(\beta_{5} = \frac{{e_{2} \omega_{2}^{2} }}{{\delta_{0} \omega_{1}^{2} }}\), \(\beta_{6} = \frac{1}{{m_{2} \omega_{1}^{2} \delta_{0} }}\), \(\beta_{7} = \frac{g}{{\omega_{1}^{2} \delta_{0} }}\), \(\beta_{8} = \frac{{L_{3}^{2} c_{3} }}{{J_{{{\text{d}}2}} \omega_{1} }}\), \(\beta_{9} = \frac{{LL_{3} c_{3} }}{{J_{{{\text{d}}2}} \omega_{1} }}\), \(\beta_{10} = \frac{{J_{{{\text{p}}2}} \omega_{2} }}{{J_{{{\text{d}}2}} \omega_{1} }}\), \(\beta_{11} = \frac{{L_{3}^{2} k_{3} }}{{J_{{{\text{d}}2}} \omega_{1}^{2} }}\), \(\beta_{12} = \frac{{LL_{3} k_{3} }}{{J_{{{\text{d}}2}} \omega_{1}^{2} }}\), \(\beta_{13} = \frac{{LL_{4} }}{{J_{{{\text{d2}}}} \omega_{1}^{2} }}\), \(F_{X}\) and \(F_{Y}\) representing the dimensionless bearing forces are as follows

$$ \left[ {\begin{array}{*{20}c} {F_{X} } \\ {F_{Y} } \\ \end{array} } \right] = H\left( {E - \Delta } \right)k_{{\text{b}}} \left( {1 - \frac{\Delta }{E}} \right)\left[ {\begin{array}{*{20}c} {X_{{\text{b}}} } \\ {Y_{{\text{b}}} } \\ \end{array} } \right] $$
(10)

where \(E = \sqrt {X_{{\text{b}}}^{2} + Y_{{\text{b}}}^{2} }\), \(X_{{\text{b}}} = \left( {q_{1} - \frac{{L_{2} - L_{5} }}{L}q_{4} } \right) - \left( {q_{5} - \frac{{L_{4} }}{L}q_{8} } \right)\), \(Y_{{\text{b}}} = \left( {q_{2} + \frac{{L_{2} - L_{5} }}{L}q_{3} } \right) - \left( {q_{6} + \frac{{L_{4} }}{L}q_{7} } \right)\), \(\Delta = \frac{\delta }{{\delta_{0} }}\).

The values of parameters of the system[38] are as follows

$$ \begin{aligned} &m_{1} = {\text{20 kg}}, \, J_{{{\text{p}}1}} = {0}{\text{.18 kg m}}^{{2}} , \, J_{{{\text{d}}1}} = {0}{\text{.09 kg m}}^{{2}} , \, m_{2} = {\text{13 kg}}, \, J_{{{\text{p2}}}} = 1{\text{ kg m}}^{{2}} , \, J_{{{\text{d2}}}} = {0}{\text{.5 kg m}}^{{2}} {, } \hfill \\ & k_{1} = 5 \times 10^{6} {\text{ N m}}^{ - 1} {, }k_{2} = 5 \times 10^{6} {\text{ N m}}^{ - 1} {, }k_{3} = 1 \times 10^{7} {\text{ N m}}^{ - 1} {, }c_{1} = 100{\text{ N s m}}^{ - 1} , \, c_{2} = {\text{100 N s m}}^{ - 1} {, } \hfill \\ & c_{3} = {\text{100 N s m}}^{ - 1} {, }e_{1} = {1} \times 10^{ - 6} {\text{ m, }}e_{2} = {3} \times 10^{ - 6} {\text{ m, }}L = {\text{1 m, }}k_{{\text{b}}} = 1 \times 10^{7} {\text{ N m}}^{ - 1} {, }\delta_{0} = {5 }\upmu {\text{m}}{.} \hfill \\ \end{aligned} $$
(11)

3 Methodology

The HB-AFT proposed in [32] is employed to obtain the periodic solutions for Eq. (9), in which the AFT (alternating frequency/time domain) procedure is employed to get the harmonic expending coefficients of the harmonic balance residuals in time domain, and then construct the relations between the coefficients of the nonlinear forces and that of the supposed solution. After that, an arc length continuation procedure [40] is introduced into the HB-AFT method, then all solution branches of the system are grasped, including the unstable solutions. In addition, the Floquet theory [41, 42] is employed to analyze the stabilities of the solutions. The details of the methodology formulation are as follow.

3.1 Harmonic balance method

With the consideration of the unbalance excitations of two different frequencies from the two rotors, the solution of Eq. (9) and the nonlinear forces of the inter-shaft bearing can be expressed as Fourier series, i.e.,

$$ q_{p} = a_{p00} + \sum\limits_{i = - m}^{m} {\sum\limits_{j = - n}^{n} {\left( {a_{pij} \cos \left( {i\Omega_{1} + j\Omega_{2} } \right)\tau - b_{pij} \sin \left( {i\Omega_{1} + j\Omega_{2} } \right)\tau } \right)} } $$
(12a)
$$ F_{l} = c_{l00} + \sum\limits_{i = - m}^{m} {\sum\limits_{j = - n}^{n} {\left( {c_{lij} \cos \left( {i\Omega_{1} + j\Omega_{2} } \right)\tau - d_{lij} \sin \left( {i\Omega_{1} + j\Omega_{2} } \right)\tau } \right)} } $$
(12b)

in which \(F_{1} = F_{X}\), \(F_{2} = F_{Y}\), \(i = - m, \, \cdots , \, m\), \(j = - n, \, \cdots , \, n\), excluding \(i\Omega_{1} + j\Omega_{2} \le 0\). The coefficients are unknowns to be determined. Herein, the harmonic terms of the two unbalanced excitation frequencies and their combinations are all considered.

Substituting (12) into Eq. (9), and using the harmonic balance procedure, one can get.

(i) constant terms

$$ g_{100} = \alpha_{3} a_{100} + \alpha_{4} a_{400} + \alpha_{6} c_{100} $$
(13a)
$$ g_{200} = \alpha_{3} a_{200} - \alpha_{4} a_{300} + \alpha_{6} c_{200} $$
(13b)
$$ g_{300} = \alpha_{11} a_{300} - \alpha_{12} a_{200} - \alpha_{13} c_{200} $$
(13c)
$$ g_{400} = \alpha_{11} a_{400} + \alpha_{12} a_{100} + \alpha_{13} c_{100} $$
(13d)
$$ g_{500} = \beta_{3} a_{500} + \beta_{4} a_{800} - \beta_{6} c_{100} $$
(13e)
$$ g_{600} = \beta_{3} a_{600} - \beta_{4} a_{700} - \beta_{6} c_{200} $$
(13f)
$$ g_{700} = \beta_{11} a_{700} - \beta_{12} a_{600} + \beta_{13} c_{200} $$
(13g)
$$ g_{800} = \beta_{11} a_{800} + \beta_{12} a_{500} - \beta_{13} c_{100} $$
(13h)

(ii) cosine terms

$$ g_{1ij} = \left( {\alpha_{3} - \left( {i\Omega_{1} + j\Omega_{2} } \right)^{2} } \right)a_{1ij} - \left( {i\Omega_{1} + j\Omega_{2} } \right)\left( {\alpha_{1} b_{1ij} + \alpha_{2} b_{4ij} } \right) + \alpha_{4} a_{4ij} + \alpha_{6} c_{1ij} - \gamma \alpha_{5} $$
(13i)
$$ g_{2ij} = \left( {\alpha_{3} - \left( {i\Omega_{1} + j\Omega_{2} } \right)^{2} } \right)a_{2ij} - \left( {i\Omega_{1} + j\Omega_{2} } \right)\left( {\alpha_{1} b_{2ij} - \alpha_{2} b_{3ij} } \right) - \alpha_{4} a_{3ij} + \alpha_{6} c_{2ij} $$
(13j)
$$ g_{3ij} = \left( {\alpha_{11} - \left( {i\Omega_{1} + j\Omega_{2} } \right)^{2} } \right)a_{3ij} - \left( {i\Omega_{1} + j\Omega_{2} } \right)\left( {\alpha_{8} b_{3ij} - \alpha_{9} b_{2ij} + \alpha_{10} b_{4ij} } \right) - \alpha_{12} a_{2ij} - \alpha_{13} c_{2ij} $$
(13k)
$$ g_{4ij} = \left( {\alpha_{11} - \left( {i\Omega_{1} + j\Omega_{2} } \right)^{2} } \right)a_{4ij} - \left( {i\Omega_{1} + j\Omega_{2} } \right)\left( {\alpha_{8} b_{4ij} + \alpha_{9} b_{1ij} - \alpha_{10} b_{3ij} } \right) + \alpha_{12} a_{1ij} + \alpha_{13} c_{1ij} $$
(13l)
$$ g_{5ij} = \left( {\beta_{3} - \left( {i\Omega_{1} + j\Omega_{2} } \right)^{2} } \right)a_{5ij} - \left( {i\Omega_{1} + j\Omega_{2} } \right)\left( {\beta_{1} b_{5ij} + \beta_{2} b_{8ij} } \right) + \beta_{4} a_{8ij} - \beta_{6} c_{1ij} - \gamma \beta_{5} $$
(13m)
$$ g_{6ij} = \left( {\beta_{3} - \left( {i\Omega_{1} + j\Omega_{2} } \right)^{2} } \right)a_{6ij} - \left( {i\Omega_{1} + j\Omega_{2} } \right)\left( {\beta_{1} b_{6ij} - \beta_{2} b_{7ij} } \right) - \beta_{4} a_{7ij} - \beta_{6} c_{2ij} $$
(13n)
$$ g_{7ij} = \left( {\beta_{11} - \left( {i\Omega_{1} + j\Omega_{2} } \right)^{2} } \right)a_{7ij} - \left( {i\Omega_{1} + j\Omega_{2} } \right)\left( {\beta_{8} b_{7ij} - \beta_{9} b_{6ij} - \beta_{10} b_{8ij} } \right) - \beta_{12} a_{6ij} + \beta_{13} c_{2ij} $$
(13o)
$$ g_{8ij} = \left( {\beta_{11} - \left( {i\Omega_{1} + j\Omega_{2} } \right)^{2} } \right)a_{8ij} - \left( {i\Omega_{1} + j\Omega_{2} } \right)\left( {\beta_{8} b_{8ij} + \beta_{9} b_{5ij} + \beta_{10} b_{7ij} } \right) + \beta_{12} a_{5ij} - \beta_{13} c_{1ij} $$
(13p)

(iii) sine terms

$$ g_{9ij} = \left( {\alpha_{3} - \left( {i\Omega_{1} + j\Omega_{2} } \right)^{2} } \right)b_{1ij} + \left( {i\Omega_{1} + j\Omega_{2} } \right)\left( {\alpha_{1} a_{1ij} + \alpha_{2} a_{4ij} } \right) + \alpha_{4} b_{4ij} + \alpha_{6} d_{1ij} $$
(13q)
$$ g_{10ij} = \left( {\alpha_{3} - \left( {i\Omega_{1} + j\Omega_{2} } \right)^{2} } \right)b_{2ij} + \left( {i\Omega_{1} + j\Omega_{2} } \right)\left( {\alpha_{1} a_{2ij} - \alpha_{2} a_{3ij} } \right) - \alpha_{4} b_{3ij} + \alpha_{6} d_{2ij} + \gamma \alpha_{5} $$
(13r)
$$ g_{11ij} = \left( {\alpha_{11} - \left( {i\Omega_{1} + j\Omega_{2} } \right)^{2} } \right)b_{3ij} + \left( {i\Omega_{1} + j\Omega_{2} } \right)\left( {\alpha_{8} a_{3ij} - \alpha_{9} a_{2ij} + \alpha_{10} a_{4ij} } \right) - \alpha_{12} b_{2ij} + \alpha_{13} d_{2ij} $$
(13s)
$$ g_{12ij} = \left( {\alpha_{11} - \left( {i\Omega_{1} + j\Omega_{2} } \right)^{2} } \right)b_{4ij} + \left( {i\Omega_{1} + j\Omega_{2} } \right)\left( {\alpha_{8} a_{4ij} + \alpha_{9} a_{1ij} - \alpha_{10} a_{3ij} } \right) + \alpha_{12} b_{1ij} - \alpha_{13} d_{1ij} $$
(13t)
$$ g_{13ij} = \left( {\beta_{3} - \left( {i\Omega_{1} + j\Omega_{2} } \right)^{2} } \right)b_{5ij} + \left( {i\Omega_{1} + j\Omega_{2} } \right)\left( {\beta_{1} a_{5ij} + \beta_{2} a_{8ij} } \right) + \beta_{4} b_{8ij} - \beta_{6} d_{1ij} $$
(13u)
$$ g_{14ij} = \left( {\beta_{3} - \left( {i\Omega_{1} + j\Omega_{2} } \right)^{2} } \right)b_{6ij} + \left( {i\Omega_{1} + j\Omega_{2} } \right)\left( {\beta_{1} a_{6ij} - \beta_{2} a_{7ij} } \right) - \beta_{4} b_{7ij} - \beta_{6} d_{2ij} + \gamma \beta_{5} $$
(13v)
$$ g_{15ij} = \left( {\beta_{11} - \left( {i\Omega_{1} + j\Omega_{2} } \right)^{2} } \right)b_{7ij} + \left( {i\Omega_{1} + j\Omega_{2} } \right)\left( {\beta_{8} a_{7ij} - \beta_{9} a_{6ij} - \beta_{10} a_{8ij} } \right) - \beta_{12} b_{6ij} + \beta_{13} d_{2ij} $$
(13w)
$$ g_{16ij} = \left( {\beta_{11} - \left( {i\Omega_{1} + j\Omega_{2} } \right)^{2} } \right)b_{8ij} + \left( {i\Omega_{1} + j\Omega_{2} } \right)\left( {\beta_{8} a_{8ij} + \beta_{9} a_{5ij} + \beta_{10} a_{7ij} } \right) + \beta_{12} b_{5ij} - \beta_{13} d_{1ij} $$
(13x)

Letting the right side of Eq. (13) be equal to zero, then one can rewrite Eq. (13) as the following matrix equation, i.e.,

$$ {\mathbf{g}} = {\varvec{A}}{\mathbf{X}} + {\mathbf{B}} = {\mathbf{0}} $$
(14)

where g is the residual vector and \({\mathbf{X}} = \left[ {a_{100} , \, a_{200} , \, a_{300} , \, a_{400} , \, a_{500} , \, a_{600} , \, a_{700} , \, a_{800} , \, a_{1ij} , \, a_{2ij} , \, a_{3ij} , \, a_{4ij} , \, a_{5ij} , \, a_{6ij} , \, a_{7ij} , \, a_{8ij} , \, b_{1ij} , \, b_{2ij} , \, b_{3ij} , \, b_{4ij} , \, b_{5ij} , \, b_{6ij} , \, b_{7ij} , \, b_{8ij} } \right]^{{\text{T}}}\) is the matrix of unknowns for the solution, \({\varvec{A}}\) is the coefficient matrix, and the rest terms including the unknowns for the nonlinear inter-shaft bearing forces are contained in the vector B.

Then the Newton–Raphson iterative procedure is employed to get the fixed point \({\mathbf{X}}\) for Eq. (14), i.e.,

$$ {\mathbf{X}}^{(k + 1)} = {\mathbf{X}}^{(k)} - {\varvec{J}}^{ - 1} {\mathbf{g}}^{(k)} $$
(15)

where \({\varvec{J}}\) is the Jacobian matrix, i.e.,

$$ {\varvec{J}} = \frac{{\partial {\mathbf{g}}}}{{\partial {\mathbf{X}}}} = {\varvec{A}} + \frac{{\partial {\mathbf{B}}}}{{\partial {\mathbf{X}}}} $$
(16)

in which, A is a constant matrix corresponding to the linear part, but the vector B is corresponding to the nonlinear forces of the inter-shaft bearing, the coefficients for which are unknown. In order to get \(\partial {\mathbf{B}}/\partial {\mathbf{A}}\), one can employ the alter frequency/time domain technique (AFT) to construct the relations between the coefficients of the nonlinear forces and that of the supposed solution.

3.2 The AFT procedure

For a given \({\mathbf{X}}\), equally divide the time period into N points, i.e.,

$$ \tau_{r} = \frac{{{2}K{\uppi }r}}{N} $$
(17)

in which, K = 5, and N is the number of sampling points of a common time period.

Then the responses \(q_{p}\) at the \(r{\text{th}}\) discrete time can be obtained as follows

$$ q_{p} \left( r \right) = a_{p00} + \sum\limits_{i = - m}^{m} {\sum\limits_{j = - n}^{n} {\left( {a_{pij} \cos \frac{{{2}K{\uppi }r\left( {i\Omega_{1} + j\Omega_{2} } \right)}}{\rm N} - b_{pij} \sin \frac{{{2}K{\uppi }r\left( {i\Omega_{1} + j\Omega_{2} } \right)}}{\rm N}} \right)} } $$
(18)

where \(r = 0, \, 1, \, \cdots , \, N - 1\).

Substituting Eq. (17) and Eq. (18) into Eq. (10), the nonlinear forces \(F_{Y}\) and \(F_{Z}\) at the \(r{\text{th}}\) discrete time can be obtained as follows

$$ \left[ {\begin{array}{*{20}c} {F_{X} \left( r \right)} \\ {F_{Y} \left( r \right)} \\ \end{array} } \right] = H\left( {E\left( r \right) - \Delta } \right)k_{{\text{b}}} \left( {1 - \frac{\Delta }{E\left( r \right)}} \right)\left[ {\begin{array}{*{20}c} {X_{{\text{b}}} \left( r \right)} \\ {Y_{{\text{b}}} \left( r \right)} \\ \end{array} } \right] $$
(19)

where \(X_{{\text{b}}} \left( r \right) = \left( {q_{1} \left( r \right) - \frac{{L_{2} - L_{5} }}{L}q_{4} \left( r \right)} \right) - \left( {q_{5} \left( r \right) - \frac{{L_{4} }}{L}q_{8} \left( r \right)} \right)\), \(Y_{{\text{b}}} \left( r \right) = \left( {q_{2} \left( r \right) + \frac{{L_{2} - L_{5} }}{L}q_{3} \left( r \right)} \right) - \left( {q_{6} \left( r \right) + \frac{{L_{4} }}{L}q_{7} \left( r \right)} \right)\), \(E\left( r \right) = \sqrt {X_{{\text{b}}} \left( r \right)^{2} + Y_{{\text{b}}} \left( r \right)^{2} }\).

Using the DFT for Eq. (19), and considering Eq. (12b), the corresponding coefficients of \(F_{l}\) (\(F_{1} = F_{X}\), \(F_{2} = F_{Y}\)) in the frequency domain can be obtained as follows

$$ c_{l00} = \frac{1}{N}\sum\limits_{r = 0}^{N - 1} {F_{l} \left( r \right)} \quad l = 1,2,3,4 $$
(20a)
$$ c_{lij} = \frac{2}{N}\sum\limits_{r = 0}^{N - 1} {F_{l} \left( r \right)\cos \frac{{{2}K{\uppi }\left( {i\Omega_{1} + j\Omega_{2} } \right)r}}{\rm N}}\quad l = 1,2,3,4 $$
(20b)
$$ d_{lij} = - \frac{2}{N}\sum\limits_{r = 0}^{N - 1} {F_{l} \left( r \right)\sin \frac{{{2}K{\uppi }\left( {i\Omega_{1} + j\Omega_{2} } \right)r}}{\rm N}}\quad l = 1,2,3,4 $$
(20c)

Letting \({\mathbf{Q}} = \left[ {c_{10} , \, c_{20} , \, c_{1ij} , \, c_{2ij} , \, d_{1ij} , \, d_{2ij} } \right]^{{\text{T}}}\), and according to Eq. (18) to (20), we can calculate \(\frac{{\partial {\mathbf{B}}}}{{\partial {\mathbf{X}}}}\) by using the following formula

$$ \frac{{\partial {\mathbf{B}}}}{{\partial {\mathbf{X}}}} = \frac{{\partial {\mathbf{B}}}}{{\partial {\mathbf{Q}}}}\frac{{\partial {\mathbf{Q}}}}{{\partial {\mathbf{X}}}} $$
(21)

Finally, the Jacobian matrix \({\varvec{J}}\) can be obtained by substituting Eq. (21) into Eq. (16). Then substituting it into Eq. (15), one can update X by using the Newton–Raphson iterative procedure, i.e., \({\mathbf{X}}^{(k + 1)} = {\mathbf{X}}^{(k)} - {\varvec{J}}^{ - 1} {\mathbf{g}}^{(k)}\). When \(||{\mathbf{X}}^{(k)} - {\mathbf{X}}^{(k - 1)} ||\) is less than the allowed error, the result converges. Furthermore, the pseudo-arclength continuation method is employed to get all branches of solutions, and the Floquet theory is used to analyze the stability of the solutions obtained through the HB-AFT method. Finally, the flowchart of the HB-AFT method is shown in Fig. 2.

Fig. 2
figure 2

Flowchart of the HB-AFT method

Full size image

4 Results and discussions

4.1 Nonlinear response of the dual-rotor system

IN the following sections, the nonlinear responses of the dual-rotor system are detected by using the HB-AFT method. In the calculations, ten frequencies are supposed, that are \(\omega_{1}\), \(\omega_{2}\), \(2\omega_{2} - \omega_{1}\), \(2\omega_{1} - \omega_{2}\), \(3\omega_{2} - 2\omega_{1}\), \(3\omega_{1} - 2\omega_{2}\), \(4\omega_{2} - 3\omega_{1}\), \(4\omega_{1} - 3\omega_{2}\), \(\omega_{2} - \omega_{1}\), \(2\omega_{1}\), the error for every iteration process is less than 10–12.

Figure 3 shows the frequency response curves of the system for \(\lambda = 1.2\) and \(\delta = \delta_{0} = {5}\) μm. The response amplitudes of the inner rotor and the outer rotor are defined by

$$ R_{1} = \sqrt {q_{1}^{2} + q_{2}^{2} } $$
(28a)
$$ R_{2} = \sqrt {q_{5}^{2} + q_{6}^{2} } $$
(28b)

where \(R_{1}\) is the response amplitudes of the inner rotor, \(R_{2}\) is the response amplitudes of the outer rotor,\(q_{1}\), \(q_{2}\), \(q_{5}\), \(q_{6}\) are defined in Eq. (12a).

Fig. 3
figure 3

Frequency response curves of the dual-rotor system. a for inner rotor, b for outer rotor

Full size image

In Fig. 3a and b, the resonance peak at \(\omega_{1} \approx 681{\text{ rad/s}}\) is induced by the primary resonance due to the unbalance excitation of the outer rotor, in this case \(\omega_{2} \approx 817{\text{ rad/s}}\). while the resonance peak at \(\omega_{1} \approx 815{\text{ rad/s}}\) is induced by the primary resonance due to the unbalance excitation of the inner rotor, and in this case \(\omega_{1} \approx 980{\text{ rad/s}}\). The relative location of the two resonance peaks is determined by the speed ratio, since \(\lambda = 1.2\), so the rotation speed corresponding to the first resonance peak is about 681 rad/s, and the other is about 815 rad/s. Besides these two resonance peaks, there are three more resonance regions nearby, which are excited by the combination frequencies that are close to the critical speed of the rotor system, and marked by B, C and D. In these resonance regions, the vibration amplitudes of the system are not so large compared with the primary resonances, but jump phenomena are observed, which are harmful to the safe and steady operation of the dual-rotor system. In addition, region A is also a bi-stable region with vibration jumps. The maximum jump magnitude of region A and region D is larger for the inner rotor, while that of region B and region C is larger for the outer rotor. Nevertheless, all of these nonlinear resonances are induced by the clearance of the inter-shaft bearing.

In addition, in order to give an insight into the system motions, the x response time history and rotors’ orbits of the inner rotor corresponding to the points (\(\omega_{1} {\text{ = 650 rad/s}}\),\(\omega_{1} {\text{ = 680 rad/s}}\), \(\omega_{1} {\text{ = 810 rad/s}}\),\(\omega_{1} {\text{ = 860 rad/s}}\)) of Fig. 3 are shown in Figs. 4 and 5, where \(\omega_{1} {\text{ = 680 rad/s}}\) and \(\omega_{1} {\text{ = 810 rad/s}}\) are corresponding to the resonance area of the system in Fig. 3, and \(\omega_{1} {\text{ = 650 rad/s}}\) and \(\omega_{1} {\text{ = 860 rad/s}}\) are corresponding to the non-resonance area of the system in Fig. 3. The solid line denotes the results calculated by the HB-AFT method, and the dotted line represents the results of the Runge–Kutta method in all subfigures of Figs. 4 and 5. It is shown that the motions of the system are periodic motion, and the calculation results including time history and rotors’ orbits obtained by the Runge–Kutta method and the HB-AFT method are basically consistent, which indicates that the accuracies of the two methods are almost the same. As for the calculation efficiency, the average time consuming to get the steady-state response of the system is about 3.2 s by using the Runge–Kutta method, but the corresponding time consuming is just about 0.11 s by using the HB-AFT method, i.e., the calculation efficiency of the HB-AFT method is about 29 times that of the Runge–Kutta method. Furthermore, the Runge–Kutta method can’t find the unstable periodic solutions of the system as shown in Fig. 3 (red lines), as a result it can’t reflect the whole picture of the solution. In addition, using the HB-AFT method could obtain a further understanding of the combination resonances of the system by the separated frequency responses, the details will be discussed next.

Fig. 4
figure 4

x response time history of the inner rotor. a \(\omega_{1} {\text{ = 650 rad/s}}\), b \(\omega_{1} {\text{ = 680 rad/s}}\), c \(\omega_{1} {\text{ = 810 rad/s}}\), d \(\omega_{1} {\text{ = 860 rad/s}}\)

Full size image
Fig. 5
figure 5

rotors’ orbits of the inner rotor. a \(\omega_{1} {\text{ = 650 rad/s}}\), b \(\omega_{1} {\text{ = 680 rad/s}}\), c \(\omega_{1} {\text{ = 810 rad/s}}\), d \(\omega_{1} {\text{ = 860 rad/s}}\)

Full size image

Furthermore, since the exact expression of Eq. (12a) can be obtained through the HB-AFT method, the responses of the system can be decomposed separately into different harmonic components. The definitions of amplitudes for the separated harmonic components are presented as follows

$$ R_{1ij} = \sqrt {a_{1ij}^{2} + b_{1ij}^{2} + a_{2ij}^{2} + b_{2ij}^{2} } $$
(29a)
$$ R_{2ij} = \sqrt {a_{5ij}^{2} + b_{5ij}^{2} + a_{6ij}^{2} + b_{6ij}^{2} } $$
(29b)

where \(R_{1ij}\) is the separated harmonic components response amplitudes of the inner rotor, \(R_{2ij}\) is the separated harmonic components response amplitudes of the outer rotor.

The separated frequency responses of the system for parameters having the same value as Fig. 3 are shown in Fig. 6, which are meaningful to know exactly how much each frequency component contributes to the vibration responses of the system. It can be observed that apart from the basic components of \(\omega_{1}\) and \(\omega_{2}\), the components of \(2\omega_{2} - \omega_{1}\) and \(2\omega_{1} - \omega_{2}\) are notable in the response of the inner rotor in Fig. 6a, while the components of \(2\omega_{2} - \omega_{1}\), \(3\omega_{2} - 2\omega_{1}\) and \(4\omega_{2} - 3\omega_{1}\) take a prominent role in the response of the outer rotor in Fig. 6b. The latter three frequency components play a decisive role in the appearance of the resonance regions B, C and D in Fig. 3. The resonances are the corresponding combination resonances. Specifically, region B is induced by the combination resonance of \(2\omega_{2} - \omega_{1}\), while region C and region D are corresponding to the combination resonances of \(3\omega_{2} - 2\omega_{1}\) and \(4\omega_{2} - 3\omega_{1}\), respectively. The reason of the combination resonance is that the clearance and the fractional Hertz contact restoring force of the inter-shaft bearing are essentially nonlinear, especially the clearance would change the contact state of the rollers, thus causing the stiffness change of inter-shaft bearing.

Fig. 6
figure 6

Separated frequency responses of the dual-rotor system for the same parameters as Fig. 3. a for inner rotor, b for outer rotor. Harbin Institute of Technology

Full size image

4.2 Effect of inter-shaft bearing clearance

The inter-shaft bearing clearance is one of the main inducements of the combination resonance of the dual-rotor system, so it is very important to analyze the influence of the clearance for revealing the mechanism of the combination resonance. This section presents the effect of the inter-shaft bearing clearance on the nonlinear responses of the dual-rotor system. Firstly, the frequency response curves of the dual-rotor system for \(\delta = 0\), \(\delta = 1\) μm, \(\delta = 3\) μm and \(\delta = 5\) μm are shown in Fig. 7, in which the amplitudes of the system are calculated by Eq. (28), and the stability of the periodic solutions are analyzed by the Floquet theory. In addition, for all the subfigures of Fig. 7, the solid lines and the dotted lines represent the stable and unstable solutions branches, respectively.

Fig. 7
figure 7

Frequency response curves of the dual-rotor system for different values of inter-shaft bearing clearance. a for inner rotor, b for outer rotor

Full size image

As shown in Fig. 7, for \(\delta = 0\), there are only two primary resonance peaks on the frequency response curve, since in this case the dual-rotor system is a linear system. When the inter-shaft bearing clearance increases from \(\delta = 0\) to \(\delta = 5\) μm, both the resonance amplitude and the resonant frequency of the primary resonance peaks change very little. It is observed from Fig. 7 that as the inter-shaft bearing clearance increases, the amplitude of the first resonance peak decreases gradually but the amplitude of the other resonance peak changes slightly. Furthermore, as the inter-shaft bearing clearance increases from \(\delta = 0\) to \(\delta = 5\) μm, both the locations of the two resonance peaks move to the left gradually, which indicates that increasing the clearance will weaken the stiffness of the system. This is because changing the clearance will induce the change of the contact state of the inter-shaft bearing rollers, including number of rollers in contact.

In addition, it is shown in Fig. 7 that increasing the clearance of the inter-shaft bearing will change the nonlinear dynamic characteristics of the dual-rotor system significantly, including the number of periodic solutions both for the primary resonance regions and the combination resonance regions, and the existence of the combination resonance regions. For the primary resonance regions, it can be observed from Fig. 7 that when the clearance is 0 to 4 μm, there is only one solution branches, however, when \(\delta = 5\) μm, there are three solution branches and thus make the bi-stable phenomena emerge. Furthermore, for the combination resonance regions, when the clearance is 0 to 3 μm, the combination resonance phenomena are not obvious, but when the clearance increases to 4 and 5 μm, obvious combination resonance phenomena could be observed in the system. In addition, as the clearance increasing from 4 μm to 5 μm, it can be clearly observed that the combination resonance peaks move a lot to the left, indicating a significant decrease of the corresponding resonant frequencies.

In order to give an insight into the evolution of the frequency components in the frequency response of the outer rotor shown in Fig. 7b, the separated frequency responses for frequency components of \(\omega_{1}\), \(\omega_{2}\), \(2\omega_{2} - \omega_{1}\), \(2\omega_{1} - \omega_{2}\), \(3\omega_{2} - 2\omega_{1}\) and \(4\omega_{2} - 3\omega_{1}\) are shown in Fig. 8, in which The effective values of response amplitude for each frequency component are also calculated by Eq. (29); the solid lines and the dotted lines represent the stable and unstable solutions branches corresponding to each frequency, respectively.

Fig. 8
figure 8figure 8

Separated frequency responses of the outer rotor for the same parameters as Fig. 7. a for frequency component of \(\omega_{1}\), b for frequency component of \(\omega_{2}\), c for frequency component of \(2\omega_{2} - \omega_{1}\), d for frequency component of \(2\omega_{1} - \omega_{2}\), (e) for frequency component of \(3\omega_{2} - 2\omega_{1}\), (f) for frequency component of \(4\omega_{2} - 3\omega_{1}\)

Full size image

Subfigures (a) and (b) of Fig. 8 show the effect of clearance on the separated frequency response of \(\omega_{1}\) and \(\omega_{2}\), which are corresponding to the primary resonance. In Fig. 8a, the main resonance peak is subject to the unbalance excitation of the inner rotor, which is excited when the inner rotor passes through the first critical rotational speed. With the increase of the inter-shaft bearing clearance, the resonant frequency has a little decrease, and the resonance amplitude also decreases slightly, since the rigidity of the system is reduced. Similarly, in Fig. 8b, the resonance peak subject to the unbalance excitation of the outer rotor also has a decrease in both the resonant frequency and the resonance amplitude, which is excited when the outer rotor passes through the first critical rotational speed. Furthermore, when \(\delta = 5\) μm, a bi-stable region emerges.

Subfigures (c) to (f) of Fig. 8 show the effect of clearance on the separated frequency response of \(2\omega_{2} - \omega_{1}\), \(2\omega_{1} - \omega_{2}\), \(3\omega_{2} - 2\omega_{1}\) and \(4\omega_{2} - 3\omega_{1}\), which are corresponding to the combination resonance. As shown in subfigures 8(c) to 8(f), when \(\delta = 0\), there is no vibration response, with the increase of the inter-shaft bearing clearance, the vibration responses emerge and increase in general, and there emerge several resonance peaks. In Fig. 8c, the most prominent resonance peak is in the frequency region between \(\omega_{1} = 820{\text{ rad/s}}\) and \(\omega_{1} = 900{\text{ rad/s}}\). With the increase of the inter-shaft bearing clearance, the resonant frequency decreases, but the resonance amplitude increases dramatically, and a crossover structure emerges on the frequency response curve in the cases of \(\delta = 3\) μm and \(\delta = 5\) μm, leading to the presence of the coexistence of soft characteristic and hardening characteristic. In Fig. 8d, there are several resonance peaks, but the vibration amplitudes are really small in comparison with that in Fig. 8c, e and f. In Fig. 8e, the most prominent resonance peak is in the frequency region between \(\omega_{1} = 680{\text{ rad/s}}\) and \(\omega_{1} = 820{\text{ rad/s}}\). Similarly to Fig. 8c, with the increase of the inter-shaft bearing clearance, the resonant frequency has a decrease, while the resonance amplitude has an increase, and a crossover structure is presented on the frequency response curves for \(\delta = 1\) μm, \(\delta = 3\) μm and \(\delta = 5\) μm.

As shown in Fig. 3, there are three combination resonance regions in the frequency response curves of the dual-rotor system, marked as B, C and D, respectively. It can be seen from the previous analysis that the inter-shaft bearing clearance would affect the combination resonance characteristics of the system, and the influence on that of the high-pressure rotor is more significant. Next, we will explore the influence of the clearance on the combination resonance characteristics of region B, C and D. The separated frequency responses of the outer rotor of each combination resonance region are shown in Figs. 9, 10, 11, respectively, in which the effective values of response amplitude for each frequency component are also calculated by Eq. (29), the solid lines and the dotted lines represent the stable and unstable solutions branches corresponding to each frequency, respectively.

Fig. 9
figure 9

Separated frequency responses of the outer rotor of region D for the same parameters as Fig. 7. a for frequency component of \(2\omega_{2} - \omega_{1}\), b for frequency component of \(2\omega_{1} - \omega_{2}\), c for frequency component of \(3\omega_{2} - 2\omega_{1}\), d for frequency component of \(4\omega_{2} - 3\omega_{1}\)

Full size image
Fig. 10
figure 10

Separated frequency responses of the outer rotor of region C for the same parameters as Fig. 7. a for frequency component of \(2\omega_{2} - \omega_{1}\), b for frequency component of \(2\omega_{1} - \omega_{2}\), c for frequency component of \(3\omega_{2} - 2\omega_{1}\), d for frequency component of \(4\omega_{2} - 3\omega_{1}\)

Full size image
Fig. 11
figure 11

Separated frequency responses of the outer rotor of region B for the same parameters as Fig. 7. a for frequency component of \(2\omega_{2} - \omega_{1}\), b for frequency component of \(2\omega_{1} - \omega_{2}\), c for frequency component of \(3\omega_{2} - 2\omega_{1}\), d for frequency component of \(4\omega_{2} - 3\omega_{1}\)

Full size image

Figure 9 shows the separated frequency responses of the outer rotor of region D for the same parameters as Fig. 7 with different clearance of the inter-shaft bearing.

Subfigure (a) is corresponding to the separated frequency response of frequency component \(2\omega_{2} - \omega_{1}\), it is shown that increasing the inter-shaft bearing clearance will increase the response, and make the resonance frequency reduction. Subfigure (b) is corresponding to the separated frequency response of frequency component \(2\omega_{1} - \omega_{2}\), which shows that the frequency responses of region D contain little response of this frequency component, and the change of the clearance has little influence on this situation. Subfigure (c) is corresponding to the separated frequency response of frequency component \(3\omega_{2} - 2\omega_{1}\), it is indicated that this frequency component has some contribution to the combination resonance response of region D, and the change of the inter-shaft bearing clearance has little influence on the response amplitude, but make the resonance frequency reduction significantly. Subfigure (d) is corresponding to the separated frequency response of frequency component \(4\omega_{2} - 3\omega_{1}\), it is shown that the frequency component has some contribution to the combination resonance response of region D, and the change of the clearance will affect the separated frequency response significantly, i.e., when the clearance amplitude is 1 μm, a resonance peak emerges in the separated frequency response of the frequency component; when the clearance amplitude increases to \({2}\) μm, both the amplitude and the frequency of the peak keep increasing; besides, the increasing the clearance will make the amplitude and the frequency of the peak induction.

To sum up, it can be seen from Fig. 9 that the combination resonance response of region D is mainly dominated by the combined frequency component of \(2\omega_{2} - \omega_{1}\) and \(4\omega_{2} - 3\omega_{1}\), and almost independent of other frequency components. Furthermore, the inter-shaft bearing clearance will not only affect the response amplitudes of the combination resonance in this region, but also show a certain "stiffness weakening effect" on the rotor system in this region.

Figure 10 shows the separated frequency responses of the outer rotor of region C for the same parameters as Fig. 5 with different clearance of the inter-shaft bearing.

Subfigure (a) is corresponding to the separated frequency response of frequency component \(2\omega_{2} - \omega_{1}\); it is shown that the frequency component has some contribution to the combination resonance response of this region. Moreover, increasing the inter-shaft bearing clearance will hardly change the response amplitude, but make the resonance frequency reduction. Subfigure (b) is corresponding to the separated frequency response of frequency component \(2\omega_{1} - \omega_{2}\), which shows that the frequency responses of region C contain little response of this frequency component, and the change of the clearance will hardly influence this situation. Subfigure (c) is corresponding to the separated frequency response of frequency component \(3\omega_{2} - 2\omega_{1}\), it is indicated that this frequency component has some contribution to the combination resonance response of region C, and the increasing of the inter-shaft bearing clearance will make the response amplitude increasing, meanwhile make the resonance frequency reduction significantly. Furthermore, a kind of circle structure emerges in the separated frequency response of the frequency component when the clearance is more than zeros, which makes the separated frequency response curves behaving both “stiffness hardening characteristic” and “stiffness softening characteristic”. Subfigure (d) is corresponding to the separated frequency response of frequency component \(4\omega_{2} - 3\omega_{1}\); it is shown that there is a resonance peak in the response curve, which indicates that the frequency component has some contribution to the combination resonance response of region C. It is worth noting that the amplitudes of the resonance peaks are much less than that of Subfigure (c). Furthermore, the response curves behave like a hardening characteristic when the clearance is 1 μm, 2 μm and 3 μm, however, there emerges a circle structure, which makes the response curve behaves both “stiffness hardening characteristic” and “stiffness softening characteristic” when the clearance increases to \({4}\) μm. When the clearance amplitude is \({5}\) μm, the circular structure is more obvious.

In a word, it can be seen from Fig. 10 that the combination resonance response of region C is mainly dominated by the combined frequency component of \(3\omega_{2} - 2\omega_{1}\). Furthermore, the inter-shaft bearing clearance will not only affect the response amplitudes of the combination resonance in this region, but also show a certain "stiffness weakening effect" on the rotor system in this region.

Figure 11 shows the separated frequency responses of the outer rotor of region B for the same parameters as Fig. 7 with different clearance of the inter-shaft bearing.

Subfigure (a) is corresponding to the separated frequency response of frequency component \(2\omega_{2} - \omega_{1}\), it is shown that the frequency component has some contribution to the combination resonance response of this region. Besides, increasing the inter-shaft bearing clearance will make the response amplitudes increasing, meanwhile make the resonance frequency reduction. When the clearance is 1 μm, the separated frequency response curve behave like a linear characteristic, but when the clearance increases to 2 μm, there is a circular structure in the curve, which makes the curve behave as both “softening characteristic” and “hardening characteristic”. Subfigures (b) and (d) are corresponded to the separated frequency response of frequency components \(2\omega_{1} - \omega_{2}\) and \(4\omega_{2} - 3\omega_{1}\), respectively, which shows that the frequency responses of region B contain little response of these frequency components, and the change of the clearance will hardly influence this situation. Subfigure (c) is corresponding to the separated frequency response of frequency component \(3\omega_{2} - 2\omega_{1}\), it is indicated that this frequency component has some contribution to the combination resonance response of region B, and the increasing of the inter-shaft bearing clearance will hardly influence the response amplitude, but make the resonance frequency reduction significantly.

In conclusion, it is shown in Fig. 11 that the combination resonance response of region B is mainly dominated by the combined frequency component of \(2\omega_{2} - \omega_{1}\). Furthermore, the inter-shaft bearing clearance will not only affect the response amplitudes of the combination resonance in this region, but also show a certain "stiffness weakening effect" on the rotor system in this region.

In summary, there are two primary resonance peaks, and three more combination resonance regions in the frequency response curves of the system are found, in which the jump and bi-stable phenomena are observed. Furthermore, clearance of the inter-shaft bearing is one of the main inducements of the nonlinear phenomena of rotor system, including bi-stable, multiple solutions and combination resonance.

5 Conclusions

In this paper, the dynamic model of a dual-rotor-bearing system has been formulated by the Lagrange equation, in which the unbalanced excitations of the two rotors and the nonlinearities of the inter-shaft bearing are taken into consideration. The modified HB-AFT method has been employed to obtain all the periodic solutions including the unstable solutions of the system. The combination resonance characteristics of the system have been analyzed in detail. The main conclusions are as follows:

  1. (1)

    There are two primary resonance peaks induced by the unbalance excitation of the two rotors in the frequency response curves of the system, bi-stable and vibration jump phenomena are observed in the first primary resonance region.

  2. (2)

    Besides the two resonance peaks, there are three more combination resonance regions in the frequency response curves of the system, in which the jump phenomena are observed, which are harmful to the safe and steady operation of the dual-rotor system.

  3. (3)

    The combination resonance of the system is mainly dominated by the combined frequency component of \(2\omega_{2} - \omega_{1}\),\(4\omega_{2} - 3\omega_{1}\), \(3\omega_{2} - 2\omega_{1}\) and is almost independent of other frequency components.

  4. (4)

    Increasing the inter-shaft bearing clearance will not only affect the response amplitudes of the combination resonance and change the “softening and hardening characteristic” of the frequency response curves, but also show a certain "stiffness weakening effect" on the rotor system.

The study in this paper is of great significance in selecting the parameters of the dual-rotor system reasonably so as to avoid harmful combination resonance.

6 Future scope

The HB-AFT method has great advantages in the nonlinear dynamic characteristics analysis of rotor system with complex nonlinearities such as clearance, piecewise linearity, nonlinear faults, etc. Future works will be focused on detecting the nonlinear dynamics of dual-rotor system based on high dimensional model with complex nonlinearities by employing the modified HB-AFT method, and extending the application of the HB-AFT method in the dynamic analysis of other complex rotating machinery such as aero-engines and gas turbines.